Закон Ома для магнитной цепи
Как в электрической цепи сила тока зависит от приложенного напряжения и от сопротивления, оказываемого элементами цепи, так и в магнитной цепи магнитный поток Ф зависит от приложенной магнитодвижущей силы (м.д.с.) численно равной Iw и от сопротивления R магнитному потоку: (1) Эта формула выражает закон Ома для магнитной цепи. Магнитное сопротивление RМ определяют в зависимости от длины силовых линий l (м), площади поперечного сечения силового потока S (м2) и абсолютной магнитной проницаемости а (Вб/Ам): (2) Не трудно уловить аналогию формулы №2 формуле: — для определения сопротивления проводника электрическому току. Подставим в выражение №1 вместо RМ его значение из формулы №2, получим: (3) При расчете магнитной цепи задача чаще всего сводится к определению необходимой э.д.с. для того, чтобы получить в магнитопроводе определенный магнитный поток или заданную магнитную индукция, например воздушном зазоре. Ниже излагается путь расчета применительно к магнитопроводу, показанному на рисунке №1. Магнитный поток замыкается через сердечник и воздушный зазор . Отдельные участки сердечника могут быть выполнены из различных материалов и неодинакового сечения. Через сечение каждого из участков каждого из участков сердечника проходит один и тот же магнитный потокЗакон Ома для магнитных цепей.
Как в электрической цепи сила тока зависит от приложенного напряжения и от сопротивления, оказываемого элементами цепи, так и в магнитной цепи магнитный поток Ф зависит от приложенной магнитодвижущей силы (м.д.с.) численно равной Iw и от сопротивления R магнитному потоку:
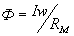
Эта формула выражает закон Ома для магнитной цепи.
Магнитное сопротивление RМ определяют в зависимости от длины силовых линий l (м), площади поперечного сечения силового потока S (м2) и абсолютной магнитной проницаемости 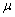 а (Вб/А
а (Вб/А  м):
м):
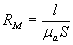 (2)
(2)
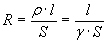 — для определения сопротивления проводника электрическому току.
— для определения сопротивления проводника электрическому току.
Подставим в выражение №1 вместо RМ его значение из формулы №2, получим:
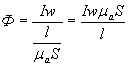 (3)
(3)
При расчете магнитной цепи задача чаще всего сводится к определению необходимой э.д.с. для того, чтобы получить в магнитопроводе определенный магнитный поток или заданную магнитную индукция, например воздушном зазоре. Ниже излагается путь расчета применительно к магнитопроводу, показанному на рисунке №1.
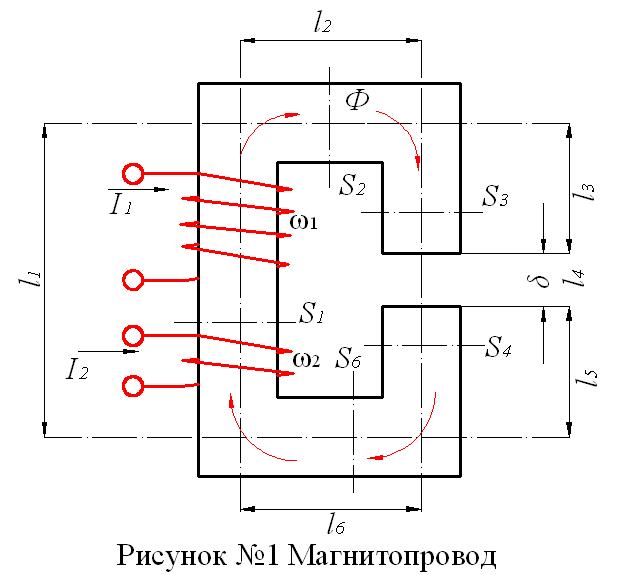
Магнитный поток замыкается через сердечник и воздушный зазор 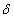 . Отдельные участки сердечника могут быть выполнены из различных материалов и неодинакового сечения. Через сечение каждого из участков каждого из участков сердечника проходит один и тот же магнитный поток Ф:
. Отдельные участки сердечника могут быть выполнены из различных материалов и неодинакового сечения. Через сечение каждого из участков каждого из участков сердечника проходит один и тот же магнитный поток Ф:
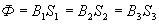 и т.д.
и т.д.
По закону Ома для магнитной цепи
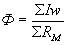
где 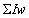 -алгебраическая сумма ампер-витков, численно равная общей м.д.с. обмотки;
-алгебраическая сумма ампер-витков, численно равная общей м.д.с. обмотки; 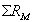 — сумма магнитных сопротивлений участков, на которых индукция В напряженность Н постоянны.
— сумма магнитных сопротивлений участков, на которых индукция В напряженность Н постоянны.
Пользуясь формулой № 2 для магнитной цепи, показанной на рисунке №1, можно найти:
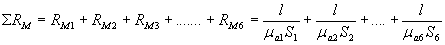 (6)
(6)
где 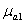 ,
, 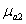
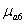 — магнитные проницаемости участков магнитной цепи.
— магнитные проницаемости участков магнитной цепи.
После подстановки значения 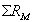 из №6 в №4
из №6 в №4
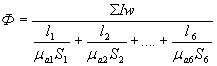
откуда
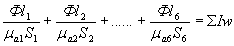 (7)
(7)
Ввиду того что
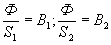
а также что
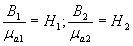 и т.д.
и т.д.
равенство №7 принимает следующий вид:
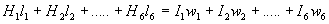 (8)
(8)
где произведения Н1 l1 ; H2 l2 являются м.д.с. отдельных участков.
16.Электромагнитная индукция.
Это когда всякое изменение магнитного потока пронизывает поток или контур наводит ЭДС в данном витке. Величина, возникающая ЭДС пропорцианальна числу витков, величине магнитного потока и измениению магнитного потока : e= — dФ/dt.
Перед приизводной стоит знак «-« ,который показывает ,что ЭДС ,проводимое в ветке создает свой магнитный поток, который направлен противоположно внешнему магнитному потоку и если внешний магнитный поток приближается к витку ,то внутренний поток старается его ослабить , уменьшить, а если виток удаляется от внешнего поля, то внутреннее поле старается поддержать магнитный поток.
17. Индуктивность
Ф= Iw/Rµ
Rµ-магнитное сопротивление витка
w- число витков.
Если число витков в цепи не меняется ,то Ф не изменяется. Если изменять величину R на dr, то ток будет изменяться и будет изменяться величина магнитного потока Ф на dФ.
dr→ dI →dФ = wdI/ Rµ
По закону электромагнитной индукции при применении магнитного потока,создавать витком в контуре возникает ЭДС :
e=- wdФ/dt= — 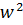 dI/ Rµ dt= — L dI/dt
dI/ Rµ dt= — L dI/dt
L dI/dt –коффициент индуктивности
Индуктивность – международ. Ед-ца [L]=Гн (Генри)
Индуктивность –коэффициент пропорциональности между ЭДС и скоростью изменения тока в цепи dI/dt
Если ток не изменяется dI=0, L =0.
Индуктивность зависит от числа витков в квадрате и обратно пропорционально магнитному сопротивлению среды.
18.Понятие о переменном синусоидальном токе
На постоянном токе ЭДС всегда постоянно, ток течет от + к – всегда и может изменяться при изменении сопротивления по величине, т.е. постоянным во времени. Переменный ток изменяется по величине и по направлению
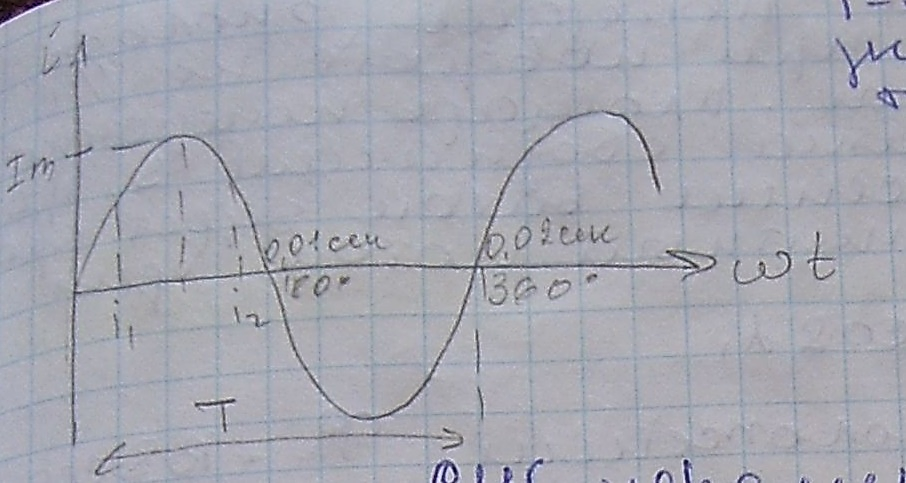
i-мгновенное значение тока.
В странах СНГ переменный ток f=50 ГЦ
Интервал через, который переменный ток периодически повторяет свои значения называется периодом(Т):
Т=1/f= 0,02сек→360®
Наибольшее мгновенное значение тока, называется амплитудой и обознач. 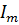 : I =
: I = 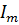 sin wt, по этому этот ток называется СИНУСОИДАЛЬНЫМ
sin wt, по этому этот ток называется СИНУСОИДАЛЬНЫМ
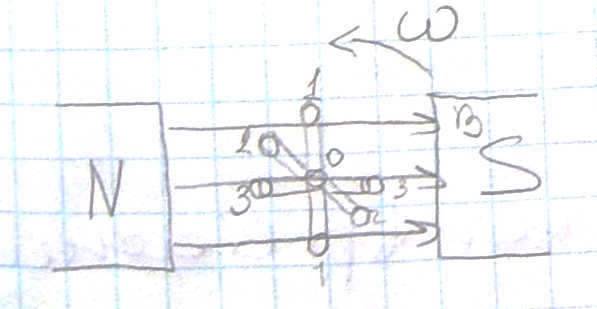
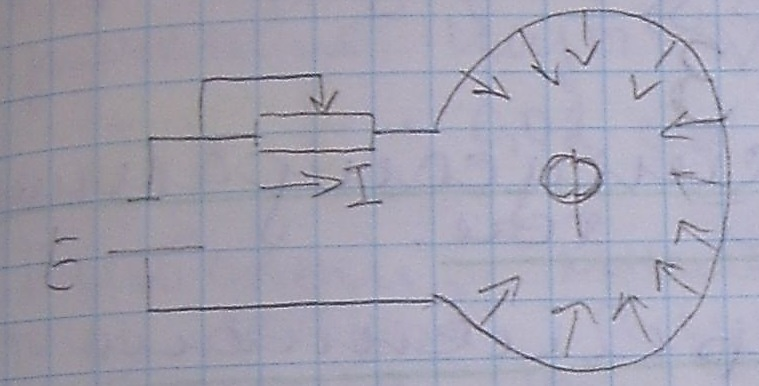
В однородном магнитном поле с индукцией В, между полюсами постоянного магнита расположена катушка их w витков. Катушка приводится во вращательное движение вокруг оси О внешней силой.
На рисунке показано 3 положения катушки при повороте на ¼ окружности. Площадь поперечного сечения витки обозначены S. При 1 положении виток будет пронизывать магнитный поток 1: 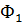 =B S cos
=B S cos 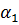
При втором положении : 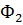 =B S cos
=B S cos 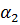 , 3:
, 3: 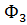 =B S cos
=B S cos 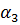
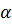 — угол между плоскостью катушки и магнитным потоком:
— угол между плоскостью катушки и магнитным потоком: 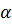 = wt
= wt
w- частота вращения катушки : w=2πf
тогда: 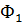 =B S cos
=B S cos 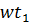 ,
, 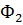 =B S cos
=B S cos 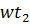 ,
, 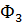 =B S cos
=B S cos 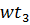
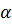 = w
= w 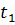 ,
, 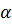 = w
= w 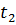 ,
, 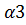 = w
= w 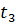
В любой момент времени: 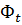 =B S cos
=B S cos 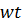
t- мгновенный момент времени.
Если обозначим BS= 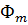 ,
, 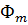 -мах(амплитудное) значение магнитного потока
-мах(амплитудное) значение магнитного потока 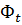 =
= 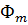 cos wt
cos wt
Витки будет пронизывать магнитный поток ,изменяющийся по закону косинуса, т.е. виток все время будет пронизывать изменяющий магнитный поток , значит в витке будет образовываться по з-ну электромагнитной индукции ЭДС: e=-W dФ/dt
Как видно из рис магнитный поток по направлению не изменяется ,но поскольку меняется угол витка , то в ней каждая ¼ окружности будет изменятся и величина направл. Тока и ЭДС
Периодич выражение ЭДС : e = W 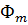 w sin wt
w sin wt
отсюда видно ,что ЭДС будет изменятся по синусоидальному закону.
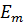 =W w
=W w 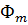 , е =
, е = 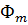 sin wt
sin wt
Магнитный поток изменяется по з-ну косинуса, а ЭДС по з-ну синуса, то они сдвинуты на 90® между собой или находятся в противофазе.
20. Действующее значение переменного тока
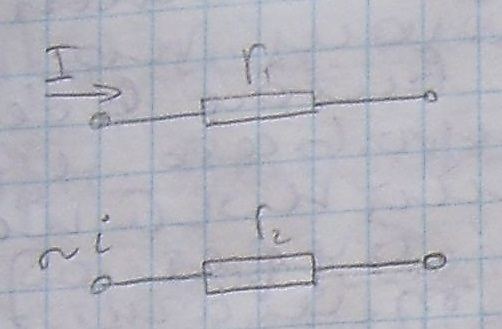 r1=r2=r
r1=r2=r
i = 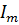 sin wt
sin wt
Определение количества тепла Q, которое выдел в сопротивлении за одинаковое время одного периода T=0.02с
Q= r1 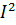 =T
=T
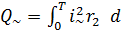 t
t
Приравниваем эти уравнения между собой :

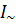 =I=
=I= 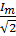
В действит значениях проградуированы все приборы раб на переменном токе. Действит значение переменного тока = такой величине постоянного тока , которое производит одинаковый тепловой эффект при одних и тех же условиях за одно и тоже время.
Фазовый сдвиг
1.Цепь с резистивным элементом.Сдвиг по фазе между напряжением и током цепи:
φ = ψu — ψi = 0° — 0° = 0°2.Цепь с емкостным элементом.Сдвиг по фазе между напряжением и током цепи:
φ = ψu — ψi = 0º — 90º = — 90º. (ток опережает по фазе напряжение на 90)
3.Цепь с индуктивным элементом. Сдвиг по фазе между напряжением и током цепи
φ = 0° – (-90° ) = +90
Таким образом, синусоида тока в цепи с идеальной индуктивной катушкой отстает от синусоиды напряжения на угол 90º.
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
Закон Ома для магнитной цепи — Википедия. Что такое Закон Ома для магнитной цепи
Материал из Википедии — свободной энциклопедииЗако́н О́ма для магни́тной цепи́ (зако́н Го́пкинсона) — физический закон для магнитной цепи, аналогичный закону Ома для электрической цепи. Определяет связь между магнитодвижущей силой, магнитным сопротивлением и магнитным потоком в магнитной цепи.
Формулировка
В неразветвлённой магнитной цепи магнитный поток равен частному от деления магнитодвижущей силы на полное магнитное сопротивление[1].
Вывод
Рассмотрим неразветвлённую магнитную цепь, состоящую из ярма с площадью поперечного сечения S{\displaystyle S} из материала c магнитной проницаемостью μ{\displaystyle \mu } и зазора из другого материала, имеющего то же сечение и магнитную проницаемость μ1{\displaystyle \mu _{1}}. На ярмо надета катушка с числом витков N{\displaystyle N}, по которой идёт ток i{\displaystyle i}. Рассмотрим среднюю линию магнитной цепи и применим теорему о циркуляции магнитного поля.
- Hl+h2l1=4πNic.(1){\displaystyle Hl+H_{1}l_{1}={\frac {4\pi Ni}{c}}.\qquad (1)}
Здесь H{\displaystyle H} — напряжённость магнитного поля внутри ярма, h2{\displaystyle H_{1}} — напряжённость магнитного поля внутри зазора, l{\displaystyle l} — длина ярма, измеренная вдоль средней линии индукции, l1{\displaystyle l_{1}} — длина зазора. Так как линии индукции непрерывны, то значения магнитного потока Φ{\displaystyle \Phi } внутри ярма и внутри зазора одинаковы. Из соотношений Φ=BS,B=μH{\displaystyle \Phi =BS,B=\mu H} выражаем напряжённость магнитного поля через поток H=ΦμS,{\displaystyle H=\Phi \mu S,} h2=Φμ1S.{\displaystyle H_{1}=\Phi \mu _{1}S.} Подставляя эти выражения в формулу (1), получаем из неё значение магнитного потока Φ{\displaystyle \Phi }:
- Φ=4πNiclμS+l1μ1S.{\displaystyle \Phi ={\frac {\frac {4\pi Ni}{c}}{{\frac {l}{\mu S}}+{\frac {l_{1}}{\mu 1S}}}}.}
Полученная формула подобна закону Ома для замкнутой электрической цепи. При этом величина Fm=4πNic{\displaystyle F_{m}={\frac {4\pi Ni}{c}}} играет роль электродвижущей силы и поэтому по аналогии она получила название магнитодвижущей силы. Её отличие от электродвижущей силы состоит в том, что в магнитном потоке не движутся никакие частицы. Сумма Rm=lμS+l1μ1S{\displaystyle R_{m}={\frac {l}{\mu S}}+{\frac {l_{1}}{\mu _{1}S}}} входит в формулу так же, как полное сопротивление электрической цепи в законе Ома, и поэтому её называют полным магнитным сопротивлением цепи. Итак, закон Ома для магнитной цепи можно записать в виде Φ=FmRm.{\displaystyle \Phi ={\frac {F_{m}}{R_{m}}}.} В неразветвлённой магнитной цепи магнитный поток равен частному от деления магнитодвижущей силы на полное магнитное сопротивление.
История
Идею о том, что величину магнитного потока в магнитной цепи можно записать аналогично закону Ома для электрической цепи, первым высказал американский физик Генри Роуланд в 1873 году[2]. Закон часто называют формулой Гопкинсона или законом Гопкинсона в честь английского физика и инженера Джона Гопкинсона (Хопкинсона), который вместе со своим братом Эдвардом в 1886 году разработал формализм для расчёта магнитных цепей.
Примечания
Литература
Магнитная цепь — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 февраля 2017; проверки требуют 10 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 февраля 2017; проверки требуют 10 правок.Магнитная цепь — последовательность взаимосвязанных магнетиков, по которым проходит магнитный поток.[1]
При расчётах магнитных цепей используется почти полная формальная аналогия с электрическими цепями.
В схожем математическом аппарате также присутствует закон Ома, правила Кирхгофа и другие термины и закономерности.[2] Принципиальным различием между магнитной и электрической цепями является то, что в магнитной цепи с неизменным по времени магнитным потоком не выделяется джоулева теплота[3].
Магнитная цепь и сопутствующий математический аппарат используется для расчётов электромагнитных устройств: трансформаторов, электрических машин, магнитных усилителей и т. п.[2][4]
В зависимости от источника магнитного потока магнитные цепи подразделяют[1] на поляризованные и нейтральные. В отличие от нейтральных, поляризованные магнитные цепи содержат постоянные магниты.[1]
- ↑ 1 2 3 Магнитная цепь — статья из Большой советской энциклопедии.
- ↑ 1 2 Теоретические основы электротехники. Лекц.32
- ↑ Магнитная цепь // Физический энциклопедический словарь. — под ред. Ю. В. Прохорова — М., Большая Российская энциклопедия, 2003. — ISBN 5-85270-306-0. — с. 368
- ↑ Теоретические основы электротехники. Лекц.33
- Герасимов В. Г., Кузнецов Э. В., Николаева О. В. Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. — М.: Энергоатомиздат, 1996. — 288 с. — ISBN 5-283-05005-X.
- Калашников С. Г. Электричество. — М.: ГИТТЛ, 1956. — 664 с.
- Бессонов Л. А. Теоретические основы электротехники. — М.: Высшая школа, 1967. — 756 с.
Закон Ома для магнитной цепи — Википедия. Что такое Закон Ома для магнитной цепи
Материал из Википедии — свободной энциклопедииЗако́н О́ма для магни́тной цепи́ (зако́н Го́пкинсона) — физический закон для магнитной цепи, аналогичный закону Ома для электрической цепи. Определяет связь между магнитодвижущей силой, магнитным сопротивлением и магнитным потоком в магнитной цепи.
Формулировка
В неразветвлённой магнитной цепи магнитный поток равен частному от деления магнитодвижущей силы на полное магнитное сопротивление[1].
Вывод
Рассмотрим неразветвлённую магнитную цепь, состоящую из ярма с площадью поперечного сечения S{\displaystyle S} из материала c магнитной проницаемостью μ{\displaystyle \mu } и зазора из другого материала, имеющего то же сечение и магнитную проницаемость μ1{\displaystyle \mu _{1}}. На ярмо надета катушка с числом витков N{\displaystyle N}, по которой идёт ток i{\displaystyle i}. Рассмотрим среднюю линию магнитной цепи и применим теорему о циркуляции магнитного поля.
- Hl+h2l1=4πNic.(1){\displaystyle Hl+H_{1}l_{1}={\frac {4\pi Ni}{c}}.\qquad (1)}
Здесь H{\displaystyle H} — напряжённость магнитного поля внутри ярма, h2{\displaystyle H_{1}} — напряжённость магнитного поля внутри зазора, l{\displaystyle l} — длина ярма, измеренная вдоль средней линии индукции, l1{\displaystyle l_{1}} — длина зазора. Так как линии индукции непрерывны, то значения магнитного потока Φ{\displaystyle \Phi } внутри ярма и внутри зазора одинаковы. Из соотношений Φ=BS,B=μH{\displaystyle \Phi =BS,B=\mu H} выражаем напряжённость магнитного поля через поток H=ΦμS,{\displaystyle H=\Phi \mu S,} h2=Φμ1S.{\displaystyle H_{1}=\Phi \mu _{1}S.} Подставляя эти выражения в формулу (1), получаем из неё значение магнитного потока Φ{\displaystyle \Phi }:
- Φ=4πNiclμS+l1μ1S.{\displaystyle \Phi ={\frac {\frac {4\pi Ni}{c}}{{\frac {l}{\mu S}}+{\frac {l_{1}}{\mu 1S}}}}.}
Полученная формула подобна закону Ома для замкнутой электрической цепи. При этом величина Fm=4πNic{\displaystyle F_{m}={\frac {4\pi Ni}{c}}} играет роль электродвижущей силы и поэтому по аналогии она получила название магнитодвижущей силы. Её отличие от электродвижущей силы состоит в том, что в магнитном потоке не движутся никакие частицы. Сумма Rm=lμS+l1μ1S{\displaystyle R_{m}={\frac {l}{\mu S}}+{\frac {l_{1}}{\mu _{1}S}}} входит в формулу так же, как полное сопротивление электрической цепи в законе Ома, и поэтому её называют полным магнитным сопротивлением цепи. Итак, закон Ома для магнитной цепи можно записать в виде Φ=FmRm.{\displaystyle \Phi ={\frac {F_{m}}{R_{m}}}.} В неразветвлённой магнитной цепи магнитный поток равен частному от деления магнитодвижущей силы на полное магнитное сопротивление.
История
Идею о том, что величину магнитного потока в магнитной цепи можно записать аналогично закону Ома для электрической цепи, первым высказал американский физик Генри Роуланд в 1873 году[2]. Закон часто называют формулой Гопкинсона или законом Гопкинсона в честь английского физика и инженера Джона Гопкинсона (Хопкинсона), который вместе со своим братом Эдвардом в 1886 году разработал формализм для расчёта магнитных цепей.
Примечания
Литература
Закон Ома для магнитной цепи — КиберПедия
Рассмотрим магнитную цепь, образованную обмоткой навитой на магнитопровод в виде кольца (тороида). При протекании тока I по обмотке в магнитопроводе возбуждается магнитное поле, которое все сосредоточено в объеме кольца (поле рассеяния отсутствует). Выбрав контур интегрирования в виде окружности с радиусом R и применяя закон полного тока:
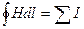
— линейный интеграл от вектора напряженности по замкнутому контуру равен алгебраической сумме токов, охватываемых этим контуром – полному току (Iполн). Для практических целей наибольший интерес представляет частный случай, когда контур интегрирования проходит внутри обмотки с числом витков w и током IВ этом случае полный ток 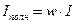 , запишем
, запишем
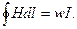
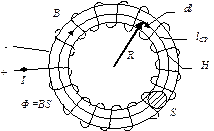
|
Сумму токов — wI через поверхность, ограниченную контуром интегрирования, называют магнитодвижущей силой F,
F = wI.
Если учесть, что угол между векторами Ни dl равен нулю и значение Н в любой точке контура интегрирования одинаково, среднее значение напряженности магнитного поля определится как
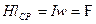 .
.
Из полученного соотношения следует, что напряженность магнитного поля Н не зависит от магнитных свойств магнитопровода, а прямо пропорциональна току в обмотке. Точнее равна МДС обмотки, приходящейся на единицу длины средней силовой линии магнитопровода.
Исходя из соотношений Ф =ВS и В = μa Н получим
Ф = μa НS = μa S(I w / l) = I w / ( l / μa S) = F/Rм.
Это выражение называют законом Ома для магнитной цепи. При этом величину Rм = l / μa S принято называть магнитным сопротивлением магнитопровода (по аналогии с электрическим сопротивлением).
При анализе магнитных цепей вводят понятие разности магнитных потенциалов между двумя точками магнитной цепи, которая приравнивается к магнитному напряжению Uм ab
Uм ab = Н l ab .
Расчет неразветвленной магнитной цепи постоянного тока
Формула, выражающая закон полного тока магнитной цепи, была получена для кольцевого магнитопровода постоянного поперечного сечения и с равномерно распределенной обмоткой. Эту формулу распространяют и на магнитные цепи, где намагничивающая обмотка сосредоточена на ограниченном участке магнитопровода, а отдельные участки цепи выполнены из различных ферромагнитных и неферромагнитных материалов и имеют различное поперечное сечение.
В приближенных расчетах магнитных цепей принимают, что магнитный поток на всех участках цепи остается одним и тем же, хотя на самом деле в магнитной цепи образуются также потоки рассеяния Фр, которые замыкаются по воздуху, а не следуют по пути магнитопровода.
В расчетах магнитных цепей различают прямую и обратную задачи.
Прямая задача
Задано: 1) геометрические размеры магнитной цепи; 2) характеристика B = f(H) (кривая намагничивания) ферромагнитных материалов, из которых выполнена магнитная цепь; 3) магнитный поток Ф, который надо создать в магнитной цепи.
Требуется найти намагничивающую силу обмотки F = IW.
Решение задачи рассматривается применительно к магнитопроводу, представленному на рисунке.
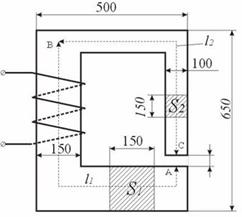
Рис. 10. Магнитная цепь
1. Магнитная цепь разбивается на ряд участков с одинаковым поперечным сечением S, выполненном из однородного материала.
2. Намечается путь прохождения средней магнитной линии (на рис. показано пунктиром).
3. Т.к. магнитный поток на всех участках цепи остается постоянным, то магнитная индукция B = Ф / S на каждом из участков и напряженность магнитного поля Н неизменны. Это позволяет сравнительно просто определить значение 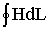 для контура, образованного средней магнитной линией, а следовательно, найти искомую величину намагничивающей силы, поскольку
для контура, образованного средней магнитной линией, а следовательно, найти искомую величину намагничивающей силы, поскольку 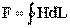 .
.
Запишем интеграл 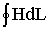 в виде суммы интегралов с границами интегрирования, совпадающими с началом и концом каждого участка цепи. Тогда
в виде суммы интегралов с границами интегрирования, совпадающими с началом и концом каждого участка цепи. Тогда
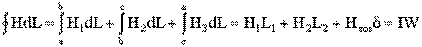 .
.
где: L1 и L2 – длины ферромагнитных участков цепи [м].
d – ширина воздушного зазора, [м].
4. Значения Н1 и Н2 определяют по известным величинам магнитной индукции В с помощью кривых намагничивания, соответствующих ферромагнитных материалов.
А для воздушного зазора
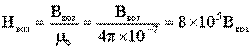 А/м.
А/м.
Разделим каждое слагаемое на магнитный поток Ф, получим:
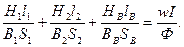 (*)
(*)
Обозначим:
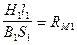 — магнитное сопротивление участка 1;
— магнитное сопротивление участка 1;
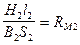 — магнитное сопротивление участка 2;
— магнитное сопротивление участка 2;
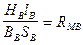 — магнитное сопротивление воздушного зазора.
— магнитное сопротивление воздушного зазора.
С учетом обозначений перепишем выражение (*):
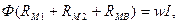
или
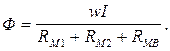 (**)
(**)
Последнее выражение, т.е. зависимость магнитного потока от магнитодвижущей силы (wI) и магнитных сопротивлений участков магнитной цепи называют основным законом магнитной цепи.
Заметна аналогия между уравнением (**) и законом Ома для полной цепи:
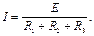
Составим таблицу аналогий соответствующих величин.
Таблица
| Магнитные величины | Электрические величины | ||||
| Наименование | Обозначение | Ед. измерения | Наименование | Обозначение | Ед. измерения |
| Магнитный поток | Ф | Вб | Сила тока | I | A |
| Магнитодвижущая сила | wI | A | Электродвижущая сила | Е | В |
| Магнитное сопротивление | RM | 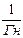 | Электрическое сопротивление | R | Ом |
| Магнитное напряжение | UM=RMФ =H l | А | Электрическое напряжение | U=RI | B |
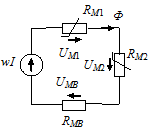
|
Пользуясь аналогиями, можно изобразить схему замещения магнитной цепи, изображенной ранее, в виде. Полученная цепь содержит последовательно соединенные нелинейные элементы RM1 и RM2. Их нелинейность обусловлена зависимостью от напряженности магнитного поля Н или от силы тока в обмотке I, т.е. от МДС действующей в контуре.
Обратная задача
Задано:
- Геометрические размеры магнитной цепи;
- Характеристики ферромагнитных материалов;
- Намагничивающая сила обмотки F.
Требуется определить магнитный поток Ф.
Непосредственное использование формулы 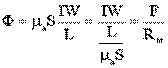 для определения магнитного потока Ф оказывается невозможным, поскольку магнитное сопротивление цепи переменное и само зависит от величины магнитного потока. Такие задачи решаются методом последовательного приближения в следующем порядке. Задаются рядом произвольных значений магнитного потока в цепи и для каждого из этих значений определяют необходимую намагничивающую силу обмотки так, как это делается при решении прямой задачи.
для определения магнитного потока Ф оказывается невозможным, поскольку магнитное сопротивление цепи переменное и само зависит от величины магнитного потока. Такие задачи решаются методом последовательного приближения в следующем порядке. Задаются рядом произвольных значений магнитного потока в цепи и для каждого из этих значений определяют необходимую намагничивающую силу обмотки так, как это делается при решении прямой задачи.
По полученным данным строят кривую Ф(F) – вебер-амперную характеристику. Имея эту зависимость, нетрудно для заданного значения намагничивающей силы найти величину магнитного потока.
Для оценки необходимого значения Ф можно пренебречь сопротивлением ферромагнитного участка и посчитать поток, который получится под действием намагничивающей силы F при сопротивлении воздушного участка. Это значение Ф заведомо больше расчетного.
Остальные значения можно давать меньше.
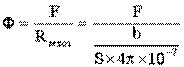 .
.
Закон Ома для магнитной цепи — Википедия
Материал из Википедии — свободной энциклопедии
Зако́н О́ма для магни́тной цепи́ (зако́н Го́пкинсона) — физический закон для магнитной цепи, аналогичный закону Ома для электрической цепи. Определяет связь между магнитодвижущей силой, магнитным сопротивлением и магнитным потоком в магнитной цепи.
Формулировка
В неразветвлённой магнитной цепи магнитный поток равен частному от деления магнитодвижущей силы на полное магнитное сопротивление[1].
Вывод
Рассмотрим неразветвлённую магнитную цепь, состоящую из ярма с площадью поперечного сечения S{\displaystyle S} из материала c магнитной проницаемостью μ{\displaystyle \mu } и зазора из другого материала, имеющего то же сечение и магнитную проницаемость μ1{\displaystyle \mu _{1}}. На ярмо надета катушка с числом витков N{\displaystyle N}, по которой идёт ток i{\displaystyle i}. Рассмотрим среднюю линию магнитной цепи и применим теорему о циркуляции магнитного поля.
- Hl+h2l1=4πNic.(1){\displaystyle Hl+H_{1}l_{1}={\frac {4\pi Ni}{c}}.\qquad (1)}
Здесь H{\displaystyle H} — напряжённость магнитного поля внутри ярма, h2{\displaystyle H_{1}} — напряжённость магнитного поля внутри зазора, l{\displaystyle l} — длина ярма, измеренная вдоль средней линии индукции, l1{\displaystyle l_{1}} — длина зазора. Так как линии индукции непрерывны, то значения магнитного потока Φ{\displaystyle \Phi } внутри ярма и внутри зазора одинаковы. Из соотношений Φ=BS,B=μH{\displaystyle \Phi =BS,B=\mu H} выражаем напряжённость магнитного поля через поток H=ΦμS,{\displaystyle H=\Phi \mu S,} h2=Φμ1S.{\displaystyle H_{1}=\Phi \mu _{1}S.} Подставляя эти выражения в формулу (1), получаем из неё значение магнитного потока Φ{\displaystyle \Phi }:
- Φ=4πNiclμS+l1μ1S.{\displaystyle \Phi ={\frac {\frac {4\pi Ni}{c}}{{\frac {l}{\mu S}}+{\frac {l_{1}}{\mu 1S}}}}.}
Полученная формула подобна закону Ома для замкнутой электрической цепи. При этом величина Fm=4πNic{\displaystyle F_{m}={\frac {4\pi Ni}{c}}} играет роль электродвижущей силы и поэтому по аналогии она получила название магнитодвижущей силы. Её отличие от электродвижущей силы состоит в том, что в магнитном потоке не движутся никакие частицы. Сумма Rm=lμS+l1μ1S{\displaystyle R_{m}={\frac {l}{\mu S}}+{\frac {l_{1}}{\mu _{1}S}}} входит в формулу так же, как полное сопротивление электрической цепи в законе Ома, и поэтому её называют полным магнитным сопротивлением цепи. Итак, закон Ома для магнитной цепи можно записать в виде Φ=FmRm.{\displaystyle \Phi ={\frac {F_{m}}{R_{m}}}.} В неразветвлённой магнитной цепи магнитный поток равен частному от деления магнитодвижущей силы на полное магнитное сопротивление.
История
Идею о том, что величину магнитного потока в магнитной цепи можно записать аналогично закону Ома для электрической цепи, первым высказал американский физик Генри Роуланд в 1873 году[2]. Закон часто называют формулой Гопкинсона или законом Гопкинсона в честь английского физика и инженера Джона Гопкинсона (Хопкинсона), который вместе со своим братом Эдвардом в 1886 году разработал формализм для расчёта магнитных цепей.

