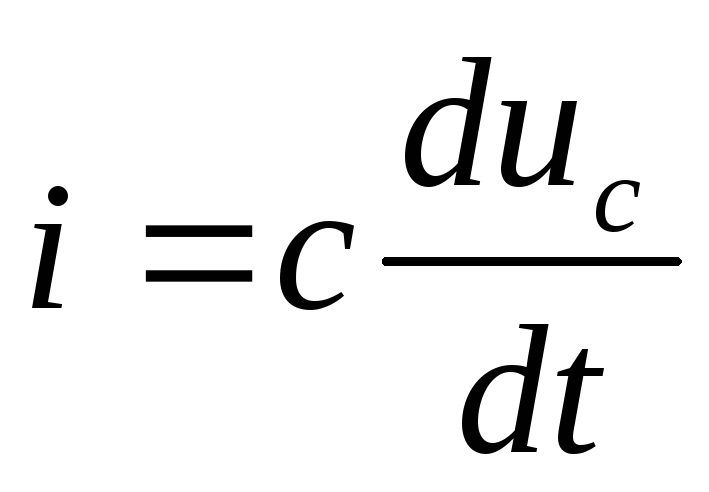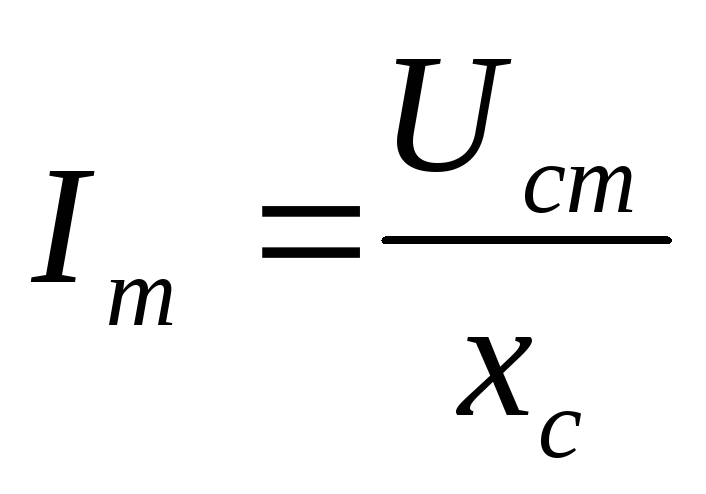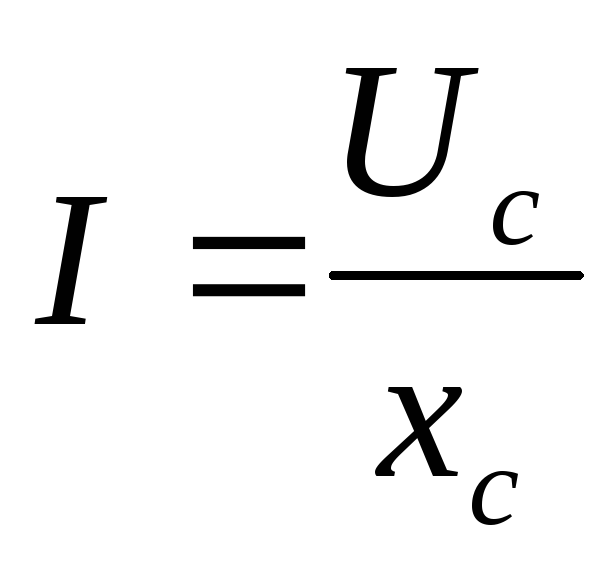Закон Ома для цепи переменного тока. Мощность
RIR=UR; 1ωCIC=UC; ωLIL=UL.
Указанные выше формулы внешне могут напоминать закон Ома на участке цепи постоянного тока, но стоит заметить, что в этом случае вместо величин постоянных токов и напряжений на участке цепи, в них входят амплитудные значения напряжений и переменных токов.
Формулы, указанные выше, выражают собой закон Ома для переменного тока, который содержит один из элементов R, L и C.
Определение 1R – активное сопротивление резистора.
1ωС – емкостное сопротивление конденсатора.
ωL – индуктивное сопротивление катушки в цепи переменного тока.
Движение переменного тока по участку цепи провоцирует электромагнитное поле выполнять работу, благодаря чему выделяется джоулево тепло.
Определение 2Мгновенной мощностью в цепи называется произведение мгновенных значений тока и напряжения: p=J·u.
Прикладной интерес у нас вызывает среднее значение мощности за некоторый период переменного тока:
P=Pcα=I0U0cos ωt cos ωt+φ.
В приведенной выше формуле I0 и U0 являются амплитудными значениями тока и напряжения на выбранном участке цепи, а φ – фазовым сдвигом между током и напряжением. Черта же представляет собой символ усреднения. В случае, когда цепь содержит только резистор с сопротивлением R, то фазовый сдвиг φ будет равен нулю:
PR=IRURcos2ωt=IRUR2=IR2R2.
Действующие значения силы тока и напряжения
Определение 3По причине необходимости совпадения с уравнением для мощности постоянного тока, нам приходится ввести определения действующих значений силы тока и напряжения:
IД=l02; UД=U02.
Мощность переменного тока на участке цепи
Определение 4Средняя величина мощности переменного тока на участке цепи, включающем в себя резистор, равняется:
PR=IДUД.
Если в цепи содержится лишь конденсатор емкости C, то φ=π2. Отсюда, справедливо следующее выражение:
PC=ICUCcos ωt cosωt+π2=ICUCcos ωt
Энергетический процесс в цепи с идеальной катушкой
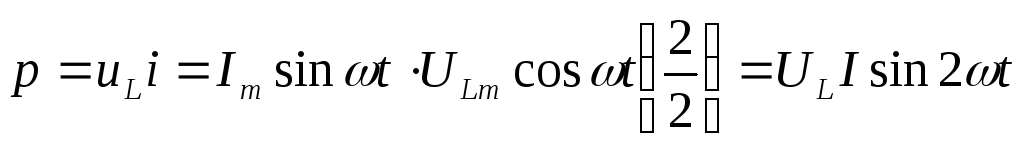
Перемножим напряжение и ток на временной диаграмме:
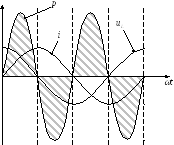
Вывод:в цепи с идеальной катушкой
индуктивностикатушка и источник
обмениваются энергией. Энергия из
цепи не уходит. Мерой этого обмена
является реактивная мощность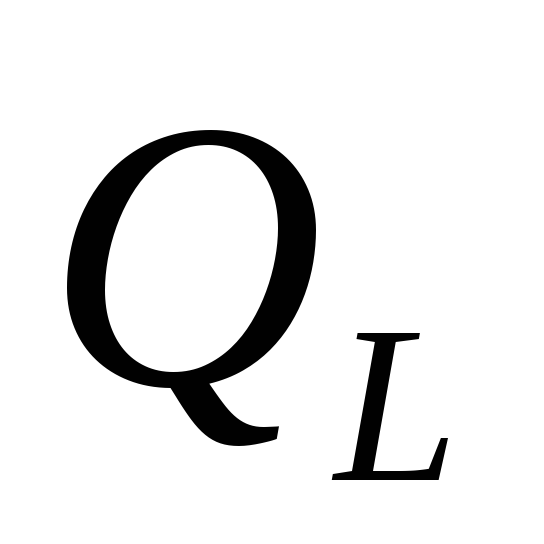
:
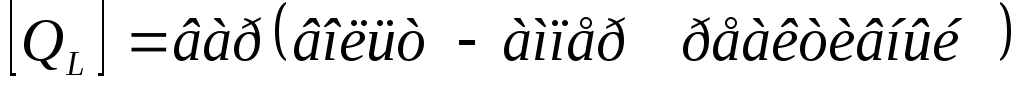
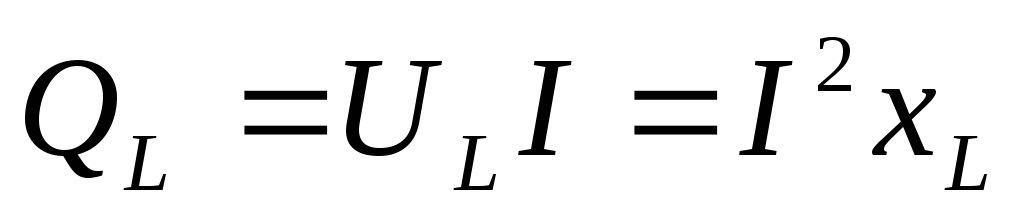
Сопротивление идеальной катушки в комплексной (символической) форме
Зададимся напряжением
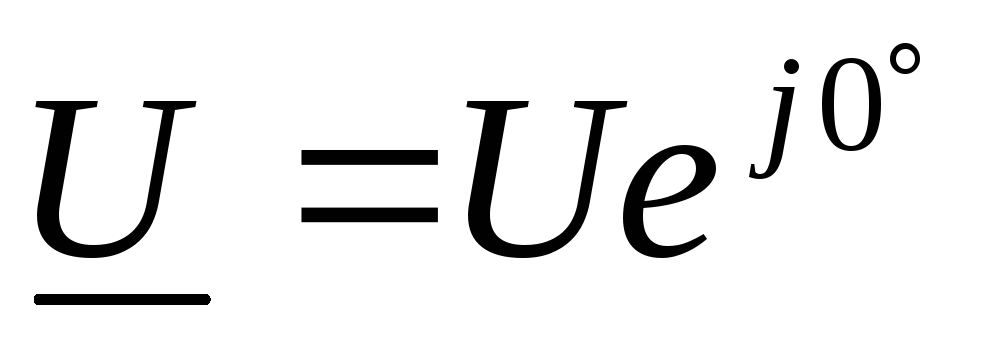
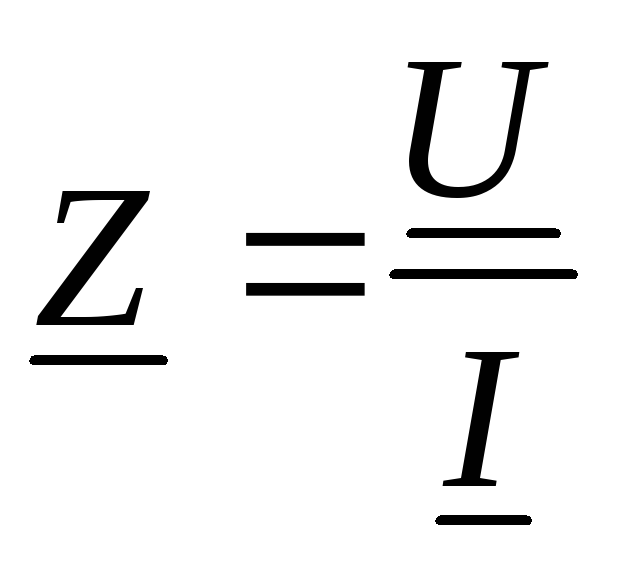— закон Ома в комплексной форме
В идеальной катушке индуктивности:
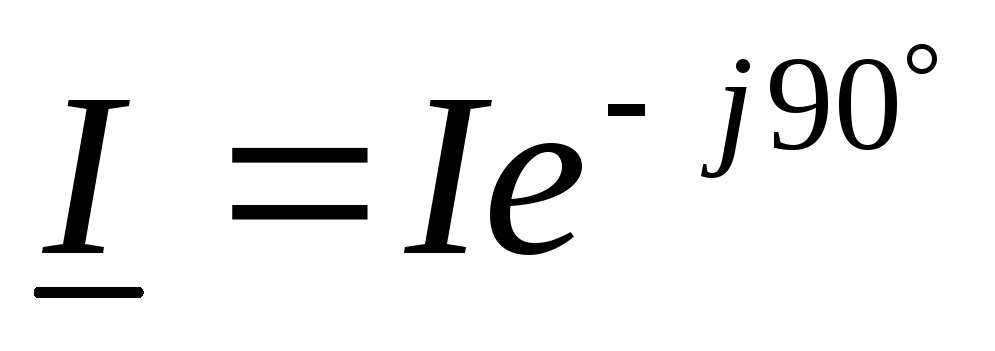
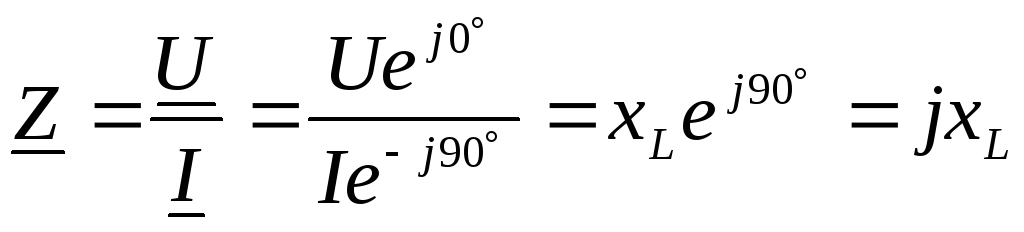
Вывод:в комплексной форме
сопротивление идеальной катушки
индуктивности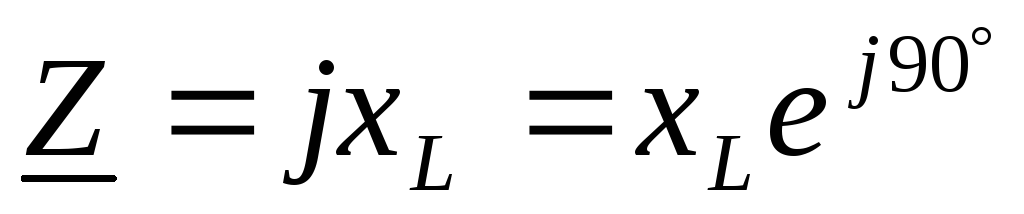
.
Вопрос 32. Цепь с конденсатором при гармоническом воздействии. Закон Ома. Емкостное сопротивление. Энергетический процесс. Реактивная (емкостная) мощность. Временная и векторная диаграммы. Входное сопротивление цепи в комплексной форме.
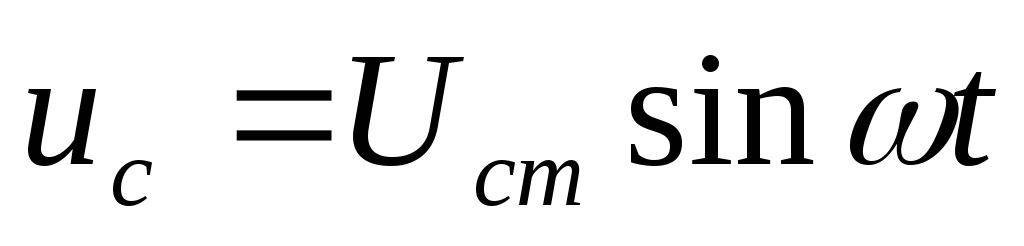
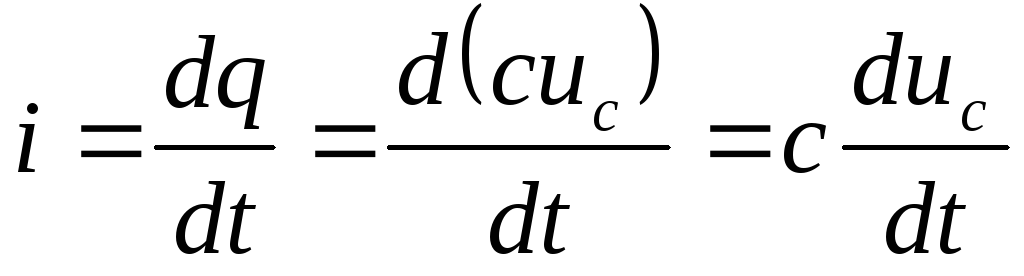
| — формула, связывающая мгновенные значения напряжения и тока в цепи с конденсатором |
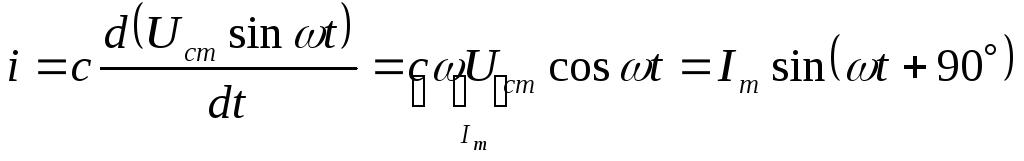
Тогда 
.
Вывод: в цепи с конденсатором ток опережает напряжение на угол 90°.
Построим напряжение и ток на временной и векторной диаграмме:
Закон Ома:
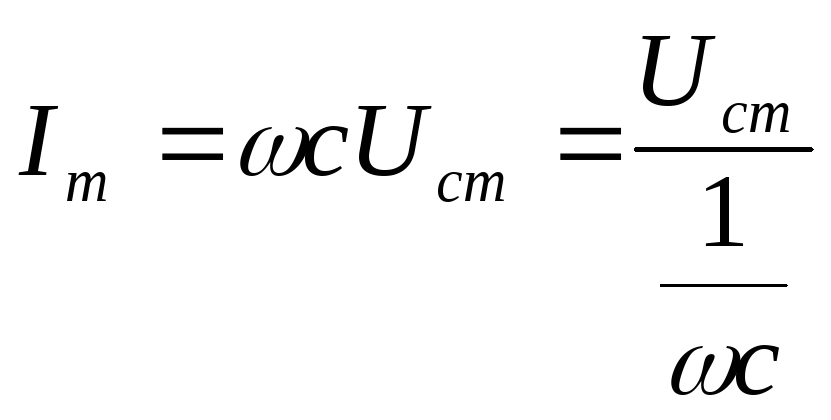
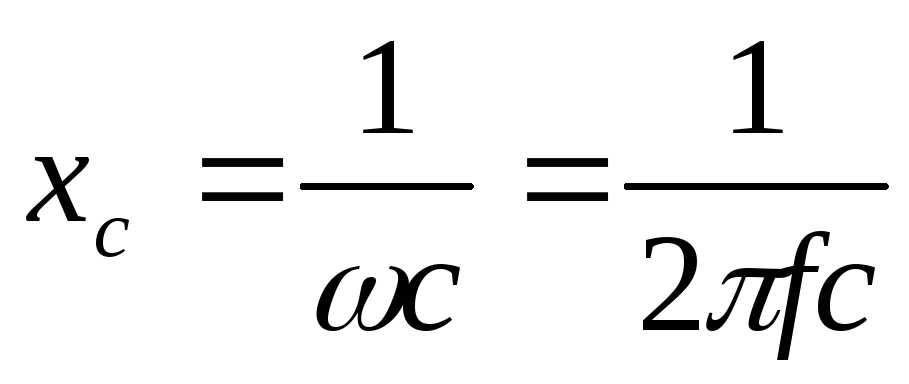— емкостное сопротивление
|
|
закон Ома для максимальных значений | закон Ома для действующих значений |
Вывод:в цепи с конденсатором закон Ома справедлив для максимальных и действующих значений, но не справедлив для мгновенных.
(
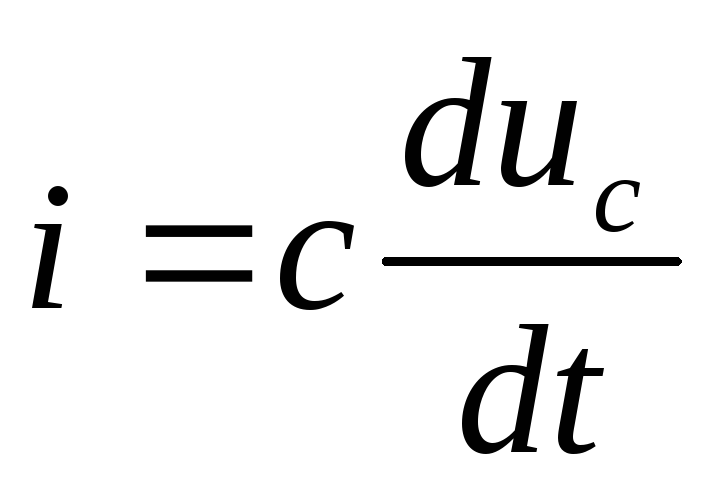— для мгновенных значений)
С ростом частоты емкостное сопротивление уменьшается, поэтому конденсатор хорошо пропускает токи верхних частот, и плохо токи нижних частот. Конденсатор — фильтр верхних частот
На постоянном токе 
,
а это значит, что в схеме замещения на
постоянном токе вместо конденсатора
надо ставить разрыв цепи.
Конденсатор не пропускает постоянный ток.
Энергетический процесс в цепи с конденсатором
Мгновенная мощность:
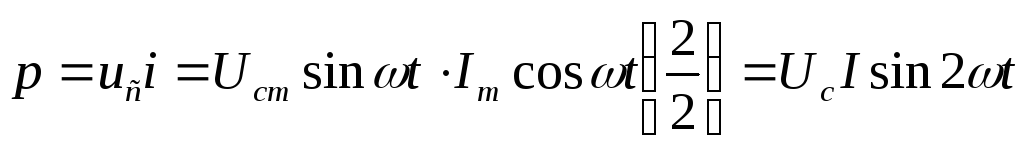
Перемножим напряжение и ток на временной диаграмме:
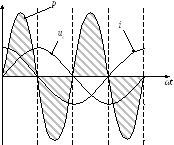
В первой и третьей четверти напряжение и ток имеют одинаковые знаки, источник работает в режиме генератора. Конденсатор заряжается от источника, мгновенная мощность положительна. Вторую и четвёртую четверть напряжение и ток имеют разные знаки. Источник работает в режиме потребителя, и конденсатор разряжается на источник. Мгновенная мощность отрицательна.
Вывод:
В цепи с конденсатором источник и
конденсатор обмениваются энергией.
Мерой этого обмена является реактивная
мощность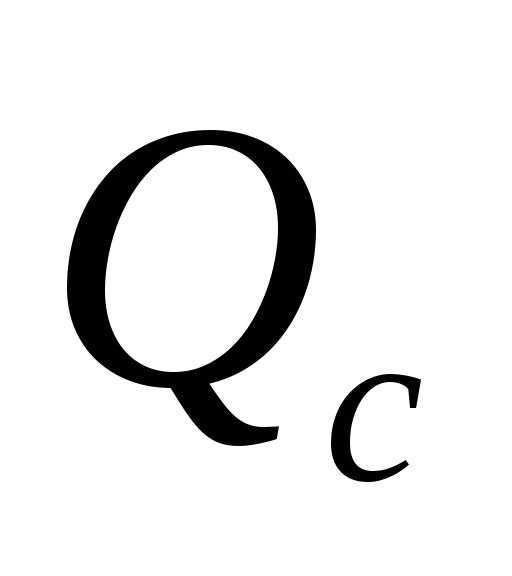
.
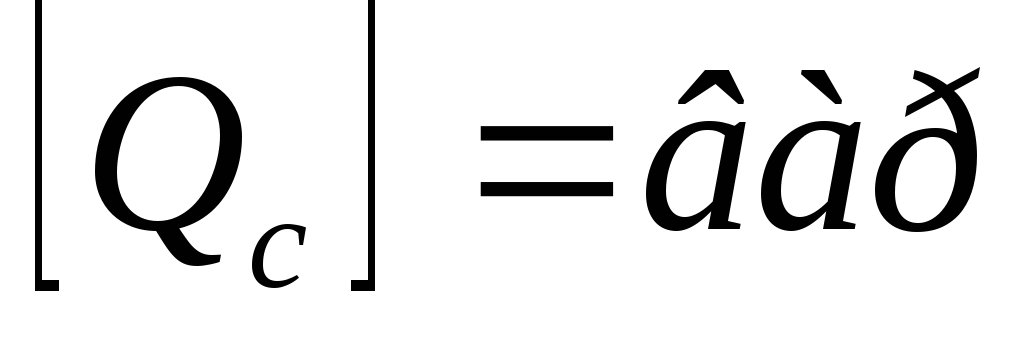
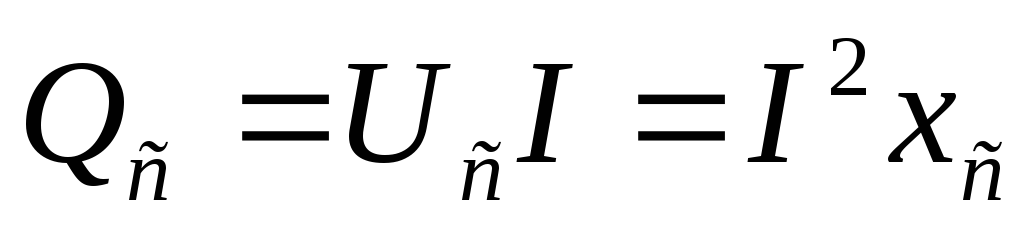
Сопротивление конденсатора в комплексной (символической) форме
Зададимся напряжением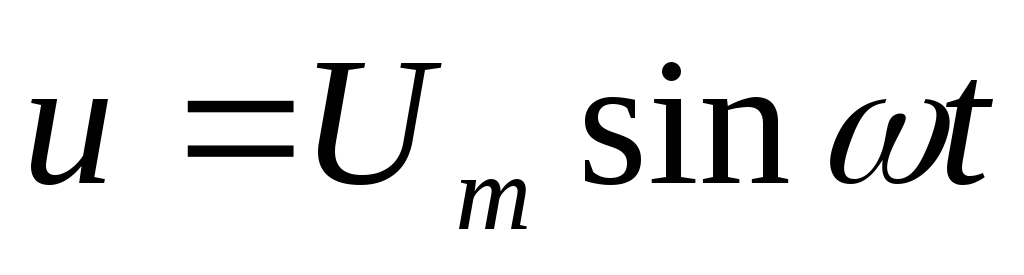 
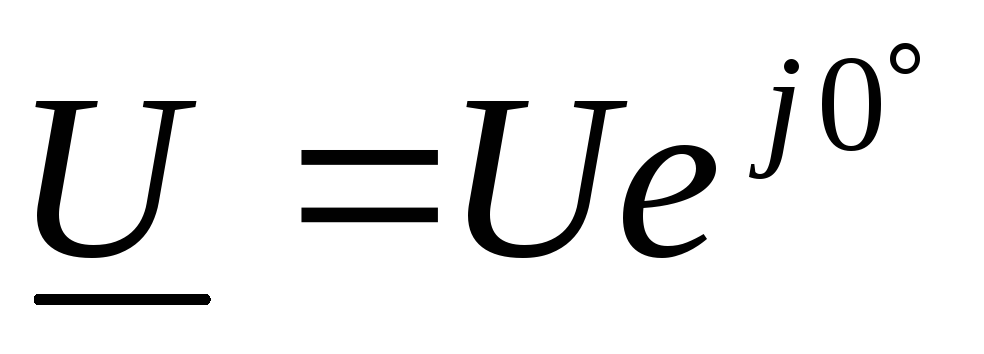
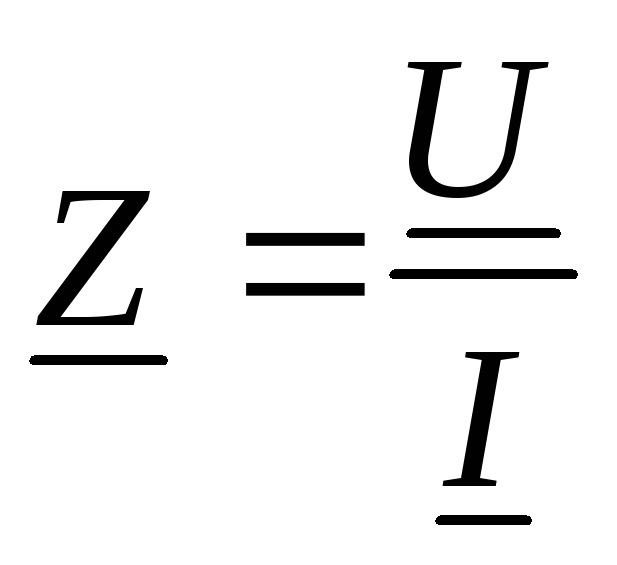— закон Ома в комплексной форме
В идеальной катушке индуктивности:
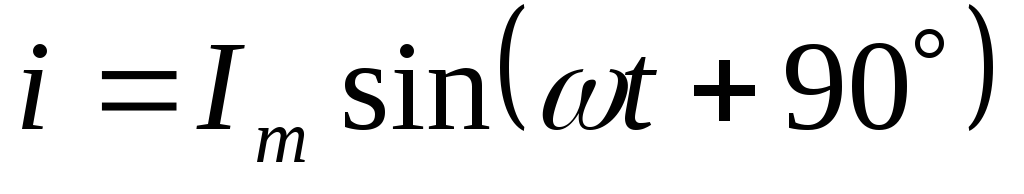
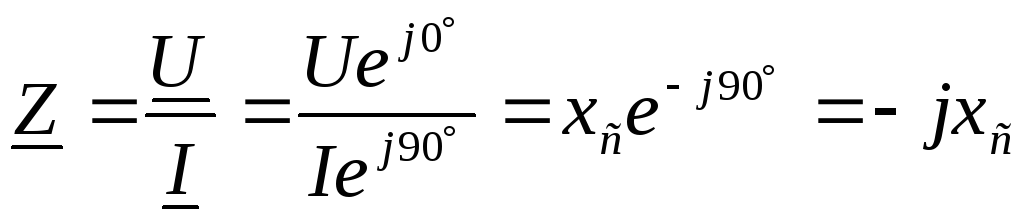
Вывод:в комплексной форме
сопротивление конденсатора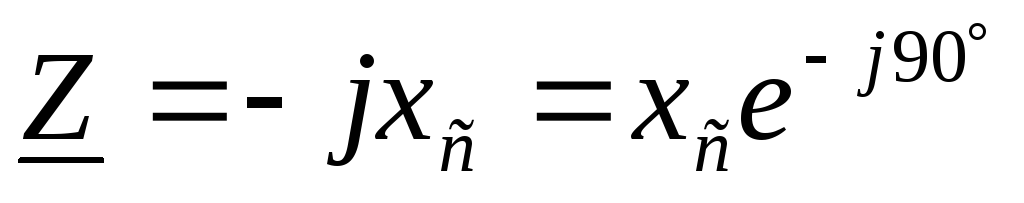
.
Вопрос 33. Неразветвлённая RL электрическая цепь при гармоническом воздействии. Свойства реальной катушки индуктивности. Закон Ома. Энергетический процесс. Треугольник напряжений, сопротивлений и мощностей. Входное сопротивление цепи в комплексной форме.
Цепь RL при гармоническом воздействии
В реальной катушке происходит процесс нагревания, поэтому в схеме замещения реальной катушки появляется резистивное сопротивление.
Пусть ток изменяется по закону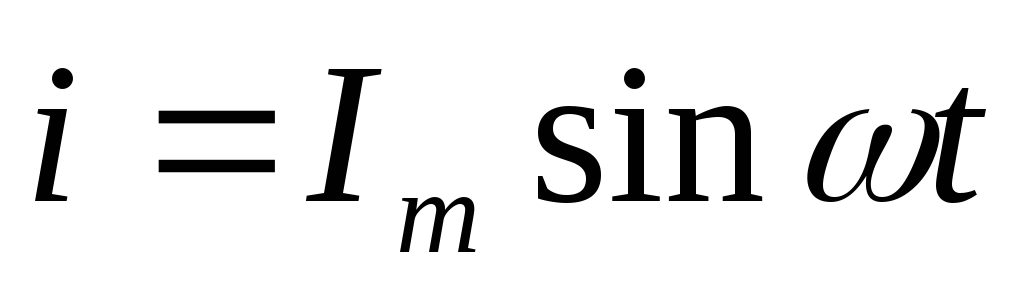 
— активная составляющая напряжения
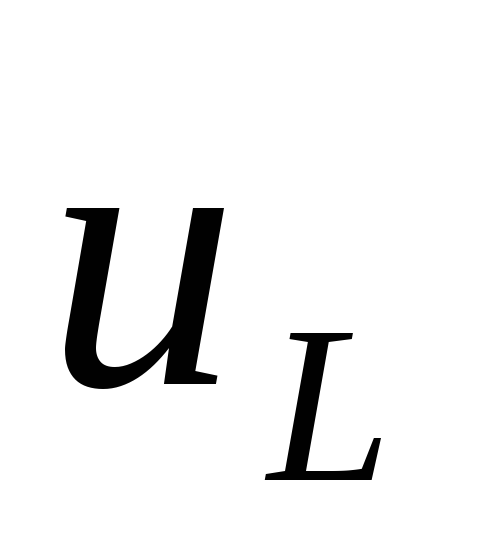— индуктивная составляющая напряжения
(Вместо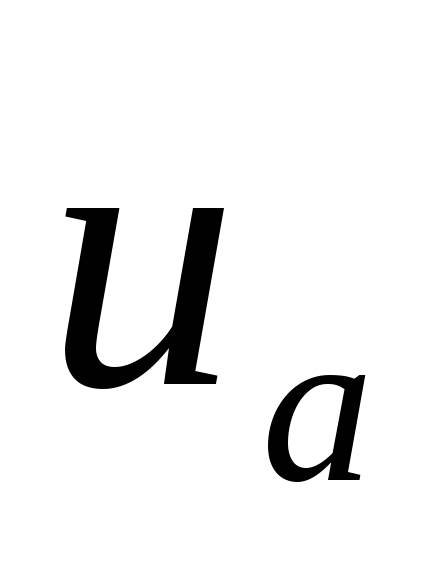 
можно писать
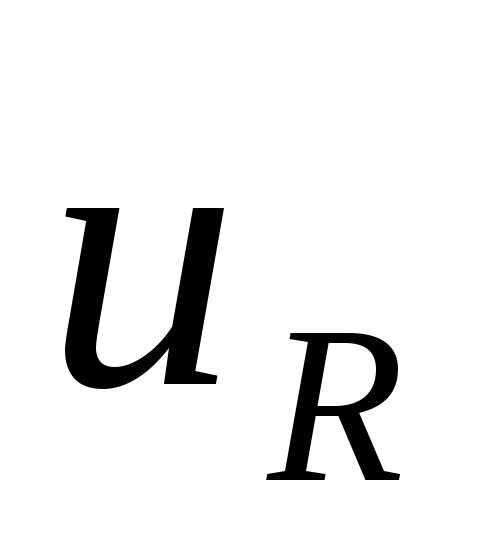— резистивная составляющая напряжения)
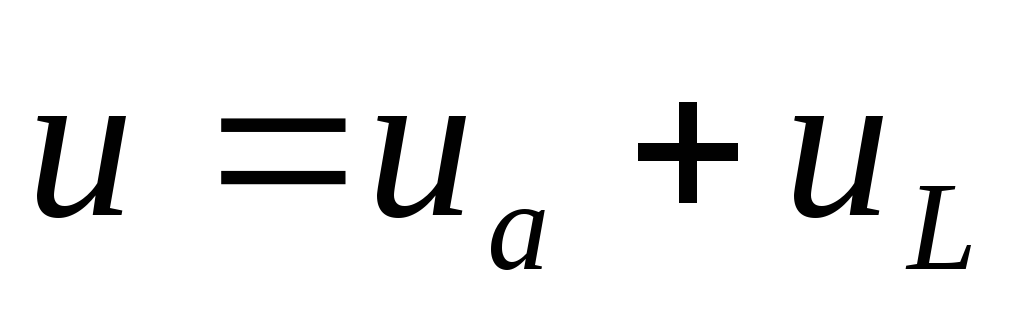
(формула справедлива для мгновенных, векторных и комплексных значений)
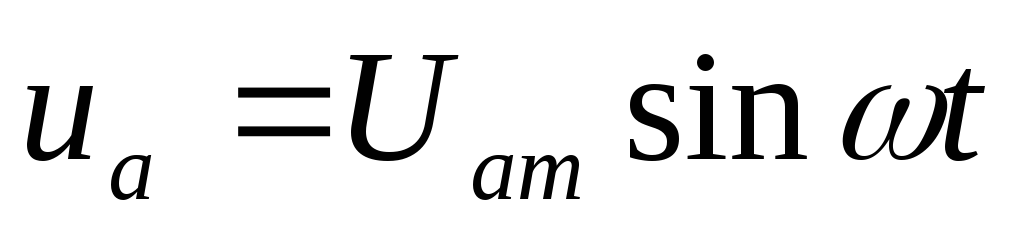
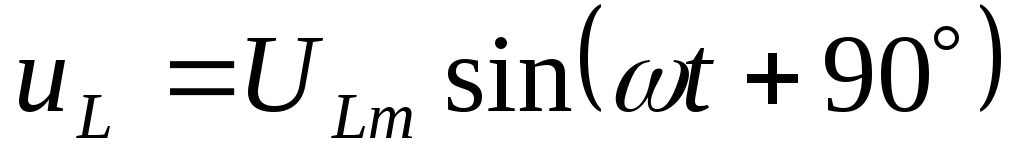
Сложим напряжения участков на векторной диаграмме:
В цепи RL напряжение
опережает ток на угол 
,
меньший 90°.
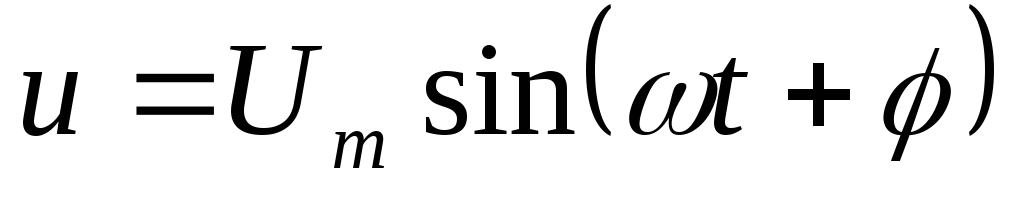
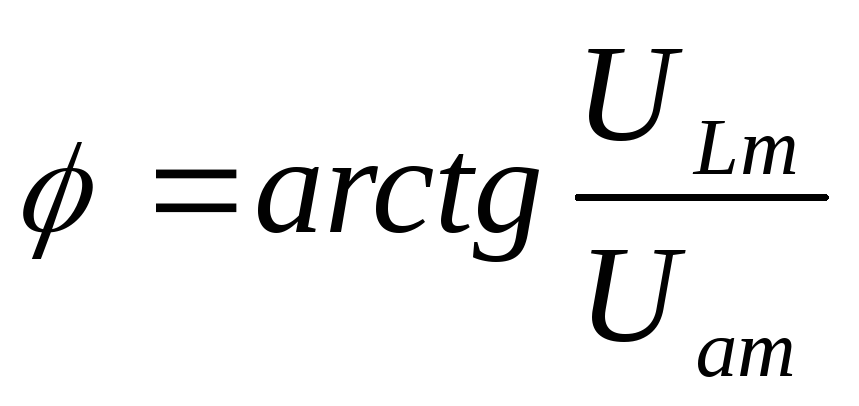
Закон Ома для цепи переменного тока. Мощность
В 2.3 были выведены соотношения, связывающие амплитуды переменных токов и напряжений на резисторе, конденсаторе и катушке индуктивности:
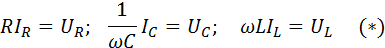
Эти соотношения во виду напоминают закон Ома для участка цепи постоянного тока, но только теперь в них входят не значения постоянных токов и напряжений на участке цепи, а амплитудные значения переменных токов и напряжений.
Соотношения (*) выражают закон Ома для участка цепи переменного тока, содержащего один из элементов R, L и C.
Физические величины R,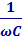 
и ωL называются активным сопротивлением резистора, емкостным сопротивлением конденсатора и индуктивным сопротивлением катушки.
При протекании переменного тока по участку цепи электромагнитное поле совершает работу, и в цепи выделяется джоулево тепло. Мгновенная мощность в цепи переменного тока равна произведению мгновенных значений тока и напряжения: p = J · u. Практический интерес представляет среднее за период переменного тока значение мощности
Здесь I0 и U0 – амплитудные значения тока и напряжения на данном участке цепи, φ – фазовый сдвиг между током и напряжением. Черта означает знак усреднения. Если участок цепи содержит только резистор с сопротивлением R, то фазовый сдвиг φ = 0:
Для того, чтобы это выражение по виду совпадало с формулой для мощности постоянного тока, вводятся понятия действующих или эффективных значений силы тока и напряжения:
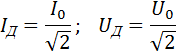
Средняя мощность переменного тока на участке цепи, содержащем резистор, равна
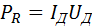
Если участок цепи содержит только конденсатор емкости C, то фазовый сдвиг между током и напряжением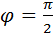 
. Поэтому
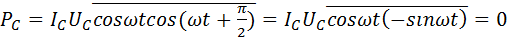
Аналогично можно показать, что PL = 0.
Таким образом, мощность в цепи переменного тока выделяется только на активном сопротивлении. Средняя мощность переменного тока на конденсаторе и катушке индуктивности равна нулю.
Рассмотрим теперь электрическую цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки. Цепь подключена к источнику переменного тока частоты ω. На всех последовательно соединенных участках цепи протекает один и тот же ток. Между напряжением внешнего источника e (t) и током J (t) возникает фазовый сдвиг на некоторый угол φ. Поэтому можно записать
J (t) = I0 cos ωt; e (t) = |
Такая запись мгновенных значений тока и напряжения соответствует построениям на векторной диаграмме (рис. 2.3.2). Средняя мощность, развиваемая источником переменного тока, равна
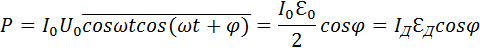
Как видно из векторной диаграммы, UR =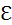 
0 · cos φ, поэтому
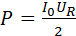. Следовательно, вся мощность, развиваемая источником, выделяется в виде джоулева тепла на резисторе, что подтверждает сделанный ранее вывод.
В 2.3 было выведено соотношение между амплитудами тока I0 и напряжения 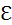0 для последовательной RLC-цепи:
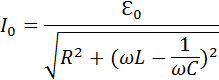
Величину
называют полным сопротивлением цепи переменного тока. Формулу, выражающую связь между амплитудными значениями тока и напряжения в цепи, можно записать в виде
ZI0 = | (**) |
Это соотношение называют законом Ома для цепи переменного тока. Формулы (*), приведенные в начале этого параграфа, выражают частные случаи закона Ома (**).
Понятие полного сопротивления играет важную роль при расчетах цепей переменного тока. Для определения полного сопротивления цепи во многих случаях удобно использовать наглядный метод векторных диаграмм. Рассмотрим в качестве примера параллельный RLC-контур, подключенный к внешнему источнику переменного тока (рис. 2.4.1).
|
Рисунок 2.4.1. Параллельный RLC-контур |
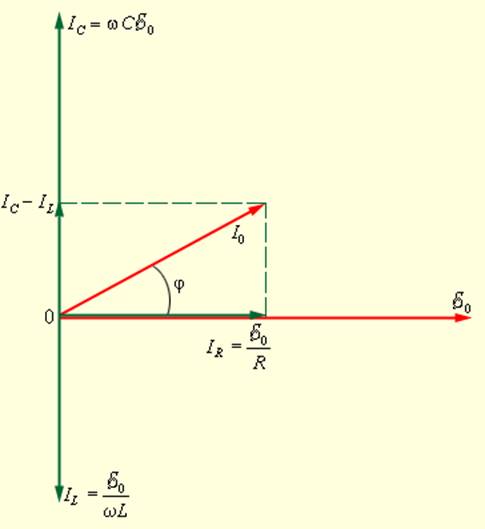
При построении векторной диаграммы следует учесть, что при параллельном соединении напряжение на всех элементах R, C и L одно и то же и равно напряжению внешнего источника. Токи, текущие в разных ветвях цепи, отличаются не только по значениям амплитуд, но и по фазовым сдвигам относительно приложенного напряжения. Поэтому полное сопротивление цепи нельзя вычислить по законам параллельного соединения цепей постоянного тока. Векторная диаграмма для параллельного RLC-контура изображена на рис. 2.4.2.
|
Рисунок 2.4.2. Векторная диаграмма для параллельного RLC-контура |
Из диаграммы следует:
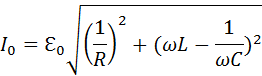
Поэтому полное сопротивление параллельного RLC-контура выражается соотношением
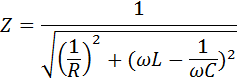
При параллельном резонансе (ω2 = 1 / LC) полное сопротивление цепи принимает максимальное значение, равное активному сопротивлению резистора:
Фазовый сдвиг φ между током и напряжением при параллельном резонансе равен нулю.
Проверка закона ома для переменного тока
Министерство образования РФ
ВОСТОЧНО-СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра физики
Лабораторная работа № 2.
Магнетизм
Улан-Удэ 2001
Контрольные вопросы
1. Как формулируется закон Ома ?
2. Что называется индуктивным сопротивлением катушки, емкостным сопротивлением конденсатора, от чего они зависят ? Как находят полное сопротивление цепи при последовательном и параллельном соединении R, L, C ?
3. Как экспериментально в работе проверяется R и L катушки, емкость С конденсатора ?
Литература: Савельев И.В. Курс общей физики т.2.
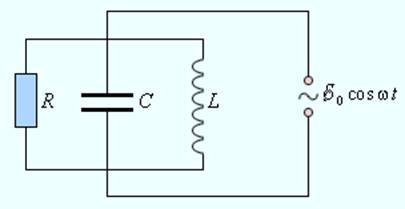
Часть IV. Проверка закона Ома при параллельном соединении катушки и конденсатора
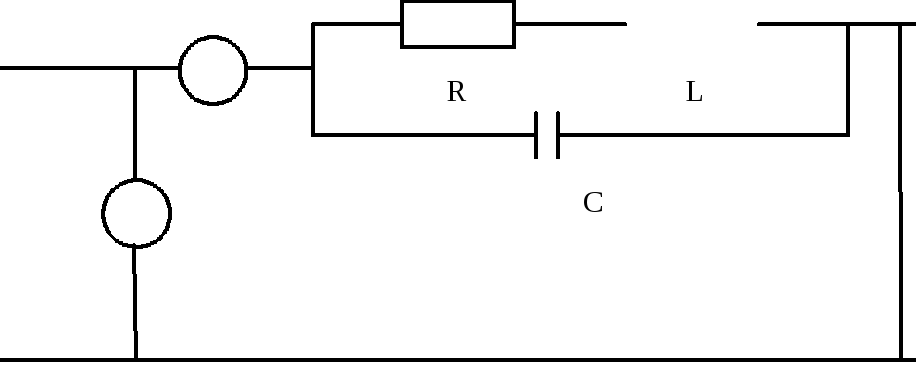
Рис. 6. Электрическая схема.
Для параллельного соединения катушки и конденсатора (рис. 6) полное сопротивление Z согласно формуле (8) можно записать
, 
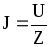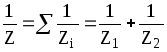(21)
, 
,
, 
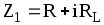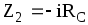
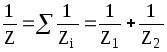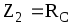
Модуль полного комплексного сопротивления Z в приближенной форме запишется
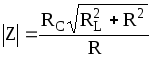(22)
так как в нем опущены слагаемые, величина которых мала.
Экспериментальное значение Z определяют как и в других случаях, измеряя ток и напряжение. Вычислив экспериментальное значение Z, сравнивают его со значением, рассчитанным по формуле (22).
Лабораторная работа № 2.
Проверка закона ома для переменного тока
Цель работы: 1. Определить омическое R и индуктивное RL
сопротивление катушки;
2. Емкостное сопротивление RС конденсатора;
3. Проверить закон Ома для переменного тока
с различными элемента цепи.
Приборы и принадлежности:
1. Катушка индуктивности;
2. Конденсатор;
3. Многопредельный амперметр;
4. Вольтметр;
5. Источник питания.
Краткая теория
Электрические цепи переменного тока нельзя описать методами, которые используются для цепей постоянного тока. Для их описания необходимо исходить из того, что в более совершенных физических теориях сохраняется вид физических законов, изменяется лишь представление физических величин, связь между которыми устанавливают эти законы. Поэтому закон Ома постоянного и переменного тока записывается одинаково. Вопрос в другом, как должны быть представлены физические величины, которые входят в этот закон. В современной физике хорошо разработано представление физических величин, которые, как правило, изображаются или комплектными числами, или векторами в п — мерном векторном пространстве, или операторами, или матрицами. Для переменного тока достаточно использование комплексной плоскости, где скалярные физические величины — сила тока, напряжение, сопротивление, эдс — представлены точками, которым соответствуют радиусы — векторы на этой плоскости, поэтому необходимо знание операций сложения, умножения, деления комплексных чисел и их геометрической интерпретации.
Рассмотрим, как изменяется ток в цепи, где имеется омическое сопротивление R (рис.1а), индуктивность L (рис. 1б) и емкость С (рис. 1в).
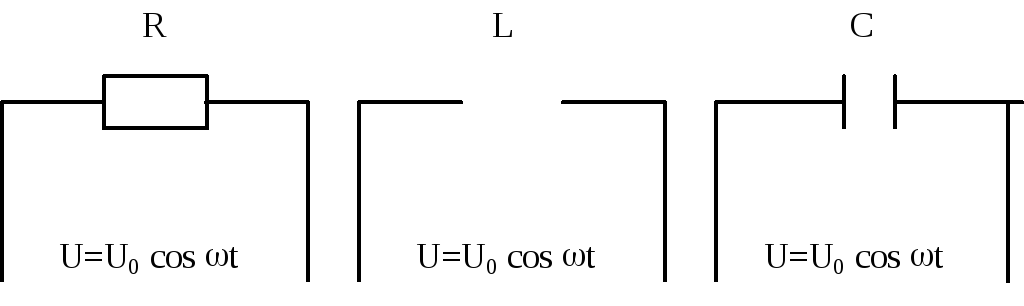
а) б) в)
Рис. 1. Омическое сопротивление, индуктивность
и емкость в цепи переменного тока.
Для цепи с омическим сопротивлением R (рис. 1а) имеем
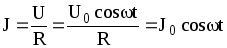(1)
где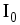 
—
амплитудное значение тока, равное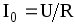 
.
В цепи с индуктивностью L переменный магнитный поток наводит в катушке индукционный ток, направленный против основного тока, уменьшая его. Поэтому катушку индуктивности можно рассматривать как некоторое сопротивление, которое называется индуктивным RL. Найдем закон изменения тока I и величину индуктивного сопротивления (рис. 1б).
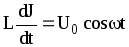
(2)
Интегрируя (2), получаем
(3)
где R=wL (4)
— индуктивное сопротивление катушки.
Конденсатор С в цепи переменного тока (рис. 1в) периодически перезаряжается, в цепи проходит ток, величина которого зависит от частоты w и емкости С
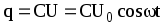
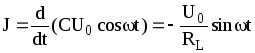(5)
, 
, 
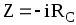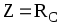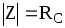(17)
22 Электрический ток в цепи последовательно соединенных конденсаторов, резисторов!закон ома для учаска цепи
у конденсаторов существует 2 вида соединения:последовательное и паралельное
последовательное сопротивления-в этом случае обкладка одного конденсатора,
соединена с обкладкой другого конденсатора,заряженного положительно.
величина,обратная емкости батареи конденсаторов при последовательном соединении,равна сумме величин,обратных емкостям отдельных
конденсаторов.:1/c=1/c1+1/c2+1/c3+…при этом типе соединения емкость ботореи конденсаторов меньше емкости любого из конденсаторов.
Последовательное соединение резисторов. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго,
конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит один и тот же ток I.
закон ома для учаска цепи
Величина тока на участке цепи прямо пропорциональна напряжению приложенному к этому участку и обратно пропорциональна его сопротивлению.
I=U/R
I-сила тока,U-напряжение,R-сопротивления
23!Законы Кирхгофа!определения
ЗАКОНЫ КИРХГОФА, два правила, основанные на законах сохранения заряда и энергии, которые применимы к цепям электрического тока. По сути, они гласят что (1) ни в какой точке сети не может происходить ни накопления, ни убыли электрического заряда; и (2) во всяком замкнутом контуре сумма ЭЛЕКТРОДВИЖУЩИХ СИЛ равна сумме РАЗНОСТИ ПОТЕНЦИАЛОВ на каждом участке сопротивления.
СуммаI=0 первый закон
Сумма E+суммаIR-второй закон
Вопрос 24.Назночение конструкция применения интегральных микросхем
делится на гибридное и полупроводниковые
гибридное:
на основе тонких и толстых пленок посивных элементы формируются в пленки.
а-активные в виде полупроводниковых приборов размещающихся под пленкой
собраную гибридную м.с заключают в металический корпус.Изолирующий ее от внешних воздействий контактных вывода размещаются в определенном порядки.
гибридные делятся на:
толстопленочные и тонкопленочные
к тонкопленочным от 10 до 100доли мкм
применяют различные маталлы-аллюминий,медь,серебро,золото,никиль,хром,олово итд!наносятся тонкой пленкой,вакумным напылением итд
к толстопленочным относится менее 1 мкм
поста ,трафорет,подложка!достоинства недорогая
к полупроводниковым : изготовляется на одном кристале введением примесей в определенные микро обмотки основной полупроводниковой схемы
25Конденсаторы.Электрическая емкость конденсатора,единица измерения
ёмкость, это количественная характеристика, отражающая способность какого либо транспортного объекта размещать в себе транспортируемое вещество. Ещё проще, ёмкость — это вместительность.
еденица измерения
Емкость измеряется в Фарадах. Эта единица измерения пошла из классики и связана с Кулоновским «электрическим зарядом». В классической электротехнике принято считать, что электрическая ёмкость в 1 фарад соответствует конденсатору,
заряженному электрическим зарядом в 1 кулон при разности потенциалов на его обкладках в 1 вольт. Но, поскольку мы знаем, что электрических зарядов не существует, больше мы данной классической формулировкой пользоваться не будем.
Стоит только знать, что ёмкость конденсатора напрямую зависит от количества электронов, которые он способен накопить в нормальном режиме работы. С одной стороны Фарады можно было бы поменять на мегаэлектроны, или, например,
гигаэлектроны, но мы этого делать не станем, поскольку Фарад принципиально отражает ту же самую ёмкость, только трактуется немного иначе, и на расчёты электрических параметров схем влиять не будет.
Электрический конденсатор — электротехническое устройство, предназначенное для быстрого накопления, хранения и отдачи электрической энергии. В электронике и электротехнике имеет самое разнообразное целевое назначение.
В мощных энергетических системах электроснабжения используются для компенсации реактивной мощности, генерируемой индуктивностью протяжённых линий электропередач. В различных электротехнических решениях конденсаторы
применяют для смещения фазы напряжения или тока, поглощения высокочастотных гармоник питающего переменного напряжения, снижения уровня пульсаций по постоянному напряжению в блоках питания бытовой и промышленной электроники,
фильтрации сигнала, в качестве времязадающих цепей, и для многого другого.
Контрольные вопросы
1. Записать выражение закона Ома для цепи с последовательным соединением конденсатора и индуктивной катушки. Чему равны полное сопротивление цепи и коэффициент мощности cos ?
I=U/Z
Коэффициент мощности cosφ при резонансе напряжений равен единице.
Cosφ=P/s= UR/U
2. Условие, признак и применение резонанса напряжений. В каком случае резонанс напряжений вреден? Почему?
Режим, при котором в цепи с последовательным соединением индуктивного и емкостного элемента напряжение на входе совпадает по фазе с током, резонанс напряжения.
внезапное возникновение резонансного режима в цепях большой мощности может вызывать аварийные ситуацию, привести к пробою изоляции проводов и кабелей и создать опасность для персонала.
3. Какими способами можно достичь резонанса напряжений?
При подключении колебательного контура, состоящего из катушки индуктивности и конденсатора, к источнику энергии могут возникнуть резонансное явление. Возможны два основных типа резонанса: при последовательном соединение катушки и конденсатора- резонанс напряжений, при их параллельном соединении- резонансов токов.
4. Почему при резонансе напряжений U2>U1?
Где R – активное сопротивление
I – сила тока
XL – индуктивное сопротивление катушки
XC – емкостное сопротивление конденсатора
Z – полное сопротивление переменного тока
При резонансе: UL = UС,
Где UС – напряжение катушки,
UL – напряжение конденсатора
Напряжение можно найти:
U=UR+UL+UC =>U=UR,
Где UR – напряжение катушки, к которой подключен вольтметр V2, значит напряжение V2=V1
5. Какова особенность резонанса напряжений? Объяснить ее.
Следовательно, режим резонанса может быть достигнут изменением индуктивности катушки L, емкости конденсата С или частоты входного напряжения ω.
6. Записать выражение закона Ома через проводимости для цепи с параллельным соединением конденсатора и индуктивной катушки. Чему равна полная проводимость?
Закон Ома через проводимости для цепи переменного тока с параллельным соединение ветвей.
7. Условие, признак и применение резонанса токов.
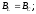
т.е равенство индуктивной и емкостной проводимостей.
8. Какими способами можно достичь резонанса токов?
Режим, при котором в цепи, содержащей параллельное ветви с индуктивным и емкостным элементами, ток неразветвленного участка цепи совпадает по фазе с напряжением , резонансом токов.
9. Почему при резонансе токов I2>I1?
Потому что, исходя из векторной диаграммы токов при резонансе график будет представлять собой прямоугольный треугольник, где токи I и I1 будут являться катетами, а ток I2 – гипотенузой. Следовательно, и I2 будет больше чем I1.
10. Какова особенность резонанса токов? Объяснить ее.
При резонансе токов токи в ветвях значительно больше тока неразветвленной части цепи. Это свойство-усилие тока- является важнейшей особенностью резонанса токов.
11. Объяснить построение векторных диаграмм.
Целью ее построения является определение активной и реактивной составляющих напряжения на катушке и угла сдвига фаз между напряжением на входе цепи и током
Расчеты
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. — B 3-х кн.: кн.1 /В. Г. Герасимов и др.; Под ред. В. Г. Герасимова. М.: Энергоатомиздат, 1996. – 288 с.
Касаткин А. С., Немцов М. В. Электротехника. М.: Высш. шк., 1999. – 542 с.
Электротехника /Под ред. Ю. Л. Хотунцева. М.: АГАР, 1998. – 332с.
Борисов Ю. М., Липатов Д. Н., Зорин Ю. Н. Электротехника. Энергоатомиздат, 1985. – 550 с.
ГОСТ 19880-74. Электротехника. Основные понятия. Термины и определения. М.: Издательство стандартов, 1974.
ГОСТ 2.710-81 ЕСКД. Обозначения буквенно-цифренные в электрических схемах.
Открытая Физика. Закон Ома для цепи переменного тока. Мощность
В § 2.3 были выведены соотношения, связывающие амплитуды переменных токов и напряжений на резисторе, конденсаторе и катушке индуктивности: RIR=UR; 1ωCIC=UC; ωLIL=UL.
Эти соотношения во виду напоминают закон Ома для участка цепи постоянного тока, но только теперь в них входят не значения постоянных токов и напряжений на участке цепи, а амплитудные значения переменных токов и напряжений.
Соотношения (*) выражают закон Ома для участка цепи переменного тока, содержащего один из элементов R, L и C. Физические величины R, 1ωC и ωL называются активным сопротивлением резистора, емкостным сопротивлением конденсатора и индуктивным сопротивлением катушки.
При протекании переменного тока по участку цепи электромагнитное поле совершает работу, и в цепи выделяется джоулево тепло. Мгновенная мощность в цепи переменного тока равна произведению мгновенных значений тока и напряжения: p = J ċ u. Практический интерес представляет среднее за период переменного тока значение мощности P=Pср=I0 U0cosωtcos(ωt+φ)¯.
Здесь I0 и U0 – амплитудные значения тока и напряжения на данном участке цепи, φ – фазовый сдвиг между током и напряжением. Черта означает знак усреднения. Если участок цепи содержит только резистор с сопротивлением R, то фазовый сдвиг φ = 0: PR=IRURcos2ωt¯=IRUR2=IR2R2.
Для того, чтобы это выражение по виду совпадало с формулой для мощности постоянного тока, вводятся понятия действующих или эффективных значений силы тока и напряжения: Iд=I02; Uд=U02.
Средняя мощность переменного тока на участке цепи, содержащем резистор, равна PR=IдUд.
Если участок цепи содержит только конденсатор емкости C, то фазовый сдвиг между током и напряжением φ=π2. Поэтому PC=ICUCcosωtcos(ωt+π2)¯=ICUCcosωt( -sin ωt)¯=0.
Аналогично можно показать, что PL = 0.
Таким образом, мощность в цепи переменного тока выделяется только на активном сопротивлении. Средняя мощность переменного тока на конденсаторе и катушке индуктивности равна нулю.
Рассмотрим теперь электрическую цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки. Цепь подключена к источнику переменного тока частоты ω. На всех последовательно соединенных участках цепи протекает один и тот же ток. Между напряжением внешнего источника e (t) и током J (t) возникает фазовый сдвиг на некоторый угол φ. Поэтому можно записать J (t) = I0 cos ωt; e (t) = ℰ0 cos (ωt + φ).
Такая запись мгновенных значений тока и напряжения соответствует построениям на векторной диаграмме (рис. 2.3.2). Средняя мощность, развиваемая источником переменного тока, равна P=I0ℰ0cosωtcos(ωt+φ)¯=I0ℰ02cosφ=Iдℰдcosφ.
Как видно из векторной диаграммы, UR = ℰ0 · cos φ, поэтому P=I0UR2. Следовательно, вся мощность, развиваемая источником, выделяется в виде джоулева тепла на резисторе, что подтверждает сделанный ранее вывод.
В § 2.3 было выведено соотношение между амплитудами тока I0 и напряжения ℰ0 для последовательной RLC-цепи: I0=ℰ0R2+(ωL-1ωC)2.
Величину Z=R2+(ωL-1ωC)2 называют полным сопротивлением цепи переменного тока. Формулу, выражающую связь между амплитудными значениями тока и напряжения в цепи, можно записать в виде ZI0 = ℰ0.
Это соотношение называют законом Ома для цепи переменного тока. Формулы (*), приведенные в начале этого параграфа, выражают частные случаи закона Ома (**).
Понятие полного сопротивления играет важную роль при расчетах цепей переменного тока. Для определения полного сопротивления цепи во многих случаях удобно использовать наглядный метод векторных диаграмм. Рассмотрим в качестве примера параллельный RLC-контур, подключенный к внешнему источнику переменного тока (рис. 2.4.1).
При построении векторной диаграммы следует учесть, что при параллельном соединении напряжение на всех элементах R, C и L одно и то же и равно напряжению внешнего источника. Токи, текущие в разных ветвях цепи, отличаются не только по значениям амплитуд, но и по фазовым сдвигам относительно приложенного напряжения. Поэтому полное сопротивление цепи нельзя вычислить по законам параллельного соединения цепей постоянного тока. Векторная диаграмма для параллельного RLC-контура изображена на рис. 2.4.2.
Из диаграммы следует: I0=ℰ0(1R)2+(ωL-1ωC)2.
Поэтому полное сопротивление параллельного RLC-контура выражается соотношением Z=1(1R)2+(ωL-1ωC)2.
При параллельном резонансе (ω2 = 1 / LC) полное сопротивление цепи принимает максимальное значение, равное активному сопротивлению резистора: Z = Zmax = R.
Фазовый сдвиг φ между током и напряжением при параллельном резонансе равен нулю.
