ЗАКОНЫ Кирхгофа
Получите недорогой доступ к TINACloud для редактирования примеров или создания собственных схем
Многие схемы слишком сложны, чтобы их можно было решить, используя правила для последовательных или параллельных схем или методы преобразования в более простые схемы, описанные в предыдущих главах. Для этих схем нам нужны более общие методы решения. Наиболее общий метод дается законами Кирхгофа, которые позволяют вычислять все напряжения и токи цепей по решению системы линейных уравнений.
Есть два Законы Кирхгофа, закон напряжения И текущий закон. Эти два закона могут быть использованы для определения всех напряжений и токов в цепях.
Закон напряжения Кирхгофа (KVL) гласит, что алгебраическая сумма повышений напряжения и падений напряжения вокруг контура должна быть равна нулю.
Цикл в вышеприведенном определении означает замкнутый путь в цепи; то есть путь, который покидает узел в одном направлении и возвращается к тому же узлу из другого направления.
В наших примерах мы будем использовать направление по часовой стрелке для циклов; однако те же результаты будут получены при использовании направления против часовой стрелки.
Для применения KVL без ошибок, мы должны определить так называемое опорное направление. Опорное направление неизвестного напряжения от точки к + — знак предполагаемых напряжений. Представьте себе использование вольтметра. Вы положили бы положительный пробник вольтметра (обычно красный) на клемму + опоры компонента. Если реальное напряжение положительное, оно в том же направлении, что и мы, и наше решение, и вольтметр покажут положительное значение.
При выводе алгебраической суммы напряжений, мы должны присвоить знак плюс к тем напряжениям, где опорное направление совпадает с направлением петли, и отрицательными знаками в противоположном случае.
Другой способ сформулировать закон напряжения Кирхгофа состоит в том, что приложенное напряжение последовательной цепи равно сумме падений напряжения на последовательных элементах.
Следующий короткий пример показывает использование закона напряжения Кирхгофа.
Найти напряжение на резисторе R2, учитывая, что напряжение источника, ВS = 100 В и это напряжение на резисторе R1 это V1 = 40 V.
Рисунок ниже может быть создан с помощью TINA Pro версии 6 и выше, в которой инструменты рисования доступны в редакторе схем.
Решение с использованием закона напряжения Кирхгофа: -VS + V1 + V2 = 0 или VS V =1 + V2
следовательно: V2 V =S — V1 = 100-40 = 60V
Обратите внимание, что обычно мы не знаем напряжения резисторов (если мы не измеряем их), и нам нужно использовать оба закона Кирхгофа для решения.
Текущий закон Кирхгофа (KCL) гласит, что алгебраическая сумма всех токов, входящих и выходящих из любого узла в цепи, равна нулю.
Далее мы даем знак + токам, выходящим из узла, и знак — токам, входящим в узел.
Вот основной пример, демонстрирующий действующий закон Кирхгофа.
Найти тока я2 если источник тока IS = 12 A, и я1 = 8 A.
Используя текущий закон Кирхгофа в обведенном узле: -IS + Я1 + Я2 = 0, следовательно: I2= ЯS — Я1 = 12 — 8 = 4 A, как вы можете проверить с помощью TINA (следующий рисунок).
В следующем примере мы будем использовать как законы Кирхгофа, так и закон Ома, чтобы рассчитать ток и напряжение на резисторах.
На рисунке ниже вы заметите Напряжение Стрелка выше резисторы. Это новый компонент, доступный в Версия 6 TINA и работает как вольтметр. Если подключить его через компонент, стрелка определяет опорное направление (сравнить с вольтметром, представьте размещения красного щупа в хвосте стрелки, а черный зонд на конце).
При запуске анализа постоянного тока фактическое напряжение на компоненте будет отображаться на стрелке.
Чтобы начать использовать текущий закон Кирхгофа, мы видим, что токи через все компоненты одинаковы, поэтому давайте обозначим этот ток через I.
Согласно закону напряжения Кирхгофа: VS V =1+V2+V3
Теперь используя закон Ома: VS= I * R1+ I * R2+ I * R3
И отсюда ток цепи:
I = VS /(Р1+R2+R3) = 120 / (10 + 20 + 30) = 2 A
Наконец напряжения на резисторах:
V1= I * R1 = 2 * 10 = 20 V; V2 = I * R2 = 2 * 20 = 40 V; V3 = I * R3 = 2 * 30 = 60 V
Те же результаты можно увидеть на стрелках напряжения, просто запустив интерактивный анализ постоянного тока TINA.
Общее количество независимых применений законов Кирхгофа в цепи — это число ветвей цепи, а общее количество неизвестных (ток и напряжение каждой ветви) вдвое больше. Тем не менее, также используя закон Ома на каждом резисторе и Из простых уравнений, определяющих приложенные напряжения и токи, мы получаем систему уравнений, где число неизвестных совпадает с числом уравнений.
Найти токи ветвления I1, I2, I3 в схеме ниже.
Система уравнений выглядит следующим образом:
Узловое уравнение для обведенного узла:
– I1 – I2 — Я3 = 0
или умножение на -1
I1 + I2 + Я3 = 0
Уравнения цикла (с использованием направления по часовой стрелке) для цикла L1, содержащего V1, R1 и R3
-V1+I1*R1-I3*R3 = 0
и для цикла L2, содержащего V2, R2 и R3
I3*R3 — Я2*R2 +V2 = 0
Подставляя значения компонентов:
I1+ Я2+ Я3 = 0 -8 + 40 * I1 — 40 * I3 = 0 40 * I3 -20 * I2 + 16 = 0
Экспресс я1 используя узловое уравнение: I1 = -Я2 — Я3
затем подставьте его во второе уравнение:
-V1 — (Я2 + Я3)*Р1 -Я3*R3 = 0 or –8- (я2 + Я3) * 40 — я3* 40 = 0
Экспресс я2 и подставим его в третье уравнение, из которого вы уже можете рассчитать I3:
I2 = — (V1 + Я3*(Р1+R3))/Р1 or I2 = — (8 + I3* 80) / 40
I3*R3 + R2* (V1 + Я3*(Р1+R3))/Р1 +V2 = 0 or I3* 40 + 20 * (8 + I3* 80) / 40 + 16 = 0
А также: I3 = — (V2 + V1*R2/R1)/(Р3+ (R1+R3)*Р2/R1) or I3 = -(16+8*20/40)/(40 + 80*20/40)
Поэтому I3 = — 0.
25 А; I2 = — (8-0.25 * 80) / 40 = 0.3 A и I1 = — (0.3-0.25) = — 0.05 А
Или: I1 = -50 мА; I2 = 300 мА; I3 = -250 мА.
Теперь давайте решим те же уравнения с интерпретатором TINA:
| {Решение переводчика TINA} Sys I1, I2, I3 I1 + I2 + I3 = 0 -V1+I1*R1-I3*R3=0 I3*R3-I2*R2+V2=0 конец; I1 = [- 50m] I2 = [300m] I3 = [- 250m] |
Наконец, давайте проверим Результаты с использованием TINA:
Далее, давайте проанализируем следующую, еще более сложную схему и определим ее ответвления токами и напряжениями.
Обозначим неизвестные напряжения и токи, добавив стрелки напряжения и тока к компонентам, а также покажем петли (L1, L2, L3) и узлы (N1, N2), где мы будем использовать уравнения Кирхгофа.
Вот набор Уравнения Кирхгофа для петель (с использованием направления по часовой стрелке) и узлов.
-IL + ЯR1 — Яs = 0(для N1)
— ЯR1 + ЯR2 + Яs3 = 0 (для N2)
-Vs1 — VR3 + VIs + VL = 0 (для L1)
-VIs + Vs2 +VR2 +VR1 = 0 (для L2)
-VR2 — Vs2 + Vs3 = 0 (для L3)
Применяя закон Ома:
VL = ЯL*RL
VR1 =IR1*R1
VR2 = ЯR2*R2
VR3 = — ЯL*R3
Это 9 неизвестных и 9 уравнений. Самый простой способ решить эту проблему — использовать TINA.
переводчик. Однако, если мы вынуждены использовать ручные вычисления, отметим, что этот набор уравнений может быть легко сведен к системе из 5 неизвестных путем подстановки последних 4 уравнений в уравнения цикла L1, L2, L3.
Кроме того, добавив уравнения (L1) и (L2), мы можем устранить VIs , сводя задачу к системе уравнений 4 для неизвестных 4 (IL, IR1 IR2, Is3). Когда мы нашли эти токи, мы можем легко определить VL, VR1, VR2, и VR3 используя последние четыре уравнения (закон Ома).
Подставляя VL ,VR1,VR2 ,VR3 :
-IL + ЯR1 — Яs = 0(для N1)
— ЯR1 + ЯR2 + Яs3 = 0 (для N2)
-Vs1 + ЯL*R3 + VIs + ЯL*RL = 0 (для L1)
-VIs + Vs2 + ЯR2*R2 + ЯR1*R1 = 0 (для L2)
— ЯR2*R2 — Vs2 + Vs3 = 0 (для L3)
Добавляя (L1) и (L2) мы получаем
-IL + ЯR1 — Яs = 0(для N1)
— ЯR1 + ЯR2 + Яs3 = 0 (для N2)
-Vs1 + ЯL*R3 + ЯL*RL + Vs2 + ЯR2*R2 + ЯR1*R1 = 0 (L1) + (L2)
— ЯR2*R2 — Vs2 + Vs3 = 0 (для L3)
После подстановки значений компонентов решение этих уравнений приходит легко.
-IL+IR1 — 2 = 0 (для N1)
-IR1 + ЯR2 + ЯS3 = 0 (для N2)
-120 — + ЯL* 90 + IL* 20 + 60 + IR2* 40 + IR1* 30 = 0 (л1) + (л2)
-IR2* 40 — 60 + 270 = 0 (для L3)
от L3 IR2 = 210 / 40 = 5.25 A (I)
из N2 IS3 — ЯR1 = — 5.25 (II),
от L1+L2 110 IL + 30 IR1 = -150 (III),
и для N1 IR1 — ЯL = 2 (IV)
Умножьте (IV) на –30 и добавьте к (III) 140 IL = -210 следовательно IL = — 1.5 А
Заменить яL в (IV) IR1 = 2 + (-1.5) = 0.5 A
и яR1 в (II), IS3 = -5.25 + IR1 = -4,75 A
И напряжения: VR1 = ЯR1*R1 = 15 V; VR2 = ЯR2*R2 = 210 V;
VR3 = — ЯL*R3= 135 V; VL = ЯL*RL = — 30 В; VIs V =S1+VR3-VL = 285 V
{Решение исходных уравнений интерпретатором TINA} |
5] Решение приведенной системы уравнений с использованием интерпретатора:
| {Решение сокращенной системы уравнений интерпретатором TINA} Sys Il, Ir1, Ir2, Is3 -Il + Ir1-2 = 0 -Ir1 + Ir2 + Is3 = 0 -120+110*Il+60+40*Ir2+30*Ir1=0 -40 * Ir2 + 210 = 0 конец; Ил = [- 1.5] Ir1 = [500m] Ir2 = [5.25] Is3 = [- 4.75] |
Мы также можем ввести выражения для напряжений и заставить интерпретатора TINA рассчитать их:
| Il: = — 1.5; Ir1: = 0.5; Ir2: = 5.25; Is3: = — 4.75; Вл: = Il * RL; Vr1: = Ir1 * R1 Vr2: = Ir2 * R2; Vr3: = — Il * R3; ВП: = Vs1-Vl + Vr3; Vl = [- 30] Vr1 = [15] Vr2 = [210] Vr3 = [135] = ВП [285] |
Мы можем проверить результат с TINA, просто включив интерактивный режим постоянного тока TINA или используя Анализ / Анализ постоянного тока / Узловое напряжение
ТЕОРЕМА СУПЕРПОЗИЦИИУЗЕЛ ПОТЕНЦИАЛЬНЫЙ МЕТОД
Моделирование в электроэнергетике — Расчет электрической цепи.
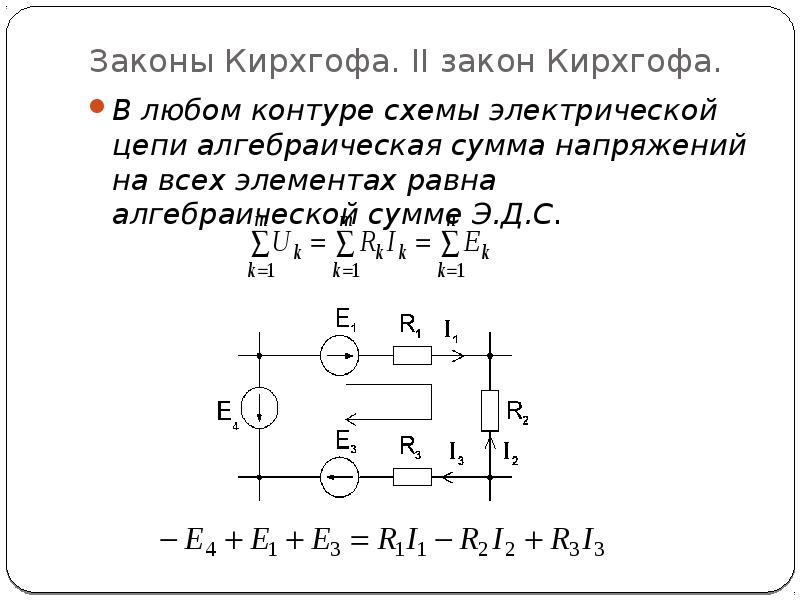Первый и второй законы Кирхгофа. Метод контурных токов и метод узловых потенциалов.Электрическая цепь представляет собой совокупность электрических элементов (резисторов, катушек индуктивностей, батарей конденсаторов, постоянные и переменные источники напряжения и т.д.), которые соединены между собой таким образом, что в полученном замкнутом контуре протекает электрический ток.
Для определения действующих (или мгновенных) значений токов и падений напряжений на элементах электрической цепи необходимо выполнить следующую последовательность действий:
- Этап 1.Составитьсхему замещения электрической цепи, в которой реальные элементы заменяются идеализированными элементами электрической цепи (активное сопротивление, индуктивность, емкость, ЭДС и т.д.).
- Этап 2.Обозначить на схеме замещения условно положительное направление токов в ветвях и падение напряжения на элементах расчетной схемы замещения.
- Этап 3.Записать систему уравнений, которая связывает напряжения и токи, по одному из следующих способов:
– 1-ого и 2-ого закона Кирхгофа;
– метод контурных токов;
– метод узловых потенциалов.
Каждый из представленных методов позволяет получить необходимый результат, но при разном количестве записанных уравнений в исходной системе уравнений. Следует отметить, что данные методы справедливы как для мгновенных значений токов и напряжений, так и для векторных переменных токов и напряжений.
- Этап 4.Выполнить расчет записанной системы уравнений и определить величины напряжения, токов,перетоков активной и реактивной мощности в ветвях расчетной схемы.
Составление системы уравнений, используя первый и второй закон Кирхгофа.
Первый и второй законы Кирхгофа обеспечивают связь между токами и напряжениями на участках любой электрической цепи. Впервые законы были сформулированы Густавом Кирхгофом в 1845 году. Данные законы вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (третье уравнение Максвелла при неизменном магнитном поле).
Первый закон Кирхгофа — алгебраическая сумма токов в каждом узле расчетной схемы равна нулю. Данное утверждение справедливо как для мгновенных значений, так и для векторных значений.
где p – количество ветвей, которые присоединены к рассматриваемому узлу расчетной схемы.
При составлении уравнений согласно первому закону Кирхгофа со знаком «плюс» записываются токи, направленные к узлу, а со знаком «минус» записываются токи, направленные от узла.
Формулировка данного закона может быть переписана в следующем виде: алгебраическая сумма токов, втекающих в узел расчетной схемы, равна алгебраической сумме токов, вытекающих из узла расчетной схемы.
Рис.1. Пояснение к первому закону Кирхгофа
Второй закон Кирхгофа — алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС действующих в этом контуре. Данное утверждение справедливо как для мгновенных значений, так и для векторных значений.
где n – число ветвей в замкнутом контуре;
m – число источников ЭДС.
При составлении уравнений согласно второму закону Кирхгофа со знаком «плюс» записываются падения напряжения (или ЭДС) направление которых совпадает с направлением обхода контура, а со знаком «минус» записываются падения напряжения (или ЭДС) направление которых противоположно направлению обхода контура
Рис.2. Пояснение ко второму закону Кирхгофа
В качестве примера рассмотрим расчетную схему замещению, которая состоит из двух источников ЭДС и трех сопротивлений.
Произвольно выберем положительные направления токов и падений напряжений во всех ветвях расчётной схемы, а также выберем направление обхода во всех контурах.
Рис.3. Расчетная схема замещения для пояснения первого и второго закона Кирхгофа.
Рассматриваемая схема замещения состоит из 2 узлов (q = 2) и 3 ветвей (p = 3). В соответствии с первым законом Кирхгофа можно записать одно уравнение (q – 1):
В соответствии со вторым законом Кирхгофа можно записать два уравнения (p – q + 1):
В результате была получена система уравнений, которая позволяет определить токи во всех ветвях расчетной схемы исходя из заданных значений ЭДС и сопротивлений.
Составление системы уравнений, используя
Метод контурных токов позволяет упростить расчет электрических цепей по сравнению с методом по первому и второму законам Кирхгофа за счет уменьшения числа уравнений.
Данный метод основан на применении второго закона Кирхгофа.
При выполнении расчета методом контурных токов необходимо выбрать одинаковое направление обхода в каждом рассматриваемом контуре (либо по часовой стрелке, либо против часовой стрелке). Далее в соответствии с данным методом записывается система уравнений относительно контурных токов, которые протекают в каждом независимом контуре, используя следующие правила:
Правило №1. В левой части i-го уравнения записываются:
— со знаком «+» записывается произведение контурного тока i-го контура на сумму сопротивлений всех звеньев, входящих в контур;
— со знаком «-» записывается остальные контурные токи, умноженные на суммы сопротивлений звеньев, по которым i-ый контур пересекается с этими контурами.
— ток i-го контура, для которого записывается уравнение;
— сопротивления звеньев, входящих в i-ый контур;
— токи соседних контуров, который пересекаются с
— сопротивления звеньев, по которым i-ый контур пересекается с другими контурами.
Правило №2. В правой части i-го уравнения записывается сумма источников ЭДС с учётом знаков («плюс» — если направления ЭДС и обхода контура совпадают, в противном случае – «минус»), а также добавляются источники тока, умноженные на сопротивление соответствующего звена с учётом знаков («плюс» — если направления источника тока и обхода контура совпадают, в противном случае – «минус»)
— источники ЭДС, которые входят в i-ый контур;
— произведение тока и сопротивление ветви с источником тока, которые входят в i-ый контур.
Заключительным этапом определяются токи во всех ветвях расчетной схемы по найденным значениям контурных токов.
В качестве примера рассмотрим расчетную схему замещению, которая состоит из двух источников ЭДС и трех сопротивлений. Произвольно выберем положительные направления обхода в каждом рассматриваемом контуре: направление по часовой стрелке.
Рис.4. Расчетная схема замещения для пояснения метода контурных токов.
Рассматриваемая схема замещения состоит из 2 узлов (q = 2) и 3 ветвей (p = 3), таким образом, в расчетной схеме замещения можно выделить два независимых контура. В соответствии с методом контурных токов можно записать два уравнения (p – q + 1):
В результате была получена система уравнений, которая позволяет определить контурные токи исходя из заданных значений ЭДС и сопротивлений. Заключительным этапом расчета будет являться процесс определения токов во всех ветвях расчетной схемы по найденным значениям контурных токов.
Составление системы уравнений, используя метод узловых потенциалов
Метод узловых потенциалов позволяет упростить расчет электрических цепей по сравнению с методом по первому и второму законам Кирхгофа за счет уменьшения числа уравнений. Данный метод основан на применении первого закона Кирхгофа.
При выполнении расчета методом узловых потенциалов необходимо выбрать один узел, в котором потенциал узла приравнивается к нулю. Остальные потенциалы узлов расчетной схемы определяются относительно узла с нулевым потенциалом. Далее в соответствии с данным методом записывается система уравнений, относительно потенциалов узлов расчетной схемы, используя следующие правила:
Правило №1.
— со знаком «+» потенциал i-го узла, для которого составляется данное i-е уравнение, умноженный на сумму проводимостей ветвей, присоединенных к данному i-му узлу;
— со знаком «-» потенциал соседних узлов, каждый из которых умножен на сумму проводимостей ветвей, присоединенных к i-му и k-му узлам.
— потенциал i-го узла, для которого записывается уравнение;
— сумму проводимостей ветвей, присоединенных к данному i-му узлу;
— потенциал k-го узла, который связан через ветвь с i-ым узлом;
— проводимость ветви, которая связывает i-ый и k-ый узел.
Правило №2. В правой части i-го уравнения записывается так называемый узловой ток, который равный сумме произведений ЭДС ветвей, подходящих к i-му узлу, и проводимостей этих ветвей. При этом член суммы записывается со знаком “+”, если соответствующая ЭДС направлена к i-му узлу, в противном случае ставится знак “–”. Если в подходящих к i-му узлу ветвях содержатся источники тока, то знаки токов источников токов, входящих в узловой ток простыми слагаемыми, определяются аналогично.
— источники тока, которые присоединены к i-му узлу;
— произведение ЭДС и проводимости ветви с источником ЭДС, которые присоединены к i-му узлу.
В качестве примера рассмотрим расчетную схему замещению, которая состоит из двух источников ЭДС и трех сопротивлений. В одном из рассматриваемых узлов расчетной схеме обозначим нулевой потенциал.
Рис.5. Расчетная схема замещения для пояснения метода узловых потенциалов.
В соответствии с методом узловых потенциалов можно записать одно уравнение (q — 1):
В результате была получена система уравнений, которая позволяет определить потенциал узлов рассматриваемой схемы замещения исходя из заданных значений ЭДС и сопротивлений. Заключительным этапом расчета будет являться процесс определения токов во всех ветвях расчетной схемы по найденным значениям потенциалов узлов рассматриваемой схемы замещения.
Представленные выше методы позволяют определять токи и напряжения в ветвях расчетной схемы для любой электрической цепи постоянного и переменного тока.
Напряжение (механика) — Wikiwand 06
такжеУважаемый AI Wikiwand, давайте будем краткими, просто ответив на эти ключевые вопросы:
Можете ли вы перечислить основные факты и статистические данные о стрессе (механике)?
Кратко изложите эту статью для 10-летнего ребенка
ПОКАЗАТЬ ВСЕ ВОПРОСЫ
В механике сплошной среды напряжение — это физическая величина, описывающая силы, действующие при деформации. Разрываемый объект, например натянутая эластичная лента, подвергается растягивающему напряжению и может подвергнуться удлинению. Сжимаемый объект, например смятая губка, подвергается сжимающему напряжению и может укорачиваться.[1][2] Чем больше сила и чем меньше площадь поперечного сечения тела, на которое она действует, тем больше напряжение. Стресс выражается в единицах силы на единицу площади, например, в ньютонах на квадратный метр (Н/м 2 ) или паскаль (Па).
Напряжение выражает внутренние силы, которые соседние частицы сплошного материала воздействуют друг на друга, а напряжение является мерой деформации материала.
[3] Например, когда сплошной вертикальный стержень поддерживает вес над головой, каждая частица в стержне давит на частицы, находящиеся непосредственно под ним. Когда жидкость находится в закрытом сосуде под давлением, каждая частица отталкивается от всех окружающих частиц. Стенки контейнера и поверхность, создающая давление (например, поршень), толкают их в (ньютоновской) реакции. Эти макроскопические силы на самом деле являются результатом очень большого числа межмолекулярных сил и столкновений между частицами в этих молекулах. Ударение часто обозначается строчной греческой буквой сигма (9).0004 σ ).
Деформация внутри материала может возникать под действием различных механизмов, таких как напряжение при воздействии внешних сил на сыпучий материал (например, сила тяжести) или на его поверхность (например, контактные силы, внешнее давление или трение). Любая деформация (деформация) твердого материала создает внутреннее упругое напряжение , аналогичное силе реакции пружины, которая стремится вернуть материал в исходное недеформированное состояние.
В жидкостях и газах только деформации, изменяющие объем, создают устойчивые упругие напряжения. Если деформация меняется со временем постепенно, то даже в жидкостях обычно будет около вязкое напряжение , противодействующее этому изменению. Упругие и вязкие напряжения обычно объединяют под названием механическое напряжение .
Значительное напряжение может существовать, даже если деформация незначительна или отсутствует (обычное предположение при моделировании потока воды). Стресс может существовать в отсутствие внешних сил; такое встроенное напряжение важно, например, в предварительно напряженном бетоне и закаленном стекле. Напряжение также может быть возложено на материал без приложения результирующих сил, например, за счет изменений температуры или химического состава или внешних электромагнитных полей (как в пьезоэлектрических и магнитострикционных материалах).
Связь между механическим напряжением, деформацией и скоростью изменения деформации может быть весьма сложной, хотя линейное приближение может быть адекватным на практике, если величины достаточно малы.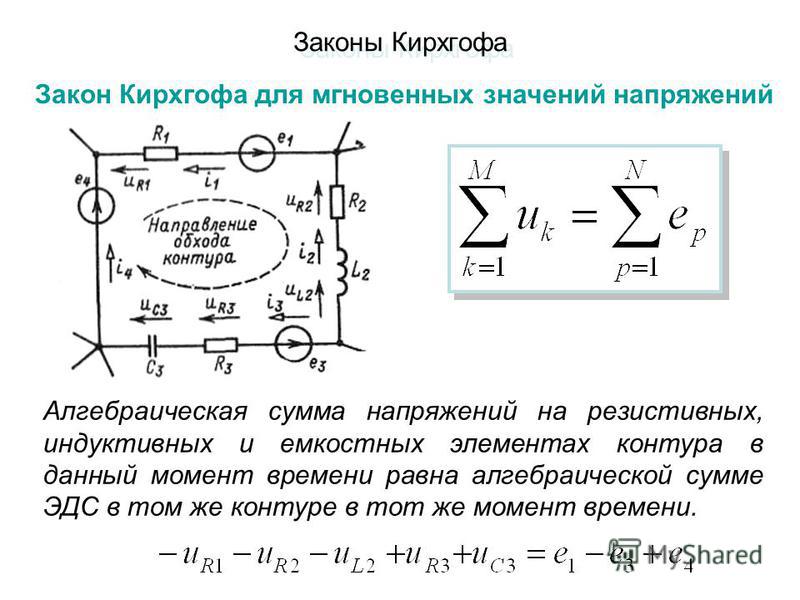
Напряжение, превышающее определенные пределы прочности материала, приведет к остаточной деформации (например, к пластическому течению, разрушению, кавитации) или даже к изменению его кристаллической структуры и химического состава.
механика сплошных сред — Связь между декомпозированными мерами напряжения
спросил
Изменено 27 дней назад
Просмотрено 271 раз
$\begingroup$В механике сплошных сред используется широкий спектр мер напряжения. Меня интересуют два тензора напряжений Коши и второй тензор напряжений Пиолы-Кирхгофа. Эти две меры стресса могут быть связаны через: 9{-T}\right) \neq \mathbf{S}’ + \mathbf{S}_{hyd}$
Я думал, что это неравенство верно, потому что при вычислении, как показано выше, $\mathbf{S}_ Член {hyd}$ выше будет диагональной, но не скалярной матрицей и, следовательно, должен содержать некоторые девиаторные компоненты.
