30 Закон Максвелла для распределения молекул идеального газа по скоростям и энергиям теплового движения
При выводе основного уравнения молекулярно-кинетической теории молекулам задавали различные скорости. В результате многократных соударений скорость каждой молекулы изменяется по модулю и направлению. Однако из-за хаотического движения молекул все направления движения являются равновероятными, т. е. в любом направлении в среднем движется одинаковое число молекул.
По
молекулярно-кинетической теории, как
бы ни изменялись скорости молекул при
столкновениях, средняя квадратичная
скорость молекул массой m0 в газе, находящемся в состоянии
равновесия при Т
= const,
остается постоянной и равной <vкв>
=3kT/m0.
Это объясняется тем, что в газе, находящемся
в состоянии равновесия, устанавливается
некоторое стационарное, не меняющееся
со временем распределение молекул по
скоростям, которое подчиняется вполне
определенному статистическому закону.
Этот закон теоретически выведен Дж.
Максвеллом.
При выводе закона распределения молекул по скоростям Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что силовые поля на газ не действуют.
Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на
малые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), имеющих скорость, заключенную в этом интервале. Функция
е.откуда
f(v)=dN(v)/Ndv
Применяя методы теории вероятностей, Максвелл нашел функцию f(v) — закон для распределения молекул идеального газа по скоростям:
Из (44.1) видно, что конкретный вид функции зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры Т).
График функции (44.1) приведен на рис. 65. Так как при возрастании v множитель уменьшается быстрее, чем растет множитель v2, то функция f(v), начинаясь от нуля, достигает максимума при vв и затем асимптотически стремится к нулю. Кривая несимметрична относительно vв.
Относительное число молекул dN(v)/N, скорости которых лежат в интервале от
65. Площадь, ограниченная кривой
распределенияи осью абсцисс, равна единице. Это означает, что функция f(v) удовлетворяет условию нормировки
Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью. Значение наиболее вероятной скорости можно найти продифференцировав выражение (44.1) (постоянные множители опускаем) по аргументу
Значенияv=0 и v= соответствуют минимумам выражения (44.1), а значение v, при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная скорость vв:
Из формулы (44.
2)
следует, что при повышении температуры
максимум функции распределения
молекул по скоростям (рис. 66) сместится
вправо (значение наиболее вероятной
скорости становится больше). Однако
площадь, ограниченная кривой, остается
неизменной, поэтому при повышении
температуры кривая распределения
молекул по скоростям будет растягиваться
и понижаться.
Средняя скорость молекулы <v> (средняя арифметическая скорость)
определяется по формуле
Подставляя сюда f(v) и интегрируя, получим
Скорости,
характеризующие состояние газа: 1)
наиболее вероятная vв=2RT/М;
2) средняя <v>=8RT/(М)=1,13v
31. Барометрическая формула. Распределение Больцмана
При
выводе основного уравнения
молекулярно-кинетической теории газов
и макcсвелловского
распределения молекул по скоростям
предполагалось, что на молекулы газа
внешние силы не действуют, поэтому
молекулы равномерно распределены по
объему.
Однако молекулы любого газа
находятся в потенциальном поле тяготения
Земли. Тяготение, с одной стороны, и
тепловое движение молекул — с другой,
приводят к некоторому стационарному
состоянию газа, при котором давление
газа с высотой убывает.
Выведем закон изменения давления с высотой, предполагая, что поле тяготения однородно, температура постоянна и масса всех молекул одинакова. Если атмосферное давление на высоте А равно р (рис. 67), то на высоте h + dh оно равно p+dp (при dh>0 dp<0, так как давление с высотой убывает). Разность давлений р и p + dp равна весу газа, заключенного в объеме цилиндра высотой Ah с основанием площадью, равной единице площади:
где
— плотность газа на высоте h (dh настолько
мало, что при изменении высоты в этом
пределе плотность газа можно считать
постоянной).
Следовательно,
dр=-gdh. (45.1)
Воспользовавшись уравнением состояния идеального газа pV = (m/M)RT (т — масса газа, М—молярная масса газа),
находим, что
Подставив это выражение в (45.1), получим
С изменением высоты от h1 до h2. давление изменяется от р1 до p2 (рис. 67), т. е.
Выражение (45.2) называется барометрической формулой. Она позволяет найти атмосферное давление в зависимости от высоты или, измерив давление, найти высоту. Так как высоты обозначаются относительно уровня моря, где давление считается нормальным, то выражение (45.2) может быть записано в виде
где р —
давление на высоте h.
Прибор для определения высоты над земной поверхностью называется высотомером (или альтиметром). Его работа основана на использовании формулы (45.3). Из этой формулы следует, что давление с высотой убывает тем быстрее, чем тяжелее газ.
Барометрическую формулу (45.3) можно преобразовать, если воспользоваться выражением (42.6) p=nkT:
где n — концентрация молекул на высоте h, n0 — то же на высоте h=0. Так как M = m0NA(NA— постоянная Авогадро, m
где m0gh=П — потенциальная энергия молекулы в поле тяготения, т. е.
Выражение
(45.5) называется распределением
Больцмана во
внешнем потенциальном поле.
Из него
следует, что при постоянной температуре
плотность газа больше там, где меньше
потенциальная энергия его молекул.
Если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределение Больцмана (45.5) справедливо в любом внешнем потенциальном поле, а не только в поле сил тяжести.
1,2,3,4 уравнения Максвелла для электромагнитного поля, смысл, суть, решение
Уравнения Максвелла в электродинамике – это как законы Ньютона в классической механике или как постулаты Эйнштейна в теории относительности. Фундаментальные уравнения, в сущности которых мы сегодня будем разбираться, чтобы не впадать в ступор от одного их упоминания.
Полезная и интересная информация по другим темам – у нас в телеграм.
Уравнения Максвелла – это система уравнений в дифференциальной или интегральной форме, описывающая любые электромагнитные поля, связь между токами и электрическими зарядами в любых средах.
Уравнения Максвелла неохотно принимались и критически воспринимались учеными-современниками Максвелла. Все потому, что эти уравнения не были похожи ни на что из известного людям ранее.
Тем не менее, и по сей день нет никаких сомнений в правильности уравнений Максвелла, они «работают» не только в привычном нам макромире, но и в области квантовой механики.
Уравнения Максвелла совершили настоящий переворот в восприятии людьми научной картины мира. Так, они предвосхитили открытие радиоволн и показали, что свет имеет электромагнитную природу.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
По порядку запишем и поясним все 4 уравнения. Сразу уточним, что записывать их будем в системе СИ.
Первое уравнение Максвелла
Современный вид первого уравнения Максвелла таков:
Тут нужно пояснить, что такое дивергенция. Дивергенция – это дифференциальный оператор, определяющий поток какого-то поля через определенную поверхность.
Уместным будет сравнение с краном или с трубой. Например, чем больше диаметр носика крана и напор в трубе, тем большим будет поток воды через поверхность, которую представляет собой носик.
В первом уравнении Максвелла E – это векторное электрическое поле, а греческая буква «ро» – суммарный заряд, заключенный внутри замкнутой поверхности.
Так вот, поток электрического поля E через любую замкнутую поверхность зависит от суммарного заряда внутри этой поверхности. Данное уравнение представляет собой закон (теорему) Гаусса.
Третье уравнение Максвелла
Сейчас мы пропустим второе уравнение, так как третье уравнение Максвелла – это тоже закон Гаусса, только уже не для электрического поля, но для магнитного.
Оно имеет вид:
Что это значит? Поток магнитного поля через замкнутую поверхность равен нулю. Если электрические заряды (положительные и отрицательные) вполне могут существовать по отдельности, порождая вокруг себя электрическое поле, то магнитных зарядов в природе просто не существует.
Второе уравнение Максвелла
Второе уравнение Максвелла представляет собой ни что иное, как закон Фарадея. Его вид:
Ротор электрического поля (интеграл через замкнутую поверхность) равен скорости изменения магнитного потока, пронизывающего эту поверхность. Чтобы лучше понять, возьмем воду в ванной, которая сливается через отверстие. Вокруг отверстия образуется воронка. Ротор – это сумма (интеграл) векторов скоростей частиц воды, которые вращаются вокруг отверстия.
Как Вы помните, на основе закона Фарадея работают электродвигатели: вращающийся магнит порождает ток в катушке.
Четвертое уравнение Максвелла
Четвертое — самое важное из всех уравнений Максвелла. Именно в нем ученый ввел понятие тока смещения.
Это уравнение еще называется теоремой о циркуляции вектора магнитной индукции. Оно говорит нам о том, что электрический ток и изменение электрического поля порождают вихревое магнитное поле.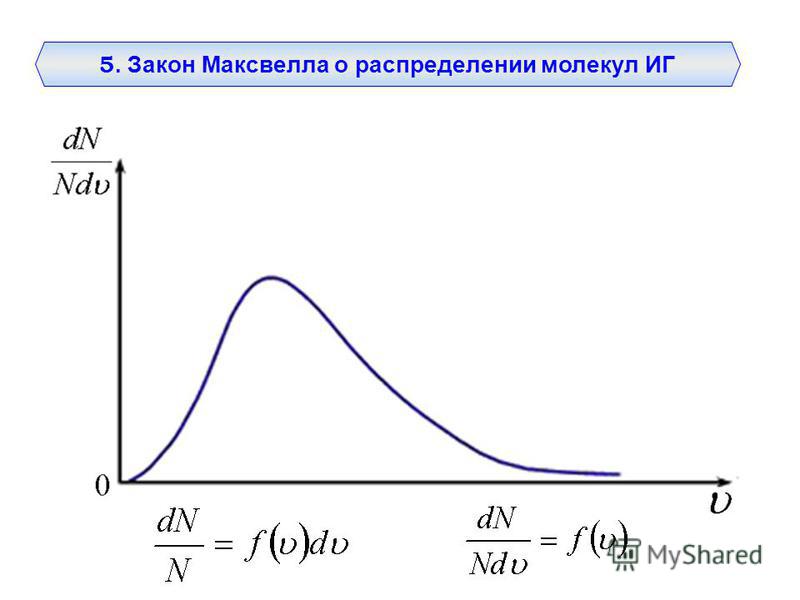
Приведем теперь всю систему уравнений и кратко обозначим суть каждого из них:
Первое уравнение: электрический заряд порождает электрическое поле
Второе уравнение: изменяющееся магнитное поле порождает вихревое электрическое поле
Третье уравнение: магнитных зарядов не существует
Четвертое уравнение: электрический ток и изменение электрической индукции порождают вихревое магнитное поле
Решая уравнения Максвелла для свободной электромагнитной волны, мы получим следующую картину ее распространения в пространстве:
Надеемся, эта статья поможет систематизировать знания об уравнениях Максвелла. А если понадобиться решить задачу по электродинамике с применением этих уравнений, можете смело обратиться за помощью в студенческий сервис. Подробное объяснение любого задания и отличная оценка гарантированы.
уравнений Максвелла
уравнений МаксвеллаСвойства электрического и магнитного полей, предсказанные уравнениями Максвелла
Классическая физика — это наша модель законов, управляющих
поведение и взаимодействие макроскопических объектов в окружающем нас мире.
Все законы классической физики были известны к концу 199005-го -го года.
век. Классическая физика хорошо описывает и предсказывает почти все
повседневные явления, но начинает глючить, когда становится слишком… .
(Здесь можно вставить любые крайности, например большой, маленький,
горячий, холодный, быстрый и т. д.)
В классической физике мир состоит из материи частиц , которые ведут себя согласно закону Ньютона
законы движения. Чтобы использовать законы Ньютона, нам нужно знать, какие силы действуют
на частицы. Взаимодействия, приводящие к возникновению сил между
частицы представлены полями .
Электрические и магнитные поля представляют собой электромагнитные взаимодействия. Если мы
знаем поля, знаем электрические и магнитные силы, действующие на заряженные
частицы.
F = F электрический + F магнитный = q E + q v × B = q( E + v × B ).
В классической физике наша модель электромагнитного полей представляет собой набор из четырех уравнений, называемых уравнениями Максвелла. уравнения . Они позволяют нам предсказать E и Б . У них есть более широкий диапазон применимости, чем у законов Ньютона. Они относительно правильно и правильно описывать поля, когда относительные скорости приближаются к скорость света. Но классической модели для электромагнитных полей нет. более правильно описывает наблюдения в масштабе атомов или элементарных частицы.
Статические поля
Уравнения Максвелла предсказывают, что статических
электрические поля , т. е. поля, не меняющиеся во времени, создаются зарядами. Сборы
источники и стоки силовых линий. Линии статического электрического поля начинаются на положительном
и заканчиваются на отрицательных зарядах.
Статическое электрическое поле
линии НИКОГДА не образуют петли.
Статическое электрическое поле – это
консервативное поле.
Если вы работаете над зарядом против статического электричества
поля эта работа запасается в виде потенциальной энергии. Потенциальная энергия представляет собой
функция только положения. Вы можете позволить электрическому полю совершить работу, чтобы
восстановить энергию, затраченную на перемещение заряда.
В статике уравнения Максвелла для электрического поля объединить, чтобы дать вам закон Кулона и принцип суперпозиции. Все остальное — просто сложение векторов.
Уравнения Максвелла предсказывают, что статических магнитных полей производится постоянными токами. магнитных зарядов нет и поэтому нет источников и стоков для силовых линий магнитного поля.
Линии статического магнитного поля ВСЕГДА образуют замкнутые контуры.
Они окружают движущиеся заряды по правилу правой руки.
Наведенные поля
Если мы НЕ ограничимся устойчивым состоянием
условиях в уравнениях Максвелла появляются два дополнительных члена.
| (1) | ∮ А Е ∙d А = Q внутри /ε 0 |
| (2) | ∮ Γ E ∙d с = -∂/∂t∫ А В ·d А |
| (3) | ∮ А В ∙d А = 0 |
| (4) | ∮ Γ B ∙d с = μ 0 I по Γ + (1/c 2 )∂/∂t∫ A E ·d A |
Уравнения Максвелла говорят нам, что есть еще один источник электрических и магнитных полей, когда любое из этих полей изменяется со временем.
- Изменяющиеся магнитные поля являются источником электрических полей.
- Изменяющиеся электрические поля являются источником магнитных полей.
Ключевое слово ИЗМЕНЕНИЕ. Поля, создаваемые этим ИЗМЕНЕНИЕМ, называются динамическими или индуцированными полями .
Индуцированные поля не
имеют источники или стоки.
Силовые линии индуцированных динамических полей ВСЕГДА образуют замкнутые контуры. У них всегда тираж .
Математическое определение циркуляции векторного поля:
Возьмем любой замкнутый контур, например окружность. По фиксированному
время, двигайтесь небольшими шагами ∆ r один раз вокруг петли. (Ты должен взять
бесконечно малыми шагами.) На каждом шаге вычисляйте произведение
тангенциальная составляющая поля времени ∆ r . Для электрического поля, для
например, вычислить E∙ ∆ r . Суммируйте все эти продукты, когда вы проходите цикл.
Пример
The circulation of E around a closed loop = lim ∆ r —>0 Σ around loop E∙ ∆ r = ∫ around loop E· d r .
Для индуцированных полей циркуляция всегда отлична от нуля.
Сколько там тираж?
Уравнения Максвелла говорят нам о величине и направлении циркуляции.
Одно из уравнений называется Закон Фарадея . Для абсолютного значения
или величина, закон Фарадея гласит, что циркуляция
электрическое поле E вокруг любого замкнутого контура равно скорости изменения
магнитного потока через площадь, ограниченную контуром.
Запомнить поток:
Поток векторного поля через площадь поверхности равен количество того, что поле представляет, проходящего через область. общий поток зависит от напряженности поля, размера площади поверхности его проходит, и от того, как область ориентирована по отношению к полю.
Мы определили электрический поток как dΦ E = E dA cosθ, Φ E = ∫ А Е ·d А .
Магнитный поток определяется в
аналогично dΦ B = B dA cosθ, Φ B = ∫ A B · d A .
Другим уравнением Максвелла является уравнение Ампера-Максвелла.
закон . В нем говорится, что циркуляция магнитного поля Б вокруг любой замкнутой петли является суммой двух терминов. Статический член пропорционален
к току, протекающему через контур, а динамический член пропорционален
скорость изменения электрического потока через площадь, ограниченную петлей.
Это взаимодействие между индуцированными электрическими и магнитными полями приводит к
производство электромагнитной волны.
Электромагнитные волны являются решениями уравнений Максвелла даже в свободном пространстве, когда
заряды и токи отсутствуют.
Проблема:
Найдите магнитный поток через каждую из приведенных ниже катушек.
(a) Магнитное поле с величиной B = 5 мТл по нормали к круговому витку проволоки радиусом r = 1 см.
(б)
Магнитное поле величиной B = 5 мТл создает
угол θ = 20 o с нормалью треугольной катушки из 50 витков
с основанием b = 5,0 см и высотой h = 4 см.
Решение:
Рассуждение:
Магнитное поле B постоянно по всей площади. магнитный поток Φ B = B A cosθ.Детали расчета:
(a) Φ B = B A cosθ = B A = (5*10 -3 T)(π*10 -4 м 2 ) = 1,57*10 -6 Тм 2 .
(б) Φ Б = B A cosθ. Так как катушка имеет 50 витков, А = 50-кратной площади треугольника.
Φ B = (5*10 -3 T)(50*5*10 -2 *2*10 -2 m 2 )*cos(20 o ) = 2,35*10 -4 Tm 2 .
Проблема:
Прямоугольная петля из N витков вращается вокруг оси в области однородного магнитного поля, как показано на рисунке справа.
Опишите, как магнитный поток через контур меняется со временем.
Решение:
- Рассуждение:
Φ B = B A cosθ = B N A прямоугольник cosθ.
Произведение B N A прямоугольник постоянно, но θ, угол B делает с нормальным, меняется со временем.
(Для плоской области можно выбрать направление нормали. Предположим, плоская область лежит в плоскости xy. Нормалью для этой области является ось z, для ее направления можно выбрать положительное или отрицательное Z-направление.)
Если магнитное поле в момент t = 0 совпадает с нормали, то поток имеет максимальное положительное значение при t = 0,
. Он спадает к нулю, когда θ приближается к максимальное отрицательное значение при θ = 180 o снова приближается к нулю когда θ приближается к 270 o и достигает максимального положительного значение снова при θ = 360 o .
Поток постоянно меняется.
13.2 Уравнения Максвелла
13.2 Уравнения Максвелла
|
Далее: 13.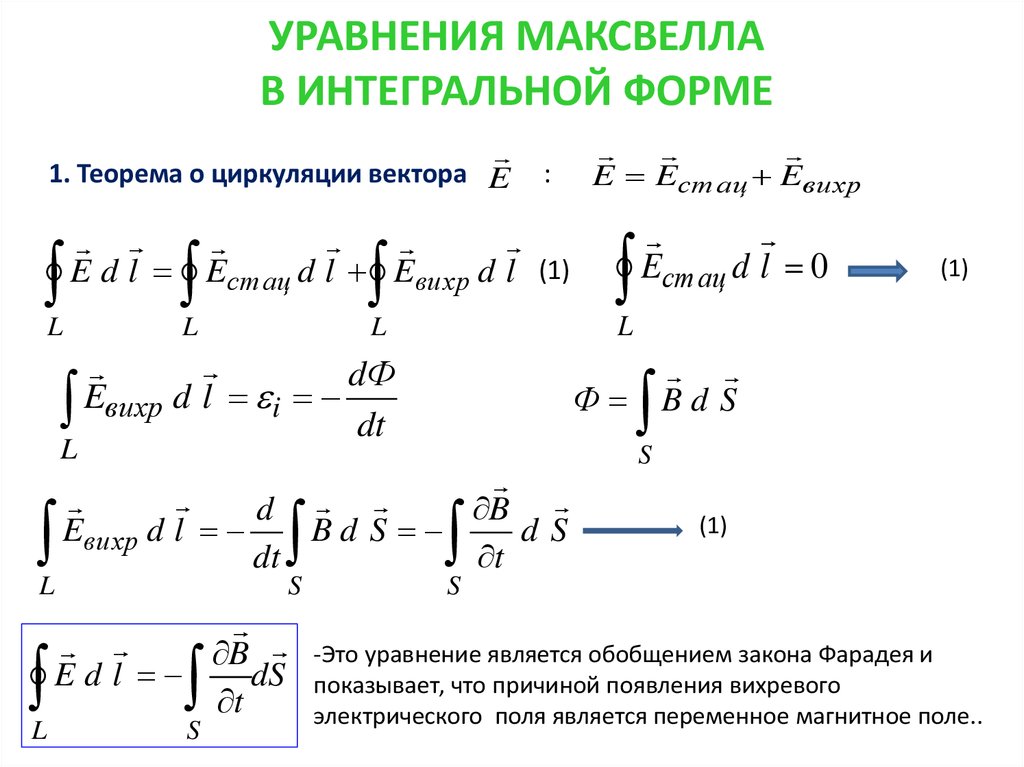 3 Пример статических электромагнитных полей |
13.2 Уравнения Максвелла
Уравнения Максвелла обычно не рассматриваются в типичном инженерная программа. Хотя эти законы не имеют прямого отношения к квантовой механике, они имеют тенденцию появляться в нанотехнологиях. Этот раздел намерен дать вам некоторые идеи. Описание на основе операторов пространственной производной дивергенции и ротора, а также связанные теоремы Гаусса и Стокса, обычно встречающиеся в курсах математического анализа (Исчисление III в системе США.)
Пока пропускаем первое уравнение, второе уравнение Максвелла
уравнений вытекает непосредственно из квантово-механического описания
предыдущий раздел. Рассмотрим выражение для магнитного поля производное
(угадал) там, (13.3).
Если вы возьмете его расходимость (предварительно умножив на ), вы получите
избавиться от векторного потенциала , так как расходимость любого
curl всегда равен нулю, поэтому вы получаете
(13. 4) |
и это вторая из четырех прекрасно сжатых фраз Максвелла. уравнения. (Компактная современная запись с использованием дивергенции и завитка правда, благодаря Хевисайду и Гиббсу.)
Первое из уравнений Максвелла представляет собой аналогичное выражение для
электрическое поле , но его дивергенция не равна нулю:
| (13.5) |
где — электрический заряд на единицу объема, который присутствует а постоянная 8,85 10 Кл/Дж·м называется диэлектрическая проницаемость пространства.
Что все это значит? Ну, первое, что нужно проверить, это то, что
Первое уравнение Максвелла — это просто очень умный способ записать
Закон Кулона для электрического поля точечного заряда.
Рассмотрим
поэтому электрический точечный заряд силы, а представьте себе
этот заряд окружен полупрозрачной сферой радиусом , как
показано на рисунке 13.1. По симметрии электрическое поле
во всех точках сферической поверхности является радиальным и везде имеет
одинаковая величина; фигура
13.1 показано это для восьми выбранных точек.
Теперь посмотрите, что произойдет, если вы интегрируете обе стороны уравнения Максвелла.
первое уравнение (13.5) над внутренностью этого
сфера. Начнем с правой части, поскольку плотность заряда
— заряд на единицу объема, по определению его интеграл по
объем. Таким образом, правая часть интегрируется
просто к. Как насчет левой стороны?
Что ж, теорема Гаусса, или теорема о дивергенции, говорит, что
дивергенция любого вектора, в данном случае интегрированного по
объем сферы равен радиальному электрическому полю
интегрированы по поверхности сферы. Так как это
постоянна на поверхности, а поверхность сферы просто
, правая часть интегрируется в
.
Так что в сумме вы получаете за интегрированный первый
Уравнение Максвелла, которое. Возьмите на другую сторону и
вот вам кулоновское электрическое поле точечного заряда:
| (13.6) |
Умножьте на, и вы получите электростатическую силу, действующую на электрон. в этом поле согласно уравнению Лоренца (13.1). Интегрируйте по отношению к и у вас есть потенциальная энергия который использовался ранее для анализа атомов и молекулы.
Конечно, все это вызывает вопрос, а зачем заморачиваться? Если у Максвелла
первое уравнение — это просто переписанный закон Кулона, почему бы просто не
придерживаться закона Кулона в первую очередь? Ну, чтобы описать
электрическое поле в данной точке по закону Кулона требует
вам рассмотреть каждое обвинение в любом другом месте. Напротив,
Уравнение Максвелла включает только локальные величины в
данной точки, а именно, производные локального электрического поля и
местный заряд на единицу объема.
Бывает так, что в числовом или
аналитическая работа, большую часть времени гораздо удобнее заниматься
с локальными величинами, даже если это производные, чем с глобальными
те.
Конечно, вы также можете проинтегрировать первое уравнение Максвелла по
более общие области, чем сфера с центром вокруг заряда. За
в качестве примера на рис. 13.2 показана сфера со смещенным центром
обвинять. Но напряженность электрического поля уже не постоянна
поверхность, и теорема о дивергенции теперь требует, чтобы вы интегрировали
составляющая электрического поля, нормальная к поверхности над
поверхность. Ясно, что это не имеет особого интуитивного смысла.
Однако, если вы готовы немного развлечься в математике
точность, есть лучший способ взглянуть на это.
Это с точки зрения линии электрического поля
, линии, которые повсюду
проследить направление электрического поля. Левая фигура на рисунке
13.2 показаны линии поля через выбранные точки;
одиночный заряд имеет радиальные силовые линии.
Предположим, что вы рисуете линии поля плотно, как на рисунке.
13.3 говорят, и сверх того, что вы делаете число
силовые линии, выходящие из заряда, пропорциональны силе
этот заряд. В этом случае локальная плотность силовых линий на
точка становится мерой напряженности электрического поля в этой точке.
точка, и в этих терминах первое интегрированное уравнение Максвелла
говорит, что чистое число линий поля, выходящих из региона, равно
пропорциональна чистому заряду внутри этой области. Что
остается верным, когда вы добавляете больше зарядов внутри региона.
В этом
случае линии поля будут уже не прямыми, а чистым числом
выход на улицу по-прежнему будет мерой чистого заряда внутри.
Теперь рассмотрим вопрос, почему второе уравнение Максвелла
говорит, что дивергенция магнитного поля равна нулю. Для
электрическое поле можно распихать, скажем, какие-то электроны в области к
создать чистый отрицательный заряд, или вы можете засунуть некоторые ионизированные
молекулы для создания чистого положительного заряда. Но магнитный
эквиваленты таких частиц, называемые «магнитными
монополи», являющиеся отдельными магнитными частицами северного полюса или
частиц магнитного южного полюса просто не существует,
{N.31}. Может показаться, что ваш стержневой магнит
имеет северный полюс и южный полюс, но если разобрать его на
маленькие кусочки, вы не получите кусочки северного полюса и южного полюса
штуки. Каждая маленькая деталь сама по себе по-прежнему является маленьким магнитом, с
одинаково сильны северный и южный полюса. Единственная причина, по которой
магнит, кажется, имеет северный полюс в том, что все микроскопические
магниты, из которых он состоит, имеют свои северные полюса преимущественно
указывал в том направлении.
Если все микроскопические магниты имеют одинаковую силу северного и южного полюсов,
то такое же количество силовых линий магнитного поля, выходящих из
северные полюса возвращаются к южным полюсам, как показано на рисунке 13.4.
иллюстрирует. Таким образом, чистые силовые линии магнитного поля, выходящие из заданного
регион будет равен нулю; все, что уходит, возвращается обратно. Правда, если вы
окружить северный полюс длинного стержневого магнита воображаемой сферой,
вы можете получить довольно хорошее магнитное приближение к электрическому
случай рисунка 13.1. Но даже тогда, если вы посмотрите
внутри магнита, где он торчит через сферическую
поверхности, линии поля будут направлены в сторону
Северный полюс, а не от него.
Вы понимаете, почему второй Максвелл
уравнение также называется отсутствие магнитных монополей.
И почему, скажем, электроны могут иметь суммарный отрицательный заряд, но иметь нулевой заряд?
сила магнитного полюса; их спин и орбитальный угловой момент производят
одинаково сильные магнитные северный и южный полюса, магнитное диполь
(ди означает два.)
Вы можете получить третье уравнение Максвелла из электрического поля является производным
из предыдущего раздела. Если вы возьмете его
curl, (предварительно умножив на ), вы избавитесь от потенциального
, так как завиток любого градиента всегда равен нулю, и
ротор — это магнитное поле. Итак, третий из
Уравнения Максвелла:
| (13.7) |
Завиток
, , также часто обозначается как
гниль.
5: Производство электроэнергии. Что это значит? Ну, первое, что нужно проверить в этом
Дело в том, что это просто умная переписка закона Фарадея.
индукция, регулирующая выработку электроэнергии. Предположим, что вы хотите
чтобы создать напряжение для какой-либо нагрузки (лампочки или чего-то еще, не
волнуйтесь, какая нагрузка, только как получить напряжение для нее.) Просто
возьмите кусок медной проволоки и согните его в круг, как показано на
рисунок 13.5. Если вы можете создать разницу в напряжении
между концами провода вы в деле; просто зацепи лампочку
или что там на концах провода и он загорится. Но чтобы получить
такое напряжение, вам понадобится электрическое поле, как показано на рисунке
13.5, потому что разница напряжений между концами
интеграл напряженности электрического поля по длине
провод. Теперь теорема Стокса исчисления говорит, что электрическое поле
прочность вдоль проволоки, интегрированная по длине проволоки
равен интегралу ротора напряженности электрического поля
интегрированы внутри провода, другими словами, над
воображаемый полупрозрачный круг на рис.
13.5. Итак, чтобы получить
напряжения, нужен ненулевой ротор электрического поля на
полупрозрачный круг. И третье уравнение Максвелла выше говорит, что
это означает изменяющееся во времени магнитное поле на полупрозрачном круге.
Перемещение конца сильного магнита ближе к кругу должно сделать это,
как показано на рисунке 13.5. Лучше не делай этого
большая лампочка, если вы не обмотаете проволоку намного больше раз, чтобы сформировать
катушка, но тем не менее. {N.32}.
Четвертое и последнее уравнение Максвелла представляет собой аналогичное выражение для
вихрь магнитного поля:
| (13.8) |
где плотность электрического тока
,заряд, протекающий через единицу площади поперечного сечения, и есть скорость света. (Возможно масштабирование с коэффициентом, чтобы получить скорости света, чтобы они в равной степени отражались в уравнениях для завихрения и завиток , но тогда закон силы Лоренца должен тоже подкорректировать)
6: Два способа
генерировать магнитное поле: с помощью тока (слева) или с помощью
переменное электрическое поле (справа).Большим отличием от третьего уравнения является внешний вид плотность тока. Итак, есть два способа создания циркулирующее магнитное поле, как показано на рис. 13.6: 1) пропустить ток через замкнутый круг (плотность тока интегрируется по площади окружности в ток через круг) и (2) путем создания переменного электрического поля по кругу, подобно тому, как это было сделано для электрического поля на рис. 13.5.
Тот факт, что ток создает окружающее магнитное поле, был
уже известный как закон Ампера, когда Максвелл провел свой анализ. Максвелл
однако сам добавил производную электрического поля по времени к
уравнение, чтобы математика имела смысл. Проблема заключалась в том, что
дивергенция любого завитка должна быть равна нулю, и само по себе дивергенция
плотность тока в правой части четвертого уравнения равна
не ноль.
Точно так же, как дивергенция электрического поля
чистые силовые линии, выходящие из области на единицу объема,
расхождение плотности тока — это выходной чистый ток. И
совершенно нормально, чтобы чистый заряд вытекал из области: это просто
уменьшает заряд, остающийся в регионе, на эту сумму. Этот
выражается уравнение непрерывности:
| (13.9) |
Итак, четвертое уравнение Максвелла без производной по времени от электрическое поле математически невозможно. Но после того, как он добавил это, если вы возьмете дивергенцию полной правой части, то вы сделаете действительно получить ноль, как вы должны. Чтобы проверить это, используйте непрерывность уравнение выше и первое уравнение.
В пустом пространстве уравнения Максвелла упрощаются: зарядов нет
поэтому и плотность заряда, и плотность тока
будет нулевым. В этом случае решения уравнений Максвелла
представляют собой просто комбинации «бегущих волн».
Бегущая волна принимает вид
| (13.10) |
где для простоты ось -системы координат была совмещены с направлением, в котором распространяется волна, и осью - с амплитудой электрического поля волны. Такая волна называется «линейно поляризованной» в -направлении. Постоянная — угловая частота волны, равная временам его частота в циклах в секунду и связана с его волной длина по. константа — это просто фазовый угол. Для этих простых волн магнитное и электрическое поля должны быть перпендикулярны друг другу, а также к направлению распространения волны.
Вы можете подставить приведенное выше волновое решение в уравнения Максвелла и
поэтому убедитесь, что он удовлетворяет их всех. С большим усилием и знаниями
анализа Фурье, можно показать, что они являются наиболее общими
возможные решения, которые принимают эту форму бегущей волны, и что любое
произвольное решение представляет собой комбинацию этих волн (если все направления
направления распространения и электрического поля относительно него,
включены.
)
Дело в том, что волны распространяются со скоростью . Когда Максвелл записал свои уравнения, была для него просто константой, но когда скорость распространения электромагнитных волн сравнялась с экспериментально измерить скорость света, это было слишком совпадение, и он правильно сделал вывод, что свет должен быть бегущими электромагнитными волнами.
Это была великая победа математического анализа. Давным-давно греки
пытался использовать математику, чтобы делать предположения о физическом мире,
и это был ужасный провал. Вы не хотите об этом слышать. Только
когда Ренессанс начал измерять, как на самом деле работает природа,
правильные законы были открыты для таких людей, как Ньютон и другие, чтобы
придать математическую форму. Но тут Максвелл успешно исправляет
Измеренный закон Ампера, только потому, что математика не имела смысла. Более того, выяснив, как
двигаются быстрые электромагнитные волны, он открывает самые фундаментальные
природа загадочного физического явления, которое люди называли
свет.
Для тех, кто знаком с уравнениями в частных производных, отдельно волновые уравнения для электрического и магнитного полей и их потенциалы приведены в добавлении {A.37}.
Электромагнитное поле, очевидно, содержит энергию; вот как
Солнце переносит тепло на нашу планету. Электромагнитная энергия внутри
в противном случае пустой том можно найти как
| (13.11) |
Обычно это получается путем сравнения энергии разряда конденсатора к электрическому полю, которое он первоначально удерживает, и от сравнивая энергию разряда катушки с магнитным полем, которое она изначально держит. Слишком много подробностей для этой книги.
Но по крайней мере результат можно сделать правдоподобным. Прежде всего обратите внимание, что
производная по времени от приведенной выше энергии может быть записана как
Вот поверхность объема, а единица вектор нормали к элементу поверхности.
Чтобы убедиться в этом
выражение, приведите производную по времени внутрь интеграла в
(13.11), затем избавьтесь от производных по времени, используя
Третий и четвертый законы Максвелла используют стандартное векторное тождество
[41, 20.40] и, наконец, теорема о расходимости.Теперь предположим, что у вас есть конечное количество радиации в пустом пространстве. пространство. Если количество излучения конечно, поле должно исчезнуть в бесконечности. Итак, приняв объем за все пространство, интеграл в правой части выше будет равен нулю. Так будет быть постоянным. Это указывает на то, что должно быть как минимум кратно энергии. В конце концов, какая другая скалярная величина, кроме энергия будет постоянной? И фактор нужен из-за единиц. Это пропускает только фактор в выражение для энергии.
Тогда для произвольного объема поверхностный интеграл должен
– отток энергии через поверхность объема. Что
предполагает, что скорость потока энергии на единицу площади определяется выражением
так называемый «вектор Пойнтинга».
| (13.12) |
К сожалению, этот аргумент ошибочен. Вы не можете вывести местные значений потока энергии от его интеграла по всему замкнутому поверхность. В частности, вы можете найти различные векторы, описывающие поток энергии также непротиворечив. Просто добавьте произвольное соленоидальный вектор, вектор с нулевой дивергенцией, к вектору Пойнтинга вектор. Например, добавление кратного магнитного поля сделает Это. Однако, если вы посмотрите на простые световые волны, такие как (13.10), вектор Пойнтинга кажется интуитивным выбором. Этот абзац был включен, потому что в других книгах есть векторы Пойнтинга. и вы были бы очень разочарованы, если бы у вас этого не было.
Обычно вы не найдете уравнения Максвелла в точной форме.
описано здесь. Чтобы объяснить, что происходит внутри материалов, вы
пришлось бы учитывать электрические и магнитные поля каждого
электрон и протон (и нейтрон!) материала.
Это просто
невыполнимая задача, поэтому физики разработали способы усреднения всех
эти эффекты, искажая уравнения Максвелла. Но тогда
ошибка в одном из уравнений Максвелла больше не является
такой же, как испорченный в другом, и такой же для .
Поэтому физики переименовывают одну лажу в, может быть, плотность электрического потока
, и испорченный
магнитное поле как, может быть, вспомогательное поле
. И
они определяют множество других символов и даже относятся к вспомогательному полю
как магнитное поле, все для того, чтобы инженеры не
нанотехнологии. Не позволяйте им! Когда нужно понять
запутанные уравнения Максвелла, в Википедии есть список
бесчисленное множество определений.
Далее: 13.  |