Закон Джоуля — Ленца. Основные формулы и применение в быту
Автор newwebpower На чтение 7 мин. Просмотров 823 Опубликовано Обновлено
Джеймс Прескотт Джоуль (слева) и Эмилий Христианович Ленц (справа)Электрические нагреватели всевозможных типов используются человечеством уже столетия, благодаря свойству электрического тока выделять тепло при прохождении через проводник. У этого явления есть и негативный фактор – перегретая электропроводка из-за слишком большого тока часто становилась причиной короткого замыкания и возникновения пожаров. Выделение тепла от работы электрического тока изучалось в школьном курсе физики, но многие позабыли эти знания.
Впервые зависимость выделения теплоты от силы электрического тока была сформулирована и математически определена Джеймсом Джоулем в 1841 году, и чуть позже, в 1842 г.
Определение закона Джоуля – Ленца
В словесном определении, согласно исследований Джоуля и Ленца закон звучит так:
Количество теплоты, выделяемой в определенном объеме проводника при протекании электрического тока прямо пропорционально умножению плотности электрического тока и величины напряженности электрического поля
В виде формулы данный закон выглядит следующим образом:
Выражение закона Джоуля — ЛенцаВ словесном определении закон Джоуля Ленца звучит так:
Словесное определение закона Джоуля — ЛенцаЕсли принять, что сила тока и сопротивление проводника не меняется в течение времени, то закон Джоуля — Ленца можно записать в упрощенном виде:
Применив закон Ома и алгебраические преобразования, получаем приведенные ниже эквивалентные формулы:
Применение и практическое значение закона Джоуля – Ленца
Исследования Джоуля и Ленца в области тепловыделения от работы электрического тока существенно продвинули научное понимание физических процессов, а выведенные основные формулы не претерпели изменений и используются по сей день в различных отраслях науки и техники. В сфере электротехники можно выделить несколько технических задач, где количество выделяемой при протекании тока теплоты имеет критически важное значение при расчете таких параметров:
В сфере электротехники можно выделить несколько технических задач, где количество выделяемой при протекании тока теплоты имеет критически важное значение при расчете таких параметров:
- теплопотери в линиях электропередач;
- характеристики проводов сетей электропроводки;
- тепловая мощность (количество теплоты) электронагревателей;
- температура срабатывания автоматических выключателей;
- температура плавления плавких предохранителей;
- тепловыделение различных электротехнических аппаратов и элементов радиотехники.
Тепловое действие электрического тока в проводах линий электропередач (ЛЭП) является нежелательным из-за существенных потерь электроэнергии на тепловыделение.
По различным данным в линиях электропередач теряется до 40% всей производимой электрической энергии в мире. Для уменьшения потерь при передаче электроэнергии на большие расстояния, поднимают напряжение в ЛЭП, производя расчеты по производным формулам закона Джоуля – Ленца.
Очень упрощенно тепловую работу тока можно описать следующим образом: двигаются электроны между молекулами, и время от времени сталкиваются с ними, отчего их тепловые колебания становятся более интенсивными. Наглядная демонстрация тепловой работы тока и ассоциативные пояснения процессов показаны на видео ниже:
Расчеты потерь электроэнергии в линиях электропередач
В качестве примера можно взять гипотетический участок линии электропередач от электростанции до трансформаторной подстанции. Поскольку провода ЛЭП и потребитель электроэнергии (трансформаторная подстанция) соединены последовательно, то через них течет один и тот же ток I. Согласно рассматриваемому тут закону Джоуля – Ленца количество выделяемой на проводах теплоты Qw (теплопотерь) рассчитывается по формуле:
Производимая электрическим током мощность (Qc) в нагрузке рассчитывается согласно закону Ома:
Таким образом, при равенстве токов, в первую формулу можно вставить вместо I выражение Q
Если проигнорировать зависимость сопротивления проводников от изменения температуры, то можно считать Rw неизменным (константой). Таким образом, при стабильном энергопотреблении потребителя (трансформаторной подстанции), тепловыделение в проводах ЛЭП будет обратно пропорционально квадрату напряжения в конечной точке линии. Другими словами, чем больше напряжение электропередачи, тем меньше потери электроэнергии.
Таким образом, при стабильном энергопотреблении потребителя (трансформаторной подстанции), тепловыделение в проводах ЛЭП будет обратно пропорционально квадрату напряжения в конечной точке линии. Другими словами, чем больше напряжение электропередачи, тем меньше потери электроэнергии.
Работа закона Джоуля – Ленца в быту
В бытовых сетях электропроводки расстояния крайне малы, чтобы уменьшения тепловых потерь поднимать напряжение, поэтому при расчете проводки учитывается тепловая работа тока, согласно закону Джоуля – Ленца при выборе поперечного сечения проводов, чтобы их  Выбор кабеля по мощности и расчеты сечения электропроводки проводятся согласно таблиц и нормативных документов ПУЭ, и подробно описаны на других страницах данного ресурса.
Выбор кабеля по мощности и расчеты сечения электропроводки проводятся согласно таблиц и нормативных документов ПУЭ, и подробно описаны на других страницах данного ресурса.
При расчете температуры нагрева радиотехнических элементов, биметаллической пластины автоматического выключателя или плавкого предохранителя используется закон Джоуля – Ленца в интегральной форме, так как при росте температуры изменяется сопротивление данных материалов. При данных сложных расчетах также учитываются теплоотдача, нагрев от других источников тепла, собственная теплоемкость и множество других факторов.
Полезная тепловая работа электрического тока
Тепловыделяющая работа электрического тока широко применяется в электронагревателях, в которых используется последовательное соединение проводников с различным сопротивлением. Данный принцип работает следующим образом: в соединенных последовательно проводниках течет одинаковый ток, значит, согласно закону Джоуля – Ленца, тепла выделится больше у материала проводника с большим сопротивлением.
Таким образом, шнур питания и подводящие провода электроплитки остаются относительно холодными, в то время как нагревательный элемент нагревается до температуры красного свечения. В качестве материала для проводников нагревательных элементов используются сплавы с повышенным (относительно меди и алюминия электропроводки) удельным сопротивлением — нихром, константан, вольфрам и другие.
Нить лампы накаливания изготовляют из тугоплавких вольфрамовых сплавовЕсли прозвонить омметром лампочки, то окажется, что у более мощной лампы сопротивление меньше. На видео ниже автор демонстрирует последовательное и параллельное подключение, но к сожалению, он ошибся в комментарии — будет ярче светить лампа с
На видео ниже автор демонстрирует последовательное и параллельное подключение, но к сожалению, он ошибся в комментарии — будет ярче светить лампа с
формулировка закона, расчет теплоты по формуле i2rt
Одной из основополагающих, теоретически и практически значимых закономерностей физики можно смело назвать закон Джоуля Ленца, который англичанин Дж. Джоуль и россиянин Э.Х. Ленц вывели примерно в одно время (в 1840-1841 годах), однако при этом, не работая совместно.
Авторы закона: Джеймс Джоуль и Эмилий Ленц
Как был открыт закон
Оба физика проводили множество экспериментов, в которых главным действующим прибором был калориметр. Агрегат представлял собой устройство, изолированное от теплопотерь, у которого была измерена и зафиксирована теплоемкость. Калориметр был оснащен термометром, в него также вставлялся проводник с определенным электросопротивлением.
Калориметр был оснащен термометром, в него также вставлялся проводник с определенным электросопротивлением.
В результате опытов физики заметили, что при подключении проводника к электропитанию начинает выделяться тепло.
Воспроизведение опытов, с помощью которых была сформулирована закономерность Джоуля-Ленца
Джоуль проводил эти исследования в рамках изучения закона сохранения энергии. Он хотел оценить, какова величина механической энергии, давшей полученное количество теплоты. Для этого к динамо-машине, вращавшей ротор для выработки электричества, он привязывал некий груз и делал вывод, что разница между механической энергией груза в поле и вне поля тяготения и есть искомая величина. Англичанин доказал, что сделанные им выводы о преобразовании энергии применимы и для электролитических растворов.
Опыты Ленца более точные. Он определил, что открытая им закономерность не действует, если проводники двигаются, когда через них течет электроток (они называются проводники второго типа), такие как индуктивная катушка, находящаяся внутри электромотора.
Суть теплового закона
В проводнике, являющимся активным сопротивлением, по которому пропускается постоянное электричество, имеется электрическое поле, в котором упорядоченно протекают заряженные частицы. Электрофизические силы, присущие ему, оказывают воздействие на электроны, что имеет определение «работа тока» (Aэл.). Та работа, которая замеряется в единицу времени (как правило, час), считается мощностью тока (Nэл.). Обозначенные электромеханические показатели измеряются при помощи приборов: амперметра, вольтметра и ваттметра. Эти 2 понятия: работа и мощность тока, формируют закон Джоуля Ленца.
Работа тока на подключенном участке преобразовывает электроэнергию во внутреннюю. Это происходит за счет того, что свободные электроны натыкаются на нейтральные молекулы (лишенные электронов) проводника, и присущая им механическая энергия превращается в тепловую. Она способствует увеличению температуры проводника. Согласуясь со всемирным законом сохранения энергии, тот объем тепла (q) приравнивается к работе тока.
Всякое преодоление сопротивления неизбежно сопровождается затратами энергии. Если, к слову, что-то тяжелое приходится тянуть, преодолевая силу трения, то работа по ее преодолению становится теплом. В случае с током и полупроводником электросопротивление выступает в роли трения.
Российский и английский ученые пришли к выводу, что количество теплоты q, получаемое в полупроводнике при прохождении постоянного тока, прямо пропорционально величине тока (I), возведенной во вторую степень, и тому времени (t), что ток пропускался по проводнику, испытывая сопротивление (R).
Знаменитый закон Лжоуля Ленца можно описать формулой:
Q =I2Rt.
Это закономерность – закон Джоуля-Ленца, применимый на однородном участке электроцепи. При этом количество тепла q может вычисляться в Джоулях (если сила тока равна 1) и в малых калориях (если сила тока 0,24). Малая калория – это количество тепла, расходуемое на нагрев 1 грамма воды на один градус.
Интегральная и дифференциальная формулы закона
Если обратить внимание на величину, представляющую разность внутренней энергии проводника за время прохождения по нему тока, можно заметить, что постепенно при нагревании эта энергия будет увеличиваться. Следуя закону Ньютона, можно предположить, что увеличится и мощность отдачи тепла q проводником. Через определенный промежуток времени температура полупроводника зафиксируется и перестанет расти. В это время внутренняя энергия перестанет меняться, и значение «дельта U» станет равно нулю. В таком равновесии формулировка 1-го термодинамического закона будет следующей:
Следуя закону Ньютона, можно предположить, что увеличится и мощность отдачи тепла q проводником. Через определенный промежуток времени температура полупроводника зафиксируется и перестанет расти. В это время внутренняя энергия перестанет меняться, и значение «дельта U» станет равно нулю. В таком равновесии формулировка 1-го термодинамического закона будет следующей:
A = – Q, т.е. работа тока полностью переходит в тепло.
Основываясь на этом выводе, можно представить тепловую закономерность Джоуля Ленца в несколько другом виде, а именно в ее интегральном и дифференциальном видах.
Закон Джоуля Ленца в интегральной и дифференциальной формах
Формула интегрального закона Джоуля-Ленца справедлива при любых данных, поэтому она считается законом. Другие же формулировки типа:
q=I*Ut и q=u2/R*t
работают лишь при определенных условиях, и их нельзя считать законом.
Дополнительная информация. Если углубляться в теорию и проводить дальнейшие расчеты, то можно вывести и другие формы данного теплового закона.
Теоретическая значимость
Открытие двух знаменитых физиков стало заметной вехой на пути к исследованию и всемирному принятию закона сохранения энергии. Благодаря ему, сегодня общеизвестно, что и тепло, и электроток, и движение механических частиц – есть формы материи, обладающие своей энергией, которую можно измерить. Закон Джоуля-Ленца (и последующие работы Джоуля) помогли установить соответствия для электрического, механического и теплового вида энергии и определить переводные соотношения между единицами различных видов (калории и джоули). Тепловая закономерность применяется и в разработке теории тока в металлах.
Обратите внимание! Поскольку тепло всегда вырабатывается в проводнике, находящемся под электрическим током, может случиться его перегрев и, как следствие, выход из строя электрических устройств. Особенно опасным явлением является короткое замыкание, когда сопротивление проводников стремится к нулю, ток становится очень сильным, соответственно, выделяется огромное количество тепла, приводящее к аварийным состояниям.
Чрезмерное выделение тепловой энергии при коротком замыкании
С помощью закона Джоуля-Ленца можно рассчитать оптимальную силу электротока, чтобы предотвратить перегрев проводников.
Попробуйте сформулируйте положение о том, как электричество переходит в тепло? Англичанину Джоулю и россиянину Ленцу это блестяще удалось: в открытом ими тепловом законе, гласящем, что электрический ток, проходящий по проводнику, выделяет тепло, равное работе электрических сил. Это наблюдение оказало большое влияние на дальнейшее развитие физики как науки.
Видео
Оцените статью:Определение и применение на практике закона Джоуля-Ленца — формула и правила расчета
Физики из Англии Джеймс Джоуль и Эмилий Ленц, по отдельности, но примерно в одно время 1841-1842 годах выяснили взаимосвязь количества тепла и поток тока внутри проводника. Эта зависимость была названа «Закон Джоуля-Ленца».
Эта зависимость была названа «Закон Джоуля-Ленца».
Английский физик заметил эту зависимость, раньше, чем русский физик на 1 год, однако назвали закон, соединив обе фамилии, т.к. как вклад каждого из них был велик. Закон Джоуля-Ленца описывает не теорию, а практику.
Давайте рассмотрим закон Джоуля-Ленца, его определение и применение в жизни.
Когда в проводнике протекает ток, то происходит работа поперек силам трения. При движении электроном через провод происходит столкновение электронов с иными электронами, атомами и другими частицами, в следствие чего вырабатывается тепло.
Рассматриваемый нами закон объясняет то количество тепла, которое вырабатывается при движении тока по проводнику.
При увеличении силы тока, сопротивления и времени протекания, количество тепла тоже увеличится, и наоборот при уменьшении этих показателей произойдет уменьшение количества тепла.
Формула закона Джоуля-Ленца представлена на рисунке.рис.1
Рисунок 1. Формула закона Джоуля-Ленца, при последовательном соединении
Формула закона Джоуля-Ленца, при последовательном соединении
Сила тока – I считается в амперах, сопротивление- R в омах, время t- в секундах. Теплота Q измеряется в джоулях. Для перевода в калории умножаем на 0,24. 1 калория рассчитывается, как то тепло, которое необходимо дать воде, чтобы повысить ее на 1 градус.
Эта формула применяется, если проводники соединяются последовательно, при проходе равной величины тока, а на концах падает разное напряжение. Мощность определяется как сила тока в квадрате, умноженная на сопротивление.
Увеличение мощности сопровождает увеличение квадрата напряжения и уменьшает сопротивление, и наоборот. Если электрические цепи соединяются параллельно, то закон Джоуля-Ленца выглядит: рис.2
Рисунок 2. Формула закона Джоуля-Ленца, при параллельном соединении
При использовании дифференциальной формы, формула такая: рис.3
Рисунок 3. Дифференциальная форма формулы закона Джоуля-Ленца
j является плотностью тока в А/см2, E — напряженностью электрического поля, сигма — удельным сопротивлением проводника.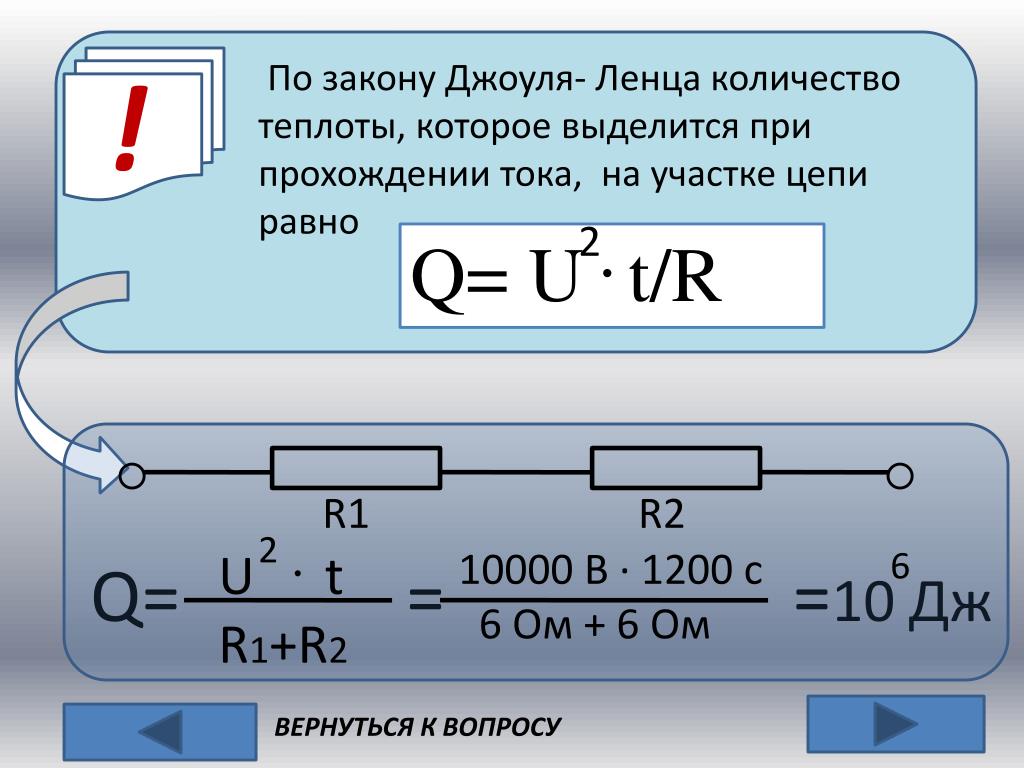
Если участок цепи однородный, то сопротивление будет одинаково. При наличии в цепях проводников с различным сопротивлением, то самое большое тепло выделится там, где находится максимальное сопротивление. К такому выводу мы приходим, анализируя формулу Джоуля-Ленца.
Нередкие проблемы
Итак, проблема нахождения времени, т.е. тот период, когда ток проходит по проводнику (замкнутая цепь)
Вторая проблема, нахождение сопротивления проводника. Используется формула рельс:рис.4
Рисунок 2. Формула нахождение сопротивления проводника
«Р» удельное сопротивление, измеряемое в Ом*м/см2, l и S является длина и площадь поперечного сечения. При математических операциях метры и сантиметры2 сокращаются и получаются Омы.
Удельным сопротивлением является величина, указанная в таблице, индивидуальная для каждого металла. Рассмотрим с какой целью это используется.
При электротехнических подсчетах широко используется закон Джоуля-Ленца.
Можно использовать его, когда рассчитываются приборы нагревания. Нагревающий элемент – проводник с высоким сопротивлением, например нихром.
Для расчета мощности тепла прибора нужно определить, что и в каком объеме нужно нагреть, количество теплоты и времени на передачу тепла телу.
После расчета определится сопротивление и сила тока в данной цепи. Учитывая полученные данные, выбирается материал сечение и длина проводника.
Использование закона Джоуля-Ленца для передачи электроэнергии на расстояние
Закон Джоуля-Ленца
Когда происходит передача электричества на расстояние, появляется проблема потери на линиях передач. Закон показывает количество тепла, которое выделяется проводником при проходе тока.
ЛЭП используются предприятиями и городами, следственно необходимо больше мощности и больше тока.
Количество теплоты связано с сопротивлением тока и проводника, для того чтобы избежать нагрева, необходимо уменьшить количество тепла.
Не всегда можно использовать сечение провода, это дорого стоит из-за цены меди и веса кабелей, следовательно, увеличивается стоимость несущей конструкции.
На рисунке показаны высоковольтные линии электропередач. Это огромные конструкции из металла, создающиеся для поднятия кабеля на высоту, безопасную для людей на земле, чтобы избежать удара током.
Для этого необходимо снизить ток, следовательно, повышается напряжение.
Линии электропередач между городами используют напряжение 220 и 110 кВ, а у того, кто потребляет, понижают до необходимой величины, используя трансформатные подстанции. Или множеством КТП медленно понижая до безопасной величины, например, 6кВ.
То есть ток уменьшится в тысячи раз, но при той же потребляемой мощности. По закону Джоуля-Ленца, теплота в данном случае определится мощностью, которая теряется на кабеле.
Плавкие предохранители
Закон Джоуля-Ленца используется для расчета плавких предохранителей. Это элементы, защищающие электрическое устройство от высоких для него токов, которые могут появится из-за скачка напряжения, короткого замыкания для охраны от поломки электрической системы и пожара. Они представляют собой корпус, изолятор и тонкую проволоку.
Это элементы, защищающие электрическое устройство от высоких для него токов, которые могут появится из-за скачка напряжения, короткого замыкания для охраны от поломки электрической системы и пожара. Они представляют собой корпус, изолятор и тонкую проволоку.
Проволока используется с сечением, подходящим для прохода номинального тока через нее, но при увеличении выделения тепла, она пережигается.
Следовательно, можно сделать вывод, что рассматриваемый нами закон Джоуля-Ленца очень широко применяется и сильно значим для электротехники.
Используя информацию про количество теплоты, исчисляемое по рассмотренным формулам, можно разузнать о режимах работы устройств, определить подходящий материал и сечение для обеспечения безопасности, увеличения срока использования прибора или цепи.
На этом я закончу данную статью. Надеюсь, эта информация стала полезной и интересной для вас.
Определение и формула закона Джоуля-Ленца: работа и мощность тока
Основные понятия
Базовое определение можно сформулировать следующим образом: количество тепла, которое выделяет проводник, пропорционально проходящему через него току и электрическому сопротивлению контрольного участка. С учетом классических отношений, установленных законом Ома, можно выражать эту зависимость через проводимость и разницу потенциалов, которая провоцирует движение заряженных частиц.
С учетом классических отношений, установленных законом Ома, можно выражать эту зависимость через проводимость и разницу потенциалов, которая провоцирует движение заряженных частиц.
Что это за закон
Закон джоуля ленца определение гласит, что это физический норматив, который определяет количественный вид меры теплового действия электротока. В девятнадцатом столетии, вне зависимости друг от друга Джоуль с российским ученым Ленцем стали изучать, как нагреваются проводники в момент прохождения электротока и нашли некую закономерность. Они узнали, что в момент прохождения электротока по проводниковому элементу получается тепло, которое равно силе тока, времени и проводниковому сопротивлению.
Обратите внимание! Это закономерность была названа законом в честь двух ученых. Стоит указать, что эта закономерность активно используется с момента открытия и по сегодняшний день и помогает решить многие вопросы, связанные с электрикой.
История появления формулировки закона ученых
Немного истории
Многочисленные опыты, проведенные в конце XVIII – начале XIX века, позволили не только установить основные свойства и законы электричества, но и сформулировать эпохальный по своей значимости вывод об эквивалентности между теплотой и механической работой: работа, или, как впоследствии стали формулировать, «энергия», никогда не теряется, а лишь переходит из одного вида в другой. Этот вывод, получивший впоследствии название закона сохранения и превращения энергии (см. подраздел 1.2), и заключался в том, что теплоту можно обратить в механическую работу и наоборот и что из определенного количества теплоты можно получить только определенное количество механической работы. Можно привести тысячи примеров, когда с помощью этого закона нашли свое объективное толкование результаты опытов в различных областях естествознания.
Этот вывод, получивший впоследствии название закона сохранения и превращения энергии (см. подраздел 1.2), и заключался в том, что теплоту можно обратить в механическую работу и наоборот и что из определенного количества теплоты можно получить только определенное количество механической работы. Можно привести тысячи примеров, когда с помощью этого закона нашли свое объективное толкование результаты опытов в различных областях естествознания.
Закон Джоуля Ленца кратко
Основными положениями закона сохранения энергии воспользовались и электротехники при определении, например, количества тепловой энергии, выделяющегося в гальванической батарее вследствие химической реакции и превращающегося впоследствии в электрическую энергию. Однако особенность электрической энергии состоит в том, что само по себе электричество неприменимо. Человечество не может использовать его непосредственно подобно тому, как оно согревается теплотой, видит благодаря свету и т.п. Можно пользоваться только действием электрического тока, при котором электричество переходит в другие формы энергии.
Одним из первых глубоко исследовал свойства электрического тока в 1801–1802 годах петербургский академик В.В. Петров (1761– 1834), который провел множество экспериментов по изучению неизвестных в то время законов электрического тока. Изучив работы своих предшественников, Петров пришел к выводу, что более полное и всестороннее исследование электрического тока возможно лишь с помощью крупных гальванических батарей, действие которых будет более интенсивным и легче наблюдаемым. Для своих опытов Петров построил самую крупную в мире в те годы батарею из 4200 медных и цинковых кружков, уложенных в четырех деревянных ящиках, и получил от нее электродвижущую силу около 1700 вольт. Благодаря «лежачей» конструкции тяжелые металлические кружки не выдавливали жидкости, которой пропитывались бумажные кружки, разделяющие цинковые и медные элементы. Для изоляции он покрыл внутренние стенки ящиков сургучным лаком. Общая длина батареи составила 12 м. Все это позволило ему построить «огромную наипаче» батарею, которой не знал ещё мир. Уже в 1801 году он нашел зависимость силы тока от поперечного сечения проводника, в то время как немецкий физик Ом, работавший над этими проблемами, опубликовал результаты своих опытов только в 1827 году. Очень скоро им было замечено, что при прохождении электрического тока по проводнику последний нагревается.
Уже в 1801 году он нашел зависимость силы тока от поперечного сечения проводника, в то время как немецкий физик Ом, работавший над этими проблемами, опубликовал результаты своих опытов только в 1827 году. Очень скоро им было замечено, что при прохождении электрического тока по проводнику последний нагревается.
В своих работах В.В. Петров описывает опыты по электролизу растительных масел, в результате которых он обнаружил высокие электроизоляционные свойства этих масел. Позднее масла получили широкое применение в качестве электроизоляционного материала. Желая продемонстрировать явление электролиза одновременно в нескольких трубках с водой, Петров впервые применил параллельное соединение приемников электрического тока. Работы этого выдающегося ученого установили возможность практического использования электрического тока для нагревания проводников.
Эмилий Христианович Ленц (1804–1865) – известный российский физик и электротехник, академик Петербургской академии наук, ректор Петербургского университета – родился в Дерпте (ныне Тарту, Эстония) в семье чиновника.
После второго курса Дерптского университета отправился в 1823 году в трехлетнее кругосветное плавание. С помощью сконструированных им приборов (глубометра и батометра) занимался физическими исследованиями в водах Берингова пролива, Тихого и Индийского океанов, установил происхождение теплых и холодных морских течений, открыл закон океанических циркуляций. В 1829 г. принял участие в экспедиции на Кавказ, где проводил магнитные, термометрические и барометрические измерения в горных районах Кавказа и на побережье Каспийского моря. В 1830 году был назначен экстраординарным профессором и директором физического кабинета при Петербургской АН, в 1836 г. возглавил кафедру физики в Петербургском университете, а в 1863 г. стал ректором этого университета. Основные его работы посвящены электромагнетизму, вопросам теории и практического применения электричества, исследования в области которого Ленц начал в 1831 году в лаборатории первого русского электротехника – академика В.В. Петрова. Ленц стоял у истоков первой в России школы физиков-электротехников, последователями которой стали А.
С. Попов, Ф.Ф. Петрушевский, В.Ф. Миткевич и др.
Зависимость количества выделяемой теплоты от силы тока изучали английский физик Джеймс Джоуль и русский физик Эмилий Ленц. Они пропускали ток по спирали, помещенной в калориметр с водой. Через некоторое время вода нагревалась. По её температуре легко было вычислить количество выделившейся теплоты. Из проведенных опытов практически одновременно Джоуль и Ленц пришли к выводу, что при прохождении гальванического тока I по проводнику, обладающему определенным сопротивлением R, в течение времени t совершается работа А :
А = I 2 Rt,
проявляющаяся в виде выделившейся теплоты.
Этот важнейший вывод обратимости электрической и тепловой энергии, теоретически обоснованный Уильямом Томсоном, получил название закона Джоуля–Ленца, а именем Джоуля названа единица механической работы в системе СИ.
Комбинируя проводники различного сопротивления, включенные последовательно в общую цепь, можно добиться концентрированного выделения большого количества теплоты на малом участке проводника с большим сопротивлением. На таком концентрировании выделения теплоты были основаны все первоначальные опыты превращения энергии электрического тока в тепловую и даже в световую энергию.
На таком концентрировании выделения теплоты были основаны все первоначальные опыты превращения энергии электрического тока в тепловую и даже в световую энергию.
Суть данного закона
Всю свою жизнь В.В. Петров – член двух академий – прожил скромно и незаметно. 41 год он проработал в Медико-хирургической академии. За это время он провел много физических опытов, написал три книги и учебник по физике, которым пользовались в гимназиях всей России. Книги и научные статьи Петров писал на русском языке, чтобы их читало как можно больше людей, хотя в то время научные работы было принято писать на латыни. Он писал: «Я надеюсь, что просвещенные и беспристрастные физики по крайней мере некогда согласятся отдать трудам моим ту справедливость, которую важность сих последних опытов заслуживает».
Где может пригодиться этот закон Джоуля-Ленца?
В электротехнике есть понятие длительно допустимого тока протекающего по проводам. Это такой ток, который провод способен выдержать длительное время (то есть, бесконечно долго), без разрушения провода (и изоляции, если она есть, потому что провод может быть и без изоляции). Конечно, данные вы теперь можете взять из ПУЭ (Правила устройства электроустановок), но получали эти данные исключительно на основе закона Джоуля-Ленца.
Конечно, данные вы теперь можете взять из ПУЭ (Правила устройства электроустановок), но получали эти данные исключительно на основе закона Джоуля-Ленца.
В электротехнике так же используются плавкие предохранители. Их основное качество – надёжность срабатывания. Для этого используется проводник определенного сечения. Зная температуру плавления такого проводника можно вычислить количество теплоты, которое необходимо, чтобы проводник расплавился от протекания через него больших значений тока, а вычислив ток, можно вычислить и сопротивление, которым такой проводник должен обладать. В общем, как вы уже поняли, применяя закон Джоуля-Ленца можно рассчитать сечение или сопротивление (величины взаимозависимы) проводника для плавкого предохранителя.
А ещё, помните, мы говорили про последовательное и параллельное соединение сопротивлений. Там на примере лампочки я рассказывал парадокс, что более мощная лампа в последовательном соединении светит слабее. И наверняка помните почему: падение напряжения на сопротивлении тем сильнее, чем меньше сопротивление.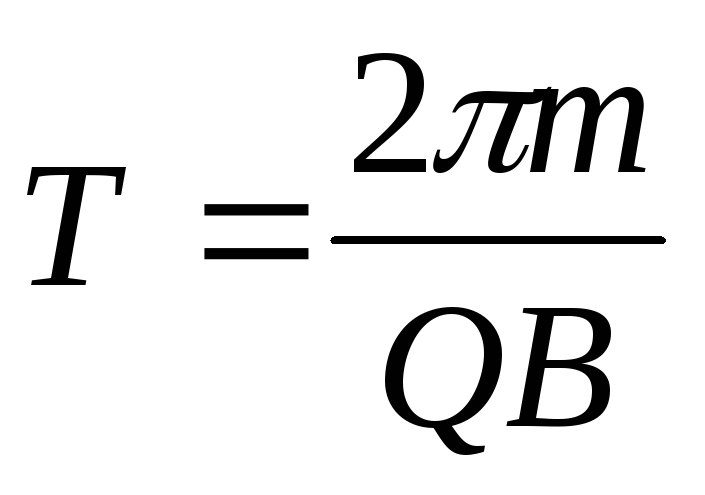 А поскольку мощность — это произведение силы тока и напряжения, а напряжение очень сильно падает, то и выходит, что большое сопротивление выделит большое количество тепла, то есть, току придется больше потрудиться, чтобы преодолеть большое сопротивление. И количество тепла, которое выделит ток при этом можно посчитать с помощью закона Джоуля-Ленца. Если брать последовательное соединение сопротивлений, то использовать лучше выражение через квадрат тока, то есть, изначальный вид формулы:
А поскольку мощность — это произведение силы тока и напряжения, а напряжение очень сильно падает, то и выходит, что большое сопротивление выделит большое количество тепла, то есть, току придется больше потрудиться, чтобы преодолеть большое сопротивление. И количество тепла, которое выделит ток при этом можно посчитать с помощью закона Джоуля-Ленца. Если брать последовательное соединение сопротивлений, то использовать лучше выражение через квадрат тока, то есть, изначальный вид формулы:
А для параллельного соединения сопротивлений, поскольку ток в параллельных ветвях зависит от сопротивления, в то время, как напряжение на каждой параллельной ветви одинаковое, то формулу лучше всего представить через напряжение:
Ну и наконец, если мы хотим посчитать, сколько тепла выделяет вся цепь, включая даже сопротивление проводов, нам достаточно взять напряжение цепи и ток цепи и формула будет выглядеть так:
Примерами работы закона Джоуля-Ленца вы все пользуетесь в повседневной жизни – в первую очередь это всевозможные нагревательные приборы. Как правило, в них используется нихромовая проволока и толщина (поперечное сечение) и длина проводника подбираются с учётом того, чтобы длительное тепловое воздействие не приводило к стремительному разрушению проволоки. Точно таким же образом добиваются свечения вольфрамовой нити в лампе накаливания. По этому же закону определяют степень возможного нагрева практически любого электротехнического и электронного устройства.
Как правило, в них используется нихромовая проволока и толщина (поперечное сечение) и длина проводника подбираются с учётом того, чтобы длительное тепловое воздействие не приводило к стремительному разрушению проволоки. Точно таким же образом добиваются свечения вольфрамовой нити в лампе накаливания. По этому же закону определяют степень возможного нагрева практически любого электротехнического и электронного устройства.
В общем, несмотря на кажущуюся простоту, закон Джоуля-Ленца играет в нашей жизни очень огромную роль. Этот закон дал большой толчок для теоретических расчётов: выделение тепла токами короткого замыкания, вычисление конкретной температуры дуги, проводника и любого другого электропроводного материала, потери электрической мощности в тепловом эквиваленте и т.д.
Вы можете спросить, а как перевести Джоули в Ватты и это довольно частый вопрос в интернете. Хотя вопрос несколько неверный, читая далее, вы поймёте почему. Ответ довольно прост: 1 дж = 0.000278 Ватт*час, в то время, как 1 Ватт*час = 3600 Джоулей.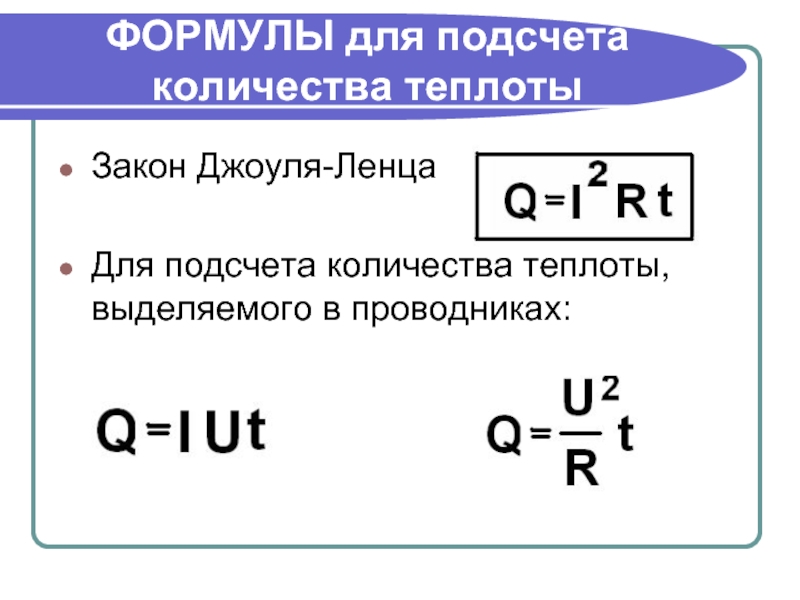 Напомню, что в Ваттах измеряется потребляемая мгновенная мощность, то есть непосредственно используемая пока включена цепь. А Джоуль определяет работу электрического тока, то есть мощность тока за промежуток времени. Помните, в законе Ома я приводил аллегорическую ситуацию. Ток – деньги, напряжение – магазин, сопротивление – чувство меры и денег, мощность – количество продуктов, которые вы сможете на себе унести (увезти) за один раз, а вот как далеко, как быстро и сколько раз вы сможете их увезти – это работа. То есть, сравнить работу и мощность никак не получается, но можно выразить в более понятных нам единицам: Ваттах и часах.
Напомню, что в Ваттах измеряется потребляемая мгновенная мощность, то есть непосредственно используемая пока включена цепь. А Джоуль определяет работу электрического тока, то есть мощность тока за промежуток времени. Помните, в законе Ома я приводил аллегорическую ситуацию. Ток – деньги, напряжение – магазин, сопротивление – чувство меры и денег, мощность – количество продуктов, которые вы сможете на себе унести (увезти) за один раз, а вот как далеко, как быстро и сколько раз вы сможете их увезти – это работа. То есть, сравнить работу и мощность никак не получается, но можно выразить в более понятных нам единицам: Ваттах и часах.
Думаю, что теперь вам не составит труда применить закон Джоуля-Ленца в практике и теории, если таковое потребуется и даже сделать перевод Джоулей в Ватты и наоборот. А благодаря пониманию, что закон Джоуля-Ленца это произведение электрической мощности на время, вы сможете более легко его запомнить и даже, если вдруг забыли основную формулу, то помня всего лишь закон Ома можно снова получить закон Джоуля-Ленца.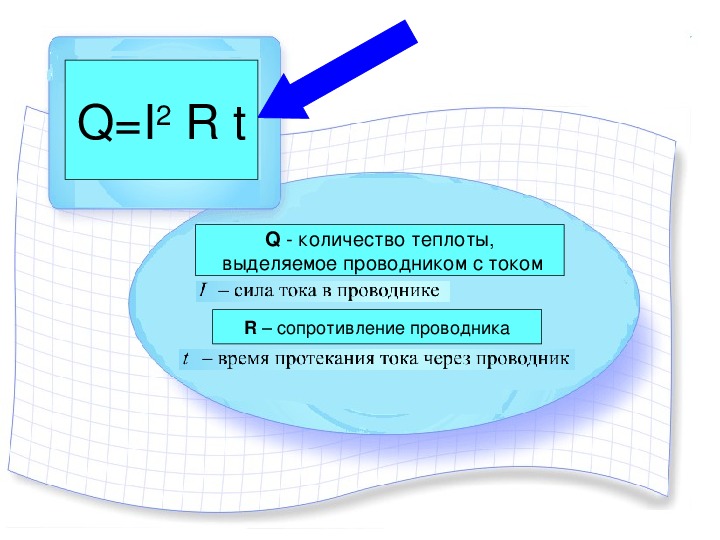 А я на этом с вами прощаюсь.
А я на этом с вами прощаюсь.
Тепловое действие электрического тока
Еще в девятнадцатом веке опыты по изучению проводимости свидетельствовали, что ток, проходящий по нагрузке, нагревает ее. Исследования показали, что нагревается не только нагрузка, но и проводники.
Рис. 1. Тепловое действие электрического тока.
Данный факт легко объясним, если вспомнить, что электрический ток – это перемещение зарядов в веществе нагрузки. При движении заряды взаимодействуют с ионами кристаллической решетки, и отдают им часть энергии, которая и переходит в тепло.
Свойства электрического тока
Когда электрический ток проходит через металлический проводник, его электроны постоянно сталкиваются с различными посторонними частицами. Это могут быть обычные нейтральные молекулы или молекулы, потерявшие электроны. Электрон в процессе движения может отщепить от нейтральной молекулы еще один электрон.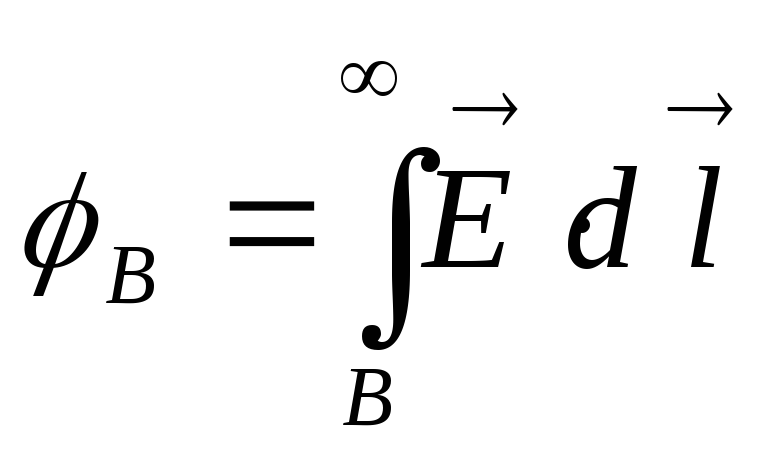 В результате, его кинетическая энергия теряется, а вместо молекулы происходит образование положительного иона. В других случаях электрон, наоборот, соединиться с положительным ионом и образовать нейтральную молекулу.
В результате, его кинетическая энергия теряется, а вместо молекулы происходит образование положительного иона. В других случаях электрон, наоборот, соединиться с положительным ионом и образовать нейтральную молекулу.
В процессе столкновений электронов и молекул происходит расход энергии, в дальнейшем превращающейся в тепло. Затраты определенного количества энергии связаны со всеми движениями, во время которых приходится преодолевать сопротивление. В это время происходит превращение работы, затраченной на преодоление сопротивления трения, в тепловую энергию.
Сопротивление в электрических проводниках обладает теми же качествами, как и у обычного сопротивления. Для того чтобы провести ток через проводник, источником тока затрачивается определенное количество энергии, превращающейся в тепло. Данное превращение как раз и отражает закон Джоуля – Ленца, известного также, как закон теплового действия тока.
Формулировка
Закон джоуля ленца формулировка словесно выглядит следующим образом: мощность тепла, которая выделяется в проводниковом элементе в момент протекания в нем электротока имеет пропорциональную зависимость умножения плотности электрополя на напряженность.
Его по-другому можно сформулировать так: энергия, протекая по проводнику, перемещает электрозаряд в электрополе. Так, электрополе совершает работу. Работа производится благодаря проводниковому нагреванию. Энергия превращается в тепло.
Однако, из-за чрезмерного проводникового нагрева при помощи тока и электрооборудования, может повредиться проводка и сами аппараты. Сильное перегревание опасно, когда есть короткое замыкание в проводах. Из-за этого проводники могут иметь большое токовое значение.
Что касается интегральной формы тонких проводников правило или уравнение Джоуля — Ленца звучит так: то тепло, которое выделяется за время в конкретном участке электроцепи, определяется квадратным произведением токовой силы на сопротивление участка.
Обратите внимание! Закон Джоуля-Ленца обладает достаточно общим характером, потому что не имеет зависимости от природы, силу которой генерирует электроток.
Из практики можно утверждать, что он справедлив, как для электролитов, так проводников и полупроводников.
Упрощенная формулировка
Частые вопросы
Как найти время? Здесь имеется в виду период протекания тока через проводник, то есть когда цепь замкнута.
Как найти сопротивление проводника? Для определения сопротивления используют формулу, которую часто называют “рельс”, то есть:
Здесь буквой «Ро» обозначается удельное сопротивление, оно измеряется в Ом*м/см2, l и S это длина и площадь поперечного сечения. При вычислениях метры и сантиметры квадратные сокращаются и остаются Омы.
Удельное сопротивление — это табличная величина и для каждого металла она своя. У меди на порядки меньше, чем у высокоомных сплавов типа вольфрама или нихрома. Для чего это применяется мы рассмотрим ниже.
О законе Джоуля Ленца
Рассмотрим произвольный участок цепи постоянного тока, к концам которого приложено напряжение U. За время t через каждое сечение проводника проходит заряд . Это равносильно тому, что заряд q переносится за время t из одного конца проводника в другой.
Интересный материал:Все о законе Ома
При этом силы электростатического поля и сторонние силы, действующие на данном участке, совершают работу . Разделив работу на время t, за которое она совершается, получим мощность, развиваемую током на рассматриваемом участке .
Эмилий Ленц
Эта мощность может расходоваться на совершение работы над внешними телами; на протекание химических реакций; на нагревание данного участка цепи и др.
В случае, когда проводник неподвижен и химических превращений в нем не совершается, работа тока затрачивается на увеличение внутренней энергии проводника, в результате чего проводник нагревается. Принято говорить, что при протекании тока в проводнике выделяется тепло
Это соотношение называется законом Джоуля – Ленца. Оно было экспериментально установлено английским физиком Д. П. Джоулем и подтверждено точными опытами Э. Х. Ленца.
Если сила тока изменяется со временем, то количество теплоты, выделяющееся в проводнике за время t, вычисляется по формуле
От формулы (4. 1), можно перейти к выражению, характеризующему выделение тепла в различных точках проводника. Выделим в проводнике элементарный объем в виде цилиндра. Согласно закону Джоуля – Ленца, за время dt, в этом объеме выделится количество теплоты
1), можно перейти к выражению, характеризующему выделение тепла в различных точках проводника. Выделим в проводнике элементарный объем в виде цилиндра. Согласно закону Джоуля – Ленца, за время dt, в этом объеме выделится количество теплоты
где – dV элементарный объем. Разделив это выражение на dV и dt, найдем количество теплоты, выделяющееся в единице объема в единицу времени:
Величину называют удельной тепловой мощностью тока. Эта формула представляет собой дифференциальную форму закона Джоуля – Ленца.
Вопросы
- В чем заключается физический смысл удельной тепловой мощности тока
2) Напишите закон Джоуля-Ленца в интегральной и дифференциальной формах
В чем измеряется
Единица теплового измерения это джоуль. Формула состоит из напряжения, измеряемого в вольтах, силы тока, измеряемого в амперах, и времени, измеряемой в секундах. Тогда выходит, что показатели будут измеряться в джоулях или одном вольте, перемноженном на ампер и секунду.
Единица измерения тепла, выделяемого электричеством
Использование теплового действия электричества
Тепловое действие электрического тока находит широкое применение, в первую очередь, в нагревательных приборах.
Еще одним важным направлением использования теплового действия являются плавкие предохранители. Если необходимо отключить электрическую цепь при превышение допустимого тока, то в цепь можно включить плавкий предохранитель.
Рис. 3. Устройство плавкого предохранителя.
Это небольшая колба из негорючего материала, внутри которой проходит плавкая проволочка или лента, сопротивление которой рассчитано так, чтобы при превышении предельного тока она расплавилась, тем самым разорвав электрическую цепь.
Квартирные предохранители
Чтобы улучшить защиту и обезопасить электрические цепи, используются особые предохранители. В роли главной части выступает проволока из легкоплавкого металла. Она проходит в пробке из фарфора, имеет винтовую нарезку и контакт в центре. Пробку вставляют в патрон, расположенный в фарфоровой коробке.
Пробку вставляют в патрон, расположенный в фарфоровой коробке.
Свинцовая проволока является частью общей цепи. Если тепловое действие электрического тока резко возрастет, сечение проводника не выдержит, и он начнет плавиться. В результате этого сеть разомкнется, и не случится токовых перегрузок.
Почему греется проводник
Как же объясняется нагрев проводника? Почему он именно греется, а не остаётся нейтральным или охлаждается? Нагрев происходит из-за того, что свободные электроны, перемещающиеся в проводнике под действием электрического поля, бомбардируют атомы молекул металла, тем самым передавая им собственную энергию, которая переходит в тепловую. Если изъясняться совсем просто: преодолевая материал проводника, электрический ток как бы “трётся”, соударяется электронами о молекулы проводника. Ну а , как известно, любое трение сопровождается нагревом. Следовательно, проводник будет нагреваться пока по нему бежит электрический ток.
Из формулы также следует – чем выше удельное сопротивление проводника и чем выше сила тока протекающего по нему, тем выше будет нагрев . Например, если последовательно соединить проводник-медь (удельное сопротивление 0,018 Ом·мм²/м) и проводник-алюминий (0,027 Ом·мм²/м), то при протекании через цепь электрического тока алюминий будет нагреваться сильнее чем медь из-за более высокого сопротивления. Поэтому, кстати, не рекомендуется в быту делать скрутки медных и алюминиевых проводов друг с другом – будет неравномерный нагрев в месте скрутки. В итоге – подгорание с последующим пропаданием контакта.
Например, если последовательно соединить проводник-медь (удельное сопротивление 0,018 Ом·мм²/м) и проводник-алюминий (0,027 Ом·мм²/м), то при протекании через цепь электрического тока алюминий будет нагреваться сильнее чем медь из-за более высокого сопротивления. Поэтому, кстати, не рекомендуется в быту делать скрутки медных и алюминиевых проводов друг с другом – будет неравномерный нагрев в месте скрутки. В итоге – подгорание с последующим пропаданием контакта.
Интегральная и дифференциальная формулы закона
Если обратить внимание на величину, представляющую разность внутренней энергии проводника за время прохождения по нему тока, можно заметить, что постепенно при нагревании эта энергия будет увеличиваться. Следуя закону Ньютона, можно предположить, что увеличится и мощность отдачи тепла q проводником. Через определенный промежуток времени температура полупроводника зафиксируется и перестанет расти. В это время внутренняя энергия перестанет меняться, и значение «дельта U» станет равно нулю. В таком равновесии формулировка 1-го термодинамического закона будет следующей:
В таком равновесии формулировка 1-го термодинамического закона будет следующей:
A = – Q, т.е. работа тока полностью переходит в тепло.
Основываясь на этом выводе, можно представить тепловую закономерность Джоуля Ленца в несколько другом виде, а именно в ее интегральном и дифференциальном видах.
Закон Джоуля Ленца в интегральной и дифференциальной формах
Формула интегрального закона Джоуля-Ленца справедлива при любых данных, поэтому она считается законом. Другие же формулировки типа:
q=I*Ut и q=u2/R*t
работают лишь при определенных условиях, и их нельзя считать законом.
Дополнительная информация. Если углубляться в теорию и проводить дальнейшие расчеты, то можно вывести и другие формы данного теплового закона.
Применение и практический смысл
Непосредственноепревращение электричества в тепловую энергию нельзя назвать экономическивыгодным. Однако, с точки зрения удобства и доступности современногочеловечества к источникам электроэнергии различные нагревательные приборыпродолжают массово применяться как в быту, так и на производстве.
Перечислим некоторые из них:
- электрочайники;
- утюги;
- фены;
- варочные плиты;
- паяльники;
- сварочныеаппараты и многое другое.
На рисунке 3 изображены бытовые нагревательные приборы, которыми мы часто пользуемся.
Рис. 3. Бытовые нагревательные приборы
Использование тепловых мощностей в химической, металлургической и в других промышленных отраслях тесно связно с использованием электрической энергии.
Без знания физического закона Джоуля-Ленца было бы невозможно сконструировать безопасный нагревательный прибор. Для этого нужны расчёты, которые невозможно сделать без применения рассмотренных нами формул. На основе расчётов происходит выбор материалов с нужным удельным сопротивлением, влияющим на нагревательную способность устройств.
Закон Джоуля-Ленца без преувеличения можно назвать гениальным. Это один из тех законов, которые повлияли на развитие электротехники.
Лампочка накаливания
Тепловое действие тока и открытие закона способствовали развитию электротехники и увеличению возможностей для использования электричества. То, как применяются результаты исследований, можно рассмотреть на примере обычной лампочки накаливания.
То, как применяются результаты исследований, можно рассмотреть на примере обычной лампочки накаливания.
Она устроена таким образом, что внутри протягивается нить, изготовленная из вольфрамовой проволоки. Этот металл является тугоплавким с высоким удельным сопротивлением. При проходе через лампочку осуществляется тепловое действие электрического тока.
Энергия проводника трансформируется в тепловую, спираль нагревается и начинает светиться. Недостаток лампочки заключается в больших энергетических потерях, так как лишь за счет незначительной части энергии она начинает светиться. Основная же часть просто нагревается.
Чтобы лучше это понять, вводится коэффициент полезного действия, который демонстрирует эффективность работы и преобразования в электроэнергию. КПД и тепловое действие тока используются в разных областях, так как имеется множество устройств, изготовленных на основании этого принципа. В большей степени это нагревательные приборы, электрические плиты, кипятильники и другие подобные аппараты.
Задача из ЕГЭ
По проводнику сопротивлением R течёт ток I. Как изменится количество теплоты, выделяющееся в проводнике в единицу времени, если его сопротивление увеличить в два раза, а силу тока уменьшить в два раза? Варианты ответа: а) увеличится в два раза; б) уменьшится в два раза; в) не изменится; г) уменьшится в восемь раз.
Решение
Воспользуемся законом Джоуля – Ленца:
Количество теплоты, выделяющееся в проводнике в единицу времени, равно:
Так как сопротивление увеличивается в два раза, а сила тока уменьшается в два раза:
Следовательно, новое значение количества теплоты будет равно:
Ответ: б) уменьшится в два раза
Плагиат или нет?
Ещё в 1832-1833-х годах Эмилий Христианович Ленц обратил внимание на то, что проводимость проводника сильно зависит от его нагревания, это осложняло расчёты электрических цепей, так как не представлялось возможным вычислить зависимость тока от теплоты, которую он выделяет.
Рис. 3. Опыт Ленца
Ленц сконструировал специальный прибор-сосуд, служивший для измерения количества тепла, выделявшегося в проволоке. В сосуд учёный заливал разбавленный спирт (спирт обладает меньшей электропроводностью, чем вода, которую использовал в своих опытах Джеймс Джоуль). В раствор спирта помещалась платиновая проволока, через которую пропускался электрический ток (см. Рис. 3). Была произведена большая серия опытов, в которых Ленц замерял время, затраченное на нагревание раствора на . Получив достаточное количество убедительных данных, в 1843 году учёный опубликовал закон: «нагревание проволоки гальваническим током пропорционально квадрату служащего для нагревания тока». Однако аналогичный закон уже был опубликован Джоулем в 1841 году, но Ленц вполне обоснованно обратил внимание на то, что англичанин провёл свои эксперименты с большим количеством погрешностей. Именно поэтому закон о тепловом действии тока был назван в честь двух выдающихся учёных.
Суть теплового закона
Тепловое действие тока
Упомянутые выше ученые (Джоуль Ленц) практически одновременно (1841-1842 гг. ) установили зависимость нагрева от силы тока. Для наглядного эксперимента можно использовать следующий комплект:
) установили зависимость нагрева от силы тока. Для наглядного эксперимента можно использовать следующий комплект:
- проводник размещают в емкости с водой;
- термометром будет измеряться изменение температуры жидкости при подключении цепи к источнику электропитания;
- с помощью вольтметра и амперметра уточняют напряжение и ток в контрольных точках.
Аналогичный опыт можно воспроизвести в емкости с раствором соли, который обладает определенной проводимостью
По закону Ома ток (I) можно определить через напряжение (U) и электрическое сопротивление (R):
I= U/R.
Выполняемую работу (A) записать следующим образом:
A = I * U * t = I * (I*R) * t = (U/R) * U * t = I2*R*t = (U2/R) * t.
Здесь t обозначает соответствующий интервал времени.
На этом этапе следует вспомнить первый закон термодинамики, который определяет сохранение энергии в замкнутой системе. Этот постулат позволяет описывать рассматриваемое явление с помощью созданной формулы. Подразумевается равенство количества тепла (Q) выполненной работе (A). Итоговое выражение (закон Ленца):
Этот постулат позволяет описывать рассматриваемое явление с помощью созданной формулы. Подразумевается равенство количества тепла (Q) выполненной работе (A). Итоговое выражение (закон Ленца):
Q = I2*R*t = (U2/R) * t = I * U * t.
Суть явления объясняется столкновением заряженных частиц с молекулами проводника. Если образец – твердый материал, речь идет об электронах и компонентах кристаллической решетки, соответственно.
( 2 оценки, среднее 5 из 5 )
Физический смысл закона джоуля ленца. «Закон Джоуля-Ленца и его применение
Эмилий Христианович Ленц (1804 — 1865) — русский знаменитый физик. Он является одним из основоположников электромеханики. С его именем связано открытие закона, определяющего направление и закона, определяющего электрическое поле в проводнике с током.
Кроме того, Эмилий Ленц и английский учёный-физик Джоуль, изучая на опыте независимо один от другого открыли закон, согласно которому количество теплоты, которое выделяется в проводнике, будет прямо пропорционально квадрату электрического тока, который проходит по проводнику, его сопротивлению и времени, в течение которого электрический ток поддерживается неизменным в проводнике.
Данный закон получил название закон Джоуля — Ленца, формула его выражает следующим образом:
где Q — количество выделившейся теплоты, l — ток, R — сопротивление проводника, t — время; величина k называется тепловым эквивалентом работы. Численное значение этой величины зависит от выбора единиц, в которых производятся измерения остальных величин, входящих в формулу.
Если количество теплоты измерять в калориях, ток в амперах, сопротивление в Омах, а время в секундах, то k численно равно 0,24. Это значит, что ток в 1а выделяет в проводнике, который обладает сопротивлением в 1 Ом, за одну секунду число теплоты, которое равно 0,24 ккал. Исходя из этого, количество теплоты в калориях, выделяющееся в проводнике, может быть рассчитано по формуле:
В системе единиц СИ энергия, количество теплоты и работа измеряются единицами — джоулями. Поэтому коэффициент пропорциональности в законе Джоуля — Ленца равен единице. В этой системе формула Джоуля — Ленца имеет вид:
Закон Джоуля — Ленца можно проверить на опыте. По проволочной спиральке, погружённой в жидкость, налитую в калориметр, пропускается некоторое время ток. Затем подсчитывается количество теплоты, выделившейся в калориметре. Сопротивление спиральки известно заранее, ток измеряется амперметром и время секундомером. Меняя ток в цепи и используя различные спиральки, можно проверить закон Джоуля — Ленца.
По проволочной спиральке, погружённой в жидкость, налитую в калориметр, пропускается некоторое время ток. Затем подсчитывается количество теплоты, выделившейся в калориметре. Сопротивление спиральки известно заранее, ток измеряется амперметром и время секундомером. Меняя ток в цепи и используя различные спиральки, можно проверить закон Джоуля — Ленца.
На основании закона Ома
Подставляя значение тока в формулу (2), получим новое выражение формулы для закона Джоуля — Ленца:
Формулой Q = l²Rt удобно пользоваться при расчёте количества теплоты, выделяемого при последовательном соединении, потому что в этом случае во всех проводниках одинаков. Поэтому, когда происходит нескольких проводников, в каждом из них будет выделено такое количество теплоты, которое пропорционально сопротивлению проводника. Если соединить, например, последовательно три проволочки одинаковых размеров — медную, железную и никелиновую, то наибольшее количество теплоты будет выделяться из никелиновой, так как её наибольшее, она сильнее и нагревается.
Если то электрический ток в них будет различен, а напряжение на концах таких проводников одно и то же. Расчёт количества теплоты, которое будет выделяться при таком соединении, лучше вести, используя формулу Q = (U²/R)t.
Эта формула показывает, что при параллельном соединении каждый проводник выделит такое количество теплоты, которое будет обратно пропорционально его проводимости.
Если соединить три одинаковой толщины проволоки — медную, железную и никелиновую — параллельно между собой и пропустить через них ток, то наибольшее количество теплоты выделится в она и нагреется сильнее остальных.
Беря за основу закон Джоуля — Ленца, производят расчёт различных электроосветительных установок, отопительных и нагревательных электроприборов. Также широко используется преобразование энергии электричества в тепловую.
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка
Закон Джоуля Ленца в интегральной форме в тонких проводах:
Если сила тока изменяется со временем, проводник неподвижен и химических превращений в нем нет, то в проводнике выделяется тепло.
Преобразование электрической энергии в тепловую широко используется в электрических печах и различных электронагревательных приборах. Тот же эффект в электрических машинах и аппаратах приводит к непроизвольным затратам энергии (потере энергии и снижении КПД). Тепло, вызывая нагрев этих устройств, ограничивает их нагрузку; при перегрузке повышение температуры может вызвать повреждение изоляции или сокращение срока службы установки.
В формуле мы использовали:
Количество теплоты
Работа тока
Напряжение в проводнике
Сила тока в проводнике
Промежуток времени
Рассмотрим Закон Джоуля-Ленца и его применение.
При прохождении электрического тока по проводнику он нагревается. Это происходит потому, что перемещающиеся под действием электрического поля свободные электроны в металлах и ионы в растворах электролитов сталкиваются с молекулами или атомами проводников и передают им свою энергию. Таким образом, при совершении током работы увеличивается внутренняя энергия проводника , в нём выделяется некоторое количество теплоты, равное работе тока, и проводник нагревается: Q = А или Q = IUt .
Таким образом, при совершении током работы увеличивается внутренняя энергия проводника , в нём выделяется некоторое количество теплоты, равное работе тока, и проводник нагревается: Q = А или Q = IUt .
Учитывая, что U = IR , в результате получаем формулу:
Q = I 2 Rt , гдеQ — количество выделяемой теплоты (в Джоулях)
I — сила тока (в Амперах)
R — сопротивление проводника (в Омах)
t — время прохождения (в секундах)
Где применяется закон Джоуля-Ленца?
1. Например, в лампах накаливания и в электронагревательных приборах применяется закон Джоуля-Ленца. В них используют нагревательный элемент, который является проводником с высоким сопротивлением. За счет этого элемента можно добиться локализованного выделения тепла на определенном участке. Выделение тепла будет появляться при повышении сопротивления, увеличении длины проводника, выбором определенного сплава.
За счет этого элемента можно добиться локализованного выделения тепла на определенном участке. Выделение тепла будет появляться при повышении сопротивления, увеличении длины проводника, выбором определенного сплава.
2. Одной из областей применения закона Джоуля-Ленца является снижение потерь энергии . Тепловое действие силы тока ведет к потерям энергии. При передаче электроэнергии, передаваемая мощность линейно зависит от напряжения и силы тока, а сила нагрева зависит от силы тока квадратично, поэтому если повышать напряжение, при этом понижая силу тока перед подачей электроэнергии, то это будет более выгодно. Но повышение напряжения ведет к снижению электробезопасности. Для повышения уровня электробезопасности повышают сопротивление нагрузки соответственно повышению напряжения в сети.
3. Также закон Джоуля-Ленца влияет на выбор проводов для цепей . Потому что при неправильном подборе проводов возможен сильный нагрев проводника, а также его возгорание. Это происходит когда сила тока превышает предельно допустимые значения и выделяется слишком много энергии.
Это происходит когда сила тока превышает предельно допустимые значения и выделяется слишком много энергии.
Знаменитый русский физик Ленц и английский физик Джоуль, проводя опыты по изучению тепловых действий электрического тока, независимо друг от друга вывели закон Джоуля-Ленца. Данный закон отражает взаимосвязь количества теплоты, выделяемого в проводнике, и электрического тока, проходящего по этому проводнику в течение определенного периода времени.
Свойства электрического тока
Когда электрический ток проходит через металлический проводник, его электроны постоянно сталкиваются с различными посторонними частицами. Это могут быть обычные нейтральные молекулы или молекулы, потерявшие электроны. Электрон в процессе движения может отщепить от нейтральной молекулы еще один электрон. В результате, его кинетическая энергия теряется, а вместо молекулы происходит образование положительного иона. В других случаях электрон, наоборот, соединиться с положительным ионом и образовать нейтральную молекулу.
В процессе столкновений электронов и молекул происходит расход энергии, в дальнейшем превращающейся в тепло. Затраты определенного количества энергии связаны со всеми движениями, во время которых приходится преодолевать сопротивление. В это время происходит превращение работы, затраченной на преодоление сопротивления трения, в тепловую энергию.
Закон джоуля Ленца формула и определение
Согласно закону джоуля Ленца, электрический ток, проходящий по проводнику, сопровождается количеством теплоты, прямо пропорциональным квадрату тока и сопротивлению, а также времени течения этого тока по проводнику.
В виде формулы закон Джоуля-Ленца выражается следующим образом: Q = I 2 Rt, в которой Q отображает количество выделенной теплоты, I — , R — сопротивление проводника, t — период времени. Величина «к» представляет собой тепловой эквивалент работы и применяется в тех случаях, когда количество теплоты измеряется в калориях, сила тока — , сопротивление — в Омах, а время — в секундах. Численное значение величины к составляет 0,24, что соответствует току в 1 ампер, который при сопротивлении проводника в 1 Ом, выделяет в течение 1 секунды количество теплоты, равное 0,24 ккал. Поэтому для расчетов количества выделенной теплоты в калориях применяется формула Q = 0,24I 2 Rt.
Численное значение величины к составляет 0,24, что соответствует току в 1 ампер, который при сопротивлении проводника в 1 Ом, выделяет в течение 1 секунды количество теплоты, равное 0,24 ккал. Поэтому для расчетов количества выделенной теплоты в калориях применяется формула Q = 0,24I 2 Rt.
При использовании системы единиц СИ измерение количества теплоты производится в джоулях, поэтому величина «к», применительно к закону Джоуля-Ленца, будет равна 1, а формула будет выглядеть: Q = I 2 Rt. В соответствии с I = U/R. Если это значение силы тока подставить в основную формулу, она приобретет следующий вид: Q = (U 2 /R)t.
Основная формула Q = I 2 Rt очень удобна для использования при расчетах количества теплоты, которое выделяется в случае последовательного соединения. Сила тока во всех проводниках будет одинаковая. При последовательном соединении сразу нескольких проводников, каждый из них выделит столько теплоты, которое будет пропорционально сопротивлению проводника. Если последовательно соединить три одинаковые проволочки из меди, железа и никелина, то максимальное количество теплоты будет выделено последней. Это связано с наибольшим удельным сопротивлением никелина и более сильным нагревом этой проволочки.
Если последовательно соединить три одинаковые проволочки из меди, железа и никелина, то максимальное количество теплоты будет выделено последней. Это связано с наибольшим удельным сопротивлением никелина и более сильным нагревом этой проволочки.
При параллельном соединении этих же проводников, значение электрического тока в каждом из них будет различным, а напряжение на концах — одинаковым. В этом случае для расчетов больше подойдет формула Q = (U 2 /R)t. Количество теплоты, выделяемое проводником, будет обратно пропорционально его проводимости. Таким образом, закон Джоуля — Ленца широко используется для расчетов установок электрического освещения, различных отопительных и нагревательных приборов, а также других устройств, связанных с преобразованием электрической энергии в тепловую.
Закон Джоуля-Ленца. Работа и мощность электрического тока
Закон Джоуля-Ленца — формула, применение на практике, вывод
Этот урок посвящён изучению теплового действия электрического тока.
 Мы проведём ряд опытов, демонстрирующих зависимость количества теплоты от силы тока и сопротивления, а также рассмотрим закон Джоуля – Ленца
Мы проведём ряд опытов, демонстрирующих зависимость количества теплоты от силы тока и сопротивления, а также рассмотрим закон Джоуля – ЛенцаБлок: 1/8 | Кол-во символов: 209
Источник: https://interneturok.ru/lesson/physics/8-klass/belektricheskie-yavleniyab/nagrevanie-provodnikov-elektricheskim-tokom-zakon-dzhoulya-lentsa-grebenyuk-yu-v?konspekt=
Введение
Мы уже знаем, что при прохождении тока через электрическую лампочку её спираль нагревается и излучает видимый свет. Таким образом, мы наблюдаем тепловое действие электрического тока. Благодаря этому действию, нагреваются, например, утюг или чайник. Но при работе вентилятора или пылесоса практически не наблюдается тепловое действие, также в нормальном состоянии слабо греются провода. На этом уроке, тема которого: «Нагревание проводников электрическим током. Закон Джоуля – Ленца», мы определим, от чего зависит тепловое действие электрического тока.
Блок: 2/8 | Кол-во символов: 562
Источник: https://interneturok. ru/lesson/physics/8-klass/belektricheskie-yavleniyab/nagrevanie-provodnikov-elektricheskim-tokom-zakon-dzhoulya-lentsa-grebenyuk-yu-v?konspekt=
ru/lesson/physics/8-klass/belektricheskie-yavleniyab/nagrevanie-provodnikov-elektricheskim-tokom-zakon-dzhoulya-lentsa-grebenyuk-yu-v?konspekt=
Определения
В словесной формулировке звучит следующим образом:
Мощность тепла, выделяемого в единице объёма среды при протекании постоянного электрического тока, равна произведению плотности электрического тока на величину напряженности электрического поля.
Математически может быть выражен в следующей форме:
где — мощность выделения тепла в единице объёма, — плотность электрического тока, — напряжённость электрического поля, σ — проводимость среды, а точкой обозначено скалярное произведение.
Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах:
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивления участка.
В интегральной форме этот закон имеет вид
где — количество теплоты, выделяемое за промежуток времени , — сила тока, — сопротивление, — полное количество теплоты, выделенное за промежуток времени от до . В случае постоянных силы тока и сопротивления:
Применяя закон Ома, можно получить следующие эквивалентные формулы:
Блок: 2/5 | Кол-во символов: 1115
Источник: https://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%BA%D0%BE%D0%BD_%D0%94%D0%B6%D0%BE%D1%83%D0%BB%D1%8F_%E2%80%94_%D0%9B%D0%B5%D0%BD%D1%86%D0%B0
Физический смысл закона Джоуля – Ленца
Закон можно объяснить следующим образом: ток, протекая по проводнику, представляет собой перемещение электрического заряда под воздействием электрического поля. Таким образом, электрическое поле совершает некоторую работу. Эта работа расходуется на нагрев проводника.
Другими словами, энергия переходит в другое свое качество – тепло.
Но чрезмерный нагрев проводников с током и электрооборудования допускать нельзя, поскольку это может привести к их повреждению. Опасен сильный перегрев при коротких замыканиях проводов, когда по проводниках могут протекать достаточно большие токи.
Опасен сильный перегрев при коротких замыканиях проводов, когда по проводниках могут протекать достаточно большие токи.
В интегральной форме для тонких проводников закон Джоуля – Ленца звучит следующим образом: количество теплоты, которое выделяется в единицу времени в рассматриваемом участке цепи, определяется как произведение квадрата силы тока на сопротивление участка.
Математически эта формулировка выражается следующим образом:
Q = ∫ k • I² • R • t,
при этом Q – количество выделившейся теплоты;
I – величина тока;
R — активное сопротивление проводников;
t – время воздействия.
Значение параметра k принято называть тепловым эквивалентом работы. Величина этого параметра определяется в зависимости от разрядности единиц, в которых выполняются измерения значений, используемых в формуле.
Закон Джоуля-Ленца имеет достаточно общий характер, поскольку не имеет зависимости от природы сил, генерирующих ток.
Из практики можно утверждать, что он справедлив, как для электролитов, так проводников и полупроводников.
Блок: 3/4 | Кол-во символов: 1521
Источник: https://pue8.ru/elektrotekhnik/823-zakon-dzhoulya-lentsa-opredelenie-formula-fizicheskij-smysl.html
Формула Джоуля-Ленца
В итоге, спустя десятилетие, в 1843 году Эмилий Ленц выставил на всеобщее обозрение научного сообщества результат своих опытов в виде закона. Однако, оказалось, что его опередили! Пару лет назад английский физик Джеймс Прескотт Джоуль уже проводил аналогичные опыты и также представил общественности свои результаты. Но, тщательно проверив все работы Джеймса Джоуля, русский учёный выяснил что собственные опыты гораздо точнее, наработан больший объём исследований, потому, русской науке есть чем дополнить английское открытие.
Научное сообщество рассмотрело оба результата исследований и объединила их в одно, тем самым закон Джоуля переименовали в закон Джоуля-Ленца. Закон утверждает, что количество теплоты, выделяемое проводником при протекании по нему электрического тока , равно произведению силы этого тока в квадрате, сопротивлению проводника и времени, за которое по проводнику течёт ток. Или формулой:
Или формулой:
Q=I2Rt
где
Q — количество выделяемого тепла (Джоули)
I — сила тока, протекающего через проводник (Амперы)
R — сопротивление проводника (Омы)
t — время прохождения тока через проводник (Секунды)
Блок: 3/6 | Кол-во символов: 1135
Источник: https://www.RusElectronic.com/zakon-dzhoulja-ljentsa/
Применение и практический смысл
Непосредственное превращение электричества в тепловую энергию нельзя назвать экономически выгодным. Однако, с точки зрения удобства и доступности современного человечества к источникам электроэнергии различные нагревательные приборы продолжают массово применяться как в быту, так и на производстве.
Перечислим некоторые из них:
- электрочайники;
- утюги;
- фены;
- варочные плиты;
- паяльники;
- сварочные аппараты и многое другое.
На рисунке 3 изображены бытовые нагревательные приборы, которыми мы часто пользуемся.
Рис. 3. Бытовые нагревательные приборы
Использование тепловых мощностей в химической, металлургической и в других промышленных отраслях тесно связно с использованием электрической энергии.
Без знания физического закона Джоуля-Ленца было бы невозможно сконструировать безопасный нагревательный прибор. Для этого нужны расчёты, которые невозможно сделать без применения рассмотренных нами формул. На основе расчётов происходит выбор материалов с нужным удельным сопротивлением, влияющим на нагревательную способность устройств.
Закон Джоуля-Ленца без преувеличения можно назвать гениальным. Это один из тех законов, которые повлияли на развитие электротехники.
Блок: 4/4 | Кол-во символов: 1209
Источник: https://www.asutpp.ru/zakon-dzhoulya-lentsa.html
Почему греется проводник
Как же объясняется нагрев проводника? Почему он именно греется, а не остаётся нейтральным или охлаждается? Нагрев происходит из-за того, что свободные электроны, перемещающиеся в проводнике под действием электрического поля, бомбардируют атомы молекул металла, тем самым передавая им собственную энергию, которая переходит в тепловую. Если изъясняться совсем просто: преодолевая материал проводника, электрический ток как бы “трётся”, соударяется электронами о молекулы проводника. Ну а , как известно, любое трение сопровождается нагревом. Следовательно, проводник будет нагреваться пока по нему бежит электрический ток.
Если изъясняться совсем просто: преодолевая материал проводника, электрический ток как бы “трётся”, соударяется электронами о молекулы проводника. Ну а , как известно, любое трение сопровождается нагревом. Следовательно, проводник будет нагреваться пока по нему бежит электрический ток.
Из формулы также следует – чем выше удельное сопротивление проводника и чем выше сила тока протекающего по нему, тем выше будет нагрев . Например, если последовательно соединить проводник-медь (удельное сопротивление 0,018 Ом·мм²/м) и проводник-алюминий (0,027 Ом·мм²/м), то при протекании через цепь электрического тока алюминий будет нагреваться сильнее чем медь из-за более высокого сопротивления. Поэтому, кстати, не рекомендуется в быту делать скрутки медных и алюминиевых проводов друг с другом – будет неравномерный нагрев в месте скрутки. В итоге – подгорание с последующим пропаданием контакта.
Блок: 4/6 | Кол-во символов: 1255
Источник: https://www.RusElectronic.com/zakon-dzhoulja-ljentsa/
Опыты Ленца
Перенесемся в 19 век-эпоху накопления знаний и подготовки к технологическому прыжку 20 века. Эпоха, когда по всему миру различные учёные и просто изобретатели-самоучки чуть ли не ежедневно открывают что-то новое, зачастую тратя огромное количество времени на исследования и, при этом, не представляя конечный результат.
Эпоха, когда по всему миру различные учёные и просто изобретатели-самоучки чуть ли не ежедневно открывают что-то новое, зачастую тратя огромное количество времени на исследования и, при этом, не представляя конечный результат.
Один из таких людей, русский учёный Эмилий Христианович Ленц, увлекался электричеством, на тогдашнем примитивном уровне, пытаясь рассчитывать электрические цепи. В 1832 году Эмилий Ленц “застрял” с расчётами, так как параметры его смоделированной цепи “источник энергии – проводник – потребитель энергии” сильно разнились от опыта к опыту. Зимой 1832-1833 года учёный обнаружил, что причиной нестабильности является кусочек платиновой проволоки, принесённый им с холода. Отогревая или охлаждая проводник, Ленц также заметил что существует некая зависимость между силой тока, электрическим сопротивлением и температурой проводника.
При определённых параметрах электрической цепи проводник быстро оттаивал и даже слегка нагревался. Измерительных приборов в те времена практически никаких не существовало – невозможно было точно измерить ни силу тока, ни сопротивление. Но это был русский физик, и он проявил смекалку. Если это зависимость, то почему бы ей не быть обратимой?
Но это был русский физик, и он проявил смекалку. Если это зависимость, то почему бы ей не быть обратимой?
Для того чтобы измерить количество тепла, выделяемого проводником, учёный сконструировал простейший “нагреватель” – стеклянная ёмкость, в которой находился спиртосодержащий раствор и погружённый в него платиновый проводник-спираль. Подавая различные величины электрического тока на проволоку, Ленц замерял время, за которое раствор нагревался до определённой температуры. Источники электрического тока в те времена были слишком слабы, чтобы разогреть раствор до серьёзной температуры, потому визуально определить количество испарившегося раствора не представлялось возможным. Из-за этого процесс исследования очень затянулся – тысячи вариантов подбора параметров источника питания, проводника, долгие замеры и последующий анализ.
Блок: 2/6 | Кол-во символов: 2044
Источник: https://www.RusElectronic.com/zakon-dzhoulja-ljentsa/
Итоги урока
На этом уроке мы узнали о том, что прохождение тока в проводнике сопровождается выделением тепла, при этом количество теплоты, выделяющееся при прохождении тока в проводнике, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока. Таким образом, мы сформулировали закон Джоуля – Ленца.
Таким образом, мы сформулировали закон Джоуля – Ленца.
Блок: 5/8 | Кол-во символов: 337
Источник: https://interneturok.ru/lesson/physics/8-klass/belektricheskie-yavleniyab/nagrevanie-provodnikov-elektricheskim-tokom-zakon-dzhoulya-lentsa-grebenyuk-yu-v?konspekt=
Применение закона Джоуля-Ленца в жизни
Открытие закона Джоуля-Ленца имело огромные последствия для практического применения электрического тока. Уже в 19 веке стало возможным создать более точные измерительные приборы, основанные на сокращении проволочной спирали при её нагреве протекающим током определённой величины – первые стрелочные вольтметры и амперметры. Появились первые прототипы электрических обогревателей, тостеров, плавильных печей – использовался проводник с высоким удельным сопротивлением, что позволяло получить довольно высокую температуру.
Были изобретены плавкие предохранители, биметаллические прерыватели цепи (аналоги современных тепловых реле защиты), основанные на разнице нагрева проводников с разным удельным сопротивлением. Ну и, конечно же, обнаружив что при определённой силе тока проводник с высоким удельным сопротивлением способен нагреться докрасна , данный эффект использовали в качестве источника света. Появились первые лампочки.
Ну и, конечно же, обнаружив что при определённой силе тока проводник с высоким удельным сопротивлением способен нагреться докрасна , данный эффект использовали в качестве источника света. Появились первые лампочки.
Проводник (угольная палочка, бамбуковая нить, платиновая проволока и т.д.) помещали в стеклянную колбу, откачивали воздух для замедления процесса окисления и получали незатухаемый, чистый и стабильный источник света – электрическую лампочку
Блок: 5/6 | Кол-во символов: 1219
Источник: https://www.RusElectronic.com/zakon-dzhoulja-ljentsa/
Задача из ЕГЭ
По проводнику сопротивлением R течёт ток I. Как изменится количество теплоты, выделяющееся в проводнике в единицу времени, если его сопротивление увеличить в два раза, а силу тока уменьшить в два раза? Варианты ответа: а) увеличится в два раза; б) уменьшится в два раза; в) не изменится; г) уменьшится в восемь раз.
Решение
Воспользуемся законом Джоуля – Ленца:
Количество теплоты, выделяющееся в проводнике в единицу времени, равно:
Так как сопротивление увеличивается в два раза, а сила тока уменьшается в два раза:
Следовательно, новое значение количества теплоты будет равно:
Ответ: б) уменьшится в два раза
Блок: 6/8 | Кол-во символов: 651
Источник: https://interneturok. ru/lesson/physics/8-klass/belektricheskie-yavleniyab/nagrevanie-provodnikov-elektricheskim-tokom-zakon-dzhoulya-lentsa-grebenyuk-yu-v?konspekt=
ru/lesson/physics/8-klass/belektricheskie-yavleniyab/nagrevanie-provodnikov-elektricheskim-tokom-zakon-dzhoulya-lentsa-grebenyuk-yu-v?konspekt=
Заключение
Таки образом, можно сказать что на законе Джоуля-Ленца держится чуть ли не вся электрика и электротехника. Открыв этот закон, появилась возможность уже заранее предсказать некоторые будущие проблемы в освоении электричества. Например, из-за нагрева проводника передача электрического тока на большое расстояние сопровождается потерями этого тока на тепло. Соответственно, чтобы компенсировать эти потери нужно занизить передаваемый ток, компенсируя это высоким напряжением. А уже на оконечном потребителе, понижать напряжение и получать более высокий ток.
Закон Джоуля-Ленца неотступно следует из одной эпохи технологического развития в другую. Даже сегодня мы постоянно наблюдаем его в быту – закон проявляется всюду, и не всегда люди ему рады. Сильно греющийся процессор персонального компьютера, пропадание света из-за обгоревшей скрутки «медь-алюминий»,выбитая вставка-предохранитель, выгоревшая из-за высокой нагрузки электропроводка – всё это тот самый закон Джоуля-Ленца.
Блок: 6/6 | Кол-во символов: 993
Источник: https://www.RusElectronic.com/zakon-dzhoulja-ljentsa/
Решение задач
Задача 1
Определите длину нихромового провода, с площадью сечения 0,25 , из которого изготовлен нагреватель электрического чайника. Чайник питается от сети напряжением 220 В и нагревает 1,5 литра воды от до за 10 минут. КПД чайника составляет .
Дано: ; ; ; ; ; ; – теплоёмкость воды; – плотность воды; – удельное сопротивление нихрома;
Найти:l
Решение
Так как вся электрическая энергия идёт на нагревание воды, то воспользуемся законом Джоуля – Ленца:
Отсюда сопротивление проводника (нихромового провода) Rравно:
Также сопротивление проводника можно вычислить по формуле:
Приравняем сопротивление в обеих формулах и выразим длину проводника (l):
В этой формуле неизвестно количество теплоты, то есть мощность чайника. Найдём её, зная, что чайник нагревает 1,5 л воды от от до за 10 минут.
Найдём её, зная, что чайник нагревает 1,5 л воды от от до за 10 минут.
Так как не вся теплота идёт на нагревание, то необходимо учитывать КПД чайника, равный:
Отсюда общее количество теплоты () будет равно:
Подставим значение в формулу для длины проводника:
Проверив единицы измерения, подставляем известные значения:
Ответ:
Задача 2
С какой целью провода в местах соединения не просто скручивают, но ещё и спаивают? Ответ обоснуйте.
Решение
Рис. 4. Иллюстрация к задаче
Сила тока в обоих проводах одинакова, так как проводники соединены последовательно (см. Рис. 4):
Если место контакта двух проводников не будет спаяно, то его сопротивление будет достаточно большое, по сравнению с сопротивлением самих проводников. Следовательно, в месте контакта будет выделяться наибольшее количество теплоты, что приведёт к расплавлению места контакта и размыканию электрической цепи. Поэтому провода в местах соединения не просто скручивают, но ещё и спаивают с целью уменьшения сопротивления.
Поэтому провода в местах соединения не просто скручивают, но ещё и спаивают с целью уменьшения сопротивления.
Задача 3
Какой длины нихромовый провод нужно взять, чтобы изготовить электрический камин, работающий при напряжении 120 В и выделяющий 1 МДж теплоты в час? Диаметр провода 0,5 мм.
Дано: ; ; ; ;
Найти:l
Решение
Так как вся электрическая энергия расходуется на нагревание, то согласно закону Джоуля-Ленца:
Отсюда сопротивление провода равно:
Также сопротивление проводника можно вычислить по формуле:
Приравняем сопротивление в обеих формулах и выразим длину проводника (l):
В этой формуле неизвестна площадь сечения проволоки. Зная диаметр проволоки, вычислим площадь сечения проволоки по формуле площади круга:
Подставим значение в формулу для длины проводника:
Проверив единицы измерения, подставляем известные значения:
Ответ:
Список литературы
- Генденштейн Л.
 Э, Кайдалов А.Б., Кожевников В.Б. / Под ред. Орлова В.А., Ройзена И.И. Физика 8. – М.: Мнемозина.
Э, Кайдалов А.Б., Кожевников В.Б. / Под ред. Орлова В.А., Ройзена И.И. Физика 8. – М.: Мнемозина. - Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
- Фадеева А.А., Засов А.В., Киселев Д.Ф. Физика 8. – М.: Просвещение.
Домашнее задание
- В чем проявляется тепловое действие тока?
- Как можно объяснить нагревание проводника с током?
- Известно, что безопасным для человека является постоянный ток 100 мкА. Какое количество теплоты выделится за 1 мин в теле человека при прохождении тока от конца одной руки до конца другой руки (при сухой коже), если сопротивление этого участка равно 15000 Ом?
- Участок цепи состоит из двух резисторов сопротивлением 8 Ом каждый, соединенных параллельно. Сила тока в цепи – 0,3 А. Какое количество теплоты выделится в участке за 1 мин?
- Сколько электроэнергии потребляет электрический утюг за 4 ч работы, если он включен в сеть напряжением 220 В при силе тока 4,55 А?
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Блок: 8/8 | Кол-во символов: 3560
Источник: https://interneturok. ru/lesson/physics/8-klass/belektricheskie-yavleniyab/nagrevanie-provodnikov-elektricheskim-tokom-zakon-dzhoulya-lentsa-grebenyuk-yu-v?konspekt=
ru/lesson/physics/8-klass/belektricheskie-yavleniyab/nagrevanie-provodnikov-elektricheskim-tokom-zakon-dzhoulya-lentsa-grebenyuk-yu-v?konspekt=
Количество использованных доноров: 5
Информация по каждому донору:
- https://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%BA%D0%BE%D0%BD_%D0%94%D0%B6%D0%BE%D1%83%D0%BB%D1%8F_%E2%80%94_%D0%9B%D0%B5%D0%BD%D1%86%D0%B0: использовано 2 блоков из 5, кол-во символов 3640 (17%)
- https://pue8.ru/elektrotekhnik/823-zakon-dzhoulya-lentsa-opredelenie-formula-fizicheskij-smysl.html: использовано 2 блоков из 4, кол-во символов 1809 (9%)
- https://www.asutpp.ru/zakon-dzhoulya-lentsa.html: использовано 1 блоков из 4, кол-во символов 1209 (6%)
- https://interneturok.ru/lesson/physics/8-klass/belektricheskie-yavleniyab/nagrevanie-provodnikov-elektricheskim-tokom-zakon-dzhoulya-lentsa-grebenyuk-yu-v?konspekt=: использовано 6 блоков из 8, кол-во символов 7684 (37%)
- https://www.
 RusElectronic.com/zakon-dzhoulja-ljentsa/: использовано 5 блоков из 6, кол-во символов 6646 (32%)
RusElectronic.com/zakon-dzhoulja-ljentsa/: использовано 5 блоков из 6, кол-во символов 6646 (32%)
Закон электромагнитной индукции — формулы, определение, примеры
Магнитный поток
Прежде, чем разобраться с тем, что такое электромагнитная индукция, нужно определить такую сущность, как магнитный поток.
Представьте, что вы взяли обруч в руки и вышли на улицу в ливень. Чем сильнее ливень, тем больше через этот обруч пройдет воды — поток воды больше.
Если обруч расположен горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.
Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).
Магнитный поток по сути своей — это тот же самый поток воды через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя. 2]
2]
n — вектор нормали (перпендикуляр к поверхности) [-]
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла α магнитный поток может быть положительным (α < 90°) или отрицательным (α > 90°). Если α = 90°, то магнитный поток равен 0. Это зависит от величины косинуса угла.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура, магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Ученики Skysmart не боятся сложных понятий по физике и чувствуют себя уверенее на контрольных в школе. А еще — не могут оторваться от домашки: захватывает не хуже, чем тик-ток.
А еще — не могут оторваться от домашки: захватывает не хуже, чем тик-ток.
Запишите ребенка на вводное занятие: покажем, как все проходит на интерактивной платформе и вдохновим на учебу!
Электромагнитная индукция
Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Майкл Фарадей провел ряд опытов, которые помогли открыть явление электромагнитной индукции.
Опыт раз. На одну непроводящую основу намотали две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.
При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.
Опыт три. Катушка замкнута на гальванометр, а магнит движется вдвигается (выдвигается) относительно катушки
Вот, что показали эти опыты:
- Индукционный ток возникает только при изменении линий магнитной индукции.
- Направление тока будет различно при увеличении числа линий и при их уменьшении.
- Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Почему возникает индукционный ток? Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции. |
Закон электромагнитной индукции
Закон электромагнитной индукции (закон Фарадея) звучит так:
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.
Математически его можно описать формулой:
Закон Фарадея
ΔФ/Δt — скорость изменения магнитного потока [Вб/с] |
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.
Закон Фарадея для контура из N витков
ΔФ/Δt — скорость изменения магнитного потока [Вб/с] N — количество витков [-] |
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением R:
Закон Ома для проводящего контура
I — сила индукционного тока [А] R — сопротивление контура [Ом] |
Если проводник длиной l будет двигаться со скоростью v в постоянном однородном магнитном поле с индукцией B ЭДС электромагнитной индукции равна:
ЭДС индукции для движущегося проводника
B — магнитная индукция [Тл] v — скорость проводника [м/с] l — длина проводника [м] |
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
- вследствие изменения во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Чтобы определить направление индукционного тока, нужно воспользоваться правилом Ленца.
Академически это правило звучит следующим образом: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Давайте попробуем чуть проще: катушка в данном случае — это недовольная бабуля. Забирают у нее магнитный поток — она недовольна и создает магнитное поле, которое этот магнитный поток хочет обратно отобрать.
Дают ей магнитный поток, забирай, мол, пользуйся, а она такая — «Да зачем сдался мне ваш магнитный поток!» и создает магнитное поле, которое этот магнитный поток выгоняет.
Закон индукции Фарадея: Закон Ленца
Цели обучения
К концу этого раздела вы сможете:
- Рассчитайте ЭДС, ток и магнитные поля, используя закон Фарадея.
- Объясните физические результаты Закона Ленца
Закон Фарадея и Ленца
Эксперименты Фарадея показали, что ЭДС, вызванная изменением магнитного потока, зависит только от нескольких факторов. Во-первых, ЭДС прямо пропорциональна изменению магнитного потока Δ Φ .Во-вторых, ЭДС является наибольшей, когда изменение во времени Δ t наименьшее, то есть ЭДС обратно пропорциональна Δ t . Наконец, если катушка имеет Н витков, будет создана ЭДС, которая в Н, раз больше, чем для одиночной катушки, так что ЭДС прямо пропорциональна Н . Уравнение для ЭДС, вызванной изменением магнитного потока, равно
[латекс] \ text {emf} = — N \ frac {\ Delta \ Phi} {\ Delta t} \\ [/ latex].
Это соотношение известно как закон индукции Фарадея .Обычно единицами измерения ЭДС являются вольты. Знак минус в законе индукции Фарадея очень важен. Минус означает, что ЭДС создает ток I и магнитное поле B, которые препятствуют изменению потока Δ Φ — это известно как закон Ленца . Направление (обозначенное знаком минус) ЭДС настолько важно, что оно было названо законом Ленца в честь русского Генриха Ленца (1804–1865), который, подобно Фарадею и Генри, независимо исследовал аспекты индукции. Фарадей знал о направлении, но Ленц так ясно изложил его, что ему приписывают его открытие.(См. Рисунок 1.)
Рис. 1. (a) Когда стержневой магнит вставляется в катушку, сила магнитного поля в катушке увеличивается. Ток, наведенный в катушке, создает другое поле в направлении, противоположном стержневому магниту, чтобы противодействовать увеличению. Это один из аспектов закона Ленца: индукция препятствует любому изменению потока. (b) и (c) — две другие ситуации. Убедитесь сами, что показанное направление индуцированной катушки B действительно противодействует изменению магнитного потока и что показанное направление тока согласуется с RHR-2.
Стратегия решения проблем закона ЛенцаЧтобы использовать закон Ленца для определения направлений индуцированных магнитных полей, токов и ЭДС:
- Сделайте набросок ситуации для использования при визуализации и записи направлений.
- Определите направление магнитного поля B.
- Определите, увеличивается или уменьшается поток.
- Теперь определите направление индуцированного магнитного поля B. Оно противостоит изменению магнитного потока путем добавления или вычитания из исходного поля.
- Используйте RHR-2 для определения направления индуцированного тока I, ответственного за индуцированное магнитное поле B.
- Направление (или полярность) наведенной ЭДС теперь будет управлять током в этом направлении и может быть представлено как ток, выходящий из положительного вывода ЭДС и возвращающийся к его отрицательному выводу.
Для практики примените эти шаги к ситуациям, показанным на Рисунке 1, и другим, которые являются частью следующего текстового материала.
Применение электромагнитной индукции
Существует множество применений закона индукции Фарадея, которые мы исследуем в этой и других главах. На этом этапе позвольте нам упомянуть несколько, которые связаны с хранением данных и магнитными полями. Очень важное приложение связано с аудио и видео , записывающими лентами . Пластиковая лента, покрытая оксидом железа, проходит мимо записывающей головки. Эта записывающая головка представляет собой круглое железное кольцо, вокруг которого намотана катушка с проволокой — электромагнит (рис. 2).Сигнал в виде переменного входного тока от микрофона или камеры поступает на записывающую головку. Эти сигналы (которые являются функцией амплитуды и частоты сигнала) создают переменные магнитные поля на записывающей головке. Когда лента движется мимо записывающей головки, ориентация магнитного поля молекул оксида железа на ленте изменяется, таким образом записывая сигнал. В режиме воспроизведения намагниченная лента проходит мимо другой головки, аналогичной по конструкции записывающей головке. Различная ориентация магнитного поля молекул оксида железа на ленте индуцирует ЭДС в проволочной катушке в воспроизводящей головке.Затем этот сигнал отправляется на громкоговоритель или видеоплеер.
Рис. 2. Головки для записи и воспроизведения, используемые с аудио- и видеомагнитными лентами. (кредит: Стив Юрветсон)
Аналогичные принципы применимы и к жестким дискам компьютера, только с гораздо большей скоростью. Здесь записи находятся на вращающемся диске с покрытием. Исторически считывающие головки создавались по принципу индукции. Однако входная информация передается в цифровой, а не аналоговой форме — на вращающемся жестком диске записывается серия нулей или единиц.Сегодня большинство считывающих устройств с жестких дисков не работают по принципу индукции, а используют технологию, известную как гигантское магнитосопротивление . (Открытие того факта, что слабые изменения магнитного поля в тонкой пленке из железа и хрома могут вызывать гораздо большие изменения электрического сопротивления, было одним из первых крупных успехов нанотехнологии.) Еще одно применение индукции можно найти на магнитной полосе на магнитной полосе. на оборотной стороне вашей личной кредитной карты, которая использовалась в продуктовом магазине или в банкомате.Это работает по тому же принципу, что и аудио- или видеопленка, упомянутая в последнем абзаце, в которой голова считывает личную информацию с вашей карты.
Другое применение электромагнитной индукции — это когда электрические сигналы должны передаваться через барьер. Рассмотрим кохлеарный имплант , показанный ниже. Звук улавливается микрофоном на внешней стороне черепа и используется для создания переменного магнитного поля. Ток индуцируется в приемнике, закрепленном в кости под кожей, и передается на электроды во внутреннем ухе.Электромагнитная индукция может использоваться и в других случаях, когда электрические сигналы должны передаваться через различные среды.
Рисунок 3. Электромагнитная индукция, используемая при передаче электрического тока через среды. Устройство на голове ребенка индуцирует электрический ток в приемнике, закрепленном в кости под кожей. (кредит: Бьорн Кнетч)
Еще одна современная область исследований, в которой электромагнитная индукция успешно реализуется (и имеет значительный потенциал), — это транскраниальное магнитное моделирование.Множество расстройств, включая депрессию и галлюцинации, можно объяснить нерегулярной локальной электрической активностью в головном мозге. В транскраниальной магнитной стимуляции быстро меняющееся и очень локализованное магнитное поле помещается рядом с определенными участками, идентифицированными в головном мозге. В идентифицированных участках индуцируются слабые электрические токи, которые могут привести к восстановлению электрических функций в тканях мозга.
Апноэ сна («остановка дыхания») поражает как взрослых, так и младенцев (особенно недоношенных детей и может быть причиной внезапной детской смерти [SID]).У таких людей дыхание может многократно останавливаться во время сна. Прекращение действия более чем на 20 секунд может быть очень опасным. Инсульт, сердечная недостаточность и усталость — вот лишь некоторые из возможных последствий для человека, страдающего апноэ во сне. У младенцев проблема заключается в задержке дыхания на это более длительное время. В одном из типов мониторов, предупреждающих родителей о том, что ребенок не дышит, используется электромагнитная индукция. В проводе, обмотанном вокруг груди младенца, проходит переменный ток. Расширение и сжатие грудной клетки младенца во время дыхания изменяет площадь спирали.В расположенной рядом катушке датчика индуцируется переменный ток из-за изменения магнитного поля исходного провода. Если ребенок перестанет дышать, наведенный ток изменится, и родители могут быть предупреждены.
Подключение: сохранение энергииЗакон Ленца является проявлением сохранения энергии. Индуцированная ЭДС создает ток, который противодействует изменению потока, потому что изменение потока означает изменение энергии.Энергия может входить или уходить, но не мгновенно. Закон Ленца — следствие. Когда изменение начинается, закон говорит, что индукция противодействует и, таким образом, замедляет изменение. Фактически, если бы индуцированная ЭДС была в том же направлении, что и изменение потока, была бы положительная обратная связь, которая не давала бы нам бесплатную энергию из любого видимого источника — закон сохранения энергии был бы нарушен.
Пример 1. Расчет ЭДС: насколько велика наведенная ЭДС?Рассчитайте величину наведенной ЭДС, когда магнит, показанный на Рисунке 1 (а), вдавливается в катушку, учитывая следующую информацию: одноконтурная катушка имеет радиус 6.00 см, а среднее значение B cos θ (это дано, поскольку поле стержневого магнита сложное) увеличивается с 0,0500 Тл до 0,250 Тл за 0,100 с.
СтратегияЧтобы найти величину ЭДС , мы используем закон индукции Фарадея, как указано в [latex] \ text {emf} = — N \ frac {\ Delta \ Phi} {\ Delta t} \\ [/ latex], но без знака минус, указывающего направление:
[латекс] \ text {emf} = N \ frac {\ Delta \ Phi} {\ Delta t} \\ [/ latex].
РастворНам дано, что N = 1 и Δ t = 0.100 с, но мы должны определить изменение потока Δ Φ , прежде чем мы сможем найти ЭДС. Поскольку площадь петли фиксирована, мы видим, что
ΔΦ = Δ ( BA cos θ ) = AΔ ( B cos θ ).
Теперь Δ ( B cos θ ) = 0,200 Тл, поскольку было задано, что B cos θ изменяется от 0,0500 до 0,250 Тл. Площадь контура A = πr2 = (3,14…) ( 0,060 м) 2 = 1,13 × 10 −2 м 2 .{2} \ right) \ left (0.200 \ text {T} \ right)} {0.100 \ text {s}} = 22.6 \ text {mV} \\ [/ latex].
ОбсуждениеХотя это напряжение легко измерить, его явно недостаточно для большинства практических приложений. Больше петель в катушке, более сильный магнит и более быстрое движение делают индукцию практическим источником напряжения.
Исследования PhET: Электромагнитная лаборатория ФарадеяПоиграйте с стержневым магнитом и катушками, чтобы узнать о законе Фарадея.Поднесите стержневой магнит к одной или двум катушкам, чтобы лампочка загорелась. Просмотрите силовые линии магнитного поля. Измеритель показывает направление и величину тока. Просмотрите силовые линии магнитного поля или используйте измеритель, чтобы показать направление и величину тока. Вы также можете играть с электромагнитами, генераторами и трансформаторами!
Щелкните, чтобы загрузить симуляцию. Запускать на Java.
Сводка раздела
Концептуальные вопросы
- Человек, работающий с большими магнитами, иногда помещает голову в сильное поле.Она сообщает, что у нее кружится голова, когда она быстро поворачивает голову. Как это может быть связано с индукцией?
- Ускоритель частиц отправляет заряженные частицы с высокой скоростью по откачанной трубе. Объясните, как катушка с проволокой, намотанная вокруг трубы, может обнаруживать прохождение отдельных частиц. Нарисуйте график выходного напряжения катушки при прохождении через нее одиночной частицы.
Задачи и упражнения
1. Как показано на Рисунке 5 (а), каково направление тока, индуцируемого в катушке 2: (а) Если ток в катушке 1 увеличивается? (b) Если ток в катушке 1 уменьшается? (c) Если ток в катушке 1 постоянный? Ясно покажите, как вы следуете шагам из приведенной выше стратегии решения проблем для закона Ленца .
Рис. 5. (a) Катушки лежат в одной плоскости. (б) Проволока находится в плоскости катушки.
2. Как показано на Рисунке 5 (b), в каком направлении индуцируется ток в катушке: (a) Если ток в проводе увеличивается? (б) Если ток в проводе уменьшится? (c) Если ток в проводе внезапно меняет направление? Ясно покажите, как вы следуете шагам из приведенной выше стратегии решения проблем для закона Ленца .
3. Как показано на рисунке 6, каковы направления токов в катушках 1, 2 и 3 (предположим, что катушки лежат в плоскости цепи): (a) Когда переключатель в первый раз замкнут? (б) Когда переключатель был замкнут в течение длительного времени? (c) Сразу после размыкания переключателя?
Рисунок 6.
4. Повторите предыдущую проблему с перевернутой батареей.
5. Убедитесь, что единицами измерения Δ Φ / Δ т являются вольты. То есть показать, что 1 Тл м 2 / с = 1 В.
6. Предположим, что 50-витковая катушка лежит в плоскости страницы в однородном магнитном поле, направленном внутрь страницы. Змеевик изначально имел площадь 0,250 м 2 . Он растягивается, чтобы не было площади за 0,100 с. Каковы направление и величина наведенной ЭДС, если однородное магнитное поле имеет напряженность 1.50 т?
7. (a) Техник МРТ перемещает свою руку из области очень низкой напряженности магнитного поля в поле 2,00 Тл сканера МРТ, указывая пальцами в направлении поля. Найдите среднюю ЭДС, индуцированную в его обручальном кольце, учитывая его диаметр 2,20 см и предполагая, что для его перемещения в поле требуется 0,250 с. (б) Обсудите, может ли этот ток существенно изменить температуру кольца.
8. Integrated Concepts Обратимся к ситуации в предыдущей задаче: (a) Какой ток индуцируется в кольце, если его сопротивление равно 0.0100 Ом? (б) Какая средняя мощность рассеивается? (c) Какое магнитное поле индуцируется в центре кольца? (d) Каково направление индуцированного магнитного поля относительно поля МРТ?
9. ЭДС индуцируется вращением катушки с 1000 витками диаметром 20,0 см в магнитном поле Земли 5,00 × 10 −5 Тл. Какая средняя ЭДС индуцируется, если плоскость катушки изначально перпендикулярна полю Земли и повернута параллельно полю за 10,0 мс?
10.Катушка с 500 витками радиусом 0,250 м поворачивается на одну четверть оборота за 4,17 мс, первоначально ее плоскость перпендикулярна однородному магнитному полю. (Это 60 об / с.) Найдите напряженность магнитного поля, необходимую для индукции средней ЭДС 10 000 В.
11. Integrated Concepts Примерно как ЭДС, наведенная в петле на рисунке 5 (b), зависит от расстояния центра петли от провода?
12. Integrated Concepts (a) Молния создает быстро меняющееся магнитное поле.Если болт ударяется о землю вертикально и действует как ток в длинном прямом проводе, он вызывает напряжение в петле, выровненной, как показано на рисунке 5 (b). Какое напряжение индуцируется в петле диаметром 50,0 м 1,00 м от удара молнии 2,00 × 10 6 , если ток падает до нуля за 25,0 мкс? (b) Обсудите обстоятельства, при которых такое напряжение может привести к заметным последствиям.
Глоссарий
- Закон индукции Фарадея:
- средство вычисления ЭДС в катушке из-за изменения магнитного потока, заданное как [latex] \ text {emf} = — N \ frac {\ Delta \ Phi} {\ Delta t} \\ [/ latex]
- Закон Ленца:
- знак минус в законе Фарадея, означающий, что ЭДС, индуцированная в катушке, противодействует изменению магнитного потока.
Избранные решения проблем и упражнения
1.(a) CCW (b) CW (c) Нет наведенного тока
3. (a) 1 против часовой стрелки, 2 против часовой стрелки, 3 по часовой стрелке (b) 1, 2 и 3 без тока индуцированного (c) 1 CW, 2 CW, 3 CCW
7. (a) 3,04 мВ (b) В качестве нижнего предела для кольца, оценка R = 1,00 мОм. Передаваемое тепло составит 2,31 мДж. Это небольшое количество тепла.
9. 0,157 В
11. пропорционально [латексу] \ frac {1} {r} \\ [/ latex]
Закон Ленца — Определение, формула и пример
Что такое закон Ленца?
Закон Ленца, названный в честь физика Эмиля Ленца, был сформулирован в 1834 году.Он утверждает, что направление тока, индуцированного в проводнике изменяющимся магнитным полем, таково, что магнитное поле, создаваемое индуцированным током, противодействует начальному изменяющемуся магнитному полю.
Когда ток индуцируется магнитным полем, то магнитное поле, создаваемое индуцированным током, создает свое магнитное поле. Таким образом, этому магнитному полю будет противостоять создавшее его магнитное поле.
Закон Ленца основан на законе индукции Фарадея, который гласит, что изменяющееся магнитное поле индуцирует ток в проводнике, тогда как закон Ленца сообщает нам направление индуцированного тока, которое противодействует начальному изменяющемуся магнитному полю, которое его породило.Следовательно, это обозначено в формуле закона Фарадея отрицательным знаком.
\ [\ epsilon = — \ frac {d \ Phi_ {B}} {dt} \]
Магнитное поле можно изменить, изменив его силу, либо перемещая магнит к катушке или от нее, либо перемещая катушка находится в магнитном поле или вне его.
Следовательно, мы можем сказать, что величина электромагнитного поля, индуцированного в цепи, пропорциональна скорости изменения магнитного потока.
\ [\ varepsilon \ propto \ frac {d \ Phi} {dt} \].
Формула закона Ленца:
Согласно закону Ленца, когда электромагнитное поле генерируется изменением магнитного потока, полярность индуцированного электромагнитного поля создает индуцированный ток, магнитное поле которого противодействует начальному изменяющемуся магнитному полю, создавшему его.
Формула закона Ленца показана ниже:
\ [\ epsilon = — N \ frac {\ partial \ Phi_ {B}} {\ partial t} \]
Где,
ε = индуцированная ЭДС
δΦB = изменение магнитного потока
N = количество витков в катушке
Применения закона Ленца:
Применения закона Ленца включают:
Когда источник электромагнитного поля подключается к катушке индуктивности, ток начинает течь через него.Обратное электромагнитное поле будет противодействовать этому увеличению тока через катушку индуктивности. Чтобы установить ток, внешний источник электромагнитного поля должен проделать некоторую работу для преодоления этого противостояния.
Закон Ленца используется в электромагнитных тормозах и индукционных варочных панелях.
Применяется также для электрогенераторов, генераторов переменного тока.
Вихретоковые весы
Металлодетекторы
Вихретоковые динамометры
Тормозные системы в поезде
Картридеры
- Чтобы найти направление наведенной электродвижущей силы и тока, воспользуемся законом Ленца.Ниже приведены некоторые эксперименты.
(изображение будет скоро загружено)
Первый эксперимент:
В первом эксперименте, когда ток в катушке протекает в цепи, создаются силовые линии магнитного поля. По мере того, как ток, протекающий через катушку, увеличивается, магнитный поток увеличивается. Направление потока индуцированного тока должно быть таким, чтобы оно было противоположным при увеличении магнитного потока.
Второй эксперимент:
Во втором эксперименте, когда катушка с током намотана на железный стержень, левый конец которого ведет себя как N-полюс, и перемещается к катушке S, возникает индуцированный ток.
Третий эксперимент:
В третьем эксперименте катушка притягивается к магнитному потоку, связанная катушка продолжает уменьшаться, что означает, что площадь катушки внутри магнитного поля уменьшается.
Согласно закону Ленца, катушка движется противоположно, когда индуцированный ток прикладывается в том же направлении.
Для выработки тока магнит в петле прикладывает силу. Чтобы противодействовать изменению, сила тока на магните должна быть приложена.
Закон Ленца (физика) Определение, уравнение и примеры
Обновлено 28 декабря 2020 г.
Ли Джонсон
Генрих Ленц (также известный как Эмиль Ленц) был физиком из прибалтийской Германии, который, возможно, не имел славы некоторых из его сверстников начала 19 века, таких как Майкл Фарадей, но который все же внес ключевой вклад в разгадку загадок электромагнетизма.
В то время как некоторые из его коллег делали аналогичные открытия, имя Ленца было присвоено закону Ленца в значительной степени из-за его скрупулезного ведения записей, исчерпывающей документации своих экспериментов и приверженности научному методу необычно для того времени.Сам закон является важной частью закона об электромагнитной индукции Фарадея и конкретно указывает направление , в котором течет индуцированный ток.
Поначалу может быть сложно осмыслить закон, но как только вы поймете ключевую концепцию, вы будете на пути к гораздо более глубокому пониманию электромагнетизма, включая практические вопросы, такие как проблема вихревых токов.
Закон Фарадея
Закон индукции Фарадея гласит, что индуцированная электродвижущая сила (ЭДС, обычно называемая «напряжение») в катушке с проволокой (или просто вокруг петли) минус скорость изменения магнитного потока через этот контур.Математически, заменив производную на более простое «изменение» (представленное ∆), закон гласит:
\ text {индуцированная ЭДС} = −N \ frac {∆ϕ} {∆t}
Где t — время, N, — количество витков в катушке с проволокой, а phi (ϕ) — магнитный поток. Определение магнитного потока очень важно для этого уравнения, поэтому стоит помнить, что это:
ϕ = \ bm {B ∙ A} = BA \ cos (θ)
, которое связывает силу магнитного поля, B , к области петли A , и угол между петлей и полем ( θ ), причем угол петли определяется как перпендикулярно области (т.е.е., указывая прямо из петли). Поскольку в уравнении используется cos, он имеет максимальное значение, когда поле прямо выровнено с петлей, и 0, когда оно перпендикулярно петле (т. Е. «Сбоку»).
Взятые вместе, эти уравнения показывают, что вы можете создать ЭДС в катушке с проволокой, изменив площадь поперечного сечения A , силу магнитного поля B или угол между областями и магнитное поле. Величина наведенной ЭДС прямо пропорциональна скорости изменения этих величин, и, конечно, не обязательно должно быть просто одно из этих изменений, чтобы вызвать ЭДС.
Закон Фарадея был использован Джеймсом Клерком Максвеллом в качестве одного из его четырех законов электромагнетизма, хотя обычно он выражается как линейный интеграл магнитного поля вокруг замкнутого контура (который, по сути, является другим способом обозначить индуцированную ЭДС) и скорость изменения выражается производной.
Закон Ленца
Закон Ленца заключен в закон Фарадея, поскольку он сообщает нам направление, в котором течет индуцированный электрический ток. Самый простой способ сформулировать закон Ленца состоит в том, что изменения магнитного потока индуцируют токи в направлении, которое противодействует изменению , вызвавшему его.
Другими словами, поскольку при протекании тока он генерирует собственное магнитное поле, направление индуцированного тока таково, что новое магнитное поле находится в направлении, противоположном направлению изменений потока, которые его создали. Это заключено в законе Фарадея из-за отрицательного знака; это говорит вам, что наведенная ЭДС противодействует первоначальному изменению магнитного потока.
В качестве простого примера представьте катушку с проволокой с внешним магнитным полем, направленным прямо на нее с правой стороны (т.е.е., в центр катушки и с силовыми линиями, направленными влево), а внешнее поле затем увеличивается по величине, но сохраняет то же направление. В этом случае индуцированный ток в проводе будет течь так, чтобы создать магнитное поле, направленное из катушки вправо.
Если бы внешнее поле вместо этого уменьшилось по величине, индуцированный ток протекал бы так, чтобы создать магнитное поле в том же направлении, что и исходное поле, потому что он противодействует изменениям потока , а не просто противодействует полю.Поскольку он противодействует изменению, а не обязательно направлению , это означает, что иногда он создает поле в противоположном направлении, а иногда в том же направлении.
Вы можете использовать правило правой руки (иногда называемое правилом правой руки, чтобы отличить его от другого правила правой руки, используемого в физике), чтобы определить направление возникающего электрического тока. Правило довольно легко применить: определите направление магнитного поля, создаваемого индуцированным током, и направьте большой палец правой руки в этом направлении, а затем согните пальцы внутрь.Направление, в котором сгибаются ваши пальцы, — это направление, в котором ток течет через катушку с проволокой.
Примеры закона Ленца
Некоторые конкретные примеры того, как закон Ленца работает на практике, помогут закрепить концепции, и самый простой очень похож на приведенный выше пример: катушка провода, движущаяся в магнитное поле или из него. . По мере того, как петля движется в поле, магнитный поток через петлю будет увеличиваться (в направлении, противоположном движению катушки), индуцируя ток, который противодействует скорости изменения потока, и, таким образом, создает магнитное поле в направлении его движения.
Если катушка движется к вам, правило правой руки и закон Ленца показывают, что ток будет течь против часовой стрелки. Если бы катушка двигалась на из поля, изменяющийся магнитный поток был бы в основном постепенным уменьшением, а не увеличением, поэтому индуцировался бы прямо противоположный ток.
Эта ситуация аналогична перемещению стержневого магнита в центр катушки или из центра, потому что при перемещении магнита внутрь поле будет становиться сильнее, а индуцированное магнитное поле будет работать, чтобы противодействовать движению магнита, поэтому , против часовой стрелки с точки зрения магнита.При перемещении из центра катушки с проволокой магнитный поток будет уменьшаться, и индуцированное магнитное поле снова будет работать, чтобы противодействовать движению магнита, на этот раз по часовой стрелке с точки зрения магнита.
Более сложный пример включает катушку с проволокой, вращающуюся в фиксированном магнитном поле, потому что при изменении угла также будет изменяться поток через петлю. Во время уменьшения потока индуцированный электрический ток будет создавать магнитное поле, препятствующее изменениям потока, так что оно будет в том же направлении, что и внешнее поле.Во время увеличения магнитного потока происходит обратное, и индуцируется ток, чтобы противодействовать увеличению магнитного потока, то есть в направлении, противоположном внешнему полю. Это генерирует переменное напряжение (потому что индуцированная ЭДС переключается каждый раз, когда контур поворачивается на 180 градусов), и это можно использовать для генерации переменного тока.
Закон Ленца и вихревые токи
Вихревой ток — это название малых электрических токов, которые подчиняются закону Ленца. В частности, это название используется в отношении небольших петлевых токов в проводниках, аналогичных вихрям, которые вы видите вокруг своих весел во время гребли в воде.
Когда проводник перемещается в магнитном поле — например, как металлический маятник, раскачивающийся между полюсами подковообразного магнита, — индуцируются вихревые токи, которые в соответствии с законом Ленца противодействуют эффекту движения. Это приводит к магнитному затуханию (так как индуцированное поле обязательно работает против движения, которое его создало), которое можно продуктивно использовать в таких вещах, как магнитные тормозные системы для американских горок, но это причина потери энергии для таких устройств, как генераторы и трансформаторы.
Когда необходимо уменьшить вихревые токи, проводник разделяется на несколько секций тонкими изоляционными слоями, которые ограничивают размер вихревых токов и уменьшают потери энергии. Однако, поскольку вихревые токи являются необходимым следствием законов Фарадея и Ленца, полностью предотвратить их невозможно.
Закон электромагнитной индукции Ленца
Что такое закон электромагнитной индукции Ленца
Что такое закон Ленца?Согласно закону Ленца (который был введен русским физиком из Балтии и Германии Генрихом Фридрихом Эмилем Ленцем в 1834 году) направление тока можно определить.когда ток через катушку изменяет магнитное поле, напряжение создается в результате изменения магнитного поля, направление индуцированного напряжения таково, что оно всегда противодействует изменению тока.
Закон Ленца влечет за собой способ определения направления наведенной ЭДС в катушке. «Таким образом, он утверждает, что направление наведенной ЭДС таково, что оно противодействует вызывающему ее изменению.
Другими словами, закон Ленца гласит, что, когда в цепи индуцируется Э. М. Ф., текущая установка всегда противодействует движению или изменению тока, которое его вызывает.OR
Индуцированная ЭДС вызовет протекание тока в замкнутой цепи в таком направлении, что его магнитный эффект будет противодействовать вызвавшему его изменению.
Очень простыми словами, закон Ленца гласит, что индуцированный эффект всегда таков, что противоречит причине, его вызвавшей.
Объяснение закона ЛенцаЗакон Ленца (который немного сложен и сбивает с толку новичков) можно понять с помощью приведенной выше схемы, на которой изолированная катушка соединена с чувствительным гальванометром и статическим и сплошной стержневой магнит.Давайте посмотрим, как это работает
- Когда и стержневой магнит, и катушка находятся в статическом положении, не течет ток или наведена ЭДС (даже небольшое количество магнитного потока (полюса N статического магнитного стержня), связанное с движением катушки), следовательно, нет прогиба гальванометра.
- Когда стержень магнита быстро движется к катушке, в гальванометре, например, происходит быстрое отклонение. Имейте в виду, что отклонение будет оставаться постоянным до тех пор, пока стержень магнита не будет непрерывно перемещаться по отношению к катушке (т.е.е. относительный момент между стержнем магнита и катушкой). Если и стержень магнита, и катушка достигают статического положения, отклонение гальванометра будет в нулевом положении (как показано на рис. 1 A).
- Когда стержень магнита отодвигается от катушки, гальванометр снова будет отклоняться до тех пор, пока относительное перемещение стержня магнита и катушки не станет неподвижным или статическим. Имейте в виду, что направление гальванометра противоположно направлению, показанному на рис. 1A (как показано на рис. 1 B).
- То же самое происходит (этапы 2 и 3), если стержень магнита находится в статическом положении, в то время как катушка движется к стержню статического магнита или удаляется от него.
Это ясно показывает, что когда магнитный стержень (в движении) находится рядом с катушкой, он разрезает или соединяется с большой частью магнитного потока, тогда как скорость магнитной связи меньше в случае, когда магнитный стержень удаляется от катушки. .
Отклонение гальванометра показывает наведенную ЭДС в катушке, вызванную внезапным перемещением или удалением стержня магнита к катушке.Точной причиной наведенной ЭДС является изменение магнитной связи по отношению к катушке, которое продолжается до тех пор, пока движение как стержня магнита, так и катушки не будет остановлено. Другими словами, сильное магнитное поле или магнитный поток не вызывает ЭДС в проводнике статического электричества. Следовательно, изменение магнитного потока является обязательным явлением для индукции ЭДС в катушке или проводниках.
Приведенное выше объяснение показывает, что, когда полюс «N» магнита перемещается к катушке, в катушке индуцируется ЭДС и протекает ток в ней против часовой стрелки (если смотреть на катушку сбоку), следовательно, передний конец катушки становится «N» полюсом (рис. 1.А).
Таким образом, северный полюс магнита отражает нейтральный полюс катушки N. Для управления этой силой отталкивания используется механическая энергия, которая преобразуется в электрическую энергию в форме ЭДС в катушке.
Аналогично, когда Северный полюс магнита перемещается от катушки, обращенный конец катушки становится S-полюсом. Таким образом, полюс N магнитного стержня притягивает полюс S. Чтобы контролировать эту силу притяжения между катушкой и стержнем магнита, снова требуется механическая энергия, которая преобразуется в электрическую энергию в форме индуцированной ЭДС в катушке.
Это доказывает, что индуцированный ток всегда течет в таком направлении, что он противодействует изменению магнитного поля (перемещение к / от магнитного стержня к катушке), которое его вызвало.
Похожие сообщения:
Формула и уравнения для закона ЛенцаОсновная версия закона Ленца может быть математически выражена следующим образом.
e = — (dΦ B / dt)
Фактически, символ «-» в законе электромагнитной индукции Фарадея представляет закон Лена.Поскольку он основан на принципе сохранения энергии, а также на третьем законе Ньютона (каждое действие имеет равную реакцию, но величина имеет противоположное направление.
Другие формы уравнений и формул для закона Ленца следующие.
- e = — N (dΦ B / dt)
- e = — N (ΔΦ / Δt)
- e = — N (δΦ B / δt)
Где:
- e = Наведенная ЭДС в катушке / проводнике
- N = Число витков или витков в катушке
- dΦ B , ΔΦ, δΦ B = Изменение скорости магнитного потока
- dt, Δt, δt = Изменение скорости времени
Применение закона Ленца
Существует множество вариантов использования и применения, основанных на законе Лена e.грамм. основной принцип закона Ленца используется в
- Электромагнитное торможение в поездах.
- Индукционные горелки, варочные панели и индукционный нагрев.
- Электрогенераторы, трансформаторы и двигатели (противо-ЭДС).
- Микрофоны, устройства чтения карт, ленты для записи аудио / видео, жесткий диск и вращающиеся диски, а также дебетовые / кредитные карты.
- Вихретоковые весы.
- Динамометры и металлоискатели.
- Для анализа основной концепции накопленной энергии в индукторах.
Похожие сообщения
Закон Фарадея и закон электромагнитной индукции Ленца
Законы электромагнитной индукции Фарадея объясняют взаимосвязь между электрической цепью и магнитным полем. Этот закон является основным принципом работы большинства электродвигателей, генераторов, трансформаторов, индукторов и т. Д.Первый закон Фарадея:
Всякий раз, когда проводник помещается в переменное магнитное поле, ЭДС индуцируется поперек проводника (называемая индуцированной ЭДС), и если проводник представляет собой замкнутую цепь, то индуцированный ток течет через него.
Магнитное поле можно варьировать различными методами —
1. Путем перемещения магнита
2. Перемещая катушку
3. Вращением катушки относительно магнитного поляВторой закон Фарадея:
Второй закон электромагнитной индукции Фарадея утверждает, что величина наведенной ЭДС равна скорости изменения магнитных связей с катушкой. Магнитопровод представляет собой произведение числа витков, и магнитного потока, связанного с катушкой.Формула закона Фарадея:
Если считать, что проводник движется в магнитном поле, тогда
потокосцепление с катушкой в исходном положении проводника = NΦ 1 (Wb) (N — скорость двигателя, Φ — поток)
потокосцепление с катушкой в конечном положении проводника = NΦ 2 (Wb)
изменение потокосцепления с начального на конечное = N (Φ 1 — Φ 2 )
пусть Φ 1 — Φ 2 = Φ
следовательно, изменение потокосцепления = NΦ
и скорость изменения потокосцепления = NΦ / t
взяв производную от RHS
скорость изменения магнитных связей = N (dΦ / dt)Согласно закону электромагнитной индукции Фарадея , скорость изменения магнитных связей равна наведенной ЭДС
Итак, E = N (dΦ / dt) (вольт )
Феномен взаимной индукции
Переменный ток, протекающий в катушке, создает вокруг нее переменное магнитное поле.Когда две или более катушек магнитно связаны друг с другом, тогда переменный ток, протекающий через одну катушку, вызывает наведенную ЭДС на других связанных катушках. Это явление называется взаимной индукцией.
Закон ЛенцаЗакон электромагнитной индукции Ленца гласит, что, когда ЭДС индуцируется в соответствии с законом Фарадея, полярность (направление) этой индуцированной ЭДС такова, что она противодействует причине ее возникновения.
Таким образом, учитывая закон Ленца
E = -N (dΦ / dt) (вольт)Отрицательный знак показывает, что направление наведенной ЭДС и направление изменения магнитных полей имеют противоположные знаки.
Важность, формула, значение и применение
Закон Ленца был первоначально предложен Генрихом Фридрихом Ленцем, и вся его карьера была полностью связана с физикой и химией. Его первоначальное наблюдение было связано с эффектом Пельтье, который означает природу проводимости металлов и изменение значения электрического сопротивления в зависимости от температуры. Затем исследования Ленца перешли к электропроводности и открыли эффект Джоуля. Исследование независимости электрических вариаций было направлено на провозглашение закона Ленца в 1834 году.Таким образом, этот подход способствовал развитию закона Ленца, который делает возможным знание направления и вибрации, возникающих при изменении потока энергии. В этой статье дается четкое описание закона Ленца, его формулы, значения и применения.
Что такое закон Ленца?
Закон Ленца об электромагнитной индукции определяет, что направление тока, развивающееся в проводнике за счет изменения магнитного поля (которое является магнитным полем, создаваемым индуцированным током), противоположно начальному изменяющемуся магнитному полю, создавшему его.Направление тока представлено с использованием принципа правой руки Флеминга.
Поначалу кажется трудным понять концепцию закона Ленца. Чтобы упростить это, рассмотрим приведенный ниже пример.
Когда моделирование тока выполняется с помощью магнитного поля, то магнитное поле, создаваемое этим моделируемым током, будет генерировать собственное магнитное поле. И генерируемое магнитное поле будет противодействовать магнитному полю, которое его изначально создало.
Принцип закона Ленца
Это качественный принцип, который указывает смоделированное направление тока, но не объясняет ничего, связанного с величиной.Закон Ленца определяет путь множественных эффектов в электромагнетизме, таких как путь напряжения, моделируемый в индукторе или проводе через переменный ток, или тянущая сила вихревых токов, приложенных к движущимся объектам в магнитном поле.
Приведенный ниже пример четко объясняет сценарий, когда при увеличении магнитного поля моделируемое магнитное поле будет действовать противоположным образом. В то время как, когда магнитное поле уменьшается, моделируемое магнитное поле также действует противоположно ему.Но здесь противоположный путь соответствует тому, что он действует, чтобы усилить поле, поскольку оно сопротивляется снижению скорости изменения.
Этот закон в основном зависит от принципа индукции Фарадея. Согласно этому принципу, изменяющееся магнитное поле будет стимулировать прохождение тока через проводник. Принцип Ленца гласит, что путь симулированного тока противоречит действительному изменяющемуся магнитному полю, которое его генерировало. Этот сценарий можно представить в виде формулы, которая показана ниже:
Є = — (dФ B / dt)
Изменение магнитного поля может быть связано с изменением напряженности магнитного поля либо по изменение положения магнита близко или далеко от катушки или изменение положения катушки в соответствии с магнитным полем.Также можно сказать, что величина ЭДС, которая моделируется в схеме, будет прямо пропорциональна скорости изменения магнитного потока.
Формула
Закон Ленца определяет, что при возникновении ЭДС из-за изменения магнитного поля поляризация смоделированной ЭДС такова, что она генерирует смоделированный ток, где его магнитное поле противоречит начальному изменяющемуся магнитному полю. поле, которое его сгенерировало. А формула закона Ленца имеет следующий вид:
Є = -N (dФ B / dt)
Где «correspond» соответствует смоделированной ЭДС
«dФ B » соответствует изменяющемуся магнитному полю
А «N» означает витки катушки.
Отрицательный знак в формуле означает, что смоделированная ЭДС и изменяющееся магнитное поле имеют противоположные знаки.
Закон Ленца и сохранение энергии
Чтобы соответствовать принципу сохранения энергии, смоделированный путь тока по закону Ленца должен генерировать магнитное поле, которое противоречит магнитному полю, которое его произвело. Этот закон является следствием принципа сохранения энергии.
Когда магнитное поле, создаваемое моделируемым током, аналогично полю, создавшему его, тогда оба поля объединяются и развивают увеличенное магнитное поле.Это увеличенное поле будет генерировать другой моделируемый ток внутри проводника, который в два раза превышает величину фактического моделируемого тока. Опять же, это создает еще один симулированный ток, и этот процесс продолжается.
Итак, можно констатировать, что закон Ленца сам генерирует симулированный ток, который противоречит полю, которое его произвело, — так что можно заключить, используя бесконечную петлю положительной обратной связи, тем самым блокируя сохранение энергии.
Закон Ленца также соответствует третьему принципу Ньютона.В соответствии с этим, когда моделируемый ток генерирует магнитное поле, которое является таким же и противоречит траектории магнитного поля, которое его произвело, тогда только он обладает способностью отражать изменение магнитного поля в этом месте.
Объясните закон Ленца
Чтобы четко понять феномен, лежащий в основе закона Ленца, рассмотрим следующие две ситуации.
Ситуация 1: Когда магнит движется близко к катушке.
Когда северный полюс магнита приближается к катушке, поток, который соединяется с катушкой, также увеличивается.Согласно принципу Фарадея, при изменении магнитного потока и ЭДС происходит моделирование тока в катушке, и это создает собственное магнитное поле.
Понимание закона Ленца — Случай 1
И согласно закону Ленца, магнитное поле само противоречит или противодействует увеличению потока через катушку, и это возможно только тогда, когда катушка приобретает северную полярность, потому что полюса того же типа отталкивает друг друга. Зная магнитную полярность катушки, можно также узнать путь симулированного тока.Здесь направление тока будет против часовой стрелки.
Ситуация 2: Когда магнит движется далеко от катушки.
Когда северный полюс магнита удаляется от катушки, поток, который соединяется с катушкой, уменьшается. Согласно принципу Фарадея, при изменении магнитного потока и ЭДС происходит моделирование тока в катушке, и это создает собственное магнитное поле.
Понимание закона Ленца — Случай 2
И согласно закону Ленца, магнитное поле само противоречит или противодействует уменьшенному потоку через катушку, и это возможно только тогда, когда катушка приобретает южную полярность, поскольку неидентичные полюса притягиваются. друг с другом.Зная магнитную полярность катушки, можно также узнать путь симулированного тока. Здесь направление тока будет по часовой стрелке.
Это считается подробным значением закона Ленца .
С помощью принципа большого пальца правой руки можно узнать направление тока или магнитного поля. Когда пальцы правой руки расположены поперек провода, то направление большого пальца соответствует направлению тока, а направление согнутых пальцев соответствует направлению магнитного поля, создаваемого проводом.
С помощью этого правила большого пальца правой руки закон Ленца определяется как:
Когда магнитный поток Ф, который соединяется с катушкой, увеличивается, тогда направление тока таково, что оно противоречит приращению потока, и поэтому моделируемый ток будет генерировать свой поток в направлении.
Правило большого пальца правой руки
Когда магнитный поток Ф, который соединяется с катушкой, уменьшается, тогда направление тока таково, что оно похоже на направление уменьшающегося потока, и поэтому моделируемый ток будет генерировать свой поток в направление, как показано на рисунке ниже.
Процедура решения проблем
Проблемы, которые должны быть разрешены в соответствии с законом Ленца, можно легко решить, выполнив следующие шаги:
- Знайте вопрос и четко представляйте, что необходимо решить.
- Определите путь магнитного поля
- Узнайте, увеличивается или уменьшается скорость магнитного потока
- Теперь найдите путь моделируемого магнитного поля. Это противоречит изменению магнитного потока путем вычитания или объединения с фактическим полем
- Вычислите смоделированный ток, который генерирует смоделированное магнитное поле
- Путь смоделированной ЭДС теперь будет запускать ток на этом пути и может быть указан как ток, который развивается от положительного фронта ЭДС и возвращается к отрицательному.
Приложения
Это несколько приложений закона Ленца :
- Благодаря этому закону известна теория накопленной магнитной энергии в индукторе. Когда исходная ЭДС подключена через катушку индуктивности, через нее будет протекать ток. Обратная ЭДС будет противоречить приращению тока через катушку индуктивности. Итак, чтобы вызвать протекание тока, должен быть другой периферийный источник ЭДС, который устраняет противоречие. Это достигается за счет ЭДС, которая накапливается в катушке индуктивности, и ее также можно восстановить после удаления периферийного источника ЭДС из схемы.
- Этот закон определяет, что моделируемая ЭДС и изменение потока будут иметь разные знаки, и это показывает физический анализ выбора знаков в принципе индукции Фарадея.
- Закон Ленца также применим к электрическим генераторам. Когда в генераторе происходит имитация тока, это противоречит ему и запускает вращение генератора, поэтому устройству требуется дополнительная механическая энергия. Это также обеспечивает обратную ЭДС, когда устройства представляют собой электродвигатели.
- Применяется в посуде с электромагнитным торможением и индукционной посуде.
- Используется в вихретоковых компенсаторах и вихретоковых динамометрах.
- Использованные микрофоны, тормозное оборудование в поездах и генераторы переменного тока.
- Устройства, работающие по закону Ленца, также можно использовать в кардридерах.
Это все о концепции закона Ленца. Эта статья предоставила исчерпывающую информацию о принципе закона Ленца, его формуле, сохранении энергии, значении и применении. Еще более важно знать еще несколько примеров закона Ленца в реальных приложениях.
13.3: Закон Ленца — Physics LibreTexts
Цели обучения
К концу этого раздела вы сможете:
- Используйте закон Ленца для определения направления наведенной ЭДС при изменении магнитного потока
- Используйте закон Фарадея с законом Ленца для определения наведенной ЭДС в катушке и соленоиде.
Направление, в котором индуцированная ЭДС движет ток по проволочной петле, можно определить через отрицательный знак.Однако обычно это направление легче определить с помощью закона Ленца, названного в честь его первооткрывателя Генриха Ленца (1804–1865). (Фарадей также открыл этот закон, независимо от Ленца.) Мы формулируем закон Ленца следующим образом:
Закон Ленца
Направление наведенной ЭДС направляет ток вокруг проволочной петли, чтобы всегда противодействовать изменению магнитного потока, вызывающему ЭДС.
Закон Ленца также можно рассматривать с точки зрения сохранения энергии.Если толкание магнита в катушку вызывает ток, энергия в этом токе должна исходить откуда-то. Если индуцированный ток вызывает магнитное поле, противодействующее увеличению поля магнита, который мы втолкнули, тогда ситуация ясна. Мы приложили магнит к полю и поработали с системой, и это проявилось как ток. Если бы индуцированное поле не препятствовало изменению магнитного потока, магнит был бы втянут, создавая ток без каких-либо действий. Была бы создана электрическая потенциальная энергия, нарушив закон сохранения энергии.
Чтобы определить наведенную ЭДС \ (\ epsilon \), вы сначала вычисляете магнитный поток \ (\ Phi_m \), а затем получаете \ (d \ Phi_m / dt \). Величина \ (\ epsilon \) равна
.\ [\ epsilon = \ left | \ dfrac {d \ Phi_m} {dt} \ right |. \]
Наконец, вы можете применить закон Ленца, чтобы определить смысл \ (\ epsilon \). Это будет развиваться на примерах, которые иллюстрируют следующую стратегию решения проблем.
Стратегия решения проблем: закон Ленца
Чтобы использовать закон Ленца для определения направлений индуцированных магнитных полей, токов и ЭДС:
- Сделайте набросок ситуации для использования при визуализации и записи направлений.
- Определите направление приложенного магнитного поля \ (\ vec {B} \).
- Определите, увеличивается или уменьшается его магнитный поток.
- Теперь определите направление индуцированного магнитного поля \ (\ vec {B} \). Индуцированное магнитное поле пытается усилить магнитный поток, который уменьшается, или противодействует магнитному потоку, который увеличивается. Следовательно, индуцированное магнитное поле добавляет или вычитает приложенное магнитное поле в зависимости от изменения магнитного потока.
- Используйте правило правой руки 2 (RHR-2; см. Магнитные силы и поля), чтобы определить направление индуцированного тока I , который отвечает за индуцированное магнитное поле \ (\ vec {B} \).
- Направление (или полярность) наведенной ЭДС теперь может управлять обычным током в этом направлении.
Давайте применим закон Ленца к системе на рисунке \ (\ PageIndex {1a} \). Мы обозначаем «перед» замкнутой проводящей петли как область, содержащую приближающийся стержневой магнит, а «заднюю часть» петли как другую область.По мере того, как северный полюс магнита движется к петле, поток через петлю из-за поля магнита увеличивается, потому что напряженность силовых линий, направленных от передней части петли к задней, увеличивается. Поэтому в контуре индуцируется ток. По закону Ленца направление индуцированного тока должно быть таким, чтобы его собственное магнитное поле было направлено так, чтобы противодействовало изменяющемуся потоку, вызванному полем приближающегося магнита. Следовательно, индуцированный ток циркулирует так, что силовые линии его магнитного поля через петлю направлены от задней части петли к передней.При использовании RHR-2 поместите большой палец напротив силовых линий магнитного поля, то есть к стержневому магниту. Ваши пальцы сгибаются против часовой стрелки, если смотреть со стороны стержневого магнита. В качестве альтернативы, мы можем определить направление индуцированного тока, рассматривая токовую петлю как электромагнит, который противодействует приближению северного полюса стержневого магнита. Это происходит, когда индуцированный ток течет, как показано, поскольку тогда поверхность петли ближе к приближающемуся магниту также является северным полюсом.
Рисунок \ (\ PageIndex {1} \): изменение магнитного потока, вызванное приближением магнита, индуцирует ток в контуре. (а) Приближающийся северный полюс индуцирует ток против часовой стрелки по отношению к стержневому магниту. (b) Приближающийся южный полюс индуцирует ток по часовой стрелке относительно стержневого магнита.На части (b) рисунка показан южный полюс магнита, движущийся к проводящей петле. В этом случае поток через петлю из-за поля магнита увеличивается, потому что количество силовых линий, направленных от задней части петли к передней, увеличивается.Чтобы противодействовать этому изменению, в петле индуцируется ток, силовые линии которого через петлю направлены спереди назад. Точно так же можно сказать, что ток течет в таком направлении, что поверхность петли, расположенная ближе к приближающемуся магниту, является южным полюсом, который затем отталкивает приближающийся южный полюс магнита. При использовании RHR-2 ваш большой палец направлен в сторону от стержневого магнита. Ваши пальцы сгибаются по часовой стрелке, что соответствует направлению индуцированного тока.
Другой пример, иллюстрирующий использование закона Ленца, показан на рисунке \ (\ PageIndex {2} \).Когда переключатель разомкнут, уменьшение тока через соленоид вызывает уменьшение магнитного потока через его катушки, что вызывает ЭДС в соленоиде. Эта ЭДС должна противодействовать вызывающему его изменению (прекращению тока). Следовательно, наведенная ЭДС имеет указанную полярность и движется в направлении исходного тока. Это может вызвать дугу на выводах переключателя при его размыкании.
Рисунок \ (\ PageIndex {2} \): (а) Соленоид, подключенный к источнику ЭДС.(b) Размыкающий переключатель S прекращает подачу тока, что, в свою очередь, индуцирует ЭДС в соленоиде. (c) Разность потенциалов между концами заостренных стержней создается за счет индукции ЭДС в катушке. Эта разность потенциалов достаточно велика, чтобы образовалась дуга между острыми точками.Упражнение \ (\ PageIndex {1A} \)
Найдите направление индуцированного тока в проволочной петле, показанной ниже, когда магнит входит, проходит и покидает петлю.
Решение
Для показанного наблюдателя ток течет по часовой стрелке по мере приближения магнита, уменьшается до нуля, когда магнит центрируется в плоскости катушки, а затем течет против часовой стрелки, когда магнит покидает катушку.
Упражнение \ (\ PageIndex {1B} \)
Проверьте направления наведенных токов на рисунке 13.2.2.
Пример \ (\ PageIndex {1A} \): круглая катушка в изменяющемся магнитном поле
Магнитное поле \ (\ vec {B} \) направлено наружу перпендикулярно плоскости круглой катушки радиуса \ (r = 0.50 \, m \) (рисунок \ (\ PageIndex {3} \)). Поле цилиндрически симметрично относительно центра катушки, и его величина экспоненциально убывает согласно \ (B = (1.{-2} s \) и \ (t_3 = 1.0 \, s \). (b) Определите ток в катушке в эти три момента, если ее сопротивление равно \ (10 \, \ Omega \).
Рисунок \ (\ PageIndex {3} \): круглая катушка в убывающем магнитном поле.Стратегия
Поскольку магнитное поле перпендикулярно плоскости катушки и постоянно в каждом месте в катушке, скалярное произведение магнитного поля \ (\ vec {B} \) и нормали к единичному вектору площади \ (\ hat { n} \) превращается в умножение. Магнитное поле можно вывести из интеграции, оставив магнитный поток как произведение магнитного поля на площадь.{-1}) t} V. \] Поскольку \ (\ vec {B} \) направлено за пределы страницы и уменьшается, индуцированный ток должен течь против часовой стрелки, если смотреть сверху, так что магнитное поле, которое он создает через катушка также указывает за пределы страницы. Для всех трех времен значение ε направлено против часовой стрелки; его величины равны \ [\ epsilon (t_1) = 6,0 В; \, \ epsilon (t_2) = 4,7 \, В; \, \ epsilon (t_3) = 0040 \, V. \]
- Согласно закону Ома, соответствующие токи равны \ [I (t_1) = \ frac {\ epsilon (t_1)} {R} = \ frac {6.{-3} \, А. \]
Значение
Напряжение ЭДС создается изменением магнитного потока во времени. Если мы знаем, как магнитное поле изменяется со временем в постоянной области, мы можем взять его производную по времени для расчета наведенной ЭДС.
Пример \ (\ PageIndex {1B} \): изменение магнитного поля внутри соленоида
Ток через обмотки соленоида с \ (n = 2000 \) витками на метр изменяется со скоростью \ (dI / dt = 3,0 \, А / с \).(См. «Источники магнитных полей» для обсуждения соленоидов.) Соленоид имеет длину 50 см и диаметр поперечного сечения 3,0 см. Небольшая катушка, состоящая из \ (N = 20 \) тесно намотанных витков, обернутых в круг диаметром 1,0 см, помещается в середину соленоида так, чтобы плоскость катушки была перпендикулярна центральной оси соленоида. Предполагая, что приближение бесконечного соленоида применимо в месте расположения небольшой катушки, определите величину ЭДС, индуцированной в катушке.
Стратегия
Магнитное поле в середине соленоида имеет однородное значение \ (\ mu_0 nI \). Это поле создает максимальный магнитный поток через катушку, поскольку он направлен по длине соленоида. Следовательно, магнитный поток, проходящий через катушку, является произведением магнитного поля соленоида на площадь катушки. Закон Фарадея включает производную от магнитного потока по времени. Единственная величина, изменяющаяся во времени, — это ток, остальное можно извлечь из производной по времени.{-5} \, V. \]
Значение
Когда ток включается в вертикальном соленоиде, как показано на рисунке \ (\ PageIndex {4} \), кольцо имеет наведенную ЭДС от изменяющегося магнитного потока соленоида, которая препятствует изменению. В результате кольцо взлетает вертикально в воздух.
Рисунок \ (\ PageIndex {4} \): прыгающее кольцо. Когда в вертикальном соленоиде включается ток, в металлическом кольце индуцируется ток. Поле рассеяния, создаваемое соленоидом, заставляет кольцо соскакивать с соленоида.Примечание
Демонстрация прыжкового кольца из Массачусетского технологического института.
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).



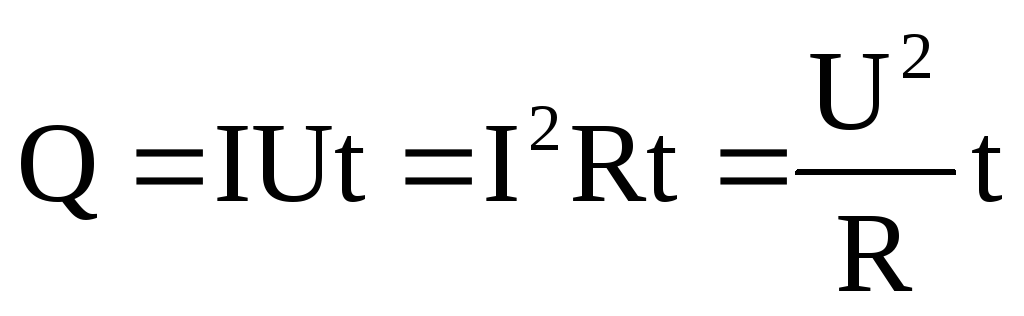 Можно использовать его, когда рассчитываются приборы нагревания. Нагревающий элемент – проводник с высоким сопротивлением, например нихром.
Можно использовать его, когда рассчитываются приборы нагревания. Нагревающий элемент – проводник с высоким сопротивлением, например нихром. После второго курса Дерптского университета отправился в 1823 году в трехлетнее кругосветное плавание. С помощью сконструированных им приборов (глубометра и батометра) занимался физическими исследованиями в водах Берингова пролива, Тихого и Индийского океанов, установил происхождение теплых и холодных морских течений, открыл закон океанических циркуляций. В 1829 г. принял участие в экспедиции на Кавказ, где проводил магнитные, термометрические и барометрические измерения в горных районах Кавказа и на побережье Каспийского моря. В 1830 году был назначен экстраординарным профессором и директором физического кабинета при Петербургской АН, в 1836 г. возглавил кафедру физики в Петербургском университете, а в 1863 г. стал ректором этого университета. Основные его работы посвящены электромагнетизму, вопросам теории и практического применения электричества, исследования в области которого Ленц начал в 1831 году в лаборатории первого русского электротехника – академика В.В. Петрова. Ленц стоял у истоков первой в России школы физиков-электротехников, последователями которой стали А.
После второго курса Дерптского университета отправился в 1823 году в трехлетнее кругосветное плавание. С помощью сконструированных им приборов (глубометра и батометра) занимался физическими исследованиями в водах Берингова пролива, Тихого и Индийского океанов, установил происхождение теплых и холодных морских течений, открыл закон океанических циркуляций. В 1829 г. принял участие в экспедиции на Кавказ, где проводил магнитные, термометрические и барометрические измерения в горных районах Кавказа и на побережье Каспийского моря. В 1830 году был назначен экстраординарным профессором и директором физического кабинета при Петербургской АН, в 1836 г. возглавил кафедру физики в Петербургском университете, а в 1863 г. стал ректором этого университета. Основные его работы посвящены электромагнетизму, вопросам теории и практического применения электричества, исследования в области которого Ленц начал в 1831 году в лаборатории первого русского электротехника – академика В.В. Петрова. Ленц стоял у истоков первой в России школы физиков-электротехников, последователями которой стали А. С. Попов, Ф.Ф. Петрушевский, В.Ф. Миткевич и др.
С. Попов, Ф.Ф. Петрушевский, В.Ф. Миткевич и др.

 Э, Кайдалов А.Б., Кожевников В.Б. / Под ред. Орлова В.А., Ройзена И.И. Физика 8. – М.: Мнемозина.
Э, Кайдалов А.Б., Кожевников В.Б. / Под ред. Орлова В.А., Ройзена И.И. Физика 8. – М.: Мнемозина.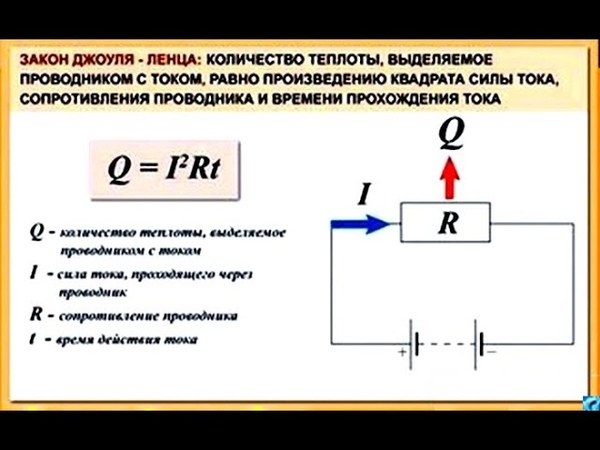 RusElectronic.com/zakon-dzhoulja-ljentsa/: использовано 5 блоков из 6, кол-во символов 6646 (32%)
RusElectronic.com/zakon-dzhoulja-ljentsa/: использовано 5 блоков из 6, кол-во символов 6646 (32%) Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС.
Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС.