Законы Кирхгофа — Технарь

Закон Ома устанавливает зависимость между силой тока, напряжением и сопротивлением для простейшей электрической цепи, представляющей собой один замкнутый контур. В практике встречаются более сложные (разветвленные) электрические цепи, в которых имеются несколько замкнутых контуров и несколько узлов, к которым сходятся токи, проходящие по отдельным ветвям. Значе­ния токов и напряжений для таких цепей можно находить при помощи законов Кирхгофа.

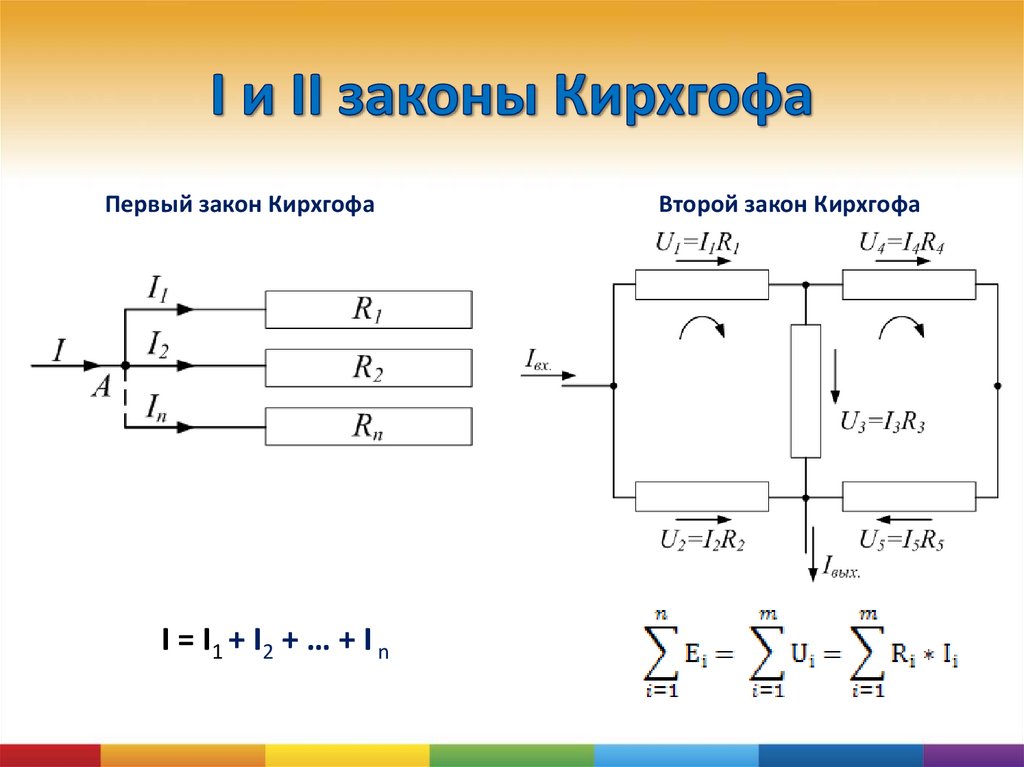
Первый закон Кирхгофа устанавливает зависимость между то­ками для узлов электрической цепи, к которым подходит несколько ветвей. Согласно этому закону алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю:

∑I = 0 (16)

При этом токи, направленные к узлу, берут с одним знаком (например, положительным), а токи, направленные от узла,— с противоположным знаком (отрицательным). Например, для узла А.

I1 + I2 + I3 – I4 – I5 = 0 (17)

Преобразуя это уравнение, получим, что сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от этого узла:

I1 + I2 + I3 = I4 + I5 (17′)

В данном случае имеет место полная аналогия с распределением потоков воды в соединенных друг с другом трубопроводах.

Второй закон Кирхгофа устанавливает зависимость между э. д. с. и напряжением в замкнутой электрической цепи. Согласно этому закону во всяком замкнутом контуре алгебраическая сумма э. д. с. равна алгебраической сумме падений напряжения на сопротивлениях, входящих в этот контур:

∑E = ∑IR (18)

При составлении формул, характеризующих второй закон Кирхгофа, значения э. д. с. E и падений напряжений IR считают положительными, если направления э. д. с. и токов на соответствующих участках контура совпадают с произвольно выбранным направлением обхода контура. Если же направления э. д. с. и токов на соответствующих участках контура противоположны выбранному направлению обхода, то такие э. д. с. и падения напряжения считают отрицательными.

Рассмотрим в качестве примера электрическую цепь, в которой имеются два источника с электродвижущими силами E1 и E2 (рис. 24, а), внутренними сопротивлениями Ro1, Ro2 и два приемника с сопротивлениями R1 и R2.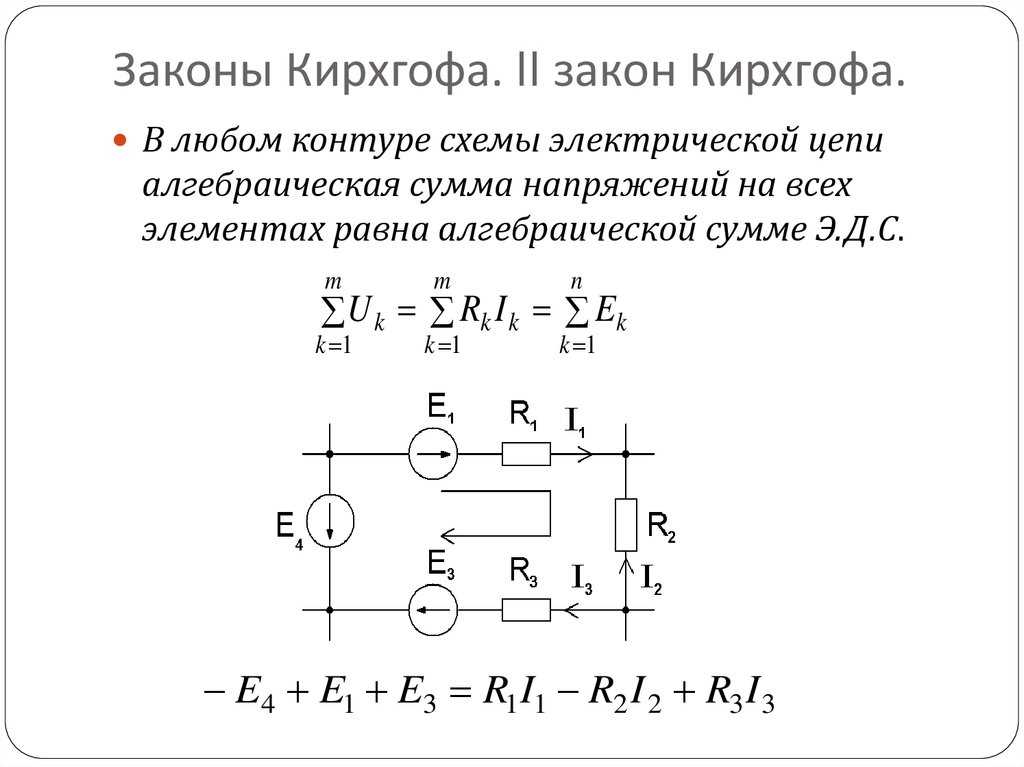 Применяя второй закон Кирхгофа для «этой цепи и выбирая направление ее обхода по часовой стрелке,
получим:

E₁ – E₂ = IR₀₁ + IR₀₂ + IR₁ + IR

При этом э. д. с. E1 и ток I совпадают с выбранным направлением обхода контура и считаются положительными, а э. д. с. Е2, противоположная этому направлению, считается отрицательной.

Если в электрической цепи э. д. с. источников электрической энергии при обходе соответствующего контура направлены навстречу друг другу (см. рис. 24, а), то такое включение называют встречным. В этом случае на основании второго закона Кирхгофа ток I = (E1-E2)/(R1+R2+R01+R02).Встречное направление э. д. с. имеет место, например, на э. п. с.при включении электродвигателей постоянного тока (их можно рассматривать как некоторые источники э. д. с.) в две параллельные группы, а также при параллельном включении аккумуляторов в батарее.

Рис 24. Схемы электрических цепей с несколькими источниками и приемниками электрической энергии: а и б — неразветвленных; в — разветвленной

Если же э. д. с. источников электрической энергии имеют по контуру одинаковое направление (рис. 24, б), то такое включение называют согласным и ток I = (E1-E2)/(R1+R2+R01+R02). В некоторых случаях такое включение недопустимо, так как ток в цепи резко возрастает.

Если в электрической цепи имеются ответвления (рис. 24, в), то по отдельным ее участкам проходят различные токи I1 и I2. Согласно второму закону Кирхгофа E1-E2=I1R01+I1R1-I2R2-I2R02-I2R3+I1R4

При составлении этого уравнения э. д. с. Е1 и ток I1 считаются положительными, так как совпадают с принятым направлением обхода контура, э. д. с. Е2 и ток I2 — отрицательными.

Метки: второй закон Кирхгофазакон ОмаЗаконы Кирхгофапервый закон Кирхгофатокэдсэлектрической цепи

ЗАКОНЫ Кирхгофа

Нажмите или коснитесь приведенных ниже примеров схем, чтобы вызвать TINACloud, и выберите интерактивный режим DC, чтобы проанализировать их в Интернете.
Получите недорогой доступ к TINACloud для редактирования примеров или создания собственных схем

ТЕОРЕМА СУПЕРПОЗИЦИИ

УЗЕЛ ПОТЕНЦИАЛЬНЫЙ МЕТОД

Многие схемы слишком сложны, чтобы их можно было решить, используя правила для последовательных или параллельных схем или методы преобразования в более простые схемы, описанные в предыдущих главах. Для этих схем нам нужны более общие методы решения. Наиболее общий метод дается законами Кирхгофа, которые позволяют вычислять все напряжения и токи цепей по решению системы линейных уравнений.

Есть два Законы Кирхгофа, закон напряжения И текущий закон. Эти два закона могут быть использованы для определения всех напряжений и токов в цепях.

Закон напряжения Кирхгофа (KVL) гласит, что алгебраическая сумма повышений напряжения и падений напряжения вокруг контура должна быть равна нулю.

Цикл в вышеприведенном определении означает замкнутый путь в цепи; то есть путь, который покидает узел в одном направлении и возвращается к тому же узлу из другого направления.

В наших примерах мы будем использовать направление по часовой стрелке для циклов; однако те же результаты будут получены при использовании направления против часовой стрелки.

Для применения KVL без ошибок, мы должны определить так называемое опорное направление. Опорное направление неизвестного напряжения от точки к + — знак предполагаемых напряжений. Представьте себе использование вольтметра. Вы положили бы положительный пробник вольтметра (обычно красный) на клемму + опоры компонента. Если реальное напряжение положительное, оно в том же направлении, что и мы, и наше решение, и вольтметр покажут положительное значение.

При выводе алгебраической суммы напряжений, мы должны присвоить знак плюс к тем напряжениям, где опорное направление совпадает с направлением петли, и отрицательными знаками в противоположном случае.

Другой способ сформулировать закон напряжения Кирхгофа состоит в том, что приложенное напряжение последовательной цепи равно сумме падений напряжения на последовательных элементах.

Следующий короткий пример показывает использование закона напряжения Кирхгофа.

Найти напряжение на резисторе R_2, учитывая, что напряжение источника, В_S = 100 В и это напряжение на резисторе R₁ это V₁ = 40 V.

Рисунок ниже может быть создан с помощью TINA Pro версии 6 и выше, в которой инструменты рисования доступны в редакторе схем.

Решение с использованием закона напряжения Кирхгофа: -V_S + V₁ + V₂ = 0 или V_S V =₁ + V₂

следовательно: V₂ V =_S — V₁ = 100-40 = 60V

Обратите внимание, что обычно мы не знаем напряжения резисторов (если мы не измеряем их), и нам нужно использовать оба закона Кирхгофа для решения.

Текущий закон Кирхгофа (KCL) гласит, что алгебраическая сумма всех токов, входящих и выходящих из любого узла в цепи, равна нулю.

Далее мы даем знак + токам, выходящим из узла, и знак — токам, входящим в узел.

Вот основной пример, демонстрирующий действующий закон Кирхгофа.

Найти тока я₂ если источник тока I_S = 12 A, и я₁ = 8 A.

Используя текущий закон Кирхгофа в обведенном узле: -I_S + Я₁ + Я₂ = 0, следовательно: I₂= Я_S — Я₁ = 12 — 8 = 4 A, как вы можете проверить с помощью TINA (следующий рисунок).

В следующем примере мы будем использовать как законы Кирхгофа, так и закон Ома, чтобы рассчитать ток и напряжение на резисторах.

На рисунке ниже вы заметите Напряжение Стрелка выше резисторы. Это новый компонент, доступный в Версия 6 TINA и работает как вольтметр. Если подключить его через компонент, стрелка определяет опорное направление (сравнить с вольтметром, представьте размещения красного щупа в хвосте стрелки, а черный зонд на конце). При запуске анализа постоянного тока фактическое напряжение на компоненте будет отображаться на стрелке.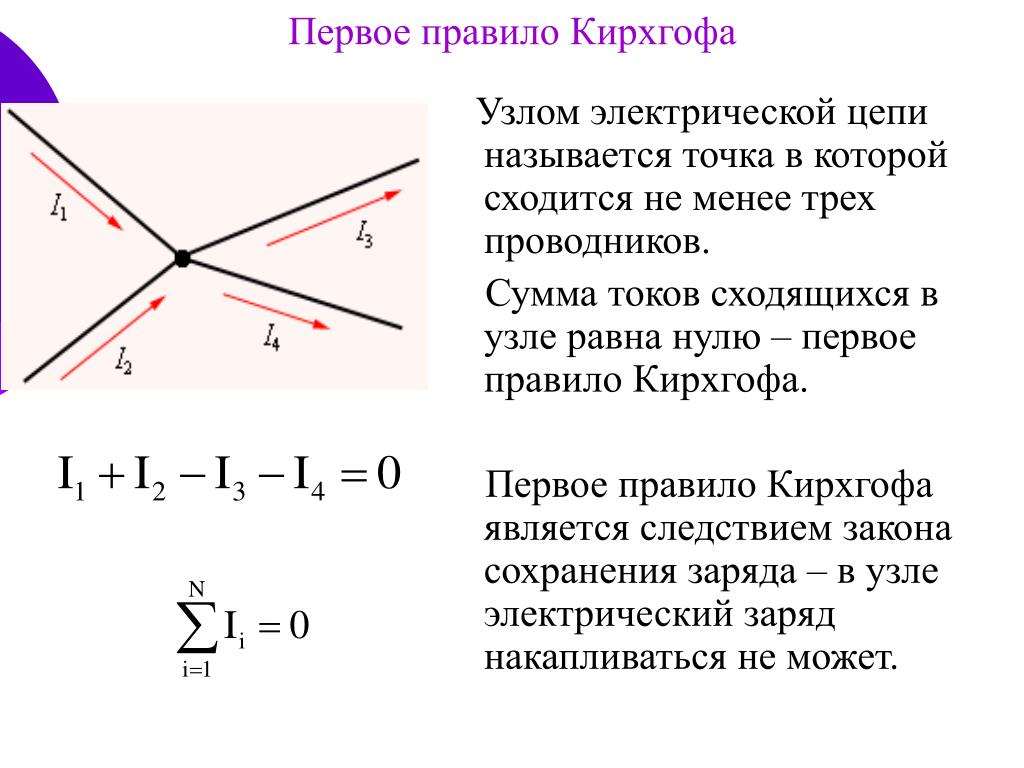

Чтобы начать использовать текущий закон Кирхгофа, мы видим, что токи через все компоненты одинаковы, поэтому давайте обозначим этот ток через I.

Согласно закону напряжения Кирхгофа: V_S V =₁+V₂+V₃

Теперь используя закон Ома: V_S= I * R₁+ I * R₂+ I * R₃

И отсюда ток цепи:

I = V_S /(Р₁+R₂+R₃) = 120 / (10 + 20 + 30) = 2 A

Наконец напряжения на резисторах:

V₁= I * R₁ = 2 * 10 = 20 V; V₂ = I * R₂ = 2 * 20 = 40 V; V₃ = I * R₃ = 2 * 30 = 60 V

Те же результаты можно увидеть на стрелках напряжения, просто запустив интерактивный анализ постоянного тока TINA.

В этой следующей, более сложной схеме мы также используем как законы Кирхгофа, так и закон Ома, но мы обнаруживаем, что мы наиболее решаем линейную систему уравнений.

Общее количество независимых применений законов Кирхгофа в цепи — это число ветвей цепи, а общее количество неизвестных (ток и напряжение каждой ветви) вдвое больше. Тем не менее, также используя закон Ома на каждом резисторе и Из простых уравнений, определяющих приложенные напряжения и токи, мы получаем систему уравнений, где число неизвестных совпадает с числом уравнений.

Найти токи ветвления I1, I2, I3 в схеме ниже.

Система уравнений выглядит следующим образом:

Узловое уравнение для обведенного узла:

– I₁ – I₂ — Я₃ = 0

или умножение на -1

I₁ + I₂ + Я₃ = 0

Уравнения цикла (с использованием направления по часовой стрелке) для цикла L1, содержащего V₁, R₁ и R₃

-V₁+I₁*R₁-I₃*R₃ = 0

и для цикла L2, содержащего V₂, R₂ и R₃

I₃*R₃ — Я₂*R₂ +V₂ = 0

Подставляя значения компонентов:

I₁+ Я₂+ Я₃ = 0 -8 + 40 * I₁ — 40 * I₃ = 0 40 * I₃ -20 * I₂ + 16 = 0

Экспресс я₁ используя узловое уравнение: I₁ = -Я₂ — Я₃

затем подставьте его во второе уравнение:

-V₁ — (Я₂ + Я₃)*Р₁ -Я₃*R₃ = 0 or –8- (я₂ + Я₃) * 40 — я₃* 40 = 0

Экспресс я₂ и подставим его в третье уравнение, из которого вы уже можете рассчитать I₃:

I₂ = — (V₁ + Я₃*(Р₁+R₃))/Р₁ or I₂ = — (8 + I₃* 80) / 40

I₃*R₃ + R₂* (V₁ + Я₃*(Р₁+R₃))/Р₁ +V₂ = 0 or I₃* 40 + 20 * (8 + I₃* 80) / 40 + 16 = 0

А также: I₃ = — (V₂ + V₁*R₂/R₁)/(Р₃+ (R₁+R₃)*Р₂/R₁) or I₃ = -(16+8*20/40)/(40 + 80*20/40)

Поэтому I₃ = — 0.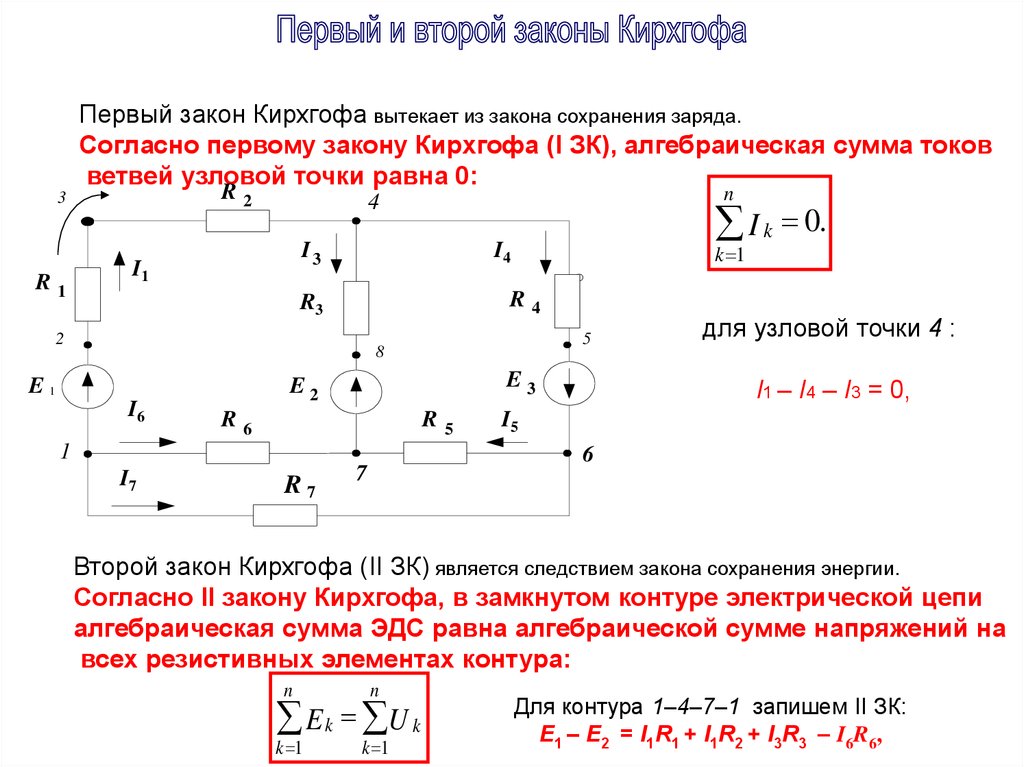 25 А; I₂ = — (8-0.25 * 80) / 40 = 0.3 A и I₁ = — (0.3-0.25) = — 0.05 А

Или: I₁ = -50 мА; I₂ = 300 мА; I₃ = -250 мА.

Теперь давайте решим те же уравнения с интерпретатором TINA:

Наконец, давайте проверим Результаты с использованием TINA:

Далее, давайте проанализируем следующую, еще более сложную схему и определим ее ответвления токами и напряжениями.

Обозначим неизвестные напряжения и токи, добавив стрелки напряжения и тока к компонентам, а также покажем петли (L1, L2, L3) и узлы (N1, N2), где мы будем использовать уравнения Кирхгофа.

Вот набор Уравнения Кирхгофа для петель (с использованием направления по часовой стрелке) и узлов.

-I_L + Я_R1 — Я_s = 0_{(для N1)}

— Я_R1 + Я_R2 + Я_s3 = 0 (для N2)

-V_s1 — V_R3 + V_Is + V_L = 0 (для L1)

-V_Is + V_s2 +V_R2 +V_R1 = 0 (для L2)

-V_R2 — V_s2 + V_s3 = 0 (для L3)

Применяя закон Ома:

V_L = Я_L*R_L

_{VR1 =IR1*R1}

V_R2 = Я_R2*R₂

V_R3 = — Я_L*R₃

Это 9 неизвестных и 9 уравнений. Самый простой способ решить эту проблему — использовать TINA.

переводчик. Однако, если мы вынуждены использовать ручные вычисления, отметим, что этот набор уравнений может быть легко сведен к системе из 5 неизвестных путем подстановки последних 4 уравнений в уравнения цикла L1, L2, L3. Кроме того, добавив уравнения (L1) и (L2), мы можем устранить V_Is , сводя задачу к системе уравнений 4 для неизвестных 4 (I_L, I_R1 I_R2, I_s3). Когда мы нашли эти токи, мы можем легко определить V_L, V_R1, V_R2, и V_R3 используя последние четыре уравнения (закон Ома).

Подставляя V_L ,V_R1,V_R2 ,V_R3 :

-I_L + Я_R1 — Я_s = 0_{(для N1)}

— Я_R1 + Я_R2 + Я_s3 = 0 (для N2)

-V_s1 + Я_L*R₃ + V_Is + Я_L*R_L = 0 (для L1)

-V_Is + V_s2 + Я_R2*R₂ + Я_R1*R₁ = 0 (для L2)

— Я_R2*R₂ — V_s2 + V_s3 = 0 (для L3)

Добавляя (L1) и (L2) мы получаем

-I_L + Я_R1 — Я_s = 0_{(для N1)}

— Я_R1 + Я_R2 + Я_s3 = 0 (для N2)

-V_s1 + Я_L*R₃ + Я_L*R_L + V_s2 + Я_R2*R₂ + Я_R1*R₁ = 0 (L1) + (L2)

— Я_R2*R₂ — V_s2 + V_s3 = 0 (для L3)

После подстановки значений компонентов решение этих уравнений приходит легко.

-I_L+I_R1 — 2 = 0 (для N1)

-I_R1 + Я_R2 + Я_S3 = 0 (для N2)

-120 — + Я_L* 90 + I_L* 20 + 60 + I_R2* 40 + I_R1* 30 = 0 (л₁) + (л₂)

-I_R2* 40 — 60 + 270 = 0 (для L₃)

от L₃ I_R2 = 210 / 40 = 5.25 A (I)

из N₂ I_S3 — Я_R1 = — 5.25 (II),

от L₁+L₂ 110 I_L + 30 I_R1 = -150 (III),

и для N₁ I_R1 — Я_L = 2 (IV)

Умножьте (IV) на –30 и добавьте к (III) 140 I_L = -210 следовательно I_L = — 1.5 А

Заменить я_L в (IV) I_R1 = 2 + (-1.5) = 0.5 A

и я_R1 в (II), I_S3 = -5.25 + I_R1 = -4,75 A

И напряжения: V_R1 = Я_R1*R₁ = 15 V; V_R2 = Я_R2*R₂ = 210 V;

V_R3 = — Я_L*R₃= 135 V; V_L = Я_L*R_L = — 30 В; V_Is V =_S1+V_R3-V_L = 285 V

{Решение исходных уравнений интерпретатором TINA} Sys IL,IR1,IR2,Is3,VIs,VL,VR1,VR3,VR2 -IL-Is + IR1 = 0 -IR1 + IR2 + Is3 = 0 -Vs1 + VR3 + Вис-VL = 0 -Vis + VR1 + VR2 + Vs2 = 0 -Vs3 + VR2 + Vs2 = 0 VR1 = IR1 * R1 VR2 = IR2 * R2 VR3 = -IL * R3 VL = IL * RL конец; IL = [- 1. 5] IR1 = [500m] IR2 = [5.25] Is3 = [- 4.75] = ВП [285] VL = [- 30] VR1 = [15] VR2 = [210] VR3 = [135]

Решение приведенной системы уравнений с использованием интерпретатора:

{Решение сокращенной системы уравнений интерпретатором TINA} Sys Il, Ir1, Ir2, Is3 -Il + Ir1-2 = 0 -Ir1 + Ir2 + Is3 = 0 -120+110*Il+60+40*Ir2+30*Ir1=0 -40 * Ir2 + 210 = 0 конец; Ил = [- 1.5] Ir1 = [500m] Ir2 = [5.25] Is3 = [- 4.75]

Мы также можем ввести выражения для напряжений и заставить интерпретатора TINA рассчитать их:

Il: = — 1.5; Ir1: = 0.5; Ir2: = 5.25; Is3: = — 4.75; Вл: = Il * RL; Vr1: = Ir1 * R1 Vr2: = Ir2 * R2; Vr3: = — Il * R3; ВП: = Vs1-Vl + Vr3; Vl = [- 30] Vr1 = [15] Vr2 = [210] Vr3 = [135] = ВП [285]

Мы можем проверить результат с TINA, просто включив интерактивный режим постоянного тока TINA или используя Анализ / Анализ постоянного тока / Узловое напряжение

---

ТЕОРЕМА СУПЕРПОЗИЦИИ

УЗЕЛ ПОТЕНЦИАЛЬНЫЙ МЕТОД

ЗАКОНЫ КИРХГОФА

/images/bkgleft.gif» valign=»top»>

Посылка Мы уже видели, что любая цепь, состоящая из комбинации резисторов, соединенных последовательно и/или параллельно, какой бы сложной она ни была, ее можно упростить до получения единого эквивалентного сопротивления. Сделано это, с помощью закона Ома можно рассчитать значение полного тока и тока для каждой ветви цепи. Это относится к цепям с одним источником энергии (ЭДС, ЭДС), но при наличии двух или больше источника электроэнергии, закона Ома уже недостаточно для расчета электрических параметров. Для таких цепей необходимо использовать законы или принципы Кирхгофа. Принципы Кирхгофа для электротехники. цепей, две: одна для узлов и одна для сеток. Узлы и сетки: Узел считается местом встречи трех или более ветвей цепи, в то время как сетка определяется как замкнутый контур, часть более сложного контура. Сложная схема имеет как минимум три сетки. Чтобы решить любую задачу с помощью принципов Кирхгофа, необходимо создать систему уравнений, состоящих из n-1 узлов и n-1 сетки. В схеме ниже то же самое состоит из двух узлов и трех сеток необходимо составить систему из трех уравнений (один узел и две сетки). и и 1   б  и 2 в R1    я   R3 ч д Е1 Р1  я   E2 г и 1   ф  и 2 и   С приведенными выше определениями в примере схемы слева: (объект последующего упражнения):   Узлы: шарнир б шарнир ф наоборот, узлы не являются соединениями d и h   Сетки являются цепями: а б е г б в д е е г Закон Кирхгофа №1: В узле сумма входящих токов равна сумме выходящих токов. Например, в математическом выражении для узла b вышеприведенной схемы:   I = i 1 + i 2 или также   я 1 + я 2 — я = 0 Закон Кирхгофа №2: В сетке сумма э.д.с. (алгебраический) равен сумме падающих напряжений. Referring to the mesh a b f g of the same circuit, in mathematical terms we have:   E 1 = R 1 * i 1 + R 2 * I or also   Р 1 * i 1 + Р 2 * I — E 1 = 0   УПРАЖНЕНИЕ   На следующем рисунке в интерактивном режиме предлагается схема, приведенная ранее в качестве примера. Введя в соответствующие поля значения: ЭДС в вольтах для генераторов постоянного тока E 1 и E 2 , электрическое сопротивление в омах для R 1 и R 2 , R 3 , и помня, что вы должны ввести (. ) для обозначения десятичной точки вместо запятой (, используемой в Европе). . При нажатии кнопки «Отправить» появится схема со значениями и направлением силы тока, которая будет течь. в различных ответвлениях (сопротивлением проводника пренебрегаем). Ваша задача, чтобы упражняться, состоит в том, чтобы вычислить значения и направление на силу тока по законам Кирхгофа, а затем сравнить их с теми, которые появляются в интерактивной схеме. Вы также можете увидеть, как меняются токи, изменив введенные параметры схемы. Номер цепи 1   Номер цепи 2     Контур номер 3

Законы Кирхгофа для электрических и магнитных цепей закон. Немецкий ученый Густав Кирхгоф имел достижения не только в физике, но и в химии, теоретической механике и термодинамике.

В электротехнике используется закономерность, которую он установил для электрической цепи, из двух соотношений. Законы Кирхгофа (также называемые правилами) описывают распределение токов в узлах и падения напряжения на элементах цепи. Далее мы попытаемся объяснить простыми словами, как применять соотношения Кирхгофа для решения задач.

• Первый закон Кирхгофа
• Второй закон Кирхгофа
• Методы расчета первого и второго законов Кирхгофа
• Законы Кирхгофа для магнитной цепи

Первый закон Кирхгофа

Определение первого закона: « «Алгебраическая сумма токов, протекающих через узел, равна нулю». Можно сказать немного в другой форме: « Сколько токов втекало в узел, столько же и вытекало, что говорит о постоянстве тока» .

Узел цепи – это точка соединения трех и более ветвей. Токи в этом случае распределяются пропорционально сопротивлению каждой ветви.

I ₁ = I ₂ + I ₃

Эта форма записи действительна для цепей постоянного тока.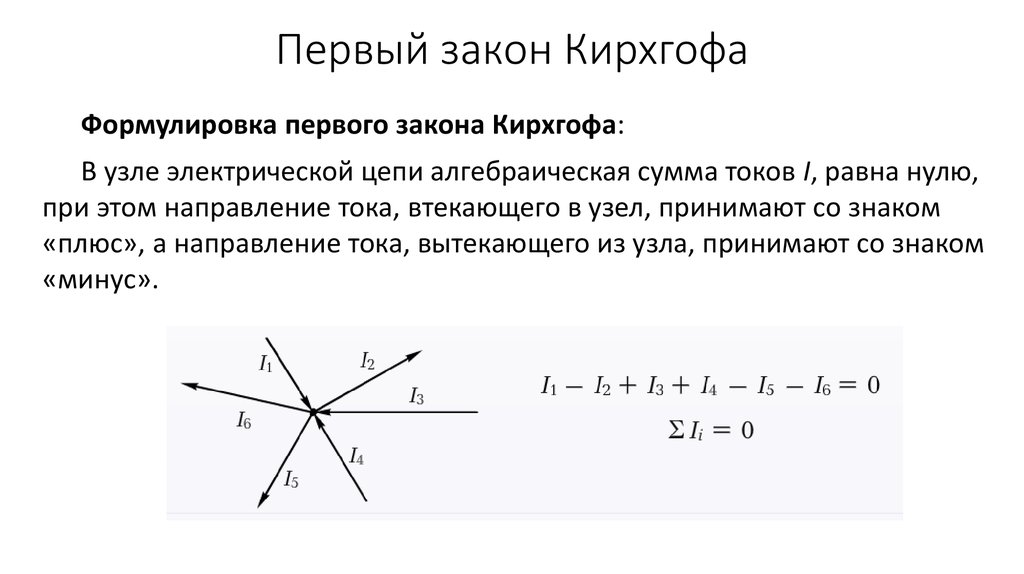 Если использовать первый закон Кирхгофа для цепи переменного тока, то используются мгновенные значения напряжения, обозначаются буквой İ и записываются в комплексной форме, а метод расчета остается прежним:

Комплексная форма учитывает как активные, так и реактивные компоненты.

Второй закон Кирхгофа

Если первый описывает распределение токов в ветвях, то второй закон Кирхгофа таков: « Сумма падений напряжения в цепи равна сумме всех ЭДС. Простыми словами формулировка звучит так: «ЭДС, приложенная к участку цепи, будет распределяться между элементами этой цепи пропорционально сопротивлениям, т.е. по закону Ома.

Тогда как для переменного тока это звучит так: « Сумма амплитуд комплексной ЭДС равна сумме комплексных падений напряжения на элементах» .

Z — полное сопротивление или комплексное сопротивление, оно включает в себя как активную часть, так и реактивную (индуктивность и емкость), которая зависит от частоты переменного тока (в постоянном токе есть только активное сопротивление). Ниже приведены формулы комплексного сопротивления конденсатора и индуктивности:

Вот картинка, иллюстрирующая вышесказанное:

Тогда:

Методы расчета первого и второго законов Кирхгофа

Приступим к практическому применению теоретического материала. Чтобы правильно расставить знаки в уравнениях, нужно выбрать направление цепи. Взгляните на схему:

Мы предлагаем выбрать направление по часовой стрелке и отметить его на рисунке:

Штрихпунктирная линия показывает, как следовать пути при составлении уравнений.

Следующим шагом будет составление уравнений по законам Кирхгофа. Сначала используем второй. Знаки ставим так: перед ЭДС ставится знак минус, если она направлена ​​против часовой стрелки (направление, которое мы выбрали на предыдущем шаге), то для ЭДС по часовой стрелке ставим знак минус . Составляем для каждой схемы с учетом знаков.

Для первого смотрим на направление ЭДС, оно совпадает со штрихпунктирной линией, ставим Е1 плюс Е2:

Для второго:

Для третьего:

Знаки для IR (напряжение) зависят от направления контурных токов.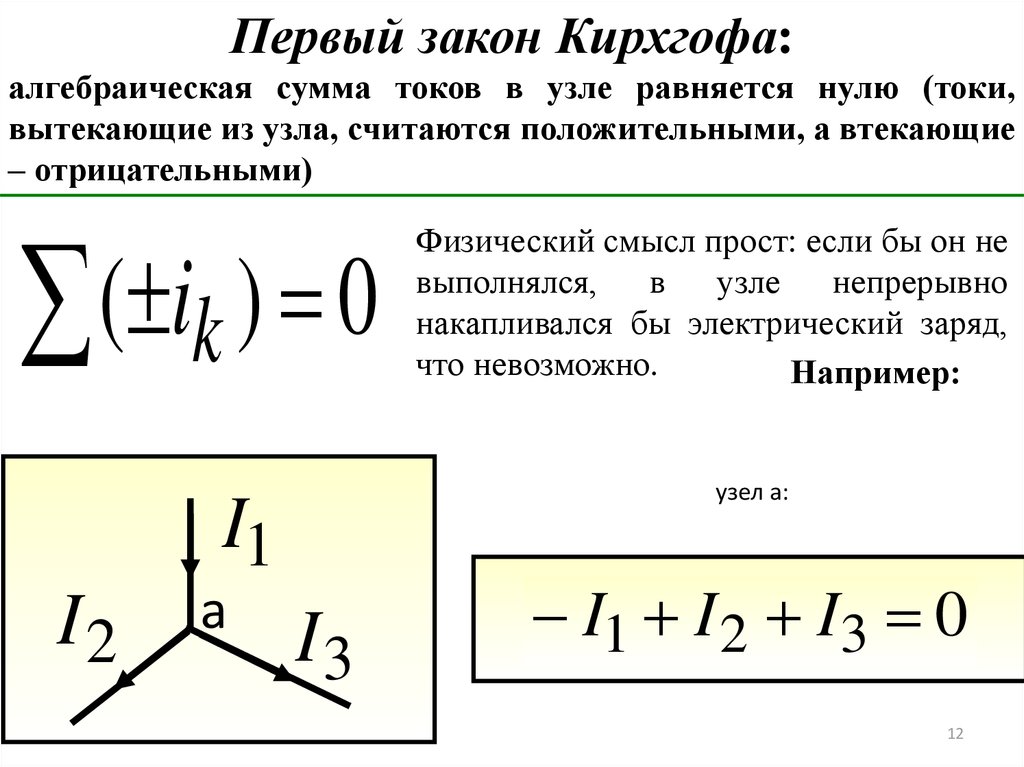 Здесь правило знаков такое же, как и в предыдущем случае.

IR записывается с положительным знаком, если ток течет в направлении обхода цепи. И со знаком «-», если ток течет против направления цепи.

Направление обхода цепи – величина условная. Он нужен только для расстановки знаков в уравнениях, выбирается произвольно и на правильность расчетов не влияет. В некоторых случаях неудачно выбранное направление обхода может усложнить расчет, но это не критично.

Рассмотрим другую схему:

Источников ЭДС целых четыре, но порядок расчета тот же, сначала выбираем направление составления уравнений.

Теперь нужно составить уравнения по первому закону Кирхгофа. Для первого узла (цифра 1 слева на схеме):

I ₃ втекает, а I ₁ , I ₄ следует, отсюда и знаки. Для второго:

Для третьего:

Вопрос: « Узлов четыре, а уравнений всего три, почему?» Дело в том, что количество уравнений первого правила Кирхгофа равно:

N _{уравнений} = n _узлов -1

Т. е., уравнений всего на 1 меньше, чем узлов, ибо этого достаточно для описания токов во всех ветвях, советую еще раз подойти к схеме и проверить все токи записаны в уравнениях

Теперь приступим к построению уравнений по второму правилу. Для первичной цепи:

Для второй цепи:

Для третьей цепи:

Если подставить значения реальных напряжений и сопротивлений, то окажется, что первый и второй законы справедливы и выполняются. Это простые примеры; на практике приходится решать гораздо более объемные задачи.

Заключение . Главное при расчете с помощью первого и второго законов Кирхгофа — соблюдение правила составления уравнений, т.е. учитывать направление протекания тока и обход цепи для правильного расположения знаков каждого элемента цепи .

Законы Кирхгофа для магнитной цепи

Расчеты магнитных цепей также важны в электротехнике, оба закона нашли здесь свое применение. Суть остается той же, но меняется тип и размер, давайте рассмотрим этот вопрос подробнее. Сначала нужно разобраться с понятиями.

Магнитодвижущая сила (МДС) определяется произведением числа витков катушки, на ток через нее:

F = w * i

Магнитное напряжение есть произведение напряженности магнитного поля и тока через нее a section, measured in Amperes:

U _m = H * I

Or magnetic flux through magnetic resistance:

U _m = F * R _m

L is the средняя длина участка, мк _r и μ ₀ — относительная и абсолютная магнитная проницаемость.

Проводя аналогию, запишем первый закон Кирхгофа для магнитной цепи:

То есть сумма всех магнитных потоков через узел равна нулю. Вы заметили, что это звучит почти так же, как для электрической цепи?

Тогда второй закон Кирхгофа звучит как «Сумма МДС в магнитопроводе равна сумме U _M (магнитное напряжение).

Магнитный поток равен:

Для переменного магнитного поля:

Зависит только от напряжения на обмотке, а не от параметров магнитопровода.

В качестве примера рассмотрим такой контур:

Тогда для ABCD получим следующую формулу:

Для цепей с воздушным зазором справедливы следующие соотношения:

Магнитное сопротивление:

А сопротивление воздушного зазора (справа на сердечнике):

Где S — площадь сердечника.

Для полного понимания материала и наглядного ознакомления с некоторыми нюансами использования правил рекомендуем ознакомиться с лекциями, которые представлены на видео:

Существенный вклад внесли открытия Густава Кирхгофа к развитию науки, особенно электротехники.