2.2 Законы Кирхгофа
Законы Кирхгофа лежат в основе анализа электрических цепей.
2.2.1 Первый закон Кирхгофа.
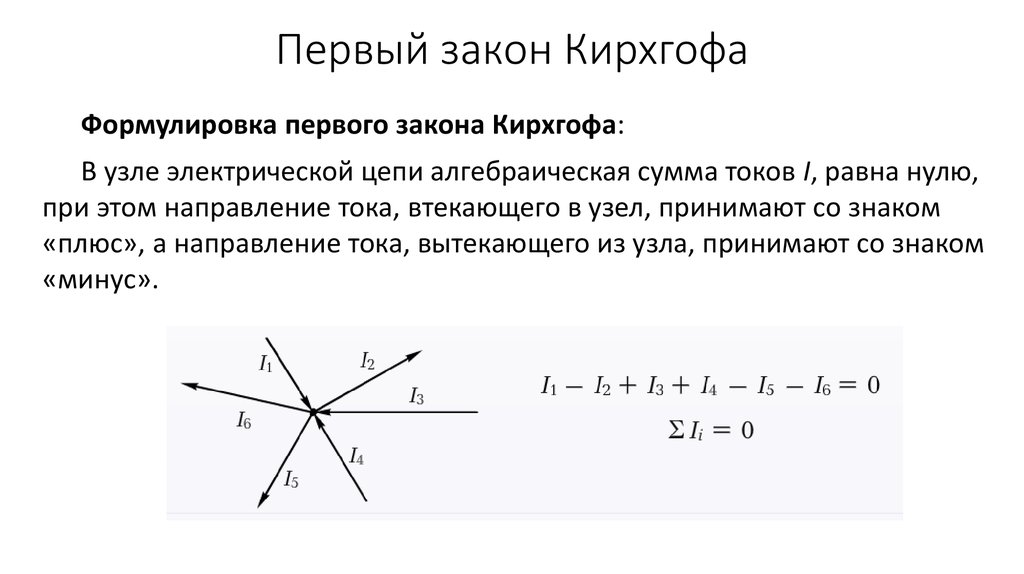
Алгебраическая сумма токов в узле электрической цепи равна нулю.
Математически это записывается так: |
|
∑I = 0 . | (2.1) |
Всем токам, направленным от узла, в уравнении (2.1) приписывается одинаковый знак, например, положительный, тогда все токи, направленные к узлу, войдут в уравнение с отрицательным знаком.
Рисунок 2.1 – Иллюстрация к первому закону Кирхгофа
На рисунке 2.1 показан узел, в котором сходятся четыре ветви. Уравнение (2.1) в этом случае принимает вид:
− I1 − I2 + I3 + I4 = 0 ,
Первый закон Кирхгофа отражает тот факт, что в узле электрический заряд не накапливается и не расходуется. Сумма электрических зарядов, приходящих к узлу, равна сумме зарядов, уходящих от узла за один и тот же промежуток времени.
2.2.2 Второй закон Кирхгофа.
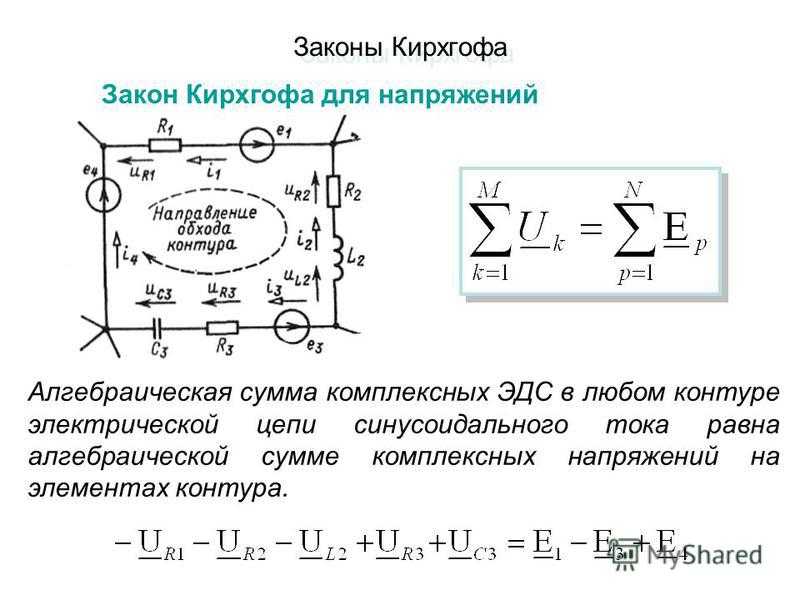
Алгебраическая сумма ЭДС в любом контуре цепи равна алгебраи-
ческой сумме напряжений на элементах этого контура: |
|
∑E = ∑U . | (2.2) |
Если в рассматриваемом контуре отсутствуют ЭДС, то уравнение | |
(2.2) принимает вид: |
|
∑U = 0 . | (2.3) |
92
Обход контура совершается в произвольно выбранном направлении. При этом ЭДС и напряжения, совпадающие с направлением обхода, берутся с одинаковыми знаками, например, со знаками «+».
Например, для схемы (рисунок 2.2) имеем:
E1 − E2 =U1 +U 2 +U3 −U 4
Второй закон Кирхгофа можно применять и для контуров, которые состоят не только из участков схемы, но и из напряжений между какимилибо точками схемы.
Так для контура 4-5-3-6-4, состоящего из участка цепи 4-5-3 и напряжения 4-6-3, можно составить уравнение:
E2 = −I3 R3 −U 43
где U 43 – напряжение между точками 4 и 3 схемы, В.
U1
Е1 | I1 |
| R1 2 |
|
1 |
|
|
| I2 |
R4 |
|
|
| |
направление |
| U2 | ||
U4 |
| |||
обхода |
|
| R2 | |
I4 | 5 |
|
| |
|
| 3 | ||
4 I3 | Е2 |
| R3 | |
| 6 | U3 |
| |
|
| U43 |
| |
|
|
|
| |
Рисунок 2. 2 – Иллюстрация ко второму закону Кирхгофа
2 – Иллюстрация ко второму закону Кирхгофа
2.3 Распределение потенциала вдоль электрической цепи
Рассмотрим неразветвленную электрическую цепь постоянного тока (ЭЦПТ), содержащую резисторы с сопротивлениями R и источниками ЭДС E (рисунок 2.3).
Примем потенциал одной из точек ЭЦПТ равным нулю ϕ0 = 0. Тогда
можем найти потенциалы остальных точек схемы при известных значениях силы тока I , ЭДС E1, E2 , E3 и сопротивлений R1, R2 , R3 :
93
ϕ1 =ϕ0 + E1 |
|
| ||||
ϕ | 2 | =ϕ | 1 | − IR |
|
|
|
| 1 |
|
| ||
ϕ3 | =ϕ2 | − E2 |
| (2. | ||
ϕ4 | =ϕ3 |
|
| |||
− IR2 |
| |||||
ϕ5 | =ϕ4 + E3 |
|
| |||
|
|
|
|
|
|
|
ϕ0 =ϕ5 |
|
|
| |||
− IR3 |
| |||||
График изменения потенциала в соответствии с формулами (2.4) представлен на рисунке 2.3, б.
Этот график служит графической иллюстрацией второго закона Кирхгофа.
Е1 | 1 R1 | 2 Е2 | 3 R2 | 4 Е3 | 5 | R 3 |
| ϕ1 UR1 | ϕ2 | ϕ3 UR2 | ϕ4 | ϕ5 UR3 | |
0 |
|
| I |
|
|
|
|
|
|
|
|
| |
ϕ |
|
| а) |
|
|
|
|
| ϕ5 |
|
|
| |
| ϕ1 | ϕ2 |
|
|
| |
|
|
|
|
| ||
|
|
|
|
|
| |
Е1 | Е |
| Е |
|
|
|
| 2 |
| 3 |
|
|
|
0 |
|
|
|
|
| 0 |
ϕ3 |
|
|
|
| R | |
|
| ϕ |
| R3 | ||
| R1 | R2 |
|
| ||
| 4 |
|
| |||
б)
Рисунок 2.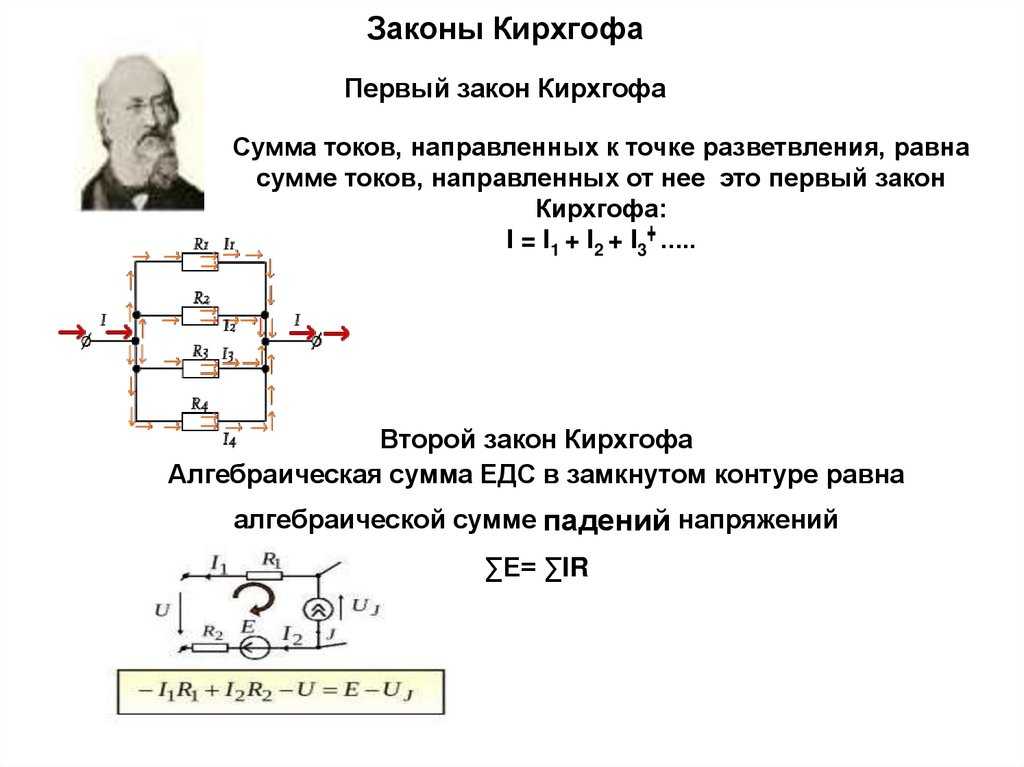 3 – Схема ЭЦПТ (а) и график изменения потенциала (б) вдоль этой цепи
3 – Схема ЭЦПТ (а) и график изменения потенциала (б) вдоль этой цепи
2.4 Последовательное и параллельное соединения резистивных элементов
2.4.1 Последовательное соединение.
Рассмотрим цепь с последовательным соединением резисторов с соответствующими сопротивлениями R1, R2 (рисунок 2.4)
94
Ток I , протекающий по этим резисторам один и тот же. Напряжения U1 и U 2 на каждом из резисторов различны.
На основании второго закона Кирхгофа можно записать:
U =U1 +U2 , | (2.5) |
где U – напряжение источника ЭДС, приложенное к обоим резисторам, В. Применяя закон Ома, перепишем уравнение (2.5)
U = IR1 | + IR2 | ; | (2.6) | |
U = I (R1 + R2 ) = IR12 , | ||||
| ||||
где R12 – общее (эквивалентное) сопротивление всей цепи относительно зажимов 1 и 2, Ом.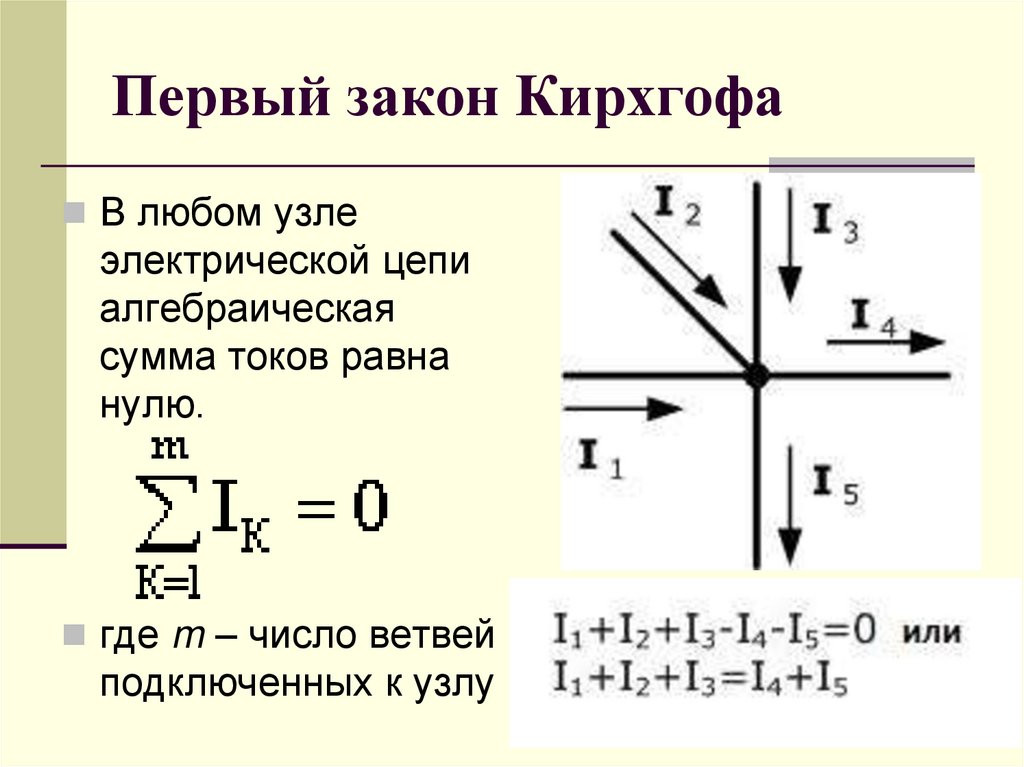
R1 | R2 | I |
| R12 | I |
U 1 | U2 |
|
|
|
|
1 | U | 2 | 1 | U | 2 |
Е |
|
|
| Е |
|
| а) |
|
|
|
Рисунок 2.4 – Схема ЭЦ с последовательным соединением резисторов (а) и упрощенная схема этой цепи с эквивалентным сопротивлением (б)
Полученные результаты можно распространить на n последовательно соединенных резисторов:
R1,2,…,n = R1 + R2 + … + Rn , | (2. |
Сопротивление цепи, состоящей из нескольких последовательно соединенных резистивных элементов, равно сумме их сопротивлений.
2.4.2 Параллельное соединение
При параллельном соединении элементов (рисунок 2.5,а) к ним приложено одно и то же напряжение.
На основании первого закона Кирхгофа можно записать
I = I1 + I 2
95
| U |
| U |
| U |
| 1 |
| 1 |
|
|
| ||
|
|
|
|
|
|
|
| |||||||
или |
| = |
| + |
|
| =U |
| + |
|
|
| , | (2. |
R | R | R | 2 | R | R | 2 | ||||||||
| 12 |
| 1 |
|
|
| 1 |
|
|
|
|
| ||
откуда
1 = 1 + 1 .
R12 R1 R2
где R12 – общее эквивалентное сопротивление цепи, Ом.
I1 | R1 |
| R |
|
|
I 1 | 2 | 1 | 2 | I | |
12 |
| ||||
| R2 |
|
|
| |
|
|
|
|
| |
I2 | U |
| U |
|
|
|
|
|
|
| |
Е |
|
| Е |
|
|
| а) |
| б) |
|
|
Рисунок 2. 5 – Схема ЭЦ с параллельным соединением резисторов (а) и упрощенная схема этой цепи с эквивалентным сопротивлением (б)
5 – Схема ЭЦ с параллельным соединением резисторов (а) и упрощенная схема этой цепи с эквивалентным сопротивлением (б)
Выражение (2.8) можно распространить на случай n параллельно соединенных резистивных элементов. Тогда
1 | = | 1 | + | 1 |
| + … + |
| 1 | , | (2.9) | |||
| R1,2…,n |
|
|
| Rn | ||||||||
|
| R1 | R2 |
|
|
| |||||||
Если вместо сопротивлений резисторов ввести понятие электриче- | |||||||||||||
ской проводимости, равной G = | 1 | , G | 2 | = | 1 | и т. | |||||||
|
|
| |||||||||||
|
| 1 |
| R1 |
|
| R2 |
| |||||
|
|
|
|
|
|
|
|
|
| ||||
| G1,2,…,n =G1 + G2 + … + Gn , | (2.10) | |||||||||||
Общая эквивалентная проводимость G1,2,…n электрической цепи, со-
стоящей из n параллельно соединенных резистивных элементов, равна сумме их проводимостей G1 +G2 +…+Gn
Параллельное включение – основой способ включения в ЭЦ различных приемников (потребителей) электрической энергии.
Цепь, питающая током какой-нибудь населенный пункт, представляет собой систему параллельно соединенных приемников электрической энергии. Основная линия распадается на параллельные линии, идущие к
Основная линия распадается на параллельные линии, идущие к
96
5. Первый закон Кирхгофа
В любом узле электрической цепи алгебраическая сумма токов равна нулю =0 , гдеm – число подключенных к узлу ветвей.
При записи уравнений по первому закону Кирхгофа токи, направленные к узлу, берут со знаком «плюс», а токи, направленные от узла – со знаком «минус». Например, для узла а (см. рис. 1.3) I — I1— I2= 0. Рис. 1.3
6. Второй закон Кирхгофа
В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках:
== ,где n – число источников ЭДС в контуре; m – число элементов с сопротивлением Rк в контуре;
Uк = RкIк – напряжение или падение напряжения
на к-м элементе контура.
Для схемы (рис. 1.3) запишем уравнение по второму закону Кирхгофа: E = UR + U1.
Если в электрической цепи включены источники напряжений, то второй закон Кирхгофа формулируется в следующем виде: алгебраическая сумма напряжений на всех элементах контру, включая источники ЭДС, равна нулю.
При записи уравнений по второму закону Кирхгофа необходимо:
1) задать условные положительные направления ЭДС, токов и напряжений;
2) выбрать направление обхода контура, для которого записывается уравнение;
3) записать уравнение, пользуясь одной из формулировок второго закона Кирхгофа, причем слагаемые, входящие в уравнение, берут со знаком «плюс», если их условные положительные направления совпадают с обходом контура, и со знаком «минус», если они противоположны.
Запишем уравнения
по II закону Кирхгофа для контуров
электрической схемы (рис. 1.3):
1.3):
контур I: E = RI + R1I1 + r0I,
контур II: R1I1 + R2I2 = 0,
контур III: E = RI + R2I2 + r0I.
7. Уравнение баланса мощностей
В действующей цепи электрическая энергия источника питания преобразуется в другие виды энергии. На участке цепи с сопротивлением R в течение времени t при токе I расходуется электрическая энергия W = I2Rt.
Скорость преобразования электрической энергии в другие виды представляет электрическую мощность
.
Из закона сохранения энергии следует, что мощность источников питания в любой момент времени равна сумме мощностей, расходуемой на всех участках цепи:
Это соотношение
называют уравнением
баланса мощностей. При составлении уравнения баланса
мощностей следует учесть, что если
действительные направления ЭДС и тока
источника совпадают, то источник ЭДС
работает в
режиме источника питания, и произведение EI подставляют в это уравнение знаком
плюс. Если не совпадают, то источник
ЭДС работает в режиме потребителя
электрической энергии, и произведение E I подставляют
в это уравнение знаком минус. Для цепи,
показанной на рис. 4 уравнение баланса
мощностей запишется в виде: EI
= I2(r0 + R) + I12R1 + I22R2.
При составлении уравнения баланса
мощностей следует учесть, что если
действительные направления ЭДС и тока
источника совпадают, то источник ЭДС
работает в
режиме источника питания, и произведение EI подставляют в это уравнение знаком
плюс. Если не совпадают, то источник
ЭДС работает в режиме потребителя
электрической энергии, и произведение E I подставляют
в это уравнение знаком минус. Для цепи,
показанной на рис. 4 уравнение баланса
мощностей запишется в виде: EI
= I2(r0 + R) + I12R1 + I22R2.
Кроме основных
единиц измерения при расчете электрических
цепей используют дольные и кратные
единицы измерения: 1 миллиампер (1мA =
10–3 А), 1 килоампер (1кA = 1000А), 1 милливольт
(1мВ = 10–3 В), 1 киловольт (1кВ = 1000В), 1 килоом (1кОм
= 1000 Ом), 1 мегаом (1МОм = 1000м), 1
киловатт (1кВт = 1000Вт), 1 киловатт-час
(1кВт-час = 1000 ватт-час).
21.3: Правила Кирхгофа — Физика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2690
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Анализировать сложную схему, используя правила Кирхгофа, используя соглашения для определения правильных знаков различных термов.
Многие сложные цепи, такие как показанная на рисунке \(\PageIndex{1}\), не могут быть проанализированы с помощью последовательно-параллельных методов, разработанных в разделе Резисторы в последовательном и параллельном соединении и Электродвижущая сила: напряжение на клеммах. Однако есть два правила анализа цепей, которые можно использовать для анализа любой схемы, простой или сложной. Эти правила являются частными случаями законов сохранения заряда и сохранения энергии. Эти правила известны как правила Кирхгофа в честь их изобретателя Густава Кирхгофа (1824–1887).
Однако есть два правила анализа цепей, которые можно использовать для анализа любой схемы, простой или сложной. Эти правила являются частными случаями законов сохранения заряда и сохранения энергии. Эти правила известны как правила Кирхгофа в честь их изобретателя Густава Кирхгофа (1824–1887).
Определение: Правила Кирхгофа
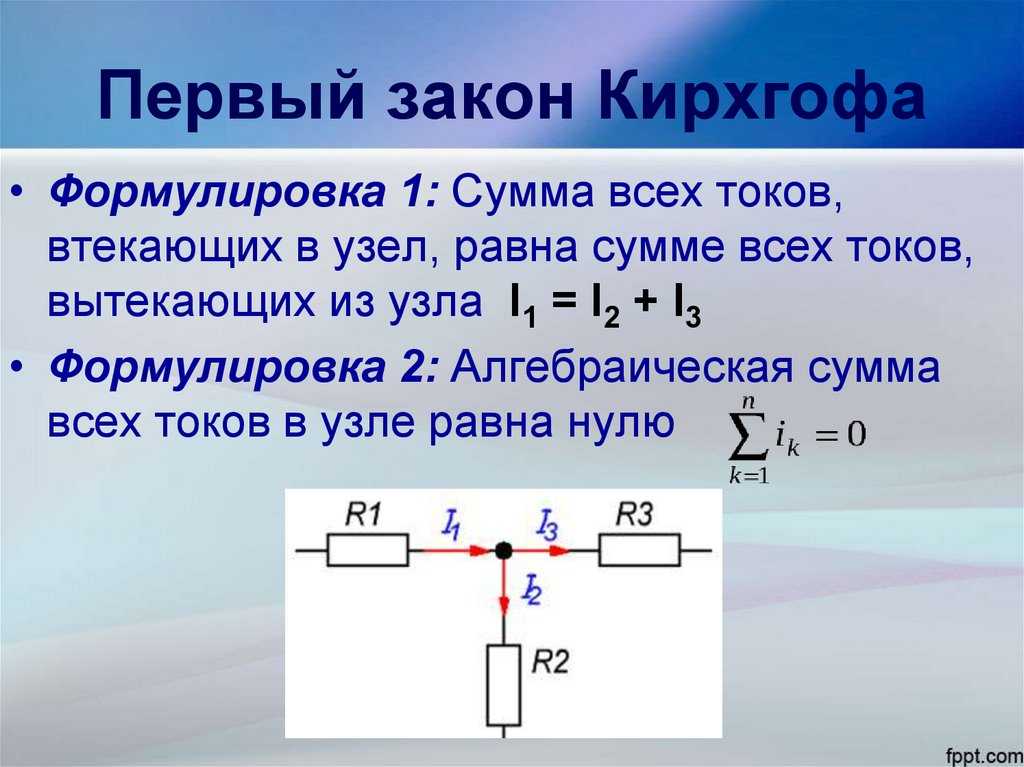
- Первое правило Кирхгофа — правило соединения: Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения. перекресток.
- Второе правило Кирхгофа — правило петли: Алгебраическая сумма изменений потенциала вокруг любого замкнутого контура (петли) должна быть равна нулю.
Теперь будут даны объяснения двух правил, за которыми следуют советы по решению проблем для применения правил Кирхгофа и рабочий пример, который их использует.
Первое правило Кирхгофа (правило соединения)
Первое правило Кирхгофа (правило соединения) является применением закона сохранения заряда к соединению; это показано на рисунке \(\PageIndex{2}\). Ток — это поток заряда, а заряд сохраняется; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу. Первое правило Кирхгофа требует, чтобы \(I_1 = I_2 + I_3\) (рис. \(\PageIndex{2}\)). Подобные уравнения могут и будут использоваться для анализа схем и решения схемных задач.
Рисунок \(\PageIndex{2}\): Правило соединения. На диаграмме показан пример первого правила Кирхгофа, в котором сумма токов, поступающих в соединение, равна сумме токов, выходящих из соединения. В этом случае ток, входящий в переход, разделяется и выходит в виде двух токов, так что \(I_1 = I_2 + I_3\). Здесь \(I_1\) должно быть 11 А, так как \(I_2\) равно 7 А, а \(I_3\) равно 4А.Второе правило Кирхгофа (правило цикла)
Второе правило Кирхгофа (правило цикла) является приложением закона сохранения энергии. Правило петли сформулировано в терминах потенциала, а не потенциальной энергии, но они связаны, поскольку \(PE_{elec} = qV\). Напомним, что ЭДС — это разность потенциалов источника при отсутствии тока. В замкнутом контуре любая энергия, поставляемая ЭДС, должна быть переведена в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в контур или из него. На рисунке \(\PageIndex{3}\) показаны изменения потенциала в простой последовательной цепи.
Правило петли сформулировано в терминах потенциала, а не потенциальной энергии, но они связаны, поскольку \(PE_{elec} = qV\). Напомним, что ЭДС — это разность потенциалов источника при отсутствии тока. В замкнутом контуре любая энергия, поставляемая ЭДС, должна быть переведена в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в контур или из него. На рисунке \(\PageIndex{3}\) показаны изменения потенциала в простой последовательной цепи.
Второе правило Кирхгофа требует \(ЭДС — Ir — IR_1 — IR_2 = 0\). В перестановке это \(ЭДС = Ir + IR_1 + IR_2\), что означает, что ЭДС равна сумме падений \(IR\) (напряжения) в контуре.
Рисунок \(\PageIndex{3}\): Правило цикла. Пример второго правила Кирхгофа, согласно которому сумма изменений потенциала вокруг замкнутого контура должна быть равна нулю. (a) На этой стандартной схеме простой последовательной цепи ЭДС подает напряжение 18 В, которое сводится к нулю сопротивлениями, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки, для всего 18 В.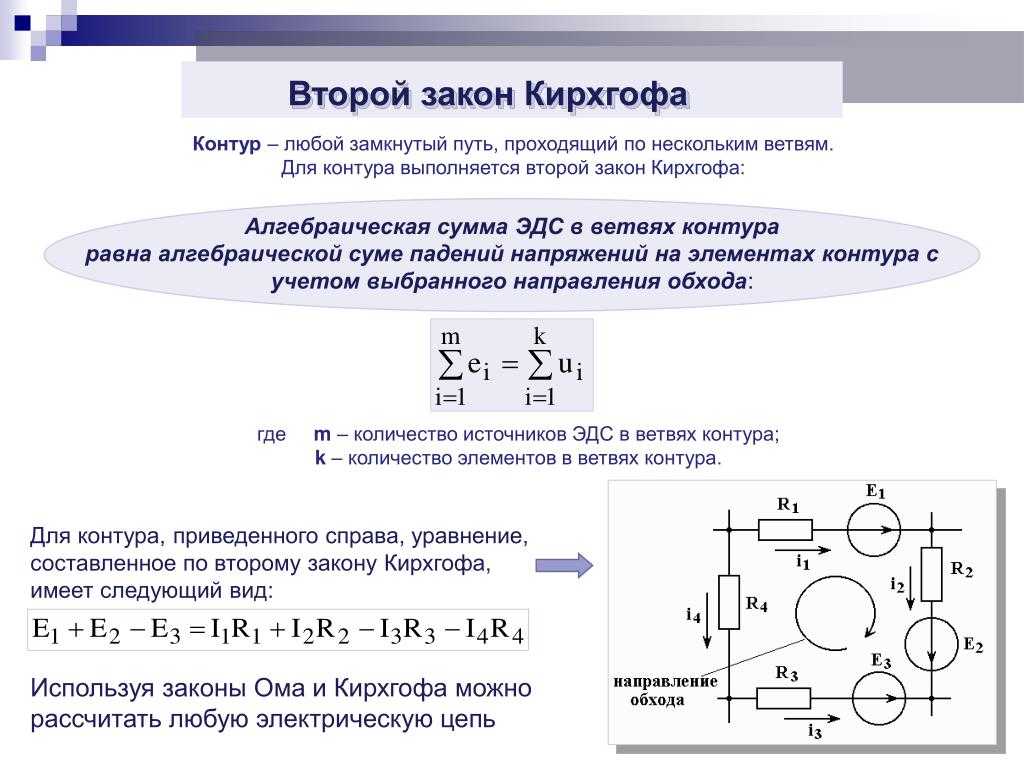 (b) Этот вид в перспективе представляет потенциал как что-то вроде американских горок, где потенциал повышается за счет ЭДС и снижается за счет сопротивления. (Обратите внимание, что буква E означает ЭДС.)
(b) Этот вид в перспективе представляет потенциал как что-то вроде американских горок, где потенциал повышается за счет ЭДС и снижается за счет сопротивления. (Обратите внимание, что буква E означает ЭДС.)Применение правил Кирхгофа
Применяя правила Кирхгофа, мы получаем уравнения, позволяющие находить неизвестные в цепях. Неизвестными могут быть токи, ЭДС или сопротивления. Каждый раз, когда применяется правило, создается уравнение. Если независимых уравнений столько же, сколько неизвестных, то задача решаема. При применении правил Кирхгофа вы должны принять два решения. Эти решения определяют знаки различных величин в уравнениях, которые вы получаете, применяя правила.
- Применяя первое правило Кирхгофа, правило соединения, вы должны обозначить ток в каждой ветви и решить, в каком направлении он течет. Например, на рисунке, рисунке и рисунке токи помечены \(I_1, \, I_2, \, I_3\) и \(I\), а стрелки указывают их направления. Здесь нет никакого риска, потому что, если вы выберете неправильное направление, ток будет правильной величины, но отрицательным.

- Применяя второе правило Кирхгофа, правило петли, вы должны определить замкнутую петлю и решить, в каком направлении ее обойти, по часовой или против часовой стрелки. Например, на рисунке петля была пройдена в том же направлении, что и ток (по часовой стрелке). Опять же, нет никакого риска; Обход цепи в противоположном направлении меняет знак каждого члена в уравнении, что похоже на умножение обеих частей уравнения на -1.
Рисунок \(\PageIndex{4}\) и следующие пункты помогут правильно расставить знаки плюс или минус при применении правила цикла. Обратите внимание, что резисторы и ЭДС пересекаются при переходе от a к b. Во многих схемах будет необходимо построить более одного контура. При обходе каждого цикла необходимо соблюдать последовательность знака изменения потенциала (пример \(\PageIndex{1}\)).
Рисунок \(\PageIndex{4}\): Каждый из этих резисторов и источников напряжения проходит от a до b. Возможные изменения показаны под каждым элементом и пояснены в тексте. (Обратите внимание, что буква E означает ЭДС.)
(Обратите внимание, что буква E означает ЭДС.)- Когда резистор перемещается в том же направлении, что и ток, изменение потенциала равно \(-IR\). (См. рисунок.)
- Когда резистор перемещается в направлении, противоположном току, изменение потенциала равно \(+IR\). (См. рисунок.)
- Когда ЭДС перемещается от — к + (в том же направлении, что и положительный заряд), изменение потенциала составляет +ЭДС. (См. рисунок.)
- Когда ЭДС перемещается от + к — (противоположно направлению движения положительного заряда), изменение потенциала равно -ЭДС. (См. рис.)
Пример \(\PageIndex{1}\): Расчет силы тока: использование правил Кирхгофа
Найдите токи, протекающие в цепи на рисунке \(\PageIndex{5}\).
Рисунок, но указаны сопротивления и ЭДС. (Каждая ЭДС обозначена буквой E.) Токи в каждой ветви помечены и предполагается, что они движутся в показанных направлениях. В этом примере для нахождения токов используются правила Кирхгофа.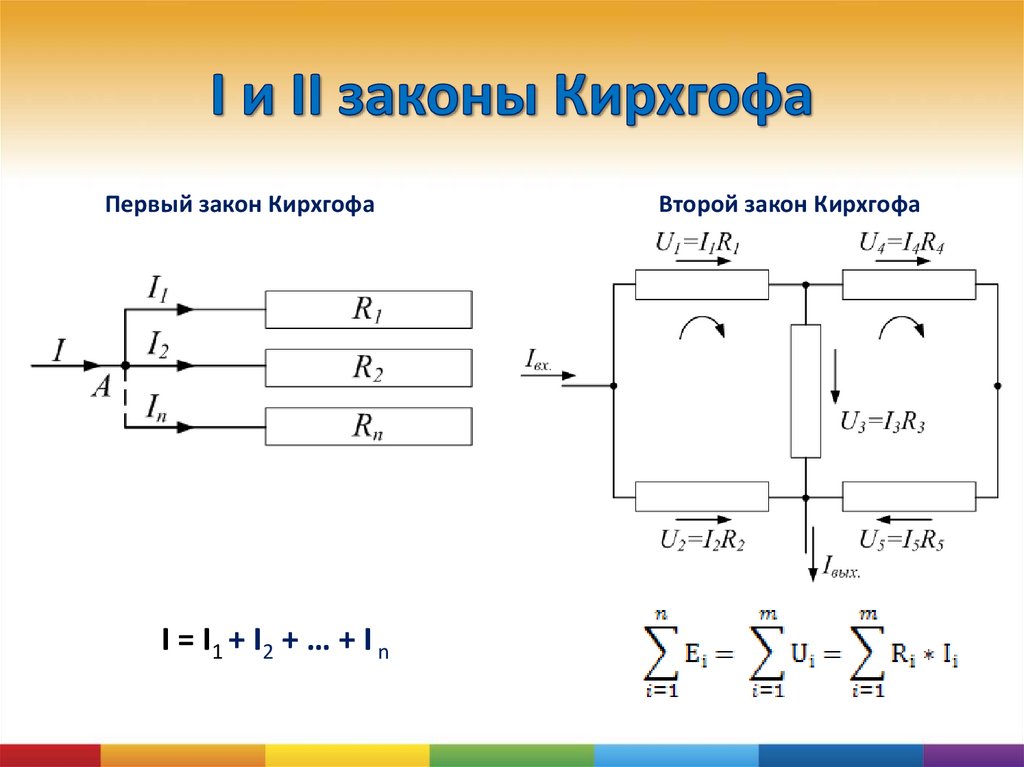
Стратегия
Эта схема настолько сложна, что токи нельзя найти с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. Токи были помечены \(I_1, \, I_2,\) и \(I_3\)
на рисунке, и были сделаны предположения об их направлениях. Места на схеме обозначены буквами от a до h. В решении мы будем применять правила соединения и петли, ища три независимых уравнения, которые позволят нам найти три неизвестных тока.
Решение
Начнем с применения первого правила Кирхгофа или правила соединения в точке а. Это дает
\[I_1 = I_2 + I_3,\]
, так как \(I_1\) впадает в соединение, а \(I\) и \(I_3\) вытекают. Применение правила соединения в точке e дает точно такое же уравнение, так что никакой новой информации не получается. Это одно уравнение с тремя неизвестными — нужны три независимых уравнения, поэтому необходимо применить правило цикла.
Теперь рассмотрим цикл abcdea. Переходя от a к b, мы пересекаем \(R_2\) в том же (предполагаемом) направлении тока \(I_2\), поэтому изменение потенциала равно \(-I_2R_2\). Затем, переходя от b к c, мы переходим от — к +, так что изменение потенциала равно \(+ЭДС_1\). Перемещение внутреннего сопротивления \(r_1\) от c к d дает \(-I_2r_1\). Завершение цикла путем перехода от d к a снова пересекает резистор в том же направлении, что и его ток, что дает изменение потенциала \(-I_1R_1\).
Переходя от a к b, мы пересекаем \(R_2\) в том же (предполагаемом) направлении тока \(I_2\), поэтому изменение потенциала равно \(-I_2R_2\). Затем, переходя от b к c, мы переходим от — к +, так что изменение потенциала равно \(+ЭДС_1\). Перемещение внутреннего сопротивления \(r_1\) от c к d дает \(-I_2r_1\). Завершение цикла путем перехода от d к a снова пересекает резистор в том же направлении, что и его ток, что дает изменение потенциала \(-I_1R_1\).
Правило цикла гласит, что сумма изменений потенциала равна нулю. Таким образом,
\[-I_2R_2 + эдс_1 -I_2r_1 — I_1R_1 = -I_2(R_2 + r_1) + эдс_1 — I_1R_1 = 0.\]
Обратите внимание, что знаки меняются местами по сравнению с другим циклом, потому что элементы проходятся в противоположное направление. С введенными значениями это становится \[+6I_1 + 2I_3 -45 = 0.\] Этих трех уравнений достаточно, чтобы решить для трех неизвестных токов. Сначала решите второе уравнение для \(I_2\).
\[I_2 = 6 — 2I_1.\]
Теперь решите третье уравнение для \(I_3\):
\[I_3 = 22,5 — 3I_1. \]
\]
Подстановка этих двух новых уравнений в первое позволяет нам найти значение для
\[I_1 = I_2 + I_3 = (6 — 2I_1) + (22,5 — 3I_1) = 28,5 — 5I_1.\]
Объединение членов дает
\[6I_1 = 28,5, \, и\]\[I_1 = 4,75 \, A.\ ]
Подстановка этого значения вместо \(I\) обратно в четвертое уравнение дает
\[I_2 = 6 — 2I_1 = 6 — 9,50\]\[I_2 = -3,50 \, A\]
Знак минус означает, что \(I_2\) течет в направлении, противоположном предполагаемому на рисунке .
Наконец, подстановка значения \(I_1\) в пятое уравнение дает
\[I_3 = 22,5 — 3I_1 = 22,5 — 14,25\]\[I_3 = 8,25 \, A.\]
Обсуждение
Просто для проверки отметим, что действительно \(I_1 = I_2 + I_3\). Результаты также можно проверить, введя все значения в уравнение для цикла abcdefgha.
Стратегии решения проблем для правил Кирхгофа
- Убедитесь, что имеется четкая принципиальная схема, на которой вы можете отметить все известные и неизвестные сопротивления, ЭДС и токи.
 Если ток неизвестен, вы должны присвоить ему направление. Это необходимо для определения признаков потенциальных изменений. Если вы зададите направление неправильно, то обнаружится, что ток имеет отрицательное значение — никакого вреда не будет.
Если ток неизвестен, вы должны присвоить ему направление. Это необходимо для определения признаков потенциальных изменений. Если вы зададите направление неправильно, то обнаружится, что ток имеет отрицательное значение — никакого вреда не будет. - Примените правило соединения к любому соединению в цепи. Каждый раз, когда применяется правило соединения, вы должны получать уравнение с током, которого не было в предыдущем приложении — если нет, то уравнение избыточно.
- Примените правило цикла к такому количеству циклов, которое необходимо для поиска неизвестных в задаче. (Независимых уравнений должно быть столько же, сколько и неизвестных.) Чтобы применить правило цикла, вы должны выбрать направление обхода цикла. Затем тщательно и последовательно определите знаки потенциальных изменений для каждого элемента, используя четыре маркированных пункта, рассмотренных выше в сочетании с рисунком.
- Решите уравнения для неизвестных. Это может включать в себя множество алгебраических шагов, требующих тщательной проверки и перепроверки.

- Проверить разумность и последовательность ответов. Числа должны быть правильного порядка, ни чрезмерно большими, ни исчезающе малыми. Признаки должны быть разумными — например, отсутствие сопротивления не должно быть отрицательным. Убедитесь, что полученные значения удовлетворяют различным уравнениям, полученным в результате применения правил. Например, токи должны удовлетворять правилу соединения.
Материал в этом разделе теоретически верен. Мы должны быть в состоянии проверить это, произведя измерения тока и напряжения. На самом деле, некоторые из устройств, используемых для проведения таких измерений, представляют собой прямое применение принципов, рассмотренных до сих пор, и рассматриваются в следующих модулях. Как мы увидим, отсюда вытекает очень простой, даже глубокий факт: проведение измерения изменяет измеряемую величину.
Упражнение \(\PageIndex{1}\)
Можно ли применять правила Кирхгофа к простым последовательным и параллельным схемам, или они ограничены для использования в более сложных схемах, которые не являются комбинацией последовательной и параллельной?
- Ответить
Правила Кирхгофа можно применить к любой схеме, поскольку они являются приложениями к схемам двух законов сохранения.
 Законы сохранения являются наиболее широко применимыми принципами в физике. Обычно математически проще использовать правила для последовательной и параллельной схемы в более простых схемах, поэтому мы подчеркиваем правила Кирхгофа для использования в более сложных ситуациях. Но правила последовательностей и параллелей можно вывести из правил Кирхгофа. Кроме того, правила Кирхгофа могут быть распространены на устройства, отличные от резисторов и ЭДС, такие как конденсаторы, и являются одним из основных устройств анализа в анализе цепей.
Законы сохранения являются наиболее широко применимыми принципами в физике. Обычно математически проще использовать правила для последовательной и параллельной схемы в более простых схемах, поэтому мы подчеркиваем правила Кирхгофа для использования в более сложных ситуациях. Но правила последовательностей и параллелей можно вывести из правил Кирхгофа. Кроме того, правила Кирхгофа могут быть распространены на устройства, отличные от резисторов и ЭДС, такие как конденсаторы, и являются одним из основных устройств анализа в анализе цепей.
Резюме
- Правила Кирхгофа можно использовать для анализа любой схемы, простой или сложной.
- Первое правило Кирхгофа — правило соединения: сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения.
- Второе правило Кирхгофа — правило петли: алгебраическая сумма изменений потенциала вокруг любого замкнутого контура (петли) должна быть равна нулю.

- Два правила основаны соответственно на законах сохранения заряда и энергии.
- При расчете потенциала и тока по правилам Кирхгофа необходимо соблюдать ряд правил для определения правильных знаков различных членов.
- Простые ряды и параллельные правила являются частными случаями правил Кирхгофа.
Глоссарий
- Правила Кирхгофа
- набор из двух правил, основанных на сохранении заряда и энергии, регулирующих ток и изменения потенциала в электрической цепи
- правило соединения
- первое правило Кирхгофа, применяющее закон сохранения заряда к соединению; ток — это поток заряда; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу; можно указать правило \(I_1 = I+2 + I_3\)
- правило цикла
- Второе правило Кирхгофа, которое гласит, что в замкнутом контуре любая энергия, поставляемая ЭДС, должна быть переведена в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в контур или из него.
 Таким образом, ЭДС равна сумме падений \(IR\) (напряжения) в контуре и может быть сформулирована следующим образом: \(ЭДС = Ir + IR_1 + IR_2\)
Таким образом, ЭДС равна сумме падений \(IR\) (напряжения) в контуре и может быть сформулирована следующим образом: \(ЭДС = Ir + IR_1 + IR_2\)
- законы сохранения
- требуют сохранения энергии и заряда в системе
Эта страница под названием 21.3: Правила Кирхгофа распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа ООР или издатель
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- Законы сохранения
- правило соединения
- Первое правило Кирхгофа
- Второе правило Кирхгофа
- Правило соединения Кирхгофа
- Правило петли Кирхгофа
- правило цикла
- источник@https://openstax.
 org/details/books/college-physics
org/details/books/college-physics
Закон Кирхгофа • Инженерные каракули
Перейти к содержимомуПредыдущий Следующий
Закон КирхгофаВ этом разделе закон Кирхгофа поможет нам понять, как анализировать цепь постоянного тока. Постоянный ток означает постоянный ток, когда ток течет в одном направлении, от положительной клеммы источника напряжения (батареи) к отрицательной клемме.
Зачем анализировать цепь постоянного тока?
И что это значит?
Ну, это означает, что мы берем компоненты, значение которых мы знаем в цепи, и вычисляем то, что мы не знаем. Например, значение резистора или протекание тока.
Цепи увеличиваются. Действительно большой. С помощью анализа цепи постоянного тока мы могли бы упростить большую схему , так что несколько компонентов представляли бы большую схему. Теоретически, конечно, например, мы можем заменить 100 резисторов на 1: это будет сумма их всех. Но мы доберемся до этого в ближайшее время.
Но мы доберемся до этого в ближайшее время.
Давайте сосредоточимся на мистере Кирхгофе. У него есть 2 важных закона:
1. Текущий закон Кирхгофа
Возьмем для примера этот перекресток. Это часть случайной цепи.
- Имеется 4 провода , соединенных вместе в узле
- В каждом проводе разный ток
- I1 и I2 текут к узлу
- Поскольку ток течет от клеммы +ve к клемме -ve, этот узел имеет более низкий потенциал, чем то, что у нас есть на другой стороне проводов I1 и I2.
- I3 и I4 текут в сторону от узла
- для них узел находится в потенциале найма, чем туда, куда текут токи I3 и I4.
Токи можно выразить следующим образом:
Из уравнения становится ясно, почему I3 и I4 отрицательны. Но подумайте об этом так: они находятся в противоположном направлении, как I1 и I2 таким образом, что они не идут в сторону узла, а уходят от него.
Но подумайте об этом так: они находятся в противоположном направлении, как I1 и I2 таким образом, что они не идут в сторону узла, а уходят от него.
Сумма полного тока, входящего в соединение, равна сумме полного тока, выходящего из соединения.
Другими словами, сумма всех токов равна нулю. Знак сигма представляет собой математическое представление суммы:
2. Закон напряжения Кирхгофа
Чтобы понять это, давайте начнем с небольшой схемы:
- Имеем 1 источник напряжения : E и два резистора R1 и R2.
- Красные стрелки обозначают падение напряжения
- Стрелка указывает на более высокий потенциал .
- В цепи есть ток I .
- Падение напряжения на R1: В(R1) = IR1 и на R2: В(R2) = IR2 .
- Ток одинаков на обоих резисторах.

- Падение напряжения на R1 плюс падение напряжения на R2 равно источнику напряжения E.
- E это EMF .
Вышесказанное можно выразить так:
Второй закон Кирхгофа гласит, что сумма напряжений в замкнутой цепи равна нулю.
Итак, сумма всех ЭДС (несколько батарей) за вычетом падений напряжения на всех элементах (резисторах) равна 0:
Решенный Пример:Найдите ток, протекающий через R1.
Решение:
1. Используйте правило тока Кирхгофа
- У нас есть 3 тока , из которых мы знаем только значение I . Узел X соединяет их вместе.
- I1 и текущий источник I текут к узлу X , в то время как I2 течет от .
- отсюда мы можем написать следующие уравнения.
 Обратите внимание, что I1 и I2 отрицательны, поскольку они текут к узлу.
Обратите внимание, что I1 и I2 отрицательны, поскольку они текут к узлу.
2. Подставим уравнения 2 и 3 в уравнение 2
- Наша цель – найти напряжение в узле X.
- Зная Vx , мы узнаем падение напряжения на R1. Значение резистора R1 задано, таким образом, используя закон Ома, мы можем вычислить I1 .
3. Подстановка в уравнение:
4. Используйте уравнение 2 для нахождения I1 и уравнение 3 для нахождения I2
Решено индивидуальное падение напряжения на каждом резисторе. Решение:1. Используйте правило напряжения Кирхгофа
- В цепи 4 резистора и 2 источника напряжения
- Все резисторы в серии . таким образом, через них протекает тот же ток
- Согласно закону Кирхгофа о напряжении сумма падений напряжения на каждом резисторе равна сумме падений всех источников напряжения.




 7)
7) 8)
8) д., получим:
д., получим:
 Если ток неизвестен, вы должны присвоить ему направление. Это необходимо для определения признаков потенциальных изменений. Если вы зададите направление неправильно, то обнаружится, что ток имеет отрицательное значение — никакого вреда не будет.
Если ток неизвестен, вы должны присвоить ему направление. Это необходимо для определения признаков потенциальных изменений. Если вы зададите направление неправильно, то обнаружится, что ток имеет отрицательное значение — никакого вреда не будет.
 Законы сохранения являются наиболее широко применимыми принципами в физике. Обычно математически проще использовать правила для последовательной и параллельной схемы в более простых схемах, поэтому мы подчеркиваем правила Кирхгофа для использования в более сложных ситуациях. Но правила последовательностей и параллелей можно вывести из правил Кирхгофа. Кроме того, правила Кирхгофа могут быть распространены на устройства, отличные от резисторов и ЭДС, такие как конденсаторы, и являются одним из основных устройств анализа в анализе цепей.
Законы сохранения являются наиболее широко применимыми принципами в физике. Обычно математически проще использовать правила для последовательной и параллельной схемы в более простых схемах, поэтому мы подчеркиваем правила Кирхгофа для использования в более сложных ситуациях. Но правила последовательностей и параллелей можно вывести из правил Кирхгофа. Кроме того, правила Кирхгофа могут быть распространены на устройства, отличные от резисторов и ЭДС, такие как конденсаторы, и являются одним из основных устройств анализа в анализе цепей.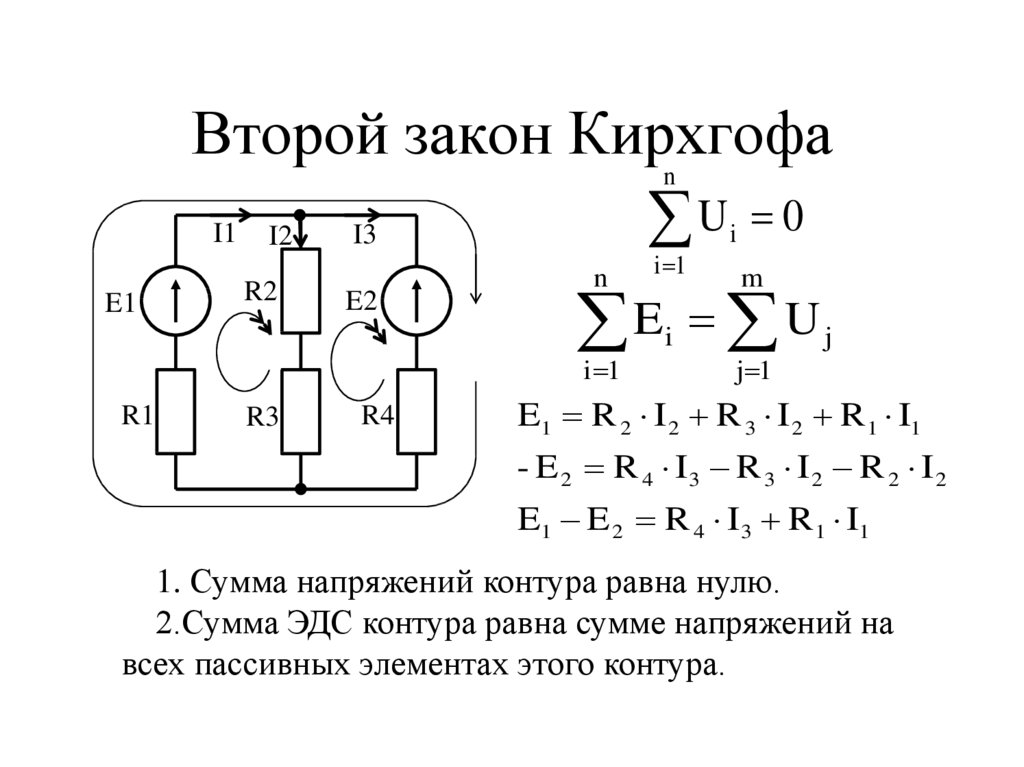
 Таким образом, ЭДС равна сумме падений \(IR\) (напряжения) в контуре и может быть сформулирована следующим образом: \(ЭДС = Ir + IR_1 + IR_2\)
Таким образом, ЭДС равна сумме падений \(IR\) (напряжения) в контуре и может быть сформулирована следующим образом: \(ЭДС = Ir + IR_1 + IR_2\) org/details/books/college-physics
org/details/books/college-physics
 Обратите внимание, что I1 и I2 отрицательны, поскольку они текут к узлу.
Обратите внимание, что I1 и I2 отрицательны, поскольку они текут к узлу.