Законы Кирхгофа, теория и примеры задач

Законы Кирхгофа (или правила Кирхгофа) – это приемы, которые используют для того, чтобы упрощать процедуру составления систем уравнений необходимых при расчетах сложных разветвленных цепей постоянного тока. Разветвленными цепями называют цепи, которые содержат несколько замкнутых контуров с несколькими источниками ЭДС.

Узлом цепи называют такую точку цепи, в которой сошлись три или более проводников с токами.

Первый закон Кирхгофа

Первый закон Кирхгофа еще называют правилом узлов. Так как он касается именно узлов цепи и токов в них. Словесно этот закон формулируется следующим образом: Сумма токов в цепи с учетом их знаков равна нулю. В математическом виде этот закон представляют как формулу:

   

Знак у тока (плюс или минус) выбирают произвольно, но при этом следует считать, что все входящие в узел токи имеют одинаковые знаки, а все исходящие из узла токи имеют противоположные входящим, знаки.

Допустим, все входящие токи мы примем за положительные, тогда все исходящие их этого узла токи будут отрицательными.

Первый закон Кирхгофа является следствием закона сохранения заряда. Если в цепи текут только постоянные токи, то нет в этой цепи точек, которые накапливали бы заряд. Иначе токи не были бы постоянными.

Первый закон Кирхгофа дает возможность составить независимое уравнение, если в цепи k узлов.

Второй закон Кирхгофа

Во втором законе Кирхгофа рассматривают контуры, поэтому он еще называется правилом контуров. Формулируется второй закон Кирхгофа так: Суммы произведений алгебраических величин сил тока на внешние и внутренние сопротивления всех участков замкнутого контура равны алгебраической сумме величин сторонних ЭДС (), которые входят в рассматриваемый контур. В математическом виде второй закон Кирхгофа записывают как:

   

Величины еще называют падениями напряжения. Прежде, чем применять второй закон Кирхгофа определяются с направлением положительного обхода контура. Выбирается направление произвольно, либо по часовой стрелке, либо против нее. Если направление обхода совпадает с направлением течения тока в рассматриваемом элементе контура, то падение напряжения в формулу второго закона для данного контура входит с положительным знаком. ЭДС считают положительной, если при движении по контуру (в избранном направлении) первым встречается отрицательный полюс источника.

Второй закона Кирхгофа является следствием закона Ома.

Любую цепь можно рассчитать при помощи закона сохранения заряда и закона Ома, правила Кирхгофа являются лишь подходами, упрощающими расчетные задачи.

При составлении уравнение, используя законы Кирхгофа, следует внимательно следить за расстановкой знаков у токов и ЭДС.

Примеры решения задач

как они проявляются в работе электромагнитной цепи, примеры расчета

Считается, что каждый образованный человек должен обладать минимальными знаниями физики, например, знать закон Ома.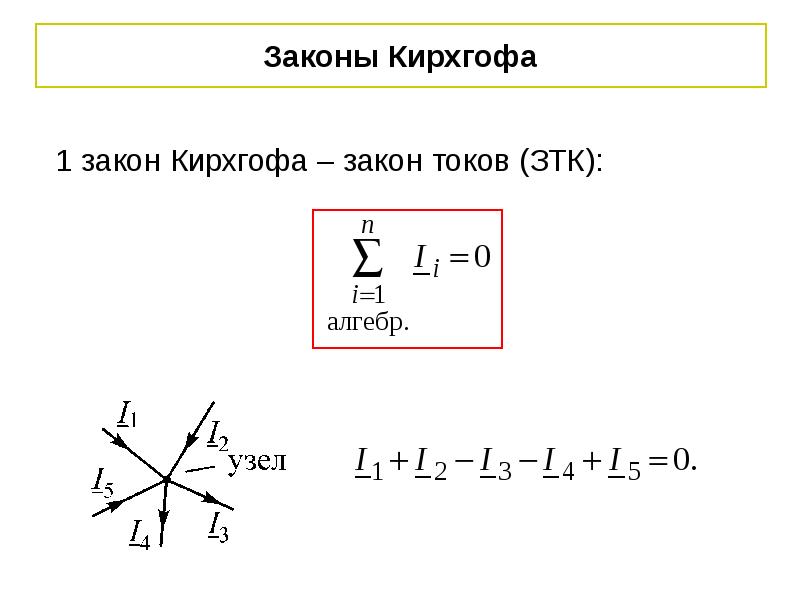

Но знать закон Ома мало, ведь вокруг нас действует гораздо больше. Ученый из Германии Г. Кирхгоф, занимавшийся рядом естественных наук, вывел закон, по которой сегодня работают все электрические цепи.

Закон Кирхгофа объясняют, как распределяется ток на контуре цепи. Поговорим о правилах, которые вывел немецкий учёный.

Первое правило

В первом определении закона Кирхгофа описано, что общее суммирование токов, проходящим по веткам, равняется 0. Постоянство токов объясняется тем, что неважно, сколько токов втекает в узлы пересечения — такое же количество будет вытекать.

Точку в соединении ветвей обозначают как узел в электрической цепи. В каждой ветке на своё сопротивление есть свой ток.

Эта формула соответствует тем электрическим цепям, где ток считается постоянным.

Когда закон Кирхгофа применяется для цепи, где ток считается переменным, используется I, обозначающее мгновенное напряжение.

Формула производится в форме комплекса, но расчёт при этом не изменится:

Благодаря такому подходу к расчётам учитывается реактивные и активные значения, присутствующие в цепи.

Второе правило Кирхгофа

Первое правило закона Кирхгофа существует для описания распределения тока среди веток цепи.

Второе правило Кирхгофа описывает, что суммарное падение напряжения будет равно суммарному количеству электродвижущих сил.

Это значит, что электродвижущие силы, воздействующие на определённые места в цепи, распределятся пропорционально сопротивлению. Об этом говорится в законах Ома.

Для переменного тока суммарное количество электродвижущих сил будет равна сумме падений напряжений в ветках электрической цепи.

В формуле Z означает абсолютное сопротивление, включающее реактивную и резистивную элементы, зависящие от частоты переменного тока. Формула суммы сопротивления и индуктивности:

Более наглядно данная формула может выглядеть следующим образом:

При этом:

Какими могут быть варианты расчёта правила Кирхгофа

Теперь рассмотрим, как можно применять описанные правила в жизни. Выбрав направления обходов контура Вы сможете верно разместить знаки в формуле. Рассмотрим следующий вариант:

Выберем путь, идущий параллельно стрелке часов, отметим на примере:

Пунктиром мы обозначили, как будет проходить ток в схеме.

Далее составим само уравнение закона Кирхгофа согласно правилам, сначала по второму.

Перед ЭДС ставим минус, если сила будет двигаться против часовой стрелки. Для всех контуров используются свои знаки.

При первом контуре сила будет совпадать с направлением контура. Первый будет выглядеть так:

Второе будет выглядеть так:

Третий будет выглядеть так:

Напряжение зависит от направления. По часовой стрелке значения будут положительными. Против часовой стрелки значения будут отрицательными.

Обход контура является своего рода условным значением, который нужен для того, чтобы правильно поставить знаки в формулах. На правильность вычисления это значение не влияет. Иногда это может затруднить расчёт в целом, но скорее всего значение останется то же.

Теперь посмотрим на эту цепь:

В этой схеме у электродвижущей силы четыре источника. Не забудьте сначала выбрать направление контура.

Составляем формулу по первому рассмотренному закону. Начальный узел рассчитывается следующим образом:

Второй будет таким:

Третий таким:

Узла 4, но уравнения при этом 3, и эти цифры не являются ошибкой. Число формул согласно первому правилу выглядит так:

Так, уравнений будет на одно меньше, чем узлов, и при этом все токи будут описаны.

Строим формулы по второму закону Кирхгофа. Первый контур будет выглядеть так:

Второй контур будет таким:

Третий контур вычисляется следующим образом:

Подставляя значения из реальной жизни Вы сможете убедиться, что все эти законы действующие и правильные. Примеры к закону Кирхгофа, о которых мы рассказали, достаточно лёгкие, задачи из жизни бывают гораздо сложнее.

При вычислении путём применения данных правил главным образом нужно следить за тем, куда направлен ток и как обходит контур, чтобы подставить в уравнение правильные значения.

Действие правил и закона Кирхгофа в электромагнитной цепи

Расчёты магнитных цепей необходимы для вычислений верных значений. Расчёт будет тем же, но числа изменятся.

МДС, или магнитная движущая силы, определена витками в катушке и проходящее через них электричество:

МДС является множителем поля и тока.

Можно провести вычисление через сопротивление:

В этих формулах средняя длина участок цепи и проницаемость магнита разделены. Для магнитной цепи формула будет выглядеть следующим образом:

Через узел общее число магнитного потока будет равно нулю.

Сумма магнитной движущей силы в контуре равно сумме напряжения магнита.

Магнитный поток можно высчитать следующим образом:

А переменное поле магнита рассчитывается так:

Применяя эти знания на практике, посмотрим на следующий вариант контура.

Математическая формула будет следующей:

При наличии зазора рисунок будет выглядеть так:

Сопротивление магнитного потока будет вычисляться согласно описанным законам:

Сопротивление в зазоре будет таким:

Лучше понять всё написанное помогут наглядный урок по закону Кирхгофа от ведущего эксперта и профессора в области физики. Для того, чтобы разобраться в написанном и понять происходящее, советуем посмотреть данный урок:

Учёные веками вносили неоценимый вклад в развитие науки и объяснения жизни вокруг нас, это касается и Г.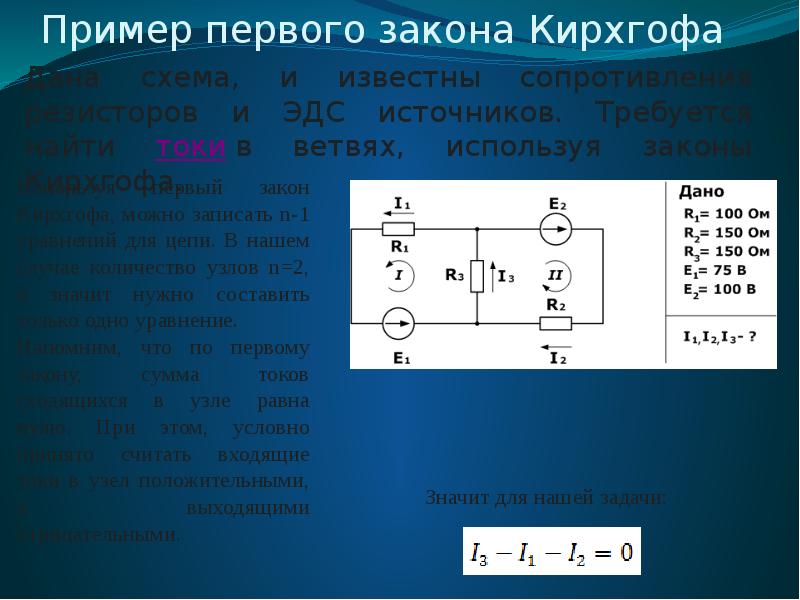 Кирхгофа.

Благодаря его правилам и выведенному закону можно рассчитать многие значения в электрической цепи. Пользуйтесь ими, чтобы легко проводить расчёты!

Алгоритм решения задач на законы Кирхгофа

Задачи на применение закона Кирхгофа решаются в школе не часто, и не во всех классах. Работая в школе, я давала законы Кирхгофа только тем ребятам, кто готовился к олимпиадам по физике, и учащимся, которые готовились в ВУЗы.

Задачи на использование законов Кирхгофа есть даже не всех сборниках задач, рекомендованных для использования в средней школе.

Ниже приведён алгоритм решения задач по данной теме. Алгоритм не сложен. Использование данного алгоритма поможет Вам в решении задач по этой теме.

Итак, начнем. Сначала необходимо выполнить некоторые подготовительные операции.

• перерисовать схему
• указать направление ЭДС источников тока
• указать предполагаемое направление токов, текущих в каждом резисторе (если итоговый ответ будет отрицательным, то направление тока было изначально выбрано не верно)
• выбрать направление обхода для всех линейно независимых контуров

После проведения предварительных операций, приступаем собственно к решению самой задачи.

• Записываем первый  закон Кирхгофа: сумма токов, втекающих и вытекающих в данный узел, равна нулю.

Важно! Если ток втекает в узел, то он берётся со знаком «плюс», если вытекает, то со знаком «минус». Число уравнений второго закона Кирхгофа равно n-1, где n — число узлов в данной схеме. (Узел — точка, в которой соединяются три проводника и более).

• Записываем второй закон Кирхгофа для всех линейно независимых контуров: Сумма ЭДС в контуре равно сумме падений напряжений в каждом из этих контуров.

Важно! Если направление ЭДС  совпадает с направлением обхода контура, то значение ЭДС берётся со знаком «плюс». Если направление ЭДС не совпадает с направлением обхода контура, то значение ЭДС берётся со знаком «минус». Если направление тока совпадает с направлением обхода контура, то падение напряжения на данном участке берётся со знаком «плюс». Если направление тока через какой-либо резистор не совпадает с направлением обхода в данном контуре, то падение напряжения берётся со знаком «минус».

 

Решаем систему получившихся уравнений, относительно неизвестных величин.

Чаще всего в задачах этого типа, основную сложность представляет именно решение системы получившихся уравнений.

Ниже показан пример решения задачи с использованием законов Кирхгофа. Обратите внимание ещё раз на основные этапы решения. Они полностью соответствуют алгоритму, описанному выше.

Вот условие этой задачи.

Электрическая цепь состоит из двух гальванических элементов, трех резисторов и амперметра. В этой цепи R₁ = 100 Ом, R₂ = 50 Ом, R₃ = 20 Ом, ЭДС элемента ?₁ = 2 В. Амперметр регистрирует ток I₃ = 50 мА, идущий в направлении, указанном стрелкой. Определить ЭДС ?₂ второго элемента. Сопротивлением амперметра и внутренним сопротивлением источников пренебречь.

Удачи в освоении этой довольно сложной темы!

Возникающие вопросы можете оставлять в комментариях.

Вы можете оставить комментарий, или поставить трэкбек со своего сайта.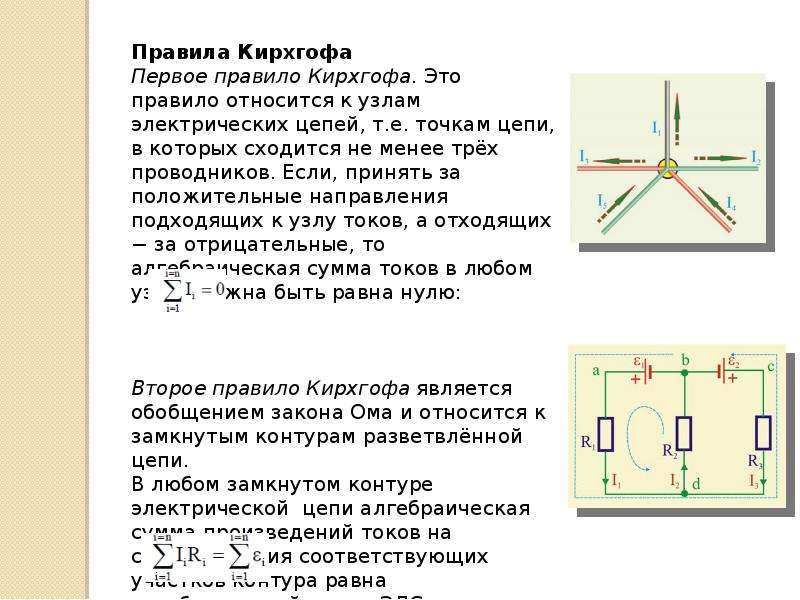

Написать комментарий

7.2. Порядок решения задач на законы Кирхгофа

1. Нарисовать схему цепи. На рисунке выбрать и показать направления токов на всех участках цепи, при этом надо учесть, что в узел токи не могут только входить или только выходить из узла. Это следует из первого закона Кирхгофа.

2. Выбрать замкнутые контуры обхода для применения второго закона Кирхгофа. Показать на рисунке направление обхода по контуру. Контуров может быть несколько. Число независимых уравнений, которые можно составить по второму закону Кирхгофа, меньше чем число контуров. Чтобы составить необходимое число независимых уравнений надо придерживаться следующего правила: Выбирать контуры так, чтобы в каждый новый контур входил хотя бы один участок цепи, которого бы не было нив одном ранее рассмотренных контуров.

3. Используя первый закон Кирхгофа можно написать ( n – 1) уравнений, где n— число узлов в рассматриваемой цепи.

4. Воспользоваться вторым законом Кирхгофа и записать такое число уравнений, чтобы число уравнений, составленных по первому и второму законам Кирхгофа, равнялось числу неизвестных величин в задаче. При этом надо учитывать следующее правило знаков: падение напряжения на каждом участке записывается со знаком «+», если направление обхода по этому участку совпадает с направлением тока на нем. И наоборот, если обход совершался по этому сопротивлению обратно направлению тока, то ставится знак « – ».

ЭДС записывается со знаком «+» в том случае, когда направление обхода совпадает с направлением поля сторонних сил в источнике тока и наоборот.

Поле сторонних сил внутри источника всегда направлено от отрицательного полюса к положительному.

5. Решить полученную систему уравнений и найти искомые величины.

В результате решения полученной системы уравнений определяемые величины могут получаться отрицательными. Отрицательное значение тока указывает на то, что фактическое направление тока на данном участке цепи обратно тому, которое мы выбрали.

7.3. Примеры решения задач на законы Кирхгофа

П р и м е р 1.

Два элемента с одинаковыми ЭДС e₁ = e₂ = 2В и внутренними сопротивлениями r₁ = 1 Ом, r₂ = 2 Ом замкнуты на внешнее сопротивление R. Через первый элемент течет ток I₁ = 1 А. Найдите сопротивление R, ток I₂, текущий через второй элемент, и ток I, текущий через сопротивление R. Схема соединения показана на рисунке.

Дано:

e₁ = e₂ = 2 D;

r₁ = 1 Ом;

r₂ = 2 Ом;

I₁ = 1 A

________

Найти:

I₂ =? R=? I=?

Решение:

1. Выберем направления токов на всех участках цепи так, как показано на рисунке. Видим, что в узлах 1 и 2 есть входящие и есть выходящие токи, значит, направления токов выбраны разумно.

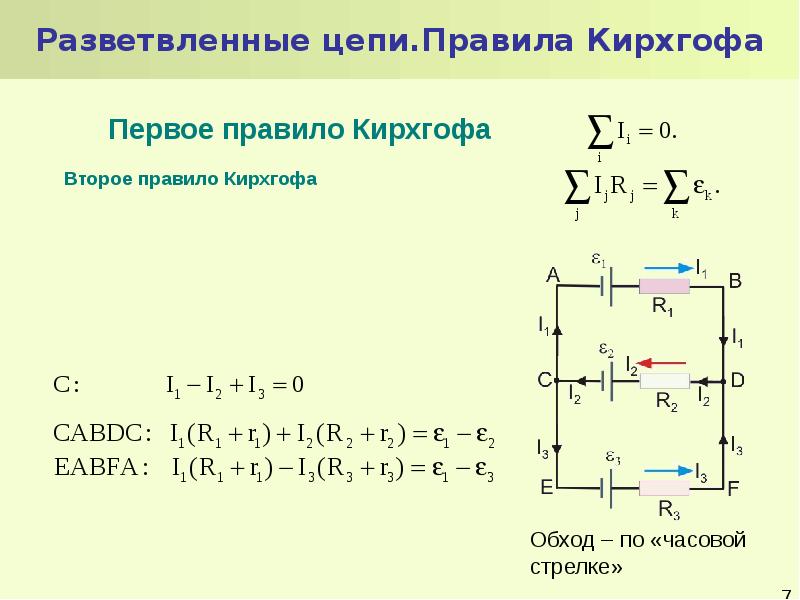
2. Выберем контуры обхода и покажем направления обхода по ним. Контуров выбрали два и нарисовали направления обхода по ним.

3. Составим уравнение, используя первый закон Кирхгофа. Узлов два, поэтому можно составить только одно уравнение, например для первого узла:

I₁ + I₂ — I = 0.

Токи, входящие в узел, пишем со знаком «+», а выходящие с знаком»–». Уравнение для второго узла будет тождественно первому.

4. Применим второй закон Кирхгофа для первого контура обхода. Падение напряжения на всех участках этого контура пишем со знаком «+», т.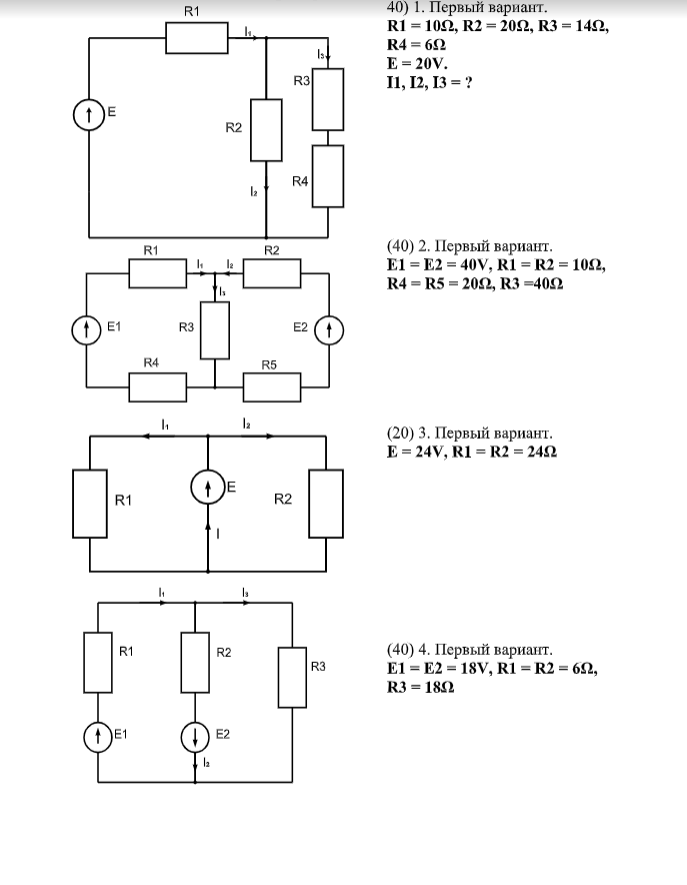 к. направление обхода на всех участках совпадает с направлением тока на этих участках

U_å = IR +I₁ r.

В этот контур входит только один источник тока e₁, и направление обхода по контуру совпадает с направлением поля сторонних сил, т.к. силы этого поля направлены от отрицательного полюса к положительному, т.е. вниз.

Запишем уравнение

IR + I₁r₁ = e₁.

Для второго контура, рассуждая аналогично, получим U₂ = +I₂r₂ + IR. ЭДС будет входить в уравнение также со знаком «+».

Второе уравнение имеет вид: I₂R₂ + IR = e₂.

5. Получили систему из трех уравнений с тремя неизвестными.

Решая систему, находим величину тока I₂

.

Полный ток через сопротивление R равен сумме токов

I = I₁ + I₂ = 1,5 A.

Сопротивление R находим из одного из уравнений системы:

.

Ответ: ток через второй источник равен I₂ = 0,5 А, суммарный ток

I = I₁ + I₂ = 1,5 А. Внешнее сопротивление R = 0,66 Ом.

П р и м е р 2.

Два одинаковых элемента имеют ЭДС e₁ = e₂ = 2 В и внутренние сопротивления r₁ = r ₂ = 0,5 Ом. Найдите токи I₁ и I₂, текущие через сопротивления R₁ = 0,5 Ом и R₂ = 1,5 Ом, а также ток I через первый элемент. Схема заданной цепи изображена на рисунке.

Дано:

e₁ = e₂ = 2 В;

r₁=r₂=0,5 Ом;

R₁ = 0,5 Ом;

R₂ = 1,5 Ом

I₁ – ? I₂ – ? I – ?

Решение:

1. Выберем направления токов на всех участках так, как показано на рисунке. Видим, что в узлах 1 и 2 есть входящие и есть выходящие токи, значит, направления токов выбраны верно.

2. Выберем два контура обхода: большой и малый. Укажем направления обходов по контурам. Контуров обхода в заданной цепи можно выбрать три, но для нахождения трех неизвестных величин достаточно трех уравнений. Узлов всего два, поэтому можно составить только одно уравнение, применяя первый закон Кирхгофа. Недостающих два уравнения составим используя второй закон Кирхгофа.

3. Для первого узла запишем:

I₂ + I₁ – I = 0.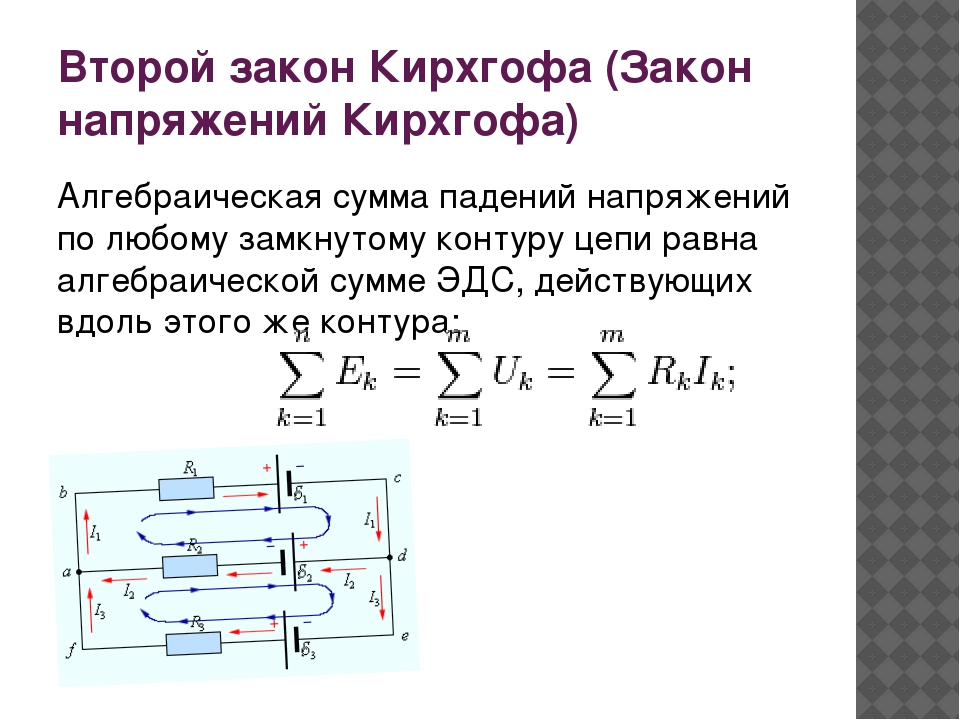

4. Учитывая правила определения знаков всех слагаемых при применении второй закон Кирхгофа для большого контура, получаем уравнение:

I r₁ + I₂r₂ + I₂R₂ = e₁ + e₂.

Для малого контура:

I r₁ + I₁R₁ = e₁.

5.Получили систему из трех уравнений с тремя неизвестными величинами I₁; I₂ и I.

Решать систему линейных уравнений можно разными способами. В случае, когда система состоит из большого числа уравнений удобно пользоваться методом Крамера (методом определителей). Проиллюстрируем применение этого метода решения на нашей системе уравнений. Для этого перепишем систему ещё раз:

или в численном виде; если поделить правую и левую части второго и третьего уравнении на « 0,5» получим

Искомые величины токов по методу определителей находятся следующим образом: и ,

где определители — определитель системы уравнений, и -определители, которые получаются заменой соответствующих столбцов определителя столбцами, полученными из свободных членов уравнений образующих систему (с учетом заданных числовых значений). Запишем эти определители:

По приведенным выше формулам, получаем

и .

Значение третьего тока можно найти аналогичным способом, но проще его значение получить из первого уравнения нашей системы:

I₂ + I₁ – I = 0 или I = I₂ + I₁ = 1,33 + 1,33 = 2,66 А

Знаки у всех полученных значений силы тока положительные, это свидетельствует о том, что при произвольном выборе направлений токов, указанных на рисунке, все направления токов были выбраны правильно.

Ответ: I₁ = 1,33 А ; I₂ = 1.33 А;I = I₁ + I₂ = 2.66 А.

П р и м е р 3.

Два элемента с одинаковыми ЭДС ₁ = ₂ = 2В и внутренними сопротивлениями r₁ = 1 Ом, r₂ = 2 Ом замкнуты на внешнее сопротивление R.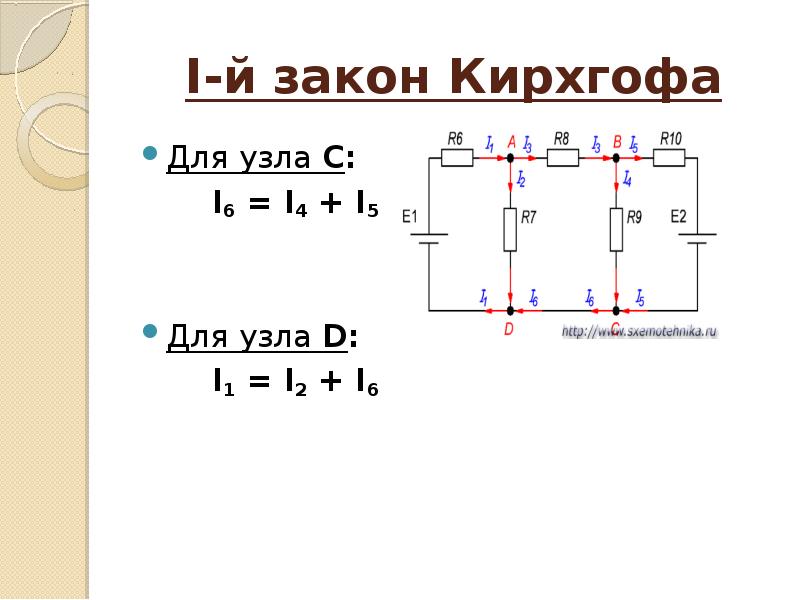 Через элемент с ЭДС ₁ — течет ток I₁ = 1 А. Найти сопротивление R и ток I₂, текущий через элемент с ЭДС ₂. Какой ток течет через сопротивление R. Схема соединения показана на рисунке.

Д ано:

₁ = ₂ = 2 D;

r₁ = 1 Ом;

r₂ = 2 Ом;

I₁ = 1 A

__________

+I₂ — ?

R — ? I — ?

Выберем направления токов на всех участках цепи. Видим, что в узлах 1 и 2 есть входящие и есть выходящие токи, значит, направления токов выбраны разумно.

Выберем контуры обхода и покажем направления обхода по ним.

Составим уравнение, используя первый закон Кирхгофа для первого узла:

I₁ + I₂ — I = 0.

Токи, входящие в узел, пишем со знаком «+», а входящие с «–». Всего можно написать одно уравнение, т.к. второе будет тождественно первому.

Воспользуемся вторым законом Кирхгофа. Запишем уравнение для первого контура обхода. Падение напряжения на всех участках 1-го контура напишем со знаком «+», т.к. направление обхода на этих участках совпадает с направлением тока

U_ = IR +I₁ r.

В этот контур входит только ЭДС ₁, и направление обхода по контуру совпадает с направлением поля сторонних сил, т.к. силы этого поля направлены от отрицательного полюса к положительному.

Запишем уравнение

IR + I₁r₁ = ₁.

Для второго контура U₂ = +I₂r₂ + IR. И ЭДС будет входить в уравнение также со знаком «+».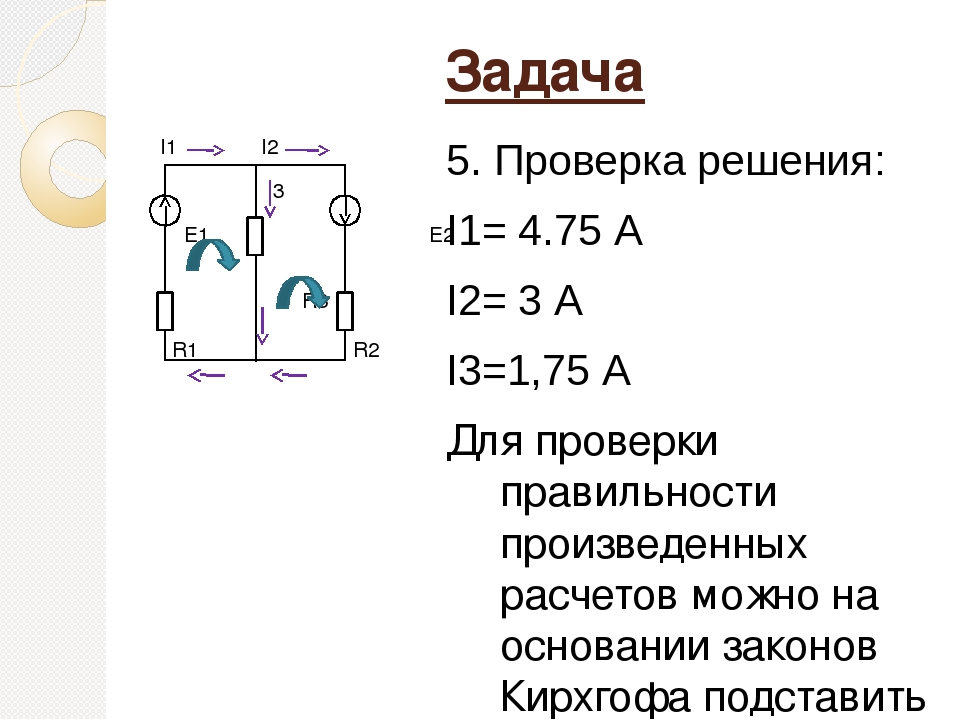

Запишем уравнение I₂R₂ + IR = ₂.

Получим систему из трех уравнений с тремя неизвестными.

Решая систему, получаем

.

Полный ток через сопротивление R равен сумме токов

I = I₁ + I₂ = 1,5 A.

Сопротивление R находим из одного из уравнений

.

Ответ. Ток через второй источник равен I₂ = 0,5 А, суммарный ток

I = I₁ + I₂ = 1,5 А. Внешнее сопротивление R = 2/3 Ом.

П р и м е р 4.

Два одинаковых элемента имеют ЭДС ₁ = ₂ = 2 В и внутренние сопротивления r₁ = l₂ =0,5 Ом. Найти токи I₁ и I₂, текущие через сопротивления R₁ = 0,5 Ом и R₂ = 1,5 Ом, а также ток I через элемент с ЭДС.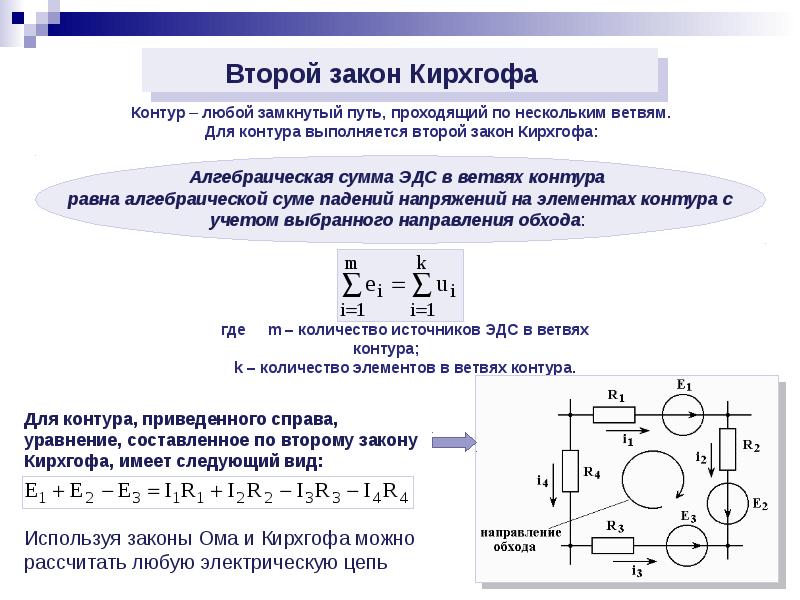 Схема изображена на рисунке.

Д ано:

₁ = ₂ = 2 В;

r₁ = r₂ = 0,5 Ом;

R₁ = 0,5 Ом;

R₂ = 1,5 Ом

_____________

I₁ — ?

I₂ — ?

I — ?

Решение:

Выберем направления токов на всех участках. Запишем первый закон Кирхгофа для 1-го узла

I₂ + I₁ = I .

Выберем большой и малый контуры обхода. Для большого контура уравнение будет иметь вид:

Ir₁ + I₂r₂ + I₂R₂ = ₁ + ₂.

Для малого контура

Ir₁ + I₁R₁ = ₁.

Получили три уравнения

В эти уравнения входят три неизвестных величины I₁; I₂ и I. Решаем систему уравнений и находим

I₁ = 2,28 А ; I₂ = 0,56 А;I = I₁ + I₂ = 1,72 А.

Объясняю 1 и 2 законы Кирхгофа простыми словами | ASUTPP

Законы Кирхгофа, которые касаются тока и напряжения — это два закона, которые действительно полезны, когда вы работаете с электрическими цепями.

Знание их значительно облегчит понимание принципиальных схем, конструирование электроники, ремонт электроники и многого другого.

Хотя эти законы могут показаться сложными — это не так.

Первый закон Кирхгофа

Первый закон Кирхгофа гласит: весь ток, поступающий в узел, равен всему току, выходящему из узла.

Другими словами можно перефразировать:

«То, что входит, должно выйти»

Рис. 1.

Рис. 1.

Согласно 1 закона Кирхгофа получаем: I1=I2+I3

Примеры первого закона Кирхгофа на практике:

• Ток, который «втекает в цель», должен выходить из цепи.
• Ток, который течет в резисторе, должен выходить из резистора.
• Ток, который течет в четыре резистора параллельно, должен выходить из четырех резисторов параллельно.

Рис. 2. Пример схемы

Рис. 2. Пример схемы

В схеме выше (рис. 2), вы можете использовать первый закон Кирхгофа, чтобы найти ток через компоненты:

То, что входит в резистор R1, должно из него выйти. И этому току больше некуда идти, кроме как на две ветви со светодиодами. И тот ток, который входит в две ветви со светодиодами, должен выходить из этих двух ветвей.

Итак, вы знаете, что ток через резистор такой же, как суммарный ток двух светодиодов.

И пока светодиоды одного типа, половина тока будет уходить в левый светодиод, а половина в светодиод справа.

Два параллельных светодиода 2 В не влияют на падение напряжения, которое все еще равно 2 В. Теперь вы можете рассчитать ток точно так же, как мы это сделали в приведенном ниже примере со 2 законом Кирхгофа. Затем разделите ток пополам, чтобы получить текущее значение для каждого светодиода.

Когда вы знаете как применять 1 закон Кирхгофа, вы можете многое упростить. Если у вас большая цепь с множеством компонентов, включенных параллельно и последовательно, может быть сложно найти отдельные токи.

Но, может быть, вам это и не нужно?

Иногда достаточно просто знать, что если 500 мА входит в этот участок цепи — 500 мА выйдет из него.

Второй закон Кирхгофа

Второй закон Кирхгофа гласит, что если вы просуммируете все падения напряжения в цепи — вы получите напряжение источника питания.

Когда я узнал об этом впервые, я подумал «ВАУ! НЕУЖЕЛИ ЭТО ТАК?». Но потом это стало очевидным явлением.

ПРИМЕР:

На рисунке 3 ниже у вас есть 9-вольтовая батарея, подключенная к трем резисторам последовательно. Если вы измеряете напряжения на компонентах — сумма их составит 9 вольт.

Рис. 3.

Рис. 3.

Vr1 + Vr2 + Vr3 = 9 Вольт

Как это помогает вам понимать и читать принципиальные схемы?

Ну, часто у вас есть компоненты в цепи, которые, как вы знаете, имеют определенное падение напряжения.

Например: светодиод с прямым напряжением 2 В будет иметь падение напряжения 2 В, когда он горит (рисунок 4).

Рис. 4

Рис. 4

Итак, если у вас есть такой светодиод в цепи с резистором и батарея 9 В питает цепь, вы знаете это:

Резистор будет иметь падение напряжения 7 В (9 В минус 2 В равно 7 В).

Зная падение напряжения на резисторе, давайте посчитаем ток через резистор.

Просто используйте закон Ома:

• Ток = напряжение / сопротивление
• Ток = 7В / 350 Ом
• Ток = 0,02А

Итак, просто зная закон напряжения Кирхгофа, вы можете обнаружить, что ток в цепи составляет 20 мА.

Законы кирхгофа 1 и 2 примеры. Первый закон кирхгофа

Большое количество электрических цепей на практике являются сложными. Однако в цепь любого уровня сложности имеет элементы двух простейших видов. Это узлы и замкнутые контуры. Узел — это любая точка разветвления цепи, в которой сошлось три или более проводников, по которым текут токи.

Второе правило (закон) Кирхгофа является следствием обобщенного закона Ома. Так, если в изолированной замкнутой цепи есть один источник ЭДС, то сила тока в цепи будет такой, что сумма падения напряжения на внешнем сопротивлении и внутреннем сопротивлении источника будет равна сторонней ЭДС источника. Если источников ЭДС несколько, то берут их алгебраическую сумму. Знак ЭДС выбирается положительным, если при движении по контуру в положительном направлении первым встречается отрицательный полюс источника. (За положительное направление обхода контура принимают направление обхода цепи либо по часовой стрелке, либо против нее).

Формулировка второго закона Кирхгофа

Произведение алгебраической величины силы тока (I) на сумму вешних и внутренних сопротивлений всех участков замкнутого контура равно сумме алгебраических значений сторонних ЭДС () рассматриваемого контура:

Каждое произведение определяет разность потенциалов, которая существовала бы между концами соответствующего участка, если бы ЭДС в нем была равно нулю.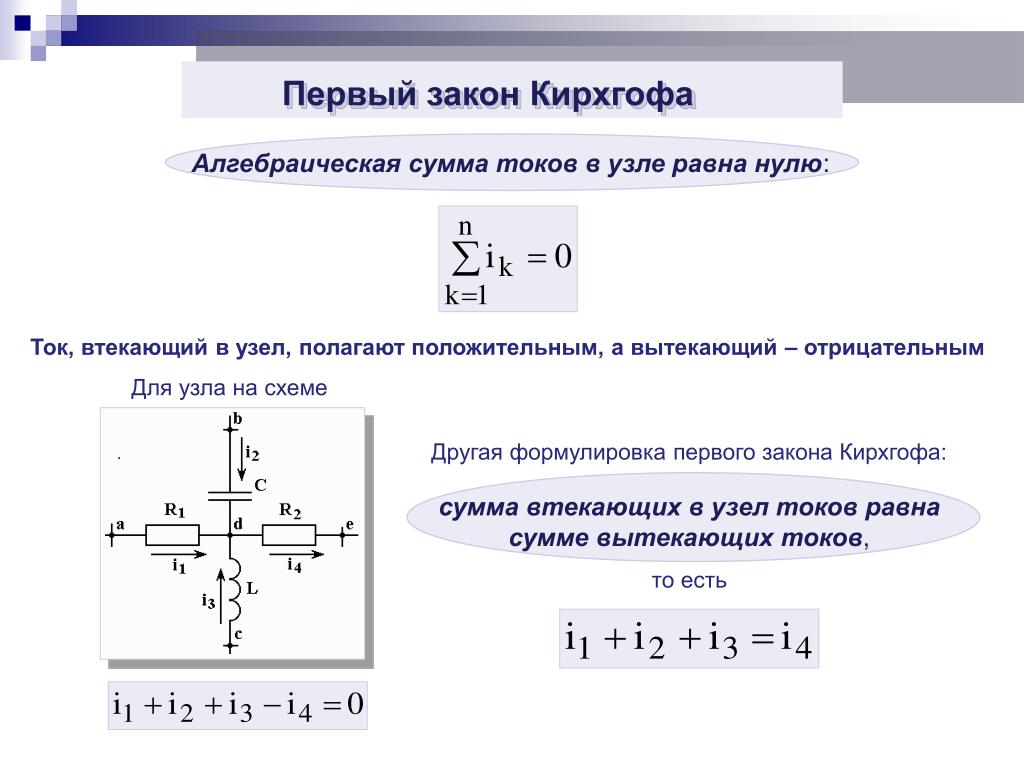 Величину называют падением напряжения, которое вызывается током.

Второй закон Кирхгофа иногда формулируют следующим образом:

Для замкнутого контура сумма падений напряжения есть сума ЭДС в рассматриваемом контуре.

Правила Кирхгофа служат для того, чтобы составить систему уравнений, позволяющих найти силу тока для сложной цепи. Направление положительного обхода выбирают для всех контуров одинаковым. При составлении уравнений, используя правила Кирхгофа необходимо внимательно следить за расстановкой знаков токов и ЭДС.

Система уравнений, которая получается при использовании первого и второго закона Кирхгофа является полной и дает возможность отыскать все токи. При составлении уравнений, используя правила Кирхгофа, надо следить за тем, чтобы новое уравнение имело хотя бы одну величину, которая еще не вошла в предыдущие уравнения. Кроме того, необходимо, чтобы система уравнений имела число уравнений равное количеству неизвестных.

Второй закон Кирхгофа следует из того, что электрическое напряжение по замкнутому контуру равно нулю, то есть это правило является следствием основного свойства электростатического поля, которое заключается в том, что работа поля при движении заряда по замкнутой траектории равна нулю.

Примеры решения задач

ПРИМЕР 1

Задание	Примените второе правило Кирхгофа для рис.1 и запишите уравнения рассмотрев контуры: ABDCA; ABFEA
Решение	Направление обхода контура зададим при помощи последовательности букв в его обозначении. Так для контура имеем направление обхода по часовой стрелке. Рассматривая эту цепь в дальнейшем направления обхода контуров изменять нельзя. Положительными будем считать токи, которые совпадают с направлением обхода контура. Для контура со знаком плюс будут во второе правило Кирхгофа входить ток: , со знаком минус ток . В соответствии с правилом выбора знака ЭДС, сформулированном в теоретической части, в рассматриваемый контур и будут положительными. Уравнение, соответствующее второму правилу Кирхгофа для контура запишем как: где и — внутренние сопротивления источников ЭДС; и — внешние сопротивления. Рассмотрим контур . Ток согласно избранным нами направлениям будет положительным во втором законе Кирхгофа, то — отрицательным. ЭДС войдет в уравнение со знаком минус. Получим:
Ответ	Для контура . Для контура получили:

ПРИМЕР 2

Задание

Пусть n одинаковых источников ЭДС соединены последовательно и замкнуты на внешнюю цепь (рис.2). Чему равна ЭДС данной цепи, если ЭДС каждого источника равна , внутренне сопротивление каждого источника ? Сопротивление внешней цепи R.

В цепях, состоящих из последовательно соединенных источника и приемника энергии, соотношения между током, ЭДС и сопротивлением всей цепи или, между напряжением и сопротивлением на каком-либо участке цепи определяется законом Ома .

На практике в цепях, токи, от какой-либо точки, идут по разным путям.
Точки, где сходятся несколько проводников, называются узлами, а участки цепи, соединяющие два соседних узла, ветвями.

В замкнутой электрической цепи ни в одной ее точке не могут скапливаться электрические заряды так, как это вызвало бы изменение потенциалов точек цепи. Поэтому электрические заряды притекающие к какому-либо узлу в единицу времени, равны зарядам, утекающим от этого узла за ту же единицу.
Разветвлённая цепь.
В узлеА цепь разветвляется на четыре ветви, которые сходятся в узел В .

Обозначим токи в неразветвленной части цепи —I , а в ветвях соответственно

I1 , I2 , I3 , I4 .

У этих токов в такой цепи будет соотношение:

I = I1+I2+I3+I4;

Cумма токов, подходящих к узловой точке электрической цепи,
равна сумме токов, уходящих от этого узла.

При параллельном соединении резисторов ток проходит по четырем направлениям, что уменьшает общее сопротивление или увеличивает общую проводимость цепи, которая равна сумме проводимостей ветвей.

Обозначим силу тока в неразветвленной ветви буквойI .
Силу тока в отдельных ветвях соответственно I1 , I2 , I3 и I4 .
Напряжение между точками A и B — U .
Общее сопротивление между этими точками — R .

По закону Ома напишем:

I = U/R ; I1 = U/R1 ; I2 = U/R2 ; I3 = U/R3 ; I4 = U/R4 ;

Согласно первому закону Кирхгофа:

I = I1+I2+I3+I4 ; или U/R = U/R1+U/R2+U/R3+U/R4 .

Сократив обе части полученного выражения на U получим:

1/R = 1/R1+1/R2+1/R3+1/R4 , что и требовалось доказать.

Cоотношение для любого числа параллельно соединенных резисторов.
В случае, если в цепи содержится два параллельно соединенных резистора
R1 и R2 , то можно написать равенство:

1/R =1/R1+1/R2 ;

Из этого равенства найдем сопротивление R , которым можно заменить два параллельно соединенных резистора:

Полученное выражение имеет большое практическое применение.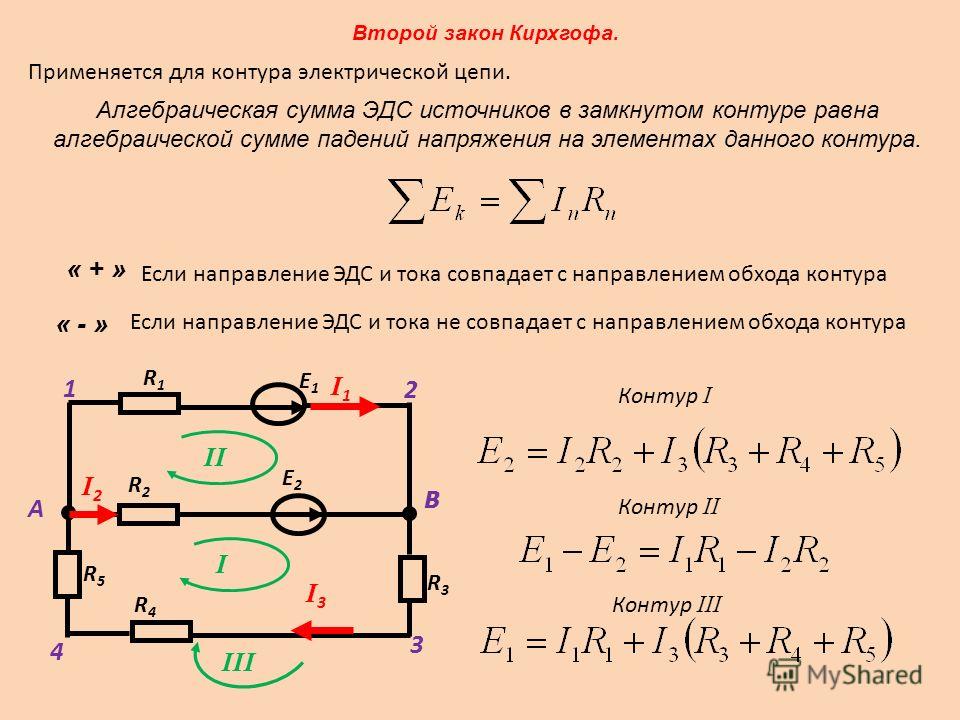
Благодаря этому закону производятся расчёты электрических цепей.

Второй закон Кирхгофа

В замкнутом контуре электрической цепи сумма всех эдс равна
сумме падения напряжения в сопротивлениях того же контура.

E1 + E2 + E3 +…+ En = I1R1 + I2R2 + I3R3 +…+ InRn . При составлении уравнений выбирают направление обхода цепи и произвольно задаются направлениями токов.

Если в электрической цепи включены два источника энергии, эдс которых совпадают по направлению, т. е. согласно изо1, то эдс всей цепи равна сумме эдс этих источников,
т. е.
E = E1+E2 .

Если же в цепь включено два источника, эдс которых имеют противоположные направления, т. е. включены встречно изо2, то общая эдс цепи равна разности эдс этих источников
Е = Е1-Е2 .

Благодаря этим законам производятся расчёты электрических цепей.
Существует несколько методов расчёта, один из них «Метод узловых напряжений»

Два приема, которые применяют для упрощения процесса составления уравнений, необходимых при расчетах сложных разветвленных цепей постоянного тока называют законами (вернее было бы сказать правилами) Кирхгофа. Прежде чем перейти к самим правила Кирхгофа введем два необходимых определения.

Разветвлёнными цепями названы цепи, которые имеют несколько замкнутых контуров, несколько источников электродвижущей силы (ЭДС).

Узлом разветвлённой цепи называют точку, в которой сходятся три или более проводников с токами.

Первый закон (правило) Кирхгофа, простыми словами

Первое правило Кирхгофа называют правилом узлов, так как оно касается сил токов в узах цепи. Словесно первый закон Кирхгофа формулируют следующим образом: Алгебраическая сумма сил токов в узле равна нулю. В виде формулы это правило запишем как:

С каким знаком сила тока будет входить в сумму (1), зависит от произвольного выбора. Но при этом следует считать, что все входящие в узел токи имеют одинаковые знаки, а все исходящие из узла токи имеют противоположные входящим, знаки. Пусть все входящие токи мы примем за положительные, тогда все исходящие их этого узла токи будут отрицательными. Если направления токов изначально не заданы, то их задают произвольно. Если при расчетах получено, что сила тока отрицательна, значит, что верное направление тока является противоположным тому, которое предполагали.

Первый закон Кирхгофа является следствием закона сохранения заряда. Если в цепи текут только постоянные токи, то нет в этой цепи точек, которые накапливали бы заряд. Иначе токи не были бы постоянными.

Первый закон Кирхгофа дает возможность составить независимое уравнение, при наличии в цепи k узлов.

Второй закон (правило) Кирхгофа, простыми словами

Второй закон Кирхгофа относят к замкнутым контурам, поэтому его называют правилом контуров. Согласно этому правилу суммы произведений алгебраических величин сил тока на внешние и внутренние сопротивления всех участков замкнутого контура равны алгебраической сумме величин сторонних ЭДС (), входящих в рассматриваемый контур. В виде формулы второй закон Кирхгофа запишем как:

где величину часто называют падением напряжения; N — число рассматриваемых участков избранного контура. При использовании второго правила Кирхгофа важно помнить о направлении обхода контура. Как это делается? Произвольно выберем направление обхода рассматриваемого в задаче контура (по часовой стрелке или против нее). В случае совпадения направления обхода контура с направлением силы тока в рассматриваемом элементе, величина входит в (2) со знаком плюс. ЭДС войдет в сумму правой части выражения (2) со знаком плюс, если при движении вдоль контура, в соответствии с избранным направлением обхода первым мы встречаем отрицательный полюс источника ЭДС.

Используя второе правило Кирхгофа можно получить независимые уравнения для тех контуров цепи, которые не получены наложением уже описанных контуров. Количестов независимых контуров (n) равно:

где p — количество ветвей в цепи; k — число узлов.

Количество независимых уравнений, которые дадут оба правила Кирхгофа равно (s):

Делаем вывод о том, что число независимых уравнений будет равно числу разных токов в исследуемой цепи.

Второе правило Кирхгофа — следствие закона Ома. В принципе любую цепь можно рассчитать, применяя только закон Ома и закон сохранения заряда. Правила Кирхгофа являются всего лишь упрощающими приемами для решения задач, рассматривающих цепи постоянного тока.

Используя правила Кирхгофа для составления уравнений необходимо внимательно следить за расстановкой знаков токов и ЭДС.

Первое и второе правила Кирхгофа дают метод расчета цепи, то есть используя их можно найти все токи в цепи, если известны все ЭДС и сопротивления, в том числе и внутренние сопротивления источников.

Примеры решения задач

ПРИМЕР 1

Задание	Как следует записать уравнение для токов, используя первое правило Кирхгофа для узла А, изображенного на рис.1
Решение	Прежде чем применять первое правило Кирхгофа определим для себя, что положительными будут токи, которые входят в узел А, тогда выходящие из этого узла токи мы должны будем записать в первом правиле Кирхгофа со знаком минус. Из рис. 1 в узел А входят токи: Из узла А выходят токи: Тогда согласно правилу узлов имеем:
Ответ

ПРИМЕР 2

Задание	Составьте систему независимых уравнений, используя правила Кирхгофа, которая позволит найти все токи в цепи, представленной на рис.2, если известны все ЭДС и все сопротивления (они указаны на рисунке)?
Решение	Направления токов выберем произвольно, обозначим их на рис.1. Пусть через сопротивление течет ток . На рис.2 видно, что в нашей цепи два узла. Это точки A и С. Запишем первое правило Кирхгофа для узла А:

При расчете электрических цепей нам часто приходится встречаться с цепями, которые образуют замкнутые контуры. В состав таких контуров, помимо сопротивлений, могут входить еще электродвижущие силы, то есть источники напряжений. На рисунке 1 представлен участок сложной электрической цепи. Задана полярность всех (э. д. с.). Произвольно выбираем положительные направления токов. Обходим контур от точки А в произвольном направлении, например по часовой стрелке. Рассмотрим участок АБ . На этом участке происходит падение потенциала (ток идет от точки с высшим потенциалом к точке с низшим потенциалом).

На участке АБ :

φ А + E 1 – I 1 × r 1 = φ Б .

На участке БВ :

φ Б – E 2 – I 2 × r 2 = φ В .

На участке ВГ :

φ В – I 3 × r 3 + E 3 = φ Г .

На участке ГА :

φ Г – I 4 × r 4 = φ А .

Складывая почленно четыре приведенных уравнения, получим:

φ А + E 1 – I 1 × r 1 + φ Б – E 2 – I 2 × r 2 + φ В – I 3 × r 3 + E 3 + φ Г – I 4 × r 4 = φ Б + φ В + φ Г + φ А

E 1 – I 1 × r 1 – E 2 – I 2 × r 2 – I 3 × r 3 + E 3 – I 4 × r 4 = 0.

Перенеся произведения I × r в правую часть, получим:

E 1 – E 2 + E 3 = I 1 × r 1 + I 2 × r 2 + I 3 × r 3 + I 4 × r 4 .

В общем виде

Это выражение представляет собой . Формула второго закона Кирхгофа показывает, что во всяком замкнутом контуре алгебраическая сумма э. д. с. равна алгебраической сумме падений напряжений. Бывают случаи, когда в замкнутом контуре отсутствуют источники э. д. с., тогда применимо другое определение второго закона Кирхгофа – алгебраическая сумма падений равна нулю.

Видео 1. Второй закон Кирхгофа

Рассмотрим простой замкнутый контур (рисунок 2).

Рисунок 2. Простой замкнутый контур

По второму закону Кирхгофа

E = I × r 0 + I × r = I × (r 0 + r ),

Имеем три уравнения с тремя неизвестными. Решая их, находим величину и направление токов. Подставляя значение тока I 3 из уравнения (3) в уравнение (1), получим:

6 = 2 × I 1 + 5 × I 1 + 5 × I 2 ;

Сложим уравнения для двух контуров почленно:

(6 = 7 × I 1 + 5 × I 2) + (2 = I 1 – 2 × I 2)

(12 = 14 × I 1 + 10 × I 2) + (10 = 5 × I 1 – 10 × I 2).

Сложив два последних уравнения, имеем:

22 = 19 × I 1 , откуда I 1 = 1,156 А,

подставляем значение I 1 в уравнение (1):

6 = 2 × 1,156 + 5 × I 3 ,

Подставляем значение I 1 в уравнение (2):

2 = 1,156 – 2 × I 2 ,

Знак минус показывает, что действительное направление тока I 2 обратно принятому нами направлению.

Правило токов Кирхгофа (первый закон Кирхгофа)

Добавлено 15 января 2021 в 07:01

Сохранить или поделиться

Что такое правило токов Кирхгофа (первый закон Кирхгофа)?

Закон Кирхгофа, часто называемый правилом токов Кирхгофа, гласит, что «алгебраическая сумма всех токов, входящих и выходящих из узла, равна нулю».

Этот закон используется для описания того, как заряд входит и покидает точку соединения (узел) проводов.

Вооружившись этой информацией, давайте теперь рассмотрим пример применения этого закона на практике, почему он важен и как он был разработан.

Обзор параллельной цепи

Давайте подробнее рассмотрим последний пример параллельной схемы:

Рисунок 1 – Пример параллельной схемы

Решение для всех значений напряжений и токов в этой схеме:

Рисунок 2 – Значения напряжений и токов

На данный момент мы знаем значения токов каждой ветви и полного тока в цепи. Мы знаем, что полный ток в параллельной цепи должен равняться сумме токов ветвей, но в данной цепи происходит нечто большее. Взглянув на токи в каждой точке (узле) соединения проводов в цепи, мы должны увидеть что-то еще:

Рисунок 3 – Пример параллельной схемы

Токи, входящие в узел и выходящие из него

В каждом узле положительной «шины» (провод 1-2-3-4) у нас есть отделение тока от основного потока к резистору каждой последующей ветви. В каждом узле отрицательной «шины» (провод 8-7-6-5) у нас есть объединение токов из каждой последующей ветви вместе, чтобы сформировать основной поток. Этот факт должен быть довольно очевиден, если взять для аналогии контур водопровода с узлами, действующими как тройники, в которых происходит разделение или объединение водяного потока с основным трубопроводом, когда он движется от выхода водяного насоса обратно в резервуар.

Если мы внимательно рассмотрим один конкретный узел «тройник», такой как узел 6, то увидим, что токи, входящие в узел, равны по величине току, выходящему из узла:

Рисунок 4 – Узел

Сверху и справа у нас есть два тока, входящие в соединение проводов, обозначенное как узел 6. Слева у нас есть один ток, выходящий из узла, равный по величине сумме двух входящих токов. Если обратиться к аналогии с водопроводом: пока в трубопроводе нет утечек, поток, поступающий в фитинг, должен также выходить из него. Это верно для любого узла («фитинга»), независимо от того, сколько потоков входит или выходит. Математически мы можем выразить это общее соотношение следующим образом:

I_{входящий} = I_{выходящий}

Правило токов Кирхгофа (первый закон Кирхгофа)

Кирхгоф решил выразить его в несколько иной форме (хотя и математически эквивалентной), назвав это правилом токов Кирхгофа:

I_{входящий} + (–I_{выходящий}) = 0

Кратко говоря, закон токов Кирхгофа гласит:

«Алгебраическая сумма всех токов, входящих и выходящих из узла, равна нулю»

То есть, если мы присвоим каждому току математический знак (полярность), обозначающий, входит ли он (+) или выходит (-) из узла, мы можем сложить их вместе, чтобы гарантированно получить в сумме ноль.

Взяв наш пример узла (номер 6), мы можем определить величину тока, выходящего слева, выразив уравнение первого закона Кирхгофа с этим током в качестве неизвестного значения:

I₂ + I₃ + I = 0

2 мА + 3 мА + I = 0

Решаем уравнение для I…

I = -2 мА — 3 мА

I = -5 мА

Отрицательный (-) знак в значении 5 миллиампер говорит нам, что ток выходит из узла, в отличие от токов в 2 и 3 миллиампер, которые оба должны быть положительными (и, следовательно, входить в узел). Неважно, обозначает ли отрицательное или положительное значение входящий или выходящий ток, если для противоположных направлений используются противоположные знаки, и мы остаемся последовательными в наших обозначениях. Правило токов Кирхгофа (первый закон Кирхгофа) будет работать.

Вместе законы напряжений и токов Кирхгофа представляют собой прекрасную пару инструментов, полезных при анализе электрических цепей. Их полезность станет еще более очевидной в следующей главе («Анализ цепей»), но достаточно сказать, что эти законы заслуживают того, чтобы человек, изучающий электронику, запомнил не меньше их, чем закон Ома.

Резюме

• Правило токов Кирхгофа (первый закон Кирхгофа): «Алгебраическая сумма всех токов, входящих и выходящих из узла, равна нулю»

Оригинал статьи:

Теги

Анализ цепейДля начинающихОбучениеПараллельная цепьПолярностьПравило токов Кирхгофа / Первый закон КирхгофаЭлектрический ток

Сохранить или поделиться

правил Кирхгофа | Физика

Найдите токи, протекающие в цепи, показанной на Рисунке 5.

Рис. 5. Эта схема аналогична схеме на рис. 1, но указаны сопротивления и ЭДС. (Каждая ЭДС обозначена буквой E.) Токи в каждой ветви помечены и предполагается, что они движутся в показанных направлениях. В этом примере для нахождения токов используются правила Кирхгофа.

Стратегия

Эта схема достаточно сложна, поэтому токи не могут быть найдены с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа.Токи обозначены на рисунке I ₁ , I ₂ и I ₃ , и были сделаны предположения об их направлениях. Места на схеме обозначены буквами от a до h. В решении мы будем применять правила соединения и петли, ища три независимых уравнения, которые позволят нам решить три неизвестных тока.

Решение

Начнем с применения правила Кирхгофа первого или перекрестка в точке а.Это дает

I ₁ = I ₂ + I ₃ ,

, так как I ₁ течет в стык, а I ₂ и I ₃ вытекает. Применение правила соединения в e дает точно такое же уравнение, так что новая информация не получается. Это одно уравнение с тремя неизвестными — необходимы три независимых уравнения, поэтому необходимо применять правило цикла.Теперь рассмотрим цикл abcdea. Двигаясь от a к b, мы проходим R ₂ в том же (предполагаемом) направлении тока I ₂ , поэтому изменение потенциала составляет — I ₂ R ₂ . Затем, переходя от b к c, мы переходим от — к +, так что изменение потенциала равно + ЭДС ₁ . Прохождение внутреннего сопротивления r ₁ от c до d дает — I ₂ r ₁ .Завершение цикла путем перехода от d к a снова проходит через резистор в том же направлении, что и его ток, давая изменение потенциала — I ₁ R ₁ . Правило цикла гласит, что изменения в потенциале равны нулю. Таким образом,

— I ₂ R ₂ + ЭДС ₁ — I ₂ r ₁ — I ₁ R ₁ = — I ₂ ( R ₂ + r ₁ ) + ЭДС ₁ — I ₁ R ₁ = 0.

Подставляя значения из принципиальной схемы для сопротивлений и ЭДС и отменяя единицу измерения ампер, получаем

−3 I ₂ + 18 — 6 I ₁ = 0.

Теперь, применяя правило цикла к aefgha (мы могли бы также выбрать abcdefgha), аналогично дает

+ I ₁ R ₁ + I ₃ R ₃ + I ₃ r ₂ — ЭДС ₂ = + I ₁ R ₁ + I ₃ ( R ₃ + r ₂ ) — ЭДС ₂ = 0.

Обратите внимание, что знаки меняются местами по сравнению с другим циклом, потому что элементы перемещаются в противоположном направлении. С введенными значениями это становится

+6 I ₁ + 2 I ₃ — 45 = 0.

Этих трех уравнений достаточно для решения трех неизвестных токов. Сначала решите второе уравнение относительно I ₂ :

I ₂ = 6-2 I ₁ .

Теперь решите третье уравнение относительно I ₃ :

I ₃ = 22,5 — 3 I ₁ .

Подстановка этих двух новых уравнений в первое позволяет нам найти значение для I ₁ :

I ₁ = I ₂ + I ₃ = (6−2 I ₁ ) + (22,5− 3 I ₁ ) = 28,5 — 5 Я ₁ .

Объединение терминов дает

6 I ₁ = 28,5 и

I ₁ = 4,75 А.

Подставляя это значение вместо I ₁ обратно в четвертое уравнение, получаем

I ₂ = 6 — 2 I ₁ = 6 — 9,50

I ₂ = −3,50 A.

Знак минус означает, что I ₂ течет в направлении, противоположном предполагаемому на рисунке 5.Наконец, подстановка значения I ₁ в пятое уравнение дает

I ₃ = 22,5 — 3 I ₁ = 22,5 — 14. 25

I ₃ = 8,25 А.

Обсуждение

В качестве проверки отметим, что действительно I ₁ = I ₂ + I ₃ . Результаты также можно было проверить, введя все значения в уравнение для цикла abcdefgha.

10.4: Правила Кирхгофа — Physics LibreTexts

Мы только что видели, что некоторые схемы можно анализировать, сводя схему к одному источнику напряжения и эквивалентному сопротивлению. Многие сложные схемы не могут быть проанализированы с помощью последовательно-параллельных методов, разработанных в предыдущих разделах. В этом разделе мы подробно рассмотрим использование правил Кирхгофа для анализа более сложных схем. Например, схема на рисунке \ (\ PageIndex {1} \) известна как многоконтурная схема , которая состоит из переходов.Соединение, также известное как узел, представляет собой соединение трех или более проводов. В этой схеме нельзя использовать предыдущие методы, потому что не все резисторы имеют четкую последовательную или параллельную конфигурацию, которую можно уменьшить. Попробуйте. Резисторы \ (R_1 \) и \ (R_2 \) включены последовательно и могут быть уменьшены до эквивалентного сопротивления. То же самое и с резисторами \ (R_4 \) и \ (R_5 \). Но что же тогда делать?

Несмотря на то, что эта схема не может быть проанализирована с использованием уже изученных методов, два правила анализа схемы могут использоваться для анализа любой схемы, простой или сложной.Правила известны как Правила Кирхгофа , в честь их изобретателя Густава Кирхгофа (1824–1887).

Теперь мы даем объяснения этих двух правил, за которыми следуют советы по их применению и рабочий пример, в котором они используются.

Первое правило Кирхгофа

Первое правило Кирхгофа (правило соединения ) применяется к заряду, входящему в соединение и выходящему из него (рисунок \ (\ PageIndex {2} \)). Как было сказано ранее, соединение или узел — это соединение трех или более проводов.Ток — это поток заряда, и заряд сохраняется; таким образом, любой заряд, попадающий в переход, должен вытекать.

Рисунок \ (\ PageIndex {2} \): Заряд должен сохраняться, поэтому сумма токов в переходе должна быть равна сумме токов на выходе.

Хотя это и является чрезмерным упрощением, можно провести аналогию с водопроводными трубами, соединенными в водопроводной разводке. Если провода на рисунке \ (\ PageIndex {2} \) были заменены водопроводными трубами и вода считалась несжимаемой, объем воды, текущей в соединение, должен быть равен объему воды, вытекающей из соединения.

Второе правило Кирхгофа

Второе правило Кирхгофа (правило петли ) применяется к разности потенциалов. Правило цикла сформулировано в терминах потенциала В , а не потенциальной энергии, но они связаны между собой, поскольку \ (U = qV \). В замкнутом контуре, какая бы энергия ни поступала от источника напряжения, энергия должна быть передана в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в цепь или из нее.Правило петли Кирхгофа гласит, что алгебраическая сумма разностей потенциалов, включая напряжение, подаваемое источниками напряжения и резистивными элементами, в любой петле должна быть равна нулю. Например, рассмотрим простой цикл без стыков, как на рисунке \ (\ PageIndex {3} \).

Рисунок \ (\ PageIndex {3} \): простой цикл без соединений. Правило петли Кирхгофа гласит, что алгебраическая сумма разностей напряжений равна нулю.

Схема состоит из источника напряжения и трех внешних нагрузочных резисторов.Ярлыки a , b , c и d служат в качестве ссылок и не имеют другого значения. Скоро станет очевидна полезность этих этикеток. Цепь обозначается как Loop abcda , и метки помогают отслеживать разницу напряжений при перемещении по цепи. Начните с точки a и двигайтесь к точке b . Напряжение источника напряжения добавляется к уравнению и вычитается падение потенциала резистора \ (R_1 \).От точки b до c падение потенциала на \ (R_2 \) вычитается. Из c до d вычитается падение потенциала на \ (R_3 \). От точек d до a ничего не делается, потому что нет компонентов.

На рисунке \ (\ PageIndex {4} \) показан график напряжения при перемещении по контуру. Напряжение увеличивается при прохождении через батарею, тогда как напряжение уменьшается при прохождении через резистор. Падение потенциала , или изменение электрического потенциала, равно току через резистор, умноженному на сопротивление резистора.Поскольку провода имеют незначительное сопротивление, напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.

Рисунок \ (\ PageIndex {4} \): график напряжения при движении по цепи. Напряжение увеличивается, когда мы пересекаем батарею, и уменьшается, когда мы пересекаем каждый резистор. Поскольку сопротивление провода довольно мало, мы предполагаем, что напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.

Тогда правило петли Кирхгофа утверждает

\ [V — IR_1 — IR_2 — IR_3 = 0.\]

Уравнение контура можно использовать для определения тока в контуре:

\ [I = \ frac {V} {R_1 + R_2 + R_3} = \ frac {12.00 \, V} {1.00 \, \ Omega + 2.00 \, \ Omega + 3.00 \, \ Omega} = 2.00 \, A . \]

Этот цикл можно было бы проанализировать с помощью предыдущих методов, но мы продемонстрируем мощь метода Кирхгофа в следующем разделе.

Применение правил Кирхгофа

Применяя правила Кирхгофа, мы генерируем набор линейных уравнений, которые позволяют нам находить неизвестные значения в схемах.Это могут быть токи, напряжения или сопротивления. Каждый раз, когда применяется правило, оно создает уравнение. Если независимых уравнений столько же, сколько неизвестных, то проблема может быть решена.

Использование метода анализа Кирхгофа требует нескольких шагов, перечисленных в следующей процедуре.

Стратегия решения проблем: правила Кирхгофа

1. Обозначьте точки на принципиальной схеме строчными буквами a , b , c ,….Эти ярлыки просто помогают сориентироваться.
2. Найдите соединения в цепи. Соединения — это точки соединения трех или более проводов. Обозначьте каждое соединение токами и направлениями в него и из него. Убедитесь, что по крайней мере один ток направлен на соединение, а по крайней мере один ток выходит из соединения.
3. Выбрать петли в схеме. Каждый компонент должен содержаться по крайней мере в одном цикле, но компонент может содержаться более чем в одном цикле.
4. Примените правило соединения. Опять же, некоторые стыки не следует включать в анализ. Вам нужно использовать достаточно узлов только для включения каждого тока.
5. Примените правило цикла. Используйте карту на рисунке \ (\ PageIndex {5} \).

Рисунок \ (\ PageIndex {5} \): Каждый из этих резисторов и источников напряжения проходит от до до до . (a) При перемещении через резистор в том же направлении, что и ток, вычтите падение потенциала. (b) При перемещении через резистор в направлении, противоположном току, добавьте падение потенциала.(c) При перемещении источника напряжения от отрицательного вывода к положительному, добавьте падение потенциала. (d) При перемещении через источник напряжения от положительной клеммы к отрицательной вычтите падение потенциала.

Давайте подробнее рассмотрим некоторые этапы этой процедуры. При размещении переходов в цепи не обращайте внимания на направление токов. Если направление потока тока неочевидно, выбора любого направления достаточно, если хотя бы один ток направлен в соединение и хотя бы один ток выходит из соединения.Если стрелка находится в направлении, противоположном обычному потоку тока, результат для рассматриваемого тока будет отрицательным, но ответ все равно будет правильным.

Количество узлов зависит от схемы. Каждый ток должен быть включен в узел и, таким образом, включен по крайней мере в одно уравнение соединения. Не включайте узлы, которые не являются линейно независимыми, то есть узлы, содержащие одинаковую информацию.

Рассмотрим рисунок \ (\ PageIndex {6} \). В этой цепи два перехода: переход b и переход e .Точки a , c , d и f не являются перекрестками, потому что стык должен иметь три или более соединений. Уравнение для соединения b — \ (I_1 = I_2 + I_3 \), а уравнение для соединения e — \ (I_2 + I_3 = I_1 \). Это эквивалентные уравнения, поэтому необходимо оставить только одно из них.

Рисунок \ (\ PageIndex {6} \): На первый взгляд, эта схема содержит два соединения, соединение b и соединение e , но следует рассматривать только один, поскольку их уравнения соединения эквивалентны.

При выборе петель в схеме вам необходимо достаточное количество петель, чтобы каждый компонент был покрыт один раз, без повторения петель. На рисунке \ (\ PageIndex {7} \) показаны четыре варианта циклов для решения примерной схемы; варианты (a), (b) и (c) имеют достаточное количество циклов для полного решения схемы. Вариант (d) отражает больше петель, чем необходимо для решения схемы.

Рисунок \ (\ PageIndex {7} \): Панели (a) — (c) достаточно для анализа схемы. В каждом случае два показанных контура содержат все элементы схемы, необходимые для полного решения схемы.На панели (d) показаны три использованных контура, что больше, чем необходимо. Любые две петли в системе будут содержать всю информацию, необходимую для решения схемы. Добавление третьего цикла дает избыточную информацию.

Рассмотрим схему на рисунке \ (\ PageIndex {8a} \). Давайте проанализируем эту схему, чтобы найти ток через каждый резистор. Сначала промаркируйте схему, как показано в части (b).

Рисунок \ (\ PageIndex {8} \): (a) Многоконтурная схема. (b) Пометьте цепь, чтобы облегчить ориентацию.

Далее определяем перекрестки.В этой схеме точки b и e имеют по три соединенных провода, что делает их соединениями. Начните применять правило соединения Кирхгофа \ (\ left (\ sum I_ {in} = \ sum I_ {out} \ right) \), рисуя стрелки, представляющие токи, и маркируя каждую стрелку, как показано на рисунке \ (\ PageIndex {9 } \). Соединение b показывает, что \ (I_1 = I_2 + I_3 \), а соединение e показывает, что \ (I_2 + I_3 = I_1 \). Поскольку соединение e дает ту же информацию, что и соединение b , ее можно не принимать во внимание.Эта схема имеет три неизвестных, поэтому для ее анализа нам понадобятся три линейно независимых уравнения.

Рисунок \ (\ PageIndex {9} \): (a) Эта схема имеет два соединения, помеченных b и e, но в анализе используется только узел b. (b) Обозначенные стрелки представляют токи в переходах и на выходе из них.

Далее нам нужно выбрать петли. На рисунке \ (\ PageIndex {10} \) контур abefa включает источник напряжения \ (V_1 \) и резисторы \ (R_1 \) и \ (R_2 \). Цикл начинается в точке a , затем проходит через точки b , e и f , а затем возвращается к точке a .Второй контур, Loop ebcde , начинается в точке e и включает резисторы \ (R_2 \) и \ (R_3 \), а также источник напряжения \ (V_2 \).

Рисунок \ (\ PageIndex {10} \): Выберите петли в схеме.

Теперь мы можем применить правило цикла Кирхгофа, используя карту на рисунке \ (\ PageIndex {5} \). Начиная с точки a и двигаясь к точке b , резистор \ (R_1 \) пересекается в том же направлении, что и ток \ (I_1 \), поэтому падение потенциала \ (I_1R_1 \) вычитается.Двигаясь от точки b к точке e , резистор \ (R_2 \) пересекается в том же направлении, что и ток \ (I_2 \), поэтому падение потенциала \ (I_2R_2 \) вычитается. При перемещении от точки e к точке f источник напряжения \ (V_1 \) пересекается от отрицательной клеммы к положительной клемме, поэтому добавляется \ (V_1 \). Между точками f и a нет компонентов. Сумма разностей напряжений должна равняться нулю:

\ [Петля \, abefa: \, -I_1R_1 — I_2R_2 + V_1 = 0 \ или \, V_1 = I_1R_1 + I_2R_2.\]

Наконец, проверяем цикл ebcde . Мы начинаем с точки e и переходим к точке b , пересекая \ (R_2 \) в направлении, противоположном текущему потоку \ (I_2 \). Потенциальное падение \ (I_2R_2 \) добавлено. Затем мы пересекаем \ (R_3 \) и \ (R_4 \) в том же направлении, что и текущий поток \ (I_3 \), и вычитаем потенциальные падения \ (I_3R_3 \) и \ (I_3R_4 \). Обратите внимание, что ток через резисторы \ (R_3 \) и \ (R_4 \) одинаков, потому что они соединены последовательно. Наконец, источник напряжения пересекается с положительной клеммы на отрицательную, а источник напряжения \ (V_2 \) вычитается.Сумма этих разностей напряжений равна нулю и дает уравнение контура

\ [Петля \, ebcde: \, I_2R_2 — I_3 (R_3 + R_4) — V_2 = 0. \]

Теперь у нас есть три уравнения, которые мы можем решить относительно трех неизвестных.

\ [\ text {Перекресток b:} \, I_1 — I_2 — I_3 = 0. \ label {eq1} \]

\ [\ text {Петля abefa:} \, I_1R_1 + I_2R_2 = V_1. \ label {eq2} \]

\ [\ text {Loop ebcde:} \, I_2R_2 — I_3 (R_3 + R_4) = V_2. \ label {eq3} \]

Чтобы решить три уравнения для трех неизвестных токов, начните с исключения тока \ (I_2 \).Сначала добавьте уравнение \ ref {eq1} times \ (R_2 \) к уравнению \ ref {eq2}. Результатом будет уравнение \ ref {eq4}:

.

\ [(R_1 + R_2) I_1 — R_2I_3 = V_1. \]

\ [6 \, \ Omega I_1 — 3 \ Omega I_3 = 24 \, V. \ label {eq4} \]

Затем вычтите уравнение \ ref {eq3} из уравнения \ ref {eq2}. Результатом будет уравнение \ ref {eq5}:

.

\ [I_1R_1 + I_3 (R_3 + R_4) = V_1 — V_2. \]

\ [3 \ Omega I_1 + 7 \ Omega I_3 = -5 \, V. 2R_4 = 130 \, W.\ nonumber \]

Обратите внимание, что решение для текущего \ (I_3 \) отрицательно. Это правильный ответ, но он предполагает, что стрелка, первоначально нарисованная при анализе соединений, имеет направление, противоположное направлению обычного тока. Мощность, отдаваемая вторым источником напряжения, составляет 58 Вт, а не −58 Вт.

Пример \ (\ PageIndex {1} \): Расчет тока с использованием правил Кирхгофа

Найдите токи, протекающие в цепи, показанной на рисунке \ (\ PageIndex {11} \).

Рисунок \ (\ PageIndex {11} \): Эта схема представляет собой комбинацию последовательной и параллельной конфигураций резисторов и источников напряжения.Эта схема не может быть проанализирована с использованием методов, обсуждаемых в «Электродвижущей силе», но может быть проанализирована с использованием правил Кирхгофа.

Стратегия

Эта схема достаточно сложна, поэтому токи не могут быть найдены с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. На рисунке токи обозначены \ (I_1, \, I_2 \) и \ (I_3 \), и были сделаны предположения об их направлениях. Места на схеме обозначены буквами от до до h .В решении мы применяем правила соединения и петли, ища три независимых уравнения, которые позволят нам решить три неизвестных тока.

Решение

Применение правил соединения и петли дает следующие три уравнения. У нас есть три неизвестных, поэтому требуется три уравнения.

\ [Перекресток \, c: \, I_1 + I_2 = I_3. \]

\ [Петля \, abcdefa: \, I_1 (R_1 + R_4) — I_2 (R_2 + R_5 + R_6) = V_1 — V_3. \]

\ [Петля \, cdefc: \, I_2 (R_2 + R_5 + R_6) + I_3R_3 = V_2 + V_3.\]

Упростите уравнения, поместив неизвестные в одну сторону уравнений.

\ [Перекресток \, c: \, I_1 + I_2 — I_3 = 0. \]

\ [Петля \, abcdefa: \, I_1 (3 \ Omega) — I_2 (8 \ Omega) = 0,5 \, V — 2,30 \, V. \]

\ [Цикл \, cdefc: \, I_2 (8 \ Omega) + I_3 (1 \ Omega) = 0,6 \, V + 2. 2R_1 = 0.2R_1 = 0,18 \, W. \]

\ [P_ {рассеивается} = 1.09 \, W. \]

\ [P_ {источник} = I_1V_1 + I_2V_3 + I_3V_2 = 0,10 \, + 0,69 \, W + 0,30 \, W = 1,09 \, W. \]

Подаваемая мощность равна мощности, рассеиваемой резисторами.

Упражнение \ (\ PageIndex {1} \)

При рассмотрении следующей схемы и мощности, подаваемой и потребляемой схемой, всегда ли источник напряжения обеспечивает питание схемы или может ли источник напряжения потреблять энергию?

Ответ

Схема может быть проанализирована с использованием правила петли Кирхгофа.2R_2 = 7,2 \, мВт. \)

Пример \ (\ PageIndex {2} \): расчет тока с использованием правил Кирхгофа

Найдите ток, протекающий в цепи, показанной на рисунке \ (\ PageIndex {12} \).

Рисунок \ (\ PageIndex {12} \): Эта схема состоит из трех резисторов и двух последовательно соединенных батарей. Обратите внимание, что батареи подключены с противоположной полярностью.

Стратегия

Эту схему можно проанализировать с помощью правил Кирхгофа. Есть только один цикл и нет узлов.Выберите направление тока. В этом примере мы будем использовать направление по часовой стрелке от точки a до точки b . Рассмотрим цикл abcda и воспользуйтесь рисунком \ (\ PageIndex {5} \), чтобы написать уравнение цикла. Обратите внимание, что согласно рисунку \ (\ PageIndex {5} \), батарея \ (V_1 \) будет добавлена, а батарея \ (V_2 \) вычтена.

Решение

Применение правила соединения дает следующие три уравнения. У нас есть одно неизвестное, поэтому требуется одно уравнение:

\ [Цикл \, abcda: \, -IR_1 -V_1 -IR_2 + V_2 -IR_3 = 0.\]

Упростите уравнения, поместив неизвестные в одну сторону уравнений. Используйте значения, указанные на рисунке.

\ [I (R_1 + R_2 + R_3) = V_2 — V_1. \]

\ [I = \ frac {V_2 — V_1} {R_1 + R_2 + R_3} = \ frac {24 \, V — 12 \, V} {10.0 \, \ Omega + 30.0 \, \ Omega + 10.0 \, \ Омега} = 0,20 \, А. \]

Значение

Мощность, рассеиваемая или потребляемая схемой, равна мощности, подаваемой в схему, но обратите внимание, что ток в батарее \ (V_1 \) течет через батарею от положительной клеммы к отрицательной клемме и потребляет энергию.2R_3 = 0,80 \, Вт \]

\ [P_ {V_1} = IV_1 = 2,40 \, W \]

\ [P_ {рассеивается} = 4.80 \, Вт \]

\ [P_ {источник} = IV_2 = 4.80 \, W \]

Подаваемая мощность равна мощности, рассеиваемой резисторами и потребляемой батареей \ (V_1 \).

Упражнение \ (\ PageIndex {2} \)

При использовании законов Кирхгофа вам необходимо решить, какие петли использовать, и направление тока, протекающего через каждую петлю. При анализе схемы в примере \ (\ PageIndex {2} \) было выбрано направление тока по часовой стрелке от точки a до точки b .Как бы изменились результаты, если бы направление тока было выбрано против часовой стрелки, от точки b до точки a ?

Ответ

Расчетный ток будет равен \ (I = -0.20 \, A \) вместо \ (I = 0.20 \, A \). Сумма рассеиваемой мощности и потребляемой мощности все равно будет равна подаваемой мощности.

Несколько источников напряжения

Для многих устройств требуется более одной батареи.Несколько источников напряжения, например батареи, могут быть подключены в последовательной конфигурации, параллельной конфигурации или их комбинации.

Последовательно положительная клемма одной батареи соединена с отрицательной клеммой другой батареи. Любое количество источников напряжения, в том числе аккумуляторы, можно подключать последовательно. Две последовательно соединенные батареи показаны на рисунке \ (\ PageIndex {13} \). Использование правила петли Кирхгофа для схемы в части (b) дает результат

\ [\ epsilon_1 — Ir_1 + \ epsilon_2 — Ir_2 — IR = 0, \]

\ [[(\ epsilon_1 + \ epsilon_2) — I (r_1 + r_2)] — IR = 0.\]

Рисунок \ (\ PageIndex {13} \): (a) Две батареи, соединенные последовательно с нагрузочным резистором. (b) Принципиальная схема двух батарей и нагрузочного резистора, каждая из которых моделируется как идеализированный источник ЭДС и внутреннее сопротивление.

Когда источники напряжения включены последовательно, их внутренние сопротивления можно складывать, а их ЭДС можно складывать вместе, чтобы получить общие значения. Последовательное соединение источников напряжения является обычным явлением, например, в фонариках, игрушках и других приборах.Обычно ячейки включены последовательно, чтобы обеспечить большую суммарную ЭДС. На рисунке \ (\ PageIndex {13} \) напряжение на клеммах равно

.

\ [V_ {терминал} = (\ epsilon_1 — Ir_1) + (\ epsilon_2 — Ir_2) = [(\ epsilon_1 + \ epsilon_2) — I (r_1 + r_2) — I (r_1 + r_2)] = (\ epsilon_1 + \ epsilon_2) + Ir_ {eq}. \]

Обратите внимание, что одинаковый ток I присутствует в каждой батарее, потому что они соединены последовательно. Недостаток последовательного соединения ячеек в том, что их внутренние сопротивления складываются.

Батареи соединены последовательно для увеличения напряжения, подаваемого в цепь. Например, светодиодный фонарик может иметь две батареи типа AAA, каждая с напряжением на клеммах 1,5 В, чтобы обеспечить 3,0 В для фонарика.

Любое количество батарей можно подключить последовательно. Для последовательно включенных батарей N напряжение на зажимах равно

Примечание

\ [V_ {терминал} = (\ epsilon_1 + \ epsilon_2 +… + \ Epsilon_ {N-1} + \ epsilon_N) — I (r_1 + r_2 +.№ р_и \]

Когда нагрузка подключается к источникам напряжения последовательно, как показано на рисунке \ (\ PageIndex {14} \), мы можем найти ток:

\ [(\ epsilon_1 — Ir_1) + (\ epsilon_2 — Ir_2) = IR, \]

\ [Ir_1 + Ir_2 + IR = \ epsilon_1 + \ epsilon_2, \]

\ [I = \ frac {\ epsilon_1 + \ epsilon_2} {r_1 + r_2 + R}. \]

Как и ожидалось, внутренние сопротивления увеличивают эквивалентное сопротивление.

Рисунок \ (\ PageIndex {14} \): две батареи подключаются последовательно к светодиодной лампе, как в фонарике.

Источники напряжения, такие как батареи, также можно подключать параллельно. На рисунке \ (\ PageIndex {15} \) показаны две батареи с одинаковыми ЭДС, соединенные параллельно и подключенные к сопротивлению нагрузки. Когда батареи подключаются параллельно, положительные клеммы соединяются вместе, отрицательные клеммы соединяются вместе, а сопротивление нагрузки подключается к положительной и отрицательной клеммам. Обычно источники напряжения, включенные параллельно, имеют идентичные ЭДС. В этом простом случае, поскольку источники напряжения подключены параллельно, общая ЭДС равна индивидуальной ЭДС каждой батареи.

Рисунок \ (\ PageIndex {15} \): (a) Две батареи подключаются параллельно к нагрузочному резистору. (b) На принципиальной схеме показана батарея как источник ЭДС и внутренний резистор. Два источника ЭДС имеют идентичные ЭДС (каждый помечен как \ (\ epsilon \)), соединенные параллельно, которые производят одинаковую ЭДС.

Рассмотрим анализ Кирхгофа схемы на рисунке \ (\ PageIndex {15b} \). {- 1} \]

Например, в некоторых грузовиках с дизельным двигателем параллельно используются две батареи на 12 В; они производят полную ЭДС 12 В, но могут обеспечивать больший ток, необходимый для запуска дизельного двигателя.

Таким образом, напряжение на клеммах последовательно соединенных батарей равно сумме индивидуальных ЭДС минус сумма внутренних сопротивлений, умноженная на ток. Когда батареи соединены параллельно, они обычно имеют равные ЭДС, а напряжение на клеммах равно ЭДС минус эквивалентное внутреннее сопротивление, умноженное на ток, где эквивалентное внутреннее сопротивление меньше, чем отдельные внутренние сопротивления. Аккумуляторы подключаются последовательно для увеличения напряжения на клеммах нагрузки.Аккумуляторы подключаются параллельно для увеличения тока нагрузки.

Законы Кирхгофа

• Действующий закон Кирхгофа (KCL)

• Закон Кирхгофа о напряжении (KVL)

Действующий закон Кирхгофа (KCL) :

Алгебраическая сумма всех токов, входящих в узел, всегда должна быть равна нулю , где i n — это n -й ток .N — количество ветвей. Обычное задание: , если ток входит в узел, присвойте отрицательный знак «-» и , если ток покидает узел, присвойте положительный знак «+». Для следующего рисунка Уравнение узла можно записать как Чтобы использовать KCL для анализа схемы, Запишите уравнения KCL для токов Используйте закон Ома, чтобы записать токи через напряжения Боде (одно уравнение для каждого резистора) Решить, чтобы найти значения напряжения и тока узла

---

Пример: Найдите ток через сопротивление 20 Ом и ток через сопротивление 40 Ом

---

Закон Кирхгофа о напряжении (KVL):

Алгебраическая сумма всех напряжений в замкнутом контуре всегда должна быть равна нулю.

, где v n — напряжение n -го . N — количество элементов в контуре Обычное задание: Если положительная (+) сторона напряжения встречается первой, присвойте положительный знак «+» напряжению на элементе. Если сначала встречается отрицательная (-) сторона напряжения, присвойте отрицательный знак «-» напряжению на элементе. Для следующего рисунка Чтобы использовать KVL для анализа схемы, Запишите уравнения КВЛ для напряжений Используйте закон Ома, чтобы записать напряжения через сопротивления и токи. Решите, чтобы найти значения токов, а затем напряжений.

---

Примеры:

Пример 2 : Найдите ток i и напряжение v на каждом резисторе.

---

Пример 3: Найдите v1 и v2 в следующей схеме
(примечание: стрелки указывают положительное положение прямоугольника, а отрицательное — в конце поля)

---

Пример 4 : Найдите V1, V2 и V3.
(примечание: стрелки указывают положительное положение поля, а отрицательное — в конце поля)

---

Пример 5: Найдите V1, V2, V3 и V4
(примечание: стрелки указывают положительное положение поля, а отрицательное — в конце поля)

---

Практические задачи :

(Щелкните изображение, чтобы просмотреть решение)

Задача 1: Найдите V1 в следующей цепи.

Посмотреть решение

---

Задача 2: Найдите V0 в следующей схеме.

Посмотреть решение

---

Задача 3: Найдите V1, V2 и V3 в следующей схеме.

Посмотреть решение

---

Задача 4 : Найдите I ₁ , I ₂ , I ₃ в следующей схеме

Посмотреть решение

---

Проблема 5 : Найдите значение резистора R в следующей цепи.

Посмотреть решение

---

Операции:

1. В ₁ = 8 В, В ₂ = -4 В, В ₄ = 14 В. Найдите V ₃ и V ₅ в следующей схеме

2. Найдите V _x и V _y в следующей схеме
   
3. Найдите V _x , V _y и V _z в следующей схеме
   
4. Найдите уравнения узлов KCL в узлах A, B, C и D

5. Если I ₁ = 4A, I ₂ = 5A и I ₃ = 3A, то с помощью KCL найдите I ₄ и, I ₅ в следующей схеме
   

Ответов:
1. В ₃ = 12 В и ₅ = -2 В
2. В _x = 12 В и В _y = 9 В
3. V _x = 35 В, V _y = 5 В и V _z = 15 В
4. На узле A:
   
   На узле B:
   
   На узле C:
   
   На узле D:
   
   
5. I ₄ = 2A и I ₅ = 1A

6.3 Правила Кирхгофа — Введение в электричество, магнетизм и электрические цепи

ЦЕЛИ ОБУЧЕНИЯ

---

К концу раздела вы сможете:

• Государственное правило Кирхгофа
• Государственное правило петли Кирхгофа
• Анализировать сложные схемы по правилам Кирхгофа

Мы только что видели, что некоторые схемы можно проанализировать, сведя схему к одному источнику напряжения и эквивалентному сопротивлению. Многие сложные схемы не могут быть проанализированы с помощью последовательно-параллельных методов, разработанных в предыдущих разделах.В этом разделе мы подробно рассмотрим использование правил Кирхгофа для анализа более сложных схем. Например, схема на рисунке 6.3.1 известна как многоконтурная схема , которая состоит из переходов. Соединение, также известное как узел, представляет собой соединение трех или более проводов. В этой схеме нельзя использовать предыдущие методы, потому что не все резисторы имеют четкую последовательную или параллельную конфигурацию, которую можно уменьшить. Попробуйте. Резисторы и включены последовательно и могут быть уменьшены до эквивалентного сопротивления.То же самое и с резисторами и. Но что же тогда делать?

Несмотря на то, что эта схема не может быть проанализирована с помощью уже изученных методов, два правила анализа схемы могут использоваться для анализа любой схемы, простой или сложной. Правила известны как Правила Кирхгофа , в честь их изобретателя Густава Кирхгофа (1824–1887).

(рисунок 6.3.1)

Рисунок 6.3.1 Эта схема не может быть сведена к комбинации последовательного и параллельного соединения.Однако мы можем использовать правила Кирхгофа для его анализа.

ПРАВИЛА КИРХГОФА

---

• Первое правило Кирхгофа — правило соединения . Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения:
  

  (6.3.1)

• Второе правило Кирхгофа — правило петли. Алгебраическая сумма изменений потенциала вокруг любого пути (контура) замкнутой цепи должна быть равна нулю:
  

  (6.3.2)

Теперь мы даем объяснения этих двух правил, сопровождаемые советами по решению проблем по их применению и работающим примером, в котором они используются.

Первое правило Кирхгофа

Первое правило Кирхгофа (правило соединения) применяется к заряду, входящему в соединение и выходящему из него (рисунок 6.3.2). Как было сказано ранее, соединение или узел — это соединение трех или более проводов. Ток — это поток заряда, и заряд сохраняется; таким образом, любой заряд, попадающий в переход, должен вытекать.

(рисунок 6.3.2)

Рисунок 6.3.2 Заряд должен сохраняться, поэтому сумма токов в переходе должна быть равна сумме токов на выходе.

Хотя это и является чрезмерным упрощением, можно провести аналогию с водопроводными трубами, соединенными в водопроводной разводке. Если провода на рисунке 6.3.2 были заменены водопроводными трубами и вода считалась несжимаемой, объем воды, поступающей в разветвление, должен быть равен объему воды, вытекающей из разветвления.

Второе правило Кирхгофа

Второе правило Кирхгофа (правило петли ) применяется к разности потенциалов. Правило петли сформулировано в терминах потенциальной, а не потенциальной энергии, но они связаны между собой.В замкнутом контуре, какая бы энергия ни поступала от источника напряжения, энергия должна быть передана в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в цепь или из нее. Правило петли Кирхгофа гласит, что алгебраическая сумма разностей потенциалов, включая напряжение, подаваемое источниками напряжения и резистивными элементами, в любой петле должна быть равна нулю. Например, рассмотрим простую петлю без стыков, как на рисунке 6.3.3.

(рисунок 6.3.3)

Рисунок 6.3.3 Простая петля без стыков. Правило петли Кирхгофа гласит, что алгебраическая сумма разностей напряжений равна нулю.

Схема состоит из источника напряжения и трех внешних нагрузочных резисторов. Ярлыки,, и служат в качестве ссылок и не имеют другого значения. Скоро станет очевидна полезность этих этикеток. Петля обозначена как петля, и метки помогают отслеживать разницу напряжений при перемещении по цепи.Начните с точки и двигайтесь к ней. Напряжение источника напряжения добавляется к уравнению, а падение потенциала на резисторе вычитается. От точки до потенциальный перепад вычитается. От до вычитается потенциальный перепад. От пунктов до ничего не делается, потому что нет компонентов.

На рис. 6.3.4 показан график напряжения при перемещении по контуру. Напряжение увеличивается при прохождении через батарею, тогда как напряжение уменьшается при прохождении через резистор.Падение потенциала , или изменение электрического потенциала, равно току через резистор, умноженному на сопротивление резистора. Поскольку провода имеют незначительное сопротивление, напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.

(рисунок 6.3.4)

Рисунок 6.3.4 График напряжения при перемещении по цепи. Напряжение увеличивается, когда мы пересекаем батарею, и уменьшается, когда мы пересекаем каждый резистор. Поскольку сопротивление провода довольно мало, мы предполагаем, что напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.

Тогда правило петли Кирхгофа утверждает

Уравнение контура можно использовать для определения тока в контуре:

Этот цикл можно было бы проанализировать с помощью предыдущих методов, но мы продемонстрируем мощь метода Кирхгофа в следующем разделе.

Применение правил Кирхгофа

Применяя правила Кирхгофа, мы генерируем набор линейных уравнений, которые позволяют нам находить неизвестные значения в схемах. Это могут быть токи, напряжения или сопротивления.Каждый раз, когда применяется правило, оно создает уравнение. Если независимых уравнений столько же, сколько неизвестных, то проблема может быть решена.

Использование метода анализа Кирхгофа требует нескольких шагов, перечисленных в следующей процедуре.

---

Стратегия решения проблем: правила Кирхгофа

1. Обозначьте точки на принципиальной схеме строчными буквами. Эти ярлыки просто помогают сориентироваться.
2. Найдите соединения в цепи. Соединения — это точки соединения трех или более проводов.Обозначьте каждое соединение токами и направлениями в него и из него. Убедитесь, что по крайней мере один ток направлен на соединение, а по крайней мере один ток выходит из соединения.
3. Выбрать петли в схеме. Каждый компонент должен содержаться по крайней мере в одном цикле, но компонент может содержаться более чем в одном цикле.
4. Примените правило соединения. Опять же, некоторые стыки не следует включать в анализ. Вам нужно использовать достаточно узлов только для включения каждого тока.
5. Примените правило цикла.Используйте карту на рисунке 6.3.5.

(рисунок 6.3.5)

Рисунок 6.3.5 Каждый из этих резисторов и источников напряжения проходит от до. (a) При перемещении через резистор в том же направлении, что и ток, вычтите падение потенциала. (b) При перемещении через резистор в направлении, противоположном току, добавьте падение потенциала. (c) При перемещении источника напряжения от отрицательного вывода к положительному, добавьте падение потенциала.(d) При перемещении через источник напряжения от положительной клеммы к отрицательной вычтите падение потенциала.

Давайте подробнее рассмотрим некоторые этапы этой процедуры. При размещении переходов в цепи не обращайте внимания на направление токов. Если направление потока тока неочевидно, выбора любого направления достаточно, если хотя бы один ток направлен в соединение и хотя бы один ток выходит из соединения. Если стрелка находится в направлении, противоположном обычному потоку тока, результат для рассматриваемого тока будет отрицательным, но ответ все равно будет правильным.

Количество узлов зависит от схемы. Каждый ток должен быть включен в узел и, таким образом, включен по крайней мере в одно уравнение соединения. Не включайте узлы, которые не являются линейно независимыми, то есть узлы, содержащие одинаковую информацию.

Рассмотрим рисунок 6.3.6. В этой цепи есть два соединения: соединение и соединение. Точки,, и не являются соединениями, потому что соединение должно иметь три или более соединений. Уравнение для соединения есть, а уравнение для соединения есть.Это эквивалентные уравнения, поэтому необходимо оставить только одно из них.

(рисунок 6.3.6)

Рисунок 6.3.6 На первый взгляд, эта схема содержит два соединения, соединение и соединение, но следует рассматривать только один, поскольку их уравнения соединения эквивалентны.

При выборе петель в схеме вам необходимо достаточное количество петель, чтобы каждый компонент был покрыт один раз, без повторения петель. На рис. 6.3.7 показаны четыре варианта петель для решения типовой схемы; варианты (a), (b) и (c) имеют достаточное количество циклов для полного решения схемы.Вариант (d) отражает больше петель, чем необходимо для решения схемы.

(рисунок 6.3.7)

Рисунок 6.3.7 Панели (a) — (c) достаточно для анализа схемы. В каждом случае два показанных контура содержат все элементы схемы, необходимые для полного решения схемы. На панели (d) показаны три использованных контура, что больше, чем необходимо. Любые две петли в системе будут содержать всю информацию, необходимую для решения схемы. Добавление третьего цикла дает избыточную информацию.

Рассмотрим схему на Рисунке 6.3.8 (a). Давайте проанализируем эту схему, чтобы найти ток через каждый резистор. Сначала промаркируйте схему, как показано в части (b).

(рисунок 6.3.8)

Рисунок 6.3.8 (a) Многоконтурная схема. (b) Пометьте цепь, чтобы облегчить ориентацию.

Далее определяем перекрестки. В этой схеме точки и каждая имеют по три соединенных провода, что делает их соединениями. Начните применять правило соединения Кирхгофа, нарисовав стрелки, представляющие токи, и пометив каждую стрелку, как показано на рисунке 6.3.9 (б). Junction показывает это, а Junction это показывает. Поскольку Junction предоставляет ту же информацию, что и Junction, ее можно не принимать во внимание. Эта схема имеет три неизвестных, поэтому для ее анализа нам понадобятся три линейно независимых уравнения.

(рисунок 6.3.9)

Рисунок 6.3.9 (a) Эта схема имеет два соединения, помеченных b и e, но в анализе используется только узел b. (b) Обозначенные стрелки представляют токи в переходах и на выходе из них.

Далее нам нужно выбрать петли.На рисунке 6.3.10 контур включает источник напряжения, резисторы и. Цикл начинается с точки, затем проходит через точки, и, а затем возвращается к точке. Вторая петля, петля, начинается в точке и включает резисторы и источник напряжения.

(рисунок 6.3.10)

Рисунок 6.3.10 Выберите петли в схеме.

Теперь мы можем применить правило цикла Кирхгофа, используя карту на рис. 6.3.5. Начиная с точки и двигаясь к точке, резистор пересекается в том же направлении, что и ток, поэтому падение потенциала вычитается.При перемещении от точки к точке резистор пересекается в том же направлении, что и ток, поэтому падение потенциала вычитается. При перемещении от точки к точке источник напряжения пересекается от отрицательной клеммы к положительной, поэтому добавляется. Между точками и нет компонентов. Сумма разностей напряжений должна равняться нулю:

Наконец, проверяем цикл. Мы начинаем с точки и переходим к точке, пересекаясь в направлении, противоположном текущему потоку.Потенциальное падение добавлено. Затем мы пересекаем и в том же направлении, что и ток, и вычитаем падения потенциала и. Обратите внимание, что через резисторы и ток одинаковый, потому что они соединены последовательно. Наконец, источник напряжения пересекается с положительной клеммы на отрицательную, а источник напряжения вычитается. Сумма этих разностей напряжений равна нулю и дает уравнение контура

Теперь у нас есть три уравнения, которые мы можем решить относительно трех неизвестных.

Чтобы решить три уравнения для трех неизвестных токов, начните с исключения тока. Сначала добавьте уравнение. (1) раз к формуле. (2). Результат обозначен как уравнение. (4):

Затем вычтите уравнение. (3) из уравнения. (2). Результат обозначен как уравнение. (5):

Мы можем решить уравнения. (4) и (5) для тока. Сложив в семь раз уравнение. (4) и троекратное уравнение. (5) приводит к, или. Используя уравнение.(4) приводит к. Наконец, уравнение. (1) дает. Один из способов проверить соответствие решений — проверить мощность, подаваемую источниками напряжения, и мощность, рассеиваемую резисторами:

Обратите внимание, что решение для тока отрицательное. Это правильный ответ, но он предполагает, что стрелка, первоначально нарисованная при анализе соединений, имеет направление, противоположное направлению обычного тока. Питание от второго источника напряжения есть и нет.

ПРИМЕР 6.3.1

---

Расчет тока по правилам Кирхгофа

Найдите токи, протекающие в цепи, показанной на рисунке 6.3.11.

(рисунок 6.3.11)

Рисунок 6.3.11 Эта схема представляет собой комбинацию последовательной и параллельной конфигураций резисторов и источников напряжения. Эта схема не может быть проанализирована с использованием методов, обсуждаемых в «Электродвижущей силе», но может быть проанализирована с использованием правил Кирхгофа.

Стратегия

Эта схема достаточно сложна, поэтому токи не могут быть найдены с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа.На рисунке обозначены токи, и сделаны предположения об их направлениях. Места на схеме отмечены сквозными буквами. В решении мы применяем правила соединения и петли, ища три независимых уравнения, которые позволят нам решить три неизвестных тока.

Решение

Применение правил соединения и петли дает следующие три уравнения. У нас есть три неизвестных, поэтому требуется три уравнения.

Упростите уравнения, поместив неизвестные в одну сторону уравнений.

Упростите уравнения. Уравнение первого цикла можно упростить, разделив обе части на. Уравнение второго цикла можно упростить, разделив обе части на.

Результатов:

Значение

Метод проверки расчетов заключается в вычислении мощности, рассеиваемой резисторами, и мощности, подаваемой источниками напряжения:

Подаваемая мощность равна мощности, рассеиваемой резисторами.

ПРОВЕРЬТЕ ПОНИМАНИЕ 6.6

---

При рассмотрении следующей схемы и мощности, подаваемой и потребляемой схемой, всегда ли источник напряжения обеспечивает питание схемы или может ли источник напряжения потреблять энергию?

ПРИМЕР 6.3.2

---

Расчет тока по правилам Кирхгофа

Найдите ток, протекающий в цепи, показанной на рисунке 6.3.12.

(рисунок 6.3.12)

Рисунок 6.3.12 Эта схема состоит из трех последовательно соединенных резисторов и двух батарей. Обратите внимание, что батареи подключены с противоположной полярностью.

Стратегия

Эту схему можно проанализировать с помощью правил Кирхгофа. Есть только один цикл и нет узлов. Выберите направление тока. В этом примере мы будем использовать направление по часовой стрелке от точки к точке. Рассмотрим цикл и воспользуйтесь рисунком 6.3.5, чтобы написать уравнение цикла. Обратите внимание, что согласно рисунку 6.3.5, батарея будет добавлена, а батарея вычтена.

Решение

Применение правила соединения дает следующие три уравнения. У нас есть одно неизвестное, поэтому требуется одно уравнение:

Упростите уравнения, поместив неизвестные в одну сторону уравнений. Используйте значения, указанные на рисунке.

Значение

Мощность, рассеиваемая или потребляемая схемой, равна мощности, подаваемой в схему, но обратите внимание, что ток в батарее течет через батарею от положительной клеммы к отрицательной клемме и потребляет мощность.

Подаваемая мощность равна мощности, рассеиваемой резисторами и потребляемой батареей.

ПРОВЕРЬТЕ ПОНИМАНИЕ 6.7

---

При использовании законов Кирхгофа вам необходимо решить, какие петли использовать, и направление тока, протекающего через каждую петлю. При анализе схемы в Примере 6.3.2 направление тока было выбрано по часовой стрелке от точки a до точки b .Как бы изменились результаты, если бы направление тока было выбрано против часовой стрелки, от точки к точке?

Несколько источников напряжения

Для многих устройств требуется более одной батареи. Несколько источников напряжения, например батареи, могут быть подключены в последовательной конфигурации, параллельной конфигурации или их комбинации.

Последовательно положительная клемма одной батареи соединена с отрицательной клеммой другой батареи. Любое количество источников напряжения, в том числе аккумуляторы, можно подключать последовательно.Две последовательно соединенные батареи показаны на рисунке 6.3.13. Использование правила петли Кирхгофа для схемы в части (b) дает результат

(рисунок 6.3.13)

Рисунок 6.3.13 (a) Две батареи, соединенные последовательно с нагрузочным резистором. (b) Принципиальная схема двух батарей и нагрузочного резистора, каждая из которых моделируется как идеализированный источник ЭДС и внутреннее сопротивление.

Когда источники напряжения включены последовательно, их внутренние сопротивления можно складывать, а их ЭДС можно складывать вместе, чтобы получить общие значения.Последовательное соединение источников напряжения является обычным явлением, например, в фонариках, игрушках и других приборах. Обычно ячейки включены последовательно, чтобы обеспечить большую суммарную ЭДС. На рисунке 6.3.13 напряжение на клеммах равно

.

Обратите внимание, что в каждой батарее присутствует одинаковый ток, поскольку они соединены последовательно. Недостаток последовательного соединения ячеек в том, что их внутренние сопротивления складываются.

Батареи соединены последовательно для увеличения напряжения, подаваемого в цепь.Например, светодиодный фонарик может иметь две батарейки типа AAA, каждая с напряжением на клеммах, чтобы обеспечить фонарик.

Любое количество батарей можно подключить последовательно. Для аккумуляторов, подключенных последовательно, напряжение на зажимах равно

.

(6.3.3)

, где эквивалентное сопротивление.

Когда нагрузка подключается к источникам напряжения последовательно, как показано на рисунке 6.3.14, мы можем найти ток:

Как и ожидалось, внутренние сопротивления увеличивают эквивалентное сопротивление.

(рисунок 6.3.14)

Рисунок 6.3.14 Две батареи подключаются последовательно к светодиодной лампе, как в фонарике.

Источники напряжения, такие как батареи, также можно подключать параллельно. На рисунке 6.3.15 показаны две батареи с одинаковыми ЭДС, включенные параллельно и подключенные к сопротивлению нагрузки. Когда батареи подключаются параллельно, положительные клеммы соединяются вместе, отрицательные клеммы соединяются вместе, а сопротивление нагрузки подключается к положительной и отрицательной клеммам.Обычно источники напряжения, включенные параллельно, имеют идентичные ЭДС. В этом простом случае, поскольку источники напряжения подключены параллельно, общая ЭДС равна индивидуальной ЭДС каждой батареи.

(рисунок 6.3.15)

Рисунок 6.3.15 (a) Две батареи подключаются параллельно к нагрузочному резистору. (b) На принципиальной схеме показана батарея как источник ЭДС и внутренний резистор. Два источника ЭДС имеют идентичные ЭДС (каждый помечен значком), соединенные параллельно, которые создают одинаковую ЭДС.

Рассмотрим анализ Кирхгофа схемы на рис. 6.3.15 (b). В точке и есть две петли и узел.

Расчет тока через нагрузочный резистор дает, где. Напряжение на клеммах равно падению потенциала на нагрузочном резисторе. Параллельное соединение снижает внутреннее сопротивление и, таким образом, может производить больший ток.

Параллельно можно подключить любое количество батарей. Для параллельно включенных аккумуляторов напряжение на зажимах равно

.

(6.3.4)

, где эквивалентное сопротивление.

Например, в некоторых грузовиках с дизельным двигателем параллельно используются две батареи; они производят полную ЭДС, но могут обеспечить больший ток, необходимый для запуска дизельного двигателя.

Таким образом, напряжение на клеммах последовательно соединенных батарей равно сумме индивидуальных ЭДС минус сумма внутренних сопротивлений, умноженная на ток. Когда батареи соединены параллельно, они обычно имеют равные ЭДС, а напряжение на клеммах равно ЭДС минус эквивалентное внутреннее сопротивление, умноженное на ток, где эквивалентное внутреннее сопротивление меньше, чем отдельные внутренние сопротивления.Аккумуляторы подключаются последовательно для увеличения напряжения на клеммах нагрузки. Аккумуляторы подключаются параллельно для увеличения тока нагрузки.

Массив солнечных батарей

Другой пример работы с несколькими источниками напряжения — комбинация из солнечных элементов , соединенных как последовательно, так и параллельно, чтобы обеспечить желаемое напряжение и ток. Фотогальваническая генерация, которая представляет собой преобразование солнечного света непосредственно в электричество, основана на фотоэлектрическом эффекте.Фотоэлектрический эффект выходит за рамки этого учебника, но, как правило, фотоны, ударяясь о поверхность солнечного элемента, создают в нем электрический ток.

Большинство солнечных элементов изготовлено из чистого кремния. Большинство отдельных ячеек имеют выходное напряжение около, в то время как выходной ток зависит от количества солнечного света, падающего на элемент (падающее солнечное излучение, известное как инсоляция). При ярком полуденном солнечном свете типичные монокристаллические элементы вырабатывают ток на единицу площади, примерно равную площади поверхности ячейки.

Отдельные солнечные элементы электрически соединены в модулях для удовлетворения потребностей в электроэнергии. Их можно соединить последовательно или параллельно — как батареи, о которых говорилось ранее. Матрица или модуль солнечных элементов обычно состоит из промежуточных ячеек и с выходной мощностью до.

Солнечные элементы, как и батареи, вырабатывают напряжение постоянного тока. Ток от источника постоянного напряжения однонаправлен. Для большинства бытовых приборов требуется напряжение переменного тока.

Candela Citations

Лицензионный контент CC, конкретная атрибуция

• Загрузите бесплатно по адресу http://cnx.org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution

21.3 Правила Кирхгофа — College Physics

Расчет силы тока: с использованием правил Кирхгофа

Найдите токи, протекающие в цепи на Рисунке 21.25.

Рисунок 21.25 Эта схема аналогична схеме на рисунке 21.21, но указаны сопротивления и ЭДС. (Каждая ЭДС обозначена буквой E.) Токи в каждой ветви помечены и предполагается, что они движутся в показанных направлениях. В этом примере для нахождения токов используются правила Кирхгофа.

Стратегия

Эта схема достаточно сложна, поэтому токи не могут быть найдены с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа.Токи обозначены как I1I1 размер 12 {I rSub {размер 8 {1}}} {}, I2I2 размер 12 {I rSub {размер 8 {2}}} {} и I3I3 размер 12 {I rSub {размер 8 {3 }}} {} на рисунке, и были сделаны предположения об их направлениях. Места на схеме обозначены буквами от a до h. В решении мы будем применять правила соединения и петли, ища три независимых уравнения, которые позволят нам решить три неизвестных тока.

Решение

Начнем с применения правила Кирхгофа первого или перекрестка в точке а.Это дает

I1 = I2 + I3, I1 = I2 + I3, размер 12 {I rSub {размер 8 {1}} = I rSub {размер 8 {2}} + I rSub {размер 8 {3}}} {}

21,54

, поскольку I1I1 размером 12 {I rSub {размер 8 {1}}} {} течет в соединение, в то время как I2I2 размером 12 {I rSub {размер 8 {2}}} {} и I3I3 размером 12 {I rSub {размер 8 {3}}} {} вытекать. Применение правила соединения в e дает точно такое же уравнение, так что новая информация не получается. Это одно уравнение с тремя неизвестными — необходимы три независимых уравнения, поэтому необходимо применять правило цикла.

Теперь рассмотрим цикл abcdea. Двигаясь от a к b, мы пересекаем R2R2 размера 12 {R rSub {size 8 {2}}} {} в том же (предполагаемом) направлении, что и текущий размер I2I2 12 {I rSub {size 8 {2}}} {} , поэтому изменение потенциала равно −I2R2-I2R2 размер 12 {- I rSub {размер 8 {2}} R rSub {размер 8 {2}}} {}. Затем, переходя от b к c, мы переходим от –– к +, так что изменение потенциала составляет + emf1 + emf1 размер 12 {+ «emf» rSub {size 8 {1}}} {}. Пересечение внутреннего сопротивления r1r1 размером 12 {r rSub {размер 8 {1}}} {} от c до d дает −I2r1-I2r1 размер 12 {- I rSub {размер 8 {2}} r rSub {размер 8 {1} }} {}.Завершение цикла путем перехода от d к a снова проходит через резистор в том же направлении, что и его ток, давая изменение потенциала −I1R1 − I1R1 размер 12 {- I rSub {размер 8 {1}} R rSub {размер 8 { 1}}} {}.

Правило цикла гласит, что сумма изменений потенциала равна нулю. Таким образом,

−I2R2 + emf1 − I2r1 − I1R1 = −I2 (R2 + r1) + emf1 − I1R1 = 0. − I2R2 + emf1 − I2r1 − I1R1 = −I2 (R2 + r1) + emf1 − I1R1 = 0. размер 12 {- I rSub {размер 8 {2}} R rSub {размер 8 {2}} + «emf» rSub {размер 8 {1}} — I rSub {размер 8 {2}} r rSub {размер 8 { 1}} — I rSub {размер 8 {1}} R rSub {размер 8 {1}} = — I rSub {размер 8 {2}} \ (R rSub {размер 8 {2}} + r rSub {размер 8 {1}} \) + «emf» rSub {size 8 {1}} — I rSub {size 8 {1}} R rSub {size 8 {1}} = 0} {}

21.55

Подставляя значения из принципиальной схемы для сопротивлений и ЭДС и отменяя единицу измерения ампер, получаем

−3I2 + 18−6I1 = 0. − 3I2 + 18−6I1 = 0. размер 12 {- 3I rSub {размер 8 {2}} + «18» — 6I rSub {размер 8 {1}} = 0} {}

21,56

Теперь применим правило цикла к aefgha (мы могли бы выбрать abcdefgha как ну) аналогично дает

+ I1R1 + I3R3 + I3r2 − emf2 = + I1R1 + I3R3 + r2 − emf2 = 0. + I1R1 + I3R3 + I3r2 − emf2 = + I1R1 + I3R3 + r2 − emf2 = 0. размер 12 {+ I rSub {размер 8 {1}} R rSub {размер 8 {1}} + I rSub {размер 8 {3}} R rSub {размер 8 {3}} + I rSub {размер 8 {3} } r rSub {размер 8 {2}} — «emf» rSub {размер 8 {2}} «= +» I rSub {размер 8 {1}} R rSub {размер 8 {1}} + I rSub {размер 8 {3}} слева (R rSub {размер 8 {3}} + r rSub {размер 8 {2}} справа) — «emf» rSub {size 8 {2}} = 0} {}

21.57

Обратите внимание, что знаки меняются местами по сравнению с другим циклом, потому что элементы перемещаются в противоположном направлении. С введенными значениями это становится

+ 6I1 + 2I3−45 = 0. + 6I1 + 2I3−45 = 0. размер 12 {+ 6I rSub {размер 8 {1}} + 2I rSub {размер 8 {3}} — «45» = 0} {}

21,58

Этих трех уравнений достаточно для решения трех неизвестных токов. Сначала решите второе уравнение для I2I2 размером 12 {I rSub {size 8 {2}}} {}:

I2 = 6−2I1.I2 = 6−2I1. размер 12 {I rSub {размер 8 {2}} = 6 — 2I rSub {размер 8 {1}}} {}

21.59

Теперь решите третье уравнение для I3I3 размера 12 {I rSub {size 8 {3}}} {}:

I3 = 22,5−3I1.I3 = 22,5−3I1. размер 12 {I rSub {размер 8 {3}} = «22» «.» 5 — 3I rSub {size 8 {1}}} {}

21.60

Подстановка этих двух новых уравнений в первое позволяет нам найти значение для I1I1 размера 12 {I rSub {size 8 {1}}} {} :

I1 = I2 + I3 = (6−2I1) + (22,5−3I1) = 28,5−5I1.I1 = I2 + I3 = (6−2I1) + (22,5−3I1) = 28,5−5I1. размер 12 {I rSub {размер 8 {1}} = I rSub {размер 8 {2}} + I rSub {размер 8 {3}} = \ (6 — 2I rSub {размер 8 {1}} \) + \ («22» ».»5 — 3I rSub {size 8 {1}} \) =» 28 «». «5 — 5I rSub {size 8 {1}}} {}

21,61

Объединение терминов дает

6I1 = 28,5 и 6I1 = 28,5, а размер 12 {6I rSub {size 8 {1}} = «28» «.» 5} {}

21,62

I1 = 4,75 A.I1 = 4,75 A. размер 12 {I rSub {size 8 {1}} = 4 «.» «75» «A»} {}

21,63

Подставляя это значение вместо I1I1 размера 12 {I rSub {size 8 {1}}} {} обратно в четвертое уравнение, получаем

I2 = 6−2I1 = 6−9,50 I2 = 6−2I1 = 6−9,50 размер 12 {I rSub {size 8 {2}} = 6 — 2I rSub {size 8 {1}} = 6–9 дюймов.»» 50 «} {}

21,64

I2 = −3,50 A.I2 = −3,50 A. размер 12 {I rSub {size 8 {2}} = — 3″. «» 50 «» A «} {}

21.65

Знак минус означает, что I2I2 размером 12 {I rSub {size 8 {2}}} {} течет в направлении, противоположном предполагаемому на рисунке 21.25.

Наконец, подстановка значения для I1I1 размера 12 {I rSub {size 8 {1}}} {} в пятое уравнение дает

I3 = 22,5−3I1 = 22,5−14,25 I3 = 22,5−3I1 = 22,5−14,25 размер 12 {I rSub {size 8 {3}} = «22» «.» 5 — 3I rSub {size 8 {1}} = «22» «.»5 -» 14 «». «» 25 «} {}

21,66

I3 = 8,25 A.I3 = 8,25 A. размер 12 {I rSub {size 8 {3}} = 8″. «» 25 «» A «} {}

21,67

Обсуждение

Для проверки отметим, что действительно I1 = I2 + I3I1 = I2 + I3 размер 12 {I rSub {размер 8 {1}} = I rSub {размер 8 {2}} + I rSub {размер 8 {3} }} {}. Результаты также можно было проверить, введя все значения в уравнение для цикла abcdefgha.

Закон Кирхгофа по току и напряжению (KCL и KVL)

Первый и второй законы Кирхгофа с решенным примером

Немецкий физик Роберт Кирхгоф ввел в 1847 году два важных электрических закона, с помощью которых мы можем легко найти эквивалентное сопротивление сложная сеть и протекающие токи в разных проводниках.Цепи переменного и постоянного тока могут быть решены и упрощены с помощью этих простых законов, известных как закон Кирхгофа по току (KCL) и закон Кирхгофа по напряжению (KVL).

Также обратите внимание, что KCL выводится из уравнения непрерывности заряда в электромагнетизме, в то время как KVL выводится из уравнения Максвелла-Фарадея для статического магнитного поля (производная B по времени равна 0)

Закон Кирхгофа (KCL):

Согласно KCL, в любой момент алгебраическая сумма текущих токов через точку (или соединение) в сети равна нулю (0) или в любой электрической сети алгебраическая сумма токов, встречающихся в точке (или соединение) равно нулю (0).Этот закон также известен как Точечный закон или Текущий закон.

В любой электрической сети алгебраическая сумма входных токов в точку и выходных токов из этой точки равна нулю. Или токи на входе в точку равны токам на выходе из этой точки.

Другими словами, сумма токов, текущих к точке, равна сумме токов, текущих от нее. Или алгебраическая сумма токов, входящих в узел, равна алгебраической сумме выходящих из него токов.

Объяснение KCL:

Предположим, что некоторые проводники встречаются в точке «A», как показано на рис. 1.a. в некоторых проводниках токи поступают в точку «А», в то время как в других проводниках токи уходят или исходят из точки «А».

Считайте входящие или входящие токи «положительными (+) в направлении точки« A », в то время как уходящие или исходящие токи из точки« A »считаются« отрицательными (-) ».
, затем:

I ₁ + (-I ₂ ) + (-I ₃ ) + (-I ₄ ) + I ₅ = 0

OR

I ₁ + I ₅ -I ₂ -I ₃ -I ₄ = 0

OR

I ₁ + I ₅ = I ₂ + I ₃ + I ₄ = 0

и.е.
Входящие или входящие токи = выходящие или исходящие токи
или
ΣI Вход = ΣI Выход

Например, 8A приближается к точке, а 5A плюс 3A выходят из этой точки на рис. 1.b, следовательно,
8A = 5A + 3А
8А = 8А.

Демонстрация текущего закона Кирхгофа (KCL)

Закон Кирхгофа о напряжении (KVL):

Второй закон Кирхгофа гласил:
В любом замкнутом пути (или цепи) в сети алгебраическая сумма IR-продукта равна ЭДС в этом пути.
Другими словами, в любом замкнутом контуре (который также известен как Mesh) алгебраическая сумма приложенной ЭДС равна алгебраической сумме падений напряжения в элементах. Второй закон Кирхгофа также известен как закон напряжения или закон сетки.
ΣIR = ΣE

Пояснение к KVL:

Замкнутый контур показан на рис., Который содержит два соединения батарей E ₁ и E ₂ . Общая сумма E.M.F батарей обозначена E ₁ -E ₂ .Воображаемое направление тока также показано на рис.

E ₁ управляют током в таком направлении, которое должно быть положительным, в то время как E ₂ мешает в направлении тока (то есть в направлении, противоположном предполагаемому направлению тока), следовательно, это принято как отрицательный. Падение напряжения в этой замкнутой цепи зависит от произведения напряжения и тока.

Падение напряжения в предполагаемом направлении тока известно как положительное падение напряжения, а другое — отрицательное падение напряжения.

На приведенном выше рисунке I ₁ R ₁ и I ₂ R ₂ — положительное падение напряжения, а I ₃ R ₃ и I ₄ R ₄ — отрицательное напряжение V.D.
Если мы обойдем замкнутую цепь (или каждую сетку) и умножим сопротивление проводника на протекающий в нем ток, то сумма IR будет равна сумме приложенных источников ЭДС, подключенных к цепи.

Общее уравнение для вышеуказанной схемы:

E ₁ -E ₂ = i ₁ R ₁ + i 2R ₂ — _{i 3} R ₃ — _{i 4} R ₄

Если мы пойдем в предполагаемом направлении тока, как показано на рисунке, то произведение IR будет положительным, в противном случае отрицательным.

Полезно знать:
Направление тока:
Очень важно определять направление тока при решении схем по законам Кирхгофа.
Направление тока можно предполагать по часовой стрелке или против часовой стрелки. После того, как вы выберете собственное направление тока, вам нужно будет применить и поддерживать одно и то же направление для всей цепи до окончательного решения схемы.

Если мы получили окончательное значение как положительное, это означает, что предполагаемое направление тока было правильным.В случае отрицательных значений, тогда ток направления меняется на противоположный по сравнению с предполагаемым.

Анализ цепи по законам Кирхгофа

Решенный пример для KCL и KVL (законы Кирхгофа)

Пример:

Резисторы R ₁ = 10 Ом, R ₂ = 4 = 8 Ом подключаются до двух батарей (с незначительным сопротивлением), как показано. Найдите ток через каждый резистор.

Решение:
Предположим, что токи текут в направлениях, указанных стрелками.
Примените KCL к соединениям C и A.
Следовательно, ток в сети ABC = i ₁
Ток в сети CA = i ₂
Тогда ток в Mesh CDA = i ₁ — i ₂

Теперь примените KVL к сетке ABC, 20 В действуют по часовой стрелке. Приравнивая сумму IR произведений, получаем:
10 i ₁ + 4 i ₂ = 20 ……………. (1)

В сети ACD 12 вольт действуют по часовой стрелке, затем:
8 ( i ₁ — i ₂ ) — 4 i ₂ = 12

8 i ₁ — 8 i ₂ — 4 i ₂ = 12
8 i ₁ — 12 i ₂ = 12 …………….(2)

Умножение уравнения (1) на 3;
30 i ₁ + 12 i ₂ = 60

Решение для i ₁
30 i ₁ + 12 i ₂ = 60
8 i ₁ — 12 i ₂ = 12

______________
38 i ₁ = 72

Приведенное выше уравнение также можно упростить с помощью правила исключения или правила Крамера.

i ₁ = 72/38 = 1,895 Ампер = Ток в резисторе 10 Ом

Подставляя это значение в (1), получаем:
10 (1,895) + 4 i ₂ = 20

4 i ₂ = 20 — 18,95

i ₂ = 0,263 Ампер = Ток в резисторах 4 Ом.

Сейчас,
i ₁ — i ₂ = 1.895 — 0,263 = 1,632 Ампер

Применение законов Кирхгофа

• Законы Кирхгофа можно использовать для определения значений неизвестных значений, таких как ток, напряжение, ток, а также направление потока. значения в цепи.
• Эти законы могут быть применены к любой цепи * (см. Ограничение законов Кирхгофа в конце статьи), но полезны для поиска неизвестных значений в сложных схемах и сетях.
• Также используется в узловом и сеточном анализе для определения значений тока и напряжения.
• Ток через каждую независимую петлю передается путем применения KVL (каждая петля) и тока в любом элементе схемы путем подсчета всего тока (применимо в методе тока петли).
• Ток через каждую ветвь передается за счет применения KCL (каждый переход) KVL в каждом контуре цепи (применимо в методе тока контура).
• Законы Кирхгофа полезны для понимания передачи энергии через электрическую цепь.

Полезно знать:

Эти полезные правила необходимо учитывать при упрощении и анализе электрических цепей по законам Кирхгофа:

• Падение напряжения в контуре из-за тока по часовой стрелке считается положительным (+) Падение напряжения.
• Падение напряжения в контуре из-за тока, направленного против часовой стрелки, считается отрицательным (-) падением напряжения.
• Ток, потребляемый батареей по часовой стрелке, считается положительным (+).
• Ток, потребляемый батареей против часовой стрелки, считается положительным (-).

Ограничения по закону Кирхгофа:

• KCL применяется при условии, что ток течет только по проводам и проводам. В то время как в высокочастотных цепях, где паразитная емкость больше не может игнорироваться. В таких случаях ток может течь в разомкнутой цепи, потому что в этих случаях проводники или провода действуют как линии передачи.
• KVL применимо при условии отсутствия флуктуирующего магнитного поля, связывающего замкнутый контур.В то время как в присутствии изменяющегося магнитного поля в высокочастотных, но коротковолновых цепях переменного тока электрическое поле не является консервативным векторным полем. Таким образом, электрическое поле не может быть градиентом какого-либо потенциала, а линейный интеграл электрического поля вокруг петли не равен нулю, что прямо противоречит KVL. Поэтому КВЛ в таком состоянии неприменим.
• Во время передачи энергии от магнитного поля к электрическому, когда в KVL необходимо ввести помадку, чтобы заставить P.d (разность потенциалов) вокруг цепи равна 0.

Вы также можете проверить другие схемы, анализируя теоремы:

Законы Кирхгофа

Законы Кирхгофа

Вот несколько терминов для электрических цепей:

• Узел: точка, в которой три или более токоведущих элемента (ветви) связаны;
• Ветвь: путь, соединяющий два узла, по которому проходит один или несколько элементов последовательно;
• Цикл: последовательность нескольких путей, образующих замкнутый цикл.

На принципиальной схеме как направление тока, так и полярность напряжения на элементе может быть обозначена произвольно. Фактическое направление и полярность будут определяться знаком конкретные значения, полученные после решения схемы. Например, ток, обозначенный слева направо с отрицательным значением на самом деле течет справа налево.

Законы Кирхгофа

• Действующий закон Кирхгофа (KCL)

  Алгебраическая сумма токов в узле равна нулю:

  (70)

  за счет принципа сохранения электрического заряда (электрический заряд не может быть создан или разрушен в цепи).

  Здесь можно предположить направления всех токов через элементы находятся либо в узле, либо вне его.

• Закон Кирхгофа о напряжении (KVL)

  Алгебраическая сумма всех падений напряжения в контуре равна нулю:

  (71)

  за счет принципа сохранения энергии (энергия не может быть созданы или уничтожены в цепи).

  Здесь мы можем предположить полярности всех напряжений на элементах от высокого (+) до низкого (-), при обходе цикла в любом по часовой стрелке или против часовой стрелки.

Пример 1:

Предположим, что токи, текущие в узел, положительны, а токи, выходящие из узел отрицательный, KCL утверждает: .

Предположим, что ток течет по петле по часовой стрелке, KVL состояния: .

Пример 2: Для приведенной ниже схемы найти,,, а также .

По закону Ома имеем .

Нанесите КВЛ на петлю справа, чтобы получить:

(72)

По закону Ома имеем .

Примените KCL к среднему узлу сверху, чтобы получить:

(73)

Опять же по закону Ома получаем .

Нанесите КВЛ на петлю слева, чтобы получить:

(74)

Последовательные и параллельные комбинации компонентов схемы

• Последовательные резисторы:

  Согласно КВЛ, сумма напряжений на резисторы равны входному напряжению:
  

  
  где

  (76)

  а также

  (77)

• Делитель напряжения:

  По закону Ома напряжение на k-м резисторе может быть равным найдено, что:

  (78)

  В частности, если мы имеем

  (79)

• Сопротивление параллельно:

  Согласно KCL сумма токов через резисторы равна входной ток:
  

  
  где

  (81)

  а также

  (82)

  В частности, когда,

  (83)

• Делитель тока:

  По закону Ома ток через k-й резистор может быть найдено, что:

  (84)

  В частности, если мы имеем

  (85)

  (86)

• Последовательные индукторы: Согласно KVL, сумма напряжений на индуктивности равно входному напряжению:

  (87)

  я.е.,

  (88)

• Параллельные индукторы: Согласно KCL, сумма токов через индуктивности равняется входному току:

  (89)

  мы получили

  (90)

• Конденсаторы, включенные параллельно: Согласно KCL, сумма токов через резисторы равны входному току:

  (91)

  я.е.,

  (92)

• Последовательные конденсаторы: По КВЛ сумма напряжений на конденсаторы равны входному напряжению:

  (93)

  т.е.

  (94)

Пример 3 Рассмотрим следующие шесть цепей как ток или делители напряжения.

• Для каждой из трех параллельных цепей найдите и в условия данного тока и сопротивлений, емкостей или индуктивности.
  • Цепь резистора:

    (95)

  • Цепь конденсатора:

    (96)

  • Цепь индуктивности:

    (97)

• Для каждой из трех последовательных цепей найдите и в с точки зрения данного напряжения и сопротивлений, емкостей или индуктивности.
  • Цепь резистора:

    (98)

  • Цепь конденсатора:

    (99)

  • Цепь индуктивности:

    (100)

.