5. Теорема Гаусса для электрического поля в вакууме

Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.

СГС	СИ

где

• —поток вектора напряжённости электрического поля через замкнутую поверхность .

• —полный заряд, содержащийся в объёме, который ограничивает поверхность .

• — электрическая постоянная.

Данное выражение представляет собой теорему Гаусса в интегральной форме.

В дифференциальной форме теорема Гаусса выражается следующим образом:

СГС	СИ

Здесь — объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а — оператор набла.

• Теорема Гаусса может быть доказана как теорема в электростатике исходя из закона Кулона (см. ниже). Формула однако также верна в электродинамике, хотя в ней она чаще всего не выступает в качестве доказываемой теоремы, а выступает в качестве постулируемого уравнения (в этом смысле и контексте ее логичнее называть 

  законом Гаусса^[2].

6. Применение теоремы Гаусса к расчету электростатического поля равномерно заряженной длинной нити (цилиндра)

Поле равномерно заряженного бесконечного цилиндра (нити). Бесконечный цилиндр радиуса R (рис. 6) равномерно заряжен слинейной плотностью τ (τ = –dQ/dt заряд, который приходится на единицу длины). Из соображений симметрии мы видим, что линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. Мысленно построим в качестве замкнутой поверхности коаксиальный цилиндр радиуса r и высотой l. Поток вектора Е

 сквозь торцы коаксиального цилиндра равен нулю (торцы и линии напряженности параллельны), а сквозь боковую поверхность равен 2πrlЕ. Используя теорему Гаусса, при r>R 2πrlЕ = τl/ε₀, откуда   (5) 

Если r<R, то замкнутая поверхность внутри зарядов не содержит, поэтому в этой области E=0. Значит, напряженность поля вне равномерно заряженного бесконечного цилиндра задается выражением (5), внутри же его поле равно нулю. 

7. Применение теоремы Гаусса к расчету электростатического поля равномерно заряженной плоскости

 Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость (рис. 1) заряжена с постоянной поверхностной плотностью +σ (σ = dQ/dS — заряд, который приходится на единицу поверхности). Линии напряженности перпендикулярны данной плоскости и направлены от нее в каждую из сторон. Возьмем в качестве замкнутой поверхности цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей.

Так как образующие цилиндра параллельны линиям напряженности поля (соsα=0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания Е_n совпадает с Е), т. е. равен 2ES. Заряд, который заключен внутри построенной цилиндрической поверхности, равен σS. Согласно теореме Гаусса, 2ES=σS/ε ₀, откуда 

 (1)  Из формулы (1) следует, что Е не зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях равна по модулю, иными словами, поле равномерно заряженной плоскости однородно. 

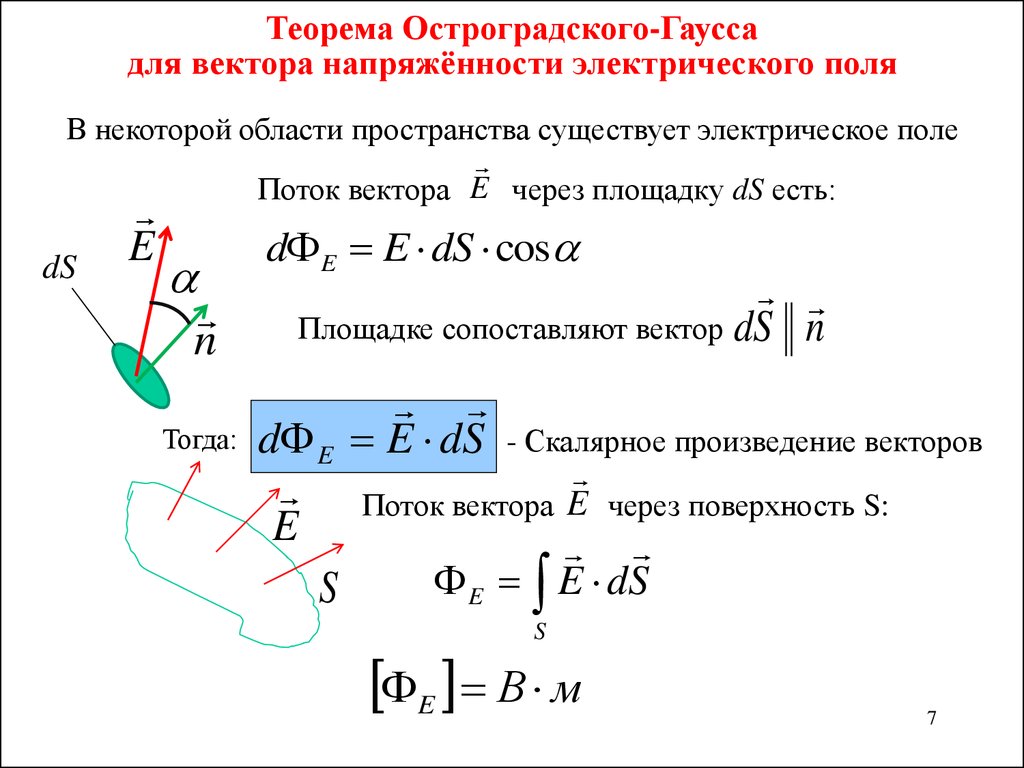
§81. Теорема Гаусса для электростатического поля в вакууме

Вычисление напряженности поля системы электрических зарядов с помощью при­нципа суперпозиции электростатических полей можно значительно упростить, ис­пользуя выведенную немецким ученым К. Гауссом (1777—1855) теорему, опреде­ляющую поток вектора напряженности электрического поля через произвольную замкнутую поверхность.

В соответствии с формулой (79.3) по­ток вектора напряженности сквозь сфери­ческую поверхность радиуса r, охватывающую точечный заряд Q, находящийся в ее центре (рис. 124),

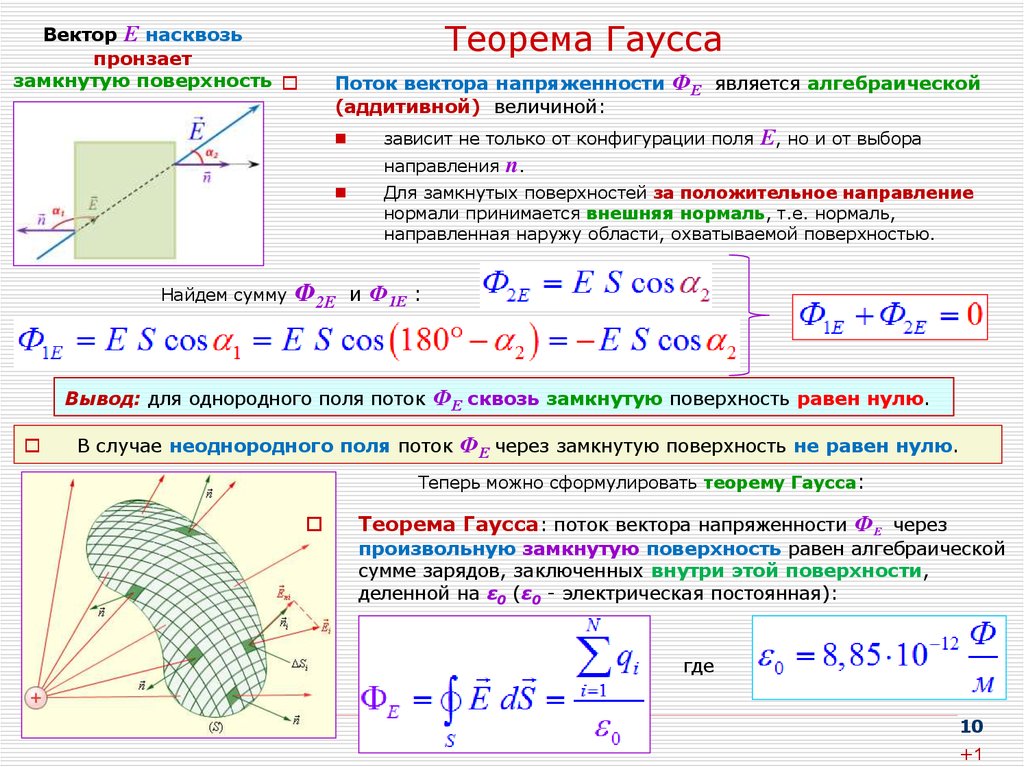
Этот результат справедлив для замкнутой поверхности любой формы. Действитель­но, если окружить сферу (рис. 124) про­извольной замкнутой поверхностью, то каждая линия напряженности, пронизыва­ющая сферу, пройдет и сквозь эту по­верхность.

Если замкнутая поверхность произ­вольной формы охватывает заряд (рис. 125), то при пересечении любой вы­бранной линии напряженности с поверхно­стью она то входит в нее, то выходит из нее. Нечетное число пересечений при вы­числении потока в конечном счете сводит­ся к одному пересечению, так как поток считается положительным, если линии на­пряженности выходят из поверхности, и отрицательным для линий, входящих

134

в поверхность.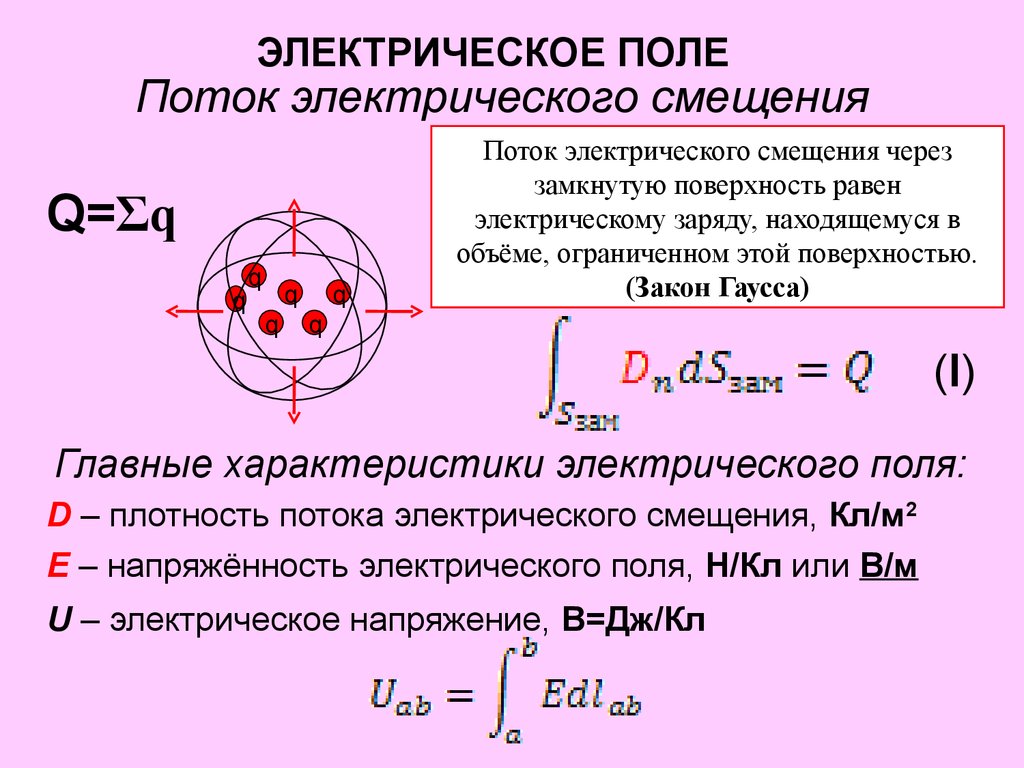 Если замкнутая поверх­ность не охватывает заряда, то поток сквозь нее равен нулю, так как число линий напряженности, входящих в повер­хность, равно числу линий напряженности, выходящих из нее.

Таким образом, для поверхности лю­бой формы, если она замкнута и заключа­ет в себя точечный заряд

Q, поток вектора Е будет равен Q/₀, т. е.

Знак потока совпадает со знаком заряда Q. Рассмотрим общий случай произволь­ной поверхности, окружающей n зарядов. В соответствии с принципом суперпозиции (80.2) напряженность Е поля, создаваемо­го всеми зарядами, равна сумме напря-женностей Е_i, создаваемых каждым за­рядом в отдельности:_;. Поэтому

Согласно (81.1), каждый из интегралов, стоящий под знаком суммы, равен Q_i/₀. Следовательно,

Формула (81. 2) выражает теорему Га­усса для электростатического поля в ваку­уме: поток вектора напряженности элек­тростатического поля в вакууме сквозь произвольную замкнутую поверхность ра­вен алгебраической сумме заключенных внутри этой поверхности зарядов, делен­ной на ₀. Эта теорема выведена матема­тически для векторного поля любой при­роды русским математиком М. В. Остро­градским (1801 —1862), а затем неза­висимо от него применительно к электро­статическому полю — К. Гауссом.

В общем случае электрические заряды могут быть «размазаны» с некоторой

объемной плотностью =dQ/dV, различной

в разных местах пространства. Тогда сум­марный заряд, заключенный внутри замкнутой поверхности S, охватывающей не­который объем V,

Используя формулу (81.3), теорему Гаус­са (81.2) можно записать так:

1. Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость (рис. 126) заряжена с постоянной поверхностной плотно­стью +  (=dQ/dS—заряд, приходящийся на единицу поверхности). Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим ци­линдр, основания которого параллельны заря­женной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (cos=0), то поток вектора напряженности сквозь боковую повер­хность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания

E_n совпадает с Е), т.е. равен 2ES. Заряд, заключенный внутри построенной цилин­дрической поверхности, равен S. Согласно теореме Гаусса (81.2), 2ES = S/₀,

откуда

E=/(2₀). (82.1)

Из формулы (82.1) вытекает, что Е не зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях одинакова по модулю, ины-

135

ми словами, поле равномерно заряженной плоскости однородно.

2. Поле двух бесконечных параллельных разноименно заряженных плоскостей (рис. 127). Пусть плоскости заряжены равномерно разнои­менными зарядами с поверхностными плотно­стями + и -. Поле таких плоскостей найдем как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. На рисунке верх­ние стрелки соответствуют полю от положитель­но заряженной плоскости, нижние — от отрица­тельной плоскости. Слева и справа от плоско­стей поля вычитаются (линии напряженности направлены навстречу друг другу), поэтому здесь напряженность поля

E=0. В области между плоскостями E=E₊+E_— (E₊ и E_—определяются по формуле (82.1)), поэтому ре­зультирующая напряженность

E=/₀. (82.2)

Таким образом, результирующая напряжен­ность поля в области между плоскостями описы­вается формулой (82.2), а вне объема, ограни­ченного плоскостями, равна нулю.

3. Поле равномерно заряженной сфериче­ской поверхности. Сферическая поверхность ра­диуса R с общим зарядом Q заряжена равно­мерно с поверхностной плотностью +0. Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией.

Поэтому линии напря­женности направлены радиально (рис. 128). Построим мысленно сферу радиуса r, имеющую общий центр с заряженной сферой. Если r>R, то внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле, и, по теореме Гаусса (81.2), 4r²E=Q/₀, откуда

При r>R поле убывает с расстоянием r по такому же закону, как у точечного заряда. Гра­фик зависимости E от r приведен на рис. 129. Если r‘<R, то замкнутая поверхность не со­держит внутри зарядов, поэтому внутри равно­мерно заряженной сферической поверхности электростатическое поле отсутствует (E=0).

Электрическое поле, сферическая геометрия

Электрическое поле, сферическая геометрия

Электрическое поле точечного заряда Q можно получить прямым применением закона Гаусса. Рассматривая гауссову поверхность в виде сферы радиусом r , электрическое поле имеет одинаковую величину в каждой точке сферы и направлено наружу. Тогда электрический поток равен произведению электрического поля на площадь сферы. Электрическое поле на радиусе r определяется как: Если другой заряд q разместить на r , это будет испытать силу , так что это считается согласующимся с законом Кулона. Заряженная проводящая сфера Сфера однородного заряда Поля для другой геометрии заряда	Индекс Концепции электрического поля
Гиперфизика***** Электричество и магнетизм R Ступица		Назад

999999999004

Электрическое поле проводящего шара с зарядом Q можно получить прямым применением закона Гаусса. Рассматривая гауссову поверхность в виде сферы радиусом r > R , электрическое поле имеет одинаковую величину в каждой точке поверхности и направлено наружу. Тогда электрический поток равен произведению электрического поля на площадь сферической поверхности. Видно, что электрическое поле идентично полю точечного заряда Q в центре сферы. Поскольку весь заряд будет находиться на проводящей поверхности, поверхность Гаусса при r Point заряда Сфера равномерного заряда Потенциал проводящей сферы

Fields для других геометрий зарядки

.

Индекс Концепции электрического поля

Гиперфизика***** Электричество и магнетизм R Ступица

Назад

Электрическое поле сферы с однородной плотностью заряда и полным зарядом заряда Q можно получить, применяя закон Гаусса. Рассматривая гауссову поверхность в виде сферы с радиусом r > R , электрическое поле имеет одинаковую величину в каждой точке поверхности и направлено наружу. Тогда электрический поток равен произведению электрического поля на площадь сферической поверхности. Видно, что электрическое поле вне сферы ( r > R ) идентично полю точечного заряда Q в центре сферы. Для радиуса r гауссова поверхность будет охватывать меньше, чем полный заряд, и электрическое поле будет меньше. Внутри сферы заряда поле определяется как: Точечный заряд Заряженная проводящая сфера Поля для другой геометрии заряда	Индекс Концепции электрического поля
Гиперфизика***** Электричество и магнетизм R Ступица		Назад

Электрическое поле внутри сферы с однородным зарядом направлено радиально наружу (по симметрии), но сферическая гауссова поверхность заключала бы в себе меньше полного заряда Q. Заряд внутри радиуса r определяется отношением объемов: Тогда электрический поток определяется как и электрическое поле Обратите внимание, что предел при r = R согласуется с выражением для r >= R. Сферически-симметричный заряд вне радиуса r не влияет на электрическое поле при r. Отсюда следует, что внутри сферической заряженной оболочки у вас будет нулевое электрическое поле. Поле вне заряженной сферы

Индекс Концепции электрического поля

Гиперфизика***** Электричество и магнетизм R Ступица

Назад

Электрическое поле, линейный заряд

Электрическое поле, линейный заряд

Электрическое поле линии заряда можно найти путем наложения полей точечных зарядов бесконечно малых зарядовых элементов. Радиальная часть поля от элемента заряда равна Интеграл, необходимый для получения выражения поля, равен . Бесконечная зарядка линии Электрический потенциал конечного линейного заряда Поля для другой геометрии заряда	Индекс Концепции электрического поля
Гиперфизика***** Электричество и магнетизм R Ступица	Назад

Электрическое поле кольца заряда на оси кольца можно найти путем наложения точечных полей зарядов бесконечно малых элементов заряда. Затем кольцевое поле можно использовать как элемент рассчитать электрическое поле заряженный диск. Электрические поля в плоскости xy компенсируются по симметрии, а z-компоненты из элементы заряда могут быть просто добавлены. Если заряд характеризуется плотность площади и кольцо на инкрементная ширина dR’ , тогда: Это подходящий элемент для расчета электрического поля заряженного диска. Электрический потенциал кольца заряда Поля для другой геометрии заряда 9 9 9	Индекс Концепции электрического поля
Гиперфизика***** Электричество и магнетизм R Ступица		Назад

Электрическое поле заряженного диска можно найти, наложив поля точечных зарядов бесконечно малых зарядовых элементов. alexxlab Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Прост Радио Разное Своими руками Советы Схем Схемы Транзист Транзисторы Электрон Электроника