«Закон не всегда то, чем кажется»

Максим Никонов – об актуальности «формулы Радбруха»

Недавно российские адвокаты провели публичную дискуссию о допустимости работы на «присоединённых» территориях. Один из участников беседы заявил коллегам, что считает своим долгом руководствоваться российским законодательством – а оно считает «новые регионы» частью страны. Ему в ответ напомнили про Нюрнбергский процесс, который зафиксировал, что законы могут быть несправедливыми и даже преступными. Адвокат Максим Никонов решил развить эту тему подробнее. В своей колонке он рассказывает про «формулу Радбруха», которая использовалась в процессах над теми, кто предал идею права в угоду законам.

I

О хота на ведьм. Рабство. Расовая сегрегация. Холокост. ГУЛАГ. «Грязная война» в Аргентине и другие акты государственного терроризма в Латинской Америке… Всё это когда-то существовало не без ссылок на «закон».

Именно поэтому «право» не равно «закону», а «верховенство права» не тождественно «диктатуре закона».

Это объясняют на любом более-менее приличном юридическом факультете. Потом, правда, у многих вчерашних студентов эти лекции выветриваются. И для обоснования своей работы появляются другие тезисы: «То – теория, а то – практика», «Не мы такие – система такая», «Закон есть закон, его надо исполнять»…

Точно так же часто забывается один важный исторический пример. Тот, что после Второй мировой войны называют и применяют как «формулу Радбруха».

II

Густав Радбрух – адвокат по уголовным делам, затем министр юстиции Веймарской республики, профессор права. После прихода Гитлера к власти он по политическим мотивам был отстранён от преподавания. После поражения нацистов Радбрух вернулся в право – и в 1945-1946 годах был вынужден констатировать: вера в принцип «закон есть закон» сделала немецких юристов беззащитными перед законами преступного и произвольного содержания. И вот какой вывод он сделал: «Если законы намеренно попирают волю к справедливости, например, произвольно предоставляя тому или иному лицу права человека или отказывая в них, то такие законы недействительны, люди не обязаны им подчиняться, а юристы должны найти в себе мужество не признавать их правовую природу».

Иными словами, суть «формулы Радбруха» состоит в следующем. Там, где к справедливости даже не стремятся; где равенство, являющееся основой правосудия, отвергается и в законодательном процессе – там закон не просто «неправовой». На самом деле он вообще не имеет юридической природы. И потому должен «нуллифицироваться» судьёй в пользу справедливости.

Назначение этой «формулы» двояко. Во-первых, она нужна, чтобы разрешать конфликт между несправедливым по сути, но действующим по форме законом – и справедливым, но не выраженным в форме закона правом.

Во-вторых, она объясняет, почему ссылка на «всего лишь» следование внутригосударственным законам, действующим в определённый исторический период, не может в последующем сама по себе освобождать от возможной ответственности создателей этих законов – и их исполнителей «на местах». Поскольку не всё, что называется «закон», имеет правовую природу.

III

Несмотря на, казалось бы, абстрактный характер, эти идеи из области теоретической юриспруденции напрямую использовались в судебных актах – от приговоров Нюрнбергского трибунала до решений судов Германии разного уровня. Например, в 1947 году – в ходе «малого» Нюрнбергского трибунала над нацистскими судьями, прокурорами и высокопоставленными чиновниками юстиции. Тогда сторона защиты ссылалась на формальную трактовку принципов nulla poena sine lege и ex post facto – которые не позволяют задним числом менять юридические последствия или статус действий. Подсудимые подчёркивали: их работа соответствовала действовавшим на тот момент внутригосударственным законам, поэтому они не могут нести за неё ответственность.

Трибунал очень подробно объяснил, почему этот довод не может быть принят с точки зрения сути права. Он указал: обвиняемые знали или должны были знать, что поступали несправедливо. Что принятые ими судебные решения с международно-правовой точки зрения означали участие в организованной государством системе несправедливости и преследований, оскорбляющей нравственное чувство человечности.

В том же году Апелляционный суд Франкфурта рассматривал дело врачей, участвовавших в «экспериментальных убийствах». И почти дословно цитировал Радбруха: «Право должно быть определено как постановление или предписание, разработанное для служения справедливости. Всякий раз, когда конфликт между принятым законом и истинной справедливостью достигает невыносимых размеров, принятый закон должен уступить место справедливости и считаться “неправовым”. Обвиняемый не может оправдать своё поведение апелляцией к существующему закону, если этот закон оскорбляет определённые очевидные принципы естественного права».

Федеральный верховный суд Германии писал в 1952 году: «Те, кто находились у власти во времена Третьего рейха, издавали многочисленные нормативные документы, заявленные как “законные” и устанавливающие “закон”. Однако им не хватало [сущностного] качества законов – потому что они нарушали те основные принципы, которые не зависят от официального признания правительствами и сильнее, чем любой законодательный акт; действия, которые соответствуют [таким “законам”], остаются правонарушениями».

А Федеральный конституционный суд Германии в 1968 году рассматривал вопрос, как влияют на право получать наследство положения Закона о гражданстве Рейха 1941 года – те, что лишали экспатриированных евреев гражданства и обращали их имущество в пользу государства. В итоге Суд констатировал, что у этих положений нет и не может быть юридической силы – «поскольку они настолько явно противоречат основным принципам справедливости, что судья, который хотел бы применить их или признать их правовые последствия, стал бы вершить несправедливость вместо правосудия».

IV

Интеллектуальное влияние «формулы Радбруха» на немецких юристов оказалось настолько сильным, что её применяли и развивали в судебной практике даже спустя полвека после опубликования – в 1990-х по делам против пограничников ГДР, стрелявших по перебежчикам из Восточной в Западную Германию. А также в процессах «об искажении права» против судей ГДР – чьи решения привели к длительным срокам лишения свободы или даже смертной казни по политически мотивированным делам.

Например, в 1995 году Федеральный верховный суд Германии оставил в силе обвинительный приговор в отношении судьи Ганса Райнварта за факты искажения права при вынесении смертных приговоров. Суд не только скрупулёзно и очень подробно мотивировал свои выводы, но и особо подчеркнул: «Судья, который в слепом повиновении правителям государства считает, что находится в гармонии с законом и порядком, даже когда выполняет волю руководства страны сверх того, что разрешено законом, и тем самым нарушает права человека описанным [в данном деле] образом, не может ссылаться на ошибку. То же самое относится и к случаям, когда он осуществляет “правосудие” исходя из государственных соображений таким образом, который явно выходит за пределы известных ему фундаментальных, нерушимых правовых принципов». Сходную формулировку использовал Федеральный конституционный суд Германии в 1998 году при отклонении жалобы судьи Герды Клабун, осуждённой за искажение права.

Удивительно, но подход, близкий идеям Радбруха, закреплён и в ст. 18 российского закона «О реабилитации жертв политических репрессий». Там говорится: «Работники органов ВЧК, ГПУ – ОГПУ, УНКВД – НКВД, МГБ, прокуратуры, судьи, члены комиссий, “особых совещаний”, “двоек”, “троек”, работники других органов, осуществлявших судебные полномочия, лица, участвовавшие в расследовании и рассмотрении дел о политических репрессиях, несут уголовную ответственность на основании действующего уголовного законодательства». Иными словами, именно действующее «здесь и сейчас» – после принятия этого закона в 1991 году – правовое регулирование определяло ответственность за участие в репрессиях прошлых лет. Пусть и формально имевших легальную основу для них «там и тогда».

Но эта норма осталась лишь на бумаге – по разным причинам. Несмотря на реабилитацию репрессированных – включая признание фактов фальсификации уголовных дел, отсутствия состава или даже события преступления – мне неизвестны публичные процессы над теми, кто участвовал в вынесении подобных приговоров.

Разумеется, по делам 1930-х эти люди физически не смогли бы предстать перед правосудием в 1990-е. Однако оставались, например, те, кто выносили приговоры по ст. 70 УК РСФСР (антисоветская агитация и пропаганда) или ст. 190.1 (распространение заведомо ложных измышлений, порочащих советский государственный и общественный строй). С 1967 по 1987 годы по ним осудили 2356 человек; в последующем обе статьи были декриминализированы, а люди – реабилитированы.

Тем не менее в опыте российского юридического сообщества, по-видимому, в принципе нет дел «об искажении права». Которые самим своим существованием служили бы не только напоминанием, но и предостережением: закон не всегда то, чем кажется.

Переместительный закон сложения – формула

4.1

Средняя оценка: 4.1

Всего получено оценок: 93.

4.1

Средняя оценка: 4.1

Всего получено оценок: 93.

Переместительный закон сложения иногда ставит учеников в тупик. Ведь все учат свойства сложения, поэтому понятие законов сложения выглядит страшно и пугающе. Чтобы не допускать досадных ошибок разберем отличие переместительного закона сложения от переместительного свойства сложения, а также поговорим о правилах использовании этого закона.

Сложение

Если представить себе пенал, куда складывают карандаши и ручки, то количество карандашей это первое слагаемое, количество ручек второе слагаемое, а их общее количество в пенале – сумма.

Но глупо говорить о ручках, когда речь идет о сложении и вычитании огромных чисел, поэтому в математике принято более общее определение. Считается, что сложение это перемещение числа по числовой прямой вправо, то есть в сторону увеличения чисел.

Иногда ученикам кажется, что большие числа или дроби не получится отметить на числовой прямой. Это грубая ошибка. Запомните, на числовой прямой можно отметить абсолютно любое действительное число. А если у вас что-то не получается, значит дело в единичном отрезке.

Законы сложения

Законов сложения, как и свойств, всего два: переместительный и сочетательный.

Сочетательный закон гласит, что в примерах, где три и более слагаемых, выполнять сложение можно в любом порядке. Значит, можно сложить первое число со вторым, а потом результат сложить с третьим, а можно первое слагаемое сложить с третьим, а к результату прибавить второе и так далее.

Переместительный закон гласит, что от перемены мест слагаемых сумма не меняется.

Кажется, что законы и свойства это одно и то же, ведь количество законов такое же, формулировка и смысл так же не изменились в сравнении со свойствами сложения. Дело в том, что свойства и законы это действительно одно и то же в этом конкретном случае. Просто под законами обычно понимают формулы, которые выражают словесные формулировки свойств.

Значит, если мы видим перед собой формулу, то это считается законом, если словесную формулировки – свойством. Вот и все различие.

Запишем формулу переместительного закона сложения:

а+в=в+а

Формула сочетательного закона выглядит так:

а+в+с=(а+с)+в

Стоит запомнить, что любые математические формулы работают в обе стороны. То есть, как справа налево, так и слева направо. Для сложения это так важно, но лучше понять это сразу.

Переместительный закон сложения

Поговорим о том, как можно использовать переместительный закон в математике. Для этого решим небольшую задачу.

Найти значение примера: а+с+р+х, если а+р=3, с+9=12, а х=3

Для начала сгруппируем пример.

а+с+р+х=(а+р)+с+х – нам известно значение одной скобки а+р=3 и х=3. Подставим эти значения в пример.

а+с+р+х=(а+р)+с+х=3+с+3 – теперь сделаем так, чтобы получилась скобка (с+9)

а+с+р+х=(а+р)+с+х=6+с=с+9-3 – мы не нарушили равенства, ведь 9-3=6. Зато теперь получится посчитать пример до конца.

а+с+р+х=(а+р)+с+х=6+с=с+9-3=12-3=9 – пример было бы невозможно решить без переместительного закона сложения.

Но такие задачи встречаются не часто. Гораздо чаще свойства сложения применяются для ускорения вычислений. Правильное использование законов сложения, поможет сэкономить вам много времени для более трудных примеров и задач.

Что мы узнали?

Мы поговорили о том, что такое сложение. Узнали, чем законы сложения отличаются от свойств. Поняли, что отличий практически нет. Выделили переместительный закон сложения и применили его, решив интересную задачу.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Лариса Доля

  10/10

• Татьяна Попкова

  9/10

• Артём Мещеряков

  8/10

• Татьяна Зобкова

  10/10

Оценка статьи

4.1

Средняя оценка: 4.1

Всего получено оценок: 93.

---

А какая ваша оценка?

Калькулятор закона Чарльза

Создано Wojciech Sas, PhD

Отредактировано Bogna Szyk и Jack Bowater

Последнее обновление: 22 декабря 2022 г. Примеры закона Чарльза

Как закон Чарльза применяется в реальной жизни?

Другие термодинамические процессы

Калькулятор закона Шарля — это простой инструмент, который описывает основные параметры идеального газа в изобарическом процессе .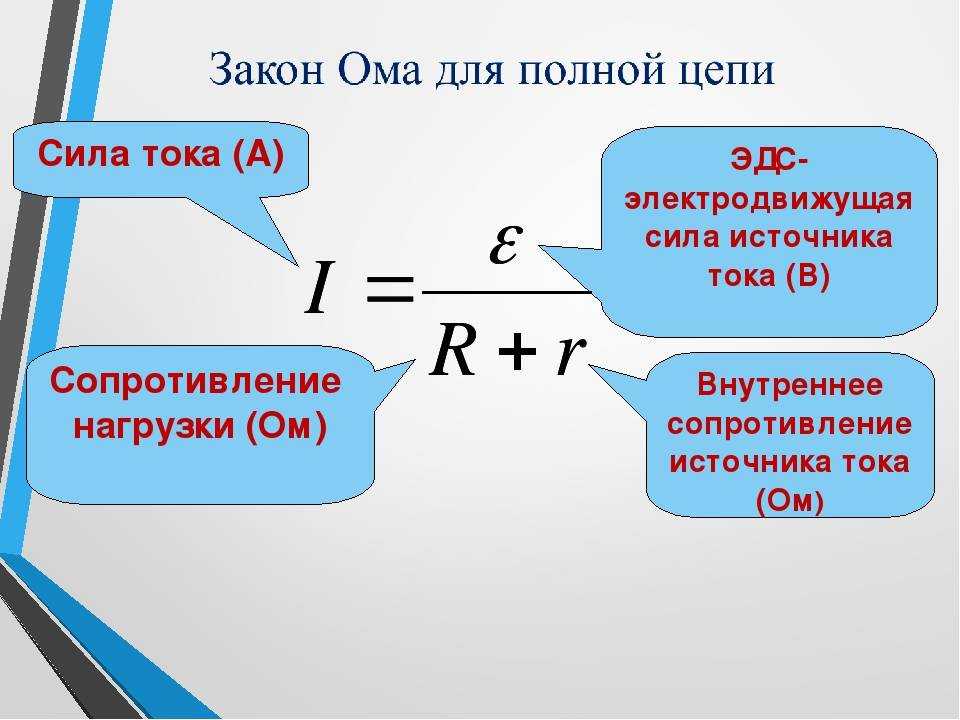 В тексте вы можете найти ответ на вопрос «Что такое закон Шарля?», узнать, как выглядит формула закона Шарля, и прочитать, как решать термодинамические задачи с некоторыми примерами закона Шарля.

Если вам нужно рассчитать результаты для изохорного процесса, воспользуйтесь нашим калькулятором закона Гей-Люссака.

Определение закона Шарля

Закон Шарля (иногда называемый законом объемов) описывает зависимость между объемом газа и его температурой , когда давление и масса газа постоянны . В нем говорится, что объем пропорционален абсолютной температуре .

Есть несколько других способов записать определение закона Шарля, один из которых таков: соотношение объема и температуры газа в замкнутой системе остается постоянным, пока не изменяется давление.

Закон Шарля описывает поведение идеального газа (газов, которые мы можем охарактеризовать уравнением закона идеального газа) в течение изобарический процесс , что означает, что давление остается постоянным во время перехода.

Формула закона Чарльза

Основываясь на определении закона Чарльза, мы можем написать уравнение закона Чарльза следующим образом: T₁ — начальный объем и температура соответственно. Точно так же В₂ и Т₂ являются конечными значениями этих параметров газа.

Как работает калькулятор закона Чарльза? Сначала вам нужно вставить три параметра, а четвертый будет рассчитан автоматически. Допустим, мы хотим найти окончательный объем, тогда формула закона Шарля дает:

V₂ = V₁ / T₁ × T₂ .

Если вы предпочитаете задать конечный объем и хотите оценить результирующую температуру, то уравнение закона Шарля изменится на:

T₂ = T₁ / V₁ × V₂ .

В расширенном режиме , вы также можете определить давление и посмотреть, сколько молей атомов или молекул содержится в сосуде.

💡 Если температура постоянна во время перехода , это изотермический процесс. В таком случае вы можете быстро оценить его параметры с помощью калькулятора закона Бойля от Omni!

Примеры закона Шарля

Мы можем использовать калькулятор закона Чарльза для решения некоторых термодинамических задач. Давайте посмотрим, как это работает:

1. Представьте, что у нас есть мяч, накачанный воздухом. Его начальный объем равен 2 литра , и он лежит на пляже с температурой 35 °C . Затем мы перемещаем его в кондиционируемую комнату с температурой 15 °C . Как изменится объем мяча?

   • Во-первых, формула закона Шарля требует абсолютных значений температуры , поэтому мы должны преобразовать их в кельвины:

     T₁ = 35 °C = 308,15 K ,
     T₂ = 15 °C = 288,15 K .

   • Тогда мы можем применить уравнение закона Шарля в форме, где оценивается конечный объем:

     V₂ = V₁ / T₁ × T₂
     = 2 л / 308,15 К × 288,15 К
     = 1,8702 л .

   Мы видим, что объем уменьшается, когда мы перемещаем мяч из более теплого места в более прохладное . Иногда вы можете испытать этот эффект, меняя свое местоположение или просто оставляя объект в покое, когда погода меняется. Мяч кажется недостаточно надутым, и кто-то может подумать, что в нем есть дырка, через которую выходит воздух. К счастью, это всего лишь физика, поэтому вам не нужно покупать еще один мяч — просто надуйте тот, который у вас есть, и наслаждайтесь!

   Одно маленькое замечание: воздух является примером реального газа, так что результат будет лишь приблизительным , но до тех пор, пока мы избегаем экстремальных условий (давление, температура). Результат достаточно близок к реальному значению.

2. Во второй задаче нагреваем легко растягивающийся контейнер. Он заполнен азотом, что является хорошим приближением к идеальному газу. Мы можем найти, что его начальный объем составляет 0,03 фут3 при комнатной температуре, 295 K . Затем ставим близко к источнику тепла и оставляем на некоторое время. Через несколько минут его объем увеличился до 0,062 ft³ . Имея все эти данные, можем ли мы оценить температуру нашего обогревателя?

   • Применим формулу закона Шарля и перепишем ее в такой форме, чтобы можно было вычислить температуру:

     T₂ = T₁ / V₁ × V₂
     = 295 K × 0,03 фут³ / 0,062 фут³
     = 609,7 K .

   • Мы можем записать результат в более любезной форме T₂ = 336,55 °C или T₂ = 637,79 °F .

   Это отличный пример, который показывает нам, что мы можем использовать этот тип устройства в качестве термометра ! Что ж, это не очень практичный метод и, возможно, не такой точный, как обычные, но все же заставляет задуматься, а какие еще необычные приложения можно получить из других повседневных предметов?

Как закон Чарльза применяется в реальной жизни?

Существуют различные области, в которых мы можем использовать закон Чарльза. Вот список нескольких самых популярных и интригующих примеров:

• Полет на воздушном шаре — Вы, должно быть, видели воздушный шар в небе хотя бы раз в жизни. Вы когда-нибудь задумывались, как он может летать и почему на его борту есть огонь или другие источники тепла? Закон Чарльза — ответ! Всякий раз, когда воздух нагревается, его объем увеличивается . В результате одно и то же количество (масса) газа занимает большее пространство, а значит плотность уменьшается. Плавучесть окружающего воздуха делает остальную часть работы, поэтому воздушный шар начинает плавать.

  Рулевое управление в любом заданном направлении — это, вероятно, отдельная история, но мы можем объяснить общую концепцию движения вверх и вниз с помощью закона Шарля .

• Эксперименты с жидким азотом . Вы когда-нибудь видели эксперимент, в котором кто-то кладет мяч или воздушный шар в контейнер, наполненный жидким азотом, а затем перемещает его наружу? Во-первых, он сжимается независимо от того, насколько большим он был в начале. Затем, после освобождения, возвращается в исходное состояние. Опять же, всякий раз, когда изменяется температура, изменяется и объем.

• Термометр – Как показано в предыдущем разделе, можно сконструировать устройство, измеряющее температуру на основе закона Шарля. Хотя мы должны знать о его ограничениях, которые в основном связаны с прочностью объекта на растяжение и устойчивостью к высоким температурам, мы можем изобрести оригинальное устройство, которое идеально подходит для наших нужд. Всякий раз, когда вы не уверены в результате, проверьте этот калькулятор закона Чарльза, чтобы найти ответ.

Другие термодинамические процессы

Закон Шарля, закон Бойля и закон Гей-Люссака входят в число основных законов, описывающих подавляющее большинство термодинамических процессов. Мы собрали все основные газовые переходы в нашем калькуляторе комбинированного газового закона, где вы можете оценить не только конечную температуру, давление или объем, но также изменение внутренней энергии или работу, совершаемую газом.

Войцех Сас, доктор философии

Начальные параметры

Начальный объем (V₁)

Начальная температура (T₁)

Окончательные параметры

Окончательный объем (V₂)

Окончательная температура (T₂)

Проверьте 42 аналогичные термодинамики и тепловые калькуляторы 🌡

Biot Numberboltzmann Factorbyle — GeeksforGeeks

Недоказанный газовый закон называется законом Чарльза. Это объясняет, почему горячие газы обычно расширяются. Количество газа при постоянном давлении было исследовано французским ученым Шарлем в зависимости от температуры. Согласно этому закону газ расширяется при повышении его температуры, а понижение температуры приводит к уменьшению его объема. Формула закона Чарльза будет рассмотрена в этой статье.

Согласно Чарльзу Лоу, «объем данной массы газа при постоянном давлении точно пропорционален абсолютной температуре или температуре Кельвина».

Чарльз Law Formula

Уравнение Закона Чарльза гласит, что

V α T

V ₁ /T ₁ = V ₂ /T ₁ = V ₂ /T ₁ = V ₂ /T ₁ = V ₂ /T ₁ = V ₂ /T ₁ = V ₂ /T ₁ = V ₂ /T ₁ .

• V ₁ Начальный том,
• T ₁ — Начальная температура в Кельвинах,
• V ₂ — Конечный объем,
• T ₂ — Конечная температура в Кельвинах.

Вывод формулы закона Чарльза

Объем прямо пропорционален его температуре при постоянном давлении , это формулировка закона Чарльза. (при постоянном давлении)0003

V = kT

В соответствии с математической формулой Чарльза Лоу

V ₂ = V ₁ (273+t/273)

₁

∴ V ₂ = V ₁ (T ₂ /T ₁ )

∴ V ₂ /V ₁ = T ₂ /T ₁

ИЛИ

∴ 1/V ₁ = T ₂ /V ₂ T ₁

∴ T ₁ /V ₁ = T ₂ /V ₂

∴ V ₁ /T ₁ = V ₂ /T ₂

Актуальность Чарльза Лоу в реальной жизни

Использование воздушных шаров для спортивных мероприятий, а также для наблюдений за погодой — интригующее применение закона Чарльза. Газы расширяются при нагревании, согласно закону. Из-за того, что масса газа постоянна, при нагревании плотность газа или количество молекул в единице объема падает. Тепло делает воздух менее плотным, чем холод. Это заставляет более холодный воздух в атмосфере вытесняться, что помогает воздушным шарам подниматься.

Недостаток

Ограничение закона Чарльза состоит в том, что он применим только к совершенному газу. Это справедливо только для реальных газов при высоких температурах и низких давлениях; тем не менее, при высоких давлениях зависимость между объемом и температурой не является линейной.

Примеры задач

Задача 1. При 19°C образец газа занимает 2,55 л. Каков будет новый объем газа, если давление останется прежним, а температуру повысят до 30°C?

Answer:

T ₁ = 273 + 19 = 292 K

T ₂ = 273 + 30 = 303 K

Since,

V ₁ /T ₁ = V ₂ /T ₂

∴ 2. 55 / 292 = V2 /303

∴ V ₂ = 2.55 × 303 / 292

∴ V ₂ = 772.65 / 292

∴ V ₂ = 2,64 л

Задача 2. При 123 градусах Цельсия газообразный гелий имеет объем 1690 мл. Определить температуру, при которой емкость увеличивается до 472 мл. Рассчитывайте на стабильное давление.

Answer :

T ₁ = 273 + 123 = 396 K

Since,

V ₁ /T ₁ = V ₂ /T ₂

∴ V ₁ /T ₁ V ₂ = 1 /T ₂

∴ T ₂ = T ₁ V ₂ /V ₁ V ₂ /V ₁ V ₂ /V ₁ 2 2 2 2 2 2 2 .0236 2 = 396 × 1690 /472

∴ T ₂ = 669240 /472

∴ T ₂ = 1417,9 K

OR

= 1417,9 K

OR

9002 1 k

OR

9002

7 = 1417,9 K

OR

9002

7. C

Задача 3. Каким будет начальный объем газа при 400 К, если конечный объем составит 13 л при 270 К?

Ответ :

С,

В ₁ /Т ₁ = В ₂ /Т _{7 2}

30002 ∴ V ₁ = V ₂ T ₁ / T ₂

∴ V ₁ = 13 × 400 /270

∴ v ₁ = 500 /270

∴ V ₁ = 500 /270

∴ V ₁ = 500 /270 / 2703937. 9000. 9000. 9000. 9000. . 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. . /500 /270

. 1 = 19,26 л

Задача 4. Что произойдет с объемом газа, если его 55 мл охладить с 67°С до 30°С?

Ответ :

T ₁ = 273 + 67 = 340 К

T ₂ = 273 + 30 = 303 К

002 Since,

V ₁ /T ₁ = V ₂ /T ₂

∴ V ₂ = V ₁ T ₂ / T ₁

∴ V ₂ = 55 × 303 /340

∴ V ₂ = 16665 /340

∴ V ₂ = 49,015 мл

9 Проблема 5: A -GAS AST AGAFIC 1,5 L. 5. При температуре 333 К определить объем.

Ответ :

Since,

V ₁ /T ₁ = V ₂ /T ₂

∴ V ₂ = V ₁ T ₂ / T ₁

∴ v ₂ = 1,5 × 333 /273

∴ V ₂ = 499,5 / 273

∴ V ₂ = 1,8 л

Задача. л, определите температуру, при которой объем станет 34 л.

Answer :

Since,

V ₁ /T ₁ = V ₂ /T ₂

∴ V ₁ /T ₁ V ₂ = 1/ T ₂

∴ T ₂ = T ₁ V ₂ / V ₁

∴ T ₂ = 280 × 34 / 20

∴ T ₂ = 9520 / 20

∴ T ₂ = 476 K

Задача 7. При стандартной температуре объем равен 30 л, найти при конечной температуре объем 50 л.

Answer :

Since,

V ₁ /T ₁ = V ₂ /T ₂

∴ V ₁ /T ₁ V ₂ = 1/T ₂

∴ T ₂ = T ₁ V ₂ / V ₁

∴ T ₂ = 273 × 30 / 50

∴ T ₂ = 8190 / 50

∴ T ₂ = 163,8

Задача 8. Для чего используется формула закона Шарля?

Ответ :

Используя следующее уравнение, закон Шарля используется для определения неизвестного объема или температуры реакции или процесса при постоянном давлении.

V ₁ /T ₁ = V ₂ /T ₂  …(при постоянном давлении)

Задача 9.