PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
- 2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
- 3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
- 4 Электродинамика
- 4.
 1 Электростатика
1 Электростатика - 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
- 4.
- 5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.
 6 СТО
6 СТО
- 6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный
 справку), обсуждать уже созданные.
справку), обсуждать уже созданные.Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
| Принцип ферма | Fiziku5
Задача 1. Параллельный пучок света c длиной волны 500 нм падает на экран с круглым отверстием диаметра d. Прошедший сквозь отверстие свет, попадает на экран для наблюдения, расположенный на расстоянии L от экрана с отверстием. Каков будет диаметр светлого пятна? Используя полученный результат, получите критерий применимости геометрической оптики.
Каков будет диаметр светлого пятна? Используя полученный результат, получите критерий применимости геометрической оптики.
3. Закон отражения
3.1 Принцип Ферма
Законы геометрической оптики: закон прямолинейного распространения света в оптически однородной среде, закон отражения и закон преломления света могут быть получены из принципа Ферма, который формулируется так:
В пространстве между двумя точками свет распространяется по такому пути, вдоль которого время его прохождения минимально.
Задача 2. Используя принцип Ферма, выведите закон отражения света.
Решение. Пусть свет от точечного источника S, отразившись от зеркала, попадает в точку P. Будем исходить из установленного ранее факта, что свет в однородной среде распространяется прямолинейно. Изменение направления происходит при отражении света от зеркала.
Рассмотрим произвольный ход луча SOP. Пусть угол между перпендикуляром к зеркалу OH и направлением падающего луча равен a, а угол между перпендикуляром к зеркалу и направлением отраженного луча равен b. Время между выходом из источника и достижением светом точки P равно длине ломаной SOP, деленной на скорость распространения c. Так как скорость распространения света везде одна и та же, минимальность времени прохождения траектории эквивалентна минимальности длины ломаной SOP. Таким образом, формулировка задачи об отыскании траектории минимального времени достижения точки
Время между выходом из источника и достижением светом точки P равно длине ломаной SOP, деленной на скорость распространения c. Так как скорость распространения света везде одна и та же, минимальность времени прохождения траектории эквивалентна минимальности длины ломаной SOP. Таким образом, формулировка задачи об отыскании траектории минимального времени достижения точки
Проведем геометрическое решение. Решение сводится к нахождению такого расположения точки O на зеркале, которое обеспечит минимальность длины ломаной SOP. Построим дополнительную точку S`, которая расположена симметрично точке S относительно поверхности зеркала. Из построения точки S` ясно, что длина ломаной SOP равна длине ломаной S`OP. Получаем еще одну формулировку задачи — надо найти такое положение точки O, которое обеспечит минимальность длины ломаной S`OP.
3.2 Построение изображения в плоском зеркале
Дополнительная точка S`, которая использовалась при доказательстве закона отражения является ничем иным, как изображением источника S. Изображение источника расположено в его зеркальном отражении относительно плоскости отражения. Наблюдатель может увидеть изображение не из любой точки. Чтобы изображение было видимым, необходимо, чтобы прямая, соединяющая изображение и точку наблюдения, пересекала плоскость отражения. Отсюда также ясно, что между источником и его видимым изображением необязательно должна находиться отражающая поверхность.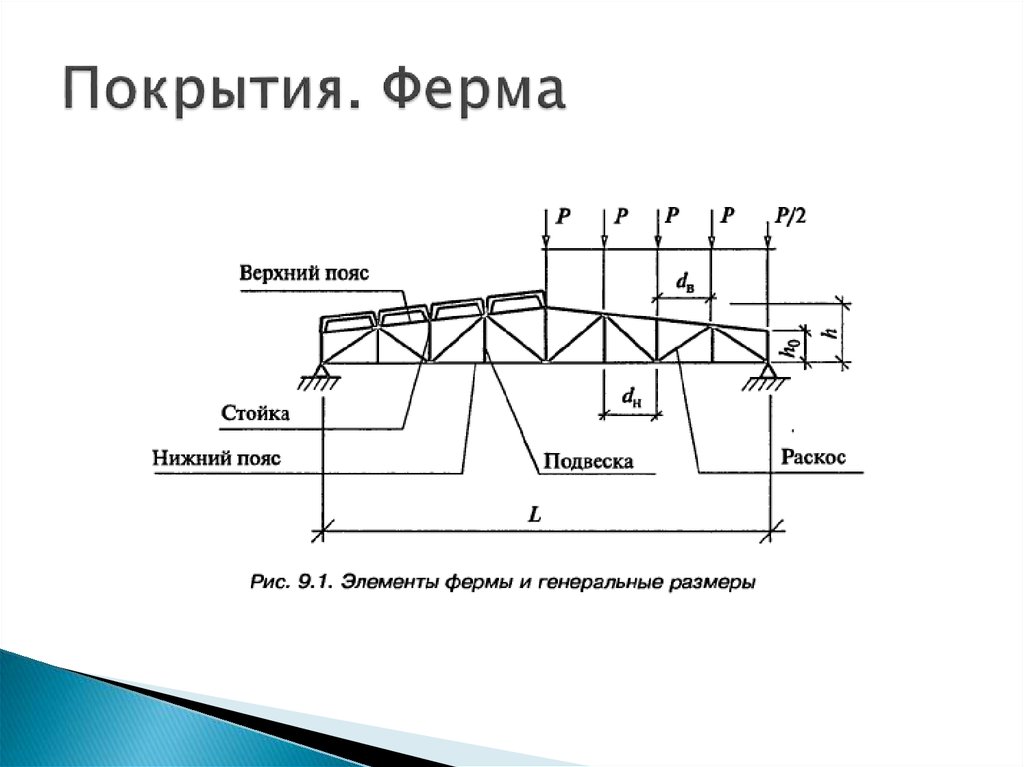
Оптическое отражение является физическим воплощением одноименной математической операции симметрии.
Задача 3. Горящая миниатюрная лампочка находится вблизи прямого угла, образованного двумя плоскими зеркалами. Сколько изображений имеет лампочка? Постройте все изображения.
Задача 4. Луч света падает под углом a на одно из двух зеркал, образующих друг с другом прямой угол. Каково направление отраженного от системы зеркал луча?
3.3 Построение изображения в сферическом зеркале
3.3.1 Основные точки и линии сферического зеркала
Изображение предмета создается светом, отраженным от предмета, прошедшим оптическую систему и попавшим в глаза наблюдателю. Для построения изображения предмета можно пользоваться любыми из лучей, однако, изо всех лучей есть наиболее удобные для этих целей. У сферического зеркала есть несколько опорных линий и точек, используемых при построении изображения. Они показаны на рисунке 81. Во-первых, ось симметрии зеркала
 Далее: центр кривизны зеркала O, точка P — полюс зеркала, точка F — фокус, он расположен на главной оптической оси зеркала на расстоянии R/2 от центра. Фокус вогнутого зеркала находится перед, а выпуклого — за зеркалом. Фокус вогнутого зеркала замечателен тем, что все лучи, идущие параллельно главной оптической оси, пересекаются в фокусе. Это свойство используется при построении изображения.
Далее: центр кривизны зеркала O, точка P — полюс зеркала, точка F — фокус, он расположен на главной оптической оси зеркала на расстоянии R/2 от центра. Фокус вогнутого зеркала находится перед, а выпуклого — за зеркалом. Фокус вогнутого зеркала замечателен тем, что все лучи, идущие параллельно главной оптической оси, пересекаются в фокусе. Это свойство используется при построении изображения.3.3.2 Построение изображения в вогнутом зеркале
Пусть AB — предмет, изображение которого следует построить (рисунок 81). Из всех лучей, которые идут из точки
При построении изображения точки, лежащей на главной оптической оси, используется одна из побочных оптических осей (прямая, проходящая через полюс). Все лучи, идущие параллельно побочной оптической оси пересекаются в точке, лежащей на фокальной плоскости.
3.3.3 Формула сферического зеркала
Задача 5. Выведите уравнение, связывающее фокусное расстояние F с расстояниями от предмета и изображения до полюса зеркала a и b:
. (1)
Отдельно рассмотрите случаи: a>F; a<F. Что означает результат b<0? (Величина называется оптической силой зеркала, измеряется в
м-1 или диоптриях.)
Формула сферического зеркала (1) применима и для выпуклого зеркала. Для выпуклого зеркала F<0. При этом надо иметь в виду, что расстояние дор изображения может быть также отрицательным. Это означает, что изображение находится по ту же сторону от линзы, что и сам предмет.
Задача 6. Свеча длины h=20 см стоит в фокусе выпуклого зеркала. Определите увеличение зеркала , если F=30 см.
Определите увеличение зеркала , если F=30 см.
4. Закон преломления
4.1 Повторение содержания закона преломления
Вопрос 1. На рисунке 82 показан ход луча через границу раздела двух прозрачных сред с разными показателями преломления.
а) В какой среде показатель преломления больше?
б) Укажите какие из обозначенных на рисунке углов являются: углом падения, углом отражения, углом преломления?
в) Сформулируйте закон преломления и запишите его математическое выражение.
4.2 Полное внутреннее отражение
При падении луча на границу двух сред из более в менее плотную оптическую среду (из среды с большим в среду с меньшим показателем преломления) угол преломления оказывается больше угла падения. По мере увеличения угла падения угол преломления приближается к прямому углу. Угол падения g0, при котором угол преломления становится прямым, называется углом полного внутреннего отражения.
Задание 1.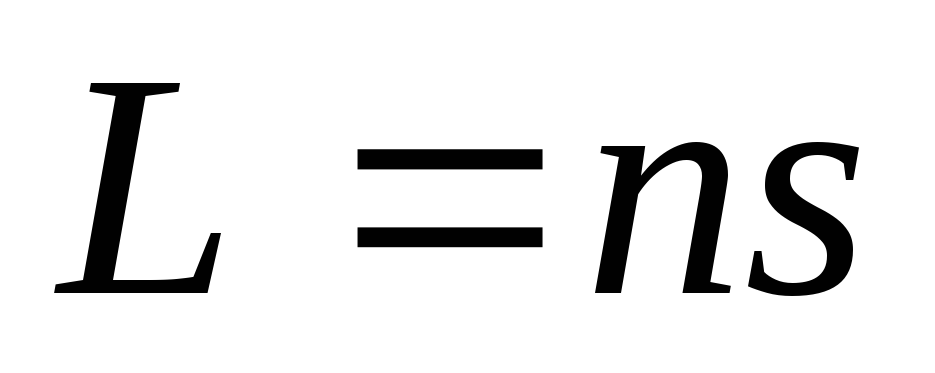 Выразите угол полного внутреннего отражения через показатели преломления сред. Как изменится формула для границы раздела среды и вакуума?
Выразите угол полного внутреннего отражения через показатели преломления сред. Как изменится формула для границы раздела среды и вакуума?
4.3 Решение задач
Задача 7. Луч света падает на границу раздела двух сред под углом 30о. Показатель преломления первой среды равен 2,4. Определите показатель преломления второй среды, если отраженный и преломленный лучи перпендикулярны друг другу.
Задача 8. В блоке оптического стекла с показателем преломления имеется наполненная воздухом полость в виде плоскопараллельной пластинки толщиной 0,2 см. Луч света падает на границу раздела стекло-воздух под углом 30о. Определите смещение луча после прохождения через воздушную полость.
Задача 9. Сечение стеклянной призмы имеет форму равностороннего треугольника. Луч света падает из воздуха на одну из граней перпендикулярно ей. Найдите угол между лучом, выходящим из призмы, и продолжением падающего луча. Показатель преломления стекла равен 1,5.
5. Домашнее задание
5.2 Решение задач
Задача 1. Человек видит свое изображение в плоском зеркале. На какое расстояние нужно передвинуть зеркало, чтобы изображение сместилось на 1 м от человека,
Задача 2. Отражающая поверхность зеркала составляет с плоскостью стола угол 1350. По направлению к зеркалу катится шар со скоростью
2 м/с. В каком направлении и с какой скоростью движется изображение шара?
Принцип Ферма
- Главная страница 🏠
- 📚 Библиотека
- 👉 Оптика 👈 org/ListItem»> Курс лекций по оптике
- Принцип Ферма
Нужна помощь в написании работы?
Узнать стоимость
Распространение света из одной точки А в другую точку В проходит таким образом, чтобы вариация времени dt была равна нулю. Если среда оптически неоднородна, весь путь разбивают на элементарные dli участки и тогда
, а , а (1)
Учитывая принцип Ферма запишем
(2)
Это и есть математическое выражение принципа Ферма. Ввиду того, что минимальное расстояние между двумя точками есть прямая линия, скрепляющая эти точки, прямолинейное распространение света в однородной среде является прямым следствием принципа Ферма. На основе принципа Ферма выводятся законы отражения и преломления света.
Пусть из т. А луч света падает на зеркальную поверхность и, отражаясь, попадает в т. В (рис. 1). Он может идти или по пути АОВ или АО1В. Исходя из принципа Ферма, найдем вариацию времени и приравняем нулю. Спроецируем т. А и В получим А1 и В1. А1О обозначим через х, а А1В1=а=const.
AA1=h2; BB1=h3 (3)
Время прохождения света из т.А в т.В
(4)
Видим, что время t зависит от х, т.е. от положения т.О. Согласно принципу Ферма имеем
(5)
Отсюда
sinα+sinα1=0 и α=-α1 (6)
Знак минус показывает, что углы a и a1 расположены по разные стороны нормали. Таким образом, минимальным является путь при котором a=-a1. Аналогичным образом выводится и закон преломления.
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
Расчет стоимостиГарантииОтзывы
Поможем написать любую работу на аналогичную тему
Реферат
Принцип Ферма
От 250 руб
Контрольная работа
Принцип Ферма
От 250 руб
Курсовая работа
Принцип Ферма
От 700 руб
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Поделись с друзьями
- Содержание
- Меню
Введение в волновую теорию света
Энергетические величины
Фотометрические величины
Интерференция света.
 Когерентность
КогерентностьЦвета тонких пленок
Многолучевая интерференция
Применение интерференции
Дифракция света. Принцип Гюйгенса-Френеля
Метод зон Френеля
Добавить в избранное (необходима авторизация)
Принцип Ферма — frwiki.wiki
Не следует путать с теоремой Ферма .
Принцип Ферма — это физический принцип , приписываемый Пьеру де Ферма , который является основой оптической геометрии. Он описывает форму оптического пути о наличии светового луча и формулируется следующим образом :
Свет распространяется от одной точки к другой по таким траекториям, что продолжительность путешествия является локально экстремальной (локально означает: для «малой» траектории).
Основное следствие принципа Ферма — прямолинейное распространение световых лучей в однородных средах . В самом деле, в однородной среде время прохождения пропорционально длине пути, а кратчайший путь в евклидовом пространстве от одной точки к другой — это прямая линия .
Он позволяет найти большинство результатов геометрической оптики , в частности законы отражения на зеркалах, законы преломления , закон Снеллиуса-Декарта и т. Д.
Резюме
- 1 История
- 2 Стационарное или минимальное время в пути
- 3 Формулировка принципа Ферма с использованием оптического пути
- 3.
 1 Случай однородной среды
1 Случай однородной среды - 3.2 Случай неопределенной сплошной среды
- 3.
- 4 Последствия
- 4.1 Принцип обратного возврата света
- 4.2 Законы Снеллиуса-Декарта
- 4.3 Обобщение законов Декарта на случай любой сплошной среды
- 4.3.1 Случай плоского пути
- 4.3.2 Общий случай
- 5 Примечания и ссылки
- 6 См. Также
- 6.1 Библиография
- 6.2 Статьи по теме
- 6.3 Внешние ссылки
Исторический
Этот принцип получил свое название от Пьера де Ферма , который сформулировал его в 1657 году, но не представил свою диссертацию « Synthèse pour les réfractions» до 1662 года . В то время как Рене Декарт в « La Dioptrique» объяснил законы оптики, проводя «аналогию между световыми лучами и траекториями мяча, отправленного играющим на ладони» , Ферма основывается на этом принципе финалиста, который он считает наиболее «вероятным. «:
«Эта природа всегда действует простейшими средствами, то есть кратчайшими путями, когда не требуется больше времени, или, во всяком случае, в кратчайшие сроки, чтобы сократить его работу и подойти к концу.
операция раньше. »
В 1746 году Мопертюи использовал эквивалентный принцип финалиста, чтобы ввести принцип наименьшего действия , который позже разработали Эйлер и Лагранж .
В 1924 году Луи де Бройль идентифицировал принцип Ферма и принцип наименьшего действия, предложив, чтобы каждая массивная частица была связана с волной: это открыло путь для дуальности волна-частица, ведущего к уравнению Шредингера , фундаментальному в квантовой механике .
Стационарное или минимальное время в пути
Стационарные оптические пути при отражении в вогнутом зеркале
Принцип Ферма был изложен выше в его общей форме, но должен быть изложен в более строгой форме:
Свет распространяется из одной точки в другую по таким траекториям, что продолжительность поездки остается неизменной .
Действительно, если в большинстве случаев мы встречаем пути с минимальным временем в пути, мы не должны забывать, что могут существовать и другие ситуации. Например, чтобы перейти из точки A в точку B, расположенную внутри вогнутого зеркала, показанного напротив, отражаясь от поверхности только один раз, свет может пройти два пути минимальной продолжительности (красный) и путь максимальной продолжительности (зеленый ) среди маршрутов, состоящих из двух участков AM и BM. Изучение длины пути выявило бы три локальных экстремума, два минимума и один максимум, для этого типа путешествия.
ВMBзнак равноВM+MB{\ displaystyle AMB = AM + MB}
Например, чтобы перейти из точки A в точку B, расположенную внутри вогнутого зеркала, показанного напротив, отражаясь от поверхности только один раз, свет может пройти два пути минимальной продолжительности (красный) и путь максимальной продолжительности (зеленый ) среди маршрутов, состоящих из двух участков AM и BM. Изучение длины пути выявило бы три локальных экстремума, два минимума и один максимум, для этого типа путешествия.
ВMBзнак равноВM+MB{\ displaystyle AMB = AM + MB}
Термин « стационарный» можно понять из этого примера. Если какая-либо точка M выполняет бесконечно малое смещение первого порядка на поверхности зеркала, изменение оптического пути также является первым порядком. С другой стороны, если мы рассмотрим три зоны, которые соответствуют экстремумам, то смещение точки первого порядка приводит к изменению оптического пути второго порядка или даже ниже. Другими словами, когда точка M движется по зеркалу, изменение оптического пути происходит быстро почти везде, но очень медленно в окрестности трех конкретных точек, где он становится почти нулевым, отсюда и использование слова «стационарный». «.
«.
Однако, если две точки соединены достаточно коротким путем, этот путь минимизирует продолжительность по сравнению с другими ближайшими возможными путями. Вернемся к примеру с вогнутым зеркалом, если две точки находятся на зеленой траектории и достаточно близки к его точке «отскока» на вогнутом зеркале, то для длины траектории больше нет трех экстремумов, а только один, который является минимумом. В общем случае траектория света между двумя точками является точкой пересечения или минимумом для множества геометрически возможных траекторий, соединяющих их. ВMBзнак равноВM+MB{\ displaystyle AMB = AM + MB}
Та же проблема обнаруживается в формулировке принципа наименьшего действия , который для механики является тем же, что принцип Ферма для оптики, в определении минимальных поверхностей (которые не обязательно … минимальны) или в определении геодезических .
Формулировка принципа Ферма с использованием оптического пути
Случай однородной среды
Оптический путь света , чтобы перейти от точки к точке в однородной среде, обозначается , определяется как число пропорционально времени , затраченному луча , чтобы перейти от к , коэффициент пропорциональности такова , что равен дистанция для курса в вакууме. Призывая к быстроте света в середине и в вакууме, мы, следовательно, имеем и , откуда ; коэффициент пропорциональности называется показателем преломления среды. Таким образом, оптический путь определяется:
В{\ displaystyle A}B{\ displaystyle B}L(В,B){\ Displaystyle L (А, В)}В{\ displaystyle A}B{\ displaystyle B}L(В,B){\ Displaystyle L (А, В)}ВB{\ displaystyle AB}v{\ displaystyle v}против{\ displaystyle c}L(ВB)знак равноαВBv{\ Displaystyle L (AB) = \ альфа {\ tfrac {AB} {v}}}αВBпротивзнак равноВB{\ Displaystyle \ альфа {\ tfrac {AB} {c}} = AB}L(В,B)знак равнопротивvВB{\ Displaystyle L (A, B) = {\ tfrac {c} {v}} AB}нетзнак равнопротивv{\ Displaystyle п = {\ tfrac {c} {v}}}
Призывая к быстроте света в середине и в вакууме, мы, следовательно, имеем и , откуда ; коэффициент пропорциональности называется показателем преломления среды. Таким образом, оптический путь определяется:
В{\ displaystyle A}B{\ displaystyle B}L(В,B){\ Displaystyle L (А, В)}В{\ displaystyle A}B{\ displaystyle B}L(В,B){\ Displaystyle L (А, В)}ВB{\ displaystyle AB}v{\ displaystyle v}против{\ displaystyle c}L(ВB)знак равноαВBv{\ Displaystyle L (AB) = \ альфа {\ tfrac {AB} {v}}}αВBпротивзнак равноВB{\ Displaystyle \ альфа {\ tfrac {AB} {c}} = AB}L(В,B)знак равнопротивvВB{\ Displaystyle L (A, B) = {\ tfrac {c} {v}} AB}нетзнак равнопротивv{\ Displaystyle п = {\ tfrac {c} {v}}}
Свет «с большим трудом» распространяется в средах, отличных от вакуума. Пример: луч света проходит через слой воды толщиной 5 см. В то же время другой луч света проходит через 5 см воздуха. Вода имеет показатель преломления, а воздух — показатель, практически равный показателю вакуума . В воде луч света прошел большое расстояние . В воздухе луч пройдет большое расстояние . Луч пройдет более длинный оптический путь в воде, чем в воздухе.
нетзнак равно1,33{\ displaystyle n = 1,33}нетзнак равно1{\ Displaystyle п = 1}Dзнак равно1,33⋅5знак равно6,65противм{\ Displaystyle D = 1,33 \ cdot 5 = 6,65 \ mathrm {см}}D′знак равно1⋅5знак равно5противм{\ Displaystyle D ‘= 1 \ cdot 5 = 5 \ mathrm {см}}
В воде луч света прошел большое расстояние . В воздухе луч пройдет большое расстояние . Луч пройдет более длинный оптический путь в воде, чем в воздухе.
нетзнак равно1,33{\ displaystyle n = 1,33}нетзнак равно1{\ Displaystyle п = 1}Dзнак равно1,33⋅5знак равно6,65противм{\ Displaystyle D = 1,33 \ cdot 5 = 6,65 \ mathrm {см}}D′знак равно1⋅5знак равно5противм{\ Displaystyle D ‘= 1 \ cdot 5 = 5 \ mathrm {см}}
Случай любой сплошной среды
Мы рассматриваем две точки, бесконечно соседние и удаленные на расстояние . Оптический путь, разделяющий эти две точки, определяется как ; — это разность оптического пути или даже бесконечно малый унитарный элемент оптического пути. Чтобы найти оптический путь, разделяющий две точки и на этой кривой, достаточно произвести интегральную сумму всех элементов по криволинейной координате, разделенной точками и : ds{\ displaystyle \ mathrm {d} s}dLзнак равнонет.ds{\ Displaystyle \ mathrm {d} L = п. \ mathrm {d} s}dL{\ displaystyle \ mathrm {d} L}L(ВB){\ Displaystyle L (AB)}В{\ displaystyle A}B{\ displaystyle B}dL{\ displaystyle \ mathrm {d} L}s{\ displaystyle s}В{\ displaystyle A}B{\ displaystyle B}
Затем формулируется принцип Ферма:
Между двумя точками и , достигаемые светом, оптический путь, проходящий вдоль пути, является стационарным.
В{\ displaystyle A}B{\ displaystyle B}
Последствия
Принцип обратного возврата света
Путь, по которому свет идет от одной точки к другой, не зависит от направления распространения света.
Стационарность оптического пути позволяет сделать некоторые соображения. Между двумя точками A и B, обе на криволинейной траектории светового луча, распространяющегося в неоднородной среде, мы можем выразить интеграл оптического пути следующим образом:
Учитывая, что это криволинейный элемент координат от B до A, мы можем написать . В случае исследования оптической системы это означает, что мы можем изучать распространение света и путь световых лучей, не беспокоясь о направлении распространения.
ds′знак равно-ds{\ displaystyle \ mathrm {d} s ‘= — \ mathrm {d} s}L(ВB)знак равноL(BВ){\ Displaystyle L (AB) = L (BA)}
В случае исследования оптической системы это означает, что мы можем изучать распространение света и путь световых лучей, не беспокоясь о направлении распространения.
ds′знак равно-ds{\ displaystyle \ mathrm {d} s ‘= — \ mathrm {d} s}L(ВB)знак равноL(BВ){\ Displaystyle L (AB) = L (BA)}
Предупреждение: на практике бездумное использование этого принципа приводит к абсурду. Мы знаем, например, что объектив никогда не дает точного изображения световой точки, а дает всегда более или менее размытое изображение. Было бы ребячеством думать, что лучи, образующие это пятно, отраженные обратно в линзу плоским зеркалом, могут преобразовать точку четкого изображения на другой стороне … Здесь идет речь не о принципе, а о факте. о желании применить это неправильно.
Законы Снеллиуса-Декарта
Плоскость вектора нормали разделяет две среды с показателями преломления и . Световой луч начинается от точки , расположенной в первой среде, пересекает в и достигает точку . Проблема состоит в том, чтобы найти положение из принципа Ферма. п{\ displaystyle P}нет→{\ displaystyle {\ vec {n}}}нет1{\ displaystyle n_ {1}}нет2{\ displaystyle n_ {2}}В1{\ displaystyle A_ {1}}п{\ displaystyle P}M{\ displaystyle M}В2{\ displaystyle A_ {2}}M{\ displaystyle M}
п{\ displaystyle P}нет→{\ displaystyle {\ vec {n}}}нет1{\ displaystyle n_ {1}}нет2{\ displaystyle n_ {2}}В1{\ displaystyle A_ {1}}п{\ displaystyle P}M{\ displaystyle M}В2{\ displaystyle A_ {2}}M{\ displaystyle M}
Оптический путь от к является , следовательно: В1{\ displaystyle A_ {1}}В2{\ displaystyle A_ {2}}Lзнак равнонет1В1M+нет2В2M{\ displaystyle L = n_ {1} A_ {1} M + n_ {2} A_ {2} M}
dLзнак равнонет1В1M→В1MdM→+нет2В2M→В2MdM→знак равно(нет1В1M→В1M+нет2В2M→В2M)dM→{\ displaystyle \ mathrm {d} L = n_ {1} {{\ overrightarrow {A_ {1} M}} \ over A_ {1} M} \ mathrm {d} {\ overrightarrow {M}} + n_ {2 } {{\ overrightarrow {A_ {2} M}} \ over A_ {2} M} \ mathrm {d} {\ overrightarrow {M}} = \ left (n_ {1} {{\ overrightarrow {A_ {1}) M}} \ over A_ {1} M} + n_ {2} {{\ overrightarrow {A_ {2} M}} \ over A_ {2} M} \ right) \ mathrm {d} {\ overrightarrow {M} }}
Стационарное состояние , поэтому результаты ортогональны плоскости , коллинеарны с ; световой луч, таким образом , включается в плоскости , проходящей через и ортогонально (первый закон Декарта) и дает: ( второй закон Декарта ). L{\ displaystyle L}dLзнак равно0{\ Displaystyle \ mathrm {d} L = 0}нет1В1M→В1M+нет2В2M→В2M{\ displaystyle n_ {1} {\ tfrac {\ overrightarrow {A_ {1} M}} {A_ {1} M}} + n_ {2} {\ tfrac {\ overrightarrow {A_ {2} M}} {A_ {2} M}}}п{\ displaystyle P}нет→{\ displaystyle {\ vec {n}}}В1{\ displaystyle A_ {1}}В2{\ displaystyle A_ {2}}п{\ displaystyle P}(нет1В1M→В1M+нет2В2M→В2M)∧нет→знак равно0→{\ displaystyle \ left (n_ {1} {\ tfrac {\ overrightarrow {A_ {1} M}} {A_ {1} M}} + n_ {2} {\ tfrac {\ overrightarrow {A_ {2} M}) } {A_ {2} M}} \ right) \ wedge {\ vec {n}} = {\ vec {0}}}нет1грехя1знак равнонет2грехя2{\ Displaystyle п_ {1} \ грех i_ {1} = n_ {2} \ грех i_ {2}}
L{\ displaystyle L}dLзнак равно0{\ Displaystyle \ mathrm {d} L = 0}нет1В1M→В1M+нет2В2M→В2M{\ displaystyle n_ {1} {\ tfrac {\ overrightarrow {A_ {1} M}} {A_ {1} M}} + n_ {2} {\ tfrac {\ overrightarrow {A_ {2} M}} {A_ {2} M}}}п{\ displaystyle P}нет→{\ displaystyle {\ vec {n}}}В1{\ displaystyle A_ {1}}В2{\ displaystyle A_ {2}}п{\ displaystyle P}(нет1В1M→В1M+нет2В2M→В2M)∧нет→знак равно0→{\ displaystyle \ left (n_ {1} {\ tfrac {\ overrightarrow {A_ {1} M}} {A_ {1} M}} + n_ {2} {\ tfrac {\ overrightarrow {A_ {2} M}) } {A_ {2} M}} \ right) \ wedge {\ vec {n}} = {\ vec {0}}}нет1грехя1знак равнонет2грехя2{\ Displaystyle п_ {1} \ грех i_ {1} = n_ {2} \ грех i_ {2}}
Эта демонстрация в основном принадлежит Мопертюи в 1744 году, почти через столетие после того, как Ферма сформулировал свой принцип.
Иллюстрацией этому служит так называемая проблема «спасателя». Этот, расположенный на пляже, должен отправиться на спасение утонувшего человека, находящегося в . Поскольку он бежит быстрее, чем плывет, его оптимальный путь (во времени) соответствует законам преломления, которые мы только что определили. {\ alpha} \; \ mathrm {d} t \ end {case}}}.
{\ alpha} \; \ mathrm {d} t \ end {case}}}.
Это кривая Рибокура .
Например, для (показатель преломления обратно пропорционален абсциссе) получаем αзнак равно1{\ Displaystyle \ альфа = 1}
другими словами, траектории — это круги.
Для (показатель преломления обратно пропорционален квадратному корню из абсциссы) получаем αзнак равно2{\ Displaystyle \ альфа = 2}
кривая — циклоида . Этот случай исторически интересен: именно этим методом Жан Бернулли доказал, что кривая брахистохрона (минимизирующая время пробега материальной точки) является циклоидой, показав, что проблемы механики и оптики фактически эквивалентны. Бернард Pire, » La Dioptrique (Р. Декарт) » , на энциклопедический universlis (доступ к 20 марта 2015 года ) .
Бернард Pire, » La Dioptrique (Р. Декарт) » , на энциклопедический universlis (доступ к 20 марта 2015 года ) .
— Луи Кутюрат , Логика Лейбница из неопубликованных документов , Париж, Алкан,( читать онлайн ), По принципу наименьшего действия , с. 577-581.

Смотрите также
Библиография
- Хосе-Филипп Перес и Эрик Антерье, Оптика: основы и приложения , Dunod, 2004.
- Общие механические работы серии Schaum
- Born & Wolf, Принципы оптики
- Жорж Брюа, Оптика
- Жан Басс, Упражнения по математике , Masson, 1965, стр. 381–385
Статьи по Теме
- Преломление
- Принцип наименьшего действия
Внешние ссылки
- Глава викиучебника фотографии, посвященная распространению света и особенно принципу Ферма .
- Жан Гунон, Принцип Ферма: приложения к отражению и преломлению (файл PDF)
- Геометрическая демонстрация в связи с Гюйгенсом принципа Ферма применяется к рефракции.
- Курс оптики: принцип Ферма (фемто-физика)
<img src=»https://fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
Теорема Ферма и 380 лет на ее доказательство
Не много идей и рассуждений занимали мысли и внимание ученых-математиков и самоучек так долго, как Великая теорема Ферма. Эта теорема – самое известное математическое утверждение, на доказательство которого понадобилось больше 380 лет. Более того, в 1908 году ажиотаж вокруг нее был накален после обещания присудить премию за ее решение.
Эта теорема – самое известное математическое утверждение, на доказательство которого понадобилось больше 380 лет. Более того, в 1908 году ажиотаж вокруг нее был накален после обещания присудить премию за ее решение.
Вся сложность доказательства этой теоремы состояла в том, что нужно было доказать отсутствие решения. Казалось, что ее суть так легко понять, но как тяжело было ее решить!
Доказательство этой единой математической теоремы тесно связано с развитием истории математики, формированием новых направлений и углублением человеческого знания об абстракциях. О том, кто доказал теорему Ферма и сколько времени на это ушло, мы поговорим в этой статье.
Юрист Пьер де Ферма – «король среди любителей математики»
Пьер де Ферма (1601-1665) – французский судья и самоучка, известен как автор самой сложной теоремы всех времен. Свою карьеру и жизненный путь Ферма связал с юриспруденцией, и работал в местном парламенте маленького городка Кастр (до 1789 года «парламентом» во Франции называли суды).
Помимо блестящей карьеры в суде, Пьер также увлекался математикой, был самоучкой, черпая свои знания из книг и переписки со своими сверстниками, учеными и философами того времени – Декартом, Паскалем, Бернардом де Бесси и другими. Несмотря на его статус любителя, профессиональные математики ценили переписку с Пьером Ферма и называли его «королем среди любителей». Главный интерес он проявлял к теории чисел, которая в начале 17 столетия стала очень популярной во Франции благодаря новым изданиям трудов древнегреческих математиков. Изучая их, Ферма смог обосновать основные проблемы решения многочисленных задач, которые стали основными для развития классической теории чисел.
Больше всего влияния на Пьера Ферма оказала книга «Арифметика», изучая которую он исписывал поля собственными рассуждениями, впоследствии изменившими развитие математического мышления. В этой книге греческий математик и отец алгебры Диофант Александрийский описывал натуральные числа Пифагора. На основании «Арифметики» Ферма, решая задачи сложных уравнений с несколькими неизвестными, сформулировал легендарное утверждение, позже названное в его честь Великой теоремой Ферма. Доказательство теоремы заняло около 380 лет.
Доказательство теоремы заняло около 380 лет.
Наибольший научный вклад Ферма в развитие математики в том, что он обратил внимание на роль, которую занимают простые числа.
Великая теорема Ферма
Рассуждения Ферма о натуральных числах были не единственными, и даже не Пифагор первым их обосновал. История исчислений натуральных чисел была известна еще в Шумере и Древней Индии, но только Пифагор записал эти рассуждения в современной математической формуле: x2 + y2 = z2, а Ферма увеличил количество неизвестных: xn + yn = zn.
Особый интерес к натуральным числам возродился в начале 17 столетия, после издания «Арифметики» Диофанта. Эта книга стала особо популярной среди ученых и философов, которые пытались рационально объяснить мироустройство, исключая всякое божественное начало. Среди них был и Пьер Ферма.
Во время чтения «Арифметики» ему в голову пришла идея заменить показатель степени 2 в теореме Пифагора любым другим числом. Тогда он понял: решения такому суждению не существует, и это можно доказать. Но само доказательство не записал из-за отсутствия места в книжке. На страницах книги II, обдумывая задачу 8, Ферма записал только следующее:
Тогда он понял: решения такому суждению не существует, и это можно доказать. Но само доказательство не записал из-за отсутствия места в книжке. На страницах книги II, обдумывая задачу 8, Ферма записал только следующее:
«Невозможно разложить куб на два куба, биквадрат на два биквадрата, на две степени с тем же показателем. Я нашел этому поистине чудесное доказательство, но поля книги слишком узки для него».
Доказать выдвинутое утверждение Ферма, что нет простого решения для уравнения, например, 32+42=52, когда n˃2, являющегося целым числом, впоследствии смогли немногие. Сегодня известно, что Ферма доказал отсутствие решения для n = 4. А из его переписки известно, что он также осуществил и доказательство для n = 3, но найти его среди писем не удалось.
Рассуждение Ферма о простых числах стало широко известным после того, как в 1670 году его сын Самюэль опубликовал книгу «Арифметика», но уже с комментариями отца. Путь доказательства занял более чем 350 лет. Сотни математиков пытались доказать утверждение Ферма, а получилось это лишь у Эндрю Уайлса в 1993 году.
Сотни математиков пытались доказать утверждение Ферма, а получилось это лишь у Эндрю Уайлса в 1993 году.
Знаменательно, что очевидной практической ценности Великая теория Ферма не имеет. Но ее формулировка будоражила умы сотен математиков, что, в свою очередь, действительно приносило плоды в развитии теории математики. Помимо легендарной Великой (или «Последней», как ее еще называют) теоремы Ферма, не менее важную роль в развитии математики занимает другая теорема – малая.
Малая теорема Ферма – это еще одно знаменитое рассуждение, которое Ферма описал в письме к своему другу в 1640 году. Читается эта теорема так: если целое число п не делится на простое число р, то пр — 1—1 делится на число р.
Доказательство этой теоремы не заняло столько времени и усилий, как в случае с ее предшественницей, но ее роль в развитии математического мышления несомненно бесценна. Сегодня она является одной из самых важных теорем элементарной теории чисел, криптографии и современной алгебры.
Великая теорема Ферма: доказательство
Великая теорема Ферма не была детально объяснена даже самым автором. Может быть, его бумаги затерялись, но, скорее всего, в этом он сам не видел необходимости.
Все дело в том, что скупое, на наш взгляд, объяснение утверждения на полях книжки «Арифметика» непонятно для нас, но так не будет казаться, если учесть контекст, в котором Ферма развивал свои идеи. На протяжении своей жизни он вел активную переписку с другими учеными и любителями математики, и это были долгие дискуссии в письменной форме, где очень важно было понимание логичности и чередования писем. Это было общество, члены которого понимали друг друга с полуслова. Поэтому в многословности в такой среде просто не было необходимости.
Другим предположением, почему Ферма не развил детальное объяснение своей теоремы, в том, что он не был профессиональным математиком, как, к примеру, Рене Декарт или Франсуа Виет, и тем более он не пытался достичь признания в этой сфере, помимо одобрения друзей и единомышленников, которое, очевидно, уже получил. Но, тем не менее, Ферма понимал оригинальность своих идеи и подходов, а также то, что его методы мышления помогают другим математикам.
Но, тем не менее, Ферма понимал оригинальность своих идеи и подходов, а также то, что его методы мышления помогают другим математикам.
Увлекаясь теорией простых чисел, Ферма понимал, что натуральные числа не являются бесконечными. Он полагал, что найденный им метод является общим, и его можно будет использовать, чтобы доказать любые теоремы натуральных чисел. Но реальность оказалась иной. Метод оказался не таким универсальным, как рассуждал Ферма. И на доказательство этого ученым понадобилось более трех столетий.
В начале 1990-х годов теорему Ферма уже доказали для показателей разных степеней вплоть до 4 000 000. Но все-таки ученые продолжали искать показатель, для которого теорема окажется ложной.
Математик из Принстонского университета Эндрю Уайлс смог доказать теорему в 1993 году, исполнив свою мечту, которая появилась у него в 10-летнем возрасте. На протяжении долгих лет он следил за многочисленными методами, с помощью которых разные ученые пытались доказать теорему Ферма. И в 1986 году, оставив все свои проекты, он сам занялся доказательством этой теории, которое заняло 7 лет.
И в 1986 году, оставив все свои проекты, он сам занялся доказательством этой теории, которое заняло 7 лет.
В своем доказательстве он использовал сложные методы вычисления. Его работа опиралась на труды гигантов из разных направлений математики. Теорема Ферма – это сложная головоломка, решить которую стало возможным, сочетая поэтапно разные подходы и методы доказательства. Исписывая тысячи страниц, Уайлс смог доказать Великую теорему Ферма.
Это был долгий путь, который заключался в подсчете бесконечностей, рассмотрении всех ранее использованных подходов с целью найти собственный метод доказательства. Сначала Уайлс подсчитал все эллиптические функции, а также модулярные эллиптические функции, где как одних, так и других бесконечно много, чтобы показать, что их вычисления эквивалентны. Хотя этот подход оказался неэффективным, он помог осознать, куда двигаться дальше. Эти вычисления помогли Уайлсу понять, что нужно вместо доказательства гипотезы Таниямы-Симуры для эллиптических кривых, доказать эту же гипотезу лишь для полустабильных кривых.
Далее он обратился к теории Галуа, и с ее помощью смог определить эллиптические уравнения и доказать, что можно провести ассоциацию с элементами модулярных форм. Так Уайлсу удалось переформулировать задачу в более податливые понятия. Но это был только первый шаг, который занял два года.
Позднее он пробовал решить теорему с помощью теории Ивасавы, но ее оказалось недостаточно, поэтому Уайлс использовал еще и инструменты системы Эйлера. Однако позже он понял, что самым подходящим подходом является подход Колывагина-Флаха. И здесь новая тактика начала приносить плоды.
В начале 1993 года Уайлс подключил к решению теоремы друга Ника Каца. Они решили, что в основании нового университетского курса «Вычисления на эллиптических кривых» они смогут поэтапно изложить теорему Ферма. Во время этого курса проверялись разные этапы доказательства.
Окончательные результаты и первое публичное доказательство Уайлс представил на конференции в Кембридже в июне 1993 года. Для этого эму понадобилось три часа. Рукопись занимала 200 страниц. Потом решение задачи подтвердил комитет экспертов, и, после уточнения нескольких неточностей, в 1995 году теорема Ферма официально была доказана.
Рукопись занимала 200 страниц. Потом решение задачи подтвердил комитет экспертов, и, после уточнения нескольких неточностей, в 1995 году теорема Ферма официально была доказана.
Вклад Пьера Ферма в развитие науки
История математики просто немыслима без вклада ученого-самоучки Пьера Ферма. Но из-за уединенного образа жизни и узкого круга общения его идеи ученые смогли оценить лишь после его смерти и благодаря его сыну Сэмюелю, который в 1870 году начал публиковать наброски и размышления отца.
Ферма и его идеи во многом стали основополагающими для развития новых математических теорий. Его сильной стороной был творческий подход и неограниченность рамками одной дисциплины: Ферма применял алгебраические методы в геометрических задачах, что заложило основания аналитической геометрии. Поэтому справедливо считать, что Ферма, наравне с Декартом, повлиял на формирование аналитической геометрии, а также то, что в своей переписке с Паскалем он заложил основы теории вероятности.
Идеи и подходы Пьера Ферма были настолько неординарными, что его рассуждения и толкования решения задач повлияли на Ньютона и даже Галилея, а другой французский математик Марен Мерсенн в своей книге «Универсальная гармония» вообще назвал Ферма математическим гением.
Кстати, если вам интересно, как развить мышление, лучше понимать абстракции и удерживать в голове длинные формулы, замечать закономерности и создавать новые идеи, предлагаем вам попробовать наши программы «Мнемотехники» и «ТРИЗ на практике». И пусть напрямую с математикой они не связаны, зато представленная в них информация, упражнения и задания прекрасно подходят для повышения уровня интеллекта, а его, как вы знаете, можно использовать в любой области.
Желаем удачи и до встречи на уроках наших курсов!
Ключевые слова:1LLL
Теорему Ферма снова «доказали» — Российская газета
Завистники утверждают, что французский математик Пьер Ферма вписал свое имя в историю всего одной фразой. На полях рукописи с формулировкой знаменитой теоремы в 1637 году он сделал пометку: «Я нашел удивительное решение, но здесь маловато места, чтобы его поместить». Тогда и началась удивительная математическая гонка, в которую наряду с выдающимися учеными включилась армия дилетантов.
В чем коварство задачи Ферма? На первый взгляд, она понятна даже школьнику.
В основе — известная каждому теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: х2 + у2 = z2. Ферма утверждал: уравнение при любых степенях больше двух не имеет решения в целых числах.
Казалось бы, просто. Протяни руку, и вот ответ. Неудивительно, что академии разных стран, научные институты, даже редакции газет были завалены десятками тысяч доказательств. Их число беспрецедентно, уступает разве что проектам «вечных двигателей». Но если эти сумасшедшие идеи серьезная наука давно не рассматривает, то работы «фермистов» честно и заинтересованно изучает. И, увы, находит ошибки. Говорят, что за три с лишним века образовалось целое математическое кладбище решений теоремы.
Не зря говорят: близок локоть, а не укусишь. Проходили года, десятилетия, века, и задача Ферма представлялась все более удивительной и заманчивой. Вроде бы простенькая, она оказалась не по зубам стремительно наращивающему мускулы прогрессу. Человек уже расщепил атом, добрался до гена, ступил на Луну, а Ферма не давался, продолжая манить потомков ложными надеждами.
Человек уже расщепил атом, добрался до гена, ступил на Луну, а Ферма не давался, продолжая манить потомков ложными надеждами.
Однако попытки одолеть научную вершину не прошли даром. Первый шаг сделал великий Эйлер, доказав теорему для четвертой степени, затем для третьей. В конце XIX века немец Эрнст Куммер довел число степеней до ста. Наконец, вооружившись компьютерами, ученые увеличили эту цифру до 100 тысяч. Но Ферма-то говорил о любых степенях. В этом состояла вся загвоздка.
Конечно, мучились ученые над задачей не из-за спортивного интереса. Знаменитый математик Давид Гильберт говорил, что теорема — это пример, как вроде бы малозначительная проблема может оказать на науку огромное влияние. Работая над ней, ученые открыли совершенно новые математические горизонты, например, были заложены фундаменты теории чисел, алгебры, теории функций.
И все же Великая теорема была в 1995 году покорена. Ее решение представил американец из Принстонского университета Эндрю Уайлс, и оно официально признано научным сообществом. Более семи лет жизни отдал он, чтобы найти доказательство. По мнению ученых, эта выдающаяся работа свела воедино труды многих математиков, восстановив утраченные связи между разными ее разделами.
Более семи лет жизни отдал он, чтобы найти доказательство. По мнению ученых, эта выдающаяся работа свела воедино труды многих математиков, восстановив утраченные связи между разными ее разделами.
— Итак, вершина взята, и наука ответ получила, — сказал корреспонденту «РГ» ученый секретарь Отделения математики Российской академии наук, доктор технических наук Юрий Вишняков. — Теорема доказана, пусть и не простейшим способом, на чем настаивал сам Ферма. А теперь желающие могут печатать свои варианты.
Однако семейство «фермистов» вовсе не собирается признавать доказательство Уайлса. Нет, они не опровергают решение американца, ведь оно очень сложное, а потому понятно лишь узкому кругу специалистов. Но не проходит недели, чтобы в Интернете ни появилось новое откровение очередного энтузиаста, «наконец-то поставившего точку в многолетней эпопее».
Кстати, буквально вчера в редакцию «РГ» позвонил один из старейших в нашей стране «фермистов» Всеволод Ярош: «А вы знаете, что теорему Ферма я доказал еще до Уайлса. Более того, потом нашел у него ошибку, о чем написал выдающемуся нашему математику академику Арнольду с просьбой напечатать об этом в научном журнале. Теперь жду ответа. Переписываюсь по этому поводу и с французской академией наук».
Более того, потом нашел у него ошибку, о чем написал выдающемуся нашему математику академику Арнольду с просьбой напечатать об этом в научном журнале. Теперь жду ответа. Переписываюсь по этому поводу и с французской академией наук».
И вот только что, как сообщается в ряде СМИ, с «легким изяществом раскрыл великую тайну математики», еще один энтузиаст — бывший генеральный конструктор ПО «Полет» из Омска, доктор технических наук Александр Ильин. Решение оказалось настолько простым и коротким, что поместилось на маленьком участке газетной площади одного из центральных изданий.
Редакция «РГ» обратилась в ведущий в стране Институт математики им. Стеклова РАН с просьбой оценить это решение. Ученые были категоричны: нельзя комментировать газетную публикацию. Но после долгих уговоров и учитывая повышенный интерес к знаменитой задаче, согласились. По их словам, в опубликованном очередном доказательстве допущено несколько принципиальных ошибок. Кстати, их вполне мог бы заметить даже студент математического факультета.
И все же редакция хотела получить информацию из первых рук. Тем более что вчера в академии авиации и воздухоплавания Ильин должен был представить свое доказательство. Однако оказалось, что о такой академии мало кто знает даже среди специалистов. А когда все-таки с величайшим трудом удалось разыскать телефон ученого секретаря этой организации, то, как выяснилось, он даже не подозревал, что именно у них должно состояться столь историческое событие. Словом, корреспонденту «РГ» стать свидетелем мировой сенсации так и не удалось.
Law Farm — Район сохранения почв и водных ресурсов округа Пискатакис
перейти к содержаниюЮридическая фермаКейси Вебер2022-07-05T16:33:19+00:00
Юридическая ферма округа Пискатакис по сохранению почвы и воды
Ознакомьтесь с картами ниже, чтобы узнать о них, чтобы узнать о них наши последние проекты и дополнения к Law Farm и истории земли!
The Law Farm предоставляет посетителям возможность узнать о том, как планирование и содержание общественного леса может оказать долгосрочное положительное влияние на множество важных факторов, таких как биоразнообразие экосистемы, здоровье наших жителей, доступ к отдыху на природе и для него. и доступ к безопасным общественным землям.
и доступ к безопасным общественным землям.
Через Law Farm PCSWCD предоставляет уникальные возможности для отдыха и обучения в округе Пискатакис, а также общественное пространство для активного обучения. В округе Пискатакис леса обеспечивают средства к существованию для многих наших жителей, а процветающий общественный лес представляет собой здоровую экономику, возможности для наших детей, красоту нашего дома и нашу любовь и уважение к природе.
Пожалуйста, просмотрите все разделы ниже, чтобы увидеть все развлечения, исследования и красоту, которые ждут на ферме закона!
Образовательные туры можно организовать через PCSWCD по электронной почте [email protected] или по телефону 564-2321, добавочный номер 3.
Подробнее о Law Farm!
НОВИНКА! Учебный класс — Возможна аренда!
Вам нужно место для следующей встречи? Подумайте об аренде открытого класса Law Farm! В этом здании есть боковые двери, которые полностью открываются, создавая защищенное, свежее и живописное место. На территории также есть столы для пикника и компостная уборная.
На территории также есть столы для пикника и компостная уборная.
Все доходы от аренды классной комнаты пойдут на поддержку образовательных программ PCSWCD.
FMI по аренде, пожалуйста, свяжитесь с отделом почво-водосбережения округа Пискатакис по адресу [email protected], 207-564-2321 доб. 3.
The Law Farm History
Акры общественного леса Law Farm дают возможность семьям путешествовать пешком, заниматься спортом и устраивать пикники вместе, а также предоставляют место, чтобы узнать больше о методах ведения лесного хозяйства. , природоохранные мероприятия и агролесоводство.
Стивен и Элейн Лоу приобрели эту землю в 1945 году и передали ее в 2009 году округу охраны почвы и воды округа Пискатакис после поиска организации, которая могла бы лучше всего выполнять двойную миссию управления лесами для настоящего и будущих поколений и также обучая других важности рационального использования наших природных ресурсов.
С тех пор наш округ работает с грантодателями, волонтерами, местными предприятиями и организациями, чтобы превратить собственность в привлекательное и динамичное общественное пространство под открытым небом.
Развлечение на юридической ферме
Май 2022 — Учебный класс юридической фермы ЗАВЕРШЕН! Спасибо Кори Хиллу и его команде из Чарльстонского исправительного учреждения за то, что взялись за этот проект!
Бесплатная библиотека Томпсона объединилась с PCSWCD, чтобы организовать прогулку по истории на ферме закона! Отправляйся туда и посмотри!
PCSWCD посвятил Bluebird Trail Линн Любас! Чтобы отпраздновать 12-летие службы Линн в PCSWCD, мы построили и выделили Линн новую тропу. На Тропе синих птиц есть смотровая скамейка, с которой открывается вид на поле, полное полевых цветов и три ящика для синих птиц. Кроме того, мы поделимся фотографиями этой тропы с камеры, чтобы мы все могли увидеть, что затевают твари на ферме закона!
Район сохранения почв и водных ресурсов округа Пискатакис приглашает вас исследовать общественный лес на ферме закона. Наши тропы проходят через заболоченные леса, демонстрационные участки агролесоводства и заболоченные земли северного белого кедра. Мы добавили несколько информационных знаков, которые предоставляют общественности информацию о многих природоохранных мероприятиях и проектах, реализуемых на ферме закона.
Наши тропы проходят через заболоченные леса, демонстрационные участки агролесоводства и заболоченные земли северного белого кедра. Мы добавили несколько информационных знаков, которые предоставляют общественности информацию о многих природоохранных мероприятиях и проектах, реализуемых на ферме закона.
The Law Farm — отличное место, чтобы прогуляться по лесу, устроить пикник с семьей, посмотреть и узнать о широком разнообразии местных видов деревьев, посаженных в лесу, покататься на снегоступах, беговых лыжах, понаблюдать за птицами и дикой природой. , пригласите молодежные группы для активного отдыха на природе и многое другое.
Надеемся, вам понравится красота и разнообразие Юридической фермы!
Проекты и достопримечательности фермы права
С тех пор как ферма права была передана в собственность Округа охраны почвы и воды округа Пискатакис, мы курировали несколько проектов по благоустройству земли.
Вот несколько проектов, в которых мы принимали участие:
Программа Dedicated Bench Program at the Law Farm:
Бесплатная библиотека Томпсона объединилась с PCSWCD, чтобы организовать Story Walk at the Law Farm! Отправляйтесь и посмотрите на это забавное дополнение к природным тропам! Делайте фотографии на ходу и делитесь ими, используя хэштег #dfstorywalk2021
21 июня 2019 года сотрудники PCSWCD, волонтеры Law Farm и участники лагеря PRYMCA Camp Katahdin посадили наш Детский сад опылителей «Круг подсолнухов» на Law Farm. Земля была подготовлена перед посадкой круга 21 июня и добавлен компост, который был щедро пожертвован компанией Jackson ReGenerational Farm. PCSWCD получил в дар сотни прекрасных многолетних растений от нескольких местных ферм и предприятий: Marr Pond Farm, Checkerberry Farm, Ellis’ Greenhouse & Nursery, Ripley Farm, Thompson Free Library, Trailside Gardens, Dover True Value и Bob’s Home and Garden. Это садовое пространство представляет собой общественное пространство, где можно устроить пикник, почитать книгу, насладиться природой и узнать о местных опылителях и растениях.
Земля была подготовлена перед посадкой круга 21 июня и добавлен компост, который был щедро пожертвован компанией Jackson ReGenerational Farm. PCSWCD получил в дар сотни прекрасных многолетних растений от нескольких местных ферм и предприятий: Marr Pond Farm, Checkerberry Farm, Ellis’ Greenhouse & Nursery, Ripley Farm, Thompson Free Library, Trailside Gardens, Dover True Value и Bob’s Home and Garden. Это садовое пространство представляет собой общественное пространство, где можно устроить пикник, почитать книгу, насладиться природой и узнать о местных опылителях и растениях.
Мы приветствовали Марту на юридической ферме в августе 2019 года! Теперь вы можете проехать мимо Law Farm и насладиться прекрасным видом «Марты», металлической скульптуры, созданной в сотрудничестве с Брюсом Таулом, Меррили Шон из Aeons by Design, Питером Крокеттом из Argyle Iron Works и Фредом Паттерсоном из Трой Индастриалз. 7-футовая скульптура является частью мультимедийной выставки «В промежутке между снежинками — выращивание органических фруктов и овощей на сельской ферме в штате Мэн». «Цель выставки — помочь тем из нас, кто не может по многим причинам — выращивать себе еду, ценить и — в некотором смысле — чтить тяжелую, утомительную, временами пыльную, грязную, а иногда и опасную работу, которую выполняют фермеры и сельскохозяйственные бригады. изгибается, чтобы собрать еду для многих из нас», — объясняет Брюс Таул. «Марта» — это один из «бендеров», способ почтить и прославить фермы, фермеров и фермеров, выращивающих органические фрукты и овощи в короткий вегетационный период штата. Она будет приветствоваться в своем новом доме на ферме Ло как раз к осеннему сезону сбора урожая.
«Цель выставки — помочь тем из нас, кто не может по многим причинам — выращивать себе еду, ценить и — в некотором смысле — чтить тяжелую, утомительную, временами пыльную, грязную, а иногда и опасную работу, которую выполняют фермеры и сельскохозяйственные бригады. изгибается, чтобы собрать еду для многих из нас», — объясняет Брюс Таул. «Марта» — это один из «бендеров», способ почтить и прославить фермы, фермеров и фермеров, выращивающих органические фрукты и овощи в короткий вегетационный период штата. Она будет приветствоваться в своем новом доме на ферме Ло как раз к осеннему сезону сбора урожая.
рождественских елок были посажены на ферме закона в рамках программы Стивена и Элейн Лоу «Дети и деревья». Теперь наш округ поддерживает их с целью, чтобы любая выручка от продажи рождественских елок пошла на образовательные программы на Law Farm. В 2013 году наш округ провел семинар по обрезке рождественских елок, и было интересно использовать этот ресурс как способ расширить наши образовательные предложения.
На Юридической Ферме 9 было проведено несколько заготовок древесины 0007 . Эти урожаи были запланированы, чтобы открыть землю, чтобы обеспечить доступ к демонстрационным участкам лесного хозяйства и освободить место для пород деревьев, лучше подходящих для ландшафта. Кроме того, в 2014 году PCSWCD получил грант Project Canopy, который помог профинансировать крупные посадки местных лиственных пород как на вырубленных участках общественного леса, так и на новых демонстрационных участках агролесоводства.
Этот же грант Project Canopy профинансировал ярких и информативных указателей троп и участков , которые значительно улучшают природные зоны Law Farm.
Для получения дополнительной информации о любом из этих замечательных проектов Law Farm обращайтесь в PCSWCD!
Сад сохранения зародышевой плазмы американских каштанов на ферме Law Farm
В феврале 2018 года The Commons at Central Hall предоставила Району сохранения почв и вод округа Пискатакис (PCSWCD) средства, присужденные The Commons от Фонда семьи Куимби чтобы внести изменения в Law Farm, расположенную на Lee Cemetery Rd в Dover-Foxcroft.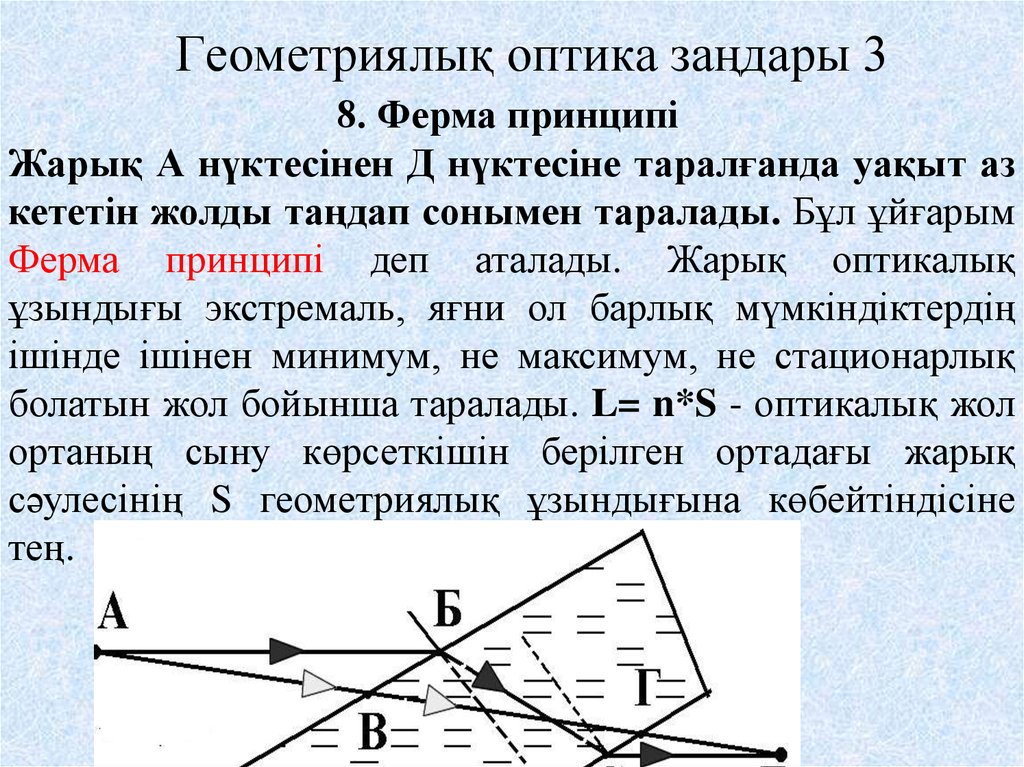 Средства, выделенные округу, пошли на новые вывески, модернизацию туалетов и новые скамейки, чтобы увеличить общественное использование существующих троп для использования несколькими поколениями. PCSWCD установил один из новых знаков в четверг, 2 августа, в 16:00.
Средства, выделенные округу, пошли на новые вывески, модернизацию туалетов и новые скамейки, чтобы увеличить общественное использование существующих троп для использования несколькими поколениями. PCSWCD установил один из новых знаков в четверг, 2 августа, в 16:00.
В сотрудничестве с исполняющим обязанности директора отдела совместных исследований лесного хозяйства Университета штата Мэн Брайаном Ротом, преподавателями естественных наук Академии Фокскрофт Робертом Вебером и Брайаном Краузе, а также Томасом Клаком, главой Американского фонда каштанов в штате Мэн, 18 июля 2017 г. было посажено 104 саженца. находится под контролем PCSWCD для Сада сохранения зародышевой плазмы каштанов (GCO). С добавлением этого красивого нового знака на Юридическую ферму посетители могут осмотреть сад, получая больше информации о новом саду сохранения зародышевой плазмы каштанов.
Сад по сохранению зародышевой плазмы каштанов — это захватывающее исследовательское предприятие Района охраны почвы и воды округа Пискатакис, и мы с нетерпением ждем возможности поделиться информацией об этом проекте со всеми вами.
Направления, карта, брошюра и обновленные маршруты
Карта маршрута
Направления
Из центра Дувра-Фокскрофта проехать 1,25 мили направо по трассе Lee 16 (Milo Rd.) и проехать 1,25 мили направо на Lee Rd. Кладбищенская улица. Автостоянка Law Farm расположена в полумиле вниз по Lee Cemetery Rd. справа. На 16-м маршруте есть дополнительная парковка по адресу 477 Milo Road. Эта парковка была щедро подарена PCSWCD компанией Pleasant River Lumber.
Брошюра «Юридическая ферма»
Информация и обновления маршрута
«Юридическая ферма» теперь представлена в системе поиска маршрутов штата Мэн! Нажмите здесь, чтобы увидеть страницу о природных тропах Law Farm в системе поиска троп штата Мэн!
Тропы фермы законов готовы для вас! Отправляйтесь туда и наслаждайтесь!
Переключатель Область скользящей панели
Это настраиваемый виджет
Эту скользящую панель можно включать и выключать в параметрах темы, и она может принимать любой виджет, который вы ей добавляете, или даже заполнять его вашим собственным HTML-кодом. Это идеально подходит для привлечения внимания ваших зрителей. Выберите между 1, 2, 3 или 4 столбцами, установите цвет фона, цвет разделителя виджета, активируйте прозрачность, верхнюю границу или полностью отключите его на настольном компьютере и мобильном телефоне.
Это идеально подходит для привлечения внимания ваших зрителей. Выберите между 1, 2, 3 или 4 столбцами, установите цвет фона, цвет разделителя виджета, активируйте прозрачность, верхнюю границу или полностью отключите его на настольном компьютере и мобильном телефоне.
Это настраиваемый виджет
Эту ползунковую панель можно включать и выключать в параметрах темы, и она может принимать любой виджет, который вы ей добавляете, или даже заполнять его вашим собственным HTML-кодом. Это идеально подходит для привлечения внимания ваших зрителей. Выберите между 1, 2, 3 или 4 столбцами, установите цвет фона, цвет разделителя виджета, активируйте прозрачность, верхнюю границу или полностью отключите его на настольном компьютере и мобильном телефоне.
Это настраиваемый виджет
Эту ползунковую панель можно включать и выключать в параметрах темы, и она может принимать любой виджет, который вы ей добавляете, или даже заполнять его вашим собственным HTML-кодом. Это идеально подходит для привлечения внимания ваших зрителей. Выберите между 1, 2, 3 или 4 столбцами, установите цвет фона, цвет разделителя виджета, активируйте прозрачность, верхнюю границу или полностью отключите его на настольном компьютере и мобильном телефоне.
Выберите между 1, 2, 3 или 4 столбцами, установите цвет фона, цвет разделителя виджета, активируйте прозрачность, верхнюю границу или полностью отключите его на настольном компьютере и мобильном телефоне.
Это настраиваемый виджет
Эту ползунковую панель можно включать и выключать в параметрах темы, и она может принимать любой виджет, который вы ей добавляете, или даже заполнять его вашим собственным HTML-кодом. Это идеально подходит для привлечения внимания ваших зрителей. Выберите между 1, 2, 3 или 4 столбцами, установите цвет фона, цвет разделителя виджета, активируйте прозрачность, верхнюю границу или полностью отключите его на настольном компьютере и мобильном телефоне.
Адвокаты по травмам и трудоустройству
ЛИЧНЫЕ ТРАВМЫ | ЗАНЯТОСТЬ | АВИАЦИЯ | КЛАСС АКЦИЯ
Более $ 1 МЛРД взыскано для клиентов с 2007 года
ТРАВМЫ | ЗАНЯТОСТЬ | АВИАЦИЯ | CLASS ACTION
ATTORNEYS
More than $ 1 BILLION recovered for clients since 2007
FEATURED ON
$28. 7M
7M
SCHOOL DISTRICT LIABILITY
$17.1M
PEDESTRIAN V. BUS
$14M
AUTO V. TRUCK
$12M
ПОМЕЩЕНИЕ ОТВЕТСТВЕННОСТЬ
10 миллионов долларов США
ОТВЕТСТВЕННОСТЬ ЗА ПРОДУКЦИЮ
4,75 миллиона долларов США
AUTO V. AUTO
КАК МЫ МОЖЕМ ПОМОЧЬ
Автомобильные аварии
ваши права. В Wilshire Law Firm наши отмеченные наградами адвокаты и профессиональные юристы могут помочь вам восстановиться, убедившись, что ваше дело о несчастном случае находится в надежных руках.
Телесные повреждения
Наши отмеченные наградами адвокаты имеют многолетний опыт в получении максимальной компенсации для клиентов. Наша юридическая фирма готова защитить ваши права, начиная с ответственности за помещение и заканчивая катастрофическими авариями и исками о совместном использовании.
Наша юридическая фирма готова защитить ваши права, начиная с ответственности за помещение и заканчивая катастрофическими авариями и исками о совместном использовании.
Авиационное право
Наши всемирно признанные юристы по авиационным происшествиям участвовали в некоторых из самых сложных и громких дел о авиакатастрофах и обладают квалификацией для понимания технической сущности авиационного права.
Закон о занятости
Нарушал ли ваш работодатель законы штата или федеральные законы о занятости? Если это так, вы заслуживаете компенсации, но вам не нужно добиваться ее в одиночку. Наши юристы по трудоустройству помогают работникам добиваться справедливости, которой они заслуживают, когда работодатели нарушают закон.
КОЛЛЕКТИВНЫЕ ИСКИ
Подача иска против крупной корпорации или бизнеса может показаться сложной задачей. Наши адвокаты по коллективным искам с самым высоким рейтингом занимаются самыми сложными делами и дают потребителям возможность защищать свои права от влиятельных деловых интересов.
Наши адвокаты по коллективным искам с самым высоким рейтингом занимаются самыми сложными делами и дают потребителям возможность защищать свои права от влиятельных деловых интересов.
Типы травм
ПОЧЕМУ ОБРАЩАТЬСЯ В ЮРИДИЧЕСКУЮ ФИРМУ WILSHIRE ДЛЯ ВАШЕГО ДЕЛА?
Независимо от того, были ли вы ранены в результате несчастного случая, несправедливо уволены или подверглись жестокому обращению со стороны работодателя, или ваши права как потребителя были нарушены, наши отмеченные наградами адвокаты могут помочь. Мы можем защитить ваши права и получить МАКСИМАЛЬНУЮ компенсацию по вашему делу!
Как признанные на национальном уровне юристы, заслужившие репутацию в обеспечении некоторых из крупнейших судебных исков и вердиктов в США , мы не отступаем перед трудностями. На самом деле, многие юристы обращаются к нам со своими самыми сложными делами.
Когда вы нанимаете нашу команду увлеченных своим делом профессионалов в области права, вы можете рассчитывать на то, что мы будем заботиться о ваших интересах на каждом шагу и будем бороться за наилучший возможный исход вашего дела.
СИЛЬНАЯ КОМАНДА НА ВАШЕЙ СТОРОНЕ
С более чем 50 адвокатами и 250 членами команды у нас есть ресурсы и ноу-хау, чтобы выступать против страховых компаний и крупных корпораций от вашего имени.
ПОБЕДИТЕЛЬНЫЙ РЕЗУЛЬТАТ
Вам нужна юридическая фирма с доказанными результатами. Испытанная фирма с успешным послужным списком, мы возместили ущерб на сумму более 1 миллиарда долларов для наших достойных клиентов.
СЕРВИС ДЛЯ ВАС
Вы заслуживаете того, чтобы быть на первом месте. Как юридическая фирма, ориентированная на людей, мы всегда будем поддерживать вас и ставить во главу угла ваше благополучие. Мы полны решимости бороться за урегулирование, которое вы заслуживаете.
Мы полны решимости бороться за урегулирование, которое вы заслуживаете.
БЕЗ ВОЗВРАТА, БЕЗ КОМИССИИ
Не беспокойтесь о первоначальных затратах. Наша фирма работает на основе непредвиденных расходов, что означает, что вы не платите нам НИКАКИХ СБОРОВ, если мы не выиграем ваше дело.
ПРИЗНАНИЕ «ЛУЧШЕЙ ЮРИДИЧЕСКОЙ ФИРМЫ»
Положитесь на отмеченную наградами фирму. Нас назвали среди «Лучших юридических фирм» U.S. News & World Report и Best Lawyers® три года подряд в 2020, 2021 и 2022 годах.
ДОСТУПНО 24/7
юридические вопросы. Мы здесь каждый день, круглосуточно, чтобы дать вам БЕСПЛАТНУЮ консультацию.
СИЛЬНАЯ КОМАНДА НА ВАШЕЙ СТОРОНЕ
С более чем 50 адвокатами и 250 членами команды у нас есть ресурсы и ноу-хау, чтобы выступать против страховых компаний и крупных корпораций от вашего имени.
ПОБЕДИТЕЛЬНЫЙ РЕЗУЛЬТАТ
Вам нужна юридическая фирма с доказанными результатами. Испытанная фирма с успешным послужным списком, мы возместили ущерб на сумму более 1 миллиарда долларов для наших достойных клиентов.
ОБСЛУЖИВАНИЕ ДЛЯ ВАС
Вы заслуживаете того, чтобы быть на первом месте. Как юридическая фирма, ориентированная на людей, мы всегда будем поддерживать вас и ставить во главу угла ваше благополучие. Мы полны решимости бороться за урегулирование, которое вы заслуживаете.
БЕЗ ВОЗВРАТА, БЕЗ ПЛАТЫ
Не беспокойтесь о первоначальных затратах. Наша фирма работает на основе непредвиденных расходов, что означает, что вы не платите нам НИКАКИХ СБОРОВ, если мы не выиграем ваше дело.
ПРИЗНАНИЕ «ЛУЧШЕЙ ЮРИДИЧЕСКОЙ ФИРМЫ»
Положитесь на отмеченную наградами фирму. Мы были названы среди «Лучших юридических фирм» по версии U.S. News & World Report и Best Lawyers® три года подряд в 2020, 2021 и 2022 годах. чтобы получить своевременную помощь после аварии или когда у вас есть юридические вопросы. Мы здесь каждый день, круглосуточно, чтобы дать вам БЕСПЛАТНУЮ консультацию.
Мы были названы среди «Лучших юридических фирм» по версии U.S. News & World Report и Best Lawyers® три года подряд в 2020, 2021 и 2022 годах. чтобы получить своевременную помощь после аварии или когда у вас есть юридические вопросы. Мы здесь каждый день, круглосуточно, чтобы дать вам БЕСПЛАТНУЮ консультацию.
НЕ ЖДИТЕ — СВЯЖИТЕСЬ С НАМИ ДЛЯ БЕСПЛАТНОЙ КОНСУЛЬТАЦИИ!
ЗАПРОСИТЬ БЕСПЛАТНУЮ КОНСУЛЬТАЦИЮ
ПОЗНАКОМЬТЕСЬ С НАШИМИ УЧАСТНИКАМИ ЮРИСТОВ
БОББИ СААДЬЯН, ESQ.
Президент-основатель
КОЛИН ДЖОНС, ESQ.
Старший партнер
А. ИЛЬЯС АКБАРИ, ESQ.
Старший партнер | Биоинженер
ДЖАСТИН МАРКЕС, ESQ.
Старший партнер
ДЖОН ТЕЛЛЕР, ESQ.
Партнер
НИКОЛ ХАДЖАР, ESQ.
Адвокат по судебным разбирательствам
Опытные и квалифицированные юристы нашей фирмы готовы вам помочь. Вам нужно выбрать ЛУЧШЕГО адвоката для рассмотрения вашего дела о травмах, трудоустройстве, авиации или коллективном иске. Ваш выбор может означать разницу между урегулированием, которое даже не покроет ваши счета, или восстановлением десятков тысяч или даже миллионов долларов. У нас есть юристы, которые были выбраны Национальной ассоциацией выдающихся юрисконсультов, Американским советом судебных адвокатов, Super Lawyers, Best Lawyers и другими организациями в список «1 процент лучших юристов страны».
Узнайте больше о нашей команде юристов прямо сейчас!
ПОЧЕМУ ВАЖНО ИМЕТЬ ОПЫТНОГО ЮРИСТА?
Когда вы подаете иск против страховой компании или корпорации, они сделают все, что в их силах, чтобы ослабить или опровергнуть ваше требование. У оппозиции, как правило, против вас работает большая команда юристов, пытающихся доказать, что вы заслуживаете меньше денег, чем на самом деле. Опытный адвокат может сразу определить эту тактику и использовать правильные доказательства, чтобы получить вам компенсацию, которую вы заслуживаете.
У оппозиции, как правило, против вас работает большая команда юристов, пытающихся доказать, что вы заслуживаете меньше денег, чем на самом деле. Опытный адвокат может сразу определить эту тактику и использовать правильные доказательства, чтобы получить вам компенсацию, которую вы заслуживаете.
В юридической фирме Уилшир мы знаем все хитрости, описанные в книге. Что еще более важно, мы знаем, как их отключить. Мы будем бороться за то, чтобы вы получили справедливую компенсацию.
КАК Я УЗНАЮ, ЧТО МОГУ ПОЛУЧИТЬ ПОЛЬЗОВАНИЕ ХОРОШЕГО АДВОКАТА?
Многие люди ошибаются, думая, что не могут позволить себе хорошего адвоката, и в результате наносят ущерб своему делу. К счастью, можно получить доступ к высококачественному юридическому представительству без финансовых затруднений.
Юридическая фирма Уилшира работает на основе оплаты непредвиденных расходов. Это означает, что вы, как клиент, не должны платить нам судебные издержки до тех пор, пока не получите компенсацию в своем деле. После того, как вы получите мировое соглашение или решение суда, сборы взимаются оттуда, поэтому вам не нужно иметь дело с авансовыми расходами. Мы даже можем помочь вам найти медицинскую помощь, которая может быть отложена до тех пор, пока ваше дело не будет решено.
После того, как вы получите мировое соглашение или решение суда, сборы взимаются оттуда, поэтому вам не нужно иметь дело с авансовыми расходами. Мы даже можем помочь вам найти медицинскую помощь, которая может быть отложена до тех пор, пока ваше дело не будет решено.
ЧТО ГОВОРЯТ НАШИ КЛИЕНТЫ
Я определенно рекомендую юридическую фирму Wilshire. Я действительно не смог бы иметь дело со страховыми компаниями, получить всю необходимую мне медицинскую помощь и получить хорошее урегулирование от страховых сторон без помощи и опыта Юридической фирмы Уилшир и особенно Лидии. Спасибо
Сохейл М.
Ломита, Калифорния
Компания Wilshire Law предоставила услуги, наиболее близкие к услугам консьержа в моем American Express. Они предоставили мне выделенную линию, которая [дала мне] доступ к моему куратору Энни Роблес в любое время. Энни координировала самые требовательные и непонятные запросы и поддерживала ощущение роскоши на протяжении всей службы.
Энни координировала самые требовательные и непонятные запросы и поддерживала ощущение роскоши на протяжении всей службы.
Рохан Г.
Ньюпорт-Бич, Калифорния
Персонал очень дружелюбный и очень знающий. Мой адвокат Дэниел был великолепен в урегулировании дела, а специалист по залогам Эми Ву быстро и очень эффективно урегулировала мои залоговые права для меня в процентах, которые я искал. Я могу продолжать перечислять имена людей в этом офисе, которые действительно помогали мне. От моего куратора Энни до Бобби. WLF — это фирма, к которой я бы отослал своих друзей и семью.
Крис М.
Лос-Анджелес, Калифорния
ПОЛУЧИТЕ БЕСПЛАТНУЮ КОНСУЛЬТАЦИЮ
Наша команда доступна 24/7, чтобы обсудить с вами ваш случай! Заполните эту форму, чтобы получить БЕСПЛАТНУЮ консультацию, чтобы мы могли помочь вам определить наилучший план действий для вашего юридического вопроса.
Домашняя форма
Пожалуйста, включите JavaScript в вашем браузере, чтобы заполнить эту форму.Имя *
Фамилия *
Телефон *
Эл.0003
Чем мы можем помочь? *
Покрываются все иммиграционные потребности | Закон о фермерах, ПК
Мы не просто юристы, мы стратегические юридические консультанты, преследующие одну цель
— привести наших клиентов туда, где они хотят быть.
Свяжитесь с нами сегодня
Мы не просто юристы, мы стратегические юридические консультанты, преследующие одну цель
— привести наших клиентов туда, где они хотят быть.
Свяжитесь с нами сегодня
Чем мы занимаемся
Инновационные иммиграционные решения с полным спектром услуг
Наша команда занимается всеми аспектами иммиграционного процесса, будь то рабочие, инвестиционные или семейные визы. Наша цель — помочь нашим клиентам полностью соблюдать федеральные иммиграционные законы и правила.
Иммиграция по месту работы
Работодатели квалифицированных кандидатов могут получить рабочие визы в Соединенных Штатах для соответствующих иностранных работников. Временная,
Работник-неиммигрант — это лицо, желающее въехать в Соединенные Штаты с определенной целью трудоустройства на временной период времени.
По прибытии в Соединенные Штаты лица, которым выдана неиммиграционная виза
для работы по найму, ограничены деятельностью или целью, по которой их неиммиграционная виза…
Читать далее
Служба найма и соблюдения требований
Управление долгом и банкротство
Услуги корпоративного права
Что отличает нас от других
Мы предлагаем общение и отзывчивость мирового класса для всех наших клиентов, а наш комплексный подход может упростить даже самые сложные визовые программы. Независимо от того, насколько велика или мала ваша работа, у нас есть решение для вас.
Отзывчивый
Ваша потребность в рабочей силе заставляет нас чувствовать срочность. Оперативность была ключом к успеху наших клиентов.
Эффективные коммуникаторы
Мы понимаем важность общения. Вот почему у нас есть политика отвечать на запросы клиентов в течение 24 часов с момента их получения.
Стратегическая экспертиза
Истинное, глубокое знание нормативных требований к подаче документов, чтобы мы могли действовать в качестве стратегического консультанта в надлежащем иммиграционном проспекте, а не просто проталкивать бумаги.
Дружелюбный!
Мы профессионально работаем с нашими клиентами, но выбираем искренние отношения с ними, что отражается в том, как мы общаемся с нашими клиентами. Мы всегда уважительны.
Преподаватели и поставщики ресурсов
Мы не хотим, чтобы иммиграция была загадкой для наших клиентов. Мы поняли, что чем больше мы учим наших клиентов, тем лучше они становятся. Вот почему мы часто проводим сеансы вопросов и ответов, вебинары и другой образовательный контент.
Что говорят наши клиенты
— Блейк Алевелт, Alewelt Concrete Inc. «Команда Farmer Law PC делает все возможное, когда дело доходит до соблюдения требований и помогает нам узнавать больше каждый день. ”
— Синди Бутикофер, Reicks View Farms «Farmer Law сделал все возможное, чтобы помочь Reicks View Farms нанимать работников. Они усердно и своевременно выполняют наши запросы, что оказало большое влияние на наши трудовые проблемы».
At Farmer Law PC…
…мы предлагаем первоклассное общение и оперативность для всех наших клиентов, а наш комплексный подход может упростить даже самые сложные визовые программы. Независимо от того, насколько велика или мала ваша работа, у нас есть решение для вас.
Познакомьтесь с нашими адвокатами
Свяжитесь с нами
Свяжитесь с нами
Имя/Фамилия*
Название организации
Эл.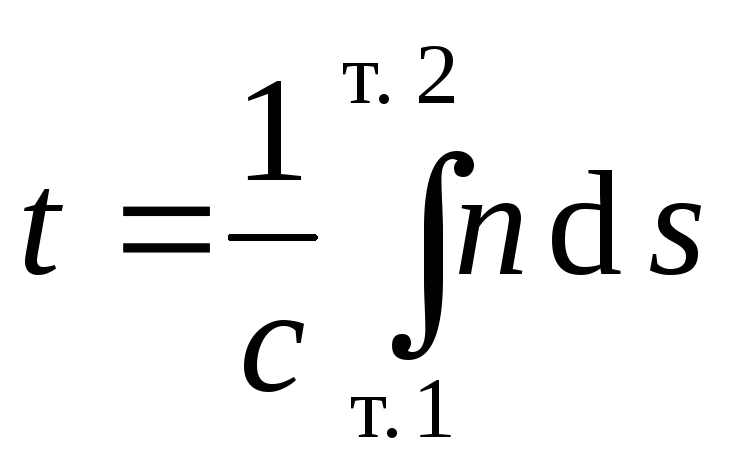 нам, чтобы связаться с вами по поводу наших продуктов и услуг. Вы можете отказаться от подписки на эти сообщения в любое время. Для получения информации о том, как отказаться от подписки, а также о наших методах обеспечения конфиденциальности и обязательствах по защите вашей конфиденциальности, ознакомьтесь с нашей Политикой конфиденциальности.
нам, чтобы связаться с вами по поводу наших продуктов и услуг. Вы можете отказаться от подписки на эти сообщения в любое время. Для получения информации о том, как отказаться от подписки, а также о наших методах обеспечения конфиденциальности и обязательствах по защите вашей конфиденциальности, ознакомьтесь с нашей Политикой конфиденциальности.
Последние статьи
Пресс-релиз Farmer Law PC обращается к изменениям в ставках заработной платы от Министерства труда [post_date] Благодаря трехлетнему росту выручки на 770%, Farmer Law PC получает № рейтинга. 824 среди самых быстрорастущих частных компаний Америки. 6 сентября 2022 г. Остин, Техас. Министерство труда (DOL) объявило об изменении методологии расчета […]
Подробнее
Блог FARMER LAW PC занимает 824-е место в ежегодном списке 2022 Inc. 5000 [post_date] Благодаря трехлетнему росту выручки на 770%, Farmer Law PC получает 824-е место в рейтинге. 824 среди самых быстрорастущих частных компаний Америки. НЬЮ-ЙОРК, 16 августа 2022 г. — 16 августа 2022 г. Inc. сообщила, что Farmer Law PC занимает 824-е место в годовом […]
5000 [post_date] Благодаря трехлетнему росту выручки на 770%, Farmer Law PC получает 824-е место в рейтинге. 824 среди самых быстрорастущих частных компаний Америки. НЬЮ-ЙОРК, 16 августа 2022 г. — 16 августа 2022 г. Inc. сообщила, что Farmer Law PC занимает 824-е место в годовом […]
Подробнее
Центры по контролю за заболеваниями в апреле пояснили, что дети-неграждане в возрасте до 18 лет, которые не являются иммигрантами, путешествующими из других стран в США, в настоящее время не обязаны предъявлять доказательство отпуска от Covid-19. Приказ учитывает глобальную доступность вакцины и потенциальные трудности, с которыми могут столкнуться семьи, путешествующие вместе. Однако […]
Подробнее
Посмотреть больше статей
Решите свою трудовую проблему
Юристы Farmer Law PC понимают ценность диверсифицированной рабочей силы и хорошо ориентируются во всех аспектах иммиграционного законодательства. Мы предлагаем комплексные решения для всех ваших нехватки рабочей силы. Наша команда находит честных, опытных работников, чтобы обеспечить работодателей исключительными талантами со всех уголков земного шара.
Мы предлагаем комплексные решения для всех ваших нехватки рабочей силы. Наша команда находит честных, опытных работников, чтобы обеспечить работодателей исключительными талантами со всех уголков земного шара.
Давай поговорим
- 7700 TX-71, Ste 350 Остин,
Техас 78735
Facebook-f Твиттер Линкедин YouTube
Иммиграционное право
- ОБМЕН J-1
ПОСЕТИТЕЛИ - ТН-1/2 НАФТА
ПРОФЕССИОНАЛЫ - ВИЗЫ H-2A
- ВИЗЫ H-2B
- I-601 ОТКАЗ
- И-601А
- ВИЗА Е-2
- виза ЕВ-3
- ВИЗА H-1B
- К-1 ВИЗА
- ВИЗА L-1A
Подпишитесь на нашу рассылку новостей
Юристы Farmer Law PC понимают ценность диверсифицированной рабочей силы и хорошо ориентируются во всех аспектах иммиграционного законодательства. Мы предлагаем комплексные решения для всех ваших нехватки рабочей силы. Наша команда находит честных, опытных работников, чтобы обеспечить работодателей исключительными талантами со всех уголков земного шара.
Наша команда находит честных, опытных работников, чтобы обеспечить работодателей исключительными талантами со всех уголков земного шара.
Отказ от ответственности: информация, которую вы получаете на этом сайте, не является и не предназначена для юридической консультации. Вам следует обратиться к адвокату за консультацией относительно вашей индивидуальной ситуации.
Copyright by Farmer Law PC | Все права защищены
Политика конфиденциальности Отказ от ответственности
Husch Blackwell: юридическая фирма, ориентированная на ценность, ориентированная на отрасль, построенная на отношениях
, ориентированная на отрасль. Построен на отношениях.
В Husch Blackwell мы построили нашу юридическую фирму вокруг одной идеи: вести наших клиентов оттуда, где они есть, туда, где они хотят быть.
Что мы можем вам помочь найти?
Эл. адресБизнес больше не обычный. Не наш подход.
Наш отраслевой подход дает нам глубокое понимание того, с чем наши клиенты сталкиваются каждый день. Но более того, это создает общее видение, которое продвигает наших клиентов вперед.
Но более того, это создает общее видение, которое продвигает наших клиентов вперед.
человек
Найти юридическийчлен команды
Возможности
Узнайте, что мымогу сделать для вас
Идейное лидерство
Смотрите наши знанияна работе
Выпуск новостей
Law360 признал Husch Blackwell десяткой лучших юридических фирм по версии Summer Associates.
Читать об этом признании >
Отзывы Эрик Лоран, исполнительный директор Roo
«Мы выбрали Husch Blackwell за ее готовность ориентироваться в водах экономики совместного потребления, а также за ее дружелюбие и поддержку предпринимательства.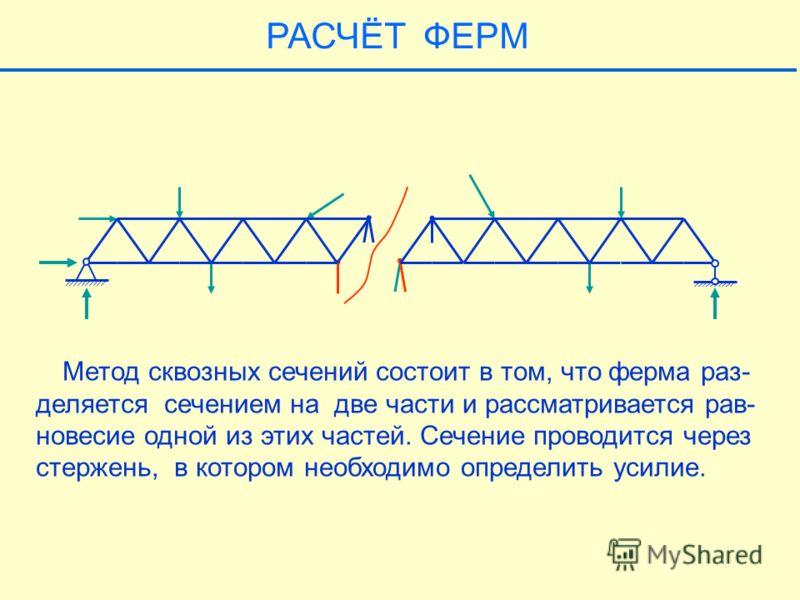 Размер Husch предоставляет нам широкий спектр услуг, которые удовлетворяют потребности нашей компании по всем направлениям. . У нас есть доступ к отличным юридическим консультациям во многих различных областях, которые, как мы знаем, нам понадобятся как сейчас, так и в будущем. Наконец, репутация Husch говорит сама за себя и предоставляет нам доступ к сети высококвалифицированных и готовых помочь людей в Сент-Луисе».
Размер Husch предоставляет нам широкий спектр услуг, которые удовлетворяют потребности нашей компании по всем направлениям. . У нас есть доступ к отличным юридическим консультациям во многих различных областях, которые, как мы знаем, нам понадобятся как сейчас, так и в будущем. Наконец, репутация Husch говорит сама за себя и предоставляет нам доступ к сети высококвалифицированных и готовых помочь людей в Сент-Луисе».
Отзывы Кай Уилсон, старший штатный аналитик — Раздел VI, Управление деловых возможностей
«Мероприятие Husch Blackwell, посвященное разнообразию и инклюзивности, было фантастическим. Мне особенно понравилась возможность услышать Сэнди Хеллумс-Гомез и Артуро Мишеля и узнать, что делают другие организации. Я хочу поблагодарить вас за вашу приверженность как частным, так и государственным организациям. Я с нетерпением жду возможности узнать больше и принять участие в такой значимой работе».
Отзывы Тони Мецнер, финансовый директор, Manna Pro Products
«Как одна из ведущих мировых компаний по уходу за животными и кормлению, наш бизнес охватывает несколько линеек продуктов, которые, в свою очередь, регулируются несколькими государственными и федеральными агентствами. Глубокий опыт Husch Blackwell в области здоровья животных оказался ценным для нас на протяжении всего жизненного цикла продукта, от исследований и разработок, разработки продукта, продаж и маркетинга, разрешения споров и заключения контрактов. Фирма предоставляет интегрированные ресурсы с преданными своему делу профессионалами, которые могут решать юридические и деловые вопросы по всем нашим операциям, включая вопросы, связанные с приобретением и трудоустройством».
Отзывы Дэн Фитцджеральд, генеральный директор Horizon Construction Group
«Husch Blackwell помогла нам расти, предоставляя превосходные услуги во всех областях, от прав, финансирования, приобретений, составления контрактов и разрешения споров.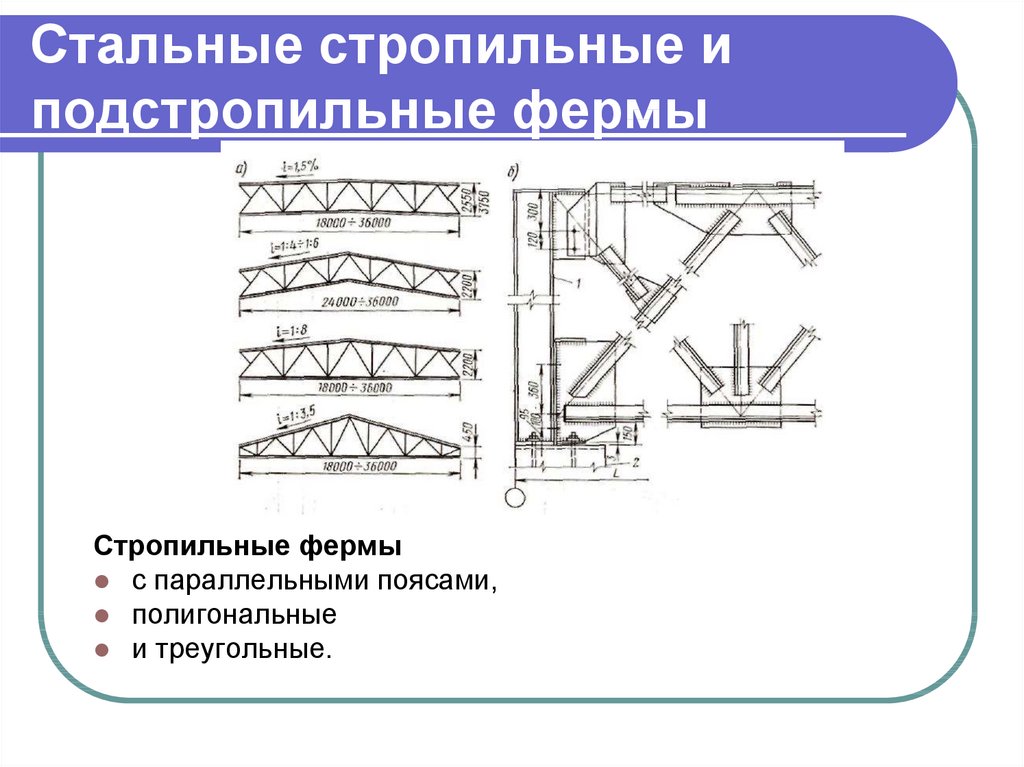 Их группа по строительству и проектированию обладает глубокими отраслевыми знаниями, которые вселяют в нас уверенность в том, что нам нужно любую возможность в любом штате».
Их группа по строительству и проектированию обладает глубокими отраслевыми знаниями, которые вселяют в нас уверенность в том, что нам нужно любую возможность в любом штате».
Отзывы Бренда Филлипс, вице-президент по персоналу, Alden Torch Financial, LLC
«Я начал составлять список вещей, которые нам нужно было рассмотреть перед повторным открытием из-за COVID-19. Затем я получил электронное письмо от Хаша Блэквелла о «генераторе политик». Спасибо, что сделали мою работу намного проще и за всю вашу помощь в создании нашей политики возврата к работе. Как приятно было уже иметь подробный план вместо того, что будет дальше!»
Отзывы Марк Савит, генеральный директор Predictive Compliance LLC
«Я работал с Маршаллом Кастером и командой Husch Blackwell над корпоративными и транзакционными консультациями в отношении сделки обратного выкупа.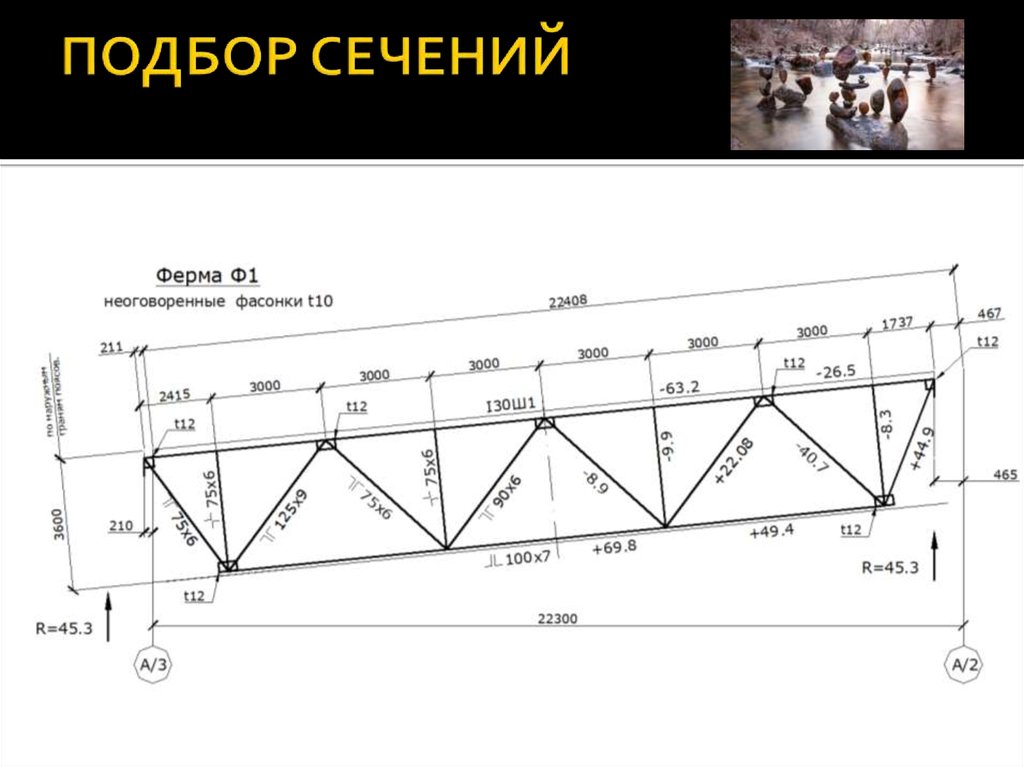 Команда была прямой, практичной и чуткой к нашему небольшому размеру и меняющимся потребностям. Их советы были точны с точки зрения достижения наилучшей цели с наименьшими затратами».
Команда была прямой, практичной и чуткой к нашему небольшому размеру и меняющимся потребностям. Их советы были точны с точки зрения достижения наилучшей цели с наименьшими затратами».
Отзывы Эми Канниццо-Бреннан, вице-президент по совершенствованию и корпоративному соответствию, Trustbridge
«Наш некоммерческий хоспис работает очень добросовестно. Наши партнеры по хоспису Husch Blackwell понимают это и часто помогают нам принимать доступные решения, которые также отвечают нашим потребностям. Мы уверены в юристах, которые помогают нам и высоко ценим знания команды о нашей организации и операциях. Они предвидят наши потребности и осмысленно доносят стратегии. Они превосходно осведомлены!»
Отзывы Д-р Чиринджиев Катурия, сопредседатель и соучредитель UpHealth
«То, что наша компания торгуется на Нью-Йоркской фондовой бирже, является огромным свидетельством способностей всей команды Husch Blackwell. Husch Blackwell успешно провел нас через сложный процесс SPAC, который теперь позволяет нам масштабировать нашу деятельность на рынке здравоохранения, созревшем для столь необходимых изменений и инноваций».
Husch Blackwell успешно провел нас через сложный процесс SPAC, который теперь позволяет нам масштабировать нашу деятельность на рынке здравоохранения, созревшем для столь необходимых изменений и инноваций».
Отзывы Барб Хансен, главный исполнительный директор Орегонской ассоциации хосписов и паллиативной помощи
«Мэг Пекарске «самая лучшая и умнейшая», и я очень высокого мнения о Хаш Блэквелл и ее коллегах. Я всегда многому учусь на вебинарах и подкастах, которые предоставляет Хуш Блэквелл . Это отличный сервис для индустрии хосписов . »
Козен О’Коннор: Юридическая фирма с полным спектром услуг
Козен О’Коннор: юридическая фирма с полным спектром услуг За помощью в реализации своей бизнес-стратегии CardX обратилась к Группе генеральных прокуроров штата (AG) Козена О’Коннора, чтобы работать с AG штата для борьбы с запретами штатов на дополнительные сборы с кредитных карт и правилами, регулирующими, как дополнительные сборы могут быть доведены до сведения потребителей.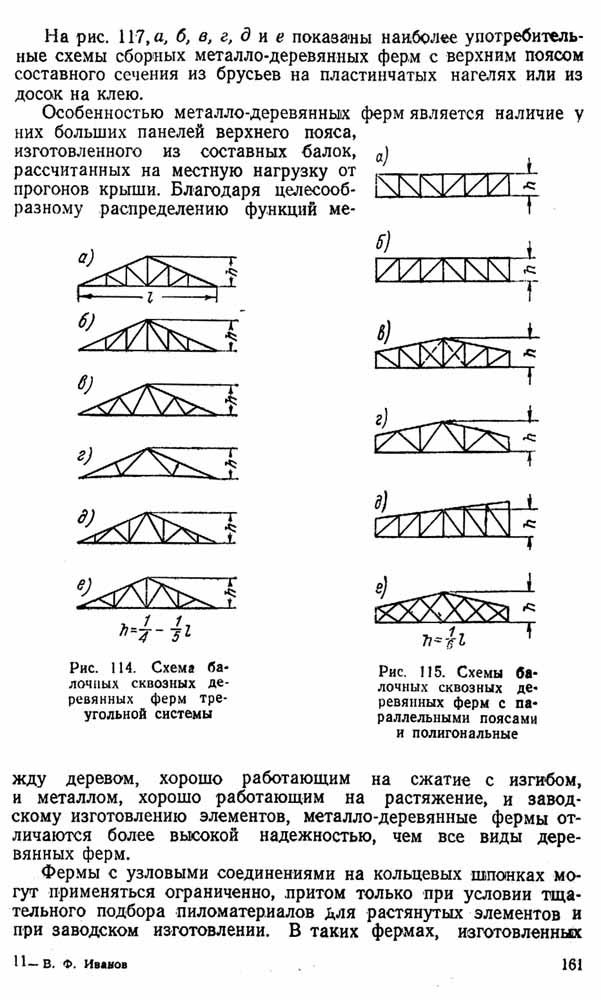
Прочитать историю клиентаНаш опыт
Последние новости фирмы
800+ адвокатов
Поиск людей
Индекс адвокатов
Козен О’Коннор имеет широко признанную национальную практику судебных разбирательств, корпоративный, интеллектуальная собственность, недвижимость и труд и занятость и большой опыт работы в различных областях практики. Наши талантливые специалисты работают в тесном сотрудничестве дисциплины и беспрепятственно во всех наших 32 офисах для достижения наших бизнес-цели клиентов.
Последние обновления
Возможности
Ответственность за продукциюПросмотр
Генеральные прокуроры штатаПросмотр
Труд и занятостьПросмотр
Возможности поиска
Просмотреть все возможности
О нас
Мы процветаем благодаря результатам
Уже более 50 лет мы определяем себя нашими
успех клиентов. Как юридическая фирма с полным спектром услуг, Козен О’Коннор направляет и защищает бесчисленное количество клиентов.
с широким спектром наших юридических услуг, включая судебные, корпоративные и
регулирующее право. Наша непоколебимая преданность делу делает нас одной из лучших юридических фирм в стране. В
индустрия, построенная на разговорах, мы сделали себе имя, делая.
Как юридическая фирма с полным спектром услуг, Козен О’Коннор направляет и защищает бесчисленное количество клиентов.
с широким спектром наших юридических услуг, включая судебные, корпоративные и
регулирующее право. Наша непоколебимая преданность делу делает нас одной из лучших юридических фирм в стране. В
индустрия, построенная на разговорах, мы сделали себе имя, делая.
800+ адвокатов 32 офиса
Cozen O’Connor входит в число 100 лучших юридических фирм страны и имеет более 800
адвокатов в 31 городе на двух континентах. Мы являемся фирмой с полным спектром услуг с национальными
признанная практика в судебных процессах, коммерческом праве и отношениях с государственными органами, и наша
адвокаты имеют опыт работы во всех отраслях экономики. Наш разнообразный клиент
список включает глобальные компании из списка Fortune 500, фирмы среднего размера, готовые к росту,
амбициозные стартапы и известные личности.
Одна победа за раз
В индустрии, построенной на разговорах, Козен О’Коннор сделал себе имя на деле. Мы построили наша фирма одно дело, одна победа за раз. Наши адвокаты имеют безупречную академическую полномочия и способны сочетать интеллектуальную строгость с практичностью и эффективностью. Мы предоставляем сложные, ориентированные на бизнес советы, направленные на одну простую цель: получить правильный результат для наших клиентов. Какими бы сложными, спорными или критическими ни были предпринимая, мы настойчиво, пока работа не будет сделана.
- Руководство фирмы
- Награды и награды
- Про Боно
- Разнообразие и инклюзивность
- Женская инициатива
- Общественные работы
Фирменное лидерство
Награды и почести
Про Боно
Разнообразие и инклюзивность
Женская инициатива
Общественная служба
То, что вы построили, мы можем защитить.
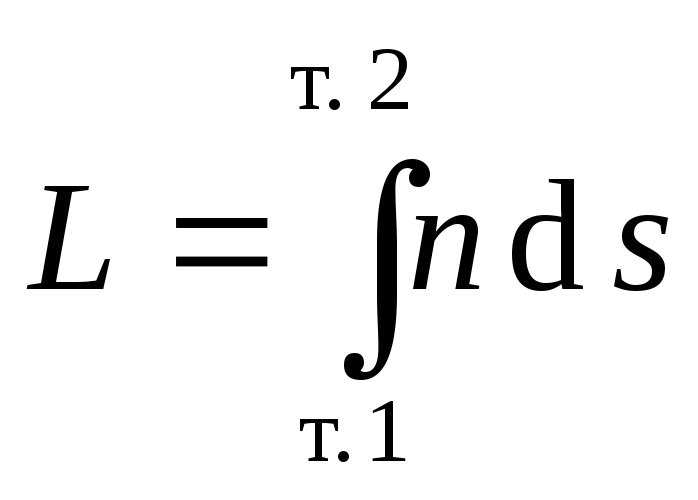
Что вы представляете, мы можем помочь построить.
Наши офисы
Atlanta
Boca Raton
Boston
Charlotte
Cherry Hill
Chicago
Dallas
Denver
Harrisburg
Houston
Las Vegas
London
Los Angeles
Miami
Minneapolis
Монреаль
Нью-Йорк
Newark
Philadelphia
Pittsburgh
Richmond
San Diego
San Francisco
Santa Monica
Seattle
Toronto
Vancouver
Washington, D.C.
West Conshohocken
West Palm Beach
Wilkes -Барре
Уилмингтон
Wright & Moore Law Co. LPA – основное внимание уделяется юридическим вопросам, связанным с сельским хозяйством и фермами
- (740) 990-0750
- Свяжитесь с нами
Facebook-f Инстаграм
Акцент на правовых вопросах, связанных с сельским хозяйством и фермерскими хозяйствами
Узнайте больше о нас
Просто проверяю овцу!
Wright & Moore Update: COVID-19
Каждое утро, собираясь на встречу в виртуальном офисе, мы переоцениваем ситуацию с COVID-19.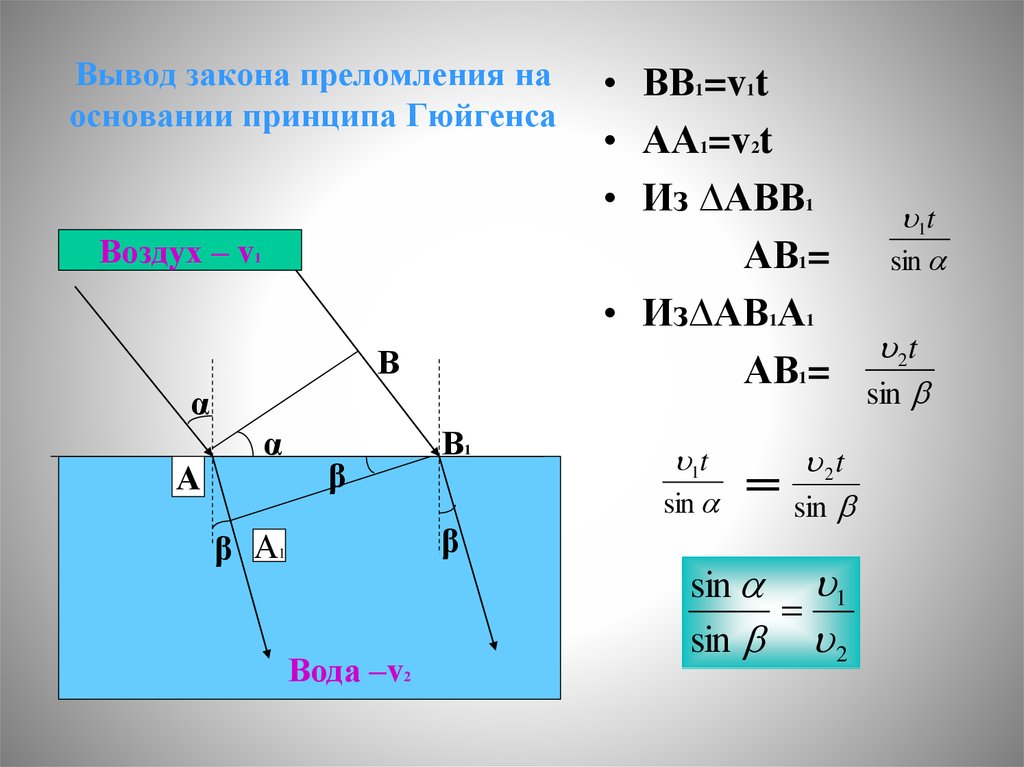 Хотя наш физический офис закрыт, а наши сотрудники в безопасности дома, мы по-прежнему «открыты» для бизнеса. Мы предпринимаем следующие шаги, чтобы уменьшить путаницу и обеспокоенность, продолжая при этом обслуживать наших клиентов как можно лучше в сложившихся обстоятельствах. Мы звоним каждому нашему клиенту, у которого запланирована встреча, и обсуждаем возможность телефонного или видеозвонка. Мы находимся в процессе сертификации Эшли и Эвин в качестве онлайн-нотариусов, что позволит нам назначать встречи для подписания видео. Мы пытаемся перенести все наши сезонные встречи на следующие пару недель, чтобы убедиться, что планы по недвижимости и планы преемственности завершены. Наш офисный телефон переадресован на сотовый телефон Эшли, поэтому, пожалуйста, не стесняйтесь оставлять сообщение, даже если вы не слышите «обычное» голосовое сообщение Wright & Moore. Мы всегда доступны по телефону.
Хотя наш физический офис закрыт, а наши сотрудники в безопасности дома, мы по-прежнему «открыты» для бизнеса. Мы предпринимаем следующие шаги, чтобы уменьшить путаницу и обеспокоенность, продолжая при этом обслуживать наших клиентов как можно лучше в сложившихся обстоятельствах. Мы звоним каждому нашему клиенту, у которого запланирована встреча, и обсуждаем возможность телефонного или видеозвонка. Мы находимся в процессе сертификации Эшли и Эвин в качестве онлайн-нотариусов, что позволит нам назначать встречи для подписания видео. Мы пытаемся перенести все наши сезонные встречи на следующие пару недель, чтобы убедиться, что планы по недвижимости и планы преемственности завершены. Наш офисный телефон переадресован на сотовый телефон Эшли, поэтому, пожалуйста, не стесняйтесь оставлять сообщение, даже если вы не слышите «обычное» голосовое сообщение Wright & Moore. Мы всегда доступны по телефону.
В настоящее время необходимы гибкость и творческий подход, и мы продолжим придумывать творческие способы выполнения работы. Мы все знаем, каково это принимать сложные решения для нашего семейного бизнеса. Мы сделаем все возможное, чтобы развеять ваши страхи, ответить на ваши вопросы и продолжить служить фермерскому сообществу в новом «нормальном» режиме.
Мы все знаем, каково это принимать сложные решения для нашего семейного бизнеса. Мы сделаем все возможное, чтобы развеять ваши страхи, ответить на ваши вопросы и продолжить служить фермерскому сообществу в новом «нормальном» режиме.
Как всегда, мы продолжим принимать все необходимые меры для обеспечения безопасности нашей семьи Райт и Мур!
Офисный переход
План преемственности Wright & Moore
2022 год принесет компании Wright & Moore год перемен! После десяти лет владения фирмой Роберт и Келли Мур нашли своего преемника в лице Райана Конклина. Муры передают управление и право собственности на Wright & Moore Райану, чтобы уделить больше времени семье, и чтобы Роберт мог согласиться на новую роль в штате Огайо.
Сейчас Эвин делит время между Wright & Moore и фирмой в своем родном городе Селина. Тем временем Эшли продолжает свое юридическое образование с целью стать адвокатом в Wright & Moore. Наконец, недавно мы добавили нового офис-менеджера, Тори Сноу, чтобы Эшли могла уделять больше времени оплачиваемой работе. Много интересных изменений в нашей офисной семье!
Много интересных изменений в нашей офисной семье!
Офис Celina
Расширение нашего присутствия в штате Огайо
Хотя компания Wright & Moore всегда поддерживала свое обязательство помогать фермерам по всему Огайо, географические границы неизбежны при попытке работать за пределами центрального штата Огайо. В 2021 году Эвин предоставил нам прекрасную возможность расширить нашу фирму и расширить охват фермеров и землевладельцев в нашем штате.
В рамках покупки Purdy Lammers & Schiavone в Селине Эвин теперь помогает клиентам и партнерам Wright & Moore в этой области. Эвин рад работать дома, продолжая работать в нашей фирме. Открытие нового офиса за пределами штата Делавэр является важным шагом для нашей фирмы, и мы с нетерпением ждем возможности удовлетворить потребности наших клиентов и партнеров в западном Огайо.
Планирование фермы/поместья
Мы работаем с фермерами над разработкой и реализацией надежного и индивидуального плана, чтобы передать ферму следующему поколению.
Планирование бизнеса
Мы работаем с фермерами, землевладельцами и малым бизнесом для разработки и реализации бизнес-планов.
Агротуризм
Агротуризм ежегодно привлекает тысячи посетителей на фермы Огайо. Давайте работать вместе над безопасным и веселым опытом для ваших гостей.
Аренда недвижимости/энергии
Сельскохозяйственные угодья – это самое ценное, что есть у вашей семьи. Используете ли вы эту землю для выращивания урожая или собираете арендную плату как землевладелец, ваша земля требует особого внимания.
Обсуждение семейной фермы
Часто, когда семья борется с передачей фермы, полезно встретиться с третьей стороной, которая может способствовать обсуждению и общению.
Государственное образование
Wright & Moore ежегодно участвует во многих презентациях для различных фермерских групп. Мы можем говорить на различные темы, связанные с сельскохозяйственным правом.
Кто мы
Роберт Э.

Мур
Адвокат
Келли Брейкфилд
Мур
Адвокат
Райан
Конклин
Адвокат
Эвин
Бакалавр
Адвокат
Эшли
Доннелли
Помощник по правовым вопросам
Тори
Сноу
Офис-менеджер
Последние новости
Интернет-продажи оборудования: охота за выгодными покупками или покупатель должен быть осторожен?
by Ryan Conklin По большей части наши клиенты очень хорошо отзываются о своем опыте покупки оборудования в Интернете, главным образом потому, что они ценят простоту
Подробнее »
Несовершеннолетние дети являются важной частью планирования преемственности
Райан Конклин В почтенном возрасте 33 лет меня окружают дети. У многих моих друзей есть дети или ждут, мой
Подробнее »
Завещания: центральный элемент любого плана преемственности
Райан Конклин Концепция завещания восходит к Римской империи, и многие принципы завещания берут свое начало в
Подробнее »
Что такое умственная недееспособность, согласно закону Огайо
by Robert Moore Сельский юрисконсульт: Врачи, как правило, являются лучшими людьми для определения недееспособности.


 1 Электростатика
1 Электростатика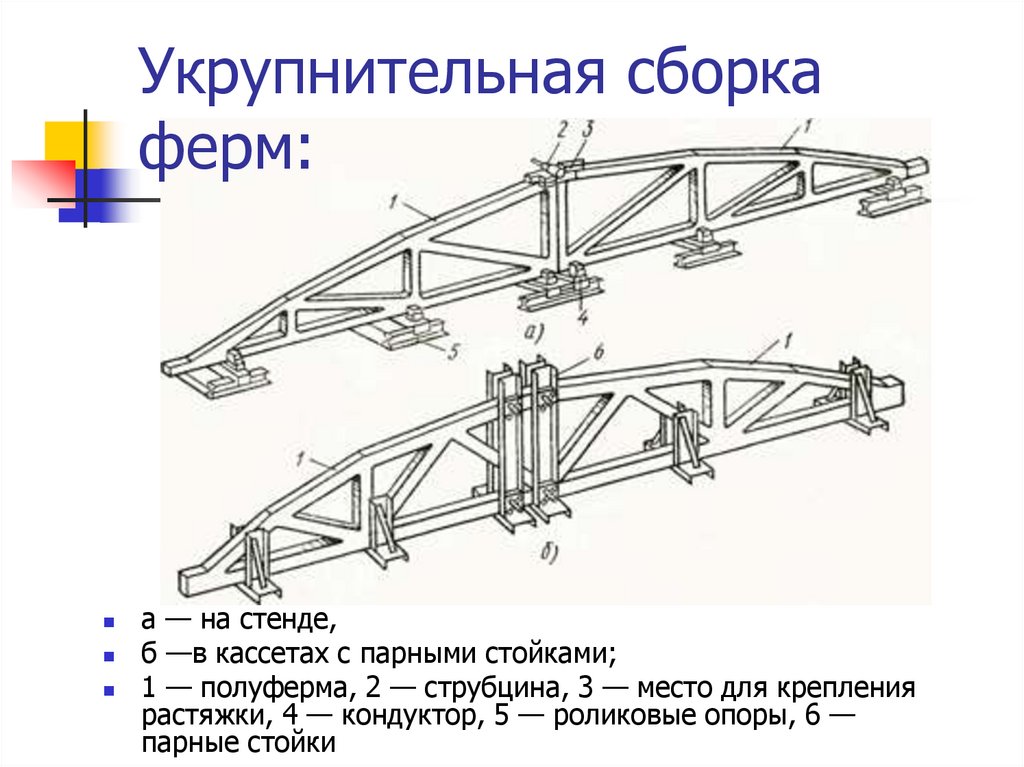 6 СТО
6 СТО 1 Случай однородной среды
1 Случай однородной среды операция раньше. »
операция раньше. » В{\ displaystyle A}B{\ displaystyle B}
В{\ displaystyle A}B{\ displaystyle B}