Что такое электромагнитная индукция. Закон электромагнитной индукции
История
Около 1830 г. Майкл Фарадей установили, что химические реакции на каждой из двух поверхностей раздела электрод-электролит обеспечивают «место действия ЭДС» для гальванического элемента. То есть эти реакции приводят в движение ток, а не являются бесконечным источником энергии, как предполагалось изначально. [11] В случае разомкнутой цепи разделение зарядов продолжается до тех пор, пока электрическое поле разделенных зарядов не станет достаточным для остановки реакций. Годами ранее, Алессандро Вольта, который измерял контактную разность потенциалов на границе металл – металл (электрод – электрод) своих ячеек, ошибочно полагал, что только контакт (без учета химической реакции) является источником ЭДС.
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Фарадеем.
Опыты Фарадея
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.
Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.

Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ), площади поверхности ( S ), пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
Обозначение – ( Phi ), единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла ( alpha ) магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.
Если ( alpha ) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции
Закон электромагнитной индукции (закон Фарадея) звучит так:
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.
Математически его можно описать формулой:
| Закон Фарадея Ɛi — ЭДС индукции [В] ΔФ/Δt — скорость изменения магнитного потока [Вб/с] |
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.
| Закон Фарадея для контура из N витков Ɛi — ЭДС индукции [В] ΔФ/Δt — скорость изменения магнитного потока [Вб/с] N — количество витков [-] |
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением R:
| Закон Ома для проводящего контура Ɛi — ЭДС индукции [В] I — сила индукционного тока [А] R — сопротивление контура [Ом] |
Если проводник длиной l будет двигаться со скоростью v в постоянном однородном магнитном поле с индукцией B ЭДС электромагнитной индукции равна:
| ЭДС индукции для движущегося проводника Ɛi — ЭДС индукции [В] B — магнитная индукция [Тл] v — скорость проводника [м/с] l — длина проводника [м] |
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках.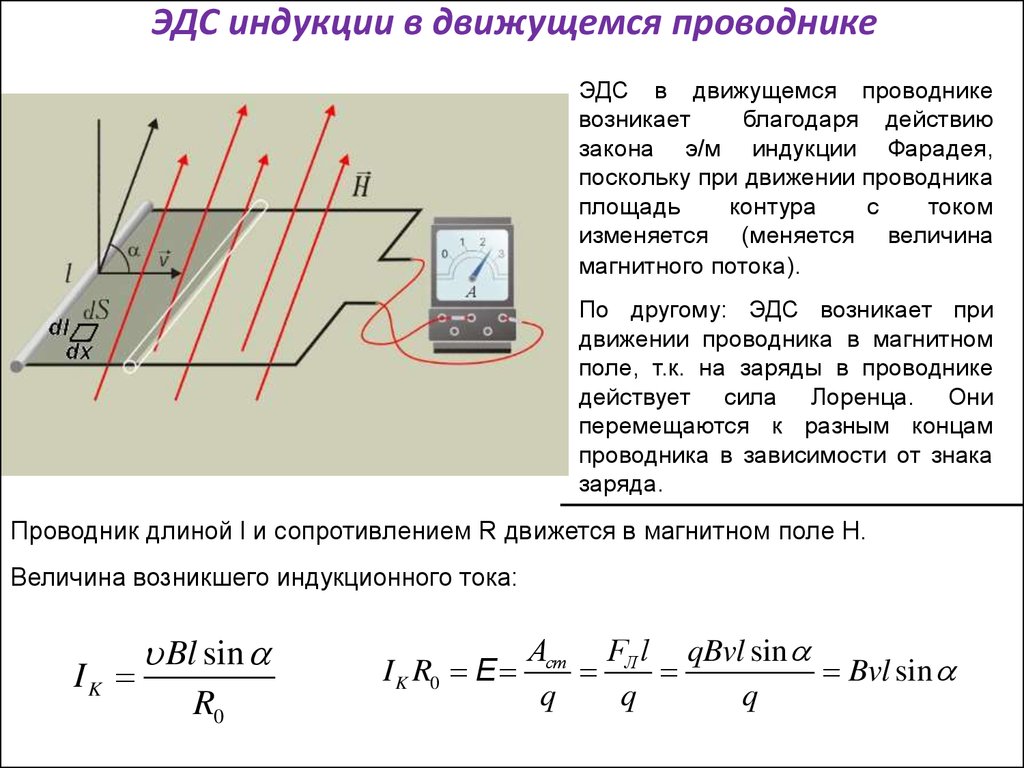 Сила Лоренца играет в этом случае роль сторонней силы.
Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
- вследствие изменения во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Правило Ленца
Чтобы определить направление индукционного тока, нужно воспользоваться правилом Ленца.
Академически это правило звучит следующим образом: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Давайте попробуем чуть проще: катушка в данном случае — это недовольная бабуля. Забирают у нее магнитный поток — она недовольна и создает магнитное поле, которое этот магнитный поток хочет обратно отобрать.
Дают ей магнитный поток, забирай, мол, пользуйся, а она такая — «Да зачем сдался мне ваш магнитный поток!» и создает магнитное поле, которое этот магнитный поток выгоняет.
Закон электромагнитной индукции Фарадея
Явление электромагнитной индукции описывается законом Фарадея, первооткрывателя и исследователя этого явления.
Представьте себе простейший контур с подвижной стороной, помещенный в магнитное поле так, чтобы поверхность контура была перпендикулярна линиям магнитного поля (рис. 2.).
2.).
Рис. Контур с подвижной стороной (перекладиной)
Мы перемещаем контур со скоростью v вправо. Это изменяет поток магнитной индукции, пронизывающий поверхность, охватываемую контуром, обозначенным на рисунке более темным цветом.
Вспоминая определение магнитного потока индукции, мы можем понять, почему изменяется поток ФB (рис.) – потому что, значение площади S поверхности увеличивается .
Вследствие изменения потока магнитной индукции в рассматриваемой цепи возникнет электродвижущая сила индукции и, следовательно, потечет электрический ток.
Рис. Внешняя сила Fz уравновешивает электродинамическую силу Fed , действующую на контур, движущийся с постоянной скоростью v
В рассматриваемом нами случае легко вычислить работу внешней силы, предполагая постоянную скорость движения контура. Внешняя сила Fz действует в соответствии со смещением контура (и вектором скорости) и в любой момент уравновешивает электродинамическую силу (силу Ампера) Fed, действующую в противоположном направлении (рис. 3.). Согласно определению работы Az = F * Δx где Δx – смещение контура во времени Δt.
3.). Согласно определению работы Az = F * Δx где Δx – смещение контура во времени Δt.
Величина силы Fz равна величине электродинамической силы (силе Ампера) Fed, действующей на контур. Поэтому Az = I * L * B * Δx, где – I сила индукционного тока, протекающего в цепи (и в контуре), L – длина контура (той части, где протекает электрический ток), B – величина магнитной индукции. Давайте введем наше выражение в определение ЭДС индукции. Зная, что q = I * Δt, получаем:
| εинд | = Az / q = I * L * B * Δx / I * Δt = B * L * Δx / Δt = B * ΔS / Δt = dФB / dt.
Мы получили интересный результат. Абсолютное значение ЭДС индукции равно скорости изменения потока магнитной индукции.
В рассматриваемом здесь случае поток магнитной индукции изменяется равномерно во времени. В общем случае это совсем не обязательно. Вот почему мы пишем: εинд = ΔФB / Δt , где Δt → 0, который в сокращенном виде записывается как dФB / dt . Это производная магнитного потока по времени.
Хотя наш вывод формулы относится к одному примеру, оказывается, что выведенное отношение является общим. Необходимо сделать лишь небольшую поправку. Это знак минус, который связан с определенной условностью и принципом сохранения энергии.
Необходимо сделать лишь небольшую поправку. Это знак минус, который связан с определенной условностью и принципом сохранения энергии.
Таким образом, закон электромагнитной индукции Фарадея записывается следующим образом: εинд = – dФB / dt и формулируется так:
Для любого контура индуцированная электродвижущая сила (ЭДС) равна скорости изменения магнитного потока, проходящего через этот контур, взятой со знаком минус.
Знак “минус” означает, что ЭДС индукции действует так, что индукционный ток препятствует изменению потока. Этот факт отражён в правиле Ленца.
Этот закон верен независимо от того, как изменяется поток магнитного поля; когда изменение вызвано относительным движением источника магнитного поля и контура, или когда движения вообще нет, но значение магнитной индукции меняется.
Закон Фарадея – это универсальный, всеобъемлющий и полный математический отчет о явлении электромагнитной индукции.
Вернемся на мгновение к нашему примеру и отметим, что скорость изменения потока, а значит и абсолютное значение ЭДС индукции, в данном случае равна произведению B*L*v. Это следует из ранее написанных соотношений, а именно:
Это следует из ранее написанных соотношений, а именно:
| εинд | = Az / q = I * L * B * Δx / I * Δt = B * L * Δx / Δt = B * L * ( Δx / Δt ) = B * L * v .
Правило Ленца.
Правило Ленца позволяет быстро и легко определить направление индукционного тока. Это действительно одна из форм принципа сохранения энергии. Правило гласит, что индукционный ток, наведенный в проводнике под действием переменного потока магнитной индукции, всегда имеет такое направление, что магнитное поле, создаваемое этим индукционным током, противодействует причине (т.е. изменению потока магнитного поля), которая его вызвала.
Обозначение и единицы измерения
Вектор магнитной индукции: формула
ЭДС в формулах обозначают вектором Е. Подразумевается напряженность, которую создают сторонние силы. Соответствующим образом эту величину можно оценивать по разнице потенциалов. По действующим международным стандартам (СИ), единица измерения – один вольт. Большие и малые значения указывают с применением кратных приставок: «микро», «кило» и др.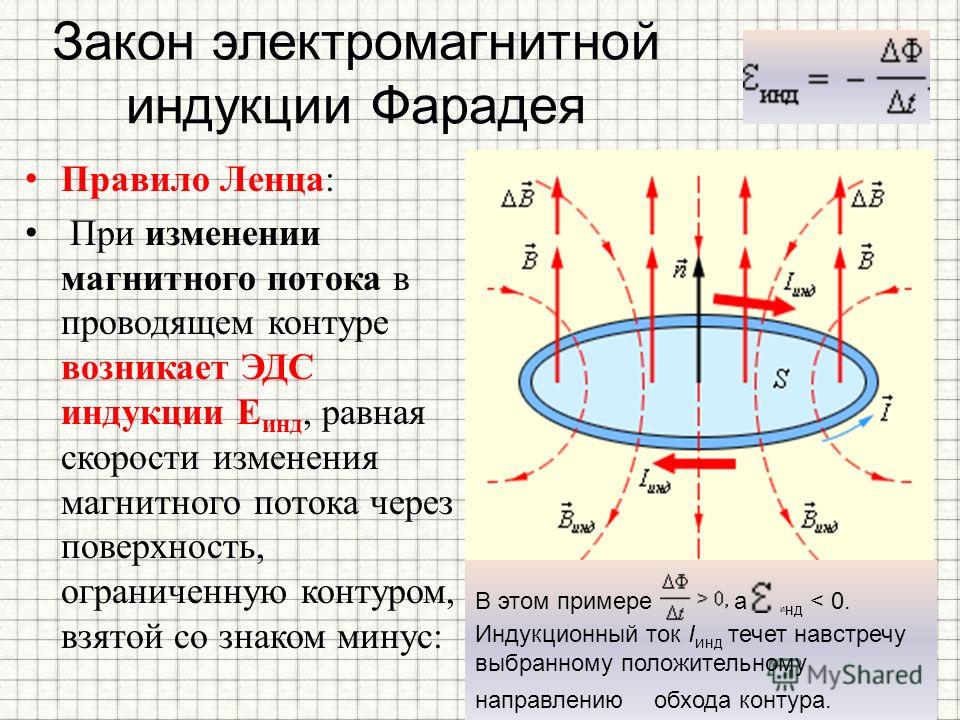
Движение провода в магнитном поле
Значение индуктированной ЭДС определяется в зависимости от длины проводника, пересекаемого силовыми линиями поля. При большем количестве силовых линий возрастает величина индуктируемой ЭДС. При увеличении магнитного поля и индукции, большее значение ЭДС возникает в проводнике. Таким образом, значение ЭДС индукции в движущемся в магнитном поле проводнике находится в прямой зависимости от индукции магнитного поля, длины проводника и скорости его движения.
Данная зависимость отражена в формуле Е = Blv, где Е — ЭДС индукции; В — значение магнитной индукции; I — длина проводника; v —скорость его перемещения.
Отметим, что в проводнике, который движется в магнитном поле, ЭДС индукции появляется, только когда он пересекает силовые линии магнитного поля. Если проводник движется по силовым линиям, тогда ЭДС не индуктируется. По этой причине формула применяется только в случаях, когда движением проводника направлено перпендикулярно силовым линиям.
Направление индуктированной ЭДС и электротока в проводнике определяется направлением движения самого проводника. Для выявления направления разработано правило правой руки. Если держать ладонь правой руки таким образом, чтобы в ее направлении входили силовые линии поля, а большой палец указывает направление движения проводника, тогда остальные четыре пальца показывают направление индуктированной ЭДС и направление электротока в проводнике.
Вращающаяся катушка
Функционирование генератора электротока основывается на вращении катушки в магнитном потоке, где имеется определенное количество витков. ЭДС индуцируется в электрической цепи всегда при пересечении ее магнитным потоком, на основании формулы магнитного потока Ф = B x S х cos α (магнитная индукция, умноженная на площадь поверхности, через которую проходит магнитный поток, и косинус угла, сформированный вектором направления и перпендикулярной плоскости линии).
Согласно формуле, на Ф воздействуют изменения в ситуациях:
- при изменении магнитного потока меняется вектор направления;
- изменяется площадь, заключенная в контур;
- меняется угол.

Допускается индуцирование ЭДС при неподвижном магните или неизменном токе, а просто при вращении катушки вокруг своей оси в пределах магнитного поля. В данном случае магнитный поток изменяется при смене значения угла. Катушка в процессе вращения пересекает силовые линии магнитного потока, в итоге появляется ЭДС. При равномерном вращении возникает периодическое изменение магнитного потока. Также число силовых линий, которые пересекаются ежесекундно, становится равным значениям через равные временные промежутки.
На практике в генераторах переменного электротока катушка остается в неподвижном состоянии, а электромагнит выполняет вращения вокруг нее.
ЭДС самоиндукции
При прохождении через катушку переменного электротока генерируется переменное магнитное поле, которое характеризуется меняющимся магнитным потоком, индуцирующим ЭДС. Данное явление называется самоиндукцией.
В силу того, что магнитный поток пропорционален интенсивности электротока, тогда формула ЭДС самоиндукции выглядит таким образом:
Ф = L x I, где L – индуктивность, которая измеряется в Гн. Ее величина определяется числом витков на единицу длины и величиной их поперечного сечения.
Ее величина определяется числом витков на единицу длины и величиной их поперечного сечения.
Где используются разные виды ЭДС
Перемещение проводника в магнитном поле применяют для генерации электроэнергии. Вращение ротора обеспечивают за счет разницы уровней жидкости (ГЭС), энергией ветра, приливами, топливными двигателями.
Различное количество витков (взаимоиндукцию) применяют для изменения нужным образом напряжения во вторичной обмотке трансформатора. В таких конструкциях взаимную связь увеличивают с помощью ферромагнитного сердечника. Магнитную индукцию применяют для возникновения мощной отталкивающей силы при создании ультрасовременных транспортных магистралей. Созданная левитация позволяет исключить силу трения, значительно увеличить скорость передвижения поезда.
Взаимодействие магнита с контуром
Итак, приближение или удаление магнита приводит к появлению в контуре индукционного тока, направление которого определяется правилом Ленца. Но ведь магнитное поле действует на ток! Появится сила Ампера, действующая на контур со стороны поля магнита. Куда будет направлена эта сила?
Куда будет направлена эта сила?
Если вы хотите хорошо разобраться в правиле Ленца и в определении направления силы Ампера, попробуйте ответить на данный вопрос самостоятельно. Это не очень простое упражнение и отличная задача для С1 на ЕГЭ. Рассмотрите четыре возможных случая.
1. Магнит приближаем к контуру, северный полюс направлен на контур.
2. Магнит удаляем от контура, северный полюс направлен на контур.
3. Магнит приближаем к контуру, южный полюс направлен на контур.
4. Магнит удаляем от контура, южный полюс направлен на контур.
Не забывайте, что поле магнита не однородно: линии поля расходятся от северного полюса и сходятся к южному. Это очень существенно для определения результирующей силы Ампера. Результат получается следующий.
Если приближать магнит, то контур отталкивается от магнита. Если удалять магнит, то контур притягивается к магниту. Таким образом, если контур подвешен на нити, то он всегда будет отклоняться в сторону движения магнита, словно следуя за ним. Расположение полюсов магнита при этом роли не играет .
Расположение полюсов магнита при этом роли не играет .
Уж во всяком случае вы должны запомнить этот факт — вдруг такой вопрос попадётся в части А1
Результат этот можно объяснить и из совершенно общих соображений — при помощи закона сохранения энергии.
Допустим, мы приближаем магнит к контуру. В контуре появляется индукционный ток. Но для создания тока надо совершить работу! Кто её совершает? В конечном счёте — мы, перемещая магнит. Мы совершаем положительную механическую работу, которая преобразуется в положительную работу возникающих в контуре сторонних сил, создающих индукционный ток.
Итак, наша работа по перемещению магнита должна быть положительна . Это значит, что мы, приближая магнит, должны преодолевать силу взаимодействия магнита с контуром, которая, стало быть, является силой отталкивания .
Теперь удаляем магнит. Повторите, пожалуйста, эти рассуждения и убедитесь, что между магнитом и контуром должна возникнуть сила притяжения.
Вихревое электрическое поле
Рассмотрим неподвижный контур, находящийся в переменном магнитном поле. Каков же механизм возникновения индукционного тока в контуре? А именно, какие силы вызывают движение свободных зарядов, какова природа этих сторонних сил?
Каков же механизм возникновения индукционного тока в контуре? А именно, какие силы вызывают движение свободных зарядов, какова природа этих сторонних сил?
Пытаясь ответить на эти вопросы, великий английский физик Максвелл открыл фундаментальное свойство природы: меняющееся во времени магнитное поле порождает поле электрическое . Именно это электрическое поле и действует на свободные заряды, вызывая индукционный ток.
Линии возникающего электрического поля оказываются замкнутыми, в связи с чем оно было названо вихревым электрическим полем . Линии вихревого электрического поля идут вокруг линий магнитного поля и направлены следующим образом.
Пусть магнитное поле увеличивается. Если в нём находится проводящий контур, то индукционный ток потечёт в соответствии с правилом Ленца — по часовой стрелке, если смотреть с конца вектора. Значит, туда же направлена и сила, действующая со стороны вихревого электрического поля на положительные свободные заряды контура; значит, именно туда направлен вектор напряжённости вихревого электрического поля.
Итак, линии напряжённости вихревого электрического поля направлены в данном случае по часовой стрелке (смотрим с конца вектора.
Рис. Вихревое электрическое поле при увеличении магнитного поля
Наоборот, если магнитное поле убывает, то линии напряжённости вихревого электрического поля направлены против часовой стрелки (рис).
Рис. Вихревое электрическое поле при уменьшении магнитного поля
Теперь мы можем глубже понять явление электромагнитной индукции. Суть его состоит именно в том, что переменное магнитное поле порождает вихревое электрическое поле. Данный эффект не зависит от того, присутствует ли в магнитном поле замкнутый проводящий контур или нет; с помощью контура мы лишь обнаруживаем это явление, наблюдая индукционный ток.
Вихревое электрическое поле по некоторым свойствам отличается от уже известных нам электрических полей: электростатического поля и стационарного поля зарядов, образующих постоянный ток.
1. Линии вихревого поля замкнуты, тогда как линии электростатического и стационарного полей начинаются на положительных зарядах и оканчиваются на отрицательных.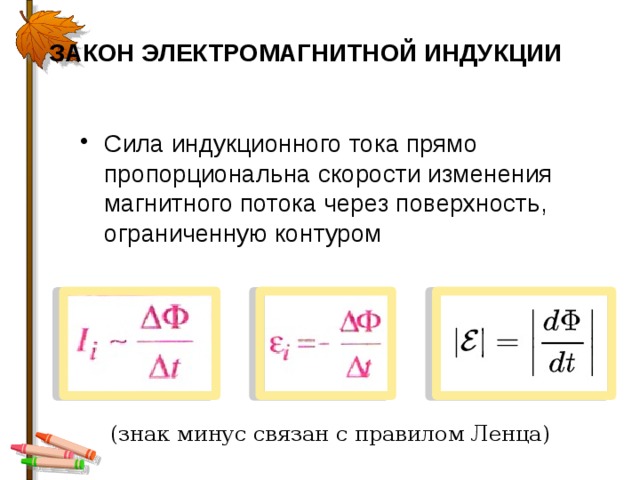
2. Вихревое поле непотенциально: его работа перемещению заряда по замкнутому контуру не равна нулю. Иначе вихревое поле не могло бы создавать электрический ток! В то же время, как мы знаем, электростатическое и стационарное поля являются потенциальными.
Итак, ЭДС индукции в неподвижном контуре — это работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура .
Пример задачи
Дано:
Контур в форме квадрата со стороной d = 0,5 м “втягивается” с постоянной скоростью v = 4 м/с в область однородного магнитного поля, величина индукции которого B = 1 Тл (см. рис. 4). Электрическое сопротивление цепи равно R = 2 Ом.
Рис. . Пример задачи по электростатической индукции
Нам нужно найти ответы на следующие вопросы:
a) Когда (в какой момент/моменты) в рамке будет протекать электрический ток?
б) Определите направление этого электрического тока.
(в) Вычислите значение силы, действующей на рамку при ее перемещении в соответствии с направлением вектора скорости. Предположите отсутствие механического сопротивления движению.
Предположите отсутствие механического сопротивления движению.
Решение.
(a) Индукционный ток протекает при изменении потока магнитной индукции через поверхность, охваченную контуром. В ситуации, показанной на рисунке 4, магнитный поток равен нулю и будет оставаться таковым до тех пор, пока правый край контура не коснется границы области магнитного поля. Затем, по мере движения контура, он будет все больше и больше заполняться магнитным полем – магнитный поток будет увеличиваться. Поэтому выполняется условие электромагнитной индукции, т.е. начинает протекать индукционный ток. Как долго? Это легко вычислить, поскольку движение рамы равномерно:
t = d / v = 0,5 / 2 = 0,25 секунд
Ток будет течь до тех пор, пока весь квадрат не войдет в магнитное поле. Тогда поток будет ненулевым, но больше не будет меняться.
б) Воспользуемся правилом Ленца. Мы уже заметили, что поток магнитной индукции при “втягивании” контура в магнитное поле увеличивается. Поэтому индукционный ток будет протекать в таком направлении, чтобы противодействовать увеличению потока.
Магнитное поле, создаваемое индукционным током с вектором индукции Bинд, будет противоположно вектору B.
Таким образом, вектор Bинд направлен в нашу сторону. Если расположить таким образом большой палец правой руки, остальные согнутые пальцы покажут направление индукционного тока. Ток будет течь против часовой стрелки.
(в) Снова воспользуемся равномерностью движения рамы. Обратите внимание, что сила, которая действует на рамку при ее перемещении по вектору скорости (например, сила моей руки), не может быть единственной силой, действующей на квадрат. Если бы это было так, он бы двигался с ускорением. Поскольку движение равномерное, это означает, что в каждый момент времени существует сила, которая уравновешивает силу моей руки. Это и есть электродинамическая сила. Ведь теперь в рамке течет ток, и часть его протекает в магнитном поле (см. рис. 5).
Рис.
Красная стрелка показывает направление электрического тока. Электродинамическая сила (сила Ампера) действует слева (я определил ее с помощью правила трех пальцев).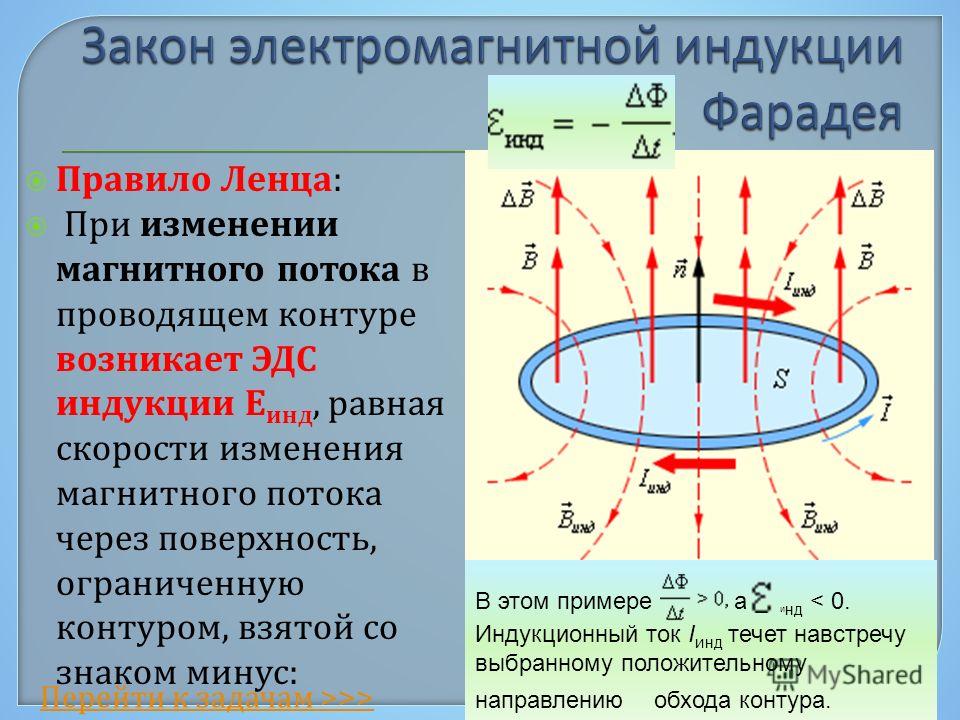 На верхнюю часть рамки и нижнюю часть также действуют электродинамические силы, но они аннулируют друг друга.
На верхнюю часть рамки и нижнюю часть также действуют электродинамические силы, но они аннулируют друг друга.
Подведем итог: электродинамическая сила уравновешивает силу моей руки. Таким образом, я могу сравнить значения обеих сил, то есть F = Fed = B * I * d, где I – сила индукционного тока. Теперь достаточно рассчитать значение силы этого тока. Мы будем использовать закон Фарадея и закон Ома для участка цепи. Давайте начнем с последнего: поскольку нас интересует только значение I, мы напишем
I = εинд / R .
| εинд | = ΔФB / Δt = Δx * d * B / Δt = ( Δx / Δt ) * d * B = v * d * B .
После подстановки в I получаем: I = εинд / R = v * d * B / R .
В конечном итоге искомое значение силы будет выражено через: Fed = B * I * d = ( B * d * v * d * B ) / R = ( B2 * d2 * v ) / R .
Подставляя численные значения получим: Fed = F = ( 12 * 0,52 * 4 ) / 2 = 0,5 Н .
Что мы узнали?
Кратко и понятно явление электромагнитной индукции можно описать, как возникновение электрического тока в проводящем контуре при изменении магнитного потока, проходящего через этот контур. При этом возникающий ток направлен так, чтобы противодействовать причине, его создавшей.
При этом возникающий ток направлен так, чтобы противодействовать причине, его создавшей.
Источники
- https://wikibgu.ru/wiki/Electromotive_Force
- https://fizi4ka.ru/egje-2018-po-fizike/jelektromagnitnaja-indukcija.html
- https://skysmart.ru/articles/physics/zakon-elektromagnitnoj-indukcii
- https://www.asutpp.ru/elektromagnitnaya-induktsiya.html
- https://amperof.ru/teoriya/formula-eds-indukcii.html
- https://odinelectric.ru/knowledgebase/chto-takoe-eds-induktsii-i-kogda-voznikaet
- https://ege-study.ru/ru/ege/materialy/fizika/elektromagnitnaya-indukciya/
- https://obrazovaka.ru/fizika/elektromagnitnaya-indukciya-formula.html
Как вам статья?
Павел
Бакалавр «210400 Радиотехника» – ТУСУР. Томский государственный университет систем управления и радиоэлектроники
Написать
Пишите свои рекомендации и задавайте вопросы
ЭДС индукции. Основные определения и формулы.
 Электромагнитная индукция. Закон электромагнитной индукции
Электромагнитная индукция. Закон электромагнитной индукцииФизика \ Физика
Страницы работы
15 страниц (Word-файл)
Посмотреть все страницы
Скачать файл
Фрагмент текста работы
ЭДС ИНДУКЦИИ
Электромагнитная индукция: в замкнутом проводящем контуре при изменении магнитного потока (т.е. вектора B! ), охватываемого этим контуром, возникает электрический ток индукционный ток.
Правило Ленца: индукционный ток всегда направлен так, чтобы противодействовать причине его вызывающей.
Закон электромагнитной индукции: εi = − ddtΦ возникающая в контуре
ЭДС индукции.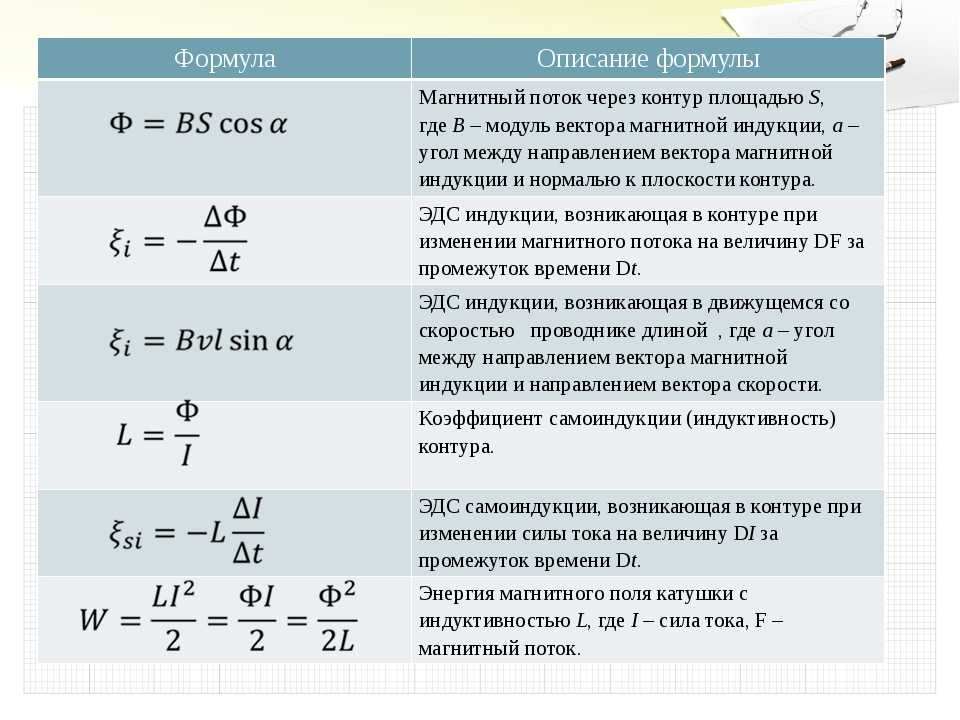
Если замкнутый контур, в котором индуцируется ЭДС состоит не из одного витка, а из N витков и, если, магнитный поток, охватываемый каждым витком одинаков и равен Φ1, то суммарный поток Φ сквозь поверхность, натянутую на данный контур: Φ = NΦ1 полный магнитный поток или потокосцепление. εi = −N ddtΦ1 .
Изменение тока в контуре, которое ведет к возникновению ЭДС индукции в этом же контуре называется самоиндукцией.
Если в пространстве, где находится контур с током I , нет ферромагнетиков, то полный магнитный поток через контур пропорционален силе тока
Взаимная индукция:
Рассмотрим два неподвижных контура 1 и 2, расположенных
достаточно близко друг к другу. Если в контуре 1 течет ток I1, то он создает через контур
2 полный магнитный поток Φ2, пропорциональный (при отсутствии ферромагнетиков)
току I1: Φ
=2 L I21 1.
Аналогично, если в контуре 2 течет ток
Коэффициенты L12 и L21 называют взаимной индуктивностью контуров.
Теорема взаимности: при отсутствии ферромагнетиков коэффициенты L12 и L21 одинаковы: L12 = L21.
Взаимная индукция: при всяком изменении тока в одном из контуров в другом контуре возникает ЭДС индукции.
Согласно закону электромагнитной индукции, ЭДС, возникающие в контурах 1 и 2 равны, соответственно: ε1 = −
ε2 = − ddtΦ = −L21 dIdt1 .
С учетом явления электромагнитной индукции, закон Ома для контура 1:
R I1 1 =ε1 −
L1 dIdt1 −
L12 dIdt2 , где ε1 сторонняя ЭДС в контуре
1 (помимо индукционных ЭДС), L1 индуктивность контура
1.
Энергия магнитного поля:
Дополнительная работа, совершаемая сторонними силами против ЭДС самоиндукции в процессе установления тока: δAдоп = IdΦ .
При отсутствии ферромагнетиков контур с индуктивностью L, по которому течет ток I обладает энергией: W = 12 LI2 = 12 IΦ = Φ2L2 магнитная
W dV энергия магнитного поля.
W = L I1 12 2 + L I2 22 2 + L I I12 1 2 магнитная энергия
двух контуров с токами; первые два слагаемых собственная энергия, последнее
слагаемое взаимная энергия.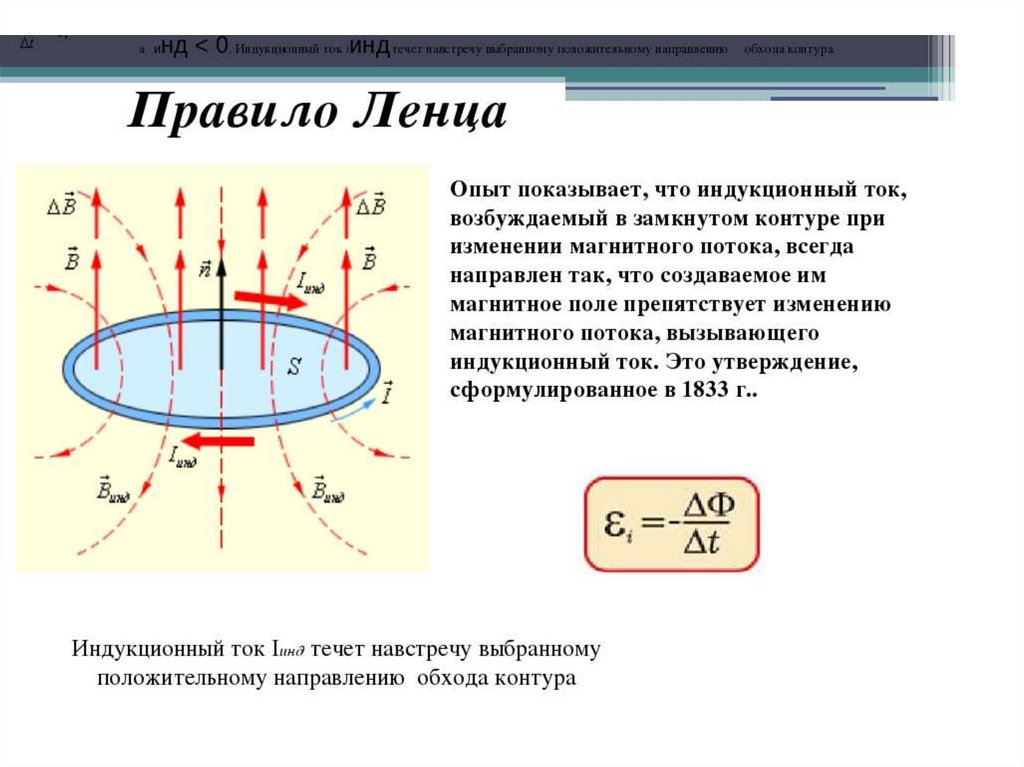
W dV dV dV полевая трактовка энергии, где
ЗАДАЧИ ЭДС индукции, ЭДС самоиндукции:
1. Провод, имеющий форму параболы y = kx2 , находится в однородном магнитном поле B! , перпендикулярном плоскости параболы. Из вершины параболы перемещают поступательно и без начальной скорости перемычку с постоянным ускорением a. Найти ЭДС индукции в образовавшемся контуре как функцию времени.
Решение:
За время dt перемычка переместится на
Если S! ↑↑ B! , то dΦ = BdS .
Поток Φ возрастает и
индукционный ток Iи течет против часовой
стрелки, порождая поле B!и ↑↓
B!
компенсируя изменение Φ .
Тогда εи = − ddtΦ = −B 2xdydt . Но dy
Поэтому εи = −B⋅2at at2k2 = −Ba 2kat2.
Ответ: Ba t2.
2.
Плоская спираль с большим числом N витков, плотно прилегающих друг к другу, находится
в однородном магнитном поле, перпендикулярном в плоскости спирали. Наружный радиус
спирали равен a. Магнитное
поле изменяется со временем по закону B = B
Решение:
Выделим участок спирали толщиной dr . В нем dN = Na dr витков по форме совпадающих
с окружностью радиуса r .
В нем dN = Na dr витков по форме совпадающих
с окружностью радиуса r .
Полный магнитный поток через этот участок спирали равен dΦ = B r dNπ 2 = B Nπa r dr2 .
Полный магнитный поток через всю спираль равен
Φ = ∫0a dΦ = B Nπa r33 0a=πNa3 2 B0 sinωt.
Тогда B t и амплитуда εи0 = −πNa3 2ωB0.
Ответ: εи0 = −πNa3 2ωB0.
3. По двум металлическим столбам, поставленным вертикально
Похожие материалы
Информация о работе
Скачать файл
4.
 2. Вывод основного закона электромагнитной индукции из закона сохранения и превращения энергии
2. Вывод основного закона электромагнитной индукции из закона сохранения и превращения энергииОсновной закон электромагнитной индукции (закон Фарадея) можно вывести из закона сохранения и превращения энергии, что и было сделано Гельмгольцем (1847 г.).
Пусть имеется замкнутая цепь (контур с током), содержащая источник ЭДС, величина которой , и пусть полное сопротивление этой цепи равно R. Обозначим силу тока в цепи через I. Количество энергии, затрачиваемое источником ЭДС за время dt, как известно, равно
.
Если внешнее магнитное поле отсутствует или контур неподвижен, то вся эта энергия превращается в тепло, количество которого определяется законом Джоуля-Ленца:
.
Имеем
.
Откуда после сокращения на dt получим закон Ома для замкнутой (полной) цепи в интегральной форме:
и . (4.11)
При перемещении
такого контура с источником ЭДС (с током)
в магнитном поле часть энергии источника
тока будет расходоваться против
перемещения контура в магнитном поле,
а часть выделяться в контуре в виде
тепла. Расходование энергии источника
тока против перемещения контура с током
в магнитном поле связано с тем, что для
получения индукционных токов методом
перемещения проводника в магнитном
поле необходимо совершить работу, так
как сила, действующая на индукционный
ток, препятствует перемещению проводника.
Расходование энергии источника
тока против перемещения контура с током
в магнитном поле связано с тем, что для
получения индукционных токов методом
перемещения проводника в магнитном
поле необходимо совершить работу, так
как сила, действующая на индукционный
ток, препятствует перемещению проводника.
Известно, что работа по перемещению проводника с током в магнитном поле dA = IdФ, где dФ – величина изменения магнитного потока, сцепленного с данным контуром.
Так как при таком перемещении магнитное поле остается неизменным, то эта работа может совершаться лишь за счет энергии источника тока.
На основании закона сохранения и превращения энергии будем иметь
или
.
Откуда
. (4.12)
Решая уравнение (4.12) относительно силы тока, найдем
. (4.13)
Принимая равенство
(4. 13) за математическое выражение закона
Ома и сравнивая его с полученным ранее
для этого же контура в отсутствие
магнитного поля, можно установить, что
благодаря изменению потока магнитной
индукции к имевшейся в цепи ЭДС источника
прибавилась ЭДС:
13) за математическое выражение закона
Ома и сравнивая его с полученным ранее
для этого же контура в отсутствие
магнитного поля, можно установить, что
благодаря изменению потока магнитной
индукции к имевшейся в цепи ЭДС источника
прибавилась ЭДС:
. (4.14)
Как видно, величина ЭДС электромагнитной индукции не зависит от величины источника тока и, значит, сохранит свое значение и при = 0, т.е. будет возникать вне зависимости от всяких других ЭДС, действующих в той же цепи.
Знак «минус» служит математическим выражением правила (закона) Ленца.
Таким образом, формула (4.14) является математическим выражением основного закона электромагнитной индукции (в формулировке Максвелла).
Аналогично можно получить вывод этого закона и для отрезка проводника (в формулировке Фарадея).
4.3. Явление самоиндукции. Магнитное поле бесконечно длинного соленоида. Коэффициенты индуктивности и взаимной индуктивности
Известно,
что вокруг любого проводника с током
возникает магнитное поле. Следовательно,
с любым контуром тока всегда связан
поток магнитной индукции. Этот поток
будет изменяться при изменении силы
тока в контуре, а также формы контура
или магнитной проницаемости окружающей
среды. Изменение же магнитного потока,
согласно закону электромагнитной
индукции, возбудит в контуре ЭДС. ЭДС
электромагнитной индукции, которая
возникает в каком-либо контуре вследствие
изменения магнитного потока, создаваемого
электрическим током этого контура,
называют ЭДС самоиндукции (рис. 4.4).
Следовательно,
с любым контуром тока всегда связан
поток магнитной индукции. Этот поток
будет изменяться при изменении силы
тока в контуре, а также формы контура
или магнитной проницаемости окружающей
среды. Изменение же магнитного потока,
согласно закону электромагнитной
индукции, возбудит в контуре ЭДС. ЭДС
электромагнитной индукции, которая
возникает в каком-либо контуре вследствие
изменения магнитного потока, создаваемого
электрическим током этого контура,
называют ЭДС самоиндукции (рис. 4.4).
Величина ЭДС самоиндукции может быть определена по общей формуле, выражающей основной закон электромагнитной индукции:
.
Рассчитаем ЭДС самоиндукции, возникающую в бесконечно длинном соленоиде, магнитное поле которого однородно находится внутри объема соленоида, заполненного средой с магнитной проницаемостью .
Магнитный поток Ф1, пронизывающий каждый виток соленоида сечением S,
. (4.15)
(4.15)
При изменении тока в соленоиде в каждом витке возникает ЭДС самоиндукции:
. (4.16)
В N последовательно соединенных витках соленоида возникает ЭДС самоиндукции:
(4.17)
где — коэффициент самоиндукции или индуктивность.
Индуктивность L зависит от формы, размеров проводника и магнитной проницаемости среды, окружающей проводник.
При с = L, т.е. индуктивность (коэффициент самоиндукции) – это физическая величина, численно равная ЭДС самоиндукции, возникающей в проводнике при скорости изменения тока в нем, равной 1 А/с. В системе СИ индуктивность проводников измеряется в «генри» (Гн).
Один Гн (генри) – это индуктивность такого проводника, в котором при скорости изменения тока в 1 А/с индуцируется ЭДС самоиндукции, равная 1 В.
Если L = const,
. (4.18)
(4.18)
Следовательно, ЭДС самоиндукции прямо пропорциональна скорости изменения тока в проводнике. Оказывается, что данное утверждение справедливо для любых проводников.
Если L const, что возможно при = f(H),
. (4.19)
То есть при наличии ферромагнетиков и в переменных магнитных полях коэффициент пропорциональности в выражении для ЭДС самоиндукции не равен L.
Таким образом, в проводниках с переменным током существуют одновременно две ЭДС — источника тока и самоиндукции.
При возрастании тока ,с<0, а это означает, что ЭДС самоиндукции «тормозит» движение зарядов в проводнике, совершая отрицательную работу, т.е. уменьшает ток в проводнике.
Если ток в проводнике убывает ,с>0 — ЭДС самоиндукции препятствует уменьшению тока в проводнике.
Следовательно, с противодействует причине, которая
порождает ее (препятствует изменению
тока в проводнике).
Сравнивая выражения идля магнитного потока, имеем
Ф = LI. (4.20)
4.3.1. Взаимная индукция. Коэффициент взаимной индукции
Взаимная индукция, явление, в котором обнаруживается магнитная связь двух или более электрических цепей. Благодаря этой связи возникает ЭДС индукции в одном из контуров при изменении тока в другом. Количественной характеристикой магнитной связи электрических цепей является взаимная индуктивность.
Если два контура (два замкнутых проводника) находятся в магнитных полях друг друга, то при всяком изменении тока в одном из них происходит изменение магнитного потока, пронизывающего (сцепленного) другой контур, что вызывает в нем появление ЭДС индукции (рис. 4.5).
Магнитный поток через первый контур с током I1 частично пронизывает площадь, ограниченную вторым контуром. Причем магнитный поток Ф12 через контур два прямо пропорционален току I1:
,
(4. 21)
21)
где М12 — коэффициент пропорциональности, зависящий от размеров, формы контуров, расстояния между ними, от их взаимного расположения, а также от магнитной проницаемости окружающей среды. Он называется взаимной индуктивностью или коэффициентом взаимной индукции контуров. В системе СИ измеряется в генри (Гн).
Если ток I2 течет в контуре «два», то магнитный поток Ф21 через контур «один» также пропорционален току I2:
. (4.22)
Согласно закону электромагнитной индукции,
; (4.23)
, (4.24)
где 2 и 1 — возникающие во втором и в первом контурах ЭДС индукции;
и — скорости изменения магнитных потоков через соответствующие контуры.
Взаимная индукция лежит в основе действия трансформаторов.
10.3 Закон электромагнитной индукции Фарадея | Электромагнетизм
Предыдущий 10. | Следующий 10.4 Краткое содержание главы |
10.3 Закон электромагнитной индукции Фарадея (ESBPY)
Ток, индуцированный изменяющимся магнитным полем (ESBPZ)
В то время как неожиданное открытие Эрстедом электромагнетизма проложило путь к более практическим применениям электричество, именно Майкл Фарадей дал нам ключ к практическому производству электричества: электромагнитная индукция .
Фарадей обнаружил, что когда он подносил магнит к проводу, на нем возникало напряжение. Если бы магнит был
удерживался неподвижно, никакого напряжения не генерировалось, напряжение существовало только во время движения магнита. Мы называем это
напряжение ЭДС индукции (\(\mathcal{E}\)).
Контур цепи, подключенный к чувствительному амперметру, будет регистрировать ток, если он настроен так, как показано на этом рисунке, и магнит перемещается вверх и вниз:
Магнитный поток
Прежде чем мы перейдем к определению закона электромагнитной индукции Фарадея и примерам, нам сначала нужно провести некоторое время, наблюдая за магнитным потоком. Для петли площади \(A\) при наличии равномерного магнитное поле, \(\vec{B}\), магнитный поток (\(φ\)) определяется как: \[\фи = БА\cos\тета\] Где: \начать{выравнивать*} \theta & = \text{угол между магнитным полем B и нормалью к петле площади A}\\ A & = \text{площадь петли}\\ B & = \text{магнитное поле} \end{выравнивание*}
Единицей магнитного потока в системе СИ является вебер (Вб).
Вы можете спросить себя, почему угол \(\theta\) включен. Поток зависит от магнитного поля, которое
проходит через поверхность. Мы знаем, что поле, параллельное поверхности, не может индуцировать ток, потому что оно не
пройти через поверхность. Если магнитное поле не перпендикулярно поверхности, то есть составляющая
которая является перпендикулярной и компонентой, которая параллельна поверхности. Параллельный компонент не может
вклад в поток может вносить только вертикальная составляющая.
Мы знаем, что поле, параллельное поверхности, не может индуцировать ток, потому что оно не
пройти через поверхность. Если магнитное поле не перпендикулярно поверхности, то есть составляющая
которая является перпендикулярной и компонентой, которая параллельна поверхности. Параллельный компонент не может
вклад в поток может вносить только вертикальная составляющая.
На этой диаграмме мы показываем, что магнитное поле под углом, отличным от перпендикулярного, может быть разбито на составные части. Компонент, перпендикулярный поверхности, имеет величину \(B\cos(\theta)\), где \(\theta\) угол между нормалью и магнитным полем.
temp text- Закон электромагнитной индукции Фарадея
ЭДС, \(\mathcal{E}\), возникающая вокруг контура проводника, пропорциональна скорости изменения магнитный поток φ через площадь контура A. Математически это можно выразить так:
\[\mathcal{E} = -N\frac{\Delta\phi}{\Delta t}\], где \(\phi =B·A\) и B — напряженность магнитного поля.
 \(N\) — количество контуров цепи.
Магнитное поле измеряется в единицах тесла (Тл). Знак минус указывает направление и то, что индуцированное
ЭДС стремится противодействовать изменению магнитного потока. Знак минус можно не учитывать при расчете
величины.
\(N\) — количество контуров цепи.
Магнитное поле измеряется в единицах тесла (Тл). Знак минус указывает направление и то, что индуцированное
ЭДС стремится противодействовать изменению магнитного потока. Знак минус можно не учитывать при расчете
величины.
Закон Фарадея связывает ЭДС индукции со скоростью изменения потока, которая является произведением магнитного поля и площадь поперечного сечения, через которое проходят силовые линии.
Это не площадь самого провода, а область, которую окружает провод. Это означает, что если согнуть проволоки в круг, площадь, которую мы будем использовать при расчете потока, — это площадь поверхности круга, а не провод.
На этом рисунке, где магнит находится в той же плоскости, что и петля цепи, тока не будет даже
если бы магнит был перемещен ближе и дальше. Это связано с тем, что силовые линии магнитного поля не проходят через
замкнутую область, но параллельны ей.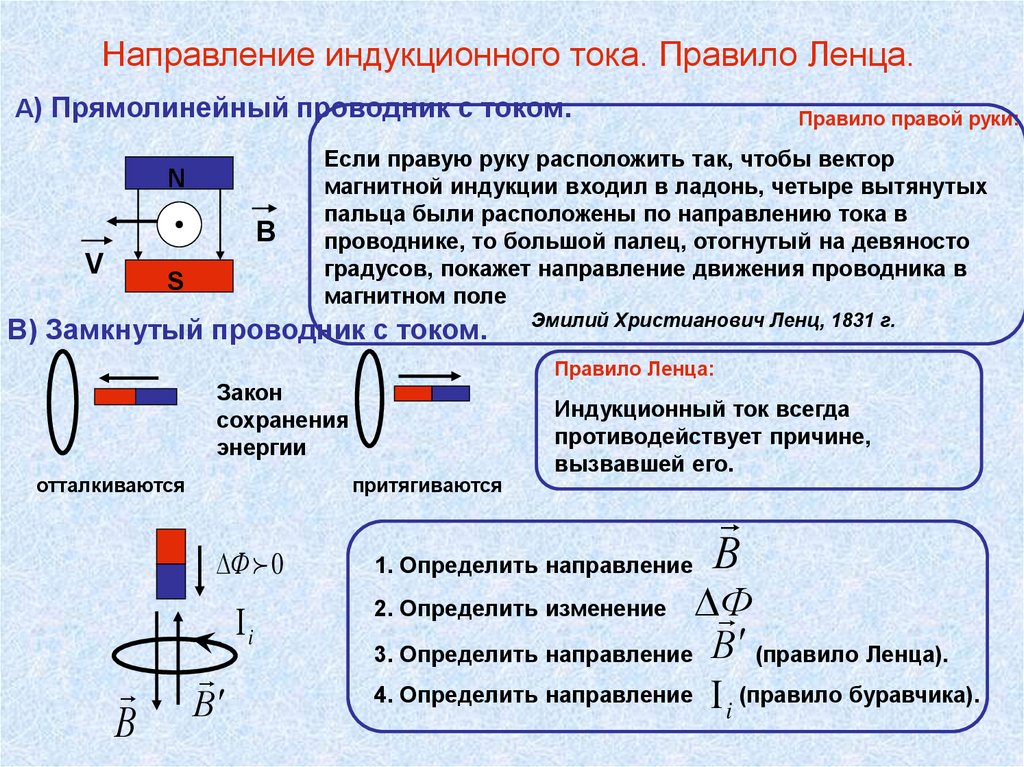 Линии магнитного поля должны проходить через область, ограниченную
петля цепи для индукции ЭДС.
Линии магнитного поля должны проходить через область, ограниченную
петля цепи для индукции ЭДС.
Направление индуктивного тока (ESBQ2)
Самое важное, что нужно помнить, это то, что индуцированный ток противостоит любым происходящим изменениям.
На первом рисунке (слева) южный полюс магнита приближается к петле цепи. Величина поле от магнита увеличивается. Ответом от ЭДС индукции будет попытка сопротивляться полю к полюсу становится сильнее. Поле является вектором, поэтому ток будет течь в таком направлении, что поля, вызванные током, имеют тенденцию нейтрализовать поля от магнита, сохраняя результирующее поле прежним.
Чтобы противостоять изменению от приближающегося южного полюса сверху, ток должен привести к линиям поля, которые
отойти от приближающегося полюса. Следовательно, индуцированное магнитное поле должно иметь силовые линии, идущие вниз.
внутреннюю часть петли. Направление тока, указанное стрелками на контуре цепи, позволит достичь этого. Проверьте это, используя правило правой руки. Поместите большой палец правой руки в направлении одной из стрелок и обратите внимание
что поле закручивается вниз в область, ограниченную петлей.
Проверьте это, используя правило правой руки. Поместите большой палец правой руки в направлении одной из стрелок и обратите внимание
что поле закручивается вниз в область, ограниченную петлей.
На второй диаграмме южный полюс удаляется. Это означает, что поле от магнита будет получать слабее. Реакцией на индуцированный ток будет создание магнитного поля, которое добавляется к существующему. от магнитного, чтобы сопротивляться его уменьшению в силе.
Другой способ представить ту же функцию — использовать столбы. Чтобы противостоять приближающемуся южному полюсу тока
индуцированное создает поле, похожее на еще один южный полюс со стороны приближающегося южного полюса.
Подобно тому, как полюса отталкиваются, вы можете представить себе течение, создающее южный полюс, чтобы отразить приближающийся южный полюс. В
на второй панели течение устанавливает северный полюс, чтобы притянуть южный полюс, чтобы остановить его удаление.
Мы также можем использовать вариацию правила правой руки, помещая пальцы в направлении тока, чтобы направьте большой палец в направлении линий поля (или на северный полюс).
Мы можем проверить все это на примере северного полюса, приближающегося или удаляющегося от контура. Для В первом случае приближения к северному полюсу ток будет сопротивляться изменению, создав поле в противоположное направление полю от магнита, который становится сильнее. Используйте правило правой руки для подтверждения что стрелки создают поле с линиями поля, которые закручиваются вверх в замкнутой области, отменяя эти закручивается вниз от северного полюса магнита.
Подобно тому, как шесты отталкиваются, в качестве альтернативы проверьте, что, положив пальцы правой руки в направлении ток оставляет ваш большой палец вверх, указывая на северный полюс.
Для второй фигуры, где северный полюс удаляется, ситуация обратная.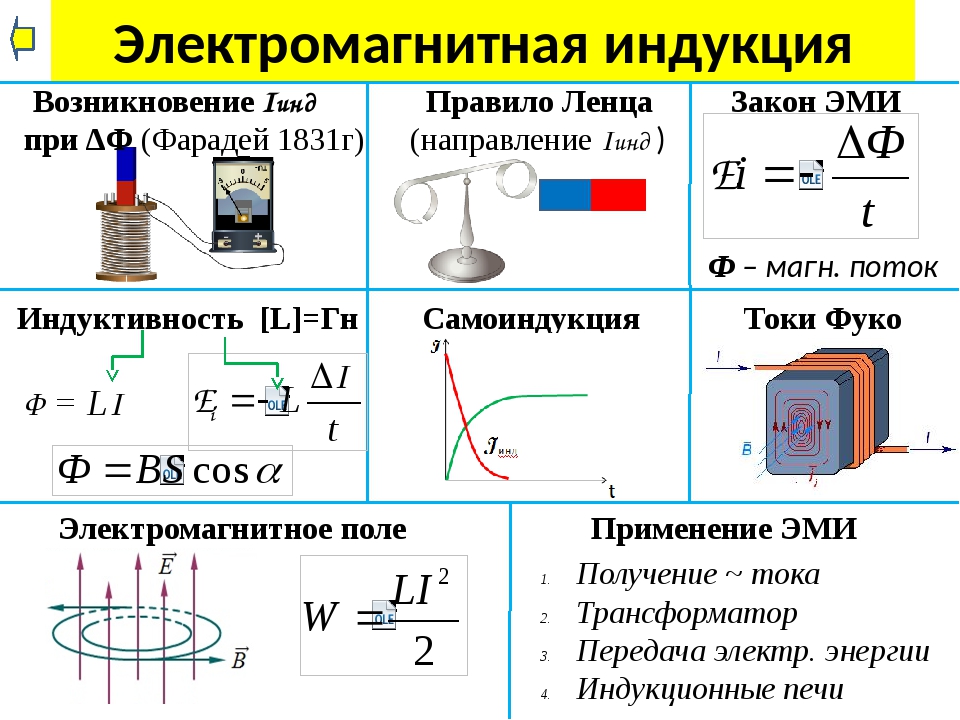
Направление индукционного тока в соленоиде (ESBQ3)
Подход для определения направления тока в соленоиде аналогичен подходу, описанному выше. Единственное отличие состоит в том, что в соленоиде есть несколько витков проволоки, поэтому величина наведенного ЭДС будет другой. Поток можно рассчитать, используя площадь поверхности соленоида, умноженную на количество петель.
Помните: направления токов и связанных с ними магнитных полей можно найти с помощью только Правило правой руки. Когда пальцы правой руки направлены в сторону магнитного поля, большой палец указывает направление течения. Когда большой палец направлен в сторону магнитного поле, пальцы указывают в направлении тока.
Направление тока будет препятствовать изменению. Мы будем использовать настройку, как в этом скетче, чтобы сделать тест:
В случае, когда северный полюс подведен к соленоиду, ток будет течь так, что северный полюс установленный на конце соленоида, ближайшем к приближающемуся магниту, чтобы оттолкнуть его (проверьте с помощью правого Ручное правило):
В случае, когда северный полюс удаляется от соленоида, ток будет течь так, что южный полюс устанавливается на конце соленоида, ближайшем к удаляющемуся магниту, для его притяжения:
В случае, когда южный полюс удаляется от соленоида, ток будет течь так, что северный полюс устанавливается на конце соленоида, ближайшем к удаляющемуся магниту, для его притяжения:
В случае, когда южный полюс подведен к соленоиду, ток будет течь так, что южный полюс будет устанавливается на конце соленоида, ближайшем к приближающемуся магниту, для его отражения:
temp text Простой способ создать магнитное поле с изменяющейся интенсивностью — переместить постоянный магнит рядом с проводом или проводом. моток проволоки. Магнитное поле должно увеличиваться или уменьшаться по интенсивности перпендикулярно проводу (так
что силовые линии магнитного поля «пересекают» проводник), иначе не будет индуцироваться напряжение.
моток проволоки. Магнитное поле должно увеличиваться или уменьшаться по интенсивности перпендикулярно проводу (так
что силовые линии магнитного поля «пересекают» проводник), иначе не будет индуцироваться напряжение.
Наведенный ток создает магнитное поле. Наведенное магнитное поле имеет направление, которое стремится к компенсировать изменение магнитного поля в петле провода. Таким образом, вы можете использовать правило правой руки, чтобы найти направление индуцированного тока, помня, что индуцированное магнитное поле противоположно по направлению к изменению магнитного поля.
Индукция
Электромагнитная индукция находит практическое применение в конструкции электрических генераторов, использующих
механическая сила для перемещения магнитного поля мимо катушек провода для создания напряжения. Однако это отнюдь не
единственное практическое применение этого принципа.
Если мы помним, магнитное поле, создаваемое проводом с током, всегда перпендикулярно проводу, и что интенсивность потока этого магнитного поля зависит от количества тока, проходящего через него. Мы поэтому можно видеть, что провод способен индуцировать напряжение по собственной длине если ток меняется. Этот эффект называется самоиндукцией . Самоиндукция – это когда переменное магнитное поле производится изменением тока через провод, индуцируя напряжение по длине того же провода.
Если магнитный поток усиливается за счет сгибания проволоки в форме катушки и/или наматывания этой катушки вокруг материала с высокой проницаемостью этот эффект самоиндуцируемого напряжения будет более интенсивным. Устройство созданный для использования этого эффекта, называется индуктор .
Помните, что индуцированный ток создаст магнитное поле, противодействующее изменению магнитного потока. Это известно как закон Ленца.
Это известно как закон Ленца.
Рабочий пример 1: Закон Фарадея
Рассмотрим плоскую квадратную катушку с 5 витками. Катушка имеет размер \(\text{0,50}\) \(\text{m}\) с каждой стороны и имеет магнитное поле \(\text{0,5}\) \(\text{T}\), проходящее через него. Плоскость катушки перпендикулярна магнитное поле: поле направлено за пределы страницы. Используйте закон Фарадея для расчета ЭДС индукции, если магнитное поле равномерно увеличивается от \(\text{0,5}\) \(\text{T}\) до \(\text{1}\) \(\text{T}\) в \(\text{10}\) \(\text{s}\). Определить направление индукционного тока.
Определите, что требуется
Мы должны использовать Закон Фарадея для расчета ЭДС индукции.
Запишите закон Фарадея
\[\mathcal{E}=-N\frac{\Delta\phi}{\Delta t}\]
Мы знаем, что магнитное поле направлено под прямым углом к поверхности и, таким образом, выровнено с нормалью. Это означает
нам не нужно беспокоиться об угле, который поле образует с нормалью и \(\phi=BA\). Старт
или начальное магнитное поле, \(B_i\), задается как окончательная величина поля, \(B_f\). Мы хотим определить
величина ЭДС, поэтому мы можем игнорировать знак минус. 92(\текст{1} — \текст{0,50})}{\текст{10}} \\
&=\текст{0,0625}\текст{В}
\конец{выравнивание*}
Это означает
нам не нужно беспокоиться об угле, который поле образует с нормалью и \(\phi=BA\). Старт
или начальное магнитное поле, \(B_i\), задается как окончательная величина поля, \(B_f\). Мы хотим определить
величина ЭДС, поэтому мы можем игнорировать знак минус. 92(\текст{1} — \текст{0,50})}{\текст{10}} \\
&=\текст{0,0625}\текст{В}
\конец{выравнивание*}
Индуцированный ток направлен против часовой стрелки, если смотреть со стороны возрастающего магнитного поля.
Рабочий пример 2: Закон Фарадея
Рассмотрим соленоид из 9 витков неизвестного радиуса \(r\). На соленоид действует магнитное поле
\(\text{0,12}\) \(\text{T}\). Ось соленоида параллельна магнитному полю. Когда поле
равномерно переключается на \(\text{12}\) \(\text{T}\) в течение 2 минут ЭДС величиной
\(-\text{0,3}\) \(\text{V}\) индуцируется.
Определить радиус соленоида.
Определите, что требуется
Нам необходимо определить радиус соленоида. Мы знаем, что связь между индуцированным ЭДС и поле подчиняются закону Фарадея, который включает в себя геометрию соленоида. Мы можем использовать это соотношение для нахождения радиуса.
Запишите закон Фарадея
\[\mathcal{E}=-N\frac{\Delta\phi}{\Delta t}\]
Мы знаем, что магнитное поле направлено под прямым углом к поверхности и, таким образом, выровнено с нормалью. Это означает
нам не нужно беспокоиться об угле, который поле образует с нормалью и \(\phi=BA\). Начальный или
начальное магнитное поле, \(B_i\), задается как окончательная величина поля, \(B_f\). Можем скинуть минус
знак, потому что мы работаем только с величиной ЭДС. 9{-\text{2}}\) \(\text{m}\).
соленоид подвергается воздействию переменного магнитного поля, которое равномерно изменяется от \(\text{0,4}\) \(\text{T}\) до
\(\text{3,4}\) \(\text{T}\) в интервале \(\text{27}\) \(\text{s}\).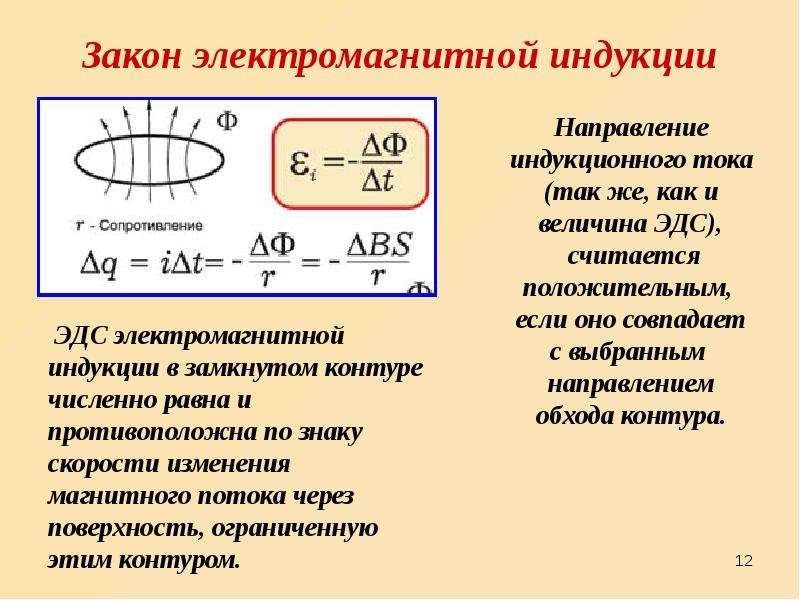 Ось соленоида делает
угол \(\text{35}\)\(\text{°}\) к магнитному полю. Найдите ЭДС индукции.
Ось соленоида делает
угол \(\text{35}\)\(\text{°}\) к магнитному полю. Найдите ЭДС индукции.
Определите, что требуется
Мы должны использовать Закон Фарадея для расчета ЭДС индукции.
Запишите закон Фарадея
\[\mathcal{E}=-N\frac{\Delta\phi}{\Delta t}\] Мы знаем, что магнитное поле направлено под углом к нормали к поверхности. Это означает, что мы должны учитывать угол, который поле образует с нормалью и \(\phi=BA\cos(\theta)\). Стартовый или начальный магнитный поле, \(B_i\), задается как окончательная величина поля, \(B_f\). Мы хотим определить величину ЭДС, поэтому мы можем игнорировать знак минус. 9{-\текст{3}}\текст{В} \конец{выравнивание*}
Индуцированный ток направлен против часовой стрелки, если смотреть со стороны возрастающего магнитного поля.
временный текстМоделирование: 23ZW
Реальные приложения
Следующие устройства используют закон Фарадея в своей работе.
индукционные плиты
магнитофон
металлоискатели
трансформаторы
Применение закона Фарадея в реальной жизни
Выберите одно из следующих устройств и поищите в Интернете или в библиотеке, как работает ваше устройство. работает. Вам нужно будет обратиться к закону Фарадея в вашем объяснении.
индукционные плиты
магнитофон
металлоискатели
трансформаторы
Закон Фарадея
Учебник Упражнение 10.2
Сформулируйте закон электромагнитной индукции Фарадея словами и запишите математическое соотношение.
ЭДС, \(\mathcal{E}\), возникающая вокруг контура проводника, пропорциональна скорости изменения магнитного потока φ через площадь контура A. Это можно сформулировать математически как:
\[\mathcal{E} = -N\frac{\Delta\phi}{\Delta t}\]
где \(\phi =B·A\) и B — напряженность магнитного поля. \(N\) — количество цепей петли. Магнитное поле измеряется в единицах тесла (Тл). Знак минус указывает направление и что ЭДС индукции стремится противодействовать изменению магнитного потока. Знак минус можно игнорировать при вычислении величин.
Опишите, что происходит, когда стержневой магнит вставляется или вытягивается из соленоида, соединенного с амперметр. Нарисуйте картинки, подтверждающие ваше описание.
В случае, когда северный полюс подведен к соленоиду, ток будет течь так, что северный полюс устанавливается на конце соленоида, ближайшем к приближающемуся магниту, чтобы оттолкнуть его (проверьте с использованием правила правой руки):
В случае, когда северный полюс удаляется от соленоида, ток будет течь так, что южный полюс устанавливается на конце соленоида, ближайшем к удаляющемуся магниту, чтобы притягивать его:
В случае, когда южный полюс удаляется от соленоида, ток будет течь так, что северный полюс устанавливается на конце соленоида, ближайшем к удаляющемуся магниту, чтобы притягивать его:
В случае, когда южный полюс приближается к соленоиду, ток будет течь так, что полюс устанавливается на конце соленоида, ближайшем к приближающемуся магниту, чтобы отталкивать его:
Объясните, как магнитный поток может быть равен нулю, когда магнитное поле не равно нулю.
Поток связан с магнитным полем:
\(\фи = БА \cos\тета\)
Если \(\cos \theta\) равно 0, то магнитный поток будет равен 0, даже если есть магнитное поле. В этом случае магнитное поле параллельно поверхности и не проходит через нее.
Используйте правило правой руки, чтобы определить направление индуцированного тока в соленоиде ниже.
Южный полюс магнита приближается к соленоиду. Закон Ленца говорит нам, что ток будет течь чтобы противостоять изменениям. Южный полюс на конце соленоида будет противодействовать приближающемуся югу. столб. Ток будет циркулировать по странице в верхней части катушки, так что большой палец правой рука указывает налево.
Рассмотрим круглую катушку из 5 витков радиусом \(\text{1,73}\) \(\text{м}\). Катушка подвергается
к переменному магнитному полю, которое равномерно изменяется от \(\text{2,18}\) \(\text{T}\) до
\(\text{12,7}\) \(\text{T}\) с интервалом \(\text{3}\) \(\text{минуты}\). {2} & = \текст{0,0479} \\
г & = \текст{0,22}\текст{м}
\end{align*}
{2} & = \текст{0,0479} \\
г & = \текст{0,22}\текст{м}
\end{align*}
Найдите изменение потока, если ЭДС равна \(\text{12}\) \(\text{V}\) за период \(\text{12}\) \(\текст{ы}\).
\begin{выравнивание*} \mathcal{E} &= N\frac{\Delta\phi}{\Delta t} \\ 12 & = 5 \ влево ( \ гидроразрыва {\ Delta \ phi} {12} \ вправо) \\ \Дельта\фи & = \текст{28,8}\текст{Wb} \end{align*}
Если угол изменить на \(\text{45}\)\(\text{°}\), какой временной интервал должен измениться? изменить на , чтобы ЭДС индукции осталась прежней?
\начать{выравнивать*} \mathcal{E} &= N\frac{\Delta\phi}{\Delta t} \\ & = N\frac{\phi_{f} — \phi_{i}}{\Delta t} \\ & = N\frac{B_{f}A\cos\theta — B_{i}A \cos\theta}{\Delta t} \\ & = \cos\theta \times N\frac{B_{f}A — B_{i}A}{\Delta t} \конец{выравнивание*}
Все значения остаются одинаковыми между двумя описанными ситуациями, за исключением угла и
время. Мы можем приравнять уравнения для двух сценариев:
Мы можем приравнять уравнения для двух сценариев:
\начать{выравнивать*} \mathcal{E}_1 &= \mathcal{E}_2 \\ \cos\theta_1 \times N\frac{B_{f}A — B_{i}A}{\Delta t_1} & = \cos\theta_2 \times N\frac{B_{f}A — B_{i}A}{\Delta t_2} \\ \cos\theta_1 \frac{1}{\Delta t_1} & = \cos\theta_2 \frac{1}{\Delta t_2} \\ \Delta t_2 & = \frac{\Delta t_1 \cos\theta_2}{\cos \theta_1} \\ \Delta t_2 & = \frac{(\text{12} \cos(\text{45}}{\cos(\text{23})} \\ \Дельта t_2 & = \text{9,22}\text{ с} \конец{выравнивание*}
Предыдущий 10.2 Магнитное поле, связанное с током | Оглавление | Следующий 10. |
Физика | Бесплатный полнотекстовый | Закон Фарадея и магнитная индукция: причина и следствие, эксперимент и теория. проводящая катушка заменена.
Это явление компактно описывается математической моделью, связывающей «электродвижущую силу» (ЭДС) V вокруг замкнутой цепи с временными изменениями магнитного потока Φ — интеграла магнитного поля по поверхности, очерченной этим замыканием. Закон индукции Фарадея можно напрямую связать с векторным уравнением Максвелла–Фарадея ([1], с. 160). Используя обозначения, где ∂t≡d/dt, уравнения записываются как
где E — электрическое поле, а B — магнитное поле.
Однако фундаментальный закон причинности требует, чтобы следствия не могли произойти раньше их причин; и это ожидание имеет математические последствия. Эти следствия порождают, в частности, знаменитые соотношения Крамерса-Кронига [2,3,4], которые можно использовать для ограничения как спектральных свойств физических величин, так и моделей, используемых для их описания.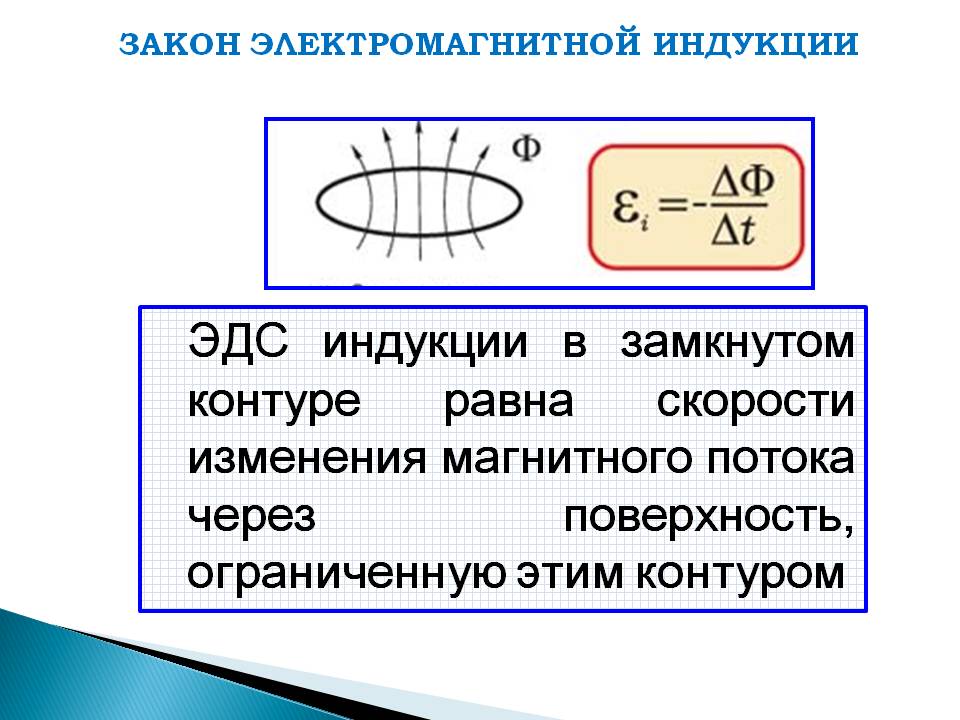
Здесь мы принимаем локальный взгляд на причинность, а не глобальный, и используем временную область, наиболее естественную для выражения причинного поведения. В этом случае существует схема [5] приписывания конкретных причинно-следственных ролей компонентам математических моделей, основанная на дифференциальных уравнениях во времени (подробности см. также в [6,7]). Проще говоря, это означает, что в любой уравнение математической модели это член производной по времени высшего порядка, который следует рассматривать как следствие, а остальные члены как причины; но обратите внимание, что его также можно применять к системам связанных уравнений (например, уравнениям Максвелла ([5], раздел V), а также позже в этой статье в разделе 5.2). В качестве простого примера, поскольку второй закон Ньютона можно записать в виде ∂tv=F/m, то согласно [5] мы можем утверждать, что сила F вызывает изменение скорости v массы m. Использование этой интерпретации особенно естественно при рассмотрении численного решения динамических физических моделей; см. Приложение A в [8], где основное внимание уделяется тому, что происходит при обновлении текущего состояния системы [9].,10] (т. е. интегрированные вперед во времени), или по мере того, как вселенная расширяется в свое «будущее» (как, например, в подходе причинных множеств [11]).
Приложение A в [8], где основное внимание уделяется тому, что происходит при обновлении текущего состояния системы [9].,10] (т. е. интегрированные вперед во времени), или по мере того, как вселенная расширяется в свое «будущее» (как, например, в подходе причинных множеств [11]).
Обратите внимание, что существуют другие обсуждения и подходы к причинно-следственной связи в электродинамике, имеющие отношение к закону Фарадея [12,13,14]. В частности, одна значительная школа мысли предпочитает связывать все обратно с первоначальными исходными терминами (см., например, [12] и примечания в Приложении B к [8]). К сожалению, поскольку закон Фарадея не содержит явных ссылок на исходные заряды, мы не можем анализировать его с точки зрения причин и следствий на этой основе — нам потребовалась бы другая модель, которая действительно ссылалась на исходные заряды и их движение (например, см. [15]). ).
Следовательно, в дальнейшем мы решили использовать только локальное и совместимое с Крамерсом-Кронигом определение [5] для того, что представляет собой каузальную интерпретацию математической модели.
Используя локальный взгляд на причинность, описанный в [5] и во вставке 1, поскольку уравнение (1) не имеет производных по времени, применяемых к V, но одна производная по времени применяется к Φ, это означает, что ЭДС V следует рассматривать как причину , где изменение потока ∂tΦ является его следствием. Как следствие, было бы более интуитивно переписать уравнение (1) как
где мы также вынуждены описывать пространственные градиенты электрического поля ∇×E как причину, а результирующие временные изменения поля B как его следствие. Несколько тревожно то, что теперь это означает, что мы не можем интерпретировать нашу математическую модель закона индукции Фарадея как наше предпочтительное причинно-следственное утверждение: то есть, где изменения в потоке индуцируют ЭДС (и, следовательно, управляют токами) [16,17,18]. Однако, основываясь на нашей математической модели, мы по-прежнему можем сделать более слабое утверждение, когда эти два утверждения просто приравниваются друг к другу или связаны друг с другом [19]. ].
].
Эта ситуация предполагает, что уравнение (2), несмотря на его полезность, просто не является хорошим причинным представлением эксперимента, который мы имели в виду. Чтобы решить эту проблему, нам нужно провести четкое различие между причинностью, очевидной в эксперименте, и причинной интерпретацией математической модели, которая обязательно является лишь приближением к этому эксперименту. Хотя обычно мы надеемся, что они совпадают, кажется, что в случае закона Фарадея это не так, и в разделе 2 мы обсуждаем, почему (или как) это может быть.
Очевидно, было бы желательно, чтобы наше математическое описание индукции явно показывало, как ЭДС или электрический ток могут генерироваться в проводнике, будь то за счет изменяющихся свойств магнитного поля или за счет движения проводника в этих полях. В дальнейшем мы попробуем три (нерелятивистских) подхода к поиску математической модели, которая описывает, как некоторое свойство или поведение магнитного потока (или, возможно, только магнитного поля) явно приписывается как причина ЭДС.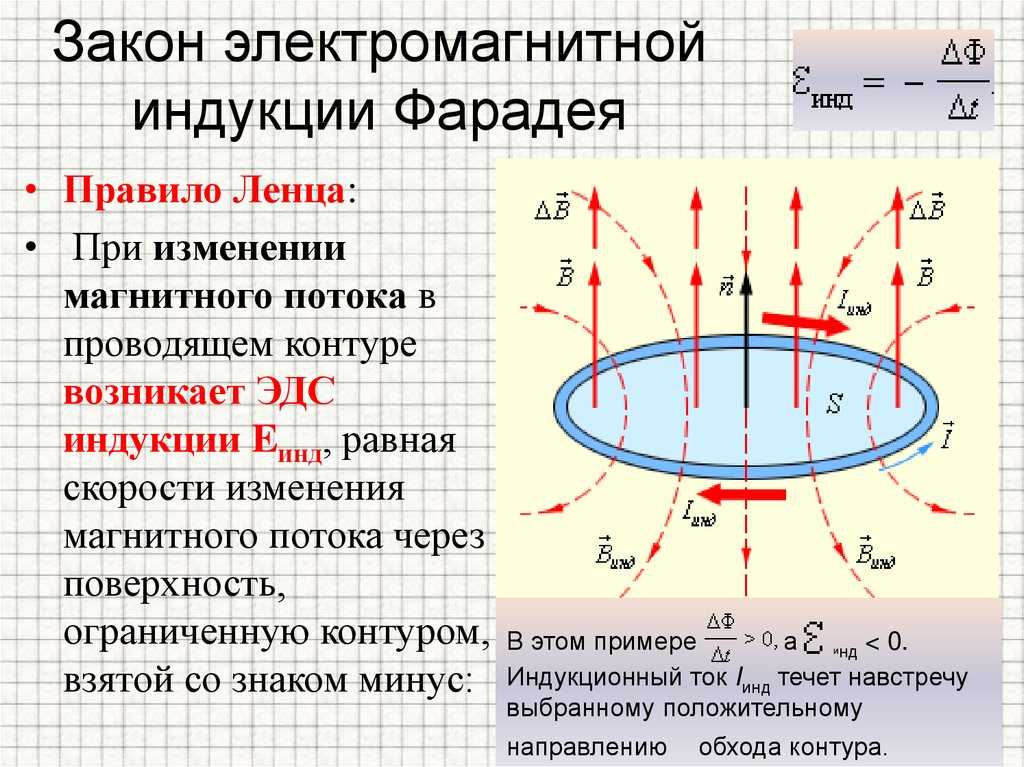
Первый, в разделе 3, основан на уравнении Максвелла-Фарадея и не работает. Второй, в разделе 4, вместо этого основан на уравнении Максвелла-Ампера и достигает этой важной цели, но, возможно, не очень удовлетворительным образом. Третий, в разделе 5, основан на законе силы Лоренца, и мы пробуем как простой абстрактный расчет, так и конкретную установку, распространенную во многих курсах бакалавриата, и выводим модель тока, вызванного магнитными полями и движением. Наконец, в разделе 6 мы делаем вывод.
Вставка 1. Как быть причинным: Рассмотрим простое модельное уравнение ∂tR(t)=Q(t), которое в используемой здесь интерпретации интерпретируется как «Q вызывает изменения в R». Используя математическое определение производной, в некоторый произвольный момент времени t0 уравнение модели имеет вид
Непосредственно перед тем, как перейти к пределу, и для некоторого достаточно малого значения δ мы имеем
Теперь давайте попробуем использовать это как предсказатель будущего.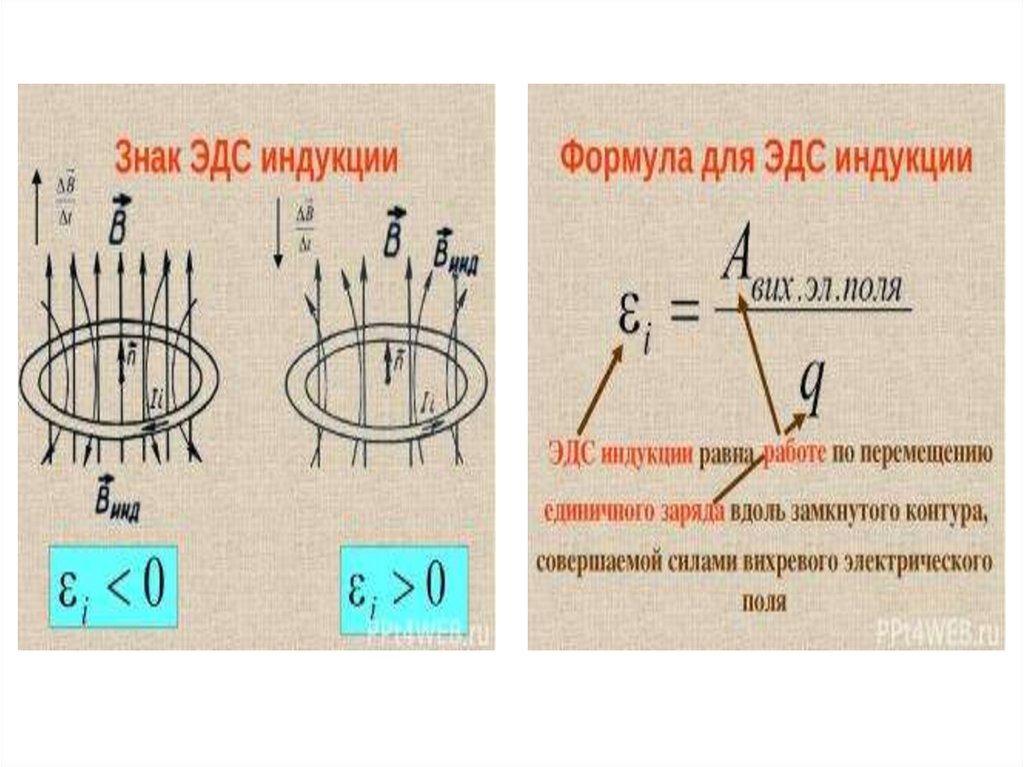 Мы сразу видим, что самая последняя (или наиболее близкая к будущему) величина равна R(t0+δ), поэтому мы переставляем ее слева и получаем
Мы сразу видим, что самая последняя (или наиболее близкая к будущему) величина равна R(t0+δ), поэтому мы переставляем ее слева и получаем
Здесь мы видим, что для обновления наших знаний о R до его следующего значения в момент t+δ требуется (а) прошлое знание R (т. е. R(t0−δ)) и (б) текущее знание Q (т. е. Q( т0)). Таким образом, ясно, что значение Q вызывает изменения в R. Если бы вместо этого мы захотели вычислить Q, надеясь сказать что-то вроде «R вызывает Q», мы бы сначала преобразовали уравнение (4) в форму
но сразу увидим, что Q(t0) зависит от будущего значения R, а именно R(t0+δ) – а зависимость от будущих значений несовместима со стандартными представлениями о причинности.
Эта презентация на уровне бакалавриата, в которой обсуждается магнитная индукция, подчеркивает различие между любой предполагаемой экспериментальной причинностью и причинностью, закодированной в ее математической модели. Это показывает, что очевидно полезное определение ЭДС на самом деле работает против наших попыток создать модель, в которой оно индуцируется изменениями магнитного потока. Напротив, альтернативный подход к электрическим токам, генерируемым движением и/или изменением магнитного поля, не имеет таких ограничений.
Это показывает, что очевидно полезное определение ЭДС на самом деле работает против наших попыток создать модель, в которой оно индуцируется изменениями магнитного потока. Напротив, альтернативный подход к электрическим токам, генерируемым движением и/или изменением магнитного поля, не имеет таких ограничений.
2. Эксперимент
Рассмотрим пример эксперимента, состоящего из двух частей устройства: (i) магнита и (ii) петли или катушки с прикрепленным вольтметром, как показано на рисунке 1. Когда мы перемещаем магнит поблизости петли, мы видим индуцированное напряжение. Поэтому на основе этого экспериментального опыта вполне естественно — и действительно точно — сделать вывод, что движение магнита вызывало появление напряжения (или ЭДС). Если мы также изучаем физику, мы могли бы также связать движение магнита с величиной магнитного потока, пересекающего петлю, и, таким образом, сказать, что наш эксперимент показывает, что «изменение потока вызывает ЭДС».
Только что описанная «экспериментальная причинность» не вызывает сомнений. Однако здесь исследуется объединение этого экспериментального опыта причинности с любой причинной интерпретацией математического выражения закона Фарадея, то есть уравнения (2).
Однако здесь исследуется объединение этого экспериментального опыта причинности с любой причинной интерпретацией математического выражения закона Фарадея, то есть уравнения (2).
Для лучшего понимания нам нужно начать с более ясного понимания того, почему мы можем сделать вывод, что напряжение было вызвано нашими действиями по перемещению магнита. Примечательно, что мы должны понимать, что это происходит не только потому, что мы видели конечное напряжение, зарегистрированное на вольтметре, так как оно могло быть просто плохо обнулено и всегда иметь какое-то конечное значение или компенсировано эффектами какого-то внешнего поля, не относящегося к индукционному эксперименту. . Вместо этого мы говорим «вызвано», потому что после того, как (и когда) мы переместили магнит рядом с петлей, напряжение, регистрируемое вольтметром, изменилось. Изменение напряжения — это видимый эффект, который заставляет нас искать его причину. По крайней мере, мы должны хотеть, чтобы наша каузальная модель индукции описывала, как происходят изменения напряжения («ЭДС») из-за внешних раздражителей.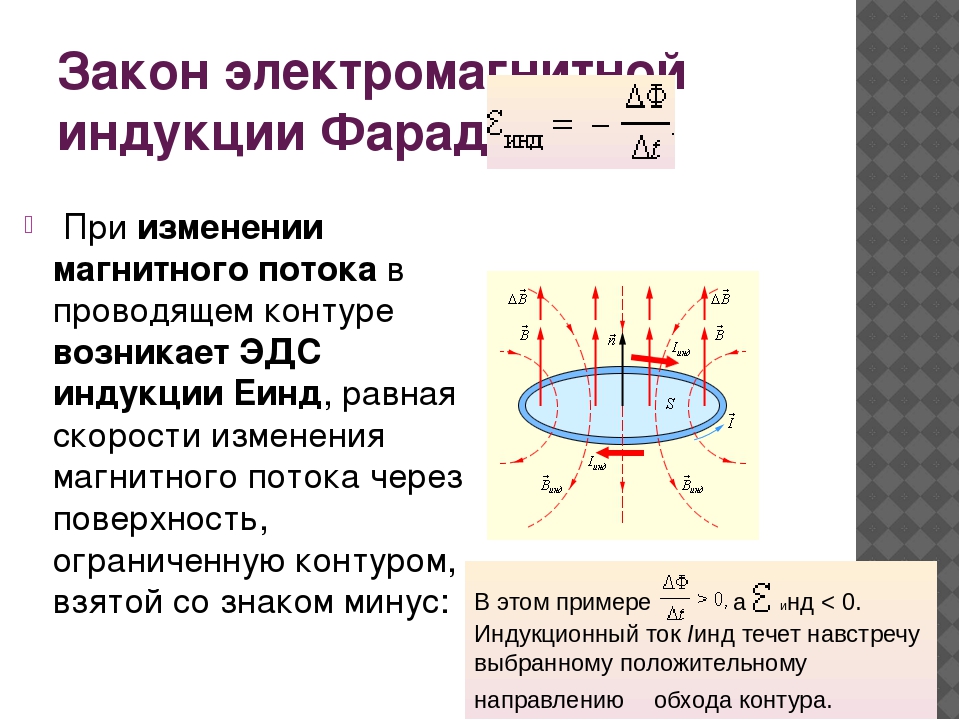
Теперь попробуем математически систематизировать наш эксперимент, учитывая предопределенный вход (движение магнита) и наблюдая за результирующим эффектом на выходе (ЭДС V). Предполагая для простоты магнит фиксированной силы с одинаково фиксированной ориентацией, единственным входом в нашу модель должна быть только его скорость v(t). Это v(t) есть причина; это то, что мы указываем в плане эксперимента, а затем реализуем. Мы надеемся или ожидаем, что эта причина приведет к изменению. Это изменение должно быть видно как влияние на измеряемую ЭДС, так что в один момент она может быть равна нулю, а в следующий момент уже будет другой, т. ). Таким образом, мы могли бы написать
где L () — это функция или оператор, который содержит всю необходимую информацию об электромагнетизме, структуре поля, создаваемого магнитом, законе силы Лоренца для зарядов и теории цепей.
Теперь мы можем с первого взгляда увидеть, что структура математической модели Уравнение (7) для нашего эксперимента не имеет той же формы, что и закон Фарадея: Уравнение (2) явно относится только к изменениям потока ∂tΦ, а не к изменения ЭДС. В самом деле, это не должно вызывать удивления, поскольку уравнение (2) не является даже попыткой микроскопической модели экспериментального процесса, когда движущийся магнит создает изменяющееся распределение электромагнитного поля, которое затем влияет на движение электронов. создавая или изменяя электрические токи (например, [15]), и, таким образом, впоследствии вызывая ЭДС. Поскольку в уравнении (2) опущено так много экспериментальных подробностей, на первый взгляд неясно, почему мы должны ожидать, что они вообще совпадают, не говоря уже об идеальном совпадении.
В самом деле, это не должно вызывать удивления, поскольку уравнение (2) не является даже попыткой микроскопической модели экспериментального процесса, когда движущийся магнит создает изменяющееся распределение электромагнитного поля, которое затем влияет на движение электронов. создавая или изменяя электрические токи (например, [15]), и, таким образом, впоследствии вызывая ЭДС. Поскольку в уравнении (2) опущено так много экспериментальных подробностей, на первый взгляд неясно, почему мы должны ожидать, что они вообще совпадают, не говоря уже об идеальном совпадении.
Тем не менее, в дальнейшем мы попытаемся найти фарадеевский закон, который лучше соответствует нашей экспериментальной концепции.
3. Уравнение Максвелла–Фарадея
Сначала рассмотрим стандартный вывод закона индукции Фарадея, начиная с уравнения Максвелла для ротора; обратите внимание, однако, что некоторые подходы используют обратный подход и начинают с индукции и сводят ее к уравнению завитка.
Мы начинаем с петли материала и рассматриваем эту петлю как границу C некоторой замкнутой поверхности S, и рассматриваем электрическое поле E и магнитное поле B, как показано на рисунке 2. Вывод продолжается, начиная с Максвелла-Фарадея уравнение, взяв поверхностный интеграл с обеих сторон, а затем применив теорему Стокса к левой части (левая сторона), чтобы преобразовать поверхностный интеграл по S в линейный интеграл по элементам dl вдоль C:
Причинная интерпретация этого уравнения должна состоять в том [5], что ЭДС «вызывает» изменения в потоке Φ — на самом деле мы не можем принять общепринятую интерпретацию, согласно которой изменения в потоке индуцируют (или вызывают) ЭДС. Обратите внимание, что это не интерпретация экспериментальных фактов или наблюдений, а интерпретация, основанная на математической модели.
Кроме того, обратите внимание, что ЭДС, т. е. V=∮Cdl·E, которая, как предполагается, представляет потенциал, генерирующий ток, индуцированный в проводе, не вычисляется, как мы, возможно, могли бы ожидать, т. е. следуя одиночному заряду на своем пути вокруг проводящего контура, чтобы вычислить пройденную разность напряжений. Вместо этого мы рассмотрели силы, действующие на непрерывную линию бесконечно малых зарядов на петле в один момент, и проинтегрировали эти силы. Без модели движения этих зарядов то, что мы смоделировали, больше похоже на диэлектрическое кольцо со связанными зарядами и токами, привязанными к своим местам, а не на проводящую проволочную петлю со свободно движущимися зарядами и токами [20].
е. следуя одиночному заряду на своем пути вокруг проводящего контура, чтобы вычислить пройденную разность напряжений. Вместо этого мы рассмотрели силы, действующие на непрерывную линию бесконечно малых зарядов на петле в один момент, и проинтегрировали эти силы. Без модели движения этих зарядов то, что мы смоделировали, больше похоже на диэлектрическое кольцо со связанными зарядами и токами, привязанными к своим местам, а не на проводящую проволочную петлю со свободно движущимися зарядами и токами [20].
Конечно, с практической точки зрения закон индукции Фарадея, полученный выше и показанный в уравнении (1), является чрезвычайно полезным выражением, и оно совместимо с экспериментальными измерениями. Примечательно, что в электродвигателе или генераторе скорость вращения оси дает нам собственную угловую частоту ω, так что производная потока по времени становится простым умножением на ω; и далее, в таком квазистационарном случае атрибуция причинности становится несущественной. Однако его полезность не является гарантией того, что он предоставит математическую модель, инкапсулирующую случайные свойства, на которые мы могли бы надеяться для генерации ЭМП. Тем не менее, позже в разделе 5 мы увидим, что этой трудности нет при поиске моделей, демонстрирующих влияние на ток в результате изменений магнитного поля или потока.
Тем не менее, позже в разделе 5 мы увидим, что этой трудности нет при поиске моделей, демонстрирующих влияние на ток в результате изменений магнитного поля или потока.
4. Уравнение Максвелла–Ампера
В разделе 3 мы видели, что уравнение Максвелла–Фарадея не дает желаемой причинной интерпретации. Следовательно, давайте попробуем альтернативный вывод для модели индукции, начиная с уравнения Максвелла для ротора, которое представляет закон Ампера. Цель здесь — показать, как некое подходящее свойство магнитного поля — возможно, связанное с магнитным потоком — явным образом вызывает изменение ЭДС. Это означало бы, что мы можем заняться генерацией ЭДС из ничего и использовать это, чтобы мотивировать появление индуцированного тока. Поскольку мы видели в предыдущем разделе, что, согласно [5], уравнение Максвелла-Фарадея неверно объясняет картину «магнитные поля, вызывающие (индуцирующие) ток», уравнение Максвелла-Ампера с его обратными ролями для электрических и магнитные вклады могут показаться более многообещающими.
Снова возьмем петлю, содержащую заряды, с замкнутой поверхностью S и границей C, и рассмотрим поля электрического смещения и магнитной индукции D и H, как на рис. 3. Вывод продолжается, начиная с уравнения Максвелла–Ампера, принимая поверхностный интеграл с обеих сторон, а затем применить теорему Стокса к правой части (правая сторона), чтобы преобразовать этот поверхностный интеграл в линейный интеграл:
где J — электрический ток.
Отсюда видно, что ни ЭДС, ни поток Φ не возникают. Однако некоторые дальнейшие размышления приведут нас к большему успеху, если взять завиток с обеих сторон перед применением поверхностного интеграла. Если ϵ — диэлектрическая проницаемость, а μ — проницаемость, мы имеем:
Теперь это уравнение дает нам ЭДС от левой.в.с. линейный интеграл, рассчитанный так же, как в разделе 3. Поскольку ∇·B=0, а c=1/µϵ — скорость света, мы можем написать
Этот результат представляет собой уравнение, похожее на индукцию, которому мы можем дать четко определенную причинную интерпретацию того, где возникает ЭДС: поскольку пространственные вариации B (или, при интегрировании, пространственные вариации потока) вызывают изменения ЭДС, как и токи .
Хотя мы могли бы попытаться рассмотреть этот общий случай, поучительно упростить его и взять случай нулевого тока, когда все dS ориентированы по оси z, а B в основном выровнена по оси z и изменяется в направлении z, так что только ее компонента Bz имеет большое значение. С учетом этих допущений и расчета эффективного магнитного потока как ΦA=SBz, т.е. после перемещения п.в.с. поверхностный интеграл через пространственные производные по оси z ∂z, мы можем написать упрощенное уравнение
И последнее замечание: в ситуациях, когда целесообразно заменить c∂z на ∂t, мы также можем восстановить что-то, эквивалентное обычной форме, но с дополнительной производной по времени с обеих сторон. Однако при этой замене поток ΦA снова подвергается производной по времени высшего порядка. Таким образом, индукционная модель также вернулась к той же каузальной интерпретации, противоположной нашему предпочитанию «потока как причины».
5.
 Закон силы Лоренца
Закон силы ЛоренцаНесмотря на относительно знакомый характер расчетов в разделах 3 и 4, во многих отношениях может показаться более естественным вывести модель индукции тока, исходя из закона силы Лоренца. Поскольку закон магнитной индукции Фарадея не основан на эффектах, вызванных приложенными электрическими полями (см., например, [1], стр. 160), я начинаю с импульса p электрического заряда q в чисто магнитном поле
Это сама по себе модель, в которой изменения количества движения заряда вызываются (магнитной) силой Лоренца F. Хотя рассмотрение изменений количества движения в контексте индуцированных токов необычно, в приведенных ниже расчетах это удобный способ суммирования задействованных сил.
Как и в предыдущих расчетах, теперь мы надеемся найти полезным определение величины, подобной ЭДС. Однако в то время как в этих расчетах ЭДС была получена из линейного интеграла электрического поля, здесь мы вместо этого основываем ее на интеграле по движущимся зарядам; и чтобы подчеркнуть это различие, мы обозначаем его VL, а не просто V.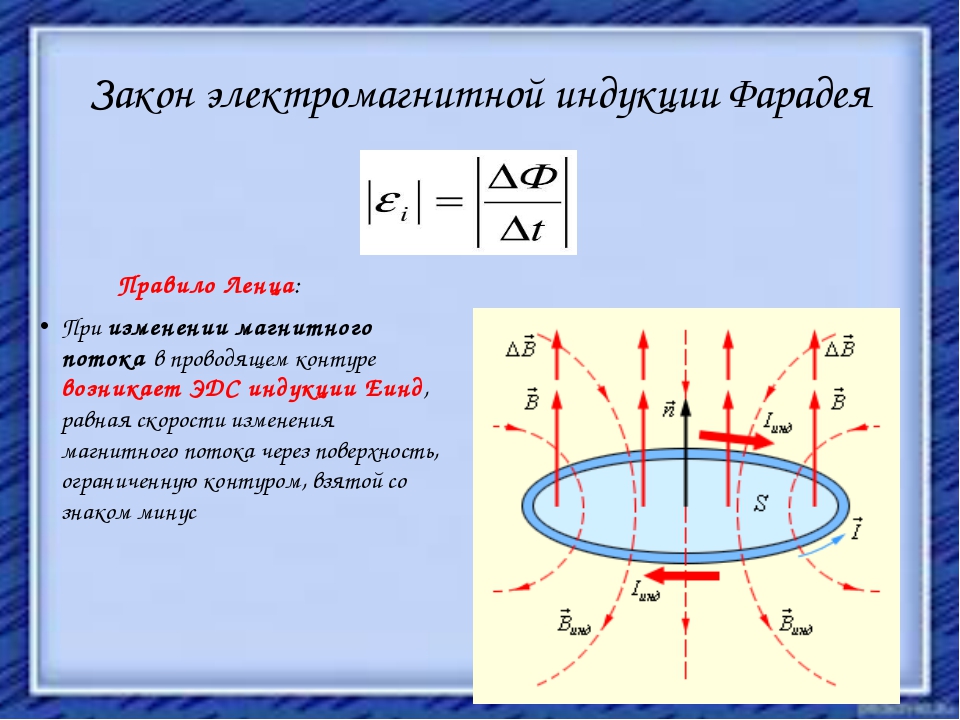
5.1. Простая петля
Здесь мы применим ее к (одному из) зарядов в нашей проводящей петле. Это более общая формулировка Блини и Блини ([1], стр. 160), но они используют ее просто как поддержку чего-то, эквивалентного стандартному вычислению, сделанному в разделе 3.
Поскольку VL=W/ q для потенциала (ЭДС) VL, работы W и заряда q, а приращение работы на заряде определяется выражением dW=F·dl с силой F вдоль линейного элемента dl,
Сначала мы линейно интегрируем по петле (контур C), содержащей заряды q и движущейся в v, чтобы получить полную ЭДС VL,
Далее мы преобразуем правую поверхность. линейный интеграл к поверхностному интегралу завитка по теореме Стокса
так что теперь мы можем использовать стандартную векторную идентичность для ∇ × (A × B),
Первый член равен нулю, так как ∇·B=0; и мы можем еще больше упростить, удалив второй член, если поле скоростей для зарядов (по сути, масштабированный ток) не имеет источников или стоков. Здесь для удобства мы пошли дальше и настаиваем на постоянном поле скоростей v, так что третий член также обращается в нуль. Результат
Здесь для удобства мы пошли дальше и настаиваем на постоянном поле скоростей v, так что третий член также обращается в нуль. Результат
Чтобы сделать этот результат более понятным, мы дополнительно упростим ситуацию, как показано на рисунке 4, рассматривая квадратную петлю в плоскости xy, которая ограничивает поверхность S, площадь которой S перпендикулярна оси z. Магнитное поле ориентировано вдоль оси z, так что единственная ненулевая составляющая — это Bz, и оно изменяется только вдоль оси x и с фиксированной скоростью. Затем мы перемещаем нашу петлю вбок параллельно оси x с фиксированной скоростью v, так что мы получаем прямое равенство, но без каких-либо производных по времени и, следовательно, без подразумеваемой причинно-следственной связи:
Это кажется наиболее тесно связанным с формулировкой Максвелла–Ампера в разделе 4, которая также зависит от пространственных градиентов B. Однако мы могли бы адаптировать это соотношение, преобразовав часть числителя dx скорости v=dx/dt, и часть знаменателя dx градиента поля dBz/dx, чтобы получить
что является нормальным выражением закона Фарадея, если предположить эквивалентность VL и V, несмотря на то, что они получены из разных исходных точек. Несмотря на это, нам все еще не удалось найти математическую модель с искомыми причинными свойствами, в которых свойства магнитного поля или его потока вызывают появление или изменение токов.
Несмотря на это, нам все еще не удалось найти математическую модель с искомыми причинными свойствами, в которых свойства магнитного поля или его потока вызывают появление или изменение токов.
5.2. U-образный стержень и подвижный стержень
Теперь попробуем продвинуться дальше, рассматривая конкретную ситуацию, а не абстрактные конструкции. Рассмотрим стандартную систему в стиле бакалавриата, состоящую из длинной прямоугольной проводящей U-образной формы в постоянном магнитном поле с проводящим стержнем, замыкающим токовую петлю, как показано на рисунке 5. Тогда говорят, что стержень скользит по плечам U, таким образом изменение площади, окруженной петлей, следовательно, изменение замкнутого потока. Тогда мы могли бы напрямую применить закон Фарадея из левой части. уравнения (1) и использовать скорость изменения потока для расчета ЭДС, а затем (если мы хотим) индукционного тока, связанного с этой ЭДС.
Однако, учитывая наше решение настаивать на существовании конкретной причинной интерпретации и поскольку закон Фарадея не согласуется с этой интерпретацией, мы должны поэтому выбрать другую математическую модель. Поскольку без предположения о пространственных градиентах поля, которые не являются необходимым свойством нашего примера, мы не можем использовать выражение, основанное на амперах, в уравнении (19), мы начнем с закона силы. Однако использование уравнения закона сил Лоренца (21) означает, что мы можем сразу увидеть, что здесь есть две силы, действующие на заряды:
Поскольку без предположения о пространственных градиентах поля, которые не являются необходимым свойством нашего примера, мы не можем использовать выражение, основанное на амперах, в уравнении (19), мы начнем с закона силы. Однако использование уравнения закона сил Лоренца (21) означает, что мы можем сразу увидеть, что здесь есть две силы, действующие на заряды:
Во-первых, на заряды в стержне действует магнитная сила из-за движения стержня в магнитном поле. Эта сила направлена вдоль стержня, изменяя скорость заряда в стержне, а затем распространяясь на всю петлю.
Во-вторых, на заряды в стержне действует магнитная сила из-за движения этих зарядов вдоль стержня в магнитном поле. Эта сила толкает заряды перпендикулярно стержню, что может быть связано с эффектом Холла. Здесь мы предполагаем, что этот эффект Холла быстро поляризует стержень в масштабе времени, намного более быстром, чем другие процессы, так что суммарный эффект проявляется только в остаточной замедляющей силе самого стержня.
Это означает, что мы можем использовать закон силы, чтобы вычислить (а) как ток J в петле реагирует на скорость v стержня, и (б) как движение стержня реагирует на ток J в петле . Естественно, это будут динамические уравнения с явной причинностью.
Здесь мы принимаем провод U фиксированным и жестким, так что любые силы, действующие на него из-за протекания по нему тока и/или наличия электромагнитных полей, не учитываются. Сама проволока U имеет сколь угодно длинные плечи с расстоянием между ними и длиной основания Lbar, каждое с линейной плотностью заряда σ. Стержень имеет массу M и скорость v, что дает импульс Pbar. Он установлен перпендикулярно плечам проволоки U на расстоянии L от их основания и (также) имеет плотность заряда σ и длину Lbar.
Ток J состоит из потока зарядов с поступательным импульсом Pcur. Он имеет полный заряд Q, но только q=Lbarσ в стержне, который является единственной частью, на которую действует магнитная сила. Если (эффективная) массовая плотность зарядов [21] равна ρ, скорость зарядов вдоль стержня равна u, а их скорость равна u=Pcur/ρLtot(t), где Ltot(t)=2Lbar+2L(t ).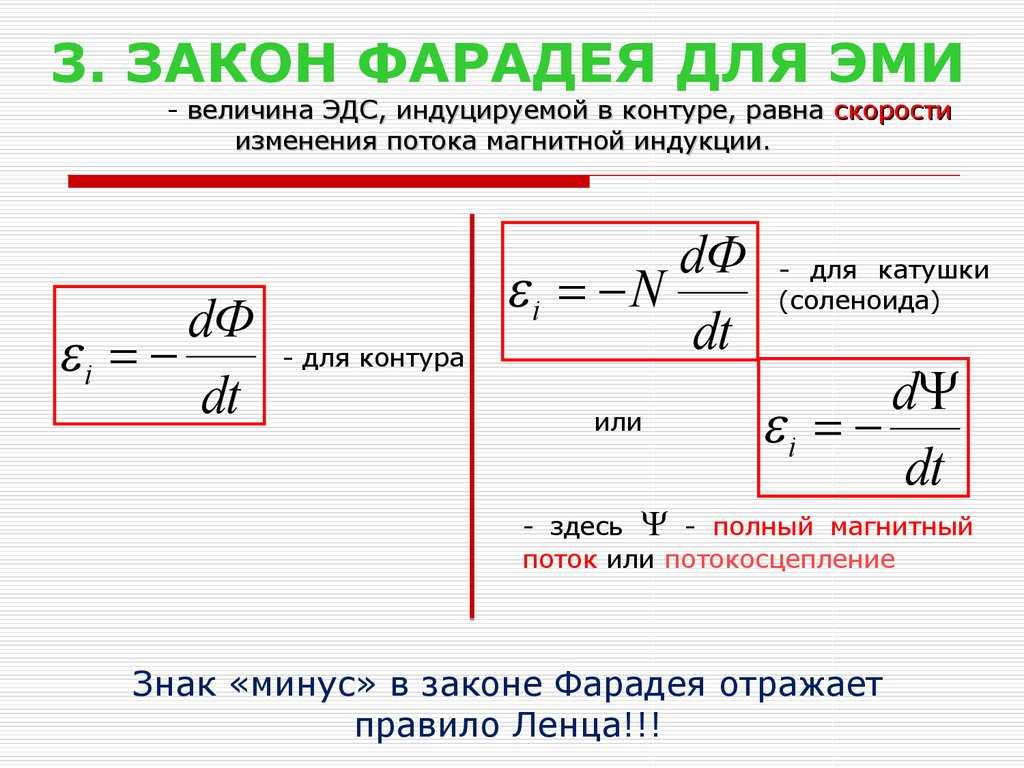 Предполагается, что углы U и контакты между U и стержнем отклоняют (например, за счет упругого отражения) заряды вокруг петли (т. е. в их новом направлении), так что Pcur направлен либо вперед (по часовой стрелке, либо рис. 5) или назад (против часовой стрелки) по петле; плотность заряда тока также предполагается фиксированной [22].
Предполагается, что углы U и контакты между U и стержнем отклоняют (например, за счет упругого отражения) заряды вокруг петли (т. е. в их новом направлении), так что Pcur направлен либо вперед (по часовой стрелке, либо рис. 5) или назад (против часовой стрелки) по петле; плотность заряда тока также предполагается фиксированной [22].
Полная сила на стержне возникает только из-за магнитной силы, которую необходимо просуммировать по длине Lbar. Обратите внимание, что поле внутри петли здесь не имеет значения, важна его напряженность в каждой точке стержня в момент интегрирования общей силы. Плотность силы на каждом элементе стержня равна
так что в сумме получаем
Суммарная сила тока представляет собой не только магнитную силу, которую необходимо просуммировать по длине стержня Lbar, но также включает линейный резистивный член γ(t), где γ(t)=rLtot(t) и r пропорциональна сопротивлению на единицу длины. Обратите внимание, что (опять же) поле внутри петли здесь не важно, важна его сила вдоль стержня в его текущем местоположении. Поскольку скорость стержня по проводам равна Pbar/M, плотность силы на каждом элементе тока равна
Обратите внимание, что (опять же) поле внутри петли здесь не важно, важна его сила вдоль стержня в его текущем местоположении. Поскольку скорость стержня по проводам равна Pbar/M, плотность силы на каждом элементе тока равна
так что в сумме имеем
Это два линейных связанных дифференциальных уравнения, которые проще всего скомбинировать, взяв производную по времени от уравнения Pcur и подставив одно в другое. Упрощая уравнения, не отображая явных зависимостей Ltot(t) и γ(t) от времени, получаем
куда
Обратите внимание, что мы не можем напрямую заменить Pcur на ток J в дифференциальных уравнениях, так как они связаны через общую длину проводника Ltot(t). Кроме того, управляющий член, зависящий от ∂tBz, пропорционален v(t)=Pbar(t)/M, что имеет свою динамику: если магнитное поле меняется во времени, недостаточно пытаться решить только уравнение ( 37), нам также необходимо рассмотреть уравнение (30).
Поскольку в этом результате содержится несколько сложных взаимозависимостей, мы теперь рассмотрим некоторые поучительные частные случаи.
5.2.1. Постоянное магнитное поле
Рассмотрим случай, когда магнитное поле постоянно во времени и во всем пространстве, так что ∂tBz=0, т. е. третья правая часть. член уравнения (37) обращается в нуль. Здесь стержень после первоначального толчка будет колебаться вперед и назад в соответствии с частотным параметром Ω(t), но амплитуда этих колебаний затухает со скоростью, определяемой γ(t).
Мы также можем видеть, что при небольших вариациях L(t) и Ltot(t) параметр частоты будет фактически постоянным и, таким образом, станет истинной частотой колебаний. В этом режиме мы можем прямо заменить Pcur на ток J=σPcur/ρLtot и получить
Это приведет к затухающим синусоидальным колебаниям тока и, следовательно, к соответствующим колебаниям скорости стержня; поскольку ускорение стержня можно связать с током уравнением (30).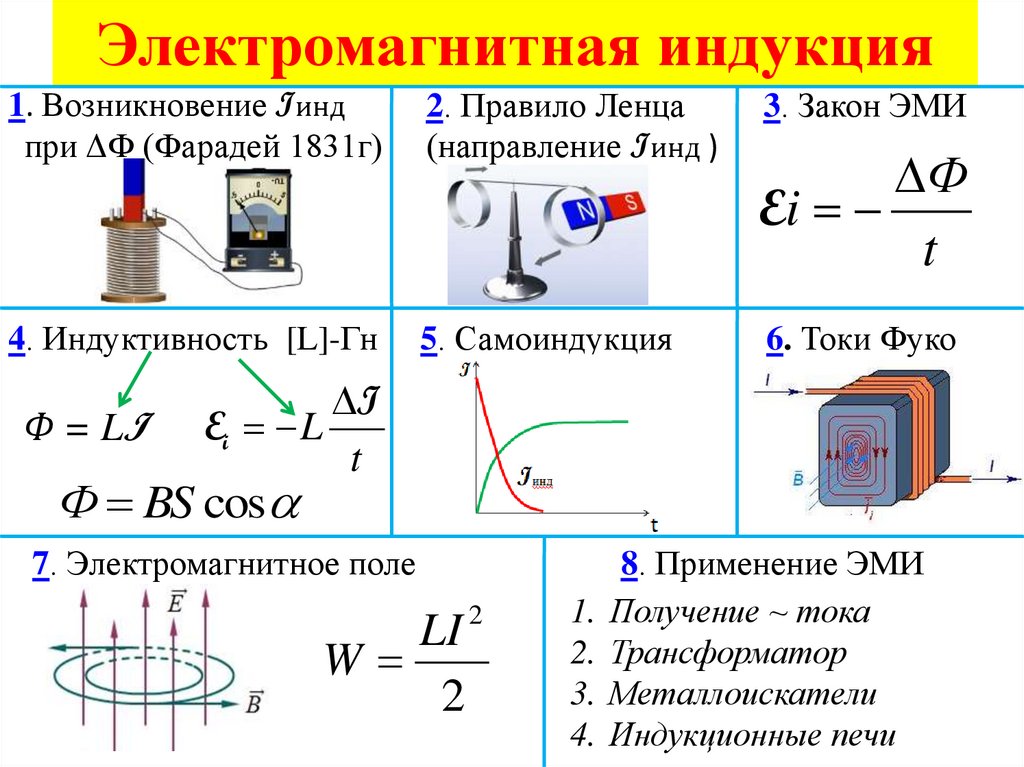
5.2.2. Изменяющееся во времени магнитное поле
Уравнение (37) сохранило возможность для зависящего от времени Bz. Мы видим, что изменение поля ∂tBz действует на ускорение тока, но способом, зависящим от Pbar (т. е. скорости стержня). Таким образом, ток по-прежнему хочет колебаться, хотя это вряд ли будет простой синусоидой, а изменения поля действуют как движущая сила.
Обратите внимание, что причинно-следственная связь сохраняется, поскольку влияние на Pcur второго порядка по времени, на один порядок больше, чем на Bz [5,23].
5.2.3. Электродвижущая сила
Теперь мы можем рассмотреть, что говорит нам уравнение (37) об ЭДС, индуцированной в контуре; поскольку то, что мы делаем, основано на законе силы Лоренца, мы используем ЭДС VL, а не обычный закон Фарадея V. Поскольку VL — это работа на единицу заряда, или линейный (петлевой) интеграл силы, а сила — это просто при изменении импульса имеем, что VL=σ−1∂tPcur. Это означает, что для небольших изменений Ltot(t) мы можем практически повторно использовать уравнение (37) напрямую — мы просто применяем другую производную по времени и заменяем Pcur, чтобы получить
Это означает, что для небольших изменений Ltot(t) мы можем практически повторно использовать уравнение (37) напрямую — мы просто применяем другую производную по времени и заменяем Pcur, чтобы получить
На первый взгляд может показаться, что уравнение показывает временные изменения магнитного поля, вызывающие изменения в ЭДС. Конечно, поскольку он содержит больше деталей, зависящих от модели, следует ожидать некоторых отличий от стандартного закона Фарадея в уравнении (2) или альтернативного закона Ампера в уравнении (19).
Трудность теперь состоит в том, что правая часть, являющаяся прямым результатом преобразования Pcur в VL, теперь имеет производную по времени второго порядка, действующую на B, точно так же, как и левая часть, действующая на VL. Поскольку они имеют одинаковые порядки производной по времени, они имеют один и тот же каузальный статус — при правильном объединении их можно интерпретировать как следствие других членов уравнения (40), т. е. причиноподобных членов VL и ∂tγVL, как а также с участием v.
Это означает, что уравнение (40) не имеет причинно-следственной интерпретации, которую мы искали, например, такой, где временные изменения первого порядка в магнитном поле вызывают изменения второго порядка в ЭДС.
5.3. Обсуждение
Здесь мы увидели, что ни для наших вычислений, основанных на силовом законе, т. е. очень простой, ни для более реалистичной системы, оба не могут дать нам результат, в котором можно было бы сказать, что свойства магнитного поля вызывают изменения в магнитном поле. ЭДС. Тем не менее причинно-следственные связи, подобные той, к которой мы стремились, все же можно сделать, не ссылаясь на ЭДС, а вместо этого используя утверждения о том, что (изменения) свойств магнитного поля вызывают токи.
6. Выводы
В этой статье мы попытались найти версию или новый вывод закона Фарадея, математическая форма которого имитирует причинно-следственную интерпретацию, которую мы хотели бы иметь, а именно изменения магнитного потока через петлю вызывают изменения в ЭДС вокруг эта петля.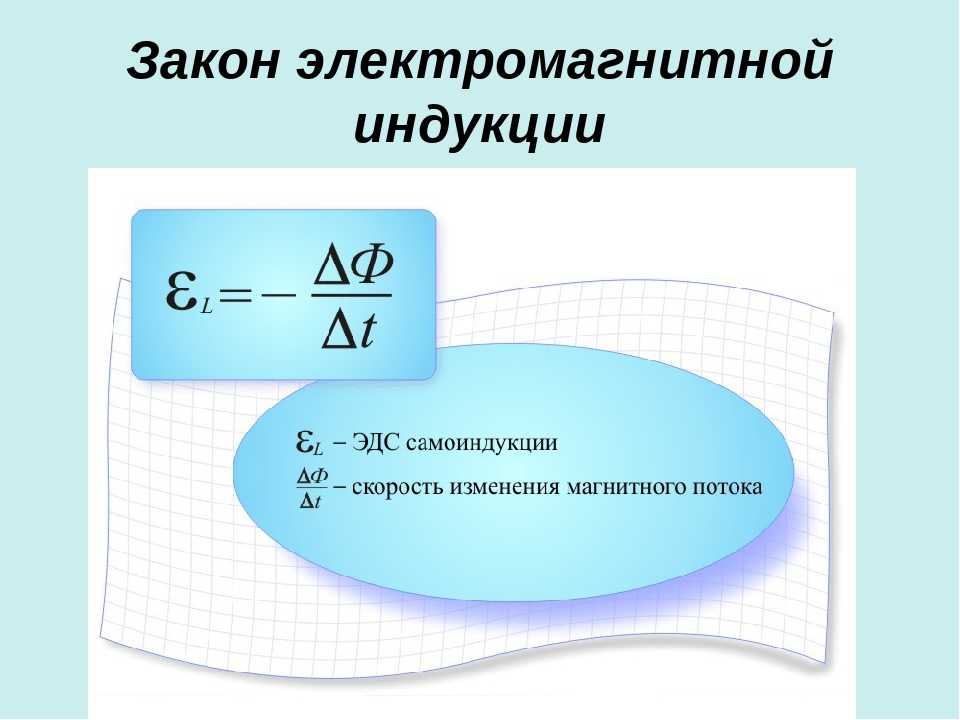 Однако обычная математическая форма закона Фарадея несовместима с этим желанием и позволяет лишь сказать, что ЭДС вызывает изменение потока.
Однако обычная математическая форма закона Фарадея несовместима с этим желанием и позволяет лишь сказать, что ЭДС вызывает изменение потока.
Чтобы устранить этот очевидный недостаток, мы вывели фарадеевский закон, основанный на уравнении Максвелла Ампера, что действительно позволило нам говорить об индуцированных изменениях ЭДС, но вместо этого они были вызваны пространственными градиентами магнитного потока, которые не совсем то, на что мы надеялись. Это побудило нас попробовать альтернативный подход, основанный на законе силы Лоренца, микроскопические основы которого показали многообещающие свойства магнитного поля, действительно индуцирующие (вызывающие) изменения тока, как в абстрактной, так и в более реалистичной обстановке. Однако, когда математическая модель была преобразована, чтобы ссылаться вместо этого на индуцированные изменения в величине VL, подобной ЭДС, мы обнаружили, что модель стала несовместимой с желаемой причинной интерпретацией, подчеркнув, что именно настойчивое использование ЭДС вносит трудности.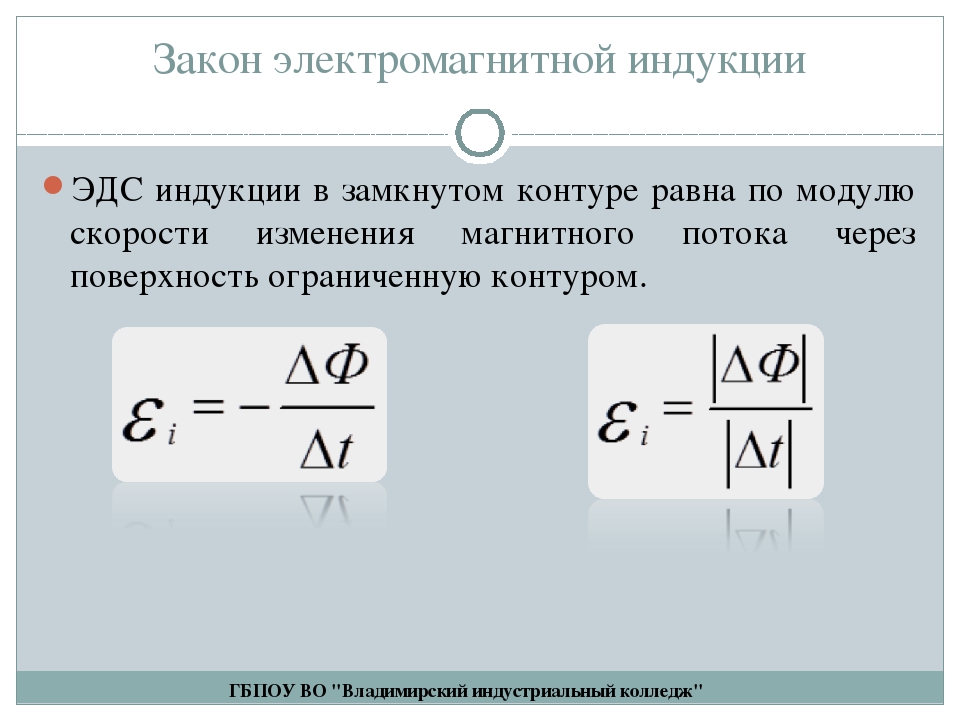
Таким образом, наше исследование показало, что следует быть осторожным при интерпретации причинно-следственных связей процессов магнитной индукции и опасаться зависимости от скрытых или неявных предположений, которые могут привести к вводящим в заблуждение выводам. Во-первых, следует четко различать интерпретации, относящиеся к эксперименту, и интерпретации, относящиеся к математической модели; различие, которое жизненно важно в случае закона Фарадея. Во-вторых, поскольку самое близкое к тому, что мы можем подобраться к «изменениям в магнитном потоке, вызывающем ЭДС», основано на уравнении Максвелла-Ампера, а не Максвелла-Фарадея, нам нужно быть осторожными при выборе причинно-следственной интерпретации эмпирических законов, полученных из эксперимента или совместимых с ним.
Финансирование
Я благодарен за поддержку, предоставленную STFC (Институт Кокрофта ST/G008248/1 и ST/P002056/1) и EPSRC (проект Alpha-X EP/N028694/1).
Благодарности
Я также хотел бы поблагодарить Имперский колледж Лондона за гостеприимство, многочисленные интересные дискуссии с Джонатаном Гратусом и Мартином В. МакКоллом, а также всех, кто внес полезные предложения.
МакКоллом, а также всех, кто внес полезные предложения.
Конфликт интересов
Автор заявляет об отсутствии конфликта интересов.
Ссылки и примечания
- Блини, Б.И.; Блини, Б. Электричество и магнетизм, 2-е изд.; Clarendon Press: Oxford, UK, 1965. [Google Scholar]
- Bohren, C.F. Что сделали Крамерс и Крониг и как они это сделали? Евро. Дж. Физ. 2010 , 31, 573. [Google Scholar] [CrossRef]
- Ландау, Л.Д.; Лифшиц, Е.М. Электродинамика сплошных сред; Пергамон: Оксфорд, Великобритания; Нью-Йорк, штат Нью-Йорк, США, 1984. [Google Scholar]
- Lucarini, V.; Сааринен, Дж. Дж.; Пейпонен, К.Е.; Вартиайнен, Э. М. Отношения Крамерса-Кронига в исследованиях оптических материалов; Springer: Берлин/Гейдельберг, Германия, 2005 г.; Том 110. [Google Scholar] [CrossRef][Green Version]
- Кинслер, П. Как быть причинным: время, пространство-время и спектры.
 Евро. Дж. Физ. 2011 , 32, 1687. [Google Scholar] [CrossRef][Green Version]
Евро. Дж. Физ. 2011 , 32, 1687. [Google Scholar] [CrossRef][Green Version] - Кордуняну, К. Функциональные уравнения с каузальными операторами; Тейлор и Фрэнсис: Лондон, Великобритания; Нью-Йорк, штат Нью-Йорк, США, 2002. [Google Scholar]
- Кордуняну, К. Существование решений нейтральных функционально-дифференциальных уравнений с каузальными операторами. Дж. Дифференц. Экв. 2000 , 168, 93–101. [Google Scholar] [CrossRef][Зеленая версия]
- Кинслер, П. Как быть причинным: время, пространство-время и спектры. arXiv 2011 , arXiv:1106.1792. [Google Scholar] В этом обновлении электронной печати есть дополнительные приложения по сравнению с [5].
- Кинслер, П. Время и пространство, частота и волновой вектор: Или о чем я говорю, когда говорю о распространении. arXiv 2014 , arXiv:1408.0128. [Google Scholar]
- Кинслер П. Однонаправленные оптические импульсы, распространение во времени, пространственная и временная дисперсия.
 Дж. опт. 2018 , 20, 025502. [Google Scholar] [CrossRef][Green Version]
Дж. опт. 2018 , 20, 025502. [Google Scholar] [CrossRef][Green Version] - Rideout, DP; Соркин Р.Д. Классическая динамика последовательного роста причинных множеств. физ. Rev. D 2000 , 61, 024002. [Google Scholar] [CrossRef][Green Version]
- Ефименко О. Изложение электромагнитной теории в соответствии с принципом причинности. Евро. Дж. Физ. 2004 , 25, 287–296. [Google Scholar] [CrossRef]
- Hill, S.E. Перефразируя закон Фарадея. физ. Учитель 2010 , 48, 410–412. [Google Scholar] [CrossRef]
- Savage, C.M. Причинность в классической электродинамике. физ. Учитель 2012 , 50, 226. [Google Scholar] [CrossRef][Green Version]
- Бойер, Т.Х. Фарадеевская индукция и носители тока в цепи. Являюсь. Дж. Физ. 2015 , 83, 263–271. [Google Scholar] [CrossRef][Green Version]
- Thide, B. Теория электромагнитного поля; Upsilon Books: Uppsala, Sweden, 2004.
 [Google Scholar]
[Google Scholar] - .Джексон, Дж. Д. Классическая электродинамика, 3-е изд.; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Reitz, J.R.; Милфорд, Ф.Дж.; Кристи, Р. В. Основы электромагнитной теории, 3-е изд.; Addison-Wesley: Reading, MA, USA, 1980. [Google Scholar]
- При поиске определения «индуцировать» мы видим, что оно, по сути, то же самое, что и «причины». Некоторые примеры различных формулировок слов «причина», «индуцировать» и «связанный с» из литературы обсуждаются в приложении к предварительной версии этой статьи по адресу arxiv:1705.0840.
- Кумар, В. Электромагнитный отклик металла: сравнительный анализ «модели свободного заряда» и «модели связанного заряда». Евро. Дж. Физ. 2017 , 38, 045203. [Google Scholar] [CrossRef]
- Попытка точно описать, как заряды реагируют как группа, трудна и сложна. Нужно как-то усреднить множество различных микроскопических влияний на каждый заряд: не только от его локального окружения в проводнике и любых внешних приложенных полей, но также необходимо учитывать множество взаимодействий между ним и другими зарядами [15,24,25].
 . Затем мы должны объединить все это в чистое влияние на сборы как группу. Здесь мы просто сводим совокупный эффект всех подобных усложнений к эффективной плотности массы зарядов.
. Затем мы должны объединить все это в чистое влияние на сборы как группу. Здесь мы просто сводим совокупный эффект всех подобных усложнений к эффективной плотности массы зарядов. - Еще одна деталь, которой здесь пренебрегают, заключается в том, что каждое движение стержня либо теряется, либо наследует некоторые дополнительные расходы из-за изменения длины стороны.
- Кинслер, П. Активные стоки и причинность. физ. Rev. A 2010 , 82, 055804. [Google Scholar] [CrossRef][Green Version]
- Darwin, C.G. Инерция электронов в металлах. проц. Р. Соц. А 1936 , 154, 61–66. [Google Scholar] [CrossRef][Green Version]
- Эссен, Х. От наименьшего действия в электродинамике к магнитомеханической энергии — обзор. Евро. Дж. Физ. 2009 , 30, 515–539. [Google Scholar] [CrossRef]
Рисунок 1. Эксперимент: ( a ) магнит (его северный полюс обозначен буквой «N») со скоростью v(t) проходит вблизи проволочной петли с вольтметром ⓥ, так что ( b ) его магнитное поле B(t,r ) также движется, что приводит к ( c ) ЭДС V, появляющейся вокруг петли.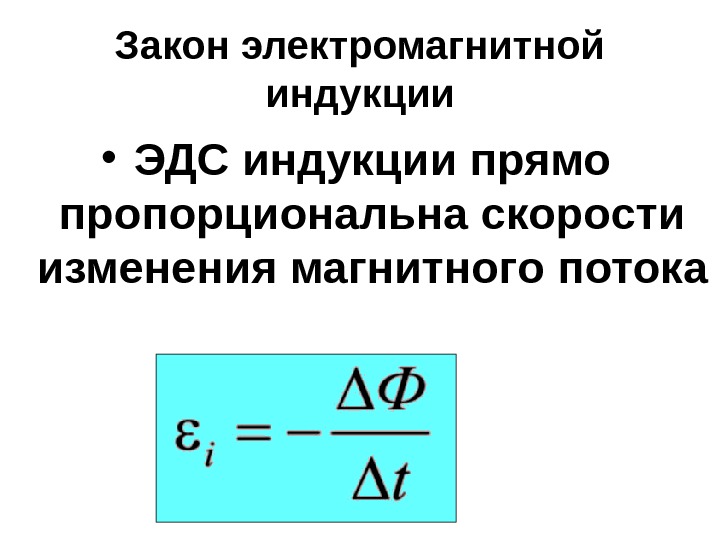 Хотя переход от ( a ) к ( b ) моделируется просто, так как это всего лишь перемещение магнитного поля магнита, в ( c ), где эти поля взаимодействуют с зарядами в контуре, индуцируя и изменяя токи, вплоть до возможного воздействия на ЭДС.
Хотя переход от ( a ) к ( b ) моделируется просто, так как это всего лишь перемещение магнитного поля магнита, в ( c ), где эти поля взаимодействуют с зарядами в контуре, индуцируя и изменяя токи, вплоть до возможного воздействия на ЭДС.
Рисунок 1. Эксперимент: ( a ) магнит (его северный полюс обозначен буквой «N») со скоростью v(t) проходит вблизи проволочной петли с вольтметром ⓥ, так что ( b ) его магнитное поле B(t,r ) также движется, что приводит к ( c ) ЭДС V, появляющейся вокруг петли. Хотя переход от ( a ) к ( b ) моделируется просто, так как это всего лишь перемещение магнитного поля магнита, в ( c ), где эти поля взаимодействуют с зарядами в контуре, индуцируя и изменяя токи, вплоть до возможного воздействия на ЭДС.
Рисунок 2. Диаграмма, показывающая конфигурацию и поля, используемые для уравнения индукции, основанного, как обычно, на уравнении Максвелла-Фарадея в полях E и B. Петля, которая позволяет нам выбрать контур интегрирования C, показана голубым цветом, а поверхность интегрирование S является его диском поперечного сечения.
Петля, которая позволяет нам выбрать контур интегрирования C, показана голубым цветом, а поверхность интегрирование S является его диском поперечного сечения.
Рис. 2. Диаграмма, показывающая конфигурацию и поля, используемые для уравнения индукции, основанного, как обычно, на уравнении Максвелла-Фарадея в полях E и B. Петля, которая позволяет нам выбрать контур интегрирования C, показана голубым цветом, а поверхность интегрирование S является его диском поперечного сечения.
Рисунок 3. Диаграмма, показывающая конфигурацию и поля, используемые для уравнения индукции, основанного на уравнении Максвелла–Ампера в полях D и H. Петля, которая позволяет нам принять решение о контуре интегрирования C, показана голубым цветом, а поверхность интегрирования S — его диск поперечного сечения.
Рисунок 3. Диаграмма, показывающая конфигурацию и поля, используемые для уравнения индукции, основанного на уравнении Максвелла–Ампера в полях D и H. Петля, которая позволяет нам принять решение о контуре интегрирования C, показана голубым цветом, а поверхность интегрирования S — его диск поперечного сечения.
Рисунок 4. Ориентации магнитного поля и петли (контура интегрирования), использованные для сведения уравнения (26) к уравнению (27). Петля в плоскости x,y движется со скоростью v в направлении x через магнитное поле, направленное по оси z, напряженность которого зависит только от x (т. е. Bz(x)).
Рис. 4. Ориентации магнитного поля и петли (контура интегрирования), использованные для сведения уравнения (26) к уравнению (27). Петля в плоскости x,y движется со скоростью v в направлении x через магнитное поле, направленное по оси z, напряженность которого зависит только от x (т. е. Bz(x)).
Рисунок 5. На диаграмме U-образный стержень показан темно-синим цветом, а движущийся стержень — темно-красным. Черные стрелки указывают текущее J, а красные стрелки показывают (положительное) движение движущейся полосы. Пурпурные стрелки указывают на две силы: одна на стержне, вызванная эффектом (его) тока, проходящего через магнитное поле; а другой на зарядах в стержне (и, следовательно, на токе), вызванном движением стержня через магнитное поле. Вдоль бара полезно выразить текущий J в виде вектора (J), чтобы помочь в вычислении направления Fbar.
Вдоль бара полезно выразить текущий J в виде вектора (J), чтобы помочь в вычислении направления Fbar.
Рисунок 5. На диаграмме U-образный стержень показан темно-синим цветом, а движущийся стержень — темно-красным. Черные стрелки указывают текущее J, а красные стрелки показывают (положительное) движение движущейся полосы. Пурпурные стрелки указывают на две силы: одна на стержне, вызванная эффектом (его) тока, проходящего через магнитное поле; а другой на зарядах в стержне (и, следовательно, на токе), вызванном движением стержня через магнитное поле. Вдоль бара полезно выразить текущий J в виде вектора (J), чтобы помочь в вычислении направления Fbar.
© 2020, автор. Лицензиат MDPI, Базель, Швейцария. Эта статья находится в открытом доступе и распространяется на условиях лицензии Creative Commons Attribution (CC BY) (http://creativecommons.org/licenses/by/4.0/).
Законы электромагнитной индукции — 1095 слов
Центральной темой этого доклада было изучение принципов физики электромагнитной индукции. В докладе рассмотрены закон Фарадея, характеризующий генерацию ЭДС в замкнутой цепи при наведении внешнего магнитного поля, и закон Ленца, иллюстрирующий способность цепи сопротивляться внешнему индуктивному воздействию. Обобщающим принципом для двух правил были мнемонические законы Флеминга, которые позволяют определять направления электромагнитных векторных величин двумя руками.
В докладе рассмотрены закон Фарадея, характеризующий генерацию ЭДС в замкнутой цепи при наведении внешнего магнитного поля, и закон Ленца, иллюстрирующий способность цепи сопротивляться внешнему индуктивному воздействию. Обобщающим принципом для двух правил были мнемонические законы Флеминга, которые позволяют определять направления электромагнитных векторных величин двумя руками.
Введение
Глубокое понимание природы электрофизических процессов является основой для успешного и вдумчивого понимания предмета. Если рассматривать физические законы по отдельности, то они представляют собой посредственную математическую конструкцию, но изучение взаимосвязи явлений позволяет расширить академические рамки. В этой статье рассматриваются три важных закона электричества: закон Фарадея, закон Ленца и правила Флеминга. Каждый закон относится к области физики электромагнитной индукции. В частности, общее представление об индукции сводится к тому, что при прохождении через проводник магнитного потока, излучаемого источником магнитного поля, в цепи возникает электрический ток. Отсюда следует, что если проводник поместить в магнитное поле и привести в движение, то в проводнике возникнет собственная ЭДС.
Отсюда следует, что если проводник поместить в магнитное поле и привести в движение, то в проводнике возникнет собственная ЭДС.
Обзор законов
Закон Фарадея
Одним из первых принципов электродинамики, определяющих взаимосвязь между внешним магнитным полем и генерацией ЭДС, является закон Фарадея. В общем виде закон Фарадея следует сформулировать как пропорциональность генерируемой ЭДС скорости изменения магнитного потока, как показано в уравнении [1] . Другими словами, изменение напряженности магнитного потока (при движении магнита) вблизи замкнутого контура приводит к ЭДС индукции, противоположной по направлению и равной по величине потоку. Следовательно, чем быстрее меняется магнитное поле, тем большее напряжение будет проявляться в цепи. Уравнение [1] указано, что ЭДС в цепи прямо пропорциональна скорости изменения магнитного потока в зависимости от времени, и в случае большого числа витков катушки индуктора их количество добавляется к формула, Н.
Этот основной закон важен для понимания электродинамических процессов в замкнутом контуре. В частности, его применяют для определения работы трансформаторов, генераторов, электродвигателей и дросселей ( Закон индукции Фарадея , 2018). Таким образом, трансформаторы переносят энергию переменного электромагнитного поля за счет явления взаимной индукции, преобразуя таким образом величину напряжения на разных клеммах. Если обратить внимание на уравнение [1] , то в уравнении есть минус, что вполне оправдано законом Ленца.
Закон Ленца
Закон Ленца постулирует второе важное электродинамическое свойство цепи, связанное с направлением индукционного тока. Стоит уточнить, что индукционный ток, возникающий в замкнутой цепи в результате изменения магнитного потока, всегда имеет определенное направление. Более того, как известно, сам поток тока создает уникальное своим направлением магнитное поле. Это означает, что силовые линии магнитного поля от магнита имеют определенное направление, согласно которому по правилу правой руки ток в цепи должен течь по часовой стрелке ( Три правила правой руки , 2018). Однако в действительности закон Ленца отражает противоположный эффект: электрический ток, генерируемый в цепи, имеет другое направление, чем ожидалось. Объяснение этого парадокса заключается в стремлении цепи сопротивляться изменению магнитного потока, чтобы ослабить действие причины, инициировавшей генерацию индукционного тока.
Однако в действительности закон Ленца отражает противоположный эффект: электрический ток, генерируемый в цепи, имеет другое направление, чем ожидалось. Объяснение этого парадокса заключается в стремлении цепи сопротивляться изменению магнитного потока, чтобы ослабить действие причины, инициировавшей генерацию индукционного тока.
Следует признать, что закон Ленца действует независимо от типа цепи или направления движения силовых линий магнитного поля. В частности, при изменении площади цепи индукционный ток индуцируется силой Лоренца, но индукционный ток ослабляет действие внешнего магнитного поля. С другой стороны, величина магнитного потока может быть увеличена, и в этом случае эффект вихревого электрического поля индуцирует индукционный ток. Однако и в этом случае ток будет направлен на подавление действия внешнего поля. Примечательно, что магнитное поле может создаваться протеканием тока в соседней цепи. Тогда в рассматриваемой цепи индукционный ток может иметь то же направление, что и линии этого поля. В частности, если внешний ток численно увеличивается, то наблюдается новый ток, уменьшающий это увеличение, и наоборот.
В частности, если внешний ток численно увеличивается, то наблюдается новый ток, уменьшающий это увеличение, и наоборот.
Правила Флеминга
Более глубокое понимание взаимосвязи между направлениями силовых линий, током и результирующей магнитной силой возможно с помощью двух мнемонических правил Флеминга. При работе с электрическими машинами это необходимые правила, будь то генераторы (правая рука) или электродвигатели (левая рука). В частности, взаимодействие внешнего магнитного поля с электромагнитным полем цепи создает вектор физической силы, направление которой можно определить с помощью мнемотехники. Примечательно, что результирующая магнитная сила всегда перпендикулярна двум полям, образуя трехосную плоскость. Для применения этих правил средний палец должен указывать в направлении тока, указательный — в направлении силовых линий, а большой палец будет описывать вектор конечной магнитной силы. Наглядным примером применения правил Флеминга может быть рассмотрение принципиальной схемы стандартного электродвигателя, имеющего ротор и статор. Базовые модели простых двигателей состоят из кольцеобразного металлического статора, в котором вращается ротор, обмотанный медной проволокой. В ротор подается электрический ток от внешнего источника, создающий электромагнитное поле. Это поле, в свою очередь, взаимодействует с магнитными полями двух постоянных магнитов в статоре, создавая новую физическую силу. Используя правило левой руки Флеминга, можно определить результирующее направление этой силы.
Базовые модели простых двигателей состоят из кольцеобразного металлического статора, в котором вращается ротор, обмотанный медной проволокой. В ротор подается электрический ток от внешнего источника, создающий электромагнитное поле. Это поле, в свою очередь, взаимодействует с магнитными полями двух постоянных магнитов в статоре, создавая новую физическую силу. Используя правило левой руки Флеминга, можно определить результирующее направление этой силы.
Заключение
В этом отчете подробно рассмотрена природа законов электромагнитной индукции. Подводя итог, можно сказать, что эти законы являются фундаментальными принципами, объясняющими электродинамические процессы при воздействии внешнего магнитного поля на замкнутую цепь. Закон Фарадея определяет равенство между ЭДС индукции и изменяющимся во времени магнитным потоком. Закон Ленца показывает, что индуктивный ток имеет направление, противоположное внешнему полю, что обусловлено стремлением подавить действие цепи. Мнемонические правила Флеминга применяются для определения направления результирующей магнитной силы, возникающей в результате взаимодействия магнитного и электромагнитного полей.



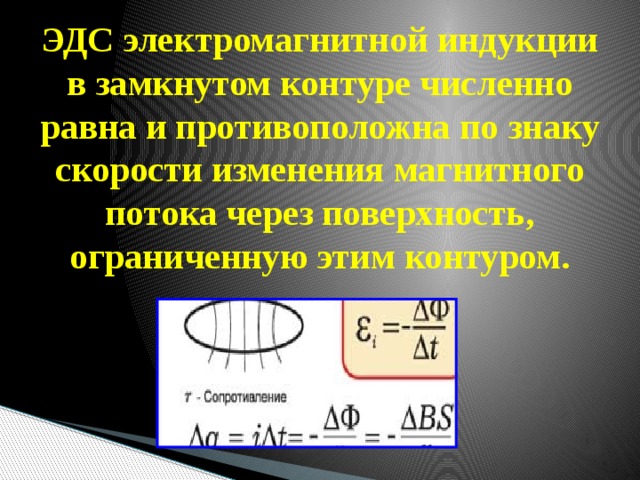

 2 Магнитное поле, связанное с током
2 Магнитное поле, связанное с током \(N\) — количество контуров цепи.
Магнитное поле измеряется в единицах тесла (Тл). Знак минус указывает направление и то, что индуцированное
ЭДС стремится противодействовать изменению магнитного потока. Знак минус можно не учитывать при расчете
величины.
\(N\) — количество контуров цепи.
Магнитное поле измеряется в единицах тесла (Тл). Знак минус указывает направление и то, что индуцированное
ЭДС стремится противодействовать изменению магнитного потока. Знак минус можно не учитывать при расчете
величины. 4 Краткое содержание главы
4 Краткое содержание главы Евро. Дж. Физ. 2011 , 32, 1687. [Google Scholar] [CrossRef][Green Version]
Евро. Дж. Физ. 2011 , 32, 1687. [Google Scholar] [CrossRef][Green Version] Дж. опт. 2018 , 20, 025502. [Google Scholar] [CrossRef][Green Version]
Дж. опт. 2018 , 20, 025502. [Google Scholar] [CrossRef][Green Version]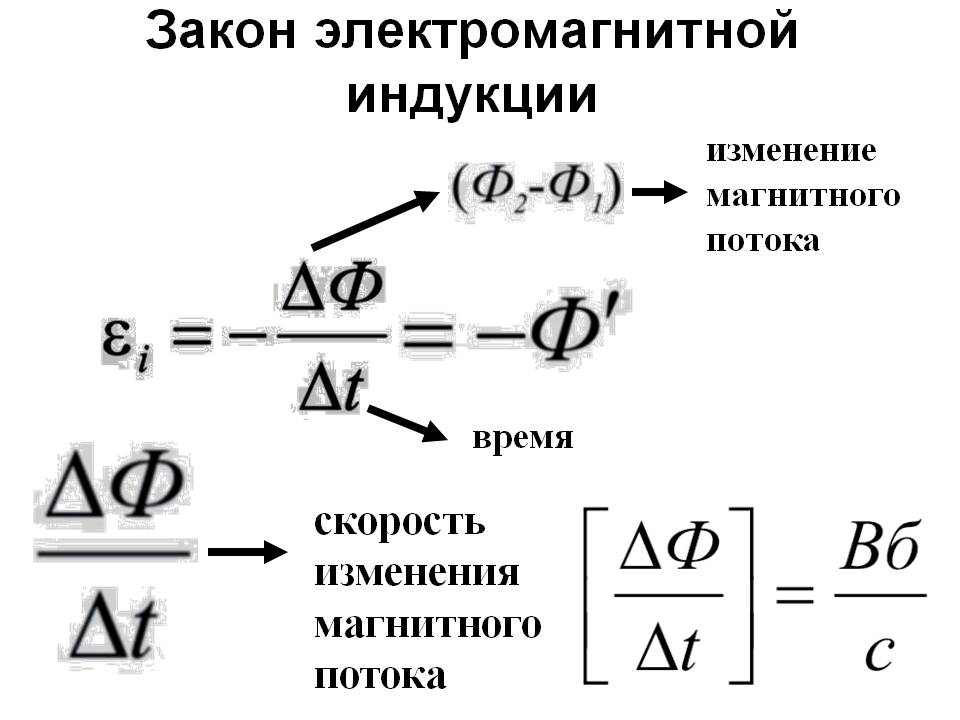 [Google Scholar]
[Google Scholar] . Затем мы должны объединить все это в чистое влияние на сборы как группу. Здесь мы просто сводим совокупный эффект всех подобных усложнений к эффективной плотности массы зарядов.
. Затем мы должны объединить все это в чистое влияние на сборы как группу. Здесь мы просто сводим совокупный эффект всех подобных усложнений к эффективной плотности массы зарядов.