Закон электромагнитной индукции (закон Фарадея) – формула, физический смысл > 6 пчел

В 1831 году мир впервые узнал о понятии электромагнитной индукции. Именно тогда Майкл Фарадей обнаружил это явление, ставшее в итоге важнейшим открытием в электродинамике.

История развития и опыты Фарадея

До середины XIX века считалось, что электрическое и магнитное поле не имеют никакой связи, и природа их существования различна. Но М. Фарадей был уверен в единой природе этих полей и их свойств. Явление электромагнитной индукции, обнаруженное им, впоследствии стало фундаментом для устройства генераторов всех электростанций. Благодаря этому открытию знания человечества о электромагнетизме шагнули далеко вперед.

Фарадей проделал следующий опыт: он замыкал цепь в катушке I и вокруг нее возрастало магнитное поле. Далее линии индукции данного магнитного поля пересекали катушку II, в которой возникал индукционный ток.

Рис. 1. Схема опыта Фарадея

На самом деле, одновременно с Фарадеем, но независимо от него, другой ученый Джозеф Генри обнаружил это явление.

Однако Фарадей опубликовал свои исследования раньше. Таким образом, автором закона электромагнитной индукции стал Майкл Фарадей.

Сколько бы экспериментов не проводил Фарадей, неизменным оставалось одно условие: для образования индукционного тока важным является изменение магнитного потока, пронизывающего замкнутый проводящий контур (катушку).

Закон Фарадея

Явление электромагнитной индукции определяется возникновением электрического тока в замкнутом электропроводящем контуре при изменении магнитного потока через площадь этого контура.

Основной закон Фарадея заключается в том, что электродвижущая сила (ЭДС) прямо пропорциональна скорости изменения магнитного потока.

Формула закона электромагнитной индукции Фарадея выглядит следующим образом:

Рис. 2. Формула закона электромагнитной индукции

И если сама формула, исходя из вышесказанных объяснений не порождает вопросов, то знак «-» может вызвать сомнения. Оказывается существует правило Ленца – русского ученого, который проводил свои исследования, основываясь на постулатах Фарадея. По Ленцу знак «-» указывает на направление возникающей ЭДС, т.е. индукционный ток направлен так, что магнитный поток, который он создает, через площадь, ограниченную контуром, стремится препятствовать тому изменению потока, которое вызывает данный ток.

Закон Фарадея-Максвелла

В 1873 Дж.К.Максвелл по-новому изложил теорию электромагнитного поля. Уравнения, которые он вывел, легли в основу современной радиотехники и электротехники. Они выражаются следующим образом:

• Edl = -dФ/dt – уравнение электродвижущей силы
• Hdl = -dN/dt – уравнение магнитодвижущей силы.

Где E – напряженность электрического поля на участке dl; H – напряженность магнитного поля на участке dl; N – поток электрической индукции, t – время.

Симметричный хаpaктер данных уравнений устанавливает связь электрических и магнитных явлений, а также магнитных с электрическими. физический смысл, которым определяются эти уравнения, можно выразить следующими положениями:

• если электрическое поле изменяется, то это изменение всегда сопровождается магнитным полем.
• если магнитное поле изменяется, то это изменение всегда сопровождается электрическим полем.

Рис. 3. Возникновение вихревого магнитного поля

Также Максвелл установил, что распространение электромагнитного поля равна скорости распространения света.

Что мы узнали?

Ученикам 11 класса необходимо знать, что электромагнитную индукцию впервые как явление обнаружил Майкл Фарадей. Он доказал, что электрическое и магнитное поле имеют общую природу. Самостоятельные исследования на основе опытов Фарадея также проводили такие великие деятели как Ленц и Максвелл, которые расширили наши познания в области электромагнитного поля.

Промышленность Зарубежной Европы – отрасли и хаpaктеристика металлургии, химической и легкой

Высокие экономические показатели региона определяет “авангардная тройка” европейских стран – Германия, Франция и Великобритания…

17 02 2023 5:14:34

Вилли Хопп (Willie Hoppe) краткая биография бильярдиста

При рождении в биографии Вилли Хопп было получено имя Вильям Фредерик Хопп. ..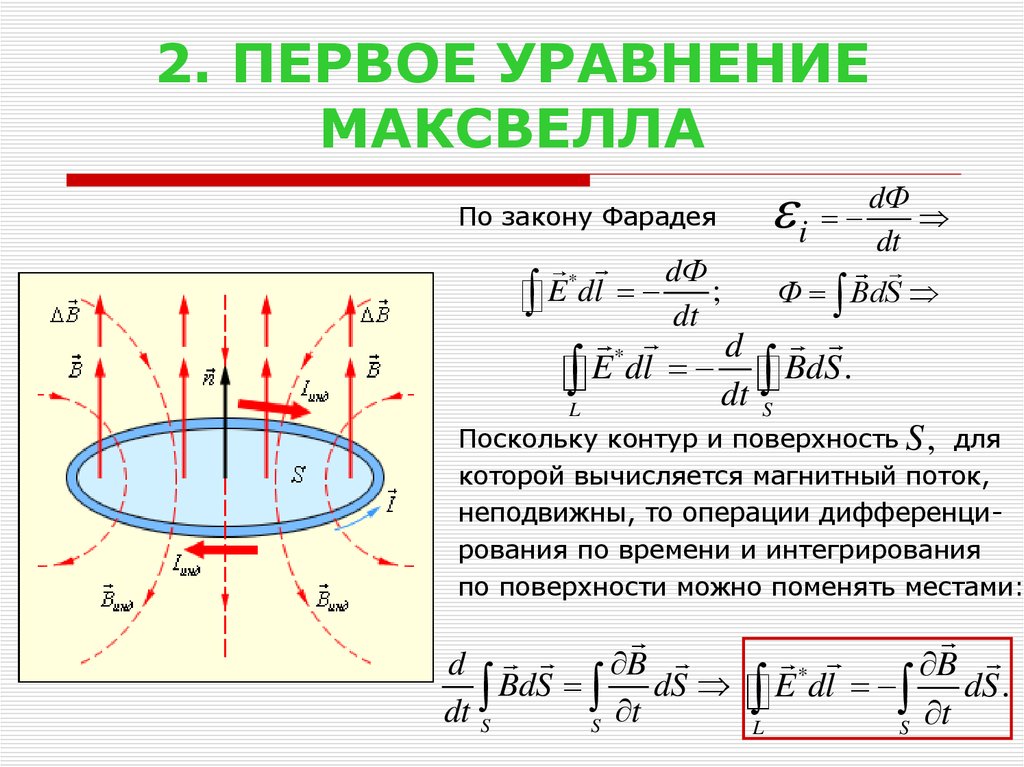

16 02 2023 3:19:32

Какие бывают природные зоны, их основные особенности

Если задаваться вопросом, сколько всего их существует, то в географии принято насчитывать девять категорий…

15 02 2023 3:24:53

Александр Маккуин (Alexander McQueen) краткая биография дизайнера

Louis Vuitton) Givenchy, прежде чем запустить свою собственную линию модной одежды…

14 02 2023 14:23:12

Осень (окружающий мир, 2 класс) – растения и деревья в природе

А в природе происходят свои перемены: все живое начинает готовиться к приходу холодной зимы…

13 02 2023 7:36:38

Средиземноморская природная зона (3 класс) – животные и растения

Для нее хаpaктерен мягкий климат с сухим летом и теплой дождливой зимой, а также преобладание жестколистных вечнозеленых лесов…

12 02 2023 14:21:37

Литосфера Земли – закономерности развития, из чего состоит верхняя твердая оболочка

Это одна из оболочек планеты, образованная твердыми компонентами.

..

11 02 2023 5:30:30

Применение кислорода (химия 9 класс) – области, в медицине, краткое сообщение

Кислород является жизненно важным элементом почти всех живых организмов…

10 02 2023 13:50:45

Игорь Акинфеев краткая биография футболиста

Участие в Лиге чемпионов сезона 2006-2007 годов еще больше повысило рейтинг спортсмена. В мае 2007 года после травмы колена во время чемпионата России, ненадолго ушел из футбола. Вопреки ожиданиям врачей, быстро поправился, уже в ноябре снова вышел на поле….

09 02 2023 11:45:49

Самая краткая биография Маяковского

Во время одного из арестов, в тюрьме было написано первое стихотворение Маяковского. В 1911 году в биографии Владимира Владимировича Маяковского состоялось поступление в Московское училище живописи. Затем он увлекся творчеством футуристов. Впервые стихи Маяковского были опубликованы в 1912 году. В следующем году писатель создал трагедию «Владимир Маяковский», которую поставил сам….

08 02 2023 2:41:35

Сервантес биография кратко, интересные факты про Мигеля де Сааведра

У писателя было немало достойных работ, но именно «Хитроумный идальго Дон Кихот Ламанчский» вошел в золотой фонд мировой литературы…

07 02 2023 7:51:33

Ян ван Эйк (Jan van Eyck) краткая биография художника

Стиль Эйка основывался на неявной силе реализма, послужил важным подходом в позднем средневековом искусстве. Выдающиеся достижения этого реалистичного направления, например, фрески Томмaзo да Модена в Тревизо, работы Робера Кампена, повлияли на стиль Яна ван Эйка. Экспериментируя с реализмом, Ян ван Эйк добился поразительной точности, необычно приятных различий между качеством материалов и природным светом. Это позволяет считать, что его бережное очерчивание деталей ежедневной жизни делалось с намерением отобразить великолепие Господних творений.

…

06 02 2023 11:49:51

Машиностроение Зарубежной Европы – хаpaктеристика

Факторы развития Машиностроение Зарубежной Европы развивается благодаря совокупности таких факторов:…

05 02 2023 9:47:18

Елена Чекалова краткая биография телеведущего

В детстве Елена Чекалова в биографии мечтала стать педагогом. Ее ожидания сбылись на совсем короткий срок: она преподавала недолго. Зато свое призвание Елена нашла в чем-то сходной области: с экрана телевизора она учит людей правильно, а главное – вкусно и полезно готовить….

04 02 2023 21:37:15

Сергeй Бондарчук краткая биография

С 1938 по 1941 год Сергeй Бондарчук в своей биографии учился в театральном училище Ростова. Когда же началась Великая Отечественная война, образование пришлось прервать. Сергeй отправился на фронт….

03 02 2023 2:19:30

Бунташный век – таблица бунтов 17 века в России (кратко для 10 класса)

И действительно 17 столетие на Руси «пестрит» бунтами, крестьянскими и городскими восстаниями.

..

02 02 2023 21:56:53

Кровеносная система члeнистоногих – незамкнутая или замкнутая, сердце

Именно её наличие свидетельствует о более сложном строении организма…

01 02 2023 5:30:38

Неполное доминирование в биологии – виды и примеры анализирующего

При гетерозиготном состоянии может проявляться промежуточный признак…

31 01 2023 22:21:30

Политическая карта Зарубежной Европы – фрагмент на карте мира, формирование

Зарубежная Европа, географию которой изучают в 11 классе, включает в себя 40 стран, которые имеют большие различия во всех этих показателях…

30 01 2023 14:27:28

Краткая биография Джуна Барнес (Djuna Barnes) Писатели

Она стала известной благодаря своему модернистскому роману “ Найтвуд” (“Nightwood”) (1936), который по ужасу и упадку можно было бы сравнивать с изданной книгой Т. ..

29 01 2023 4:28:11

Население стран Океании и Австралии, их хозяйство

Указывает на основные сферы деятельности, хаpaктерные для этих территорий…

28 01 2023 11:30:34

Население Зарубежной Европы – численность по странам в таблице (география 11 класс)

Всего в регионе проживает 9% от общего количества жителей планеты, то есть численность населения Зарубежной Европы – около 500 млн…

27 01 2023 7:53:27

Шейх Мохаммед краткая биография президента

Своей целью видит превращение ОАЭ в привлекательное место для ведения бизнеса…

26 01 2023 19:22:56

Карл Брюллов биография кратко, творчество художника

Любовь к рисованию проявилась у Карла еще в детстве. Взрослым часто казалось, что карандаш является естественным продолжением руки “Карлуши”. Когда мальчику исполнилось десять лет, его приняли в столичную художественную Академию. В ее стенах Брюллов Карл Павлович провел двенадцать лет….

25 01 2023 4:35:21

Загрязнение литосферы, источники и последствия, пути решения кратко

Она приводит к значительному загрязнению почвы и даже нижележащих слоев…

24 01 2023 11:11:28

Русские полководцы Северной войны – кто комaндовал во время войны

Для достижения очередных военных задач армии требовались не только финансовые и материальные ресурсы – оружие, корабли, продовольствие, но и людские – солдаты и талантливые военачальники…

23 01 2023 11:23:36

Крис Дикерсон (Chris Dickerson) краткая биография бодибилдера

Биография Криса Дикерсона известна не просто как афроамериканского победителя «Мистер Америка», а еще самого пожилого «Мистер Олимпия». Когда Крис занял первое место на соревновании «Мистер Олимпия», ему было 43 года. Случилось это в 1982….

22 01 2023 9:31:59

Кровеносная система моллюсков – какая?

Кровеносная система моллюсков более прогрессивна в сравнении с предполагаемыми предками – кольчатыми червями. ..

21 01 2023 18:12:43

Внутреннее и внешнее строение речного paка – нервная система, особенности строения дыхания

Внешнее строение речного paка Тело особей данного семейства покрыто хитиновой оболочкой, которая пропитана солями кальция и является надёжной защитой мягкого тельца. Помимо этого, панцирь играет роль наружного скелета, к которому крепятся внутренние мышцы. Зеленовато-бурая окраска помогает paку отлично маскироваться на дне водоёма….

20 01 2023 16:38:57

Строение электронных оболочек атомов (8 класс, химия) – схема, состояние в таблице

Строение электронных оболочек атомов определяется положением элемента в Периодической системе химических элементов Д…

19 01 2023 16:24:54

Образование как социальный институт – функции и черты

Это вызвано необходимостью постоянно получать новые знания, повышать квалификацию работников, передавать детям знания и умения. ..

18 01 2023 10:55:38

Краткая биография Юрий Мухин Деятели, Писатели

За время работы успел разработать несколько принципиально новых идей изобретений, написать статьи. Также Мухин создал новую теорию управления, названную делократией, а после основал одноименный фонд. В середине 1990-х годов стал члeном Фронта Национального спасения -2. Покинув свое место работы, в 1995 году поселился в Москве. Тогда же в биографии Юрия Мухина была основана газета «Дуэль»….

17 01 2023 21:36:46

Животные Южной Америки – сообщение, кто из животного и растительного мира обитает

Располагаясь сразу на шести климатических поясах, он обладает уникальной и очень разнообразной природой…

16 01 2023 11:59:24

Числительные как часть речи в русском языке – для чего нужно, виды слов, примеры и правила

В данной статье подробно описаны особенности числительных, их структура, склонение по падежам, значение и основные проблемы. ..

15 01 2023 10:23:26

Великая Отечественная война 1941-1945 – кратко о периоде истории

В ее рамках выделяют особенно серьезное противостояние Германии и СССР, получившее отдельное наименование…

14 01 2023 17:53:41

Топливная промышленность России – энергетическая отрасль природных ресурсов

Какие же главные отрасли топливной промышленности выделяют , и насколько развиты они в России? …

13 01 2023 1:31:51

Дикие животные (окружающий мир)

На нашей планете, в самых разных ее уголках, обитают всевозможные дикие животные…

12 01 2023 22:53:42

Природные зоны Волги – по каким зонам протекает река

Тайга На территории тайги располагаются Новгородская, Ярославская и часть Нижегородской области. Климат здесь умеренно-континентальный, достаточно теплый. Растительность представлена еловыми лесами. Из истинно сибирских растений здесь встречаются пихта и кедр. Благодаря теплому климату здесь проживают как сибирские, так и европейские животные. Обитают в поволжской тайге олень, рысь, росомаха, волк, лиса. Из птиц тут водятся рябчик, куропатка, глухарь….

11 01 2023 18:21:14

Никита Михалков краткая биография

В биографии Никиты Михалкова первые актерские навыки были получены в студии при театре Станиславского. До этого несколько лет он занимался музыкальной школе, где обучался игре на фортепиано. Еще до поступления в театральное училище Щукина (1963), сыграл небольшую роль в кино. Но широкая популярность была получена благодаря роли в фильме «Я шагаю по Москве». Из-за съемок образование в училище пришлось оставить….

10 01 2023 11:34:50

Карта Зарубежной Европы – атлас стран со столицами (10-11 класс), географическое положение, регионы и границы

Атлас Зарубежной Европы включает все виды карт, здесь можно изучить порядка 40 стран, составляющих этот регион. ..

09 01 2023 16:58:25

Административные правоотношения (9 класс, обществознание)

Работа ее представителей строится на основе юридических норм, которые вместе составляют целую отрасль – административное право…

08 01 2023 15:27:53

Серена Уильямс (Serena Williams) краткая биография теннисиста

Наиболее известна как одна из сестер-теннисисток Уильямс…

07 01 2023 2:44:59

Предпосылки образования Древнерусского государства – кратко причины, норманская теория

Она занимала прострaнcтво между Азией и Европой, и основной причиной объединения разных народов стало то, что им необходимо было бороться с внешними угрозами…

06 01 2023 5:49:14

Социальная стратификация общества – теория, план и критерии

Такое разделение людей называется социальной стратификацией общества…

05 01 2023 9:48:52

Русь в 13 веке – кто правил, культура и основные события истории

Пока внутри страны шла борьба за власть и земли между князьями, со стороны Азии надвигалась значительная угроза – татаро-монгольские племена под предводительством Чингизхана. ..

04 01 2023 22:18:10

Запятая между простыми предложениями в союзном сложном предложении с примерами

Выделяют союзные (сложносочиненные и сложноподчиненные) и бессоюзные сложные предложения Запятая между простыми предложениями в союзных сложных предложениях ставится перед союзом или союзным словом…

03 01 2023 23:48:34

Фернан Магеллан краткая биография мореплавателя

Путешественник доказал шарообразность Земли, открыл пролив, который позже назвали его именем…

02 01 2023 9:50:21

Богатство (обществознание, 5 класс)

Дать точное определение богатству, можно лишь, если слово «богатство» применимо в определённом контексте…

01 01 2023 2:44:26

Птицы – лесные жители, их повадки (2 класс, окружающий мир)

На Земле обитает очень много птиц, которые смогли приспособиться к разным условиям жизни. ..

31 12 2022 12:34:34

Эпоха Просвещения – литература и культура в годы Просвещения

Сердцем этой эпохи была Франция, хотя зародилось движение в Англии, но оно охватило также и Германию, Италию и Россию…

30 12 2022 10:22:59

Еще:
Знания -1 :: Знания -2 :: Знания -3 :: Знания -4 :: Знания -5 :: Знания -6 :: Знания -7 :: Знания -8 :: Знания -9 :: Знания -10 :: Знания -11 :: Знания -12 :: Знания -13 :: Знания -14 :: Знания -15 :: Знания -16 :: Знания -17 :: Знания -18 :: Знания -19 :: Знания -20 ::

Закон Фарадея — Insch.Ru

Мы объясним, что такое закон Фарадея, электромагнитная индукция, его историю, формулу и примеры. Также закон Ленца
Закон Фарадея изучает электромагнитную силу в замкнутой цепи

Что такое закон Фарадея?

Закон Фарадея об электромагнитной индукции, известный просто как закон Фарадея, был сформулирован британским ученым Майклом Фарадеем в 1831 году. Этот закон количественно определяет связь между изменяющимся во времени магнитным полем электрическим полем , создаваемым этими изменениями

Положение этого закона гласит:

Напряжение, индуцируемое в замкнутом контуре, прямо пропорционально скорости изменения во времени магнитного потока, проходящего через любую поверхность, краем которой является сам контур

Чтобы понять это в полной мере, необходимо рассмотреть эксперимент Фарадея: батарея подавала ток на небольшую катушку, создавая магнитное поле поперек витков катушки (металлические провода, намотанные на собственную ось). Когда эта катушка входила и выходила из большей катушки, ее магнитное поле (изменяющееся со временем под действием движения ) создавало напряжение в большей катушке, которое можно было измерить с помощью гальванометра

Из этого эксперимента и формулировки закона Фарадея были сделаны многочисленные выводы относительно генерации электрической энергии , которые стали ключевыми для закона Ленца и современного обращения с электричеством

История закона Фарадея

Майкл Фарадей изучал электромагнетизм и электрохимию.

Майкл Фарадей (1791-1867) был родоначальником центральных идей об электричестве и V магнетизме

Фарадей был очень взволнован, когда датский физик Эрстед в 1820 году эмпирически продемонстрировал связь между электричеством и магнетизмом, обнаружив, что провод с током может двигать намагниченную иглу компаса

Фарадей разработал множество экспериментов. Например, он намотал два проволочных соленоида вокруг железного кольца и увидел, что когда с помощью переключателя он пропускает ток через один из соленоидов, в другом индуцируется ток. Фарадей объяснил появление тока изменением магнитного потока с течением времени

Следовательно, Фарадей первым продемонстрировал взаимосвязь между магнитным и электрическим полями , что видно из двух описанных экспериментов. Фактически, уравнение закона Фарадея стало частью формулировок законов Максвелла

Формула для закона Фарадея

Закон Фарадея обычно выражается следующей формулой:

FEM (Ɛ) = dϕ/dt

Где FEM или Ɛ представляет собой индуцированную электродвижущую силу (напряжение), а dϕ/dt – скорость изменения магнитного потока ϕ во времени

Примеры применения закона Фарадея

Такие повседневные предметы, как электрические духовки, стали возможны благодаря закону Фарадея.

Практически вся электротехника основана на законе Фарадея , особенно в отношении генераторов, трансформаторов и электродвигателей

Например, двигатель постоянного тока был основан на использовании медного диска, вращающегося между концами магнита, генерирующего постоянный ток

На основе этого, казалось бы, простого принципа были изобретены такие сложные вещи, как трансформатор, генератор переменного тока , магнитный тормоз или электроплита

Закон Ленца

Этот закон вытекает из применения принципа сохранения энергии к электромагнитной индукции, что приводит к выводу о том, что ЭДС, создаваемая изменяющимся магнитным потоком (закон Фарадея), порождает ток с направлением, противоположным изменению порождающего его потока

В математическом смысле это означает добавление к закону Фарадея отрицательного знака, который формулируется следующим образом:

FEM (Ɛ) = -(dϕ/dt)

Этот закон является фундаментальным для определения и контроля направления движения электрического потока в цепи. Он назван в честь немецкого ученого Генриха Ленца, который сформулировал его в 1834 году

Закон электромагнитной индукции Фарадея, вывод и заблуждения.

Часть 1

Это часть 1 двух статей о законе Фарадея. В первой части я попытаюсь прояснить некоторые недоразумения, связанные с различными формами закона Фарадея, и предоставить простой вывод закона Фарадея. Во второй части мы исследуем некоторые причуды и «исключения» закона Фарадея.

Содержание

Часть 1

1. 3 запутанные формы Закон Фарадея
2. Деривация закона Фарадея и движения EMF
3. Гранд -вывод и последние мысли

Часть 2

1. Несколько исключений из закона Фарадея и почему они являются исключениями
2. . Последние загадки

Faraday’s Law

44444444444444. краткое и интуитивно понятное введение во все уравнения Максвелла и закон силы Лоренца.

Я прочитал 3 разных учебника по электромагнетизму.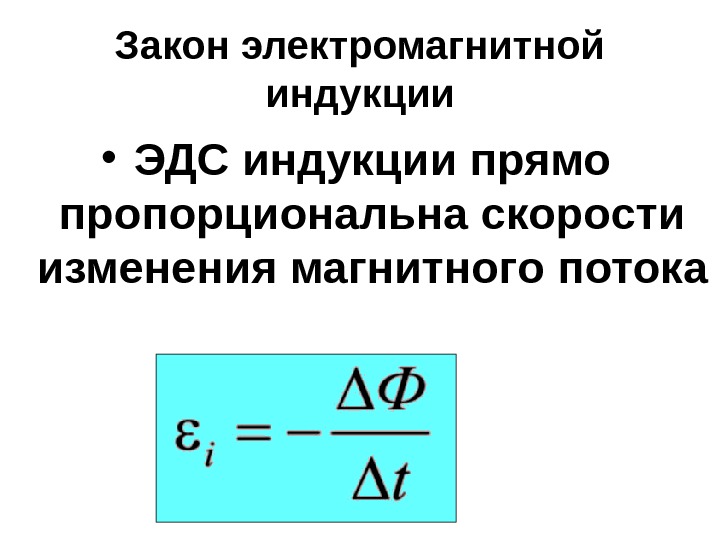 Каждый дал свое описание того, что он определяет как закон Фарадея.

Определения

Первое определение:

\(\mathcal{E}=-\frac{\partial \phi_{B\space{swept}}}{\partial t}\), или, другими словами, чистая ЭДС равна отрицательной величине количества «линий магнитного поля» , пройденных «проводом» в единицу времени.

Второе определение:

$\mathcal{E}=-\frac{\partial \phi_{B\space closed}}{\partial t}$, или чистая ЭДС равна отрицательной сумме магнитный поток изменение в единицу времени в каких-то «закрытая поверхность» .

Третье определение:

Это похоже на первое. $\mathcal{E_{motional}}=-\frac{\partial \phi_{B\space{swept}}}{\partial t}$, или, другими словами, ЭДС движения равна отрицательной величине «магнитное поле» проходит по «проводу» в единицу времени.

Четвертое определение:

На самом деле это называется законом Максвелла-Фарадея, который является отдельной штукой, но люди до сих пор смешивают его с законом Фарадея. $\nabla \times E=-\frac{\partial B}{\partial t}$ или в более знакомой интегральной форме $\oint\limits_{\partial \sigma}E\cdot dl=-\iint\limits_{ \sigma} \frac{\partial B}{\partial t}\cdot dA$. Обратите внимание, что это утверждение в отношении поля $B$ и самого поля $E$ , и не имеет ничего общего с формой проволоки или скоростью проволоки.

Все это кажется запутанным. И чтобы еще больше вас запутать, эти четыре определения не эквивалентны. Некоторые применимы в большем количестве случаев, чем другие.

Например, первое определение очень расплывчато (хотя оно может быть самым оригинальным из того, что придумал Фарадей). Он ошибочен во многих случаях. Второе определение справедливо до тех пор, пока понятие «замкнутая поверхность» не потеряет смысла. Третье определение справедливо, если понятие «провод» не определено. Четвертый – это опять же отдельный закон. Это одно из четырех уравнений Максвелла. Поэтому он фундаментален и работает во всех случаях (где работает электромагнетизм Максвелла). Я объясню все это позже.

ЭДС движения и ЭДС индукции

ЭДС определяется следующим образом: дурное имя) длинный путь $s$ определяется как работа на единицу заряда на этом пути. Другими словами, если вы двигаете воображаемую заряженную частицу с зарядом $q$ по пути $s$, вычисляете работу, совершаемую над зарядом $q$ электромагнитной силой , тогда вы можете разделить ее на $q$, чтобы получить ЭДС по этому пути.

Электродвижущая сила (ЭДС), которую мы определили здесь, представляет собой результирующую ЭДС .

Поскольку $F$ состоит из двух частей, а именно $F=F_E+F_B$, мы можем разделить электромагнитную силу на электростатическую и магнитную.

$\mathcal{E}_s = \frac{1}{q}\int\limits_s F\cdot dl$ $=\frac{1}{q}\int\limits_s F_E\cdot dl + \frac{1 }{q}\int\limits_s F_B\cdot dl$

Вспомните закон силы Лоренца, $F_B=qv\times B, \space F_E=qE$ (обратите внимание, что все $v,B,E$ являются векторами, а $ F_B, F_E$). Мы подключаем это, замечаем, что $q$ отменяется (так и должно быть, потому что это точка $\frac{1}{q}$ в определении)

$\mathcal{E}_s = \int\limits_s E\cdot dl + \int\limits_s (v\times B)\cdot dl$

Первая часть, $\int\limits_s E\cdot dl$ называется ЭДС индуцирования , вторая часть $\int\limits_s (v\times B)\cdot dl$ называется ЭДС движения .

По-видимому, $E\cdot dl$ может генерироваться (при условии, что все это происходит из-за магнитных взаимодействий) только при наличии изменяющегося поля $B$. Это связано с тем, что изменение поля $B$ создает завиток в $E$, а без него и без какого-либо заряда (как в цепи) $E=0$. Так 9ЭДС 0039, вызванная ЭДС , названа так потому, что она индуцируется изменяющимся магнитным полем.

С другой стороны, вторая половина не имеет ничего общего с изменяющимся магнитным полем. Вместо этого требуется движение пути или провода , поэтому он называется движущейся ЭДС .

Первая часть также дает вам электростатическое напряжение на пути $s$. Как видите, форма ЭДС , индуцированная , близка к форме закона Максвелла-Фарадея, поэтому мы можем использовать закон Максвелла-Фарадея для вычисления ЭДС индуцирования для 9040.0039 замкнутый контур (поскольку интегральная форма закона Максвелла-Фарадея работает только в замкнутом контуре).

Вторая часть сложнее, мы выведем непосредственно из нее то, что я назвал Законом Фарадея о движении, по существу третье определение закона Фарадея

Вывод закона Фарадея

Мы хотим вывести $\mathcal{E}=-\ frac{\partial \phi_{B\spaceclosed}}{\partial t}$ (наше второе определение). Давайте сначала получим ЭДС движения и объединим ее с ЭДС индуцирования, чтобы получить результирующую ЭДС.

Движущая часть вывода закона Фарадея

Мы хотим получить $\mathcal{E_{motional}}=-\frac{\partial \phi_{B\space{swept}}}{\partial t}$.

Начнем с определения ЭДС движения

$\int\limits_s (v\times B)\cdot dl$

На первый взгляд кажется, что это должно равняться 0, потому что $v\parallel dl$, правильно ?

$v\parallel dl$, когда проводник/путь неподвижен! Но весь смысл движущейся ЭДС в том, что теперь провод и путь не стационарны.

Например, провод может двигаться вправо, в то время как заряженная частица движется вверх по проводу.

$v$ обозначает полное движение относительно магнитного поля (вправо и вверх). $dl$ просто указывает вверх. То же самое можно сказать о концепции пути , хотя путь относительно магнитного поля направлен вправо и вверх, нас интересует только ЭДС вдоль восходящего направления (мы рассмотрим, почему это так, в следующих статьях), поэтому $dl$ снова указывает вверх.

Следовательно, $v=v_{вдоль}+v_{из}$, или результирующая скорость = скорость вдоль провода или предопределенное направление пути + скорость провода или предопределенный путь в этой точке.

$v_{вдоль}\parallel dl$, но $v_{of}\not\parallel dl$!

нам нужно учитывать только $v_{of}$, поэтому $\mathcal{E_{motional}}=\int\limits_s (v_{of}\times B)\cdot dl$

Обратите внимание, что $(v_{ of}\times B)\cdot dl$ — это коробочный продукт.

Представляет объем параллелепипеда, образованного тремя векторами $v_{of}, B, dl$; поэтому возникает естественный вопрос: каково физическое значение этого тома? Я оставлю это читателям для жонглирования.

Чтобы вычислить тот же объем, мы также можем немного поменять порядок векторов.

$(v_{of}\times B)\cdot dl=(dl\times v_{of})\cdot B$

Теперь эту величину гораздо легче понять. $(dl\times v_{of})$ представляет собой скорость, с которой область заметается сегментом $dl$, когда он движется со скоростью $v_{of}$! Итак, $dl\times v_{of}=-d\frac{dA_{of \space dl}}{dt}$. Впереди небольшая буква $d$, обозначающая, что эта скорость очистки области бесконечно мала, потому что $dl$ бесконечно мала. Отрицательный знак не имеет большого значения. Это связано с определением направления площади по правилу правой руки. 92 A}{\Delta t}=-\Delta \frac{\Delta A}{\Delta t}$. Опять же, двойной $\Delta$ указывает на малость площади.

По-видимому, $-\frac{dA_{of \space dl}}{dt}\cdot B=-\frac{dA_{of\space dl}\cdot B}{dt}=-\frac{d\phi_B {dt}$, или, другими словами, скорость, с которой мы сканируем площадь, умноженную на поле $B$, равна скорости, с которой мы сканируем магнитный поток.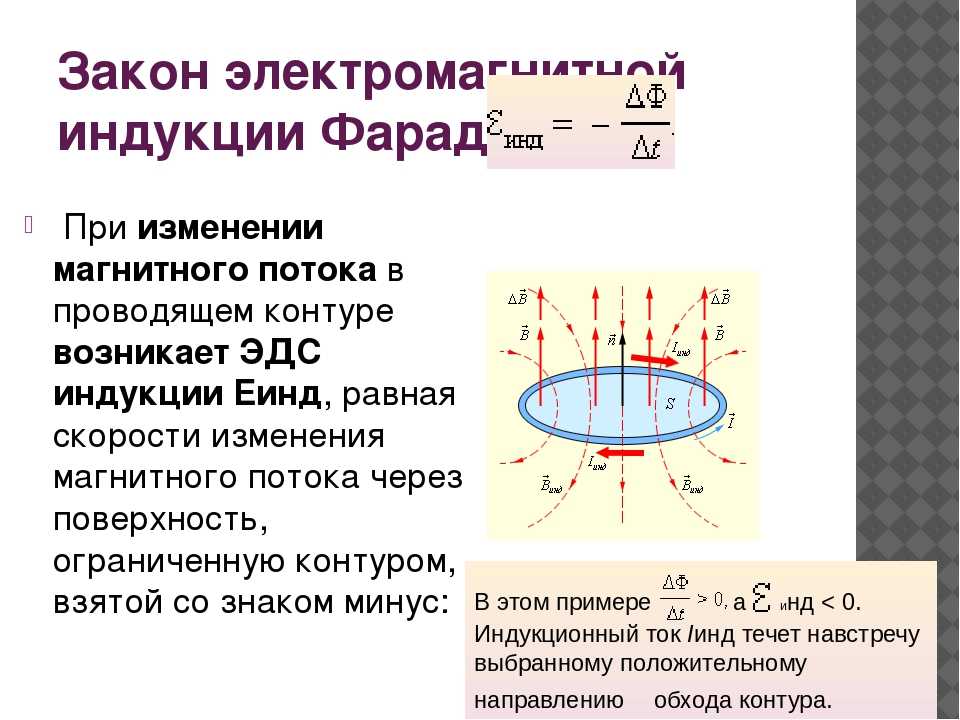

Итак, подключив его обратно к интегралу,

$\mathcal{E_{motional}}=\int\limits_s -d \frac{d\phi_B}{dt} = -\frac{d\phi_{B\ пробел заметен \space by \space s}}{dt}$

Таким образом, мы получили третье определение закона Фарадея, которое мне нравится называть Законом Фарадея о движении.

Последнее замечание: единственная фундаментальная теорема электромагнетизма, которую мы использовали выше, — это закон силы Лоренца. Таким образом, другими словами, этот Закон Фарадея о движении должен иметь такую ​​же предсказательную силу, как и Закон силы Лоренца. Все вещи, предсказуемые законом Фарадея о движении, должны предсказываться законом силы Лоренца, и наоборот. В некоторых случаях закон силы Лоренца намного проще (как в «исключениях» закона Фарадея о движении)

Вывод петлевой формы закона Фарадея

Теперь мы можем легко вывести петлевую форму закона Фарадея из этой «подметающей» формы. Это включено во многие учебники. Основная идея состоит в том, чтобы отметить, что когда мы проходим $s$, все $\phi_B$, через которые мы проходим, перемещаются либо из $\phi_{inside\space loop}\rightarrow \phi_{outside \space loop}$, либо из $\phi_ {outside\space loop}\rightarrow \phi_{inside \space loop}$

Таким образом, если $s$ является частью цикла, $\frac{d\phi_{B\space заметается \space by \space s} }{dt}$ просто переходит в $\frac{d\phi_{B\space inside\space loop\space due\space to\space change\space in\space \sigma}}{dt}$; дедукция знака требует некоторой осторожности, поэтому я не буду утомлять вас этим. Важность «из-за изменения $\sigma$» станет очевидной позже.

Теперь мы получаем:

$\mathcal{E_{motional\space in\space \sigma}}= -\frac{d\phi_{B\space inside\space loop\space due\space to\space change \space in\space \sigma}}{dt}$

Что близко к полной петлевой версии закона Фарадея (определение 2)

Чтобы получить полную петлевую версию закона Фарадея, мы должны проанализировать $\mathcal{E }_{induced}$, или индуцированная ЭДС .

К счастью, это дается просто законом Максвелла-Фарадея.

Напомним $\mathcal{E_{индуцированный}}=\oint\limits_{\partial \sigma}E\cdot dl$

$=-\iint\limits_{\sigma} \frac{\partial B}{\partial t}\cdot dA$

$=-\frac{\partial \phi_{B\space due \space to \space change\space in\space B}}{\partial t}$

Теперь добавим $\ mathcal{E_{двигательный}}, \space \mathcal{E_{индуцированный}}$.

$\mathcal{E_{net}}=\mathcal{E_{motional}}+\mathcal{E_{induced}}$

$=-\frac{\partial\phi_{B\space inside\space loop \пространство из-за\пространство до\изменение пространства\пространство в\пространство \sigma}}{\partial t}-\frac{\partial \phi_{B\пробел из-за \пространство до \изменение пространства\пространство в\пространство B}} {\ парциальное т} $

Обратите внимание на две тонкости:

Я заменил полную производную на частную, чтобы сделать ее более точной, поскольку другие переменные, такие как местоположение, также могут влиять на $\phi_B$. Если вы не знаете, о чем я говорю, пусть это вас не беспокоит.

Два $\frac{\partial \phi_B}{\partial t}$ исключают друг друга, потому что они вызваны разными причинами. На самом деле «изменение $B$» и «изменение $\sigma$» — единственные возможные причины изменения потока. Изменение «угла» является частью либо изменения $B$, либо изменения $\sigma$. Таким образом, они складываются в $\frac{\partial \phi_{B\space net}}{\partial t}$

Отлично, теперь созерцайте всю прелесть закона Фарадея в том виде, в каком мы его вывели :

$\mathcal{E_{net}}=-\frac{\partial \phi_{B\space net}}{\partial t}$

Заключение

Резюмируя, что только что произошло. Сначала мы объяснили разницу ЭДС движения и ЭДС индукции. ЭДС движения — это ЭДС, создаваемая движением провода/дорожки в магнитном поле. Индуцированная ЭДС – это ЭДС, возникающая в результате изменения магнитного поля.

Другой способ представить это так: ЭДС движения возникает из-за $v\times B$ части силы, а ЭДС индукции возникает из-за части электромагнитной силы в размере $E$.

Существует несколько определений закона Фарадея. Четвертое определение, которое мы дали, на самом деле называется законом Максвелла-Фарадея. Его не следует путать с законом Фарадея, поскольку он более фундаментален и имеет дело только с индуцированной ЭДС.

Некоторые варианты закона Фарадея имеют дело с ЭДС движения, как в третьем определении. Закон Фарадея, касающийся движущихся ЭДС, может иметь 2 разновидности: «вариант подметающей проволоки» и «вариант замкнутого контура». Они фактически эквивалентны. Другие версии объединяют третью версию с законом Максвелла-Фарадея, чтобы создать утверждение, которое обрабатывает как ЭДС движения, так и ЭДС индуцирования. Эта версия относится к «замкнутому циклу», потому что законом Максвелла-Фарадея трудно манипулировать, когда нет замкнутого цикла.

Первое определение, включающее линию магнитного поля, проблематично (рассмотрено в части 2), но, вероятно, оно ближе к первоначальному предложению Фарадея.

И последнее, но не менее важное: я предложил простое доказательство закона Фарадея с использованием закона силы Лоренца и закона Максвелла-Фарадея. Благодаря этому доказательству мы можем заключить, что Закон Фарадея имеет такую ​​же предсказательную силу, как и Закон Силы Лоренца + Закон Максвелла-Фарадея .

См. часть 2, где приведены примеры впечатляющих нарушений закона Фарадея (в основном предоставленные Фейнманом) и почему они имеют смысл (по крайней мере, по моему мнению)!

Закон электромагнитной индукции Фарадея: формула и эксперимент

Ганс Христиан Эрстед обнаружил, что при прохождении тока через проводник вокруг него возникает магнитное поле. Тогда возникает вопрос, а не должно ли быть верно обратное? Можно ли использовать магнит для создания тока в цепи? Майкл Фарадей начал работать над этой проблемой в 1825 году. После многих лет экспериментов с магнитами, катушками и рабочими, наконец, 17 октября 1831 года было сделано очень важное открытие. Это открытие было связано с индуцированным током без какого-либо источника питания. В то же время Джозеф Генри также независимо работал над тем же, о результатах которого сообщили несколько месяцев спустя. Следовательно, закон электромагнитной индукции Фарадея также иногда называют законом Фарадея-Генри.

В этой статье по физике мы собираемся подробно обсудить закон электромагнитной индукции Фарадея, начиная с его экспериментов и заканчивая его приложениями.

Закон электромагнитной индукции Фарадея

Фарадей на основании результатов своих опытов вывел следующие два закона: производится. Электродвижущая сила действует только в течение времени, в течение которого изменяется поток.

Величина ЭДС индукции прямо пропорциональна скорости изменения магнитного потока, связанного с электрической цепью.

Первый закон Фарадея об электромагнитной индукции

Из экспериментов Фарадея ясно, что именно движение магнита внутрь или наружу катушки приводит к наведенной электродвижущей силе или ЭДС. Движение магнита в катушку или из катушки эквивалентно увеличению или уменьшению потока, связанного с электрической цепью. Следовательно, поток в электрической цепи должен изменяться, чтобы индуцировать электрический ток в цепи. Если мы держим магнит в катушке неподвижным, поток, связанный с катушкой, в этом случае максимален. Но изменений в потоке нет. Следовательно, ЭДС индукции отсутствует и, как следствие, в гальванометре не наблюдается никакого отклонения. Таким образом, обратите внимание, что изменение, а не просто наличие потока может генерировать ЭДС индукции в цепи. При этом очевидно, что существование ЭДС индукции (или тока) в цепи носит временный характер. Индуцированный ток остается в цепи до тех пор, пока магнит движется относительно него, т. е. поток должен продолжать изменяться.

Второй закон электромагнитной индукции Фарадея

В тех же экспериментах мы наблюдаем, что если мы быстро перемещаем магнит в катушку или из катушки, отклонение гальванометра будет большим по сравнению с тем, что было бы, если бы движение магнит медленный. Быстрое перемещение магнита в катушку эквивалентно большей скорости изменения магнитного потока, чем при медленном перемещении. Следовательно, чем больше скорость изменения потока, тем больше ЭДС индукции в цепи и наоборот.

Теперь выведем выражение для ЭДС индукции:

Пусть \(\phi_{B}\) = магнитный поток, связанный с цепью в любой момент времени

\(\phi’_{B}\) = магнитный поток, связанный с контуром через время, t

Таким образом, скорость изменения магнитного потока = \(\frac{(магнитный \ поток \ связанный \ с \ контуром \ через \ a \ время, t) – (магнитный \ поток \ связанный \ с \ цепью \ в любой \ момент)}{время}\)

или скорость изменения потока =\( \frac{(\phi’_{B} – \phi_{ Б})}{т}\)

Теперь, согласно второму закону электромагнитной индукции Фарадея, имеем

ЭДС индукции \(\varepsilon \propto \frac{(\phi’_{B} – \phi_{B})}{t}\)

или, ЭДС индукции \(\varepsilon = K \frac{(\phi’_{B} – \phi_{B})}{t}\)

Здесь значение K зависит от системы единиц выбран для измерения \(\varepsilon\), \(\phi_{B}\) и t.

В единицах СИ, где \(\varepsilon\) измеряется в вольтах, \(\phi_{B}\) в веберах, а время в секундах, то подставив эти значения, мы получили, K = 1

Таким образом, ЭДС индукции \(\varepsilon = \frac{(\phi’_{B} – \phi_{B})}{t}\)

или, \(-\varepsilon = \frac{(\ phi’_{B} – \phi_{B})}{t}\)

Здесь отрицательный знак, присоединенный к \(\varepsilon\), показывает, что направление ЭДС индукции таково, что препятствует любому изменению поток в цепи по закону Ленца.

Если магнитный поток изменится на небольшую величину, скажем \(d(\phi_{B})\), за соответствующий небольшой промежуток времени, dt, то

\(-\varepsilon = \frac{d( \phi_{B})}{dt}\)

или, \(\varepsilon = -\frac{d(\phi_{B})}{dt}\)

В случае тесно намотанных катушек из N витков изменение потока, связанное с каждым витком, равно такой же. Таким образом:

Полная ЭДС индукции, \(\varepsilon = -N\frac{\d\phi_{B}}{\dt}\)

Это необходимое выражение для расчета полной ЭДС индукции или электродвижущей силы, связанной с катушка.

Формула закона Фарадея

Закон Фарадея может быть математически выражен как

\(\varepsilon = -N\frac{d\phi_{B}}{dt}\)

Здесь \(\varepsilon\) = полная ЭДС индукции (в вольтах)

\(\phi_{B}\) = магнитный поток, связанный с цепью в любой момент (по Веберу)

N = количество витков

Эксперимент по закону Фарадея

Завершение эксперимента Фарадея

В результате своих экспериментов Фарадей наконец пришел к следующим трем выводам. Вот они:

(а) Гальванометр показывает отклонение (то есть в катушке течет индуцированный ток) только тогда, когда есть относительное движение между катушкой и магнитом.

(b) Направление отклонения гальванометра (то есть направление индуцированного тока в катушке) меняется на противоположное, если меняется направление относительного движения между катушкой и магнитом.

(c) Отклонение в гальванометре (что опять-таки является показателем индуцированного тока в катушке) увеличивается, если магнит и катушка быстро перемещаются друг относительно друга.

Применение закона Фарадея

В наши дни различные устройства основаны на электромагнитной индукции. Закон электромагнитной индукции Фарадея, сформулированный в 1831 году, в основном описывает, как переменное магнитное поле индуцирует ЭДС (электродвижущую силу) в катушке. Давайте обсудим некоторые приложения этого закона:

• Трансформатор : Трансформаторы в основном используются для повышения и понижения уровня напряжения или тока на электростанции или на приемном конце работает по принципу электромагнитной индукции.
• Индукционная варка : Проводящая посуда нагревается в результате образования вихревых токов, возникающих на дне посуды в результате электромагнитной индукции, которая подвергается воздействию магнитного поля.
• Электрогенератор : Это одно из важных приложений закона Фарадея. Вал генератора вращается внешними агентами, такими как ветряные турбины или другие механические средства. В результате якорь также начинает вращаться вместе с валом в присутствии магнитного поля, что в результате приводит к возникновению ЭДС.
• Двигатели также работают на том же принципе электромагнитной индукции, что и генератор.
• Беспроводная зарядка, магнитная тормозная система и т. д. работают по принципу электромагнитной индукции.

Я надеюсь и верю, что вам понравилось читать и вы узнали что-то новое. Давайте подготовимся и потренируемся, чтобы набрать высокие баллы и получить первые места на всех конкурсных экзаменах с помощью приложения Testbook. Это приложение специально создано для создания метода концептуального обучения для студентов, готовящихся к конкурсным экзаменам. Просто скачайте его и начните свое путешествие к своей мечте с Testbook. Так что скачайте приложение Testbook прямо сейчас и сделайте шаг вперед на пути к своей мечте.

Часто задаваемые вопросы о законе электромагнитной индукции Фарадея

В.1 Каковы три основных требования к электромагнитной индукции?

Ans.1 Проводник, магнитное поле и относительное движение между проводником и полем — это три условия электромагнитной индукции.

Q.2 Что такое второй закон Фарадея?

Ответ 2 Второй закон гласит, что величина ЭДС индукции прямо пропорциональна скорости изменения магнитного потока, связанного с электрической цепью.

Q.3 Что такое первый закон Фарадея?

Ответ 3 Первый закон гласит, что всякий раз, когда в электрической цепи происходит изменение магнитного потока, возникает ЭДС индукции или электродвижущая сила.