Закон электромагнитной индукции (закон Фарадея).

Федун В.И. Конспект лекций по физике Электромагнетизи

Лекция 26.

Электромагнитная индукция. Открытие Фарадея.

В 1831 г. М. Фарадеем было сделано одно из важнейших фундаментальных открытий в электродинамике – обнаружено явлениеэлектромагнитной индукции.

В замкнутом проводящем контуре при изменении магнитного потока (потока вектора 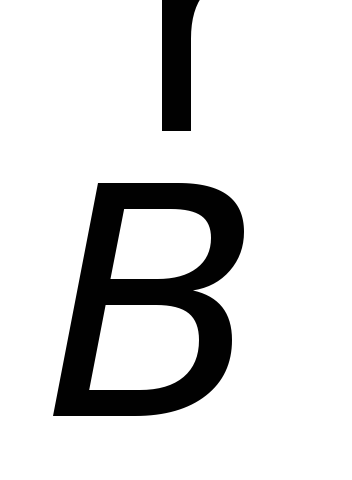), охватываемого этим контуром, возникает электрический ток.

Этот ток получил название индукционного.

Появление индукционного тока означает, что при изменении магнитного

Фарадей обнаружил, что индукционный ток можно вызвать двумя различными способами, которые удобно объяснить с помощью рисунка.

1-й способ: перемещение рамки 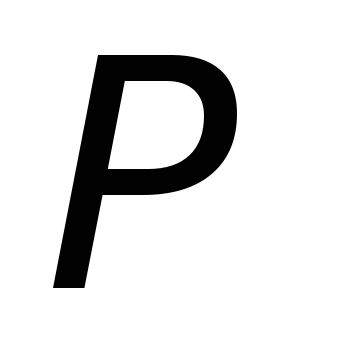в магнитном поле неподвижной катушки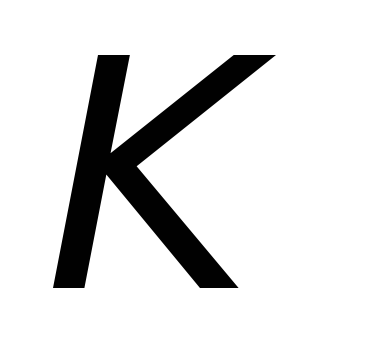(см. рис.26.1).

2-й способ: изменение магнитного поля 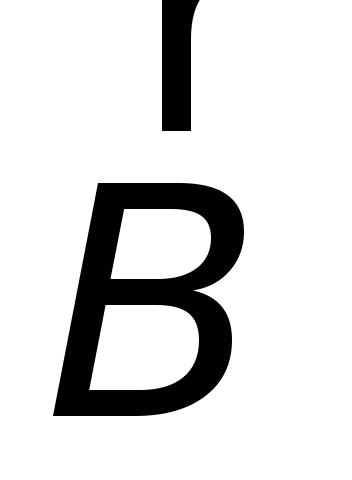, создаваемого катушкой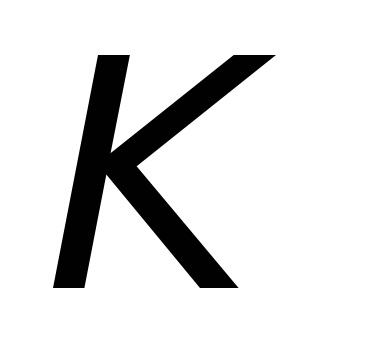, за счет ее движения или вследствие изменения силы тока

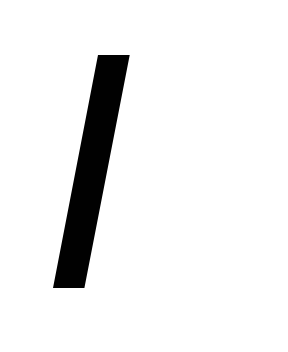
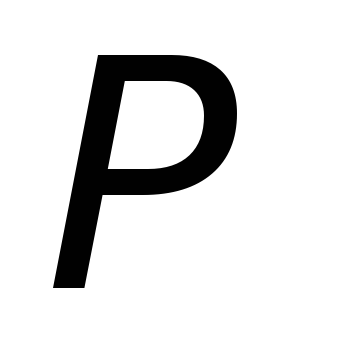в ней (или того и другого вместе). Рамкапри этом неподвижна.

В обоих этих случаях гальванометр 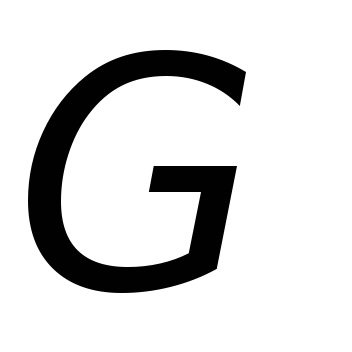будет показывать наличие индукционного тока в рамке.

Направление индукционного тока и, соответственно, знак э.д.с. индукции

определяются правилом Ленца.

Правило Ленца.

Индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей.

Правило Ленца выражает важное физическое свойство – стремление системы противодействовать изменению ее состояния. Это свойство называют электромагнитной инерцией.

Какова бы ни была причина изменения магнитного потока, охватываемого замкнутым проводящим контуром, возникающая в контуре э.д.с. индукции определяется формулой

(26.1)

Природа электромагнитной индукции.

С целью выяснения физических причин, которые приводят к возникновению э.д.с. индукции, последовательно рассмотрим два случая.

1. Контур движется в постоянном магнитном поле.

	Пусть контур с подвижной перемычкой длиной 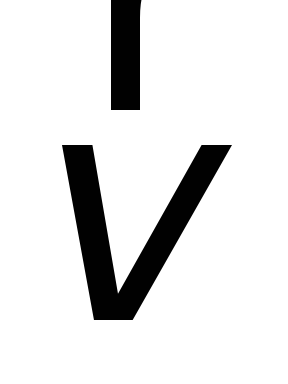находится в магнитном поле, перпендикулярном плоскости контура (см.Рисунок 26.2). Если двигать перемычку со скоростьювправо, то с такой же скоростью начнут двигаться и носители тока в перемычке – электроны. В результате на каждый электрон начинает
Рисунок 26.2

действовать сила

,

вызывающая перемещение электронов по перемычке вниз, т.е. потечет ток, направленный вверх.

Перераспределившиеся заряды создадут электрическое поле, которое возбудит ток и в остальных участках контура.

Это и есть индукционный ток.

Магнитная сила играет роль сторонней силы. Ей можно сопоставить эквивалентное поле сторонних сил

.

(26.2)

Электродвижущая сила, создаваемая этим полем, называется электродвижущей силой индукции . В нашем случае

.

(26.3)

Здесь знак «минус» поставлен потому, что стороннее поле направлено против положительного обхода контура, определяемого правилом правого винта. Произведение

есть скорость приращения площади контура (приращение площади в единицу времени), поэтому

,

где — приращение магнитного потока сквозь контур.

Тогда,

.

(26.4)

Полученный результат можно обобщить на случай произвольной ориентации вектора индукции магнитного поля 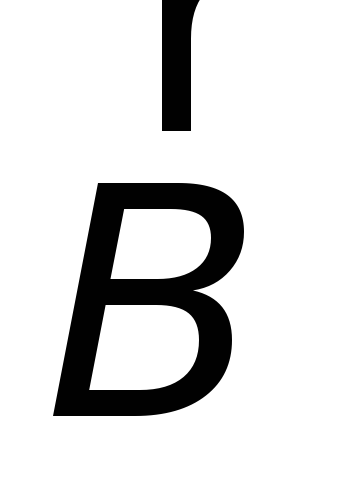относительно плоскости контура и на любой контур, движущийся (и/или деформируемый) произвольным образом в постоянном неоднородном внешнем магнитном поле.

Итак, возбуждение э.д.с. индукции при движении контура в постоянном магнитном поле объясняется действием магнитной составляющей силы Лоренца, пропорциональной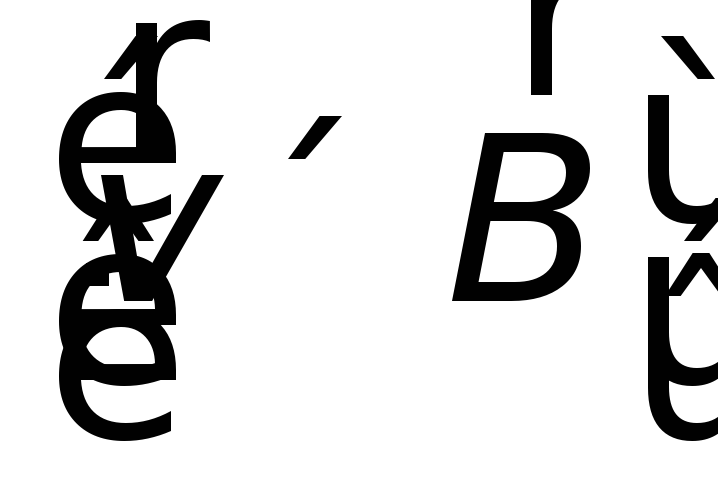

, которая возникает при перемещении проводника.

2. Контур покоится в переменном магнитном поле.

Наблюдаемое на опыте возникновение индукционного тока свидетельствует о том, что и в этом случае в контуре появляются сторонние силы, которые теперь связаны с изменяющимся во времени магнитным полем. Какова же их природа? Ответ на этот принципиальный вопрос был дан Максвеллом.

Поскольку проводник покоится, то скорость упорядоченного движения электрических зарядов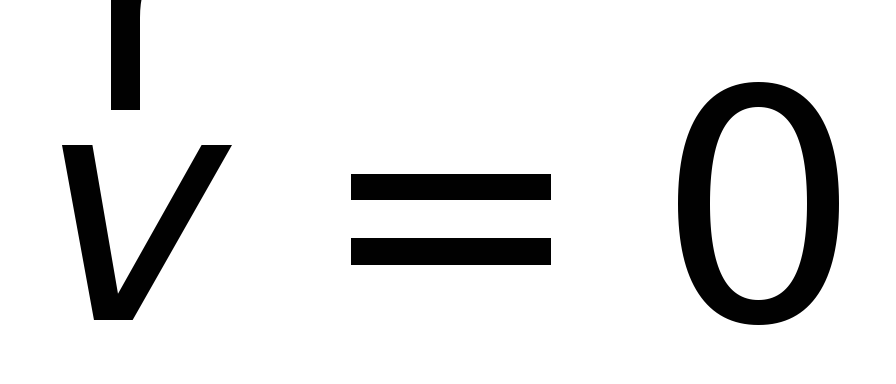

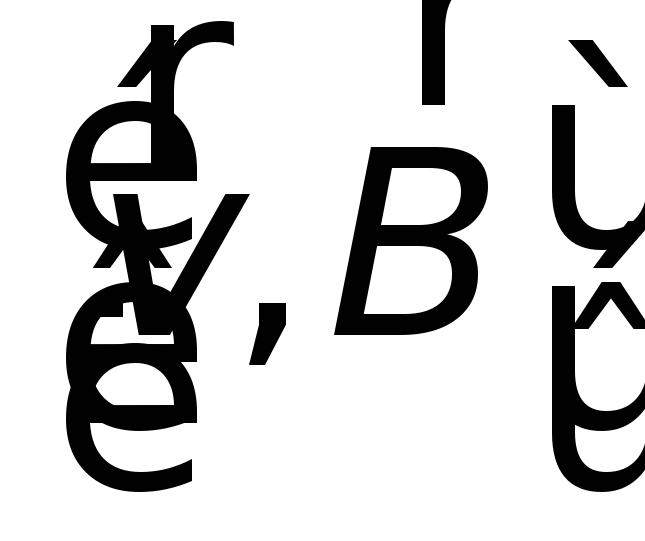и, следовательно, магнитная сила, пропорциональная, также равна нулю и уже не может привести заряды в движение. Однако кроме магнитной силы на электрический заряд может действовать только сила со стороны электрического поля, равная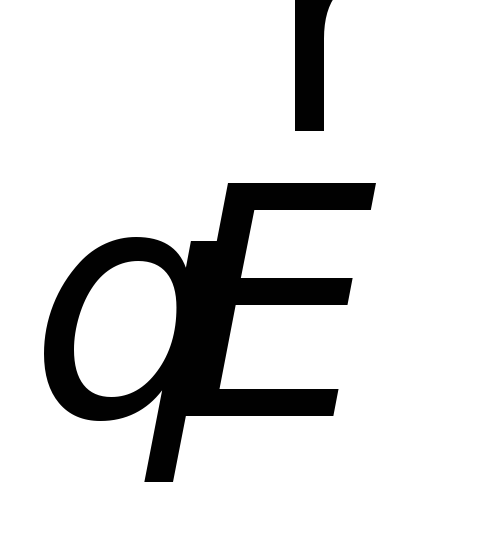. Поэтому остается заключить, чтоиндукционный ток обусловлен электрическим полем , возникающим при изменении во времени внешнего магнитного поля

. Именно это электрическое поле и ответственно за появление э.д.с. индукции в неподвижном контуре. Согласно Максвеллу,изменяющееся во времени магнитное поле порождает в окружающем пространстве электрическое поле. Возникновение электрического поля не связано с наличием проводящего контура, который лишь позволяет обнаружить по возникновению в нем индукционного тока существование этого поля.

Формулировка закона электромагнитной индукции, данная Максвеллом, принадлежит к числу наиболее важных обобщений электродинамики.

Всякое изменение магнитного поля во времени возбуждает в окружающем пространстве электрическое поле

.

Математическая формулировка закона электромагнитной индукции в понимании Максвелла имеет вид:

Циркуляция вектора напряженности 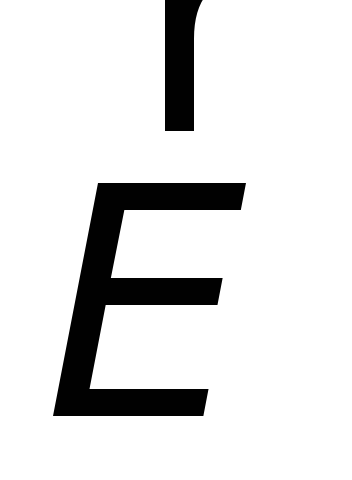этого поля по любому неподвижному замкнутому контуруопределяется выражением

,

(26.5)

где 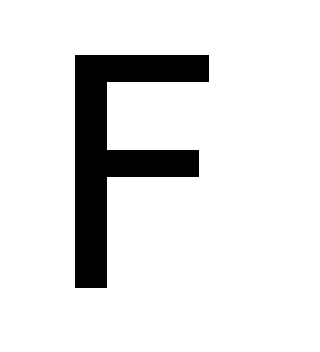— магнитный поток, пронизывающий контур.

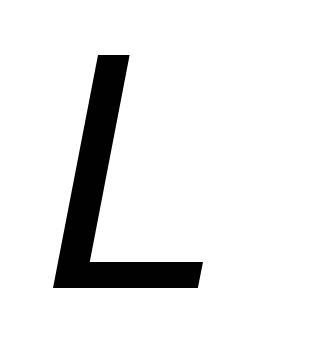Используемый для обозначения скорости изменения магнитного потока знак частной производной указывает на то, что контур является неподвижным.

Поток вектора 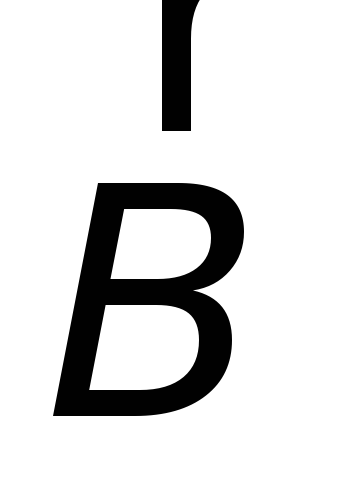через поверхность, ограниченную контуром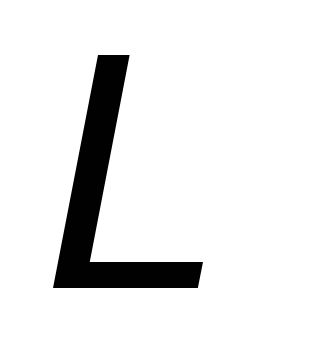, равен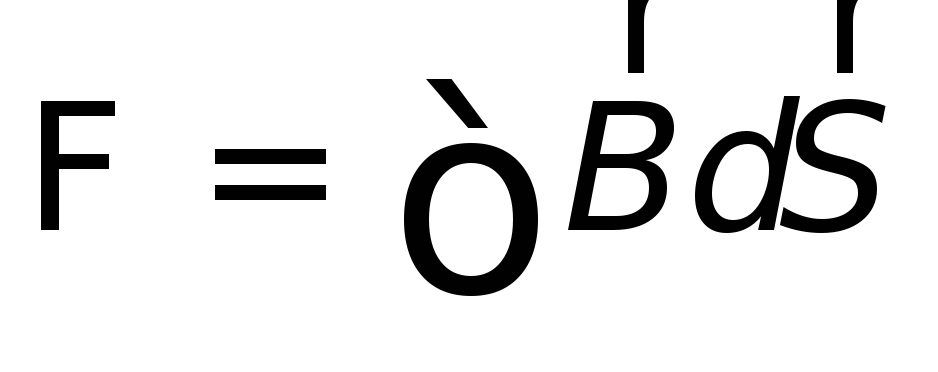, поэтому выражение закона электромагнитной индукции можно переписать следующим образом:

.

(26.6)

Воспользовавшись теоремой Стокса можно получить закон электромагнитной индукции в дифференциальной форме:

.

(26.7)

Это одно из уравнений системы уравнений Максвелла.

Тот факт, что циркуляция электрического поля, возбуждаемого переменным во времени магнитным полем, отлична от нуля, означает, что рассматриваемое электрическое поле не потенциальное.Оно, как и магнитное поле, являетсявихревым.

В общем случае электрическое поле может быть представлено векторной суммой потенциального (поля статических электрических зарядов, циркуляция которого равна нулю) и вихревого (обусловленного изменяющимся во времени магнитным полем) электрических полей.

В основе рассмотренных нами явлений, объясняющих закон электромагнитной индукции, не просматривается общего принципа, позволяющего установить общность их физической природы. Поэтому эти явления следует рассматривать как независимые, а закон электромагнитной индукции — как результат их совместного действия. Тем более удивительным оказывается тот факт, что э.д.с. индукции в контуре всегда равна скорости изменения магнитного потока сквозь контур. В тех случаях, когда меняется и поле и расположение или конфигурация контура в магнитном поле, э.д.с. индукции следует рассчитывать по формуле

,

(26.8)

а закон электромагнитной индукции можно представить в виде

.

(26.9)

Выражение, стоящее в правой части этого равенства, представляет собой полную производную магнитного потока по времени: первое слагаемое связано с изменением магнитного поля во времени, второе – с движением контура.

Можно сказать, что во всех случаях индукционный ток вызывается полной силой Лоренца

.

Какая часть индукционного тока вызывается электрической, а какая магнитной составляющей силы Лоренца — зависит от выбора системы отсчета.

О работе сил Лоренца и Ампера.

Из самого определения работы следует, что сила, действующая в магнитном поле на электрический заряд и перпендикулярная его скорости, не может совершать работы. Однако при движении проводника с током, увлекающего за собой заряды, сила Ампера все же работу совершает. Наглядным подтверждением этого служат электромоторы.

Это противоречие исчезает, если принять во внимание, что движение проводника в магнитном поле неизбежно сопровождается явлением электромагнитной индукции. Поэтому наряду с силой Ампера работу над электрическими зарядами совершает и возникающая в проводнике электродвижущая сила индукции. Т.о., полная работа сил магнитного поля складывается из механической работы, обусловленной силой Ампера, и работы э.д.с., индуцируемой при движении проводника. Обе работы равны по модулю и противоположны по знаку, поэтому их сумма равна нулю. Действительно, работа амперовой силы при элементарном перемещении проводника с током в магнитном поле равна 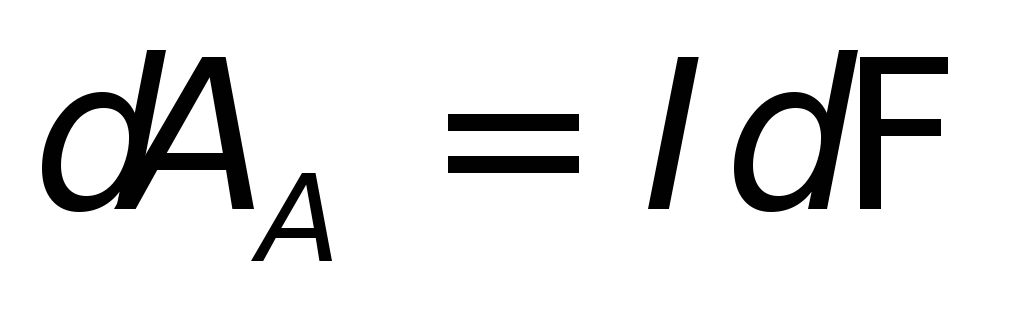, за это же время э.д.с. индукции совершает работу

,

(26.10)

тогда полная работа .

Силы Ампера совершают работу не за счет энергии внешнего магнитного поля, которое может оставаться постоянным, а за счет источника э.д.с., поддерживающего ток в контуре.

Обобщение закона электромагнитной индукции

Введём взаимосвязь между основными характеристиками ЭСП (основной силовой характеристики напряженностью и основной силовой характеристики потенциалом). Для этого воспользуемся фундаментальным физическим законом (законом магнитной индукции).

И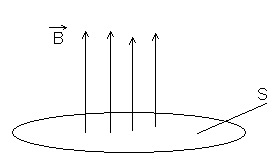з опыта известно, что в некотором замкнутом поводящем контуре охваченным поверхностью S будет возникать электрический ток (индукционный) в то случае если поток магнитной индукции через данную поверхность будет меняться с течением времени.

Данный закон получен из электромагнитной индукции.

ЭДС индукции возникающее в данном контуре

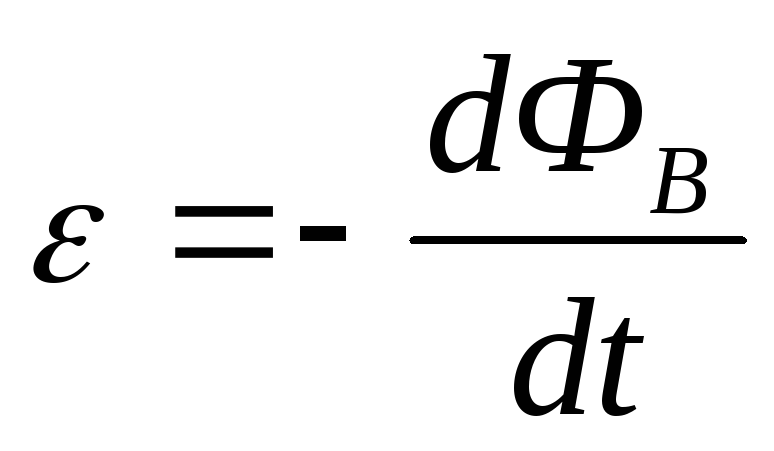
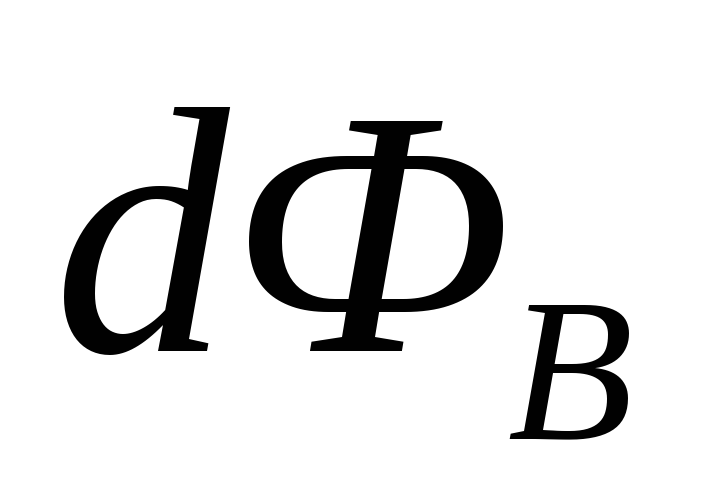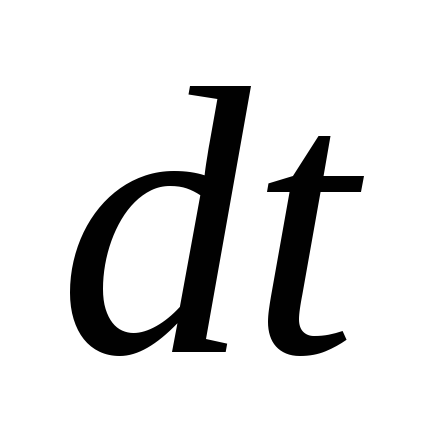— изменение потока магнитной индукции через поверхность S. — изменение промежутка времени в течение которого данное изменение произошло. Знак минус говорит о правиле Ленца согласно которому которое говорит что индукционный ток должен иметь такое направление, что создаваемое им магнитное поле должно препятствовать изменению того магнитного потока которое создаёт данный индукционный ток. Получим уравнение обобщающее данный физический закон. Это уравнение было выведено максвеллом и вошло в систему уравнений максвелла обобщающих основной закон электричества и магнетизма. Параллельно получим закон Ома в дифференциальной форме, то есть для некоторого элементарного отрезка по которому протекает ток. Согласно закону Ома для замкнутой цепи ЭДС индукции равно:

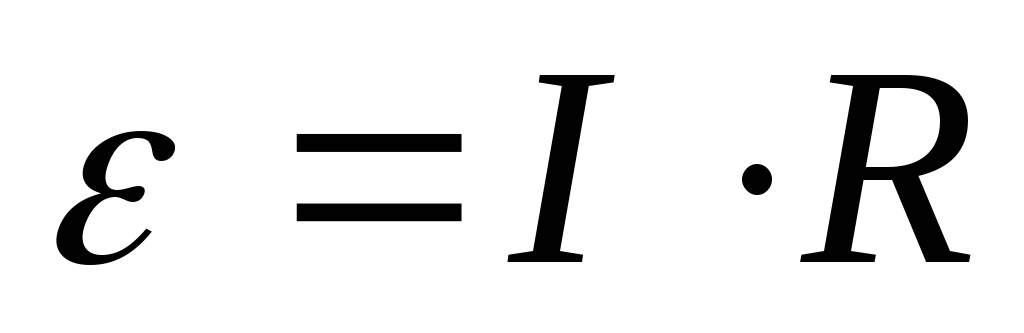
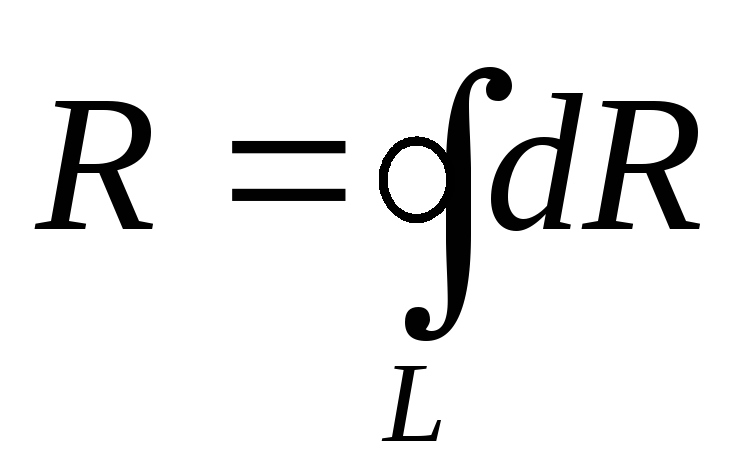
где: I – индукционный ток протекающий в данной поверхности замкнутого контура. R – сопротивление. dR – сопротивление элементарного участка данной цепи длинной dL.

Д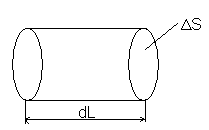анный элементарный участок замкнутого контура длинной dL имеет площадь поперечного сечения ∆S, то

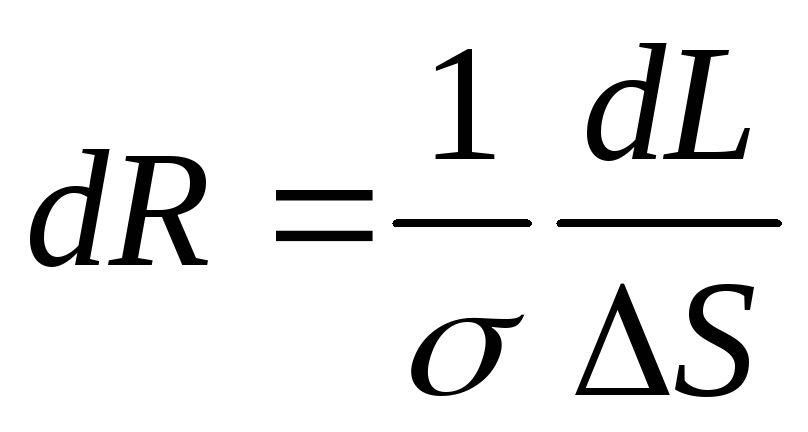
— удельная проводимость данного проводника.

Предполагаем что к некоторому проводнику длинной L и имеющему сопротивление R приложено напряжение U. То есть разность потенциалов проводника равная U. Сопротивление R данного проводника может быть определено:

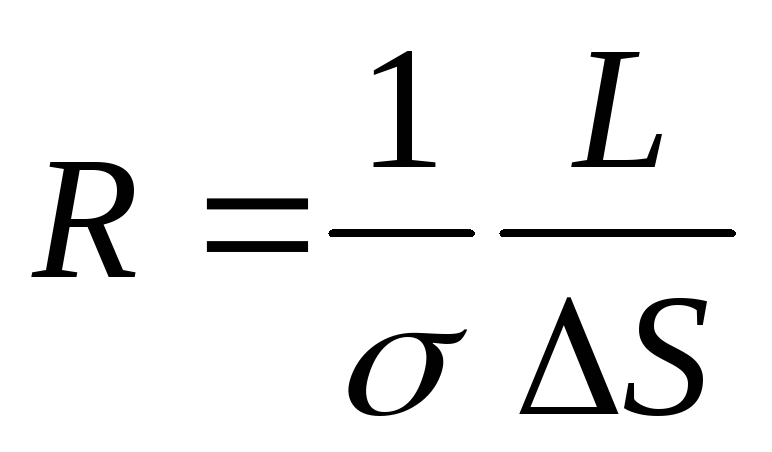
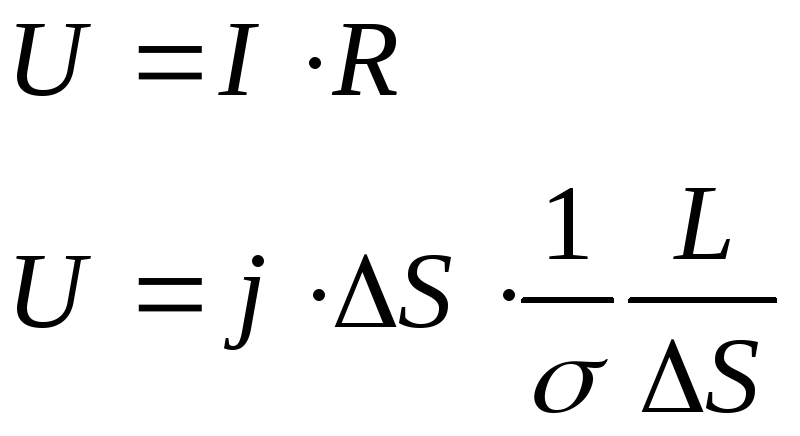
где: j – плотность тока, то есть ток проходящий через единицу поверхности поперечного сечения проводника, в том случае если проводник короткий, то можно считать что напряжённость электрического поля под действием которой происходит движение электрических зарядов связано с напряжением U.

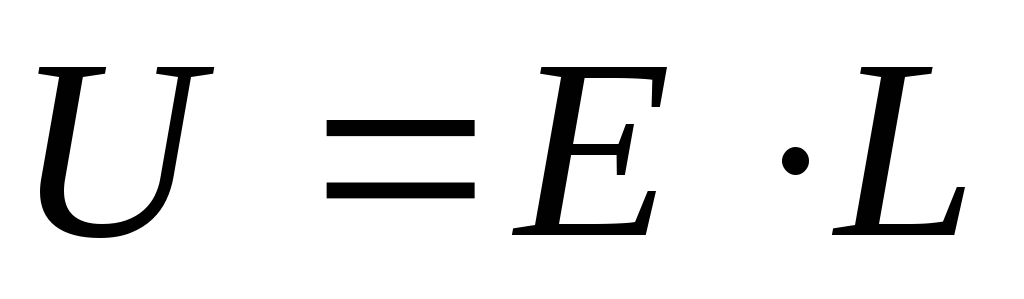
С учётом выше изложенного

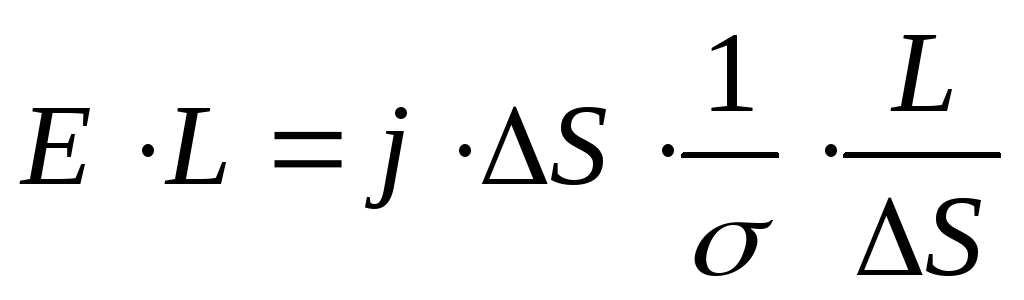
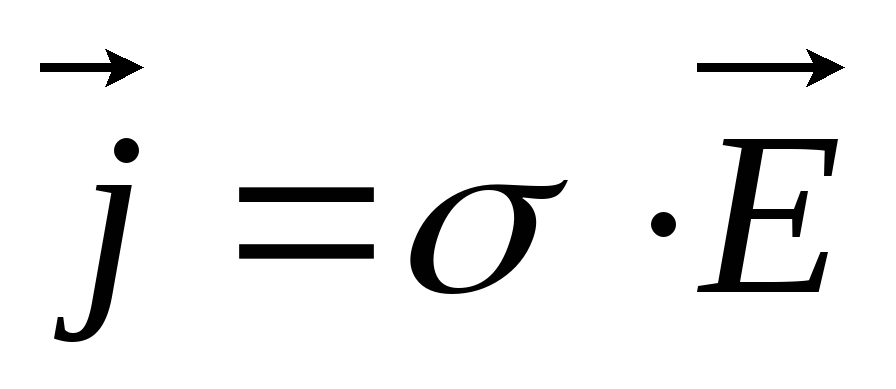
Таким образом мы получили закон Ома в дифференциальной форме. Или уравнение среды. Используя выше представленные выкладки получили обобщающее уравнение электромагнитной индукции.

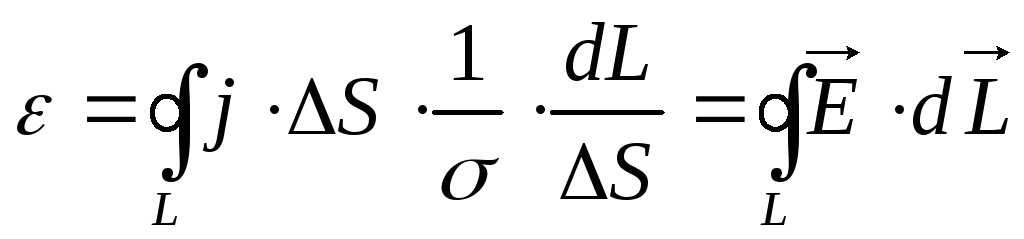
ЭДС индукции которая возникла в замкнутом контуре мы можем трактовать как циркуляцию вектора напряжённости электрического поля возникающего в результате изменения магнитного потока через поверхность которая охвачена замкнутым контуром по которому происходит выше названная циркуляция.

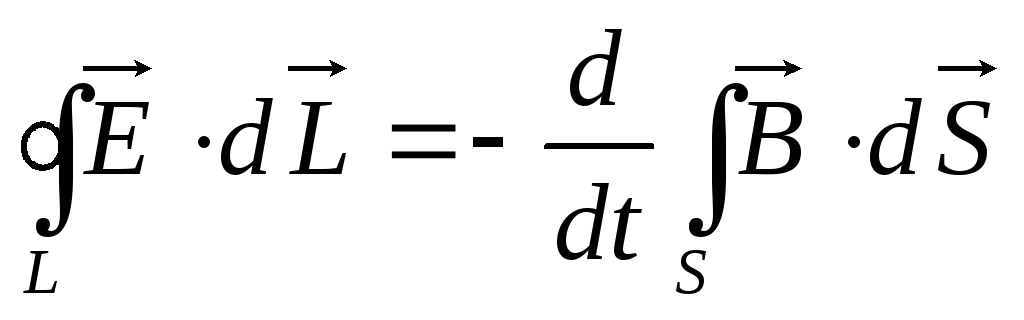
Циркуляция вектора напряжённости ЭП по замкнутому контуру L равна изменению во времени потока магнитной индукции через поверхность S которая охватывает данный замкнутый контур L взятую с обратным знаком. Из этого уравнения следует что изменяющийся во времени поток магнитной индукции порождает ЭП которое в общем случае отличается от ЭСП. Это поле наиболее легко обнаруживается если в качестве замкнутого контура охватывающего замкнутый контур S взять проводящий контур по которому будет протекать электрический ток вызывающий воздействие ЭП на свободные заряды находящиеся в проводнике. Данное уравнение является уравнением обобщающим закон электромагнитной индукции в интегральной форме. Для перехода к дифференциальной форме воспользуемся формулой Стокса.

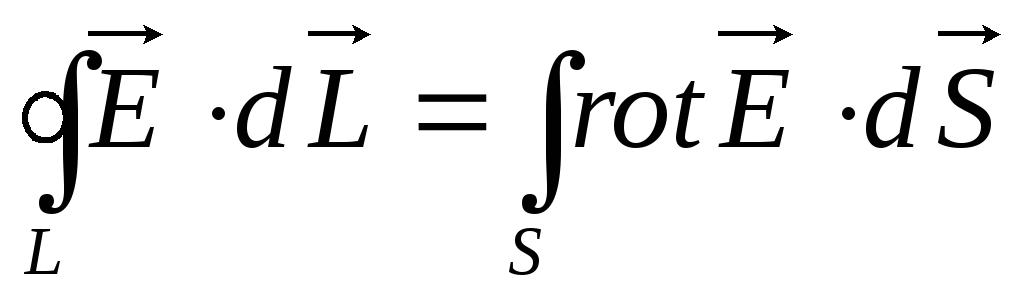
С учётом формулы стокса.

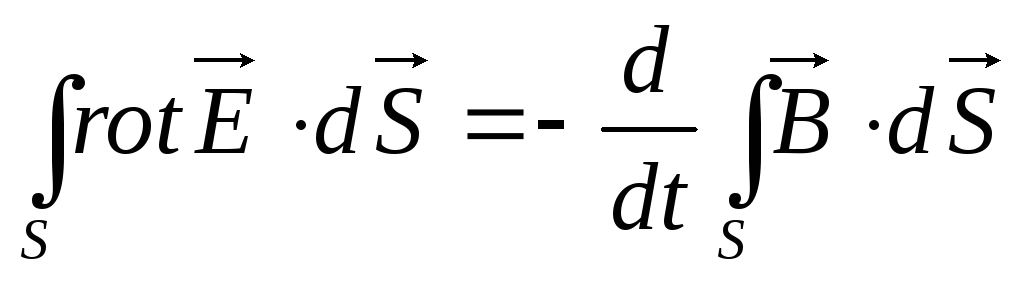
Это выражение может выполняться только в случае когда

Данное выражение есть запись уравнения обобщающего закон электромагнитной индукции для некоторой точки пространства.

В случае ЭСП все производные по времени равны нулю, а неподвижными электрическими зарядами МП не создается. Тогда для ЭСП уравнение обобщающее закон электромагнитной индукции можно записать следующим образом.

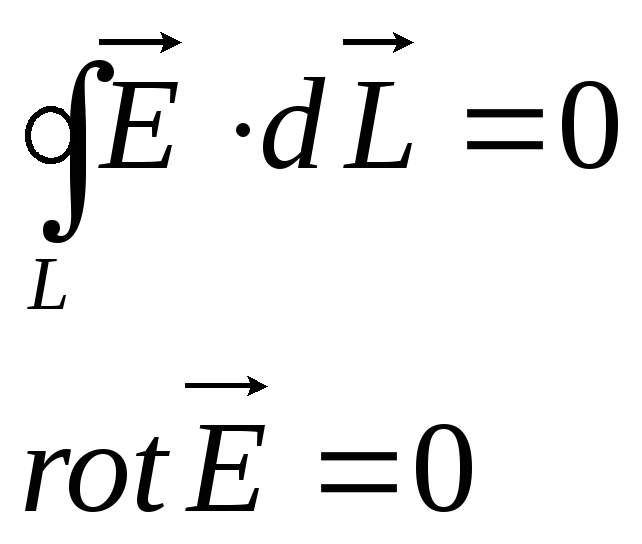
Эта запись говорит о потенциальности, консервативности ЭСП, о том что работа сил кулоновского происхождения на замкнутом контуре равна нулю. Или что работа этих сил не зависит от формы траектории, а зависит лишь от начальной и конечной точки движения заряда. Таким образом исходя из обобщённого уравнения Максвелла нами получено свойство ЭСП, а именно его консервативность (потенциальность).

В общем случае работа по перемещению заряда Uиз точки а в точку б может быть определена как:

Исходя из потенциальности ЭСП можно получить взаимосвязь между напряжённостью ЭСП (основной силовой характеристикой ЭСП) и потенциалом ЭСП (основной энергетической характеристикой ЭСП). Ранее нами было введено понятие grad скалярной функции. Определим его физический смысл. Предполагаем, что дана скалярная функция φ. В некоторый момент данная функция определена и в пространстве данную функцию можно изобразить с помощью поверхности.

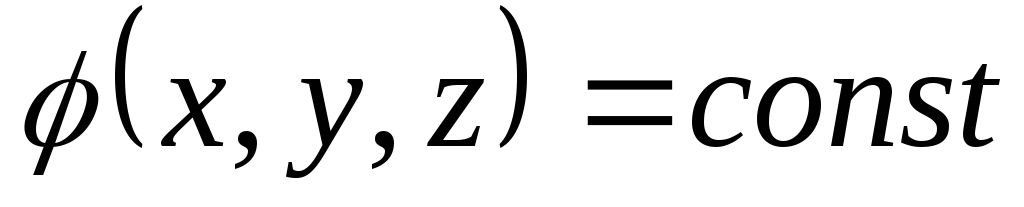
В следующий момент времени данная скалярная функция принимает другое значение и соответственно так же данная скалярная функция может быть изображена в виде новой поверхности причём можно утверждать, что за некоторый промежуток времени поверхность описанная уравнением 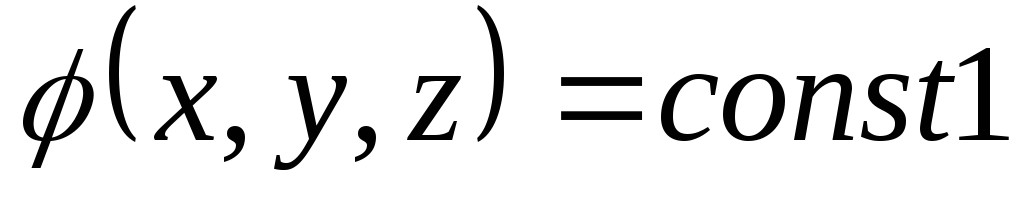сместилось в новое положение определяемое поверхностью 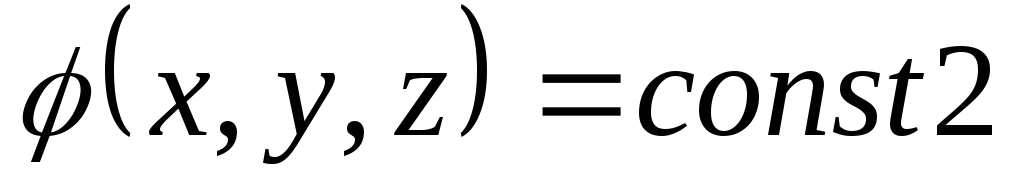. Вдоль нормали к этой поверхности. Величина равная 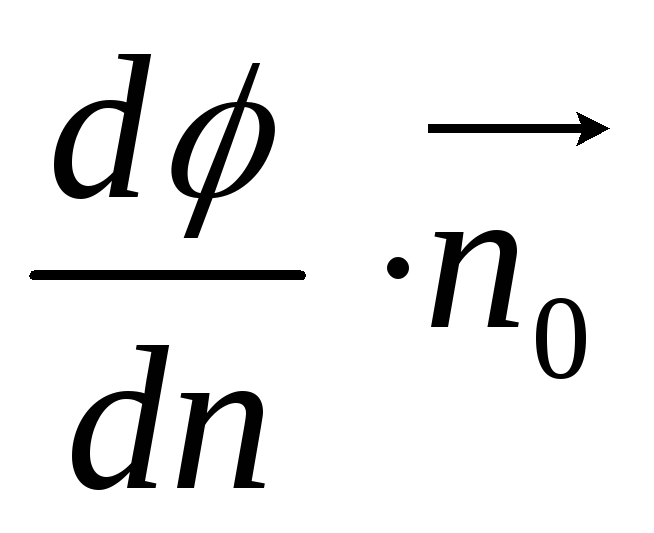получила название градиента скалярной функции φ. Таким образом градиент это вектор направленный в сторону наибольшего изменения некоторой скалярной функции.

Будем понимать под функцией φ потенциал ЭСП. Потенциал ЭСП можно определить как работу по перемещению положительного единичного пробного заряда выполненную силами ЭСП из данной точки (в которой определяется потенциал) на бесконечность.

Так как ЭСП потенциально то для него справедливо:

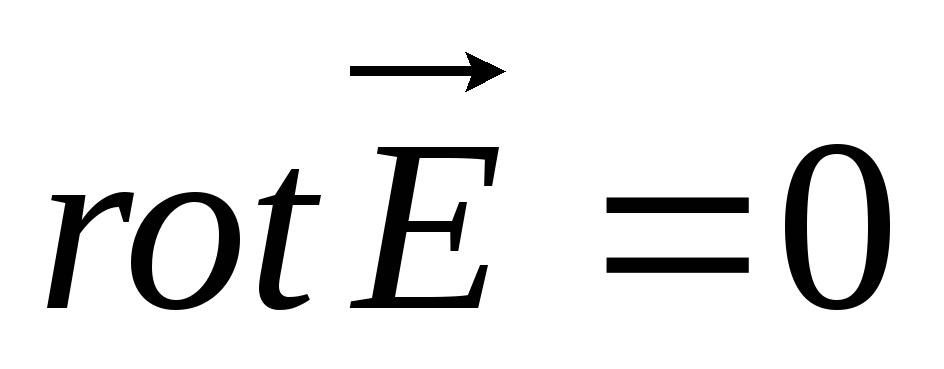
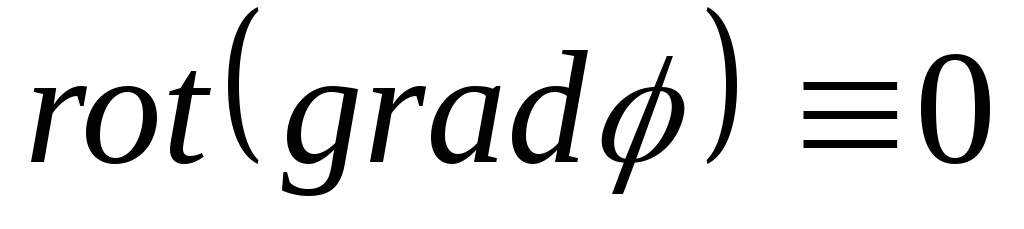
Из данного выражения следует:

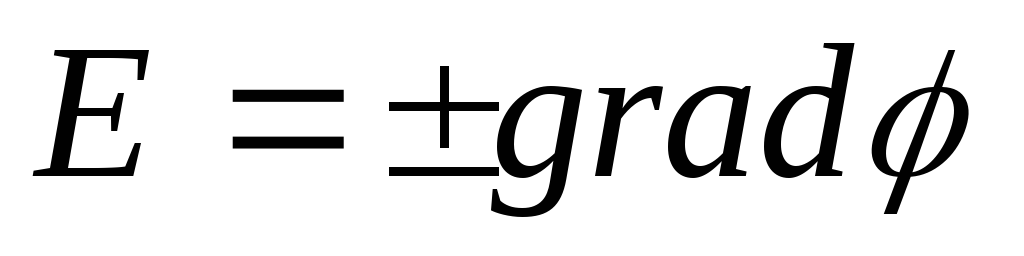
Найдём однозначную взаимосвязь между напряжённостью и потенциалом. С учетом введённого определения потенциала можно записать:

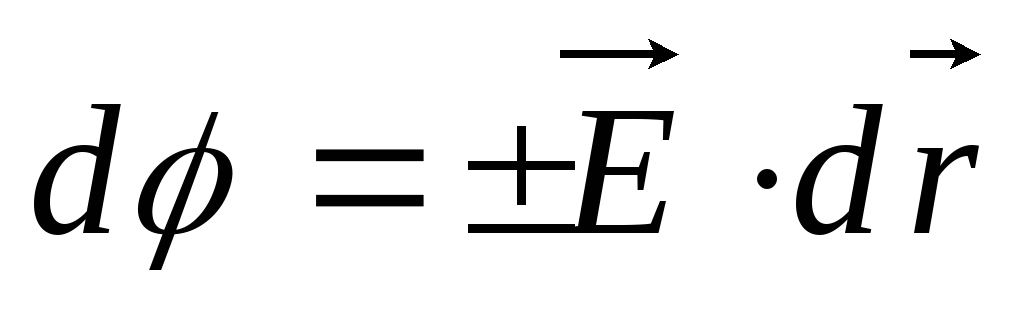
где: 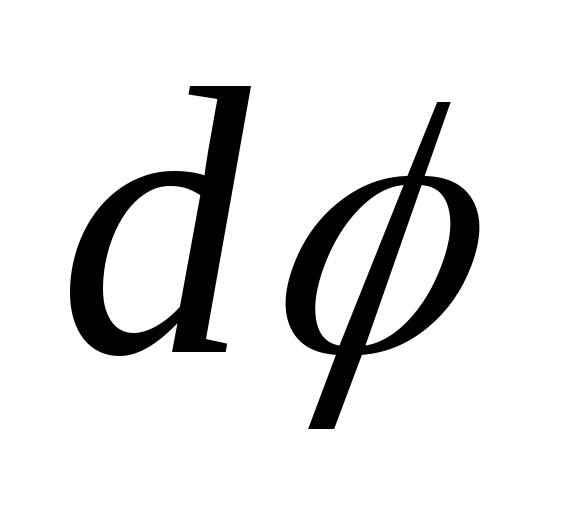— элементарное изменение потенциала; 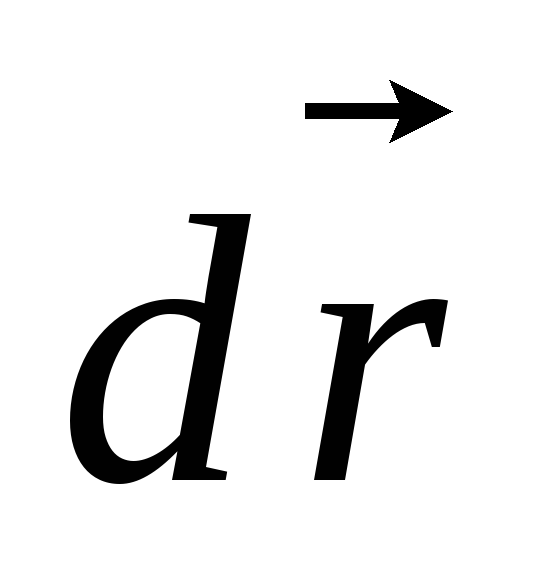— элементарное перемещение.

Так как 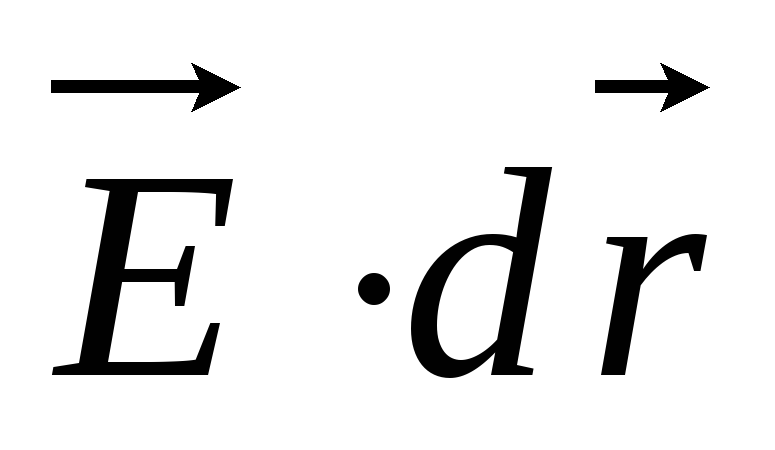можно трактовать как элементарную работу консервативных сил по перемещению единичного пробного положительного заряда на величину dr, а работа консервативных сил связанная с потенциальной энергией тела находящегося в поле данных консервативных сил:

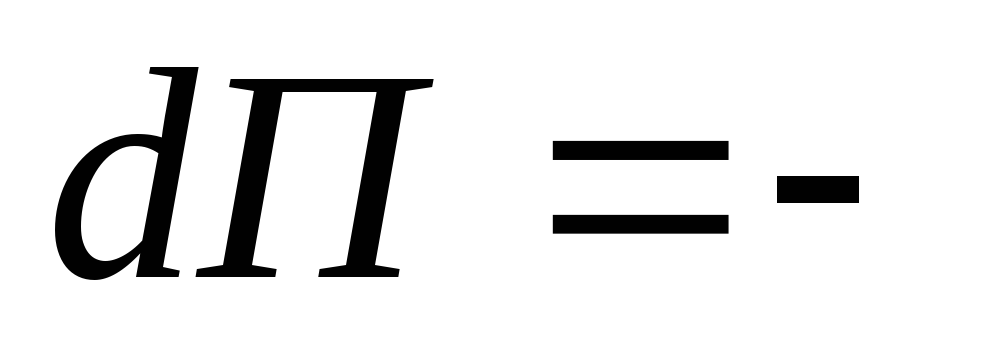
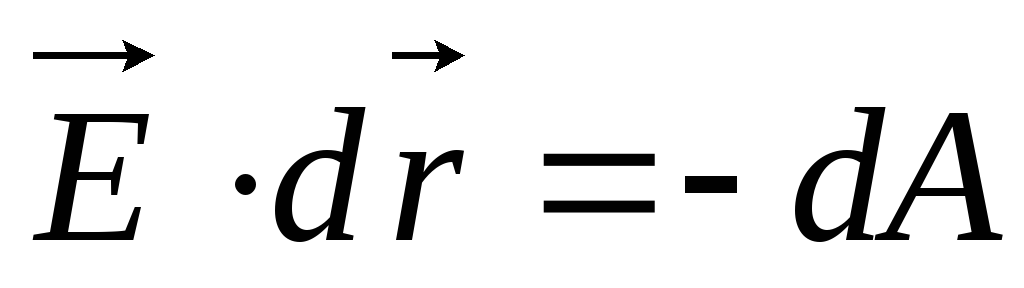
Таким образом исходя из этого можно определить:

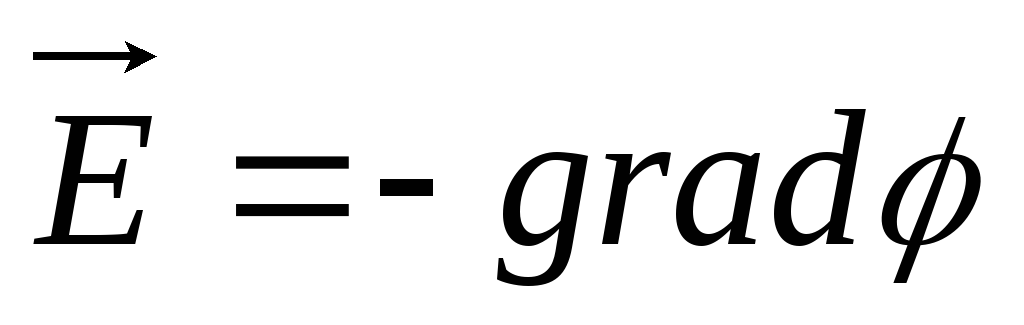
Таки образом исходя из фундаментального физического закона электромагнитной индукции получили потенциальность ЭСП и нашли взаимосвязь между двумя характеристиками ЭСП (напряжённость и потенциал).

Потенциалом можно так же дать и иное определение. Потенциал равен, той потенциальной энергии которой обладает единичный пробный положительный заряд в точке определения потенциала, находящегося в поле кулоновских сил (сил электростатического происхождения). Отсюда выражения для определения потенциальной энергии заряда q находящегося в поле кулоновских сил может быть определено:

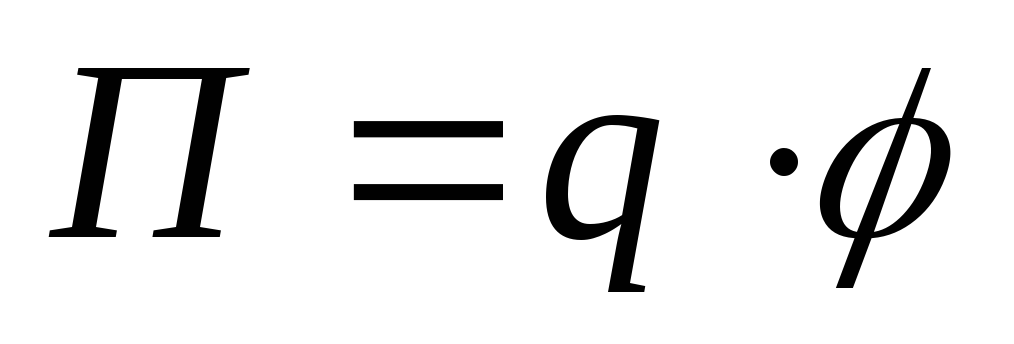
— величина заряда; — потенциал ЭСП в точке где находится заряд q.

Закон электромагнитной индукции, теория и примеры

Формулировка закона электромагнитной индукции

Эмпирически М. Фарадей показал, что сила тока индукции в проводящем контуре прямо пропорциональна скорости изменения количества линий магнитной индукции, которые проходят через поверхность ограниченную рассматриваемым контуром. Современную формулировку закона электромагнитной индукции, используя понятие магнитный поток, дал Максвелл. Магнитный поток (Ф) сквозь поверхность S – это величина, равная:

   

где модуль вектора магнитной индукции; – угол между вектором магнитной индукции и нормалью к плоскости контура. Магнитный поток трактуют как величину, которая пропорциональна количеству линий магнитной индукции, проходящих сквозь рассматриваемую поверхность площади S.

Появление тока индукции говорит о том, что в проводнике возникает определенная электродвижущая сила (ЭДС). Причиной появления ЭДС индукции является изменение магнитного потока. В системе международных единиц (СИ) закон электромагнитной индукции записывают так:

   

где – скорость изменения магнитного потока сквозь площадь, которую ограничивает контур.

Знак магнитного потока зависит от выбора положительной нормали к плоскости контура. При этом направление нормали определяют при помощи правила правого винта, связывая его с положительным направлением тока в контуре. Так, произвольно назначают положительное направление нормали, определяют положительное направление тока и ЭДС индукции в контуре. Знак минус в основном законе электромагнитной индукции соответствует правилу Ленца.

На рис.1 изображен замкнутый контур. Допустим, что положительным является направление обхода контура против часовой стрелки, тогда нормаль к контуру () составляет правый винт в направлением обхода контура. Если вектор магнитной индукции внешнего поля сонаправлен с нормалью и его модуль увеличивается со временем, тогда получим:

   

При этом ток индукции создаст магнитный поток (Ф’), который будет меньше нуля. Линии магнитной индукции магнитного поля индукционного тока () изображены на рис. 1 пунктиром. Ток индукции будет направлен по часовой стрелке. ЭДС индукции будет меньше нуля.

Формула (2) – это запись закона электромагнитной индукции в наиболее общей форме. Ее можно применять к неподвижным контурам и движущимся в магнитном поле проводникам. Производная, которая входит в выражение (2) в общем случае состоит из двух частей: одна зависит от изменения магнитного потока во времени, другая связывается с движением (деформаций) проводника в магнитном поле.

В том случае, если магнитный поток изменяется за равные промежутки времени на одну и ту же величину, то закон электромагнитной индукции записывают как:

   

Если в переменном магнитном поле рассматривается контур, состоящий из N витков, то закон электромагнитной индукции примет вид:

   

где величину называют потокосцеплением.

Примеры решения задач

§5. Закон электромагнитной индукции.

I. Краткие теоретические сведения

Закон электромагнитной индукции Фарадея: ЭДС индукции, возникающая в замкнутом контуре, численно равна изменению магнитного потока в единицу времени. Направление ЭДС индукции таково, что индукционный ток создает магнитный поток, препятствующий изменению магнитного потока, вызывающего ЭДС индукции.

.

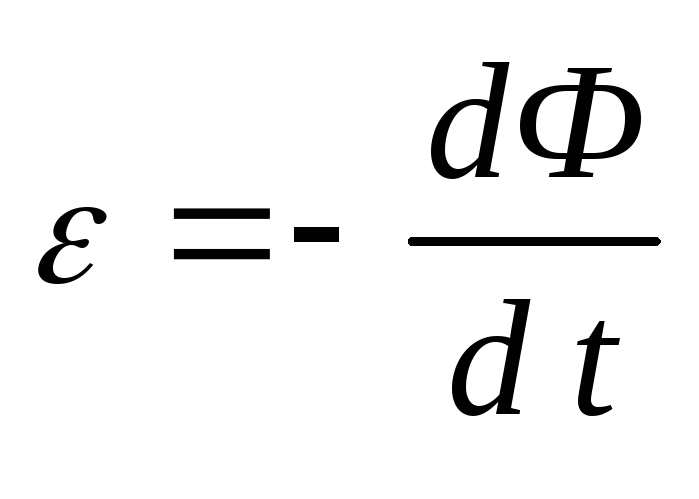Поток вектора магнитной индукции:

,

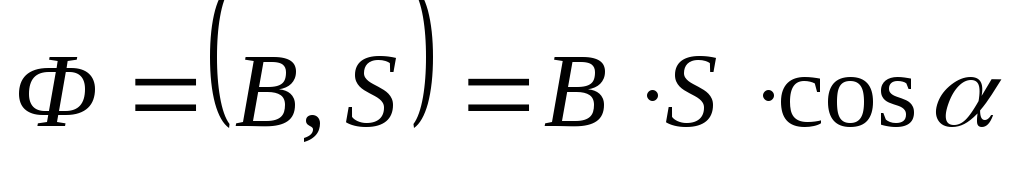где — угол между вектором магнитной индукции и нормалью к плоскости контура.

Индуктивность соленоида:

,

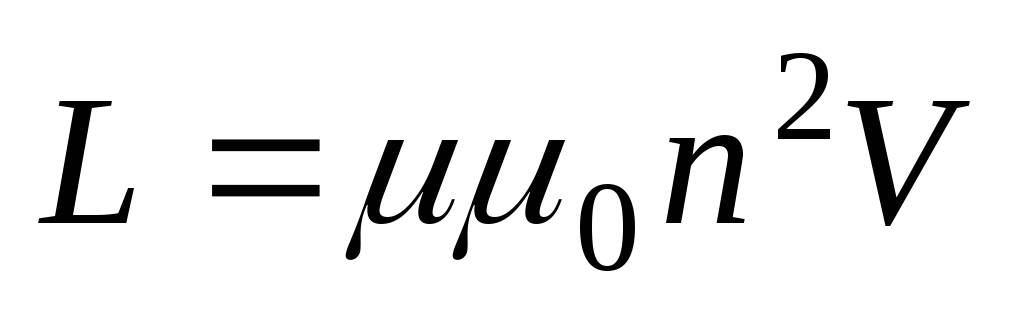где — магнитная проницаемость материала сердечника,n– число витков на единицу длины,V– объем соленоида.

II. Примеры решения задач

Пример 5.1.Короткозамкнутый виток провода сопротивлением R, имеющий форму квадрата со стороной а, поместили в однородное магнитное поле с индукцией В, перпендикулярной плоскости витка. Затем витку придали форму половины окружности (не растягивая провод, а только деформируя его). Какой заряд протечет через поперечное сечение провода в результате такой деформации.

Решение.

Из закона электромагнитной индукции:

,

где магнитный поток 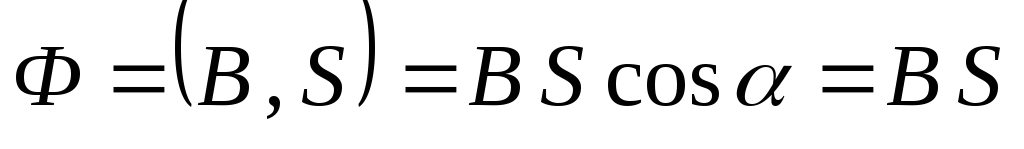, т.к. магнитное поле перпендикулярно плоскости витка, т.е. угол между вектором магнитной индукции и нормалью к плоскости витка равен нулю.

Из закона Ома,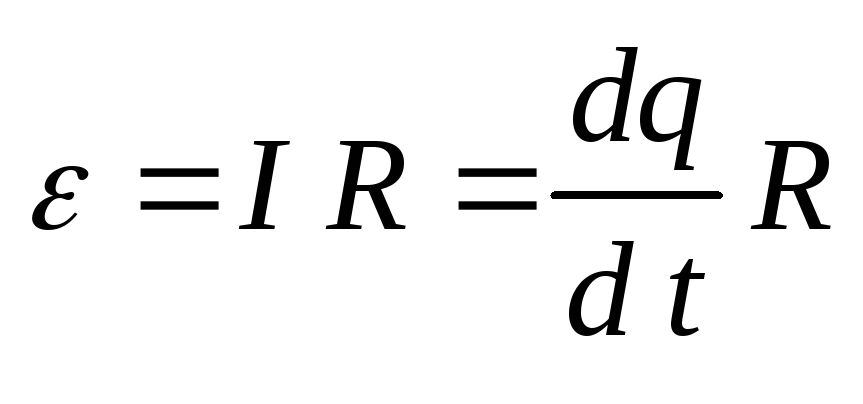

где R – сопротивление контура. Тогда:

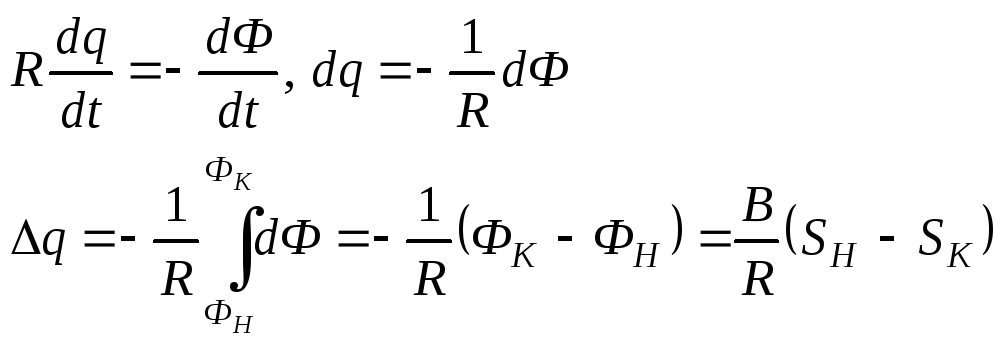
Начальная площадь контура: 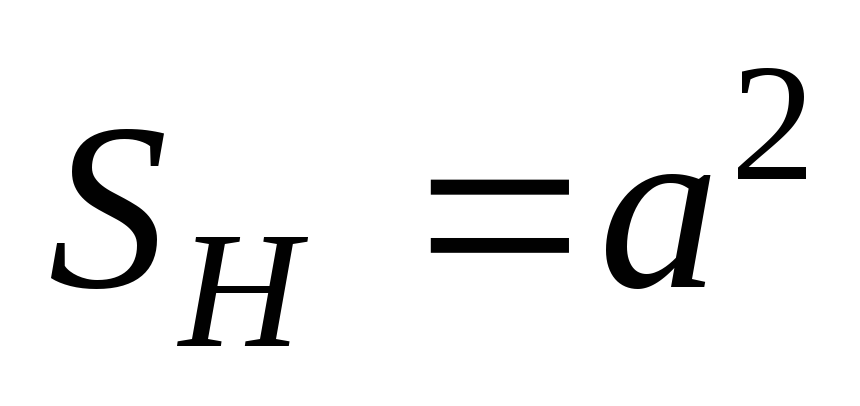, конечная площадь контура – площадь половины окружности: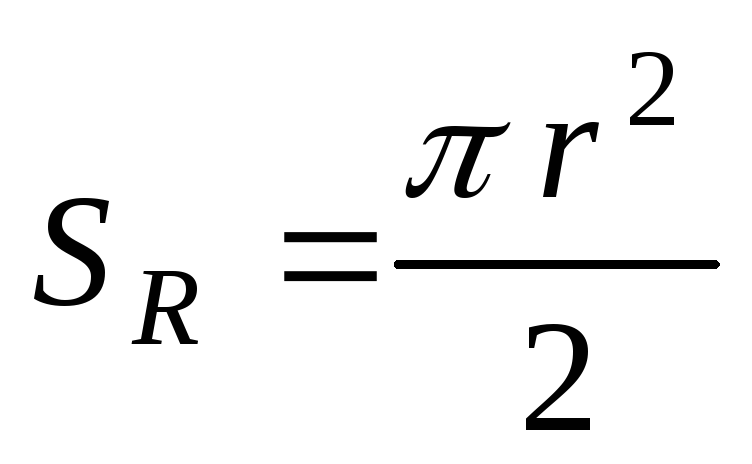, где r – радиус окружности. Радиус окружности найдем из условия, что длина провода остается неизменной: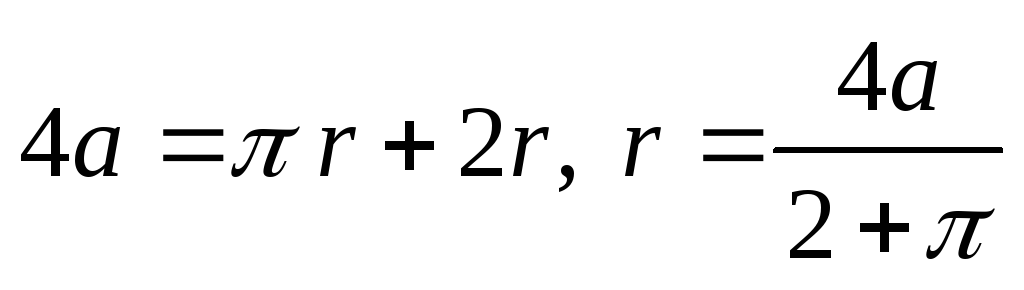. Тогда конечная площадь контура:.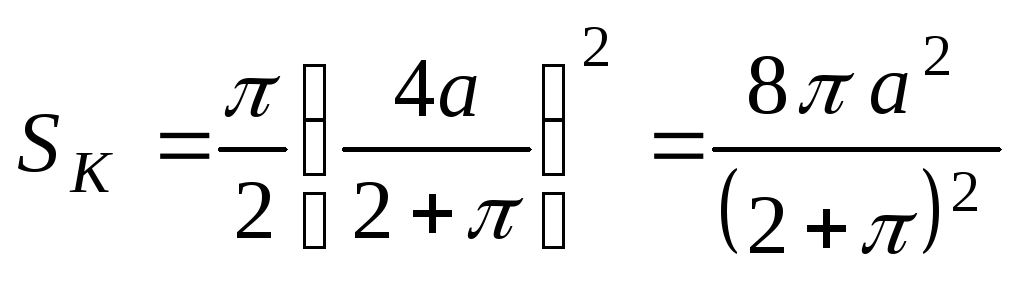

Таким образом, заряд который пройдет через поперечное сечение провода:

.

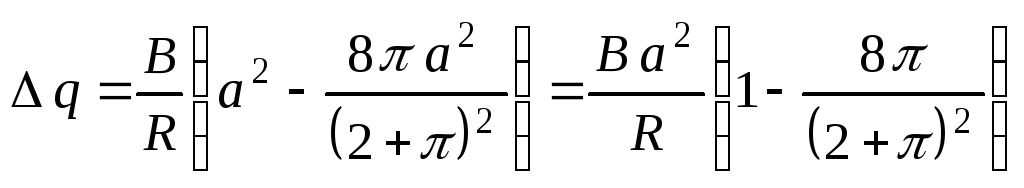Пример 5.2.Кольцо радиуса r вращается вокруг оси лежащей в его плоскости, так что угловая скорость зависит от времени по закону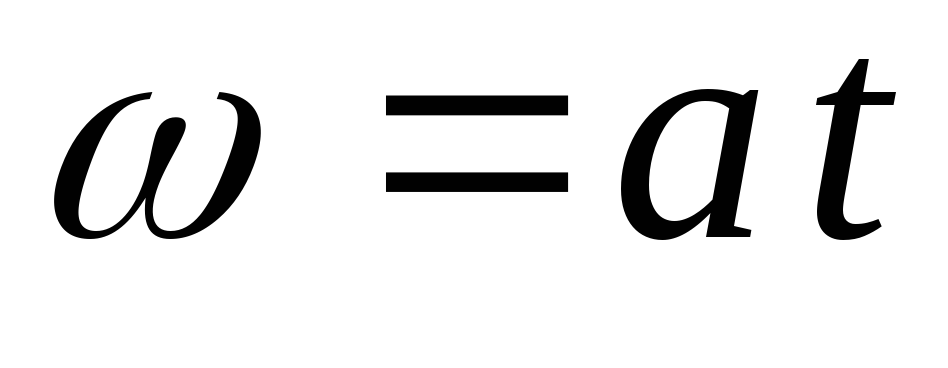(где а > 0). Кольцо помещено в однородное магнитное поле с индукцией В, направленной перпендикулярно к оси вращения. Найти индукционный ток в кольце, если его сопротивление R.

Решение.

Индукционный ток :

.

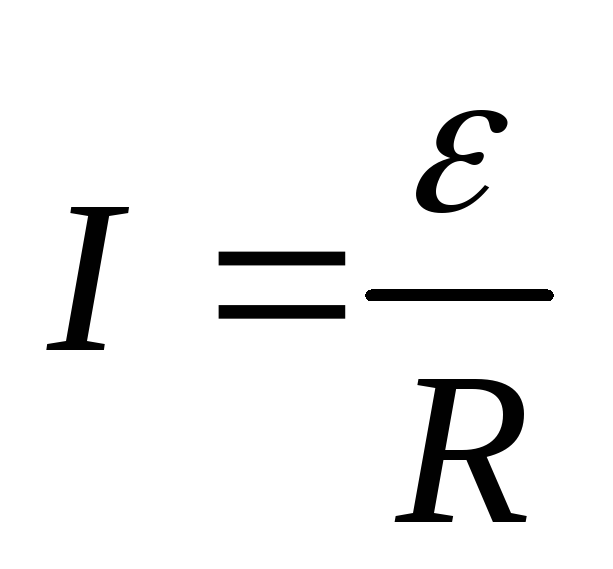Из закона электромагнитной индукции:

,

где магнитный поток 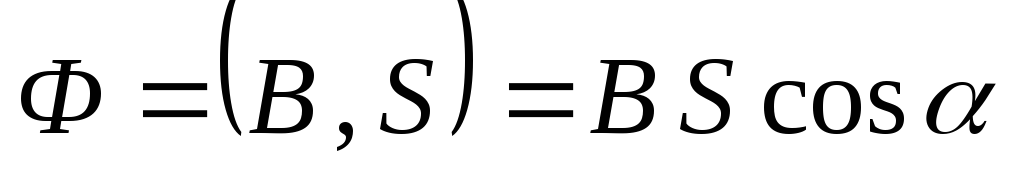,— угол между вектором магнитной индукции и нормалью к плоскости контура. Тогда:

.

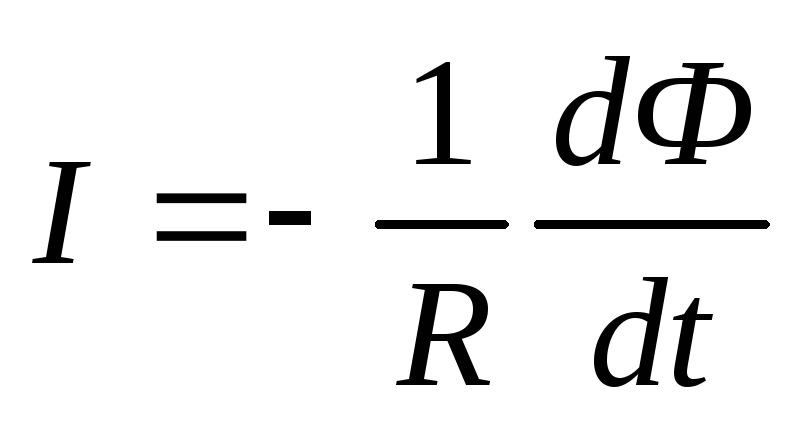В начальный момент времени нормаль к контуру совпадает с направлением вектора индукции магнитного поля:

.

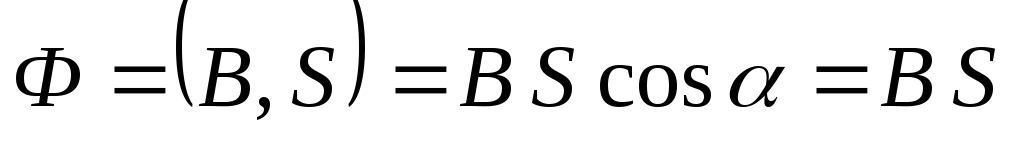В момент времени 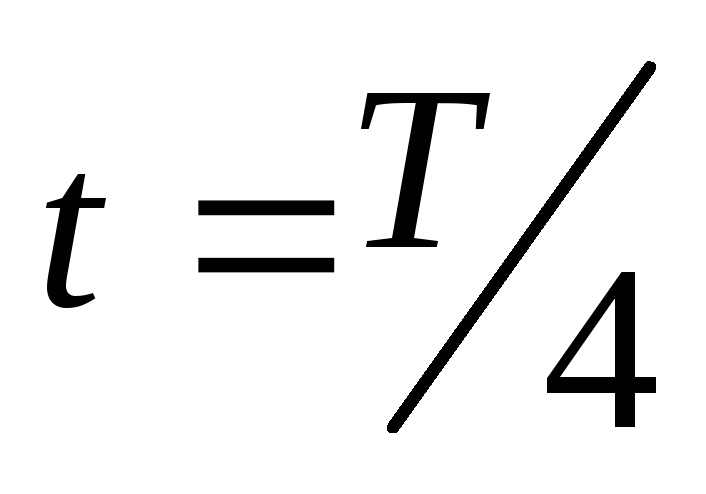, (гдеТ– период вращения, т.е. время одного полного оборота) кольцо повернется на угол 90вокруг своей оси, т.е.= 90и магнитный поток равен нулю.

В момент времени 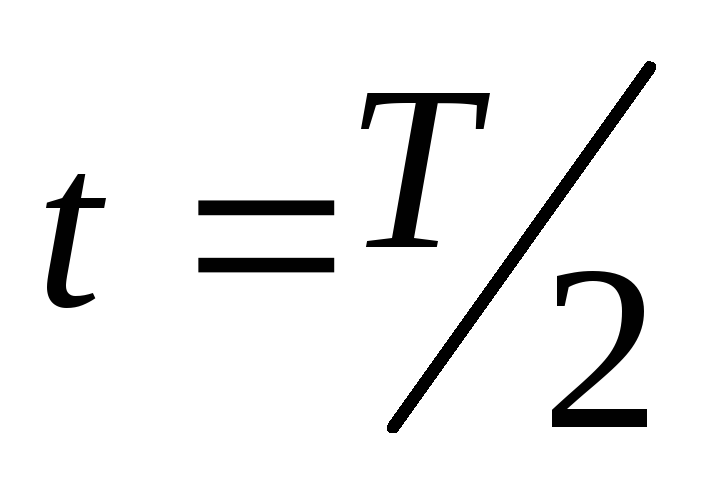, кольцо повернется на угол 180вокруг своей оси, т.е.= 180и магнитный поток равен:

.

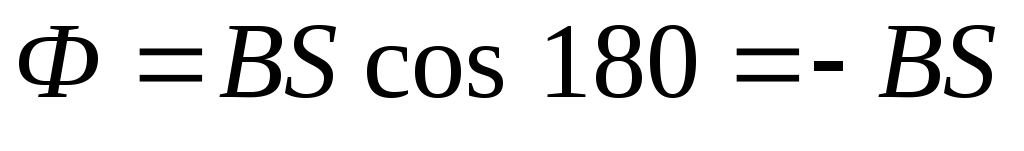В момент времени 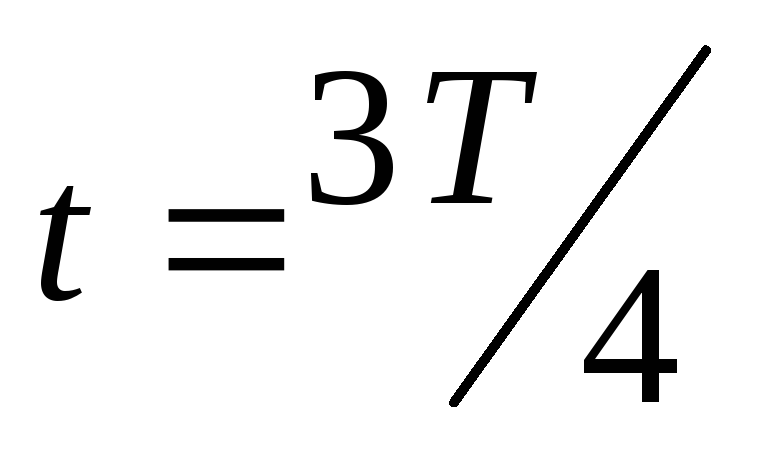, кольцо повернется на угол 270вокруг своей оси и= 270, т.е. магнитный поток равен нулю.

Таким образом, зависимость магнитного потока от времени имеет вид: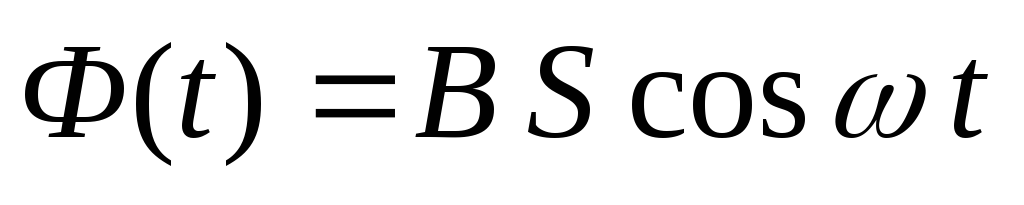, где.

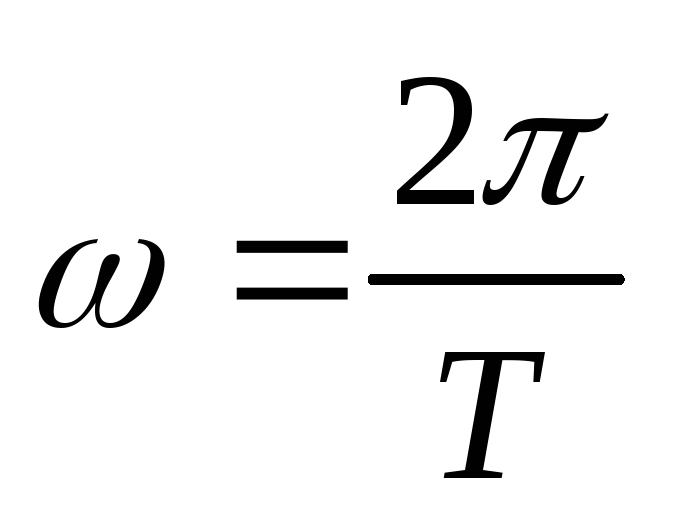Магнитный поток: 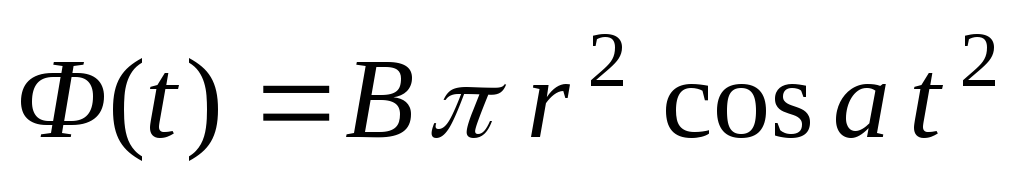и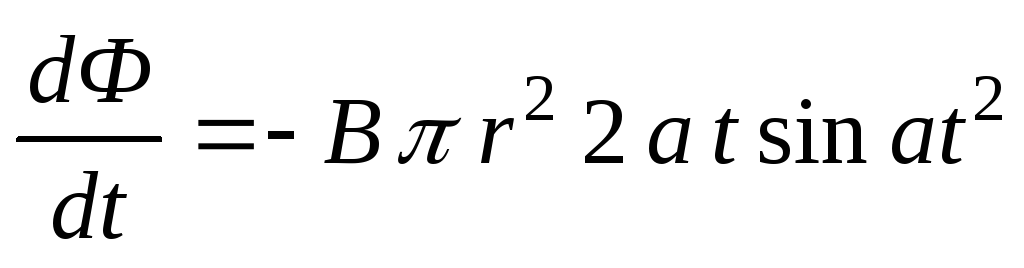. Тогда индукционный ток равен:

.

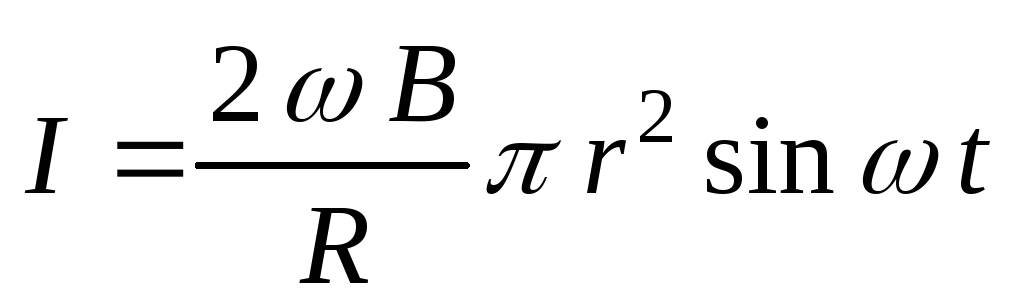Пример 5.3.В очень длинном соленоиде, радиус которого равенR, а число витков на единицу длины равноn, ток изменяется со временем по закону: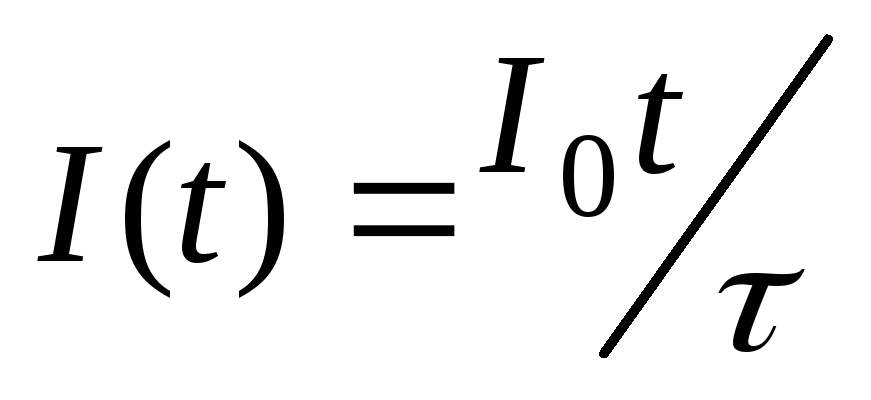(гдеI₀и— положительные постоянные). Определит напряженность электрического вихревого поляЕ(r)(внутри и снаружи соленоида) в любой момент времени.

Решение.

Закон электромагнитной индукции:

,

где 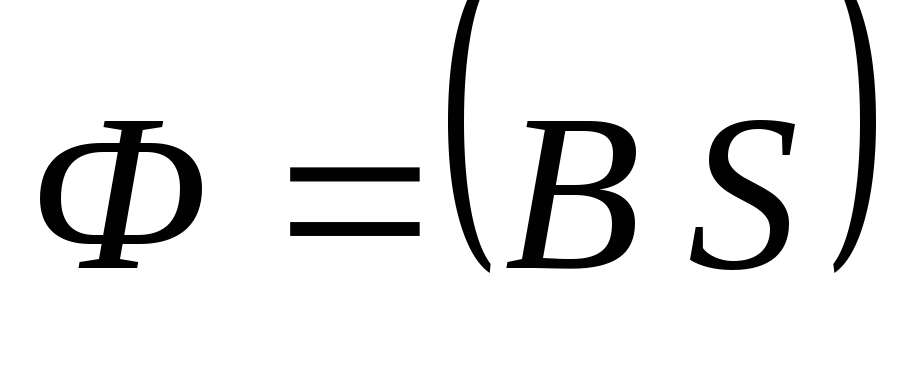— поток вектора магнитной индукции. Индукция магнитного поля внутри соленоида: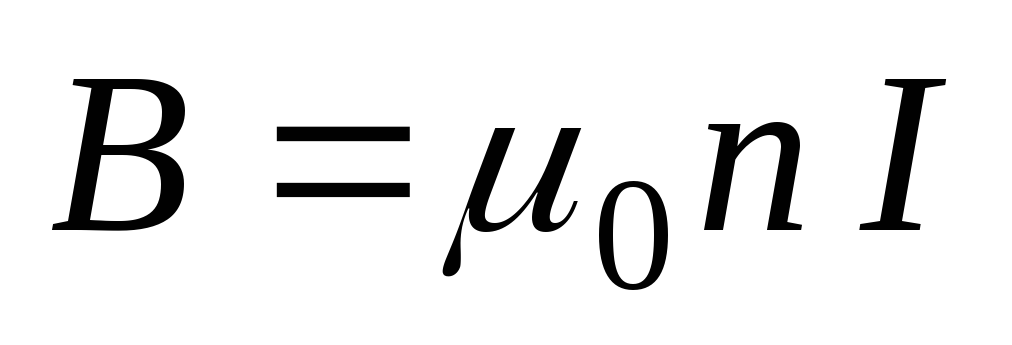, индукция магнитного поля вне бесконечного соленоида равна нулю. Силовые линии магнитного поля параллельны оси соленоида, силовые линии электрического поля – окружности, плоскости которых перпендикулярны оси соленоида. Выбираем замкнутый контур вдоль силовой линии электрического поля внутри соленоида, тогда поток вектора магнитной индукции через поверхность ограниченную данным контуром равен:

,

где r– радиус замкнутого контура.

.

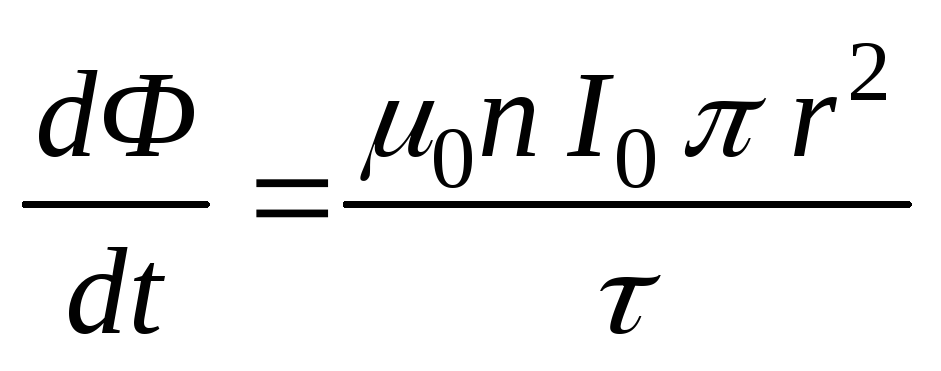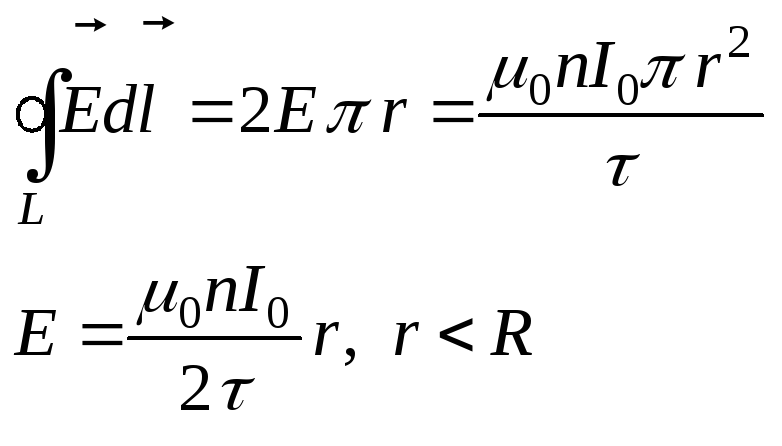
Если замкнутый контур выбираем вне соленоида, то .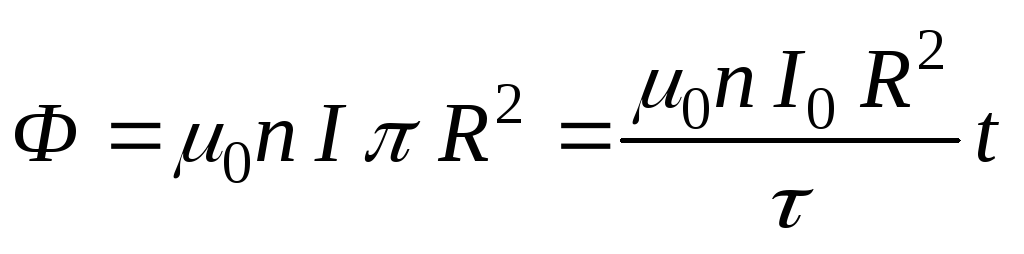

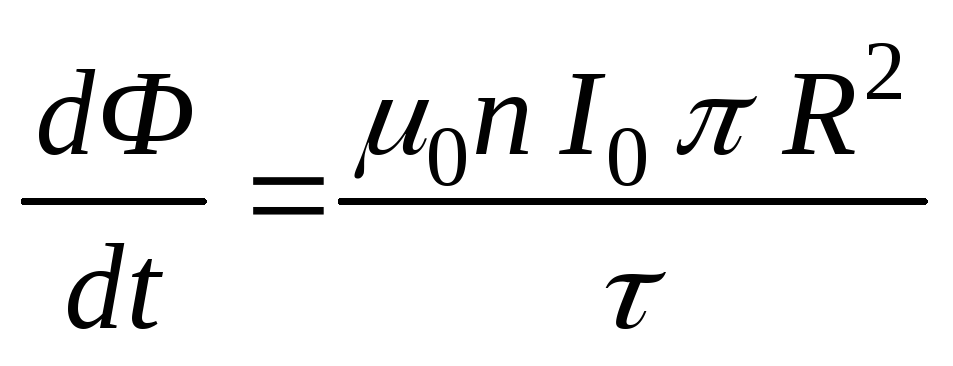
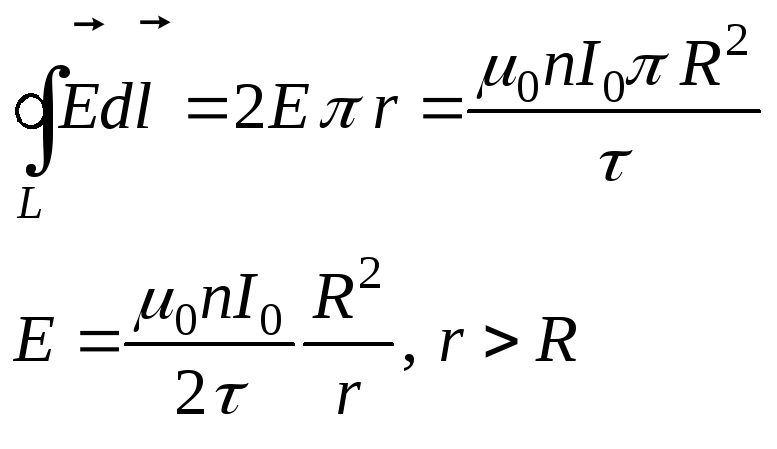
Пример 5.4.Провод, имеющий форму параболы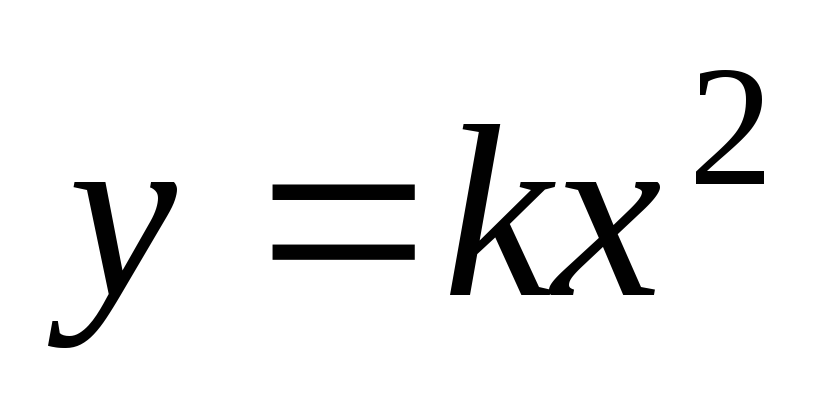, находится в однородном магнитном поле с индукциейВ. Из вершины параболы в момент времениt= 0 начали перемещать перемычку 12 (рис. 5.1 а). Найти э.д.с. в образовавшемся контуре как функциюу, если перемычку перемещают с постоянным ускорениема, причем в моментt= 0 скорость перемычки была равна нулю.

Решение.

Из закона электромагнитной индукции:

,

где магнитный поток 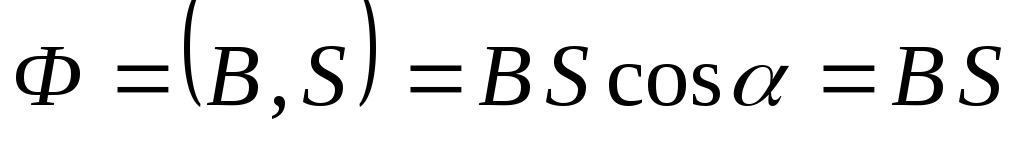,= 0 — угол между вектором магнитной индукции и нормалью к плоскости контура.

Чтобы найти площадь S, вычислим площадь заштрихованной фигурыS^/на рис. 5.1 б, учитывая, что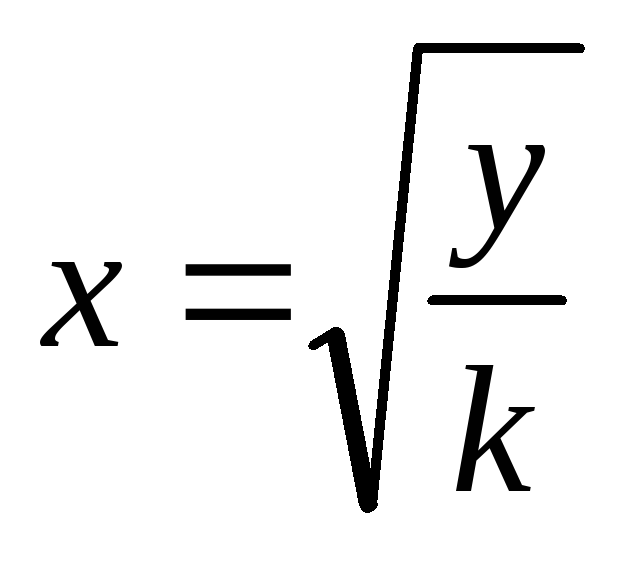и.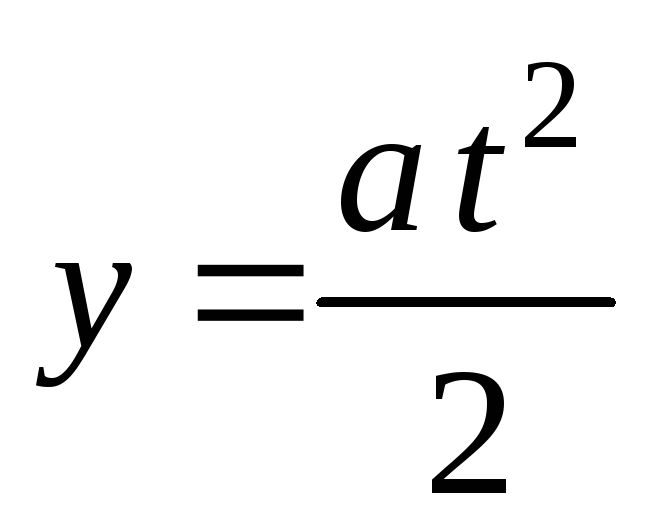

.

.

.

.

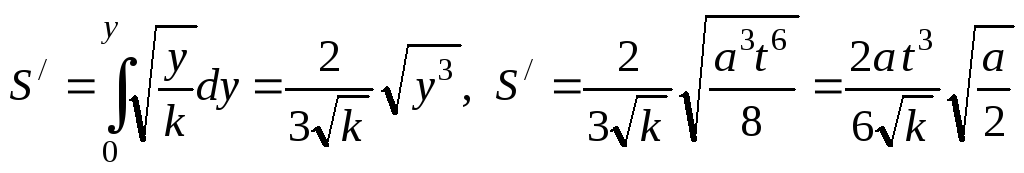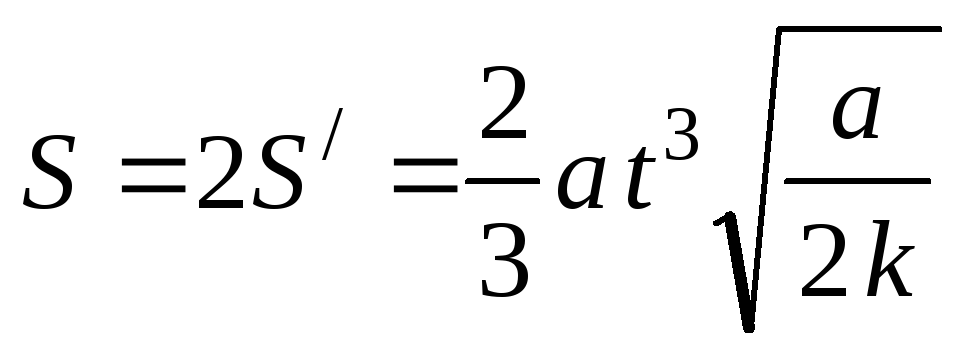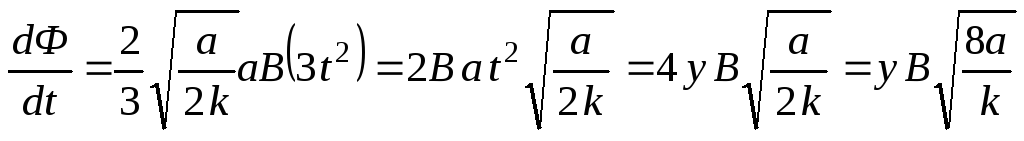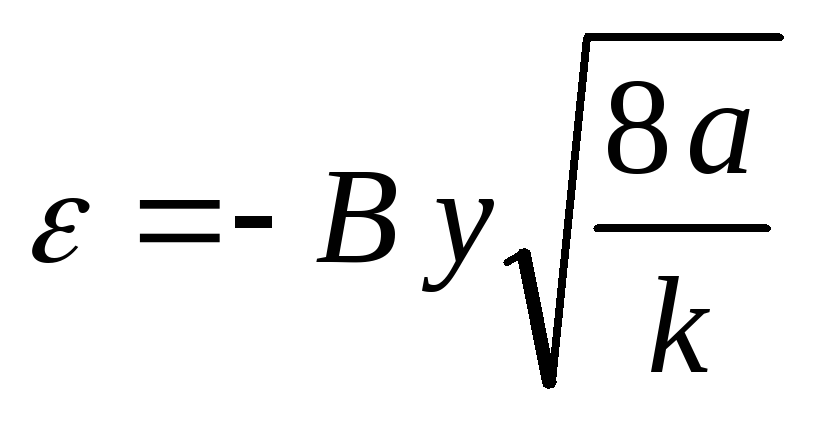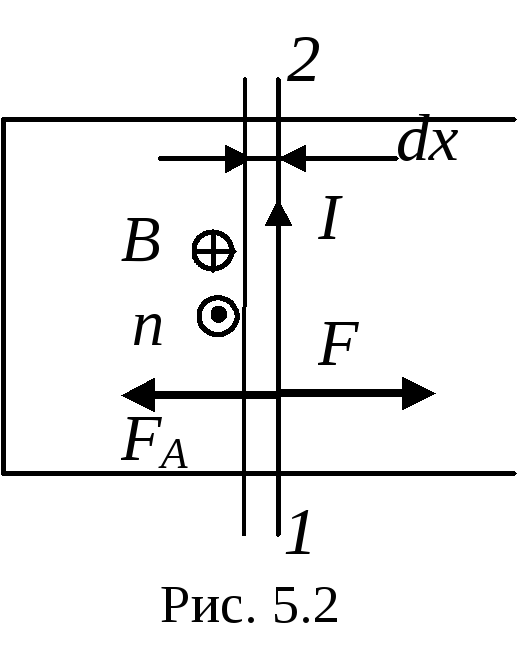
Пример 5.5.По П-образному проводнику, расположенному в горизонтальной плоскости, может скользить без трения перемычка 12 (рис. 5.2). Перемычка имеет длинуl, массуmи сопротивлениеR. Вся система находится в однородном магнитном поле с индукциейВ. В момент времениt= 0 на перемычку стали действовать постоянной горизонтальной силойF, и перемычка начала перемещаться вправо. Найти зависимость от времени скорости перемычки. Самоиндукция и сопротивление П-образного проводника малы.

Решение.

При перемещении перемычки под действием силы Fв контуре возникает ЭДС индукции и индукционный ток (направление тока указано на рис. 5.2):

,

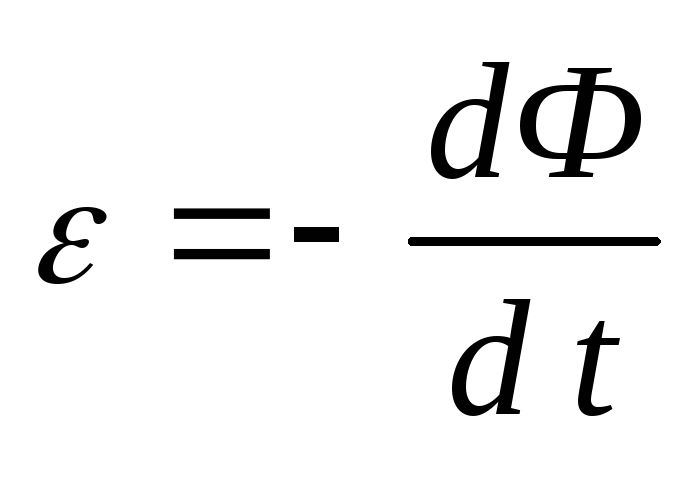где магнитный поток 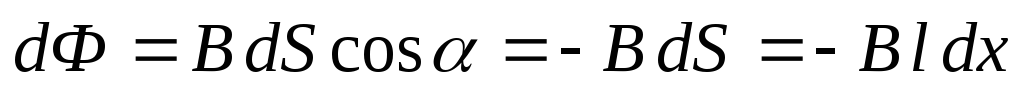,= 180 — угол между вектором магнитной индукции и нормалью к плоскости контура. Величина индукционного тока определяется выражением:

,

где v– скорость движения перемычки.

На проводник, по которому течет ток, в магнитном поле действует сила Ампера:

.

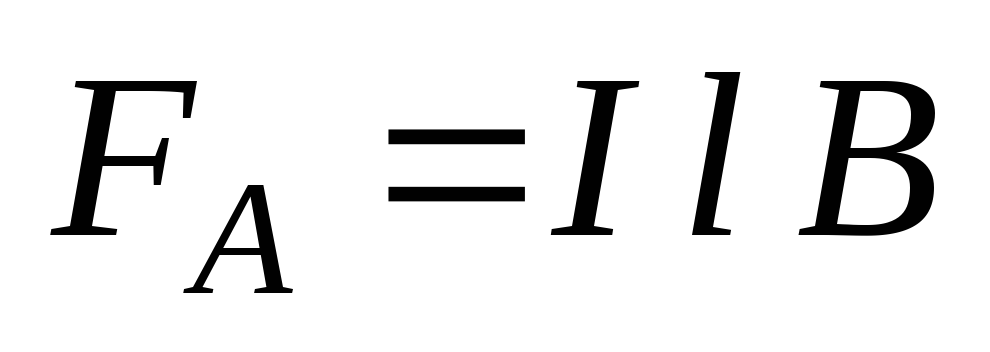Уравнение движения перемычки имеет вид:

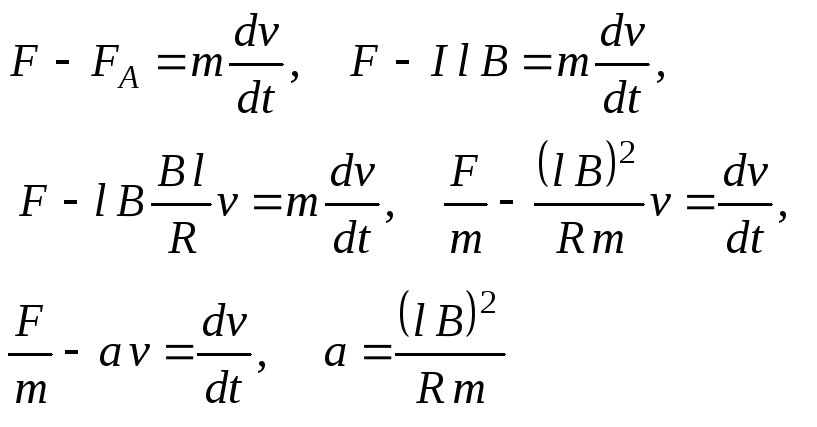
Решаем дифференциальное уравнение:

.

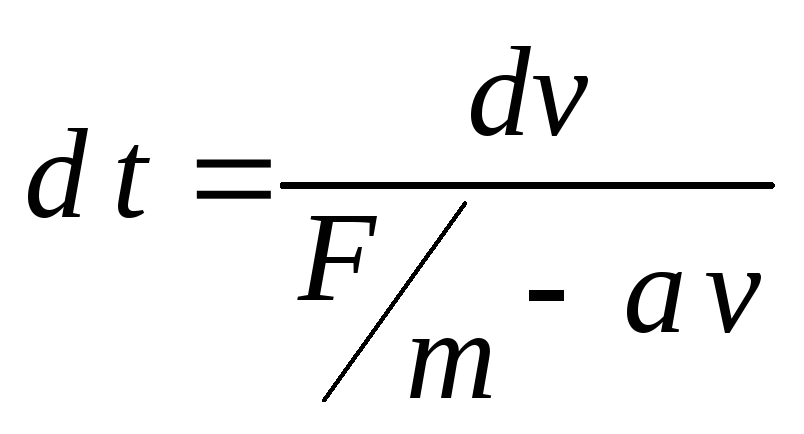
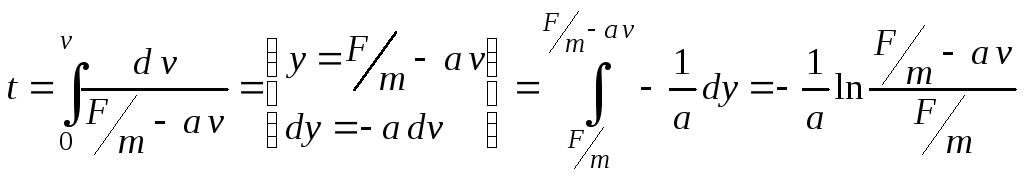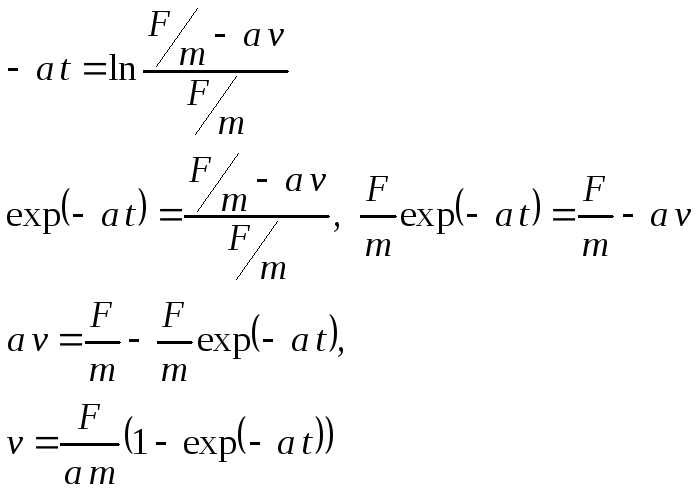
Обсуждение:Закон электромагнитной индукции Фарадея — Википедия

Материал из Википедии — свободной энциклопедии

что за бардак в статье? вы её читать пробывали?

читием заголовок: Пример 2: петля, движущаяся в постоянном магнитном поле

текст: На рис. 4 показан шпиндель, образованный двумя дисками с проводящими ободами, и проводящая петля, расположенная вертикально между этими ободами.

подпись к рисунку 4:

Рис. 4. Замкнутый прямоугольный провод вращается с угловой скоростью ω в радиальном, направленном наружу магнитном поле B фиксированной величины. Ток снимается щётками, касающимися верхнего и нижнего дисков с проводящими ободами.

ну что тут можно сказать «петля» практически тоже самое что и «Замкнутый прямоугольный провод», а нарисована ваще пластина ибо ток в одном направлении с каждой стороны. попробуйте в петле направить ток как на рисунке. так получится если это не петля, а два отдельных проводика замкнутые на обод.

к слову говоря и «ток снимается» это что? типа закон сохранения энергии не указ? и крутится и снимается — само по сибе. и проще всего обяснить не силой Лоренца, а силой Ампера там сразу блина проводна а не единичный заряд.

кстати говоря не надо мучатся что петля что пластина а что замкнутый прямоугольный провод — один провод будет отлично вращаться есали к дискам подвести ток.

интересны коментарии.

объяснениее же здесь — наукообразный бред. фишка это конструкции в том чтто тут не работает закон электромагнитной индукции Фарадея — вообще напрочь. вот такой вот парадокс Фарадея.

вот ваш эффект — так сказать наглядная демонстрация.

а вот здесь ничего написано и картинка правильная Рельсотрон

а вобще статью написал какойто вредитель.там ниже идет обяснение что если весь путь отследить, то будет изменение площади контура, одна загвоздка — он не замкунут. цитаты извесных людей притянуты за уши. тут надо все переписывать от начала и до конца.

есть графоман с физическим образованием? —109.238.81.229 08:54, 13 сентября 2016 (UTC)

и еще пять копек к правке. можно говорить об ЭДС, но нужен источник потока магнитной индукци. Меня что-то мучают некоторые сомнения(с чего бы это? опять закон сохранения энергии? — вот шайтан ведь), что ситема выйдет на самоподдержку. такой генератор называют униполярным — описан в начале статьи. вообще случай «рамки» в равномерном поле это просто часный случай униполярного двигателя или генератора. кстати исторически это называется «парадокс Фарадея». т.е. Фарадей сам не смог прикрутить туда свой закон. готов написать математику (упрощенный вывод через закон Фарадея или силу Лоренца, а можно то и то) мне нужны картинки. последовательное описание еффекта дается в ОТО — это мне не по-зубам. —109.238.81.229 11:00, 19 сентября 2016 (UTC)
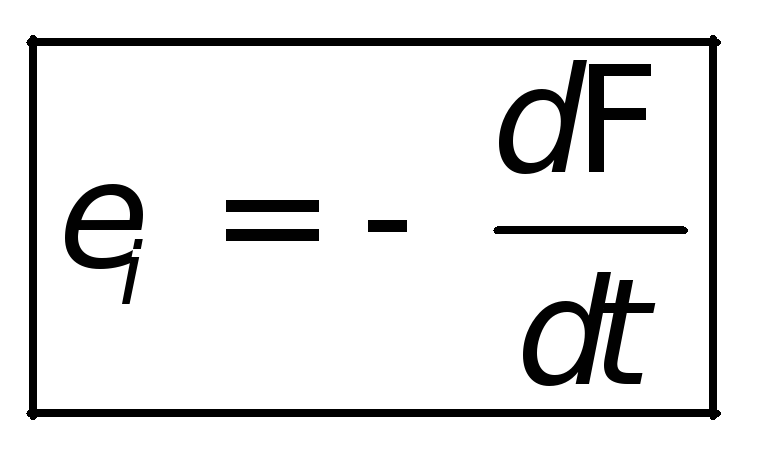
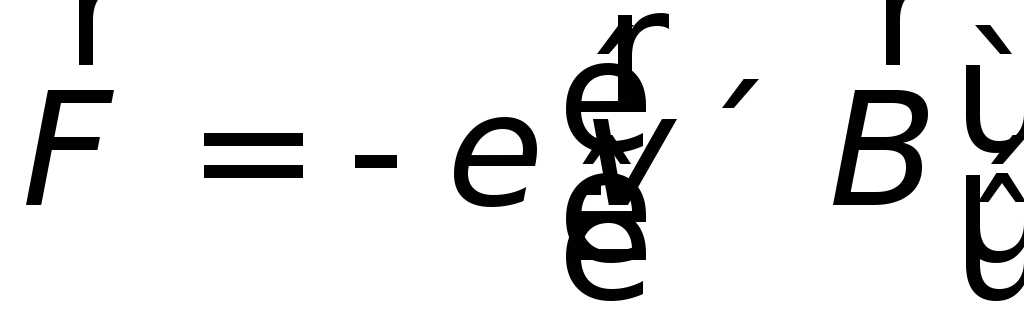
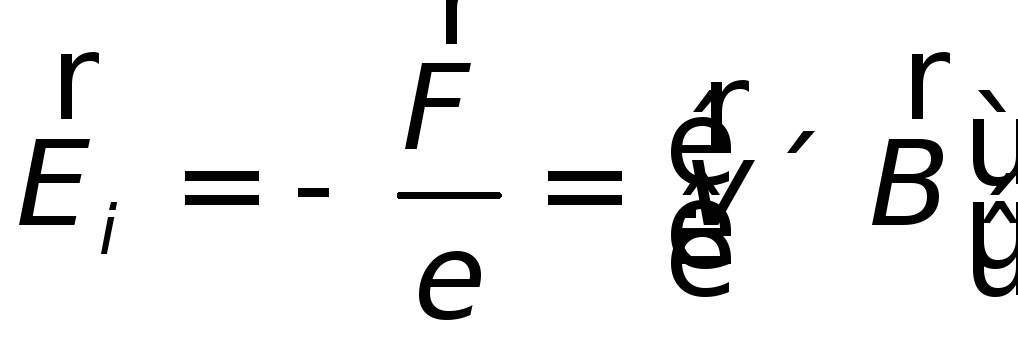
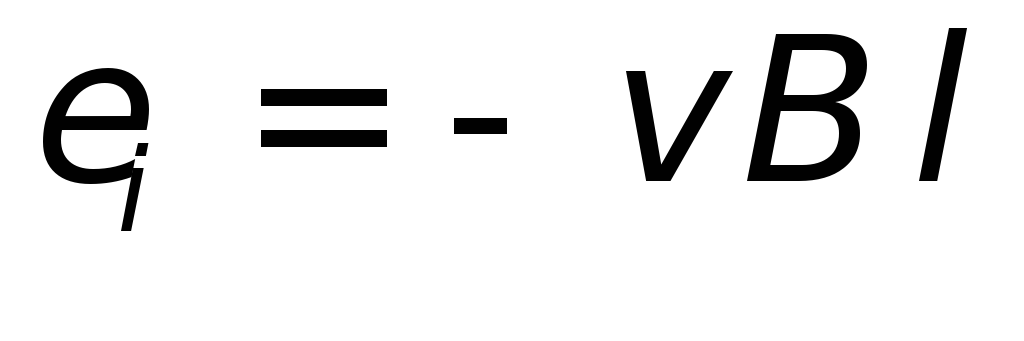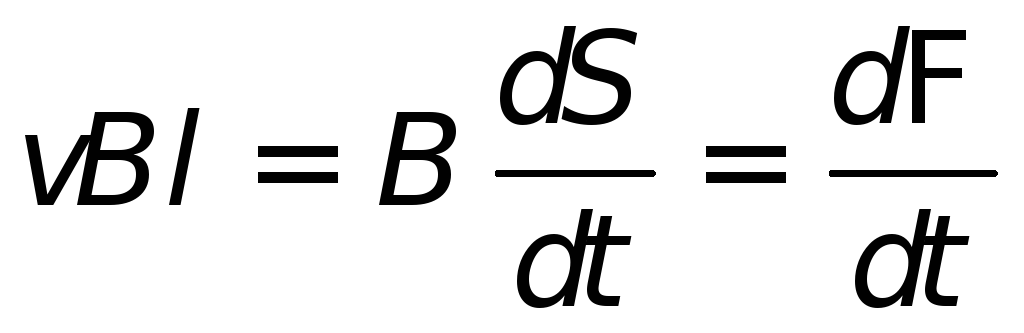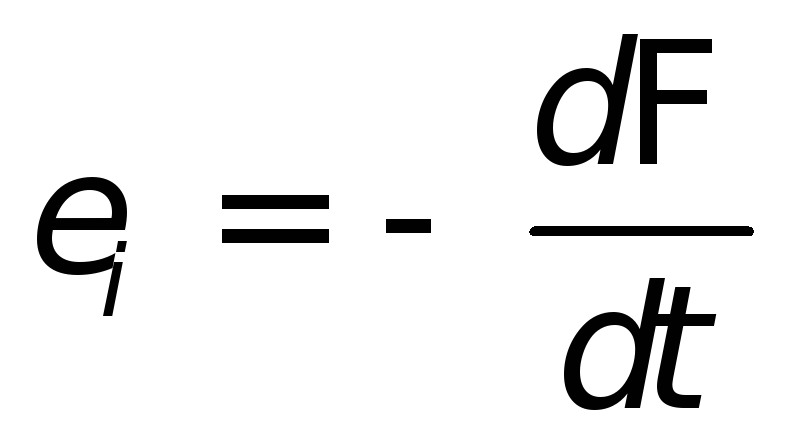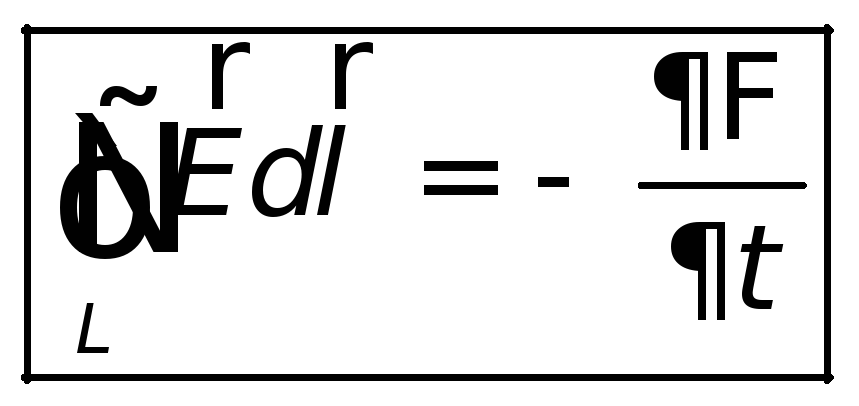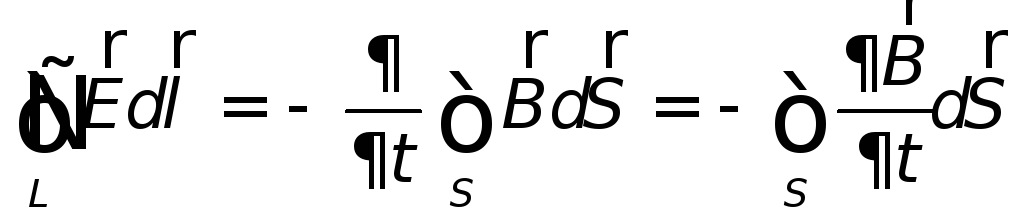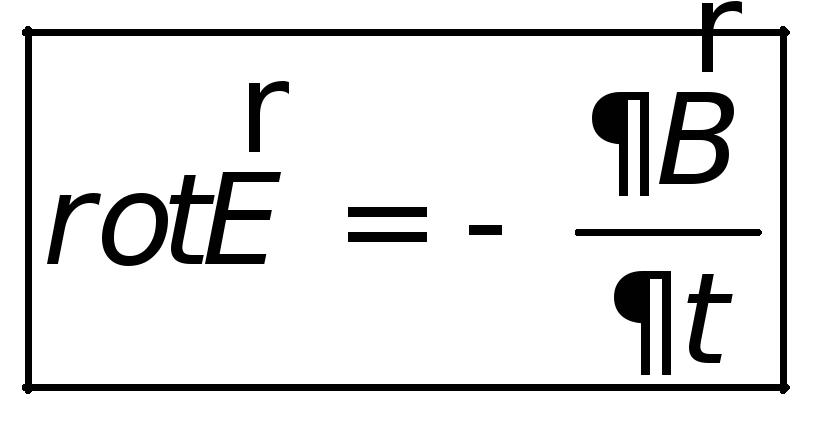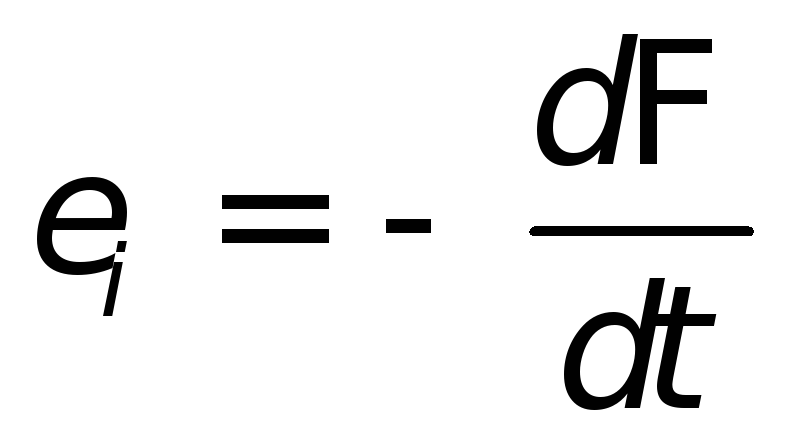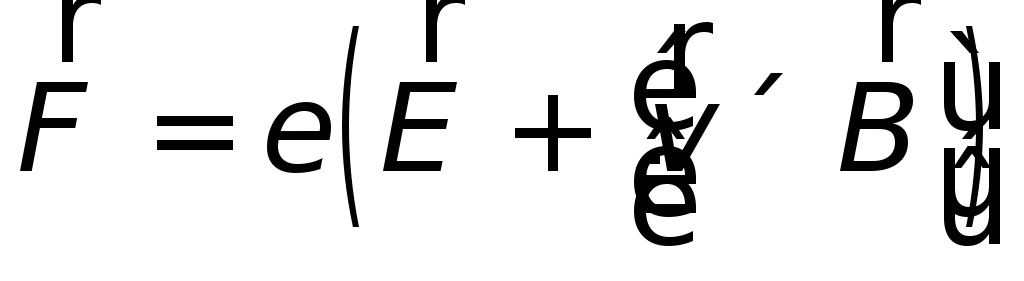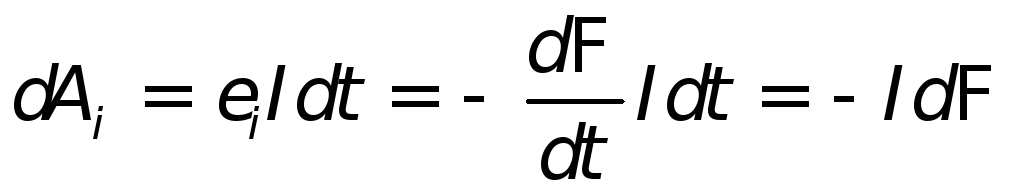