Закон Био-Савара-Лапласа. Вывод формулы для напряженности и индукции магнитного поля на оси кругового витка с током.

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Нижегородский Государственный Технический Университет им. Р.Е.Алексеева

Выксунский филиал

Кафедра общеобразовательных и общепрофессиональных дисциплин

Методическое пособие

к выполнению лабораторной работы №2-6

«Магнитное поле соленоида. Датчик Холла»

Для студентов всех специальностей и всех форм обучения ВФ НГТУ

г. Выкса

2009г.

Составители: В.П. Маслов, О.Д. Честнова, С.А.Ковыляев

Определение индукции магнитного поля соленоида на основе закона Био-Савара-Лапласа и с применением датчика Холла. : методическое пособие к выполнению лаб. работы №2-6 по дисциплине «Физика» для студентов всех специальностей и всех форм обучения ВФ НГТУ; сост.: В.П.Маслов и др. г.Н.Новгород, 2009. -9с.

Дана методика определения индукции магнитного поля соленоида на основе закона Био-Савара-Лапласа и с применением датчика Холла.. При написании использованы описания лабораторных работ НГТУ, МАИ, МИФИ, СФТИ и др. вузов.

Научный редактор А.А. Радионов

Редактор Э.Б. Абросимова

Подписано в печать Формат 60х48 1/16. Бумага газетная.

Печать офсетная. Усл. п. л. 0,75. Уч.-изд. л. 0,75. Тираж 200 экз. Заказ 14.

Нижегородский Государственный Технический Университет им. Р.Е.Алексеева

Типография НГТУ. 603950, ГСП-41, г. Нижний Новгород, ул. Минина, 24.

© Нижегородский государственный технический

университет им. Р.Е.Алексеева, 2009

Цель работы: ознакомиться с определением индукции магнитного поля соленоида на основе закона Био-Савара-Лапласа и с применением датчика Холла.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

В пространстве, окружающем проводники с током, движущиеся заряды, магниты, возникает магнитное поле, которое можно обнаружить по воздействию его на другой проводник с током или магнитную стрелку. Магнитное поле в каждой точке пространства количественно может быть описано с помощью вектора напряженности магнитного поля или с помощью вектора индукции магнитного поля . В вакууме векторы и связаны соотношением:

, (1)

где μ₀ = 4π·10 ^-7 Гн/м — магнитная постоянная.

Единицы измерения и А/м и Тл соответственно. В среде с магнитной проницаемостью μ

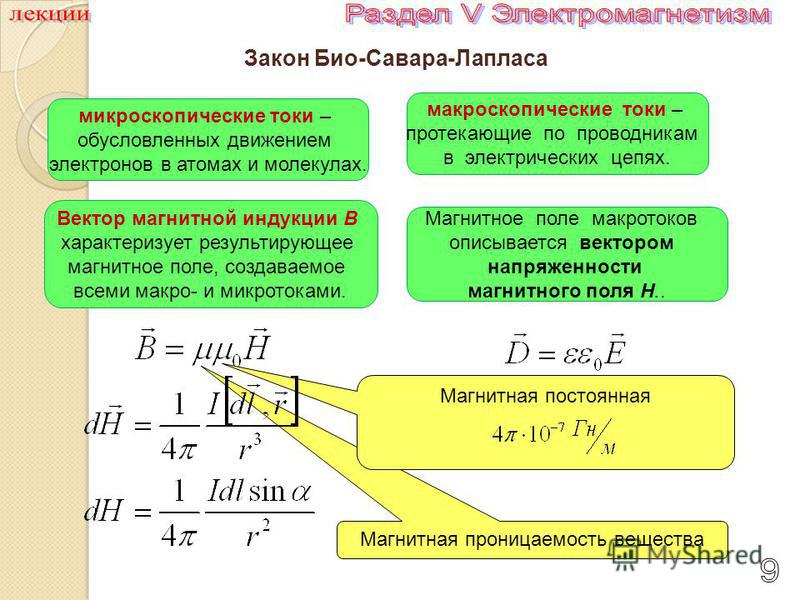
Для вычисления напряженности и индукции магнитного поля, используют закон Био-Савара-Лапласа, согласно которому элементарная напряженность магнитного поля , создаваемая элементом проводника с током в некоторой точке пространства на расстоянии , определяется выражением:

, (2)

где – единичный вектор, направленный вдоль .

Модуль вектора:

,

где – угол между векторами и .

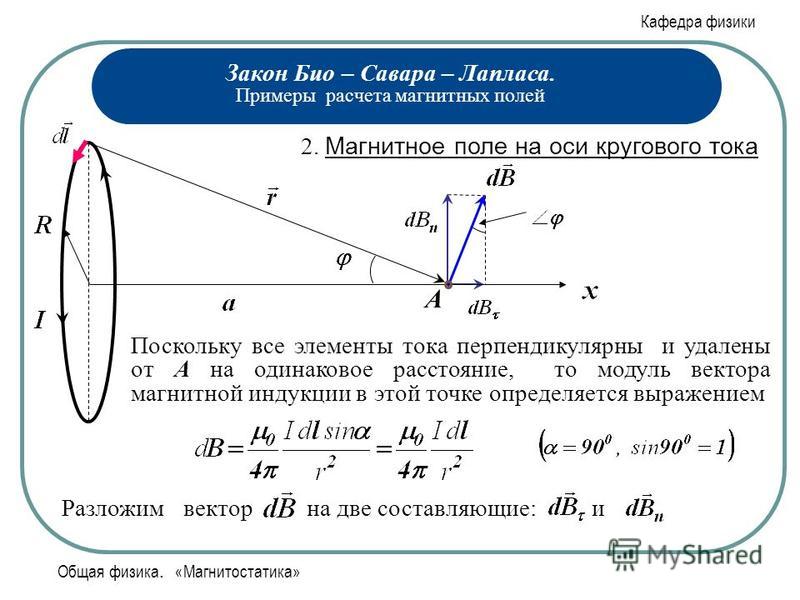
Для нахождения результирующей напряженности, создаваемой проводником конечных размеров, надо воспользоваться принципом суперпозиции магнитных полей и найти векторную сумму элементарных напряженностей от всех элементов проводника. Применим формулу (2) для вычисления напряженности магнитного поля на оси кругового витка с током (рис.1).

На рис.1 компонента , созданная элементом тока , согласно (2) определяется как

,

где учтено, что угол между и прямой. Из симметрии элементов витка по отношению к точке А видно, что результирующая напряженность магнитного поля направлена вдоль оси так, что , то есть

.

В правой части последней формулы все-величины, кроме , постоянны (для данной точки А), поэтому интегрирование no дает

,

или согласно рис. 1

(3)

Величину можно найти по формуле (1).

Вывод формулы для напряженности и индукции магнитного поля на оси соленоида (на расстоянии z от средней точки на оси)

Пусть на единицу длины соленоида приходится n витков (рис.2), тогда участок содержит витков, которые, согласно (3), в точке А на оси создадут напряженность

. (4)

На рис.2 – длина соленоида, а — радиус витков обмотки, 0 -центральная точка на оси соленоида. ОА=

z – координата точки А.

На рис. 3 отдельно изображены элементы dz, радиус-вектор и углы и . Из геометрических построений рис.2 и 3 следует:

; ; .

Подставим эти соотношения в (4) и проинтегрируем по в пределах от до :

.

Учитывая, что , получим

(5)

В случае бесконечно длинного соленоида () в центральной точке 0 ,

. (6)

Из (5) также следует, что при переходе от центра к краю полубесконечного соленоида (на краю z=0,5L, α

1=π/2, α₂→0) напряженность уменьшается вдвое:

. (7)

Индукцию, магнитного поля получим, добавив к выражениям (5), (б), (7) формулу (1). Отметим, что вывод формулы (6) для бесконечно длинного соленоида получается существенно проще на основе закона полного тока.

Курс физики (Грабовский Р.И.)

Курс физики (Грабовский Р.И.)

Грабовский Р.И. Курс физики. Учеб. пособие для с/х ин-тов. Изд. 4-е, перераб. и доп. М., «Высш. школа», 1974. — 552 с. Учебник составлен в соответствии с программой по физике для сельскохозяйственных институтов. В нем приводится достаточное количество примеров, связанных с агробиологическими науками и сельскохозяйственным производством. Настоящее издание (3-е вышло в 1970 г.) отличается от предыдущих некоторыми (небольшими по объему) дополнениями и изменениями, способствующими улучшению содержания. Предназначается для студентов неинженерных факультетов сельскохозяйственных вузов. Многие разделы учебника могут быть использованы и студентами инженерных факультетов. Оглавление Предисловие Введение § 1. Предмет физики. Связь физики с другими науками и производством § 2. О единицах измерения и размерности физических величин § 3. О некоторых математических понятиях и символах 1. Физические основы механики § 4. Общий случай криволинейного движения материальной точки; основные характеристики движения § 5. Прямолинейное движение материальной точки § 6. Движение материальной точки по окружности Глава II. Основные законы динамики § 7. Законы Ньютона. Масса и сила § 8. Закон изменения количества движения (импульса) § 9. Закон сохранения количества движения в изолированной системе § 10. Силы упругости § 11. Силы трения § 12. Силы тяготения (гравитационные силы) § 13. Центростремительная сила § 14. Инерциальные и неинерциальные системы отсчета. Силы инерции § 15. Вес тел. Ускорение силы тяжести. Невесомость Глава III. Работа и энергия § 16. Работа и мощность § 17. Энергия § 18. Закон сохранения и превращения энергии § 19. О космических скоростях § 20. Границы применимости классической механики Глава IV. Вращательное движение твердого тела § 21. Основной закон динамики вращения § 22. Моменты инерции некоторых тел § 23. Закон сохранения момента количества движения. Кинетическая энергия вращающегося тела Глава V. Движение жидкости § 24. Основные определения. Уравнение неразрывности § 25. Уравнение Бернулли § 26. О некоторых приложениях уравнения Бернулли Глава VI. Колебания и волны § 27. Гармоническое колебание и его характеристики § 28. Сложение гармонических колебаний § 29. Динамика колебательного движения. Маятник § 30. О затухающих и вынужденных колебаниях § 31. Волновой процесс § 32. Уравнение волны. Интенсивность волны § 33. Интерференция волн. Стоячие волны § 34. Фронт волны. Принцип Гюйгенса-Френеля 2. Молекулярная физика и термодинамика § 35. Основные положения молекулярно-кинетической теории § 36. О некоторых явлениях, подтверждающих основные положения молекулярно-кинетической теории § 37. О теплоте и температуре § 38. О предмете и методах молекулярной физики Глава VIII. Газы § 39. Экспериментальные газовые законы: Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро. Абсолютная температура § 40. Уравнение Клапейрона — Менделеева. Универсальная газовая постоянная § 41. Основное уравнение кинетической теории идеального газа § 42. Средняя кинетическя энергия поступательного движения молекулы идеального газа § 43. О числе степеней свободы. Внутренняя энергия газа § 44. Теплоемкости газа. Физический смысл универсальной газовой постоянной § 45. Скорость поступательного движения молекул газа. Распределение числа молекул по скоростям § 46. Средняя длина свободного пробега молекул § 47. Явления переноса в газах. Уравнение переноса § 48. Диффузия § 49. Теплопроводность § 50. Внутреннее трение (вязкость) Глава IX. Жидкости и твердые тела § 51. Особенности строения жидкостей и твердых тел § 52. Деформация твердого тела § 53. Тепловое расширение твердых и жидких тел § 54. Теплоемкость твердых и жидких тел § 55. Диффузия в жидких и твердых телах § 56. Осмос § 57. Теплопроводность жидких и твердых тел § 58. Вязкость жидкости. Турбулентное движение жидкости § 59. Внутреннее давление в жидкости. Поверхностное натяжение и свободная энергия поверхности жидкости § 60. Дополнительное давление под искривленной поверхностью жидкости. Формула Лапласа § 61. Капиллярные явления; формула Жюрена Глава X. Изменение агрегатного состояния вещества (фазовые превращения) § 62. Понятие о фазовых превращениях и диаграмме состояний вещества § 63. Реальный газ. Уравнение Ван-дер-Ваальса § 64. Опыт Эндрюса. Критическая температура § 65. Сжижение газов. Эффект Джоуля-Томсона § 66. Испарение и конденсация. Кипение § 67. Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором § 68. Плавление и затвердевание (кристаллизация). Возгонка Глава XI. Основы термодинамики § 69. О некоторых общих понятиях термодинамики. Первое начало термодинамики § 70. Работа, совершаемая при изменении объема газа. Адиабатические процессы § 71. Цикл Карно. Второе начало термодинамики § 72. Энтропия § 73. О статистическом смысле энтропии и второго начала термодинамики 3. Электричество и магнетизм § 74. Электризация тел. Электрический заряд § 75. Взаимодействие электрических зарядов в вакууме. Электрическое поле и его напряженность § 76 Электрический диполь. 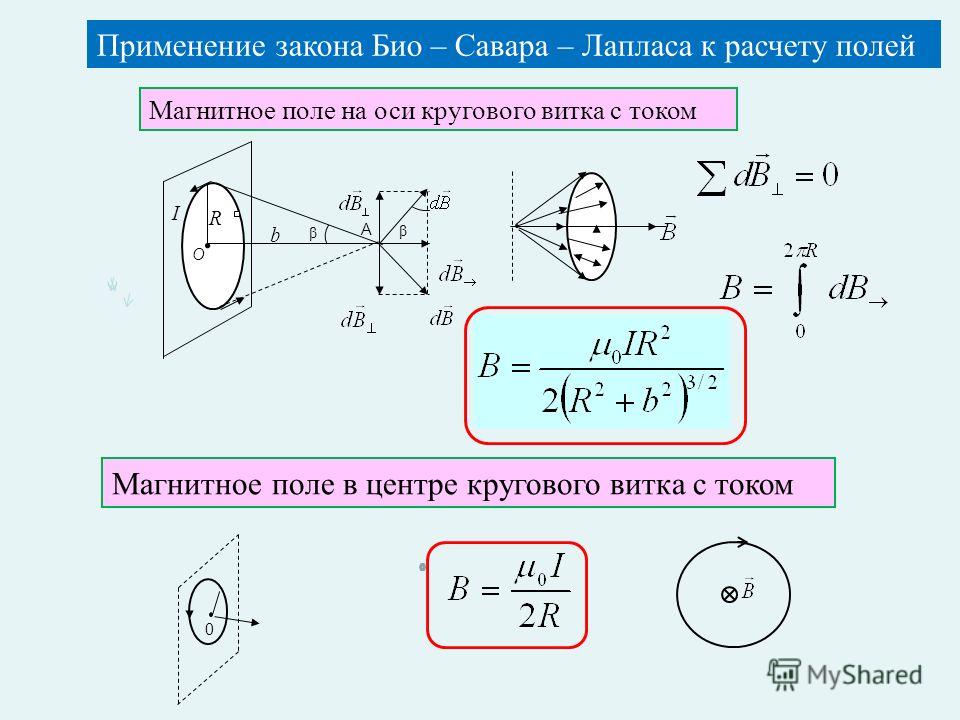Поле диполя § 77. Теорема Остроградского-Гаусса и ее приложения § 78. Работа перемещения заряда в электрическом поле. Потенциал § 79. О неустойчивости статических систем электрических зарядов § 80. Проводники в электрическом поле. Электроемкость. Энергия заряженного проводника § 81. Диэлектрики в электрическом поле. Поляризация диэлектриков § 82. Электрическое поле в диэлектрике. Диэлектрическая проницаемость. Вектор электрической индукции § 83. Конденсатор. Энергия электрического поля Глава XIII. Постоянный электрический ток § 84. Электрический ток. Сила тока. Электродвижущая сила. Напряжение § 85. Ток в металлических проводниках. Сопротивление. Законы Ома. Работа и мощность тока § 86. Разветвленная электрическая цепь. Правила Кирхгофа § 87. Контактная разность потенциалов. Термоэлектрические явления § 88. Эмиссия электронов. Термоэлектронная эмиссия. Электронные лампы § 89. Ток в полупроводниках. Собственная и примесная проводимости полупроводников § 90. Запирающий слой. Полупроводниковые выпрямители, усилители и термоэлектрические батареи § 91. Ток в жидкостях. Электролиз. Законы Фарадея § 92. Ток в газах. Несамостоятельный и самостоятельный газовые разряды § 93. Типы самостоятельного газового разряда Глава XIV. Электромагнетизм § 94. Постоянный магнит и круговой ток. Магнитные поля магнитов и токов § 95. Магнитное взаимодействие токов в вакууме; закон Ампера § 96. Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа § 97. Некоторые приложения закона Био-Савара-Лапласа § 98. Магнитные поля соленоида и тороида § 99. Диамагнитные, парамагнитные и ферромагнитные вещества. Магнитная проницаемость. Магнитная индукция. Поток магнитной индукции § 100. Действие магнитного поля на проводник с током. Определение ампера § 101. Движение заряженных частиц в электрическом и магнитном полях. Определение удельного заряда и массы электрона § 102. О некоторых приборах и установках, основанных на движении заряженных частиц в электрическом и магнитном полях Глава XV. Электромагнитная индукция и переменный ток § 103. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Токи Фуко § 104. Взаимная индукция и самоиндукция § 105. Энергия магнитного поля. Понятие об электромагнитной теории Максвелла § 106. Контур, вращающийся в магнитном поле. Синусоидальный переменный ток. Работа и мощность переменного тока § 107. Емкостное и индуктивное сопротивления § 108. Обобщенный закон Ома. Электрический резонанс. Коэффициент мощности электрической цепи § 109. Понятие о трехфазном токе Глава XVI. Электрические колебания и электромагнитные волны § 110. Электромагнитные волны § 111. Закрытый колебательный контур § 112. Вибратор Герца. Автоколебательный контур. О диапазоне частот электромагнитных волн § 113. Радиосвязь 4. Оптика и атомная физика § 114. Природа света § 115. Отражение и преломление света. Полное отражение § 116. Дисперсия света. Спектры § 117. Тонкие линзы. Микроскоп § 118. Глаз как оптическая система. Спектральная чувствительность глаза § 119. Основные фотометрические характеристики § 120. Поглощение света. О физиологическом действии света Глава XVIII. Волновые свойства света § 121. Интерференция света. Интерферометр § 122. Об интерференции света, отраженного от прозрачных пленок § 123. Дифракция света. Разрешающая способность оптических приборов § 124. Дифракция от щелей. Дифракционные спектры. Дифракционная решетка. О рассеянии света в мутной среде § 125. Дифракция рентгеновских лучей. Формула Вульфа-Брэггов § 126. О дифракции микрочастиц и волнах де-Бройля § 127. Поляризация света. Естественный и поляризованный свет. Поляризация света в турмалине. Поляроиды § 128. Двойное лучепреломление. Поляризация света в исландском шпате. Призма Николя 129. Вращение плоскости колебаний поляризованного света. Поляриметр Глава XIX. Квантовые свойства света и строение атома § 130. Тепловое лучеиспускание и лучепоглощение. Абсолютно черное тело. 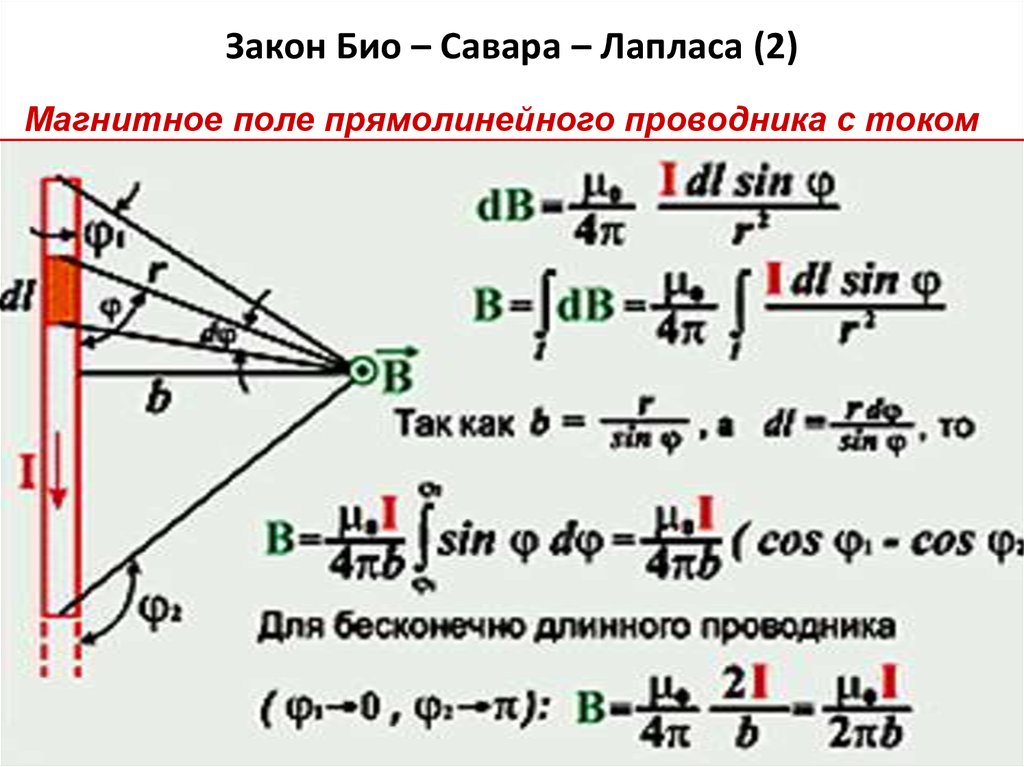Закон Кирхгофа § 131. Законы излучения абсолютно черного тела. Квантовый характер излучения. Формула Планка § 132. Строение атома (ядерная модель). Дискретность энергетических состояний атома. Постулаты Бора § 133. Квантовая теория строения атома водорода (по Бору). Объяснение спектров излучения и поглощения водорода § 134. Понятие о строении многоэлектронных атомов и образовании оптических и рентгеновских (характеристических) спектров § 135. Люминесценция. Законы фотолюминесценции и некоторые ее практические применения § 136. Фотоэффект. Законы фотоэффекта. Фотоэлементы § 137. Масса и импульс фотона. Световое давление. Эффект Комптона. Флуктуации света Глава XX. Атомное ядро и внутриядерные процессы § 138. Общие сведения об атомных ядрах. Изотопы § 139. Естественная радиоактивность. Альфа-, бета- и гамма-лучи. Законы радиоактивного распада § 140. О методах наблюдения и регистрации микрочастиц § 141. Ядерные реакции. Искусственная радиоактивность § 142. Энергия связи и дефект массы атомного ядра § 143. Реакция деления. Цепная реакция. Ядерный реактор § 144. Реакция синтеза (термоядерная реакция). Энергия звезд § 145. Космические лучи. Элементарные частицы § 146. Об использовании ядерной энергии

Закон Био-Савара | Определение, формула, диаграммы и факты

магнитное поле от токовой петли

Посмотреть все СМИ

Ключевые люди:

Жан-Батист Био

Похожие темы:

электромагнитная индукция сахариметрия

Просмотреть весь связанный контент →

Закон Био-Савара , в физике фундаментальное количественное соотношение между электрическим током I и создаваемое им магнитное поле B на основе экспериментов 1820 года французских ученых Жана-Батиста Био и Феликса Савара.

Ток в петле создает линии магнитного поля B , которые образуют петли вокруг тока. Закон Био-Савара выражает частичный вклад d B небольшого отрезка проводника в полное B поле тока в проводнике. Для отрезка проводника длиной и ориентацией d l that carries a current i , d B = ^{μ ₀} / _4π ^{I d l × r̂} / _{r ²} .В этом уравнении μ ₀ представляет собой проницаемость свободного пространства и имеет значение 4π × 10 ⁻⁷ ньютона на квадратный ампер.

Britannica Quiz

Электричество: короткие замыкания и постоянные токи

Это уравнение проиллюстрировано для небольшого отрезка провода, по которому течет ток, так что в начале системы координат небольшой отрезок провода длиной d l лежит вдоль оси x . Сравнение d B в точках 1 и 2 показывает обратную квадратическую зависимость величины поля от расстояния. Векторы в точках 1, 3 и 4, находящихся на одинаковом расстоянии от d l , показать направление d B по кругу вокруг провода. В положении 1 вклад в поле d B ₁ перпендикулярен как направлению тока, так и вектору r ₁ . Наконец, векторы 1, 5, 6 и 7 иллюстрируют угловую зависимость величины d B в точке. Величина d B varies as the sine of the angle between d l and r̂ , where r̂ is in the direction from d l к точке. Он наиболее силен под углом 90° к d l и уменьшается до нуля для местоположений, расположенных непосредственно на линии с d l . Магнитное поле тока в контуре или катушке получают суммированием отдельных парциальных вкладов всех участков контуров с учетом векторного характера поля. Хотя простые математические выражения для магнитного поля могут быть получены для нескольких текущих конфигураций, для большинства практических приложений требуется использование высокоскоростных компьютеров.

The expression for the magnetic field B a distance r from a long straight wire with current I is B = ^{μ ₀ I} / _{2π r} θ, где θ — единичный вектор, указывающий на окружность вокруг провода. То есть значение магнитного поля B в точке рядом прямо пропорционально значению тока I и обратно пропорционально перпендикулярному расстоянию r от провода до заданной точки. ( Сравните Закон Ампера.)

Редакция Британской энциклопедии Эта статья была недавно отредактирована и дополнена Эриком Грегерсеном.

Что такое Закон Био-Савара? Узнать определение, формулу и приложения

Дом »Физика

Гурприт Сингх | Обновлено: 14 февраля 2023 г. 9:34 IST

0

Сохранить

Скачать публикацию в формате PDF

Закон Био-Савара — это специфический электромагнетизм физики, это математическое выражение, объясняющее магнитное поле, создаваемое постоянным электрическим током. Этот закон является центральным для магнитостатики и играет существенную роль в электростатике, связанной с законом Кулона.

Внимательно прочтите эту статью, чтобы понять формулу закона Био-Савара и ее применение.

Что такое закон Био–Савара?

Закон Био-Савара — это уравнение, которое описывает магнитное поле, создаваемое постоянным электрическим током, и связывает магнитное поле с величиной, направлением, длиной и близостью электрического тока. Он дает соотношение напряженности магнитного поля, создаваемого его компонентом источника тока.

Жан Батист Био и Феликс Савар провозгласили это правило в 1820 году.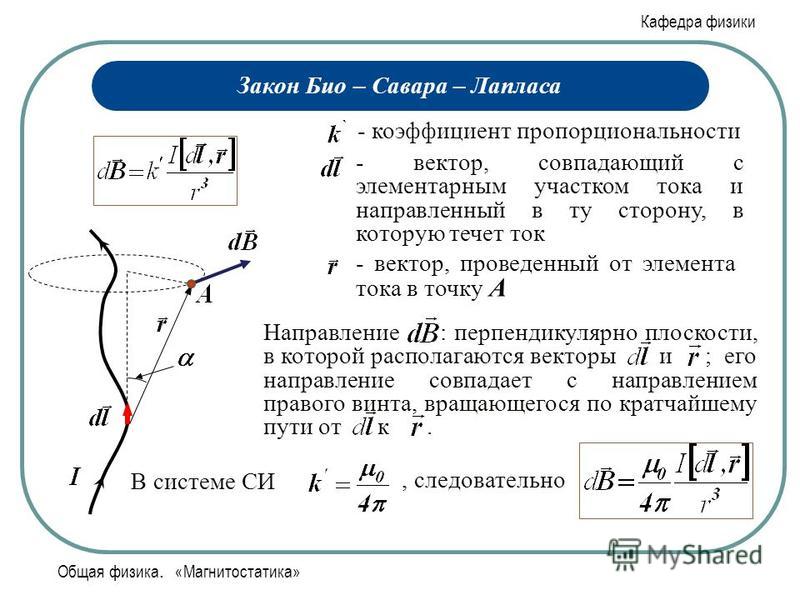 Направление магнитного поля подчиняется законам правой руки для прямого провода. Правило Био Савара также считается законом Лапласа или законом Ампера. Эти два ученых предположили, глядя на отклонение стрелки магнитного компаса, что любой существующий компонент излучает магнитное поле в окружающее его пространство.

Формула закона Био-Савара

Рассмотрим провод, по которому течет электрический ток I, находящийся на расстоянии x от точки A и провод бесконечно малой длины dl.

Био Закон Савара гласит, что: в точке A напряженность магнитного поля dH связана с током I, протекающим через небольшой элемент dl:

1. Прямо пропорциональна току (I), длине элемента ( dl), синус угла θ между направлением тока и линией, соединяющей элемент dl из точки A.
2. Обратно пропорциональна квадрату расстояния (x) точки A от элемента dl.

Здесь k постоянно и зависит от магнитных свойств среды.

Здесь µ0 – абсолютная проницаемость воздуха или вакуума, и ее значение составляет 4 x 10-7 Вб/А-м, а µr – относительная проницаемость среды.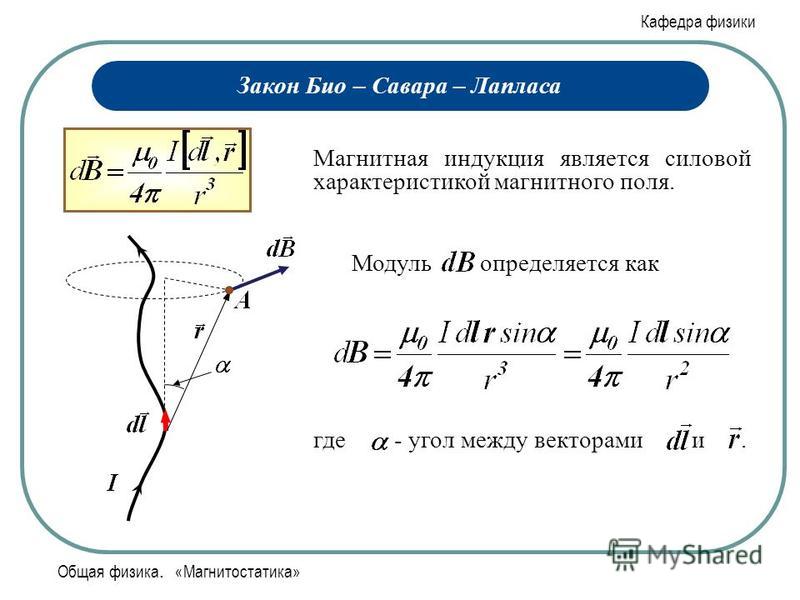

Направление магнитного поля всегда перпендикулярно линии элемента и вектору положения на плоскости. Это дается правилом большого пальца правой руки, где большой палец указывает на обычное направление тока, а остальные пальцы показывают направление магнитного поля.

Применение закона Био-Савара

Это правило можно использовать даже на химической или ядерной стадии для расчета магнитных реакций. Его можно использовать для оценки желаемой скорости вихревых линий в аэродинамической теории. Правило Био-Савара идентично электростатическому закону Кулона. Этот закон часто применяется к очень маленьким проводникам, по которым течет ток. Закон распространяется на распределение симметричного тока.

Заключение

Наконец, из приведенной выше информации мы можем сделать вывод, что этот закон можно использовать для расчета магнитного поля, создаваемого элементом тока. Однако это правило используется для оценки магнитного поля из-за некоторых условий, таких как вращающийся провод, диск или участок линии.