Закон Био-Савара-Лапласа. Вывод формулы для напряженности и индукции магнитного поля на оси кругового витка с током.
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
Нижегородский Государственный Технический Университет им. Р.Е.Алексеева
Выксунский филиал
Кафедра общеобразовательных и общепрофессиональных дисциплин
Методическое пособие
к выполнению лабораторной работы №2-6
«Магнитное поле соленоида. Датчик Холла»
Для студентов всех специальностей и всех форм обучения ВФ НГТУ
г. Выкса
2009г.
Составители: В.П. Маслов, О.Д. Честнова, С.А.Ковыляев
Определение
индукции магнитного поля соленоида на
основе закона Био-Савара-Лапласа и с
применением датчика Холла. : методическое
пособие к выполнению лаб. работы №2-6 по
дисциплине «Физика» для студентов всех
специальностей и всех форм обучения ВФ
НГТУ; сост.: В.П.Маслов и др. г.Н.Новгород,
2009. -9с.
: методическое
пособие к выполнению лаб. работы №2-6 по
дисциплине «Физика» для студентов всех
специальностей и всех форм обучения ВФ
НГТУ; сост.: В.П.Маслов и др. г.Н.Новгород,
2009. -9с.
Дана методика определения индукции магнитного поля соленоида на основе закона Био-Савара-Лапласа и с применением датчика Холла.. При написании использованы описания лабораторных работ НГТУ, МАИ, МИФИ, СФТИ и др. вузов.
Научный редактор А.А. Радионов
Редактор Э.Б. Абросимова
Подписано в печать Формат 60х48 1/16. Бумага газетная.
Печать офсетная. Усл. п. л. 0,75. Уч.-изд. л. 0,75. Тираж 200 экз. Заказ 14.
Нижегородский Государственный Технический Университет им. Р.Е.Алексеева
Типография НГТУ. 603950, ГСП-41, г. Нижний Новгород, ул. Минина, 24.
© Нижегородский государственный технический
университет им. Р.Е.Алексеева, 2009
Р.Е.Алексеева, 2009
Цель работы: ознакомиться с определением индукции магнитного поля соленоида на основе закона Био-Савара-Лапласа и с применением датчика Холла.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
В пространстве, окружающем проводники с током, движущиеся заряды, магниты, возникает магнитное поле, которое можно обнаружить по воздействию его на другой проводник с током или магнитную стрелку. Магнитное поле в каждой точке пространства количественно может быть описано с помощью вектора напряженности магнитного поля или с помощью вектора индукции магнитного поля . В вакууме векторы и связаны соотношением:
, (1)
где μ0 = 4π·10 -7 Гн/м — магнитная постоянная.
Единицы измерения и А/м и Тл соответственно. В среде с магнитной проницаемостью μ
Для вычисления напряженности и индукции магнитного поля, используют закон Био-Савара-Лапласа, согласно которому элементарная напряженность магнитного поля , создаваемая элементом проводника с током в некоторой точке пространства на расстоянии , определяется выражением:
, (2)
где – единичный вектор, направленный вдоль
.
Модуль вектора:
,
где – угол между векторами и .
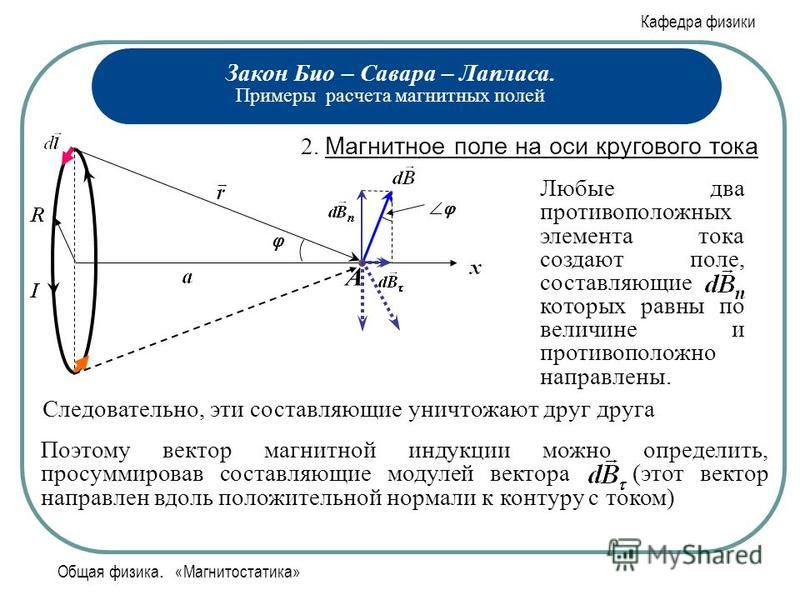
Для нахождения результирующей напряженности, создаваемой проводником конечных размеров, надо воспользоваться принципом суперпозиции магнитных полей и найти векторную сумму элементарных напряженностей от всех элементов проводника. Применим формулу (2) для вычисления напряженности магнитного поля на оси кругового витка с током (рис.1).
На рис.1 компонента , созданная элементом тока , согласно (2) определяется как
,
где учтено, что угол между и прямой. Из симметрии элементов витка по отношению к точке А видно, что результирующая напряженность магнитного поля направлена вдоль оси так, что , то есть
.
В правой части последней формулы все-величины, кроме , постоянны (для данной точки А), поэтому интегрирование no дает
,
или согласно рис. 1
1
(3)
Величину можно найти по формуле (1).
Вывод формулы для напряженности и индукции магнитного поля на оси соленоида (на расстоянии z от средней точки на оси)
Пусть на единицу длины соленоида приходится n витков (рис.2), тогда участок содержит витков, которые, согласно (3), в точке А на оси создадут напряженность
. (4)
На рис. 3 отдельно изображены элементы dz, радиус-вектор и углы и . Из геометрических построений рис.2 и 3 следует:
; ; .
Подставим эти соотношения в (4) и проинтегрируем по в пределах от до :
.
Учитывая, что , получим
(5)
В случае бесконечно длинного соленоида () в центральной точке 0 ,
. (6)
(6)
Из (5) также следует, что при переходе от центра к краю полубесконечного соленоида (на краю z=0,5L, α1=π/2, α2→0) напряженность уменьшается вдвое:
. (7)
Индукцию, магнитного поля получим, добавив к выражениям (5), (б), (7) формулу (1). Отметим, что вывод формулы (6) для бесконечно длинного соленоида получается существенно проще на основе закона полного тока.
Закон Био-Савара. Теорема о циркуляции
Французские ученые Ж. Био и Ф. Савар в 1820-м году проводили эксперименты над магнитным полем постоянных токов. Физики доказали, что индукция магнитного поля проходящих по проводнику токов зависит от совместного действия всех участков данного проводника. Работа магнитного поля основана на принципе суперпозиции.
Принцип суперпозиции: если магнитное поле работает за счет нескольких проводников с током, тогда индукция результативного поля – это совокупность индукций полей, которые создаются каждым проводником по отдельности.
Индукция B→ проводника с током представлена, как векторная сумма элементарных индукций ∆B→ вырабатываемых отдельными участками проводника. На практике нельзя отделить один участок проводника с током, поскольку постоянные токи всегда замкнутые. Возможно лишь измерить совокупную индукцию магнитного поля, которое создают все элементы тока. Как найти индукцию магнитного поля?
Закон Био–Савара
Определение 2Закон Био-Савара определил вклад ∆B→ в магнитную индукцию B→ результативного магнитного поля, образуемый маленьким участком Δl проводника с током I.
∆B=μ0·I·∆l·sin α4πr2.
В формуле r – это расстояние от заданного участка Δl до точки наблюдения, α – это угол между направлением на точку наблюдения и направлением тока на заданном участке, μ0 – это магнитная постоянная.
Используя правило буравчика, определим направление вектора ∆B→: оно указывает на ту сторону, в которую вращается рукоятка буравчика при его поступательном движении вдоль тока. Рисунок 1.
B=μ0I2πR.
Рисунок 1.17.1. Иллюстрация закона Био–Савара.
С помощью этого закона можно определять магнитные поля токов с различными конфигурациями. Запросто рассчитать магнитное поле в центре кругового витка с током. Вычисления приводят к соотношению:
B=μ0I2πR,
где R – это радиус кругового проводника.
Чтобы определить направление вектора B→ тоже используется правило буравчика, только в этом случае рукоятка вращается по направлению кругового тока, а поступательное движение буравчика указывает, куда направлен вектор магнитной индукции.
Теорема о циркуляции вектора магнитной индукции
Определение 3Вычисления магнитного поля зачастую упрощаются с учетом симметрии в конфигурации токов. В этом помогает теорема о циркуляции вектора магнитной индукции.
В этом помогает теорема о циркуляции вектора магнитной индукции.
Объясним, что означает циркуляция вектора B→. Допустим, в пространстве с магнитным полем существует какой-то условный замкнутый контур, а также положительное направление его обхода. Тогда, на каждом отдельном маленьком участке Δl данного контура определяется касательная составляющая Bl вектора B→ в этом месте, то есть определяется проекция вектора B→ на направление касательной к заданному участку контура. Рисунок 1.17.2 наглядно демонстрирует это.
Рисунок 1.17.2. Замкнутый контур (L) с заданным направлением обхода. Изображение токов I1,I2 и
I3, создающих магнитное поле.
Циркуляция вектора B→ – это сумма произведений Bl∆l, взятая по целому контуру L: B→=∑(L)Bl∆l.
Некоторые токи, при которых магнитное поле создается, пропускают выбранный контур L тем временем, как остальные токи находятся в стороне от контура.
Теорема 1Согласно теореме о циркуляции, циркуляция вектора B→ магнитного поля постоянных токов по любому из контуров L все время определяется, как произведение магнитной постоянной μ0 на сумму всех токов:
∑(L)Bl∆l=μ0∑li.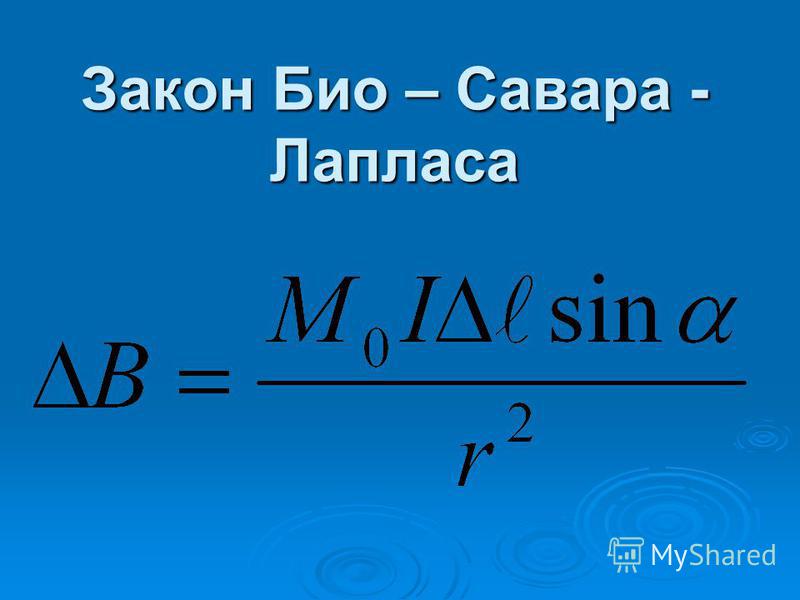
На рисунке 1.17.2 продемонстрирован пример с несколькими проводниками с токами, образующими магнитное поле. Ток I2 и ток I3 пронзают контур L в противоположных направлениях, им приписываются различные знаки. Положительным является ток, который связан с заданным направлением обхода контура по правилу буравчика.
Значит, I3>0, а I2<0. Ток I1 не пронзает контур L.
Теорема о циркуляции в этом примере математически выражается следующей формулой:
∑(L)Bl∆l=μ0(I3-I2).
Общий вид теоремы о циркуляции можно вывести из принципа суперпозиции и закона Био-Савара.
Пример 2Самый простой пример использования теоремы о циркуляции – это вывод формулы магнитного поля прямолинейного проводника с током. С учетом симметрии в этой задаче контуром L лучше выбрать окружность какого-то радиуса R, лежащую в перпендикулярной проводнику плоскости. Центр окружности задан в какой-то точке проводника. Из-за симметрии вектор B→ направляется по касательной (Bl=B), а его модуль имеет одинаковое значение по всей окружности. Использование теоремы о циркуляции приводит к выражению:
Использование теоремы о циркуляции приводит к выражению:
∑(L)Bl∆l=2πRB=μ0I,
отсюда можно вывести формулу для модуля магнитной индукции поля прямолинейного проводника с током, приведенную раньше.
Из данного примера видно, что теорема о циркуляции вектора магнитной индукции B→ можно использовать для вычисления магнитных полей, которые создаются симметричным распределением токов, когда можно наугад определить общую структуру поля.
Существует много примеров определения магнитных полей при помощи теоремы о циркуляции.
Пример 3Рассмотрим одну из них – это задачу расчета поля тороидальной катушки (рисунок 1.17.3).
Рисунок 1.17.3. Использование теоремы о циркуляции к тороидальной катушке.
Предположим, что катушка намотана виток к витку на ненамагниченный тороидальный сердечник. В ней линии магнитной индукции сходятся внутри катушки и выступают концентрическими окружностями. Они имеет такое направление, что, смотря вдоль них, наблюдатель увидел бы ток в витках, циркулирующих по часовой стрелке.
Одна линия индукции какого-то радиуса r1≤r<r2 представлена на рисунке 1.17.3. Используем теорему о циркуляции для контура L в виде окружности, которая совпадает с линией индукции магнитного поля, изображенной на рисунке 1.17.3. Опираясь на соображения о симметрии, делаем вывод, что модуль вектора B→ имеет одинаковое значение по всей линии. Исходя из теоремы о циркуляции, запишем:
B·2πr=μ0IN,
где N – это полное количество витков, а I – это ток, протекающий по виткам катушки. Значит, B=μ0IN2πr.
Так, модуль вектора магнитной индукции в тороидальной катушке находится в зависимости от радиуса r. При условии, что сердечник катушки тонкий, то есть r2–r1≪r, тогда магнитное поле внутри катушки почти однородное.
Величина n=N 2πr – это количество витков на единицу длины катушки. Следовательно, B=μ0In.
Сюда не относится радиус тора, потому оно действует и в предельном случае r→∞.
Определение 5Однако в пределе каждая часть тороидальной катушки при необходимости рассматривается в качестве длинной прямолинейной катушки, которая называется соленоид. Вдали торцов такой катушки модуль магнитной индукции определяется, как соотношение в случае с тороидальной катушкой.
Вдали торцов такой катушки модуль магнитной индукции определяется, как соотношение в случае с тороидальной катушкой.
На рисунке 1.17.4 представлено магнитное поле катушки конечной длины. Обращаем внимание, что в центре катушки магнитное поле почти однородное и намного сильнее, чем снаружи. Это объясняется густотой линий магнитной индукции. В предельном случае бесконечно длинного соленоида однородное магнитное поле полностью находится внутри него.
Рисунок 1.17.4. Магнитное поле катушки конечной длины. В центральной части соленоида магнитное поле почти однородное и существенно больше по модулю поля вне катушки.
В случае с бесконечно длинным соленоидом соотношение для модуля магнитной индукции получаем прямо из теоремы о циркуляции, применяя ее к прямоугольному контуру, изображенному на рисунке 1.17.5.
Рисунок 1.17.5. Теорема о циркуляции при расчете магнитного поля бесконечно длинного соленоида.
Проекция вектора магнитной индукции на направление обхода контура abcd только на стороне ab отлична от 0. Значит, циркуляция вектора B→ по контуру равняется Bl, где l – это длина стороны ab. Количество витков соленоида, пронзающих контур abcd, равняется n·l, где n – это количество витков на единицу длины соленоида, а полный ток, пронзающий контур, равняется Inl. Из теоремы о циркуляции, Bl=μ0Inl.
Значит, циркуляция вектора B→ по контуру равняется Bl, где l – это длина стороны ab. Количество витков соленоида, пронзающих контур abcd, равняется n·l, где n – это количество витков на единицу длины соленоида, а полный ток, пронзающий контур, равняется Inl. Из теоремы о циркуляции, Bl=μ0Inl.
Отсюда B=μ0In.
Данное вычисление совпадает с формулой для магнитного поля тонкой тороидальной катушки.
Рисунок 1.17.6. Модель магнитного поля кругового витка с током.
Рисунок 1.17.7. Модель магнитного поля прямого тока.
Рисунок 1.17.8. Модель магнитного поля соленоида.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.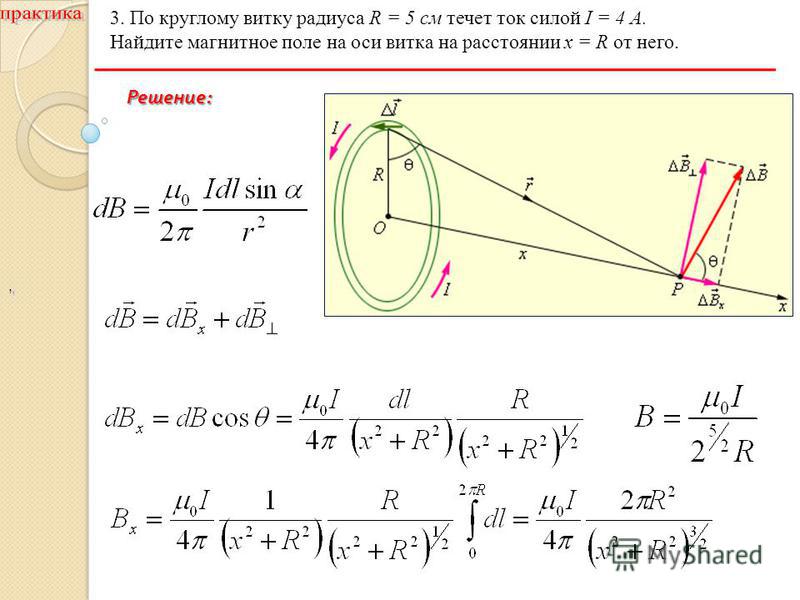 Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает. Динамика и детерминанты показателей газоанализа юных спортсменов в восстановительном периоде после лабораторных нагрузок до отказа… Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования… Интересное: Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является… Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски… Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 8 из 8 Закон Био Савара Лапласа определяет величину модуля вектора магнитной индукции в точке выбранной произвольно находящейся в магнитном поле. 38,48. Рассмотреть движение электрона в однородном магнитном поле в двух случаях: а) скорость электрона перпенд. Рассмотрим частный случай, когда нет электрического поля, но имеется магнитное поле. Предположим, что частица, обладающая начальной скоростью V0, попадает в магнитное поле с индукцией B. Это поле мы будем считать однородным и направленным перпендикулярно к скорости V0. Действующая на частицу сила Лоренца всегда перпендикулярна к скорости движения частицы. Это значит, что работа силы Лоренца всегда равна нулю; следовательно, абсолютное значение скорости движения частицы, а значит, и энергия частицы остаются постоянными при движении. Так как скорость частицы V не изменяется, то величина силы Лоренца остается постоянной. Эта сила, будучи перпендикулярной, к направлению движения, является центростремительной силой. Но движение под действием постоянной по величине центростремительной силы есть движение по окружности. Радиус r этой окружности определяется условием , откуда . ⇐ Предыдущая12345678 Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… |
Закон Био–Савара • Джеймс Трефил, энциклопедия «Двести законов мироздания»
200 законов мироздания > Физика
Магнитное поле в точке пространства, создаваемое малым отрезком проводника, по которому течет электрический ток, пропорционально силе тока, обратно пропорционально квадрату расстояния от этой точки до проводника и направлено перпендикулярно по отношению и к току, и к направлению на проводник.
Одним из величайших прорывов в естествознании XIX века стала серия открытий, позволивших установить неразрывную связь между двумя, казалось бы, не связанными между собой природными феноменами — электричеством и магнетизмом, — которые на поверку оказались просто двумя сторонами одной медали. Одним из первых фрагментов пазла, который предстояло собрать ученым, стало осознание того, что движущиеся электрические заряды (то есть электрический ток) могут порождать магнитное поле. Это открытие сделал датский ученый Ханс Кристиан Эрстед (см. открытие Эрстеда), а представил его в количественной форме французский ученый Андре-Мари Ампер (см. Закон Ампера). Обобщением этой работы стал закон Био—Савара (его еще называют «закон Био—Савара—Лапласа». — Прим. переводчика), содержащий окончательную формулировку соотношения между электрическими токами и магнитными полями, которые они производят.
Жан Батист Био, яркий и смелый ученый, был профессором физики в Сорбонне и действительным членом французской Академии наук. Сразу после открытия Эрстеда вместе со своим коллегой Феликсом Саваром он принялся за изучение взаимосвязи между электрическим током и магнитными полями.
Сразу после открытия Эрстеда вместе со своим коллегой Феликсом Саваром он принялся за изучение взаимосвязи между электрическим током и магнитными полями.
В отличие от Ампера, изучавшего магнитные поля опосредованно, путем измерения силы взаимодействия между парами проводников с током, Био и Савар предприняли прямые измерения магнитных полей, используя для этого множество легких магнитных стрелок компасов. Смысл их закона проще всего понять, если представить себе, что проводник с током разбит на крошечные отрезки — т. н. элементы тока (такой подход предложил ученым их старший коллега Пьер Симон Лаплас (Pierre-Simon Laplace, 1749–1827), стоявший у истоков дифференциального и интегрального исчисления, который затем и обобщил полученные результаты. — Прим. переводчика). На каждом из этих крошечных отрезков кривизной проводника можно пренебречь — их можно рассматривать как отрезки прямой. Так вот, согласно закону Био—Савара, магнитное поле В на расстоянии r от такого элемента тока пропорционально
IL/r2
где I — сила тока, а L — длина элемента тока.
Я уже упоминал, что закон Био—Савара является наиболее полным формальным обобщением взаимосвязи между электрическим током и магнитным полем. Это значит, что можно взять проводник с током сколь угодно сложной и асимметричной конфигурации и разбить его на элементы тока. Каждый элемент вносит свой вклад в магнитное поле в рассчитываемой точке. Сделав эти расчеты, мы можем затем просуммировать вклад от каждого элемента проводника и найти общее магнитное поле (этот процесс суммирования относится к области высшей математики и выглядит он достаточно сложно). Таким образом, закон Ампера является частным случаем закона Био—Савара для случая линейного проводника.
Я еще не сказал, что закон Био—Савара предсказывает также направление получающегося магнитного поля. Это направление можно определить с помощью так называемого правила правой руки, ставшего настоящим бичом целых поколений студентов физических и технических вузов. Правило гласит: если вытянутый указательный палец правой руки показывает направление электрического тока в элементе тока, а средний палец направлен на точку, в которой вы вычисляете магнитное поле, то выставленный под прямым углом к двум другим пальцам большой палец укажет направление магнитного поля.
Как я уже говорил, полное математическое выражение закона Био—Савара требует довольно сложных вычислений, поскольку оно представляет собой интегральное уравнение. Оно является, по сути, общим решением четвертого уравнения Максвелла.
См. также:
1864 | Уравнения Максвелла |
1879 | Эффект Холла |
Феликс САВАР
Félix Savart, 1791–1841
Французский врач и физик. Родился в Мезьере. Получив медицинское образование, Савар, тем не менее, поступил на работу в Коллеж де Франс в качестве профессора акустики. Там он изучал принцип работы музыкальных инструментов, прежде всего скрипки, на примере колебаний песчаных волн в слое песка на плоской поверхности, отражающих акустические колебания. Кроме того, он изобрел колесо Савара для точного измерения высоты музыкальных тонов и кварцевую пластину Савара для изучения поляризации света.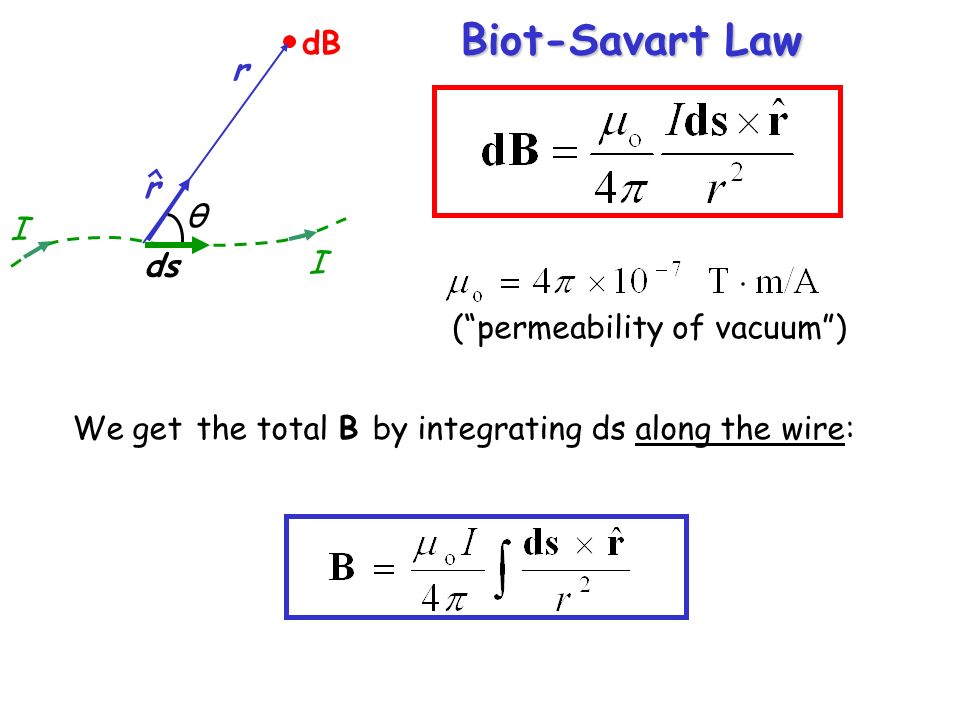 Однако самая известная работа ученого — его сотрудничество с Био, вылившееся в закон Био—Савара.
Однако самая известная работа ученого — его сотрудничество с Био, вылившееся в закон Био—Савара.
Жан Батист БИО
Jean-Baptiste Biot, 1774–1862
Французский физик. Родился в Париже, вырос в годы Великой французской революции и до начала занятий физикой успел отслужить в армии. Затем стал одним из первых студентов только что открытой Парижской политехнической школы, по окончании которой продолжал заниматься академической наукой, со временем заняв должность профессора физики в Коллеж де Франс в Париже. В 1803 году был командирован Министерством внутренних дел для расследования обстоятельств метеоритного дождя в городок Эгль. Ему впервые удалось доказать, что метеориты имеют внеземное происхождение и в буквальном смысле падают к нам с неба (в то время в это практически не верили). На следующий год Био вместе с Жозефом Луи Гей-Люссаком (Joseph-Louis Gay-Lussac, 1778–1850) впервые в истории поднялся в воздух на воздушном шаре в научно-исследовательских целях — для изучения характеристик магнитного поля Земли на больших высотах. 2/R
2/R
Ответить
Написать комментарий
1785 | Закон Кулона |
1820 | Открытие Эрстеда |
1820 | Закон Ампера |
1820 | Закон Био—Савара |
1831 | Законы электромагнитной индукции Фарадея |
1833 | Правило Ленца |
1662
Закон Бойля—Мариотта
III в. до н. э.
Закон Архимеда
Новостная рассылка
«Элементы» в соцсетях:
Обратная связь ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса — ваш вокал Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими Целительная привычка Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Тренинг уверенности в себе Вкуснейший «Салат из свеклы с чесноком» Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Как слышать голос Бога Классификация ожирения по ИМТ (ВОЗ) Глава 3. Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д. Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. |
Значение магнитной индукции для любого проводника определяется законом Био — Савара — Лапласа. Рис. 15.8.
-в векторной форме, (15.6) — в скалярной форме. (15.7) Вектор всегда перпендикулярен плоскости, построенной на векторах и . С помощью закона Био — Савара — Лапласа рассчитаем магнитную индукцию поля прямого, кругового и соленоидального токов. Вывод формулы напряжённости магнитного поля прямого тока (рис. 15.9; рис. 15.10) . Применим формулу для вычисления полей простейших токов. Рассмотрим поле, создаваемое током, текущим по бесконечному прямому проводу (Рис. 15.9) .Все dBв данной точке имеют одинаковое направление. Поэтому сложение векторов dBможно заменить сложением их модулей. Точка, для которой мы вычисляем магнитную индукцию, находится на расстоянии b от провода. Из рисунка 15.9 видно, что: Рис. 15.9.
Подставим эти значения в формулу магнитной индукции: . Угол для всех элементов бесконечно прямого тока изменяется в пределах от 0 до . . Таким образом, магнитная индукция поля прямого тока определяется формулой: . (15.8 ) Для того, чтобы получить напряженность магнитного поля, необходимо разделить правую часть формулы (15.8) на : . (15.9) Рис. 15.10
Вывод формулы напряжённости магнитного поля кругового тока (рис. 15.11). Рассмотрим поле, создаваемое током, текущим по тонкому проводу, имеющему форму окружности (круговой ток). Определим магнитную индукцию кругового тока Рис. 15.11 Рассмотрим индукции , создаваемых двумя элементами контура dl1 и dl2. Т. к. угол между r и dl равен 90°, то sin 90°=1. Закон Био — Савара — Лапласа для двух элементов: Выбрав dl1=dl2 и принимая, что r1=r2, получим: Проинтегрируем это выражение по всему контуру и заменим r на получим: (15. В частности, при x=0 имеем: (15.11) магнитная индукция в центре кругового тока Напряженность магнитного поля в центре кругового тока равна:
(15.12) Формула для расчета напряженности магнитного поля кругового тока на его оси принимает вид: (15.13) Вывод формулы напряжённости магнитного поля соленоидального тока. Соленоид представляет собой тонкий провод, навитый плотно, виток к витку, на цилиндрический каркас. В отношении создаваемого им поля соленоид эквивалентен системе одинаковых круговых токов с общей прямой осью. Бесконечно длинный соленоид симметричен относительно любой перпендикулярной к его оси плоскости. Взятые попарно симметричные относительно такой плоскости витки создают поле, магнитная индукция которого перпендикулярна к плоскости. Следовательно, в любой точке внутри и вне соленоида вектор может иметь лишь направление, параллельное оси.
Рис. 15.12.
Возьмем прямоугольный контур 1-2-3-4. Циркуляцию вектора по этому контуру можно представить следующим образом: Из четырех интегралов, стоящих в правой части, второй и четвертый равны нулю, так как вектор перпендикулярен к участкам контура, по которым они берутся. Взяв участок 3-4 на большом расстоянии от соленоида(где поле заведомо должно быть очень слабым), третьим слагаемым можно пренебречь. Следовательно, можно утверждать, что : Здесь В — магнитная индукция поля в тех точках, где располагается отрезок 1-2, -длина этого отрезка. Если отрезок 1-2 проходит внутри соленоида на любом расстоянии от его оси, контур охватывает суммарный ток , где — число витков соленоида, приходящееся на единицу его длинны, — сила тока в соленоиде. Поэтому согласно : Откуда: (15.14) а напряженность магнитного поля соленоидального тока равна: (15. Отметим, что полученный нами результат не зависит от того, на каком расстоянии от оси (но внутри соленоида) располагается отрезок 1-2. Если этот отрезок располагается вне соленоида, то охватываемый контуром ток равен нулю, вследствие чего: . Откуда В=0. Таким образом, вне бесконечного длинного соленоида магнитная индукция равна нулю, внутри — всюду одинакова и имеет величину, определяемую формулой (15.14). По этой причине в учении о магнетизме бесконечно длинный соленоид играет такую же роль, как плоский конденсатор в учении об электричестве. В обоих случаях поле однородно и полностью заключено внутри конденсатора (электрическое) и внутри соленоида(магнитное). Произведение называется числом ампер — витков на метр. Тесты к лекции №15 Тест 15.1.Магнитная индукция поля, создаваемого отрезком бесконечно тонкого прямолинейного проводника, вычисляется по формуле…
£ £ £ £
Тест 15. £ £ £ £
Тест 15.3.Форма существования материи, обладающая свойством передавать магнитное взаимодействие. £ магнитное поле £ магнитная индукция £ пробный контур £ магнитный момент Тест 15.4.Дайте определение пробного контура. £ контур, вносящий помехи в исходное поле. £ контур, усиливающий исходное поле. £ контур, ослабляющий исходное поле. £ контур, который не создает заметных искажений исходного поля.
Тест 15.5.Формула выражает: £ вектор магнитной индукции £ напряженность магнитного поля £ магнитную индукцию £ магнитный момент Вихревой характер магнитного поля. Циркуляция вектора индукции магнитного поля. 16.1. Вихревой характер магнитного поля. Циркуляция вектора индукции магнитного поля. Магнитный поток 16.2. Сила Ампера 16.3. Работа по перемещению проводника с током в магнитном поле 16.4. Сила Лоренца 16.5. Определение удельного заряда электрона
Доверь свою работу ✍️ кандидату наук! Имя Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно — исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое Нажимая кнопку «Продолжить», я принимаю политику конфиденциальности |
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 2 из 4Следующая ⇒ Магнитное поле постоянных токов различной конфигурации изучалось экспериментально французскими учеными Ж. Био и Ф. Саваром (1820 г.). Совместно с Лапласом они пришли к выводу, что индукция магнитного поля токов, текущих по проводнику, определяется совместным действием всех отдельных участков проводника. Магнитное поле подчиняется принципу суперпозиции: Если магнитное поле создается несколькими проводниками с током, то индукция результирующего поля есть векторная сумма индукций полей, создаваемых каждым проводником в отдельности. (1) Индукцию проводника с током можно представить как векторную сумму элементарных индукций , создаваемых отдельными участками проводника длиной l. (2) Закон Био–Савара-Лапласа определяет индукцию магнитного поля, создаваемого малым участком проводника с током I: , (3) где – магнитная постоянная, — радиус-вектор, проведенный от элемента проводника , имеющего направление тока в проводнике, к точке, в которой определяется индукция магнитного поля (рис. Рис.6
Пример 1. Найти индукцию магнитного поля в точке, отстоящей на расстоянии 10 см от бесконечно длинного проводника, по которому течет ток силой 5 А. Дано: ; . Решение: Разобьем проводник на элементарные отрезки . Магнитная индукция поля , создаваемого этим элементом в точке А определяется по закону Био-Савара-Лапласа: , где – магнитная постоянная, — радиус-вектор, проведенный от элемента проводника в точку А. По правилу буравчика определим направление . В нашем случае вектор магнитной индукции направлен от нас (на рисунке показан ). По принципу суперпозиции магнитная индукция равна сумме магнитных индукций от всех элементарных отрезков проводника (интегрирование ведется по длине проводника l). Так как проводник прямолинейный, то имеют одинаковые направления, поэтому можно заметить векторное интегрирование скалярным: , где , где α – угол между элементом и радиус-вектором . Из рисунка видно , где — угол, лежащий против элемента проводника с током , тогда , где . , где α1, α2 –углы между направлением тока в проводнике и радиусами – векторами, проведенными от концов проводника в точку А. Если проводник бесконечно длинный, то α1=00, cosα1=1, α2=1800, cosα2=-1. Тогда Вычисления:
Выведенная в примере 1 формула: (4) позволяет определить магнитную индукцию поля прямого бесконечно длинного проводника с током.
Пример 2. По прямому проводнику длиной 4 м течет ток I=100 А. Определить индукцию В магнитного поля в точке, равноудаленной от концов проводника и находящейся на расстоянии 1 м от него. Дано: ; ; . Решение: Разобьем проводник на элементарные отрезки . Магнитная индукция поля , создаваемого этим элементом в точке А определяется по закону Био-Савара-Лапласа: , где – магнитная постоянная, — радиус-вектор, проведенный от элемента проводника в точку А. По правилу буравчика определим направление . В нашем случае вектор магнитной индукции направлен от нас. По принципу суперпозиции магнитная индукция равна сумме магнитных индукций от всех элементарных отрезков проводника (интегрирование ведется по длине проводника l). Так как проводник прямолинейный, то имеют одинаковые направления, поэтому можно заметить векторное интегрирование скалярным: , где , где α – угол между элементом и радиус-вектором . Из рисунка видно , где — угол, лежащий против элемента проводника с током , тогда , где . Тогда . С учетом этого получаем , где α1, α2 –углы между направлением тока в проводнике и радиусами – векторами, проведенными от концов проводника в точку А. Как видно из рисунка cosα1=-cosα2= , тогда . Вычисления:
Выведенная в примере 2 формула: (5) позволяет определить магнитную индукцию поля прямого проводника с током конечной длины. Пример 3. Из проводника длиной l=3,14 м сделано кольцо. Определить индукцию В магнитного поля в точке, лежащей в центре кольца, если сила тока в проводнике равна 5 А. Дано: ; . Решение: Разобьем проводник на элементарные отрезки . Магнитная индукция поля , создаваемого этим элементом в точке О определяется по закону Био-Савара-Лапласа: , где – магнитная постоянная, — радиус-вектор, проведенный от элемента проводника в точку О. По правилу буравчика определим направление . В нашем случае вектор магнитной индукции направлен вверх. По принципу суперпозиции магнитная индукция равна сумме магнитных индукций от всех элементарных отрезков проводника (интегрирование ведется по длине кругового проводника l). В нашем случае имеют одинаковые направления, поэтому можно заметить векторное интегрирование скалярным: , где , где α – угол между элементом и радиус-вектором , проведенным от элемента в точку О. Из рисунка видно, что , так как , , где R – радиус кольца. Радиус кольца , тогда Производим расчет .
Выведенная в примере 3 формула: (6) позволяет определить магнитную индукцию поля в центре кругового проводника с током.
Пример 4. Индукция В магнитного поля в точке, лежащей на оси проводящего кольца на расстоянии b=0,6 м от плоскости кольца, равна 50 мкТл. Определить силу тока в кольце. Радиус кольца R=0,8 м. Дано: ; ; Решение: Разобьем проводящее кольцо на элементарные отрезки . Магнитная индукция поля , создаваемого этим элементом в точке А определяется по закону Био-Савара-Лапласа: , где – магнитная постоянная, — радиус-вектор, проведенный от элемента проводника в точку А. По правилу буравчика определим направление . По принципу суперпозиции магнитная индукция равна сумме магнитных индукций от всех элементарных отрезков проводника (интегрирование ведется по длине проводящего кольца). Разложим вектор на две составляющие: — перпендикулярную плоскости кольца и — параллельную плоскости кольца, то есть . Тогда . Заметим, что из соображений симметрии и что векторы от различных элементов сонаправлены, поэтому можно заметить векторное интегрирование скалярным: , где , где , где α – угол между элементом и радиус-вектором , проведенным от элемента в точку А. Из рисунка видно, что , так как , , , где R – радиус кольца, b – расстояние от плоскости кольца до точки А. С учетом этого получаем . Отсюда искомая сила тока в кольце. Тогда .
Выведенная в примере 4 формула: (7) позволяет определить магнитную индукцию поля на оси проводящего кольца. Пример 5. Два длинных прямых параллельных проводника с одинаково направленными токами I1=2 A и I2=4 A расположены на расстоянии r=10 см друг от друга. Определить индукцию магнитного поля в точке, лежащей в середине отрезка прямой, соединяющего проводники. Дано: ; ; ; . . Решение: Согласно принципу суперпозиции (формула 1) индукция магнитного поля в точке А равна , где — индукция магнитного поля, созданного в точке А проводником с током I1, — индукция магнитного поля, созданного в точке А проводником с током I2. Определим направления векторов магнитной индукции в точке А по правилу буравчика. Как видно из рисунка , поэтому модульное значение индукции магнитного поля в точке А , где — индукция магнитного поля, созданного в точке А бесконечно длинным проводником с током I1 (формула 4), — индукция магнитного поля, созданного в точке А бесконечно длинным проводником с током I2 (формула 4). Получаем , где μ0=1,26·10-6 – магнитная постоянная. Подставим числовые значения: (Тл).
Пример 6. Два прямолинейных бесконечно длинных проводника скрещены под прямым углом. По проводам текут токи силами 80 А и 60 А. Расстояние между проводниками 10 см. Определить магнитную индукцию в точке А, одинаково удаленной от обоих проводников. Дано: ; ; ; . . Решение: Согласно принципу суперпозиции (формула 1) индукция магнитного поля в точке А равна , где — индукция магнитного поля, созданного в точке А проводником с током I1, — индукция магнитного поля, созданного в точке А проводником с током I2. Определим направления векторов магнитной индукции в точке А по правилу буравчика. Как видно из рисунка , поэтому модульное значение индукции магнитного поля в точке А , где — индукция магнитного поля, созданного в точке А бесконечно длинным проводником с током I1 (формула 4), — индукция магнитного поля, созданного в точке А бесконечно длинным проводником с током I2 (формула 4). Получаем . Вычисление: .
⇐ Предыдущая1234Следующая ⇒ Читайте также: Психологические особенности спортивного соревнования Приготовление дезинфицирующих растворов различной концентрации Занятость населения и рынок труда Социальный статус семьи и её типология |
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 326; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
[PDF] О законе Био-Савара-Лапласа и его использовании для расчетов в высоковольтных установках переменного тока
- title={О законе Био-Савара-Лапласа и его использовании для расчетов в высоковольтных установках переменного тока},
автор={Клецель Марк Я. и Александр Барукин и Олжас Талипов},
журнал={Przegląd Elektrotechniczny},
год = {2017},
громкость = {1},
страницы={131-134}
}
- Клецель Марк Я., Барукин А., Талипов О.
- Опубликовано 5 ноября 2017 г.
- Наука об окружающей среде
- Przegląd Elektrotechniczny
Несколько форм записи современных магнитных методов и расчетных формул для получения магнитного закона Био-Савара-Лапласа поля даны.
 Отмечается наличие неточностей в толковании закона Био-Савара-Лапласа. Показано, что в электроэнергетике простая формула, основанная на использовании закона Био-Савара-Лапласа и экспериментально полученных поправочных коэффициентов, может быть использована для расчета магнитных полей, создаваемых переменными токами в шинах…
Отмечается наличие неточностей в толковании закона Био-Савара-Лапласа. Показано, что в электроэнергетике простая формула, основанная на использовании закона Био-Савара-Лапласа и экспериментально полученных поправочных коэффициентов, может быть использована для расчета магнитных полей, создаваемых переменными токами в шинах… View Via Publisher
PE.ORG.PL
Удаленное определение амплитуды и фазы тока с использованием переключателя Reed
- M. Kletsel ‘, A. Neftisov, P. N. Maishev
Physics, Engineering
- 20209
, Engineering
- 20209 9004
- Машрапов Б., Машрапова Ризагуль
Машиностроение
2021 Международная конференция по промышленному инжинирингу, применению и производству (ICIEAM)
- 2021
- Калтаев А., Машрапов Б., Талипов О.
Физика
2020 Международная конференция по промышленному инжинирингу, применению и производству (ICIEAM)
- 2020
- Клецель М., Барукин А., Мельников В.Ю. ЭлКонРус)
- 2021
- Барукин А.В., Калтаев А.В., Ленков Ю.В. (ICIEAM)
- 2020
- С. Апанасевич, С. Павловский, Й. Плевако
Математика
- 2013
- Н. Ида, Дж. Бастос
Физика, геология
- 1992
- J. Bastos, N. Sadowski
Physics
- 2003
- 2010
Moscow : Vysshaya shkola,
- 2002
Электромагнитное поле. – Москва : Гардарики,
- 2001
Москва: Висайя Школа,
- 1976
- 2006
Био — Савар Закон определяет магнитное поле, создаваемое токоведущим сегментом, и его применения. Это один из важных законов физики, поскольку его можно использовать для очень маленьких проводников.
Некоторые примеры геометрий, в которых закон Био -Савара может быть успешно использован при расчете магнитного поля, возникающего в результате распределения электрического тока. Индекс Концепции магнитного поля
Ответ- Да, уравнение Максвелла подразумевает закон Био-Савара.
 Рассматривая параллельно с законом Кулона и Гаусса небольшое увеличение сложности, мы можем получить закон Био-Савара из закона Ампера. Мы знаем, что векторная способность связана с магнитным полем соотношением B=∇×AB=∇×A.
Рассматривая параллельно с законом Кулона и Гаусса небольшое увеличение сложности, мы можем получить закон Био-Савара из закона Ампера. Мы знаем, что векторная способность связана с магнитным полем соотношением B=∇×AB=∇×A.Кроме того, как закон Био-Савара, так и закон Ампера поддерживают получение распределений магнитного поля, однако закон Ампера учитывает симметрию, поскольку представляет собой замкнутый линейный интеграл (петля Ампера). Оба закона можно использовать для расчета чистого магнитного поля, создаваемого в точке различными распределениями тока.
- Надеюсь, полезные комментарии о сдаче UIUC Physics 435
- Краткая история электромагнетизма
- СИ Единицы электромагнитных величин
- Краткая история развития единиц СИ
- Конспект лекций 01: Введение/Обзор, Закон Кулона, Электрическое поле, Принцип суперпозиции
- Конспект лекций 02: Закон Гаусса, Теорема о расходимости, Теорема Стокса
- Конспект лекций 03: Электростатический потенциал, уравнения Пуассона и Лапласа, граничные условия
- Конспект лекций 04: Работа и электростатическая энергия
- Конспект лекций 05: Электростатические свойства электрических проводников, емкость
- Примечания к лекциям 06: Метод изображений/проблем заряда изображений
- Примечания к лекциям 07: Уравнение Лапласа, Теорема(ы) единственности, Уравнение Лапласа в трехмерном пространстве, Разделение переменных, Ряды решений, Граничные условия
- Дополнительный раздаточный материал 1: векторные пространства, внутренние произведения, все такое.
 ..
.. - Примечания к лекции 7.5: Уравнение Лапласа в двух и трех измерениях: явные примеры
- Дополнительный раздаточный материал 2: Уравнение Лапласа в двух и трех измерениях: еще девять явных примеров
- Примечания к лекциям 08: Электрическое многополюсное расширение, электростатические многополюсные моменты
- Раздаточный материал: расширения ряда Тейлора/биномиального ряда
- Конспект лекций 09: Электростатические поля в веществе, диэлектрические материалы и их свойства
- Диэлектрические постоянные различных материалов
- Конспект лекции 10: Электростатические поля внутри диэлектрика, граничные условия для E, D и P
- Примечания к лекциям 11: Краевые задачи с линейными диэлектриками; Электростатическая энергия сил, действующих на диэлектрики
- Примечания к лекциям 12: Микроскопическая теория диэлектриков, уравнения Клаузиуса-Моссотти, уравнения Ланжевена и ДеБая; Ферро-, пьезо- и пироэлектрические материалы
- Конспект лекций 13: Установившиеся электрические токи, магнитное поле, B, закон силы Лоренца
- Конспект лекции 14: Магнитное поле от линейных/поверхностных/объемных токов, закон силы Био-Савара, магнитные моменты
- Примечания к лекциям 15: Расхождение и завиток B, Закон Ампера, Применение закона Ампера
- Конспект лекций 16: Магнитный векторный потенциал, A; B = Curl A, магнитостатические граничные условия
- Конспект лекций 17: Мультипольное разложение магнитного векторного потенциала, A; магнитные мультиполи; В = завиток А
- Конспект лекций 18: Магнитные монополи/магнитные заряды; Квантование магнитного потока, условие квантования Дирака, законы силы Кулона/Лоренца для электрических/магнитных зарядов, преобразования двойственности
- Четыре различных вида магнетизма
- Конспект лекций 19: Магнитные поля в материи I; диа-/пара-/ферро-/антиферро-магнетизм; Намагниченность, М; Связанный объем и поверхностные течения, Jm_bound, Km_bound; Закон Ампера, Curl B = mu_o * Jm_tot; Вспомогательное поле, H; 3 Уравнения непрерывности
- Конспект лекций 20: Магнитные поля в материи II; A и B-поля; Магнитное поле B внутри намагниченного вещества; Магнитный скалярный потенциал, поверхностная/объемная плотность силы магнитного полюса; Уравнение Ланжевена для парамагнитных материалов; Ферромагнитные материалы, гистерезис
- Дополнительный раздаточный материал 3: Комментарии о соотношениях вспомогательных полей для электростатики и магнитостатики
- Дополнительный раздаточный материал 4: Сводная таблица формул ЭМ для электростатики и магнитостатики
- Конспект лекций 20.
 5: Магнитостатические краевые задачи
5: Магнитостатические краевые задачи - Конспект лекций 21: Закон Ома; Электродвижущие силы, источники ЭДС; Закон Фарадея о магнитной индукции, индукция движения
- Конспект лекций 22: Индуктивность – взаимная и собственная индуктивность
- Конспект лекций 23: Вихревые токи в проводниках, Энергия, запасенная в магнитных полях, Магнитные силы, Магнитное давление
- Новые направления в измерении вихревых токов — использование вихревых токов в реальных условиях
- Дополнительный раздаточный материал: Новые направления в вихретоковом зондировании
- Дополнительный раздаточный материал 5: Эффект Холла
- Конспект лекций 24: уравнения Максвелла, ток смещения Максвелла, уравнения Максвелла в материи, граничные условия
- Дополнительный раздаточный материал 6: Свойства симметрии электромагнитных величин
- Электромагнитные моменты элементарных частиц
- Дополнительный раздаточный материал 7: Физика Фун с эффектами движения и магнитным векторным потенциалом, A: Физика E+M в различных системах отсчета
- Смульски, Дж.

.
Аннотация Предложен метод определения амплитуды и фазы тока в шинах высоковольтного электрооборудования. Метод основан на определении астрономического времени…
Геркон и дифференциальная защита на основе магниторезисторов с тестовой диагностикой для преобразователей
В статье предложена схема тестовой диагностики, которая, в отличие от других известных конструкций, имеет от трех до шести соединенных между собой обмоток управления на магниторезисторах, а также кнопочные выключатели и определены области применения такой защиты.

Помехоустойчивые измерительные устройства для защиты токов на герконах без трансформаторов тока
Отмечено, что в релейной защите можно обеспечить ресурсосбережение, построив ее на основе гораздо менее металлоемких датчиков тока по сравнению с традиционными трансформаторами тока.…
Конструкции для установки герконов в закрытых полных токопроводах и на кабельных линиях
Предложены четыре конструкции для установки герконов вблизи трехфазных замкнутых комплектных токопроводов с разделительными перегородками и на кабельных линиях и с их помощью осуществляется контроль параметров срабатывания магниточувствительных элементов.

Схема защиты от перегрузки по току с использованием герконов вместо трансформаторов тока
Указана необходимость создания защиты от перегрузки по току без применения трансформаторов тока из-за присущих им недостатков и предложен метод настройки устройства измерения схемы защиты, учитывающий неравенство расчетной и фактической индукций магнитного поля, действующего на геркон.
Герконы Дифференциальная защита преобразовательных установок с блокировкой по второй гармонике
Рассмотрены преимущества и недостатки традиционных дифференциальных защит преобразовательных установок и герконовых защит. Предлагается дифференциальная защита с герконом,…
Централизованная защита шин и подключенных к ним электродвигателей
Централизованная защита имеет ряд преимуществ перед автономной защитой; однако неправильные действия первых могут обернуться более серьезными последствиями.
 Надежность их работы может…
Надежность их работы может…Опорные конструкции для пломбировочных выключателей, расположенных вблизи автобусных линий
Авторы предлагают три конструкции опорных конструкций пломбировочных выключателей, расположенных вблизи автобусных линий электростанций. Первый имеет пластину, которая крепится к шинным линиям, расположенным в одной плоскости. Второй…
Мажоритарные схемы дифференциальных защит без трансформаторов тока с функциональной диагностикой преобразовательных агрегатов и электродвигателей
Авторы предлагают две новые схемы защиты, основанные на принципе мажоритарного голосования — сигнал отключения неисправного электроблока формируется, если хотя бы два из трех взаимно резервированных комплектов посылают аварийные сигналы, что приводит к улучшению как по надежности, так и по безопасности.
Повышение надежности диагностики цепей МТЗ на основе герконов
Для повышения надежности диагностики МТЗ на основе герконов авторы настоящего документа разработали схему, проверяющую целостность герконов, защит и их элементов.

ПОКАЗАНЫ 1-10 ИЗ 10 ССЫЛОК
Анализ квазистационарного электромагнитного поля с ферромагнитными объектами, присутствующими в пределах
Предложен метод расчета распределения квазистационарного электромагнитного поля в системах, содержащих ферромагнитные объекты с нелинейными свойствами. Итеративная версия…
Электромагнетизм и расчет полей
Это введение в теоретические расчеты электромагнитных полей связи. Начиная с идеи, что уравнения Максвелла первичны,…
Электромагнитное моделирование с помощью методов конечных элементов
ПРЕДИСЛОВИЕ МАТЕМАТИЧЕСКИЕ ПРЕДУПРЕЖДЕНИЯ Введение Вектор. Операторы больше одного…
Разработка имитационной модели магнитного поля на основе теории подобия и метода Монте-Карло
О численных методах решения задач электромагнитного поля // Известия высших учебных заведений.
 Electromechanics
ElectromechanicsTest calculation of a twodimensional magnetic field in the ring sector
A Handbook of Electrical Engineering
Theoretical Foundations of Electrical Engineering
Теория сходства и моделирования (применяется к проблемам электроэнергии
Закон Био-Савара — Формулировка, вывод и часто задаваемые вопросы
Магнитное поле, создаваемое постоянным электрическим полем, описывается уравнением закона Био-Савара.Согласно этому закону, величина, длина, направление и близость электрического тока связано с магнитным полем. Кроме того, этот закон согласуется как с теоремой Гаусса, так и с схемным законом Ампера.
 Поскольку закон Кулона является основным для электростатики, аналогичным образом закон Био-Савара также является основным для магнитостатики. В 1820 году два французских физика Жан Батист Био и Феликс Савар создали формулировку закона Био-Савара, которая вывела математическую формулу для r плотность магнитного потока в точке из-за близлежащего проводника с током. Наблюдая за отклонением стрелки магнитного компаса, эти ученые пришли к выводу, что частица тока проецирует магнитное поле в окружающее ее пространство.
Поскольку закон Кулона является основным для электростатики, аналогичным образом закон Био-Савара также является основным для магнитостатики. В 1820 году два французских физика Жан Батист Био и Феликс Савар создали формулировку закона Био-Савара, которая вывела математическую формулу для r плотность магнитного потока в точке из-за близлежащего проводника с током. Наблюдая за отклонением стрелки магнитного компаса, эти ученые пришли к выводу, что частица тока проецирует магнитное поле в окружающее ее пространство.Математическое выражение было получено путем наблюдений и расчетов, которые показали плотность магнитного потока. Эта плотность потока dB пропорциональна длине тока I, элементу dl, синусу угла θ между направлением тока и вектором, соединяющим данную точку магнитного поля и элемент тока. Он обратно пропорционален квадрату расстояния данной точки от текущего элемента r.
Вывод закона Био Савара
9{2}}\]Рассмотрим длинный провод с током I в точке p в пространстве.
 Провод показан на картинке ниже красным цветом. Также рассмотрим бесконечно малую длину провода dl на расстоянии r от точки P, как показано на схеме. Здесь r — вектор расстояния, который составляет угол θ с направлением тока в мельчайшей части провода.
Провод показан на картинке ниже красным цветом. Также рассмотрим бесконечно малую длину провода dl на расстоянии r от точки P, как показано на схеме. Здесь r — вектор расстояния, который составляет угол θ с направлением тока в мельчайшей части провода.Представьте себе условие, и вы поймете, что плотность магнитного поля в точке P из-за мельчайшей длины dl провода пропорциональна току, переносимому по этому участку провода. Поскольку ток, протекающий через мельчайшую длину провода, аналогичен току, протекающему по всему проводу, мы можем выразить его как: 9{2}}\]
Кроме того, плотность магнитного поля в точке P из-за мельчайшей части провода пропорциональна фактической длине мельчайшей длины dl провода. θ — угол между вектором расстояния r и направлением тока через этот мельчайший участок провода, составляющая dl провода, обращенного перпендикулярно к точке P, равна dlsinθ.
Следовательно, дБ ∝ dl sinθ
Теперь, объединив эти три утверждения, мы можем написать:
\[дБ\ \alpha k\frac{I.
 {2}}\] 9\theta2\]
{2}}\] 9\theta2\]= \[\frac {I\mu_0 \mu_r}{4\pi D} [\cos\theta_{1}- \cos\theta_{2}]\]
Рассмотрим провод бесконечно долго, то θ изменится от 0 до π, то есть от θ1 = 0 до θ2 = π.
Поместив эти два значения в приведенное выше окончательное выражение закона Био-Савара, мы получим,
\[B = \frac {I\mu_0 \mu_r}{4\pi D}[\cos0 — \cos\pi = \ frac {I\mu_0 \mu_r}{4\pi D} 1-(-1)\]
\[B = \frac{\mu_{0}\mu_{r}I}{2\pi D}\ ]
Применение закона Био-Савара
Применение закона Био Савара указано ниже.
Важность Закона Био-Савара
Закон Био-Савара важен по следующим причинам:
Что такое Закон Био-Савара?
В физике, особенно в электромагнетизме, закон Био–Савара (/ˈbiːoʊ səˈvɑːr/ или /ˈbjoʊ səˈvɑːr/) представляет собой уравнение, описывающее магнитное поле, создаваемое постоянным электрическим током . Он связывает магнитное поле с величиной, направлением, длиной и близостью электрического тока.

Что такое закон Био-Савара-Лапласа?
Закон Био-Савара используется для определения напряженности магнитного поля H вблизи проводника с током или, можно сказать, он дает зависимость между напряженностью магнитного поля, создаваемой его источником тока. … Закон Био-Савара также известен как закон Лапласа или закон Ампера.
Что такое вывод закона Био-Савара?
Закон Био-Савара, названный в честь Жана-Батиста Био и Феликса Савара, определяется как уравнение, объясняющее магнитное поле, создаваемое постоянным электрическим током .
 … Он играет ту же роль, что и закон Кулона в электростатике, но в магнитостатике.
… Он играет ту же роль, что и закон Кулона в электростатике, но в магнитостатике.Как получить закон Био Савара?
Закон Био-Савара начинается со следующего уравнения: → B=µ04π∫wireId→l׈rr2 . B=μ04π∫wireIrdθr2. Ток и радиус можно вытащить из интеграла, потому что они одинаковы независимо от того, где мы находимся на пути. 5 ноября 2020 г.
Почему используется закон Био Савара?
Закон Био-Савара представляет собой уравнение, которое описывает магнитное поле, создаваемое проводом с током , и позволяет рассчитать его силу в различных точках.
 … И мы также заменяем электрическое поле E на элемент магнитного поля в дБ, потому что движущийся заряд создает магнитное поле, а не электрическое поле. 11 марта 2021 г.
… И мы также заменяем электрическое поле E на элемент магнитного поля в дБ, потому что движущийся заряд создает магнитное поле, а не электрическое поле. 11 марта 2021 г.Родственный
Что такое тороид класса 12?
Тороид представляет собой полое круглое кольцо, на которое плотно намотано большое количество витков проволоки . Его можно рассматривать как соленоид, изогнутый в круглую форму, чтобы замкнуться сам на себя. 30 ноября 2016 г.
Какие выводы из закона Био-Савара?
Закон Био-Савара представляет собой уравнение, описывающее магнитное поле, создаваемое постоянным электрическим током. … Наблюдая за отклонением стрелки магнитного компаса, эти двое ученых пришли к выводу, что любой элемент тока проецирует магнитное поле в окружающее его пространство
Что такое закон Био-Савара Toppr?
Закон Био-Савара дает магнитное поле, создаваемое токоведущим сегментом .
 … Величина магнитного поля dB на расстоянии r от токоведущего элемента dl оказывается пропорциональной I и длине dl. И обратно пропорциональна квадрату расстояния |r|.
… Величина магнитного поля dB на расстоянии r от токоведущего элемента dl оказывается пропорциональной I и длине dl. И обратно пропорциональна квадрату расстояния |r|.Связанные
Что верно в отношении закона Био-Савара?
В физике, особенно в электромагнетизме, закон Био-Савара (/ˈbiːoʊ səˈvɑːr/ или /ˈbjoʊ səˈvɑːr/) равен уравнение, описывающее магнитное поле, создаваемое постоянным электрическим током . … Закон действителен в магнитостатическом приближении и согласуется как с схемным законом Ампера, так и с законом Гаусса для магнетизма.
Связанные
Что такое формула магнитного поля?
Величина силы, действующей на провод с током I длиной L в магнитном поле, определяется уравнением. … F=ILBsinθ , где θ — угол между проводом и магнитным полем. Сила перпендикулярна полю и току.

Связанные
Как Гаусс связан с Теслой?
Один гаусс соответствует 10 — 4 тесла (T) , международной системе единиц. Гаусс равен 1 максвеллу на квадратный сантиметр, или 10 − 4 веберов за квадратный метр. Магниты оцениваются в гауссах.
Связанные
Что такое ампер-петля?
Это воображаемый замкнутый контур вокруг проводника с током, через который к этому проводнику применяется закон ампера . 28 июня 2019 г.
Что такое сила Лоренца класса 12?
Сила Лоренца относится к комбинации магнитной и электрической сил, которые действуют на точечный заряд из-за наличия электромагнитных полей . Кроме того, сила Лоренца также известна специалистам как электромагнитная сила.

Связанные
Что такое закон Био-Савара?
Родственный
Можно ли использовать закон Био-Савара для расчета магнитного поля?
Связанные
Подразумевает ли уравнение Максвелла закон Био-Савара?
Связанные
Чем закон биоцаварта отличается от закона ампера?
общий Информация СМИ Нажмите галерея иллюстрация
Поделиться этой записью:
Физика 435 — Конспект лекций профессора С.
 Эрреде
ЭрредеВсе конспекты лекций, раздаточные материалы и т. д. представлены в формате Adobe PDF.
Общая ориентационная информация, краткая история электромагнетизма…
Электростатика:
Магнитостатика:
Электродинамика:
«> Вернуться на домашнюю страницу профессора С.
 Эрреде
Эрреде Dr. Baird — Все курсы
Учебные материалы
Доктор Бэрд в настоящее время преподает младшие и старшие классы бакалавриата в Западно-Техасском университете A&M, включая оптику, электромагнетизм, общую физику I и II и вычислительную физику I и II. В прошлом он преподавал курс электромагнетизма I и II в Массачусетском университете в Лоуэлле.
Выпускник Электромагнетизм I Конспект лекций
Лекция 1 — Закон Кулона, закон Гаусса, электрический потенциал, емкость
Лекция 2 — Плотность поверхностного заряда, функции Грина, плотность энергии, вычислительные подходы
Лекция 3 — Метод изображений, точечный заряд в наличие сферы
Лекция 4 — Ряды Фурье, уравнение Лапласа в прямоугольных координатах, уравнение Лапласа в полярных координатах
Лекция 5 — Уравнение Лапласа в сферических координатах, полиномы Лежандра, азимутальная симметрия
Лекция 6 — Сферические гармоники, уравнение Лапласа в цилиндрических координатах
Лекция 7 — Функции Грина в сферических координатах
Лекция 8 — Мультипольные разложения
Лекция 9 — Электростатические поля в диэлектриках, энергия в диэлектриках
Лекция 10 — Закон Био-Савара, закон Ампера , магнитная сила, векторный потенциал
Лекция 11 — Магнитные дипольные поля, магнитостатика в магнитном материале
Лекция 12 — Примерные задачи магнитостатики, закон индукции Фарадея
Лекция 13 — Уравнения Максвелла, волновое уравнение, потенциалы электродинамики
Лекция 14 — Квазистатика, функции Грина для волнового уравнения, сохранение энергииВыпускник по электромагнетизму I Дополнительные примечания
Математический справочник по электродинамике
Пошаговый метод функции Грина
Лекция 4 Дополнительные примечания
Графики электрических многополюсников
Резюме
Электростатика с диэлектриками
Реакции материалов
Методы магнитостатики
Краткий обзор уравнений магнитостатики
Магнитные зеркала, ионосфера и магнитосфера
Уникальность уравнений Максвелла
Разложение Гельмгольца векторных полей
Альтернативные потенциалыВыпускник по электромагнетизму II Конспекты лекций
Лекция 1.
7 Джексон 7.4 Решение для домашнего задания Уравнения Максвелла, плоские векторы, поляризация, параметры Стокса, вектор Джонса, отражение, преломление
Уравнения Максвелла, плоские векторы, поляризация, параметры Стокса, вектор Джонса, отражение, преломление
Лекция 2. Комплексная диэлектрическая проницаемость , резонансное поглощение, проводимость, плазменная частота
Лекция 3 — Суперпозиция волн, групповая скорость, расплывание импульса, дисперсия, соотношение Крамерса-Кронига
Лекция 4 — Поля на поверхности неидеального проводника, уравнения волновода
Лекция 5 — Прямоугольные волноводы, частота отсечки, резонансные полости, добротность
Лекция 6 — Излучение, длинноволновое приближение, волны дальнего поля, дипольное излучение
Лекция 7 — Линейные антенны
Лекция 8 — Длинноволновое рассеяние, сечения, зависящие от поляризации
Лекция 9 — Рассеяние на проводящем шаре, атмосферное рассеяние
Лекция 10 — Галилеево относительность, эфир, постулаты Эйнштейна
Лекция 11. Принцип относительности Эйнштейна, преобразования Лоренца, четырехвекторы
Лекция 12. Сложение скоростей в специальной теории относительности, релятивистский импульс и энергия
Лекция 13. Ковариантная геометрия, ковариантные уравнения Максвелла Решение для домашнего задания
Ковариантная геометрия, ковариантные уравнения Максвелла Решение для домашнего задания
Jackson 1.2 Решение для домашнего задания
Jackson 1.3 Решение для домашнего задания
Jackson 1.4 Решение для домашнего задания
Jackson 1.5 Решение для домашнего задания
Джексон 1.6 Домашнее задание Решение
Джексон 1.7 Домашнее задание Решение
Джексон 1.8 Домашнее задание Решение
Джексон 1.9 Домашнее задание Решение
Джексон 1.10 Домашнее задание Решение
Джексон 1.11 Домашнее задание Решение
Джексон 1.12 Домашнее задание Решение
Джексон 1.13 Домашнее задание 7 Джексон 1.247 Домашнее задание 1.104
Джексон 2.2 Домашнее задание
Джексон 2.3 Домашнее задание
Джексон 2.4 Домашнее задание
Джексон 2.5 Домашнее задание
Джексон 2.7 Домашнее задание
Джексон 2.9 Домашнее задание
Джексон 2.11 Домашнее задание
Джексон 2.12 Домашнее задание
Джексон 2.13 Домашнее задание
Джексон 2.14 Домашнее задание
Джексон 2. 23 Домашнее задание
23 Домашнее задание
Джексон 2.25 Домашнее задание 7 Джексон 2.24 Домашнее задание 7 Джексон 2.24
Jackson 3.1 Решение для домашних заданий
Jackson 3.2 Решение для домашних заданий
Jackson 3.4 Решение для домашних заданий
Jackson 3.5 Решение для домашних заданий
Джексон 3.6 Решение для домашних заданий
Джексон 3.7 Решение для домашних заданий
Джексон 3.9 Решение для домашних заданий
Джексон 3.10 Решение для домашних заданий
Джексон 3.12 Решение для домашних заданий
Джексон 3.14 Решение для домашних заданий
Джексон 3.15 Решение для домашних заданий
Джексон 4.1 Решение для домашних заданий
Джексон 4.2 Решение для домашних заданий
Джексон 4.2 Решение для домашних заданий
Джексон 4.5 Решение для домашних заданий
Джексон 4.7 Решение для домашних заданий
Джексон 4.8 Решение для домашних заданий
Джексон 4.9 Решение для домашних заданий
Джексон 4.10 Решение для домашнего задания
Джексон 4. 13 Решение для домашнего задания
13 Решение для домашнего задания
Джексон 5.1 Решение для домашнего задания
Джексон 5.3 Решение для домашнего задания
Джексон 5.6 Решение для домашнего задания
Джексон 5.11 Решение для домашнего задания
Джексон 5.13 Решение для домашнего задания
Джексон 5.14 Решение для домашнего задания 6 Джексон 5247 Решение для домашнего задания 5.11
Джексон 5.17 Решение для домашнего задания
Джексон 5.18 Решение для домашнего задания
Джексон 5.19 Решение для домашнего задания
Джексон 5.20 Решение для домашнего задания
Джексон 5.21 Решение для домашнего задания
Джексон 5.22 Решение для домашнего задания
Джексон 6.1 Решение для домашнего задания
Джексон 6.4 Решение для домашнего задания
Джексон 6.8 Решение для домашнего задания
Джексон 6.9 Решение для домашнего задания
Джексон 7.1 Решение для домашнего задания
Джексон 7.3 Решение для домашнего задания
Джексон 7. 12 Решение для домашних заданий
12 Решение для домашних заданий
Джексон 7.19 Решение для домашних заданий
Джексон 7.22 Решение для домашних заданий
Джексон 8.1 Решение для домашних заданий
Джексон 8.2 Домашнее задание
Джексон 8.4 Домашнее задание
Джексон 8.5 Домашнее задание
Джексон 9.3 Домашнее задание
Джексон 9.5 Домашнее задание
Джексон 10.1 Домашнее задание
Джексон 10.3 Домашнее задание
Джексон 10.4 Домашнее задание
Джексон 3 Домашнее решение 19.14
Джексон 11.14 Домашнее заданиеТочные уравнения для светового эффекта Доплера
Журнал современной физики Vol.05 No.16(2014), ID статьи:50607,5 страниц
10.4236/jmp.2014.516161 Точные уравнения для светового эффекта Доплера и Scientific Research Publishing Inc.Эта работа находится под лицензией Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
Поступила в редакцию 12 августа 2014 г.
 ; пересмотрено 7 сентября 2014 г.; принята 1 октября 2014 г.
; пересмотрено 7 сентября 2014 г.; принята 1 октября 2014 г.АННОТАЦИЯ
Рассмотрено влияние источника света на приемник в виде электромагнитного взаимодействия. Механическое воздействие движущегося заряженного тела на неподвижное определяется экспериментальными законами электродинамики. Эти законы определяют изменение параметров источника света, движущегося относительно приемника. Законы изменения частоты света и его направления движущимся источником вытекают из законов электромагнетизма. При малых скоростях движения источника они совпадают с классическими результатами: эффектом Доплера и явлением аберрации. Взаимодействие источника и приемника зависит только от скорости их движения относительно друг друга. Нет мировой среды, относительное движение которой повлияло бы на характеристики источника света.
Ключевые слова:
Источник света, Движение, Относительно, Приемник, Законы электромагнетизма, Эффект Доплера, Аберрация
1.
 Введение
Введениеперемещается относительно приемника. Я не буду их все перечислять и анализировать; здесь я просто изложу то понимание, к которому пришел.
Многочисленными экспериментами установлено, что свет — это электромагнитное воздействие одного тела на другое. Характер светового воздействия такой же, как и характер действия передающей антенны источника излучения на приемную антенну радиоприемника.
В простейшей передающей антенне, в плоском конденсаторе, заряженная частица испытывает действие, направленное перпендикулярно пластинам. Если к конденсатору с переменным напряжением подключить источник питания, то сила воздействия на эту частицу изменится, оставаясь перпендикулярной пластинам. Такое воздействие на заряженную частицу будет существовать вне конденсатора, но его величина будет уменьшаться с расстоянием. Это переменное электрическое действие называется электромагнитными волнами. Если между пластинами будет находиться намагниченное тело, то переменная сила действия на один из его полюсов будет направлена перпендикулярно силе, действующей на заряженное тело, а также перпендикулярно направлению удаления от конденсатора.
 Поэтому в любой точке пространства вблизи средней плоскости конденсатора, на помещенную в него заряженную частицу или на магнитный полюс будет действовать то, что направлено перпендикулярно направлению этой точки от конденсатора. Поэтому элементарные волны называются «поперечными».
Поэтому в любой точке пространства вблизи средней плоскости конденсатора, на помещенную в него заряженную частицу или на магнитный полюс будет действовать то, что направлено перпендикулярно направлению этой точки от конденсатора. Поэтому элементарные волны называются «поперечными».Приемником этого электромагнитного воздействия могла бы быть заряженная частица или магнитный полюс, если бы можно было измерить их поперечные колебания. Но развитие радиотехники пошло другим путем. Приемником переменного электромагнитного воздействия является аналогичный конденсатор, на обкладках которого находится переменный электрический заряд, преобразующийся в переменный ток. Этот ток усиливается, и при этом восстанавливается та информация, которую передал приемник.
Электромагнитное воздействие света отличается от электромагнитного воздействия радиоволн гораздо большей частотой. Многочисленными экспериментами установлено, что физические свойства электромагнитного воздействия существенно зависят от значения частоты.
 По-видимому, это в значительной мере относится и к свету. Есть ряд его свойств, которые для других электромагнитных волн не проявляются. Однако существует единая электромагнитная природа света и радиоволн относительно действия движущегося электромагнитного источника на приемник. В частности, существуют одинаковые законы изменения характеристик электромагнитного воздействия источника при его движении относительно приемника.
По-видимому, это в значительной мере относится и к свету. Есть ряд его свойств, которые для других электромагнитных волн не проявляются. Однако существует единая электромагнитная природа света и радиоволн относительно действия движущегося электромагнитного источника на приемник. В частности, существуют одинаковые законы изменения характеристик электромагнитного воздействия источника при его движении относительно приемника.2. Законы электромагнитного взаимодействия двух тел с относительным движением
Известно, что при движении магнита относительно конденсатора на его обкладках возникает электрический заряд. Следовательно, если поместить между пластинами конденсатора заряженную частицу, то на нее будет оказано механическое воздействие со стороны движущегося магнита, т.е. частица получит движение. Если пластинами конденсатора замкнуть проводник, то в проводнике потечет ток. Этот эффект идентичен случаю, когда магнит перемещается относительно катушки с проводником. При коротком замыкании его концов ток будет в проводнике.
 Величина тока не зависит от того, движется ли катушка или магнит. Сила течения определяется по скорости их относительного движения. Как известно [1], это явление описывается индукцией по закону Фарадея.
Величина тока не зависит от того, движется ли катушка или магнит. Сила течения определяется по скорости их относительного движения. Как известно [1], это явление описывается индукцией по закону Фарадея.Аналогичная ситуация возникает при движении наэлектризованного тела. Его движение относительно магнита тождественно току, а ток создает механическое воздействие на полюс магнита; т. е. движущийся заряд создает механическое воздействие на магнит. Это влияние описано в [1] с использованием экспериментального закона Био-Савара-Лапласа для токового элемента. Взаимодействие движущегося заряженного тела и магнита также не зависит от того, движется ли заряженное тело или магнит. Это зависит от скорости их относительного движения. Если заряд и магнит движутся относительно третьего тела, например поверхности Земли, но относительно друг друга покоятся, то в этом случае заряд и магнит не взаимодействуют. В этом случае катушка не взаимодействует с магнитом.
Переменное электромагнитное взаимодействие между источником и приемником (в современной терминологии электромагнитные волны) определяется первым и вторым уравнениями Максвелла.
 В свою очередь, эти уравнения являются другой формой записи двух экспериментальных законов [1]: закона индукции Фарадея и закона Био-Савара-Лапласа. Исключая из уравнений Максвелла магнитную напряженность H, получаем уравнение Даламбера для электрической напряженности E
В свою очередь, эти уравнения являются другой формой записи двух экспериментальных законов [1]: закона индукции Фарадея и закона Био-Савара-Лапласа. Исключая из уравнений Максвелла магнитную напряженность H, получаем уравнение Даламбера для электрической напряженности E, (1)
где – скорость света в рассматриваемых средах; – диэлектрическая проницаемость среды; – магнитная проницаемость среды; – плотность электрических зарядов, распределенных в пространстве системы координат x, y, z; v — скорость зарядов. Уравнение (1) определяет силу воздействия движущихся зарядов на неподвижную точечную частицу, заряд которой равен единице. А движение со скоростями v происходит относительно неподвижной частицы.
Мы решили уравнение Даламбера (1) для действия одной точечной заряженной частицы на другую, когда первая движется относительно второй со скоростью. Также мы получили выражение для силы:
, (2)
где — радиус-вектор от первого заряда ко второму; нормированная скорость.

Сила (2) зависит от относительной скорости движения v, и при ней переходит в закон Кулона:
, (3)
, который, как известно, определяет силу взаимодействия двух неподвижных зарядов.
Итак, все электромагнитные эксперименты и вытекающие из них результаты (1)-(2) свидетельствуют о том, что законы электромагнитного взаимодействия двух тел зависят от их относительной скорости. Отсюда следуют два важных вывода. Первый свидетельствует о ошибочности принципа относительности, когда он применяется к взаимодействию движущихся друг от друга объектов. В этом случае нельзя сказать, что Законы Природы (например, закон Кулона (3)) не зависят от движения объекта. Наоборот, закон электромагнитного взаимодействия двух тел (2) зависит от их относительного движения. Итак, принцип относительности, используемый в Теории Относительности (ТО), неверен. Второй вывод свидетельствует об отсутствии мировой среды: светоносной среды, эфира, среды физического вакуума и т. д. Отсюда следует, что электромагнитное взаимодействие двух тел зависит от их относительной скорости и не зависит от абсолютной скорости относительно среда воображаемого мира.

3. Законы, описывающие электромагнитные волны
Переменное электромагнитное воздействие (в принятой терминологии: электромагнитные волны, электромагнитное излучение, свет и т.п.) источника на приемник зависит от их относительной скорости. Эта зависимость (эффект Доплера, явление аберрации) давно установлена астрономическими наблюдениями. Однако для их теоретического объяснения привлекались различные модели распространения света. Как видим, все эти модели являются умозрительными. Реальная зависимость светового воздействия источника на приемник от их относительного перемещения может быть установлена только на основе экспериментальных законов электромагнетизма, полученных в результате измерения механических взаимодействий.
При переменном электромагнитном воздействии постоянный заряд отсутствует, а его плотность; поэтому при равенстве нулю правой части уравнения Даламбера уравнение (1) переходит в волновое уравнение
. (4)
Как показано в наших работах, например [2] [3] , частным случаем его решения является уравнение плоской волны
, (5)
где E 0 = const – амплитуда ; f – частота колебаний; – нормаль к плоскости волны; направляющие косинусы с осями координат x, y, z равны:
.

4. Взаимодействие источника и приемника при их относительном движении
Выражение (5) описывает изменение напряженности электрического поля E в любой точке системы координат x, y, z и в любой момент времени. Это изменение вызвано переменным электромагнитным источником. Из формулы (5) следует, что изменения Е в пространстве распространяются со скоростью c 1 . Если электромагнитный источник является точечным, то далеко от него уравнение (5) будет описывать его влияние при небольших изменениях расстояния. А для точного описания его действия необходимо использовать решение волнового уравнения (4) для сферической волны [2][3] . Приемник, помещенный в точку с координатами x, y, z согласно выражению (4), будет тестировать переменное действие источника.
В случае движения источника, например, со скоростью v в направлении оси x, его влияние на приемник уже будет другим. Поэтому для его расчета необходимо произвести изменение электромагнитных характеристик источника, которое вызвано его перемещением относительно приемника.
 В работах [2][3] мы пошли другим путем. Мы задались вопросом: при каких условиях выражение (2) для силы взаимодействия относительно движущихся заряженных частиц будет совпадать с законом Кулона (3) для силы взаимодействия неподвижных заряженных частиц? Очевидно, что для этого необходимо величины, входящие в выражение (3), выразить через величины, от которых зависит (2). Оказалось, что существует два варианта преобразования выражения (3) в выражение (2). Воспользуемся одним из них. При этом параметры взаимодействия относительно движущихся зарядов запишем символом «v»:
В работах [2][3] мы пошли другим путем. Мы задались вопросом: при каких условиях выражение (2) для силы взаимодействия относительно движущихся заряженных частиц будет совпадать с законом Кулона (3) для силы взаимодействия неподвижных заряженных частиц? Очевидно, что для этого необходимо величины, входящие в выражение (3), выразить через величины, от которых зависит (2). Оказалось, что существует два варианта преобразования выражения (3) в выражение (2). Воспользуемся одним из них. При этом параметры взаимодействия относительно движущихся зарядов запишем символом «v»:(6)
Здесь использована электрическая напряженность, создаваемая первым зарядом, через которую сила его действия на второй заряд записывается как.
Итак, после преобразования параметров закона Кулона (3) по выражениям (6) получается выражение (2) для силы взаимодействия относительно движущихся зарядов. Аналогичным образом, подставив в волновое уравнение (5) преобразования (6), получим выражение для воздействия движущегося переменного источника со скоростью v на приемник в следующем виде:
.
 (7)
(7)Очевидно, что уравнение (7) приводит к уравнению плоской волны
, (8)
с помощью выражений для частоты и направляющих косинусов волнового фронта движущегося источника в следующем виде вид:
, (9)
, (10)
, (11)
. (12)
Обратите внимание, что для направляющих косинусов это легко проверить.
5. Эффект Доплера и аберрация света
Рассмотрим изменение частоты света при движении источника. Пусть источник приближается по оси x с нормированной скоростью к приемнику, находящемуся впереди приемника. В этом случае нормаль фронта волны с осью x имеет нулевой угол: , т. е. при малой скорости движения источника, в выражении (9) можно пренебречь значением по сравнению с 1, и частота источника будет определяться по формуле
. (13)
Это совпадает с формулой классического эффекта Доплера. При движении источника к приемнику частота света будет увеличиваться. А по мере удаления источника от приемника частота света будет уменьшаться.
 Однако при скорости источника или приемника со скоростью, сравнимой со скоростью света, более точную формулу изменения частоты света от источника необходимо определить по формуле (9). При скорости v, сравнимой со скоростью света, изменение частоты источника будет существенно отличаться от величины, определяемой эффектом Доплера (13).
Однако при скорости источника или приемника со скоростью, сравнимой со скоростью света, более точную формулу изменения частоты света от источника необходимо определить по формуле (9). При скорости v, сравнимой со скоростью света, изменение частоты источника будет существенно отличаться от величины, определяемой эффектом Доплера (13).Рассмотрим изменение направления фронта световой волны при движении источника, т.е. аберрацию света (см. рис. 1). Пусть источник (S) движется вдоль оси x, а приемник (R) находится в плоскости x, y. Чтобы обозначения совпадали с принятыми в астрономии, заменим углы между нормалью фронта волны
Рис. 1. Изменение направления света при движении источника S. S – движущийся источник света, который наблюдается приемником R; S’ — неподвижный источник света, наблюдаемый приемником R.
движущегося источника S: и неподвижного источника:. Тогда выражение (10) для изменения фронта световой волны в источнике или при движении приемника запишется как:
.
 (14)
(14)Обозначим (см. рис. 1) разность углов нормали к фронтам световых волн неподвижного и движущегося источников символом, который называют углом световой аберрации. Из рисунка 1 видно, что
. (15)
Найдем выражение для угла аберрации. Для этого найдем из формулы (14):
(16)
Подставим из (15) в (16) и преобразуем косинус
. (17)
Как и в астрономии, используется угол аберрации, учитывающий орбитальное движение Земли. Поэтому он очень мал (около 20²) и его можно принять в (17). Поэтому из (17) находим, что:
. (18)
При малых нормированных скоростях движения источника вторым слагаемым в знаменателе можно пренебречь. Тогда угол аберрации будет определяться по формуле:
. (19)
В астрономии эта формула дает годовое движение звезд, вызванное движением Земли по орбите вокруг Солнца.
В последние десятилетия астрономы обнаружили объекты, которые движутся со скоростями, сравнимыми со скоростью света.
 Формула (19) будет для них некорректным. Изменения их угла направления фронта световой волны необходимо рассчитывать по формуле (10), или, в других обозначениях, по формуле (14).
Формула (19) будет для них некорректным. Изменения их угла направления фронта световой волны необходимо рассчитывать по формуле (10), или, в других обозначениях, по формуле (14).6. Выводы
1) Свет – электромагнитное воздействие источника на приемник.
2) Электромагнитное действие одного тела на другое зависит от скорости их относительного движения. Это действие не зависит от скорости перемещения приемника или источника из какой-либо воображаемой среды.
3) Нет светоносных сред (эфир, поле, среды физического вакуума и т.д.), относительно которых относительное движение источника или приемника изменило бы действие источника на приемник.
4) Изменение частоты света и его направления при движении источника относительно приемника полностью определяется законами электромагнетизма.
Благодарности
Благодарю доктора Синтию Колб Уитни за исправление английского языка в статье и полезные советы по его улучшению.
Ссылки


 ..
..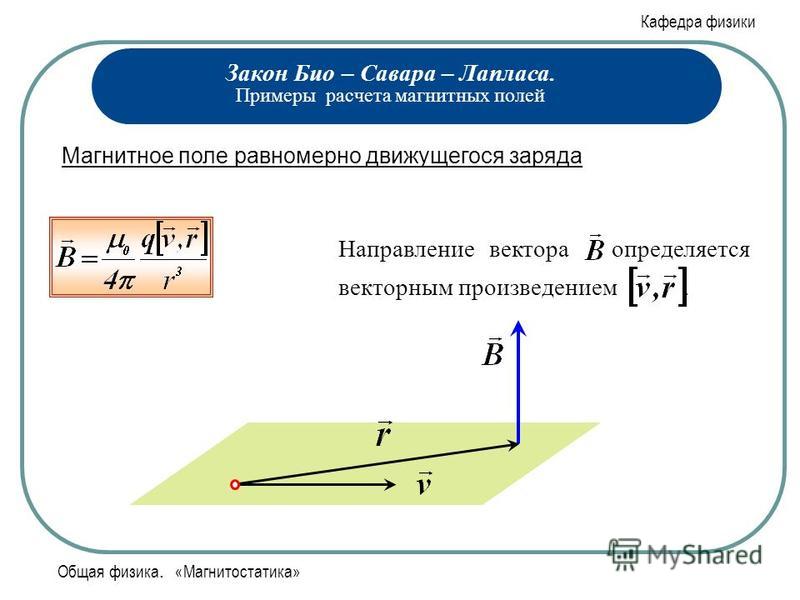 Поле при этом создано постоянным током на некотором участке. Формулировка закона Био Савара Лапласа имеет вид: При прохождении постоянного тока по замкнутому контуру, находящемуся в вакууме, для точки, отстоящей на расстоянии r0, от контура магнитная индукция будет иметь вид. . В этом случае α = π/2, sinα = 1; , где а – расстояние, отсчитываемое от центра витка до рассматриваемой точки на оси витка. Векторы образуют в этой точке конус с углом раствора при вершине 2 = π — 2β, где β – угол между отрезками а и r. Из соображений симметрии ясно, что результирующее магнитное поле на оси витка будет направлено вдоль этой оси, то есть вклад в него дают только те составляющие, которые параллельны оси витка: Результирующую величину индукции магнитного поля B на оси витка получим, проинтегрировав это выражение по длине контура от 0 до 2πR: или, подставив значение r:
Поле при этом создано постоянным током на некотором участке. Формулировка закона Био Савара Лапласа имеет вид: При прохождении постоянного тока по замкнутому контуру, находящемуся в вакууме, для точки, отстоящей на расстоянии r0, от контура магнитная индукция будет иметь вид. . В этом случае α = π/2, sinα = 1; , где а – расстояние, отсчитываемое от центра витка до рассматриваемой точки на оси витка. Векторы образуют в этой точке конус с углом раствора при вершине 2 = π — 2β, где β – угол между отрезками а и r. Из соображений симметрии ясно, что результирующее магнитное поле на оси витка будет направлено вдоль этой оси, то есть вклад в него дают только те составляющие, которые параллельны оси витка: Результирующую величину индукции магнитного поля B на оси витка получим, проинтегрировав это выражение по длине контура от 0 до 2πR: или, подставив значение r: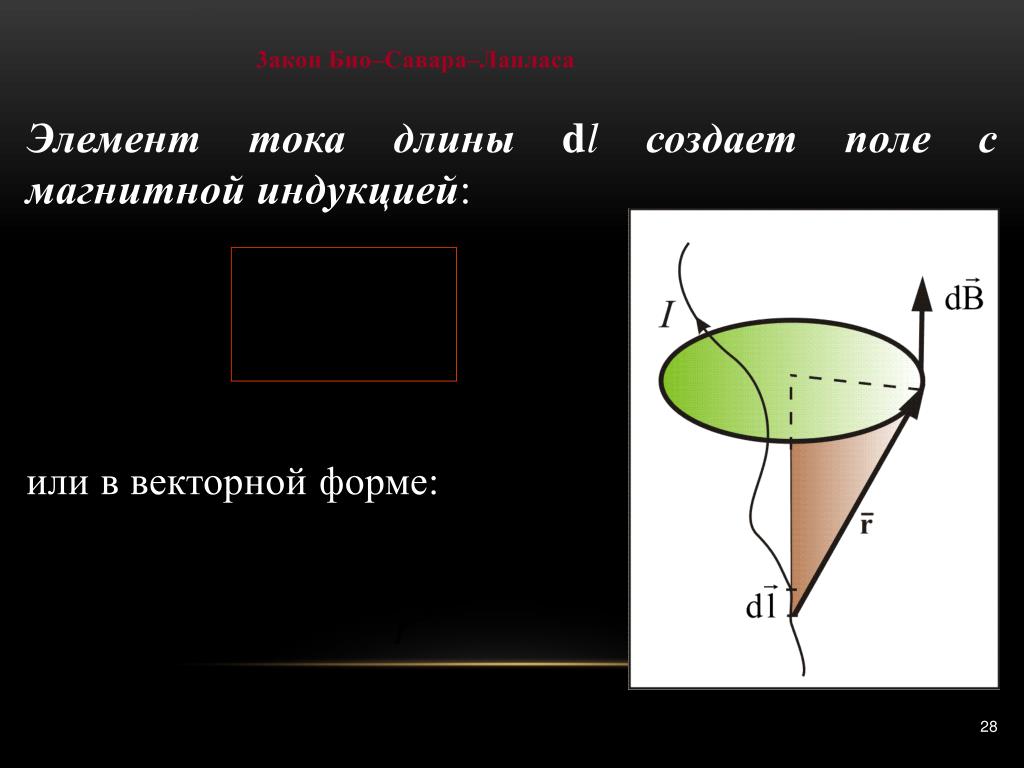 вектору магнитной индукции; б) скорость электрона направлена под углом α к полю магнитной индукции?
вектору магнитной индукции; б) скорость электрона направлена под углом α к полю магнитной индукции? Если энергия электрона выражена в эВ и равна U, то и поэтому . Кругообразное движение заряженных частиц в магнитном поле обладает важной особенностью: время полного обращения частицы по окружности (период движения) не зависит от энергии частицы. Действительно, период обращения равен Подставляя сюда вместо r его выражение, имеем: , а частота равна . Для данного типа частиц и период, и частота зависят только от индукции магнитного поля. Рассмотрим какой характер будет иметь движение, если начальная скорость частицы составляет некоторый угол с направлением поля. В этом случае удобно разложить скорость на две составляющие, одна из которых параллельна полю, а другая перпендикулярна к полю. На частицу действует сила Лоренца, и частица движется по окружности, лежащей в плоскости, перпендикулярной к полю. Составляющая Vt, не вызывает появления добавочной силы, так как сила Лоренца при движении параллельно полю равна нулю. Поэтому в направлении поля частица движется по инерции равномерно, со скоростью .
Если энергия электрона выражена в эВ и равна U, то и поэтому . Кругообразное движение заряженных частиц в магнитном поле обладает важной особенностью: время полного обращения частицы по окружности (период движения) не зависит от энергии частицы. Действительно, период обращения равен Подставляя сюда вместо r его выражение, имеем: , а частота равна . Для данного типа частиц и период, и частота зависят только от индукции магнитного поля. Рассмотрим какой характер будет иметь движение, если начальная скорость частицы составляет некоторый угол с направлением поля. В этом случае удобно разложить скорость на две составляющие, одна из которых параллельна полю, а другая перпендикулярна к полю. На частицу действует сила Лоренца, и частица движется по окружности, лежащей в плоскости, перпендикулярной к полю. Составляющая Vt, не вызывает появления добавочной силы, так как сила Лоренца при движении параллельно полю равна нулю. Поэтому в направлении поля частица движется по инерции равномерно, со скоростью . В результате сложения обоих движений частица будет двигаться по цилиндрической спирали. Шаг винта этой спирали равен подставляя вместо T его выражение, имеем:
В результате сложения обоих движений частица будет двигаться по цилиндрической спирали. Шаг винта этой спирали равен подставляя вместо T его выражение, имеем: Магнитное поле прямого, кругового и соленоидального токов.
Магнитное поле прямого, кругового и соленоидального токов. Завет мужчины с женщиной
Завет мужчины с женщиной
 Следовательно:
Следовательно: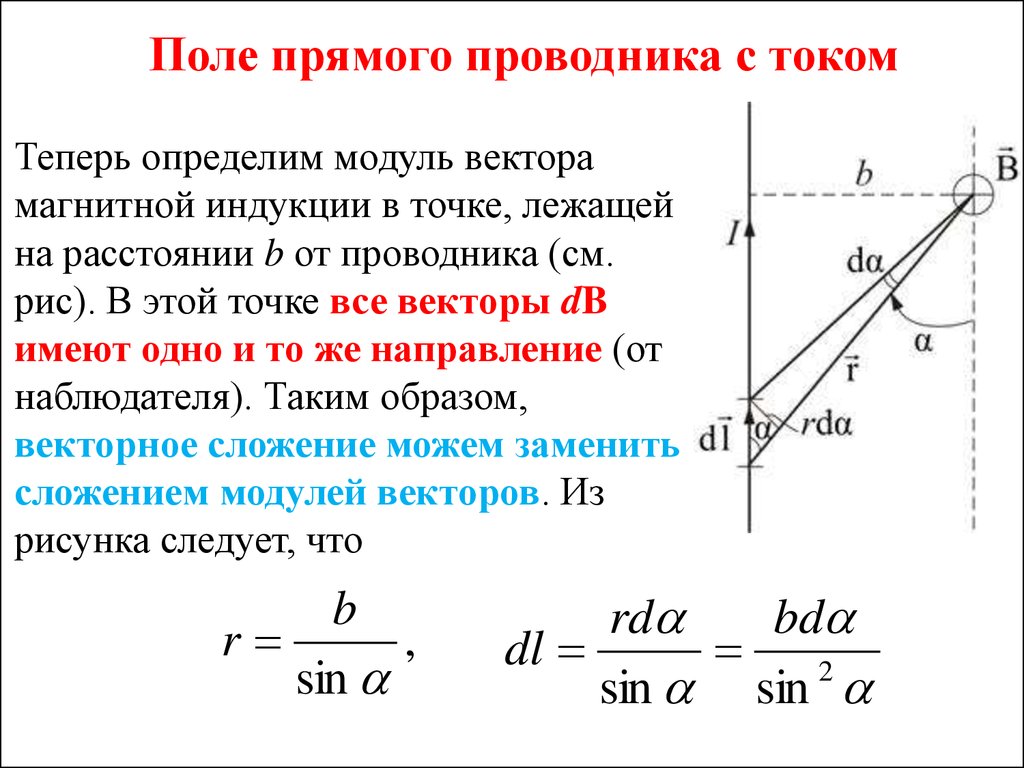 10)
10)
 15)
15)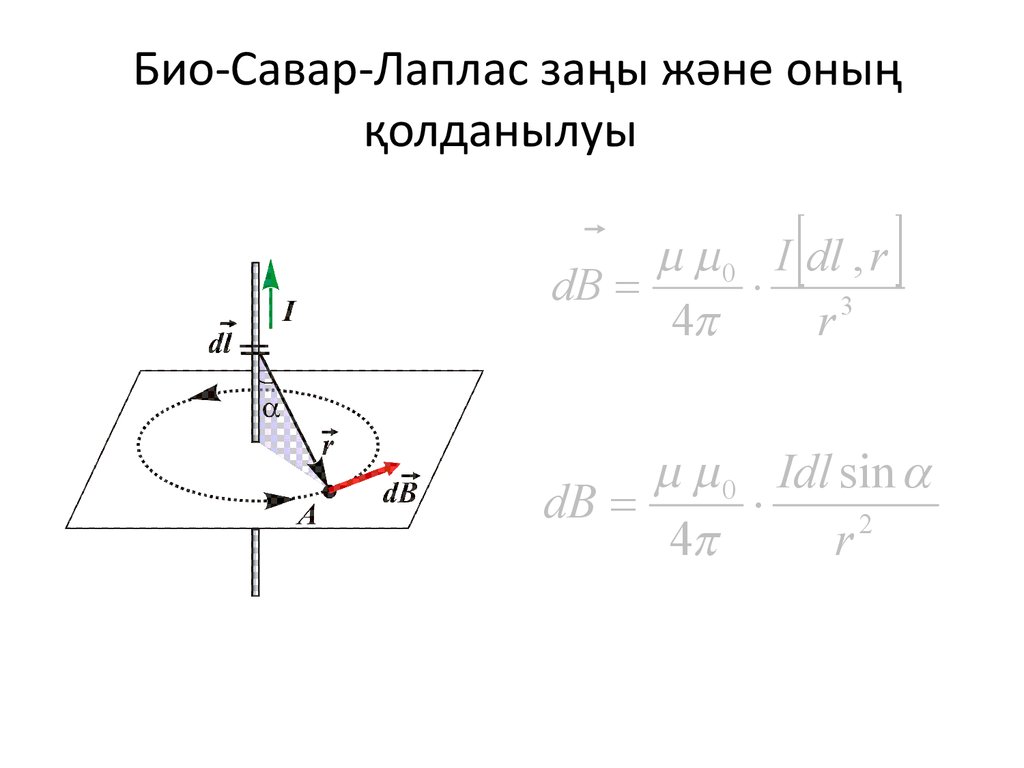 2.Магнитная индукция в центре кругового тока определяется по формуле…
2.Магнитная индукция в центре кругового тока определяется по формуле… Магнитный поток. Сила Ампера. Работа по перемещению проводника с током в магнитном поле. Сила Лоренца. Определение удельного заряда электрона[11]
Магнитный поток. Сила Ампера. Работа по перемещению проводника с током в магнитном поле. Сила Лоренца. Определение удельного заряда электрона[11] ru Все права принадлежат авторам размещенных материалов. Обратная связь…
ru Все права принадлежат авторам размещенных материалов. Обратная связь… Все правила по сольфеджио
Все правила по сольфеджио
 6).
6). Тогда . С учетом этого получаем
Тогда . С учетом этого получаем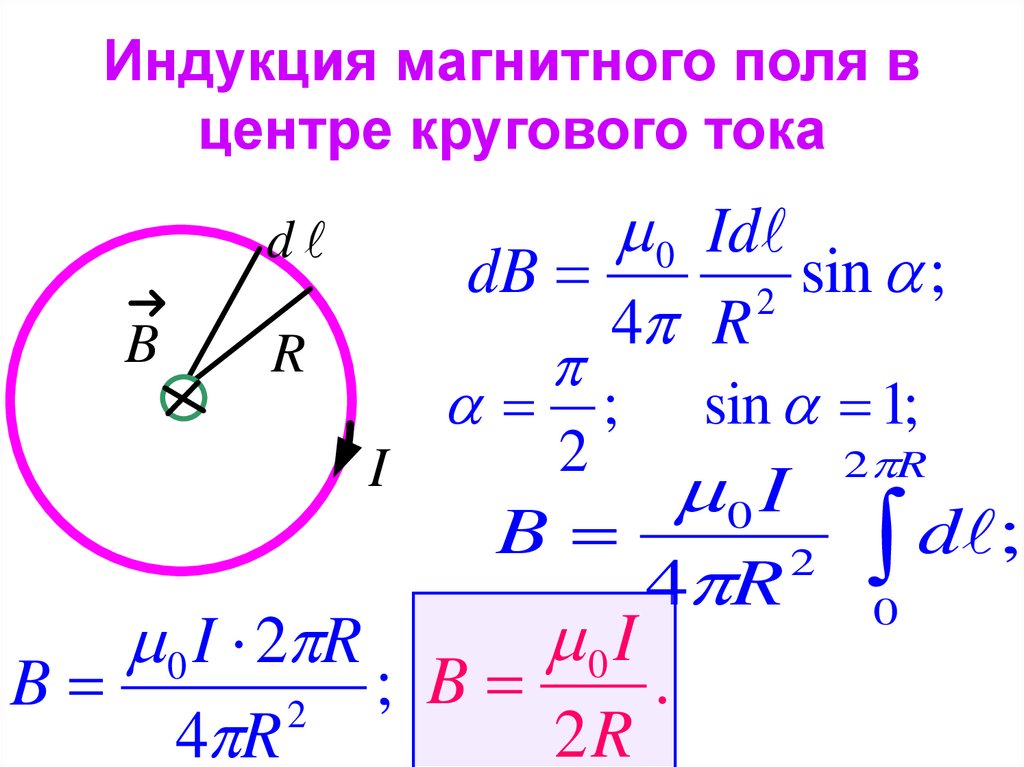

 С учетом этого получаем .
С учетом этого получаем .


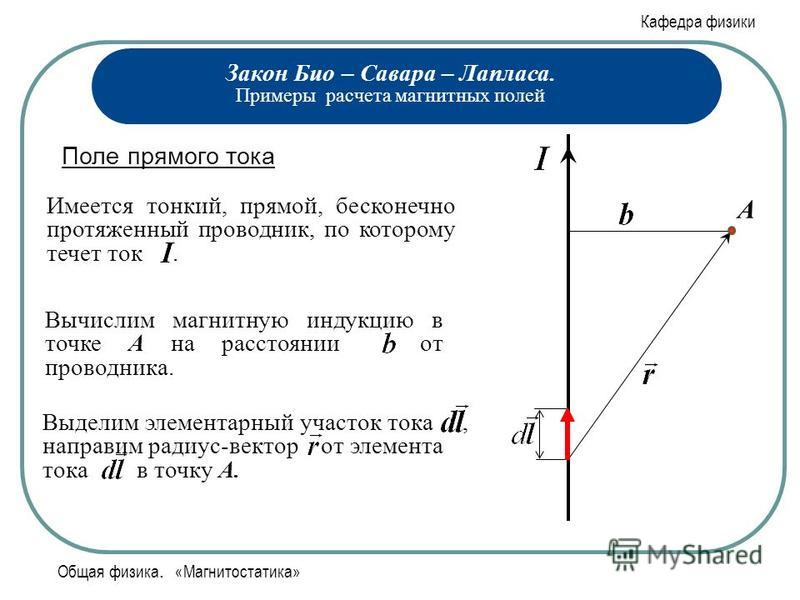 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.022 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.022 с.)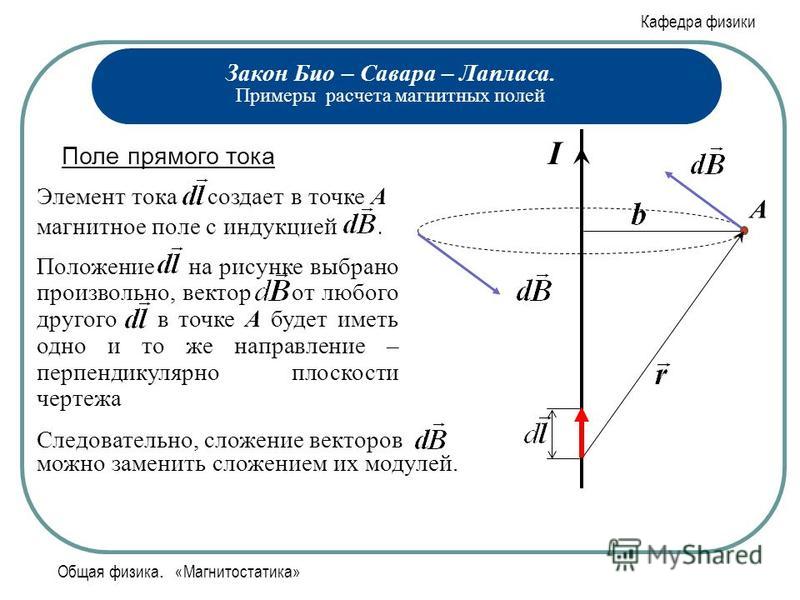 Отмечается наличие неточностей в толковании закона Био-Савара-Лапласа. Показано, что в электроэнергетике простая формула, основанная на использовании закона Био-Савара-Лапласа и экспериментально полученных поправочных коэффициентов, может быть использована для расчета магнитных полей, создаваемых переменными токами в шинах…
Отмечается наличие неточностей в толковании закона Био-Савара-Лапласа. Показано, что в электроэнергетике простая формула, основанная на использовании закона Био-Савара-Лапласа и экспериментально полученных поправочных коэффициентов, может быть использована для расчета магнитных полей, создаваемых переменными токами в шинах… 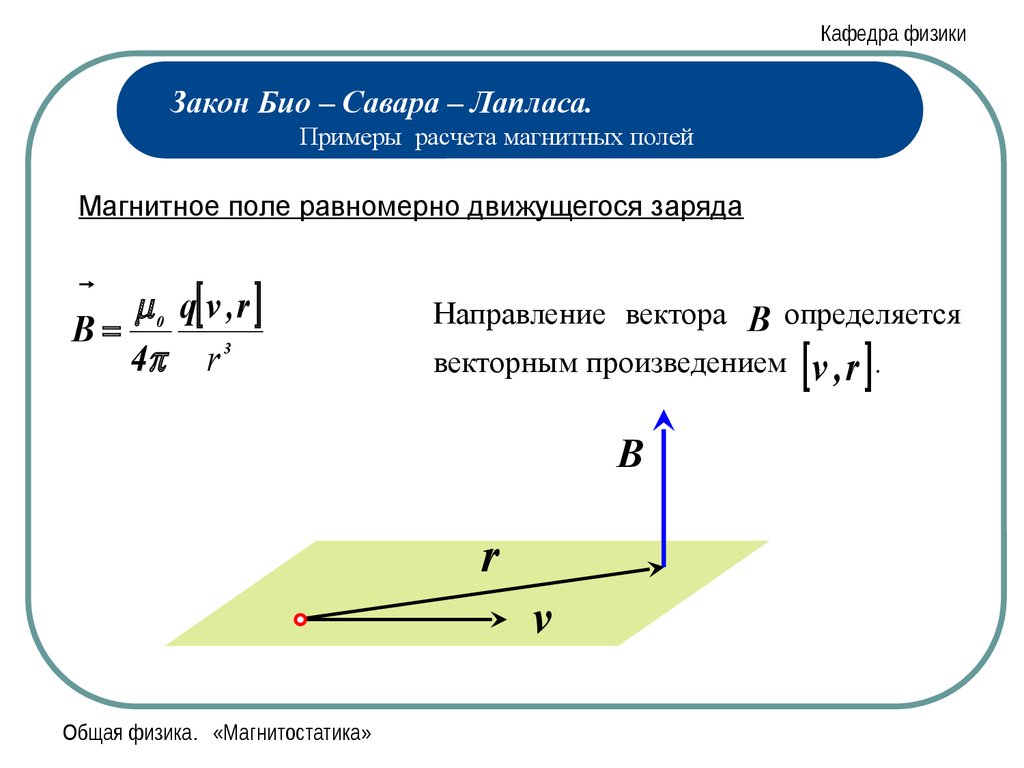
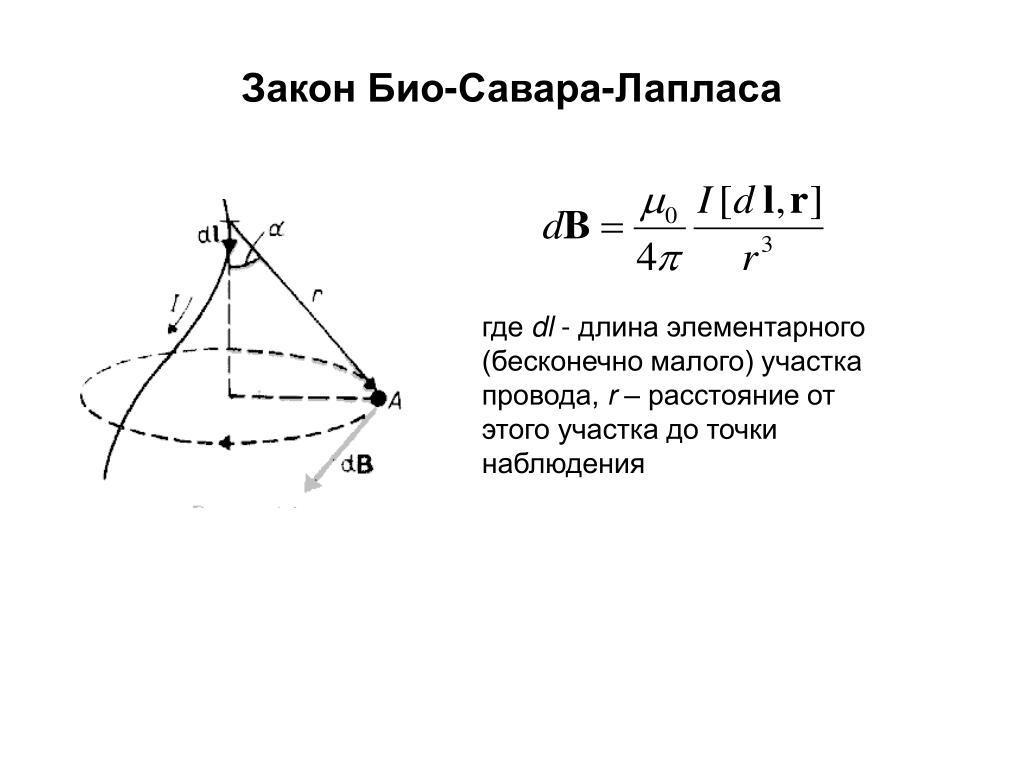
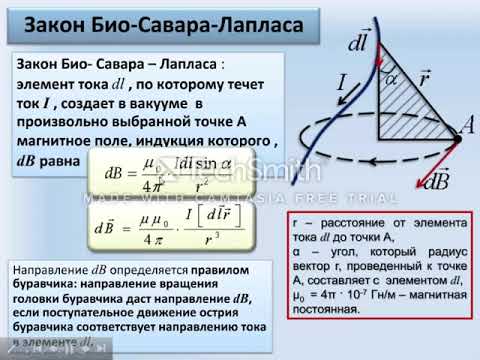 Надежность их работы может…
Надежность их работы может…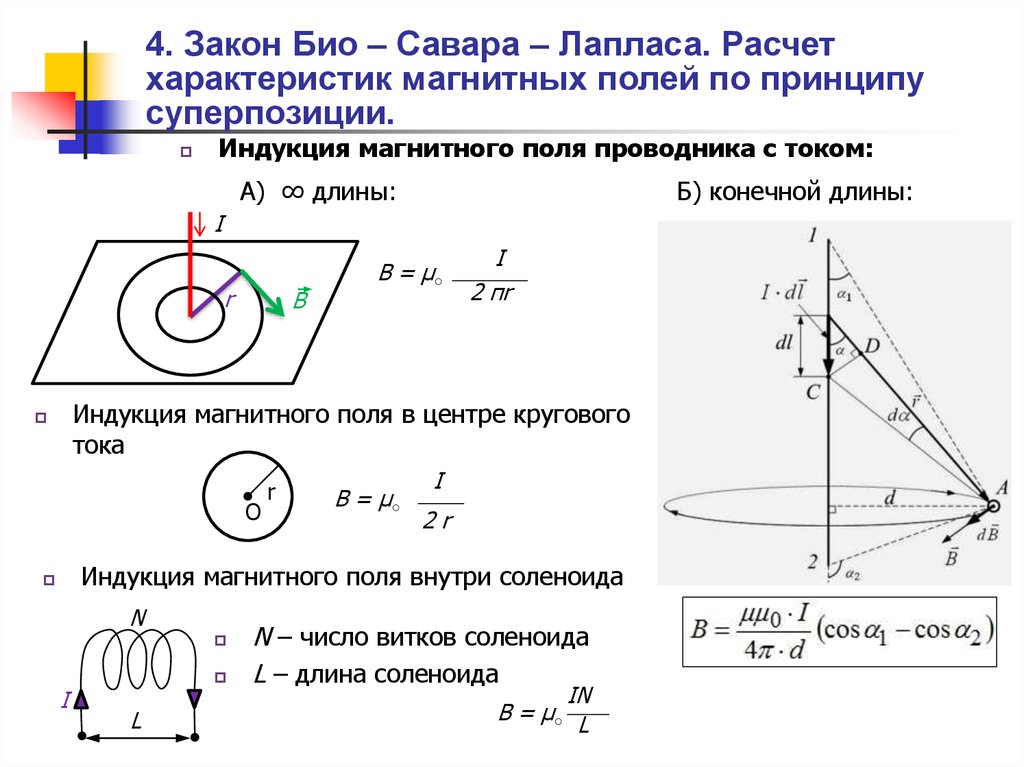
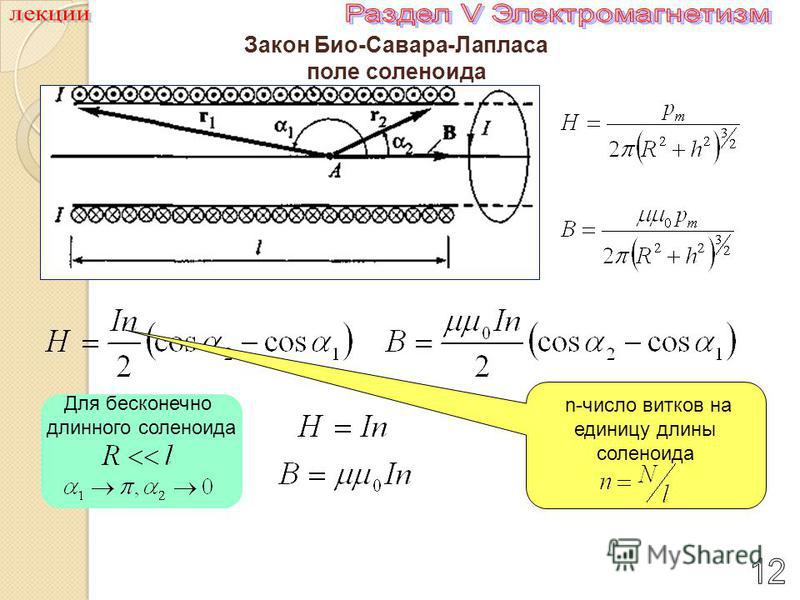 Electromechanics
Electromechanics Поскольку закон Кулона является основным для электростатики, аналогичным образом закон Био-Савара также является основным для магнитостатики. В 1820 году два французских физика Жан Батист Био и Феликс Савар создали формулировку закона Био-Савара, которая вывела математическую формулу для r плотность магнитного потока в точке из-за близлежащего проводника с током. Наблюдая за отклонением стрелки магнитного компаса, эти ученые пришли к выводу, что частица тока проецирует магнитное поле в окружающее ее пространство.
Поскольку закон Кулона является основным для электростатики, аналогичным образом закон Био-Савара также является основным для магнитостатики. В 1820 году два французских физика Жан Батист Био и Феликс Савар создали формулировку закона Био-Савара, которая вывела математическую формулу для r плотность магнитного потока в точке из-за близлежащего проводника с током. Наблюдая за отклонением стрелки магнитного компаса, эти ученые пришли к выводу, что частица тока проецирует магнитное поле в окружающее ее пространство. Провод показан на картинке ниже красным цветом. Также рассмотрим бесконечно малую длину провода dl на расстоянии r от точки P, как показано на схеме. Здесь r — вектор расстояния, который составляет угол θ с направлением тока в мельчайшей части провода.
Провод показан на картинке ниже красным цветом. Также рассмотрим бесконечно малую длину провода dl на расстоянии r от точки P, как показано на схеме. Здесь r — вектор расстояния, который составляет угол θ с направлением тока в мельчайшей части провода. {2}}\] 9\theta2\]
{2}}\] 9\theta2\]
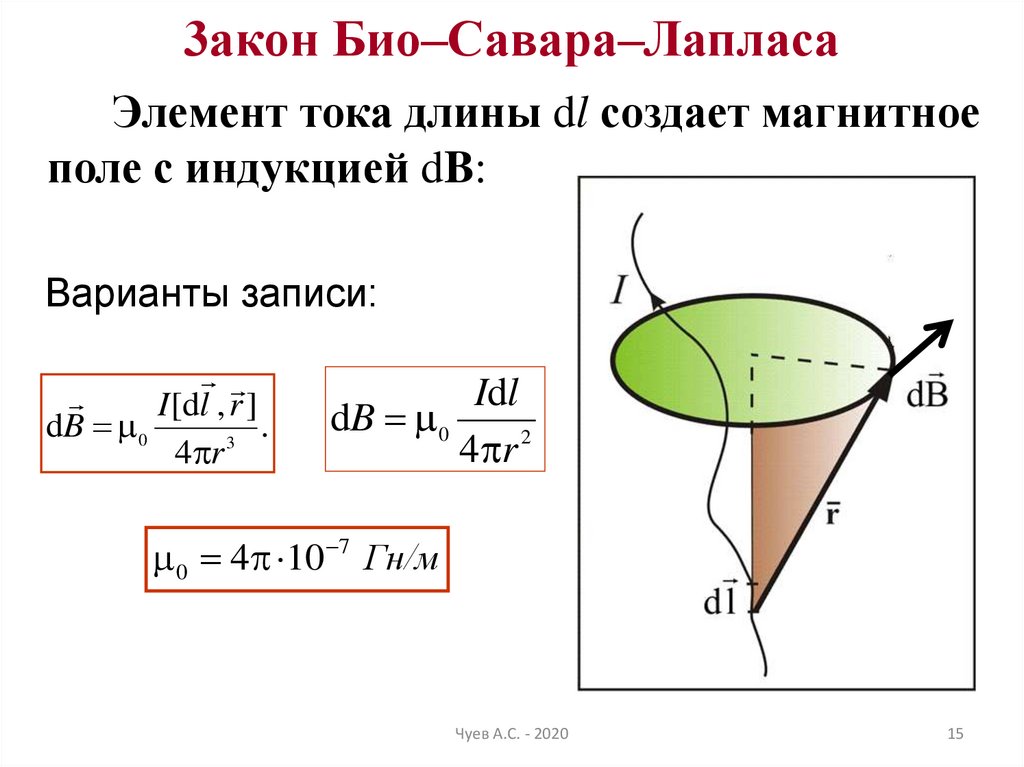 … Он играет ту же роль, что и закон Кулона в электростатике, но в магнитостатике.
… Он играет ту же роль, что и закон Кулона в электростатике, но в магнитостатике. … И мы также заменяем электрическое поле E на элемент магнитного поля в дБ, потому что движущийся заряд создает магнитное поле, а не электрическое поле. 11 марта 2021 г.
… И мы также заменяем электрическое поле E на элемент магнитного поля в дБ, потому что движущийся заряд создает магнитное поле, а не электрическое поле. 11 марта 2021 г.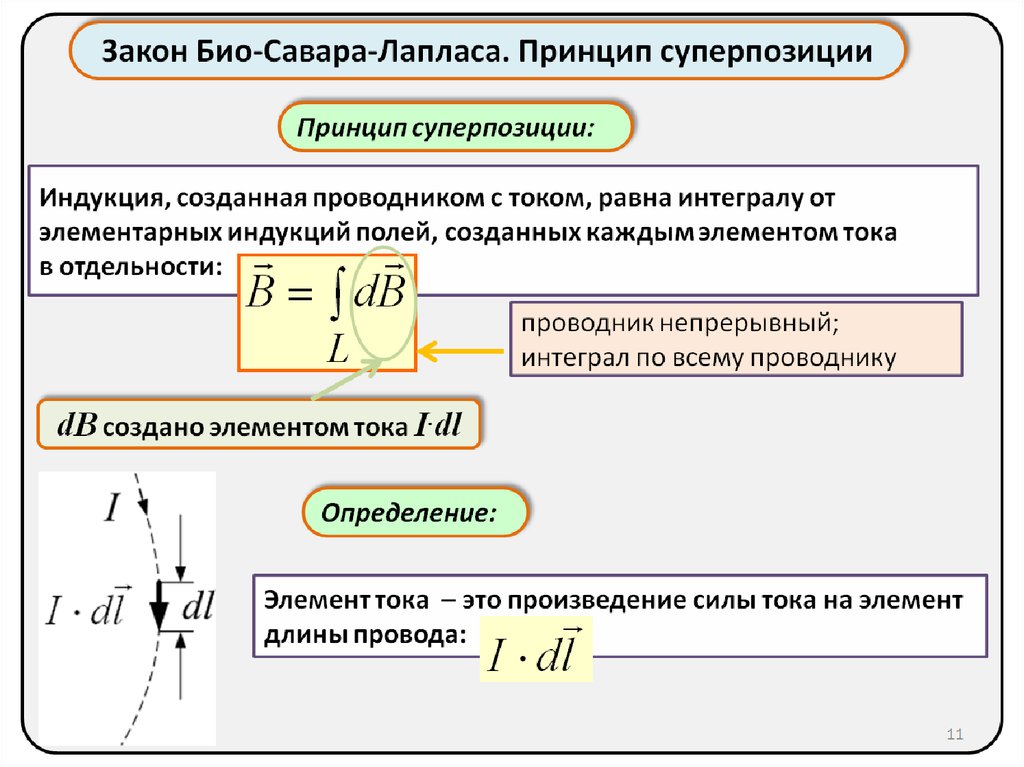 … Величина магнитного поля dB на расстоянии r от токоведущего элемента dl оказывается пропорциональной I и длине dl. И обратно пропорциональна квадрату расстояния |r|.
… Величина магнитного поля dB на расстоянии r от токоведущего элемента dl оказывается пропорциональной I и длине dl. И обратно пропорциональна квадрату расстояния |r|.
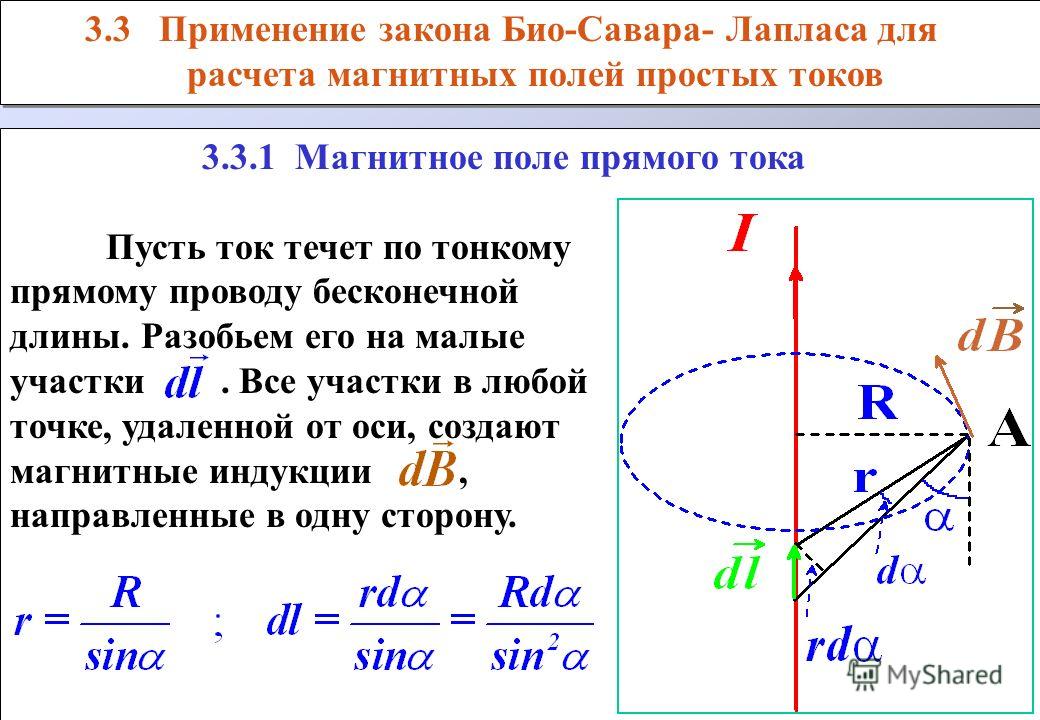
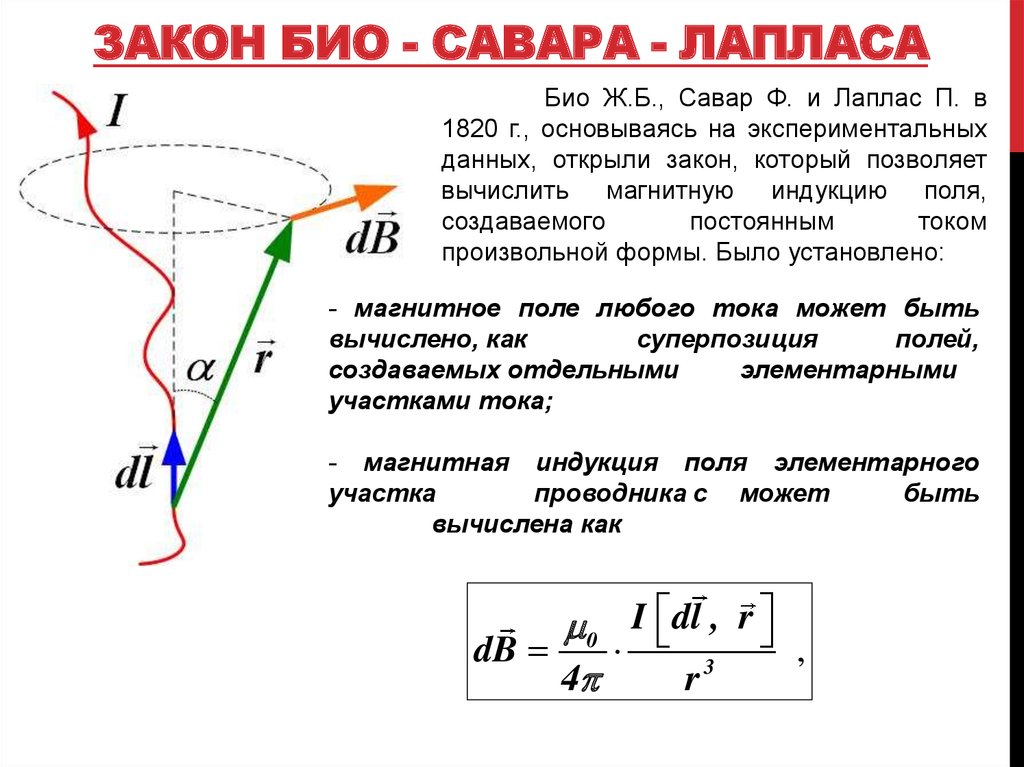 Рассматривая параллельно с законом Кулона и Гаусса небольшое увеличение сложности, мы можем получить закон Био-Савара из закона Ампера. Мы знаем, что векторная способность связана с магнитным полем соотношением B=∇×AB=∇×A.
Рассматривая параллельно с законом Кулона и Гаусса небольшое увеличение сложности, мы можем получить закон Био-Савара из закона Ампера. Мы знаем, что векторная способность связана с магнитным полем соотношением B=∇×AB=∇×A. Эрреде
Эрреде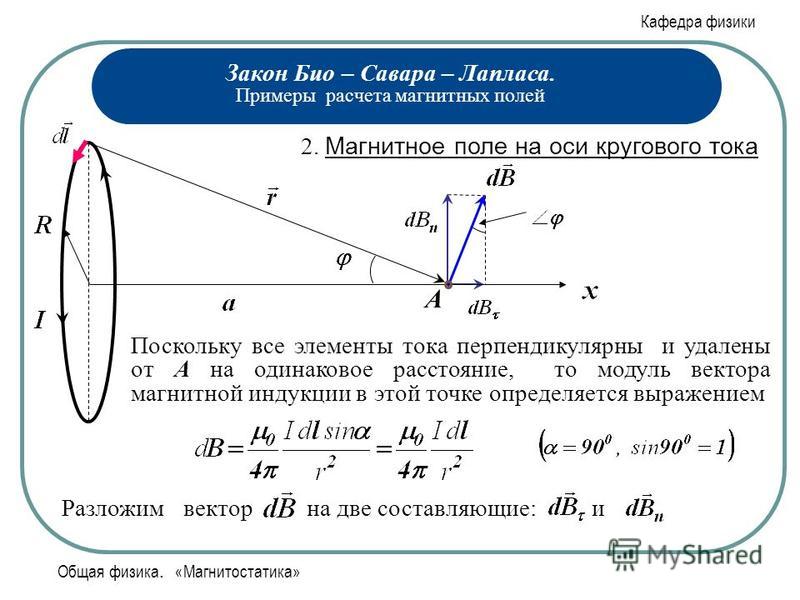 ..
..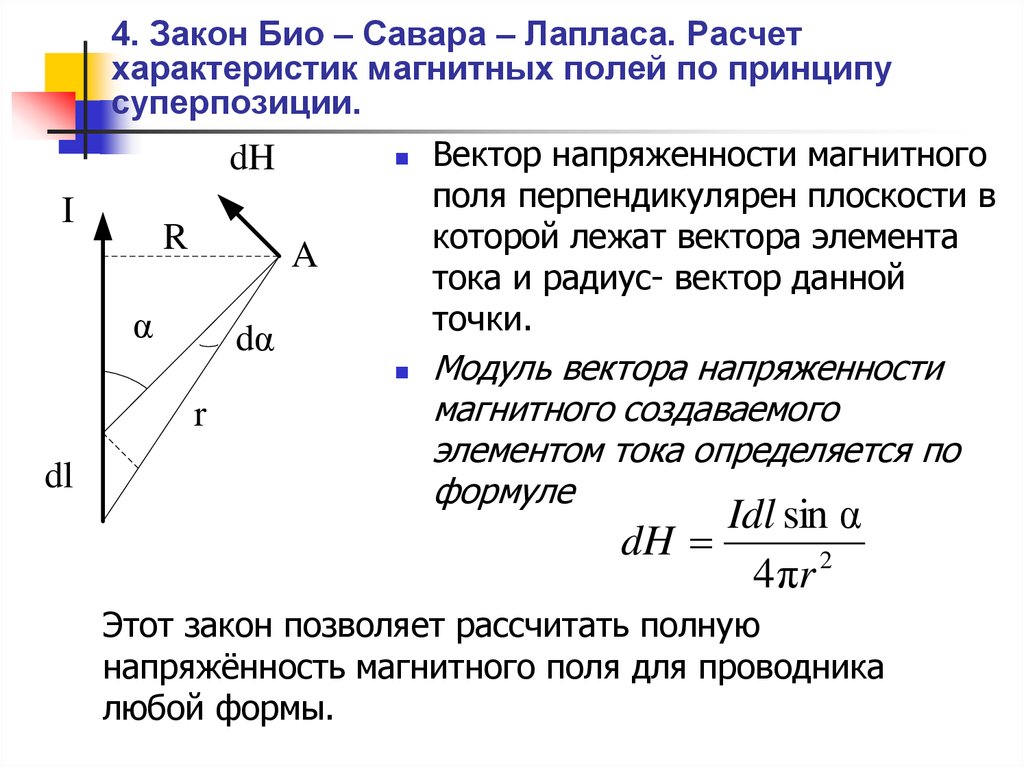 5: Магнитостатические краевые задачи
5: Магнитостатические краевые задачи Эрреде
Эрреде  Уравнения Максвелла, плоские векторы, поляризация, параметры Стокса, вектор Джонса, отражение, преломление
Уравнения Максвелла, плоские векторы, поляризация, параметры Стокса, вектор Джонса, отражение, преломление  Ковариантная геометрия, ковариантные уравнения Максвелла Решение для домашнего задания
Ковариантная геометрия, ковариантные уравнения Максвелла Решение для домашнего задания  23 Домашнее задание
23 Домашнее задание  13 Решение для домашнего задания
13 Решение для домашнего задания  12 Решение для домашних заданий
12 Решение для домашних заданий 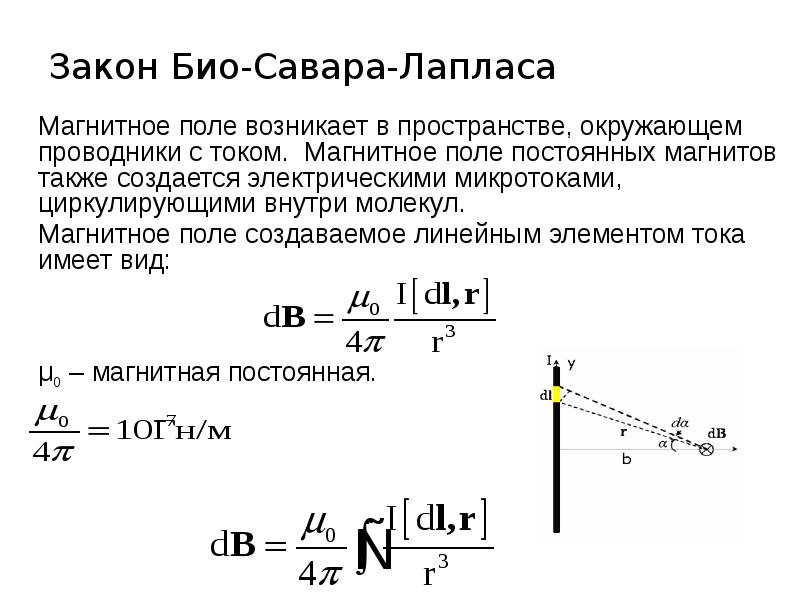 ; пересмотрено 7 сентября 2014 г.; принята 1 октября 2014 г.
; пересмотрено 7 сентября 2014 г.; принята 1 октября 2014 г.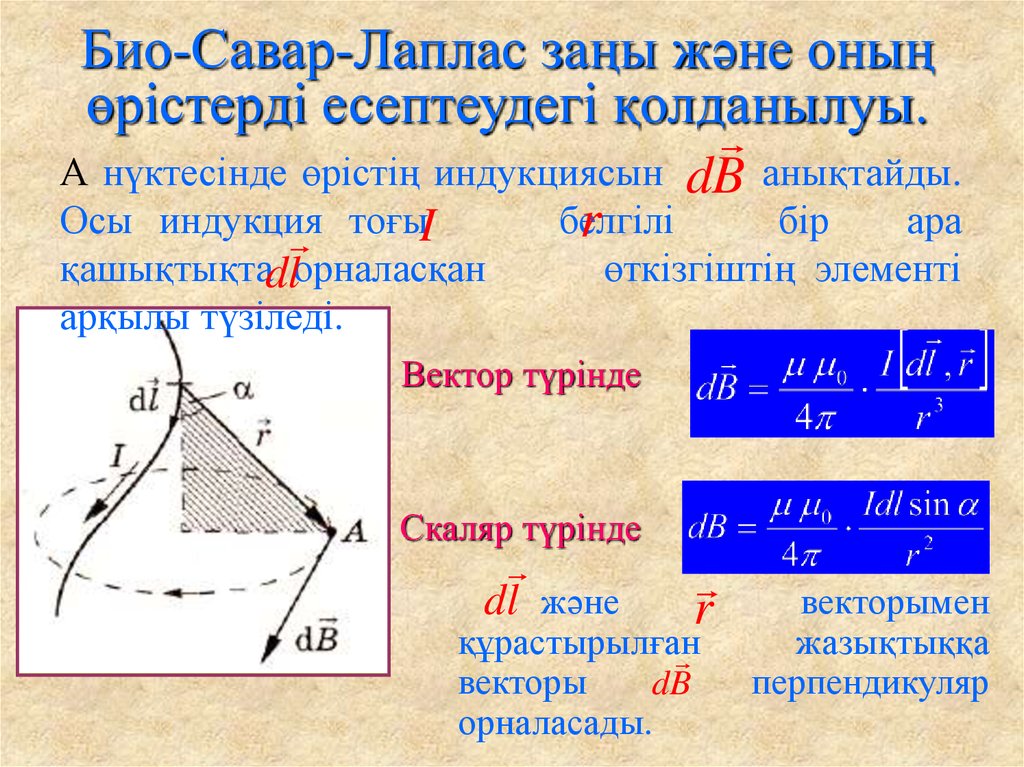 Введение
Введение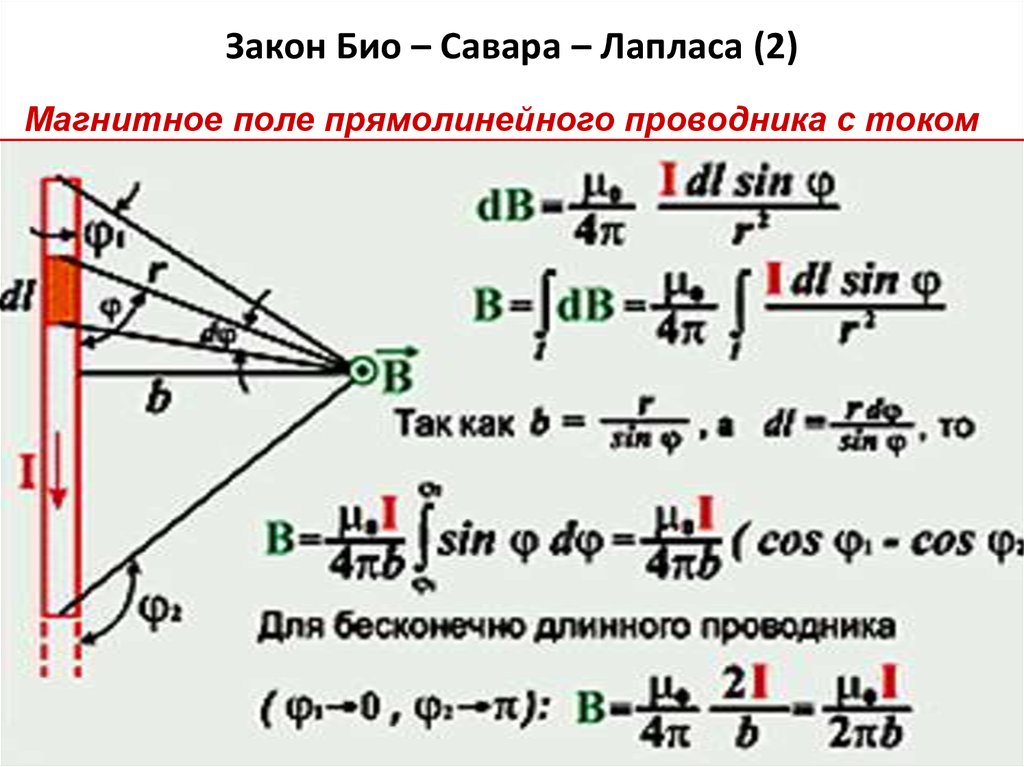 Поэтому в любой точке пространства вблизи средней плоскости конденсатора, на помещенную в него заряженную частицу или на магнитный полюс будет действовать то, что направлено перпендикулярно направлению этой точки от конденсатора. Поэтому элементарные волны называются «поперечными».
Поэтому в любой точке пространства вблизи средней плоскости конденсатора, на помещенную в него заряженную частицу или на магнитный полюс будет действовать то, что направлено перпендикулярно направлению этой точки от конденсатора. Поэтому элементарные волны называются «поперечными». По-видимому, это в значительной мере относится и к свету. Есть ряд его свойств, которые для других электромагнитных волн не проявляются. Однако существует единая электромагнитная природа света и радиоволн относительно действия движущегося электромагнитного источника на приемник. В частности, существуют одинаковые законы изменения характеристик электромагнитного воздействия источника при его движении относительно приемника.
По-видимому, это в значительной мере относится и к свету. Есть ряд его свойств, которые для других электромагнитных волн не проявляются. Однако существует единая электромагнитная природа света и радиоволн относительно действия движущегося электромагнитного источника на приемник. В частности, существуют одинаковые законы изменения характеристик электромагнитного воздействия источника при его движении относительно приемника.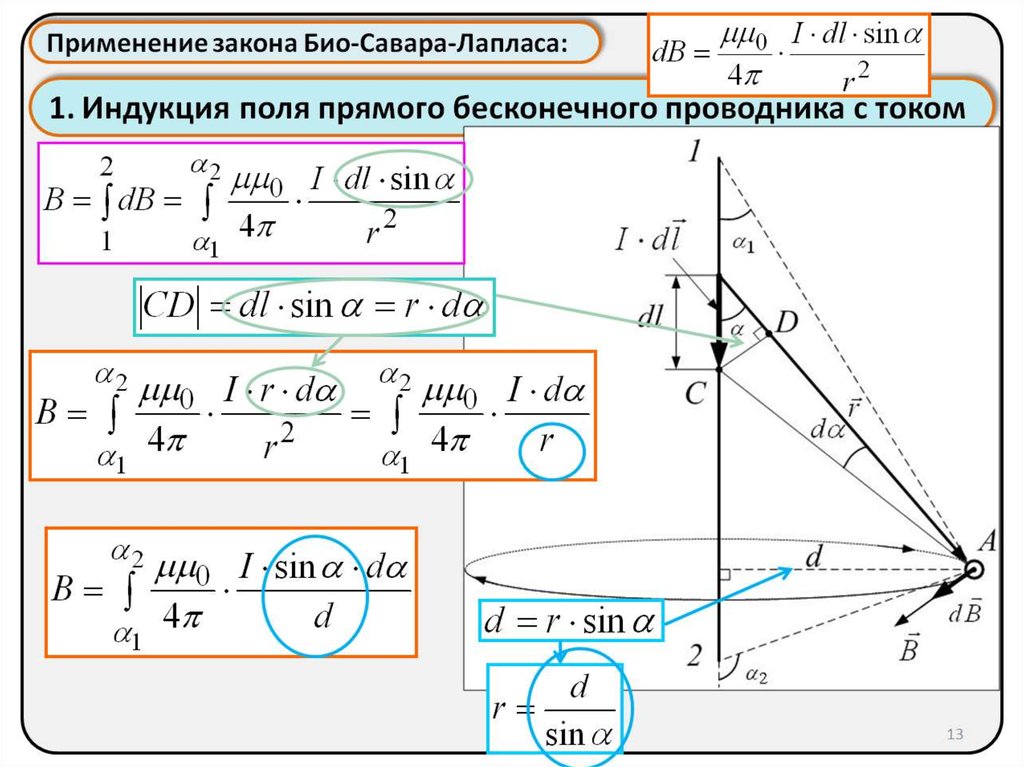 Величина тока не зависит от того, движется ли катушка или магнит. Сила течения определяется по скорости их относительного движения. Как известно [1], это явление описывается индукцией по закону Фарадея.
Величина тока не зависит от того, движется ли катушка или магнит. Сила течения определяется по скорости их относительного движения. Как известно [1], это явление описывается индукцией по закону Фарадея. В свою очередь, эти уравнения являются другой формой записи двух экспериментальных законов [1]: закона индукции Фарадея и закона Био-Савара-Лапласа. Исключая из уравнений Максвелла магнитную напряженность H, получаем уравнение Даламбера для электрической напряженности E
В свою очередь, эти уравнения являются другой формой записи двух экспериментальных законов [1]: закона индукции Фарадея и закона Био-Савара-Лапласа. Исключая из уравнений Максвелла магнитную напряженность H, получаем уравнение Даламбера для электрической напряженности E
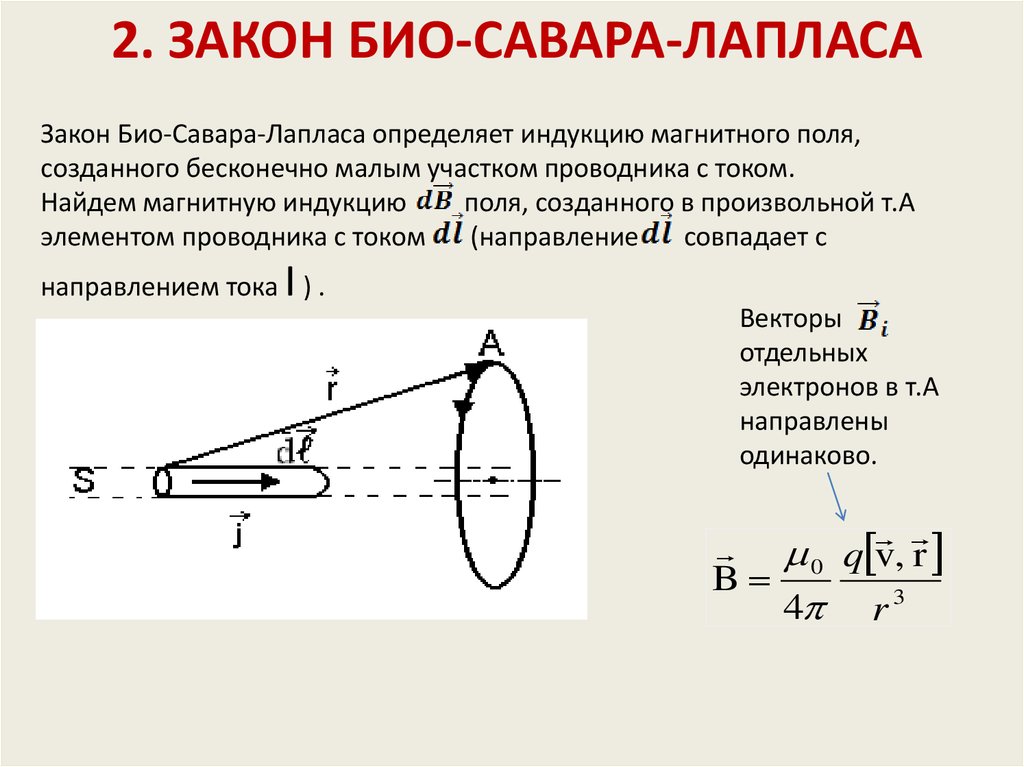

 В работах [2][3] мы пошли другим путем. Мы задались вопросом: при каких условиях выражение (2) для силы взаимодействия относительно движущихся заряженных частиц будет совпадать с законом Кулона (3) для силы взаимодействия неподвижных заряженных частиц? Очевидно, что для этого необходимо величины, входящие в выражение (3), выразить через величины, от которых зависит (2). Оказалось, что существует два варианта преобразования выражения (3) в выражение (2). Воспользуемся одним из них. При этом параметры взаимодействия относительно движущихся зарядов запишем символом «v»:
В работах [2][3] мы пошли другим путем. Мы задались вопросом: при каких условиях выражение (2) для силы взаимодействия относительно движущихся заряженных частиц будет совпадать с законом Кулона (3) для силы взаимодействия неподвижных заряженных частиц? Очевидно, что для этого необходимо величины, входящие в выражение (3), выразить через величины, от которых зависит (2). Оказалось, что существует два варианта преобразования выражения (3) в выражение (2). Воспользуемся одним из них. При этом параметры взаимодействия относительно движущихся зарядов запишем символом «v»: (7)
(7) Однако при скорости источника или приемника со скоростью, сравнимой со скоростью света, более точную формулу изменения частоты света от источника необходимо определить по формуле (9). При скорости v, сравнимой со скоростью света, изменение частоты источника будет существенно отличаться от величины, определяемой эффектом Доплера (13).
Однако при скорости источника или приемника со скоростью, сравнимой со скоростью света, более точную формулу изменения частоты света от источника необходимо определить по формуле (9). При скорости v, сравнимой со скоростью света, изменение частоты источника будет существенно отличаться от величины, определяемой эффектом Доплера (13). (14)
(14) Формула (19) будет для них некорректным. Изменения их угла направления фронта световой волны необходимо рассчитывать по формуле (10), или, в других обозначениях, по формуле (14).
Формула (19) будет для них некорректным. Изменения их угла направления фронта световой волны необходимо рассчитывать по формуле (10), или, в других обозначениях, по формуле (14).