Site Loader
Posted on 09.04.2021

Закон Ампера — Студопедия

Закон Ампера показывает, с какой силой действует магнитное поле на помещенный в него проводник. Эту силу также называют силой Ампера.

Формулировка закона: сила, действующая на проводник с током, помещенный в однородное магнитное поле, пропорциональна длине проводника, вектору магнитной индукции, силе тока и синусу угла между вектором магнитной индукции и проводником.

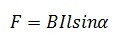
Если размер проводника произволен, а поле неоднородно, то формула выглядит следующим образом:

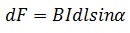
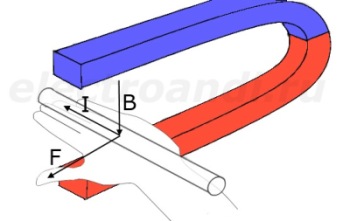
Направление силы Ампера определяется по правилу левой руки.

Правило левой руки: если расположить левую руку так, чтобы перпендикулярная составляющая вектора магнитной индукции входила в ладонь, а четыре пальца были вытянуты по направлению тока в проводнике, то отставленный на 90

°большой палец, укажет направление силы Ампера.

МП движущего заряда. Действие МП на движущийся заряд. Сила Ампера, Лоренца.

Любой проводник с током создает в окружающем пространстве магнитное поле. При этом электрический же ток является упорядоченным движением электрических зарядов. Значит можно считать, что любой движущийся в вакууме или среде заряд порождает вокруг себя магнитное поле. В результате обобщения многочисленных опытных данных был установлен закон, который определяет поле В точечного заряда Q, движущегося с постоянной нерелятивистской скоростью v. Этот закон задается формулой

(1)

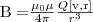
где r — радиус-вектор, который проведен от заряда Q к точке наблюдения М (рис. 1). Согласно (1), вектор В направлен перпендикулярно плоскости, в которой находятся векторы v и r: его направление совпадает с направлением поступательного движения правого винта при его вращении от v к r.


 

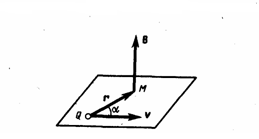
Рис.1

Модуль вектора магнитной индукции (1) находится по формуле

(2)

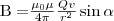
где α — угол между векторами v и r. Сопоставляя закон Био-Савара-Лапласа и (1), мы видим, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока: Idl = Qv

Действие МП на движущийся заряд.

Из опыта известно, что магнитное поле оказывает действие не только на проводники с током, но и на отдельные заряды, которые движутся в магнитном поле. Сила, которая действует на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и задается выражением: F = Q где В — индукция магнитного поля, в котором заряд движется.

Чтобы определить направление силы Лоренца используем правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q>0 направления I и v совпадают, для Q На рис. 1 продемонстрирована взаимная ориентация векторов v, В (поле имеет направление на нас, на рисунке показано точками) и F для положительного заряда. Если заряд отрицательный, то сила действует в противоположном направлении.


Модуль силы Лоренца, как уже известно, равен F = QvB sin a; где α — угол между v и В.

МП не оказывает действия на покоящийся электрический заряд. Этим магнитное поле существенно отличается от электрического. Магнитное поле действует только на движущиеся в нем заряды.

Зная действие силы Лоренца на заряд можно найти модуль и направление вектора В, и формула для силы Лоренца может быть применена для нахождения вектора магнитной индукции В.

Поскольку сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, то данная сила может менять только направление этой скорости, не изменяя при этом ее модуля. Значит, сила Лоренца работы не совершает.

В случае, если на движущийся электрический заряд вместе с магнитным полем с индукцией В действует еще и электрическое поле с напряженностью Е, то суммарная результирующая сила F, которая приложена приложенная к заряду, равна векторной сумме сил — силы, действующей со стороны электрического поля, и силы Лоренца: F = QE + Q[v,B]

Сила Ампера, Лоренца.

Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.

Сила действия однородного маг­нитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником:

F = B.I.l. sin α — закон Ампера.

Сила, действующая на заряженную движущуюся частицу в магнитном поле, называется силой Лоренца:

 

Явление электромагнитной индукции. Закон Фарадея. ЭДС индукции в движущихся проводниках. Самоиндукция.

Фарадей предположил, что если вокруг проводника с током существует магнитное поле, то естественно ожидать, что должно происходить и обратное явление – возникновение электрического тока под действием магнитного поля. И вот в 1831 г. Фарадей публикует статью, где сообщает об открытии нового явления – явления электромагнитной индукции.

Опыты Фарадея были чрезвычайно просты. Он присоединял гальванометр G к концам катушки L и приближал к ней магнит. Стрелка гальванометра отклонялась, фиксируя появление тока в цепи. Ток протекал, пока магнит двигался. При отдалении магнита от катушки гальванометр отмечал появление тока противоположного направления. Аналогичный результат отмечался, если магнит заменяли катушкой с током или замкнутым контуром с током.

Движущиеся магнит или проводник с током создают через катушку L переменное магнитное поле. В случае их неподвижности создаваемое ими поле постоянно. Если вблизи замкнутого контура поместить проводник с переменным током, то в замкнутом контуре также возникнет ток. На основе анализа опытных данных Фарадей установил, что ток в проводящих контурах появляется при изменении магнитного потока через площадь, ограниченную этим контуром.

Этот ток был назван индукционным. Открытие Фарадея было названо явлением электромагнитной индукции и легло в дальнейшем в основу работы электрических двигателей, генераторов, трансформаторов и подобных им приборов.

Итак, если магнитный поток через поверхность, ограниченную некоторым контуром, изменяется, то в контуре возникает электрический ток. Известно, что электрический ток в проводнике может возникнуть только под действием сторонних сил, т.е. при наличии э.д.с.. В случае индукционного тока э.д.с., соответствующая сторонним силам, называется электродвижущей силой электромагнитной индукции εi.

Э.д.с. электромагнитной индукции в контуре пропорциональна скорости изменения магнитного потока Фm сквозь поверхность, ограниченную этим контуром:

 

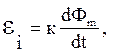где к – коэффициент пропорциональности. Данная э.д.с. не зависит от того, чем вызвано изменение магнитного потока – либо перемещением контура в постоянном магнитном поле, либо изменением самого поля.

Итак, направление индукционного тока определяется правилом Ленца: При всяком изменении магнитного потока сквозь поверхность, ограниченную замкнутым проводящим контуром, в последнем возникает индукционный ток такого направления, что его магнитное поле противодействует изменению магнитного потока.

Обобщением закона Фарадея и правила Ленца является закон Фарадея — Ленца: Электродвижущая сила электромагнитной индукции в замкнутом проводящем контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную контуром:

 

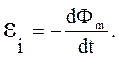Это выражение представляет собой основной закон электромагнитной индукции.

При скорости изменения магнитного потока 1Вб/с в контуре индуцируется э.д.с. в 1 В.

Пусть контур, в котором индуцируется э.д.с., состоит не из одного, а из N витков, например, представляет собой соленоид. Соленоид – это цилиндрическая катушка с током, состоящая из большого числа витков. Так как витки в соленоиде соединяются последовательно, εi в данном случае будет равна сумме э.д.с., индуцируемых в каждом из витков по отдельности

:

 


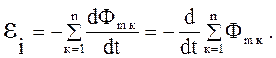Величину Ψ = ΣΦm называют потокосцеплением или полным магнитным потоком. Если поток, пронизывающий каждый из витков, одинаков (т.е. Ψ = NΦm), то в этом случае

 


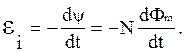Немецкий физик Г. Гельмгольц доказал, что закон Фарадея-Ленца является следствием закона сохранения энергии. Пусть замкнутый проводящий контур находится в неоднородном магнитном поле. Если в контуре течет ток I, то под действием сил Ампера незакрепленный контур придет в движение. Элементарная работа dA, совершаемая при перемещении контура за время dt, будет составлять

dA = IdФm,

где dФm – изменение магнитного потока сквозь площадь контура за время dt. Работа тока за время dt по преодолению электрического сопротивления R цепи равна I2Rdt. Полная работа источника тока за это время равна εIdt. По закону сохранения энергии работа источника тока затрачивается на две названные работы, т.е.

εIdt = IdФm + I2Rdt.

Разделив обе части равенства на Idt, получим

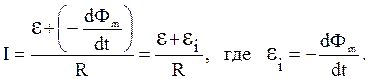
Следовательно, при изменении магнитного потока, сцепленного с контуром, в последнем возникает электродвижущая сила индукции

Электромагнитные колебания. Колебательной контур.

Электромагнитные колебания — это колебания таких величин, индуктивность, как сопротивление, ЭДС, заряд, сила тока.

Колебательный контур — это электрическая цепь, которая состоит из последовательно соединенных конденсатора, катушки и резистора. Изменение электрического заряда на обкладке кон- денсатора с течением времени описывается дифференциальным уравнением:

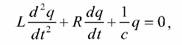
Электромагнитные волны и их свойства.

В колебательном контуре происходит процесс перехода электрической энергии конденсатора в энергию магнитного поля катушки и наоборот. Если в определенные моменты времени компенсировать потери энергии в контуре на сопротивление за счет внешнего источника, то получим незатухающие электрические колебания, которые через антенну могут быть излучены в окружающее пространство.

Процесс распространения электромагнитных колебаний, периодических изменений напряженностей электрического и магнитных полей, в окружающем пространстве называется электромагнитной волной.

Электромагнитные волны охватывают большой спектр длин волн от 105 до 10 м и по частотам от 104 до 1024 Гц. По названию электромагнитные волны разделяются на радиоволны, инфракрасное, видимое и ультрафиолетовое излучения, рентгеновские лучи и -излучение. В зависимости от длины волны или частоты свойства электромагнитных волн меняются, что является убедительным доказательством диалектико-материалистического закона перехода количества в новое качество.

Электромагнитное поле материальное и обладает энергией, количеством движения, массой, перемещается в пространстве: в вакууме со скоростью С, а в среде со скоростью: V= , где = 8,85 ;

Объемная плотность энергии электромагнитного поля . Практическое исполь­зование электромагнитных явлений весьма широкое. Это — системы и средства связи, радиовещания, телевидения, электронно-вычислительная техника, системы управления различного назна­чения, измерительные и медицинские приборы, бытовая электро- и радиоаппаратура и другие, т.е. то, без чего невозможно представить себе современное общество.

Как действует на здоровье людей мощное электромагнитное излучение, точных научных данных почти нет, есть только неподтвержденные гипотезы и, в общем-то, небезосновательные опасение, что все неестественное действует губительно. Доказано, что ультрафиолетовое, рентгеновское и -излучение большой интенсивности во многих случаях наносят реальный вред всему живому.

Геометрическая оптика. Законы ГО.

Геометрическая (лучевая) оптика использует идеализированное представление о световом луче – бесконечно тонком пучке света, распространяющемся прямолинейно в однородной изотропной среде, а также представления о точечном источнике излучения, равномерно светящем во все стороны. λ – длина световой волны, – характерный размер

предмета, находящегося на пути волны. Геометрическая оптика является предельным случаем волновой оптики и ее принципы выполняются при соблюдении условия:

h/D << 1 т. е. геометрическая оптика, строго говоря, применима лишь к бесконечно коротким волнам.

В основе геометрической оптики лежит так же принцип независимости световых лучей: лучи при перемещении не возмущают друг друга. Поэтому перемещения лучей не мешают каждому из них распространяться независимо друг от друга.

Для многих практических задач оптики можно не учитывать волновые свойства света и считать распространение света прямолинейным. При этом картина сводится к рассмотрению геометрии хода световых лучей.

Основные законы геометрической оптики.

Перечислим основные законы оптики, следующие из опытных данных:

1) Прямолинейное распространение.

2) Закон независимости световых лучей, то есть два луча, пересекаясь, никак не мешают друг другу. Этот закон лучше согласуется с волновой теорией, так как частицы в принципе могли бы сталкиваться друг с другом.

3) Закон отражения. луч падающий, луч отраженный и перпендикуляр к поверхности раздела, восстановленный в точке падения луча, лежат в одной плоскости, называемой плоскостью падения; угол падения равен углу

Отражения.

4) Закон преломления света.

Закон преломления: луч падающий, луч преломленный и перпендикуляр к поверхности раздела, восстановленный из точки падения луча, лежат в одной плоскости – плоскости падения. Отношение синуса угла падения к синусу угла отражения равно отношению скоростей света в обеих средах.

Sin i1/ sin i2 = n2/n1 = n21

где – относительный показатель преломления второй среды относительно первой среды. n21

Если вещество 1 – пустота, вакуум, то n12 → n2 – абсолютный показатель преломления вещества 2. Можно легко показать, что n12 = n2 /n1 , в этом равенстве слева относительный показатель преломления двух веществ (например, 1 – воздух, 2 – стекло), а справа – отношение их абсолютных показателей преломления.

5) Закон обратимости света (его можно вывести из закона 4). Если направить свет в обратном направлении, он пройдёт по тому же пути.

Из закона 4) следует, что если n2 > n1 , то Sin i1 > Sin i2 . Пусть теперь у нас n2 < n1 , то есть свет из стекла, например, выходит в воздух, и мы постепенно увеличиваем угол i1.

Тогда можно понять, что при достижении некоторого значения этого угла (i1)пр окажется, что угол i2 окажется равным π /2 (луч 5). Тогда Sin i2 = 1 и n1 Sin (i1)пр = n2 . Итак Sin

(i1)пр = n2 / n1 .

§ 35. ЗАКОН АМПЕРА. СИЛА ЛОРЕНЦА

Закон Био-Савара-Лапласа–Ампера экспериментально проверить нельзя, но следствия из него подтверждаются на практике.

Во всех точках пространства, окружающего произвольный ток, всегда существует обусловленное этим током поле сил, которое по сложившейся исторически терминологии называется магнитным полем.

По аналогии с электростатикой можно ввести силовую характеристику точки магнитного поля – вектор магнитной индукции:

— закон Био-Савара-Лапласа для расчета индукции магнитного поля, создаваемого элементом тока в некоторой точке (рис.69). Экспериментально проверить эту формулу нельзя, но можно рассчитать индукцию магнитного поля, созданного всем контуром с током, используя установленный на опыте принцип суперпозиции магнитных полей: . -лишь формальная запись, на практике интегрирование возможно лишь для проекций вектора магнитной индукции.

Тл (Тесла).

Если задана объемная плотность тока,

то: . Тогда

Магнитное поле порождается движущимися зарядами(токами). Если скорость направленного движения зарядов в проводнике , то . Тогда:

Индукцию магнитного поля точечного заряда, движущегося с постоянной нерелятивистской скоростью (рис.70) можно определить по формуле:

Вземли~5*10-5Тл, Вмозга~10-11Тл.

Вmax ~150 Тл — получена в виде импульса.

САМОСТОЯТ. XI: рассчитать индукцию магнитного поля: 1)бесконечного длинного прямого проводника с током I в точке на расстоянии b от него;

2)полубесконечного длинного прямого проводника с током I в точке на расстоянии b от него.

В законе Био-Савара-Лапласа-Ампера рассматривалось взаимодействие элементов токов двух контуров.

Выражение определяет индукцию магнитного поля, созданного элементом тока в месте расположения элемента тока .

Используя принцип суперпозиции магнитных полей, можно найти индукцию магнитного поля, создаваемого всем первым контуром с током в месте расположения второго элемента тока. В этом случае на второй элемент тока будет действовать сила .

Сила, действующая на элемент тока в магнитном поле, называется силой Ампера, а формула, позволяющая рассчитать эту силу – закон Ампера:

Так как , то закон Ампера может быть записан в виде:

Интегрируя эти выражения по объемным или линейным элементам тока, можно найти силу, действующую на тот или иной объем проводника или его линейный участок.

Экспериментально показано, что магнитное поле также действует на движущиеся заряды. Сила, действующая на движущийся электрический заряд со стороны электромагнитного поля, называется силой Лоренца.

Получим формулу для магнитной составляющей силы Лоренца. Используем для этого формулу для силы Ампера, действующей на элемент тока в магнитном поле:

Если ток прекращается, то исчезает сила Ампера, но сила тока

, где q0 — величина свободного заряда, а N – число свободных зарядов, проходящих через поперечное сечение проводника за dt.

Если средняя скорость направленного движения свободных зарядов , то

— сила, действующая со стороны магнитного поля на движущийся заряд.

Если заряд двигается в пространстве, в котором существуют одновременно электрическое и магнитное поле, то на него действует сила Лоренца:

Сила Лоренца является причиной появления силы Ампера.

Закон Ампера. Сила Лоренца — Мегаобучалка

Причина возникновения сил магнитного взаимодействия токов (§ 5.21) заключается в появлении вокруг проводников с током магнитного поля (§ 5.22). Это магнитное поле в свою очередь действует на второй проводник с током. Сила взаимодействия двух контуров с током конечных размеров складывается из взаимодействия отдельных элементов тока. Она зависит от размеров контуров, их формы и взаимного расположения, и поэтому сформулировать общий закон взаимодействия контуров с током нельзя. Однако такой закон можно дать для элементов тока.

Оба контура с током мысленно разбиваем на элементы тока. Применяя закон Био-Савара-Лапласа совместно с принципом суперпозиции, довольно просто рассчитать конкретное поле, создаваемое одним из контуров в точке пространства, где располагается элемент тока другого контура. Затем, используя принцип суперпозиции для силы, можно рассчитать результирующую силу магнитного взаимодействия контуров с током. Согласно третьему закону Ньютона силы взаимодействия двух контуров равны по модулю и противоположны по направлению.

Результаты опытов Ампера и последующих многочисленных исследований можно сформулировать следующим образом. Сила , действующая на элемент тока I× , равна

 

= , (24.1)

 

где — вектор магнитной индукции.

Соотношение (24.1) было установлено экспериментально Ампером и носит название закона Ампера. Полную силу, действующую на проводник, можно найти суммированием элементарных сил на отдельных элементах проводника, т.е. = . Силы, действующие на токи в магнитном поле, называют амперовыми или силами Ампера.

Если имеется прямолинейный отрезок провода и магнитная индукция во всех его точках постоянна, то сила Ампера согласно (24.1):

 

= . (24.2)

 

Величина этой силы равна

 

F = I×l×B×sina, (24.3)

 

где a — угол между векторами и .

Направление силы перпендикулярно к и и подчиняется правилу правого винта: при движении головки винта от вектора к вектору поступательное движение винта происходит в направлении силы . Взаимное расположение векторов , и показано на рисунке 33.



Закон Ампера позволяет определить единицу измерения магнитной индукции. Предположим, что проводник длиной l с током I перпендикулярен вектору магнитной индукции. Тогда закон Ампера (24.3) запишется в виде F = I×l×B, и

 

B = ,

 

откуда определяем, что 1 Тл — магнитная индукция такого однородного магнитного поля, которое действует с силой в 1 Н на каждый метр длины прямолинейного проводника, расположенного перпендикулярно направлению поля, если по этому проводнику протекает ток в 1 А, т.е. 1 Тл = 1 Н/(А×м).

Одним из методов измерения магнитной индукции В является использование зависимости электрического сопротивление висмута от величины индукции магнитного поля (примерно на 5 % на каждую десятую долю тесла). Помещая предварительно проградуированную висмутовую спираль в магнитное поле, и измеряя относительное изменение ее сопротивления, можно определить магнитную индукцию поля. Следует отметить, что у других металлов электрическое сопротивление также возрастает в магнитном поле, но в гораздо меньшей степени. У меди, например, увеличение сопротивления примерно в 104 раз меньше, чем у висмута.

Применим закон Ампера для вычисления силы взаимодействия двух находящихся в вакууме параллельных бесконечно длинных прямых токов. Если расстояние между токами R (рисунок 34), то каждый элемент тока I2 будет находиться в магнитном поле, индукция которого равна В1 = (m0/2p)×(I1/R) (см. формулу (22.4)). Угол a между элементами тока I2 и вектором прямой. Следовательно, согласно (24.3) на единицу длины (l2 = 1 м) тока I2 действует сила

 

F2 = I2l2B1 = I1I2. (24.4)

 

Нетрудно убедиться, что токи, одинаково направленные, притягиваются, а противоположно направленные – отталкиваются. Для силы F1, действующей на единицу длины тока I1, получается аналогичное (24.4) выражение.

В § 1.1 уже отмечалось, что единица силы тока (ампер) – определяется через магнитное взаимодействие токов. Если в (24.4) положить I1 = I2 = 1 А, а R = 1 м, то можно дать следующее определение: 1 А – сила постоянного тока, протекающего по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м друг от друга в вакууме, вызывающего между этими проводниками силу, равную 2×10-7 Н на каждый метр длины. Из этого определения следует, что магнитная постоянная должна иметь значение m0 = 4p×10-7 единицы системы СИ.

Так как всякий ток есть движение заряженных частиц (электронов или ионов), то очевидно, что на движущийся заряд в магнитном поле действует сила. Нетрудно определить величину этой силы. На проводник длиной l с током I в однородном магнитном поле с индукцией В действует сила Ампера

 

FA = I×l×B×sina,

 

где a — угол между векторами и .

С другой стороны

 

I×l = Nev,

 

где N – полное число движущихся заряженных частиц, е – заряд частицы (носителя тока), v — скорость движения частиц.

Учитывая, что направление совпадает с направлением скорости движения положительных частиц (с направлением тока), мы можем выражение для силы представить в следующем виде:

 

FА = Nev×B×sina,

 

где a — угол между векторами и .

Сила, действующая на проводник, пропорциональна полному числу движущихся частиц, а значит, сила, действующая на одну частицу, равна:

 

F = ev×B×sina. (24.5)

 

Заменяя в (24.5) заряд носителя тока на q, получаем

 

F = qv×B×sina. (24.6)

 

Полученный результат можно выразить в векторной форме:

 

= . (24.7)

 

Направление этой силы перпендикулярно к плоскости, в которой лежат векторы и , и подчиняется правилу правого винта. Скорость в этой формуле есть скорость заряда относительно магнитного поля. Если заряд q положителен, направление силы совпадает с направлением векторного произведения . В случае отрицательного заряда q направления и противоположны. Сила всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, сила работы не совершает. Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется. Причем на покоящуюся заряженную частицу ( =0) магнитное поле не действует ( =0).

Если одновременно имеются электрическое и магнитное поля, сила, действующая на заряженную частицу, равна:

 

= q + . (24.8)

 

Это выражение было получено Лоренцем путем обобщения экспериментальных данных, и носит название силы Лоренца.

Сила Лоренца складывается из двух слагаемых: = + , где = q и = , которые называют, соответственно, электрической и магнитной составляющими силы Лоренца. Разделение полной силы Лоренца на электрическую и магнитную составляющие зависит от выбора системы отсчета. Без указания системы отсчета такое разделение не имеет смысла.

Сила Лоренца. Закон Ампера — Студопедия

На заряд, движущийся в магнитном поле, действует сила, которую мы будем называть магнитной. Эта сила определяется зарядом q, скоростью его движения и магнитной индукцией 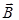в той точке, где находится заряд в рассматриваемый момент времени. Опытным путем установлено, что сила 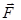, действующая на заряд, движущейся в магнитном поле, определяется формулой

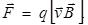(9.4)

Модуль магнитной силы равен

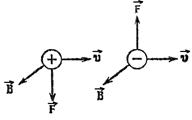
где α – угол между векторами 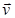и .

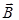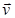Направлена магнитная сила перпендикулярно плоскости, в которой лежат векторы и 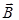. Если заряд qположителен, направление силы совпадает с направлением вектора 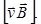В случае отрицательного qнаправления 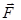и 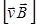противоположны (рис. 9.3).

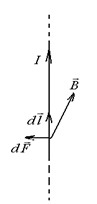Если имеются одновременно электрическое и магнитное поля, сила, действующая на заряженную частицу, равна

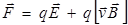. (9.5)

Это выражение было получено из опытов Лоренца и носит название силы Лоренца.

Если провод, по которому течет ток, находится в магнитном поле, на каждый из носителей тока, а, следовательно, на проводник действует магнитная сила. Опытным путем установлено, что на элемент проводника длиной с током в магнитном поле действует сила

, (9.10)

получившая название силы Ампера. Модуль этой силы вычисляется по формуле

,

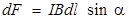где α – угол между векторам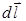и и 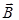(рис. 9.4).

9.3. Теорема о циркуляции вектора магнитной индукции и теорема Гаусса для вектора

Можно доказать теорему о циркуляции вектора 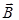для вакуума: циркуляция вектора 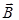по произвольному замкнутому контуру Г равна алгебраической сумме токов, охватываемых этим контуром, умноженной на :


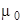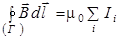. (9.11)

Знак силы тока в формуле (9.11) выбирается следующим образом: если направление тока связано с направлением обхода контура правилом правого буравчика, то это «+», если нет – «-».

В присутствии вещества в правую часть теоремы о циркуляции вектора 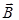необходимо ввести микротоки Iмикро, охватываемые контуром Г:

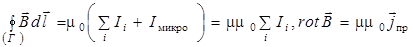, (9.12)

где μ – относительная магнитная проницаемость среды.

Под микротоками, или молекулярными токами, понимают токи, вызванные движением электронов в молекулах. Эти токи создают магнитное поле вещества, помещенного во внешнем магнитном поле.

Из формулы (9.12) следует физический смысл теоремы о циркуляции вектора 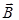, а именно источником магнитного поля являются токи проводимости и микротоки. В природе не существует магнитных зарядов, поэтому линии 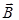являются замкнутыми.


Магнитное поле в отличие от электростатического – непотенциальное поле: циркуляция вектора 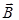магнитной индукции вдоль замкнутого контура, вообще говоря, не равна нулю и зависит от выбора контура. Такое поле называют вихревым или соленоидальным.

Так как в природе нет магнитных зарядов, линии 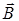являются замкнутыми, теорему Гаусса для вектора магнитной индукции 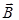запишем следующим образом:

.

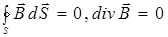3.4. Сила Лоренца и закон Ампера.

3.4.1.Сила Лоренца.

Обобщение опытных фактов приводит к выводу о том, что на движущийся заряд в магнитном поле действует сила, определяемая выражением:

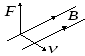
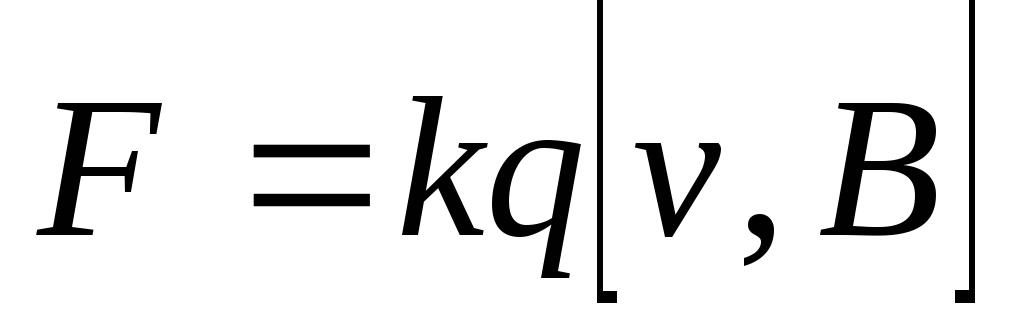, (3.15)

где 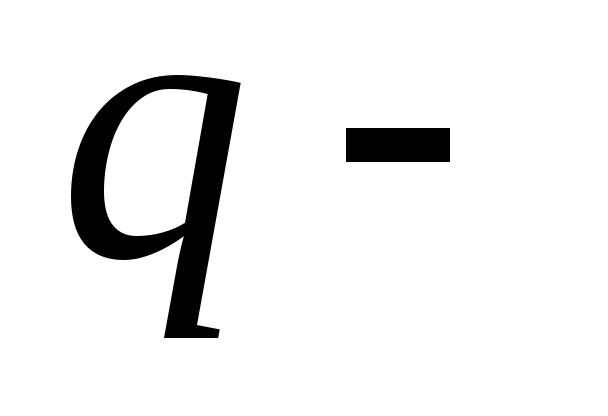заряд,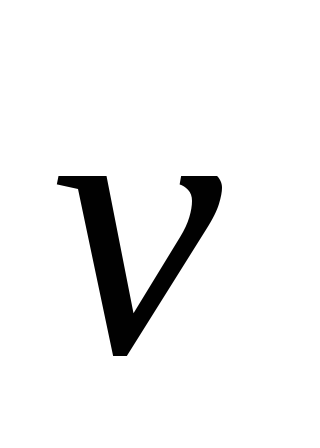— скорость заряда,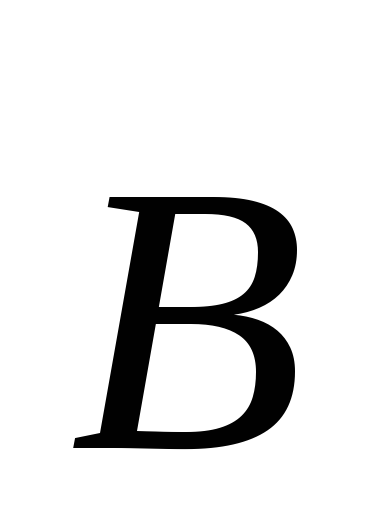— индукция магнитного поля.

Здесь 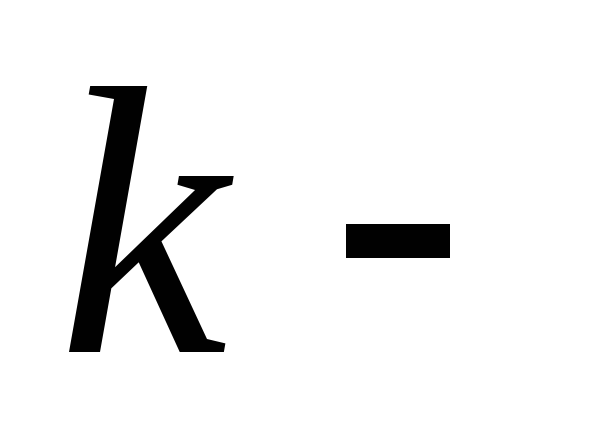некоторая константа, которая определяется выбранной

системой единиц.

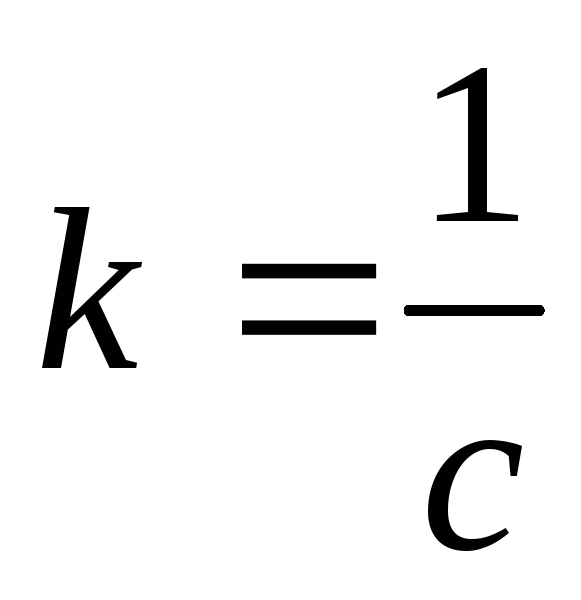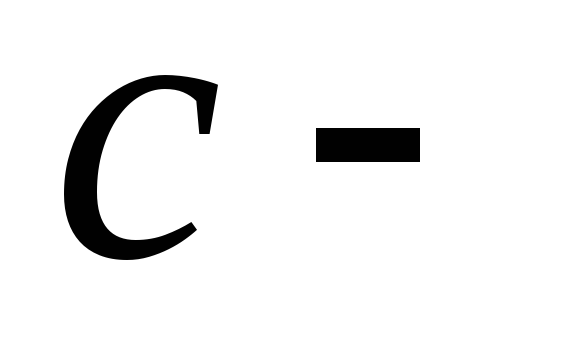В системе Гаусса , гдескорость света.

В СИ 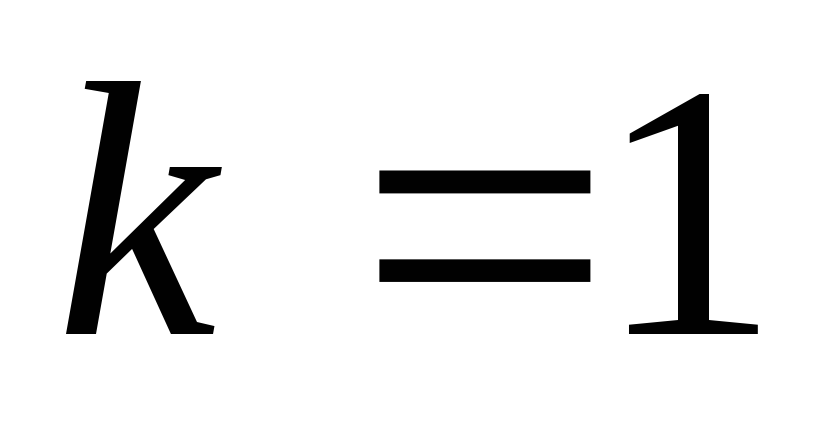,т.е. сила Лоренца выражается формулой

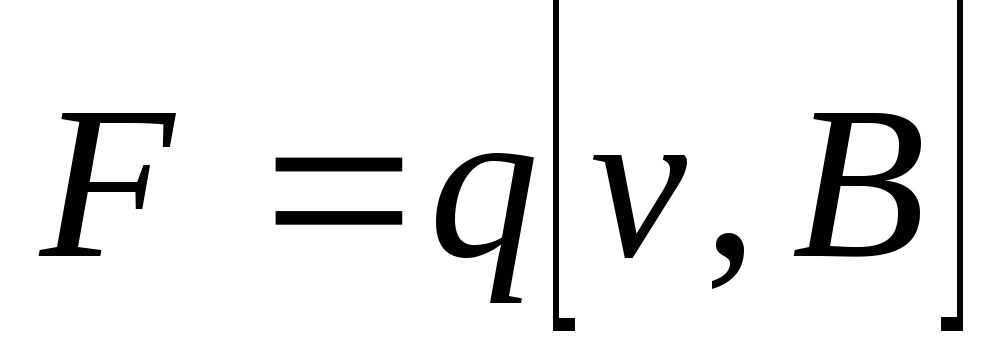. (3.16)

Таким образом, это соотношение может служить определением единиц магнитной индукции .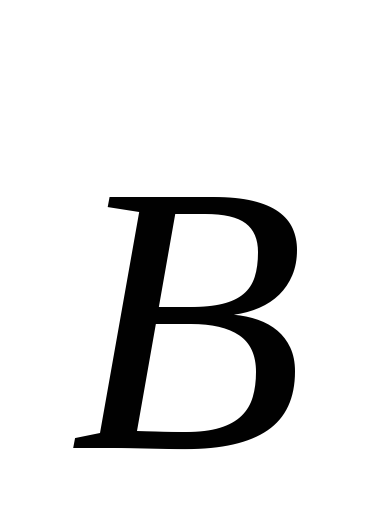

В системе СИ: 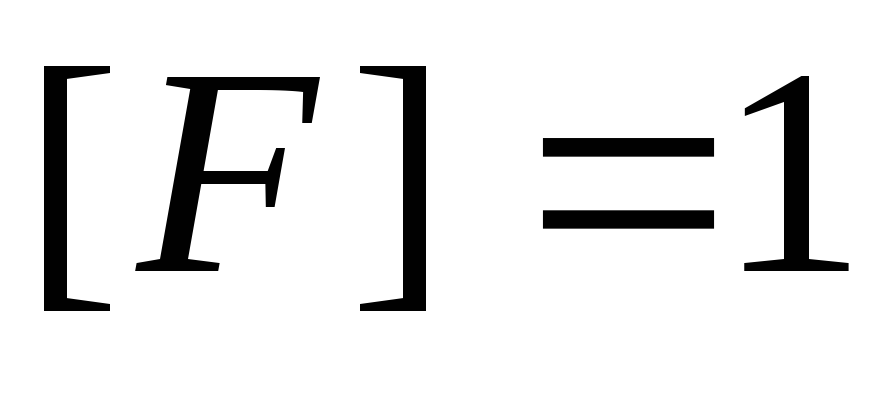Н,Кл,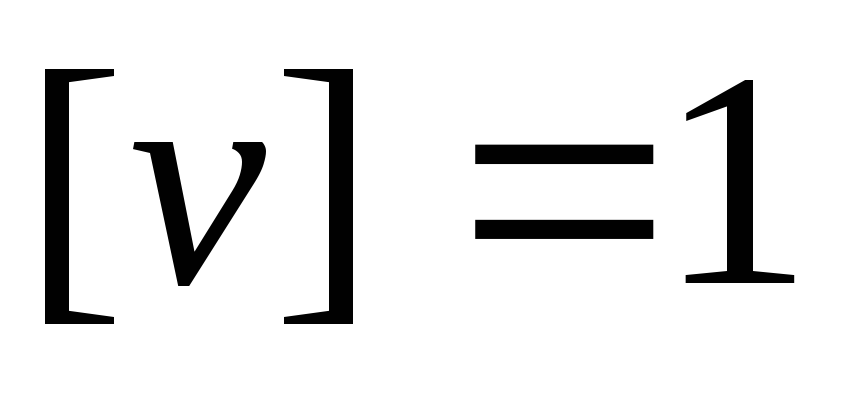м/с, тогда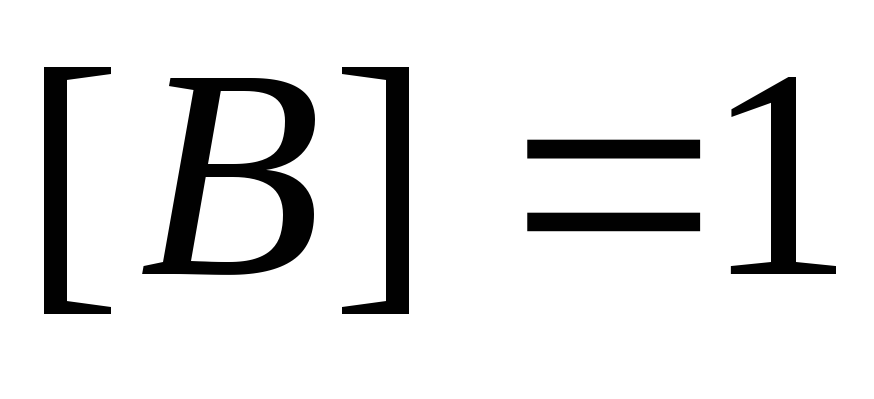Тл (тесла).

Если движение заряда происходит в магнитном и электрическом полях, то сила Лоренца приобретает вид:

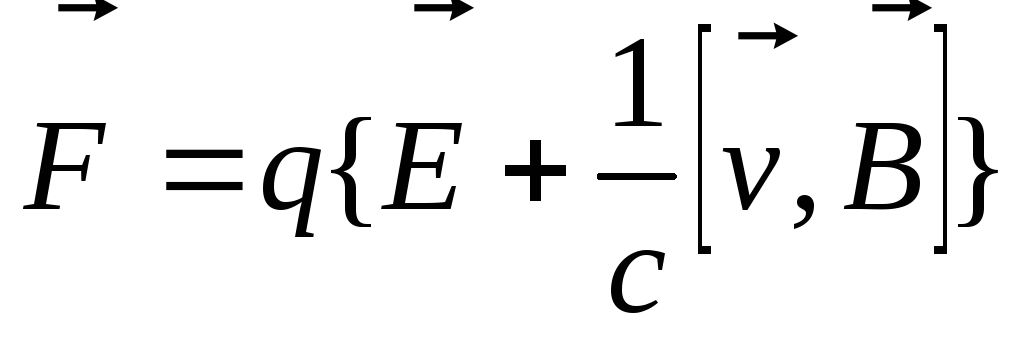. (3.17)

Примечание:В нерелятивистском приближении сила 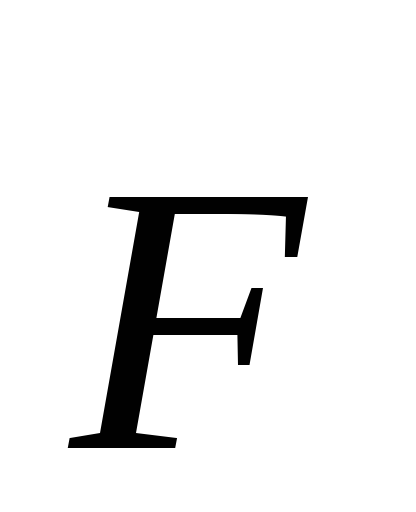не должна изменяться при переходе из одной ИСО в другую, поэтому разделение силы Лоренца на электрическую и магнитную части зависит от выбора системы отсчета. Без указания системы отсчета такое разделение теряет смысл.

  1. Движение заряда в постоянном однородном магнитном поле.

Если рассматривать движение частицы с зарядомв постоянном

однородном магнитном поле 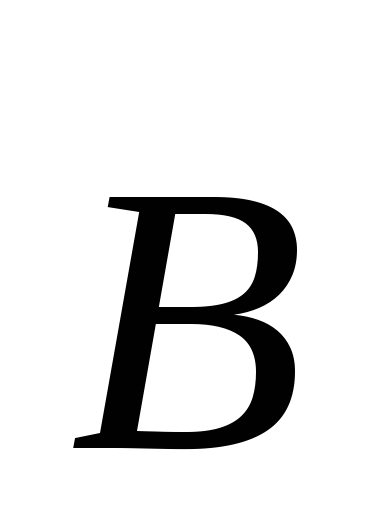, то уравнение движения примет вид

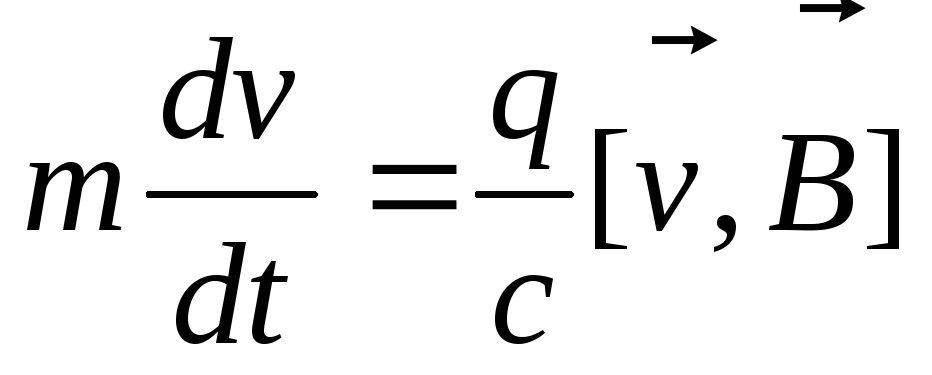. (3.18)

Чтобы определить траекторию частицы, рассмотрим её движение

в направлении вектора 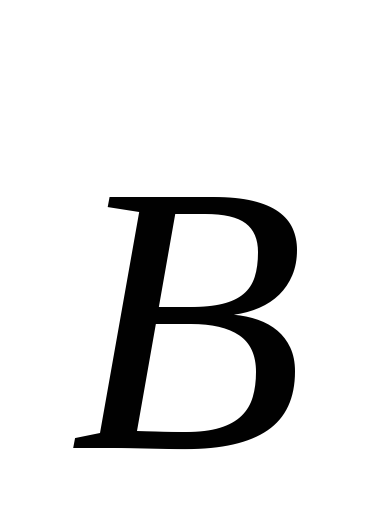и в перпендикулярном ему направлении.

Из свойств векторного произведения следует, что при движении

заряженной частицы в направлении, параллельном магнитному

полю, сила, действующая со стороны поля на заряд , равна нулю,

т.е. параллельная полю компонента скорости заряда сохраняет свое

значение.

В то же время движение в направлении, перпендикулярном полю, совершается с ускорением , определяемым уравнением

,

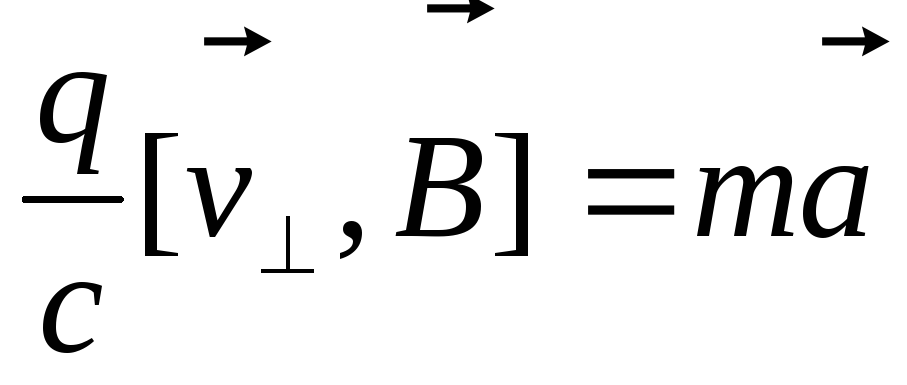откуда следует, что ускорение перпендикулярно векторам 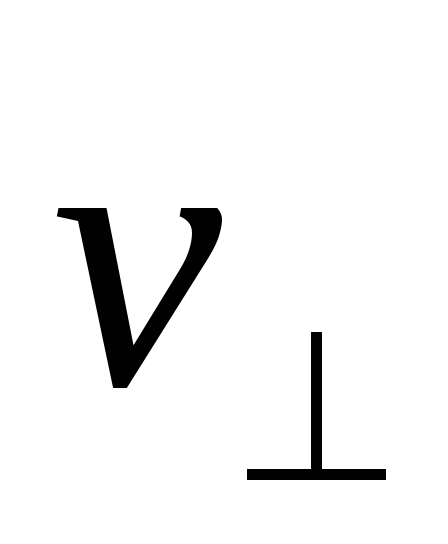и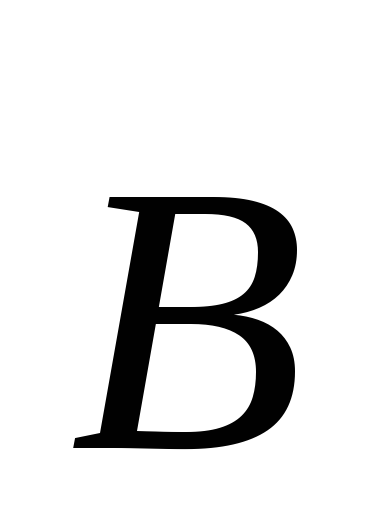, т.е. частица движется с нормальным ускорением

,

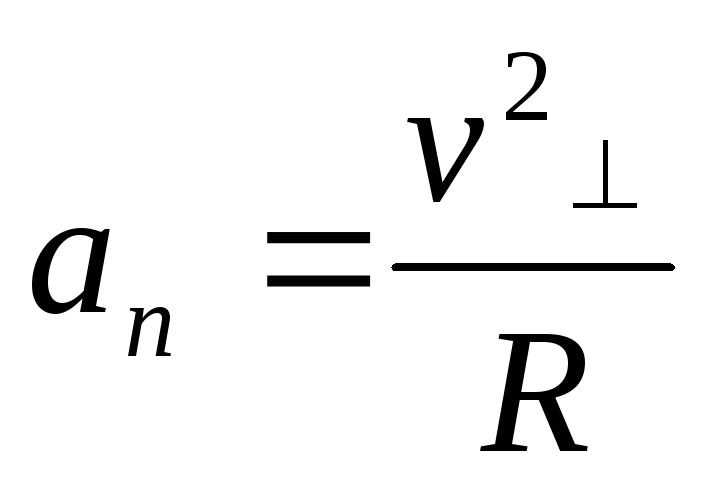по окружности радиусом:

.

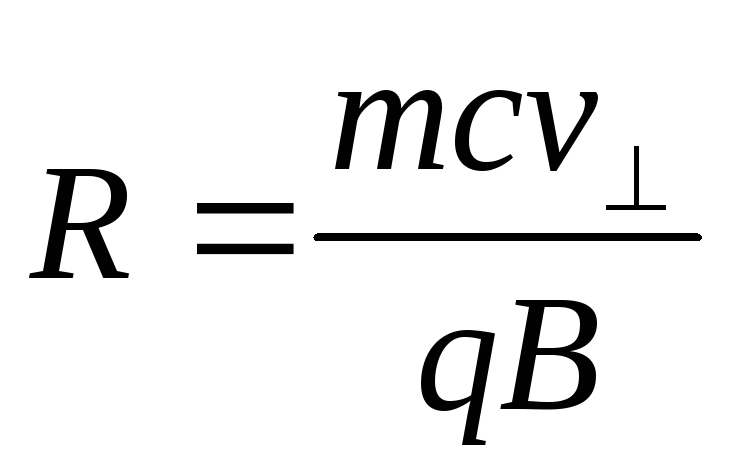Суммируя сказанное находим, что траекторией движения частицы, влетевшей в магнитное поле под произвольным угломк вектору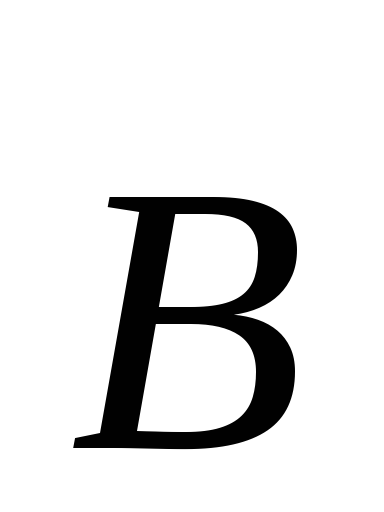, являетсявинтовая линия, вырождающаяся в прямую при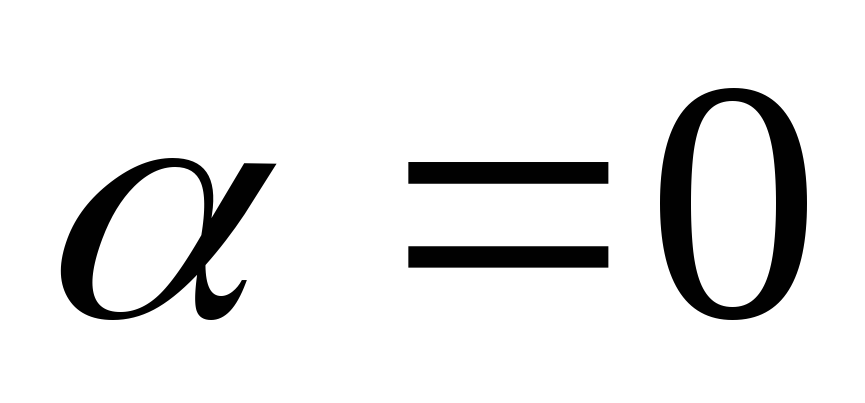и окружность при.

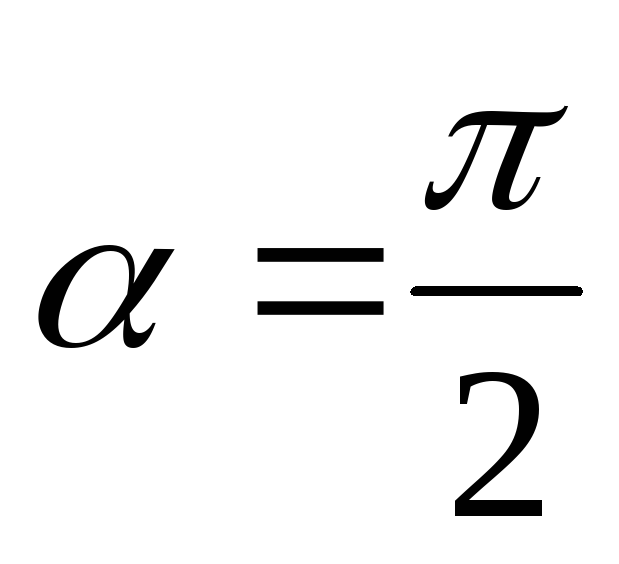Шаг винтовой линии определяется как

,

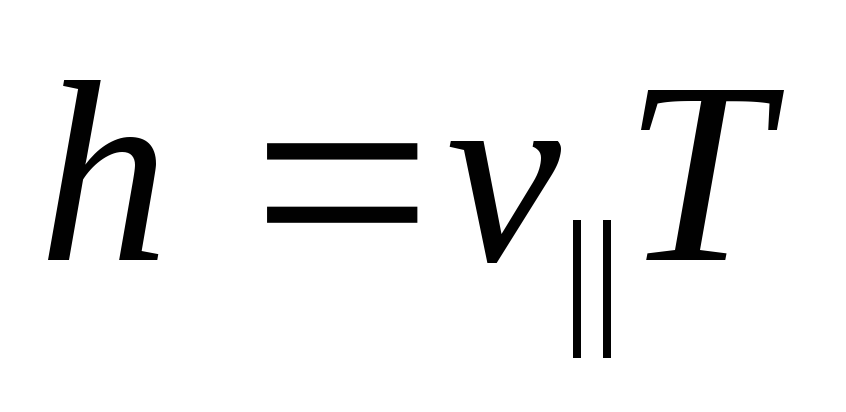где

;;.

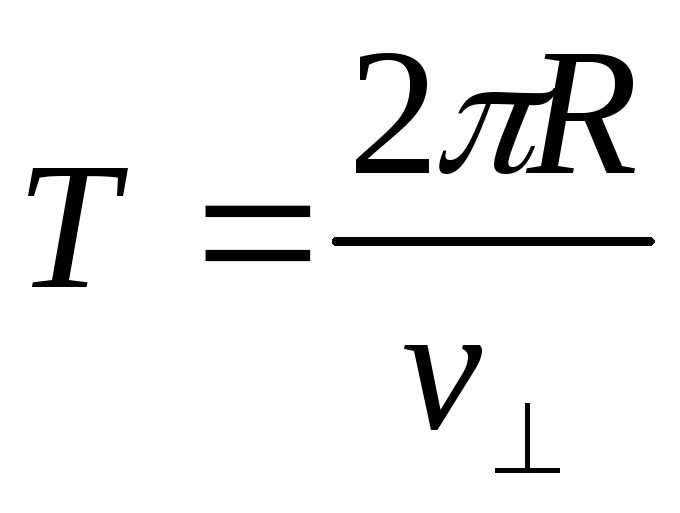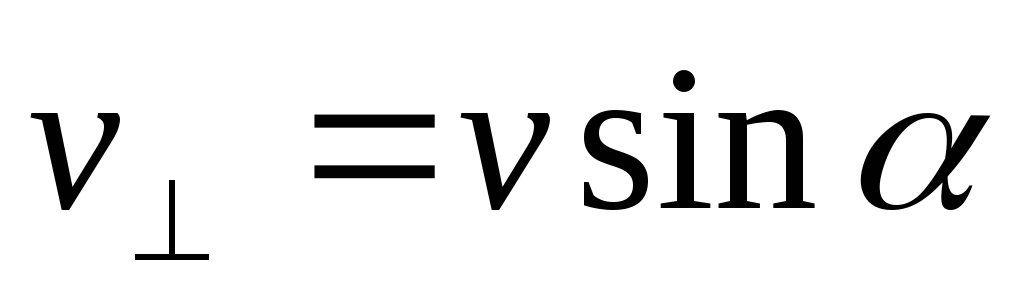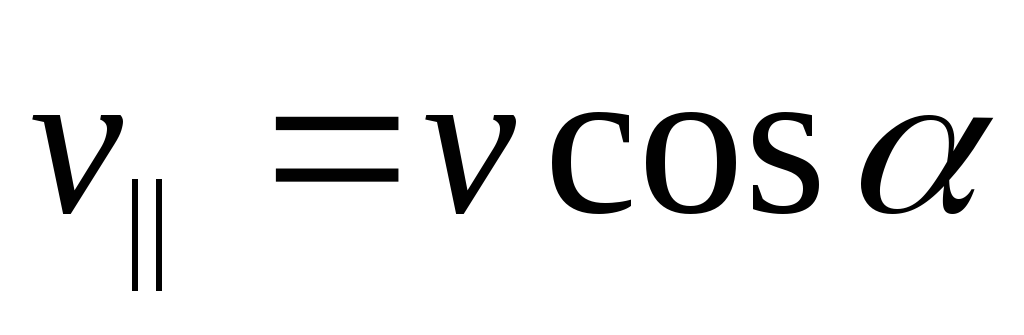3.4.3. Закон Ампера.

Каждый носитель тока в проводнике испытывает действие магнитной силы. В результате магнитное поле действует с определенной силой на сам проводник с током

Пусть имеем провод с током, помещенный в магнитное поле. На каждый заряд (носитель) действует сила Лоренца

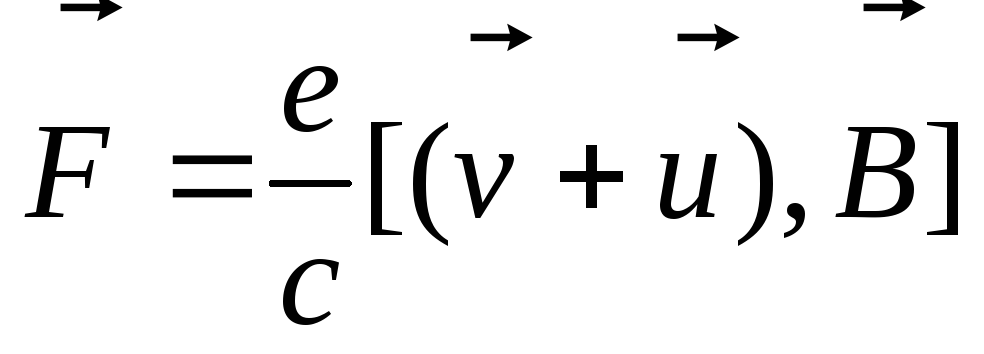, (3.19)

где — скорость хаотического движения,— скорость дрейфа носителей. Если— сечение проводника,— концентрация носителей, то на элемент тока длиной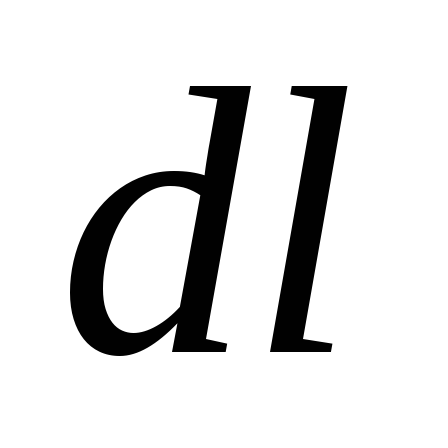будет действовать сила

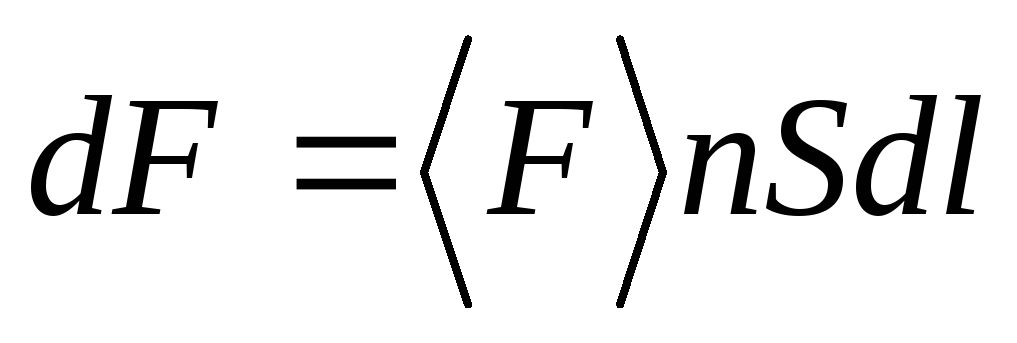, (3.20)

где — средняя сила, действующая на заряд;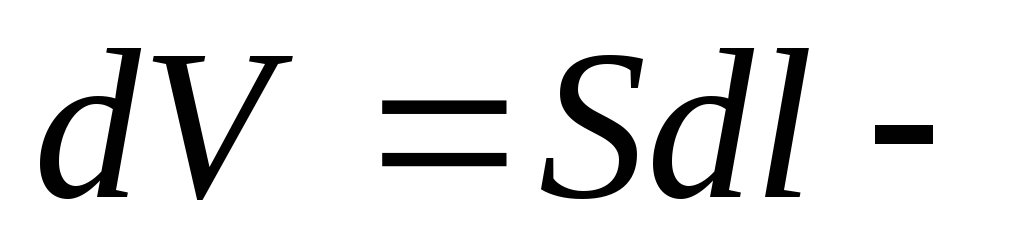элементарный объем проводника.

,

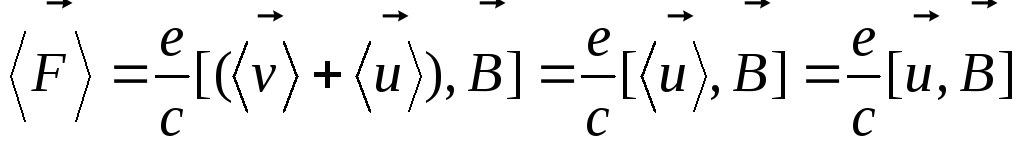т.к. и.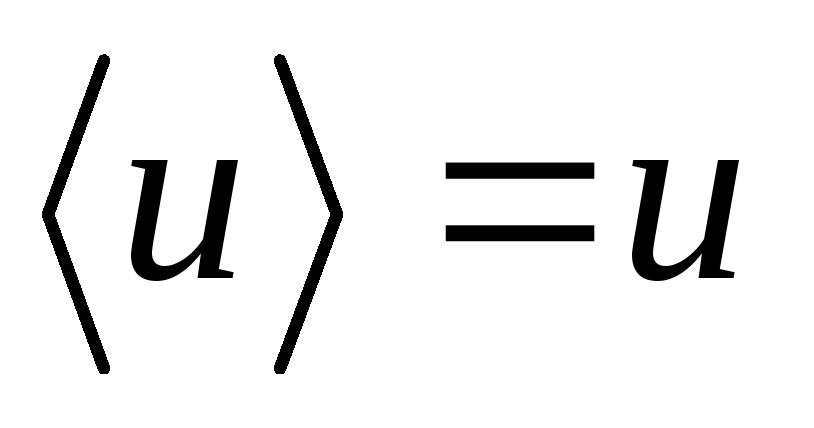

Тогда сила, действующая на элемент проводника длиной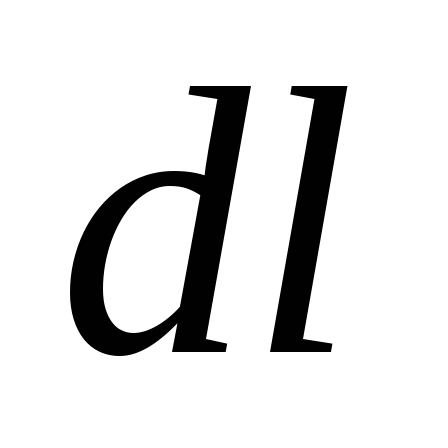

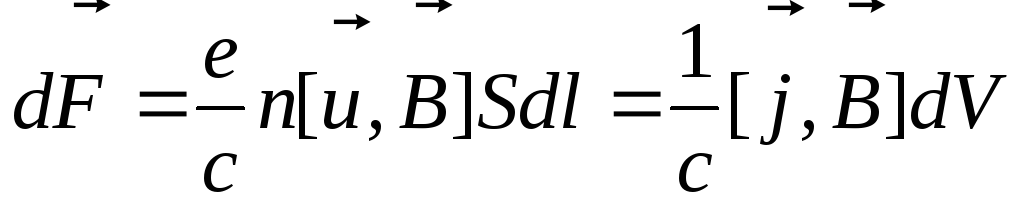, т.к..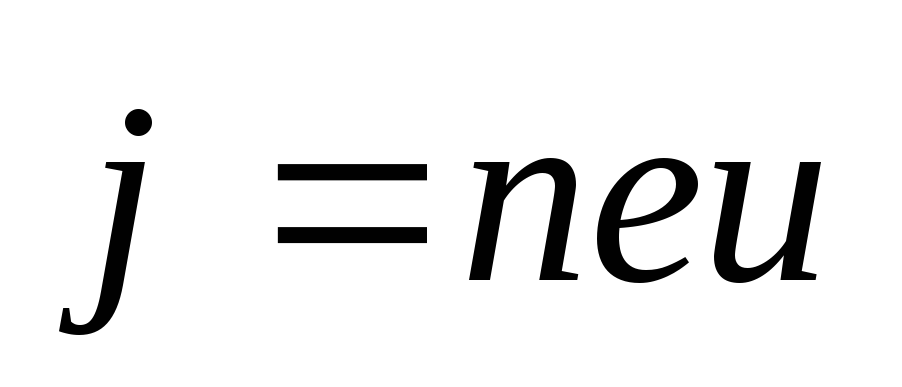

Итак,

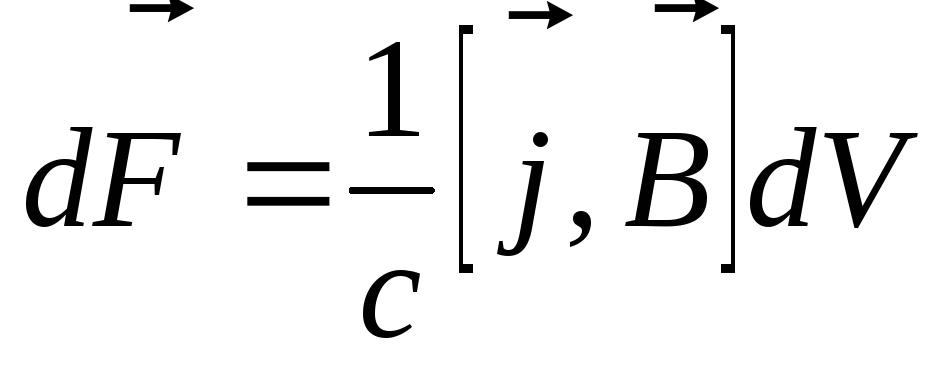. (3.21)

Если объемный элемент токавыразим черезлинейный элементтока , то для тонкого провода с площадью поперечного сеченияможно записать

. (3.22)

Тогда сила, действующая на провод длиной 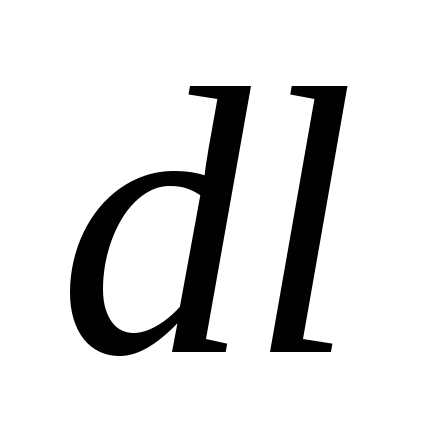, определяется как

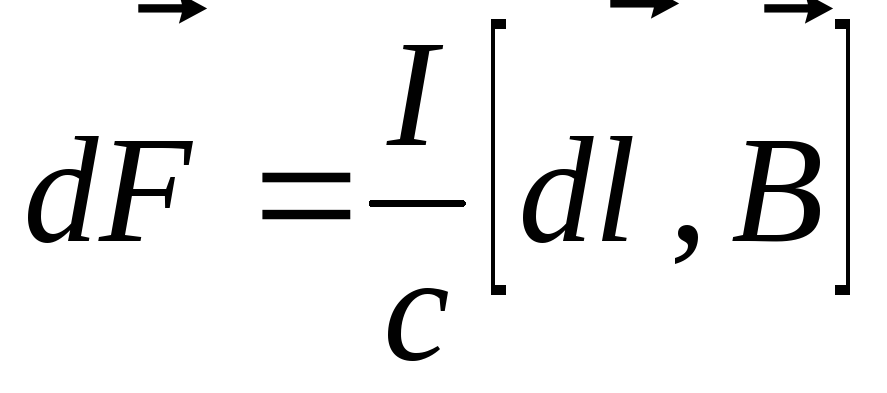. (3.23)

Сила, действующая на провод конечной длины:

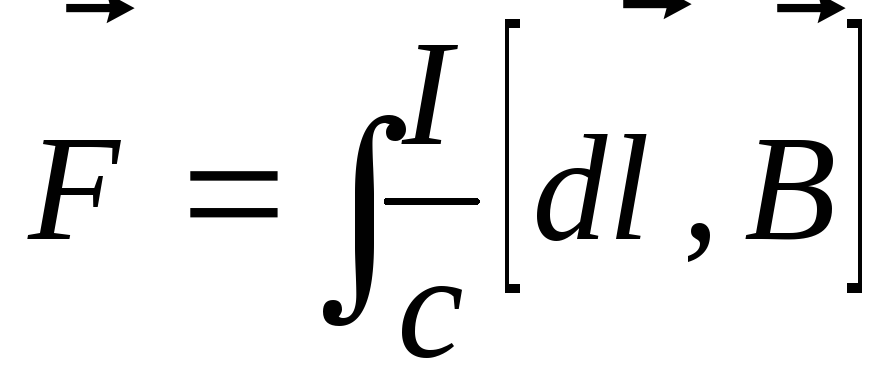. (3.24)

Эти соотношения и определяют закон Ампера (1820г.).

19. Магнитное поле. Магнитная индукция. Закон Ампера.

Магнитное поле:

Неоднородное и однородное магнитное поле. Сила, с которой поле полосового магнита действует на помещенную в это поле магнитную стрелку, в разных точках поля может быть различной как по модулю, так и по направлению. Такое поле называют неоднородным. Линии неоднородного магнитного поля искривлены, их густота меняется от точки к точке. В некоторой ограниченной области пространства можно создать однородное магнитное поле, т.е. поле, в любой точке которого сила действия на магнитную стрелку одинакова по модулю и направлению. Для изображения магнитного поля пользуются следующим приемом. Если линии однородного магнитного поля расположены перпендикулярно к плоскости чертежа и наплавлены от нас за чертеж, то их изображают крестиками, а если из-за чертежа к нам – то точками.

Магни́тное по́ле— силовоеполе, действующее на движущиесяэлектрические зарядыи на тела, обладающиемагнитным моментом, независимо от состояния ихдвижения; магнитная составляющаяэлектромагнитного поля.

Основной силовой характеристикой магнитного поля является вектор магнитной индукции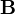

Магнитное поле макротоков описывается вектором напряжённости Н. (B=0H).

Магнитная индукция:

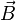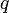Магни́тная инду́кция —векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует назаряд , движущийся со скоростью.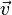

Единицы измерения: Тл.

Модуль вектора магнитной индукции B равен отношению модуля силы F, с которой магнитное поле действует на расположенный перпендикулярно магнитным линиям проводник с током, к силе тока в проводнике I и длине проводника l.

B=F / (I*l)

Магнитная индукция не зависит ни от силы тока, ни от длины проводника, она зависит только от магнитного поля. То есть, если мы, например, уменьшим силу тока в проводнике, не меняя больше ничего, то уменьшится не индукция, с которой сила тока связана прямо пропорционально, а сила воздействия магнитного поля на проводник. Величина же индукции останется постоянной. В связи с этим индукцию можно считать количественной характеристикой магнитного поля.

Магнитная индукция имеет направление. Графически ее можно зарисовывать в виде линий. Линии индукции магнитного поля это и есть то, что мы до сих пор в более ранних темах называли магнитными линиями или линиями магнитного поля. Так как мы выше вывели определение магнитной индукции, то мы можем дать определение и линиям магнитной индукции.

Линии магнитной индукции это линии, касательные к которым в каждой точке поля совпадают с направлением вектора магнитной индукции.

В однородном магнитном поле линии магнитной индукции параллельны, и вектор магнитной индукции будет направлен так же во всех точках.

В случае неоднородного магнитного поля, вектор магнитной индукции будет меняться в каждой точке пространства вокруг проводника, а касательные к этому вектору создадут концентрические окружности вокруг проводника.

Направление линий магнитной индукции определяется по правилу буравчика.

Закон Ампера:

Закон Ампера показывает, с какой силой действует магнитное поле на помещенный в него проводник. Эту силу также называют силой Ампера.

  Формулировка закона: сила, действующая на проводник с током, помещенный в однородное магнитное поле, пропорциональна длине проводника, вектору магнитной индукции, силе тока и синусу угла между вектором магнитной индукции и проводником. 

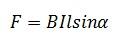
  Если размер проводника произволен, а поле неоднородно, то формула выглядит следующим образом: 

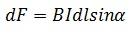
  Направление силы Ампера определяется по правилу левой руки.

  Правило левой руки : если расположить левую руку так, чтобы перпендикулярная составляющая вектора магнитной индукции входила в ладонь, а четыре пальца были вытянуты по направлению тока в проводнике, то отставленный на 90° большой палец, укажет направление силы Ампера.

закон Фарадея, закон Ампера, закон Ленца и сила Лоренца

Работа электродвигателей регулируется различными законами электричества и магнетизма, включая закон индукции Фарадея, закон Ампера, круговой закон Ленса и силу Лоренца. Первые два — закон Фарадея и круговой закон Ампера — включены в уравнения Максвелла. Вместе с законом Ленца и силой Лоренца эти принципы составляют основу электромагнетизма.

закон индукции Фарадея

Закон индукции Фарадея — это основной закон, на котором работают электродвигатели.Майклу Фарадею приписывают открытие индукции в 1831 году, но Джеймс Клерк Максвелл описал это математически и использовал в качестве основы своей количественной электромагнитной теории в 1860-х годах.

Индуктивность — это свойство устройства, которое сообщает, насколько эффективно оно вызывает эдс в другом устройстве (или на самом себе).

Закон Фарадея обычно гласит, что в замкнутой катушке (петле) провода изменение магнитного окружения катушки вызывает индуцирование напряжения или ЭДС (электродвижущей силы) в катушке.

Изменение магнитной среды может быть вызвано изменением напряженности магнитного поля, перемещением магнита к катушке или от нее, перемещением катушки в магнитное поле или из него или вращением катушки в поле.

Индуцированная ЭДС равна отрицательной скорости изменения магнитного потока, умноженной на число витков в катушке:

electromagnetism

Где:

E = ЭДС (В)

N = число витков в катушке

Φ = магнитный поток (Вебер, Wb)

t = время (с)

Обратите внимание, что магнитный поток равен среднему магнитному полю B (тесла или Вт / м 2 ), умноженному на перпендикулярную площадь катушки, которая пронизывает магнитное поле, A (м 2 ).

закон Ленца

Закон Ленца демонстрирует причину отрицательного знака в законе индукции Фарадея. Другими словами, закон Ленца объясняет , почему ЭДС, генерируемая по закону Фарадея, является отрицательной.

Распространенный способ сформулировать закон Ленца: «Когда эдс генерируется изменением магнитного потока, полярность индуцированной эдс такова, что она генерирует ток, магнитное поле которого находится в направлении, которое противодействует изменению, вызвавшему его (оригинальное магнитное поле).То есть индуцированное магнитное поле всегда работает для поддержания постоянного магнитного потока.

electromagnetism

Когда магнитный поток изменяется (ΔB), магнитное поле индуцированной эдс (B Induced ) работает для противодействия изменению.
Автор фотографии: C. R. Nave, Университет штата Джорджия

Закон Ленца аналогичен третьему закону Ньютона в механике, который гласит, что на каждое действие существует равная и противоположная реакция.

сила Лоренца

Существуют разногласия по поводу того, была ли сила Лоренца первоначально получена Джеймсом Клерком Максвеллом или Оливером Хивисайдом, но, как правило, это заслуга Хевисайда.Хендрик Лоренц вывел современную форму уравнения в 1891 году.

Сила Лоренца — это сила, которую испытывает частица из-за электрических и магнитных полей. Электрические поля воздействуют на частицу независимо от того, движется она или нет, тогда как магнитные поля создают силу только тогда, когда частица находится в движении. Комбинация сил от электрического и магнитного полей имеет вид:

electromagnetism

Что упрощает до:

electromagnetism

Где:

F = сила (Н)

q = частица заряда (кулон, C)

E = электрическое поле (N / C)

v = скорость, перпендикулярная магнитному полю (м / с)

B = магнитное поле (тесла, Т)

Поскольку ток по существу представляет собой поток движущихся заряженных частиц, он также испытывает силу, вызванную магнитным полем.В случае тока в магнитном поле уравнение силы Лоренца принимает вид:

electromagnetism

Где:

I = ток (A)

л = длина провода через поле (м)

Направление силы Лоренца определяется по правилу правой руки: направьте большой палец в направлении тока, первый палец в направлении магнитного поля, а второй (средний) палец будет указывать в направлении сила.

Ampère Circuit Law

Несмотря на свое название, закон Ампера был получен не Андре-Мари Ампера, а Джеймсом Клерком Максвеллом в 1860 году и является одним из уравнений электромагнетизма Максвелла. (Ампер сформулировал закон силы Ампера, который описывает силу притяжения или отталкивания между двумя токонесущими проводами.)

Магнитное поле оказывает силу на прямой провод, который проводит ток. С помощью закона Ампера, сила магнитного поля может быть определена следующим образом:

electromagnetism

Где:

B = магнитное поле (Т)

μ 0 = магнитная проницаемость воздуха, Т-м / А

I = ток (A)

r = расстояние от провода (м)

electromagnetism

Когда провод представляет собой петлю, магнитное поле вызывает силу в одном направлении на одной стороне петли и в противоположном направлении на другой стороне петли.Это создает вращающий момент, который заставляет катушку вращаться. Обратите внимание, что если подается постоянный ток, катушка будет колебаться взад-вперед, но не будет совершать полных оборотов — это причина, по которой двигатели постоянного тока используют коммутаторы. Двигатели с переменным током (двигатели переменного тока) не имеют этой проблемы.

Характеристика изображения: TutorVista.com

,
формула закона Ампера — формула, обозначения и решенные примеры
    • Классы
      • Класс 1 — 3
      • Класс 4 — 5
      • Класс 6 — 10
      • Класс 11 — 12
    • КОНКУРСЫ
      • BBS
      • 000000000 Книги
        • NCERT Книги для 5 класса
        • NCERT Книги Класс 6
        • NCERT Книги для 7 класса
        • NCERT Книги для 8 класса
        • NCERT Книги для 9 класса
        • NCERT Книги для 10 класса
        • NCERT Книги для 11 класса
        • NCERT Книги для 12-го класса
      • NCERT Exemplar
        • NCERT Exemplar Class 8
        • NCERT Exemplar Class 9
        • NCERT Exemplar Class 10
        • NCERT Exemplar Class 11
        • NCERT Exemplar Class 12
          • 9000al Aggar Agaris Agard Agard Agard Agard Agard 2000 12000000
          • Решения RS Aggarwal класса 10
          • Решения RS Aggarwal класса 11
          • Решения RS Aggarwal класса 10
            • 90 003 Решения RS Aggarwal класса 9
          • Решения RS Aggarwal класса 8
          • Решения RS Aggarwal класса 7
          • Решения RS Aggarwal класса 6
        • Решения RD Sharma
          • Решения класса RD Sharma
          • Решения класса 9 Шарма 7 Решения RD Sharma Class 8
          • Решения RD Sharma Class 9
          • Решения RD Sharma Class 10
          • Решения RD Sharma Class 11
          • Решения RD Sharma Class 12
        • ФИЗИКА
          • Механика
          • 000000 Электромагнетизм
        • ХИМИЯ
          • Органическая химия
          • Неорганическая химия
          • Периодическая таблица
        • МАТС
          • Теорема Пифагора
          • Отношения и функции
          • Последовательности и серии
          • Таблицы умножения
          • Детерминанты и матрицы
          • Прибыль и убыток
          • Полиномиальные уравнения
          • Делительные дроби
        • 000 ФОРМУЛЫ
          • Математические формулы
          • Алгебровые формулы
          • Тригонометрические формулы
          • Геометрические формулы
        • КАЛЬКУЛЯТОРЫ
          • Математические калькуляторы
          • S000
          • 80003 Pегипс Класс 6
          • Образцы документов CBSE для класса 7
          • Образцы документов CBSE для класса 8
          • Образцы документов CBSE для класса 9
          • Образцы документов CBSE для класса 10
          • Образцы документов CBSE для класса 11
          • Образец образца CBSE pers for Class 12
        • CBSE Предыдущий год Вопросник
          • CBSE Предыдущий год Вопросники Класс 10
          • CBSE Предыдущий год Вопросник класс 12
        • HC Verma Solutions
          • HC Verma Solutions Класс 11 Физика
          • Решения HC Verma Class 12 Physics
        • Решения Lakhmir Singh
          • Решения Lakhmir Singh Class 9
          • Решения Lakhmir Singh Class 10
          • Решения Lakhmir Singh Class 8
        • Примечания
        • CBSE
        • Notes
            CBSE Класс 7 Примечания CBSE
          • Класс 8 Примечания CBSE
          • Класс 9 Примечания CBSE
          • Класс 10 Примечания CBSE
          • Класс 11 Примечания CBSE
          • Класс 12 Примечания CBSE
        • Примечания пересмотра
        • CBSE Редакция
        • CBSE
        • CBSE Class 10 Примечания к пересмотру
        • CBSE Class 11 Примечания к пересмотру 9000 4
        • Замечания по пересмотру CBSE класса 12
      • Дополнительные вопросы CBSE
        • Дополнительные вопросы CBSE 8 класса
        • Дополнительные вопросы CBSE 8 по естественным наукам
        • CBSE 9 класса Дополнительные вопросы
        • CBSE 9 дополнительных вопросов по науке CBSE
          • 9000 Класс 10 Дополнительные вопросы по математике
        • CBSE Класс 10 Дополнительные вопросы по науке
      • Класс CBSE
        • Класс 3
        • Класс 4
        • Класс 5
        • Класс 6
        • Класс 7
        • Класс 8
        • Класс 9
        • Класс 10
        • Класс 11
        • Класс 12
      • Решения для учебников
    • Решения NCERT
      • Решения NCERT для класса 11
          Решения NCERT для физики класса 11
        • Решения NCERT для класса 11 Химия
          • Решения для класса 11 Биология
        • NCERT Решения для класса 11 Математика
          • 9 0003 NCERT Solutions Class 11 Бухгалтерия
        • NCERT Solutions Class 11 Бизнес исследования
        • NCERT Solutions Class 11 Экономика
        • NCERT Solutions Class 11 Статистика
        • NCERT Solutions Class 11 Коммерция
      • NCERT Solutions для класса 12
        • NCERT Solutions для Класс 12 Физика
        • Решения NCERT для 12 класса Химия
        • Решения NCERT для 12 класса Биология
        • Решения NCERT для 12 класса Математика
        • Решения NCERT Класс 12 Бухгалтерский учет
        • Решения NCERT Класс 12 Бизнес исследования
        • Решения NCERT Класс 12 Экономика
        • NCERT Solutions Class 12 Бухгалтерский учет Часть 1
        • NCERT Solutions Class 12 Бухгалтерский учет Часть 2
        • NCERT Solutions Class 12 Микроэкономика
        • NCERT Solutions Class 12 Коммерция
        • NCERT Solutions Class 12 Макроэкономика
      • NCERT Solutions Для Класс 4
        • Решения NCERT для математики класса 4
        • Решения NCERT для класса 4 EVS
      • Решения NCERT для класса 5
        • Решения NCERT для математики класса 5
        • Решения NCERT для класса 5 EVS
      • Решения NCERT для класса 6
        • Решения NCERT для класса 6 Maths
        • Решения NCERT для класса 6 Science
        • Решения NCERT для класса 6 Общественные науки
        • Решения NCERT для класса 6 Английский
      • Решения NCERT для класса 7
        • Решения NCERT для класса 7 Математика
        • Решения NCERT для 7 класса Science
        • Решения NCERT для 7 класса Общественные науки
        • Решения NCERT для 7 класса Английский
      • Решения NCERT для 8 класса Математические решения
        • для 8 класса Математика
        • Решения NCERT для класса 8 Science
        • Решения NCERT для класса 8 Общественные науки
        • NCERT Solutio ns для класса 8 Английский
      • Решения NCERT для класса 9
        • Решения NCERT для класса 9 Общественные науки
      • Решения NCERT для класса 9 Математика
        • Решения NCERT для класса 9 Математика Глава 1
        • Решения NCERT Для класса 9 Математика 9 класса Глава 2
        • Решения NCERT для математики 9 класса Глава 3
        • Решения NCERT для математики 9 класса Глава 4
        • Решения NCERT для математики 9 класса Глава 5
        • Решения NCERT для математики 9 класса Глава 6
        • Решения NCERT для Математика 9 класса Глава 7
        • Решения NCERT для математики 9 класса Глава 8
        • Решения NCERT для математики 9 класса Глава 9
        • Решения NCERT для математики 9 класса Глава 10
        • Решения NCERT для математики 9 класса Глава 11
        • Решения NCERT для Математика 9 класса Глава 12
        • Решения NCERT для математики 9 класса Глава 13
        • Решения NCERT для математики 9 класса Глава 14
        • Решения NCERT для математики класса 9 Глава 15
      • Решения NCERT для науки 9 класса
        • Решения NCERT для науки 9 класса Глава 1
        • Решения NCERT для науки 9 класса Глава 2
        • Решения NCERT для класса 9 Наука Глава 3
        • Решения NCERT для 9 класса Наука Глава 4
        • Решения NCERT для 9 класса Наука Глава 5
        • Решения NCERT для 9 класса Наука Глава 6
        • Решения NCERT для 9 класса Наука Глава 7
        • Решения NCERT для 9 класса Научная глава 8
        • Решения NCERT для 9 класса Научная глава
        • Научные решения NCERT для 9 класса Научная глава 10
        • Научные решения NCERT для 9 класса Научная глава 12
        • Научные решения NCERT для 9 класса Научная глава 11
        • Решения NCERT для 9 класса Научная глава 13
        • Решения NCERT для 9 класса Научная глава 14
        • Решения NCERT для класса 9 Science Глава 15
      • Решения NCERT для класса 10
        • Решения NCERT для класса 10 Общественные науки
      • Решения NCERT для математики класса 10
        • Решения NCERT для математики класса 10 Глава 1
        • Решения NCERT для математики класса 10 Глава 2
        • решения NCERT для математики класса 10 глава 3
        • решения NCERT для математики класса 10 глава 4
        • решения NCERT для математики класса 10 глава 5
        • решения NCERT для математики класса 10 глава 6
        • решения NCERT для математики класса 10 Глава 7
        • решения NCERT для математики класса 10 глава 8
        • решения NCERT для математики класса 10 глава 9
        • решения NCERT для математики класса 10 глава 10
        • решения NCERT для математики класса 10 глава 11
        • решения NCERT для математики класса 10, глава 12
        • Решения NCERT для математики класса 10, глава 13
        • соль NCERT Решения для математики класса 10 Глава 14
        • Решения NCERT для математики класса 10 Глава 15
      • Решения NCERT для науки 10 класса
        • Решения NCERT для науки 10 класса Глава 1
          • Решения NCERT для науки 10 класса Глава 2
        • Решения NCERT для науки 10 класса, глава 3
        • Решения NCERT для науки 10 класса, глава 4
        • Решения NCERT для науки 10 класса, глава 5
        • Решения NCERT для науки 10 класса, глава 6
        • Решения NCERT для науки 10 класса, глава 7
        • Решения NCERT для науки 10 класса, глава 8
        • Решения NCERT для науки 10 класса, глава 9
        • Решения NCERT для науки 10 класса, глава 10
        • Решения NCERT для науки 10 класса, глава 11
        • Решения NCERT для науки 10 класса, глава 12
        • Решения NCERT для 10 класса Science Глава 9
        • Решения NCERT для 10 класса Science Глава 14
        • Решения NCERT для науки 10 класса Глава 15
        • Решения NCERT для науки 10 класса Глава 16
      • Программа NCERT
      • NCERT
    • Коммерция
      • Класс 11 Коммерческая программа Syllabus
      • Учебный курс по бизнес-классу 11000
      • Учебная программа по экономическому классу
    • Учебная программа по коммерческому классу
      • Учебная программа по 12 классу
      • Учебная программа по 12 классу
      • Учебная программа по экономическому классу
          000000000000000000
        • Образцы коммерческих документов класса 11
        • Образцы коммерческих документов класса 12
      • Решения TS Grewal
        • Решения TS Grewal Класс 12 Бухгалтерский учет
        • Решения TS Grewal Класс 11 Бухгалтерский учет
      • Отчет о движении денежных средств
      • eurship
      • Защита потребителей
      • Что такое фиксированный актив
      • Что такое баланс
      • Формат баланса
      • Что такое акции
      • Разница между продажей и маркетингом
    • P000S Документы ICSE
    • ML Aggarwal Solutions
      • ML Aggarwal Solutions Класс 10 Математика
,

АМПЕР ЗАКОН

АМПЕРСКИЙ ЗАКОН

Магнитное поле на расстоянии r от очень длинной прямой проволоки, несущей установившийся ток I, имеет величину, равную

(31.)

и направление, перпендикулярное к r и I. Интеграл пути вдоль круга вокруг провода (см. рисунок 31.1) равно

(31.2)

Здесь мы использовали тот факт, что магнитное поле является тангенциальным в любой точке на круговом пути интеграции.

Рисунок 31.1. Магнитное поле, создаваемое током. Любой произвольный путь можно рассматривать как набор радиальных сегменты (r изменяется и [тета] остается постоянной) и круглые сегменты ([тета] изменяется и r остается постоянным). Для радиальных сегментов магнитный поле будет перпендикулярно смещению и продукту скейлера между магнитное поле и смещение равно нулю.Рассмотрим теперь небольшой круговой отрезок траектории вокруг проволоки (см. рисунок 31.2). Интеграл пути вдоль этого кругового сегмента равен

(31.3)

Рисунок 31.2. Путь интегральный по небольшой круговой дорожке. Уравнение (31.3) показывает, что вклад этого циркуляра отрезок к интегралу полного пути не зависит от расстояния r и только зависит от изменения угла дельта тета. Для закрытого пути общее изменение угла будет 2 [пи], и экв.(31.3) можно переписать как

(31.4)

Это выражение: , , закон Ампера, , :

,

. «Интеграл B вокруг любого замкнутого математического пути равен u 0 умножить на ток, перехваченный областью, охватывающей путь «

Пример: задача 31,5

Шесть параллельных алюминиевых проводов небольшого, но конечного радиуса лежат в тот же самолет. Провода разделены на равные расстояния d, и они несут равные Токи у меня в том же направлении.Найти магнитное поле в центре Первый провод. Предположим, что токи в каждом проводе распределены равномерно над его поперечным сечением.

Схематическое расположение проблемы показано на рисунке 31.3. Магнитное поле сгенерированный одним проводом равен

(31,5)

где r — расстояние от центра провода. Уравнение (31.5) исправить для всех точек за пределами провода, и, следовательно, может быть использован для определения магнитное поле, создаваемое проводом 2, 3, 4, 5 и 6.Поле на центр провода 1, из-за тока, протекающего в проводе 1, можно определить с помощью Закон Ампера и равен нулю. Общее магнитное поле в центре провод 1 можно найти векторным сложением вкладов каждого из шести провода. Поскольку направление каждого из этих вкладов одинаково, суммарное магнитное поле в центре провода 1 равно

(31.6)

Рисунок 31.3. Задача 31.5

Соленоид — это устройство, используемое для создания однородного магнитного поля.Это может быть изготовлены из тонкой проводящей проволоки, намотанной в жесткую спиральную катушку из множества витков. Магнитное поле внутри соленоида можно определить суммированием магнитного поля. поля, генерируемые N отдельными кольцами (где N — число витков соленоид). Мы ограничим наше обсуждение магнитного поля, генерируемого соленоид к тому, что генерируется идеальным соленоидом, который является бесконечно длинным, и имеет очень плотно намотанные катушки.

Идеальный соленоид обладает трансляционной и вращательной симметрией.Тем не менее, так как линии магнитного поля должны образовывать замкнутые петли, магнитное поле не может быть направлены вдоль радиального направления (в противном случае будут созданы линии поля или разрушен на центральной оси соленоида). Поэтому мы заключаем, что силовые линии в соленоиде должны быть параллельны оси соленоида. Величина магнитного поля можно получить, применяя закон Ампера.

Рисунок 31.4. Идеальный соленоид. Рассмотрим путь интеграции, показанный на рисунке 31.4. Путь интеграл магнитного поля вокруг этого пути интегрирования равен

(31.7)

где L — горизонтальная длина пути интеграции. Ток прилагается по пути интеграции равен N . I 0 где N является число витков, окруженных путем интеграции, и I 0 является ток в каждом витке соленоида. Используя закон Ампера, мы заключаем, что

(31.8)

или

(31,9)

где n — число витков соленоида на единицу длины. Уравнение (31.9) показывает, что магнитное поле B не зависит от положения внутри соленоид. Мы заключаем, что магнитное поле внутри идеального соленоида равномерная.

Пример: задача 31.14

Длинный соленоид из n витков на единицу длины несет ток I, и длинный прямой провод, лежащий вдоль оси этого соленоида, несет ток I ‘.Найти суммарное магнитное поле внутри соленоида на расстоянии r от оси. Опишите форму линий магнитного поля.

Магнитное поле, создаваемое соленоидом, является однородным, направленным параллельно ось соленоида, и имеет величину, равную

(31.10)

Магнитное поле, если длинный прямой провод, несущий ток I ‘, имеет величина равна

(31.11)

и направлен перпендикулярно направлению r и I ‘.Направление B проволока , следовательно, перпендикулярна направлению В соль . Чистое магнитное поле внутри соленоида равно векторная сумма B , провода и B , соль . Его величина равна до

(31.12)

Угол a между направлением магнитного поля и осью z задан по

(31.13)

Пример: проблема 31.15

Коаксиальный кабель состоит из длинного цилиндрического медного провода радиуса r 1 , окруженный цилиндрической оболочкой внутреннего радиуса r 2 и внешний радиус r 3 (см. рис. 31.5). Провод и оболочку несут Равные и противоположные токи я равномерно распределил по их объемам. найти формулы для магнитного поля в каждой из областей r 1 , r 1 2 , r 2 3 и r> r 3 .

Линии магнитного поля представляют собой окружности, центрированные по оси симметрии коаксиальный кабель. Сначала рассмотрим путь интеграции с r 1 . Интеграл пути B по этому пути равен

(31.14)

Ток, заключенный этим путем интеграции, равен

. (31.15)

Применяя закон Фарадея, мы можем связать ток, приложенный к интегралу пути Б

(31.16)

Следовательно, магнитное поле B равно

,

(31.17)

Рисунок 31.5. Задача 31.15. В области между проводом и оболочкой ток равен I, а интеграл пути магнитного поля определяется как э. (31.14). Закон Ампера гласит, что

(31.18)

и магнитное поле задается

(31.19)

В третьей области (r 2 3 ) интеграл по траектории магнитного поля вдоль круговой траектории с радиусом r определяется как э.(31.14). Закрытый ток равен

(31.20)

Поэтому магнитное поле равно

(31.21)

Ток, окруженный путем интегрирования с радиусом r> r 3 равно нулю (так как ток в проводе и в оболочке течет в противоположные направления). Поэтому магнитное поле в этой области также равно нулю.

Магнитная сила, действующая на частицу с зарядом q, движущимся со скоростью v, равна равно

(31.22)

Эта сила всегда перпендикулярна направлению движения частицы, и поэтому будет только менять направление движения, а не величину скорости. Если заряженная частица движется в однородном магнитном поле, с силой B, которая перпендикулярна скорости v, то величина магнитной силы задается

(31.23)

и его направление перпендикулярно v. В результате этой силы, частица будет совершать равномерное круговое движение.Радиус круга определяется требованием, что сила магнитной силы равна центростремительная сила. Таким образом

(31.24)

Радиус r орбиты равен

(31.25)

где р — импульс заряженной частицы. Расстояние, пройденное Частица за один оборот равна

(31.26)

Время T, необходимое для завершения одного оборота, равно

(31.27)

Частота этого движения равна

(31.28)

и называется циклотронной частотой . Уравнение (31.28) показывает что циклотронная частота не зависит от энергии частицы, и зависит только от его массы m и заряда q.

Можно использовать влияние магнитного поля на движение заряженной частицы. определить некоторые его свойства. Одним из примеров является измерение заряд электрона.Электрон, движущийся в однородном магнитном поле, описал круговое движение с радиусом, заданным уравнением (31.25). Предположим, электрон ускоряется потенциалом V 0 . Конечная кинетическая энергия электрона дается

(31.29)

Импульс р электрона определяется его кинетической энергией

(31.30)

Радиус кривизны траектории движения электрона при этом равен

(31.31)

Уравнение (31.31) показывает, что измерение r может использоваться для определения отношение массы к заряду электрона.

Другое приложение влияния магнитного поля на движение заряженная частица является циклотроном. Циклотрон состоит из вакуумированной полости помещен между полюсами большого электромагнита. Полость разрезана на две части D-образные фигуры (называемые dees) с зазором между ними. Колеблющийся максимум напряжение подключается к пластинам, генерируя колеблющееся электрическое поле в область между двумя деами.Заряженная частица, введенная в центр циклотрон, будет выполнять равномерное круговое движение для первой половины один ход Частота движения частицы зависит от ее массы, ее заряд и напряженность магнитного поля. Частота генератора равна выбирается таким образом, чтобы каждый раз, когда частица пересекала промежуток между деями, она будет ускоряться электрическим полем. Поскольку энергия иона увеличивается, его радиус кривизны будет увеличиваться, пока не достигнет края циклотрон и извлекается.Во время движения в циклотроне ион будет преодолеть разрыв между деями много раз, и он будет ускорен до высокой энергия.

До сих пор мы предполагали, что направление движения заряженного частица перпендикулярна направлению магнитного поля. Если это случае, равномерное круговое движение приведет. Если направление движения ион не перпендикулярен магнитному полю, в результате возникнет спиральное движение. Скорость заряженной частицы можно разложить на две составляющие: одну параллельно и один перпендикулярно магнитному полю.Магнитная сила действующее на частицу будет определяться компонентом ее скорости перпендикулярно магнитному полю. Проекция движения частица на плоскости x-y (предполагается перпендикулярной магнитному полю) будет круговой Магнитное поле не будет влиять на компонент движение параллельно полю, и эта составляющая скорости останется постоянная. Конечным результатом будет спиральное движение.

Заряженная частица, движущаяся в области с электрическим и магнитным полем, будет испытать общую силу, равную

(31.32)

Эта сила называется силой Лоренца .

Рисунок 31.6. Заряженная частица движется в скрещенных E и B поля. Рассмотрим особый случай, когда электрическое поле перпендикулярно магнитному полю. Движение заряженной частицы в такой регион может быть сложным. Заряженная частица с положительным зарядом q и скорость v движется в этом поле (см. рисунок 31.6). Направление частица показана на рисунке 31.6 перпендикулярно как электрическому полю, так и магнитное поле. Электрическая сила, действующая на частицу, направлена вдоль направления электрического поля и имеет величину, равную

(31,33)

Магнитная сила, действующая на заряженную частицу, направлена ​​перпендикулярно и V и B и имеет величину, равную

(31,34)

Чистая сила, действующая на частицу, является суммой этих двух компонентов и имеет величина равна

(31.35)

Если заряженная частица имеет скорость, равную

, то

(31.36)

тогда чистая сила будет равна нулю, а движение частицы будет быть равномерным линейным движением. Устройство со скрещенными электрическим и магнитным полями называется селектором скорости. Если щели размещены в соответствующем позиции, он будет транспортировать только те частицы, скорость которых определена по величинам электрического и магнитного полей.

Рисунок 31.7. Ток в магнитном поле. Метод, используемый для определения плотности и знака заряда носители в металле основаны на силах, оказываемых скрещенными полями E и B на носители заряда. Диаграмма, показанная на рисунке 31.7, показывает металлическую полосу проводящий ток в указанном направлении и помещенный в однородный магнитный поле с направлением магнитного поля перпендикулярно электрическое поле (которое генерирует ток I). Предположим, что носители заряда в материал электроны, чем электроны будут двигаться в направлении противоположный току (см. рисунок 31.7). Поскольку магнитное поле перпендикулярно электрическому полю, оно также перпендикулярно направлению движения электронов. В результате магнитной силы электроны отклонены вниз, и избыток отрицательного заряда будет создан на нижняя часть полосы. В то же время дефицит отрицательного заряда будет быть созданным в верхней части полосы. Это распределение заряда будет генерировать электрическое поле, которое перпендикулярно внешнему электрическому полю и, под В условиях равновесия электрическая сила, создаваемая этим полем, отменит магнитная сила, действующая на электроны.Когда это происходит, внутренний электрическое поле, E в , равно произведению электрона скорость, v d , и напряженность магнитного поля, B. Как В результате внутреннего электрического поля будет создана разность потенциалов между верхней и нижней частью полосы. Если металлическая полоса имеет ширину w, тогда разность потенциалов [Delta] V будет равна

(31.37)

Этот эффект называется эффектом Холла.

Скорость дрейфа электронов зависит от тока I в проводе, его площадь поперечного сечения A и плотность n электронов (см. главу 28):

(31,38)

Объединяя уравнения (31.38) и (31.37), получаем следующее выражение для [Delta] V

(31.39)

Измерение & delta; V может поэтому использоваться, чтобы определить n.

Ток I, протекающий через провод, эквивалентен совокупности зарядов движется с определенной скоростью v d по проволоке.Количество Заряд dq, присутствующий в сегменте dL провода, равен

(31.40)

Если провод находится в магнитном поле, магнитная сила будет действовать на каждый из носителей заряда, и, как следствие, сила будет действовать на провод. Предположим, что угол между направлением тока и направлением поля равен [тета] (см. рисунок 31.8). Магнитная сила, действующая на отрезке дл провода равен

(31.41)

Общая сила, оказываемая магнитным полем на провод, может быть найдена интегрирование уравнения (31.41) по всему проводу.

Рисунок 31.8. Магнитная сила на проводе.

Пример: проблема 31.33

Весы могут быть использованы для измерения напряженности магнитного поля. Рассмотрим петлю провода, по которой проходит точно известный ток, показанный на рисунке. 31,9, который частично погружен в магнитное поле. Сила, что Магнитное поле, воздействующее на петлю, можно измерить с помощью баланса, и это позволяет рассчитать напряженность магнитного поля.Предположим, что короткая сторона петли измеряется 10,0 см, ток в проводе составляет 0,225 А, а магнитная сила составляет 5,35 х 10 -2 Н. Какова сила магнитное поле?

Рассмотрим три сегмента токовой петли, показанных на рисунке 31.9, которые погруженный в магнитное поле. Магнитная сила, действующая на отрезки 1 и 3 имеют одинаковую величину, но направлены в противоположном направлении, и, следовательно, Отмена. Величина магнитной силы, действующей на сегмент 2, может быть рассчитывается по формуле(31.41) и равен

(31.42)

Эта сила измеряется с использованием весов и равна 5,35 x 10 -2 . Н. Напряженность магнитного поля при этом равна

(31.43)

Рисунок 31.9. Токовая петля погружена в магнитное поле.

Если токовая петля погружена в магнитное поле, чистая магнитная сила будет быть равным нулю.Однако крутящий момент на этом контуре в общем случае не будет равно нулю. Предположим, прямоугольная петля тока находится в единой магнитное поле (см. рисунок 31.10). Угол между нормалью тока петля и магнитное поле равно тета. Магнитные силы, действующие на верхняя и нижняя части токовой петли равны

и

(31.44)

где L — длина верхнего и нижнего края. Крутящий момент, оказываемый на токовая петля, относительно ее оси, равна

(31.45)

Рисунок 31.10. Токовая петля помещена в однородное магнитное поле. Используя определение магнитного дипольного момента u, обсуждалось в главе 30 уравнение (31.45) можно переписать как

(31.46)

где

(31.47)

Используя векторную нотацию, уравнение (31.45) можно переписать как

(31.48)

где направление магнитного момента определяется с помощью правой руки править.

Работа, которая должна быть сделана против магнитного поля, чтобы вращать ток петля на угол d тета равна — тау d тета. Изменение в потенциальная энергия токовой петли, когда она вращается между тета 0 и тета 1 дается

(31.49)

Обычным выбором для контрольной точки является тета 0 = 90 градусов. и U ([theta] 0 ) = 0 Дж. Если этот выбор сделан, мы можем переписать уравнение.(31,50) как

(31.50)

В векторной записи:

(31,51)

Потенциальная энергия токовой петли имеет минимум, когда u и B параллельно, и максимум, когда u и B антипараллельны.

Присылайте комментарии, вопросы и / или предложения по электронной почте [email protected] и / или посетите домашнюю страницу Фрэнка Вольфса. ,

закон Ампера — физика видео от Brightstorm

Закон Ампера был открыт в 1819 году Ампером. Закон Ампера гласит, что токи генерируют магнитные поля или, другими словами, всякий раз, когда у вас есть ток, вокруг него циркулирует магнитное поле. Закон Ампера выражается в уравнении магнитное поле x 2 (pi) x радиус = постоянный x ток (проходящий через этот путь) .

Итак, давайте поговорим о законе Ампера.Закон Ампера был обнаружен хорошо. Эффект, стоящий за законом Ампера, был обнаружен около 1819 г. фактически лектором по физике, который был в середине лекции, и он заметил, что генерировалось магнитное поле, которое перемещалось вокруг стрелки компаса, когда он пропускал большой ток через провод, поэтому закон в основном гласит, что токи, если я проведу ток, он будет генерировать магнитное поле. Есть несколько способов заявить этот закон; есть закон [IB], есть закон Эрстеда. Стандартный способ представить это с точки зрения закона Ампера, который в основном гласит, что всякий раз, когда у вас есть ток, у вас будет магнитное поле, которое циркулирует вокруг этого тока.Теперь, чтобы определить смысл этой циркуляции, вы используете правую руку и хватаете провод большим пальцем, указывающим в направлении тока. Когда вы это сделаете, ваши пальцы покажут вам смысл, в котором магнитное поле циркулирует, поэтому, если у вас есть ток, идущий таким образом, магнитное поле будет образовывать маленькие круги вокруг тока в этом смысле, так что впереди его будет спускаться сзади, он будет подниматься под проводом, который входит в плату, а над проводом он выходит из платы, так что в этом идея.

Теперь закон Ампера также говорит о том, что циркуляция магнитного поля и под этим мы в основном подразумеваем магнитное поле, умноженное на длину этой циркуляции, пропорционально тому, какой ток у нас есть, поэтому мы удваиваем величину тока, тогда мы если вдвое увеличить размер магнитного поля, это также дает нам очень очень простой способ определить выражение в замкнутой форме для магнитного поля из-за длинного провода, поэтому здесь я получил провод, в котором ток выходит из платы, так что вот почему вы не видите провод, потому что ток выходит из платы.Теперь магнитное поле — это синяя линия, обратите внимание, что я снова хватаю провод большим пальцем, указывающим в направлении тока, и мои пальцы показывают, как магнитное поле циркулирует.

Теперь закон Ампера гласит, что циркуляция магнитного поля, которая является магнитным полем, умноженным на длину этой кривой, которая равна 2 пи r, потому что наш круг пропорционален, это означает, что он равен постоянному, умноженному на ток, который выходит из платы. , Теперь, что это за константа? Ну, мы могли бы на самом деле это измерить, но на самом деле люди делают то, что они используют свободу, которую мы должны определить, как ампер, как единицу измерения, чтобы сделать эту константу ровно 4 пи 10 от минус 7 в S.I единицы, так что эти единицы Тесла, метров на ампер хорошо, так что 4 пи умножить на 10 до минус 7, что может равняться нулю, это называется проницаемостью свободного пространства. Хорошо, поэтому, когда у меня есть это выражение, я собираюсь решить для B, и это дает мне B равно mue, а не I более 2 pi r, так что это означает, что если вы удвоите расстояние, которое вы находитесь от провода, вы получите магнитное поле. Если вы утроите расстояние от провода, вы сократите его на треть.

Хорошо, давайте сделаем пример с этим результатом, поэтому я хочу знать, какое магнитное поле находится на расстоянии 2 сантиметра от провода, который хорошо переносит 5 ампер тока, почему бы мне просто не сделать это напрямую? «B» означает «больше, чем я» в течение 2 пи, так что я просто подключу 4 пи по 10 к минус 7, по 5 ампер, разделенных на 2 пи в порядке, что мы знаем, что нам нужно сделать, нам нужно изменить его на S.Я также делю, что наше магнитное поле не выйдет в Тесле, так что 2 раза 10 до минус 2, хорошо, с этой точки зрения происходят удивительные вещи, посмотрите на это 4 пи, 4 пи, пи пи, хорошо, так что теперь мы заканчиваем с 5 раз 10 до отрицательное семь плюс 2 отрицательное 5 Тесла в порядке или 50 микротесла в порядке, так что это магнитное поле, это не очень большое магнитное поле, а 5 ампер — довольно большой ток, поэтому, когда мы делаем это только с помощью длинного прямого провода, как правило, мы не делаем в конечном итоге с огромным магнитным полем у меня есть другие способы сделать это позже.

Хорошо, предположим, что я хочу определить силу между двумя длинными проводами, поэтому вот идея, что у них есть два длинных провода, которые оба несут ток. В этом длинном проводе я использую правило правой руки, и это означает, что здесь, на втором проводе, есть магнитное поле, но теперь провод, который проводит ток в магнитном поле, чувствует силу, что это за сила? Хорошо пересекают b, так что сила действительно привлекательна, в этом случае она будет тянуть провод вверх по направлению к нему. Большая сила заключается в том, что сила, ну и дела, магнитное поле на расстоянии d от провода с током II 1 больше, чем I 1 более 2 пи в порядке.

Сила — это второй ток, умноженный на длину провода, умноженную на магнитное поле, которое я могу переставить таким образом. Теперь люди обычно делят на длину и получают силу на единицу длины, заданную этой формулой. Обратите внимание, что мы получили больше, чем мы получили продукт двух продуктов, а затем мы делим на 2 пи d. Теперь это на самом деле, как определяется ампера. Усилитель — это ток, который дает силу, равную силе на единицу длины, в 2 раза по 10 минус 7 Ньютонов на метр, когда у вас два провода, несущие одинаковый ток, и они на расстоянии 1 метра друг от друга, что означает, что это 1, это 1 это 1, и мне нужно, чтобы все это было 2 от 10 до минус 7, так что это означает, что 4 пи умножить на 10 до минус 7, и вот откуда исходит определение ампер, и это закон ампера.

,

alexxlab

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *