Задачи на закон Ома с решением
Знание закона Ома на сегодняшний день – вопрос общей эрудиции каждого человека. В сегодняшней статье займемся решением задач по теме «закон Ома».
Подписывайтесь на наш телеграм и получайте интересные новости каждый день! А если хотите получить скидку и не упустить выгоду – загляните на наш второй канал с приятными акциями и бонусами для клиентов.
Закон Ома: задачи с решением
Для новичков, которые только начинают решать задачи по физике, мы подготовили специальную памятку и собрали вместе более 40 формул по разным темам. Берите и пользуйтесь!
Задача на закон Ома №1
Условие
Определите силу тока в медном проводнике сеченим 0,5 мм2, если длина проводника 100 м, а напряжение на его концах равно 6,8 В.
Решение
Сначала запишем закон Ома:
I=UR
В данном случае, чтобы найти силу тока I, нужно определить сопротивление R. Используем формулу с удельным сопротивлением и перепишем выражение для закона Ома:
R=ρlSI=USρl
Осталось подставить числа и рассчитать:
I=6,8·0,50,017·100=2 А
Значение удельного сопротивления «ро» для меди берется из таблиц. Для меди ρ=0,017Ом·мм2м
Для меди ρ=0,017Ом·мм2м
Ответ: 2 А.
Задача на закон Ома №2
Условие
По вольфрамовой проволоке длиной 3 м протекает электрический ток силой 0,04 А. Проволока находится под напряжением 5 В. Определите величину площади поперечного сечения проволоки.
Решение
Выразим площадь поперечного сечения проводника из формулы для сопротивления:
R=ρlSS=ρlR
Сопротивление R найдем из закона Ома:
I=URR=UI
Подставим выражение для R в формулу для S и рассчитаем:
S=ρl·IU=0,055·3·0,045=0,0013 мм2
Ответ: 0,0013 мм2
Задача на закон Ома №3
Условие
Каково напряжение на неоднородном участке цепи?
Решение
По закону Ома для неоднородного участка цепи:
U12=φ1-φ2+ε
Считая началом участка точку A, а концом – точку B, и беря поэтому ЭДС со знаком плюс (внутри источника направление тока от отрицательного полюса к положительному), получаем:
UAB=φA-φB+ε=5-7+3=1 В
Ответ: 1В.
Нужно больше примеров решений задач? Вы найдете их в нашем блоге!
Задача на закон Ома №4
Условие
Какова сила тока в резисторе, если его сопротивление 12 Ом, а напряжение на нем 120 В?
Решение
Это простейшая задача на закон Ома для участка цепи, которая решается в одно действие. Просто записываем закон Ома и производим расчет:
I=UR=12012=10 А
Ответ: 10 А.
Задача на закон Ома №5
Условие
Источник постоянного тока с ЭДС E = 12 В и внутренним сопротивлением г = 1 Ом замкнут на внешнее сопротивление R = 9 Ом. Определить силу тока в цепи I, падение напряжения UR на внешнем участке и падение напряжения Ur на внутреннем участке цепи.
Решение
Это задача на закон Ома для полной цепи. По закону Ома для замкнутой цепи:
I=εR+r=129+1=1,2 А
Падение напряжения на внешнем участке цепи:
UR=I·R=εRR+r=12·99+1=10,8 В
Падение напряжение на внутреннем участке цепи:
Ur=ε-UR=12-10,8=1,2 В
Ответ: 1,2 А; 10,8 В; 1,2 В.
Школьный учитель Георг Симон Ом открыл свой закон в 1826 году. Подробнее об истории открытия и самом законе Ома читайте в нашем блоге.
Вопросы на закон Ома
Вопрос 1. Сформулируйте закон Ома для однородного участка цепи.
Ответ. Закон Ома для однородного участка цепи нласит:
Ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.
Вопрос 2. Сформулируйте закон Ома для замкнутой цепи.
Ответ. Закон Ома для замкнутой цепи гласит:
Величина тока в замкнутой цепи, состоящей из источника тока, обладающего внутренним и внешним нагрузочным сопротивлениями, равна отношению электродвижущей силы источника к сумме внутреннего и внешнего сопротивлений.
Вопрос 3. От чего зависит сопротивление цепи?
Ответ. Сопротивление вещества обусловлено колебанием атомов кристаллической решетки.
Сопротивление зависит от:
- температуры;
- материала;
- поперечного сечения проводника.
Вопрос 4. Зависит ли сопротивление от напряжения и силы тока?
Ответ. Нет. Сопротивление не зависит от напряжения и силы тока в проводнике.
Вопрос 5. Всегда ли соблюдается закон Ома?
Ответ. Нет, не всегда. Например, закон Ома не действует при низких температурах для веществ, обладающих сверхпроводимостью.
Проблемы с учебой? Обращайтесь в профессиональный сервис для студентов за квалифицированной помощью.
Решение задач «ЭДС. Закон Ома для полной цепи» 10класс | Учебно-методическое пособие по физике (10 класс):
Опубликовано 17.05.2020 — 16:36 — Салей Елена Владимировна
Решение задач в рамках подготовки к к/р
Скачать:
Предварительный просмотр:
Подготовка к К/р « Законы постоянного тока»
- К источнику с ЭДС 12 В и внутренним сопротивлением 1 Ом подключен реостат, сопротивление которого 5 Ом.
 Найти силу тока в цепи и напряжение на зажимах источника.
Найти силу тока в цепи и напряжение на зажимах источника.
- При подключении лампочки к батарее элементов с ЭДС 4,5 В вольтметр показал напряжение на лампочке 4 В, а амперметр — силу тока 0,25 А. Каково внутреннее сопротивление батареи.
- В проводнике сопротивлением 2 Ом, подключенном к элементу с ЭДС 1,1В, сила тока равна 0,5 А. Какова сила тока при коротком замыкании элемента
- Элемент с ЭДС 2,1 В и внутренним сопротивлением 0,2 Ом соединён с реостатом. Определить силу тока в цепи и сопротивление реостата, если напряжение на зажимах элемента 2 В. Какой длины надо взять для изготовления реостата железную проволоку, если площадь сечения 0,75 мм.
- При подключении к батарее гальванических элементов резистора сопротивлением 9 Ом сила тока в цепи была 1 А, а при подключении резистора сопротивлением 4 Ом сила тока стала 1,5 А. Найдите ЭДС и внутреннее сопротивление батареи.
По теме: методические разработки, презентации и конспекты
«Закон Ома для полной цепи » (сценарий урока)
Представлен подробный сценарий урока. Тип урока: комбинированный. Вид: мультимедийный урок комплексного применения знаний. Материал подобран так, что триединая цель урока и задачи реализовались через …
Тип урока: комбинированный. Вид: мультимедийный урок комплексного применения знаний. Материал подобран так, что триединая цель урока и задачи реализовались через …
10 класс Презентация по физике на тему «Работа и мощность постоянного тока. Электродвижущая сила. Закон Ома для полной цепи.»
10 класс. Презентация по физике на тему «Работа и мощность постоянного тока. Электродвижущая сила. Закон Ома для полной цепи.»…
Закон Ома для полной цепи
Урок изучения нового материала для 10 класса с исследовательским заданием по теме «Закон Ома для полной цепи». При объяснении новой темы учащиеся участвуют в обсуждении вопросов, делают записи в тетра…
Решение задач на закон Ома для полной цепи
На данном уроке опробируется формирование ключевых компетентностей учащихся средствами современных педагогических технологий (технология личностно-ориентированного обучения, технология дифференц…
Контрольная работа по теме «Законы постоянного тока. Закон Ома для полной цепи», 10 класс
Контрольная работа составлена для проверки знаний обучающихся по темам «Законы постоянного тока. Закон Ома для полной цепи."…
Закон Ома для полной цепи."…
Методические рекомендации к изучению темы: « Решение квадратных уравнений» с применением теоремы Виета для решения приведенного квадратного уравнения и полного квадратного уравнени
Решать квадратные уравнения учащимся приходится часто в старших классах, Решение иррациональных, показательных , логарифмических ,тригонометрических уравнений часто сводится к решени…
Решение задач на применение закона Ома для полной цепи.
Сегодня мы разберем методики решения нескольких задач, касающихся всех ключевых тем этой главы: правил соединения, законов Ома, работы тока и правил Кирхгофа….
Поделиться:
Закон Ома: Решенные примеры задач
ЗАКОН ОМА:
Решенные примеры задачПРИМЕР 2.5
Разность потенциалов на резисторе 24 Ом составляет 12 В. Какова сила тока через резистор?
Раствор
В = 12 В и R = 24 Ом
Ток, I = ?
По закону Ома I = V/R = 12/24 = 0,5 А0007
Сопротивление провода 20 Ом. Каково будет новое сопротивление, если его равномерно растянуть в 8 раз?
Каково будет новое сопротивление, если его равномерно растянуть в 8 раз?
Решение
R1 = 20 Ом, R2 = ?
Пусть исходная длина (l1) равна l .
Новая длина, l 2 = 8 l 1 (т.е., д) l2 = 8 l
Исходное сопротивление, R = ρ [ l 1 / A1]
6 Новое сопротивление
R2 =
Хотя проволока натянута, ее объем не меняется.
Initial volume = Final volume
A1 l 1= A2 l 2 , A1 l = A28 l
A1 / A2 = 8 l / l = 8
By деля уравнение R2 на уравнение R1, получаем
. Подставляя значение А1/А2, получаем растяжение провода увеличило его сопротивление.
ПРИМЕР 2.7
Рассмотрим прямоугольный металлический брусок высотой A, шириной B и длиной C, как показано на рисунке.
Если между двумя гранями A и B блока (рисунок (a)) приложена разность потенциалов V, наблюдается текущий IAB . Найдите силу тока, если между двумя гранями В и С блока будет приложена одинаковая разность потенциалов V (рисунок (б)). Дайте свои ответы с точки зрения IAB.
Найдите силу тока, если между двумя гранями В и С блока будет приложена одинаковая разность потенциалов V (рисунок (б)). Дайте свои ответы с точки зрения IAB.
Раствор
В первом случае сопротивление блока
Резисторы последовательно и параллельно: батареи, а также найти разность потенциалов на резисторах 4 Ом и 6 Ом в цепи.
Решение
Поскольку резисторы соединены последовательно, эффективное сопротивление в цепи
= 4 Ом + 6 Ом = 10 Ом
Ток I в цепи = В/треб. = 24/10 = 2,4 А
Напряжение на резисторе 4 Ом
V1 = IR1 = 2 . 4 А × 4 Ом = 9,6 В
Напряжение на резисторе 6 Ом
V2 = IR1 = 2 . 4 А × 6 Ом = 14,4 В
ПРИМЕР 2.9
Рассчитайте эквивалентное сопротивление в следующей цепи, а также найдите ток I, I1 и I2 в данной цепи.
Решение
Поскольку сопротивления соединены параллельно, поэтому эквивалентное сопротивление в цепи равно
Сопротивления соединены параллельно, потенциал (напряжение) на каждом резисторе одинаков.
Ток I представляет собой сумму токов в двух ветвях. Тогда
I = I1 + I2 = 6 А + 4 А = 10 А
ПРИМЕР 2.10
Когда два сопротивления соединены последовательно и параллельно, их эквивалентные сопротивления составляют 15 Ом и 56/15 Ом соответственно. Найдите индивидуальные сопротивления.
Решение
Rs = R1 + R2 = 15 Ом (1)
Приведенное выше уравнение можно решить с помощью факторизации.
R12-8 R1-7 R1+ 56 = 0
R1 (R1– 8) – 7 (R1– 8) = 0
(R1– 8) (R1– 7) = 0
Если (R1= 8) Ом)
используя в уравнении (1)
8 + R2 = 15
R2 = 15 – 8 = 7 Ом ,
R2 = 7 Ом, т.е. (когда R1 = 8 Ом; R2 = 7 Ом)
7
Если (R1= 7 Ом)
Подставляя в уравнение (1)
7 + R2 = 15
R2 = 8 Ом, т. е. (когда R1 = 8 Ом; R2 = 7 Ом)
Решение
ПРИМЕР 2. 12. Рассчитайте эквивалентное сопротивление между точками а и b.
12. Рассчитайте эквивалентное сопротивление между точками а и b.
Решение
Случай (a)
Чтобы найти эквивалентное сопротивление между точками a и b, предположим, что ток входит в соединение a. Так как все сопротивления во внешнем контуре одинаковы (1 Ом), ток в ветвях ac и ad должен быть равен. Таким образом, электрический потенциал в точках c и d одинаков, поэтому ток не течет через сопротивление 5 Ом. Это означает, что 5 Ом не играют никакой роли в определении эквивалентного сопротивления и могут быть удалены. Итак, схема упрощена, как показано на рисунке.
. Эквивалентное сопротивление цепи между A и B равен REQ = 1 Ом
ТЕМПЕТАНСКАЯ ЖЕЛАСА СДЕЛИЧЕСКИЕ СДЕЛАННОСТЬ: Решающие пример задачи
Пример 2.13
, если сопротивление 3 Ом при 20 0С и α = 0,004/0С, затем определить его сопротивление при 100 0С.
Раствор
R0= 3 Ом, T = 100ºC, T0 = 20ºC
α = 0,004/ºC, RT = ?
RT= R0(1 + α(T-T0))
R100 = 3 (1 + 0,004 × 80)
R100 = 3 (1 + 0,32)
R100 = 3 (1,32)
R100 = 3,96 ω
Пример 2,14
Устойчивый при 10ºC и 40ºC составляют 45 Ом и 85 Ом соответственно. Найдите его температурный коэффициент сопротивления.
Найдите его температурный коэффициент сопротивления.
Раствор
T0 = 10ºC, T = 40ºC, R0= 45 Ом, R = 85 Ом
α = 1/R. ΔR /ΔT
α = 0,0296 на ºC
Учебный материал, Лекционные заметки, Задание, Справочник, Объяснение описания Wiki, краткая информация
Цепи постоянного тока — решение задач
Пример задачи по закону Ома: основная цепь
Вопрос
Источник ЭДС \(6,0 В\) подключен к чисто резистивной лампе и ток \(2,0\) ампер течет. Все провода без сопротивления. Каково сопротивление лампы?
Рисунок 1: Схема схемы в этой задаче.Подсказки
- Где в цепи происходит прирост потенциальной энергии?
- Где в цепи происходит потеря потенциальной энергии?
- Что такое закон Ома?
Решение
Прирост потенциальной энергии происходит при прохождении заряда через аккумулятор, то есть он приобретает потенциал \(\varepsilon = 6.0V\). Никакая энергия не теряется в проводах, так как предполагается, что они не имеют сопротивления. При сохранении энергии полученный потенциал (т. Е. \ (\ varepsilon = V = 6,0 В \)) должен быть потерян в резисторе. Итак, по закону Ома:
При сохранении энергии полученный потенциал (т. Е. \ (\ varepsilon = V = 6,0 В \)) должен быть потерян в резисторе. Итак, по закону Ома:
\(V = I R\)
\(R=V/I\)
\(R = 3,0 \Омега\)
Пример задачи о резисторах, соединенных последовательно
Вопрос
Ток, протекающий в цепи, содержащей четыре последовательно соединенных резистора, равен \(I = 1,0 А\). Падение потенциала на первом, втором и третьем резисторах соответственно: \(V = 5 В\), \(V = 8 В\) и \(V = 7 В\).
Эквивалентное сопротивление цепи равно \(R = 30 \Омега\).
Найдите общее напряжение, выдаваемое батареей, а также ток, падение напряжения и сопротивление каждого резистора в цепи.
Подсказки
- Как связаны резисторы при последовательном соединении?
- Что верно в отношении падения потенциала резисторов при последовательном соединении?
- Вам нужно будет использовать закон Ома.

Решение
Рис. 3 Пример задачи с заданными даннымиВо-первых, давайте пометим диаграмму информацией, указанной в вопросе.
Существует несколько способов решения этой проблемы (см. альтернативные решения), но в этом руководстве рассматривается только один из них.
Поскольку резисторы соединены последовательно, через каждый из них протекает одинаковый ток. Используя закон Ома, мы можем найти сопротивления первого, второго и третьего резисторов.
\(R_1 = \frac {V_1}{I}, R_2 = \frac{V_2}{I} , R_3 = \frac {V_3}{I}\)
\(R_1 = \frac {5.0}{ 1,0} = 5,0 \quad \Omega R_2 = \frac{8,0}{1,0} = 8,0 \quad \Omega R_3 = \frac {7,0}{1,0} = 7,0\Omega\)
Теперь, используя эквивалентное сопротивление, мы можно найти сопротивление в четвертом резисторе. Это последовательная цепь, поэтому эквивалентное сопротивление представляет собой сумму отдельных сопротивлений.
\(R_ \mathrm {эквивалент} = R_1 + R_2 +R_3+R_4\)
\(R_4 = R _\mathrm {эквивалент} — ( R_1+R_2+R_3)\)
\(R_4 = 30 — (5,0 + 8,0 + 7,0) = 10 \Омега\)
Ток, протекающий через четвертый резистор, также \(I=1,0А\).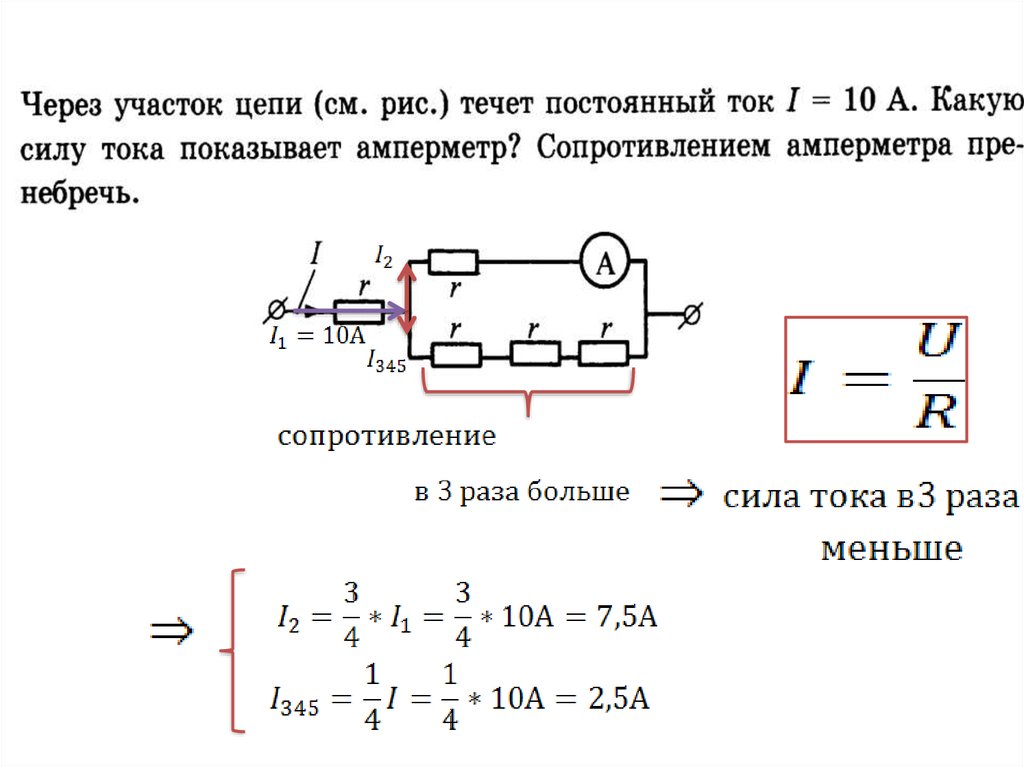 Снова используя закон Ома, мы находим напряжение на этом резисторе.
Снова используя закон Ома, мы находим напряжение на этом резисторе.
\(V_4 = I \cdot R_4\)
\(V_4 = (1.0)\cdot (10) = 10В\)
Общее напряжение, выдаваемое аккумулятором, должно равняться полному падению напряжения в цепи ( это известно как закон напряжения Кирхгофа). Значит, надо просуммировать падения напряжения на резисторах.
\(V = V_1 +V_2 +V_3 +V_4\)
\(V = 5,0+8,0+7,0+10 = 30 В\)
Пример задачи о резисторах, включенных параллельно
Вопрос
7 9 На следующей схеме найдите общий ток, I. Рисунок 4: Пример задачи: Резисторы в параллельном соединении Подсказки
- Вам понадобится закон Ома.
Как связаны резисторы при параллельном соединении?- Каково падение потенциала на каждом резисторе?
- Как ведет себя ток в параллельных ветвях?
Решение
Мы знаем общий потенциал этой цепи,
\(\varepsilon = 12,0 В\)
Итак, между точками \(A\) и \(B\) потенциал должен падать \ (12,0В\). Кроме того, падение потенциала на ветвях цепи одинаково. То есть
Кроме того, падение потенциала на ветвях цепи одинаково. То есть
\(V_1 = V_2 = V_3 = \varepsilon = 12.0V\)
Мы можем использовать закон Ома
\(V = IR\)
или
\(I = V/R\)
, чтобы найти ток через каждый резистор.
\(I_1 = \frac {V_1}{R_1} = \frac {12.0V}{2.0 \Omega} = 6.0A\)
\(I_2 = \frac{V_2}{R_2} = \frac{12.0 V}{3.0 \Omega} = 4.0A\)
\(I_3 = \frac {V_3}{R_3} = \frac {12.0V}{6.0 \Omega} = 2.0A\)
Напомним, что токи через ветви параллельной цепи складываются, чтобы получить общий ток. То есть общий ток «расщепляется», так что часть общего тока проходит по каждой ветви. Из-за сохранения заряда сумма токов в каждой ветви должна равняться сумме, поступающей в ветвь. (Это закон тока Кирхгофа.)
Итак, сложив три тока, получим:
\(I = I_1 +I_2 + I_3\)
\(= 6,0 + 4,0 +2,0 = 12,0 А\)
Итак, общий ток равен \ (I = 12,0 А\).
Примеры задач с резисторами в комбинированных цепях
Вопрос 1
Рис. 5: Комбинированная цепь 1
5: Комбинированная цепь 1 Советы
- Какие резисторы включены параллельно, а какие последовательно?
- Эта цепь состоит из небольших групп параллельных резисторов, соединенных последовательно? Или он состоит из групп последовательных резисторов, соединенных параллельно?
Решение
Эта схема состоит из 3 «элементов», соединенных последовательно: группы параллельных резисторов между \(A\) и \(B\), одного резистора \(R_3\) и группы параллельных резисторов между \(C\) и \(D\).
Сначала найдем эквивалентное сопротивление между \(A\) и \(B\).
Здесь у нас есть два резистора, \(R_1\) и \(R_2\), соединенные параллельно. Используя формулу для параллельно соединенных резисторов:
\(\frac {1}{R_\mathrm{эквивалент}} = \sum \frac{1}{R_i}\)
можно найти эквивалентное сопротивление между точками \(A\) и \(B\). Назовем это эквивалентное сопротивление \(R_{AB}\).
\(\frac {1}{R_{AB}} = \frac {1}{R_1} + \frac {1}{R_2}\)
\(= \frac {1}{10. 0}+ \ frac{1}{4.0}\)
0}+ \ frac{1}{4.0}\)
\(= 0,35\)
\(R_{AB} = 2,857 \Omega\)
Теперь найдем эквивалентное сопротивление между \(C\) и \ (D\), и назовем его \(R_{CD}\). Используя приведенное выше уравнение для параллельно соединенных резисторов,
\(\frac {1}{R_{CD}} = \frac {1}{R_4} + \frac {1}{R_5}\)
\(\frac {1}{R_{CD}} = \frac{1}{8.0}+\frac{1}{1.0}\)
\(\frac {1}{R_{CD}} = 1,125\)
\(R_{CD} = 0,889 \Омега\)
Рисунок 6: Упрощенная версия схемы 1 Заменив два параллельных участка их эквивалентными сопротивлениями и перерисовав схему, мы получим схему на рисунке 2 Мы видим, что последовательно соединены три сопротивления: \(R_{AB}\), \(R_3\) и \(R_{CD}\). Используя формулу для резисторов, соединенных последовательно,
, мы можем найти эквивалентное сопротивление цепи.
Таким образом, эквивалентное сопротивление этой цепи равно \(R = 6,7 Ом).
Вопрос 2
На рисунке 7 показана часть схемы. Он состоит из резисторов, объединенных как в параллельные, так и в последовательные конфигурации. Найдите эквивалентное сопротивление.
Найдите эквивалентное сопротивление.
Рисунок 7: Цепь 2, резисторы в комбинации Подсказки
- Каково эквивалентное сопротивление резисторов, включенных параллельно?
- Серийно?
Решение
В этой неполной цепи есть три основные ветви, ветвь \(AB\), ветвь \(CD\), ветвь \(EF\). Как видите, ветвь \(AB\) содержит два последовательно соединенных резистора, \(R_1\) и \(R_2\). Ветвь \(CD\) имеет только один резистор, \(R_3\). Наконец, в ветви \(EF\) есть два резистора.
Сначала рассмотрим ветвь \(AB\). Мы упростим эту ветвь, найдя эквивалентное сопротивление между \(A\) и \(B\). Обратите внимание, что \(R_1\) соединен последовательно с \(R_2\). Используя уравнение для последовательно соединенных резисторов
\(R_\mathrm {эквивалент} = \сумма R_i\)
, мы можем найти \(R_{AB}\).
\(R_{AB} = R_1 + R_2\)
\(R_{AB} = 1.0 + 2.0\)
\(R_{AB} = 3.0 \Омега\)
Теперь в ветке \( CD\) есть только один резистор, поэтому эту ветвь нельзя упростить дальше.
 Кроме того, падение потенциала на ветвях цепи одинаково. То есть
Кроме того, падение потенциала на ветвях цепи одинаково. То есть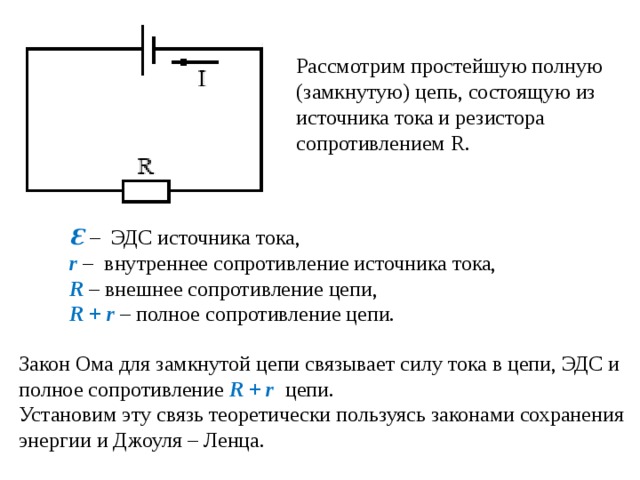 0}+ \ frac{1}{4.0}\)
0}+ \ frac{1}{4.0}\) Найдите эквивалентное сопротивление.
Найдите эквивалентное сопротивление.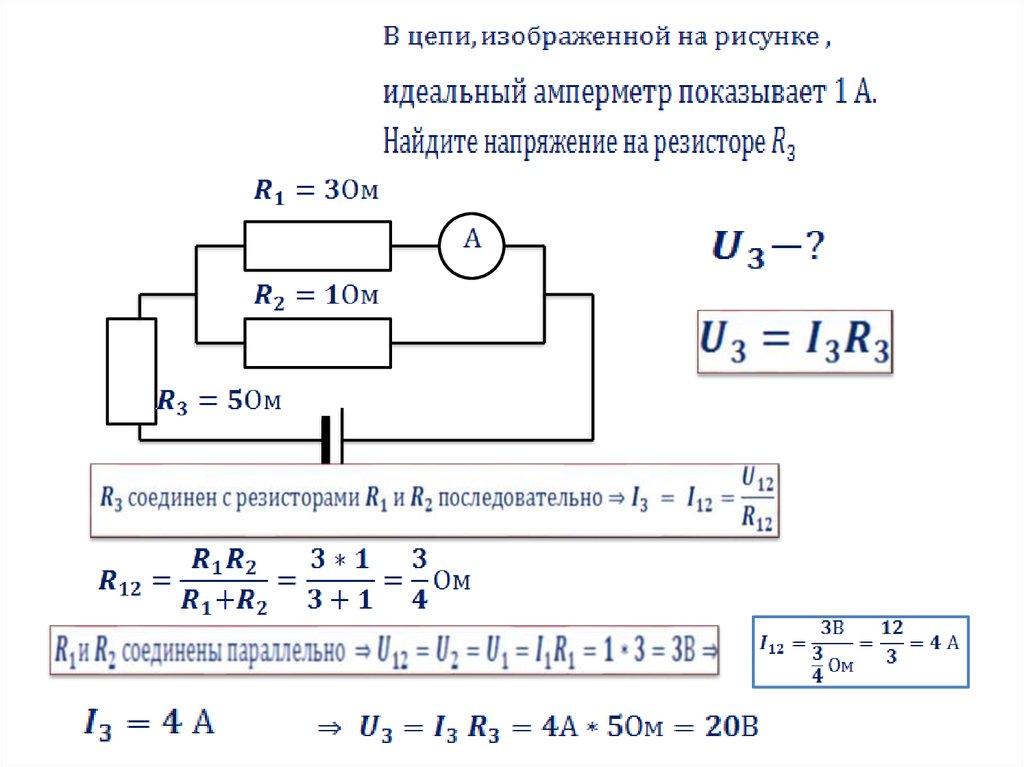


 Найти силу тока в цепи и напряжение на зажимах источника.
Найти силу тока в цепи и напряжение на зажимах источника.
 5: Комбинированная цепь 1
5: Комбинированная цепь 1