Понятие о моменте силы в физике: примеры решения задач
Часто в физике приходится решать задачи на расчет равновесия в сложных системах, имеющих множество действующих сил, рычагов и осей вращения. В этом случае проще всего использовать понятие момента силы. В данной статье приводятся все необходимые формулы с подробными объяснениями, которые следует использовать для решения задач названного типа.
О чем пойдет речь?
Многие люди наверняка обращали внимание, что если воздействовать с какой-либо силой на предмет, закрепленный в некоторой точке, то он начинает вращаться. Ярким примером может служить дверь в дом или в комнату. Если ее взять за ручку и толкнуть (приложить силу), то она начнет открываться (поворачиваться на петлях). Этот процесс представляет собой проявление в быту действия физической величины, которая получила название момента силы.
Из описанного примера с дверью следует, что рассматриваемая величина указывает на способность силы совершать вращение, что является ее физическим смыслом. Также эту величину называют моментом кручения.
Также эту величину называют моментом кручения.
Определение момента силы
Перед тем как дать определение рассматриваемой величине, приведем простой рисунок.
Итак, на рисунке изображен рычаг (синего цвета), который закреплен на оси (зеленый цвет). Этот рычаг имеет длину d, а к его концу приложена сила F. Что будет в этом случае происходить с системой? Верно, рычаг начнет вращаться против часовой стрелки, если смотреть на него сверху (отметим, что если напрячь немного свое воображение и представить, что взгляд направлен снизу на рычаг, то он будет вращаться по часовой стрелке).
Пусть точка закрепления оси называется O, а точка приложения силы — P. Тогда, можно записать следующее математическое выражение:
OP¯* F¯ = M¯FO.
Где OP¯ — это вектор, который направлен от оси к концу рычага, он также называется рычагом силы, F¯ — это вектор приложенной силы к точке P, а M¯FO — это момент силы относительно точки O (оси). Эта формула является математическим определением рассматриваемой физической величины.
Эта формула является математическим определением рассматриваемой физической величины.
Направление момента и правило правой руки
Выражение выше представляет собой векторное произведение. Как известно, его результатом также является вектор, который перпендикулярен плоскости, проходящей через соответствующие вектора-множители. Этому условию удовлетворяют два направления величины M¯FO (вниз и вверх).
Чтобы однозначно его определить, следует воспользоваться так называемым правилом правой руки. Его можно сформулировать таким образом: если согнуть в полудугу четыре пальца правой руки и направить эту полудугу так, чтобы она шла вдоль первого вектора (первый множитель в формуле) и направлялась к концу второго, тогда оттопыренный вверх большой палец укажет направление момента кручения. Отметим также, что перед тем как использовать это правило, необходимо установить умножаемые вектора так, чтобы они выходили из одной точки (их начала должны совпадать).
В случае рисунка в предыдущем пункте можно сказать, применив правило правой руки, что момент силы относительно оси будет направлен вверх, то есть на нас.
Помимо отмеченного способа определения направления вектора M¯FO, существует еще два. Приведем их:
- Момент кручения будет направлен таким образом, что если смотреть с конца его вектора на вращающийся рычаг, то последний будет двигаться против хода стрелки часов. Общепринято считать это направление момента положительным при решении разного рода задач.
- Если закручивать буравчик по часовой стрелке, то момент кручения будет направлен в сторону движения (углубления) буравчика.
Все приведенные определения являются эквивалентными, поэтому каждый может выбрать то, которое удобно для него.
Итак, было выяснено, что направление момента силы является параллельным оси, вокруг которой вращается соответствующий рычаг.
Приложенная под углом сила
Рассмотрим рисунок, который приведен ниже.
Здесь мы также видим рычаг длиной L, закрепленный в точке (указана стрелкой). На него действует сила F, однако, направлена она под некоторым углом Φ (фи) к горизонтальному рычагу. Направление момента M¯FO в этом случае будет таким же, как и на предыдущем рисунке (на нас). Чтобы вычислить абсолютное значение или модуль этой величины, необходимо воспользоваться свойством векторного произведения. Согласно ему для рассматриваемого примера, можно записать выражение: MFO = L*F*sin(180o-Φ) или, воспользовавшись свойством синуса, перепишем:
Направление момента M¯FO в этом случае будет таким же, как и на предыдущем рисунке (на нас). Чтобы вычислить абсолютное значение или модуль этой величины, необходимо воспользоваться свойством векторного произведения. Согласно ему для рассматриваемого примера, можно записать выражение: MFO = L*F*sin(180o-Φ) или, воспользовавшись свойством синуса, перепишем:
MFO = L*F*sin(Φ).
На рисунке приведен также достроенный прямоугольный треугольник, сторонами которого являются сам рычаг (гипотенуза), линия действия силы (катет) и сторона длиной d (второй катет). Учитывая, что sin(Φ) = d/L, указанная формула примет вид: MFO = d*F. Видно, что дистанция d — это расстояние от точки закрепления рычага до линии действия силы, то есть d — рычаг силы.
Обе рассмотренные в этом пункте формулы, которые следуют непосредственно из определения момента кручения, являются полезными при решении практических задач.
Единицы измерения момента кручения
Воспользовавшись определением, можно установить, что величина MFO должна измеряться в ньютонах на метр (Н*м). Действительно, в виде этих единиц она и используется в СИ.
Отметим, что Н*м — это единица измерения работы, которая выражается в джоулях, как и энергия. Тем не менее джоули для концепции момента силы не используют, поскольку эта величина отражает именно возможность осуществления последней. Однако связь с единицей работы имеется: если в результате действия силы F выполнен полный поворот рычага вокруг его точки вращения O, тогда совершенная работа будет равна A = MFO*2*pi (2*pi — угол в радианах, который соответствует 360o). В этом случае единицу измерения момента MFO можно выразить в джоулях на радиан (Дж/рад.). Последняя, наряду с Н*м, также используется в системе СИ.
Теорема Вариньона
В конце XVII века французский математик Пьер Вариньон, изучая равновесие систем с рычагами, впервые сформулировал теорему, которая теперь носит его фамилию. Она формулируется так: суммарный момент нескольких сил равен моменту результирующей одной силы, которая приложена к некоторой точке относительно той же оси вращения. Математически ее можно записать следующим образом:
Она формулируется так: суммарный момент нескольких сил равен моменту результирующей одной силы, которая приложена к некоторой точке относительно той же оси вращения. Математически ее можно записать следующим образом:
M¯1+M¯2+…+M¯n = M¯ = d¯*∑ni=1(F¯i) = d¯*F¯.
Эту теорему удобно использовать для расчета моментов кручения в системах с несколькими действующими силами.
Далее приведем пример использования приведенный выше формул для решения задач по физике.
Задача с гаечным ключом
Один из ярких примеров демонстрации важности учета момента силы является процесс откручивания гаек ключом. Чтобы открутить гайку, нужно приложить некоторый момент кручения. Необходимо рассчитать, какую силу следует приложить в точке A, чтобы начать откручивать гайку, если эта сила в точке B равна 300 Н (см. рисунок ниже).
рисунок ниже).
Из приведенного рисунка следуют две важные вещи: во-первых, расстояние OB в два раза больше, чем OA; во-вторых, силы FA и FB направлены перпендикулярно к соответствующему рычагу с осью вращения, совпадающей с центром гайки (точка O).
Момент кручения для этого случая можно записать в скалярной форме так: M = OB*FB = OA*FA. Поскольку OB/OA = 2, то это равенство будет выполняться только тогда, когда FA будет больше FB в 2 раза. Из условия задачи получаем, что FA = 2*300 = 600 Н. То есть, чем больше длина ключа, тем легче откручивать гайку.
Задача с двумя шарами разной массы
На рисунке ниже приведена система, которая находится в равновесии. Необходимо найти положение точки опоры, если длина доски равна 3 метра.
Так как система находится в равновесии, то сумма моментов всех сил равна нулю. На доску действуют три силы (веса двух шаров и сила реакции опоры). Поскольку сила опоры не создает момента кручения (длина рычага равна нулю), то остается только два момента, создаваемых весом шаров.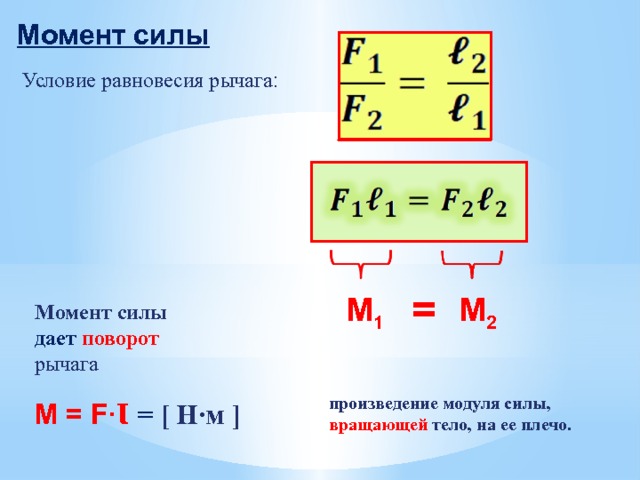
Пусть точка равновесия находится на расстоянии x от края, где лежит шар массой 100 кг. Тогда можно записать равенство: M1-M2 = 0. Поскольку вес тела определяется по формуле m*g, тогда имеем: m1*g*x — m2*g*(3-x) =0. Сокращаем g и подставляем данные, получаем: 100*x — 5*(3-x) = 0 => x = 15/105= 0,143 м или 14,3 см.
Таким образом, чтобы система находилась в равновесии, необходимо установить опорную точку на расстоянии 14,3 см от края, где будет лежать шар массой 100 кг.
Ответы на задачи по технической механике
Рейтинг ↑ не забываем
Порядок действий при демонтаже кондиционеров (посмотреть)
Свод правил вентиляции и кондиционирования 2017 год (посмотреть)
Условные обозначения систем вентиляции и кондиционирования (посмотреть)
Требования к пожарной безопастности по вентиляции и кондиционированию (посмотреть).
Если Вы не нашли свой вариант ответа, обращайтесь перейдя по ссылке в группу ВК опубликовав Ваши задачи прям в ленту группы ,по возможности постараемся Вам помочь. На данной странице не все ответы, перейдя по ссылке попадаете на другую страницу с ответами
На данной странице не все ответы, перейдя по ссылке попадаете на другую страницу с ответами
Задача № 29 Найти реакцию опор
Ответ к задачи №29
Задача № 20 Натяжка троса
Ответ к задачи № 20
Задача №7 Найти реакцию опор
Ответ к задаче №7
Задача № 9 Распределение нагрузки
Ответ к задачи № 9
Задача № 11 Определить координаты центра тяжести сечения
Ответ к задачи № 11 С решением
Задача № 12 Найти реакцию опор
Ответ к задачи №12
Задача № 13 Решить графически
Ответ к задаче №13
Задача № 33 Решить графически
Ответ к задачи № 33
Задача № 33 Силы давящие на шар
Ответ к задачи № 33 Силы давящие на шар
Задача № Задача №21 Определить координат центра тяжести
Ответ к задаче № 21 Определить координат центра тяжести
Ответ № 21 /2 Определить координат центра тяжести 30А Ответ на координат центр тяжести № 21 -27
Задача № 20 Определить опорные реакции балки. Проверить правильность их определения
Проверить правильность их определения
Ответ к задачи № 20 Определить опорные реакции балки.Проверить правильность их определения
Задача № 22 Задача № 22 найти R(a) и R(b)
Ответ к задачи Задача № 22 найти R(a) и R(b)
Задача Определить координаты центра тяжести сечения.Показать положение центра тяжести на чертеже
Ответ к задачи Определить координаты центра тяжести сечения.Показать положение центра тяжести на чертеже
Задача № 10 Найти реакцию опор
Ответ к задачи №10 Найти реакцию опор
Задача № 16 Определить опорные реакции балки.Проверить правильность их определения
Ответ к задачи № 16
Задача № 22 Определить опорные реакции балки. Проверить правильность их определения
Ответ к задачи № 22 Определить опорные реакции балки Проверить правильность их определения
Задача № 27 Определить опорные реакции балки Проверить правильность их определения
Ответ к задачи № 27 Определить опорные реакции балки Проверить правильность их определения
Задача № 26 Определить опорные реакции балки Проверить правильность их определения
Ответ к задачи № 26 Определить опорные реакции балки Проверить правильность их определения
Вариант 32 задача № 1Определить опорные реакции балки на двух опорах. Проверить правильность их определения
Проверить правильность их определения
Ответ к варианту 32 задача №1Определить опорные реакции балки на двух опорах. Проверить правильность их определения
Вариант 32 задача №2 Определить координаты центра тяжести сечения Показать положение центра на чертеже
Ответ к варианту 32 №2 Определить координаты центра тяжести сечения Показать положение центра на чертеже
Решение к варианту 32 № 2
Вариант 24 задача № 2 Определить координаты центра тяжести сечения Показать положения центра тяжести на чертеже
Ответ к варианту 24 задача № 2 Определить координаты центра тяжести сечения
Задача Указать положение центра тяжести на рисунке, придерживаясь определенного масштаба
Ответ к задачи Указать положение центра тяжести на рисунке, придерживаясь определенного масштаба
Задача — Определить величину и направления реакцию связей
Ответ к задаче -Определить величину и направления реакций связей
Задача- Определить опорные реакции балки на 2-х опорах
Ответ к задачи Определить опорные реакции балки на 2-х опорах
Задача № 9 Найти центр тяжести
Ответ к задаче № 9 найти центр тяжести
Найти центр тяжести
Решение к задаче Найти центр тяжести
Задача № 7
Решение к задаче № 7
28 задача Определить положение координаты центра тяжести
Ответ к 28 задачи Определить положение координаты центра тяжести
Задача Найти центр тяжести
Ответ к задаче Найти центр тяжести
Задача № 16 Определить положение координаты центра тяжести
Ответ к задаче № 16 Определить положение координаты центра тяжести
Ответ к задаче № 16 Определить положение координаты центра тяжести
Задача №23 Определить кординаты центра тяжести сечения
Ответ к задаче № 23 Определить координаты центра тяжести сечения
Определить опорные реакции балки
Ответ к задаче Определить опорные реакции балки
Определить опорные реакции балки
Ответ к задаче Определить опорные реакции балки
Определить координат центр тяжести
Ответ к задаче определить координат центр тяжести
Задача №20 Найти центр тяжести
Ответ к Задаче №20 Найти центр тяжести
Задача: Определить опорные реакции балки на двух опорах. Проверить правильность их определения
Проверить правильность их определения
Ответ к задаче: Определить опорные реакции балки на двух опорах. Проверить правильность их определения
Задача Определить центр тяжести
Ответ к задаче — Определить центр тяжести
Здравствуйте, помогите пожалуйста решить задачу по расчету прочности при расстяжении, сжатии
Ответ к задаче по расчету прочности при расстяжении, сжатии
Задача- Определить координат центра тяжести
Ответ к задаче Определить координат центра тяжести
Задача — Подобрать сечение стержня подвески поддерживающего брус
Ответ к задаче Подобрать сечение стержня подвески поддерживающего брус
Задача — Подобрать сечение стержня подвески поддерживающего брус
Ответ к задаче — Подобрать сечение стержня подвески поддерживающего брус
Задача: построить эпюры Qy и Mx для балки по данным в задании
Ответ построить эпюры Qy и Mx для балки по данным в задании
Задача: номер 1. Определить реакции в опорах для балки
Определить реакции в опорах для балки
Ответ к задаче номер 1. Определить реакции в опорах для балки
Задача: построить эпюр Qy и Mx для балки, по данным в задании
Ответ к Задачи: построить эпюр Qy и Mx для балки, по данным в задании
Вариант № 3
Задание № 1 Определить изгибающий момент в точке С (справа)
Вариант № 2 Задание 1
Определить изгибающий момент в точке С . Построить эпюры поперечной силы и изгибающего момента
Вариант № 2 Задание 2
Ответ к Заданию № 2 рассчитать осевой момент инерции швеллера относительно оси Х
Задача № 3 Определить координаты центра тяжести
Ответ к задаче № 3
Задача 7
Ответ к задаче 7
Задача Проверить несущую способность балки
Ответ к задаче Проверить несущую способность балки
Задача — Момент силы относительно точки
Ответ к задаче — Момент силы относительно точки
Задача — Понятие о внецентренном растяжении ( сжатии)
Ответ к задаче — Понятие о внецентренном растяжении ( сжатии)
Задание
Ответ к заданию для Натальи Добринской
Задача: Определить реакцию опор двухопорной балки
Ответ
Задача
Ответ
Задача — столбец под номером 1
Ответ к задаче
Рисунок Д вариант чисел 1 Задача
Ответ к задаче
ПЕРЕХОДИ НА ДРУГУЮ СТРАНИЦУ САЙТА
ПО ССЫЛКЕ НИЖЕ
ОТВЕТЫ ПО ТЕХ-МЕХУ НА СЛЕДУЮЩЕЙ СТРАНИЦЕ
Видео: Момент силы относительно точки в 2D: Скаляр
Стенограмма видео
В этом видео наша тема — моменты
в 2D. И хотя у нас есть такие
персонажи, нарисованные в двух измерениях, которые наслаждаются моментом, конечно, моменты
о которых мы говорим в этом уроке, разные. Мы увидим, что они
включают силы, расстояния и точки или оси вращения.
И хотя у нас есть такие
персонажи, нарисованные в двух измерениях, которые наслаждаются моментом, конечно, моменты
о которых мы говорим в этом уроке, разные. Мы увидим, что они
включают силы, расстояния и точки или оси вращения.
Для начала скажем, что у нас есть эти две вещи, сила 𝐹 и точка, которую мы назовем здесь 𝑃. Глядя на эту силу, мы видим, что оно действует по определенной линии, т. е. в определенном направлении. Имя этому — линия действие силы. И мы видим, что эта линия не пройти через нашу точку 𝑃.
Итак, давайте сделаем что-нибудь, чтобы соединиться
нашу точку 𝑃 с нашей силой 𝐹. Нарисуем стержень, который будем
скажем, имеет пренебрежимо малую массу. Но один конец этого стержня прикреплен к
точка 𝑃, а на другой конец действует сила 𝐹. И теперь мы можем видеть, что это за сила
𝐹 будет стремиться сделать стержень около точки 𝑃. Это будет стремиться заставить его вращаться. Тенденция этой силы к
вращение вокруг точки называется моментом силы. И мы представляем его с большой буквы
𝑀.
Это будет стремиться заставить его вращаться. Тенденция этой силы к
вращение вокруг точки называется моментом силы. И мы представляем его с большой буквы
𝑀.
Даже если этот термин для нас новый, идея чего-то подобного, того, что мы называем моментом силы, на самом деле привычный. Например, представьте себе эту точку 𝑃 является дверной петлей, и что наша оранжевая линия представляет собой вид сверху вниз на дверь. дверь. В этом случае будет естественно чтобы мы толкнули или потянули за этот другой конец двери — мы могли бы его назвать — для того, чтобы чтобы открыть или закрыть его. При этом сила, которую мы прикладываем создает момент.
Что касается расчета
момент силы, есть несколько способов сделать это. Чтобы увидеть, как это так, давайте
представьте, что наша сила 𝐹 действует под углом 45 градусов к оси
этот тонкий безмассовый стержень. Чтобы найти момент этой силы
создает вокруг точки 𝑃, один из способов сделать это — разбить эту силу на
вертикальную и горизонтальную составляющие, а затем умножить составляющую силы
это перпендикулярно нашему стержню на общую длину стержня. Итак, если мы скажем, что наш стержень имеет
длина 𝐿, а модуль этой составляющей силы, перпендикулярной ей, равен 𝐹
умножить на cos 45 градусов, тогда наш момент будет произведением этих двух
ценности.
Чтобы найти момент этой силы
создает вокруг точки 𝑃, один из способов сделать это — разбить эту силу на
вертикальную и горизонтальную составляющие, а затем умножить составляющую силы
это перпендикулярно нашему стержню на общую длину стержня. Итак, если мы скажем, что наш стержень имеет
длина 𝐿, а модуль этой составляющей силы, перпендикулярной ей, равен 𝐹
умножить на cos 45 градусов, тогда наш момент будет произведением этих двух
ценности.
Напоминая, что cos 45
градусов равен квадратному корню из двух из двух, этот момент упрощается до 𝐹 раз
𝐿, умноженный на квадратный корень из двух из двух. Этот метод расчета моментов,
где мы вычисляем расстояние между точкой, о которой мы рассматриваем
вращения и приложенной силы и умножить это расстояние на
перпендикулярная составляющая приложенной силы, является наиболее распространенным способом расчета
момент силы в общем. Но, как мы уже говорили, это не
единственный путь.
Но, как мы уже говорили, это не
единственный путь.
Другой подход, который мы можем использовать, это найти перпендикулярное расстояние между линией действия нашей силы и точкой о котором мы рассматриваем ротацию. Если мы расширим линию действия мы нарисовали, а затем проведем перпендикулярную линию от нашей линии действия, которая пересекает точку 𝑃, другой способ вычислить момент этой силы состоит в том, чтобы решить для этого расстояния — назовем его 𝑑 — и умножим на силу 𝐹. И заметьте, что если мы это сделаем, мы снова вычисляем плечо момента — изначально это была длина 𝐿 и теперь это расстояние 𝑑 — и умножив его на силу, перпендикулярную эта рука. Итак, что же это за расстояние 𝑑?
Мы можем решить это, распознав
что этот угол здесь должен быть 45 градусов, так как этот. И затем, поскольку это право
угол равен 90 градусов, третий внутренний угол в нашем треугольнике тоже должен быть 45
градусов.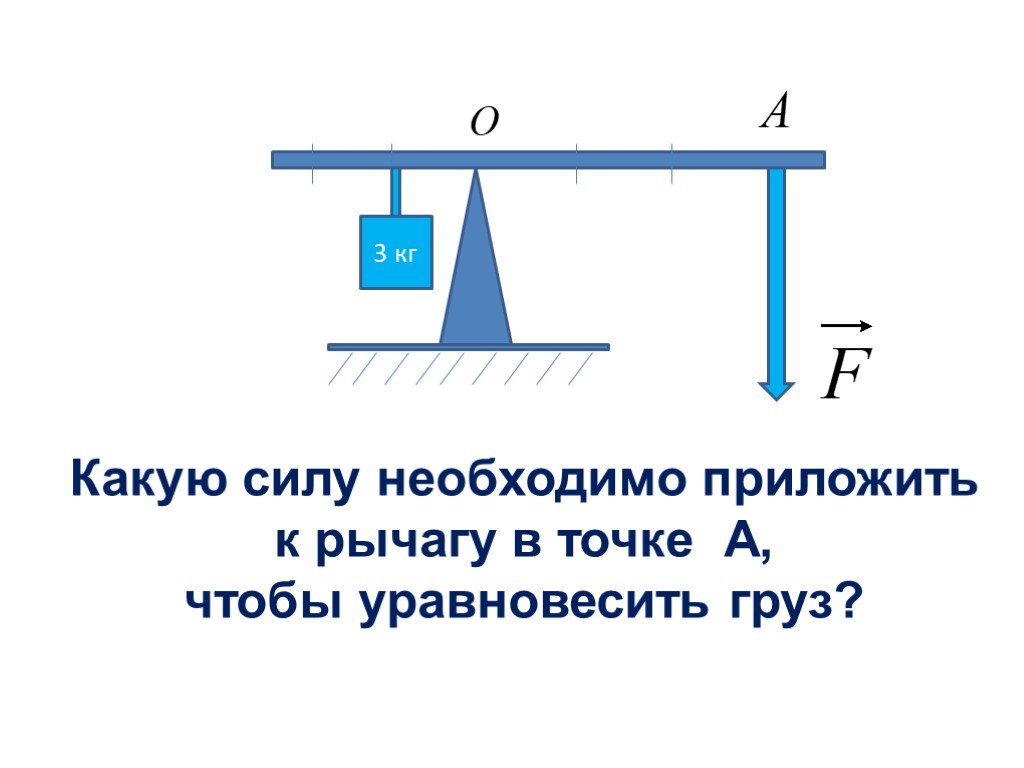 И это показывает нам, что мы можем писать
расстояние 𝑑 как 𝐿, умноженное на косинус этого угла. Таким образом, в этом втором способе
рассчитывая наш момент силы, мы умножаем расстояние 𝑑 на компонент
из 𝐹, который перпендикулярен ему. И в этом вся сила
величина. 𝑑, как мы видели, в 𝐿 раз больше, чем
cos 45 градусов. Записав этот косинус в виде
точное значение, мы находим, что момент силы равен 𝐹, умноженному на 𝐿, умноженному на квадрат
корень из двух над двумя. И теперь мы видим, что это соответствует
результат нашего предыдущего метода.
И это показывает нам, что мы можем писать
расстояние 𝑑 как 𝐿, умноженное на косинус этого угла. Таким образом, в этом втором способе
рассчитывая наш момент силы, мы умножаем расстояние 𝑑 на компонент
из 𝐹, который перпендикулярен ему. И в этом вся сила
величина. 𝑑, как мы видели, в 𝐿 раз больше, чем
cos 45 градусов. Записав этот косинус в виде
точное значение, мы находим, что момент силы равен 𝐹, умноженному на 𝐿, умноженному на квадрат
корень из двух над двумя. И теперь мы видим, что это соответствует
результат нашего предыдущего метода.
Итак, давайте напишем наше уравнение для
момент силы 𝑀 вот так. Будем говорить, что он равен
перпендикулярная составляющая силы 𝐹, умноженная на расстояние между точками, где
применяется перпендикулярная составляющая и некоторая точка вращения. И, кстати, это количество, которое
то, что мы называем моментом, в этом контексте иногда называют крутящим моментом. Так что, если мы слышим это слово крутящий момент
используется, мы знаем, что это относится к моменту силы.
Так что, если мы слышим это слово крутящий момент
используется, мы знаем, что это относится к моменту силы.
Вообще момент может быть либо положительный, отрицательный или нулевой. Мы видим, например, что это сила 𝐹 будет стремиться создать вращение этого стержня против часовой стрелки вокруг точки мы выбрали 𝑃. По соглашению, моменты в этом направление, ведущее к вращению против часовой стрелки, считаются положительными. Это означает, что мы называем моменты что приводит к отрицательному вращению по часовой стрелке. И, как мы упоминали, это также возможно на мгновение быть равным нулю.
Скажите, что вместе с нашей точкой 𝑃 мы
выбираем вторую точку — назовем ее точкой 𝑄 — и располагаем ее вдоль линии
действия нашей силы. Поскольку 𝑄 лежит вдоль этой линии,
между перпендикулярной составляющей нашей силы и этой
точка. Физически он никогда не стремился бы
создать вращение вокруг точки 𝑄. И поэтому не может породить
до отличного от нуля момента. При этом момент силы 𝐹 о
точка 𝑃 равна 𝐹 умноженному на 𝐿 умноженному на квадратный корень из двух из двух, момент 𝐹
относительно точки 𝑄 равно нулю.
Физически он никогда не стремился бы
создать вращение вокруг точки 𝑄. И поэтому не может породить
до отличного от нуля момента. При этом момент силы 𝐹 о
точка 𝑃 равна 𝐹 умноженному на 𝐿 умноженному на квадратный корень из двух из двух, момент 𝐹
относительно точки 𝑄 равно нулю.
Последнее, на что стоит обратить внимание Моменты — это единицы измерения, которые мы можем ожидать от этих величин. Мы видим, что момент задается сила в основных единицах СИ в ньютонах, умноженная на расстояние в основных единицах СИ метров. Обычно тогда дается момент в единицах ньютонов на метры. Но вне зависимости от конкретных единицы силы и расстояния, с которыми мы работаем, моменты всегда состоят из единицы сила, умноженная на единицу расстояния.
Зная все это, давайте немного
практики сейчас через пример упражнения.
Если сила, имеющая величину 498 ньютонов находится в восьми сантиметрах от точки 𝐴, найдите норму момент силы относительно точки 𝐴, давая ответ в ньютонах метров.
Хорошо, допустим, что это наша точка 𝐴 и что на расстоянии восьми сантиметров у нас есть сила мы назовем это 𝐹 с величиной 498 ньютонов. Зная все это, мы хотим вычислить норму момента этой силы относительно точки 𝐴.
Для начала вспомним
что момент силы относительно какой-то точки — назовем этот момент капитальным 𝑀
— равна составляющей приложенной силы 𝐹, перпендикулярной
линия от места приложения силы до интересующей точки, умноженная на эту
расстояние между точкой и приложенной силой. Когда мы смотрим на нашу конкретную
сценарии мы видим, что эта сила 𝐹 и расстояние в восемь сантиметров равны
уже перпендикулярны друг другу. Поэтому момент этого
сила относительно точки 𝐴 равна 𝐹, умноженной на восемь сантиметров.
Поэтому момент этого
сила относительно точки 𝐴 равна 𝐹, умноженной на восемь сантиметров.
Если заменить в заданном
значение для 𝐹, мы почти готовы умножить, чтобы вычислить 𝑀. Но прежде чем мы это сделаем, давайте вспомним
что мы хотим дать наш ответ в единицах ньютонов, умноженных на метры. Мы видим, что если мы пройдем через
наше умножение в том виде, в каком оно есть, будет выражаться в ньютонах, умноженных на сантиметры. Итак, прежде чем мы пойдем дальше,
давайте переведем это расстояние из единиц сантиметров в единицы метров. Мы можем сделать это, вспомнив
что 100 сантиметров равны одному метру, а это значит, что восемь сантиметров
равна 0,08 метра. Теперь, когда мы умножаем эти два
значения вместе, мы получаем результат ровно 390,84 ньютон-метра. Это норма момента
силы относительно точки 𝐴.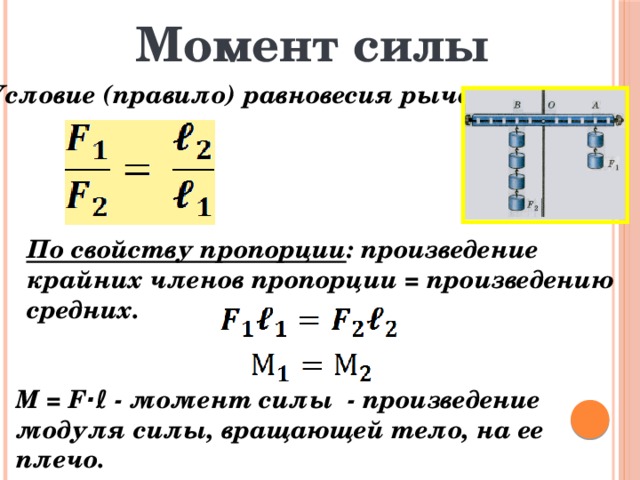
Теперь давайте рассмотрим пример, который включает в себя более сложное плечо момента.
Определить момент силы что имеет величину 11 ньютонов относительно точки 𝑂. Дайте ответ в ньютонах раз метры.
Глядя на нашу схему, мы видим
эта сила в 11 ньютонов направлена вниз и мы также видим здесь точку 𝑂. Чтобы определить момент этого
сила относительно точки 𝑂, мы можем вспомнить, что момент из-за некоторой силы относительно некоторой
точка равна составляющей этой силы, перпендикулярной прямой
между точкой приложения силы и точкой интереса, умноженной на
расстояние между этой точкой и точкой приложения силы. Практически, что все это
означает, что когда дело доходит до нашего сценария, то, если мы нарисуем линию, вдоль которой
наша сила действует — это называется линией действия силы — то
момент этой силы относительно точки 𝑂 будет равен силе, умноженной на эту
расстояние, которое мы назвали 𝑑.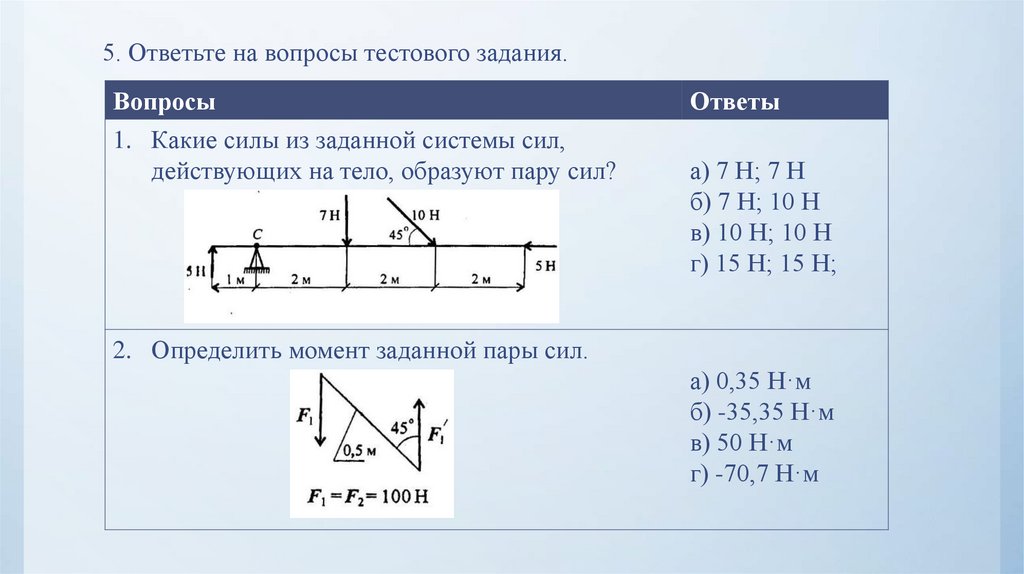
Оглядываясь назад на это уравнение для момента силы, поскольку мы уже знаем силу в 11 ньютонов, наша задача сначала решить для этого расстояния 𝑑. Если мы начнем с точки 𝑂 и затем рассмотрим то, что мы могли бы назвать тремя сегментами этого аппарата, если бы мы проехать из точки 𝑂 по первому отрезку, а затем вниз по второму сегмент и, наконец, по третьему, пока мы не достигнем линии действия наша сила, то общее горизонтальное смещение этого трехсегментного путешествия будет равно расстоянию 𝑑, которое мы хотим вычислить.
Чтобы определить это расстояние,
назначим движение вправо как движение в положительном направлении, а движение как
слева в отрицательном направлении. Это означает, что в первый
этап нашего путешествия, мы прошли положительные 36 сантиметров. А потом на вторую ногу,
путешествуя по этому 29-сантиметровому отрезку, так как этот отрезок наклонен под углом 60
градусов ниже горизонтали, то горизонтальное смещение мы покрываем перемещением
вдоль этого отрезка положительная 29сантиметры, умноженные на косинус 60 градусов. И вот, наконец, вдоль
третий сегмент, мы проходим минус 26 сантиметров. И это потому, что, как мы
указанное движение влево отрицательно.
И вот, наконец, вдоль
третий сегмент, мы проходим минус 26 сантиметров. И это потому, что, как мы
указанное движение влево отрицательно.
Когда эти три значения вместе они равны 𝑑, расстоянию, которое мы хотим найти. Напоминая, что cos 60 градусов равно половине, общее расстояние, которое мы получим, будет положительным 24,5 сантиметры. Тогда это значение, по которому мы умножим нашу силу 𝐹, чтобы решить момент, когда сила создает о пункте 𝑂. Прежде чем мы это сделаем, поскольку мы хотим, чтобы наш ответ в конце был в ньютонах, умноженных на метры, давайте конвертируем это расстояние в сантиметрах к расстоянию в метрах. Напоминая, что 100 сантиметров равняется одному метру, мы можем сказать, что 24,5 сантиметра равняются 0,245 метра.
Итак, как только мы
вычисление равно силе 𝐹, умноженной на это расстояние в метрах.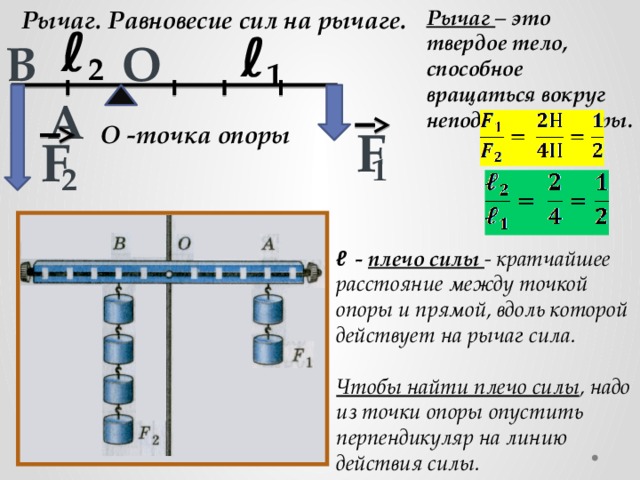 А теперь, рассмотрев
положительное и отрицательное направления для смещения, давайте сделаем то же самое для
наша сила. Наша сила, как мы видим,
направлены вниз. Мы могли бы дать этому отрицательный
значение, которое означало бы, что наша сила 𝐹 равна отрицательным 11 ньютонам. Другой способ думать об этом —
рассмотреть направление момента относительно точки 𝑂, что эта сила
создает. Мы видим, что, исходя из
положение этой силы и ее направление относительно точки 𝑂, она будет стремиться
создать момент по часовой стрелке. По соглашению, моменты в этом
направление считаются отрицательными. Это означает, что ответ мы
получить для 𝑀 должно быть отрицательное значение. И это подтверждает наш выбор
чтобы силы в этом нисходящем направлении были отрицательными.
А теперь, рассмотрев
положительное и отрицательное направления для смещения, давайте сделаем то же самое для
наша сила. Наша сила, как мы видим,
направлены вниз. Мы могли бы дать этому отрицательный
значение, которое означало бы, что наша сила 𝐹 равна отрицательным 11 ньютонам. Другой способ думать об этом —
рассмотреть направление момента относительно точки 𝑂, что эта сила
создает. Мы видим, что, исходя из
положение этой силы и ее направление относительно точки 𝑂, она будет стремиться
создать момент по часовой стрелке. По соглашению, моменты в этом
направление считаются отрицательными. Это означает, что ответ мы
получить для 𝑀 должно быть отрицательное значение. И это подтверждает наш выбор
чтобы силы в этом нисходящем направлении были отрицательными.
Все это говорит о нашей силе 𝐹
минус 11 ньютонов, что означает, что момент, который он создает относительно точки 𝑂, равен
минус 2,695 ньютон-метра. Это момент того
сила о точке 𝑂.
Это момент того
сила о точке 𝑂.
Теперь давайте рассмотрим пример, где нам нужно объединить моменты, созданные несколькими силами.
𝐴𝐵 — стержень длиной 114 см и незначительный вес. Силы величины 83 ньютонов, 225 ньютонов, 163 ньютонов и 136 ньютонов действуют на стержень как показано на следующем рисунке. 𝐶 и 𝐷 — точки трисекция 𝐴𝐵, а точка 𝑂 является серединой стержня. Найдите алгебраическую сумму моменты этих сил относительно точки 𝑂.
Итак, глядя на нашу фигуру,
мы видим этот стержень 𝐴𝐵 с точкой 𝐴 на правом конце и 𝐵 на левом. Мы также видим эти четыре силы
действующих либо вертикально вверх, либо вертикально вниз на этот стержень, а также
так, точки трисекции стержня, 𝐷 и 𝐶 — это точки, которые
делим стержень на три равные части — и середина стержня указывает
𝑂.
Сосредоточимся на этом средней точки, мы хотим вычислить общий момент относительно точки 𝑂 из-за этих четырех сил. Когда мы начнем это делать, давайте вспомним тот факт, что длина нашего стержня, длина отрезка 𝐴𝐵, равна 114 сантиметров. И мы также скажем, что мы хотим вычислить момент относительно точки 𝑂. Мы назовем это 𝑀 sub 𝑂.
Теперь мы можем убрать наш
постановка задачи. И давайте вспомним тот факт, что
когда дело доходит до моментов силы, момент 𝑀, созданный некоторой силой вокруг
данная точка равна составляющей этой силы, перпендикулярной прямой
между точкой приложения силы и интересующей точкой, умноженной на расстояние
от этой интересующей точки до приложенной силы. Чтобы вычислить 𝑀 sub 𝑂 тогда,
чистый момент относительно точки 𝑂 из-за этих четырех сил, мы сложим вместе
момент, созданный каждым в отдельности, чтобы получить эту сумму.
И обратите внимание, что у нас есть знак условное обозначение моментов, создаваемых этими силами. Если сила стремится вызвать вращение против часовой стрелки вокруг точки 𝑂, то этот момент равен считается положительным. Так, например, рассмотрим сила, приложенная в точке 𝐴. Эта сила создаст момент 83 ньютона, умноженные на это расстояние 𝐴𝑂. И мы видим, потому что это будет стремится создать вращение против часовой стрелки вокруг точки 𝑂, это индивидуальное момент будет положительным.
Чтобы следить за моментами
созданные этими четырьмя силами, давайте решим для них по отдельности. Момент, созданный этим
сила — назовем ее 𝑀 sub 83 — равна силе в 83 ньютона, умноженной на
длина этого отрезка 𝐴𝑂. Нам говорят, что 𝑂
середина отрезка 𝐴𝐵, длина которого 114 сантиметров. 114 разделить на два равно 57, а
так что это 𝑀 83, момент из-за силы в 83 ньютона относительно точки 𝑂.
114 разделить на два равно 57, а
так что это 𝑀 83, момент из-за силы в 83 ньютона относительно точки 𝑂.
Далее рассмотрим 𝑀 225 момент из-за силы в 225 ньютонов. Это равно той силе умноженное на расстояние отрезка 𝐶𝑂. Если мы вспомним, что точка 𝐶 есть в одной из точек пересечения нашего отрезка 𝐴𝐵, то это указывает что это расстояние здесь равно 114 сантиметрам, деленным на три. Это 38 сантиметров. А если вычесть это расстояние от расстояния от точки 𝐴 до точки 𝑂, равное половине длины стержня, то находим, что отрезок 𝐶𝑂 равен половине длины стержня, 57 сантиметры минус 38 сантиметров. Это равно 19сантиметры.
Мы почти закончили с этим
момент. Но заметьте, что эта сила
225 ньютонов будут стремиться создать вращение по часовой стрелке вокруг точки 𝑂. Поэтому добавим минус
подпишусь на этот момент. Таким образом, хотя сила в 83 ньютона
создал положительный момент, сила в 225 ньютонов создает отрицательный момент о
пункт 𝑂.
Таким образом, хотя сила в 83 ньютона
создал положительный момент, сила в 225 ньютонов создает отрицательный момент о
пункт 𝑂.
Переходим к следующему отряду,
163 ньютона, эта сила создает момент, равный этой силе, умноженной на величину
длина отрезка 𝑂𝐷. И мы можем заметить, что длина
этого отрезка равна 𝐶𝑂. Это потому, что точка 𝐷, просто
как и точка 𝐶, является точкой трисекции отрезка 𝐴𝐵. Итак, отрезок 𝑂𝐷 равен 19.тоже сантиметры. И мы видим, что эта сила
имеет тенденцию создавать момент против часовой стрелки относительно точки 𝑂 и, следовательно,
положительный. И тогда, наконец, мы считаем
момент, создаваемый нашей силой в 136 ньютонов. Это равно 136 ньютонам.
умножить на длину нашего отрезка 𝑂𝐵. И это расстояние мы можем
напомним, равна длине 𝐴𝑂, 57 сантиметров. Наконец, мы рассматриваем то, что
направление вращения, которое эта сила будет создавать вокруг точки 𝑂. Мы видим, что его момент
вращаться по часовой стрелке и поэтому является отрицательным по нашему знаку
соглашение.
Наконец, мы рассматриваем то, что
направление вращения, которое эта сила будет создавать вокруг точки 𝑂. Мы видим, что его момент
вращаться по часовой стрелке и поэтому является отрицательным по нашему знаку
соглашение.
Хорошо, теперь, когда мы рассчитываем каждый момент отдельно, давайте объединим их, чтобы решить для сети момент о точке 𝑂. 𝑀 sub 𝑂 равно 𝑀 83 плюс 𝑀 225 плюс 𝑀 163 плюс 𝑀 136. А если умножить и то объединив все эти термины на нашем калькуляторе, мы получим отрицательный ответ 4199 ньютон сантиметров. Это кумулятивный или чистый момент вокруг точки 𝑂.
Давайте закончим, резюмируя
несколько ключевых моментов из этого урока. В этом видео мы увидели, что
момент силы характеризует стремление силы заставить тело вращаться вокруг
конкретная точка. Далее мы узнали, что если
линия действия силы проходит через точку, то сила не создает момента
об этом моменте. И, наконец, при рассмотрении случая
сила, которая создает момент относительно некоторой точки, мы сказали, что этот момент может быть
представлен заглавной 𝑀 и равен компоненту этой силы
перпендикулярно линии между местом приложения силы и точкой
проценты, умноженные на расстояние между этими двумя точками.
Далее мы узнали, что если
линия действия силы проходит через точку, то сила не создает момента
об этом моменте. И, наконец, при рассмотрении случая
сила, которая создает момент относительно некоторой точки, мы сказали, что этот момент может быть
представлен заглавной 𝑀 и равен компоненту этой силы
перпендикулярно линии между местом приложения силы и точкой
проценты, умноженные на расстояние между этими двумя точками.
Краткое введение в физику движения
Для тех из вас, кто прочитал слово «физика» и все же открыл этот блог, я аплодирую вам как профессионалам в области фитнеса, готовым бросить вызов широте своих знаний, чтобы узнать немного больше о как силы сопротивления влияют на выбор упражнений для ваших клиентов.
Не буду вам врать: физика никогда не была моей сильной стороной. Но я действительно хотел понять эту концепцию применительно к моей профессии и поделиться ею с другими, у которых тоже могут быть проблемы с пониманием этих концепций. Это означает, что я надеюсь объяснить актуальность моментных плеч так, как научился понимать это сам. Побудьте со мной здесь минутку, и перед вами может открыться совершенно новый аспект кинезиологии.
Это означает, что я надеюсь объяснить актуальность моментных плеч так, как научился понимать это сам. Побудьте со мной здесь минутку, и перед вами может открыться совершенно новый аспект кинезиологии.
Что такое рычаги момента?
Плечо момента определяет влияние силы на создание (или предотвращение) вращения объекта вокруг оси. 1
Это кратчайший перпендикуляр расстояние между линией приложенной силы (сопротивления) и осью (сустава), пытающегося сопротивляться этой силе. Эта сила представляется как невидимая линия, которую вы должны научиться визуализировать, уходящую в бесконечность, чтобы провести другую невидимую, но перпендикулярную линию — линию плеча момента.
Ниже приведены мои грубые наброски того, как концептуализировать моментные плечи сил сопротивления . Три рисунка изображают эксцентрическую фазу сгибания рук на бицепс.
Представьте, что «А» — это ось сустава (локоть), «В» — это линия силы сопротивления (это гантель над ней без руки), а «С» — это плечо момента. (C и B — концептуальные невидимые линии).
(C и B — концептуальные невидимые линии).
Хотя это не точно в масштабе, моментная рука короче, когда локоть почти полностью согнут (1-е фото) чем когда почти 90 градусов (2-е фото).
Вот что важно понять: Чем длиннее плечо момента, тем больше сила воздействует на сустав и, следовательно, тем больше должны работать мышцы, контролирующие этот сустав, чтобы сопротивляться (или двигаться) силе.
Это означает, что когда вес находится в вашей руке и ваш локоть почти полностью согнут, его намного легче «удерживать», чем когда ваш локоть находится под углом 90 градусов.
У нас уже есть общее представление об этой концепции в отношении рычагов, верно?
Если ваша рука — это рычаг, и вы хотите поднять вес перед собой с наибольшей легкостью и эффективностью, вы будете держать этот вес ближе к себе, т. е. используя короткий рычаг. Сгибание рук на бицепс или поднятие тяжестей с согнутым локтем удерживает вес ближе к телу, а рычаг коротким; следовательно, вы можете справиться с гораздо большим весом, чем, скажем, при попытке поднять дельтовидную мышцу на прямых руках, верно?
Да, увидимся получить это!
Теперь плечо момента сила сопротивления не совпадает с плечом момента мышечной силы . Как и следовало ожидать, мышечная сила (бицепс и др.) должна быть больше, чем сила сопротивления (гантель в руке), чтобы двигать рычаг (руку) вокруг оси (локоть).
Как и следовало ожидать, мышечная сила (бицепс и др.) должна быть больше, чем сила сопротивления (гантель в руке), чтобы двигать рычаг (руку) вокруг оси (локоть).
Посмотрите, где сухожилие бицепса прикрепляется к лучевой кости. В дюйме или двух от локтя, верно? Это довольно короткий момент руки от локтя до прикрепления сухожилия бицепса. Достаточно сказать, что более длинное плечо момента сила сопротивления требует более мощной мышечной силы (с более коротким плечом момента) для ее перемещения.
Почему инструкторам важно понимать Moment Arms?
2http://ffden-2.phys.uaf.eduЭта диаграмма моментных рук в приседаниях со спиной — простой и понятный способ понять, как работают моментные руки в контексте упражнения и как их «видение» может вам помочь запрограммировать соответствующие упражнения.
Пунктирная линия представляет силовую линию. Штанга на спине (в этом высоком положении штанги) давит прямо вниз под действием силы тяжести. В нижнем приседе для этого конкретного человека (учет длины туловища и длины конечностей может изменить эти линии для всех. Это отдельный разговор!), проводя линию от тазобедренного сустава прямо к этой силовой линии (знаете, перпендикулярно) дает вам моментную руку в зеленом .
В нижнем приседе для этого конкретного человека (учет длины туловища и длины конечностей может изменить эти линии для всех. Это отдельный разговор!), проводя линию от тазобедренного сустава прямо к этой силовой линии (знаете, перпендикулярно) дает вам моментную руку в зеленом .
Синий рычаг представляет собой расстояние от коленного сустава до линии силы. На этом изображении вы можете видеть, что плечо момента для бедра немного длиннее, чем для колена. Это означает, что бедра «работают больше», чем колени, при приседаниях с высоким перекладиной, верно?
Не обязательно! Правда, более длинное плечо момента означает, что вокруг этой оси необходимо приложить больше силы, чем, условно говоря, вокруг колена. Но что мы знаем о группах мышц вокруг этих суставов?
Теперь вы можете снять шапку физика и снова надеть кепку тренера: что сильнее? Разгибатели бедра или разгибатели колена?
Даже у тех, у кого чудовищно сильные квадрицепсы, ягодицы сравнительно на сильнее . Несмотря на то, что рука с моментом бедра длиннее, скорее всего, этот присед со штангой на спине задействует квадрицепсы и ягодичные мышцы.0093 довольно равно , учитывая разницу в мышечной силе двух групп.
Несмотря на то, что рука с моментом бедра длиннее, скорее всего, этот присед со штангой на спине задействует квадрицепсы и ягодичные мышцы.0093 довольно равно , учитывая разницу в мышечной силе двух групп.
Теперь давайте посмотрим на фронтальный присед. Вы не увидите много людей, делающих это в тренажерном зале (по крайней мере, по сравнению с приседаниями со спиной).
Может быть, это потому, что хват намного сложнее освоить. Или, может быть, это потому, что людям говорили, что они делают упор на квадрицепсы, а не на ягодицы, и они пришли, чтобы забить ягодицы! (Хотя, скорее всего, это недостаток подвижности верхней части тела!) Почему фронтальные приседания больше нагружают квадрицепсы, чем ягодицы?
Беглый взгляд на эту диаграмму проясняет ситуацию. Момент руки в колене равен и равен моменту бедра, требующего большей силы от коленного сустава (относительно говоря, поскольку нагрузка на ягодичные мышцы несколько меньше на , чем при приседе на спине, что создает на больше, чем на нагрузку на ягодицы). «более слабые» квадрицепсы), следовательно, заставляя квадрицепсы больше работать, чтобы разогнуть колено.
«более слабые» квадрицепсы), следовательно, заставляя квадрицепсы больше работать, чтобы разогнуть колено.
Как насчет низкий -приседания со штангой на спине? Это когда гриф тянется вниз над лопатками, а не опирается на верхние трапеции. Может показаться, что это не окажет огромного влияния на моментные руки и силы сопротивления по сравнению с положением с высоким перекладиной, но это действительно так! Опускание штанги вниз заставляет туловище больше наклоняться вперед, изменяя силу, воздействующую на бедра и колени, чтобы задействовать больше ягодичных мышц (и нижней части спины).
Могу сказать вам, что недавно я заменил приседания с низким грифом на приседания со штангой на груди, чтобы спасти нижнюю часть спины (с которой у меня патологические проблемы. назад, если у вас уже есть проблема, как у меня). Это очень помогло мне, так как моя спина меньше нагружена, мои квадрицепсы больше нагружены (им это было нужно!), и я могу сосредоточиться на более целенаправленных упражнениях для развития ягодичных мышц, которые не усугубляют мой поясничный отдел позвоночника.
Просто царапаем поверхность руки момента
Приседания — это движение, в котором руки момента легко визуализируются и понимаются. Так же как и сгибания рук на бицепс, разгибания ног и подъемы плеч. Но все может стать действительно сложным с такими движениями, как толчки бедрами, где необходимо разработать совершенно новое уравнение, потому что векторы силы находятся не там, где вы думаете.
Перекладина на бедре, например, это только одна сила. Так же как и пол и скамья, на которой лежит верхняя часть тела. Я еще не могу полностью осознать это, но если вам интересно, вот анализ Брета Контрераса на толчок бедра.
Применение того, что вы можете
Как я уже упоминал, переход от приседаний со штангой на спине к приседаниям со штангой на груди лично помог мне сохранить поясничный отдел позвоночника, в то же время нагружая квадрицепсы и удовлетворяя мое желание поднимать тяжелые предметы. Если у вас есть клиенты с противопоказаниями, понимание момента, когда руки и силы применяются во время определенных упражнений, может помочь вам переформулировать.

