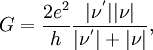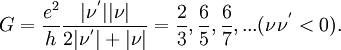ХОЛЛА ЭФФЕКТ — это… Что такое ХОЛЛА ЭФФЕКТ?
— возникновение в твёрдом проводнике с током плотностью j, помещённом в магн. поле Н, элек-трич. поля в направлении, перпендикулярном j и Н. Напряжённость электрич. поля (п о л я Х о л л а)
Здесь a — угол между векторами Н и j(a<180°). Если H | j, то поле Холла Е Н максимально: EH = RHj. Коэф. R, наз. п о с т о я н н о й Х о л л а (к о э ф. Х о л л а), является основной количеств. характеристикой X. э. Знак R положителен, если j, Н, ЕH образуют правовинтовую систему координат.
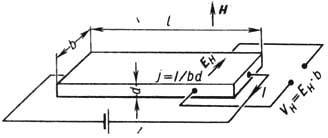
X. э. открыт Э. Г. Холлом (Е. Н. Hall) в 1879 в тонких пластинках Аu. Для наблюдения X. э. прямоуг. пластины из исследуемых веществ длиной
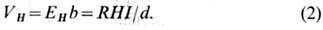
X. э. объясняется взаимодействием носителей заряда (электронов проводимости и дырок) с магн. полем. В магн. поле на электроны действует Лоренца сила F=e[Hu](u = =j/пе- ср. скорость направленного движения носителей в электрич. поле,

Знак R совпадает со знаком носителей заряда. Для металлов, у к-рых n~1022 см -3, R~10-3 см 3
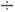 105 см 3/Кл.
105 см 3/Кл. Коэф. Холла может быть выражен через подвижность носителей зарядаm =u др/E (дрейфовая скорость носителей u др = -eEt/m, где т — эффективная масса,t — время между двумя последоват. соударениями с рассеивающими центрами) и уд. электропроводность s=j/E=enu др/E:
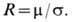
Сказанное справедливо для изотропных проводников, в частности для
В полупроводниках в электропроводимости участвуют одновременно электроны проводимости и дырки. При этом постоянная Холла выражается через парциальные проводимости электронов s э и дырок s д и их концентрации п э и n д. В случае слабых полей

Для сильных полей

При п э = п д для всех значений магнитного поля R == (1/ еn)(s э-s д)/(s э + s д), а знак R соответствует знаку осн. носителей.
Для металлов величина R зависит от зонной структуры, т. е. формы ферми-поверхности. Для замкнутых поверхностей Ферми и в сильных магн. полях постоянная Холла изотропна, а выражения для R совпадают с (3) и (4). Для открытых поверхностей Ферми
X. э.- один из наиболее эфф. методов изучения энерге-тич. спектра носителей заряда в металлах и полупроводниках. Зная R, можно определить знак носителей заряда и оценить их концентрацию, что позволяет сделать заключение о кол-ве примесей в полупроводниках. Линейная зависимость R от Н используется для измерения напряжённости магн. поля (см. Магнитометры), а также для усиления пост. токов, в аналоговых вычислит. машинах, в измерит. технике и др. (
При изучении X. э. в двумерном электронном газе кремниевого полевого транзистора, помещённого в квантующее магн. поле, К. фон Клитцинг (К. von Klitzing) в 1980 обнаружил, что холловское сопротивление (RH=VH/I), к-рое в условиях обычного X. э., как следует из ф-л (2) и (3), обратно пропорционально п, при изменении п то остаётся постоянным, то резко изменяется, переходя с одного уровня на другой. Вместо монотонного убывания в зависимости RH(n )наблюдались «ступеньки». При этом высота ступенек определяется такими фундам. константами, как постоянная Планка и заряд электрона, и не зависит от свойств вещества. Это явление получило назв.
При описании X. э. в магнетиках следует вместо поля Н рассматривать магн. индукцию В= Н+4p М, где М— намагниченность. Поле Холла в поликристаллич. ферромагнетиках может быть записано в виде
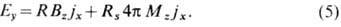
Здесь x, у, z — координатные оси. Первое слагаемое описывает нормальный X. э. Вклад в поле Холла, пропорциональный намагниченности
Аномальный X. э. обусловлен спин-орбитальным взаимодействием, к-рое пропорц. намагниченности и создаёт асимметрию рассеяния. носителей заряда, приводящую к холловскому «закручиванию» в отсутствие поля.
А. Б. Грановский.
Лит. см. при статьях Гальвано магнитные явления, Квантовый Холла эффект. Магнетизм.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
Необычный квантовый эффект Холла — это… Что такое Необычный квантовый эффект Холла?
Ква́нтовый эффе́кт Хо́лла в графене или необы́чный ква́нтовый эффе́кт Хо́лла — эффект квантования холловского сопротивления или проводимости двумерного электронного газа или двумерного дырочного газа в сильных магнитных полях в графене. Этот эффект был предсказан теоретически[1][2] и подтверждён экспериментально в 2005 году[3][4].
Уровни Ландау
| Графен | ||||||
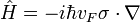 | ||||||
| Уравнение Дирака (графен) | ||||||
| Введение … Математическая формулировка …
| ||||||
Уровни Ландау в графене описываются уравнением Дирака для графена с учётом магнитного поля, которое можно записать в виде[5]
где использована калибровка Ландау для векторного потенциала 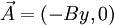 , двумерный градиент равен
, двумерный градиент равен 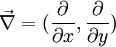 , а вектор
, а вектор 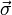 составлен из матриц Паули (σ1,σ2). В матричном виде уравнение запишется в виде
составлен из матриц Паули (σ1,σ2). В матричном виде уравнение запишется в виде
Здесь можно легко разделить переменные и в итоге прийти к спектру для релятивистских уровней Ландау
где 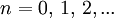 , «циклотронная частота» равна
, «циклотронная частота» равна 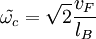 , магнитная длина
, магнитная длина 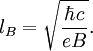
Квантовый эффект Холла
Впервые необычный (англ. unconventional) квантовый эффект Холла наблюдали в работах[3][4], где было показано, что носители в графене действительно обладают нулевой эффективной массой, поскольку положения плато на зависимости недиагональной компоненты тензора проводимости соответствовали полуцелым значениям холловской проводимости 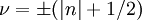 в единицах 4e2 / h (множитель 4 появляется из-за четырёхкратного вырождения энергии), то есть
в единицах 4e2 / h (множитель 4 появляется из-за четырёхкратного вырождения энергии), то есть
 .
.
Это квантование согласуется с теорией квантового эффекта Холла для дираковских безмассовых фермионов[1]. Сравнение целочисленного квантового эффекта Холла в обычной двумерной системе и графене смотрите на рисунке 1. Здесь показаны уширенные уровни Ландау для электронов (выделение красным цветом) и для дырок (синий цвет). Если уровень Ферми находится между уровнями Ландау, то на зависимости холловской проводимости σxy наблюдается ряд плато. Эта зависимость отличается от обычных двумерных систем (аналогом может служить двумерный электронный газ в кремнии, который является двухдолинным полупроводником в плоскостях эквивалентных {100}, то есть тоже обладает четырёхкратным вырождением уровней Ландау и холловские плато наблюдаются при ν = 4 | n | ).
Квантовый эффект Холла (КЭХ) может использоваться как эталон сопротивления, потому что численное значение наблюдаемого в графене плато равное h / 2e2 выполняется с хорошей точностью, хотя качество образцов уступает высокоподвижному ДЭГ в GaAs, и, соответственно, точности квантования. Преимущество КЭХ в графене в том, что он наблюдается при комнатной температуре[6] (в магнитных полях свыше 20 Т). Основное ограничение на наблюдение КЭХ при комнатной температуре накладывает не само размытие распределения Ферми-Дирака, а рассеяние носителей на примесях, что приводит к уширению уровней Ландау.
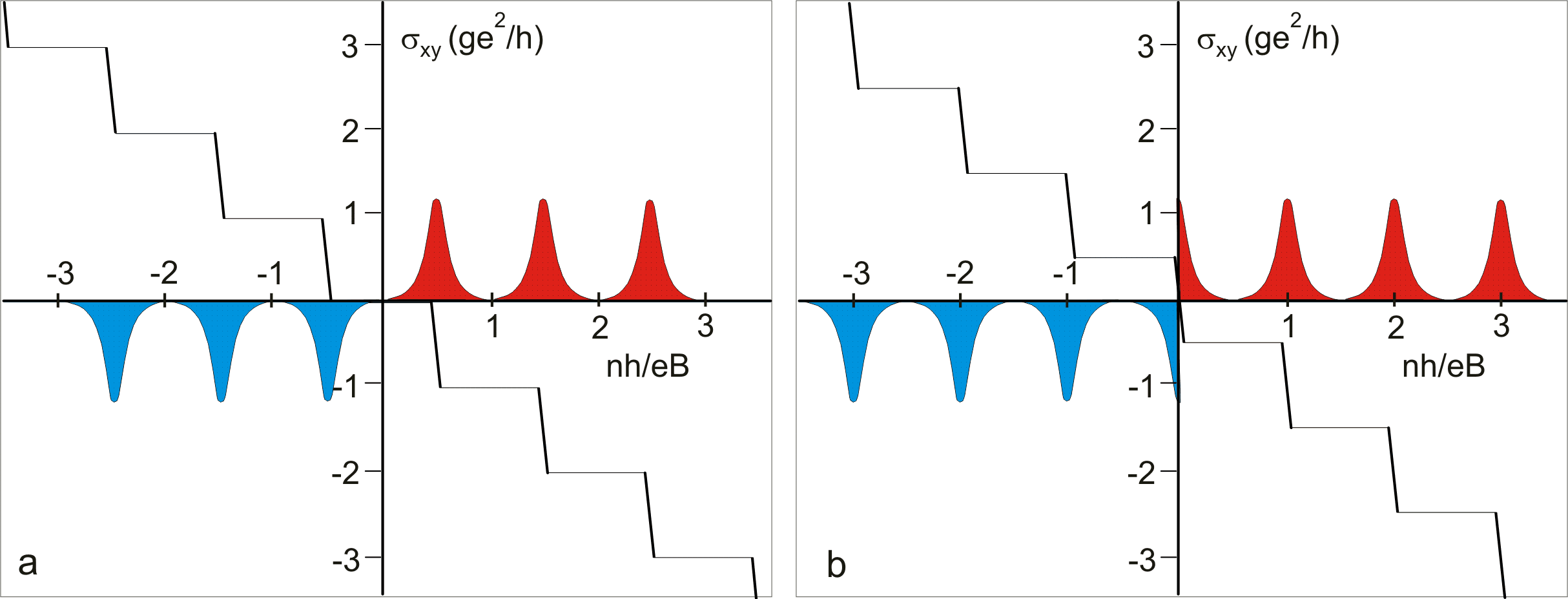
Рис. 1. a) Квантовый эффект Холла в обычной двумерной системе. b) Квантовый эффект Холла в графене. g = gsgv = 4 — вырождение спектра
p-n переход
Из-за отсутствия запрещённой зоны в графене в структурах с верхним затвором можно сформировать непрерывный p-n переход, когда напряжение на верхнем затворе позволяет инвертировать знак носителей, задаваемый обратным затвором в графене, где концентрация носителей никогда не обращается в ноль (кроме точки электронейтральности) и нет области лишённой носителей как в обычных p-n переходах. В таких структурах тоже можно наблюдать квантовый эффект Холла, но из-за неоднородности знака носителей значения холловских плато отличаются он приведённых выше. Для структуры с одним p-n переходом значения квантования холловской проводимости описываются формулой[7]
где ν и ν‘ — факторы заполнения в n- и p- области соответственно (p-область находится под верхним затвором), которые могут принимать значения 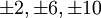 и т. д. Тогда плато в структурах с одним p-n переходом наблюдаются при значениях 1, 3/2, 3, 5/3 и т. д. Такие значения плато были наблюдены в эксперименте.[8]
и т. д. Тогда плато в структурах с одним p-n переходом наблюдаются при значениях 1, 3/2, 3, 5/3 и т. д. Такие значения плато были наблюдены в эксперименте.[8]
p-n-p переход
Для структуры с двумя p-n переходами[9] соответствующие значения холловской проводимости равны
Расщепление основного уровня Ландау
В работе[10] наблюдается спиновое расщепление релятивистских уровней Ландау и снятие четырёхкратного вырождения для наинизшего уровня Ландау вблизи точки электронейтральности. Для объяснения этого эффекта предложено несколько теорий[11].
См. также
Ссылки
- ↑ 1 2 Gusynin V. P. et al. «Unconventional Integer Quantum Hall Effect in Graphene» Phys. Rev. Lett. 95, 146801 (2005) DOI:10.1103/PhysRevLett.95.146801
- ↑ Peres N. M. R., et. al. Electronic properties of disordered two-dimensional carbon Phys. Rev. B 73, 125411 (2006) DOI:10.1103/PhysRevB.73.125411
- ↑ 1 2 Novoselov K. S. et al. «Two-dimensional gas of massless Dirac fermions in graphene», Nature 438, 197 (2005) DOI:10.1038/nature04233
- ↑ 1 2 Zhang Y.et. al. «Experimental observation of the quantum Hall effect and Berry’s phase in graphene» Nature 438, 201 (2005) DOI:10.1038/nature04235
- ↑ Peres N. M. R. et. al. „Algebraic solution of a graphene layer in transverse electric and perpendicular magnetic fields“J. Phys.: Condens. Matter 19, 406231 (2007) DOI:10.1088/0953-8984/19/40/406231
- ↑ Novoselov K. S. et. al. Room-Temperature Quantum Hall Effect in Graphene Science 315, 1379 (2007) DOI:10.1126/science.1137201
- ↑ Abanin D. A., Levitov L. S. Quantized Transport in Graphene p-n Junctions in a Magnetic Field Science 3, 641 (2007) DOI:10.1126/science.1144672
- ↑ Williams J. R. et. al. Quantum Hall Effect in a Gate-Controlled p-n Junction of Graphene Science 317, 638 (2007) DOI:10.1126/science.1144657
- ↑ Özyilmaz B. et. al. Electronic Transport and Quantum Hall Effect in Bipolar Graphene p-n-p Junctions Phys. Rev. Lett. 99, 166804 (2007) DOI:10.1103/PhysRevLett.99.166804
- ↑ Zhang Y., et al., «Landau-Level Splitting in Graphene in High Magnetic Fields» Phys. Rev. Lett. 96, 136806 (2006) DOI:10.1103/PhysRevLett.96.136806
- ↑ Fuchs J. et al. Spontaneous Parity Breaking of Graphene in the Quantum Hall Regime Phys. Rev. Lett. 98, 016803 (2007) DOI:10.1103/PhysRevLett.98.016803; Nomura K. et al., Quantum Hall Ferromagnetism in Graphene Phys. Rev. Lett. 96, 256602 (2006) DOI:10.1103/PhysRevLett.96.256602; Abanin D. A. et al., Spin-Filtered Edge States and Quantum Hall Effect in Graphene Phys. Rev. Lett. 96, 176803 (2006) DOI:10.1103/PhysRevLett.96.176803; Fertig H. A. et al., Luttinger Liquid at the Edge of Undoped Graphene in a Strong Magnetic Field Phys. Rev. Lett. 97, 116805 (2006) DOI:10.1103/PhysRevLett.97.116805; Goerbig M. O. et al., Electron interactions in graphene in a strong magnetic field Phys. Rev. B 74, 161407 (2006) DOI:10.1103/PhysRevB.74.161407; Alicea J. et al., Graphene integer quantum Hall effect in the ferromagnetic and paramagnetic regimes Phys. Rev. B 74, 075422 (2006) DOI:10.1103/PhysRevB.74.075422; Gusynin V. P. et al., Excitonic gap, phase transition, and quantum Hall effect in graphene Phys. Rev. B 74, 195429 (2006) DOI:10.1103/PhysRevB.74.195429
Wikimedia Foundation. 2010.
эффект Холла — Hall effect
Эффект Холла является производством из напряжения разницы ( напряжения Холла ) поперек электрического проводника , поперечный к электрическому току в проводнике и на приложенном магнитное поле перпендикулярно к току. Он был открыт Эдвин Холл в 1879. Для ясности, первоначальный эффект иногда называют обычный эффект Холла , чтобы отличить его от других «Холла эффектов» , которые имеют различные физические механизмы.
Коэффициент Холла определяется как отношение индуцированного электрического поля к произведению плотности тока и приложенного магнитного поля. Это является характеристикой материала , из которого изготовлен проводник, поскольку его величина зависит от типа, количества и свойств носителей заряда , которые составляют ток.
открытие
Эффект Холла был обнаружен в 1879 году Эдвин Холл , когда он работал над докторской степени в Университете Джона Хопкинса в Балтиморе , штат Мэриленд . Восемнадцать лет до того , как электрон был обнаружен, его измерение крошечного эффекта , производимым в аппарате он использовал было экспериментальный тур де силой , опубликованная под названием «О новом действии Магнита электрического тока».
теория
Эффект Холла в связи с характером тока в проводнике. Ток состоит из движения многих малых носителей заряда , как правило , электроны , дырки , ионы (см электромиграции ) или все три. Когда магнитное поле присутствует, эти заряды действует сила, называемая сила Лоренца . Когда такое магнитное поле отсутствует, заряды следуют приблизительно прямыми, «прямой видимости» пути между столкновениями с примесями, фононами и т.д. Однако, когда магнитное поле с перпендикулярной компонентой применяется, их пути между столкновениями изогнуты, таким образом , движущиеся заряды накапливаются на одной стороне материала. Это оставляет равные и противоположные заряды подвергаются на другой стороне, где есть дефицит мобильных платежей. Результатом является асимметричное распределение плотности заряда через элемент Холла, возникающий из силы, которая перпендикулярна как «прямой видимости» пути и приложенного магнитного поля. Разделение заряда создает электрическое поле , которое выступает против миграции дальнейшего заряда, поэтому устойчивый электрический потенциал устанавливается до тех пор , пока заряд течет.
В классических электромагнетизм электроны движутся в направлении, противоположном направлению тока I (по соглашению «текущий» описывает теоретическую «дыра поток»). В некоторых полупроводниках появляется «дыра» на самом деле течет , так как направление напряжения противоположно ниже вывод.

Настройка измерения эффекта Холла для электронов. Первоначально электроны следуют изогнутой стрелке, из — за магнитную силу. На некотором расстоянии от текущих контактов для введения, электроны накапливаются на левой стороне и истощать с правой стороны, который создает электрическое поле £ , у в направлении назначенного V H . V Н является отрицательным для некоторых полупроводников , где «дыра» появляется течь. В стационарном состоянии, £ , у будет достаточно сильным , чтобы точно компенсируют магнитную силу, таким образом , электроны следуют за прямой стрелкой (пунктирную).
Анимация показывает упрощенный принципДля простого металла , где есть только один тип носителей заряда (электроны), зал напряжение V Н может быть получен с помощью силы Лоренца и видеть , что в стационарном состоянии, заряды не двигаются в у оси х направление. Таким образом, магнитная сила на каждый электрона в у -Axis направления будет отменена с помощью у оси х электрической силы из — за накопление зарядов. V х член представляет собой скорость дрейфа тока , который предполагается в этой точке , чтобы быть отверстия по конвенции. V х В г слагаемое отрицательно в у -Axis направления по правилу правой руки.
- Fзнак равноQ(Е+v×В){\ Displaystyle \ mathbf {F} = {д \ Bigl (} \ mathbf {Е} + \ mathbf {v} \ раз \ mathbf {B}, {\ Bigl)}}
В стационарном состоянии, F = 0 , так что 0 = Е у — V х B г , где Е у назначается в направлении у оси х, (а не с помощью стрелок индуцированного электрического поля £ , у , как в изображении (указывая на — у направлении), который говорит вам , где поле , вызванное электронами указывает).
В проводах, электроны вместо отверстий текут, так что V х → — V х и д → — кв . Кроме того, Е у = — V Н / ш . Подставив эти изменения дает
- ВЧАСзнак равноvИксВZвес{\ Displaystyle V _ {\ mathrm {H}} = V_ {х} B_ {г} ш}
Обычный ток «дыра» находится в отрицательном направлении электронного тока , а отрицательный электрического заряд , который дает мне х = NTW (- v х ) (- е ) , где п есть плотность носителей заряда , TW представляет собой поперечное сечение площадь, и — е есть заряд каждого электрона. Решение для и затыкать в вышеперечисленного дает напряжение Холла: вес{\ Displaystyle ш}
- ВЧАСзнак равнояИксВZNTе{\ Displaystyle V _ {\ mathrm {H}} = {\ гидроразрыва {I_ {х} B_ {г}} {NTE}}}
Если заряд накопление были положительными (как представляется , в некоторых полупроводниках), то V H , заданный в изображении было бы отрицательными (положительный заряд был бы построен на левой стороне).
Коэффициент Холла определяется как
- рЧАСзнак равноЕYJИксВZ{\ Displaystyle R _ {\ mathrm {H}} = {\ гидроразрыва {Е- {у}} {J_ {х} B_ {г}}}}
где J представляет собой плотность тока электронов — носителей, а Е у является индуцированным электрическим полем. В системе единиц СИ, это становится
- рЧАСзнак равноЕYJИксВзнак равноВЧАСTяВзнак равно-1Nе,{\ Displaystyle R _ {\ mathrm {H}} = {\ гидроразрыва {Е- {у}} {J_ {х} В}} = {\ гидроразрыва {V _ {\ mathrm {H}} T} {IB}} = — {\ гидроразрыва {1} {пе}}.}
(Единицы R H , как правило , выражается в м 3 / С, или Ом · см / G , или другие варианты.) В результате, эффект Холла очень полезен в качестве средства для измерения либо плотность носителей или магнитного поля ,
Одна очень важная особенность эффекта Холла является то , что он различает положительных зарядов , движущихся в одном направлении и отрицательных зарядов , движущихся в противоположном. Эффект Холла предложил первое реальное доказательство того, что электрические токи в металлах осуществляется путем перемещения электронов, а не протонами. Эффект Холла также показал , что в некоторых веществах (особенно полупроводники р-типа ), более уместно думать о текущихах , как положительные « дырок » двигающихся , а не отрицательные электронов. Обычным источником путаницы с эффектом Холла , что дырки , движущиеся влево действительно электроны , двигаясь вправо, так что один ожидает тот же знак коэффициента Холла для электронов и дырок. Эта путаница, однако, может быть решена только современной квантово — механической теории переноса в твердых телах.
Образец Неоднородность может привести к паразитному знаку эффекта Холла, даже в идеальных ван — дер — Пау конфигурации электродов. Например, положительный эффект Холла наблюдался в полупроводниках , очевидно , п-типа. Другой источник артефакта, в однородных материалах, происходит тогда , когда соотношение сторон образца не достаточно долго: полное напряжение Холла только развивается далеко от текущих контактов для введения, так как при контактах поперечного напряжение закорочено к нулю.
Эффект Холла в полупроводниках
Когда токопроводящая полупроводниковый хранится в магнитном поле, носители заряда из опыта полупроводниковой силы в направлении , перпендикулярном как магнитного поля и тока. В равновесии напряжение появляется на полупроводниковых краях.
Простая формула для коэффициента Холла приведенного выше, как правило , хорошее объяснение , когда проводимость доминирует один носитель заряда . Однако в полупроводниках теория является более сложной, потому что в этих материалах проводимость может включать значительные, одновременно вклады от обоего электронов и дырок , которые могут присутствовать в различных концентрациях и имеют различные подвижности . Для умеренных магнитных полей коэффициент Холла
- рЧАСзнак равнопμчас2-Nμе2е(пμчас+Nμе)2{\ Displaystyle R _ {\ mathrm {H}} = {\ гидроразрыва {р \ му _ {\ mathrm {H}} ^ {2} -п \ мю _ {\ mathrm {е}} ^ {2}} {е \ влево (р \ му _ {\ mathrm {H}} + п \ му _ {\ mathrm {е}} \ справа) ^ {2}}}}
или, что эквивалентно
- рЧАСзнак равно(п-Nб2)е(п+Nб)2{\ Displaystyle R _ {\ mathrm {H}} = {\ гидроразрыва {\ влево (п-пь ^ {2} \ справа)} {е \ слева (р + пь \ справа) ^ {2}}}}
с
- бзнак равноμеμчас{\ Displaystyle Ь = {\ гидроразрыва {\ му _ {\ mathrm {е}}} {\ му _ {\ mathrm {H}}}}},
Здесь п концентрация электронов, р концентрация дырок, μ е подвижность электронов, М Н подвижности дырок и по электронной элементарному заряду.
Для больших прикладных областей проще выражение, аналогичное тому, что для типа одной несущих держит.
Отношения с звездообразования
Хотя хорошо известно, что магнитные поля играют важную роль в формировании звезд, модель исследования показывает, что диффузия Холла критически влияет на динамику гравитационного коллапса, который образует протозвезду.
Квантовый эффект Холла
Для двумерной электронной системы , которая может быть получена в МОП — транзистора , в присутствии большого магнитного поля прочности и низкой температуры , можно наблюдать квантовый эффект Холла, в котором зал проводимости σ претерпевает квантового эффекта Холла переходов взять на себя квантованное ценности.
Спин эффект Холла
Спиновый эффект Холла состоит в спиновой аккумуляции на боковых границах образца токопроводящего. Нет магнитное поле не требуется. Это было предсказано М. И. Дьяконов и В. И. Перель в 1971 и экспериментально наблюдали более чем через 30 лет, как в полупроводниках и в металлах, при криогенных, а также при комнатной температуре.
Квантовый эффект Холла спина
Для теллурида ртути два мерных квантовых ямах с сильной спин-орбитальной связи, в нулевом магнитном поле, при низкой температуре, в последнее время наблюдается квантовый спиновый эффект Холла.
Аномальный эффект Холла
В ферромагнитных материалах (и парамагнитных материалах в магнитном поле ), удельное сопротивление Холла включает в себя дополнительный вклад, известный как аномальный эффект Холла (или АЭЙ ), который непосредственно зависит от намагниченности материала, и часто намного больше чем обычный эффект Холла. (Обратите внимание , что этот эффект не за счет вклада намагниченности к общему магнитному полю ). Например, в никеле, коэффициент аномальной Холла примерно в 100 раз больше , чем обычный коэффициент Холла вблизи температуры Кюри, но два аналогично при очень низких температурах. Хотя хорошо узнаваемое явление, там до сих пор спорят о его происхождении в различных материалах. Аномальный эффект Холла может быть либо внешним (расстройства , связанные с ) эффектом , обусловленный спином -зависимого рассеяния из носителей заряда , или внутренного эффекта , который можно описать в терминах фазового Berry эффекта в импульсном пространстве кристалла ( к -пространству ).
Эффект Холла в ионизированных газах
Эффект Холла в ионизованного газа ( плазмы ) существенно отличается от эффекта Холла в твердых телах (где параметр Холла всегда много меньше единицы). В плазме, параметр Холла может принимать любое значение. Параметр Холла, β , в плазме представляет собой отношение между электронной гирочастотой , Омами е и частотой столкновений частиц электрона-тяжелым, v , :
- βзнак равноΩеνзнак равноеВмеν{\ Displaystyle \ бета = {\ гидроразрыва {\ Omega _ {\ mathrm {е}}} {\ Nu}} = {\ гидроразрыва {еВ} {т _ {\ mathrm {е}} \ Nu}}}
где
Значение параметра Холла возрастает с увеличением напряженности магнитного поля.
Физически, траектории электронов изогнуты в силу Лоренца . Тем не менее, когда параметр Холла низок, их движение между двумя столкновениями с тяжелыми частицами ( нейтральными или ионными ) близко к линейному. Но если параметр Холла высок, электронные движения сильно изогнуты. Плотность тока вектор, J , больше не коллинеарны с электрическим полем вектора, Е . Эти два вектора J и Е делают угол Холла , & thetas , который также дает параметр Холла:
- βзнак равнозагар(θ),{\ Displaystyle \ бета = \ тангенс (\ тета).}
Приложения
Датчики Холла часто используются в качестве магнитометров , то есть для измерения магнитных полей, или осмотреть материалы (например, трубы или трубопроводы) с использованием принципов магнитного потока утечки .
Эффект Холл устройства производят очень низкий уровень сигнала и , следовательно , требуют усиления. Хотя они подходят для лабораторных приборов, то вакуумные трубчатые усилители доступны в первой половине 20 — го века были слишком дорогими, энергоемкими и ненадежны для ежедневного применения. Только с развитием низкой стоимости интегральной схемы , что датчик эффекта Холла стал пригоден для массового применения. Многие устройства в настоящее время продаются как датчики эффекта Холла на самом деле содержат как датчик , как описано выше , плюс высокий коэффициент усиления интегральной схемы усилителя (IC) в одном пакете. Последние достижения дополнительно добавляют в один пакет в аналого-цифровой преобразователь и I²C (протокол связи Inter-интегральная схема) IC для прямого подключения к микроконтроллеру порта ввода / вывода «с.
Преимущества по сравнению с другими методами
эффекта Холла устройства (при надлежащем упаковывают) имеют иммунитет к пыли, грязи, грязи и воды. Эти характеристики делают эффект Холл устройство лучше для зондирования позиции по сравнению с альтернативными способами, такими как оптическое и электромеханическим зондирование.
 Эффект Холла Датчик тока с внутренним усилителем интегральной схемы. 8 мм отверстие. Нулевой ток выходного напряжения на полпути между напряжением питания, которые поддерживают вольтый дифференциал от 4 до 8. Ненулевое отклик тока пропорционально напряжению, подаваемая и линейно до 60 ампер для этого конкретного устройства (25 A).
Эффект Холла Датчик тока с внутренним усилителем интегральной схемы. 8 мм отверстие. Нулевой ток выходного напряжения на полпути между напряжением питания, которые поддерживают вольтый дифференциал от 4 до 8. Ненулевое отклик тока пропорционально напряжению, подаваемая и линейно до 60 ампер для этого конкретного устройства (25 A).Когда электроны текут через проводник, магнитное поле создается. Таким образом, можно создать бесконтактную датчик тока. Устройство имеет три терминала. Напряжение датчика подается через два терминала , а третий обеспечивает напряжение , пропорциональное току, воспринимаемого. Это имеет несколько преимуществ; никакого дополнительное сопротивление (а шунт , необходимое для наиболее распространенного текущего метода зондирования) не должно быть вставлено в первичном контуре. Кроме того , настоящее напряжение на линии , чтобы быть воспринято не передается к датчику, что повышает безопасность измерительного оборудования.
Недостатки по сравнению с другими методами
Магнитный поток из окружающей среды (например, другие проводов) может уменьшить или усилить поле зонд Холла намеревается обнаружить, что делает результаты неточными. Кроме того , как напряжение Холла часто от порядка милливольт, выходной сигнал от этого типа датчика не может быть использован для непосредственного управления исполнительных механизмов , но вместо этого должен быть усилен с помощью транзистора основанной цепи.
Способы измерения механических позиций в рамках электромагнитной системы, такие как бесщеточный двигатель постоянного тока, включают в себя (1) эффекте Холла, (2) оптический датчик положения (например, абсолютные и инкрементные датчики ) и (3) наведенное напряжение, перемещая количество из металла сердечника вставлена в трансформатор. Когда зал сравнивается с фоточувствительных методами, это труднее получить абсолютную позицию Hall. Обнаружение Холла также чувствительно к паразитным магнитным полей.
Современные приложения
Датчики на эффект Холла легко доступны из целого ряда различных производителей, и могут быть использованы в различных датчиках , такие как вращающиеся датчики скорости (колеса велосипеда шестеренных зубы, автомобильные спидометры, электронные системы зажигания), жидкие датчики потока , датчики тока и давление датчики . Общие приложения часто встречаются там , где требуется надежное и бесконтактный переключатель или потенциометр. К ним относятся: электрическое страйкбола оружие, триггерами электропневматических пейнтбольных ружей , картинг-управления скоростью, смартфоны, и некоторые системы глобального позиционирования.
Ферритовый тороидальный эффект Холла преобразователя тока
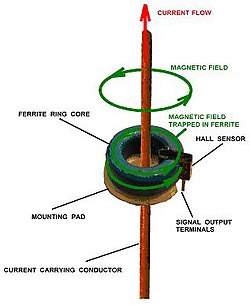 Схема эффекта Холла преобразователя тока встроен в ферритовом кольце.
Схема эффекта Холла преобразователя тока встроен в ферритовом кольце.Датчики Холла могут обнаружить паразитных магнитных полей легко, что на Земле в том числе, поэтому они хорошо работают как электронные компасы: но это также означает , что такие паразитные поля могут препятствовать точные измерения малых магнитных полей. Для того, чтобы решить эту проблему, датчики Холла часто интегрируется с магнитным экранированием некоторого вида. Например, датчик Холла встроен в ферритовом кольце (как показано) может уменьшить обнаружение полей рассеяния на коэффициент 100 или лучше (как внешние магнитные поля компенсируют через кольцо, не давая остаточного магнитного потока ). Эта конфигурация также обеспечивает улучшение отношения сигнала к шуму и дрейфу эффектов более чем в 20 раз , что голое устройство Холла.
Спектр данного датчика проходного может быть продлен вверх и вниз с помощью соответствующей разводки. Чтобы расширить диапазон на более низкие тока, несколько витков с током провода могут быть сделаны через отверстие, каждый поворот добавление к выходному сигналу датчика те же величины; когда датчик установлен на печатную плату, витки могут быть выполнены с помощью скоб на плате. Чтобы расширить диапазон на более высокие токи, может быть использован ток делителя. Делитель делит ток через два провода различной ширины и более тонкую проволоку, неся меньшей долей общего тока, проходит через датчик.
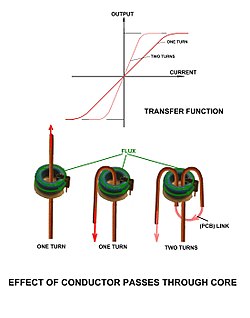 Множественный «получается» и соответствующая передаточная функция.
Множественный «получается» и соответствующая передаточная функция.Разрезное кольцо зажимного на датчике
Изменение на датчике кольца использует разделенное датчик , который зажат на линию позволяя устройству для использования во временном испытательном оборудовании. При использовании в стационарной установке, сплит датчик позволяет электрический ток , чтобы быть испытан без демонтажа существующей схемы.
Аналоговое умножение
Выход пропорционален как приложенного магнитного поля и приложенного напряжения датчика. Если магнитное поле прикладывается с помощью соленоида, то выходной сигнал датчика пропорционален произведению тока через соленоид и напряжение датчика. Поскольку большинство приложений , требующих вычисления теперь выполняются с помощью небольших цифровых вычислительных машин , остальные полезные приложения в мощности зондирования, который сочетает в себе ток зондирования с определения напряжения в одном устройстве эффекта Холла.
измерение мощности
Путем измерени ток, подаваемый на нагрузку и с помощью приложенного напряжения устройства в качестве датчика напряжения можно определить мощность, рассеиваемую устройством.
Положение и движение зондирования
Эффект Холла устройства , используемые в чувствительных движения и предельных выключателей движения может обеспечивать повышенную надежность в экстремальных условиях. Поскольку нет никаких движущихся частей , участвующих в датчике или магнита, типичная продолжительность жизни улучшается по сравнению с традиционными электромеханическими переключателями. Кроме того, датчик и магнит могут быть инкапсулированы в соответствующем защитном материале. Это приложение используется в бесщеточных двигателей постоянного тока .
Датчики на эффекте Холла, прикрепленных к механическим датчиков, которые имеют намагниченные иглы индикатора, может перевести физическое положение или ориентацию механического индикатора иглы в электрический сигнал, который может быть использован с помощью электронных индикаторов, управления или устройств связи.
Автомобильные зажигания и впрыск топлива
Обычно используется в дистрибьюторах для опережения зажигания (и в некоторых типах кривошипа и положение распределительного вала для датчиков времени впрыска импульсов, зондирования скорости и т.д.) датчик эффекта Холла используется в качестве прямой замены механических выключателей , используемых точки в более ранних автомобильных применениях. Его использование в качестве устройства опережения зажигания в различных типах дистрибьютора заключается в следующем. Стационарный постоянный магнит и полупроводниковый чип эффекта Холла установлены рядом друг с другом , разделенным воздушным зазором, образуя датчик с эффектом Холла. Металлический ротор , состоящий из окон и вкладок установлен на вал и расположен таким образом , что при вращении вала, окно и вкладки проходят через воздушный зазор между постоянным магнитом и чипом полупроводника Холла. Это эффективно защищает и выставляет чип Холла в поле постоянного магнита в соответствующем ли вкладка или окно проходит через датчик Холла. Для целей опережения зажигания, металлический ротор будет иметь ряд одинаковых по размеру вкладок и окон , соответствующих количеству цилиндров двигателя. Это производит равномерный выход прямоугольных импульсов , так как включение / выключение (экранирование и воздействие) время равно. Этот сигнал используется компьютером двигателя или ECU для контроля угла опережения зажигания. Многие автомобильные датчики на эффекте Холла имеют встроенный внутренний транзистор NPN с открытым коллектором и заземлены эмиттер, а это означает , что вместо того , напряжение производится на выходном проводе сигнала датчика Холла, транзистор включен обеспечивая замыкание на землю через сигнал выходной провод.
Чувствительный вращения колеса
Зондирования вращения колеса особенно полезно в антиблокировочной тормозной системе . Принципы таких систем были расширены и уточнены предложить более противоскольжение функции, теперь обеспечивая расширенные транспортное средство обработки усовершенствований.
Электрическое управление двигателем
Некоторые типы бесщеточных электродвигателей постоянного тока используются датчики Холла для определения положения ротора и подачи этой информации в контроллер двигателя. Это позволяет более точно контролировать двигатель.
Промышленное применение
Приложения для зондирования эффекта Холла также расширены до промышленного применения, которые в настоящее время используют эффект Холл джойстики для управления гидравлических клапанов, заменяя традиционные механические рычаги с бесконтактным зондированием. Такие приложения включают в себя карьерные самосвалы, экскаваторы — погрузчики, краны, экскаваторы, ножничные подъемники и т.д.
Космический аппарат двигательная
Эффекте Холла подруливающее (HET) представляет собой устройство , относительно низкой мощности , который используется для приведения в движение какой — то космический корабль , после того, как он попадает в орбиту или дальше в космос. В HET, атомы являются ионизируются и ускоряются электрическим полем . Радиальное магнитное поле устанавливается магнитами на подруливающем устройстве используются для улавливания электронов , которые затем вращаются и создают электрическое поле вследствие эффекта Холла. Большой потенциал устанавливаются между концом двигателя малой тяги , где подают нейтральный пропеллент, и ту частью , где производятся электроны; так, электроны попадают в ловушку в магнитном поле не может упасть до нижнего потенциала. Таким образом , они очень энергичны, что означает , что они могут ионизировать нейтральные атомы. Нейтральный газ — вытеснитель закачивает в камеру и ионизируется захваченными электронами. Положительные ионы и электроны затем выбрасываются из двигателя малой тяги в качестве квазинейтральной плазмы , создавая тягу.
Эффект Корбина
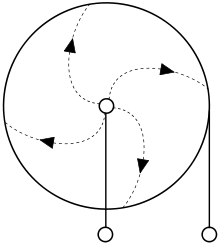
Корбино эффект представляет собой явление , с участием эффекта Холла, но в форме диска образец металла используют вместо прямоугольной. Из — за его форму диска Корбина позволяет наблюдать эффект Холл на основе магнитосопротивления без напряжения ассоциированного Холла.
Радиальный ток через круглый диск, подвергается воздействию магнитного поля, перпендикулярной к плоскости диска, производит «круговой» ток через диск.
Отсутствие свободных поперечных границ делает интерпретацию эффекта Корбина проща, чем эффект Холла.
Смотрите также
Рекомендации
источники
- Введение в физике плазмы и УТС, том 1, физике плазмы, второе издание, 1984, Фрэнсис Ф. Чена
дальнейшее чтение
внешняя ссылка
- Патенты
- Патент США 1778796 , PH Craig, система и устройство , использующее эффект Холла
- В патенте США 3596114 , JT Maupin, Е.А. Vorthmann, эффект Холла бесконтактный переключатель с prebiased триггера Шмитта
- генеральный
1 Эффект Холла и его применение в технике и в современных научных исследованиях
Постоянный
ток / пропускался через пластинку М
изготовленную из золота, и измерялась
разность потенциалов 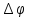 между
противолежащими точками А и С наверхней
и нижней гранях. Эти точки лежат в одном
и том же поперечном сечении проводника
М. Поэтому, как и следовало ожидать,
оказалось, что
между
противолежащими точками А и С наверхней
и нижней гранях. Эти точки лежат в одном
и том же поперечном сечении проводника
М. Поэтому, как и следовало ожидать,
оказалось, что ф
= 0. Когда пластина с гоком была помещена
в однородное магнитное поле,
перпендикулярное ее боковым граням,
то потенциалы точек А и С стали различными.
Это явление получило название явления
Холла. Было установлено, что разность
потенциалов
ф
= 0. Когда пластина с гоком была помещена
в однородное магнитное поле,
перпендикулярное ее боковым граням,
то потенциалы точек А и С стали различными.
Это явление получило название явления
Холла. Было установлено, что разность
потенциалов ф
между точками А и С пропорциональна
силе токаI,
индукции магнитного поля В и обратно
пропорциональна ширине Ь пластинки,
т. е.
ф
между точками А и С пропорциональна
силе токаI,
индукции магнитного поля В и обратно
пропорциональна ширине Ь пластинки,
т. е. 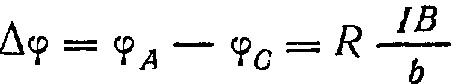
 Эффект
Холла, в некоторых случаях, позволяет
определить тип носителей заряда
(электронный или дырочный) в металле
или полупроводнике, что делает его
достаточно хорошим методом исследования
свойств полупроводников.На основе
эффекта Холла работают датчики Холла:
приборы, измеряющие напряжённость
магнитного поля. Датчики Холла получили
очень большое распространение в
бесколлекторных, или вентильных,
электродвигателях (сервомоторах).
Датчики закрепляются непосредственно
на статоре двигателя и выступают в роли
ДПР (датчика положения ротора). ДПР
реализует обратную связь по положению
ротора, выполняет ту же функцию, что и
коллектор в коллекторном ДПТ.Также на
основе эффекта Холла работают некоторые
виды ионных реактивных двигателей.
Эффект
Холла, в некоторых случаях, позволяет
определить тип носителей заряда
(электронный или дырочный) в металле
или полупроводнике, что делает его
достаточно хорошим методом исследования
свойств полупроводников.На основе
эффекта Холла работают датчики Холла:
приборы, измеряющие напряжённость
магнитного поля. Датчики Холла получили
очень большое распространение в
бесколлекторных, или вентильных,
электродвигателях (сервомоторах).
Датчики закрепляются непосредственно
на статоре двигателя и выступают в роли
ДПР (датчика положения ротора). ДПР
реализует обратную связь по положению
ротора, выполняет ту же функцию, что и
коллектор в коллекторном ДПТ.Также на
основе эффекта Холла работают некоторые
виды ионных реактивных двигателей.
2 Уравнения максвелла
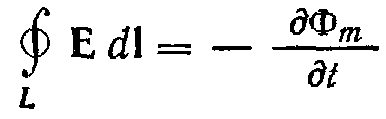 Тем
самым было выяснено, что переменное
магнитное поле создает в проводящем
замкнутом контуре вихревое электрическое
поле. Максвелл предложил считать, что
соотношение справедливо не толь-ко для
проводящего, но и для любого замкнутого
контура, мыеленно выбранного в переменном
магнитном поле. Иными словами, он
предположил, что переменное магнитное
поле создает в любой точке пространства
вихревое электрическое поле независимо
от того, находится в этой точке проводник
или нет. Обобщенное таким образом
равенство называется первым уравнением
Максвелла в интегральной форме:
циркуляция вектора напряженности
электрического поля по про- извольному
замкнутому контуру L равна взятой в
обратным знаком скорости изменения
магнитного потока сквозь поверхность,
натянутую на контур.
Тем
самым было выяснено, что переменное
магнитное поле создает в проводящем
замкнутом контуре вихревое электрическое
поле. Максвелл предложил считать, что
соотношение справедливо не толь-ко для
проводящего, но и для любого замкнутого
контура, мыеленно выбранного в переменном
магнитном поле. Иными словами, он
предположил, что переменное магнитное
поле создает в любой точке пространства
вихревое электрическое поле независимо
от того, находится в этой точке проводник
или нет. Обобщенное таким образом
равенство называется первым уравнением
Максвелла в интегральной форме:
циркуляция вектора напряженности
электрического поля по про- извольному
замкнутому контуру L равна взятой в
обратным знаком скорости изменения
магнитного потока сквозь поверхность,
натянутую на контур.
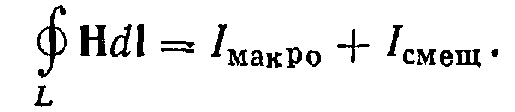 Это
равенство называется вторым уравнением
Максвелла в интегральной форме. Оно
показывает, что циркуляция вектора Н
напряженности магнитного поля по
произвольному замкнутому контуру L
равнаалгебраической сумме макротоков
и тока смещения сквозь поверхность,
натянутую на этот контур.
Это
равенство называется вторым уравнением
Максвелла в интегральной форме. Оно
показывает, что циркуляция вектора Н
напряженности магнитного поля по
произвольному замкнутому контуру L
равнаалгебраической сумме макротоков
и тока смещения сквозь поверхность,
натянутую на этот контур.
Третье
уравнение Максвелла выражает теорему
Остроградского—Гаусса для потока
вектора электрического смещения D
сквозь произвольную замкнутую поверхность
S, охватывающую суммарный свободный
заряд 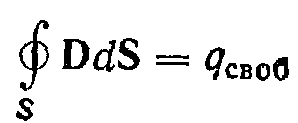
Четвертое
уравнение Максвелла является обобщением
теоремы Остроградского — Гаусса на
переменное магнитное поле: 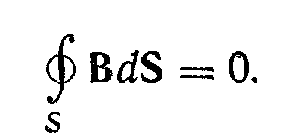
Билет29
1 Сегнетоэлектрики. Поляризация сегнетоэлектрики. Гистерезис
Сегнетоэле́ктрики
(названы по первому материалу, в котором
был открыт сегнетоэлектрический эффект
— сегнетова соль) — твёрдые диэлектрики
(некоторые ионные кристаллы и
пьезоэлектрики), обладающие в определённом
интервале температур собственным
электрическим дипольным моментом,
который может быть переориентирован
за счёт приложения внешнего электрического
поля. Сегнетоэлектрические материалы
обладают гистерезисом по отношению к
электрическому дипольному моменту.
Температура,
при которой исчезает спонтанная
поляризация (то есть собственный
дипольный момент) и происходит перестройка
кристаллической структуры, носит
название температуры (точки) Кюри (ещё
одна аналогия с ферромагнетиками).
Переход через точку Кюри означает
фазовый переход, а соответствующие
фазы обозначаются как полярная
(сегнетоэлектрик) и неполярная
(параэлектрик[1] — нелинейный диэлектрик,
не обладающий спонтанной поляризацией,
относительная диэлектрическая
проницаемость которого уменьшается с
ростом температуры).Спонтанная
поляризация в сегнетоэлектриках в
точке Кюри меняется либо непрерывно
(переход второго рода, сегнетова соль),
либо скачком (переход первого рода,
титанат бария). Другие характеристики
сегнетоэлектриков, такие как относительная
диэлектрическая проницаемость, могут
достигать в точке Кюри очень больших
значений (104 и выше).Вблизи точки Кюри в неполярной
фазе выполняется закон Кюри — Вейсса,
связывающий поляризуемость α и
температуру T сегнетоэлектрика[2] 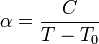 где
C и T0 — константы, определяемые видом
сегнетоэлектрика. Величина T0 носит
название температуры Кюри — Вейсса и
очень близка к значению температуры
Кюри. Если точек Кюри две, то вблизи
каждой из них в неполярной фазе
выполняется тот же закон. Вблизи верхней
— в прежней форме, а вблизи нижней — в
форме[2]:
где
C и T0 — константы, определяемые видом
сегнетоэлектрика. Величина T0 носит
название температуры Кюри — Вейсса и
очень близка к значению температуры
Кюри. Если точек Кюри две, то вблизи
каждой из них в неполярной фазе
выполняется тот же закон. Вблизи верхней
— в прежней форме, а вблизи нижней — в
форме[2]: 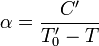 Механизм
приобретения дипольного момента в
полярной фазе (фазе сегнетоэлектрика)
может также различаться: возможен
вариант как со смещением ионов (титанат
бария; соответствующий фазовый переход
называется переходом типа смещения),
так и с упорядочиванием ориентации уже
существующих в веществе диполей
(дигидрофосфат калия, триглицинсульфат).
Механизм
приобретения дипольного момента в
полярной фазе (фазе сегнетоэлектрика)
может также различаться: возможен
вариант как со смещением ионов (титанат
бария; соответствующий фазовый переход
называется переходом типа смещения),
так и с упорядочиванием ориентации уже
существующих в веществе диполей
(дигидрофосфат калия, триглицинсульфат).
Гистере́зис
(греч. ὑστέρησις — «отстающий») —
свойство систем (физических, биологических
и т.д.), мгновенный отклик которых на
приложенные к ним воздействия зависит
в том числе и от их текущего состояния,
а поведение системы на интервале времени
во многом определяется её предысторией.
Для гистерезиса характерно явление
«насыщения», а также неодинаковость
траекторий между крайними состояниями
(отсюда наличие остроугольной петли
на графиках). Не следует путать это
понятие с инерционностью поведения
систем, которое обозначает монотонное
сопротивление системы изменению её
состояния. 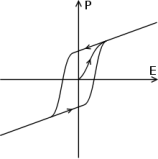
Эффект Холла — Википедия. Что такое Эффект Холла
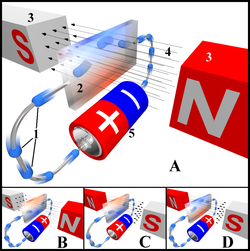
Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле. Открыт Эдвином Холлом в 1879 году в тонких пластинках золота.
Свойства
В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через проводящий брусок в слабом магнитном поле с индукцией B{\displaystyle B} течёт электрический ток с плотностью j{\displaystyle j} под действием напряжённости E{\displaystyle E}. Магнитное поле будет отклонять носители заряда к одной из граней бруса от их движения вдоль или против электрического поля. При этом критерием малости[1] будет служить условие, что при этом носители заряда не начнут двигаться по циклоиде.
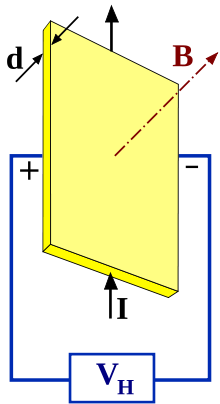
Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска, и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов E1{\displaystyle E_{1}} не скомпенсирует силу Лоренца:
- eE1=evB⇒E1=vB.{\displaystyle eE_{1}=evB\Rightarrow E_{1}=vB.}
- где e{\displaystyle e} — электрический заряд электрона.
Скорость электронов v{\displaystyle v} можно выразить через плотность тока j{\displaystyle j}:
- j=nev⇒v=jne,{\displaystyle j=nev\Rightarrow v={\frac {j}{ne}},}
- где n{\displaystyle n} — концентрация носителей заряда. Тогда
- E1=1nejB.{\displaystyle E_{1}={\frac {1}{ne}}jB.}
Коэффициент RH=1ne{\displaystyle R_{H}={\frac {1}{ne}}} пропорциональности между E1{\displaystyle E_{1}} и jB{\displaystyle jB} называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их знак заряда для большого числа металлов и полупроводников.
Несмотря на то, что носителями заряда в металлах являются электроны, имеющие отрицательный заряд, для некоторых металлов — например, таких, как свинец, цинк, железо, кобальт, вольфрам в достаточно сильном магнитном поле наблюдается положительный знак константы Холла RH{\displaystyle R_{H}}, что объясняется в полуклассической и квантовой теориях твёрдого тела.
Аномальный эффект Холла
Случай появления напряжения (электрического поля) в образце, перпендикулярного направлению пропускаемого через образец тока, наблюдающегося в отсутствие приложенного постоянного магнитного поля (то есть явление, полностью аналогичное эффекту Холла, но наблюдающееся без внешнего постоянного магнитного поля), называется аномальным эффектом Холла.
Необходимым условием для наблюдения аномального эффекта Холла является нарушение инвариантности по отношению к обращению времени в системе. Например, аномальный эффект Холла может наблюдаться в образцах с намагниченностью[2].
Квантовый эффект Холла
В сильных магнитных полях в плоском проводнике (то есть в квазидвумерном электронном газе) в системе начинают сказываться квантовые эффекты, что приводит к появлению квантового эффекта Холла: квантованию холловского сопротивления. В ещё более сильных магнитных полях проявляется дробный квантовый эффект Холла, который связан с кардинальной перестройкой внутренней структуры двумерной электронной жидкости.
Спиновый эффект Холла
В случае отсутствия магнитного поля в немагнитных проводниках может наблюдаться отклонение носителей тока с противоположными направлениями спинов в разные стороны перпендикулярно электрическому полю. Это явление, получившее название спинового эффекта Холла, было теоретически предсказано Дьяконовым и Перелем в 1971 году. Говорят о внешнем и внутреннем спиновых эффектах. Первый из них связан со спин-зависимым рассеянием, а второй — со спин-орбитальным взаимодействием.
Магнетосопротивление
Эдвин Холл проводил опыты в надежде обнаружить возрастание сопротивления проводника в магнитном поле, но в слабых полях не зарегистрировал его. Также оно не следует из теории металлов Друде, расчёты по которой приводились выше. Однако при более строгих расчётах и в сильных полях магнетосопротивление проявляется достаточно хорошо.
Применение
 Датчик Холла, используемый для измерения силы тока в проводнике. В отличие от трансформатора тока, измеряет также и постоянный ток.
Датчик Холла, используемый для измерения силы тока в проводнике. В отличие от трансформатора тока, измеряет также и постоянный ток.Эффект Холла позволяет определить концентрацию и подвижность носителей заряда, а в некоторых случаях − тип носителей заряда (электроны или дырки) в металле или полупроводнике, что делает его достаточно хорошим методом исследования свойств полупроводников (см. Метод ван дер Пау).
На основе эффекта Холла работают датчики Холла — приборы, измеряющие напряжённость магнитного поля. Датчики Холла получили очень большое распространение в бесколлекторных, или вентильных, электродвигателях (сервомоторах). Датчики закрепляются непосредственно на статоре двигателя и выступают в роли датчика положения ротора (ДПР), который реализует обратную связь по положению ротора и выполняет ту же функцию, что и коллектор в коллекторном ДПТ.
Датчики Холла применяются:
См. также
Примечания
- ↑ Критерий малости — внешние воздействия не разрушают присущих физической системе внутренних свойств, не осуществляют «насилия» над системой.
- ↑ Naoto Nagaosa, Jairo Sinova, Shigeki Onoda, A. H. MacDonald and N. P. Ong. Anomalous Hall effect (англ.) // Rev. Mod. Phys.. — 2010. — Vol. 82, iss. 2. — P. 1539—1592.
Литература
- Абрикосов А. А. Основы теории металлов. — Москва: «Наука», главная редакция физико-математической литературы, 1987. — 520 с. — ISBN нет, ББК 22.37, УДК 539.21 (075.8).
- Ашкрофт Н., Мермин Н. Физика твердого тела. — «Мир», 1979.
Ссылки
Квантовый эффект Холла — это… Что такое Квантовый эффект Холла?
Ква́нтовый эффе́кт Хо́лла — эффект квантования холловского сопротивления или проводимости двумерного электронного газа в сильных магнитных полях и при низких температурах. Квантовый эффект Холла (КЭХ) был открыт Клаусом фон Клитцингом (совместно с Г. Дордой и М. Пеппером) в 1980 году[1], за что впоследствии, в 1985 году, он получил Нобелевскую премию[2].
Введение
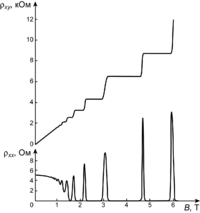 Рис. 1. Зависимости холловского сопротивления и удельного сопротивления от магнитного поля при постоянной концентрации носителей. На зависимости холловского сопротивления наблюдаются «плато»[3].
Рис. 1. Зависимости холловского сопротивления и удельного сопротивления от магнитного поля при постоянной концентрации носителей. На зависимости холловского сопротивления наблюдаются «плато»[3].Эффект состоит в том, что при достаточно низких температурах в сильных магнитных полях на зависимости поперечного сопротивления (отношения возникающего поперечного напряжения к протекающему продольному току) вырожденного двумерного электронного газа (ДЭГ) от величины нормальной составляющей к поверхности ДЭГ индукции магнитного поля (или от концентрации при фиксированном магнитном поле) наблюдаются участки с неизменным поперечным сопротивлением или «плато».
Фон Клитцинг обнаружил так называемый нормальный (или целочисленный) квантовый эффект Холла (КЭХ), когда значения сопротивления на «плато» равно , где e — заряд электрона, h — постоянная Планка, ν — натуральное число, называемое фактором заполнения уровней Ландау (рис. 1).
В 1982 году Д. Цуи и Х. Штёрмер открыли дробный квантовый эффект Холла (фактор заполнения при этом становится меньше единицы)[4].
Уже первая работа[1] по КЭХ, названная «Новый метод определения постоянной тонкой структуры с высокой точностью по квантованию холловского сопротивления» показала, что возможно его применение в качестве стандарта сопротивления. В настоящее время известно, что значения квантованного сопротивления Холла не зависят от качества образца и его материала. Поэтому, начиная с 1990 года, калибровки сопротивлений основаны на КЭХ с фиксированным значением Rэ = 25812.807557(18) Ом.
Для наблюдения КЭХ существует ряд условий, которые должны выполняться, чтобы квантование было точным. Ниже приведены основные предпосылки возникновения плато.
Двумерный электронный газ
Если ограничить трёхмерный электронный газ в одном из направлений, таким образом, что в потенциальной яме (например, с ограничивающим потенциалом по оси Z) заполнен только один уровень размерного квантования, то говорят, что электронный газ стал двумерным. В этом случае движение в плоскости, перпендикулярной оси Z остаётся свободным и энергетический спектр ДЭГ выражается формулой:
где n = 0, 1, 2…, — эффективная масса квазичастиц (электронов или дырок). Только если заполнен основной уровень размерного квантования (первая подзона размерного квантования) говорят о формировании ДЭГ[5].
Энергетический спектр носителей заряда в магнитном поле
На классические заряженные частицы, движущиеся в магнитном поле, действует сила Лоренца. Эта сила заставляет частицу двигаться по окружности с угловой скоростью , называемой циклотронной частотой (система единиц СГС). Согласно квантовой теории частицы, совершающие периодическое движение, обладают только дискретными значениями энергии, поэтому у заряженных частиц в магнитном поле появляются уровни энергии, называемые уровнями Ландау. Энергия n-го уровня, если пренебречь составляющей импульса и наличием спина у частицы, определяется выражением[6]
Энергетический спектр двумерного электронного газа становится полностью дискретным и каждый энергетический уровень обладает следующим вырождением (число орбит, которые могут принадлежать уровню Ландау)
- (1)
где Ф0 — квант магнитного потока. Это аналогично плотной упаковке циклотронных орбит в двумерном слое. Эту же величину можно получить, если представить, что из всех частиц ДЭГ, расположенных в интервале энергий, равных ħωс (то есть произведение двумерной плотности состояний на энергию ħωс), формируется отдельный уровень Ландау.
Концентрация электронов в ДЭГ в магнитном поле определяется по формуле , если уровень Ферми попадает в щель между уровнями Ландау. В общем случае частичное заполнение одного из уровней Ландау характеризуется так называемым фактором заполнения — отношение концентрации ДЭГ к вырождению уровней Ландау. Он может принимать как целые, так и дробные значения[5].
Эффект Холла
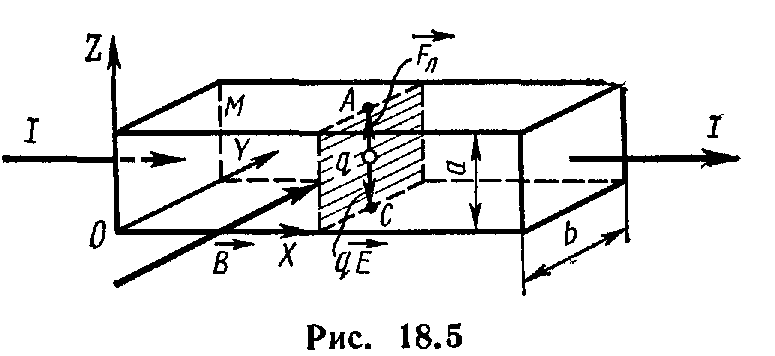
Явление, открытое Холлом в 1879 году, состоит в том, что в проводнике с током, помещённом в магнитное поле, перпендикулярное направлению тока, возникает электрическое поле в направлении, перпендикулярном направлениям тока и магнитного поля. Возникающее в проводнике электрическое поле, называемое полем Холла, вызвано действием силы Лоренца FL = eBv, заставляющей электроны отклоняться в направлении, перпендикулярном скорости v. В результате это поле EH уравновешивает силу Лоренца, и между боковыми гранями образца возникнет разность потенциалов VH, которая поддается измерению.
Ток через образец равен I = nevS, где S — площадь поперечного сечения проводника, S = bd, b — ширина, d — толщина.
Условие равновесия силы Лоренца и силы, вызванной холловским полем, — eEH = evB = eVH/b. Отсюда следует, что VH = bvB = IvB/nevd = IB/end = IRH, где RH называется холловским сопротивлением. В двумерных системах RH = B/ens, где ns — поверхностная концентрация.
Важно отметить, что RH — это отношение возникающей поперечной разности потенциалов к продольному току, RH = Rxy = Vy/Ix. При этом продольное сопротивление RL = Rxx = Vx/Ix, слабо зависит от индукции магнитного поля, оставаясь по величине близким к своему значению при B = 0[7].
Целочисленный квантовый эффект Холла
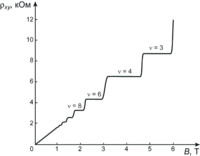 Рис. 2. Зависимости холловского сопротивления от магнитного поля. На зависимости холловского сопротивления указаны факторы заполнения для некоторых «плато».
Рис. 2. Зависимости холловского сопротивления от магнитного поля. На зависимости холловского сопротивления указаны факторы заполнения для некоторых «плато».Как было замечено Клитцингом[1], при измерении эффекта Холла в инверсном слое кремниевого МОП транзистора при низких температурах (Т ~ 1 K) и в сильных магнитных полях (B > 1 Тл) линейная зависимость холловского сопротивления сменяется чередой ступеней (плато) как показано на Рис. 2. Величина сопротивления на этих ступеньках равна комбинации фундаментальных физических констант, делённой на целое число :
Когда на зависимости холловского сопротивления RH наблюдается плато, продольное электрическое сопротивление становится очень малой величиной (оно равно нулю с высокой экспериментальной точностью). При низких температурах ток в образце может течь без диссипации (рассеяния).
Прецизионные измерения также показали, что на точности квантования RH не сказываются такие существенные параметры эксперимента, как размеры образцов, влияние границ и важное в обычном эффекте Холла закорачивание холловского напряжения омическими контактами, а также степень совершенства структур, то есть наличие большого количества примесей и дефектов, тип материала, в котором находится 2D-электронный газ, температура и сила измерительного тока. Экспериментальная точность квантования так высока, что встал вопрос о метрологических применениях КЭХ: проверке формул квантовой электродинамики с помощью прецизионного определения постоянной тонкой структуры или создания нового эталона сопротивления.
Экспериментальная установка
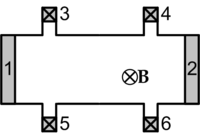 Геометрия измерения квантового эффекта Холла. RH=V35/I12 RL=V34/I12
Геометрия измерения квантового эффекта Холла. RH=V35/I12 RL=V34/I12Для наблюдения эффекта гетероструктуру со сформированным двумерным электронным газом помещают в однородное магнитное поле, перпендикулярное плоскости электронного газа. При пропускании тока через образец измеряют ток, а также возникающее напряжение вдоль и поперёк образца.
Качественная интерпретация целочисленного квантового эффекта Холла
Электроны дрейфуют вдоль линий постоянной энергии, формируя локализованные и краевые токовые состоянияЦелочисленный квантовый эффект Холла может быть просто интерпретирован на основе модели краевых состояний. Как правило, экспериментальный образец с двумерным электронным газом имеет границу, задаваемую литографическим краем или краем области под затвором. Возле края формируется обедняющее электрическое поле, направленное к краю (речь идёт об отрицательно заряженных электронах). Оно приводит к зависимости нуля отсчёта уровней Ландау от координаты, поэтому уровни Ландау «изгибаются» вверх вблизи края. Как известно в скрещенных магнитном и электрическом полях заряженная частица дрейфует вдоль линии постоянной энергии — эквипотенциали. Электроны заполняют состояния согласно статистике Ферми — Дирака до некоторого уровня Ферми, и при факторе заполнения , близком к целочисленному значению вдали от краёв формируются локализованные состояния, не участвующие в проводимости, а вблизи краёв — краевые токовые состояния. Причем ток на противоположных берегах двумерного электронного газа имеет противоположное направление, а направление обхода однозначно задаётся знаком квантующего магнитного поля. Ток переносимый каждым краевым состоянием квантован и равен , где — значение электрохимического потенциала. А число краевых каналов целое и определяется фактором заполнения . В этом случае, когда локализованные и подвижные состояния на уровне Ферми пространственно разделены и обратное рассеяние подавлено, реализуется режим квантового эффекта Холла.
Локализация состояний спектра и осцилляции компонент проводимости 2D электронного газа в сильном магнитном поле. Локализованные состояния закрашены зелёным[8].Влияние неоднородностей
Дефекты, примеси и другие неоднородности в кристалле, которые локализуют, «изолируют» отдельные электроны в «ловушках», являются причиной возникновения широких плато на графиках холловского сопротивления и широких минимумов омического сопротивления. На поверхности кристалла остаются дефекты и примеси, которые порождают энергетические «долины» и «холмы». Когда уровень Ландау оказывается заполненным, некоторые из них попадают в ловушку и изолируются. Они больше не принимают участие в процессах электропроводности через кристалл. Локализованные электроны первыми заполняют и освобождают уровни Ландау при изменении магнитного поля, поддерживая точное заполнение уровней Ландау в энергетически гладкой области кристалла для протяженных интервалов величины магнитного поля. При этом холловское сопротивление образца и магнитосопротивление остаются постоянными. Локализованные благодаря дефектам кристалла электроны представляют собой хранилище необходимых для точного заполнения уровней Ландау носителей в энергетически гладкой области кристалла для конечного интервала напряженностей магнитных полей. Cамо существование целочисленного квантового эффекта Холла зависит от наличия дефектов в кристалле. Без неоднородностей в кристалле, «идеально чистая» система приводила бы к линейному эффекту Холла, без квантованности[9].
О сопротивлении, проводимости и потенциале в условиях квантования холловского сопротивления
Эквипотенциали в образце с двумя контактами в условиях квантового эффекта Холла.Дробный квантовый эффект Холла
В 1982 году Даниэль Цуи (Daniel Tsui) и Хорст Штёрмер (Horst Störmer) заметили, что «плато» в холловском сопротивлении наблюдаются не только при целых значениях n, но и в существенно более сильных магнитных полях[4] при n=1/3. В дальнейшем были обнаружены плато электрического сопротивления и при других дробных значениях n, например при n=2/5, 3/7…
Природа дробного квантового эффекта Холла была объяснена Р. Лаффлином в 1983 году[10]. В 1998 году Цуи, Штёрмер и Лаффлин получили Нобелевскую премию по физике за открытие и объяснение этого явления[11]
Качественное объяснение дробного квантового эффекта Холла
Суть явления заключается в том, что группа электронов «объединяются» в новую «частицу», заряд которой меньше заряда электрона. Дробный квантовый эффект Холла нельзя объяснить на основе поведения одиночных электронов в магнитном поле. Причина заключается во взаимодействии между электронами. Магнитное поле создает «вихри», по одному на каждый квант магнитного потока. Принцип Паули требует, чтобы каждый электрон был окружен одним «вихрем». Когда магнитные поля превышают величину, соответствующую ЦКЭХ с i=1, вихрей становится больше, чем электронов. Принцип Паули выполняется при размещении нескольких вихрей на электроне, которые уменьшают межэлектронное кулоновское отталкивание. Электрон «захватывает» квант магнитного потока и становится «составной частицей». С точки зрения теории, такие «составные частицы» описывать гораздо легче, чем «свободные» электроны. Захваченный квант потока меняет природу частиц, «превращая» фермионы в бозоны. Электрон, захвативший четное число квантов потока, становится фермионом, а нечетное число квантов потока — бозоном. При заполнении на 1/3 нижнего уровня Ландау каждый электрон принимает три кванта магнитного потока. Таким образом получается композитный бозон. Он находится в условиях нулевого магнитного поля (оно уже включено в новую частицу) и в состоянии бозе-конденсации в новом энергетическом состоянии. Можно определить энергетическую щель, необходимую для возникновения квантования холловского сопротивления и для обращения в ноль обычного сопротивления, экспериментальными методами. Когда часть вихрей магнитного поля не захвачена, возникает дробный дефицит заряда в каждом из этих вихрей. По сравенению с электронами, это положительные дробные заряды. Квазичастицы могут свободно двигаться и проводить электрический ток. Образование плато на графиках происходит как и в целочисленном квантовом эффекте Холла, из-за флуктуаций потенциала на дефектах кристалла. Отличие в том, что носители электрического тока — не электроны, а частицы с дробным зарядом. Дробный квантовый эффект Холла объясняется захватом нечетного числа вихрей магнитного потока каждым электроном [12].
См. также
Примечания
- ↑ 1 2 3 K. v. Klitzing, G. Dorda, M. Pepper New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance Phys. Rev. Lett. 45, 494 (1980) DOI:10.1103/PhysRevLett.45.494
- ↑ Нобелевский лауреат по физике за 1985 год
- ↑ К. фон Клитцинг «Квантовый эффект Холла: Нобелевские лекции по физике — 1985 г.» УФН 150, 107 (1985).
- ↑ 1 2 D. C. Tsui, H. L. Störmer, A. C. Gossard Two-Dimensional Magnetotransport in the Extreme Quantum Limit Phys. Rev. Lett. 48, 1559 (1982). DOI:10.1103/PhysRevLett.48.1559
- ↑ 1 2 Ando T., Fowler A. B. and Stern F. Electronic properties of two-dimensional systems Rev. Mod. Phys. 54, 437 (1982).
- ↑ Л. Д. Ландау, Е. М. Лифшиц «Теоретическая физика», в 10 т, т. 3 «Квантовая механика (нерелятивистская теория)», М., Физматлит, 2002, 808 с., ISBN 5-9221-0057-2 (т. 3), гл. 15 «Движение в магнитном поле», п. 112 «Движение в однородном магнитном поле», c. 554—559;
- ↑ Askerov B. M. Electron Transport Phenomena in Semiconductors, 5-е изд.. — Singapore: World Scientific, 1994. — P. 416. — ISBN ISBN 981-02-1283-6
- ↑ Е. Н. Бормонтов Квантовый эффект Холла СОЖ 9, 81 (1999). [1]
- ↑ В. К. Воронов, А. В. Подоплелов «Современная физика», учебное пособие, М., КомКнига, 2005, 512 с., ISBN 5-484-00058-0, гл. 4 «Полупрводники», п 4.7 «Квантовый эффект Холла», пп 4.7.4 «Целочисленный квантовый эффект Холла», с. 249—253;
- ↑ R. B. Laughlin, Anomalous Quantum Hall Effect: An Incompressible Quantum Fluid with Fractionally Charged Excitations Phys. Rev. Lett. 50, 1395 (1983) DOI:10.1103/PhysRevLett.50.1395
- ↑ Нобелевские лауреаты по физике за 1998 год
- ↑ В. К. Воронов, А. В. Подоплелов «Современная физика», учебное пособие, М., КомКнига, 2005, 512 с., ISBN 5-484-00058-0, гл. 4 «Полупрводники», п 4.7 «Квантовый эффект Холла», пп 4.7.5 «Дробный квантовый эффект Холла», с. 253—259;
Литература
Ссылки
ХОЛЛА ЭФФЕКТ — это… Что такое ХОЛЛА ЭФФЕКТ?
ХОЛЛА ЭФФЕКТ — возникновение в тв. проводнике с током плотностью j, помещённом в магн. поле H, электрич. поля в направлении, перпендикулярном H и j. Напряжённость электрич. поля (поля Холла) равна: EH=RHjsina. (1) Здесь a угол между векторами Н и j (a … Физическая энциклопедия
Холла эффект — появление в проводнике с током плотностью j, помещенном в магнитное поле Н, электрического поля Ex, перпендикулярного Н и I. Напряжённость электрического поля (поля Холла) равна: Ex = Rhjsin α, (1) где α угол между… … Большая советская энциклопедия
Холла эффект — возникновение в проводнике с током плотностью j, помещённом в магнитное поле H, электрического поля (поля Холла), направленного перпендикулярно H и j. Напряжённость поля Холла EH = RjHsinα, где α угол между H и j, R постоянная Холла, зависящая… … Энциклопедический словарь
Холла эффект — Эффект Холла 1. Электроны 2. Зонд 3. Магниты 4. Магнитное поле 5. Источник тока Эффект Холла явление возникновения поперечной разности потенциалов (называемой также Холловским напряжением) при помещении проводника с постоянным током в магнитное… … Википедия
ХОЛЛА ЭФФЕКТ — возникновение в проводнике с током плотностью j, помещённом в магн. поле Н, электрич. поля (поля Холла), направленного перпендикулярно Н и j. Напряжённость поля Холла EH= RjH sin а, где а угол между Н и j, R постоянная Холла, зависящая гл. обр.… … Естествознание. Энциклопедический словарь
ХОЛЛА ЭФФЕКТ — возникновение поперечного электрич. поля в проводнике или ПП с током при помещении его в магнитное поле. Для изотропного (напр., поликристаллич.) проводника или ПП напряжённость поперечного электрич. поля ЕВ = R[В, j], где В магнитная индукция, j … Большой энциклопедический политехнический словарь
КВАНТОВЫЙ ХОЛЛА ЭФФЕКТ — макроскопич. квантовый эффект, проявляющийся в квантовании холловского сопротивления r ху (см. Холла эффект )и исчезновении уд. сопротивления r хх. К. X. э. наблюдается при низких темп pax Т в инверсионном слое носителей заряда в полупроводниках … Физическая энциклопедия
Эффект — [effect] 1. Результат, следствие каких либо причин, действий. 2. В естественных науках явление (закономерность), часто называют именем открывшего этот эффект ученого (например, эффект Холла, эффект Фарадея, эффект Томсона и т. п.): Смотри также:… … Энциклопедический словарь по металлургии
эффект Холла — гальваномагнитный эффект Холла; эффект Холла Возникновение поперечной разности потенциалов в проводнике, по которому проходит электрический ток, в том случае, когда этот проводник помещен в магнитное поле, перпендикулярное направлению потока … Политехнический терминологический толковый словарь
Холла эдс датчик — элемент автоматики, радиоэлектроники и измерительной техники, используемый в качестве измерительного преобразователя (См. Измерительный преобразователь), действие которого основано на Холла эффекте. Представляет собой топкую прямоугольную … Большая советская энциклопедия


![[\vec{\sigma}\cdot(i\hbar v_F\vec{\nabla}+e\vec{A}/c)]\psi(x,y)=\varepsilon\psi(x,y)](/800/600/https/dic.academic.ru/pictures/wiki/files/101/e8732ee3a166a90c3c924e0e348ff7a8.png)
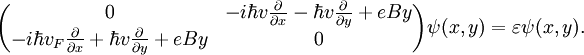
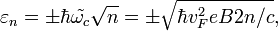
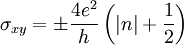 .
.