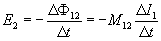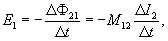Взаимоиндукция — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 июня 2017; проверки требуют 5 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 июня 2017; проверки требуют 5 правок.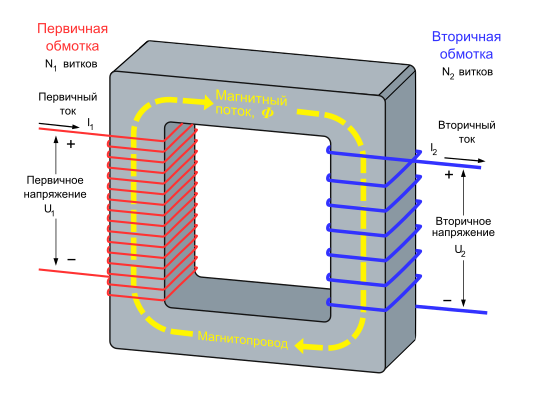

Взаимоиндукция (взаимная индукция) — явление возникновения ЭДС индукции в одном контуре при изменении силы тока во втором контуре и наоборот. Взаимоиндукция — частный случай электромагнитной индукции^[1].

При изменении силы тока в первом контуре, во втором возникает ЭДС:

E2=−dΨ1dt=−LdI1dt{\displaystyle {\mathcal {E_{2}}}=-{{d\Psi _{1}} \over dt}=-L{dI_{1} \over dt}}

где

E2{\displaystyle {\mathcal {E_{2}}}} — электродвижущая сила во втором контуре,

Ψ1{\displaystyle \Psi _{1}} — потокосцепление первого контура,

I1{\displaystyle I_{1}} — сила тока в первом контуре,

L{\displaystyle L} — взаимная индуктивность контуров^[1].

При изменении силы тока во втором контуре, в первом возникает ЭДС:

E1=−dΨ2dt=−LdI2dt{\displaystyle {\mathcal {E_{1}}}=-{{d\Psi _{2}} \over dt}=-L{dI_{2} \over dt}}

где

E1{\displaystyle {\mathcal {E_{1}}}} — электродвижущая сила в первом контуре,

Ψ2{\displaystyle \Psi _{2}} — потокосцепление второго контура,

I2{\displaystyle I_{2}} — сила тока во втором контуре,

L{\displaystyle L} — взаимная индуктивность контуров

[1].

Явление взаимоиндукции применяется для повышения и понижения напряжения переменного тока в трансформаторах^[1].

• Никеров. В. А. Физика: учебник и практикум для академического бакалавриата. — Юрайт, 2015. — 415 с. — ISBN 978-5-9916-4820-2.
• Малая Советская Энциклопедия т.2, Государственное научное издательство «Большая советская энциклопедия», 1958 г.
• Хайкин С. Э. «Словарь радиолюбителя», Госэнергоиздат, Москва 1960 г.
• Евдокимов Ф. Е. «Теоретические основы электротехники», «Высшая школа» 1981 г.
• Калантаров П.Л., Цейтлин Л.А. «Расчет индуктивностей» (справочная книга), Ленинград, ЭНЕРГОАТОМИЗДАТ Ленинградское отделение 1986 г.
• Взаимная индукция // Большая советская энциклопедия : в 66 т. (65 т. и 1 доп.) / гл. ред. О. Ю. Шмидт. — М. : Советская энциклопедия, 1926—1947.

1. ↑ ^{1 2 3 4} Никеров. В. А. Физика: учебник и практикум для академического бакалавриата.. — Юрайт, 2015. — С. 236, 237. — 415 с. — ISBN 978-5-9916-4820-2.

Индуктивность взаимная — это… Что такое Индуктивность взаимная?



Индуктивность взаимная

        величина, характеризующая магнитную связь двух или более электрических цепей (контуров). Если имеется два проводящих контура ( 1 и 2, см. рис.), то часть линий магнитной индукции, создаваемых током в первом контуре, будет пронизывать площадь, ограниченную вторым контуром (т. е. будет сцеплена с контуром 2). Магнитный поток Ф₁₂ через контур 2, созданный током I₁ в контуре 1, прямо пропорционален току:                  Коэффициент пропорциональности M₁₂ зависит от размеров и формы контуров 1 и 2, расстояния между ними, их взаимного расположения, а также от магнитной проницаемости (См. Магнитная проницаемость) окружающей среды и называется взаимной индуктивностью или коэффициентом взаимной индукции контуров 1 и 2. В системе СИ И. в. измеряется в Генри.

         Если ток I₂ течёт в контуре 2, то магнитный поток Ф₁₂ через площадь контура 1 также пропорционален току:

        

        причём M₂₁ = M₁₂.

         Наличие магнитной связи между контурами проявляется в том, что при изменении тока в одном из контуров появляется эдс индукции в соседнем контуре. Согласно закону индукции электромагнитной (См. Индукция электромагнитная),         

         (3)

        

        где E₂ и E₁ — возникающие в контурах 2 и 1 эдс индукции, а ΔФ₁₂ и Δ Ф₂₁ — изменение магнитных потоков через соответствующие контуры за время Δt.

         Через И. в. выражается взаимная энергия W₁₂ магнитного поля токов I₁ и I₂:

        

        знак в (4) зависит от направления токов.

         Лит.: Калашников С. Г., Электричество, М., 1970 (Общий курс физики, т. 2), гл. 10.

         Г. Я. Мякишев.

        

        Рис. к статье Индуктивность взаимная.

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

• Индуктивность
• Индуктивный датчик

Смотреть что такое «Индуктивность взаимная» в других словарях:

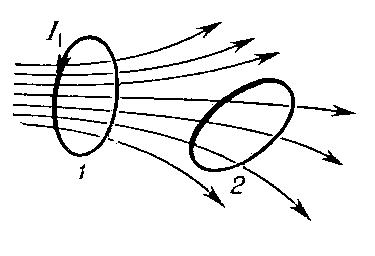
• ИНДУКТИВНОСТЬ ВЗАИМНАЯ — величина, характеризующая магн. связь двух или более электрич. цепей (контуров). Магн. поток через контур 1 с током I1 (рис.) частично пронизывает площадь, ограниченную контуром 2, причём магн. поток Ф12 через контур 2 прямо пропорционален току… …   Физическая энциклопедия

• ИНДУКТИВНОСТЬ ВЗАИМНАЯ — физическая величина, характеризующая магнитную связь электрических цепей и равная отношению потока магнитной индукции, пронизывающего площадь, ограниченную первым контуром, к силе тока во втором контуре, создающем этот поток индукции …   Большой Энциклопедический словарь

• ИНДУКТИВНОСТЬ ВЗАИМНАЯ — физ. величина, характеризующая магнитную связь электрических цепей и равная отношению (см.), пронизывающего ограниченную первым контуром площадь S, к силе тока I во втором контуре, создающем этот (см.) …   Большая политехническая энциклопедия

• индуктивность взаимная — физическая величина, характеризующая магнитную связь электрических цепей и равная отношению потока магнитной индукции, пронизывающего площадь, ограниченную первым контуром, к силе тока во втором контуре, создающем этот поток индукции. * * *… …   Энциклопедический словарь

• ИНДУКТИВНОСТЬ ВЗАИМНАЯ — физ. величина, характеризующая магн. связь электрич. цепей и равная отношению потока магн. индукции, пронизывающего площадь, ограниченную первым контуром, к силе тока во втором контуре, создающем этот поток индукции …   Естествознание. Энциклопедический словарь

• Динамическая индуктивность взаимная — скалярная величина, равная пределу, к которому стремится отношение приращения потокосцепления взаимной индукции в одной индуктивной катушке к приращению электрического тока в другой индуктивной катушке, когда последнее приращение стремится к нулю …   Официальная терминология

• ВЗАИМНАЯ ИНДУКТИВНОСТЬ — (см. ИНДУКТИВНОСТЬ ВЗАИМНАЯ). Физический энциклопедический словарь. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983 …   Физическая энциклопедия

• ИНДУКТИВНОСТЬ

  — (от лат. inductio наведение, побуждение), величина, характеризующая магн. св ва электрич. цепи. Ток, текущий в проводящем контуре, создаёт в окружающем пр ве магн. поле, причём магнитный поток Ф, пронизывающий контур (сцепленный с ним), прямо… …   Физическая энциклопедия

• взаимная индуктивность — взаимная индуктивность; статическая взаимная индуктивность; отрасл. коэффициент взаимной индукции Скалярная величина, характеризующая связь потокосцепления взаимной индукции одной электрической цепи с током в другой цепи, равная отношению… …   Политехнический терминологический толковый словарь

• взаимная индуктивность — Скалярная величина, равная отношению потокосцепления взаимной индукции одного элемента электрической цепи к электрическому току в другом элементе, обусловливающему это потоко соцепление. [ГОСТ Р 52002 2003] взаимная индуктивность По ГОСТ 19880 74 …   Справочник технического переводчика

10. Индуктивность и взаимная индуктивность.

Любой проводник имеет некоторое значение индуктивности. Индуктивность проводника показывает, насколько хорошо он может обеспечить наведение напряжения.

Элементы цепи, с определенным значением индуктивности, являющиеся катушками проволоки, называются индукторами. Индуктивность катушки зависит от его размера и материала. Чем больше число витков катушки, тем выше его индуктивность. Железный сердечник также увеличивает значение индуктивности. Катушки этого типа используются для низкочастотных токов, в то время как катушки с воздушным сердечником используются для высокочастотных токов.

Две катушки А и Bподнесены близко друг к другу и источник переменного тока(хотя нарисовано ЭДС) подключен к катушке А. Если измерительный прибор подключен к контактам катушкиBбудет установлено, что напряжение индуцируется (наводится) в этой катушки хотя две катушки не прикасаются . Вторичное напряжение , то есть напряжение в катушкеB, называется наведенным напряжением и энергия от одной катушки к другой передается по индукции. Катушка через которую течет ток называется первичной ; та, в котором индуцируется напряжение, называется вторичной. Первичная и вторичная катушки имеют взаимную индуктивность . Взаимная индуктивность измеряется в тех же единицах что и индуктивность , то есть в Генри .

Таким образом, когда скорость изменения одного ампера в секунду в первичной катушке будет производить один вольт во вторичной катушке, две катушки имеют один Генри взаимной индуктивности.

Следует учитывать, что индукция в переменном токе результат изменения тока не в текущем значении. Чем быстрее изменяется ток, тем выше наведенное напряжение.

11. Coupling . (Unit 15)

When circuits are indirect-inductively coupled energy is transferred from one circuit to another using electromagnetic field of the inductance through which a varying current is flowing. The coupling device is a transformer. It is not in series with the elements of the circuit therefore the coupling is indirect. The transformer consists of two windings: the primary and the secondary. The primary circuit is connected to the voltage source, the secondary-to the load circuit.

The coupling may be tight and loose. In case the coils of the coupling element are close together, the coupling is tight. In case the coils are separated the coupling is loose. In the loose coupling the mutual inductance is small compared with the self-inductance.

11. Взаимоиндукция.

Когда цепи являются косвенно-индуктивно связанными, энергия передается от одной схемы к другой с помощью электромагнитного поля индуктивности, через которое течет переменный ток (чушь собачья!). Сцепленное устройство представляет собой трансформатор. Это не последовательно соединенные элементы схемы, поэтому связь является косвенной. Трансформатор состоит из двух обмоток: первичной и вторичной. Первичная обмотка соединяется с источником напряжения, вторичная с нагрузкой цепи.

Взаимоиндукция может быть жесткой и свободной. В случае, если взаимоиндуктивные катушки соединены (закрыты) между собой, то связь является жесткой. В случае, если катушки разделены взаимоиндукция свободная. В слабой связи взаимная индуктивность мала по сравнению с самоиндукцией.

Взаимоиндукция

Дата публикации: 06 марта 2015.
Категория: Электротехника.

В статье «Явление электромагнитной индукции» было дано определение взаимоиндукции. Было указано, что взаимоиндукцией называется влияние изменяющегося магнитного поля одного проводника на другой проводник, в результате чего во втором проводнике возникает индуктированная электродвижущая сила (ЭДС). Пусть мы имеем два проводника I и II (рисунок 1) или две катушки, или два контура.

Рисунок 1. Явление взаимоиндукции

Ток в первом проводнике i₁ создается источником напряжения (на чертеже не показанном). Ток i₁ образует магнитный поток Ф₁, одна часть которого Ф₁₂ пересекает второй проводник, а другая часть Ф₁₁ замыкается помимо второго проводника:

Ф₁ = Ф₁₂ + Ф₁₁ .

Если вместо проводников возьмем две катушки с числом витков w₁ и w₂, то потокосцепление второго контура будет:

ψ₁₂ = w₂ × Ф₁₂ .

Так как поток Ф₁₂ пропорционален току i₁, то зависимость между потокосцеплением ψ₁₂ и током i₁ будет:

ψ₁₂ = M₁₂ × i₁ ,

откуда

где M₁₂ – коэффициент пропорциональности, называемый коэффициентом взаимоиндукции  или взаимной индуктивностью двух катушек (или контуров).

Размерность взаимной индуктивности определяется так:

Таким образом, взаимная индуктивность M измеряется в тех же единицах, что и индуктивность L.

Взаимная индуктивность зависит от числа витков катушек, их размера, взаимного расположения катушек и магнитной проницаемости среды, в которой находятся катушки.

Если пропускать ток i₂ по второму проводнику, то по аналогии можно написать:

ψ₂₁ = w₁ × Ф₂₁ .

и

ψ₂₁ = M₂₁ × i₂ ,

откуда получим формулу взаимоиндукции для второго контура

Пользуясь законом Ома для магнитной цепи, можно доказать, что

где R_м – магнитное сопротивление замкнутого контура, по которому проходят магнитные потоки Ф₁₂ и Ф₂₁.

В выражения

подставим значения ψ₁₂, ψ₂₁, Ф₁₂, Ф₂₁.

Таким образом, M₁₂ = M₂₁ = M.

Следовательно, взаимная индуктивность двух индуктивно или магнитно-связанных цепей не зависит от того, какой цепью будет создаваться магнитный поток.

При изменении тока i₁ магнитные потоки Ф₁₁ и Ф₁₂ будут изменяться и во втором контуре возникнет индуктированная ЭДС, величина которой будет равна:

аналогично:

Эти ЭДС называются ЭДС взаимоиндукции. Если первый контур обладает сопротивлением r₁ и индуктивностью L₁, то напряжение U₁, приложенное к этому контуру, должно уравновесить ЭДС самоиндукции и взаимоиндукции, а также падение напряжения в сопротивлении r₁ контура:

Для второго контура:

Между индуктивностями L₁ и L₂ контуров и взаимной индуктивностью M существует зависимость:

Однако эта формула верна когда весь поток, создаваемый первым контуром, сцепляется с витками второго контура. На практике M меньше

, то есть

Величина k меньше единицы и называется коэффициентом связи катушек. Этот коэффициент равнялся бы единице в том случае, если бы Ф₁₂ = Ф₁ и Ф₂₁ = Ф₂.

Электромагнитная связь между двумя контурами может быть изменена, если сближать контуры или удалять их один от другого, а также если менять взаимное расположение контуров.

В технике применяют приборы, работающие по принципу взаимной индукции и служащие для изменения индуктивности цепи. Такие приборы называются вариометрами. Они состоят из двух последовательно соединенных катушек, одна из которых может вращаться внутри другой.

Пусть обе катушки расположены так, чтобы оси их были параллельны одна другой и магнитные поля катушек направлены одинаково (согласное включение). В этом случае:

где индуктивность системы

L’ = L₁ + L₂ + 2 × M .

Если повернуть внутреннюю катушку на 180°, то в этом случае магнитные потоки будут направлены навстречу один другому (встречное включение).

В этом случае:

где

L’’ = L₁ + L₂ – 2 × M .

Вращая внутреннюю катушку между первым и вторым положениями, мы можем менять индуктивность системы в пределах от L’ до L’’.

По принципу взаимной индуктивности работают трансформаторы, нашедшие весьма широкое применение в технике.

Бывает, что взаимная индукция нежелательна: две линии связи (телефонные) оказывают взаимное влияние, мешая работе одна другой. Линии сильного тока, расположенные параллельно и вблизи линии связи, индуктируют в последней токи, вызывающие шум и треск, мешающие телефонным переговорам.

Рисунок 2. Взаимоиндукция

И для вашего развития посмотрите доклад доктора технических наук Ацюковского Владимира Акимовича, о взаимоиндукции проводников:

Источник: Кузнецов М.И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560с.

Явление взаимной индукции

Пусть имеются два близко расположенных контура. При протекании по одному из них тока изменяется индукция магнитного поля и, следовательно, магнитный поток, пронизывающий второй контур. В результате во втором контуре возникает ЭДС индукции, называемая в данном случае ЭДС взаимоиндукции.

Возникновение ЭДС индукции в одном из двух контуров, связанных магнитной связью, при изменении тока в другом, называется явлением взаимной индукции.

Количественно степень магнитной связи контуров (или любых электрических цепей) характеризуется взаимной индуктивностью.

Пусть ток I₁ течет по первому контуру. Часть данного магнитного потока Ф₁₂ пронизывает второй контур (рис. 3). Величина Ф₁₂ также будет пропорциональна току I₁ , т.е.

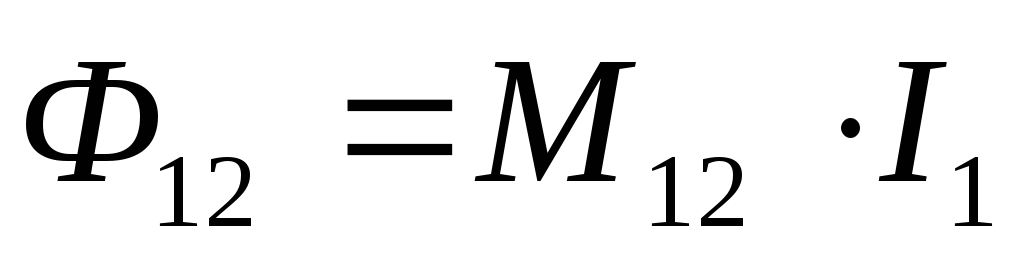, (9)

где 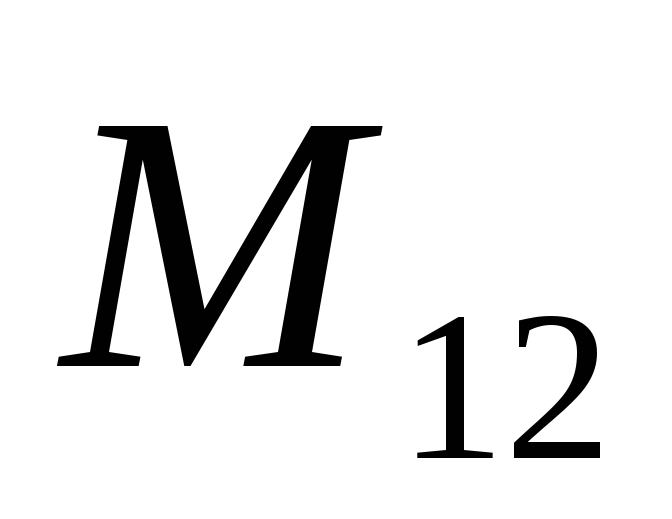— коэффициент, характеризующий влияние первого контура на второй.

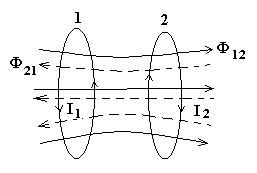
Рис.3. Возникновение ЭДС индукции в одном контуре при изменении тока в другом.

Пусть теперь ток I₂ течет по второму контуру (рис. 3). Рассуждая аналогично предыдущему случаю, для величины магнитного потока, создаваемого током I₂ и пронизывающего первый контур, можно записать:

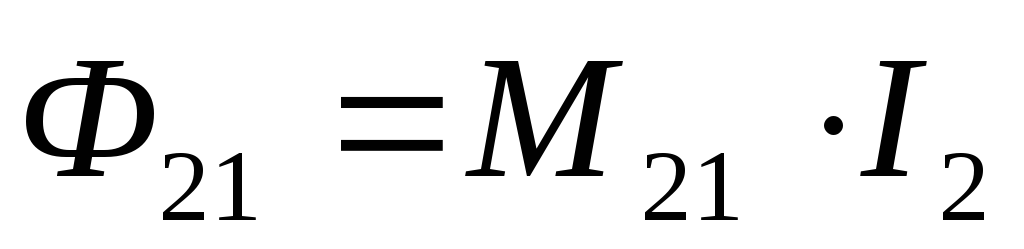
Если отсутствуют ферромагнитные сердечники, коэффициенты 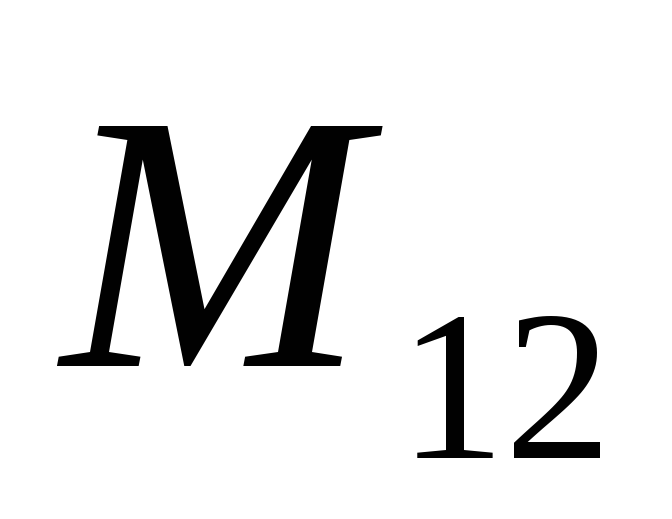и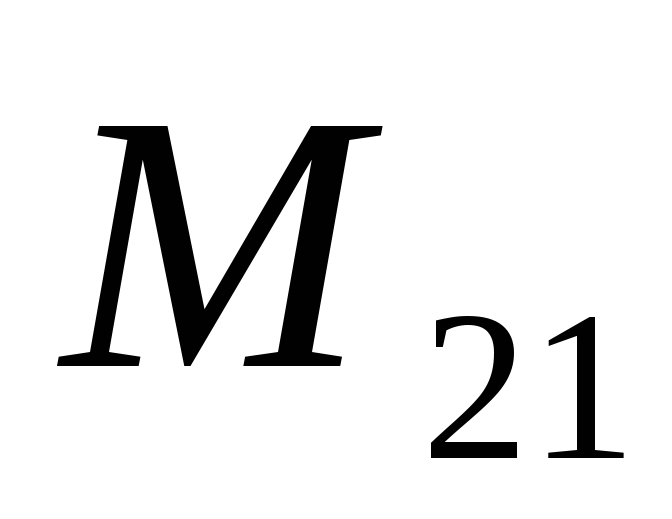тождественно равны и взаимное влияние двух контуров описывается только одним коэффициентом

= =,

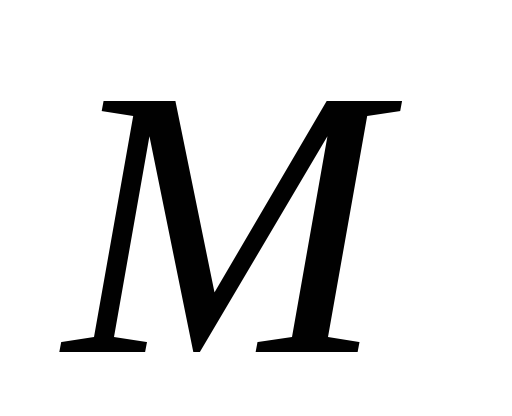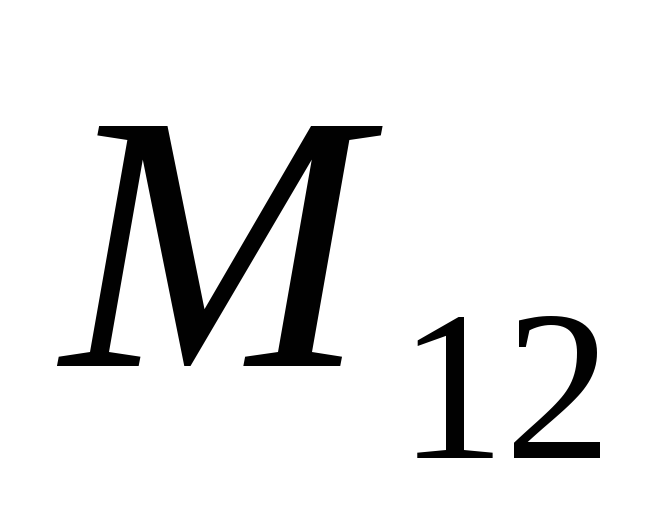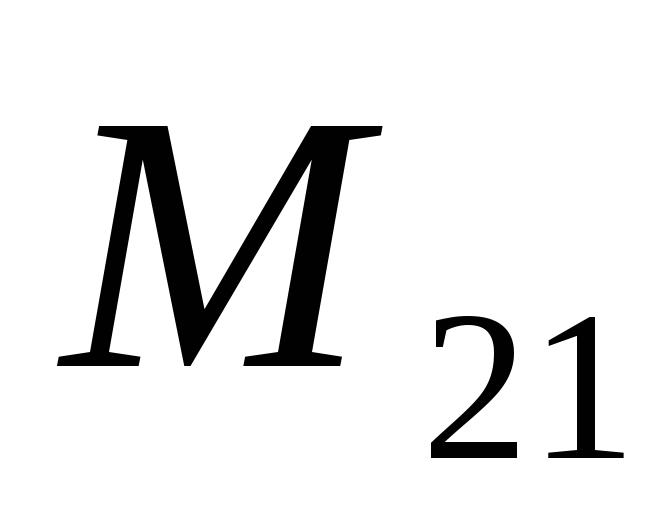который зависит от размеров и формы контуров 1 и 2, от их взаимного расположения, а также от магнитной проницаемости окружающей среды. Данный коэффициент называется взаимной индуктивностью или коэффициентом взаимной индукции контуров 1 и 2 и численно равен величине магнитного потока (в Веберах), общего для двух контуров, когда в одном из них протекает ток, равный 1 А.

При изменении тока в первом контуре, согласно закону электромагнитной индукции, в нем возникает ЭДС самоиндукции:

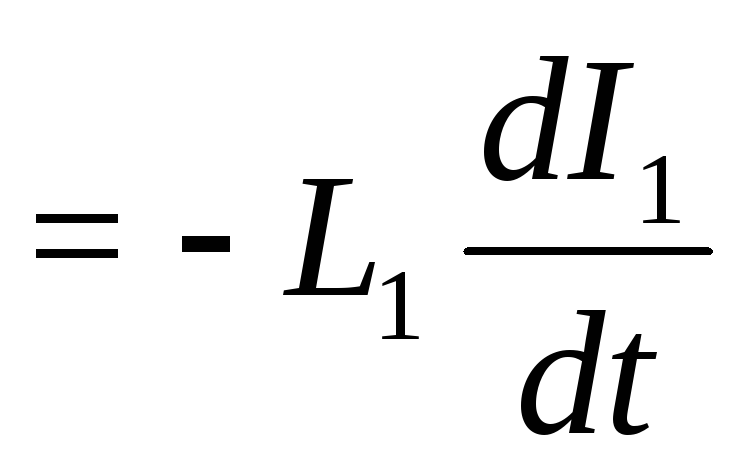Ԑ_i1(10)

Во втором контуре при этом будет индицироваться ЭДС индукции:

Ԑ_i2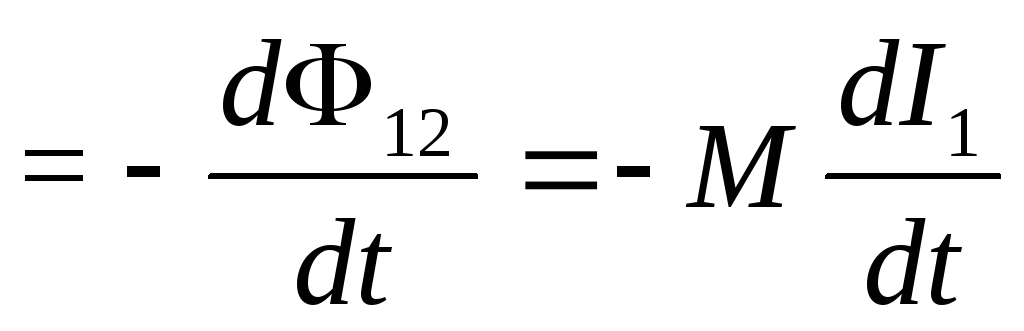(11)

Если второй контур разомкнут, то тока в нём не возникает, следовательно, обратного влияния второго контура на первый не будет. Сравнивая (10) и (11), получим:

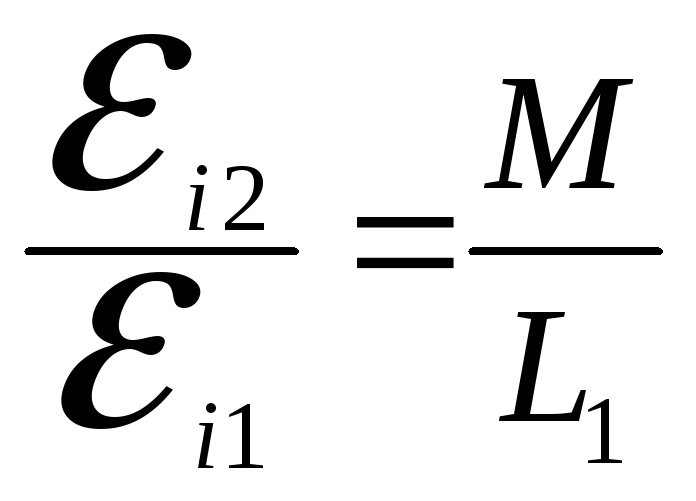(12)

Видно, что в любой момент времени отношение ЭДС, которые индуцируются в первом и во втором контуре током, протекающим по первому контуру, постоянно. Следовательно, ЭДС во втором контуре повторяет изменение ЭДС самоиндукции в первом. Это явление используется в трансформаторах для преобразования переменного напряжения в более низкое или в более высокое. Отношение М/L₁ называется КОЭФФИЦИЕНТОМ ТРАНСФОРМАЦИИ.

Описание лабораторного стенда.

Электрическая схема стенда для изучения явлений самоиндукции и взаимной индукции показана на рис.4.

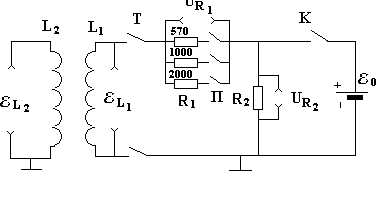
Рис.4. Схема лабораторного стенда

Он представляет собой разветвлённую цепь, содержащую источник постоянного тока Ԑ₀, активные сопротивления R₁ и R₂ и две катушки индуктивности L₁ и L₂, имеющие общий ферромагнитный сердечник (т.е. катушки являются обмотками трансформатора). Катушка L₁ может отключаться при помощи переключателя Т.

Периодическое замыкание и размыкание цепи выполняется автоматически ключом К, управляемым электромагнитным реле. Реле периодически производит замыкание ключа К на время t_о и размыкание его на время t₁.

взаимная индуктивность, собственная индуктивность, катушка индуктивности

В статье мы рассмотрим понятие индуктивности, что такое катушка индуктивности, подробно разберем закон Неймана или по-другому «взаимная индуктивность», покажем все на примере с формулами.

Взаимная индуктивность, формула Неймана

Предположим, что у нас есть две проводящие петли, петля номер один, взаимодействующая с ней, и петля номер два, вызывающая в ней магнитный поток, используя равенство индукции магнитного поля и определение индукции магнитного поля через векторный потенциал магнитного поля и изменив в этом потоке интеграл на поверхности, ограниченный замкнутым контуром, на интеграл по контуру, затем:

(1)

Из магнитостатики векторный магнитный потенциал магнитного поля из первой петли определяется как:

(2)

Если подставить формулу для векторного магнитного потенциала (2) в формулу для магнитного потока, ограниченного каким-либо произвольным контуром (1), то:

(3)

Очевидно, что формула (3) после перестановки круговых интегралов в одно место, эквивалентна:

(4)

Здесь R — расстояние друг от друга: dl(1) от dl(2)

Формула (4) может быть сохранена в виде разделения константы M ₁₂ , тогда:

(5)

где

(6)

Формула для размера взаимной индукции (6) является симметричной из-за регулировки dl(1) от dl(2), то есть взаимная индукция после этого изменения не меняется, она симметрична. Очевидно, что она не зависит от времени. Значение M_12 в формуле (6) это формула Неймана . Если подставить формулу (5) в интегральную формулу Фарадея для первого цикла, аналогично и для второго цикла, то тогда закономерность взаимной индукции второй петли относительно первой петли для электродвижущей силы для двух петель выражаются в формулах:

(7)(8)

Мы видим, что закономерности для электромагнитной силы одинаковы, но они зависят от изменений длительности электрического тока во втором контуре (формула (7) ) или в первом контуре (формула (8)).

Собственная индуктивность

Здесь мы будем иметь дело только с одним контуром, который магнитно взаимодействует с самим собой.

Закон Фарадея и собственная индукция

Мы должны иметь дело с индуктивностью, когда одна и та же цепь взаимодействует с одной и той же цепью магнетизмом, то есть это особый случай взаимной индуктивности. Мы записываем формулу для этой ситуации:

Ф = L*I (9)

Тогда формула для электромагнитной силы возникает после подстановки формулы (9) в закон Фарадея:

(10)

Формула для L такая же, как формула Неймана (6) , используется только двойное интегрирование по одному и тому же периметру, то есть геометрия применяется только к одной цепи.

Собственная энергия магнитной системы

Сила, создаваемая против ЭДС в индуктивности собственной цепи, зависит от электродвижущей силы, вызванной самоиндукцией, если ток течет в ней, и от того, что ее работа выполняется против электромагнитной силы ЭДС в единицу времени, равна:

(11)

Используя определение электродвижущей силы, обусловленной собственной индуктивностью (10), которая вытекает из закона индуктивности Фарадея, мы спрашиваем себя, что работа выполнялась системой, когда ток в системе с индуктивностью L от I равен нулю до некоторой ненулевой величины, поэтому мы приходим к выводу:

(12)

Работа, выполненная против ЭДС в системе индуктивности L, после переписывания окончательного применения (12), выражается:

(13)

Это не зависит от того, как долго протекает ток, а зависит только от геометрии системы и тока, протекающего в нашей цепи, которая взаимодействует сама с собой в результате действия магнитного поля.

Катушка индуктивности

Далее мы поговорим о катушке индуктивности и способе измерения индуктивности.

Определение и теория катушек индуктивности

Катушка индуктивности — катушка из свёрнутого изолированного проводника, обладающая значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении, способная накапливать электромагнитную энергию в собственном магнитном поле. Обозначается – L. Внешний вид может быть различным, но если вы её мотаете самостоятельно, то будет выглядеть как-то так:

Величина индуктивности измеряется в Генри [Гн].

1 Генри – очень большая величина, поэтому применяемые в технике катушки индуктивности имеют величины: микрогенри – 10^-6 (мкГн) и миллигенри – 10^-3 (мГн).

Процессы, происходящие в катушке индуктивности (далее — индуктивности) на временном графике при подключении индуктивности к источнику прямоугольного однополярного сигнала, показаны на рисунке.

Из рисунка сбоку видно, реакция индуктивности на воздействие электрического тока абсолютно противоположно реакции конденсатора (ёмкости). В момент подачи прямоугольного импульса источника тока (красный), ток индуктивности (фиолетовый) сначала равен нулю и с изменением времени увеличивается по экспоненте – индуктивность накапливает энергию, в начальный момент её внутреннее сопротивление максимально. Напряжение на выводах индуктивности (зелёный) наоборот сначала максимально, но потом по мере накопления энергии уменьшается по экспоненте до нуля. При пропадании входного импульса, так как индуктивность — элемент инерционный, напряжение на выводах индуктивности резко изменив полярность сначала максимально, а ток продолжает течь в том же направлении, уменьшаясь при этом по экспоненте – запасённая в индуктивности энергия иссякает. Напряжение из отрицательной области так же по экспоненте стремится к нулю. Скорость изменения напряжения и тока зависит от значения индуктивности. Чем больше индуктивность, тем медленнее они изменяются (экспонента более вытянута по времени). Напряжение и ток на нагрузочном резисторе ведут себя одинаково, и изображены на временном графике оранжевым цветом. Если сравнить с конденсатором — полная противоположность. Взаимосвязь тока и напряжения в индуктивности так же описывается законом Ома, с учётом реактивного сопротивления индуктивности.

Фактически, мы рассмотрели «четырёхполюсник» состоящий из катушки индуктивности и резистора, который называют интегрирующей цепочкой.

Интегрирующая цепочка чаще всего применяется для формирования пилообразных импульсов в любой радио аппаратуре и временной (ударение на «о») задержки прямоугольных импульсов. Чтобы, Вам было понятнее, интегрирующая цепочка и получение пилообразного импульса изображены на следующем рисунке. Для получения последнего, используется наиболее прямолинейный участок интегрированного импульса — его начало, и «обрезается» по времени или по амплитуде (порогу).

Для задержки импульсов используют пороговое устройство. По достижении амплитуды сигнала прошедшего через интегрирующую цепочку определённого значения (порога), пороговое устройство пропускает входной сигнал на выход. После чего, сигнал усиливается усилителем до необходимой величины. В целях уменьшения размеров (исключения громоздкости), схемы формирования пилообразных импульсов, и схемы задержки импульсов эффективнее делать на интегрирующей цепочке состоящей из резистора и конденсатора.

Кроме функции преобразования прямоугольных импульсов, интегрирующая цепочка может применяться в качестве фильтра низких частот (ФНЧ). Индуктивность – инертный элемент. Если к дросселю с большим значением индуктивности приложить переменное напряжение высокой частоты, в силу своей инертности, индуктивность будет не способной пропустить через себя ток, ведь индуктивности сначала надо будет запастись энергией в собственном сердечнике, а потом отдавать эту энергию. Свойство индуктивности сопротивляться переменному электрическому току называют реактивным сопротивлением индуктивности, которое используется при конструировании частотных фильтров и колебательных контуров. Реактивное сопротивление индуктивности обозначается X_L или Z_L и измеряется в Омах. Реактивное сопротивление индуктивности связано с частотой тока выражением:

Из формулы видно, что реактивное сопротивление индуктивности прямо пропорционально частоте. Другими словами, чем выше частота, тем больше реактивное сопротивление индуктивности.

Теперь представьте, что интегрирующая цепь, это – описанный на сайте делитель напряжения, где вместо первого резистора выступает индуктивность. А мы из формулы теперь знаем, что индуктивность легко пропускает низкие частоты – его сопротивление минимально и плохо пропускает высокие частоты – его сопротивление максимально. Не изменяя текста повторюсь: В радиоэлектронике, когда рассчитывают частотные фильтры, то считают характеристикой фильтра – частоту среза, которая определяется как значение частоты сигнала, на котором амплитуда выходного сигнала уменьшается (затухает) до значения 0,7 от входного сигнала. Чтобы было понятнее, изображу это на рисунке.

То, что изображено, называется амплитудно-частотной характеристикой, или сокращённо — АЧХ. Для фильтра высоких частот соответствует АЧХ фиолетового цвета, и частота среза равная значению f₂.

Зная, как рассчитывается делитель напряжения и реактивное сопротивление индуктивности на определённой частоте, Вы элементарно можете рассчитать простейший г-образный фильтр низкой частоты на катушке индуктивности и резисторе.

Если в интегрирующей цепочке поменять местами индуктивность и резистор, то мы получим – дифференцирующую цепочку. Все процессы в дифференцирующей цепочке происходят точно так же, как и в интегрирующей. Временные графики, показанные на первом рисунке абсолютно справедливы для дифференцирующей цепочки. Отличие заключается в том, что выходным элементом является не резистор, а катушка индуктивности.

Как описывалось в статье про конденсатор: если дифференцирующая цепочка – это фильтр высоких частот, то интегрирующая цепочка – это фильтр низких частот (ФНЧ). И рассчитывается он так же, через делитель напряжения. Для фильтра низких частот соответствует АЧХ на рисунке — оранжевого цвета, и частота среза равная значению f₁.

Cледует добавить, частотные фильтры, выполненные на катушках индуктивности и резисторах, так же, как и на конденсаторах и резисторах имеют пологую амплитудно-частотную характеристику. Другими словами у таких фильтров слабо выражен частотный срез. Более качественный срез, имеют фильтры состоящие из конденсаторов и катушек индуктивности, но об этом в следующей статье.

Способ измерения индуктивности

Наверняка прочитав данную статью, грамотный читатель подумает: «Хм, теория это конечно хорошо, но как измерить руками значение индуктивности на практике?». Однажды этим вопросом задался и я, и собрал простую схему для проверки индуктивностей.

Расчет цепей при наличии взаимной индуктивности

Рассмотрение данного вопроса начнём с простейших способов соединения двух индуктивно связанных катушек: параллельного и последовательного. При этом будем использовать комплексный метод расчета.

1. Последовательное согласное соединение катушек

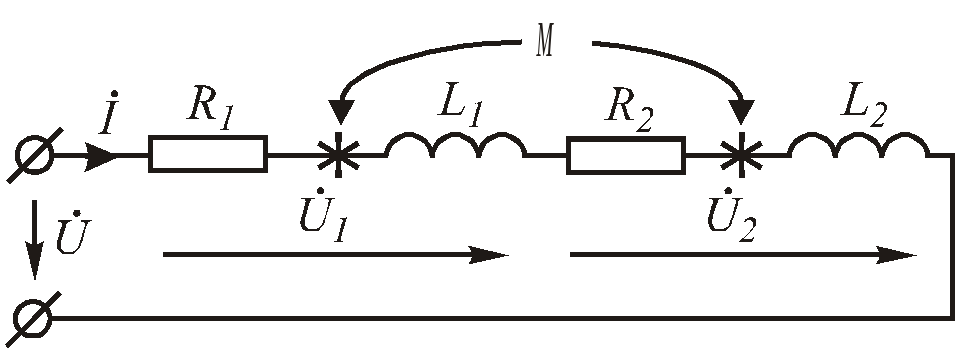
Рис.6.88. Последовательное согласное соединение двух катушек

Направление тока относительно маркированных зажимов первой и второй катушек одинаковое. Составим уравнение электрического равновесия для данного участка цепи (Рис. 6 .88) с учётом индуктивной связи по второму закону Кирхгофа:

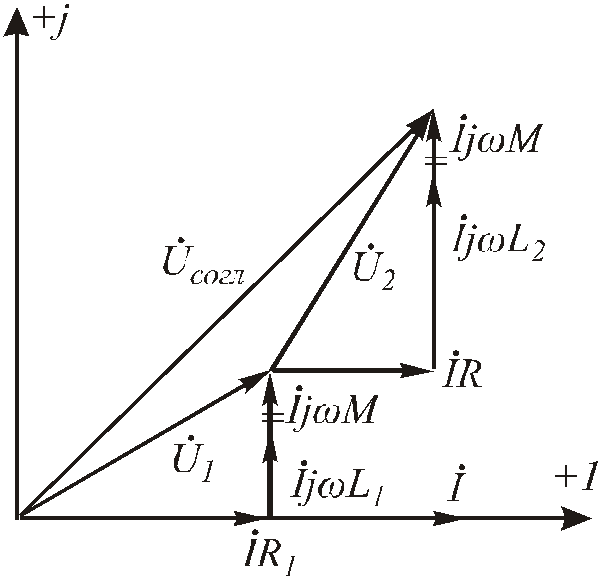
Рис.6.89.Векторная диаграмма для последовательного согласного соединения двух катушек

;

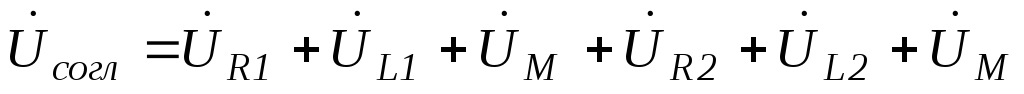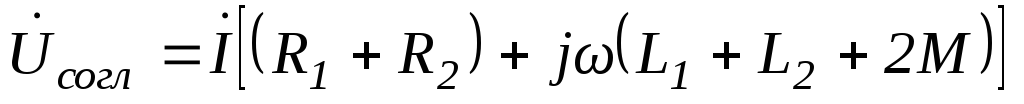.124(6.118)

Из полученного выражения следует, что при согласном соединении катушек общая индуктивность возрастает на величину 2М. В частном случае приМ = 0уравнение упрощается. Используя полученное выражение, построим векторную диаграмму для данного способа соединения (Рис. 6 .89).

Введём параметр Z_м = jωMи назовём его сопротивлением взаимной индукции.

2. Последовательное встречное соединение

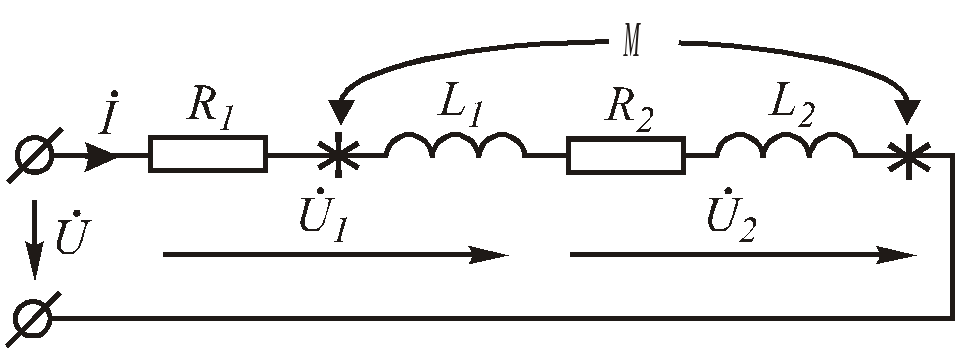
Рис.6.90. Последовательное встречное включение катушек

Используя полученные ранее соотношения, можно записать аналогичное уравнение для встречного соединения тех же катушек.

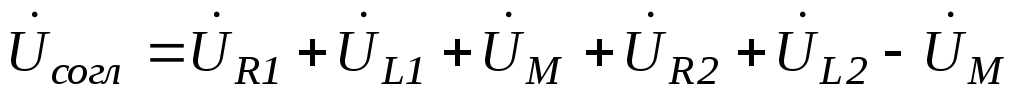
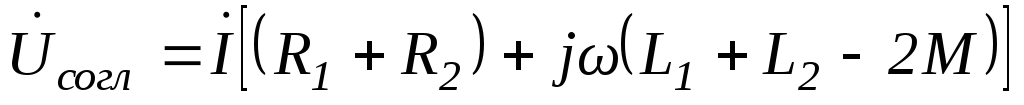125(6.119)

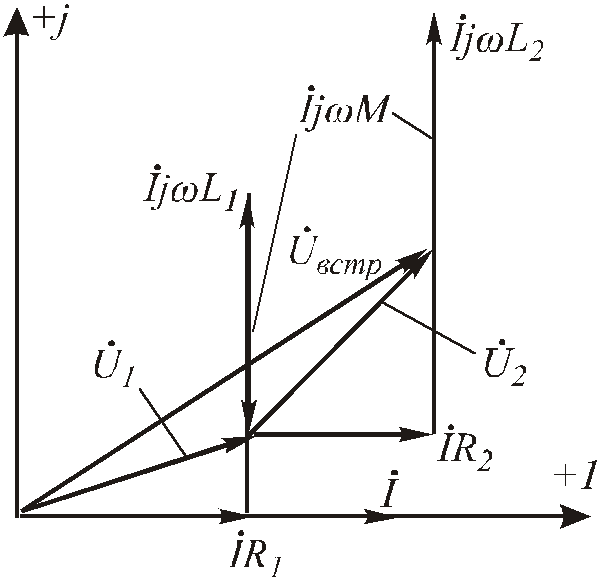
Рис.6.91. Векторная диаграмма для последовательного встречного соединения двух катушек

Для данного способа соединения общая индуктивность уменьшится на 2М.Аналогичным образом построим векторную диаграмму для встречного соединения катушек.

3. Параллельное согласное соединение

Составим систему уравнений для расчета цепи по законам Кирхгофа для схемы по рис.6.9

;

.

;

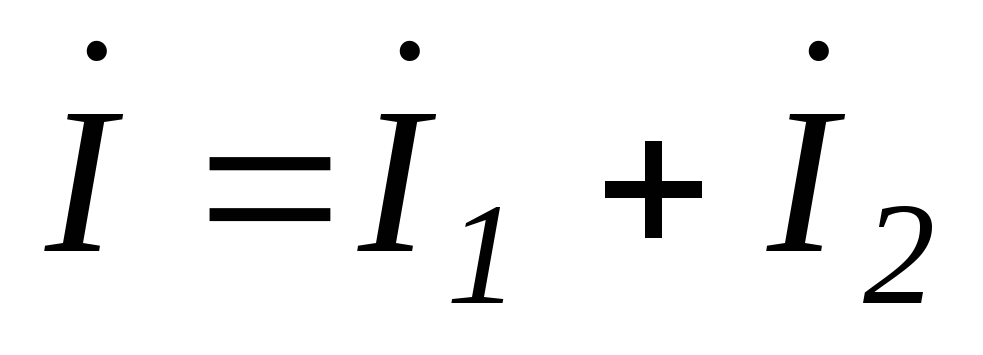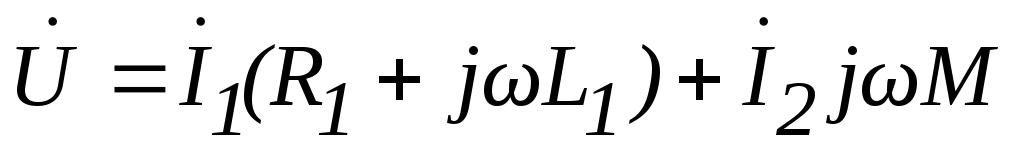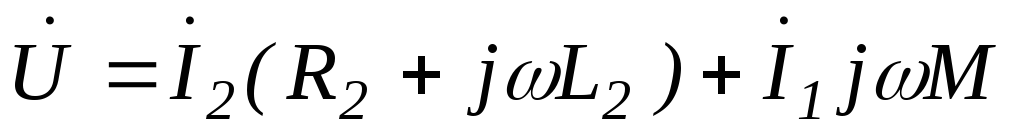Обозначим:

Z₁ = R₁ + jωL₁ ; Z₂ = R₂ + jωL₂ ; Z_m = jωM.

Решим полученную систему уравнений относительно токов.

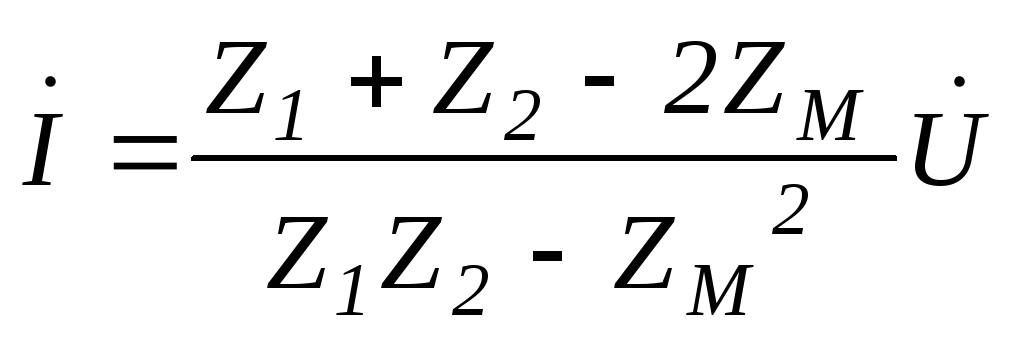;126(6.120)

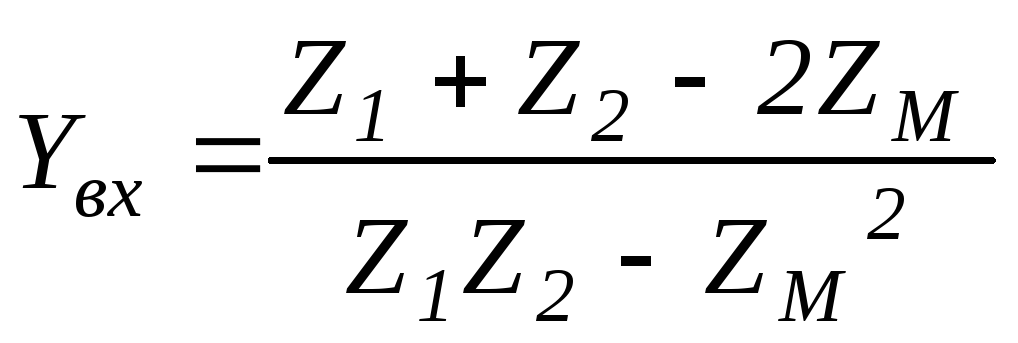;127(6.121)

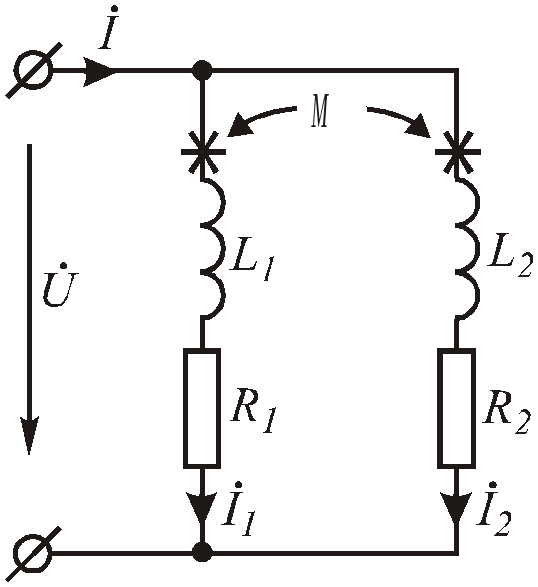
Рис.6.92. Параллельное согласное включение катушек.

В случае, когда М = 0, получим:;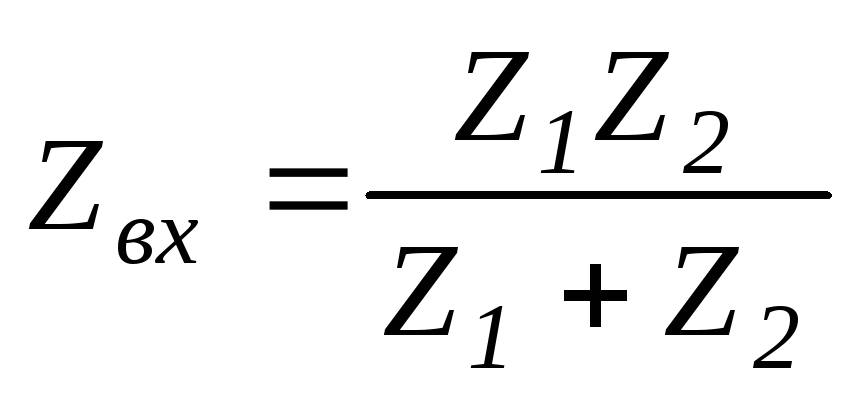

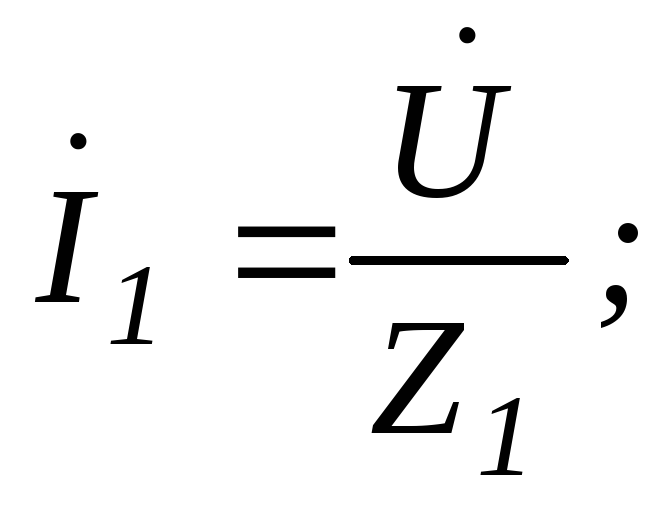
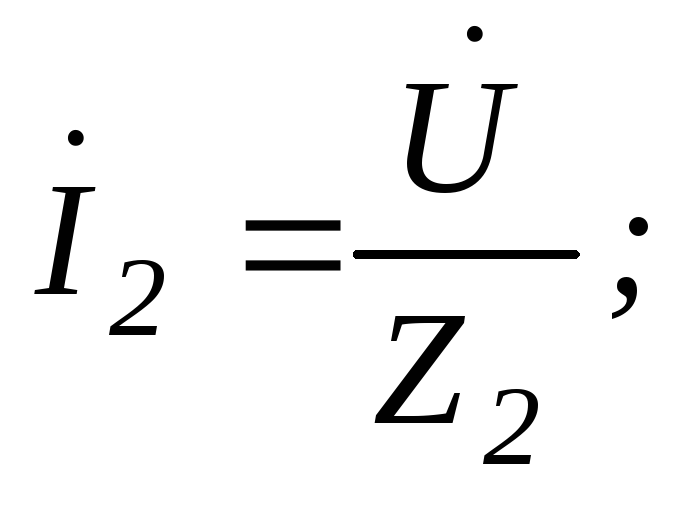
4. Параллельное встречное соединение

Для схемы, представленной на рис.6.10 уравнение электрического равновесия будет иметь вид:

;

;

;

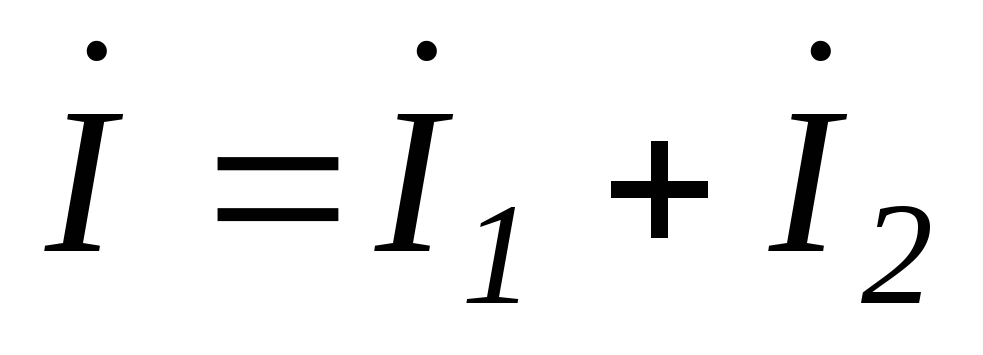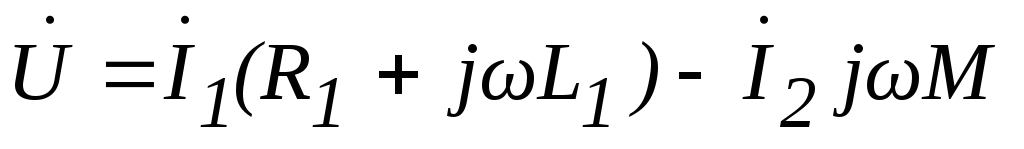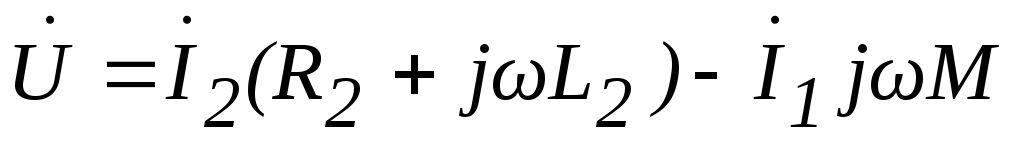Решение данной системы уравнений:

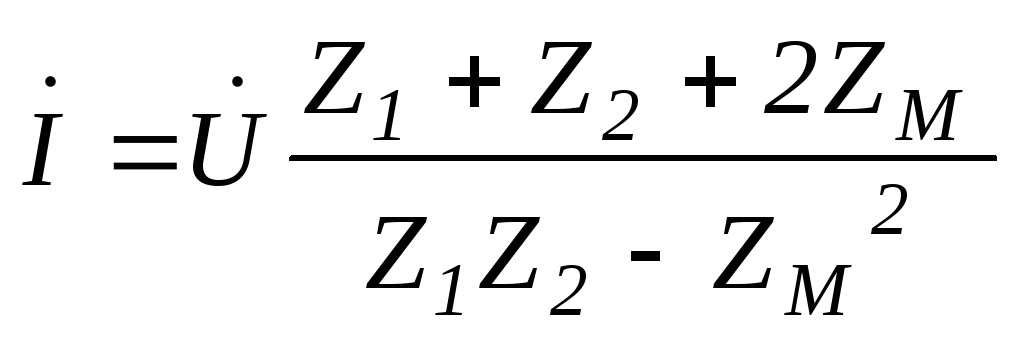(6.122)

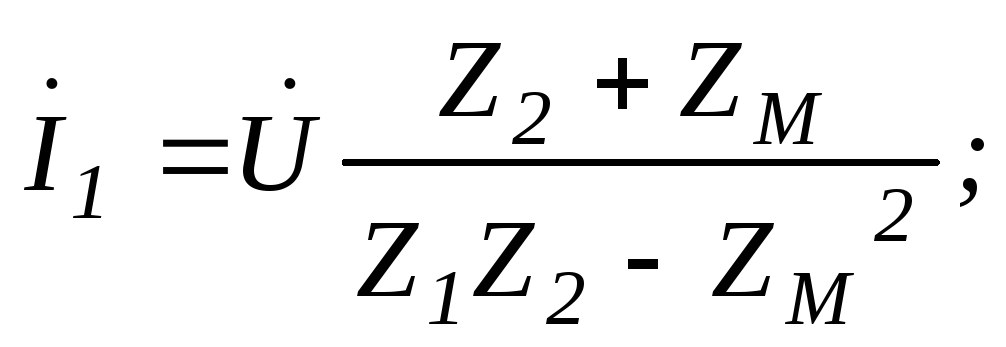
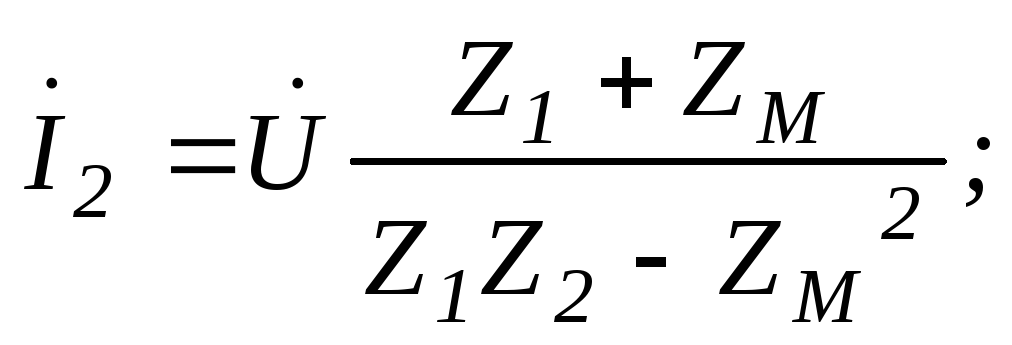
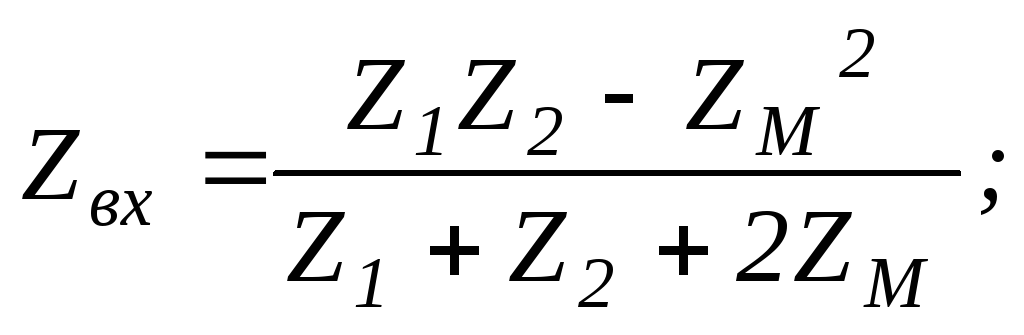
Соответствующие векторные диаграммы строятся аналогично случая последовательного соединения данных катушек.

5. Расчет разветвлённых цепей при наличии взаимной индуктивности

Расчёт разветвлённых цепей при наличии взаимной индуктивности представляется более сложным этапом. Он осуществляется с помощью законов Кирхгофа либо методов контурных токов. Отметим, что метод узловых потенциалов в данном случае не применим, поскольку токи в ветвях определяются не только разностью потенциалов соседних узлов, но и токами других ветвей, с которыми они связаны индуктивно. Пусть имеются три индуктивно связанные катушки, намотанные на общий сердечник, выполненный из немагнитного материала и подключённые к двум источникам ЭДС. Получим электрическую схему вида (Рис. 6 .93).

Выберем в качестве расчётного метод контурных токов и составим систему уравнений относительно заданных на схеме контурных токов.

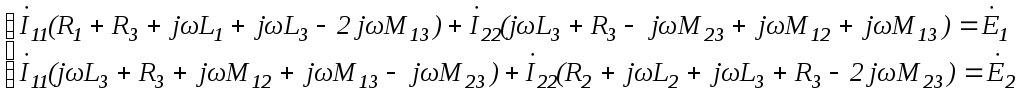Решив систему, получим:;;.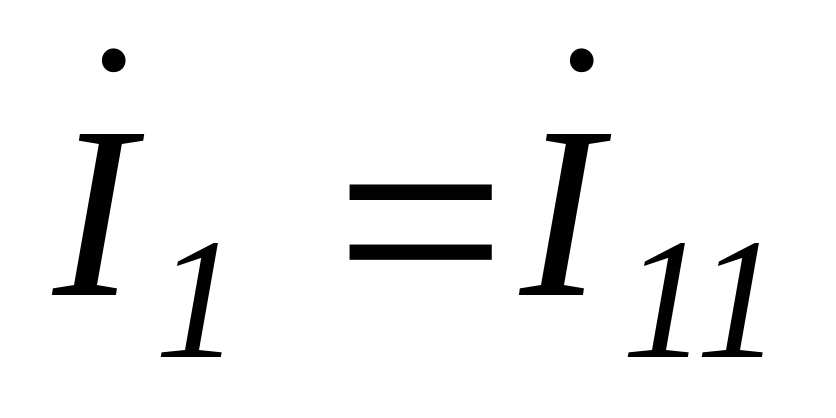

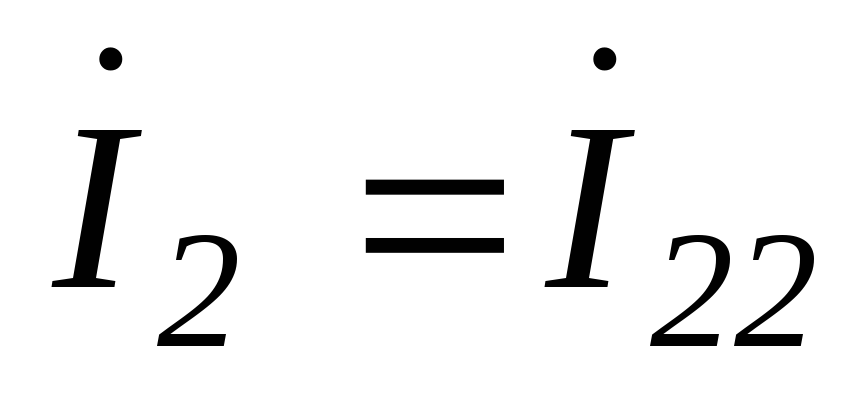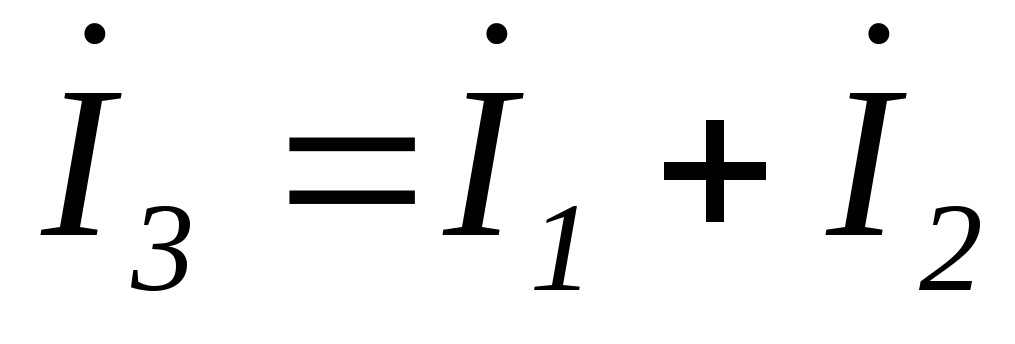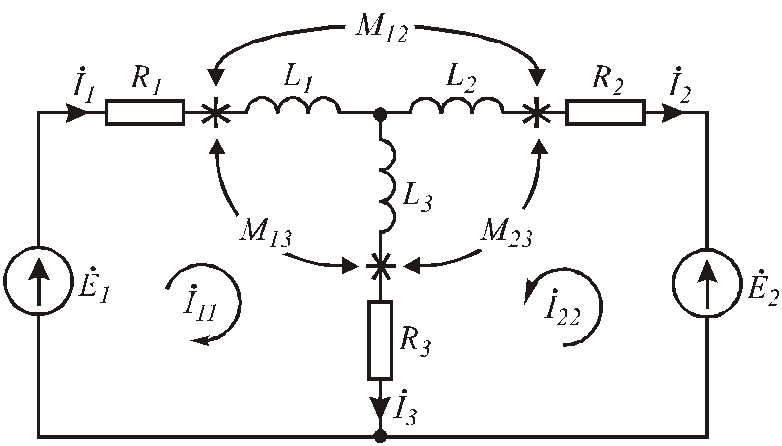
Рис.6.93. Электрическая схема с индуктивно связанными катушками

6. «Развязывание» магнитосвязанных цепей

Отличительной особенностью расчёта цепей со взаимной индуктивностью является то, что приходится одновременно учитывать электрические и магнитные связи. Расчёт цепей упростится, если теми или иными методами исключить магнитную связь и свести данную цепь к чисто электрической. Это возможно, если прибегнуть к развязыванию магнитных связей, при этом в составе цепи появятся новые дополнительные элементы.

В схеме Рис. 6 .94 катушки L₁ иL₂индуктивно связаны. Рассмотрим два варианта их соединения. В узлеС они могут соединяться как одноименными, так и разноименными зажимами.

1) Пусть в узле С катушки соединены разноимёнными зажимами. Составим уравнения по законам Кирхгофа с учётом индуктивной связи.

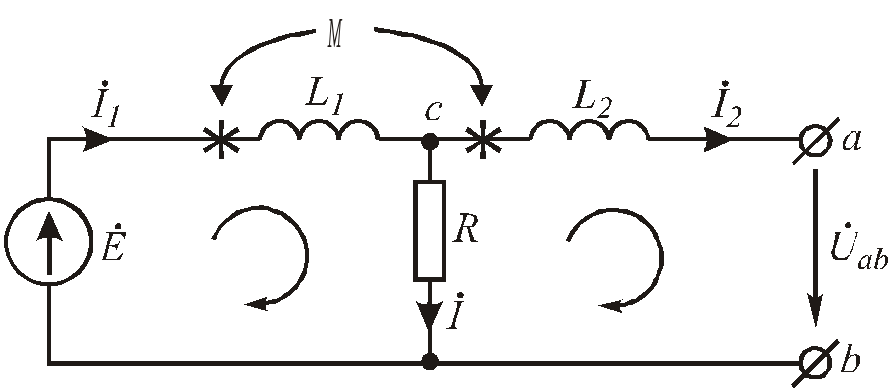
Рис.6.94. Исходная цепь

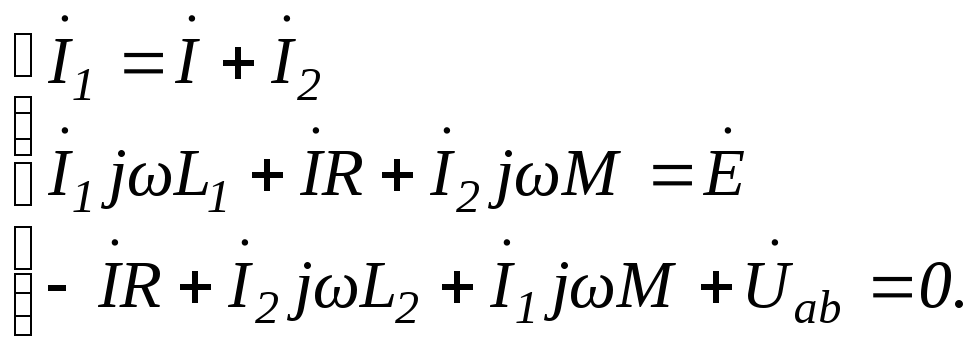
Преобразуем систему уравнений к следующему виду:

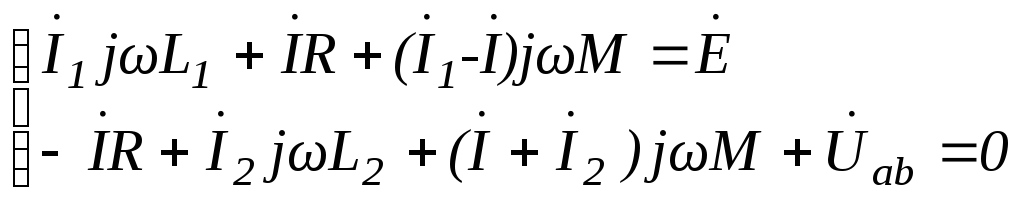
или

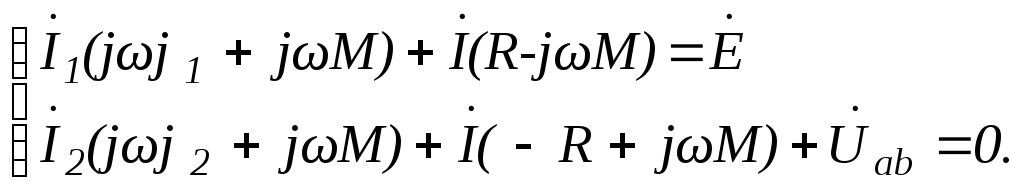
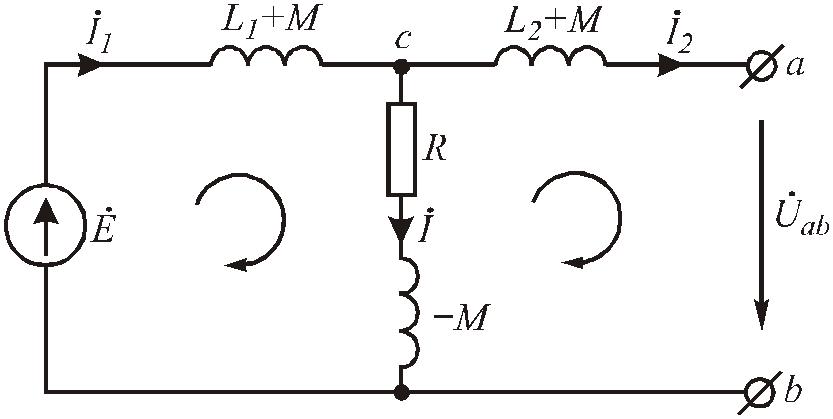
Рис.6.95. Схема после «развязывания» магнитных связей при соединении катушек в узле разноименными зажимами

2) Если в узле Скатушки соединены одноимёнными зажимами, аналогичные рассуждения позволили бы получить следующую схему:

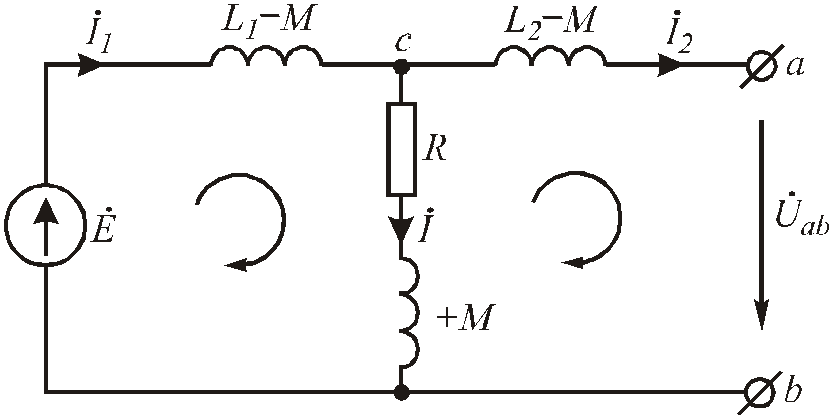
Рис.6.96. Схема после «развязывания» магнитных связей при соединении катушек в узле одноименными зажимами

Для обоих случаев определим выражения 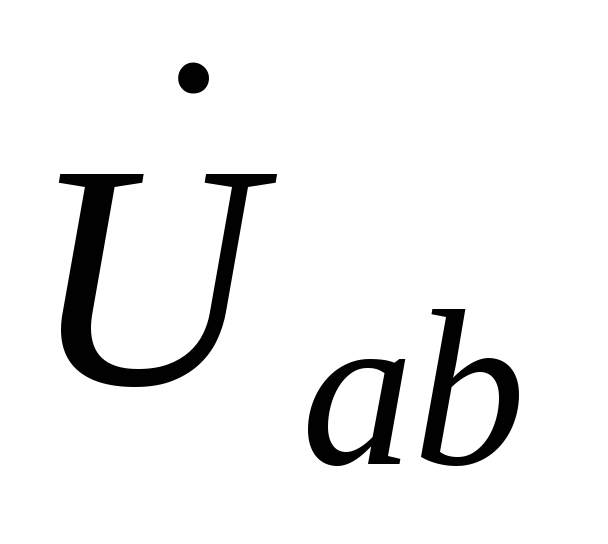при условии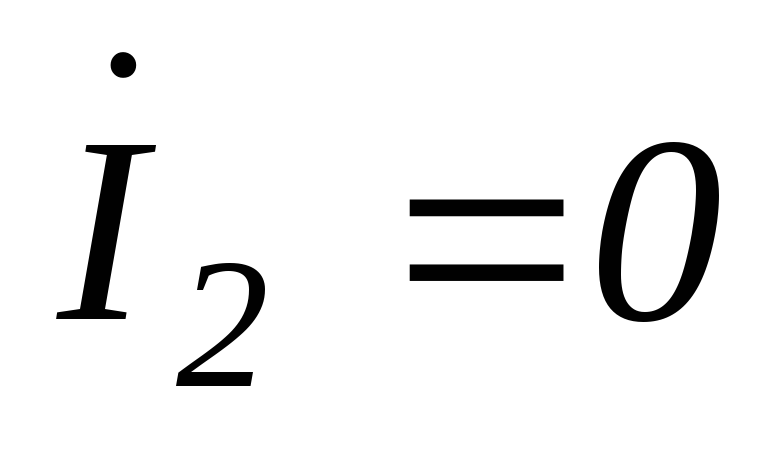, получим:, _.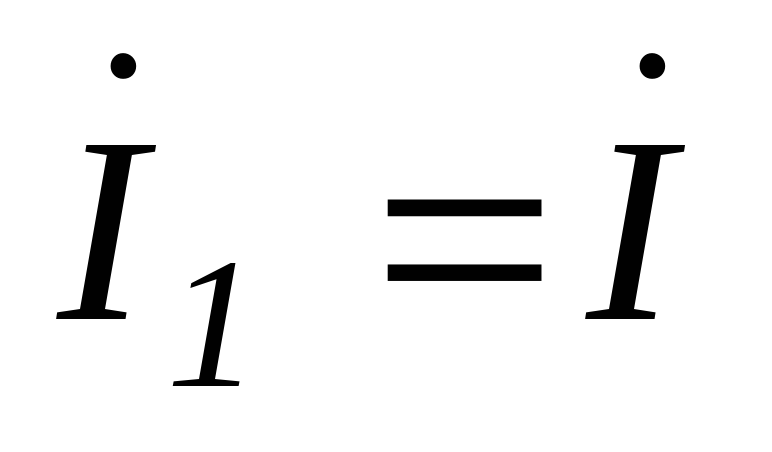

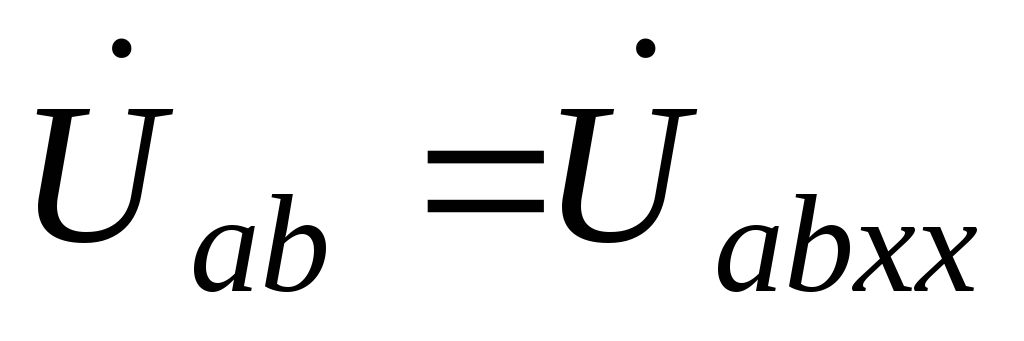Для разноимённого соединения:

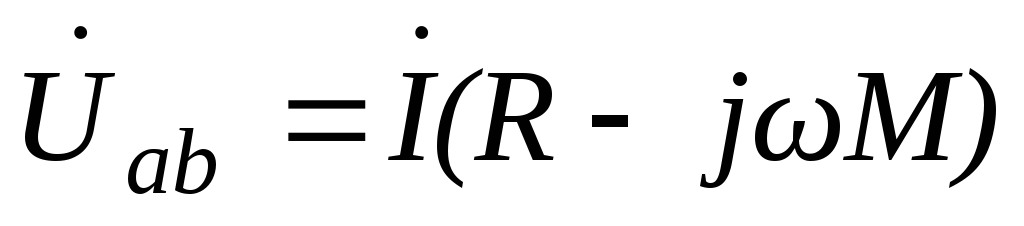. (6.123)

Для одноимённого соединения:

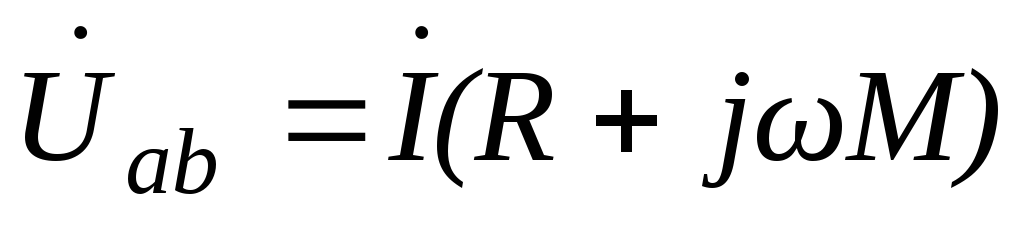. (6.124)

Оставаясь неизменным по модулю в обоих случаях, в первом случае напряжение отстаёт на определённый угол, а во втором варианте опережает ток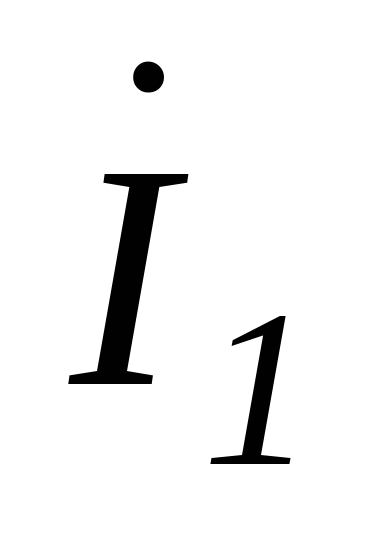. При этом ток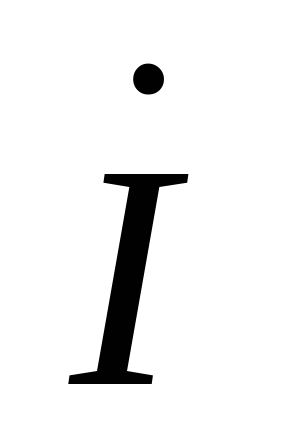 не зависит от способа соединения катушек:

;

Появление параметра Мв процессе процедуры развязывания говорит о том, что в состав цепи искусственно вводится некоторая дополнительная индуктивностьМ.Для Рис. 6 .95 введенный элемент с сопротивлением ( jωM)имеет емкостной характер, для рис.6.13 – индуктивный ( jωM).