1. Вывод формул для моментов инерции простейших фигур (прямоугольник, треугольник, круг)

Прямоугольное сечение.

Прямоугольное сечение имеет две оси симметрии, а главные центральные оси Сx и Cy проходят через середины параллельных сторон.

Главный центральный момент инерции относительно оси x

Элементарную площадку dA в этом случае можно представить в виде полоски во всю ширину сечения и толщиной dy, значит dA=b*dy. Подставим под знак интеграла значение dA и проинтегрировав по всей площади, т.е. в пределах изменения ординаты y от –h/2 до +h/2, получим

Окончательно

Аналогично получим формулу главного центрального момента инерции прямоугольника относительно оси y:

Круглое сечение

Для круга главные центральные моменты инерции относительно осей x и y равны между собой.

Поэтому из равенства

Треугольник

2.

Изменение моментов инерции при переходе от центральных осей к параллельным:

J_x1=J_x + a²А;

J_y1=J_y + b²А;

момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями. J_y1x1=J_yx + abF; («a» и «b» подставляют в формулу с учетом их знака).

3.Изменение моментов инерции при повороте осей

J_x1=J_xcos² + J_ysin² — J_xysin2; J_y1=J_ycos² + J_xsin² + J_xysin2;

J

x1y1=(J_x — J_y)sin2 + J_xycos2 ;

Угол >0, если переход от старой системы координат к новой происходит против час. стр. J_y1 + J_x1= J_y + J_x

Экстремальные (максимальное и минимальное) значения моментов инерции называются главными моментами инерции. Оси, относительно которых осевые моменты инерции имеют экстремальные значения, называются главными осями инерции. Главные оси инерции взаимно перпендикулярны. Центробежные моменты инерции относительно главных осей = 0, т.е. главные оси инерции — оси, относительно которых центробежный момент инерции = 0. Если одна из осей совпадает или обе совпадают с осью симметрии, то они главные. Угол, определяющий положение главных осей: , если

₀>0  оси поворачиваются против час.стр. Ось максимума всегда составляет меньший угол с той из осей, относительно которой момент инерции имеет большее значение. Главные оси, проходящие через центр тяжести, называются главными центральными осями инерции. Моменты инерции относительно этих осей:

J_max + J_min= J_x + J_y.

Центробежный момент инерции относительно главных центральных осей инерции равен 0. Если известны главные моменты инерции, то формулы перехода к повернутым осям:

J_x1=J_maxcos² + J_minsin²; J_y1=J_maxcos² + J_minsin²; J_x1y1=(J_max — J_min)sin2;

4.Классификация элементов конструкций

Стержнем наз. Геом тела у которых один из размеров много больше других.

Пластины или оболочки

– это геом тела у которых один из размеров << других

Массивные тела— все размеры одного порядка

5.Основные допущения о свойствах материала

Однородные – в люб. точке материалы имеют одинак. физико-химич. св-ва;

Сплошная среда – кристаллич. строение и микроскопич. дефекты не учитываются;

Изотропны – механич. св-ва не зависят от направления нагружения;

Идеальная упругость – полностью восстанавливают форму и размеры после снятия нагрузки.

6.Типы опор

а) Шарнирно – неподвижная (двухсвязная) опора: Воспринимает как вертикальные, так и горизонтальные усилия (усилия под углом).

б) Шарнирно – подвижная опора – воспринимает только вертикальные нагрузки. Реакция опоры всегда направлена вдоль опорного стержня, перпендикулярно опорной поверхности

в) Жесткая заделка (трехсвязная)

Реакции в опорах определяют из условия равновесия (уравнение статики).

7.Классификация нагрузок

1. По месту действия

Поверхностные и объемные

а) сосредоточенная сила

б) распределенная сила

прямоугольная Rq= qa

треугольная Rq= ½ qa

в) сосредоточенный момент

изгибающий

скручивающий

г) распределенный момент

Rmz= mz a –равнодейств распр мом

2. По времени действия

Постоянные и временные

3. По характеру действия

Статические и динамические

4. По характеру возникновения

Активная(известны) и реактивная (неизвестны)

8. Основные принципы изучаемого курса

При расчете сложного сопротивления используется принцип независимости действия сил. Сложный вид нагружения представляется как система простых видов нагружения действующих независимо друг от друга. Решение при сложном сопротивлении получается в результате сложения решений полученных при простых видах нагружения.

принцип Сен-Венана

на достаточном удалении от места приложения нагрузки характер её воздействия не зависит от способа её приложения, а зависит от величины равнодействующей.

9.Внутренние усилия. Метод сечений (Метод РОЗУ)

Nz=∑z (pi) нормальная с

Qx=∑x (pi) поперечная с

Qy=∑y (pi)

Mz=∑mz (pi) крутящий момент

Mx=∑mx (pi) изгибающий

My=∑my (pi)

Разрезаем мысл тело плоск

Отбрасываем одну из г внутр усил

Заменяем внутр усилиями

Уравновешив внутр ус внеш нагр

10.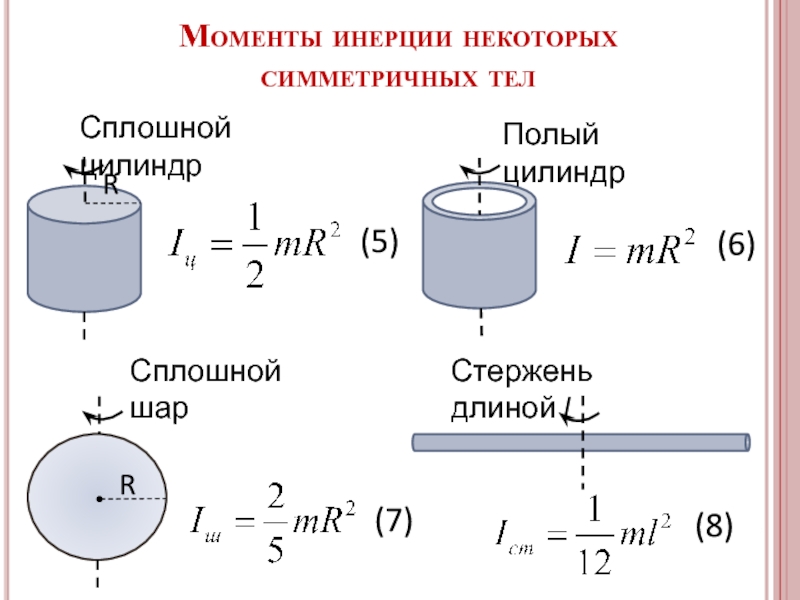 Правило знаков внутренних усилий

Правило знаков поперечных сил при изгибе:

Крутящий момент

Против ЧС при взгляде со стороны сеч то +

Правило знаков изгибающих моментов:

Правило проверки правильности построения эпюр нагружения:

В сечениях балки, где приложены внешние сосредоточенные нагрузки на эпюре д.б. скачёк на величину этой нагрузки.

11.Эпюры внутренних усилий

ПРИ РАСТЯЖЕНИИ-СЖАТИИ

ПРИ КРУЧЕНИИ

при прямом изгибе

12.Дифференциальные зависимости при изгибе

; ;

13.Следствия из дифференциальных зависимостей

1. Если на участке нет распр нагр (q=0) то поперечная сила на этом участке имеет пост вел. , а эпюры изгиб мом меняются по лин закону

2. На уч на котором присутст распр нагр пост интенсивн. Поперечная сила меняется по лин зак , а эпюры по закону квадр параболы. Причем эпюра мх всегда напр навстречу распр нагрузке. Где Qy равно 0 эпюра мх имеет экстремум. Если Qy равно 0 на всем участке, то мх постоян величину

4. На участке где Qy>0 эпюра мх возрастает слева направо

5. В том сеч. где приложена сосред сила эпюра Qy имеет скачок на вел этой силы. В сеч где сосред момент эпюра мх имеет скачок на величену этого момента

Вывод формулы момента инерции кольца : Чулан (Ф)

Сообщения без ответов | Активные темы | Избранное

Правила форума

В этом разделе нельзя создавать новые темы.

Nikolay_90	Вывод формулы момента инерции кольца 17. 12.2007, 23:52
17/12/07 1	Помогите пожалуйста вывести формулу где — момент инерции кольца, — его масса — внешний диамер, а — внутренний (вокруг оси, проход. через диаметр, а также ч-з центр.) Зарание огромное спасибо!

photon	18. 12.2007, 00:33
Экс-модератор 23/12/05 11949	!  photon: Используйте тег math (: введение, справка). После внесения исправлений сообщите одному из модераторов, чтобы тема была возвращена  !  photon: Возвращено

Eiktyrnir	Вывод формулы момента инерции кольца (рискну предположить) 18. 12.2007, 20:53
30/11/07 384	Nikolay_90 писал(а): Помогите пожалуйста вывести формулу где — момент инерции кольца, — его масса — внешний диамер, а — внутренний (вокруг оси, проход. через диаметр, а также ч-з центр.) Зарание огромное спасибо! Кольцо — плоское значит?(!) Тогда имеем плоское распределение масс. Во-первых (определение момента инерции тела): — относительно его центра масс Во-вторых (решение): Берем кольцо и из середины (или не из середины — неважно) кольца вырезаем элементарный его кусочек (представили себе). Теперь запишем элементарный момент инерции этого кусочка — Успешно интегрируем и получаем и поскольку и аналогично , а еще и то и получается восьмерочка, т.е. как на формуле В третьих (на будущее): Помни о том как вычислять момент инерции относительно произвольной оси (пригодится). Момент инерции тела относительно произвольной оси (по теореме Штейнера) равен сумме момента инерции этого тела относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела на квадрат расстояния между осями:

peregoudov	18. 12.2007, 23:35
10/03/07 ∞ 473 Москва	Никак не могу согласиться с предыдущим оратором. Вот правильное решение. Упростим немного обозначения. Пусть и — внешний в внутренний радиусы кольца, и — массы дисков из того же материала, что кольцо, радиусами и . Известно, что моменты инерции таких дисков относительно осей, перпендикулярных дискам и проходящих через их центры масс, равны и . (Если это необходимо пояснить, переспросите.) Представим теперь большой диск как наше кольцо и малый диск внутри кольца. Воспользовавшись аддитивностью массы и момента инерции, можно записать Кроме того, массы дисков, очевидно, пропорциональны квадратам их радиусов Из трех последних уравнений исключаем и и выражаем Задачу можно решить и впрямую с помощью интегрирования, только совсем не так, как предлагает Eiktyrnir.

Eiktyrnir	19.12.2007, 09:08
30/11/07 384	peregoudov писал(а): Задачу можно решить и впрямую с помощью интегрирования, только совсем не так, как предлагает Eiktyrnir. Просветите теперь и меня пожалуйста. Вы так уверенно говорите, что уже засомневался в правильности своего решения. Будьте так любезны — укажите мне на ошибку. Спасибо.

Zai	19.12.2007, 10:15
Заслуженный участник 11/04/07 1352 Москва	Ошибки нет. Прямое интегрирование в полярных координатах:

Eiktyrnir	19.12.2007, 11:52
30/11/07 384	Zai писал(а): Ошибки нет. Прямое интегрирование в полярных координатах: Ну спасибо — реабилитировали. Так это неважно — в полярных или декартовых (дело выбора системы координат) — ответ должен быть один и тот же. А почему автор сообщения о том, что я не прав — молчит? Мои сомнения ушли после вашего (Zai) сообщения. Спасибо вам.

peregoudov	19.12.2007, 18:12
10/03/07 ∞ 473 Москва	Zai писал(а): Ошибки нет. Eiktyrnir писал(а): Ну спасибо — реабилитировали. Странные утверждения. Если у вас, господа, есть глаза, почему вы ими не пользуетесь? Достаточно сравнить «решение» Eiktyrnir ‘а с решением Zai ‘я, чтобы увидеть, что между ними нет ничего общего. Если же утверждение Zai’я относится к тому, что у Eiktyrnir’а «получен» правильный ответ, так он в заглавном посте темы приведен. Под готовый ответ еще бы не подогнать. Zai, я считаю, Вам следует внимательно прочитать тему и поправить свое утверждение.

Zai	19. 12.2007, 19:29
Заслуженный участник 11/04/07 1352 Москва	Перегудов, Вы делаете впечатляющие успехи не только в поиске своих опечаток, он и в обнаружении существенных ошибок в методах решения. Я не посмотрел, что Вас привлекло в студенческой задаче и привел обычное решение не заметив подгонки. Надеюсь, что в моем предыдущем по этой теме сообщении нет ошибок.

Eiktyrnir	20. 12.2007, 16:22
30/11/07 384	peregoudov писал(а): Странные утверждения. Если у вас, господа, есть глаза, почему вы ими не пользуетесь? Достаточно сравнить «решение» Eiktyrnir ‘а с решением Zai ‘я, чтобы увидеть, что между ними нет ничего общего. Если же утверждение Zai’я относится к тому, что у Eiktyrnir’а «получен» правильный ответ, так он в заглавном посте темы приведен. Под готовый ответ еще бы не подогнать. Zai, я считаю, Вам следует внимательно прочитать тему и поправить свое утверждение. Уважаемый сударь будьте так любезны указать мне на ошибку в моем решении? Не соблаговалите ли вы привести именно свое решение (далее ссылка на вашу цитату): Цитата: Задачу можно решить и впрямую с помощью интегрирования, только совсем не так, как предлагает Eiktyrnir.

peregoudov	20.12.2007, 23:34
10/03/07 ∞ 473 Москва	Правильное решение привел Zai.

Eiktyrnir	21.12.2007, 08:49
30/11/07 384	peregoudov писал(а): Правильное решение привел Zai. Все понятно. Да действительно я ошибся. Свою спекуляцию признаю. Теперь все ясно. Увы потерянные годы практики…

Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию

Страница 1 из 1

[ Сообщений: 12 ]

Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения

Найти:

Вращательная динамика — Выведите формулу для момента инерции масс

спросил 2 года, 6 месяцев назад

Изменено 2 года, 6 месяцев назад

Просмотрено 2к раз

$\begingroup$

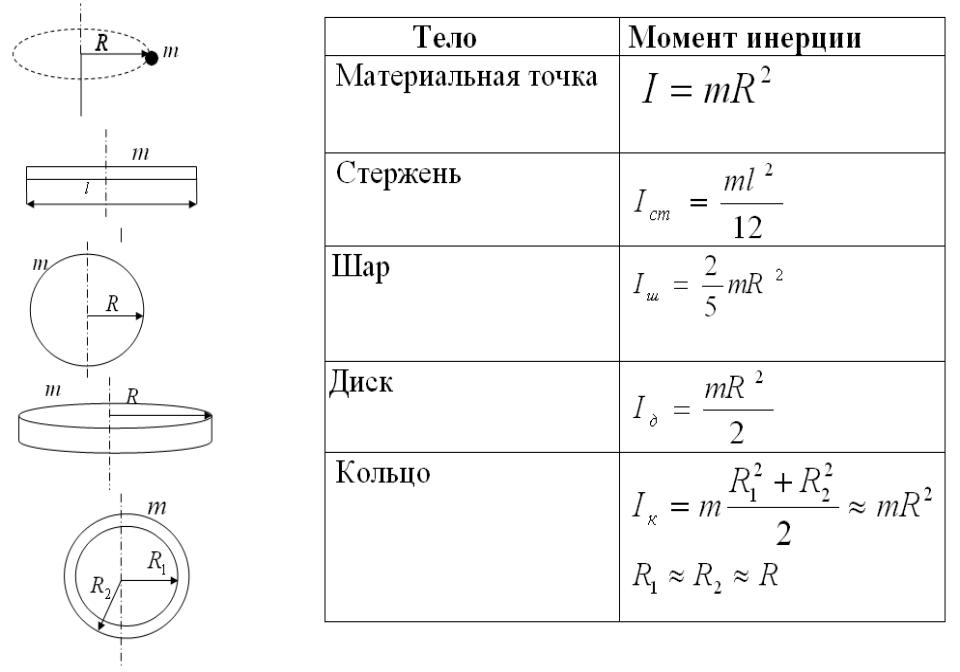
Мне всегда интересно, как на самом деле выводится формула для момента инерции. 2$, но некоторые выводят его, говоря, что момент инерции прямо пропорционален массе и квадрату расстояния, но мне нужно убийственное объяснение, почему он пропорционален квадрату расстояния от оси вращения. ?

• динамика вращения
• момент инерции

$\endgroup$

3

$\begingroup$

Массовый момент инерции определяется угловым моментом системы слипшихся частиц, вращающихся вместе. Каждая частица вносит небольшую часть углового момента, и при суммировании вращательное движение можно исключить из выражения, оставив между ними момент инерции массы. 92 } _ {\ rm mmoi} \; \омега = I \,\омега$$

Полное развитие этой идеи в 3D дано в этом ответе. Также прочитайте этот аналогичный ответ здесь.

$\endgroup$

$\begingroup$

Рассмотрим небольшую массу m, прикрепленную к концу тонкого безмассового стержня длиной r. 2\omega$$

Обратите внимание, что здесь речь идет о моменте количества движения относительно оси , в общем случае, когда мы берем его относительно точки, импульс инерции оказывается тензором 3-го ранга. Подробнее об этом здесь.

$\endgroup$

4

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

вращательная динамика — Почему момент инерции является интегралом «второго момента»? Каков вывод формулы?

Краткий ответ

Момент инерции равен, по определению , интегралу «секундного момента» относительно оси всех элементов массы $dm$, составляющих тело. В более общем смысле определение тензора инерции $\mathbf J$, принимая за точку вращения центр масс, равно

$$\mathbf J \equiv \int_{\mathcal R} \left(\left(\mathbf \pi \cdot \mathbf \ pi\right)\mathbf I — \mathbf \pi \otimes \mathbf \pi \right) \rho dv$$

где $\mathbf \pi = \mathbf x — \mathbf{\bar x}$ — позиция вектор элемента массы $\rho dv$ относительно центра масс, $\rho$ — плотность массы тела в точке $\mathbf x$, $dv$ — объем, занимаемый элементом массы, $\ mathbf I$ — единичный тензор, а $\mathbf \pi \otimes \mathbf \pi$ называется внешнее произведение $\mathbf \pi$ и $\mathbf \pi$.

Мы определяем момент инерции и тензор инерции таким образом, потому что их определения появляются в выражениях для углового момента и угловой кинетической энергии как естественное следствие обобщения ньютоновской механики — которая применима только к точечным частицам — на динамическое поведение твердых тел . В самом общем случае требуется использование тензоров вращения, но даже в более простых случаях, когда для анализа движения твердого тела достаточно только данного вами определения момента инерции, идея обобщения механики точечных частиц в твердые тела является обоснованием для этого определения.

(Чтобы получить некоторую базовую информацию о тензорах, не стесняйтесь проверить этот ответ об использовании тензоров в электромагнетизме.)

Длинный ответ

Большинство выводов для момента инерции тела массой $m $ использовать два предположения

1. Рассматриваемое тело является континуумом ; иными словами, атомной структурой тела можно пренебречь и тело можно разложить на сколь угодно много элементов сколь угодно малой массы $\rho dv$
2. Рассматриваемый кузов жесткий ; иными словами, величина вектора относительного положения $\mathbf \pi$ между двумя произвольными массовыми элементами остается постоянной при изменении конфигурации тела (например, вращении и перемещении).

Следующий вывод адаптирован и сокращен из Intermediate Dynamics for Engineers: A Unified Treatment of Newton-Euler and Lagrangian Mechanics Оливера О’Рейли. Более полное рассмотрение этого вывода, а также динамики твердого тела в целом, включая подробное обсуждение различных типов тензоров, используемых для анализа движения твердого тела, можно найти в третьей части текста.

Рассмотрим твердое тело массы $m$, занимающее область $\mathcal R$, центр масс которого, расположенный в точке $\mathbf{\bar x}$, имеет скорость $\mathbf{\bar v}$. Дополнительно рассмотрим произвольный элемент массы $\rho dv$, расположенный на теле в точке $\mathbf x$ и движущийся со скоростью $\mathbf v$. Предположение 2.) гарантирует, что элемент массы не будет испытывать поступательного движения относительно центра масс — он будет испытывать только вращательное движение относительно центра масс. Это позволяет нам выразить относительную скорость элемента массы как

$$\mathbf v — \mathbf{\bar v} = \mathbf \omega \times \left(\mathbf x — \mathbf{\bar x}\right) = \mathbf \omega \times \mathbf \pi \tag{1}$$

, где $\mathbf \omega$ — вектор угловой скорости всего тела , а не только элемента массы $\rho dv$, относительно центра масс.

Согласно ньютоновской механике, угловой момент элемента массы относительно центра масс, $d \mathbf H$, по определению равен

$$d \mathbf H = \mathbf \pi \times \rho dv \mathbf v = \mathbf \pi \times \rho dv \left(\mathbf{\bar v} + \mathbf \omega \times \mathbf \pi \right)\tag{2}$$

Интегрирование $d \mathbf H$ по всей области $\mathcal R$ дает нам полный угловой момент тела относительно центра масс, $\mathbf H$,

$$\begin{align}\mathbf H & = \int_{\mathcal R} \left(\mathbf \pi \times \left(\mathbf{\bar v} + \mathbf \omega \times \mathbf \pi \right)\right) \rho dv \ \ & = \int_{\mathcal R} \left(\mathbf \pi \times \mathbf{\bar v} + \mathbf \pi \times \left(\mathbf \omega \times \mathbf \pi \right)\right ) \ро дв \\ & = \int_{\mathcal R} \mathbf \pi \times \mathbf{\bar v} \rho dv + \int_{\mathcal R} \mathbf \pi \times \left(\mathbf \omega \times \mathbf \pi \right) \rho dv\end{align} \tag{3}$$

Рассмотрим первый член в правой части (3). Поскольку $\mathbf{\bar x}$ и $\mathbf{\bar v}$ не зависят от интегрируемой области, мы можем вынести их за пределы интеграла,

$$\begin{align} \int_{\mathcal R} \mathbf \pi \times \mathbf{\bar v} \rho dv & = \int _{\mathcal R} \mathbf \pi \rho dv \times \mathbf{\bar v} \\ & = \int_{\mathcal R} \left(\mathbf x — \mathbf{\bar x}\right) \rho dv \times \mathbf{\bar v} \\ & = \left(\int_{\mathcal R} \mathbf x \rho dv — \int_{\mathcal R} \mathbf{\bar x} \rho dv\right) \times \mathbf{\bar v} \\ & = \left(\int_{\mathcal R} \mathbf x \rho dv — \mathbf{\bar x} \int_{\mathcal R} \rho dv\right) \times \mathbf{\bar v} \\ & = \left(\int_{\mathcal R} \mathbf x \rho dv — m \mathbf{\bar x}\right) \times \mathbf{\bar v} \end{align} \tag{4}$ $

Но первый член в правой части (4) по определению центра масс равен $m \mathbf{\bar x}$, поэтому

$$\int_{\mathcal R } \mathbf \pi \times \mathbf{\bar v} \rho dv = \left(m \mathbf{\bar x} — m \mathbf{\bar x}\right) \times \mathbf{\bar v} = \mathbf 0 \times \mathbf{\bar v} = \mathbf 0 \tag{5}$$

Таким образом, из (3)

$$\begin{align}\mathbf H & = \int_{ \mathcal R} \mathbf \pi \times \left(\mathbf \omega \times \mathbf \pi \right) \rho dv \\ & = \int_{\mathcal R} \left(\left(\mathbf \pi \cdot \mathbf \pi \right) \mathbf \omega — \left(\mathbf \pi \cdot \mathbf \omega \right) \ mathbf \pi \right) \rho dv \end{align} \tag{6}$$

где мы использовали тождество векторного произведения $\mathbf a \times (\mathbf b \times \mathbf c) = (\mathbf a \cdot \mathbf c) \mathbf b — (\mathbf a \cdot \mathbf b ) \mathbf c$.