2. Векторы и операции над векторами
Вектором называется направленный отрезок в пространстве, имеющий определенную длину.
Обозначают или. Длина вектора — модуль,
обозначают ,.
Нуль-вектор — — вектор, не имеющий определенного направления, и модуль.
Вектора, расположенные на одной или параллельных прямых, называются коллинеарными.
Вектор (-) называютпротивоположным вектору , он коллинеарен векторуи направлен в противоположную сторону.
Сложение:
по правилу треугольника; по правилу параллелограмма.
++
—
—
Произведением вектора
на числоназывается вектор, модуль которого, и направление совпадает с направлением,
если,
и противоположно, если.
Вектора, лежащие на одной или параллельных плоскостях называются компланарными .
Система векторов называетсялинейно зависимой, если существуют числа λ1, λ2 , … , λnтакие, что хотя бы одно из них отлично от нуля и . В противном случае система называется
Максимальное число линейно независимых векторов в пространстве называется базисом .
Вектора — попарно перпендикулярны и, имеющие единичную длину, обозначают прямоугольный декартов базис. Всякий векторможет быть единственным образом представлен как
, где — называются координатами вектора в базисе () и представляют собой проекции векторана осиx, y, z .
аz
ax
Если
вектора заданы координатами
,,
то скалярное произведение.
Из формулы нахождения скалярного произведения можно находить косинус угла между двумя векторами
.
Векторное произведение векторов. Векторным произведением двух векторов иназывается вектор, определяемый тремя условиями :
модуль вектора численно равен площади параллелограмма , построенного на векторахи, как на сторонах;
вектор и;
вектора образуют правую тройку, т. е. если смотреть с конца векторана вектораи, то поворот от векторакпо кратчайшему расстоянию виден совершающимся против часовой стрелки.
Если вектора изаданы координатами,, то векторное произведение находится так
Пример.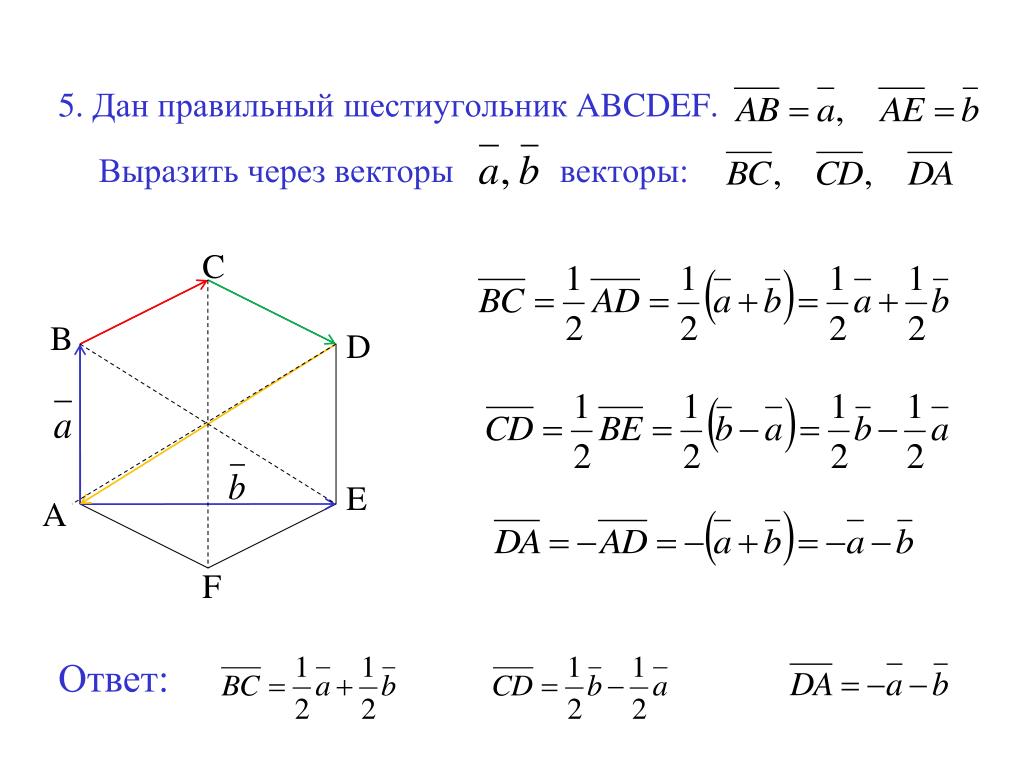
А ( 1,1,1 ), В ( 2,5,7 ), С ( 3,2,4 ) .
Решение. Рассмотрим вектора .
Найдем их векторное произведение
.
Модуль векторного произведения векторов численно равен площади параллелограмма, построенного на векторах , как на сторонах
.
Тогда площадь ΔАВС будет равна половине площади параллелограмма SΔ =.
Смешанное произведение . Смешанным произведением трех векторов называется число, равное векторно-скалярному произведению векторов. Геометрически смешанное произведение с точностью до знака численно равно объему параллелепипеда, построенного на векторах , как на ребрах.Смешанное произведение через координаты векторов выражается в виде
.
Если
три вектора
компланарны, то их смешанное произведение=0 и наоборот.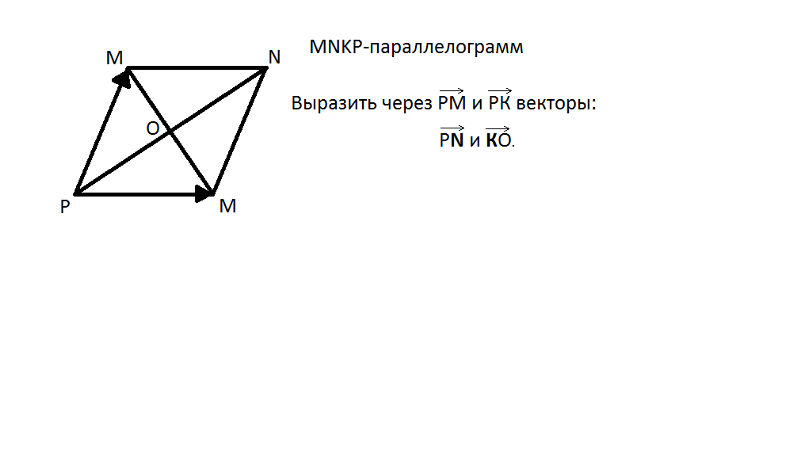
Пример. Найти объем тетраэдра с вершинами
А ( 2,-3,5 ), В ( 0,2,1 ), С ( -2,-2,3 ), D( 3,2,4 ).
Решение. Рассмотрим три вектора :
.
Найдем смешанное произведение этих векторов:
Объем тетраэдра равен объема параллелепипеда, тогда
VABCD = .
Задание 2.1.
1. Дан равносторонний треугольник АВС. Найти построением векторы .
В треугольнике ОАВ проведена медиана ОС. Доказать, что .
3. При каких значениях α и β векторы иколлинеарны ?
4.
По данным векторам
ипостроить каждый из следующих:.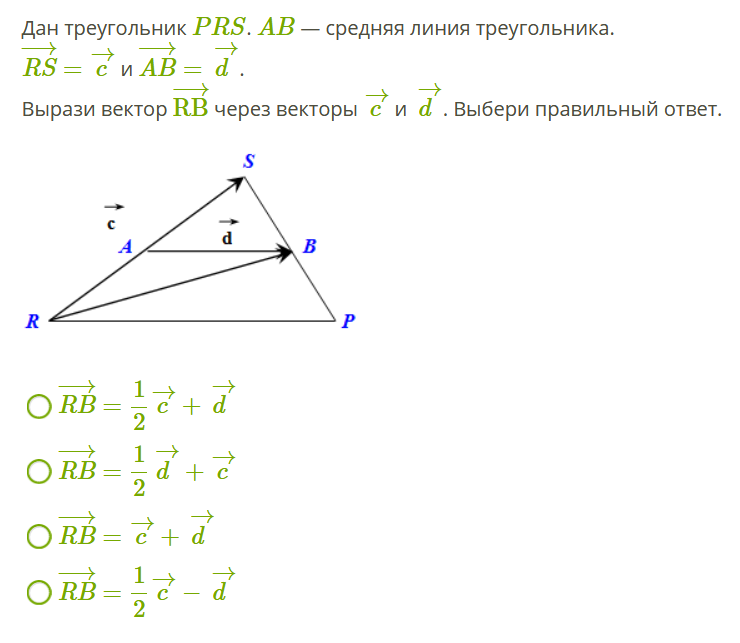
5. Заданы векторы ,,. Найти : координаты вектора; разложение векторапо базису () .
6. Дан треугольник АВС . На стороне ВС расположена точка М так, что . Найти, если.
7. В трапеции ABCD . Выразитьчерез .
8. Вне плоскости треугольника АВС взята точка О . Построить векторы .
9. ABCD — параллелограмм,
10. По сторонам ОА и ОВ прямоугольника ОАСВ отложены единичные векторы и. Выразить черезивекторы.
Выразить векторы–медианы треугольника АВС через два вектора — стороны его.
12. ABCD—
параллелограмм, О — точка пересечения его диагоналей ,
. Выразить черезвекторы.
Выразить черезвекторы.
13. ABCD — параллелограмм, . Выразить черезивекторы, где
14. ABCD — параллелограмм, О — точка пересечения его диагоналей . Выразить через векторы.
15. В треугольнике АВС сторона АВ точками М и Р разделена на три части так, что . Найти вектор, если.
16. ABCDA1B1C1D1 — параллелепипед с основанием ABCD . Выразить векторы ВD1 и DВ1 через .

18. На основании треугольникаОАВ отложен отрезок . Выразить векторчерез векторы.
19. В прямой треугольной призме АВСА1В1С1 дано: . Выразить черезвекторы, совпадающие с ребрами этой призмы.
20. Основание АВ треугольника разделено точкой М в соотношении
21. Треугольник АВС построен на векторах итак, что. Выразить черезивекторы, совпадающие с медианами данного треугольника.
22. В ромбе АВСD даны диагонали . Разложить по этим векторам все векторы , совпадающие со сторонами ромба :.
23. — медианы треугольникаАВС . Доказать равенство .
24. Заданы векторы . Найти координаты вектора.
25. Заданы векторы
. Найти координаты вектора.
Заданы векторы
. Найти координаты вектора.
26. Дан вектор . Найти вектор, если.
27. Найти длину вектора .
28. М – точка пересечения медиан треугольника АВС , О — произвольная точка пространства. Доказать равенство .
29. Даны векторы и. Проверить следующую формулу.
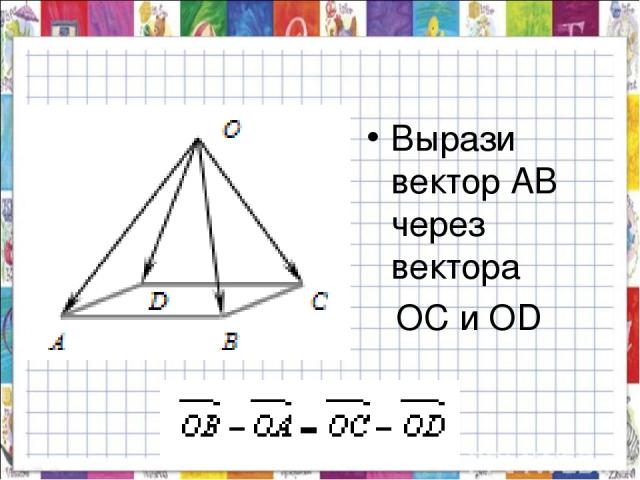
Проверить на рисунке следующие формулы : .
Задание 2.2.
Даны координаты вершин пирамиды ABCD . Требуется :
1) найти векторы и их модули ;
2) найти угол между векторами ;
3) найти площадь грани АВС ;
4) найти объем пирамиды .
А ( 2,-3,1 ) , В ( 6,1,-1 ) , С ( 4,8,-9 ) , D ( 2,-1,2 ).
А ( 5,-1,-4 ) , В ( 9,3,-6 ) , С ( 7,10,-14 ) , D ( 5,1,-3 ).

А ( 1,-4,0 ) , В ( 5,0,-2 ) , С ( 3,7,-10 ) , D ( 1,-2,1 ).
А ( -3,-6,2 ) , В ( 1,-2,0 ) , С ( -1,5,-8 ) , D ( -3,-4,3 ).
А ( -1,1,-5 ) , В ( 3,5,-7 ) , С ( 1,12,-15 ) , D ( -1,3,-4 ).
А ( -4,2,-1 ) , В ( 0,6,-3 ) , С ( -2,13,-11 ) , D ( -4,4,0 ).
А ( 0,4,3 ) , В ( 4,8,1 ) , С ( 2,15,-7 ) , D ( 0,6,4 ).
А ( -2,0,-2 ) , В ( 2,4,-4 ) , С ( 0,11,-12 ) , D ( -2,2,-1 ).
А ( 3,3,-3 ) , В ( 7,7,-5 ) , С ( 5,14,-13 ) , D ( 3,5,-2 ).
А ( 4,-2,5 ) , В ( 8,2,3 ) , С ( 6,9,-5 ) , D ( 4,0,6 ).
А ( -5,0,1 ) , В ( -4,-2,3 ) , С ( 6,2,11 ) , D ( 3,4,9 ).

А ( 1,-4,0 ) , В ( 2,-6,2 ) , С ( 12,-2,10 ) , D ( 9,0,8 ).
А ( -1,-2,-8 ) , В ( 0,-4,-6 ) , С ( 10,0,2 ) , D ( 7,2,0 ).
А ( 0,2,-10 ) , В ( 1,0,-8 ) , С ( 11,4,0 ) , D ( 8,6,-2 ).
А ( 3,1,-2 ) , В ( 4,-1,0 ) , С ( 14,3,8 ) , D ( 0,7,7 ).
А ( 8,3,-1 ) , В ( -7,1,1 ) , С ( 3,5,9 ) , D ( 0,7,7 ).
А ( 2,-1,-4 ) , В ( 3,-3,-2 ) , С ( 13,1,6 ) , D ( 10,3,4 ).
А ( 4,5,-5 ) , В ( -3,3,-3 ) , С ( 7,7,5 ) , D ( 4,9,3 ).
А ( -2,-3,2 ) , В ( -1,-5,4 ) , С ( 9,-1,12 ) , D ( 6,1,10 ).
А ( -3,4,-3 ) , В ( -2,2,-1 ) , С ( 8,6,7 ) , D ( 5,8,5 ).

А ( 3,2,-6 ) , В ( 0,-5,1 ) , С ( -2,1,0 ) , D ( 4,-1,3 ).
А ( 4,-1,0 ) , В ( -1,2,-3 ) , С ( 2,1,-2 ) , D ( 3,4,5 ).
А ( -3,6,3 ) , В ( 1,5,-7 ) , С ( -2,7,3 ) , D ( 1,-1,2 ).
А ( 1,1,-1 ) , В ( 2,3,1 ) , С ( 3,2,1 ) , D ( -3,-7,6 ).
А ( 2,3,1 ) , В ( 4,1,-2 ) , С ( 6,3,7 ) , D ( -5,-4,8 ).
А ( 2,3,8 ) , В ( 2,-2,4 ) , С ( -1,1,3 ) , D ( 1,1,2 ).
А ( 2,-1,2 ) , В ( 1,2,-1 ) , С ( 3,2,1 ) , D ( -5,3,7 ).
А ( -13,-8,16 ) , В ( 5,2,6 ) , С ( 3,0,-3 ) , D ( 1,2,0 ).
А ( 14,4,5 ) , В ( -5,-3,2 ) , С ( -2,-6,-3 ) , D ( -1,-8,7 ).

А ( -6,5,5 ) , В ( 4,-8,-4 ) , С ( -1,7,1 ) , D ( -2,0,-4 ).
Задание 2.3.
Даны три вектора ,,. Найти :
косинус угла между векторами и;
выяснить компланарны ли вектора ,,;
если вектора ,,компланарны, найти площадь параллелограмма, построенного на векторахи, как на сторонах, а если,,некомпланарны – найти объем параллелепипеда, построенного на векторах,,, как на ребрах.
( 2,1,1 ) , ( 19,11,17 ) ,( 7,4,6 ) .
( -2,4,-1 ) , ( 0,-2,-1 ) ,( -7,10,-5 ) .
( -4,7,6 ) , ( -3,3,3 ) ,( 3,0,-1 ) .
( 1,-2,1 ) , ( 3,3,1 ) ,( 1,1,1 ) .
( 6,2,6 ) , ( 4,1,1 ) ,( -9,-4,-9 ) .

( -2,-1,0 ) , ( 3,1,-1 ) ,( 5,2,-1 ) .
( 4,3,1 ) , ( 2,2,2 ) ,( 1,-2,1 ) .
( 6,7,4 ) , ( 4,3,1 ) ,( 4,0,-2 ) .
( 1,2,3 ) , ( 3,2,1 ) ,( 1,-3,-7 ) .
( 2,3,4 ) , ( 1,-1,-3 ) ,( 3,2,1 ) .
( 1,5,2 ) , ( -1,1,-1 ) ,( 1,1,1 ) .
( 2,3,4 ) , ( 3,1,-1 ) ,( 3,2,1 ) .
( 2,3,1 ) , ( 2,2,2 ) ,( -1,0,-1 ) .
( 3,1,3 ) , ( 4,1,1 ) ,( -9,-4,-9 ) .
( 4,3,6 ) , ( -1,-2,-1 ) ,( 2,1,2 ) .
( 4,-1,1 ) , ( 3,0,1 ) ,( 8,-3,1 ) .
( -1,1,1 ) , ( 6,1,8 ) ,( 3,0,3 ) .
( 0,1,3 ) , ( -5,-4,-5 ) ,( 2,1,2 ) .

( -6,-1,4 ) , ( -7,-3,1 ) ,( -4,-1,2 ) .
( 2,4,3 ) , ( 0,1,1 ) ,( 6,11,8 ) .
( 4,3,5 ) , ( 3,3,4 ) ,( 8,5,9 ) .
( 4,1,2 ) , ( 1,1,-1 ) ,( 9,2,5 ) .
( 2,1,1 ) , ( -1,-1,-1 ) ,( 2,1,2 ) .
( 1,0,-1 ) , ( 8,3,-2 ) ,( 3,1,-1 ) .
( 4,3,1 ) , ( -2,-4,-3 ) ,( 6,7,4 ) .
( 2,4,3 ) , ( -2,-2,-3 ) ,( 3,10,5 ) .
( 4,2,4 ) , ( -2,0,-2 ) ,( 5,3,4 ) .
( 4,7,5 ) , ( 2,3,2 ) ,( 2,0,-1 ) .
( 7,3,4 ) , ( -1,-2,-1 ) ,( 4,2,4 ) .
( 2,1,2 ) , ( 6,3,4 ) ,( -1,-2,-1 ) .
Выразить один вектор через другой : Чулан (М)
| Leander |
| ||
20/06/10 |
| ||
| |||
| gris |
| |||
13/08/08 |
| |||
| ||||
| Leander |
| ||
20/06/10 |
| ||
| |||
| La|Verd |
| ||
15/02/07 |
| ||
| |||
| Leander |
| ||
20/06/10 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 5 ] |
Модераторы: Модераторы Математики, Супермодераторы
Выражение вектора в компонентной форме
Все ресурсы для предварительного исчисления
12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept
Precalculus Help » Матрицы и векторы » Алгебраические векторы и параметрические уравнения » Выразите вектор в компонентной форме
Выразите следующий вектор в компонентной форме:
Возможные ответы:
Ни один из других ответов
Правильный ответ:
Объяснение:
При разделении вектора на составляющие его формы мы, по сути, создаем прямоугольный треугольник, гипотенузой которого является вектор.
Следовательно, мы можем найти каждый компонент, используя функции cos (для компонента x) и sin (для компонента y):
Теперь мы можем представить эти два компонента вместе, используя обозначения i (для компонента x) и j (для компонента y).
Сообщить об ошибке
Найдите , затем найдите его величину. и оба являются векторами.
Возможные ответы:
Правильный ответ:
Объяснение:
При сложении векторов вы просто добавляете каждый компонент вектора друг к другу.
x компонент: .
компонент y: .
z компонент: .
Новый вектор:
.
, чтобы найти величину, которую мы используем формулу,
Таким образом, ее величина составляет 5.
Отчет о ошибке
Найдите форму компонента вектора с
Начальная точка
и
точка .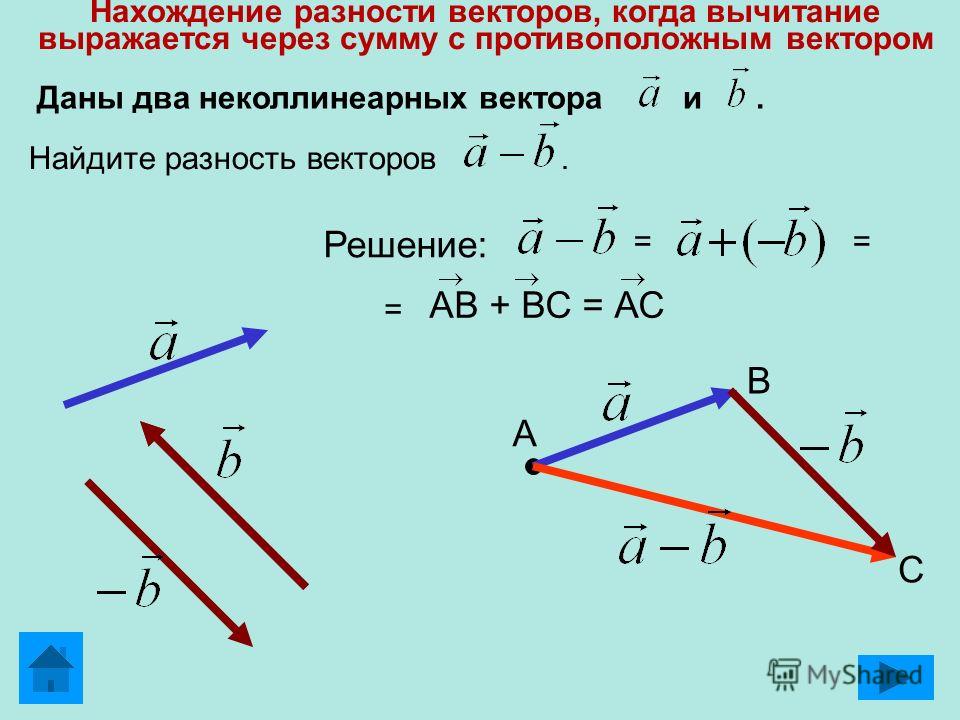
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти вектор в компонентной форме, зная начальную и конечную точки, просто вычтите начальную точку из конечной точки.
Отчет о ошибке
Найдите форму компонента вектора с
Начальная точка
и
Терминальная точка
Возможные ответы:
Правильный ответ:
9005
. Объяснение:
Чтобы найти вектор в компонентной форме с учетом начальной и конечной точек, просто вычтите начальную точку из конечной точки.
Сообщить об ошибке
Птица летит со скоростью 15 миль в час под углом 45 градусов к горизонтали. Какова скорость птицы в компонентной форме?
Какова скорость птицы в компонентной форме?
Возможные ответы:
Правильный ответ:
Пояснение:
Напишите формулу для нахождения компонентов x и y вектора.
Подставьте значения скорости и тета в уравнения.
Вектор:
Отчет о ошибке
Напишите этот вектор в форме компонента:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти горизонтальную составляющую, составим уравнение, включающее косинус с 7 в качестве гипотенузы, поскольку сторона в подразумеваемом треугольнике, представляющая горизонтальную составляющую, примыкает к углу в 22 градуса:
Сначала найдите косинус числа 22, а затем умножьте на 7
Чтобы найти вертикальную составляющую, составьте уравнение, включающее синус, поскольку сторона в подразумеваемом треугольнике, представляющая вертикальную составляющую, противоположна углу в 22 градуса. :
:
Сначала найдите синус 22, затем умножьте на 7
Мы почти закончили, но нам нужно сделать небольшую корректировку. На рисунке показано, что вектор направлен вверх и влево, поэтому горизонтальная составляющая 6,49., должно быть отрицательным:
Сообщить об ошибке
Уведомление об авторских правах
Все ресурсы Precalculus
12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept
Выражение вектора в новом базисе
$\begingroup$
Это первый раз, когда я пытался решить такую задачу и решал ее все утро. Я пытался использовать одновременные уравнения для решения переменных, но, похоже, это не работает, так что, возможно, это не тот путь…
$$\hat{\bf a} = \dfrac{1}{\sqrt{14}}({\bf i}+2{\bf j}+3{\bf k})$$ $$\шляпа{\bf b} = \dfrac{1}{\sqrt{5}}(2{\bf i}-{\bf j})$$ $$\hat{\bf c} = \dfrac{1}{\sqrt{70}}(3{\bf i}+6{\bf j}-5{\bf k})$$
Выразите вектор ${\bf d} = 5{\bf i}+3{\bf j}+2{\bf k}$ в новых $(\hat{\bf a},\hat{\bf b}, \hat{\bf c})$ базис.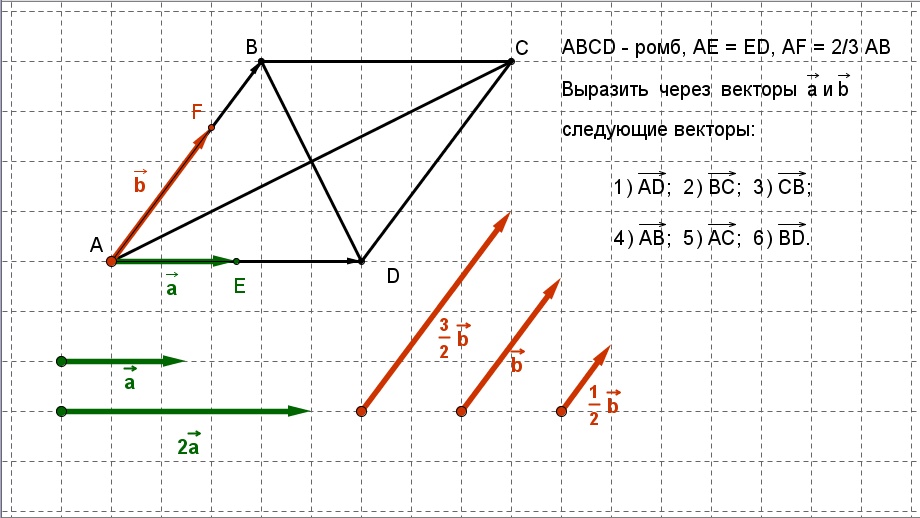
Мое решение можно увидеть здесь: https://drive.google.com/file/d/0B8CnEriPXOd1T3Z1amU4UGlMVU0/view
В моей попытке ответа есть основная арифметическая ошибка, поэтому я ответил на свой вопрос ниже. Извините за потраченное впустую чье-то время; Я постараюсь быть более осторожным.
- вектор-пространства
- векторов
$\endgroup$
3
$\begingroup$
мы сначала займемся выражением в виде линейной комбинации $\sqrt{14}\hat a, \sqrt 5\hat b,$ и $\sqrt{70}\hat c.$
нам нужно число $x, y, z$ так, что $$x(i+2j+3k)+y(2i-j)+z(3i+6j-5k)=5i+3j+2k \tag 1 $$
в матричной форме мы имеем $$\pmatrix{1&2&3&|&5\\2&-1&6&|&3\\3&0&-5&|&2}\to
\pmatrix{1&0&0&|&1.21428\\0&1&0&|&1.40000\\0&0&1&|&0.32857}$$
решения $\pmatrix{x\\y\\z}$ — последний столбец во второй матрице. теперь, умножив $x,y,z$ на $\sqrt{14}, \sqrt{5}, \sqrt{70}$, вы получите ответ.
$\endgroup$
1
$\begingroup$
Ничего себе, после всего этого и того, что я считал тщательным изучением своей работы, я перепроверил ее утром после освежающего сна и нашел элементарную арифметическую ошибку. Тета должна была быть (17 x rt(14))/14. Извините, что потратил впустую чье-то время!
$\endgroup$
$\begingroup$
Вы ищете $[r,s,t]$, где $r\hat{\bf a}+s\hat{\bf b}+t\hat{\bf c}=5{\bf i }+3{\bf j}+2{\bf k}$.
Это означает, что $\dfrac{r}{\sqrt{14}}+\dfrac{2s}{\sqrt{5}}+\dfrac{3t}{\sqrt{70}}=5$ (коэффициенты ${\bf i}$). То же самое для коэффициентов ${\bf j}$ и ${\bf k}$. Тогда остается просто разобраться с этой довольно непривлекательной системой уравнений. 🙁
$\endgroup$
1
$\begingroup$
, поэтому вы ищете [$\alpha, \beta, \gamma$], где $\vec b = \alpha \hat a + \beta \hat b + \gamma \hat c =5\hat i+3\ шляпа j+2\шляпа k$.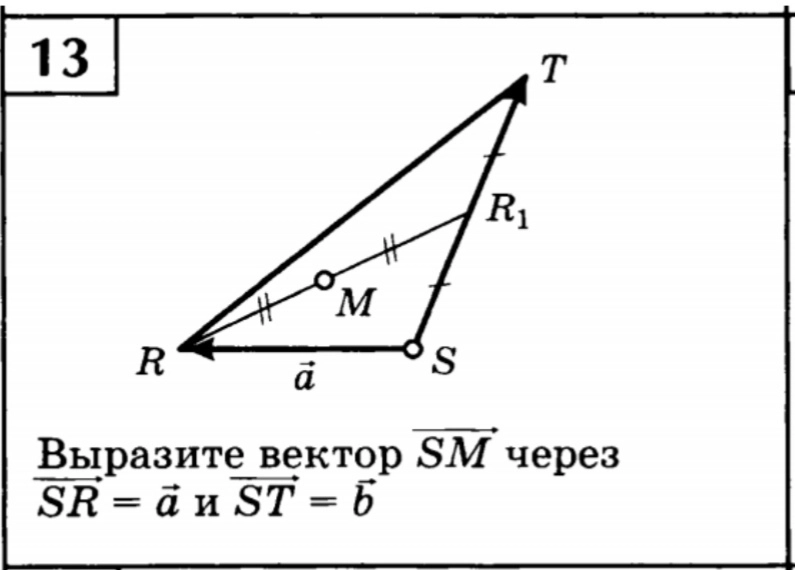







 06.2010, 17:57
06.2010, 17:57  06.2010, 18:08
06.2010, 18:08  06.2010, 18:38
06.2010, 18:38 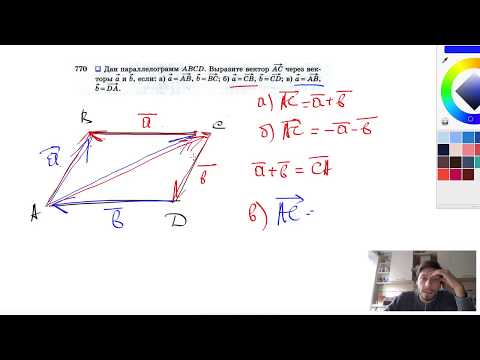 06.2010, 19:40
06.2010, 19:40  06.2010, 20:05
06.2010, 20:05