Применение векторов к решению задач 8 класс онлайн-подготовка на Ростелеком Лицей
Выражение вектора через два неколлинеарных
Напомним, что мы уже изучили некоторые факты о векторах, и теперь умеем определять равные векторы, коллинеарные векторы, сонаправленные и противоположно направленные. Также мы умеем складывать векторы по правилу треугольника и параллелограмма, складывать несколько векторов по правилу многоугольника, умеем умножать вектор на число. Решение задач с векторами использует все эти знания. Перейдем к решению некоторых примеров.
Пример 1 – задача 769: отрезок ВВ1 – медиана треугольника . Выразите через векторы и векторы , , и .
Отметим, что векторы и неколлинеарны, то есть прямые АВ и АС не параллельны.
В дальнейшем мы узнаем, что любой вектор может быть выражен через два неколлинеарных вектора.
Выразим первый вектор (см. Рис. 1): , т. к. по условию ВВ1 – медиана треугольника, значит, векторы и имеют равные модули, кроме того, очевидно, что они коллинеарны и при этом сонаправлены, значит, данные вектора равны.
Рис. 1
Для выражения следующего вектора воспользуемся правилом параллелограмма для вычитания. Мы помним, что одна из диагоналей параллелограмма, построенного на двух векторах, соответствует сумме этих векторов, а вторая – их разности. Диагональ, соответствующая разности векторов, следует от конца к началу, таким образом, если построить на заданных векторах и параллелограмм, то его диагональ будет соответствовать разности .
Вектор является противоположным к заданному вектору , отсюда .
Вектор аналогично вектору можно представить в виде разности векторов . При выражении следует учесть тот факт, что точка В1 является серединой отрезка АС, значит, векторы и равны, значит, вектор можно представить как удвоенное произведение вектора .
Перед решением задачи мы сказали, что через заданные два неколлинеарных вектора можно выразить любой вектор. Выразим, например, медиану АА1 (см. Рис. 2).
Получили систему уравнений, выполним их сложение:
Векторы в сумме составляют нулевой вектор, так как они коллинеарны и противонаправлены, а модули их равны, таким образом получаем:
Рис.
2
Поделим обе части уравнения на два, получим:
Из данной задачи можно сделать вывод, что если заданы два неколлинеарных вектора, то любой третий вектор на плоскости можно однозначно выразить через эти два вектора. Для этого необходимо применить правило сложения векторов, либо методом треугольника, либо параллелограмма, и правило умножения вектора на число.
Свойство средней линии треугольника
Пример 2: доказать с помощью векторов свойство средней линии треугольника (см. Рис. 3).
Задан произвольный треугольник , точки M и N – середины сторон АВ и АС соответственно, MN – средняя линия треугольника. Свойство средней линии: средняя линия параллельна основанию треугольника и равна его половине.
Доказательство данного свойства аналогично для треугольника и трапеции.
Рис. 3
Выразим вектор двумя способами:
Получили систему уравнений:
Выполним сложение уравнений системы:
Сумма векторов – это нулевой вектор, длины этих векторов равны по условию, кроме того, они очевидно коллинеарны и противонаправлены.
Аналогично суммой векторов будет нулевой вектор. Получаем:
Поделим обе части уравнения на два:
Таким образом, мы получили, что средняя линия треугольника равна половине его основания. Кроме того, из равенства вектора половине вектора следует, что эти векторы коллинеарны и сонаправлены, а значит, прямые MN и ВС параллельны.
Таким образом, мы доказали свойство средней линии трапеции при помощи векторов.
Свойство точки пересечения медиан треугольника
Пример 3: задан произвольный треугольник (см. Рис. 4). В нем проведены медианы АА1, ВВ1, СС1. Точка пересечения медиан – М. Вектор соответствует силе , – силе , – силе . Доказать, что .
Напомним, что медианы треугольника пересекаются в одной точке и этой точкой делятся в отношении 2:1, считая от вершины.
Иногда точку пересечения медиан называют центром тяжести треугольника.
Выполним сложение векторов , воспользуемся для этого правилом параллелограмма (см.
Рис. 5).
Рис. 4
Получаем:
С другой стороны, , так как BMCD – параллелограмм, диагонали параллелограмма точкой пересечения делятся пополам, А1 – точка пересечения диагоналей параллелограмма, значит, отрезки МА1 и А1D равны, отсюда, по свойству точки пересечения медиан, длины векторов и равны, но данные векторы противонаправлены, а значит, их сумма
Рис. 5
равна нулевому вектору. Мы помним, что вектор , а вектор , таким образом, , что и требовалось доказать.
Неравенство треугольника
Пример 4 – задача 773: докажите, что для любых векторов и справедливо следующее неравенство:
Решение: представим разность векторов в виде суммы: . Также обратим внимание на тот факт, что длины противонаправленных векторов и равны: . Таким образом, можно переписать исходное выражение:
Для удобства введем новую переменную: и перепишем выражение:
. А данное неравенство – неравенство треугольника – было доказано в предыдущем уроке.
Отметим, что равенство наблюдается в том случае, когда треугольник вырождается в отрезок.
Итак, мы рассмотрели применение векторов при решении различных задач, доказали некоторые свойства фигур и решили наиболее распространенные типы задач.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Terver.ru (Источник).
- Cleverstudents.ru (Источник).
Домашнее задание
- Задание 1: заданы два неколлинеарных вектора и . Постройте векторы: ; ; .
- Задание 2: заданы два коллинеарных вектора и . Постройте векторы: ; ; .
- Задание 3: докажите, что для любого вектора справедливы равенства: ; .
Часть I. Аналитическая геометрия
Глава 1. Векторы
§1. Сложение векторов и умножение на число
Напомним, что сумма двух векторов может быть найдена: а) по правилу треугольника; б) по правилу параллелограмма (см. рис. 1).
Рис.1.
Если векторы иколлинеарны (записывается это так:), то “работает” только первое правило. Кроме того, для любых точекплоскости или пространства имеет местоправило трёх точек: (см. рис. 2).
Рис.2.
Понятно, что равенства такого вида можно писать, даже не делая чертежа: и т.д. Если нам надо разложить какой-либо вектор (например,) в сумму, то можно попробовать разные варианты:и т.д.
Решим в качестве иллюстрации несколько задач.
Задача 1. Дан правильный шестиугольник Точка– середина стороныВыразить векторчерез векторы
Решение (см.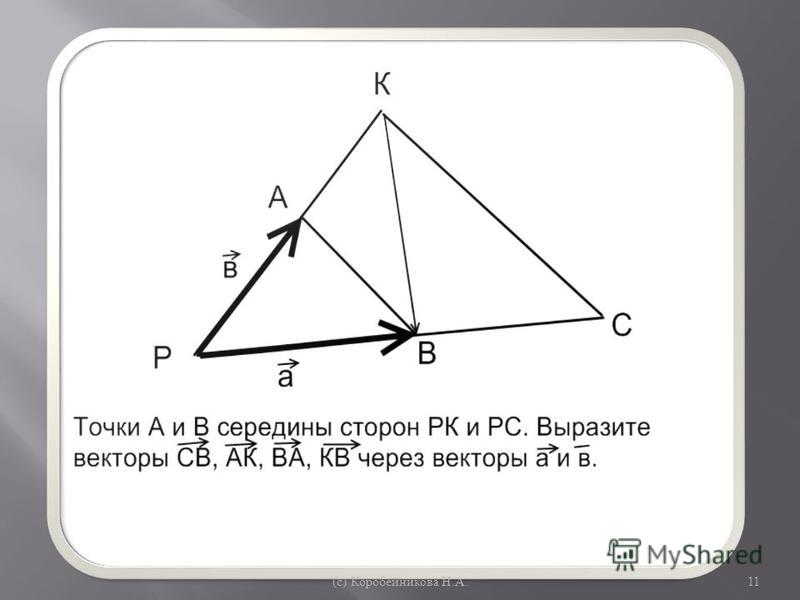
рис.3).
Известно, что правильный шестиугольник
разбивается диагоналями на 6 правильных
треугольников.
Рис.3.
Поэтому Используя правило трёх точек, получим:
Решение (см. рис. 4).
Рис.4
Имеем:
В некоторых случаях для того, чтобы выразить какой-либо вектор через другие, приходится решать отдельно задачу из элементарной геометрии или систему уравнений. Рассмотрим несколько примеров.
Задача 3. В окружности с центром проведены радиусыиРадиусделит уголпополам. Зная, чтоинайти вектор
Решение (см. рис. 5).
Рис.5.
Задача
4.
В
параллелограмме
и– середины сторонисоответственно. Выразить векторчерез векторы
Решение (см. рис 6).
Рис.6.
Введём векторы иВекторыиможно выразить черезии аналогичноНа эти равенства можно смотреть как на систему уравнений
Решим эту систему. Имеем: откуда получаем:т.е.ОтсюдаТаким образом,
Задача 5. В треугольнике – биссектриса углаВыразить векторчерез векторыи длины этих векторов.
Решение (см. рис. 7). По свойству биссектрисы имеем:
Рис.7.
Следовательно, Отсюда получаем:
Задача 6. Пусть – точка пересечения медиан треугольникаВычислить сумму
Решение (см. рис. 8).
Рис.8.
Пусть
– середины сторонсоответственно.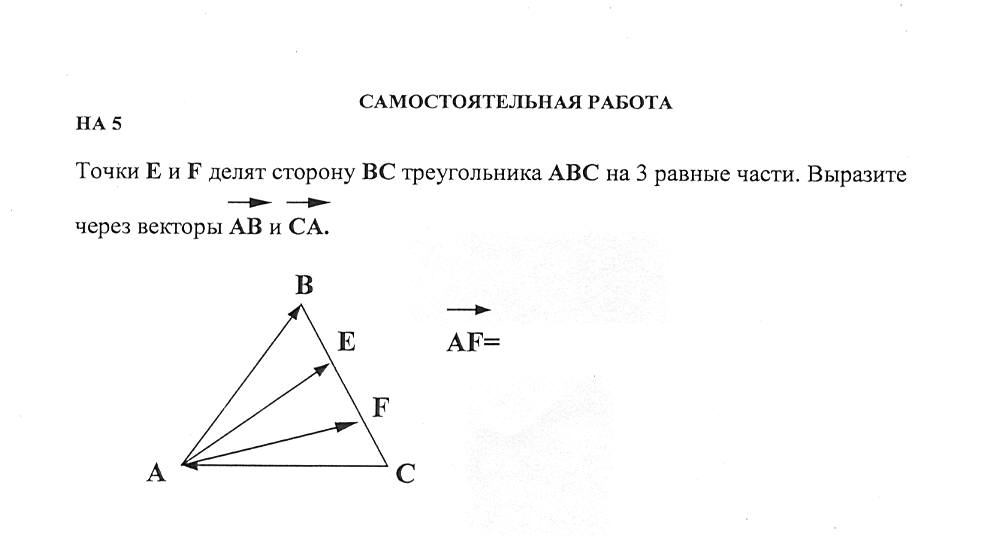
Покажем, как с помощью векторов можно доказывать утверждения. Напомним, что пространственным четырёхугольником называется четырёхугольник, вершины которого могут не лежать в одной плоскости.
Задача 7. Доказать, что отрезки, соединяющие середины противоположных сторон пространственного четырёхугольника, а также отрезок, соединяющий середины его диагоналей, пересекаются в одной точке и делятся этой точкой пополам.
Решение (см. рис. 9).
Рис.9.
Пусть
– середины сторонсоответственно. Обозначим черезисередины диагоналейисоответственно.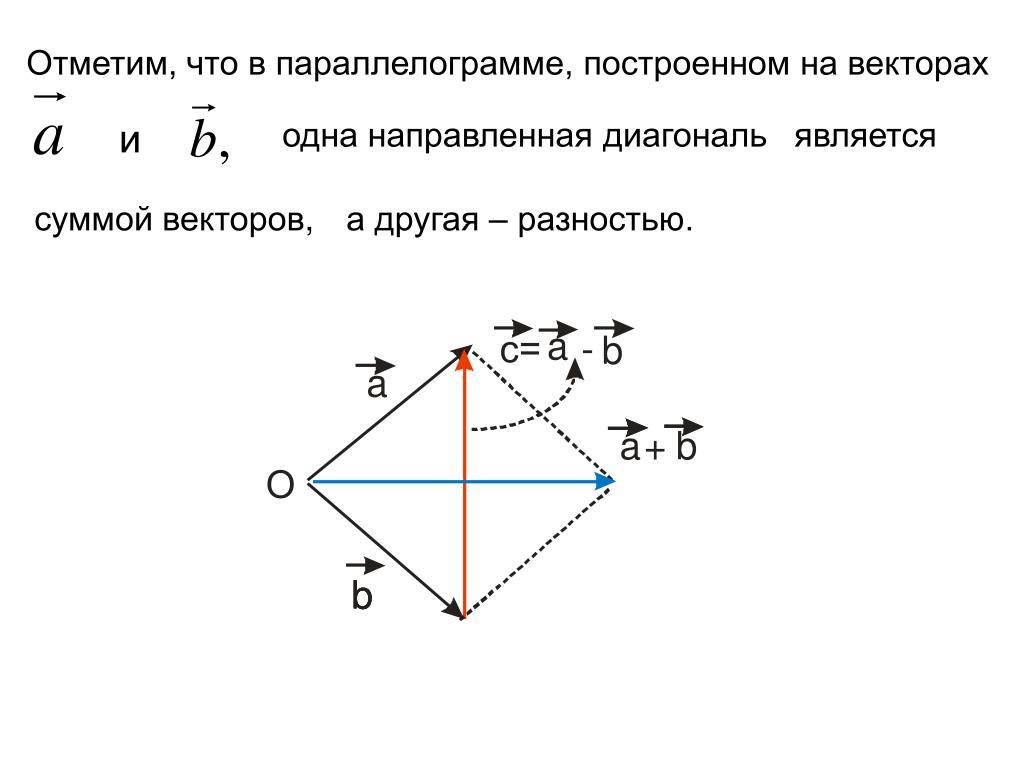
Требуется доказать,
что середины отрезковисовпадают. Пусть– середина отрезкаа– произвольная точка пространства.
Тогда получаем:
Рассуждая аналогично, получим, что если – середина отрезкатоТаким образом,откуда следует, что точкиисовпадают. Обозначим черезсередину отрезкаИмеем:
Теперь ясно, что
Векторные уравнения и интервалы
Цели
- Понимать эквивалентность между системой линейных уравнений и векторным уравнением.
- Изучите определение Span{x1,x2,…,xk} и как рисовать изображения пролетов.
- Рецепт: решить векторное уравнение с использованием расширенных матриц / определить, находится ли вектор в интервале.
- Картинки: противоречивая система уравнений, непротиворечивая система уравнений, охватывает R2 и R3.
- Словарное слово: векторное уравнение .
- Основное словарное слово: диапазон .
Уравнение, включающее векторы с n координатами, аналогично n уравнениям, включающим только числа. Например, уравнение
хC126D+yC-1-2-1D=C8163D
упрощается до
Cx2x6xD+C-y-2y-yD=C8163DorCx-y2x-2y6x-yD=C8163D.
Чтобы два вектора были равны, все их координаты должны быть равны, так что это просто система линейных уравнений
Ex-y=82x-2y=166x-y=3.
Определение
Векторное уравнение — это уравнение, включающее линейную комбинацию векторов с возможными неизвестными коэффициентами.
Спрашивать, имеет ли векторное уравнение решение, это то же самое, что спрашивать, является ли данный вектор линейной комбинацией некоторых других заданных векторов.
Например, приведенное выше векторное уравнение спрашивает, является ли вектор (8,16,3) линейной комбинацией векторов (1,2,6) и (−1,2,−1).
На самом деле нас волнует решение систем линейных уравнений, а не решение векторных уравнений. Весь смысл векторных уравнений в том, что они дают нам другой, более геометрический способ рассмотрения систем линейных уравнений.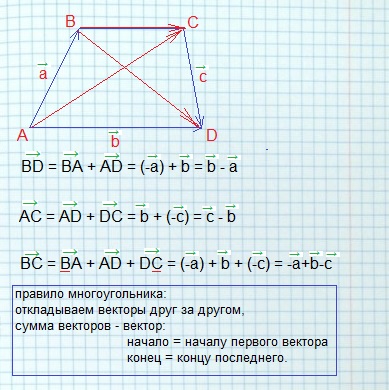
Чтобы действительно решить векторное уравнение
хC126D+yC-1-2-1D=C8163D,
нужно решить систему линейных уравнений
Ex-y=82x-2y=166x-y=3.
Это означает формирование расширенной матрицы
C1-182-2166-13Dи уменьшение ряда. Обратите внимание, что столбцы расширенной матрицы являются векторами из исходного векторного уравнения , поэтому на самом деле нет необходимости записывать систему уравнений: можно напрямую перейти от векторного уравнения к расширенной матрице, «сложив векторы вместе». ». В следующем примере мы выполняем сокращение строки и находим решение.
Пример
Рецепт: Решение векторного уравнения
В общем, векторное уравнение
x1v1+x2v2+···+xkvk=b
, чьи столбцы — это vi и b.
Теперь у нас есть три эквивалентных способа представить себе линейную систему:
- В виде системы уравнений:
ч3х1+3х2-2х3=7х1-х2-3х3=5
- В качестве расширенной матрицы: Ф23-271-1-35Г
- В виде векторного уравнения (x1v1+x2v2+···+xnvn=b):
x1F21G+x2F3-1G+x3F-2-3G=F75G
Третий по своей природе геометрический: он поддается рисованию картинок.
Будет важно знать, что такое всех линейных комбинаций набора векторов v1,v2,…,vk в Rn. Другими словами, мы хотели бы понимать множество всех векторов b в Rn таких, что векторное уравнение (относительно неизвестных x1,x2,…,xk)
x1v1+x2v2+···+xkvk=b
имеет решение (т.е. непротиворечиво).
Определение
Пусть v1,v2,…,vk — векторы в Rn. Диапазон элементов v1,v2,…,vk представляет собой набор всех линейных комбинаций элементов v1,v2,…,vk и обозначается Span{v1,v2,…,vk}. В символах:
Span{v1,v2,.
..,vk}=Ax1v1+x2v2+···+xkvk|x1,x2,…,xkinRB
Мы также говорим, что Span{v1,v2,…,vk} — это подмножество , натянутое на или , порожденное векторами v1,v2,…,vk.
Приведенное выше определение является первым из нескольких основных определений , которые мы встретим в этом учебнике. Они важны в том смысле, что составляют сущность предмета линейной алгебры: изучение линейной алгебры означает (частично) изучение этих определений. Все определения важны, но очень важно, чтобы вы выучили и поняли определения, помеченные как таковые.
Эквивалент означает, что для любого заданного списка векторов v1,v2,…,vk,b либо все три утверждения верны, либо все три утверждения ложны.
Рисунок 10. Это изображение несовместной линейной системы: вектор w в правой части уравнения x1v1+x2v2=w не лежит в промежутке v1,v2. Убедитесь в этом сами, попробовав решить уравнение x1v1+x2v2=w, перемещая ползунки и уменьшая ряды. Сравните эту цифру.
Фотографии пролетов
Рисование изображения Span{v1,v2,…,vk} аналогично рисованию всех линейных комбинаций v1,v2,…,vk.
Span{v}vSpan{v,w}vwSpan{v,w}vwFigure11Изображения пролетов в R2.Span{v}vSpan{v,w}vwvwuSpan{u,v,w}Span{u,v,w}vwuFigure12Изображения пролеты в R3. Размах двух неколлинеарных векторов — это плоскость, содержащая начало координат и головы векторов. Обратите внимание, что три компланарных (но не коллинеарных) вектора охватывают плоскость, а не трехмерное пространство, точно так же, как два коллинеарных вектора охватывают прямую, а не плоскость.Interactive: диапазон двух векторов в R2
Interactive: диапазон двух векторов в R3
Interactive: Span of three vectors in R3
Комментарии, исправления или предложения? (Требуется бесплатная учетная запись GitHub)
Условия предоставления услуг — Vector Unit
Последнее изменение: 6 декабря 2018 г.
Важно! Пожалуйста, прочтите внимательно!
Настоящие Условия обслуживания (« Условия «) регулируют отношения между вами (« Вы » или « Пользователь «) и (» Vector Unit «, » мы «) и регулирует использование вами игр, веб-сайта, форумов и приложений Vector Unit (совместно именуемые » Службы «).
BY ИСПОЛЬЗУЯ УСЛУГИ, ВЫ ПОДТВЕРЖДАЕТЕ, ЧТО ПРОЧИТАЛИ НАСТОЯЩЕЕ СОГЛАШЕНИЕ И СОГЛАШАЕТЕСЬ СОБЛЮДАТЬ ЕГО ПОЛОЖЕНИЯ И УСЛОВИЯ. Если вы не согласны с настоящими Условиями, не используйте и не покупайте Услуги.
Vector Unit оставляет за собой право пересматривать настоящие Условия в любое время. Если мы это сделаем, мы обновим Условия на этой странице и укажем дату последнего изменения выше.
Также ознакомьтесь с нашей Политикой конфиденциальности , , которая упоминается в настоящих Условиях.
1. Лицензия и ограничения
При условии соблюдения настоящих Условий Vector Unit предоставляет вам неисключительную, непередаваемую, ограниченную, отзывную лицензию на доступ к Услугам для вашего личного некоммерческого использования на авторизованных устройствах, если не указано иное. Если вы нарушите какое-либо из этих Условий, Vector Unit оставляет за собой право прекратить действие вашей лицензии без предварительного уведомления.
2. Возраст
Используя Услуги, вы подтверждаете, что вам не менее 13 лет, или что вы ознакомились с настоящими Условиями со своим родителем или опекуном, и он или она принимает эти Условия от вашего имени. Если вам еще не исполнилось 13 лет, вы должны получить разрешение от родителей или опекунов, чтобы пользоваться Услугами. Информацию об использовании вашей личной информации можно найти в Политике конфиденциальности Vector Unit .
3. Создание учетной записи
Вам может потребоваться зарегистрировать учетную запись (ваш » Учетная запись «) перед доступом к определенным Услугам. Регистрация учетной записи может быть осуществлена путем создания логина и пароля, входа через службу социальной сети или учетной записи магазина приложений, или у вас может быть учетная запись, автоматически созданная для вас на основе уникального идентификатора. Например, идентификатор устройства.
Вы несете единоличную ответственность за сохранение конфиденциальности любой и всей информации об учетной записи, а также за любые действия, которые происходят под вашей учетной записью, включая покупки, независимо от того, санкционированы ли вы или нет.
Vector Unit оставляет за собой право закрыть любую учетную запись, которая не использовалась в течение 180 дней.
4. Внутриигровая виртуальная валюта и предметы
Услуги могут включать виртуальную внутриигровую валюту (« Виртуальная валюта »), такую как монеты, драгоценные камни или билеты, или внутриигровые цифровые предметы (« Виртуальные предметы »), такие как транспортные средства, бонусы или персонажи, которые можно приобрести за «реальные» деньги или специальное взаимодействие со сторонней службой.
Виртуальная валюта и Виртуальные предметы не имеют денежной стоимости и не могут быть обменены на законную валюту или ценные предметы вне Сервисов. Вы не имеете права покупать или продавать Виртуальную валюту или Виртуальные предметы за «реальные» деньги или иным образом обменивать их на ценности вне Сервисов.
Вы также соглашаетесь с тем, что все продажи Виртуальной валюты и Виртуальных предметов являются окончательными.
Наши сторонние поставщики платежей или Vector Unit не будут возвращать средства, за исключением случаев, когда Vector Unit принимает их по собственному усмотрению. За исключением ограниченной, отзывной, непередаваемой лицензии на использование Виртуальной валюты или Виртуальных предметов в Сервисах, у вас нет никаких прав или титулов на такую Виртуальную валюту и Виртуальные предметы. В случае прекращения или приостановления действия вашей учетной записи по какой-либо причине, по единоличному и абсолютному усмотрению Vector Unit, или если Vector Unit прекращает предоставление своих Услуг, вы теряете любую и всю Виртуальную валюту и Предметы. Vector Unit имеет абсолютное право управлять, регулировать, контролировать, изменять и/или уничтожать Виртуальную валюту и/или Виртуальные предметы по своему усмотрению, и Vector Unit не несет никакой ответственности перед вами или кем-либо за осуществление такие права.
5. Сторонние продукты, услуги и ссылки
Vector Unit может предлагать сторонние продукты через Услуги.
Вы принимаете на себя все риски и ответственность, связанные с использованием любых таких сторонних продуктов. Кроме того, ваши права и обязанности в отношении таких продуктов или услуг будут регулироваться отдельными условиями использования и политиками конфиденциальности соответствующего стороннего поставщика.
Услуги могут включать гиперссылки на другие веб-сайты, над которыми Vector Unit не имеет никакого контроля. Vector Unit не несет ответственности за доступность таких внешних сайтов или ресурсов и не будет нести ответственности за любой контент, рекламу, продукты или другие материалы, доступные на таких сторонних веб-сайтах или ресурсах.
6. Кодекс поведения
Использование вами Услуг регулируется определенными правилами (« Кодекс поведения »), которые поддерживаются и применяются компанией Vector Unit. Вы несете ответственность за знание, понимание и соблюдение настоящего Кодекса поведения. Кодекс поведения регулирует все аспекты вашего взаимодействия с Услугами, включая, помимо прочего, выбор имени пользователя, публикацию сообщений на форумах или в социальных сетях, взаимодействие с другими пользователями и иной доступ к Услугам.
Следующие правила не претендуют на исчерпывающую полноту, и Vector Unit оставляет за собой право определять, какое поведение оно считает выходящим за рамки духа Кодекса поведения, и принимать дисциплинарные меры по своему усмотрению, включая изменение или удаление нарушение пункта и/или приостановка или прекращение вашего доступа к Услугам и их использования.
Вы соглашаетесь с тем, что вы не будете:
передавать или публиковать любой контент или язык, которые, по единоличному и абсолютному усмотрению Vector Unit, считаются оскорбительными, включая, помимо прочего, контент или язык, которые являются незаконными, вредными, угрожающие, оскорбительные, преследующие, клеветнические, вульгарные, непристойные, разжигающие ненависть, откровенно сексуальные или неприемлемые по расовому, этническому или иному признаку, а также вы не можете использовать орфографические ошибки или альтернативное написание, чтобы обойти ограничения содержания и языка, перечисленные выше;
сообщать или публиковать любую личную информацию пользователя, включая, помимо прочего, адрес другого пользователя, номер телефона, адрес электронной почты или номер кредитной карты, в Сервисах без явного письменного согласия пользователя, за исключением случаев, когда пользователь может сообщать его личная информация;
нарушают договорные, личные права, права интеллектуальной собственности или другие права любой стороны;
ненадлежащим образом использовать службы поддержки Vector Unit или подавать ложные сообщения о злоупотреблениях или неправомерных действиях;
использовать читы, эксплойты, программное обеспечение для автоматизации, ботов, взломы, моды или любое несанкционированное стороннее программное обеспечение, предназначенное для изменения или вмешательства в Сервисы, или без явного письменного согласия Vector Unit, изменять или вызывать изменение любого файлы, являющиеся частью Сервиса;
организовывать, помогать или участвовать в атаках любого типа, включая, помимо прочего, распространение вируса, отказ в обслуживании, атаки на Сервисы или другие попытки нарушить работу Сервисов или использование или использование Сервисов любым другим лицом.
;пытаться получить несанкционированный доступ к Услугам, Учетным записям, зарегистрированным на других лиц, или к компьютерам, серверам или сетям, подключенным к Услугам, любыми средствами, кроме пользовательского интерфейса, предоставляемого Vector Unit, включая, помимо прочего, обход или изменение, попытка обхода или изменения, а также поощрение или помощь любому другому лицу в обходе или изменении любой системы безопасности, технологии, устройства или программного обеспечения, являющихся частью Сервиса.
воспроизводить, дублировать, копировать, продавать, перепродавать или иным образом использовать Услуги, полностью или частично, для любых целей без явного письменного согласия Vector Unit;
изменять, переводить, реконструировать, обратно компилировать или декомпилировать, дизассемблировать, создавать производные работы или использовать инструменты сбора или извлечения данных в связи с Услугами;
продавать Услуги или любую их часть, включая, помимо прочего, Виртуальные предметы или Виртуальную валюту, учетные записи пользователей и доступ к ним в обмен на реальную валюту или предметы, имеющие денежную стоимость; или
заниматься мошенничеством или любой другой деятельностью, которую Vector Unit считает противоречащей духу или намерениям Сервисов.
;
7. Прекращение действия
Лицензия на использование Услуг, предоставленная в соответствии с настоящими Условиями, остается в силе до тех пор, пока она не будет прекращена вами или компанией Vector Unit.
Vector Unit оставляет за собой право закрыть или приостановить действие вашей Учетной записи или доступ к любой из Услуг в любое время по любой причине и без предварительного уведомления. Мы оставляем за собой право удалить вашу учетную запись, если вы не совершаете никаких действий в отношении учетной записи в течение 180 или более дней. Vector Unit оставляет за собой право прекратить предлагать и/или поддерживать любую Услугу или часть любой Услуги в любое время, после чего ваша лицензия на использование Услуги или ее части будет автоматически аннулирована.
Вы также можете прекратить действие своей Учетной записи в любое время и по любой причине, сообщив Vector Unit о своем желании прекратить действие своей Учетной записи.
8. Отказ от ответственности / отсутствие гарантии
Услуги предоставляются вам компанией Vector Unit «как есть».
В максимальной степени, разрешенной действующим законодательством, за исключением случаев, предусмотренных выше, Vector Unit НЕ ДАЕТ НИКАКИХ ГАРАНТИЙ ИЛИ ЗАЯВЛЕНИЙ, ЯВНЫХ ИЛИ ПОДРАЗУМЕВАЕМЫХ В ОТНОШЕНИИ УСЛУГ, ИХ КАЧЕСТВА, ПРОИЗВОДИТЕЛЬНОСТИ ИЛИ ПРИГОДНОСТИ ДЛЯ ОПРЕДЕЛЕННОЙ ЦЕЛИ. В РЕЗУЛЬТАТЕ УСЛУГИ ПРЕДОСТАВЛЯЮТСЯ «КАК ЕСТЬ» И «ПО МЕРЕ ДОСТУПНОСТИ», И ВЫ ПРИНИМАЕТЕ ВЕСЬ РИСК В ОТНОШЕНИИ ИХ КАЧЕСТВА И ПРОИЗВОДИТЕЛЬНОСТИ.
9. Возмещение убытков
Вы соглашаетесь защищать, возмещать ущерб и ограждать Vector Unit, ее аффилированных лиц, лицензиаров, партнеров и субподрядчиков от всех обязательств, претензий и расходов, включая разумные гонорары адвокатов, возникающих в связи с нарушением вами настоящих Условия или часть настоящего документа, а также любое действие или бездействие с вашей стороны в отношении Услуг. Vector Unit оставляет за собой право взять на себя защиту и / или контроль над любым вопросом, который в противном случае подлежит возмещению вами по настоящему Соглашению.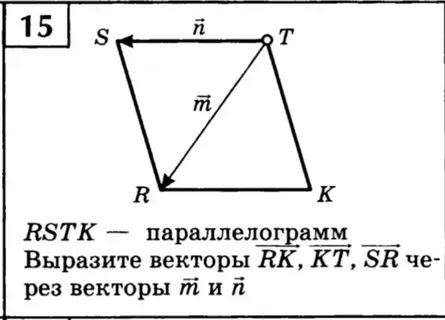
10. Ограничение ответственности
Вы понимаете и признаете, что Vector Unit не несет ответственности за какие-либо проблемы, связанные с сетью, связанные с работой Услуг, и что изменения конфигурации сети могут повлиять на производительность системы.
НАСТОЯЩИМ ВЫ ПОДТВЕРЖДАЕТЕ И СОГЛАШАЕТЕСЬ С ТЕМ, ЧТО VECTOR UNIT НЕ НЕСЕТ НИКАКОЙ ОТВЕТСТВЕННОСТИ В СВЯЗИ С ИСПОЛЬЗОВАНИЕМ ВАМИ УСЛУГ ИЛИ В РЕЗУЛЬТАТЕ ИСПОЛЬЗОВАНИЯ ВАШИМИ УСЛУГАМИ, В ТОМ ЧИСЛЕ ЗА ЛЮБОЙ ФИЗИЧЕСКИЙ ИЛИ ПРОГРАММНЫЙ ПОВРЕЖДЕНИЕ ВАШИХ УСТРОЙСТВ. ВАШЕ ЕДИНСТВЕННОЕ ПРАВО ИЛИ СРЕДСТВО В ОТНОШЕНИИ ЛЮБЫХ ПРОБЛЕМ ИЛИ НЕУДОВЛЕТВОРЕННОСТИ УСЛУГАМИ ЯВЛЯЕТСЯ УДАЛИТЬ ЛЮБЫЕ ИГРЫ ИЛИ ПРИЛОЖЕНИЯ, СВЯЗАННЫЕ С УСЛУГАМИ, И ПРЕКРАТИТЬ ИСПОЛЬЗОВАНИЕ ЛЮБЫХ ВЕБ-СТРАНИЦ, ВКЛЮЧЕННЫХ В УСЛУГИ.
VECTOR UNIT НЕ НЕСЕТ ОТВЕТСТВЕННОСТИ ЗА ЛЮБОЙ ПРЯМОЙ, КОСВЕННЫЙ, СЛУЧАЙНЫЙ, ОСОБЫЙ ИЛИ КОСВЕННЫЙ УЩЕРБ, УПУЩЕННУЮ ПРИБЫЛЬ ИЛИ ПЕРЕРЫВ В ДЕЯТЕЛЬНОСТИ, ВОЗНИКШИЙ В СВЯЗИ С ИСПОЛЬЗОВАНИЕМ ИЛИ НЕВОЗМОЖНОСТЬЮ ИСПОЛЬЗОВАНИЯ ИГРЫ, ДАЖЕ ЕСЛИ VECTOR UNIT БЫЛ УВЕДОМЛЕН О ВОЗМОЖНОСТИ ТАКИХ УЩЕРБОВ.
ОТВЕТСТВЕННОСТЬ VECTOR UNIT В ТАКИХ СЛУЧАЯХ ОГРАНИЧИВАЕТСЯ В МАКСИМАЛЬНО РАЗРЕШЕННОЙ ЗАКОНОМ МЕРЕ.
Некоторые юрисдикции могут не разрешать (некоторые) ограничения ответственности. В таких случаях некоторые ограничения могут на вас не распространяться.
11. Общие положения
Настоящие Условия вместе с Политикой конфиденциальности представляют собой полное и окончательное соглашение между Vector Unit и вами в отношении использования вами Услуг и не могут быть изменены вами, кроме как в письменной форме, должным образом подписанной вами. и уполномоченный представитель Vector Unit.
Если какое-либо положение настоящего документа будет признано неисполнимым, такое положение должно быть изменено в этом вопросе только в той мере, в какой это необходимо для обеспечения его исковой силы, и не должно влиять на исковую силу остальных положений. Неспособность любой из сторон обеспечить соблюдение какого-либо права или положения настоящих Условий не означает отказ от такого права или положения.
Vector Unit может время от времени вносить изменения в Услуги, настоящие Условия или Политику конфиденциальности. Vector Unit приложит разумные усилия, чтобы уведомить вас о любых существенных изменениях. Все такие изменения вступают в силу немедленно после уведомления и/или публикации. Vector Unit может передать или переуступить Услуги, настоящие Условия или Политику конфиденциальности, полностью или частично, любой третьей стороне по выбору Vector Unit. Настоящие Условия действуют в интересах соответствующих правопреемников и правопреемников Vector Unit и являются обязательными для них.
12. Применимое законодательство и место проведения
Настоящие Условия и Политика конфиденциальности регулируются и толкуются в соответствии с законами штата Калифорния без учета коллизионных норм. Если какой-либо иск или претензия возбуждены вами или подразделением Vector в связи с настоящими Условиями, настоящим вы подчиняетесь исключительной юрисдикции и месту рассмотрения в судах Сан-Франциско, штат Калифорния.
