Site Loader
Posted on 24.02.2023

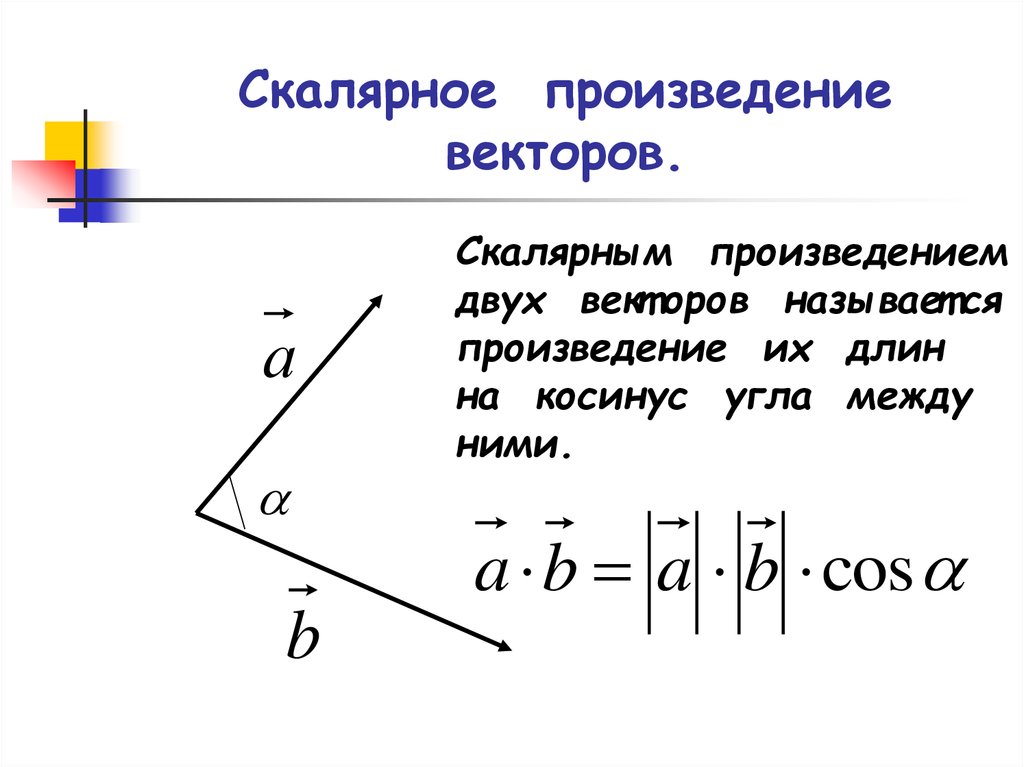
Вычисление скалярного произведения, примеры и решения.

Решение различных задач на вычисление скалярного произведения векторов сводится к использованию свойств скалярного произведения и формул

  1. ;

  2. ;

  3.  или ;

  4. .

Разберем решения наиболее часто встречающихся примеров.

Начнем с самых простых случаев, когда вычисление скалярного произведения производится на основе определения.

Пример.

Вычислите скалярное произведение двух векторов и , если их длины равны 3 и 7единиц соответственно, а угол между ними равен 60 градусам.

Решение.

У нас есть все данные, чтобы вычислить скалярное произведение по определению: .

Ответ:

.

Пример.

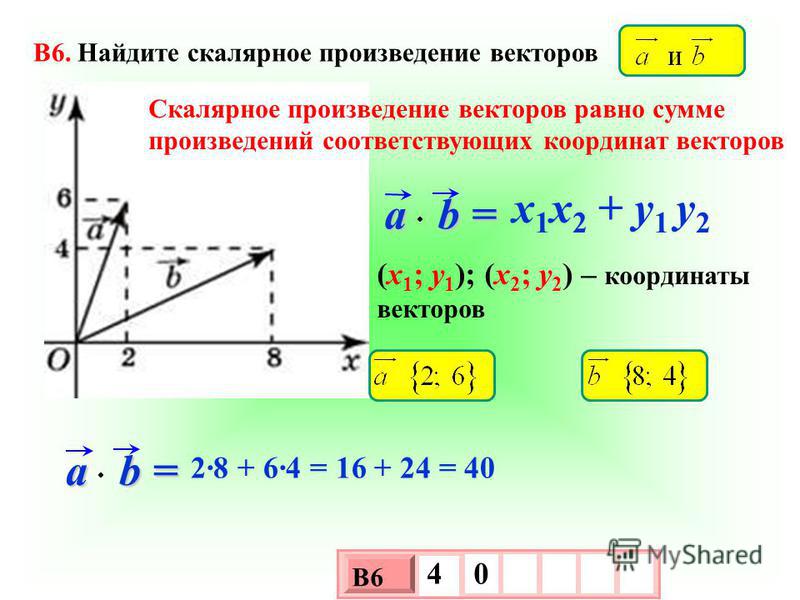
В прямоугольной системе координат заданы два вектора и , найдите их скалярное произведение.

Решение.

В этом примере целесообразно использовать формулу, позволяющую вычислить скалярное произведение векторов через их координаты:

Ответ:

.

Пример.

Вычислите скалярное произведение векторов и , если известны координаты трех точек в прямоугольной декартовой системе координат на плоскости .

Решение.

Найдем координаты векторов по координатам точек их начала и конца:

Теперь можно использовать формулу для вычисления скалярного произведения в координатах:

Ответ:

.

Сейчас рассмотрим пример, требующий сначала применить свойства скалярного произведения, и только затем переходить к вычислению.

Пример.

Вычислите скалярное произведение векторов и , если векторы и перпендикулярны и их длины равны 3

 и 2 единицы соответственно.

Решение.

. По свойству дистрибутивности скалярного произведения имеем . Сочетательное свойство позволяет нам вынести коэффициенты за знак скалярного произведения:

В силу свойства коммутативности последнее выражение примет вид .

Итак, после применения свойств скалярного произведения имеем . Осталось применить формулу для вычисления скалярного произведения через длины векторов и косинус угла между ними:

Ответ:

.

Сейчас рассмотрим пример на нахождение скалярного произведения векторов через числовую проекцию.

Пример.

Вычислите скалярное произведение векторов и , если , а проекция вектора на направление вектора имеет координаты .

Решение.

Векторы и противоположно направленные, так как , следовательно, числовая проекция вектора на направление вектора будет равна длине вектора со знаком минус: .

Вычисляем скалярное произведение .

Ответ:

.

Также встречается масса обратных задач, когда скалярное произведение векторов известно, а требуется найти, например, длину одного из векторов, угол между векторами, числовую проекцию, либо что-нибудь еще.

Пример.

При каком значении скалярное произведение векторов и равно 

-1.

Решение.

Так как скалярное произведение равно сумме произведений соответствующих координат, то . С другой стороны по условию . Тогда искомое значение находим из уравнения , откуда .

Ответ:

Определители очень полезны не только для решения симстем уравнений, но и при изучении очень многих других вопросов. Так, с помощью определителей можем вычислить векторное произведение двух векторов, заданных своими координатами в декартовой прямоугольной системе координат. Соответственно, можем использовать их в решении различных физических задач для определения моментов силы, инерции и т.д., в электричестве. Также легко вычислять площадь параллелограмма, зная координаты трех его вершин.

Определение. Векторным произведением векторов и , угол между которыми равен , называется вектор, модуль которого равен , перпендикулярный плоскости векторов , направленный так, чтобы тройка векторов была правой (если смотреть с конца третьего вектора, кратчайший поворот от первого ко второму должен происходить против часовой стрелки).

Обозначение. 2 (вольт — частотная корректировка) 3. Добавить вентиляторную…

1 Ответ

  • ПЧ
  • Скалярное управление
  • АД

14.12.2022

  • Отвеченный вопрос
  • 13.12.2022

Другое, Математика и статистика, Цифровая обработка сигналов

Здравствуйте. Подскажите пожалуйста как (и можно ли вообще) решить систему квадратных уравнений. eqn1=(x-y)/(A0-x-y)/(m0-x-2*y)==K1; eqn2=y/(x-y)/(m0-x-2*y)==K2; То есть выразить переменные x и y чер…

Здравствуйте. Подскажите пожалуйста как (и можно ли вообще) решить систему квадратных уравнений. eqn1=(x-y)/(A0-x-y)/(m0-x-2*y)==K1; eqn2=y/(x-y)/(m0-x-2*y)==K2; То есть выразить переменные x и y чер…

5 Ответов

  • Публикация
  • 07.12.2022

Электропривод и силовая электроника

Наша команда представила решение для электроэнергетической отрасли на базе КПМ РИТМ. В очередной раз мы провели демонстрацию работы стенда с терминалами РЗиА (ВАЖНО! — мы не занимаемся рекламой сипротеков, на их месте может быть любой терминал, в том числе и В. ..

На прошлой неделе прошел международный форум «Электрические сети», который объединил десятки ведущих представителей профессионального сообщества электроэнергетики, а также задал вектор развития для внедрения новых прорывных технологий.

  • Электропривод
  • электроэнергетика

07.12.2022

  • Публикация
  • 07.12.2022

Робототехника и беспилотники

В докладе будет рассказано о применении алгоритмов обучения с подкреплением к различным задачам: от простых игровых задач до задачи навигации мобильного робота. Также будут представлены результаты сравнения различных алгоритмов в задачах избежания столкновения…

Приглашаем на вебинар «Обучение с подкреплением: от игр к реальным задачам», который пройдет 13 декабря в 10:00.

В настоящее время технологии обучения с подкреплением активно применяются во многих сферах: от ритейла до автономных транспортных средств. Может быть лучше: основной сложностью этого подхода является отсутствие размеченных данных, и, к сожалению, нет формализованного подхода как данные могут быть размечены для этой задачи.

Другая сложность — это формализация функции вознаграждения. От удачного ее выбора зависит конечный успех настройки алгоритма управления.

  • MATLAB
  • Simulink
  • САУ
  • МОП
  • Модельно ориентированное проектирование
  • Искусственный интеллект

07.12.2022

  • вопрос
  • 07.12.2022

Системы связи, Цифровая обработка сигналов, ПЛИС и СнК, Другое

Здравствуйте! У меня вопрос по поводу дифференциальной квадратурной фазовой модуляции (DQPSK), которая применяется в стандарте связи TETRA.  Мне необходимо построить сигнал с данной модуляцией и…

Здравствуйте! У меня вопрос по поводу дифференциальной квадратурной фазовой модуляции (DQPSK), которая применяется в стандарте связи TETRA.  Мне необходимо построить сигнал с данной модуляцией и…

13 Ответов

  • вопрос
  • 07. 12.2022

Изображения и видео, Математика и статистика, Автоматизация испытаний, Другое

Добрый день, мне нужно выполнить в матлаб вычитание постоянного наклона для изображения, полученного атомно-силовым микроскопом. Изображение представляет собой квадратную матрицу. Для этого требуется…

Добрый день, мне нужно выполнить в матлаб вычитание постоянного наклона для изображения, полученного атомно-силовым микроскопом. Изображение представляет собой квадратную матрицу. Для этого требуется…

6 Ответов

  • вопрос
  • 06.12.2022

Математика и статистика, Системы управления, Изображения и видео, Робототехника и беспилотники, Глубокое и машинное обучение(ИИ)

Коллеги, добрый день.     Как правильно орудоватьть fprintf, чтобы получить лог-файл следующего вида дата tab событие дата tab событие ….   Я прорбую вот так: fid1=fopen(fullfile(app….

Коллеги, добрый день.     Как правильно орудоватьть fprintf, чтобы получить лог-файл следующего вида дата tab событие дата tab событие ….   Я прорбую вот так: fid1=fopen(fullfile(app….

1 Ответ

  • вопрос
  • 05.12.2022

Системы управления, Изображения и видео, Робототехника и беспилотники, Глубокое и машинное обучение(ИИ), Другое

Дорогой, hub/exponenta/   подсткажите, пожалуйста, есть ли какая-нибудь разница при запуске в среде Апп дизайнера и откомпелировангого проекта? В среде Апп дизайнера файл создается с помощью функ…

Дорогой, hub/exponenta/   подсткажите, пожалуйста, есть ли какая-нибудь разница при запуске в среде Апп дизайнера и откомпелировангого проекта? В среде Апп дизайнера файл создается с помощью функ…

1 Ответ

  • вопрос
  • 05.12.2022

Системы управления, Робототехника и беспилотники, Математика и статистика, Верификация и валидация, Встраиваемые системы, Автоматизация испытаний, Изображения и видео, Цифровая обработка сигналов, Другое

Здравствуйте, никак не пойму как нужно соединить блоки, чтобы построить систему. Пожалуйста помогите, спасибо. Задание. Моделирование работы магазина.Требуется промоделировать работу небольшого магази…

Здравствуйте, никак не пойму как нужно соединить блоки, чтобы построить систему. Пожалуйста помогите, спасибо. Задание. Моделирование работы магазина.Требуется промоделировать работу небольшого магази…

  • вопрос
  • 04.12.2022

Другое

У вас на сайте была переведенная на русский документация MATLAB? Не могу найти.

У вас на сайте была переведенная на русский документация MATLAB? Не могу найти.

4 Ответа

Maths — Vector Cross Product

Когда мы смотрели на векторы, мы видели, что они должны иметь две операции сложения и скалярного умножения.

операция обозначение объяснение
дополнение В(а+б) = В(а) + В(б) сложение двух векторов выполняется путем сложения соответствующих элементов двух векторов.
скалярное умножение В(с*а) = с * В(а) скалярное произведение вектора получается путем умножения скалярного произведения на каждый из его членов в отдельности.

Эти операции взаимодействуют в соответствии со свойством дистрибутивности: s*(b+c)=s*b+s*c

В дополнение к этим операциям у нас могут быть другие операции, которые мы можем применять к векторам, такие как векторное пересечение продукт:

Векторное перекрестное произведение

В отличие от скалярного произведения оба операнда и результат перекрестного произведения являются векторами.

Векторное перекрестное произведение обладает некоторыми полезными свойствами. Оно дает вектор, взаимно перпендикулярный двум перемножаемым векторам.

Результирующий вектор A × B определяется как:

x = Ay * Bz — By * Az
y = Az * Bx — Bz * Ax
z = Ax * By — Bx * Ay

, где x, y и z — компоненты A x B

Скалярная длина A×B равна,

|A × B| = |А| * |Б| * sin(θ)

, где θ — угол между A и B.

Интерпретация перекрестного произведения только для трехмерных векторов. Например, в 2 измерениях невозможно найти другой вектор, взаимно перпендикулярный 2 произвольных вектора, в 4 измерениях (или больше) есть много векторов, которые взаимно перпендикулярны двум произвольным векторам.

Перекрестное произведение можно использовать для вычисления нормали к поверхности как показано здесь.

Пример

На приведенной выше диаграмме трудно четко обозначить направления. представляют все 3 измерения. Поэтому я подумал, что это поможет проверить направление разработав пример с приблизительным направлением:

Если мы позволим:

Вектор A должен быть в направлении y (Ax=0 , Ay=1 , Az = 0)
Вектор B должен быть в направлении x (Bx=1, By=0, Bz = 0)

, значит, компоненты вектора A×B:

х = Ау * Бз — Ву * Аз = 0
у = Az * Bx — Bz * Ах = 0
z = Ax * By — Bx * Ay = -1

так,

AxB = (0 , 0 , -1) = вдали от зрителя

Перекрестное произведение также определяется определителем:

i и к
Топор Ай Аз
Бх По Бз

где: i,j и k — единичные векторы в измерениях x,y и z.

Важные вопросы

Мы должны быть осторожны при выполнении векторной алгебры с перекрестным умножением, потому что мы не можем использовать обычные правила:

  • Векторные векторные произведения применимы только к векторам в 3 или 7 измерениях. (на одно измерение меньше, чем в алгебрах с делением кватернион=4, октонион=8).
  • Векторные перекрестные произведения не коммутируют, они антикоммутируют (A×B = -B×A) это не обязательно плохо, например, трехмерное вращение не коммутирует, но мы должны быть осторожны.
  • Векторные перекрестные произведения не являются ассоциативными, они антиассоциативны ((A × B) × C не может равняться A × (B × C))
  • Квадрат вектора равен нулю.
  • Перекрестное умножение не имеет однозначного обратного.
  • Элемент идентичности отсутствует I × A = A

Тождества

A×B + B×A = 0 антикоммутативный, векторное перекрестное умножение не является коммутативным, изменение порядка меняет направление результирующего вектора на противоположное: A×B = — B×A.
А×(В×С) +
В × (С × А) +
С × (А × В) = 0

Тождество Якоби: антиассоциативное: антисимметричное
Таким образом, перекрестное умножение не является ассоциативным.

А × А = 0 «В квадрате» — это вектор нулевой длины, поскольку sin(0) = 0
А × (В + С) = (А × В) + (А × С) перекрестное умножение для векторов является распределительным над +
0 × А = 0  

Где:

  • A,B и C = любые векторы
  • 0 = вектор нулевой длины (все элементы равны нулю)
  • × = векторное перекрестное произведение

Например, следующее выражение:

A × A × B

Можно было бы ожидать, что оно равно нулю, поскольку A x A = 0, но это не обязательно так, поскольку перекрестное умножение не является ассоциативным. Нам нужно указать порядок, если это:

A × (A × B)

то результат не обязательно нулевой.

Родственные умножения

Существуют обобщения векторной алгебры, например,

Алгебра Клиффорда В частности, внешний продукт алгебры Грассмана, который включен в алгебру Клиффорда.
Алгебра Ли Алгебра Ли представляет собой линеаризацию групп Ли и, следовательно, связывает эту тему с группами и симметриями.

Продукт Grassmann для экстерьера обладает гораздо лучшими свойствами, чем перекрестный продукт:

  • Продукт Grassmann применим в любом количестве измерений.
  • Произведение Грассмана ассоциативно.

Сравнение с продуктом экстерьера

Произведение экстерьера объединяет два вектора и дает бивектор. В трех измерениях бивектор имеет сходные свойства с вектором, поэтому во многих случаях его можно рассматривать как вектор. Например, таблица умножения для перекрестного произведения:

a×b

 b.e1 b.e2 b.e3
a.e1 0 е3 -e2
a.e2 -e3 0 е1
а.е3 е2 -e1 0

Внешняя таблица умножения:

a/\b

 b.e1 b.e2 b.e3
a.e1 0 е1/\е2 -e3/\e1
a.e2 -e1/\e2 0 е2/\е3
а. е3 е3/\е1 -e2/\e3 0

Таким образом, результат двух типов умножения практически одинаков, разница в том, что внешнее умножение дает бивектор, а не вектор. Важно то, что таблица умножения вектора /\ бивектора не совпадает с вектором /\ вектором, на самом деле таблица умножения вектора /\ бивектора подобна скалярному произведению вектора • вектора.

Итак, когда у нас есть тройное умножение, они ассоциативны, внешний продукт 3 векторов, A, B и C дает объем, заключенный в трех векторах:

A /\ B /\ C

Это эквивалентно следующему уравнению перекрестного и скалярного произведений:

(A × B) • C

Двойственность между векторами и бивекторами в трех измерениях

Эта двойственность применима только к трем измерения, если два 2-мерных вектора перемножаются, бивектор является одномерным, если два 4-мерных вектора перемножаются, бивектор является 6-мерным. бивекторы обсуждаются здесь.

Только в трехмерной векторной алгебре бивектор также имеет три измерения, поэтому для большинства целей (в трех измерениях) мы можем рассматривать результат векторного произведения как вектор.

Кососимметричная матрица

Мы также можем разработать кососимметричную матрицу 3×3, которая эквивалентна перекрестное произведение, другими словами, если

C = A × B

Тогда мы можем найти кососимметричную матрицу [~A] такую, что:

C = [~A] B

Эта матрица:

[~А] =
0 -Аз Ай
Аз 0 -Топор
-Ай Топор 0

Как описано здесь.

Код:

Ниже приведен код Java для векторного векторного произведения.

 Void cross(sfvec3f other) {
   двойной xh = y * other.z - other.y * z;
   двойное yh = z * другое.x - другое.z * x;
   двойной ж = х * др.у - др.х * у;
   х = хч;
   у = ух;
   г = ж;
}

Ниже приведен управляемый код C++ для векторного векторного произведения.

 Недействительно sfvec3f::cross(sfvec3f* другое) {
   двойной xh = y * другое->z - другое->y * z;
   двойной yh = z * другое->x - другое->z * x;
   двойное zh = x * другое->y - другое->x * y;
   х = хч;
   у = ух;
   г = ж;
}

Этот метод будет использоваться классом sfvec3f.

Дополнительная литература

Векторами можно управлять с помощью матриц, для Пример переведен, повернут, масштабирован, отражен.

Существуют математические объекты, известные как мультивекторы, их можно использовать для выполнения многих задач, которые выполняют векторы, но у них нет некоторые ограничения (например, векторное перекрестное произведение ограничено 3 измерениями и не имеет обратного).

Перекрестные произведения единичных векторов

Перекрестные произведения единичных векторов

Часть 2: тройное скалярное произведение

Если r = № р 1 , р 2 , р 3 с , u = á u 1 , u 2 , u 3 ñ и v = á v 1 , v 2 , v 3 ñ , то из (3) следует, что

r · ( u × v ) =
Однако в силу (4) имеем
Мы называем это тождество тройным скалярным произведением : .
r · ( u × v )  =  ( r × u ) · v

Тройное скалярное произведение часто используется для получения других свойств перекрестное произведение. Например, u × u = 0 означает, что

9 об.

ПРИМЕР 3    Покажите, что u × v ортогональны u , когда u = 2,3,7 с и v = 1,4,2 с .

Решение: Для начала заметим, что

u · ( u × v ) = ( u × u ) · v = 0
б 6-28, 7-4, 8-3 –
б-22, 3, 5 –
Теперь вычислим u · ( u × v ) :
u ·( u × v ) = б2,3,7 с · б-22,3,5 с = -44+9+35 = 0
Векторы u , v и u × v показаны ниже:

Maple/javaview изображение

В качестве другого примера рассмотрим, что

i × j =    , , знак равно 0,0,1 –
То есть i × j = k , что перпендикулярно обоим i и j .

alexxlab

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *