ОглавлениеВВЕДЕНИЕЧАСТЬ ПЕРВАЯ. ВЕКТОРНАЯ АЛГЕБРА Глава I. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ 2. Скаляры и векторы. 3. Равенство векторов. 4.  Скользящие и приложенные векторные величины.6. Орт вектора. 7. Угол между двумя векторами. § 2. Сложение векторов 1. Сложение двух векторов. 2. Сложение более чем двух векторов. 3. Модуль суммы. 4. Законы сложения. § 3. Вычитание векторов § 4. Умножение и деление вектора на скаляр 2. Законы умножения вектора на скаляр. 3. Деление вектора на скаляр. 4. Выражение вектора через его модуль и орт. § 5. Линейные зависимости между векторами 2. Коллинеарные векторы. 3. Компланарные векторы. 4. Разложение вектора по трем некомпланарным векторам. 5. Метод координат. Глава II. ТЕОРИЯ ПРОЕКЦИЙ. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ § 1. Проекции векторов на ось § 3. Прямоугольная система координат в пространстве 1. Правая и левая прямоугольные системы координат. 2. Разложение вектора по ортам осей 3. Линейные операции над векторами в координатной форме.  4. Радиус-вектор и координаты точки. 5. Определение вектора по его началу и концу. 6. Деление отрезка в данном отношении. Глава III. ПРОИЗВЕДЕНИЯ ДВУХ ВЕКТОРОВ § 1. Скалярное произведение двух векторов 2. Работа силы. 3. Определение. 4. Равенство скалярного произведения нулю. 5. Законы скалярного умножения. 8. Скалярное произведение в координатной форме. 9. Неопределенность действия, обратного скалярному умножению. § 2. Векторное произведение двух векторов 3. Условия равенства нулю векторного произведения. 4. Законы векторного умножения. 5. Векторные произведения координатных ортов. 6. Определители. 7. Векторное произведение в координатной форме. 8. Неопределенность действия, обратного векторному умножению. Глава IV. ПРОИЗВЕДЕНИЯ ТРЕХ ВЕКТОРОВ § 1. Простейшее произведение трех векторов § 2. Векторно-векторное произведение трех векторов 3. Правило разложения векторно-векторного произведения.  § 3. Векторно-скалярное произведение трех векторов 2. Законы векторно-скалярного умножения 3. Обращение в нуль векторно-скалярного произведения трех векторов. 4. Векторно-скалярное произведение в координатной форме. § 4. Выражение векторно-скалярного произведения через скалярные произведения Глава V. ФУНКЦИИ ВЕКТОРОВ § 1. Произведения четырех векторов 2. Выражение скалярного произведения двух векторных произведений (а x b), (р x q) через скалярные произведения. 3. Разложение вектора (а, b, с) R по трем векторам a, b, c. 4. Разложение вектора (a, b, c) по векторным произведениям b x с, c x a, а x b 2. Разложение вектора (a, b, c) (m x n) по векторам a, b, c. 3. Выражение произведения двух смешанных произведений (a, b, c) (l, m, n) через скалярные произведения. § 3. Основные теоремы о функциях векторов 1. Рациональные функции векторов. 2. Элементарные функции векторов. 3. Произвольные скалярные функции от векторов. 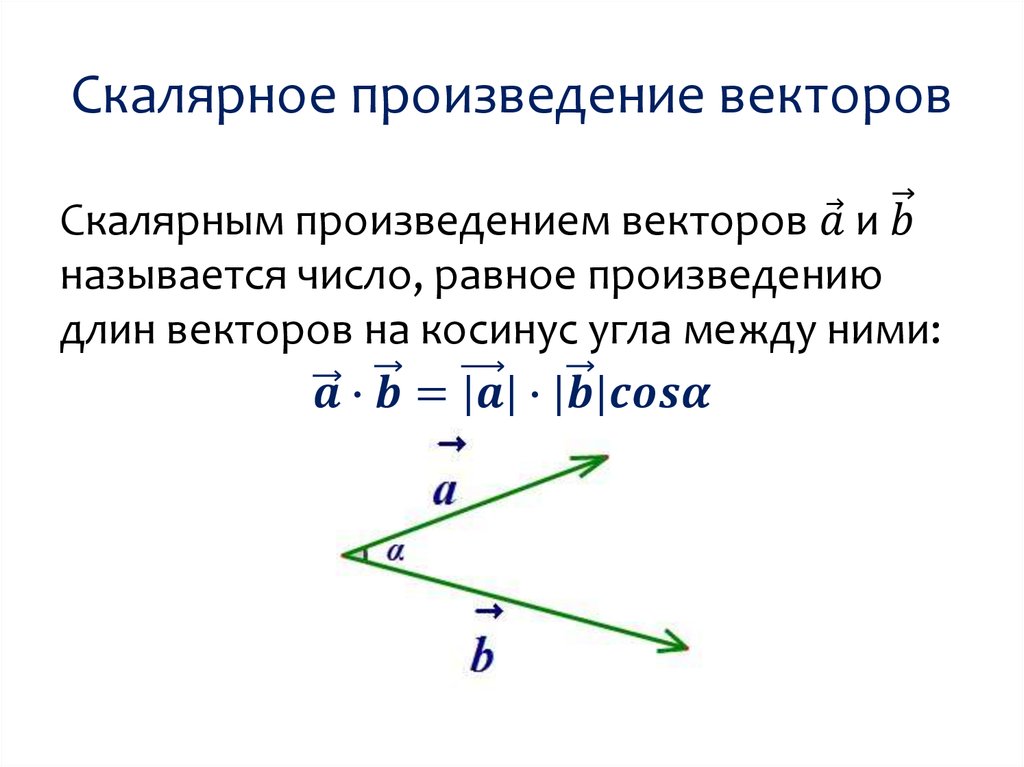 4. Произвольные векторные функции векторов. Глава VI. ОСНОВНЫЕ ЗАДАЧИ § 2. Основные задачи, связанные со скалярным умножением векторов § 3. Основные задачи, связанные с векторным умножением векторов § 5. Простейшие векторные уравнения § 6. Геометрические инварианты фигур 2. Треугольник. 3. Полные системы инвариантов треугольника. 4. Тетраэдр. 5. Полные системы инвариантов тетраэдра. 6. Гексаэдр с треугольными гранями. ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ § 1. Векторы, зависящие от скаляра 2. Вектор-функция в координатной форме. 3. Годограф вектора. 4. Предел вектора. § 2. Дифференцирование вектора по скаляру 2. Геометрический смысл производной вектора по скаляру. 3. Механический смысл производной. 5. Дифференциал вектора. 6. Инвариантность дифференциала. § 3. Формула Тейлора Глава VIII.  ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ЛИНИИ В ПРОСТРАНСТВЕ§ 1. Основные дифференциально-геометрические понятия, связанные с линией 2. Касательная. 3. Соприкасающаяся плоскость. 4. Главная нормаль и бинормаль. 5. Кривизна. 6. Кручение. 7. Длина дуги. § 2. Основные формулы дифференциальной геометрии линий в пространстве 1. Дуга как параметр. Дифференциал дуги. 2. Орт касательной. Первая основная формула. 3. Инвариантность геометрических понятий. 4. Главная нормаль и кривизна. Вторая основная формула. 6. Винтовая линия. § 3. Сопровождающий трехгранник 2. Система дифференциальных уравнений движения сопровождающего трехгранника. 3. Расположение линии относительно сопровождающего трехгранника. 4. Линии без кривизны. 5. Линии без кручения. § 4. Инвариантные формулы Глава IX. ПЛОСКИЕ ЛИНИИ § 1. Дифференциальные уравнения плоской линии § 2. Кривизна плоской линии § 3.  Круг кривизны§ 4. Эволюта § 5. Эвольвента Глава X. ПРИЛОЖЕНИЯ К МЕХАНИКЕ § 2. Движение твердого тела вокруг неподвижной точки 2. Формула Эйлера. 3. Угловая скорость. 4. Доказательстве существования угловой скорости твердого тела. § 3. Относительная производная вектора 2. Абсолютная и относительная производные вектора. 3. Общий случай движения твердого тела. Глава XI. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ § 1. Векторные функции нескольких скалярных аргументов § 2. Параметризованная поверхность 2. Поверхность в декартовых координатах. 3. Параметрическая сеть. 4. Линия на параметризованной поверхности. § 3. Касательная плоскость и нормаль 3. Нормальный вектор. 4. Преобразование параметров. 2. Площадь области на поверхности. 3. Формула для вычисления площади поверхности, заданной уравнением z=z(x,y). 4. Элемент площади поверхности. 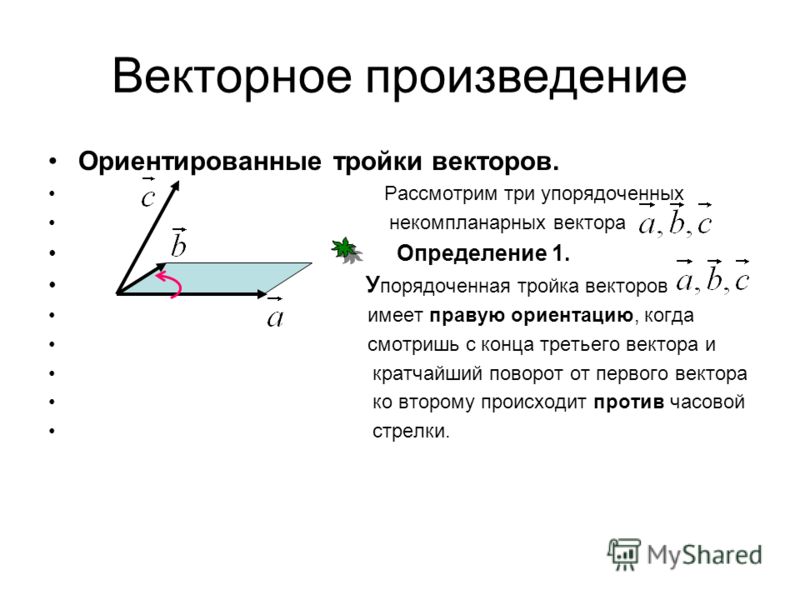 5. Векторный элемент площади поверхности. § 5. Первая квадратичная форма поверхности 2. Внутренняя геометрия поверхности. 3. Длина дуги линии на поверхности. 4. Угол между линиями на поверхности. 5. Площадь области на поверхности. § 6. Вторая квадратичная форма поверхности 2. Нормальная кривизна линии на поверхности. 3. Теорема Менье. § 7. Главные направления и главные кривизны поверхности 3. Перпендикулярность главных направлений. 4. Формула Эйлера. 5. Полная и средняя кривизны поверхности. ЧАСТЬ ТРЕТЬЯ. ТЕОРИЯ ПОЛЯ § 1. Функция поля. Поверхности уровня § 2. Градиент поля 2. Первая теорема о градиенте. § 3. Производная по направлению 2. Выражение производной по направлению через градиент. 3. Вторая теорема о градиенте. § 4. Направляющие косинусы нормали поверхности Глава XIII. КРИВОЛИНЕЙНЫЙ И ПОВЕРХНОСТНЫЙ ИНТЕГРАЛЫ § 1. Криволинейный интеграл как определенный интеграл от сложной функции 2.  Криволинейный интеграл от линейной формы по произвольной кривой.4. Обобщенный криволинейный интеграл. 5. Примеры. § 2. Криволинейный интеграл как предел криволипейной интегральной суммы § 3. Поверхностный интеграл как двойной интеграл от сложной функции 2. Определение простейшего поверхностного интеграла. 3. Поверхностный интеграл от билинейной формы по произвольной поверхности. § 4. Поверхностный интеграл как предел поверхностной интегральной суммы § 5. Поверхностный интеграл в параметрической форме 2. Параметрический поверхностный интеграл. 3. Поверхностный интеграл как предел суммы. § 6. Кратный интеграл как предел обобщенной интегральной суммы Глава XIV. ВЕКТОРНОЕ ПОЛЕ И ЕГО ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ § 1. Векторное поле § 2. Векторные линии § 3. Циркуляция поля вдоль линии § 4. Поток поля через поверхность Глава XV.  ТЕОРЕМА ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ПОЛЯ§ 1. Формула Остроградского § 2. Дивергенция поля 2. Дивергенция как предел отношения. 3. Гидромеханический смысл дивергенции. 4. Теорема Остроградского. Глава XVI. ТЕОРЕМА СТОКСА. РОТАЦИЯ ПОЛЯ § 1. Формула Стокса § 2. Ротация поля § 3. Оператор Гамильтона Глава XVII. СПЕЦИАЛЬНЫЕ ВЕКТОРНЫЕ ПОЛЯ § 1. Потенциальное поле 3. Циркуляция потенциального поля по замкнутому контуру. 4. Циркуляция потенциального поля между двумя точками. 5. Потенциал. 6. Элемент циркуляции. 7. Характеристические признаки потенциального поля. 8. Вычисление потенциала. 9. Центральное поле. 10. Вихревые шнуры. § 2. Соленоидальное поле 3. Поток соленоидального поля через замкнутую поверхность. 4. Трубчатое строение соленоидального поля. 5. Векторный потенциал. 6. Характеристические признаки соленоидального поля. 7. Источники и стоки. § 3. Потенциальное несжимаемое поле Глава XVIII.  ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ§ 1. Электростатическое поле точечного заряда 2. Дивергенция поля точечного заряда. 3. Поток поля точечного заряда через замкнутую поверхность. 4. Ротация поля точечного заряда. 5. Потенциал поля точечного заряда. § 2. Электростатическое поле системы точечных зарядов 2. Дивергенция и ротация поля системы точечных зарядов. 3. Поток поля системы точечных зарядов через замкнутую поверхность. 4. Потенциал поля системы точечных зарядов. 5. Непрерывно распределенный заряд. § 3. Магнитное поле тока 2. Напряженность магнитного поля тока, текущего по бесконечному прямолинейному проводу. 3. Векторные линии поля H. 4. Потенциал поля Н. 5. Провод как вихревой шнур. Глава XIX. ВЕКТОРНОЕ ПОЛЕ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ § 1. Криволинейные координаты 3. Координатные поверхности и линии. 4. Линейный элемент. 5. Элемент объема. 6. Подвижной репер. 7. Векторное поле в криволиненных координатах.  § 2. Дифференциальные операции в криволинейных координатах 2. Дивергенция в криволинейных координатах. 3. Ротация в криволинейных координатах. § 3. Ортогональные координаты § 4. Цилиндрические координаты 2. Линейный элемент и элемент объема в цилиндрических координатах. 3. Дифференциальные операции в цилиндрических координатах. § 5. Сферические координаты |
Векторная алгебра описывает способы выполнения различных операций над векторами, в том числе сложение, вычитание, разные типы перемножения. Здесь приводится лишь часть этого раздела математики, непосредственно относящаяся к задачам, наиболее часто возникающим в физической и инженерной практике. Понятие вектора В геометрическом смысле вектор — это направленный отрезок, определяемый точками своего начала и конца. Ограничения В силу специфики сайта векторные операции рассматриваются для наиболее частого случая — трёхмерного пространства, описываемого в декартовой системе координат (три взаимно ортогональные оси отсчёта). Для пространств меньшей мерности (двухмерной плоскости и одномерной прямой) обычно достаточно обнулить «неиспользуемые» координаты. Пространства большей мерности не рассматриваются, поскольку до сих пор являются физической экзотикой. Для работы с ними следует изучить курс векторной алгебры более серьёзно. В связи с малой практической востребованностью не рассматривается выполнение операций над векторами в полярных и других недекартовых системах координат. Не рассматривается и матричное исчисление, поскольку для трёхмерного пространства алгебраическая форма векторных операций является достаточно простой и удобной, хотя и не столь универсальной. Кроме того, матричное исчисление требует довольно специфического подхода, что затрудняет его применение теми, кто с прежде с матрицами не сталкивался. Основные понятияРассмотрим основные понятия, используемые на этой странице. Проекции и координаты вектора Любой трёхмерный вектор можно спроецировать на три взаимно перпендикулярные оси отсчёта, пересекающиеся в одной точке (декартовы оси координат). Выбор точки отсчёта и положение осей (базис системы координат) теоретически непринципиален, но на практике обычно выбирается так, чтобы как можно большее число участвующих в расчёте векторов было направлено вдоль какой-либо из осей координат — это упрощает вычисления. Каждый вектор можно охарактеризовать координатами двух точек — его начала и конца, — либо проекциями на оси координат и координатами точки привязки (обычно точкой привязки является начало вектора, но иногда бывает удобнее использовать в этом качестве его конец). В физике чаще применяется второй подход. В этом случае в трёхмерном пространстве вектор a описывается шестью величинами — координатами его точки привязки xa, ya, za и проекциями на оси ax, ay и az. Иногда точка привязки не имеет принципиального значения либо подразумевается неявно, и тогда обходятся тремя значениями — проекциями векторной величины на оси координат (ax, ay, az). Некоторые определения Модулем вектора |a| в геометрии называется его длина, а в физике — абсолютное значение направленной величины (т.е. значение, измеренное вдоль направления её действия). Среди всевозможных взаимных ориентаций векторов выделяют коллинеарные и ортогональные вектора. Коллинеарными называются такие вектора, векторное произведение которых равно нулю. Это параллельные вектора. Коллинеарные вектора могут быть сонаправленными или встречными, то есть направлеными строго в противоположные стороны. Ортогональными называются такие вектора, скалярное произведение которых равно нулю. Для любого вектора все вектора, лежащие в любой перпендикулярной ему плоскости, будут ортогональны. Понятие равных векторов менее однозначно. Иногда под этим понимают любые сонаправленные вектора одного размера, расположение точки привязки которых безразлично и может быть в любом месте пространства. Более строгое определение подразумевает и совпадение точек привязки. В физике под «равенством векторов» обычно имеют в виду первый случай (величины и направления одинаковы, положение точки привязки произвольно). Нулевым является вектор, имеющий нулевую длину, то есть тот, у которого координаты начала и конца строго совпадают. В связи с этим обычно нельзя говорить о направлении такого вектора, поэтому его считают не имеющим направления. Иногда нулевой вектор трактуют как всенаправленный, хотя в строгом смысле это не так. Операции над векторамиСложение векторовВ алгебраическом представлении при сложении векторов с = a + b проекция результирующего вектора на оси координат является суммой соответствующих проекций складываемых векторов с учётом их знака: сx = ax + bx ;сy = ay + by ; сz = az + bz . Если точка привязки не важна, а важна лишь величина (длина и направление) результирующего вектора, то сложение векторов можно считать коммутативной операцией (от перемены мест слагаемых сумма не меняется). Вычитание векторовВычитание векторов с = a – b можно представить как сложение уменьшаемого вектора с вектором, противоположным вычитаемому по направлению и равным ему по величине. Таким образом, в агебраическом представлении проекции вычитаемого вектора на оси координат меняют свой знак: сx = ax – bx ;сy = ay – by ; сz = az – bz . Умножение вектора на числоПри умножении вектора на число b = k · a в алгебраическом виде достаточно все его проекции умножить на это число: bx = k · ax ;by = k · ay ; bz = k · az .  В строго геометрическом смысле при умножении на число начало вектора остаётся на месте, а «удлиняется» его конец. Однако на физических иллюстрациях часто остаётся на месте точка конца вектора, скажем точка приложения силы, хотя в общем случае этот вопрос всегда определяется физическим смыслом решаемой задачи. Операция умножения на число является коммутативной a · k = k · a (от перемены мест сомножителей результат не меняется). При положительном множителе результирующий вектор сонаправлен с исходным, при отрицательном направление меняется на строго противоположное. Поэтому результат умножения вектора на число всегда коллинеарен с исходным вектором, за исключением случая, когда множитель или исходный вектор являются нулевыми — тогда результатом будет нулевой вектор, говорить о направлении которого некорректно. Операция умножения на число является дистрибутивной k · (a + b) = k · a + k · b (произведение суммы векторов на число равно сумме произведений слагаемых на это же число). Скалярное произведение векторовРезультатом скалярного перемножения векторов является число, равное произведению их модулей, умноженному на косинус угла между ними. Вычисление скалярного произведенияВ алгебраической форме скалярное произведение d = a · b вычисляется как d = ax · bx + ay · by + az · bz .Свойства скалярного произведенияКоммутативность: a · b = b · a . Дистрибутивность: a · (b + c) = a · b + a · c . Сочетательность (линейность) относительно скалярного множителя: k · (a · b) = (k · a) · b = a · (k · b) . Скалярный квадрат вектора равен квадрату его модуля: a · a = |a|2 (норма вектора). Векторное произведение векторов
Результатом векторного перемножения двух векторов a и b является вектор c, длина которого равна произведению их модулей, умноженному на синус угла между ними, а сам вектор ориентирован таким образом, что перпендикулярен обоим исходным векторам, и тройка a b c является правой. Вычисление векторного произведенияВ алгебраической форме векторное произведение c = [a × b] в правой системе координат вычисляется как сx = ay · bz – az · by ;сy = az · bx – ax · bz ; сz = ax · by – ay · bx . В левой системе координат знаки слагаемых меняются на противоположные. В физике обычно подразумевается, что точки привязки всех перемножаемых векторов и результирующего вектора совпадают (и вектора-сомножители, и результат их векторного произведения действуют в одной и той же точке пространства). Свойства векторного произведенияАнтикоммутативность: [a × b] = –[b × a] . Дистрибутивность: [a × (b + c)] = [a × b] + [a × c] . Сочетательность относительно скалярного множителя: k · [a × b] = [(k · a) × b] = [a × (k · b)] . Смешанное произведение: a · [b × c] = [a × b] · c . Векторный квадрат вектора всегда является нулевым вектором: [a × a] = 0 . Поэтому, когда говорят о «квадрате вектора» без уточнения типа перемножения, имеют в виду скалярный квадрат (квадрат модуля вектора). ♦ | |
| последняя правка 27.01.2011 21:01:52 |
В физическом смысле под векторами обычно понимаются величины, имеющие направление в трёхмерном пространстве. Как правило, они характеризуются абсолютной величиной, направлением и точкой приложения (точкой привязки). Во времена Ньютона эти три категории были достаточно автономны и их увязка была своего рода искусством. Применение концепции векторов позволило формализовать естественную взаимосвязь этих категорий и сделать операции над ними более наглядными и удобными.
В ортогональной системе координат модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.
Если же одинаковы и точки привязки, то речь идёт о совпадающих (эквивалентных) векторах.
В противном случае точка привязки результирующего вектора определяется исходя из физического смысла производимой операции (как правило, в физике точки привязки всех складываемых векторов и суммарного вектора совпадают, — то есть и все слагаемые, и их сумма применимы к одной и той же точке пространства или к одной и той же материальной точке).
Карта механики — Перекрестное произведение
Перекрестное произведение — это математическая операция, которая может выполняться над любыми двумя трехмерными векторами . Результатом операции перекрестного произведения будет третий вектор, который перпендикулярен обоим исходным векторам и имеет величину первого вектора, умноженную на величину второго вектора, умноженную на синус угла между векторами.
Перекрестным произведением двух векторов будет вектор, который перпендикулярен обоим исходным векторам с величиной A, умноженной на B, умноженной на синус угла между A и B.
При нахождении векторного произведения вы можете заметить, что на самом деле есть два направления, которые перпендикулярны обоим исходным векторам. Эти два направления будут прямо противоположными. Чтобы найти, какое из этих двух направлений использует перекрестное произведение, мы воспользуемся правилом правой руки .
Чтобы использовать правило правой руки, вытяните правую руку, укажите указательным пальцем в направлении первого вектора, поверните средний палец в направлении второго вектора и поднимите большой палец. Теперь ваш большой палец должен указывать в направлении вектора векторного произведения.
Мы можем использовать правило правой руки, чтобы определить направление векторного произведения. Изображение адаптировано из работы Acdx под лицензией CC-BY-SA 3.0. Еще одна вещь, которую вы можете заметить с помощью правила правой руки, заключается в том, что изменение порядка двух входных векторов (переключение A и B) приведет к тому, что векторное произведение укажет точно в противоположном направлении.
Это связано с тем, что операция перекрестного произведения не является коммуникативной , а это означает, что порядок имеет значение. В частности, переключение порядка ввода дает вам результат, прямо противоположный исходному расчету.
Чтобы найти векторное произведение вручную, самый простой способ заключается в следующем.
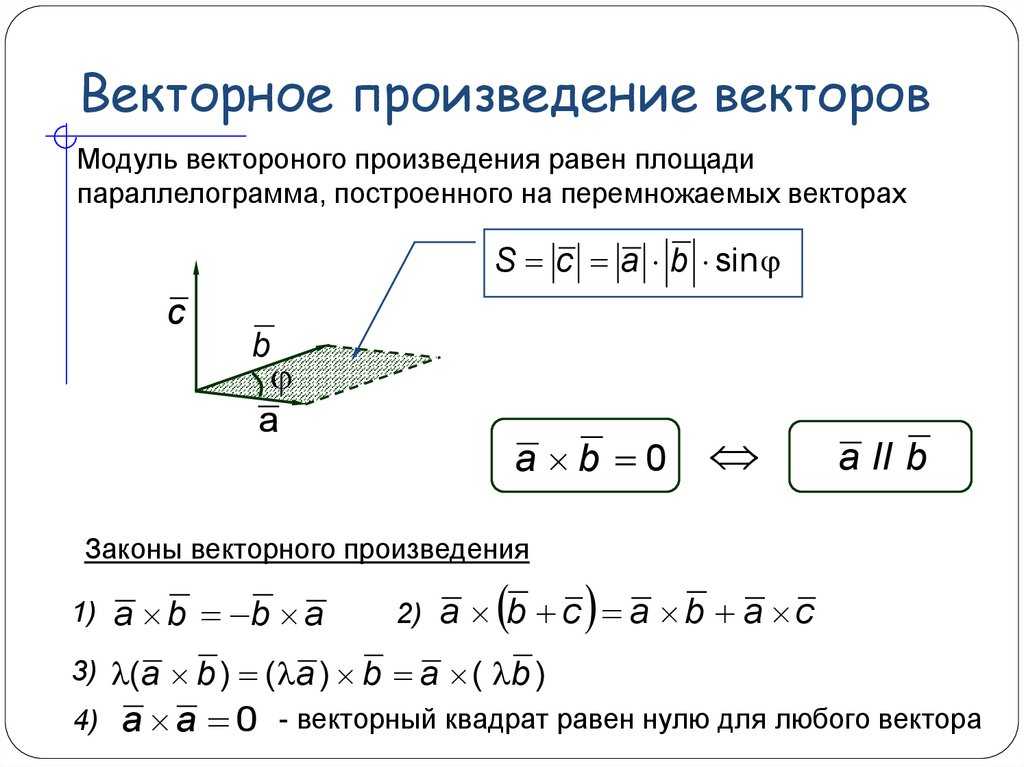
- Запишите буквы x y z x y в ряд, как показано на рисунке ниже.
- Запишите компоненты x, y и z первого вектора под соответствующими буквами выше. Повторите это для второго вектора, записав второй вектор в строке под первым вектором.
- Нарисуйте диагонали, как показано на рисунке. Диагонали, идущие вправо при движении вниз, представляют собой положительные величины, а диагонали, идущие влево при движении вниз, представляют собой отрицательные величины.
- Используя буквы, через которые проходят диагонали в верхнем ряду, в качестве руководства для того, какой компонент результата является частью каждой величины, возьмите сумму положительных и отрицательных диагональных произведений для каждого из трех компонентов в результате.
Это должно дать вам окончательную формулу, показанную на диаграмме.
Это должно дать вам окончательную формулу, показанную на диаграмме.В дополнение к вычислению перекрестного произведения вручную мы также можем использовать компьютерные инструменты, такие как команда «перекрест» в MATLAB, или веб-инструменты, такие как калькулятор векторных операций Wolfram, ссылки на которые приведены на боковой панели этой страницы. Доступ к этим инструментам позволяет очень легко и быстро вычислять векторное произведение и является основным преимуществом использования векторных операций для анализа проблем.
Формула векторного перекрестного произведения | Примеры с шаблоном Excel
Формула векторного перекрестного произведения (оглавление)
- Формула
- Примеры
В векторной алгебре и математике термин «векторное перекрестное произведение» относится к бинарным операциям между векторами в трехмерной геометрии.
Перекрестное произведение обозначается перекрестным знаком «x» между двумя векторами, а операция перекрестного произведения приводит к другому вектору, который перпендикулярен плоскости, содержащей исходные два вектора. Формула для векторного векторного произведения может быть получена путем умножения абсолютных значений двух векторов и синуса угла между двумя векторами. Математически предположим, что A и B — два вектора, такие как A = A 1 I + A 2 J + A 3 K и + A . 1 I + B 2 J + B 3 K , затем векторный поперечный продукт представлен как
A X B = | A | |б| sin θ п
, где θ = угол между a и b
|a| = √(a 1 2 + a 2 2 + a 3 2 )
|b| = √ (B 1 2 + B 2 2 + B 3 2 )
N = Единоличный вектор перпендикулярный0004
Кроме того, векторное векторное произведение также можно разложить на его трехмерные векторные компоненты, т.
е. i , j и k , которые все перпендикулярны друг другу. Формула векторного векторного произведения представлена как
a x b = i (a 2 b 3 – a 3 b 2 ) + j (a 5 0 6 7 1 3 9005 а 1 б 3 ) + к (а 1 б 2 – a 2 b 1 )
Примеры формулы векторного перекрестного произведения (с шаблоном Excel)Давайте рассмотрим пример, чтобы лучше понять расчет векторного перекрестного произведения.
Вы можете скачать этот шаблон Excel с формулой векторного перекрестного произведения здесь — Формула векторного перекрестного произведения Шаблон Excel
Формула векторного перекрестного произведения — пример № 1
Давайте рассмотрим пример двух векторов a и b такие, что их скалярная величина равна |a| = 5 и |б| = 3, а угол между двумя векторами равен 30 градусов.
Вычислите векторное перекрестное произведение двух векторов.
Решение:
Векторное перекрестное произведение двух векторов вычисляется по формуле, приведенной ниже: |б| sin θ n
- a x б = 5 * 3 * sin30 п
- a x b = 7,5 n
Следовательно, векторное произведение двух векторов равно 7,5.
Формула векторного векторного произведения – пример № 2
Рассмотрим пример двух векторов a (4, 2, -5) и b (2, -3, 7), таких, что a = 4i + 2j – 5k и b= 2i – 3j + 7k. Вычислите векторное перекрестное произведение двух векторов.
Решение:
Векторное векторное произведение двух векторов вычисляется по формуле, приведенной ниже j (a 3 b 1 – a 1 b 3 ) + k (a 1 b 2 – a 2 b 1 )
- a x б = i {2 * 7 – (-5) * (-3)} + j {(-5) * 2 – 4 * 7} + k {4 * (-3) – 2 * 2}
- a x b = -i + ( – 38 j ) + ( – 16 k 2 )
Следовательно, векторное перекрестное произведение двух векторов (4, 2, -5) и (2, -3, 7) равно (-1, -38, -16).
Формула векторного векторного произведения – Пример №3
Рассмотрим пример параллелограмма, смежные стороны которого определяются двумя векторами a (6, 3, 1) и b (3, -1, 5) такие, что a = 6i + 3j + 1k и b = 3i – 1j + 5k. Вычислите площадь параллелограмма.
Решение:
Теперь векторный поперечный продукт двух векторов можно рассчитать с использованием выше формулы,
A X B = I (A 2 B 3 — A 666 2 B 3 — A 66666. 3 б 2 ) + к (а 3 б 1 – а 1 б 3 ) + к (а 1 B 2 -A 2 B 1 )
- A X B = I {3 * 5-1 * (-1)} + j00044 j. 4 j. 1 * 3 – 6 * 5} + k {6 * (-1) – 3 * 3}
- a x b = 16 i + ( – 27 j ) + ( – 15 k 2
Теперь площадь параллелограмма может быть получена путем вычисления величины векторного векторного произведения как,
- |а х б| = √[(16) 2 + (-27) 2 + (-15) 2 ]
- |а х б| = 34,79
Следовательно, площадь параллелограмма равна 34,79.
Объяснение
Формулу векторного векторного произведения можно вывести, выполнив следующие действия:
Шаг 1: Сначала определите первый вектор a и его векторные компоненты.
Шаг 2: Затем определите второй вектор b и его компоненты вектора.
Шаг 3: Далее определите угол между плоскостями двух векторов, который обозначается как θ .
Шаг 4: Наконец, формула векторного векторного произведения между векторами a и b может быть получена путем умножения абсолютных значений a и b , который затем умножается на синус угла (шаг 3) между двумя векторами, как показано ниже.
a x b = |a| |б| sin θ n
Актуальность и использование формулы векторного перекрестного произведения
Концепция векторного перекрестного произведения имеет разнообразные применения в области инженерии, математики, вычислительной геометрии, физики, компьютерного программирования и т.
