Геометрия Умножение вектора на число

Материалы к уроку

Конспект урока

5. Умножение вектора на число

Произведением ненулевого вектора а на число k называется такой вектор  b, длина которого равна модуль |k| умноженный на модуль|а|, причем векторы а и b сонаправлены, если  k положительно и  противоположно направлены, если k отрицательно. Произведение вектора а на число k обозначается так: ka.	Текст Умножение вектора на число   Рисунок векторов
Для любого числа k и любого вектора а векторы а и ka коллинеарны. Произведением нулевого вектора на любое число считается нулевой вектор. Произведение любого вектора на число нуль есть нулевой вектор.	Текст Умножение вектора на число
Рассмотрим основные свойства умножения вектора на число. Для любых векторов а,b и любых чисел k и l справедливы равенства: Первое. Произведение k и l, умноженное на вектор а, равно произведению k на вектор lа. Это свойство известно как сочетательный закон. На рисунке, на примере показано это свойство.	Текст Свойства умножения вектора на число Сочетательный закон   Рисунок векторов   Текст
Второе свойство, первый распределительный закон. Произведение числа k на сумму векторов а и b  равно сумме произведений этого числа на векторы а и b. На рисунке, на примере показано это свойство.	Текст Свойства умножения вектора на число Первый распределительный закон
Третье свойство, второй распределительный закон. Произведение суммы чисел k и  l на вектор равно сумме произведений чисел k и l на вектор а. На рисунке, на примере показано это свойство.	Текст Свойства умножения вектора на число Второй распределительный закон
Стоит отметить, что произведение числа -1 на любой вектор дает вектор противоположный данному. Согласно определению произведения вектора на число, их длины равны, а направления противоположны. При условии, что вектор а ненулевой.	Текст
Для векторов в пространстве, как и в планиметрии, выполняется следующее условие: Если векторы a и b коллинеарны (то есть лежат на одной прямой или на параллельных прямых) и вектор а ненулевой, то существует число k такое что вектор b  равен произведению числа k на вектор а.
Решим задачу №347 (а) Необходимо упростить выражение.
Решение. Первый распределительный закон позволяет нам раскрыть скобки. А переместительное свойство сложения векторов – привести подобные.	.

Остались вопросы по теме? Наши репетиторы готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитора

Математические Законы

Переместительный закон сложения

Начнем изучать основные законы математики со сложения натуральных чисел.

Переместительный закон сложения От перестановки мест слагаемых сумма не меняется. С помощью переменных его можно записать так: m + n = n + m

Переместительный закон сложения работает для любых чисел.

Если прибавить шестерку к двойке — получим восьмерку. И наоборот, прибавим двойку к шестерке — снова получим восьмерку. Это доказывает справедливость переместительного закона сложения.

• 6 + 2 = 8
• 2 + 6 = 8

Приведем пример с весами, которые используют продавцы в магазинах.

Если мы положим на одну чашу весов 3 килограмма конфет, а на другую — такие же 3 килограмма конфет, то стрелка весов будет на нейтральной позиции. Это говорит нам о том, что чаши действительно весят одинаково.

При этом неважно, как будут лежать конфеты, в каком порядке. Если перемешать конфеты в пакете, как шары в лотерейном мешке — их вес не изменится и будет по-прежнему 3 килограмма. От перестановки мест конфет их сумма, то есть вес, не меняется.

Поэтому, между выражениями 8 + 2 и 2 + 8 можно поставить знак равенства. Это значит, что их сумма равна:

• 8 + 2 = 2 + 8
• 10 = 10

Формула переместительного закона для обыкновенных дробей:

Чтобы сложить две дроби с одинаковым знаменателем, нужно сложить числители, а знаменатель оставить прежним.

Вот так:

Демоурок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Сочетательный закон сложения

Сочетательный закон сложения помогает группировать слагаемые для удобства их вычислений.

Сочетательный закон сложения: два способа Результат сложения нескольких слагаемых не зависит от порядка действий. Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.

Чтобы лучше запомнить суть этого закона, просто выбирайте формулировку, которая вам больше нравится.

Рассмотрим сумму из трех слагаемых:

• 1 + 3 + 4

Чтобы вычислить это выражение, можно сначала сложить числа 1 и 3 и к полученному результату прибавить 4. Чтобы было удобнее, можно сумму 1 и 3 взять в скобки — так мы поймем, что ими нужно заняться в первую очередь:

• 1 + 3 + 4 = (1 + 3) + 4 = 4 + 4 = 8

Или по-другому: сложим числа 3 и 4 и к результату прибавим 1:

• 1 + 3 + 4 = 1 + (3 + 4) = 1 + 7 = 8

В обоих случаях получается один и тот же результат — что и требовалось доказать.

Между выражениями (1 + 3) + 4 и 1 + (3 + 4) можно поставить знак равенства, так как они равны одному и тому же значению:

• (1 + 3) + 4 = 1 + (3 + 4)
• 8 = 8

Отразим сочетательный закон сложения с помощью переменных:

(a + b) + c = a + (b + c)

Формула сочетательного закона для обыкновенных дробей:

Например, если к сумме одной седьмой и трёх седьмых прибавить четыре седьмых, то в результате получим восемь седьмых.

Переставим скобки — к одной седьмой прибавим сумму трёх седьмых и четырех седьмых. И снова ответ будет восемь седьмых.

Значит, сочетательный закон справедлив и для обыкновенных дробей.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Переместительный закон умножения

С каждым новым правилом решать задачки по математике все интереснее.

Переместительный закон умножения От перемены мест множителей произведение не меняется. То есть, если множимое и множитель поменять местами — их произведение никак не изменится.

Проверим, действительно ли это так. Умножим пятерку на двойку, а потом наоборот:

• 5 * 2 = 10
• 2 * 5 = 10

В обоих случаях получили один ответ — значит между выражениями 5 * 2 и 2 * 5 можно поставить знак равенства.

• 5 * 2 = 2 * 5
• 10 = 10

Переместительный закон умножения с помощью переменных выглядит так:

a * b = b * a

Бесплатные занятия по английскому с носителем

Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.

Сочетательный закон умножения

Рассмотрим еще один полезный закон в математике.

Сочетательный закон умножения Если выражение состоит из нескольких сомножителей, то их произведение не зависит от порядка действий. Другими словами, умножайте числа в любом порядке — как вам больше нравится.

Рассмотрим пример:

• 2 * 3 * 4

Это выражение можно вычислить в любом порядке. Давайте сначала перемножим числа 2 и 3, а полученный результат умножим на 4:

• 2 * 3 = 6
• 6 * 4 = 24
• 2 * 3 * 4 = 24

А теперь по-другому: перемножим числа 3 и 4, а результат умножим на 2:

• 3 * 4 = 12
• 2 * 12 = 24
• 2 * 3 * 4 = 24

Тот же ответ! Значит между выражениями (2 * 3) * 4 и 2 * (3 * 4) можно поставить знак равенства, так как они равны одному значению.

• (2 * 3) * 4 = 2 * (3 * 4)
• 6 * 4 = 2 * 12
• 24 = 24

Для любых натуральных чисел a, b и c верно равенство:

a * b * с = (a * b) * с = a * (b * с)

Пример

Вычислить: 5 * 6 * 7 * 8.

Как решаем:

Это выражение можно вычислять в любом порядке.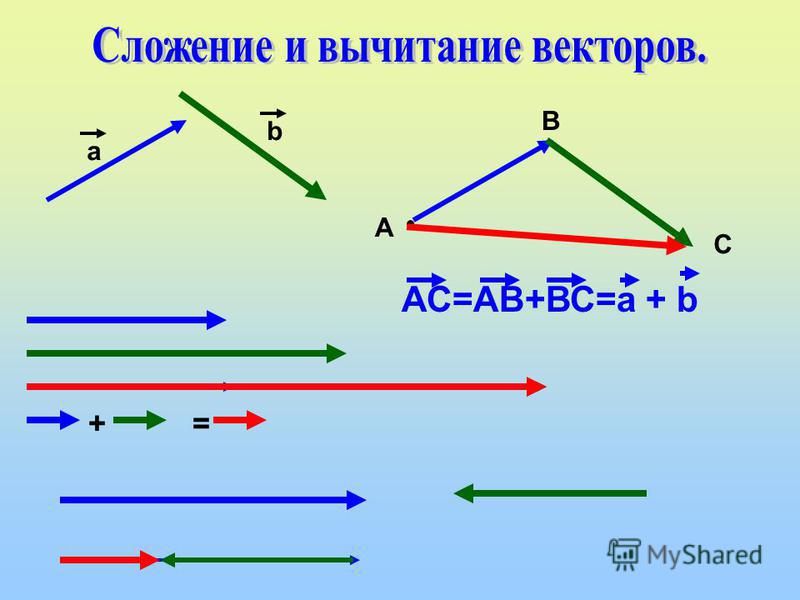 Вычислим слева направо:

5 * 6 = 30

30 * 7 = 210

210 * 8 = 1680

5 * 6 * 7 * 8 = 1680

Ответ: 1680

Распределительный закон умножения

Для умножения есть еще один закон — распределительный. На математике в 6 классе он звучит так:

Распределительный закон умножения Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить. Чтобы сумму чисел умножить на число, нужно каждое слагаемое отдельно умножить на число и полученные произведения сложить.

То есть при помощи распределительного закона умножения можно умножить сумму на число и число на сумму. Проверим на примере:

• (3 + 5) * 2

Сначала выполним действие в скобках:

• (3 + 5) = 8

В главном выражении (3 + 5) * 2 заменим выражение в скобках на восьмерку:

• 8 * 2 = 16

Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое в скобках, нужно умножить на 2, а потом сложить полученные результаты:

• (3 + 5) * 2 = 3 * 2 + 5 * 2
• 3 * 2 = 6
• 5 * 2 = 10
• 6 + 10 = 16

Отразим распределительный закон умножения с помощью переменных:

(a + b) * c = a * c + b * c

Выражение в скобках (a + b) — это множимое. Тогда переменная с — множитель, так как они соединены знаком умножения.

Из переместительного закона умножения мы знаем, что от перемены мест множимого и множителя произведение не изменится.

Если множимое (a + b) и множитель c поменять местами, то получим выражение c * (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). Для такого умножения можно применять распределительный закон умножения. Переменную c можно умножить на каждое слагаемое в скобках:

c * (a + b) = c * a + c * b

 

Пример 1

Решить: 5 * (3 + 2).

Как решаем:

Умножим пятерку на каждое слагаемое в скобках и сложим полученные результаты:

5 * (3 + 2) = 5 * 3 + 5 * 2 = 15 + 10 = 25

Ответ: 25

 

Пример 2

Найти значение выражения 2 * (5 + 2).

Как решаем:

Умножим двойку на каждое слагаемое в скобках и сложим полученные результаты:

2 * (5 + 2) = 2 * 5 + 2 * 2 = 10 + 4 = 14

Ответ: 4.

Если в скобках не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. А после из полученного первого числа вычесть второе число.

 

Пример 3

Решить: 4 * (6 − 2).

Как решаем:

Умножим четверку на каждое число в скобках. Из полученного первого числа вычтем второе число:

4 * (6 − 2) = 4 * 6 − 4 * 2 = 24 − 8 = 16

Ответ: 16

Распределительный закон умножения для суммы обыкновенных дробей:

Распределительный закон умножения для разности обыкновенных дробей:

Проверим справедливость этого закона:

Посчитаем, чему равна левая часть равенства.

Теперь посчитаем, чему равна правая часть равенства.

Так мы доказали справедливость распределительного закона.

Задания для самопроверки

Давайте потренируемся! Решите примеры и сравните с ответами — только чур, не подглядывать 🙂

Задание 1. Найти значение выражения: 8 * (1 + 6).

Задание 2. Применить распределительный закон умножения: 2 * (9 + 5).

Задание 3. Решить в порядке выполнения действий: 3 * (6 + 4) + 7 * (8 + 2).

Задание 4. Решить выражение: 4 * (5 + 4) + 9 * (3 + 2).

Задание 5. Применить распределительный закон умножения: 13 * (3 + 8) + 5 * (4 + 2)

Ответы

1. 56;


2. 28;


3. 100;


4. 81;


5. 173.

Как доказать распределительный закон скалярного произведения (т.

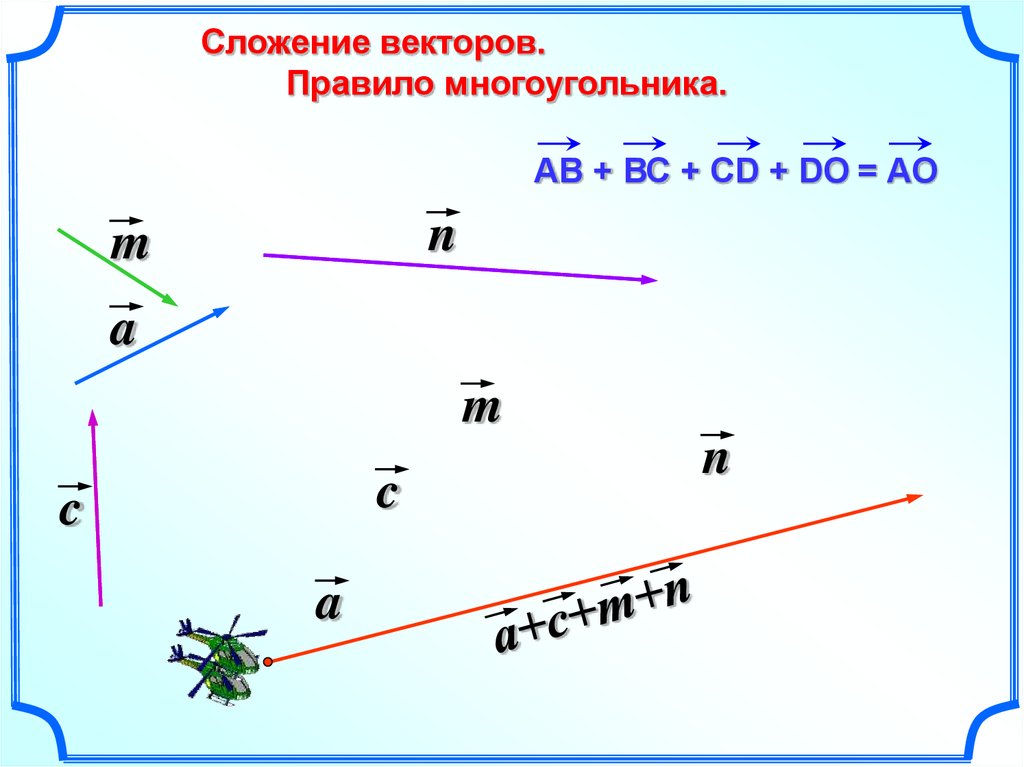е. $A.(B+C) = (A.B) + (A.C)$), когда три вектора $A , B , C$ не лежат в одной плоскости?

спросил 4 года, 1 месяц назад

Изменено 2 года, 6 месяцев назад

Просмотрено 2к раз

$\begingroup$

Как доказать закон распределения (т. е. $A.(B+C) = (A.B) + (A.C)$), когда три вектора $A , B , C$ не лежат в одной плоскости?

Я читал главу «Умножение векторов». Мне было трудно понять распределительный закон скалярного произведения, когда $A, B, C$ не лежат в одной плоскости.

Везде этот закон доказан, если предположить, что три вектора лежат в одной плоскости.

Может ли кто-нибудь помочь мне, предоставив всестороннее доказательство.

• векторов
• векторный анализ

$\endgroup$

3

$\begingroup$

Кажется, вы используете определение $${\bf a}\cdot{\bf b}:=|{\bf a}|\,|{\bf b}|\cos\phi\ ,$$ где $\phi\in[0,\pi]$ обозначает (неориентированный) угол между ${\bf a}$ и ${\bf b}$, если они оба отличны от нуля. 3\ .$$ Линейность $\pi_g$, т. е. $\pi_g({\bf x}+{\bf y})=\pi_g({\bf x})+\pi_g({\bf y})$, тогда следует $(1)$.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

геометрия — Доказательство того, что скалярный продукт является распределительным?

спросил 7 лет, 10 месяцев назад

Изменено 3 года, 8 месяцев назад

Просмотрено 30 тысяч раз

$\begingroup$

Я знаю, что можно доказать, что скалярное произведение, как оно определено «алгебраически», является дистрибутивным. Однако, чтобы показать алгебраическую формулу скалярного произведения, нужно использовать свойство дистрибутивности в геометрическом определении. Как можно было бы геометрически показать, что для евклидовых векторов $\mathbf{a},\mathbf{b},\mathbf{c}$, $$\mathbf{a}\cdot\mathbf{b}+\mathbf{a }\cdot\mathbf{c}=\mathbf{a}\cdot(\mathbf{b}+\mathbf{c})?$$

• геометрия
• векторы

$\endgroup$

7

$\begingroup$

Чтобы доказать, что геометрическое определение (двумерного) скалярного произведения является дистрибутивным, мы используем следующую диаграмму:

$\hspace{4,5 см}$

нуль) $$ \|Б_А\| = \frac{B \cdot A}{\|A\|}\\ \|С_А\| = \frac{C \cdot A}{\|A\|}\\ \|В_А + С_А\| = \frac{(B + C) \cdot A}{\|A\|} $$ Из схемы видно, что $$ \frac{(B + C) \cdot A}{\|A\|} = \|В_А + С_А\| знак равно \|Б_А\| + \|С_А\| знак равно \frac{B \cdot A}{\|A\|}+ \frac{C \cdot A}{\|A\|} $$ отсюда следует дистрибутивность скалярного произведения. ${}$

$\endgroup$

5

$\begingroup$

Это доказательство относится к общему случаю, когда рассматриваются некомпланарные векторы:

Достаточно доказать, что сумма индивидуальных проекций векторов b и c a a равно проекции векторной суммы б+с в направлении а .

Как показано на рисунке ниже, рассматриваемые некомпланарные векторы могут быть приведены к следующему расположению внутри достаточно большого цилиндра «S», который проходит параллельно вектору a . Я раскрасил векторы по-разному, просто чтобы показать, что они не обязательно должны лежать в одной плоскости.

Заметим, что проекция вектора b в направлении a — это в точности расстояние (назовем его XY) между двумя синими «перекрёстками» X (содержит хвост b ) и Y (содержит головку b).