Раздел 2. Векторная алгебра на плоскости и в пространстве

2.1 Понятие о векторах и скалярах

Векторной величиной или вектором (в широком смысле), называется всякая величина, обладающая направлением. Скалярной величиной или скаляром называется всякая величина, направлением не обладающая. Например, сила, действующая на материальную точку, есть вектор, так как она обладает направлением. Скорость также является вектором. Температура тела – это скаляр, так как с этой величиной не связано никакое направление. Масса тела и его плотность – также скалярные величины.

Если отвлечься от направления векторной величины, то ее, как и скалярную величину, можно измерить, выбрав соответствующую масштабную единицу. Но число, полученное в результате измерения, характеризует скалярную величину полностью, а векторную – лишь частично.

Векторную величину полностью можно охарактеризовать направленным отрезком, предварительно задав линейный масштаб.

2.2 Вектор в геометрии

Вектором называется направленный отрезок. Вектор с началом в точке А и концом в точке В обозначается символом (или одной буквой,,, …). Длина отрезкаАВ называется длиной, или модулем вектора и обозначается

,.

Векторы иназываютсяколлинеарными, если они лежат на одной прямой или на параллельных прямых; записывают . Коллинеарные векторы могут иметь одно и то же направление (сонаправленные векторы) или противоположное.

Три (и более) вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

Вектор, длина которого равна нулю, называется нулевым вектором и обозначается или просто 0. По определению нулевой вектор не имеет направления и коллинеарен любому вектору.

Вектор, длина которого равна единице, называется единичным вектором и обозначается через .

Единичный вектор, направление которого совпадает с направлением вектора

, называетсяортом вектора и обозначается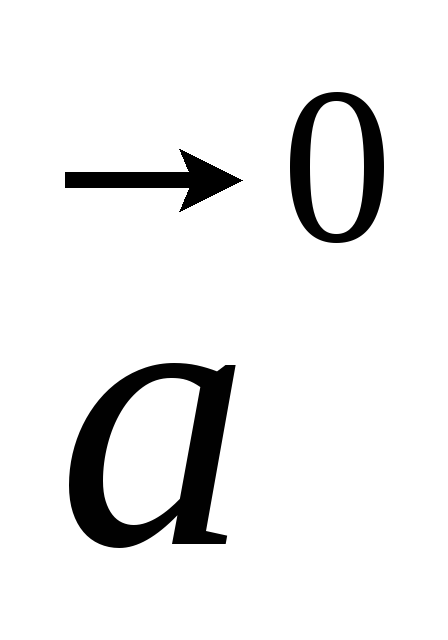. Два ненулевых вектора называютсяпротивоположными, если они имеют одинаковую длину и противоположные направления. Вектор, противоположный вектору , обозначается ; векторпротивоположен вектору().

Два коллинеарных вектора иназываютсяравными (), если они сонаправлены и имеют равные длины.

Замечание. Нельзя смешивать понятия «равенство отрезков» и «равенство векторов». Говоря: «отрезки равны», мы утверждаем, что их можно совместить наложением. Но для этого один из них может быть придется подвергнуть повороту. Два вектора будут равны лишь в том случае, когда их можно совместить, не применяя поворот.

Совместим параллельным переносом начала неколлинеарных векторов и. Начало и концы векторов образуют вершины треугольника.Углом между векторами

иназывается угол при вершине этого треугольника, соответствующий началу векторов. Если векторы сонаправлены, то угол между ними равен нулю; если противоположно направлены – угол между ними равен 180°.

2.3 Векторная алгебра

Над векторами производят действия, называемые сложением, вычитанием и умножением векторов. Эти действия имеют много общих свойств с одноименными алгебраическими действиями. Поэтому учение о действиях над векторами называется векторной алгеброй.

С

уммой двух векторов иназывается вектор, соединяющий начало векторас концом вектора, отложенного от конца вектора .

Обозначение: .

Д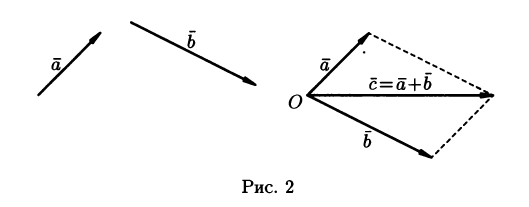ля геометрического представления суммы векторов используют правила «треугольника» и «параллелограмма», проиллюстрированные на рис. 1 и 2 соответственно.

При сложении векторов имеют место неравенства:

1) ,

2)

,

выражающие, что сторона треугольника меньше суммы и больше разности двух других сторон (неравенство треугольника). В первой формуле равенство имеет место только для сонаправленных векторов, во второй – только для противоположно направленных векторов.

Сумма противоположных векторов равна нуль-вектору: .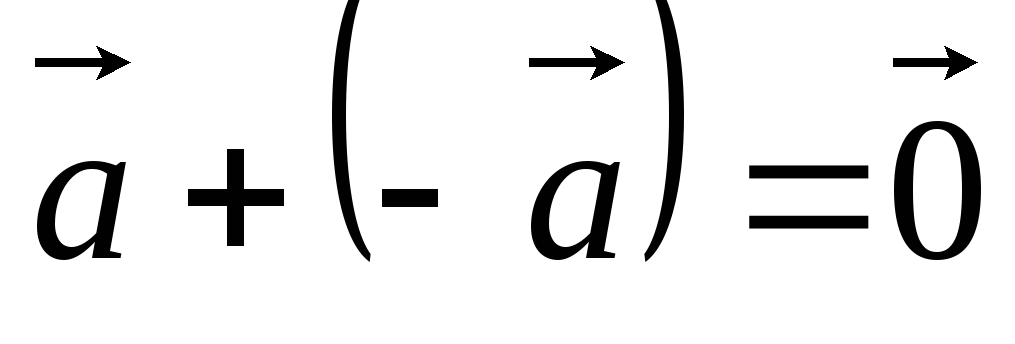

Суммой векторов называется вектор, получающийся после ряда последовательных сложений: к вектору

прибавляется вектор, к полученному вектору прибавляется вектори так далее.

Из определения вытекает следующее построение (правило многоугольника или правило цепи).

Из произвольного начала О откладываем вектор , из точкиА₁, как из начала, откладываем вектор

, из точкиА₂ строим вектор и так далее. Векторесть сумма векторов.

Сложение векторов подчиняется коммутативному и ассоциативному свойствам:

1) ,

2)

.

Коммутативность и ассоциативность сложения векторов позволяет нам находить сумму векторов в любом удобном порядке.

Правило параллелепипеда. Если три вектора ,ипосле приведения к общему началуне лежат в одной плоскости, то сумму можно найти следующим построением. Из общего началаО строим векторы ,,. На отрезкахОА, ОВ, ОС, как на ребрах, строим параллелепипед. Вектор диагонали равен сумме векторов,и, так как,,и.

Под разностью векторов ипонимается вектортакой, что. Обозначение:. Справедливо равенство.

Произведением вектора на числоназывается вектор, который имеет длину, его направление еслии противоположное направление, если.

Обозначение: .

Отметим, что , т. е. каждый вектор равен произведению его модуля на орт.

Два ненулевых вектора иколлинеарны тогда и только тогда, когда один из них есть произведение другого на некоторое число, т. е., λ – число (признак коллинеарности векторов).

Три ненулевых вектора ,,компланарны тогда и только тогда, когда один из них является линейной комбинацией других, например,(λ₁, λ₂ – числа не равные нулю одновременно) (признак компланарности векторов).

Умножение вектора на число подчиняется тем же законам, что и умножение чисел:

1. (дистрибутивный закон по отношению к числовому множителю).

2. (дистрибутивный закон по отношению к векторному множителю).

3. (ассоциативный закон).

Пример 1: В треугольнике ABC дано: ,, точкаМ – середина стороны ВС. Выразить вектор через векторыи .

Решение:

Через точкуМ проведем прямые, параллельные сторонам АВ и АС. Получим параллелограмм АВ₁МС₁ (рис. 3), в котором AM является диагональю. Следовательно, . Но,(B₁M и C₁M – средние линии, поэтому AB₁ = B₁B, AC₁ = С₁С). Получаем , т.е..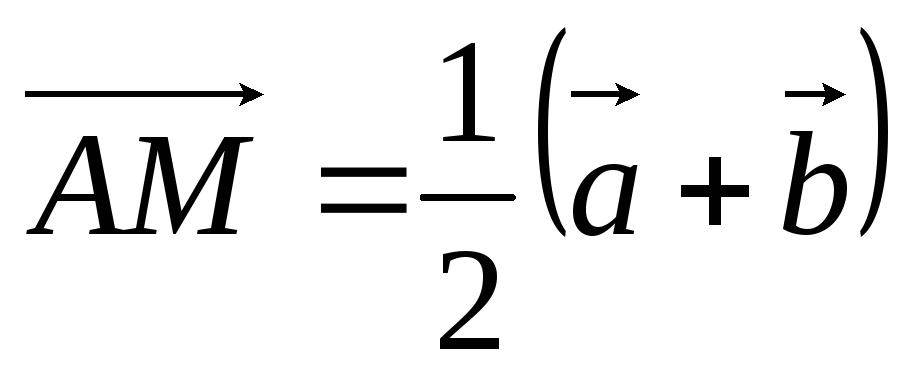

Пример 2: Какому условию должны удовлетворять ненулевые векторы и, чтобы имело место соотношение?

Решение:

Построим на векторахи, отложенных от точкиО, параллелограмм OADB (рис. 4). Тогда ,. Равенствоозначает, что длины диагоналей параллелограмма равны, т.е.. Отсюда следует, что данный параллелограмм есть прямоугольник. Следовательно, векторыиперпендикулярны.

Теория вектора (стр. 1 из 3)

Содержание:

1. Что такое вектор?

2. Сложение векторов.

3. Равенство векторов.

4. Скалярное произведение двух векторов и его свойства.

5. Свойства операций над векторами.

6. Доказательства и решение задач.

Одним из фундаментальных понятий современной математики являются вектор и его обобщение – тензор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а так же в технике.

Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.

В соответствии с требованиями новой программы по математике понятие вектора стало одним из ведущих понятий школьного курса математики.

Что же такое вектор? Как ни странно, ответ на этот вопрос представляет известные затруднения. Существуют различные подходы к определению понятия вектора; при этом даже если ограничиться лишь наиболее интересным здесь для нас элементарно-геометрическим подходом к понятию вектора, то и тогда будут иметься различные взгляды на это понятие. Разумеется, какое бы определение мы ни взяли, вектор – с элементарно-геометрической точки зрения — есть геометрический объект, характеризуемый направлением ( т.е. заданной с точностью до параллельности прямой и направлением на ней) и длиной.Однако такое определение является слишком общим, не вызывающим конкретных геометрических представлений. Согласно этому общему определению параллельный перенос можно считать вектором. И действительно, можно было бы принять такое определение: “Вектором называется всякий параллельный перенос”. Это определение логически безупречно, и на его основе может быть построена вся теория действий над векторами и развиты приложения этой теории. Однако это определение, несмотря на его полную конкретность , нас здесь также не может удовлетворить, так как представление о векторе как о геометрическом преобразовании кажется нам недостаточно наглядным и далеким от физических представлений о векторных величинах.

Итак, вектором называется семейство всех параллельных между собой одинаково направленных и имеющих одинаковую длину отрезков (рис.1).

Вектор изображают на чертежах отрезком со стрелкой (т.е. изображают не все семейство отрезков, представляющее собой вектор, а лишь один из этих отрезков). Для обозначения векторов в книгах и статьях применяют жирные латинские буквы а, в, с и так далее, а в тетрадях и на доске – латинские буквы с черточкой сверху, Той же буквой, но не жирной , а светлой (а в тетради и на доске- той же буквой без черточки) обозначают длину вектора. Длину иногда обозначают также вертикальными черточками – как модуль (абсолютную величину) числа. Таким образом, длина вектора а обозначается через а или IаI, а в рукописном тексте длина вектора а обозначается через а или IаI. В связи с изображением векторов в виде отрезков (рис.2) следует помнить , что концы отрезка, изображающего вектор, неравноправны: одного конца отрезка к другому.

Различают начало и конец вектора (точнее, отрезка, изображающего вектор).

Весьма часто понятию вектора дается другое определение:вектором называется направленный отрезок. При этом векторы (т.е. направленные отрезки), имеющие одинаковую длину и одно и то же направление (рис.3), уславливаются считать равными.

Векторы называются одинаково направленными, если их полупрямые одинаково направлены.

Сложение векторов.

Все сказанное пока еще не дает понятие вектора достаточно содержательным и полезным. Большую содержательность и богатую возможность приложений понятие вектора получает тогда, когда мы вводим своеобразную “геометрическую арифметику” – арифметику векторов, позволяющую складывать векторы, вычитать их и производить над ними целый ряд других операций. Отметим в связи с этим, что ведь и понятие числа становится интересным лишь при введении арифметических действий, а не само по себе.

Суммой векторов а и в с координатами а₁, а₂ и в₁, в₂называется вектор с с координатами а₁ + в₁, а₂ + в₂, т.е. а (а₁; а₂) + в (в₁;в₂) = с (а₁ + в₁; а₂ + в₂).
Следствие:
Для доказательства коммутативности сложения векторов на плоскости необходимо рассмотреть пример. а и в – векторы (рис.5).
Пусть

1. Строим параллелограмм ОАСВ: АМ II ОВ, ВН II ОА.

Для доказательства ассоциативности мы отложим от произвольной точки О вектор ОА = а, от точки А вектор АВ = в и от точки в – вектор ВС = с. Тогда мы имеем:АВ + ВС =АС.
откуда и следует равенство а + ( в + с ) = (а + в) + с. Заметим, что приведенное доказательство совсем не использует чертежа. Это характерно ( при некотором навыке ) для решения задач при помощи векторов. Остановимся теперь на случае, когда векторы а и в направлены в противоположные стороны и имеют равные длины; такие векторы называют противоположными. Наше правило сложения векторов приводит к тому, что сумма двух противоположных векторов представляет собой “вектор”, имеющий нулевую длину и не имеющий никакого направления; этот “вектор” изображается “отрезком нулевой длины”, т.е. точкой. Но это тоже вектор, который называется нулевым и обозначается символом 0.

Равенство векторов.

Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора.

Из данного определения равенства векторов следует, что разные векторы одинаково направлены и равны по абсолютной величине.

И обратно: если векторы одинаково направлены и равны по абсолютной величине, то они равны.

Действительно, пусть векторы АВ и СD – одинаково направленные векторы, равные по абсолютной величине (рис.6). Параллельный перенос, переводящий точку С в точку А, совмещает полупрямую СD с полупрямой АВ, так как они одинаково направлены. А так как отрезки АВ и CD равны, то при этом точка D совмещается с точкой В, то есть параллельный перенос переводит вектор CD в вектор АВ. Значит, векторы АВ и СD равны, что и требовалось доказать.

Компланарные векторы — урок. Геометрия, 10 класс.

Одно из определений компланарных векторов гласит:

векторы, которые параллельны одной плоскости или лежат на одной плоскости, называются компланарными векторами.

Тот же смысл имеет и другое определение:

три вектора называются компланарными, если они, будучи приведёнными к общему началу, лежат в одной плоскости.

Обрати внимание!

Всегда возможно найти плоскость, параллельную двум произвольным векторам, поэтому любые два вектора всегда компланарные.

Eсли из трёх векторов два коллинеарны, то очевидно, что эти три вектора компланарны.

 

Все вышеупомянутые случаи легко рассмотреть, если разместить векторы на рёбрах параллелепипеда.

 

1. Любые два вектора находятся в одной плоскости, но в одной плоскости можно разместить и векторы AA1→, CC1→ и AD→, то есть, эти векторы компланарны. Также компланарны векторы AA1→, AB→ и CC1→, так как два из этих векторов параллельны. Легко представить, что если привести их к общему началу, то вектор CC1→ совпадёт с вектором AA1→.

 

2. Например, векторы AB→, AD→ и AA1→ не компланарны, так как их нельзя разместить в одной и той же плоскости.

Признак компланарности трёх векторов:

пусть векторы a→ и b→ не коллинеарны. Если для вектора c→ существует единственная пара реальных чисел \(x\) и \(y\), такая, что c→=x⋅a→+y⋅b→, то векторы a→, b→ и c→ компланарны.

Справедливо и обратное утверждение:

если три вектора a→, b→ и c→ компланарны и векторы a→ и b→ не коллинеарны, то вектор c→ можно разложить по векторам a→ и b→ одним-единственным образом.

 

 

Если разложить вектор AC→ по векторам AA1→ и AA2→, то это можно сделать одним-единственным образом: AC→=AB→+AD→=x⋅AA1→+y⋅AA2→. 

 

Закон параллелепипеда

Если три вектора некомпланарны, то для их сложения в пространстве применяется закон параллелепипеда.

 

1. Векторы приводят к общему началу \(A\).

 

2. На этих трёх рёбрах строится параллелепипед.

3. Диагональ параллелепипеда, которая выходит из этой же точки, изображает суммы векторов AB→, AD→ и AA1→. 

 

 

Разложение вектора по трём некомпланарным векторам

Теорема о разложении по базису в пространстве
Любой вектор d→ можно разложить по трём данным некомпланарным векторам a→, b→ и c→, причём реальные коэффициенты разложения \(x\), \(y\) и \(z\) определяются единственным образом: AC1→=AD→+AB→+AA1→=x⋅AA2→+y⋅AA3→+z⋅AA4→.

Векторы. Начальные сведения

Определения

Вектор – это направленный отрезок, для которого указано, какая из его граничных точек является началом, а какая – концом.
Если \(A\) – начало вектора, \(B\) – его конец, то вектор обозначается как \(\overrightarrow{AB}\). Вектор также можно обозначать одной маленькой буквой: \(\overrightarrow{a}\).

 

Иногда говорят, что вектор – это перемещение из точки \(A\) в точку \(B\).

 

Длина (или модуль) вектора \(\overrightarrow{AB}\) – это длина соответствующего отрезка \(AB\).
Обозначение: \(|\overrightarrow{AB}|=AB\).

 

Если длина вектора равна нулю (совпадают начало и конец), то такой вектор называют нулевым.

 

Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых (\(\overrightarrow a, \overrightarrow b\) и \(\overrightarrow c\)).

В противном случае векторы называются неколлинеарными (например, \(\overrightarrow a\) и \(\overrightarrow d\)).

 

Причем если два коллинеарных вектора направлены в одну сторону, то они называются сонаправленными (\(\overrightarrow a\) и \(\overrightarrow c\)). В противном случае векторы называются противоположно направленными (\(\overrightarrow a\) и \(\overrightarrow b\)).
Обозначение: \(\overrightarrow a \uparrow \uparrow \overrightarrow c\), \(\overrightarrow a \uparrow \downarrow \overrightarrow b\).

 

Векторы называются равными, если они сонаправлены и их длины равны.

 

Правила сложения коллинеарных векторов:

 

\(\blacktriangleright\) Для того, чтобы сложить два сонаправленных вектора, можно отложить второй вектор от конца первого. Тогда их сумма – вектор, начало которого совпадает с началом первого вектора, а конец – с концом второго (рис. 1).

\(\blacktriangleright\) Для того, чтобы сложить два противоположно направленных вектора, можно отложить второй вектор от начала первого. Тогда их сумма – вектор, начало которого совпадает с началом обоих векторов, длина равна разности длин векторов, направление совпадает с направлением большего по длине вектора (рис. 2).

 

Правила сложения неколлинеарных векторов \(\overrightarrow {a}\) и \(\overrightarrow{b}\):

 

\(\blacktriangleright\) Правило треугольника (рис. 3).

Нужно от конца вектора \(\overrightarrow {a}\) отложить вектор \(\overrightarrow {b}\). Тогда сумма \(\overrightarrow {a}+\overrightarrow {b}\) – это вектор, начало которого совпадает с началом вектора \(\overrightarrow {a}\), а конец – с концом вектора \(\overrightarrow {b}\).

 

\(\blacktriangleright\) Правило параллелограмма (рис. 4).

Нужно от начала вектора \(\overrightarrow {a}\) отложить вектор \(\overrightarrow {b}\). Тогда сумма \(\overrightarrow {a}+\overrightarrow {b}\) – вектор, совпадающей с диагональю параллелограмма, построенного на векторах \(\overrightarrow {a}\) и \(\overrightarrow {b}\) (начало которого совпадает с началом обоих векторов).

 

Определение

Вектор \(\overrightarrow {-b}\) – это вектор, противоположно направленный с вектором \(\overrightarrow {b}\) и совпадающий с ним по длине.

 

\(\blacktriangleright\) Для того, чтобы найти разность двух векторов \(\overrightarrow {a}-\overrightarrow{b}\), нужно найти сумму векторов \(\overrightarrow {a}\) и \(-\overrightarrow{b}\):   \(\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+(-\overrightarrow{b})\) (рис. 5).

 

Свойства сложения векторов

1. Наличие нейтрального вектора: для любого вектора \(\overset{\rightarrow}{a}\) выполнено: \(\overset{\rightarrow}{a} + \overset{\rightarrow}{0} = \overset{\rightarrow}{a}\).

2. Наличие обратного вектора: для любого вектора \(\overset{\rightarrow}{a}\) выполнено \(\overset{\rightarrow}{a} + (-\overset{\rightarrow}{a}) = \overset{\rightarrow}{0}\).

3. Ассоциативность: для любых векторов \(\overset{\rightarrow}{a}\), \(\overset{\rightarrow}{b}\) и \(\overset{\rightarrow}{c}\) выполнено \((\overset{\rightarrow}{a} + \overset{\rightarrow}{b}) + \overset{\rightarrow}{c} = \overset{\rightarrow}{a} + (\overset{\rightarrow}{b} + \overset{\rightarrow}{c})\)

4. Коммутативность: для любых векторов \(\overset{\rightarrow}{a}\) и \(\overset{\rightarrow}{b}\) выполнено \(\overset{\rightarrow}{a} + \overset{\rightarrow}{b} = \overset{\rightarrow}{b} + \overset{\rightarrow}{a}\).

 

Замечание

Для того, чтобы сложить несколько вектором, можно отложить их последовательно: каждый следующий от конца предыдущего. Тогда суммой этих векторов будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом последнего: \[\overrightarrow {a_1}+\overrightarrow {a_2}+\overrightarrow {a_3}+ \overrightarrow {a_4}=\overrightarrow {a}\]

 

Определение

Произведением ненулевого вектора \(\overrightarrow {a}\) на число \(\lambda\) называется такой вектор \(\lambda\overrightarrow {a}\), длина которого равна \(|\lambda|\cdot |\overrightarrow {a}|\), причем векторы \(\overrightarrow {a}\) и \(\lambda \overrightarrow {a}\) сонаправлены, если \(\lambda>0\), и противоположно направлены, если \(\lambda<0\). Если \(\lambda=0\), то вектор \(\lambda\overrightarrow {a}\) равен нулевому вектору.

 

Свойства произведения вектора на число

1. Сочетательный закон: \(k(\lambda\overrightarrow {a})=(k\lambda)\overrightarrow {a}\);

 

2. Распределительный закон 1: \((k+\lambda)\overrightarrow {a}=k\overrightarrow {a}+\lambda\overrightarrow {a}\);

 

2. Распределительный закон 2: \(\lambda(\overrightarrow {a}+\overrightarrow {b})=\lambda\overrightarrow {a}+\lambda\overrightarrow {b}\).

 

Теорема

Если \(M\) – середина отрезка \(PQ\), \(O\) – произвольная точка плоскости, то \[\overrightarrow {OM}=\dfrac12 \left(\overrightarrow {OP}+\overrightarrow {OQ}\right)\]

Координаты точки и вектора — урок. Геометрия, 11 класс.

Координаты точки

Три попарно перпендикулярные прямые с выбранными направлениями и единицей измерения образуют систему координат в пространстве. Точка пересечения всех прямых является началом системы координат.

 

 

Оси координат \(Ox\), \(Oy\) и \(Oz\) называются соответственно: \(Ox\) — ось абсцисс, \(Oy\) — ось ординат, \(Oz\) — ось аппликат. 

Через две пересекающиеся прямые можно провести плоскость. Получаем три координатные плоскости: \((Oxy)\), \((Oyz)\) и \((Oxz)\).

 

 

Положение точки \(A\) в пространстве определяется тремя координатами: \(x\), \(y\) и \(z\).

 

 

Координата \(x\) называется абсциссой точки \(A\), координата \(y\) — ординатой точки \(A\), координата \(z\) — аппликатой точки \(A\).

Записываются так: \(A(x; y; z)\).

Если точка находится на оси \(Ox\), то её координаты \(X(x; 0; 0)\).

Если точка находится на оси \(Oy\), то её координаты \(Y(0; y; 0)\).

Если точка находится на оси \(Oz\), то её координаты \(Z(0; 0; z)\).

 

Если точка находится в плоскости \(Oxy\), то её координаты A1x;y;0.

Если точка находится в плоскости \(Oyz\), то её координаты A20;y;z.

Если точка находится в плоскости \(Oxz\), то её координаты A3x;0;z.

Координаты вектора

 

Если в системе координат от начальной точки отложить единичные векторы i→, j→ и k→, то можно определить прямоугольный базис. Любой вектор можно разложить по единичным векторам и представить в виде OA→=x⋅i→+y⋅j→+z⋅k→.

Коэффициенты \(x\), \(y\) и \(z\) определяются одним-единственным образом и называются координатами вектора.

 

Записываются так: OA→x;y;z.

Рассмотрим правила о том, как с помощью координат записать:

 

— координаты суммы векторов, если даны координаты векторов:

a→x1;y1;z1, b→x2;y2;z2, a→+b→x1+x2;y1+y2;z1+z2;

 

— координаты разности векторов, если даны координаты векторов:
 a→−b→x1−x2;y1−y2;z1−z2;

 

— координаты произведения вектора на число, если даны координаты вектора:

n⋅a→n⋅x1;n⋅y1;n⋅z1;

 

— длину вектора:

a→=x12+y12+z12;

— координаты вектора, если даны координаты начальной и конечной точек вектора:

AxA;yA;zA, BxB;yB;zB, AB→xB−xA;yB−yA;zB−zA;

 

— расстояние между двумя точками, если даны координаты точек:

AB→=AB=xB−xA2+yB−yA2+zB−zA2;

 

— координаты серединной точки отрезка, если даны координаты начальной и конечной точек отрезка:

xC=xA+xB2;yC=yA+yB2;zC=zA+zB2.

Векторы (повторение теории, задачи). Видеоурок. Геометрия 8 Класс

Тема: Векторы

Урок: Повторение теории. Задачи

Напомним, что существуют такие физические величины, для которых важна не только величина, но и направление. Такие величины называются векторными, или векторами, и обозначаются они направленным отрезком, то есть таким отрезком, у которого отмечены начало и конец. Введено было понятие коллинеарных векторов, то есть таких, которые лежат либо на одной прямой, либо на параллельных прямых.

Мы рассматриваем вектор, который можно отложить от любой точки, заданный вектор от произвольно выбранной точки можно отложить единственным образом.

Было введено понятие равных векторов – это такие сонаправленные векторы, длины которых равны. Сонаправленными называются коллинеарные векторы, направленные в одну сторону.

Были введены правила треугольника и параллелограмма – правила сложения векторов.

Заданы два вектора – векторы  и . Найдем сумму этих двух векторов . Для этого отложим из некоторой точки А вектор .  – направленный отрезок, точка А – его начало, а точка В – конец. Из точки В отложим вектор 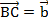. Тогда вектор  называют суммой заданных векторов:  – правило треугольника (см. Рис. 1).

Рис. 1

Задано два вектора – векторы  и . Найдем сумму этих двух векторов  по правилу параллелограмма.

Откладываем из точки А вектор  и вектор  (см. Рис. 2). На отложенных векторах можно построить параллелограмм. Из точки В откладываем вектор 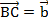, векторы  и  равны, стороны ВС и

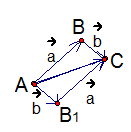
Рис. 2

АВ₁ параллельны. Аналогично параллельны и стороны АВ и В₁С, таким образом, мы получили параллелограмм. АС – диагональ параллелограмма.

Для сложения нескольких векторов применяют правило многоугольника (см. Рис. 3). Нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее, когда все векторы отложены – соединить начальную точку с концом последнего вектора, в итоге получится сумма нескольких векторов.

Рис. 3

Кроме того, мы рассмотрели понятие обратного вектора – вектора, имеющего такую же длину, как заданный, но ему противонаправленного.

Пример 1 – задача 747: выпишите пары коллинеарных сонаправленных векторов, которые определяются сторонами параллелограмма; укажите противоположно направленные векторы;

Задан параллелограмм MNPQ (см. Рис. 4). Выпишем пары коллинеарных векторов. В первую очередь это векторы  и . Они не только коллинеарные, но и равные, т.к. они сонаправлены, и длины их равны по свойству параллелограмма (в параллелограмме противоположные стороны равны). Следующая пара . Аналогично

Рис. 4

выпишем коллинеарные векторы второй пары сторон: ; .

Противоположно направленные векторы: , , , .

Пример 2 – задача 756: начертите попарно неколлинеарные векторы ,  и 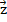. Постройте векторы ;; ;.

Для выполнения данного задания можем пользоваться правилом треугольника или параллелограмма.

Способ 1 – с помощью правила треугольника (см. Рис. 5):

Рис. 5

Способ 2 – с помощью правила параллелограмма (см. Рис. 6):

Рис. 6

Комментарий: мы применяли в первом способе правило треугольника – откладывали из произвольно выбранной точки А первый вектор, из его конца – вектор, противоположный второму, соединяли начало первого с концом второго, и таким образом получали результат вычитания векторов. Во втором способе мы применили правило параллелограмма – построили на нужных векторах параллелограмм и его диагональ – искомую разность, помня тот факт, что одна из диагоналей – это сумма векторов, а вторая – разность.

Пример 3 – задача 750: докажите, что если векторы  и  равны, то середины отрезков AD и BC совпадают. Докажите обратное утверждение: если середины отрезков AD и BC совпадают, то векторы  и  равны (см. Рис. 7).

Из равенства векторов  и  следует, что прямые АВ и CD параллельны, и что отрезки АВ и CD равны. Вспомним признак параллелограмма: если у четырехугольника пара противоположных сторон лежит на параллельных прямых, и их длины равны, то данный четырехугольник – параллелограмм.

Рис. 7

Таким образом, четырехугольник ABCD, построенный на заданных векторах, – параллелограмм. Отрезки AD и BC являются диагоналями параллелограмма, одно из свойств которого: диагонали параллелограмма пересекаются и в точке пересечения делятся пополам. Таким образом, доказано, что середины отрезков AD и BC совпадают.

Докажем обратное утверждение. Для этого воспользуемся другим признаком параллелограмма: если в некотором четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм. Отсюда четырехугольник ABCD – параллелограмм, и его противоположные стороны параллельны и равны, таким образом, векторы  и  коллинеарны, очевидно, что они сонаправлены, и модули их равны, отсюда векторы  и  равны, что и требовалось доказать.

 

Пример 4 – задача 760: докажите, что для любых неколлинеарных векторов  и  справедливо неравенство  (см. Рис. 8)

Отложим из произвольной точки А вектор , получим точку В, из нее отложим неколлинеарный ему вектор . По правилу параллелограмма или треугольника получим сумму векторов  – вектор . Имеем треугольник .

Длина суммы векторов соответствует длине стороны АС треугольника. По неравенству треугольника длина стороны АС меньше, чем сумма длин двух других сторон АВ и ВС, что и требовалось доказать.

Рис. 8

Итак, мы вспомнили все основные определения и свойства векторов, вспомнили основные операции над векторами и решили различные примеры на выполнение этих операций.

 

Список литературы

1. Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
2. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
3. Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Terver.ru (Источник).
2. Cleverstudents.ru (Источник).
3. Khd2.narod.ru (Источник).

 

Домашнее задание

1. Задание 1: дан треугольник . Найдите сумму векторов  и ;  и ;  и ;  и .
2. Задание 2: в параллелограмме ABCD диагонали пересекаются в точке М. Выразите векторы