| силы как векторы и невекторы | [авг. 24, 2014|09:54 am] Anatoly Vorobey |
| В обычном изложении ньютоновской механики (в школе, в первом университетском курсе) силу обычно называют векторной величиной. Вот есть тело, на него действует сила, направление этого действия и его величину можно обозначить с помощью вектора. Что такое вектор — в контексте обычного трехмерного эвклидового пространства, не входя в более высокие материи? С математической точки зрения это просто точка пространства, у которой есть определенные координаты. Задав другую систему координат, мы для той же точки получим другие координаты, но сама точка не изменится. Физик нарисует стрелку в пространстве от точки A до точки B и скажет: это вектор. Его направление — от A к B, его величина — расстояние между A и B. Но на самом деле конкретные точки A,B не играют роли: эту стрелку можно двигать параллельно в пространстве куда угодно, и это останется тот же вектор. Пока мы имеем дело с телами, на которые можно смотреть как на точки с массой, нет проблемы смотреть на силу как на вектор. Вот у нас есть тело в точке A, на него действует сила, мы представляем ее в виде вектора AB. Вообще говоря верно, что это тот же вектор, что CD и OV, но нам это не мешает, мы не путаем эту силу с другой силой, которая действует на другое тело в точке C (пусть даже с той же величиной и направлением). Мы знаем, когда мы рассматриваем силы в A, а когда в C. Но теперь предствим себе, что наши (твердые) тела имеют размер, которым нельзя пренебречь, как обычно и есть в реальной жизни. Пусть у меня есть куб (или другое твердое тело), на которое действуют какие-то силы: в точке A сила, которую описывает вектор AB, в точке C вектор CD, в точке E вектор EF. Для простоты предположим, что все силы лежат в одной плоскости (например: мы тянем и толкаем куб на льду в двух возможных направлениях и их комбинациях). 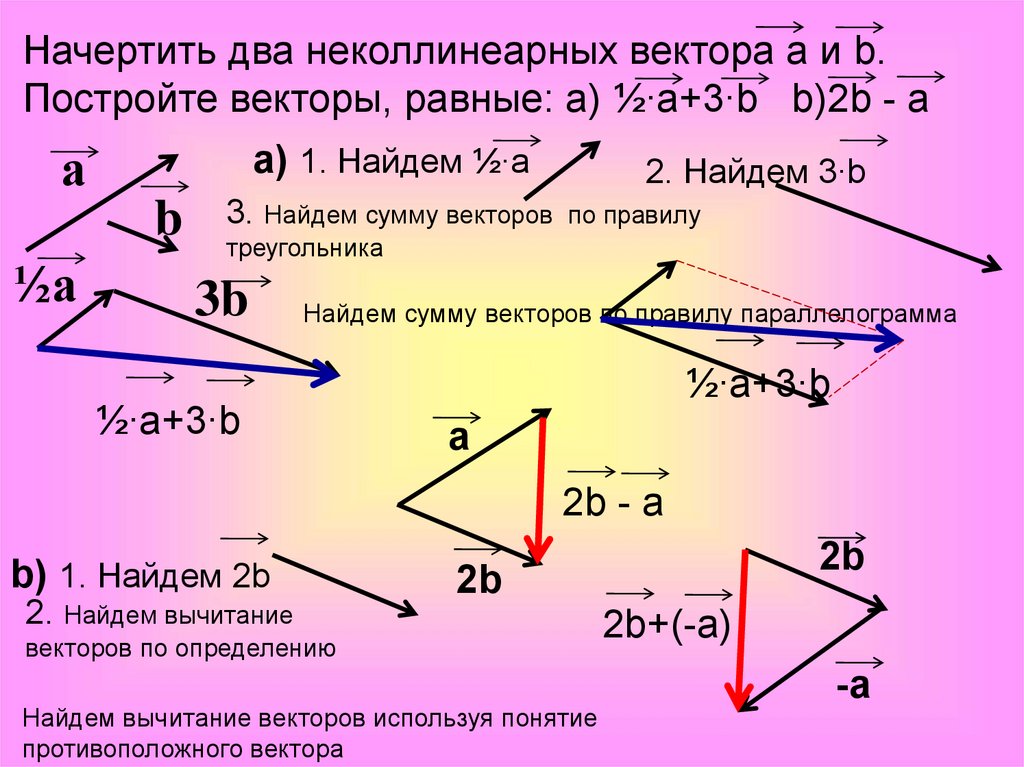 (я специально не упоминаю определенные сложности, которые возникают в этой процедуре, если некоторые из сил параллельны друг другу; их почти всегда можно решить, а когда нельзя, они решаются добавлением так называемой пары сил, но я не хочу углубляться сейчас в эти тонкости) Если присмотреться, то когда мы выполняем вышеуказанную процедуру сложения сил, прилагаемых к данному телу, мы не выполняем векторное сложение. С точки зрения векторного сложения любой вектор можно двигать параллельно куда угодно, и для того, чтобы сложить AB, CD, EF достаточно, например, сдвинуть второй и третий вектор так, чтобы они тоже начинались в A, и получить какие-то AB, AD’, AF’, после чего обычным способом сложить все три вектора. Если мы выполним эту процедуру, мы получим некий вектор AL’, который будет параллелен тому вектору KL, который мы получили раньше, и даст правильную величину и направление результирующей силы,  (есть способ обойти эту сложность, пользуясь понятием «момент силы», о котором если вы знаете — то хорошо, но я не буду сейчас подробно говорить. Момент силы описывает то, насколько данная сила стремится вращать тело вокруг заданной точки O. Если мы выберем удобную точку O, и просуммируем моменты всех исходных сил, то получим момент результирующей силы; эта величина позволить нам понять, насколько надо сдвинуть вектор AL’, чтобы получить правильную линию приложения силы KL. Но это в некотором смысле удобный «трюк», позволяющий нам складывать силы как вектора, не обращая внимания на точки приложения, а потом все «подправить»). Если мы, складывая силы описанным выше «правильным» способом — сдвигая их только вдоль их линий приложения, пока они не пересекутся — не делаем векторное сложение, то что мы на самом деле делаем? Выходит, что силы с математической точки зрения не векторы на самом деле, но что же они тогда? Когда я задал этот вопрос на физическом форуме, сначала несколько человек не поняли, о чем я вообще говорю, а потом кто-то указал мне на понятие «line vector» (не знаю, как по-русски), который является как раз вектором, «привязанным» к определенной прямой линии, которая должна быть ему параллельна: скажем, можно обозначить его парой (L, AB), где L — прямая в трехмерном пространстве, AB — обычный вектор с математической точки зрения, параллельный этой прямой, и тогда это обозначает стрелку, которая получится, если AB сдвинуть так, чтобы он лежал внутри прямой L. Если поискать «line vector» в разных книгах, то это понятие находится в многих книгах о механике, написанных для инженеров, а не физиков — а также иногда для физиков, но в старых книгах, 50 и 100 лет назад. Сейчас обычно обходятся без него, и мне хотелось бы понять получше, почему и как. Верно ли будет сказать, что ньютоновская механика в ее общей формулировке по сути дела требует этого понятия, т.е. требует того, чтобы сила была не просто вектором, а вектором, привязанным к определенной прямой? Наверное, и да и нет. На практике обычно быстро вводят понятия момента сил и центра масс; с их помощью можно любую силу, приложенную к телу в какой-то точке, разбить на две составляющие — «толкающую», которую можно считать приложенной к центру масс, и «вращающую», которая описывается с помощью момента сил. Наверное (?) по этим причинам, в школьных курсах физики или в университетских курсах механики для факультетов точных наук не рассматривается (по крайней мере по моему опыту) этот формализм «line vectors», и как бы не обращают особого внимания на точку/линию приложения силы, предпочитая считать тела точечными, а силы — векторами. Но мне лично кажется, что я бы лучше понимал простейшую ньютоновскую механику тел и сил, если бы мне в свое время преподавали ее, обращая внимание на эти обстоятельства. Поправки и замечания от знающих людей принимаются, как обычно, с благодарностью. (P.S. я понимаю, что эта запись была бы намного более понятной, если бы в ней приводилось несколько рисунков и диаграмм, и сожалею, что у меня сейчас нет времени и сил их сделать). | |
определение, примеры решения и свойства
Вектор – это отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху.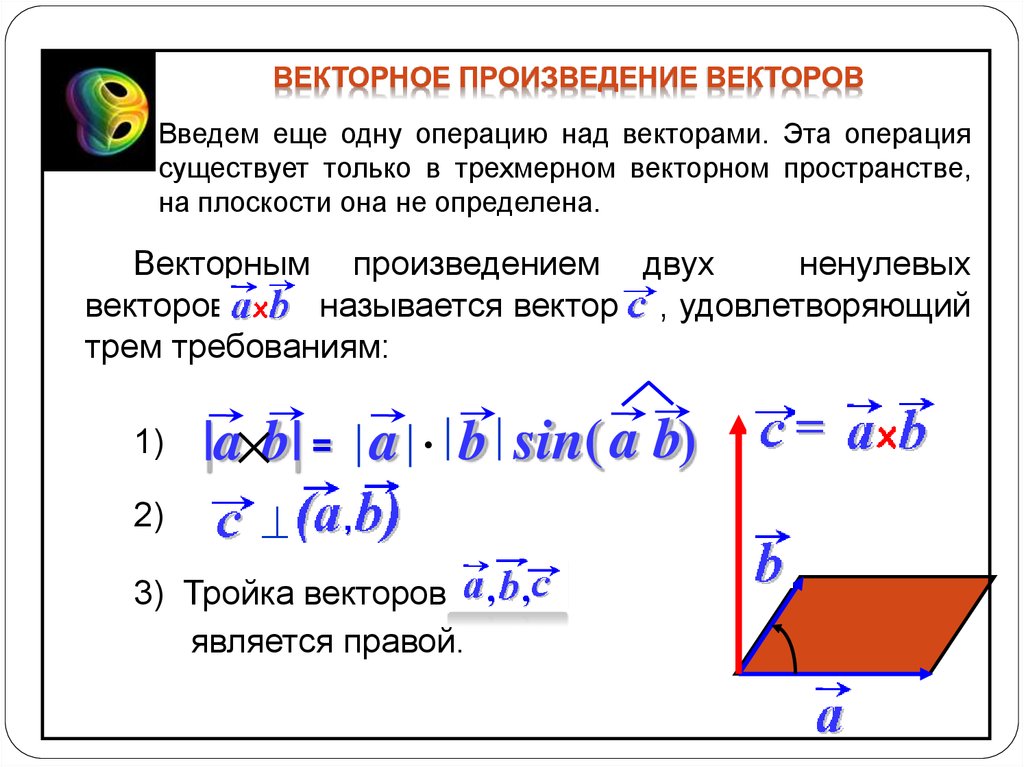 При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.
При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.
Вектор — вид представления точки, до которой требуется добраться из некоторой начальной точки.
Содержание:
- Понятие вектора
- Равенство векторов
- Сложение векторов
- Правило параллелепипеда сложения векторов
- Разность векторов
- Умножение вектора на число
- Скалярное произведение векторов
- Разложение вектора на составляющие
Понятие вектора
Векторы — это очень важное понятие, которое широко используется математиками и физиками.
Прежде всего, понятие вектора тесно связано с изучением векторных величин.
Некоторые величины в математике и физике, такие, как расстояние, площадь, объем, температура, работа, масса, характеризуются в процессе их измерения только соответствующим числом, при этом такая характеристика полная. Такие величины в математике называют скалярными. Значения скалярных величин могут быть однозначно отмечены на координатной прямой или шкале.
Такие величины в математике называют скалярными. Значения скалярных величин могут быть однозначно отмечены на координатной прямой или шкале.
Но есть и достаточно много других величин, таких, как перемещение, скорость, ускорение, сила, напряжение и др., для характеристики которых числа (числового значения) мало. Необходимо знать еще направление, в котором осуществляется действие этой величины. Поэтому все данные величины относятся к так называемым векторным величинам, которые характеризуются численным значением и направлением. Векторы придумали для того, чтобы изображать и применять векторные величины.
Рассмотрим пример.
Подъемный кран Ф за некоторый промежуток времени сместился вправо на расстояние 40 м (рис. 2.474). Это означает, что все его точки сместились вправо на 40 м. На рисунке это показано стрелками: двумя, выходящими из вершины крана В и из точки крана А, и одной общей стрелкой внизу рисунка. Таким образом, в данном примере фигура Ф при параллельном переносе в направлении луча на расстояние перешла в фигуру , а точка А перешла в точку , точка В перешла в точку и т. д.
д.
Итак,
1) лучи , сонаправленные;
2) расстояния , равны, .
В математике и физике такие отрезки принято называть направленными, это привело к появлению понятия вектора.
Определение. Вектором называют отрезок, на котором указано направление (одно из двух возможных).
Кратко говорят: вектор — это направленный отрезок. Первый по этому направлению конец отрезка называют началом вектора (или точкой приложения), второй — его концом. Вектор записывается обозначениями начала и конца слева направо (рис. 2.475), а сверху ставится черточка: .
На рисунке 2.476 изображено несколько векторов: Направления этих векторов указаны стрелками. Иногда векторы обозначают просто малыми жирными буквами или над буквами тоже ставят черту (рис. 2.477).
Определение. Два вектора называют коллинеарными, если изображающие их направленные отрезки параллельны или лежат на одной прямой.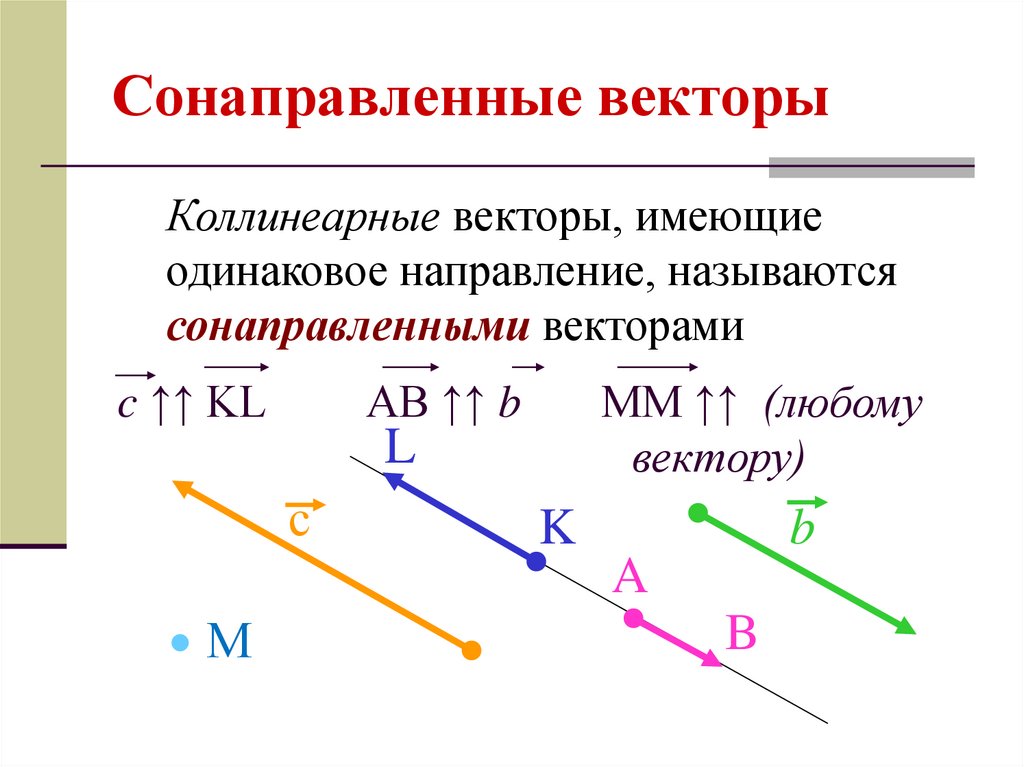
Коллинеарные векторы либо одинаково направлены, либо противоположно направлены.
На рисунке 2.478 векторы коллинеарные, а на рисунке 2.479 векторы неколлинеарные.
Кроме понятия коллинеарности векторов, вводится понятие компланарности векторов.
Определение. Три вектора называют компланарными, если изображающие их направленные отрезки лежат в параллельных плоскостях или в одной плоскости.
На рисунке 2.480 векторы компланарны, так как точки О, А, В и С лежат в одной плоскости. Векторы не компланарны, так как точки А, В, D и О не лежат в одной плоскости.
Равенство векторов
Дадим определение равных векторов.
Определение. Вектор равен вектору , если длины отрезков и равны и они одинаково направленные (сонаправленные).
Равенство векторов и записывается так: . Эта запись означает, что:
1) луч АВ сонаправлен лучу CD;
2) длины отрезков АВ и CD равны (рис.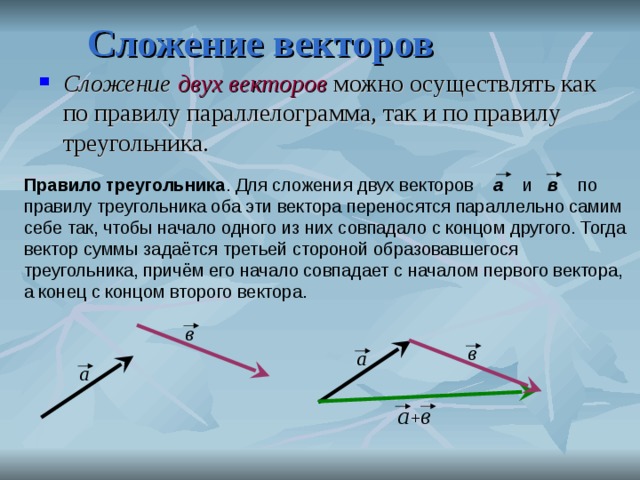 2.481).
2.481).
Определение. Длину направленного отрезка — вектора — называют модулем или абсолютной величиной вектора.
Для модуля векторов употребляется тот же знак, что и для модуля чисел. Запись = 5 читается: модуль (или длина) вектора решен 5.
Процесс изображения векторов часто называют откладыванием вектора от точки.
Отложить от данной точки вектор, равный данному, значит построить направленный отрезок с началом в этой точке, изображающий данный вектор.
На рисунке 2.482 от точки А отложен вектор , равный вектору .
Теорема 1 (об откладывании вектора). От любой точки можно отложить вектор, равный данному, и притом только один.
Определение. Если начало вектора совпадает с его концом, то такой вектор называют нулевым.
Нулевой вектор обозначается нулем с черточкой сверху: . Из определения следует, что модуль нулевого вектора решен нулю, а направления он не имеет.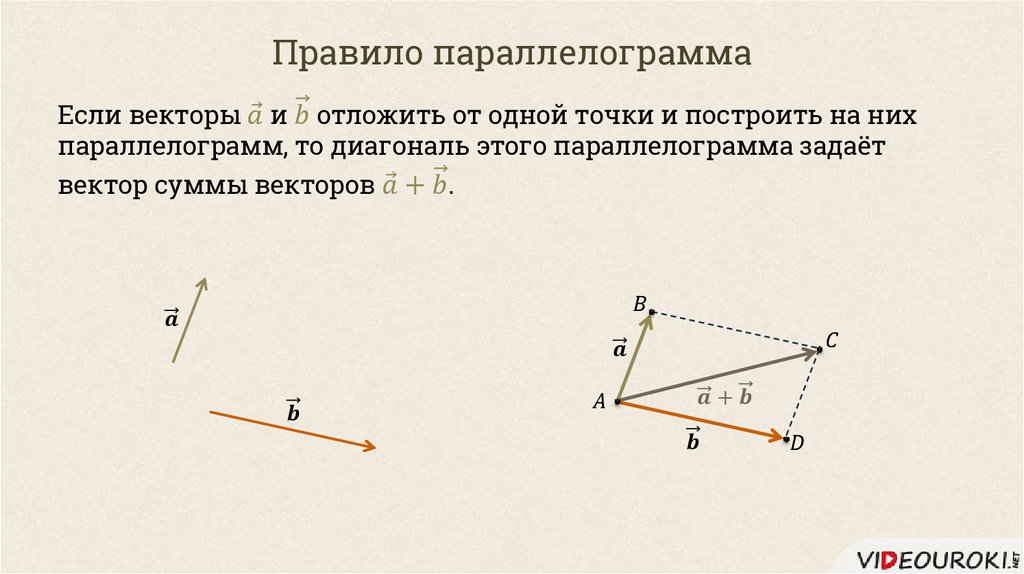 Нулевой вектор иногда называют также нуль-вектором. Изображается нулевой вектор любой точкой, которая рассматривается как начало и конец этого вектора.
Нулевой вектор иногда называют также нуль-вектором. Изображается нулевой вектор любой точкой, которая рассматривается как начало и конец этого вектора.
Сложение векторов
Первой операцией над векторами является сложение векторов.
Если материальная точка переместилась из точки А в точку В, а потом из точки В в точку С, то в результате она перейдет из точки А в точку С. Поэтому, естественно, говорят, что направленные отрезки , характеризующие эти перемещения, складываясь, дают направленный отрезок (рис. 2.483). Это записывается так:
В этом случае мы видим, что процесс сложения векторов происходит так: конец первого вектора является началом второго , а суммарный вектор соединяет начало первого вектора и конец второго.
Например, даны два вектора , задающие некоторые векторные величины, например силы (рис. 2.484). Чтобы сложить эти векторы, нужно:
1. Выбрать исходную точку А (возможно, ту точку, к которой приложена заданная сила).
2. От точки А отложить вектор , равный ,
3. От точки В отложить вектор , равный ,
4. Построить вектор , равный ( — сумма векторов и . (рис. 2.485)).
Теперь отложим вектор от точки (рис. 2.486). В этом случае в качестве суммы векторов и получим вектор . Можно доказать, что векторы и равны, т. е.
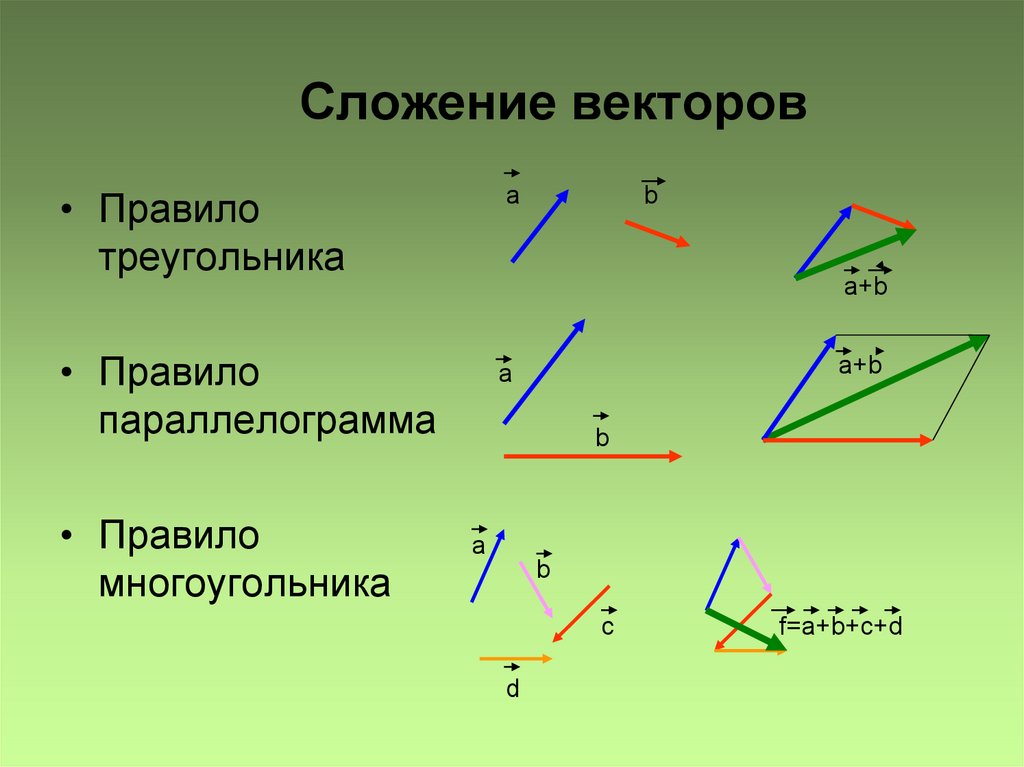
Таким образом, мы получили правило треугольника для сложения векторов.
Можно рассмотреть такой пример. Пусть, двигаясь горизонтально со скоростью , кран поднимает ящик со скоростью . На рисунке 2.487 изображены в масштабе скорость ящика относительно крана , направленная вертикально вверх, и скорость движения крана , направление которой совпадает с направлением движения крана. Сумма векторов и — вектор , который изображает скорость ящика относительно неподвижной системы отсчета:
Пусть нам даны векторы , которые неколли-неарны, то есть не лежат на одной прямой (рис. 2.488). Отложим эти вектора от некоторой точки А, то есть (рис. 2.489).
2.489).
Тогда суммарный вектор изобразится диагональю параллелограмма ABCD, построенного на векторах
Мы получили второе правило сложения векторов — правило параллелограмма: если векторы неколлинеарны, то их сумма представляется диагональю построенного на них параллелограмма.
Для операции сложения следующие свойства.
Теорема 2 (переместительный закон, или коммутативность сложения). Для любых векторов
Теорема 3 (сочетательный закон, или ассоциативность сложения). Для любых векторов
Эти законы выполняются и для коллинеарных векторов.
Из сочетательного и переместительного законов следует, что, складывая любое число векторов, можно как угодно переставлять и группировать слагаемые. Чтобы сложить несколько векторов,
например векторы , удобно построить векторную ломаную (рис. 2.490). Эта ломаная состоит из направ ленных отрезков Вектор , соединяющий начало ломаной ABCDE и ее конец, и является суммой
Если ломаная получилась замкнутой, то сумма векторов равна нуль-вектору (рис.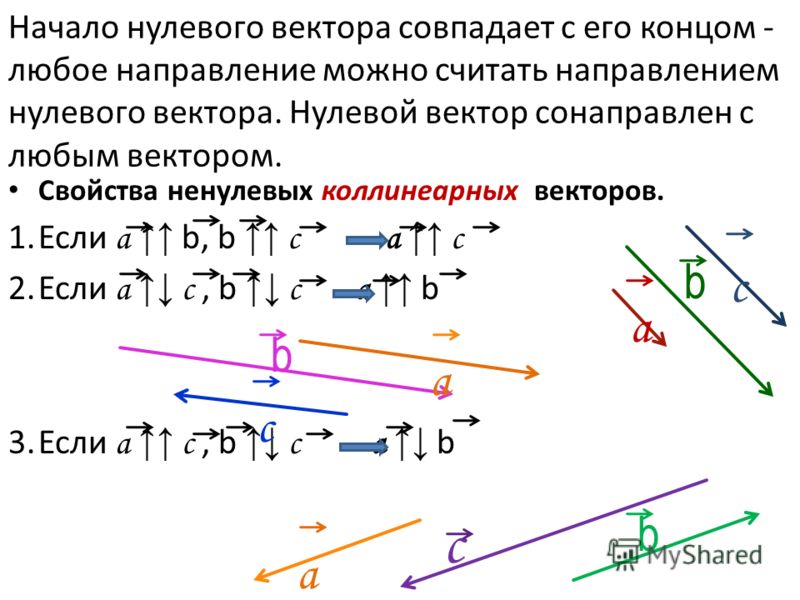 2.491), т. е.
2.491), т. е.
Отметим важное свойство нуль-вектора: для любого вектора выполняется равенство
Правило параллелепипеда сложения векторов
Пусть даны три вектора , не лежащие в одной плоскости (их называют некомпланарными) (рис. 2.492).
Выполним следующие построения.
1. Отложим от произвольной точки О векторы (построение) (рис. 2.493).
2. Построим параллелепипед так, чтобы отрезки OA, ОВ, ОС были его ребрами (построение) (рис. 2.494).
3. (2, правило параллелограмма).
4. (2, определение равенства векторов).
5. (3, 4, правило параллелограмма).
Таким образом, сумма трех векторов, не параллельных одной плоскости, представляется диагональю параллелепипеда, построенного на данных векторах, отложенных от одной точки, как на ребрах (рис. 2.494).
Получили правило параллелепипеда для сложения векторов в пространстве.
Разность векторов
Введем операцию разности двух векторов. Эта операция вводится так же, как и для чисел.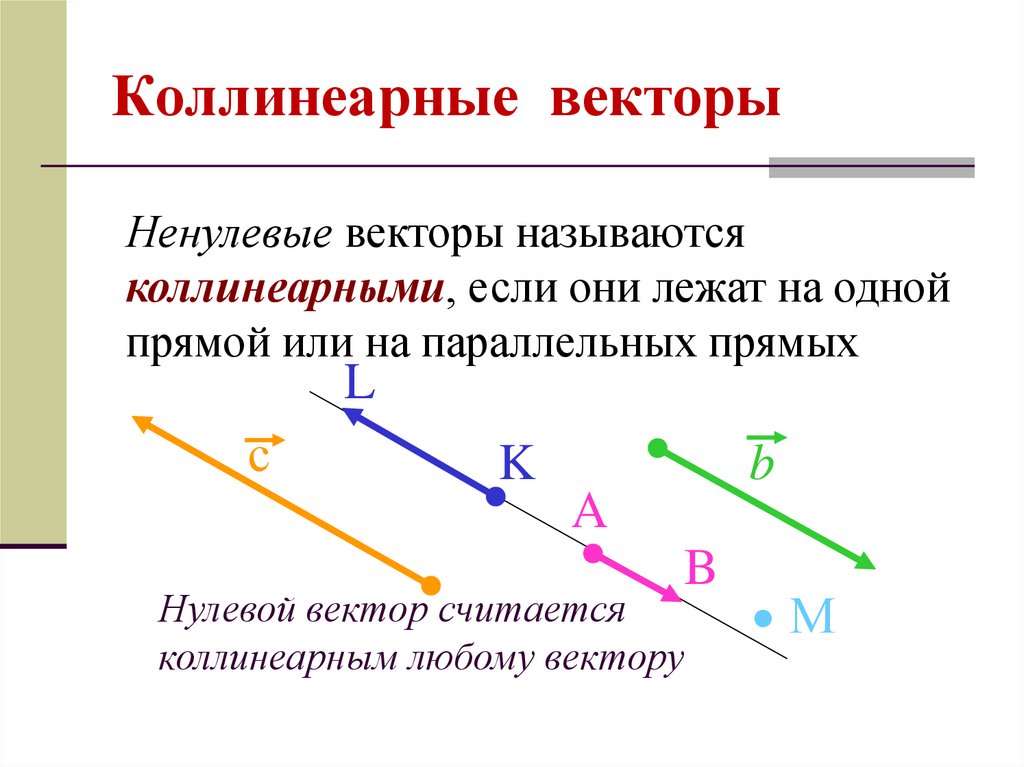
Определение. Разностью векторов называют такой вектор , что .
Разность векторов обозначается, как и для чисел, .
Построим разность двух векторов (рис. 2.495).
Отложим от какой-нибудь точки О данные векторы : (рис. 2.496). Рассмотрим вектор , мы видим, что (правило треугольника). Вектор будет разностью векторов и , т. е. Если вектор обозначить через , то .
Равенство можно назвать правилом нахождения разности двух векторов.
Определение. Два ненулевых вектора называют противоположными, если их длины равны и они направлены противоположно.
На рисунке 2.497 изображены два противоположных друг другу вектора.
Нуль-вектор считается противоположным самому себе.
Вектор, противоположный вектору , обозначается (читается: «минус а»).
Для вектора противоположным ему будет вектор .
Теорема 4. Если сложить противоположные векторы (по правилу треугольника), то в сумме получится нуль-вектор, то есть .
Верно и обратное утверждение: если сумма двух векторов равна нуль-вектору, то они противоположны.
Умножение вектора на число
В геометрии части возникает потребность в сложении двух, трех или более одинаковых векторов: и т. д. Такие суммы, как и в алгебре, удобно записывать и т. д. Эта процедура подсказывает определение операции умножения вектора на число.
Определение. Пусть даны ненулевой вектор и число . Произведением вектора на число х называют такой вектор , который, во-первых, имеет длину и, во-вторых, сонаправлен с вектором , если х > 0, и направлен противоположно вектору , если х < 0.
Итак, если, причем , то:
1)
2) сонаправлен с , если х > 0, и противоположно направлен с , если х < 0 (рис. 2.498).
3) Если или х = 0, то вектор . Для операции умножения вектора на число выполняются следующие свойства:
Векторы часто помогают изучать геометрические факты; для этого нужно научиться переводить геометрические факты на векторный язык, и наоборот, уметь векторное выражение перевести на язык геометрии.
Предположим, что нам нужно доказать, что прямые параллельны (рис. 2.499). Рассмотрим векторы и , принадлежащие соответственно прямым (рис. 2.500) (векторы и могут иметь и противоположные направления).
Если мы докажем, что векторы и коллинеарны, то по определению коллинеарности векторов получим, что прямые параллельны. Можно доказать теорему о коллине-арных векторах.
Теорема 5. Вектор коллинеарен ненулевому вектору тогда и только тогда, когда
Следствие (о векторах на прямой). Два вектора, отложенные от одной и той же точки, лежат на одной прямой тогда и только тогда, когда один из них получается из другого умножением на число.
Другими словами, точка X лежит на прямой АВ тогда и только тогда, когда (рис. 2.501).
Есть еще два более сложных свойства операций над векторами, которые относятся уже к двум операциям над векторами: сложением и умножением на число. Это два распределительных (или дистрибутивных) закона.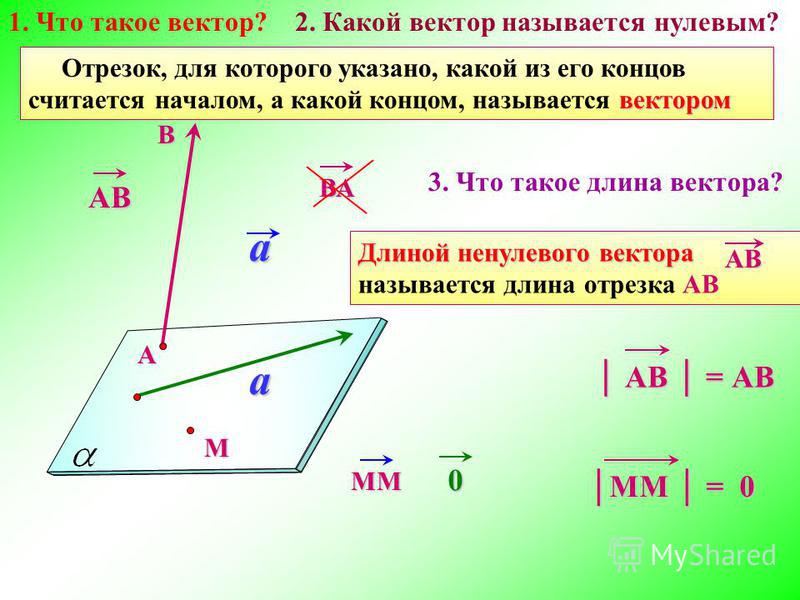
Оба эти свойства относятся к плоскости, так как выполняющиеся в них действия производятся с векторами, параллельными одной плоскости (или лежащими в одной плоскости). Если отложить эти векторы от одной точки, то изображающие их направленные отрезки окажутся лежащими в одной плоскости. Более того, свойство 6 касается лишь векторов, параллельных одной прямой (или лежащих на одной прямой). Оно непосредственно вытекает из определений сложения векторов и умножения векторов на число.
Скалярное произведение векторов
Если даны два ненулевых вектора (рис. 2.502), то углом между этими векторами называют угол, образованный направленными отрезками , отложенными от некоторой точки О (рис. 2.503).
При этом рассматривают так называемый выпуклый угол (угол, имеющий меньшую величину). Иногда угол между векторами обозначают так: (a и Ъ) = 30° читают: угол между векторами равен 30°. Определение. Углом между двумя ненулевыми векторами называют угол между соответствующими им направленными отрезками, исходящими из одной точки.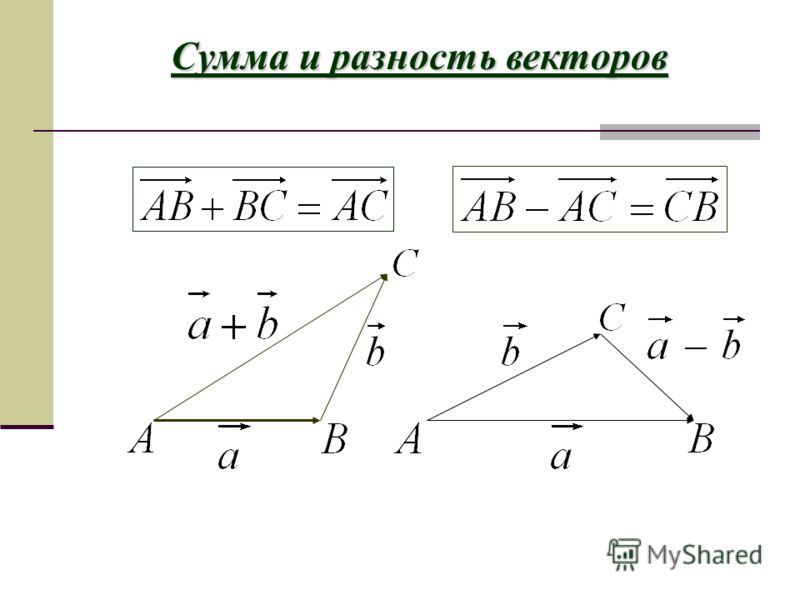 Угол между противоположно направленными векторами равен 180°, а между сонаправ ленными — 0°.
Угол между противоположно направленными векторами равен 180°, а между сонаправ ленными — 0°.
Определение. Скалярным произведением двух ненулевых векторов называют произведение длин этих векторов на косинус угла между ними. Если хотя бы один из двух векторов нулевой, то их скалярное произведение равно 0.
Если угол между векторами равен то их скалярное произведение
1. Если векторы равны, т. е. , то пишут и говорят о скалярном квадрате вектора. В этом случае , т. е. . Итак, скалярный квадрат вектора совпадает с квадратом его длины:
2. Если , то получаем . Можно сформулировать такой признак: векторы перпендикулярны в том и только в том случае, когда их скалярное произведение равно нулю.
3. ; при этом из следует Это свойство следует из первого свойства.
4.
5. Скалярное умножение связано со сложением векторов распределительным (дистрибутивным) законом:
Разложение вектора на составляющие
При изучении и использовании векторов часто приходится говорить о так называемом разложении вектора на составляющие.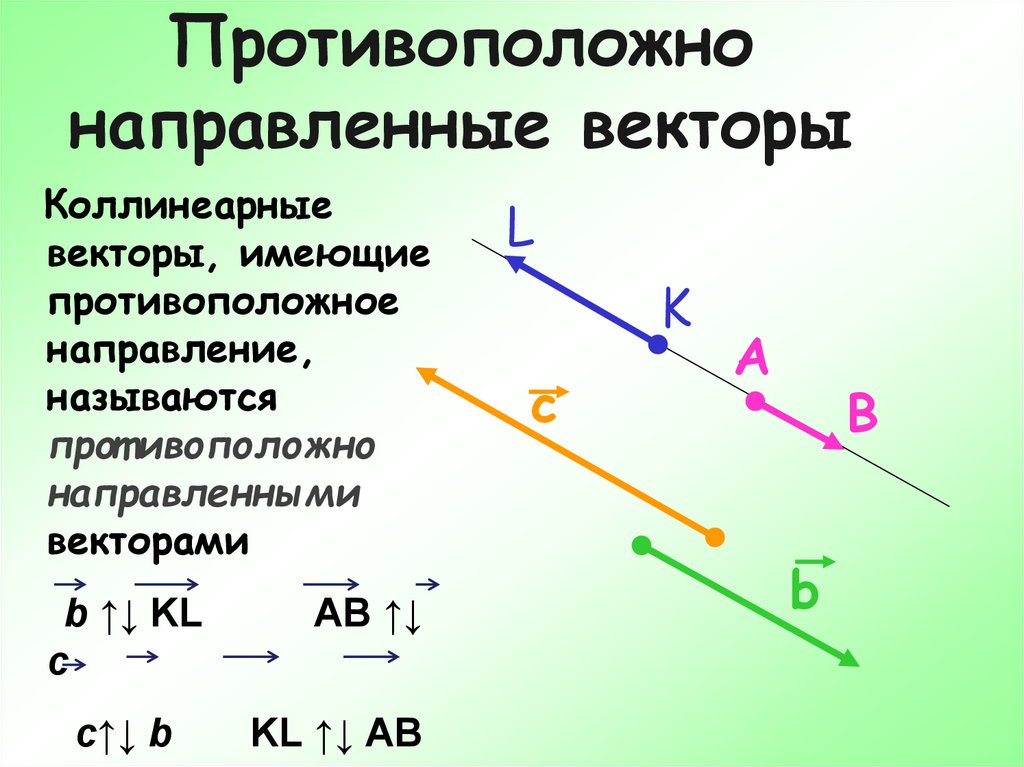
Определение. Составляющими данного вектора называют такие векторы, сумма которых равна этому вектору.
Данный вектор «составляется» из составляющих как сумма слагаемых и разлагается на них как на слагаемые, поэтому говорят о разложении на составляющие.
Пусть в плоскости даны две прямые , пересекающиеся в точке О. Возьмем какой-нибудь вектор и отложим его от точки О (рис. 2.504),
Если точка V не лежит ни на прямой , ни на прямой , то проведем через точку V прямые VA || и VB || и построим параллелограмм OAVB. Его диагональю будет отрезок OV, а его стороны OA и ОВ лежат соответственно на прямых и . По правилу параллелограмма для сложения векторов получим
Векторы являются составляющими вектора по прямым
Если а составляющая по нулевая: Аналогично в случае, когда
Мы выполнили разложение вектора по двум пересекающимся прямым.
Можно разложить вектор по двум неколлинеарным векторам.
Возьмем два неколлинеарных вектора отложим их от точки О (рис. 2.505). Пусть — вектор параллельный плоскости ОВС; отложим его от точки О, Через точку А проведем прямые, параллельные векторам , тогда
2.505). Пусть — вектор параллельный плоскости ОВС; отложим его от точки О, Через точку А проведем прямые, параллельные векторам , тогда
Векторы коллинеарны, значит,
Такое представление вектора через векторы и называют разложением вектора по неколлинеарным векторам.
Можно доказать единственность такого разложения.
Если допустить, что есть другое разложение: то есть разложение то же.
Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:
- Математика решение заданий и задач
Смотрите также дополнительные лекции по предмету «Математика»:
Объекты и типы данных R: векторы
Язык R принадлежит к семейству так называемых высокоуровневых объектно-ориентированных языков программирования. Для неспециалиста строгое определение понятия «объект» является достаточно абстрактным. Однако для простоты можно называть объектами все, что мы создаем в ходе работы с R. Их выделяют два основных типа:
Их выделяют два основных типа:
- Объекты, предназначенные для хранения данных («data objects») – это векторы, матрицы и массивы, списки, факторы, таблицы данных;
- Функции («function objects») – это поименованные программы, предназначенные для выполнения определенных действий над другими объектами.
В этом сообщении расмотрены векторы, способы их создания в R, а также основные операции над ними.
Вектор представляет собой поименованный одномерный объект, содержащий набор однотипных элементов (числовые, логические, либо текстовые значения — никакие сочетания не допускаются). Для создания векторов небольшой длины в R используется т.н. функция конкатенации c() (от «concatenate» – объединять, связывать). В качестве аргументов этой функции через запятую перечисляют объединяемые в вектор значения, например:
my.vector <- c(1, 2, 3, 4, 5) my.vector [1] 1 2 3 4 5
Вектор можно создать также при помощи функции scan(), которая «считывает» последовательно вводимые с клавиатуры значения:
X <- scan() 1: 2.9 # после каждого нового значения нажать клавишу "Ввод" 2: 3.1 3: 3.4 4: 3.4 5: 3.7 6: 3.7 7: 2.8 8: 2.5 9: # выполнение команды scan завершают введением пустой строки Read 8 items # программа сообщает о считывании 8 значений X [1] 2.9 3.1 3.4 3.4 3.7 3.7 2.8 2.5
Один из недостатков создания векторов при помощи функции scan() состоит в том, что если при вводе значений с клавиатуры допущена ошибка, то придется либо начать ввод заново, либо воспользоваться специальными инструментами корректировки (например, функцией fix(); здесь эти способы не рассматриваются).
Для создания векторов, содержащих совокупность последовательных чисел, удобна функция seq() (от «sequence» – последовательность). Так, вектор с именем S, содержащий совокупность целых чисел от 1 до 7, можно создать следующим образом:
S <- seq(1,7) S [1] 1 2 3 4 5 6 7
Идентичный результат будет получен при помощи команды
S <- 1:7 S [1] 1 2 3 4 5 6 7
В качестве дополнительного аргумента функции seq() можно задать шаг приращения чисел:
S <- seq(from = 1, to = 5, by = 0.5) S [1] 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0
Векторы, содержащие одинаковые значения, создают при помощи функции rep() (от «repeat» – повторять). Например, для формирования текстового вектора Text, содержащего пять значений «test», следует выполнить команду
Text <- rep(«test», 5)
Text [1] "test" "test" "test" "test" "test"
Система R способна выполнять самые разнообразные операции над векторами. Так, несколько векторов можно объединить в один, используя уже рассмотренную выше функцию конкатенации
v1 <- c(1, 2, 3) v2 <- c(4, 5, 6) V <- c(v1, v2) V [1] 1 2 3 4 5 6
Если попытаться объединить, например, текстовый вектор с числовым, сообщение об ошибке не появится – программа просто преобразует все значения в текстовые:
# создаем текстовый вектор text.vect:
text.vect <- c("a", "b", "c")
# объединяем числовой вектор v1 (см. выше) с текстовым вектором text. vect:
# new.vect <- c(v1, text.vect)
# просмотр содержимого нового вектора new.vect:
new.vect
[1] "1" "2" "3" "a" "b" "c"
# все значения нового вектора взяты в кавычки,
# что указывает на их текстовую природу;
# для подтверждения этого воспользуемся командой mode():
mode(new.vect)
[1] "character" # все верно: "character" значит "текстовый"
vect:
# new.vect <- c(v1, text.vect)
# просмотр содержимого нового вектора new.vect:
new.vect
[1] "1" "2" "3" "a" "b" "c"
# все значения нового вектора взяты в кавычки,
# что указывает на их текстовую природу;
# для подтверждения этого воспользуемся командой mode():
mode(new.vect)
[1] "character" # все верно: "character" значит "текстовый"Для работы c определенным элементом вектора необходимо уметь отличать его от других похожих элементов. Для этого при создании вектора всем его компонентам автоматически присваиваются индексные номера, начиная с 1. Чтобы обратится к конкретному элементу необходимо указать имя вектора и индекс этого элемента в квадратных скобках:
# создадим числовой вектор y, содержащий 5 числовых значений: y <- c(5, 3, 2, 6, 1) # проверим, чему равен третий элемент вектора y: y[3] [1] 2
Используя индексные номера, можно выполнять различные операции с избранными элементами разных векторов:
# создадим еще один числовой вектор z, содержащий 3 значения: z <- c(0.5, 0.1, 0.6) # умножим первый элемент вектора y на третий элемент вектора z (т.е. 5*0.6): y[1]*z[3] [1] 3
Индексирование является мощным инструментом, позволяющим создавать совокупности значений в соответствии с определенными критериями. Например, для вывода на экран 3-го, 4-го и 5-го значений вектора y необходимо выполнить команду
y[3:5] [1] 2 6 1
Из этого же вектора мы можем выбрать, например, только первое и четвертое значения, используя уже известную нам функцию конкатенации с():
y[с(1, 4)] [1] 5 6
Похожим образом мы можем удалить первое и четвертое значения из вектора y, применив знак «минус» перед функцией конкатенации:
y[-с(1, 4)] [1] 3 2 1
В качестве критерия для выбора значений может служить логическое выражение. Для примера выберем из вектора y все значения >2:
y[y>2] [1] 5 3 6
Ниже перечислены все используемые в R логические операторы:
- «Равно» ==
- «Не равно» !=
- «Меньше» <
- «Больше» >
- «Меньше либо равно» <=
- «Больше либо равно» >=
- «Логическое И» &
- «Логическое ИЛИ» |
- «Логическое НЕ» !
Индексирование является также удобным инструментом для внесения исправлений в имеющихся векторах. Например, так можно исправить второе значение созданного нами ранее вектора z с 0.1 на 0.3:
Например, так можно исправить второе значение созданного нами ранее вектора z с 0.1 на 0.3:
z[2] <- 0.3 z [1] 0.5 0.3 0.6
Для упорядочения значений вектора по возрастанию или убыванию используют функцию sort() в сочетании с аргументом decreasing = FALSE или decreasing = TRUE соответственно («decreasing» значит «убывающий»):
sort(z, decreasing = FALSE) [1] 0.3 0.5 0.6 sort(z, decreasing = TRUE) [1] 0.6 0.5 0.3
Дополнительную информацию на русском языке о векторах и других объектах R можно найти здесь и здесь.
--
Создано при помощи Pretty R на сайте inside-R.org
Векторов
Векторы в R n
Определение и свойства
Мы предполагаем, что вы уже знакомы с векторами в R 2 и R 3 ,
так что вы увидите, что определение расширяется естественным образом.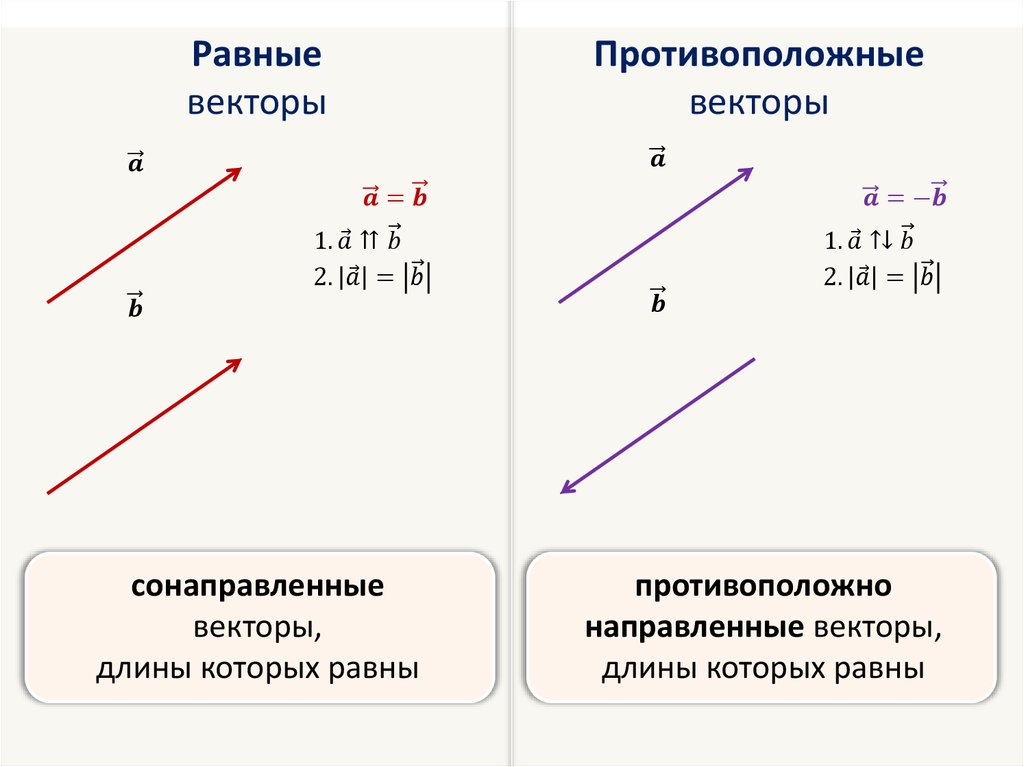
А вектор в р п является n x 1 матрицей.
набор всех векторов в R п называется n-space .
Мы определяют сумму и разность двух векторов и произведение скаляра на вектор, просто поняв, что векторы — это матрицы.
Пример
Пусть
тогда
Недвижимость векторов
Векторов пользоваться следующими свойствами.
Если и , v и w являются векторами и c и д скаляры, затем
- и + v = v + u
- и + ( v + w ) = ( u + v ) + w
- Есть это 0 с у + 0 = 0 + u = u для всех векторов u .
- Для
любые и там
это -у с u + ( -u )
= 0 .

- в и является вектором в R n .
- с( и + v ) = c u + c v
- (с +г) u = c u + d u
- с(д и ) = (кд) u
- 1 и = u
доказательства всего этого исходят из свойств действительных чисел, поскольку дано определение сложения вычитания и скалярного умножения покомпонентно. Например, чтобы доказать число 6, у нас есть
.[(с + г) и ] i = (c + d)[ u ] i = c[ u ] i + d[ u ] i = [c u ] i + [д и ] я
Скалярное произведение и длина
Так же, как мы определили скалярное произведение для векторов в R 2 и
Р 3 ,
аналогичным образом мы определяем скалярное произведение для двух векторов в более общем R n .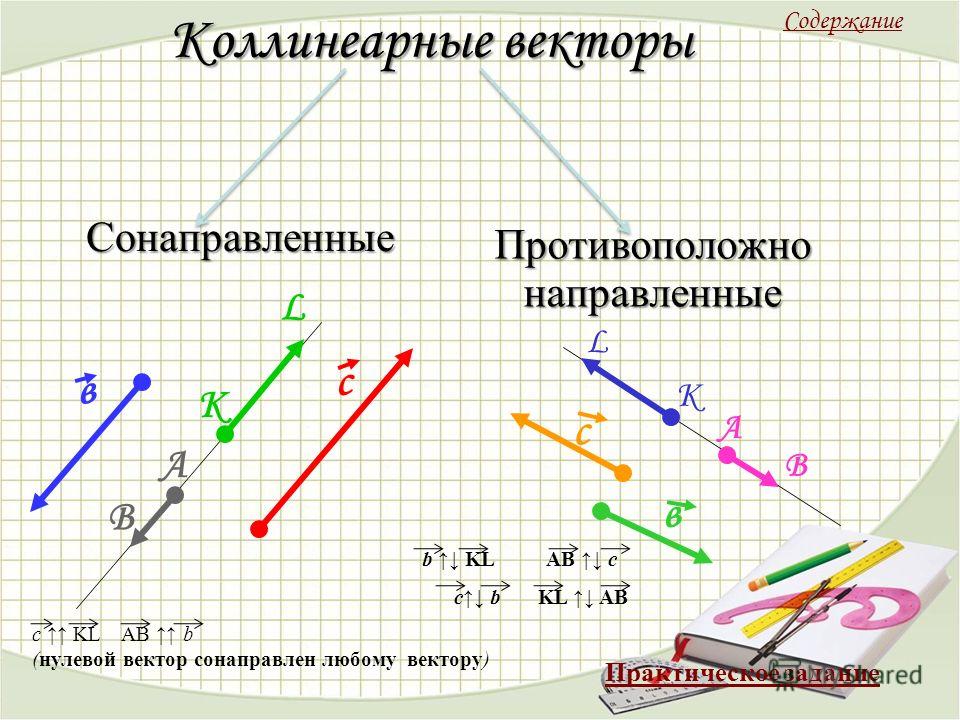
Определение
Пусть
тогда скалярное произведение (или скалярное произведение) u и против определяется
у . v = S и и в я
Определяем длину или звездной величины вектор как
А вектор представляет собой единичный вектор если он имеет длину один. Блок вектор в направлении u дано
и
|| и ||
и расстояние от до и против по
Расстояние = || и — v ||
угол q между двумя векторами определяется
у. в
потому что q
=
|| и || || v||
и и против ортогональные если
и . v = 0
Пример
Пусть
как в первом примере тогда
у . v = (1)(-4) + (4)(2) + (3)(0) +
(2)(4) = 12
v = (1)(-4) + (4)(2) + (3)(0) +
(2)(4) = 12
и расстояние между u и v это
единичный вектор в направлении u это
угол между u и v определяется
и
Недвижимость скалярного продукта
Далее мы даем некоторые основные свойства скалярного произведения.
Пусть и , против , и с быть векторами и c быть скаляром, тогда
- у . u > 0; у . и = 0 тогда и только тогда, когда и = 0,
- у . v = v . и .
- ( и + v ) . w = u . с + по сравнению с . с .

- (с и ) . v = u . (с против ) = c( u . v) .
Мы докажет свойство 2 и оставит остальные доказательства вам.
Доказательство из 2
у . v = S ты i v i = S v i u i = v . у
Еще одно важное свойство под названием Коши-Шварца неравенство достаточно важно, чтобы стоять отдельно.
Неравенство Коши-Шварца
Если и и против являются векторами, тогда
| ты . v| < ||у|| ||в||
Если выполняется равенство, мы говорим, что u и против параллельны . Это произойдет, только если u кратно против .
Доказательство
Доказательство довольно сложное.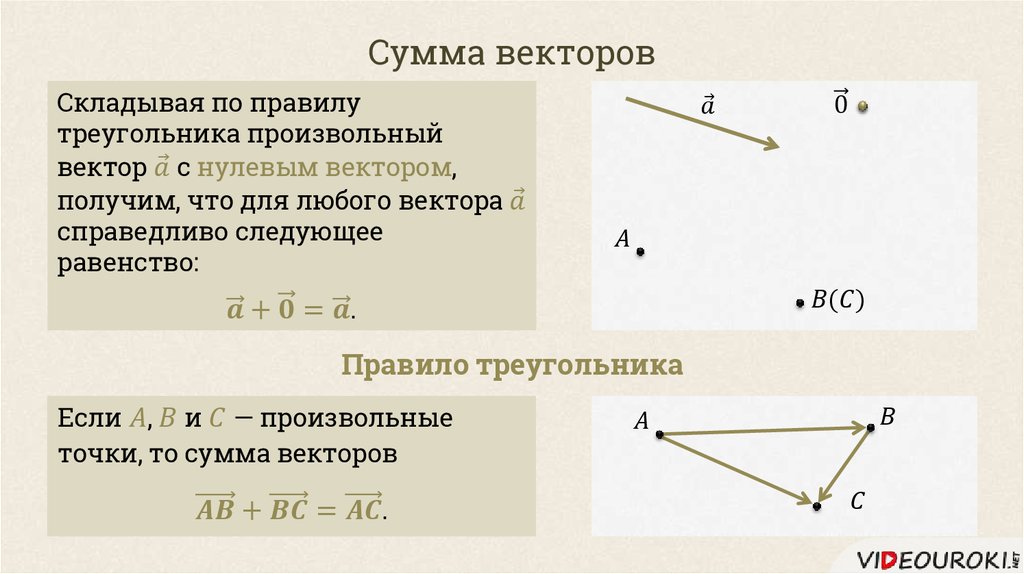 Мы позволяем х
быть скаляром и отметить из свойства 1, что
Мы позволяем х
быть скаляром и отметить из свойства 1, что
0 < (x u + v ) . (х и + против )
= u . х x 2 + 2 х . v х + v . против
Поскольку скалярное произведение дает скаляр, приведенное выше уравнение является квадратным в Икс. Квадратичный всегда положительный имеет неположительный дискриминант. Отсюда
(2 u . v ) 2 — 4( u . u )( v . v ) < 0
деление на 4 дает
( и . v ) 2 — ( u . u )( v . v ) < 0
или
( u . v ) 2 < ( и . и )( в . против )
Получение квадратного корня из обеих сторон дает результат.
Последнее свойство скалярного произведения, которое мы обсудим, исходит из геометрия. Все мы знаем, что кратчайшее расстояние между двумя точками равно прямая линия. Если мы хотим отправиться из начала координат в точку P, быстрее идти по прямому пути, чем идти в точку Q сначала, а затем в P. Если мы выберем точку P быть вершиной вектора u + v, а Q — вершиной вектора ты, тогда мы иметь следующую схему.
Это приводит нас к неравенству треугольника.
Неравенство треугольника
Если и и против векторов, затем
|| и + против || < || и || + || против ||
Доказательство
Берем квадрат левой стороны
|| и + против || 2 = ( u + v ) . ( и + v ) = u .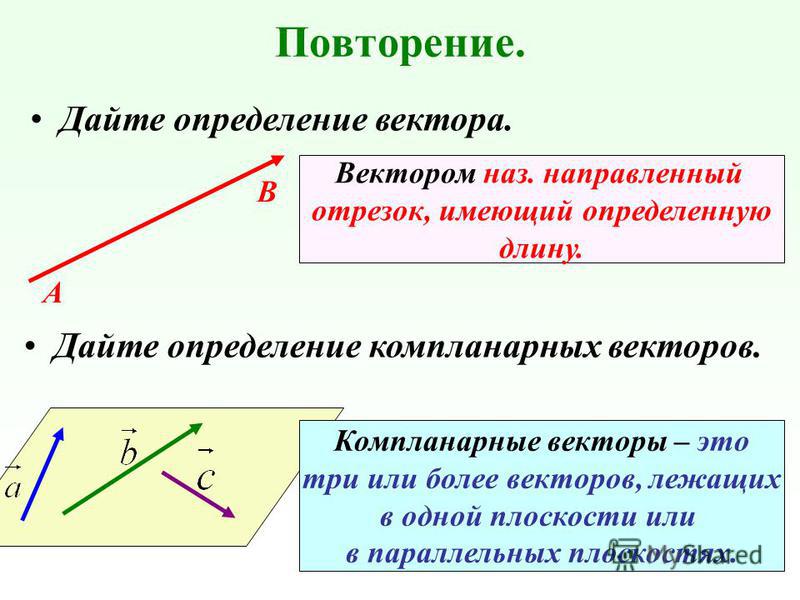 и + 2 и . В + В . против
и + 2 и . В + В . против
= || и || 2 + 2( u . v ) + || против || 2 < || и || 2 + 2|| и || || против || + || против || 2 Коши-Шварц
= (|| u || + || v ||) 2
Назад на домашнюю страницу векторов
Назад на домашнюю страницу линейной алгебры
Назад к математике Домашняя страница отдела
электронная почта Вопросы и предложения
р — Уникальная комбинация всех элементов из двух (и более) векторов
Задавать вопрос
Спросил
Изменено 2 года, 11 месяцев назад
Просмотрено 124k раз
Я пытаюсь создать уникальную комбинацию всех элементов из двух векторов разного размера в R.
Например, первый вектор
a <- c("ABC", "DEF", "GHI ")
, а второй - даты, хранящиеся в виде строк в настоящее время
b <- c("01.05.2012", "02.05.2012", "03.05.2012", "04.05.2012", "05.05.2012")
Мне нужно создать фрейм данных с двумя такими столбцами
> данные
а б
1 Азбука 2012-05-01
2 Азбука 2012-05-02
3 Азбука 2012-05-03
4 Азбука 2012-05-04
5 Азбука 2012-05-05
6 ДЕФ 2012-05-01
7 ДЭФ 2012-05-02
8 ДЕФ 2012-05-03
9 ДЭФ 2012-05-04
10 ДЕФ 2012-05-05
11 GHI 2012-05-01
12 GHI 2012-05-02
13 GHI 2012-05-03
14 GHI 2012-05-04
15 GHI 2012-05-05
В общем, я ищу уникальную комбинацию, рассматривая все элементы одного вектора (a) рядом со всеми элементами второго вектора (b).
Идеальным решением было бы обобщение на большее количество входных векторов.
См. также:
Как составить матрицу комбинаций
- r
- r-faq
0
это может быть то, что вам нужно
> expand.grid(a,b) Вар1 Вар2 1 Азбука 2012-05-01 2 ДЭФ 2012-05-01 3 GHI 2012-05-01 4 Азбука 2012-05-02 5 ДЭФ 2012-05-02 6 GHI 2012-05-02 7 Азбука 2012-05-03 8 ДЕФ 2012-05-03 9GHI 2012-05-03 10 Азбука 2012-05-04 11 ДЕФ 2012-05-04 12 GHI 2012-05-04 13 АВС 2012-05-05 14 ДЭФ 2012-05-05 15 GHI 2012-05-05
Если полученный заказ не соответствует вашим ожиданиям, вы можете отсортировать его позже. Если вы назовете аргументы expand.grid , они станут именами столбцов:
df = expand.grid(a = a, b = b) df[порядок(df$a), ]
И expand.grid обобщает любое количество входных столбцов.
4
9Пакет 0749 tidyr предоставляет хорошую альтернативу , пересекающую , которая работает лучше, чем классическая функция expand.grid , потому что (1) строки не преобразуются в множители и (2) сортировка более интуитивно понятна: библиотека
(тидыр)
а <- с ("ABC", "DEF", "GHI")
b <- c("01. 05.2012", "02.05.2012", "03.05.2012", "04.05.2012", "05.05.2012")
пересечение (а, б)
# Таблетка: 15 x 2
а б
<хр> <хр>
1 Азбука 2012-05-01
2 Азбука 2012-05-02
3 Азбука 2012-05-03
4 Азбука 2012-05-04
5 Азбука 2012-05-05
6 ДЕФ 2012-05-01
7 ДЭФ 2012-05-02
8 ДЕФ 2012-05-03
9ДЕФ 2012-05-04
10 ДЕФ 2012-05-05
11 GHI 2012-05-01
12 GHI 2012-05-02
13 GHI 2012-05-03
14 GHI 2012-05-04
15 GHI 2012-05-05
05.2012", "02.05.2012", "03.05.2012", "04.05.2012", "05.05.2012")
пересечение (а, б)
# Таблетка: 15 x 2
а б
<хр> <хр>
1 Азбука 2012-05-01
2 Азбука 2012-05-02
3 Азбука 2012-05-03
4 Азбука 2012-05-04
5 Азбука 2012-05-05
6 ДЕФ 2012-05-01
7 ДЭФ 2012-05-02
8 ДЕФ 2012-05-03
9ДЕФ 2012-05-04
10 ДЕФ 2012-05-05
11 GHI 2012-05-01
12 GHI 2012-05-02
13 GHI 2012-05-03
14 GHI 2012-05-04
15 GHI 2012-05-05
В этом обзоре r-faq отсутствует функция CJ из пакета data.table. Использование: библиотека
(data.table) CJ(a, b, уникальный = ИСТИНА)
дает:
а б 1: Азбука 2012-05-01 2: Азбука 2012-05-02 3: Азбука 2012-05-03 4: Азбука 2012-05-04 5: Азбука 2012-05-05 6: ДЕФ 2012-05-01 7: ДЕФ 2012-05-02 8: ДЕФ 2012-05-03 9: DEF 2012-05-04 10: ДЕФ 2012-05-05 11: GHI 2012-05-01 12: GHI 2012-05-02 13: GHI 2012-05-03 14: GHI 2012-05-04 15: GHI 2012-05-05
ПРИМЕЧАНИЕ: начиная с версии 1.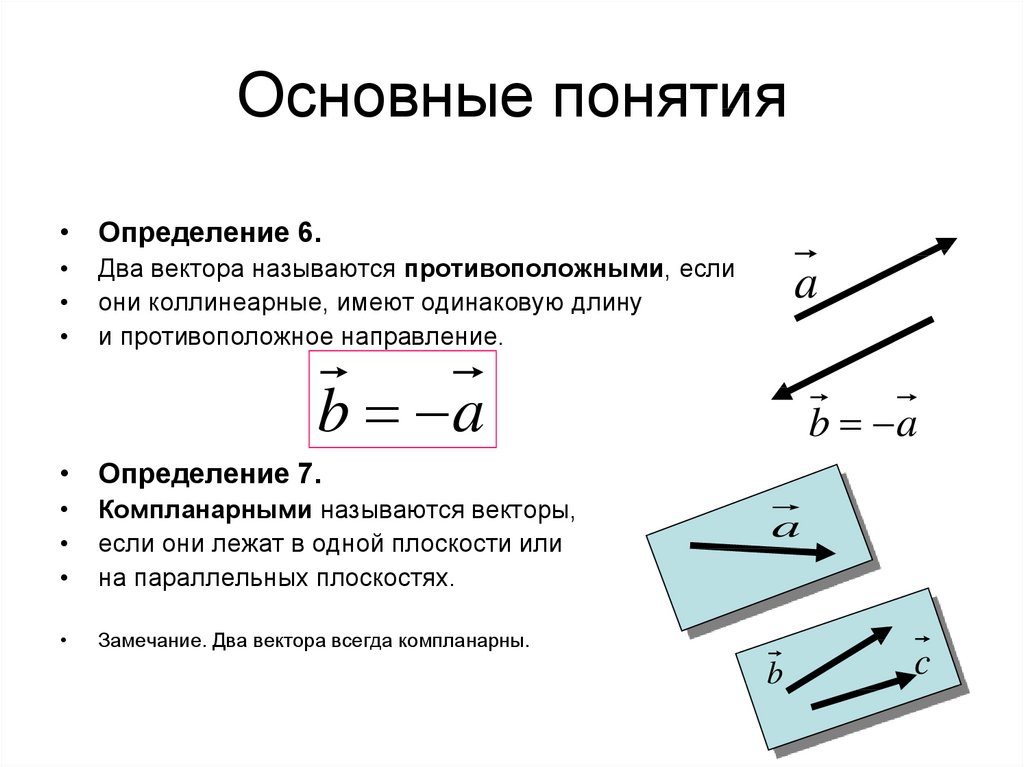 12.2
12.2 CJ автоматически присваивает имена результирующим столбцам (см. также здесь и здесь).
Начиная с версии 1.0.0, тайдыр предлагает собственную версию expand.grid() . Он дополняет существующее семейство expand() , вложенности() и crossing() низкоуровневой функцией, которая работает с векторами.
По сравнению с base::expand.grid() :
Быстрее всего меняется первый элемент. Никогда не преобразует строки в множители. Не добавляет никаких дополнительных атрибутов. Возвращает табличку, а не данные Рамка. Может расширять любой обобщенный вектор, включая фреймы данных.
а <- с ("ABC", "DEF", "GHI")
b <- c("01.05.2012", "02.05.2012", "03.05.2012", "04.05.2012", "05.05.2012")
tyr::expand_grid(а, б)
а б
<хр> <хр>
1 Азбука 2012-05-01
2 Азбука 2012-05-02
3 Азбука 2012-05-03
4 Азбука 2012-05-04
5 Азбука 2012-05-05
6 ДЕФ 2012-05-01
7 ДЭФ 2012-05-02
8 ДЕФ 2012-05-03
9ДЕФ 2012-05-04
10 ДЕФ 2012-05-05
11 GHI 2012-05-01
12 GHI 2012-05-02
13 GHI 2012-05-03
14 GHI 2012-05-04
15 GHI 2012-05-05
вы можете использовать функцию порядка для сортировки любого количества столбцов. для вашего примера
для вашего примера
df <- expand.grid(a,b) > дф Вар1 Вар2 1 Азбука 2012-05-01 2 ДЭФ 2012-05-01 3 GHI 2012-05-01 4 Азбука 2012-05-02 5 ДЭФ 2012-05-02 6 GHI 2012-05-02 7 Азбука 2012-05-03 8 ДЕФ 2012-05-03 9 GHI 2012-05-03 10 Азбука 2012-05-04 11 ДЕФ 2012-05-04 12 GHI 2012-05-04 13 АВС 2012-05-05 14 ДЭФ 2012-05-05 15 GHI 2012-05-05 > дф[порядок(дф[1], дф[2]),] Вар1 Вар2 1 Азбука 2012-05-01 4 Азбука 2012-05-02 7 Азбука 2012-05-03 10 Азбука 2012-05-04 13 АВС 2012-05-05 2 ДЭФ 2012-05-01 5 ДЭФ 2012-05-02 8 ДЕФ 2012-05-03 11 ДЕФ 2012-05-04 14 ДЭФ 2012-05-05 3 GHI 2012-05-01 6 GHI 2012-05-02 9GHI 2012-05-03 12 GHI 2012-05-04 15 GHI 2012-05-05`
0
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Бесплатные векторные изображения графического дизайна скачать
Расширенный поиск Запросить дизайн
[ Векторы ] шаблон рождественского баннера милый стилизованный декор снежинки ( .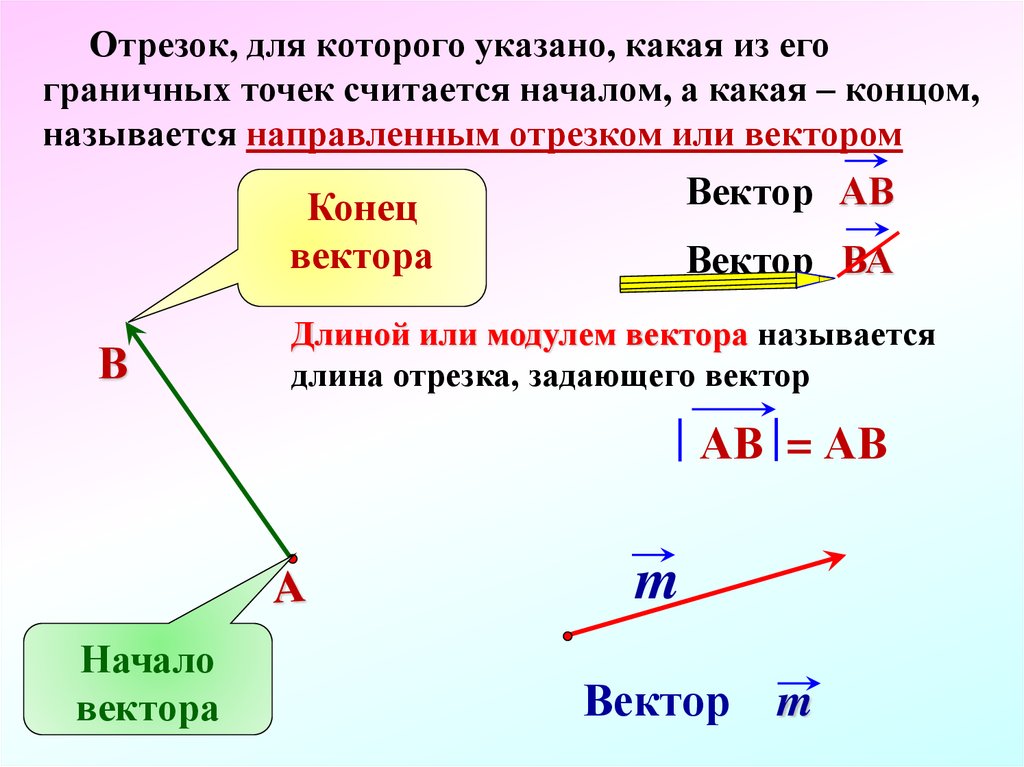 ai .eps .svg 2.42MB )
ai .eps .svg 2.42MB )
All-free-download.com
[ Векторы ] шаблон рождественского баннера висит снежинки динамический силуэт олень декор элегантный дизайн ( .ai .eps .svg 2.58MB )
All-free-download.com
[ Векторы ] все возможно, если вы попробуете шаблон типографии цитаты плоский классический черный белый текст динамический симметричный дизайн ( .ai .eps .svg 909.99KB )
All-free-download.com
[ Векторы ] будь собой все остальные уже заняты цитата типографика шаблон элегантный плоский текст элементы декора эскиз ( .ai .eps .svg 863.25KB )
All-free-download.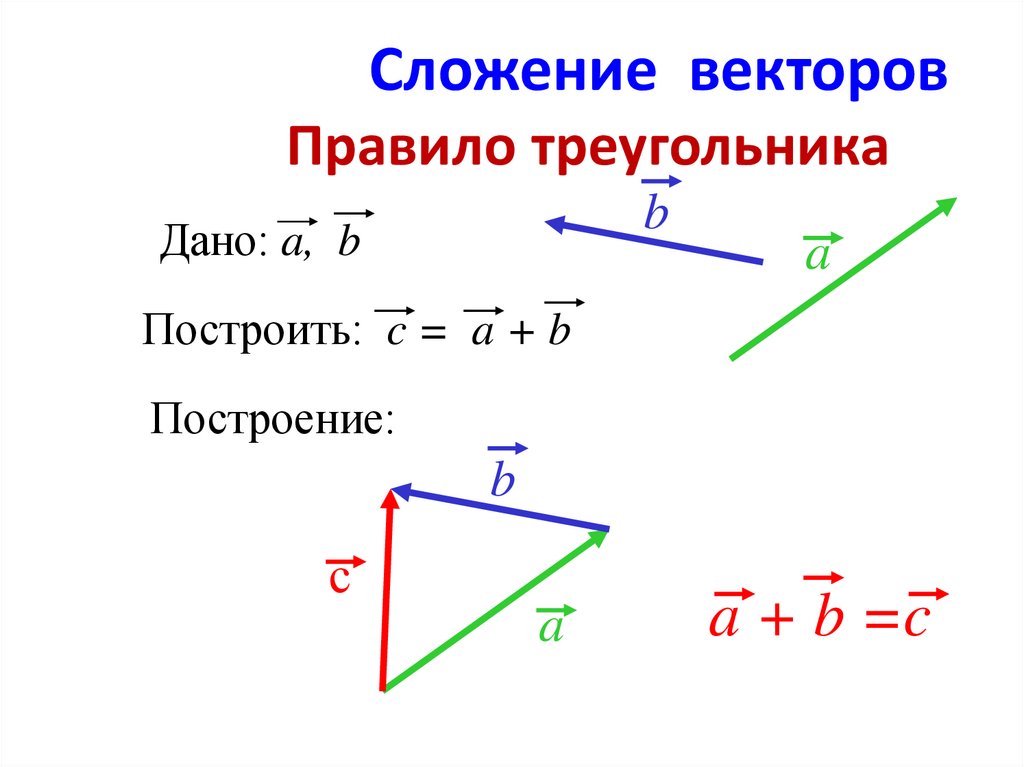 com
com
[ Векторы ] Я был создан для создания шаблона цитатной типографии плоского классического каллиграфического текста с декором ( .ai .eps .svg 1.67MB )
All-free-download.com
[ Векторы ] шаблон фона рождественской открытки элегантный размытый декор снежинки ( .ai .eps .svg 3.57MB )
All-free-download.com
[ Векторы ] Рождественский баннер шаблон элегантный темный снежинки кривые декор ( .ai .eps .svg 3.73MB )
All-free-download.com
[ Векторы ] если не сейчас то когда цитата типографика шаблон плоский классический текст декор ( .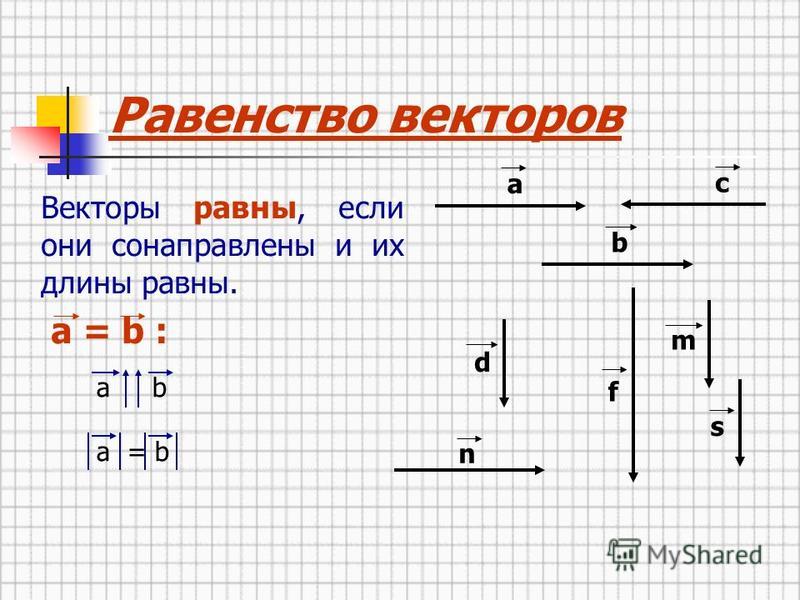 ai .eps .svg 1.43MB )
ai .eps .svg 1.43MB )
All-free-download.com
[ Векторы ] великие дела требуют времени цитата типографика шаблон элегантный современный плоский текст в верхнем регистре декор ( .ai .eps .svg 810.34KB )
All-free-download.com
[ Векторы ] офисная девушка значок мультяшный персонаж эскиз элементы рабочего места контур ( .ai 1.52MB )
Ирфан Мохаммед
векторная графика графика фон вектор фон компания вектор искусство художественная школа клипарт дизайн вектор дизайн логотип аннотация фон фон текстура рисунок рисунок логотип с днем благодарения с днем рождения рука вектор
[ Векторы ] Рождественский узор шаблон элегантный темно красный боке снежинки декор ( . ai .eps .svg 5.42MB )
ai .eps .svg 5.42MB )
All-free-download.com
[ Векторы ] шаблон меню ресторана элегантный темный размытый декор ( .ai .eps .svg 12.28MB )
All-free-download.com
[ Векторы ] каждый день создавайте новый шаблон типографики цитаты плоские динамические нарисованные от руки тексты лампочка декор ( .ai .eps .svg 1.14MB )
All-free-download.com
[ Векторы ] жизнь - это все о балансировщике цитат типографика шаблон плоский классический велосипедный текст эскиз ( .ai .eps .svg 1.48MB )
All-free-download.com
[ Векторы ] аптека шаблон плаката аптека архитектура эскиз элегантный плоский дизайн ( .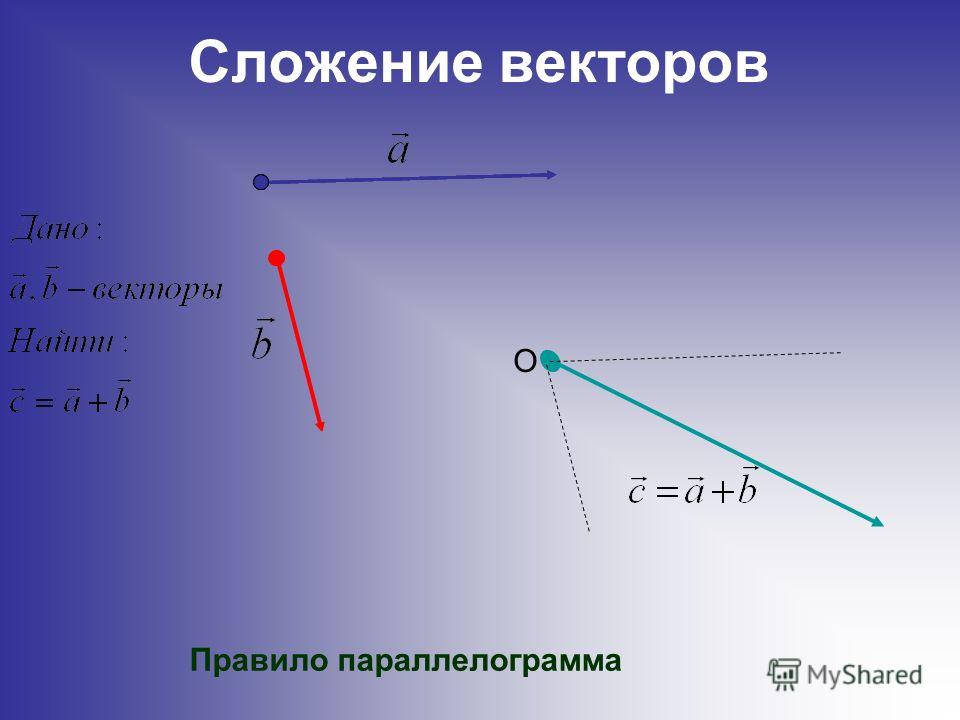 ai .eps .svg 1.98MB )
ai .eps .svg 1.98MB )
All-free-download.com
[ Векторы ] счастливого рождества с новым годом баннер плоский висит снежинки декор элегантный дизайн ( .ai .eps .svg 2.41MB )
All-free-download.com
[ Векторы ] шаблон меню ресторана плоский классический ингредиенты пищевой эскиз ( .ai .eps .svg 3.79MB )
All-free-download.com
[ Векторы ] меньше беспокойтесь и всегда улыбайтесь часто цитата типографика шаблон плоский элегантный классический текст декор ( .ai .eps .svg 834.76KB )
All-free-download.com
[ Векторы ] ничего особенного никогда не было, этот простой типографический шаблон цитаты динамический ретро-дизайн тексты декор ( . ai .eps .svg 1.47MB )
ai .eps .svg 1.47MB )
All-free-download.com
[ Векторы ] шаблон плаката аптека медицина медицинская змея эскиз символа ( .ai .eps .svg 1.89MB )
All-free-download.com
[ Векторы ] С Рождеством Христовым баннер элегантный темный декор снежинки ( .ai .eps .svg 4.21MB )
All-free-download.com
[ Векторы ] меню ресторана шаблон плоский классический темный дизайн ингредиенты еда посуда эскиз ( .ai .eps .svg 4.23MB )
All-free-download.com
[ Векторы ] просто будь вашим собственным уникальным красивым шаблоном типографии с цитатой с плоским классическим нарисованным от руки текстом вертикальный дизайн ( .



 Например, представим себе стальной куб размером метр на метр на метр. Можно представить его висящим в пустом пространстве (чтобы не заниматься силой тяжести и трением), или лежащим на очень гладкой ледяной поверхности, по которой он свободно скользит без трения. Если я толкаю (прилагаю силу) в центр грани перпендикулярно, то куб начнет двигаться прямо. Если я толкну его тоже перпендикулярно его грани, но рядом с краем, он начинет и двигаться, и вращаться. Если на куб действуют одновременно много всяких сил — я толкаю его с одной стороны, вы с другой, еще с какой-то стороны он удерживается веревкой с такой-то силой, и так далее — то для того, чтобы понять движение куба, нужно для каждой силы указать не только направление и величину, но и конкретную точку приложения.
Например, представим себе стальной куб размером метр на метр на метр. Можно представить его висящим в пустом пространстве (чтобы не заниматься силой тяжести и трением), или лежащим на очень гладкой ледяной поверхности, по которой он свободно скользит без трения. Если я толкаю (прилагаю силу) в центр грани перпендикулярно, то куб начнет двигаться прямо. Если я толкну его тоже перпендикулярно его грани, но рядом с краем, он начинет и двигаться, и вращаться. Если на куб действуют одновременно много всяких сил — я толкаю его с одной стороны, вы с другой, еще с какой-то стороны он удерживается веревкой с такой-то силой, и так далее — то для того, чтобы понять движение куба, нужно для каждой силы указать не только направление и величину, но и конкретную точку приложения.

 9 # после каждого нового значения нажать клавишу "Ввод"
2: 3.1
3: 3.4
4: 3.4
5: 3.7
6: 3.7
7: 2.8
8: 2.5
9: # выполнение команды scan завершают введением пустой строки
Read 8 items # программа сообщает о считывании 8 значений
X
[1] 2.9 3.1 3.4 3.4 3.7 3.7 2.8 2.5
9 # после каждого нового значения нажать клавишу "Ввод"
2: 3.1
3: 3.4
4: 3.4
5: 3.7
6: 3.7
7: 2.8
8: 2.5
9: # выполнение команды scan завершают введением пустой строки
Read 8 items # программа сообщает о считывании 8 значений
X
[1] 2.9 3.1 3.4 3.4 3.7 3.7 2.8 2.5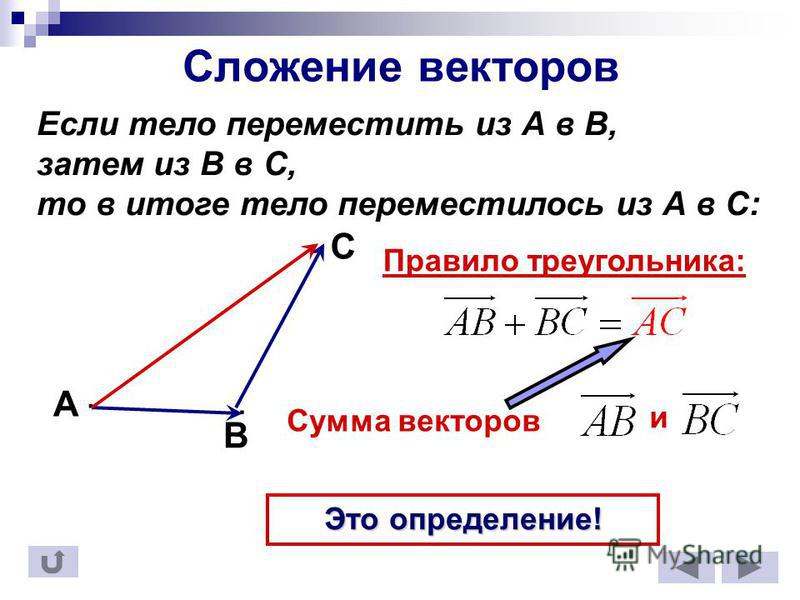 5)
S
[1] 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0
5)
S
[1] 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 vect:
# new.vect <- c(v1, text.vect)
# просмотр содержимого нового вектора new.vect:
new.vect
[1] "1" "2" "3" "a" "b" "c"
# все значения нового вектора взяты в кавычки,
# что указывает на их текстовую природу;
# для подтверждения этого воспользуемся командой mode():
mode(new.vect)
[1] "character" # все верно: "character" значит "текстовый"
vect:
# new.vect <- c(v1, text.vect)
# просмотр содержимого нового вектора new.vect:
new.vect
[1] "1" "2" "3" "a" "b" "c"
# все значения нового вектора взяты в кавычки,
# что указывает на их текстовую природу;
# для подтверждения этого воспользуемся командой mode():
mode(new.vect)
[1] "character" # все верно: "character" значит "текстовый"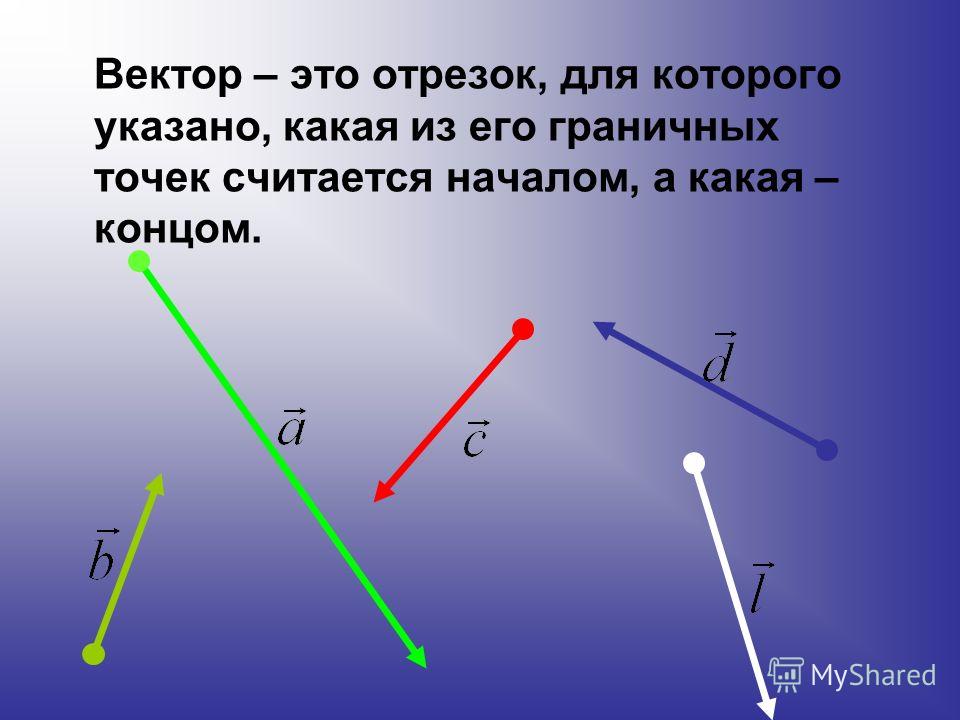 5, 0.1, 0.6)
# умножим первый элемент вектора y на третий элемент вектора z (т.е. 5*0.6):
y[1]*z[3]
[1] 3
5, 0.1, 0.6)
# умножим первый элемент вектора y на третий элемент вектора z (т.е. 5*0.6):
y[1]*z[3]
[1] 3 

 grid(a,b)
Вар1 Вар2
1 Азбука 2012-05-01
2 ДЭФ 2012-05-01
3 GHI 2012-05-01
4 Азбука 2012-05-02
5 ДЭФ 2012-05-02
6 GHI 2012-05-02
7 Азбука 2012-05-03
8 ДЕФ 2012-05-03
9GHI 2012-05-03
10 Азбука 2012-05-04
11 ДЕФ 2012-05-04
12 GHI 2012-05-04
13 АВС 2012-05-05
14 ДЭФ 2012-05-05
15 GHI 2012-05-05
grid(a,b)
Вар1 Вар2
1 Азбука 2012-05-01
2 ДЭФ 2012-05-01
3 GHI 2012-05-01
4 Азбука 2012-05-02
5 ДЭФ 2012-05-02
6 GHI 2012-05-02
7 Азбука 2012-05-03
8 ДЕФ 2012-05-03
9GHI 2012-05-03
10 Азбука 2012-05-04
11 ДЕФ 2012-05-04
12 GHI 2012-05-04
13 АВС 2012-05-05
14 ДЭФ 2012-05-05
15 GHI 2012-05-05
 05.2012", "02.05.2012", "03.05.2012", "04.05.2012", "05.05.2012")
пересечение (а, б)
# Таблетка: 15 x 2
а б
<хр> <хр>
1 Азбука 2012-05-01
2 Азбука 2012-05-02
3 Азбука 2012-05-03
4 Азбука 2012-05-04
5 Азбука 2012-05-05
6 ДЕФ 2012-05-01
7 ДЭФ 2012-05-02
8 ДЕФ 2012-05-03
9ДЕФ 2012-05-04
10 ДЕФ 2012-05-05
11 GHI 2012-05-01
12 GHI 2012-05-02
13 GHI 2012-05-03
14 GHI 2012-05-04
15 GHI 2012-05-05
05.2012", "02.05.2012", "03.05.2012", "04.05.2012", "05.05.2012")
пересечение (а, б)
# Таблетка: 15 x 2
а б
<хр> <хр>
1 Азбука 2012-05-01
2 Азбука 2012-05-02
3 Азбука 2012-05-03
4 Азбука 2012-05-04
5 Азбука 2012-05-05
6 ДЕФ 2012-05-01
7 ДЭФ 2012-05-02
8 ДЕФ 2012-05-03
9ДЕФ 2012-05-04
10 ДЕФ 2012-05-05
11 GHI 2012-05-01
12 GHI 2012-05-02
13 GHI 2012-05-03
14 GHI 2012-05-04
15 GHI 2012-05-05