«Правило моментов, 7 класс»

7 класс

Что такое момент силы?

Качели. Это устройство вы знаете с детства.

Что произойдет, если девочка сядет с краю?

O

2

Что такое момент силы ?

Что нужно сделать, чтобы качели пришли в равновесие?

O

Расчёт момента силы

Произведение модуля силы, вращающей тело, на её плечо называется МОМЕНТОМ СИЛЫ . Он обозначается буквой М .

где F – сила (Н), l – плечо силы (м)

Единица измерения момента силы — 1 Н  м.

l

О

F — вес

Момент силы характеризует действие силы и показывает, что оно зависит одновременно и от модуля силы, и от ее плеча.

Типы моментов сил

Какое действие моменты силы оказывают на рычаг силы?

(Поворачивают его в двух направлениях:

по часовой стрелке и против.)

Два типа моментов сил:

• Момент силы по

часовой стрелке

• Момент силы

против часовой стрелки

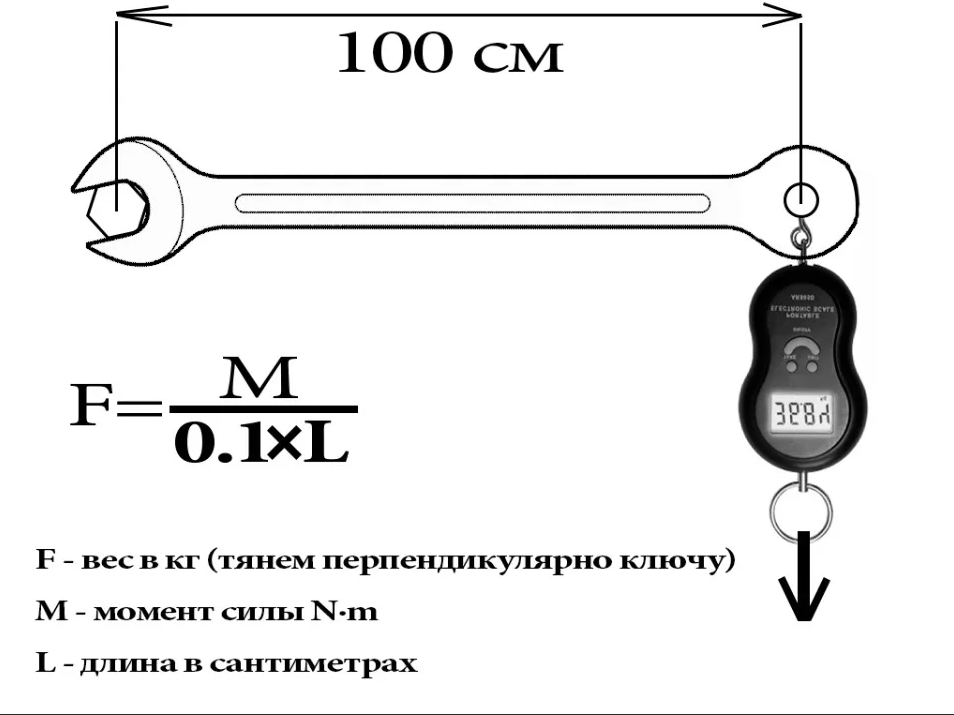
Дверь тем легче повернуть, чем дальше от оси вращения приложена действующая на нее сила.

Гайку легче отвернуть длинным гаечным ключом, чем коротким.

Гайку легче отвернуть длинным гаечным ключом, чем коротким.

6

Ведро тем легче поднять из колодца, чем длиннее ручка ворота.

Ведро тем легче поднять из колодца, чем длиннее ручка ворота.

6

Правило моментов

Рычаг находится в равновесии под действием двух сил, если момент силы, вращающий его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки.

l 1

l 2

O

_

F 2

_

F 1

М1 = М2 + М3

Рычаг находится в равновесии под действием нескольких сил, если момент силы, вращающей его против хода часовой стрелки, равен сумме моментов сил, вращающих рычаг по часовой стрелке.

Задача 1

Кот весом в 20Н сидит справа на конце качелей, расстояние между котом и центром опоры равно 3 метра.

Чему равен момент силы, действующей на качели?

_______________________________________________

Решение:

В этом случае кот вызывает момент по часовой стрелке. M = F 

l

M = 20  3 = 60 Н  м

O

l = 3 м

= 20H

Задача 2

Утка стоит в одном конце качелей, на расстоянии 5м от центра опоры.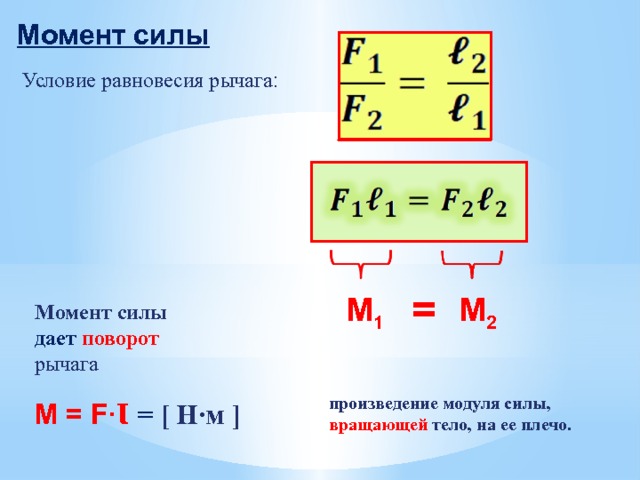 Найдите момент силы, если вес утки равен 10Н.

_________________________________________________

Решение:

Вес утки вызывает момент против часовой стрелки.

M = F 

l

M = 1 0  5 = 50 Н  м

l = 5 м

F = 10 Н

Правило моментов

Задача 3

Выполняется ли здесь правило моментов?

l

l

O

Задача 4

Момент силы F 1 равен 1 Н*м. На каком расстоянии справа от оси вращения нужно прикрепить груз весом 4Н, чтобы рычаг находился в равновесии?

4 H

F 1

Спасибо за работу

Сила. Момент силы. Закон Гука – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД

Запомнить

Восстановить пароль

Регистрация

Конспект

Сила – векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей.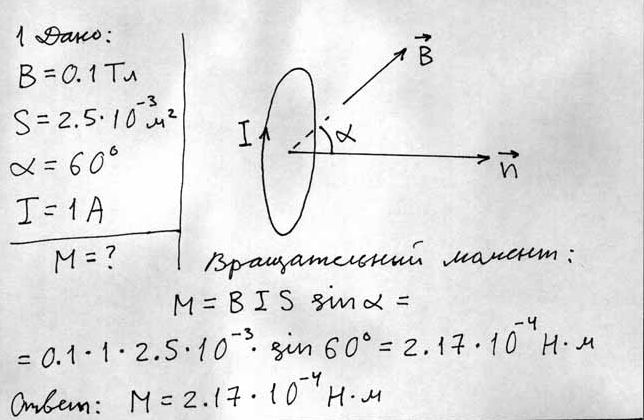 Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нем деформаций и напряжений.

Сила как векторная величина характеризуется модулем, направлением и «точкой» приложения силы. Последним параметром понятие о силе, как векторе в физике, отличается от понятия о векторе в векторной алгебре, где равные по модулю и направлению векторы, независимо от точки их приложения, считаются одним и тем же вектором. В физике эти векторы называются свободными векторами. В механике чрезвычайно распространено представление о связанных векторах, начало которых закреплено в определенной точке пространства или же может находиться на линии, продолжающей направление вектора (скользящие векторы).

Также используется понятие линия действия силы, обозначающее проходящую через точку приложения силы прямую, по которой направлена сила.

Второй закон Ньютона гласит, что в инерциальных системах отсчета ускорение материальной точки по направлению совпадает с равнодействующей всех сил, приложенных к телу, а по модулю прямо пропорционально модулю силы и обратно пропорционально массе материальной точки.

{-2}\), единицей измерения в Международной системе единиц (СИ) является ньютон (N, Н), в системе СГС – дина.

Момент силы (иногда применяют синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) – векторная физическая величина, равная векторному произведению радиус-вектора (проведенного от оси вращения к точке приложения силы – по определению), на вектор этой силы. Характеризует вращательное действие силы на твердое тело.

Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» – внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов). В физике момент силы можно часто понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами.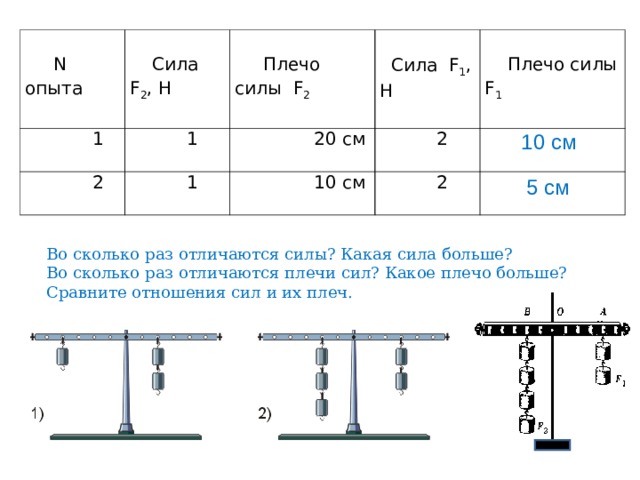

В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, создает такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения. Более точно, момент силы частицы определяется как векторное произведение:

\(\vec M = \left[ \vec r \times \vec F \right]\), где \(\vec F\) – сила, действующая на частицу, а \(\vec r\) – радиус-вектор частицы.

Закон Гука

– это основной закон, выражающий связь между напряженным состоянием и деформацией упругого тела. Установлен англ. физиком Р. Гуком в \(1660\) для простейшего случая растяжения или сжатия стержня в форме: абсолютное удлинение (укорочение) \(ΔI\) цилиндрического стержня прямо пропорционально растягивающей (сжимающей) силе N, т. е. \(ΔI = kN\), где \(k = \frac I{\frac{ES} I}\) – длина стержня, \(S\) – площадь его поперечного сечения, \(E\) – модуль продольной упругости, являющийся механической характеристикой (константой) материала. З.Г. удобно представлять также в форме \(σ= Eε\)

, где \(σ=\frac NS \) – нормальное напряжение в поперечном сечении, \(\varepsilon = \frac{ΔI}I \) – относительное удлинение (укорочение) стержня. При сдвиге этот закон записывается так: \( τ = \frac Gγ\), где \(τ\) – касательное напряжение, γ – сдвиг, \(G\) – модуль сдвига; при сдвиге касательное напряжение прямо пропорционально сдвигу.

Обобщенный закон Гука – для тела произвольной формы – утверждает, что 6 величин, определяющих напряженное состояние в точке, выражаются линейно через \(6\) величин, определяющих деформацию в окрестности рассматриваемой точки. Коэффициенты пропорциональности в этих соотношениях называются модулями упругости. В анизотропных телах, например в кристаллах, модули упругости различны в разных направлениях, поэтому в общем случае упругие свойства твердого тела характеризуются с помощью \(21\) модуля упругости. Для изотропных тел число независимых упругих постоянных сводится к двум.

Закон не имеет места, когда некоторые напряжения (или деформации) достигают предельных значений, характерных для каждого материала, и тело переходит в упруго-пластическое состояние. Закон Гука является основным соотношением, применяемым при расчете на прочность и деформируемость конструкций и сооружений.

Вопросы

1. Угол между направлением действия силы и плечом силы равен

2. Чтобы невесомый рычаг находился в равновесии, сила \(F\) должна иметь величину

3. Брусок массой 0,3 кг прижат к вертикальной стене горизонтальной силой 8 Н. Коэффициент трения между бруском и стеной равен 0,3. Сила трения скольжения бруска о стену равна

4. Чтобы вес гири увеличился в два раза, ее надо поднимать с ускорением

5. Автомобиль массой 1,5 т движется вверх по дороге с уклоном 30° с ускорением 0,5 м/с². 3\))

6. Тело массой \(m\), двигаясь со скоростью \(υ\), растягивает пружину. Если массу тела уменьшить в 4 раза, а скорость увеличить в 4 раза, то модуль абсолютного удлинения пружины

7. Диаметр стержня равен 0,4 см, в нем возникает напряжение \(\alpha\) = 150 МПа под действием силы

8. Пружины жесткостью 100 Н/м и 300 Н/м соединили параллельно. Эту систему пружин заменили одной пружиной жесткостью

9. Плечо силы \(F_2\) – это отрезок

    

10. Два тела с одинаковыми массами, которые можно считать материальными точками, взаимно притягиваются на определенном расстоянии. Если массу одного из них увеличить на 200 кг, то сила их взаимного притяжения на том же расстоянии увеличится в три раза. Первоначальная масса тел

11. Пружина с коэффициентом жесткости 100 Н/м растянется на 0,02 м под действием силы

12. Мальчик равномерно тянет санки массой \(m\) в результате приложения силы \(F\) к нити, которая составляет угол \(\alpha\) к горизонту. Выражение, по которому определяется работа силы трения при перемещении на расстояние \(s\), имеет вид

13. При растяжении пружины на 4 см возникает сила упругости в 20 Н. Жесткость этой пружины равна

14. На концах рычага действуют силы, направленные перпендикулярно вниз и равные 30 Н и 50 Н. 2}\))

15. Два тела притягиваются друг к другу. Масса каждой – 400 кг. Как изменится сила притяжения на том же расстоянии, если увеличить массу одного из них на 200 кг?

16. На рисунке представлено тело, движущееся в горизонтальном направлении со скоростью \(\vartheta\). Какая пара сил, действующих на тело, не совершает работу?

     

17. Как изменится сила тяготения между телами, размерами которых можно пренебречь, если массу одного из тел увеличить в 2 раза, а расстояние между телами сохранить прежним?

18. Определите массу груза, если при его подъеме с ускорением 4 м/с² трос подъемного крана с жесткостью 20 кН/м удлиняется на 14 см (g ≈ 10 м/c²)

19. Первая пружина имеет жесткость 35 Н/м, жесткость второй пружины – 70 Н/м.  Удлинение первой пружины равно удлинению второй. Чему будет равно отношение потенциальных энергий пружин?

20. Груз массой 2 кг поднимают вверх с ускорением 0,8 м/с на пружине жесткостью 500 Н/м. Определите модуль удлинения этой пружины.

21. Определите жесткость вертикально подвешенной пружины, которая под действием груза массой 300 г растянулась с 12 см до 16 см (g ≈ 10 м/c²)

22. Золотое правило механики состоит в том, что

23. Найдите жесткость вертикально подвешенной пружины, если она под действием груза весом 300 г растянулась от 11 см до 15 см (\(g\approx10\) м/с \(^2\))

24. Под действием какой силы пружина жесткостью 50 кН/м может сжаться на 2 см?

25. Чему равно абсолютное удлинение стальной проволоки длиной 1,5 м, если в ней возникло механическое напряжение 42 МПа? (\(Е_{ст}\) = 210 ГПа)

26. Найдите удлинение горизонтальной пружины жесткостью 50 Н/м, если она сообщает тележке массой 500 г ускорение 2 м/с².

27. Какая мощность необходима, чтобы сжать пружину на 2 см за 1 секунду, если для сжатия ее на 1 см требуется сила 22 кН?

28. Под действием силы 4 Н пружина динамометра удлинилась на 5 мм. Чему равен коэффициент упругости пружины этого динамометра?

Сообщить об ошибке

Как трехфазный двигатель может иметь крутящий момент 20 Нм при 1432 об/мин и 1,8 кВт?

спросил 4 года 9 месяцев назад

Изменено 4 года, 9 месяцев назад

Просмотрено 789 раз

\$\начало группы\$

Я пытаюсь рассчитать максимальный крутящий момент двигателя, чтобы провести анализ нагрузки на конструкцию, и мне только что предоставили детали двигателя от производителя. Они сказали, что он производит 20 Нм крутящего момента, вращается со скоростью 1432 об/мин и имеет выходную мощность 1,8 кВт . Сначала я этого не заметил, но позже обнаружил некоторые ошибки в своих расчетах, которые указывали на то, что характеристики двигателя не соответствовали друг другу. С точки зрения механики я всегда использовал Мощность [Вт] = Крутящий момент [Нм] X Угловая скорость [рад/с] для любых расчетов вращения. В этом случае, если выходная мощность и скорость правильные, крутящий момент будет 12 Нм , а не 20 Н·м .

Производитель вернулся и сказал мне, что он подтвердил исходные цифры, которые он мне предоставил, и они верны. Мне было интересно, может ли кто-нибудь сказать мне, как это будет работать?

• двигатель
• трехфазный

\$\конечная группа\$

2

\$\начало группы\$

20 Нм крутящего момента не совпадают с максимальными оборотами, поэтому вы не можете просто умножить этот крутящий момент на максимальные (без нагрузки) радианы в секунду, потому что это было бы бессмысленно.

Производитель, скорее всего, говорит вам, что двигатель может развивать максимальный крутящий момент 20 Нм при значительно более низкой скорости.

Максимальный крутящий момент достигается, когда двигатель значительно загружен и вращается со скоростью 859,4 об/мин или 60,0% от полной (без нагрузки) скорости.

\$\конечная группа\$

3

\$\начало группы\$

Асинхронные двигатели должны работать очень близко к их «синхронной скорости», которая в данном случае составляет 1500 об/мин. Это четырехполюсный двигатель, предназначенный для работы на частоте 50 Гц.

Поскольку двигатель пробуксовывает из-за потерь и нагрузок, крутящий момент увеличивается примерно пропорционально проскальзыванию, вплоть до номинального крутящего момента двигателя.

Таким образом, ваш расчет 12 Нм верен, если предположить, что число оборотов в минуту, которое они вам дали, является номинальной скоростью, а 1,8 кВт — номинальной или продолжительной мощностью двигателя. Это номинальный или постоянный крутящий момент. Существуют и другие характеристики крутящего момента двигателя, такие как пиковый крутящий момент или пробивной крутящий момент. Обычно они работают на 175-300% от номинального крутящего момента. Это, скорее всего, 20 Нм у производителя. упоминает. Работайте непрерывно в этот момент, двигатель выйдет из строя из-за перегрева.

Таким образом, производители оценивают свои двигатели по термической или непрерывной характеристике, и они дадут вам максимальный крутящий момент, который вы можете непрерывно тянуть. Они дадут вам максимальную температуру окружающей среды для этого рейтинга. Именно в этот момент мотор проскальзывал до 1432 об/мин. Если вы запускаете двигатель в более жаркой среде, вам придется снизить мощность двигателя и не нагружать его выше этой точки, так как охлаждающая способность двигателя будет снижена.

Если вы нагрузите его больше, вы можете заставить его производить более высокий пиковый крутящий момент, но вы сможете запустить его только в течение секунд или минут, пока двигатель не перегреется. Запустите более высокую нагрузку после этой точки, и крутящий момент двигателя уменьшится и все еще будет подвержен термической опасности.

\$\конечная группа\$

\$\начало группы\$

Крутящий момент (Н-м) = (кВт x 9550) / об/мин

1,8 x 9550 = 17190, разделить на 1432 = 12 Н-м Крутящий момент при полной нагрузке при номинальной скорости.

Крутящий момент пускового/заблокированного ротора в стандартном асинхронном двигателе переменного тока конструкции B составляет 160% от крутящего момента при полной нагрузке, +-10% Значение крутящего момента. Многие люди ошибочно полагают, что это максимальный крутящий момент, который может развивать двигатель, но это максимальное значение на самом деле называется крутящим моментом торможения (BDT, как упоминалось ранее) и возникает примерно при 80% номинальной скорости. Таким образом, максимальный крутящий момент, который мог бы обеспечить двигатель (опять же, при условии стандартной кривой крутящего момента конструкции B, наиболее распространенного типа), будет составлять приблизительно 220% FLT или 26,4 Н·м, но будет иметь место примерно при 1145 об/мин (при условии, что двигатель набирает обороты). напряжение при 50 Гц).

\$\конечная группа\$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Гибкая муфта EL номинальный крутящий момент 20 Нм короткая версия с пилотным отверстием из нержавеющей стали 1.4305 общая длина 65 мм внешний диаметр 38 мм Артикул: 60299023

• Описание
• Дополнительная информация

Артикул	60299023
Крутящий момент макс. [Нм]	20
Тип	С
Материал	Эдельшталь
d Направляющее отверстие [мм]	5,5
d макс. ф. Штифт [мм]	25
d макс. ф. Шпоночный паз [мм]	19
Длина [мм]	65
D [мм]	38
F [мм]	36
л [мм]	20
Скорость макс. [об/мин]	3000
Вес [кг]	0,350

КАТАЛОГ СТРАНИЦА ПРОДУКТА

ФАЙЛЫ САПР (щелкните, чтобы загрузить)

ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ

Если вам нужна доработка или изготовление изделия на заказ, пожалуйста, свяжитесь с нами напрямую с вашим запросом.

Поставляемые 3D-модели, изображения и технические чертежи выполнены с разумной тщательностью. Тем не менее ответственность за точность и правильность этих данных исключена.

Материал: Ступица 1. 4305. Пружина: Пружинная сталь 1. 4310. Эти муфты
представляют собой эластичные цельнометаллические муфты и полностью ремонтопригодны
бесплатно. Цельнометаллическая конструкция обеспечивает высокую стойкость к маслам и
более высокому температурному диапазону: от -40°C до +300°C. Эластичная часть состоит из
корпуса пружины, состоящего из трех слоев намотанных пружин. Муфты
подходят для обоих направлений вращения. Они могут быть заблокированы от вращения на
с помощью призматической шпонки или штифтов. Муфты запрессованы.
Демонтаж осуществляется нажатием или снятием. Вибрации и удары
в значительной степени поглощаются. В зависимости от длины муфты – S, L или Db –
возможен изгиб на 3-6° или осевое смещение на 3-6% от номинального диаметра вала
. Муфты поставляются предварительно просверленными на складе.
Индивидуальные отверстия и канавки под призматическую шпонку доступны за дополнительную плату.

193,66 $

Доставка в течение 1-2 недель

Гибкая муфта EL номинальный крутящий момент 20 Нм короткая версия с направляющим отверстием из нержавеющей стали 1.4305 общая длина 65 мм внешний диаметр 38 мм Артикул: 60299023 количество

05"}» data-minimum=»1″ data-product-name=»Flexible coupling EL nominal torque 20 Nm short version with pilot bore stainless steel 1.4305 overall length 65mm outer diameter 38mm SKU: 60299023″>

Количество	Скидка (%)	Цена
1 — 9	—	193,66 $
10 — 24	4,84 %	184,29 $