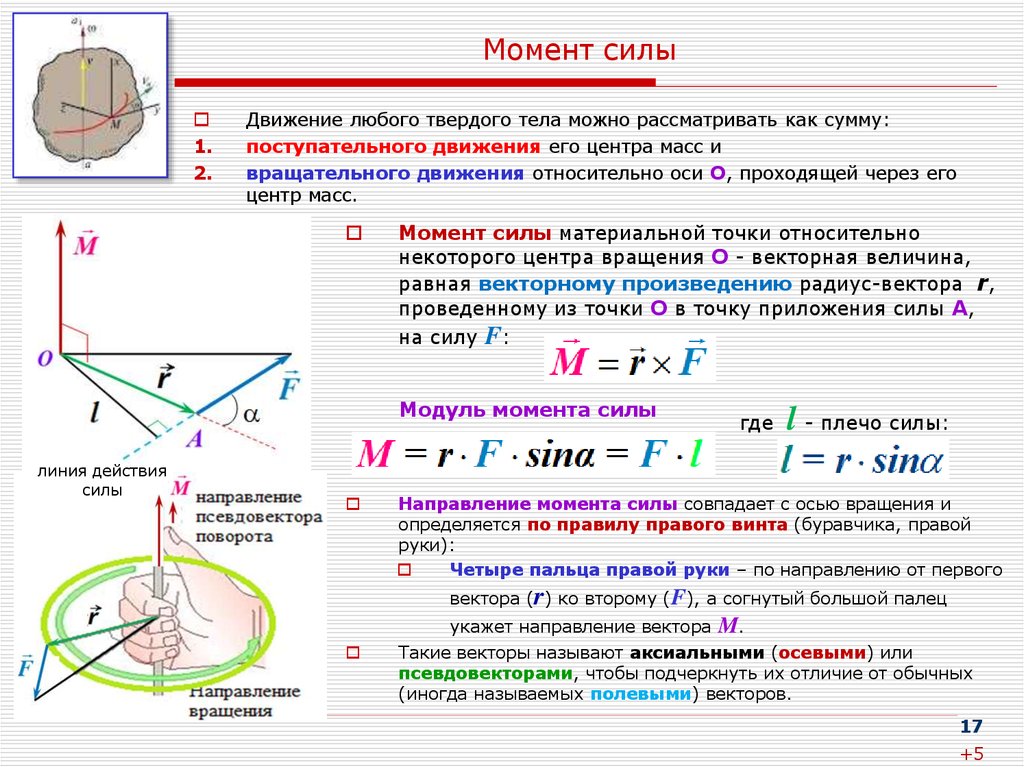
10 Момент силы
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
Общие сведения
В физике момент силы можно понимать как «вращающая
сила». В системе СИ единицами измерения для момента силы
является ньютон—метр.
Момент силы иногда называют моментом
пары сил, это понятие возникло в трудах Архимеда над рычагами.
где — сила, действующая на частицу, а — радиус-вектор частицы.
Предыстория
Строго
говоря, вектор, обозначающий момент
сил, введен искусственно, так как является
удобным при вычислении работы по
криволинейному участку относительно
неподвижной оси и удобен при вычислении
общего момента сил всей системы, так
как может суммироваться. Для того, чтобы
понять откуда появилось обозначение
момента сил и как до него додумались,
стоит рассмотреть действие силы на
рычаг, поворачивающийся относительно
неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол dφ. Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол между вектором и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус-вектор , а проекцию вектора силы на вектор , через угол .
Так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , используя соотношения для прямоугольного треугольника, можно записать следующее равенство: dl
Для
проекции вектора силы
на
вектор
,
видно, что угол ,
а так как ,
получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть не что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуль вектора момента силы .
Теперь полная работа записывается очень просто: или .
ОглавлениеОТ ИЗДАТЕЛЬСТВАИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ ВВЕДЕНИЕ Глава I. Кинематика § 1. Движение тел § 2. Кинематика. Относительность движения и покоя. § 3. Траектория движения § 4. Поступательное и вращательное движения тела § 5. Движение точки § 6. Описание движения точки § 7. Измерение длины § 8. Измерение промежутков времени § 9. Равномерное прямолинейное движение и его скорость § 11. Единицы скорости § 12. Графики зависимости пути от времени § 13. Графики зависимости скорости от времени § 14. Неравномерное прямолинейное движение § 15. Мгновенная скорость § 16. Ускорение при прямолинейном движении § 17.  Скорость прямолинейного равноускоренного движения Скорость прямолинейного равноускоренного движения§ 18. Знак ускорения при прямолинейном движении § 19. Графики скорости при прямолинейном равноускоренном движении § 20. Графики скорости при произвольном неравномерном движении § 21. Нахождение пути, пройденного при неравномерном движении, при помощи графика скорости § 23. Векторы § 24. Разложение вектора на составляющие § 25. Криволинейное движение § 26. Скорость криволинейного движения § 27. Ускорение при криволинейном движении § 28. Движение относительно разных систем отсчета § 29. Кинематика космических движений Глава II. Динамика § 30. Задачи динамики § 31. Закон инерции § 32. Инерциальные системы отсчета § 33. Принцип относительности Галилея § 34. Силы § 35. Уравновешивающиеся силы. О покое тела и о движении по инерции § 36. Сила — вектор. Эталон силы § 37. Динамометры § 39. 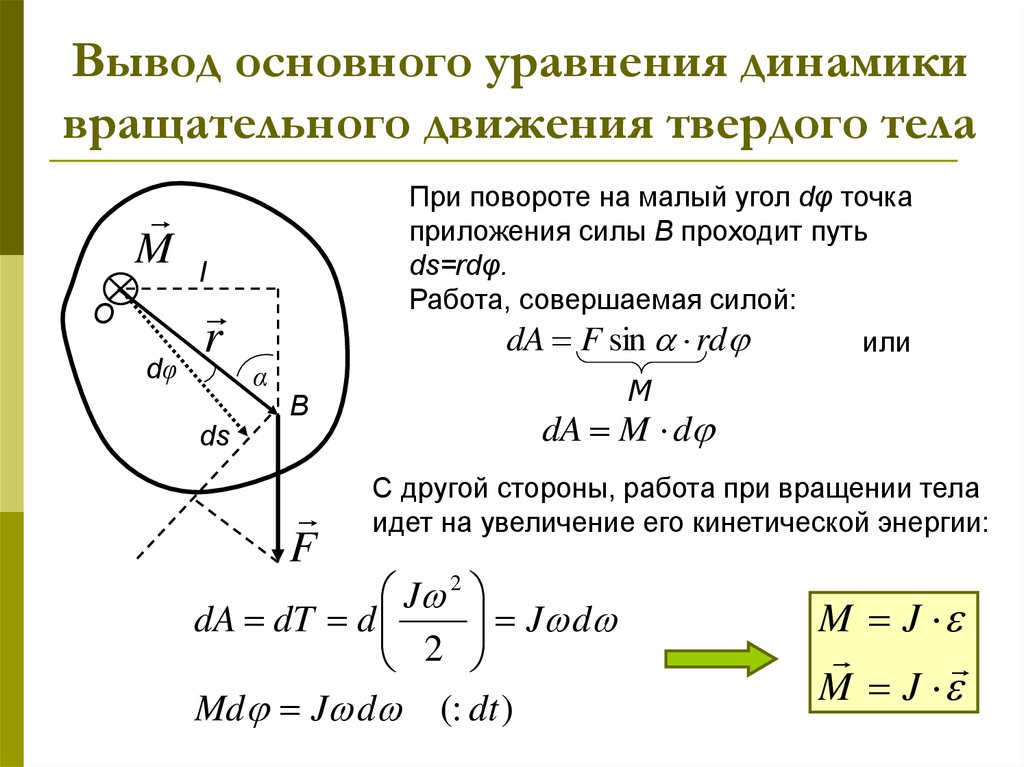 Равнодействующая сила Равнодействующая сила§ 40. Сложение сил, направленных по одной прямой § 41. Сложение сил, направленных под углом друг к другу § 42. Связь между силой и ускорением § 43. Масса тела § 44. Второй закон Ньютона § 45. Единицы силы и массы § 46. Системы единиц § 47. Третий закон Ньютона § 48. Примеры применения третьего закона Ньютона § 49. Импульс тела § 50. Система тел. Закон сохранения импульса § 51. Применения закона сохранения импульса § 52. Свободное падение тел § 53. Ускорение свободного падения § 55. Вес тела § 56. Масса и вес § 57. Плотность вещества § 58. Возникновение деформаций § 59. Деформации в покоящихся телах, вызванные действием только сил, возникающих при соприкосновении § 60. Деформации в покоящихся телах, вызванные силой тяжести § 61. Деформации тела, испытывающего ускорение § 62. Исчезновение деформаций при падении тел § 63.  Разрушение движущихся тел Разрушение движущихся тел§ 64. Силы трения § 65. Трение качения § 66. Роль сил трения § 67. Сопротивление среды § 68. Падение тел в воздухе § 69. Задачи статики § 70. Абсолютно твердое тело § 71. Перенос точки приложения силы, действующей на твердое тело § 72. Равновесие тела под действием трех сил § 73. Разложение сил на составляющие § 74. Проекции сил. Общие условия равновесия § 75. Связи. Силы реакции связей. Тело, закрепленное на оси § 76. Равновесие тела, закрепленного на оси § 77. Момент силы § 78. Измерение момента силы § 79. Пара сил § 80. Сложение параллельных сил. Центр тяжести § 81. Определение центра тяжести тел § 82. Различные случаи равновесия тела под действием силы тяжести § 83. Условия устойчивого равновесия под действием силы тяжести § 84. Простые машины Глава IV. Работа и энергия § 86. «Золотое правило» механики § 87. Применения «золотого правила» § 88.  Работа силы Работа силы§ 89. Работа при перемещении, перпендикулярном к направлению силы § 90. Работа силы, направленной под любым углом к перемещению § 91. Положительная и отрицательная работа § 92. Единица работы § 93. О движении по горизонтальной плоскости § 94. Работа силы тяжести при движении по наклонной плоскости § 95. Принцип сохранения работы § 96. Энергия § 97. Потенциальная энергия § 98. Потенциальная энергия упругой деформации § 99. Кинетическая энергия § 101. Полная энергия тела § 102. Закон сохранения энергии § 103. Силы трения и закон сохранения механической энергии § 104. Превращение механической энергии во внутреннюю энергию § 105. Всеобщий характер закона сохранения энергии § 106. Мощность § 107. Расчет мощности механизмов § 108. Мощность, быстроходность и размеры механизма § 109. Коэффициент полезного действия механизмов Глава V.  Криволинейное движение Криволинейное движение§ 110. Возникновение криволинейного движения § 111. Ускорение при криволинейном движении § 112. Движение тела, брошенного в горизонтальном направлении § 113. Движение тела, брошенного под углом к горизонту § 114. Полет пуль и снарядов § 115. Угловая скорость § 116. Силы при равномерном движении по окружности § 117. Возникновение силы, действующей на тело, движущееся по окружности § 118. Разрыв маховиков § 119. Деформация тела, движущегося по окружности § 120. «Американские горки» § 121. Движение на закруглениях пути § 122. Движение подвешенного тела по окружности § 123. Движение планет § 124. Закон всемирного тяготения § 125. Искусственные спутники Земли Глава VI. Движение в неинерциальных системах отсчета и силы инерции § 126. Роль системы отсчета § 127. Движение относительно разных инерциальных систем отсчета § 128. Движение относительно инерциальной и неинерциальной систем отсчета § 129.  Поступательно движущиеся неинерциальиые системы Поступательно движущиеся неинерциальиые системы§ 130. Силы инерции § 131. Эквивалентность сил инерции и сил тяготения § 132. Невесомость и перегрузки § 133. Является ли Земля инерциальиой системой отсчета? § 134. Вращающиеся системы отсчета § 135. Силы инерции при движении тела относительно вращающейся системы отсчета § 136. Доказательство вращения Земли § 137. Приливы Глава VII. Гидростатика § 138. Подвижность жидкости § 139. Силы давления § 140. Измерение сжимаемости жидкости § 141. «Несжимаемая» жидкость § 142. Силы давления в жидкости передаются во все стороны § 143. Направление сил давления § 144. Давление § 145. Мембранный манометр § 146. Независимость давления от ориентации площадки § 147. Единицы давления § 148. Определение сил давления по давлению § 149. Распределение давления внутри жидкости § 150. Закон Паскаля § 151. Гидравлический пресс § 152. Жидкость под действием силы тяжести § 153.  Сообщающиеся сосуды Сообщающиеся сосуды§ 154. Жидкостный манометр § 155. Устройство водопровода. Нагнетательный насос § 156. Сифон § 157. Сила давления на дно сосуда § 158. Давление воды в морских глубинах § 159. Прочность подводной лодки § 160. Закон Архимеда § 161. Измерение плотности тел на основании закона Архимеда § 162. Плавание тел § 163. Плавание несплошных тел § 164. Устойчивость плавания кораблей § 165. Всплывание пузырьков § 166. Тела, лежащие на дне сосуда Глава VIII. Аэростатика § 167. Механические свойства газов § 168. Атмосфера § 169. Давление атмосферы § 170. Другие опыты, показывающие существование атмосферного давления § 171. Разрежающие насосы § 172. Влияние атмосферного давления на уровень жидкости в трубке § 173. Максимальная высота столба жидкости § 174. Опыт Торричелли. Ртутный барометр и барометр-анероид § 175. Распределение атмосферного давления по высоте § 176. Физиологическое действие пониженного давления воздуха § 177.  Закон Архимеда для газов Закон Архимеда для газов§ 178. Воздушные шары и дирижабли § 179. Применение сжатого воздуха в технике Глава IX. Гидродинамика и аэродинамика § 180. Давление в движущейся жидкости § 181. Течение жидкости по трубам § 182. Закон Бернулли § 183. Жидкость в неинерциальных системах отсчета § 184. Реакция движущейся жидкости и ее использование § 185. Перемещение на воде § 186. Ракеты § 187. Реактивные двигатели § 188. Баллистические ракеты § 189. Взлет ракеты с Земли § 190. Сопротивление воздуха § 191. Эффект Магиуса и циркуляция § 192. Подъемная сила крыла и полет самолета § 193. Турбулентность в потоке жидкости или газа § 194. Ламинарное течение РАЗДЕЛ ВТОРОЙ. ТЕПЛОТА. МОЛЕКУЛЯРНАЯ ФИЗИКА Глава X. Тепловое расширение твердых и жидких тел § 195. Тепловое расширение твердых и жидких тел § 196. Термометры § 197. Формула линейного расширения § 198. Формула объемного расширения § 199. Связь между коэффициентами линейного и объемного расширения § 200.  Измерение коэффициента объемного расширения жидкостей Измерение коэффициента объемного расширения жидкостей§ 201. Особенности расширения воды Глава XI. Работа. Теплота. Закон сохранения энергии § 202. Изменения состояния тел § 203. Нагревание тел при совершении работы § 204. Изменение внутренней энергии тел при теплопередаче § 205. Единицы количества теплоты § 206. Зависимость внутренней энергии тела от его массы и вещества § 207. Теплоемкость тела § 208. Удельная теплоемкость § 209. Калориметр. Измерение теплоемкостей § 210. Закон сохранения энергии § 211. Невозможность «вечного двигателя» § 212. Различные виды процессов, при которых происходит передача теплоты Глава XII. Молекулярная теория § 213. Молекулы и атомы § 214. Размеры атомов и молекул § 215. Микромир § 216. Внутренняя энергия с точки зрения молекулярной теории § 217. Молекулярное движение § 218. Молекулярное движение в газах, жидкостях и твердых телах § 219. Броуновское движение § 220. Молекулярные силы Глава XIII.  Свойства газов Свойства газов§ 221. Давление газа § 222. Зависимость давления газа от температуры § 223. Формула, выражающая закон Шарля § 224. Закон Шарля с точки зрения молекулярной теории § 225. Изменение температуры газа при изменении его объема. Адиабатические и изотермические процессы § 226. Закон Бойля — Мариотта § 227. Формула, выражающая закон Бойля — Мариотта § 228. График, выражающий закон Бойля — Мариотта § 229. Зависимость между плотностью газа и его давлением § 230. Молекулярное толкование закона Бойля — Мариотта § 231. Изменение объема газа при изменении температуры § 232. Закон Гей-Люссака § 233. Графики, выражающие законы Шарля и Гей-Люссака § 234. Термодинамическая температура § 235. Газовый термометр § 236. Объем газа и термодинамическая температура § 237. Зависимость плотности газа от температуры § 238. Уравнение состояния газа § 239. Закон Дальтона § 240. Плотность газов § 241. Закон Авогадро § 242.  Моль. Постоянная Авогадро Моль. Постоянная Авогадро§ 243. Скорости молекул газа § 244. Об одном из способов измерения скоростей движения молекул газа (опыт Штерна) § 245. Удельные теплоемкости газов § 246. Молярные теплоемкости § 247. Закон Дюлонга и Пти Глава XIV. Свойства жидкостей § 248. Строение жидкостей § 249. Поверхностная энергия § 250. Поверхностное натяжение § 251. Жидкостные пленки § 252. Зависимость поверхностного натяжения от температуры § 253. Смачивание и несмачивание § 254. Расположение молекул у поверхности тел § 255. Значение кривизны свободной поверхности жидкости § 256. Капиллярные явления § 257. Высота поднятия жидкости в капиллярных трубках § 258. Адсорбция § 259. Флотация § 260. Растворение газов § 261. Взаимное растворение жидкостей § 262. Растворение твердых тел в жидкостях Глава XV. Свойства твердых тел. Переход тел из твердого состояния в жидкое § 263. Введение § 264. Кристаллические тела § 265.  Аморфные тела Аморфные тела§ 266. Кристаллическая решетка § 267. Кристаллизация § 268. Плавление и отвердевание § 269. Удельная теплота плавления § 270. Переохлаждение § 271. Изменение плотности веществ при плавлении § 272. Полимеры § 273. Сплавы § 274. Затвердевание растворов § 275. Охлаждающие смеси § 276. Изменения свойств твердого тела Глава XVI. Упругость и прочность § 277. Введение § 278. Упругие и пластические деформации § 279. Закон Гука § 280. Растяжение и сжатие § 281. Сдвиг § 282. Кручение § 283. Изгиб § 284. Прочность § 285. Твердость § 286. Что происходит при деформации тел § 287. Изменение энергии при деформации тел Глава XVII. Свойства паров § 288. Введение § 289. Пар насыщенный и ненасыщенный § 290. Что происходит при изменении объема жидкости и насыщенного пара § 291. Закон Дальтона для пара § 292. Молекулярная картина испарения § 293. Зависимость давления насыщенного пара от температуры § 294.  Кипение Кипение§ 295. Удельная теплота парообразования § 296. Охлаждение при испарении § 297. Изменение внутренней энергии при переходе вещества из жидкого состояния в парообразное § 298. Испарение при кривых поверхностях жидкости § 299. Перегревание жидкости § 300. Пересыщение паров § 301. Насыщение пара при возгонке § 302. Превращение газа в жидкость § 303. Критическая температура § 304. Сжижение газов в технике § 305. Вакуумная техника § 306. Водяной пар в атмосфере Глава XVIII. Физика атмосферы § 307. Атмосфера § 308. Тепловой баланс Земли § 309. Адиабатические процессы в атмосфере § 310. Облака § 311. Искусственные осадки § 312. Ветер § 313. Предсказание погоды Глава XIX. Тепловые машины § 314. Условия, необходимые для работы тепловых двигателей § 315. Паросиловая станция § 316. Паровой котел § 317. Паровая турбина § 318. Поршневая паровая машина § 319. Конденсатор § 320. Коэффициент полезного действия теплового двигателя § 321.  Коэффициент полезного действия паросиловой станции Коэффициент полезного действия паросиловой станции§ 322. Бензиновый двигатель внутреннего сгорания § 323. Коэффициент полезного действия двигателя внутреннего сгорания § 324. Двигатель Дизеля § 325. Реактивные двигатели § 326. Передача теплоты от холодного тела к горячему Ответы и решения к упражнениям Предметный указатель |
Сила и крутящий момент: измерение и уравнение
Предположим, вы и ваш друг гуляете по парку, когда натыкаетесь на качели. Давно никто из вас не играл на качелях, так что вы решили попробовать. Однако, зная, что вы разные по массе, вы решаете провести эксперимент. Отпуская из положения стоя, качели наклоняются в сторону вашего друга, который немного крупнее вас. В этот момент вы задаетесь вопросом, как сделать так, чтобы качели балансировали. После проб и ошибок вы обнаруживаете, что качели балансируют, когда ваш друг приближается к оси качелей. Каково физическое объяснение этого? Ответ зависит от соотношения между силой и крутящим моментом. В этой статье мы дадим определение обоим терминам, прежде чем обсуждать разницу и взаимосвязь между ними. Затем мы выведем крутящий момент из силы и обсудим, как производятся измерения крутящего момента.
В этой статье мы дадим определение обоим терминам, прежде чем обсуждать разницу и взаимосвязь между ними. Затем мы выведем крутящий момент из силы и обсудим, как производятся измерения крутящего момента.
Рис. 1 – Два друга сидят на противоположных концах качелей.
Уравнения силы и крутящего момента
Вдохновленный тем фактом, что вы нашли объяснение тому, как вам и вашему другу удалось уравновесить качели, было бы неплохо начать наше обсуждение с рассмотрения концепции силы. В физике мы определяем силу следующим образом:
Сила — это действие, приложенное к объекту для того, чтобы изменить его состояние движения либо из состояния покоя, либо из состояния равномерного поступательного движения по прямой.
Приведенное выше определение подразумевает, что всякий раз, когда объект претерпевает изменение в своем состоянии движения, задействованы силы. Мы можем выразить эту идею количественно с помощью второго закона Ньютона: \(m\) — его масса, а \(\vec{a}\) — ускорение объекта. И сила, и ускорение являются векторными величинами с величиной и направлением. По этой причине мы обозначаем их символы маленькой стрелкой. Чтобы использовать второй закон Ньютона для решения физических задач, мы придумаем следующее вспомогательное средство для запоминания:
И сила, и ускорение являются векторными величинами с величиной и направлением. По этой причине мы обозначаем их символы маленькой стрелкой. Чтобы использовать второй закон Ньютона для решения физических задач, мы придумаем следующее вспомогательное средство для запоминания:
\[\text{Сила} = \text{Масса} \times \text{Ускорение}.\]
Вспоминая качели, мы заметили, что и вы, и ваш друг вращаетесь вокруг фиксированной точка: центр качелей. Итак, вы движетесь не совсем по прямой линии; скорее, вы вращаете вокруг оси. Наличие вращения необходимо для понятия крутящего момента, который мы определяем следующим образом:
крутящий момент — это действие, оказываемое на объект для изменения его состояния кручения либо из состояния покоя, либо из равномерного углового движения вокруг оси .
Слово крутящий момент происходит от латинского термина Torquere , что означает крутить. Используя вышеприведенное определение в качестве ориентира, мы можем легко понять, почему физики любят думать о крутящем моменте как о вращательном аналоге линейной силы. На самом деле крутящий момент удовлетворяет собственному уравнению, которое мы называем вторым законом Ньютона для вращения:
На самом деле крутящий момент удовлетворяет собственному уравнению, которое мы называем вторым законом Ньютона для вращения:
\[\vec{\tau} = I\vec{\alpha}.\]
тау}\) обозначает крутящий момент, \(I\) момент инерции и \(\альфа\) (греческая буква альфа ) — угловое ускорение. Как и прежде, мы можем резюмировать вышеприведенное уравнение словами следующим образом:
\[\text{Крутящий момент} = \text{Момент инерции} \times \text{Угловое ускорение}.\]
Если вы еще не сталкивался с понятием момента инерции раньше, не волнуйтесь. Все, что вам нужно знать, это то, что, как и масса, момент инерции представляет тенденцию объекта сопротивляться изменениям в состоянии его движения. Однако, в отличие от массы, момент инерции объекта зависит от его геометрии. В инженерных приложениях момент инерции объекта можно найти в таблице.
Хорошей новостью является то, что мы можем решить многие физические задачи, связанные с крутящим моментом, с помощью более простого уравнения:
\[\begin{align}\tau &= Fr_\perp \\ &= Fr\sin(\theta). \end {align}\]
\end {align}\]
При использовании приведенного выше уравнения оборотов по часовой стрелке соответствует положительному крутящему моменту , а вращению против часовой стрелки соответствует отрицательному крутящему моменту .
Символ, который мы ввели в это выражение, \(r_\perp\) называется рычаг . Плечо рычага — это перпендикулярное расстояние от оси вращения до линии, проходящей от приложенной силы, как показано на изображении ниже. На этом изображении синий вектор положения представляет собой стержень, который вращается, когда на его конец действует сила, представленная зеленым вектором. Угол \(\тета\) (греческая буква тета ) — это угол между векторами положения и силы. Мы находим плечо рычага, продолжая линию от вектора силы наружу так, чтобы мы могли провести перпендикулярную линию от оси вращения к продолженной линии силы. Это плечо рычага. Некоторые физические задачи, которые мы можем решить с помощью этого уравнения, включают определение крутящего момента, необходимого для открытия двери или затягивания болта гаечным ключом, и, как вы уже догадались, нахождение точки равновесия качелей.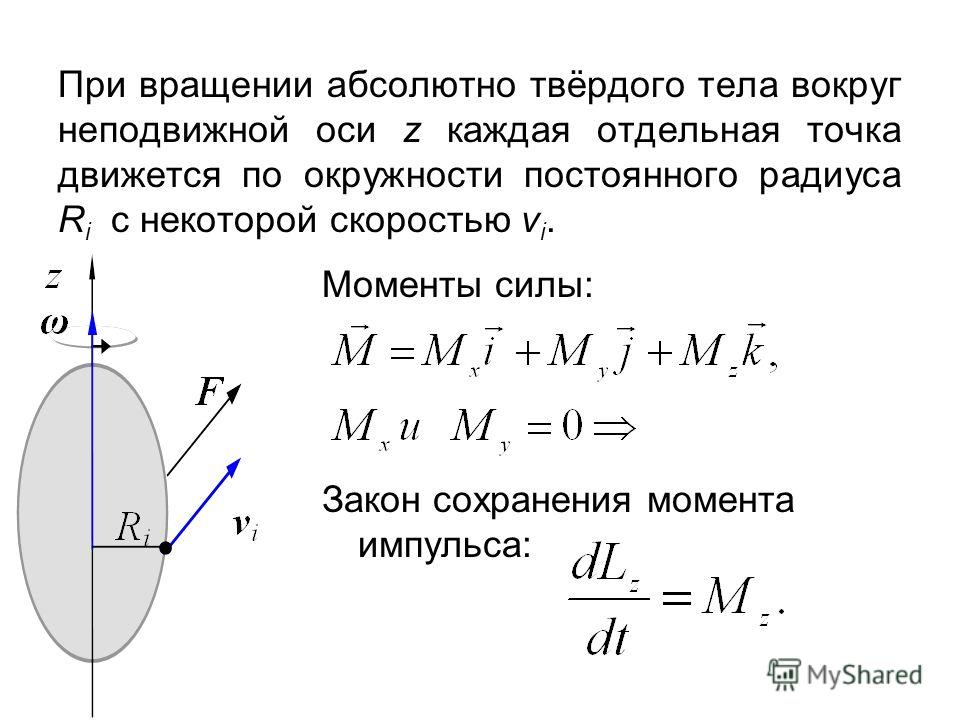
Рис. 2. Крутящий момент находится путем умножения величины приложенной силы на плечо рычага.
Другое название плеча рычага — моментное плечо . Хотя эти два термина означают одно и то же, в этой статье мы будем использовать только первый.
Обратите внимание, что, поскольку вектор силы расположен под углом к вектору положения, вектор силы имеет компонент, параллельный вектору положения, и компонент, перпендикулярный вектору положения. Параллельная составляющая не влияет на крутящий момент, поскольку она направлена в том же направлении, что и вектор положения; только перпендикулярная составляющая вносит вклад в крутящий момент. Представьте, что вы используете гаечный ключ, чтобы затянуть болт. Если вы потянете гаечный ключ наружу, болт не повернется, потому что сила параллельна гаечному ключу. Вы должны приложить перпендикулярную силу к гаечному ключу, чтобы болт повернулся.
Имея в виду вышеизложенное, самое время количественно определить, почему вы и ваш друг достигли статического равновесия после того, как ваш друг приблизился к рычагу качелей. Приведенный ниже пример предназначен для того, чтобы помочь вам разобраться с физикой.
Приведенный ниже пример предназначен для того, чтобы помочь вам разобраться с физикой.
Рис. 3 – Два человека сидят на качелях. Точка вращения находится в центре качелей.
Два человека сидят на качелях. Слева находится человек \(50\,\mathrm{kg}\), а справа — человек \(75\,\mathrm{kg}\). Всего качели \(1.2\,\mathrm{m}\) с осью в центральной точке. Левый человек сидит на расстоянии \(0,6\,\mathrm{m}\) от опорной точки. На каком расстоянии \(75\,\mathrm{kg}\) должен сидеть человек, чтобы качели находились в статическом равновесии? 9{\circ}\) угол. Итак, крутящий момент от человека слева равен
\[\begin{align*}\tau_1&=r_\perp F_1\\&=-d_1 m_1 g,\end{align*}\]
и крутящий момент от человека справа
\[\begin{align*}\tau_2&=r_\perp F_2\\&=d_2 m_2 g.\end{align*}\]
Затем мы можем найти второе расстояние установив чистый крутящий момент равным нулю:
\[\begin{align*}\sum\tau&=0\\\tau_1+\tau_2&=0\\-d_1m_1g+d_2m_2g&=0\\d_1m_1g&=d_2m_2g\\d_1m_1&= d_2m_2\\d_2&=\frac{d_1m_1}{m_2}\\&=\frac{(50\,\mathrm{kg})(0,6\,\mathrm{m})}{75\,\mathrm{kg} }\\&=0. 4\,\mathrm{m}.\end{align*}\]
4\,\mathrm{m}.\end{align*}\]
Разница между силой и крутящим моментом
Если вы сравните определения силы и крутящего момента, которые мы дали выше, вы можете заметить, что они имеют схожие характеристики. То же самое относится и к их уравнениям. В обоих случаях мы вычисляем искомое количество, взяв произведение двух вещей. Но, спрашивая себя о том, что мы умножаем в каждом случае, мы приходим к фундаментальному различию между силой и крутящим моментом. В то время как сила применяется к движению вперед в прямой линия, крутящий момент применяется к вращательному движению. Действительно, именно поэтому мы говорим о угловых и ускорений, когда думаем о крутящем моменте.
Но чем угловое ускорение отличается от линейного ускорения? Напомним, что мы определяем ускорение как скорость изменения скорости во времени:
\[\vec{a} = \frac{\Delta \vec{v}}{\Delta t}.\]
Сравните это с угловым ускорением, которое мы определяем как скорость изменения угловой скорости по отношению ко времени:
\[\vec{\alpha} = \frac{\Delta \vec{\omega}}{\Delta t}. 2}.\]
2}.\]
Это имеет смысл, поскольку сила равна массе, умноженной на ускорение, масса измеряется в килограммах, а ускорение измеряется в метрах в секунду в квадрате. С другой стороны, крутящий момент равен моменту инерции, умноженному на угловое ускорение. Единицами момента инерции являются килограммы, умноженные на метры в квадрате, где последний зависит от формы объекта. Из вышеизложенного мы видим, что угловое ускорение есть произведение расстояния от оси вращения на ускорение. Сочетание этих двух фактов позволяет нам определить единицы крутящего момента: 92} \\&= \mathrm{N} \cdot \mathrm{m}.\end{align}\]
Таким образом, сила и крутящий момент также различны, потому что они не имеют одинаковых единиц измерения.
Возможно, вы заметили, что крутящий момент имеет те же единицы измерения, что и поступательная работа. Однако мы никогда не говорим, что крутящий момент измеряется в джоулях, потому что крутящий момент сам по себе не является мерой энергии.
Связь между силой и крутящим моментом
Выше мы уже видели, что крутящий момент является вращательным аналогом линейной силы. По этой причине мы можем сказать, что отношение между силой и крутящим моментом является одним из 9.0025 логическая зависимость . Под этим мы подразумеваем, что как физическую величину мы можем вывести крутящий момент из понятия силы. Мы сделаем это в следующем разделе. Перед этим мы выделим ключевую особенность, общую как для силы, так и для крутящего момента: тот факт, что у второго закона Ньютона есть вращательный аналог.
По этой причине мы можем сказать, что отношение между силой и крутящим моментом является одним из 9.0025 логическая зависимость . Под этим мы подразумеваем, что как физическую величину мы можем вывести крутящий момент из понятия силы. Мы сделаем это в следующем разделе. Перед этим мы выделим ключевую особенность, общую как для силы, так и для крутящего момента: тот факт, что у второго закона Ньютона есть вращательный аналог.
Для объектов, испытывающих поступательное движение, мы находим уравнения движения из второго закона Ньютона, который гласит, что результирующая сила, действующая на объект, равна массе, умноженной на ускорение,
\[\sum \vec{F}=m\vec{a}.\]
Вращательный аналог второго закона Ньютона для вращающегося объекта состоит в том, что чистый крутящий момент, действующий на объект, равен моменту инерции умноженное на угловое ускорение,
\[\sum \vec{\tau}=I\vec{\alpha}.\]
Когда мы пишем второй закон Ньютона для объекта в поступательном движении, мы сначала рассматриваем все силы, вносящие вклад в результирующую силу. Точно так же для второго закона Ньютона во вращательном движении мы должны учитывать все силы, прилагающие крутящий момент к объекту. Статическое и динамическое равновесие применимо как к силе, так и к крутящему моменту, а это означает, что когда объект находится в состоянии покоя или движется с постоянной скоростью/угловой скоростью, результирующая сила/крутящий момент равна нулю.
Точно так же для второго закона Ньютона во вращательном движении мы должны учитывать все силы, прилагающие крутящий момент к объекту. Статическое и динамическое равновесие применимо как к силе, так и к крутящему моменту, а это означает, что когда объект находится в состоянии покоя или движется с постоянной скоростью/угловой скоростью, результирующая сила/крутящий момент равна нулю.
И сила, и крутящий момент также являются векторными величинами с величиной и направлением. Мы определили величину крутящего момента выше по уравнению:
\[\begin{align}\tau &= Fr_\perp.\end{align}\]
Рассматривая крутящий момент как вектор, мы должны использовать определение вектора вместо этого:
\[\vec{\tau}=\vec{r}\times\vec{F}.\]
Это уравнение говорит нам, что вектор крутящего момента равен векторному произведению векторов силы и положения. . Направление вектора крутящего момента — вдоль оси вращения, а его знак зависит от направления вращения; вращение против часовой стрелки и по часовой стрелке соответствуют положительному и отрицательному крутящему моменту соответственно, при условии, что положительное направление направлено вверх. 92}\\&=166,7\,\mathrm{\frac{rad}{s}}.\end{align*}\]
92}\\&=166,7\,\mathrm{\frac{rad}{s}}.\end{align*}\]
Вывод крутящего момента из силы
Теперь давайте посмотрим, как мы выводим уравнение для крутящего момента начиная со второго закона Ньютона с силами. Для этого вывода рассмотрим вращение частицы массы \(m\) вокруг оси вращения. Начнем с подстановки соотношения между ускорением и угловым ускорением \(\vec{a}=\vec{\alpha}\times\vec{r},\) во второй закон поступательного движения Ньютона:
\[\begin{align} \vec{F} &= m\vec{a} \\ &= m\vec{\alpha}\times\vec{r}. \end{align}\]
Векторные операции векторного произведения и скалярного произведения выходят за рамки AP Physics 1. Однако они необходимы для вывода крутящего момента из второго закона Ньютона. Вы можете думать о приведенной ниже математике как о учебнике для более строгих выводов, с которыми вы сталкиваетесь в университетских курсах физики.
Теперь возьмем перекрестное произведение обеих сторон с вектором положения:
\[\vec{r}\times\vec{F} = m\vec{r}\times(\vec{\alpha}\times\vec{r}). 2.\) Поскольку вектор ускорения, \(\vec{\alpha} ,\) указывает вдоль оси вращения, а вектор положения, \(\vec{r}\) указывает перпендикулярно ему вдоль плоскости вращения, скалярное произведение между ними стремится к нулю: \(\vec{r}\ cdot\vec{\alpha}=0.\) Таким образом, наше уравнение принимает вид: 92\) как момент инерции частицы относительно ее оси вращения, поэтому мы можем написать:
2.\) Поскольку вектор ускорения, \(\vec{\alpha} ,\) указывает вдоль оси вращения, а вектор положения, \(\vec{r}\) указывает перпендикулярно ему вдоль плоскости вращения, скалярное произведение между ними стремится к нулю: \(\vec{r}\ cdot\vec{\alpha}=0.\) Таким образом, наше уравнение принимает вид: 92\) как момент инерции частицы относительно ее оси вращения, поэтому мы можем написать:
\[\begin{align*}\vec{r}\times\vec{F} &= I\vec{\ alpha}\\&=\vec{\tau}.\end{align*}\]
Таким образом, крутящий момент на частице вокруг оси вращения равен:
\[\vec{\tau}=\vec{ r}\times\vec{F}.\]
Мы можем использовать другое правило перекрестного произведения, чтобы получить уравнение, которое мы использовали выше в терминах плеча рычага. Используемое нами перекрестное идентичность:
\[\vec{a} \times \vec{b} = \lvert \vec{a} \rvert \lvert \vec{b} \rvert \sin(\theta), \] поэтому уравнение для крутящего момента можно записать:
\[\begin{align*}\vec{\tau}&=\vec{r}\times\vec{F}\\&=\lvert \vec{r} \rvert \lvert \vec{F} \rvert \sin(\theta) \\&=(r\sin(\theta))F\\&=r_\perp F. \end{align*}\]
\end{align*}\]
Измерения силы и крутящего момента
Мы можем производить измерения силы и крутящего момента с помощью определенных инструментов в лаборатории. Для измерения силы одним из распространенных датчиков силы является пружинный измеритель. Он содержит пружину и крючок для прикрепления к измеряемому объекту и выдает усилие, необходимое (в ньютонах) для растяжения пружины. Измерение крутящего момента может быть выполнено с помощью датчика крутящего момента. Датчики крутящего момента используют датчик или преобразователь для измерения крутящего момента на объекте и выводят крутящий момент в ньютон-метрах.
Рис. 4. Датчик силы, используемый для измерения приложенной силы.
Сила и крутящий момент. Ключевые выводы
- Сила — это действие, прикладываемое к объекту для изменения его состояния движения либо из состояния покоя, либо из состояния равномерного поступательного движения по прямой линии.
- Крутящий момент – это действие, оказываемое на объект с целью изменить его состояние кручения либо из состояния покоя, либо из состояния равномерного углового движения вокруг оси.

- В то время как сила измеряется в ньютонах \(\mathrm{N}\), крутящий момент измеряется в ньютон-метрах, \(\mathrm{N}\cdot\mathrm{m}.\)
- Крутящий момент связан с силой уравнением: \(\vec{\tau}=\vec{r}\times\vec{F}.\)
- Вращательный аналог второго закона Ньютона для вращающегося объекта: \ (\vec{\tau}=I\vec{\alpha}.\)
Ссылки
- Рис. 1 — Друзья на качелях (https://pixabay.com/photos/clone-seesaw-outdoors- park-fun-4014107/) от MichaelMags (https://pixabay.com/users/michaelmags-11692883/) под лицензией Pixabay (https://pixabay.com/service/license/).
- Рис. 2 — Рычаг крутящего момента, StudySmarter Originals
- Рис. 3 — Поворотный рычаг, StudySmarter Originals
- Рис. 4 — Датчик силы (https://search-production.openverse.engineering/image/fa078701-c074- 4811-8deb-e415ee77f6d6) от SparkFun Electronics (https://www.flickr.com/photos/41898857@N04) по лицензии CC BY 2.0 (https://creativecommons.org/licenses/by/2.
 0/)
0/)
Расчет крутящего момента как векторного произведения
Содержание
- Крутящий момент относительно точки
- Крутящий момент вокруг оси
Рассмотрим винт, показанный на рисунке. Если силы приложены в разных местах, то как создаются эффекты вращения. Ось вращения проходит через центр винта и перпендикулярна плоскости диаграммы.
Во-первых, рассмотрим только силу F1{F_1}F1, создаст ли она эффект вращения? Винт не будет вращаться, поэтому сила F1{F_1}F1 не создаст крутящего момента.
Теперь, если приложить только силу F2{F_2}F2, то снова винт не будет вращаться.
Силы F3{F_3}F3 и F4{F_4}F4 будут вращать винт, поэтому они будут создавать некоторый крутящий момент или эффект вращения. Однако какой из них будет легко вращать винт? Сила F3{F_3}F3 находится далеко от оси вращения и легко вращает винт по сравнению с F4{F_4}F4.
F1{F_1}F1 и F3{F_3}F3 действуют в одной точке, но под разными углами. F1{F_1}F1 и F3{F_3}F3 имеют разные эффекты поворота. Итак, от каких факторов зависит поворотный эффект?
Поскольку F3{F_3}F3 и F4{F_4}F4 создают крутящий момент и находятся на разном расстоянии от оси вращения, то крутящий момент должен зависеть от расстояния силы от оси вращения. По этой причине ручки сделаны в конце дверей, так что расстояние действия силы увеличивается от оси вращения и может быть создан больший эффект поворота при приложении меньшего усилия.
Так как F1{F_1}F1 и F3{F_3}F3 находятся на одинаковом расстоянии от оси вращения, но под разными углами, то крутящий момент зависит от направления силы.
Крутящий момент также зависит от величины силы. Чем больше величина силы, тем больше эффект поворота. Предположим, вы хотите открыть застрявший винт, тогда вам нужно приложить большее усилие, чтобы создать больший крутящий момент.
Суммируя все вышеперечисленные факторы, можно сделать вывод, что относительно любой точки
τ⃗=r⃗×F⃗\vec \tau = \vec r \times \vec Fτ=r×F
Здесь r⃗\vec rr — вектор положения точки приложения силы относительно точки, относительно которой рассчитывается крутящий момент,
F⃗\vec FF — приложенная сила,
τ⃗\vec \tau τ — крутящий момент.
Направление крутящего момента можно рассчитать по правилам векторного произведения.
Рассмотрим приведенную выше диаграмму, на которой угол между r⃗\vec rr и F⃗\vec FF равен θ\thetaθ. В этом случае, если линия действия силы продолжена и на нее опущен перпендикуляр из точки вычисления момента, то этот перпендикуляр называется плечом момента.
Плечо момента равно rsinθr sin \thetarsinθ,
Величина крутящего момента относительно точки ‘O’ равна rFsinθr F sin \theta rFsinθ,
Следовательно, крутящий момент также может быть записан как произведение силы и плеча момента.
ПРИМЕЧАНИЕ\большой \color{#3D99F6} {ПРИМЕЧАНИЕ} ПРИМЕЧАНИЕЕсли крутящий момент вычисляется относительно точки на линии действия силы, то крутящий момент оказывается равным нулю. Это связано с тем, что в этом случае угол между вектором положения «r» и силой «F» будет равен нулю. 9\circ}30∘ на гаечный ключ на расстоянии 8 см от гайки, он как раз способен ослабить гайку.
Какой силы FFF будет достаточно, чтобы ослабить ее, если она действует перпендикулярно ключу на расстоянии 16 см от гайки?
Когда крутящий момент рассчитывается относительно точки, он автоматически указывает вдоль оси, которую можно найти с помощью правила большого пальца правой руки. Если крутящий момент должен быть рассчитан относительно какой-либо другой оси, необходимо предпринять следующие шаги,
1) Рассчитать крутящий момент относительно любой точки на оси
2) Рассчитайте составляющую крутящего момента относительно указанной оси.Рассмотрим приведенную выше диаграмму, на которой сила F действует на тело в точке P перпендикулярно плоскости рисунка. Таким образом, «r» перпендикулярно силе, а крутящий момент вокруг точки «O» находится в плоскости x-y под углом θ \ theta θ к оси y. Крутящий момент относительно ‘O’ равен τO=rF{\tau_O} = r F τO=rF
Чтобы рассчитать крутящий момент относительно оси y, возьмите компонент крутящего момента относительно оси y.
Таким образом,
τyaxis=rFcosθ{\tau_{yaxis}} = r F cos \theta τyaxis=rFcosθ
Перпендикуляр (AF), проведенный по оси Y от линии действия силы, равен AF=rcosθAF= r cos \ тета AF = rcos θ, Таким образом, крутящий момент вокруг оси можно рассчитать как произведение силы на перпендикулярное расстояние между линией действия силы и осью, относительно которой должен быть рассчитан крутящий момент.ПРИМЕЧАНИЕ\большой\цвет{#3D99F6} ПРИМЕЧАНИЕ ПРИМЕЧАНИЕ Чтобы приведенная выше формула была правильной, линия действия силы и ось, относительно которой должен быть рассчитан крутящий момент, должны быть кососимметричной линией. Кососимметричные прямые — это те, которые не параллельны и не пересекаются.
Если линия действия силы и ось, вокруг которой рассчитывается крутящий момент, параллельны, то крутящий момент вокруг оси будет равен нулю.0, Фа 0, 0 Фа, Фа Fa, 0
Сила приложена перпендикулярно ребру куба со стороной а, как показано на рисунке.




 0/)
0/)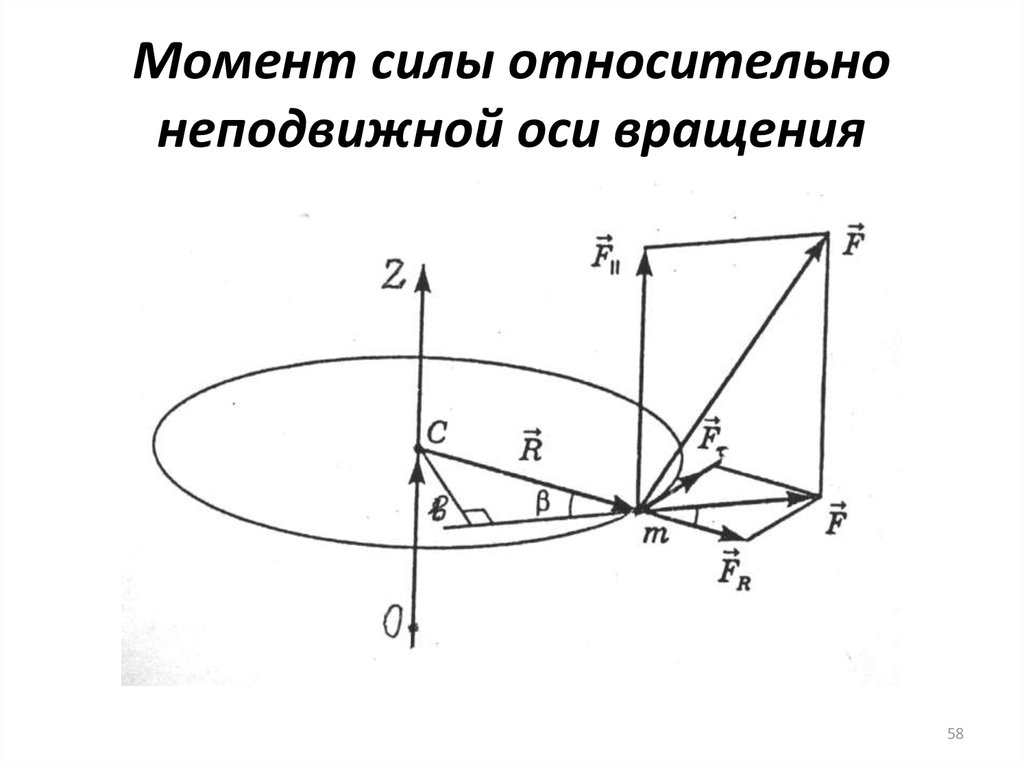 Какой силы FFF будет достаточно, чтобы ослабить ее, если она действует перпендикулярно ключу на расстоянии 16 см от гайки?
Какой силы FFF будет достаточно, чтобы ослабить ее, если она действует перпендикулярно ключу на расстоянии 16 см от гайки?