|
Random converter |
Конвертер вращающего моментаКонвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления.Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыИмпульс (количество движения)Импульс силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. Исходная величина ньютон-метрньютон-сантиметрньютон-миллиметркилоньютон-метрдина-метрдина-сантиметрдина-миллиметркилограмм-сила-метркилограмм-сила-сантиметркилограмм-сила-миллиметрграмм-сила-метрграмм-сила-сантиметрграмм-сила-миллиметрунция-сила-футунция-сила-дюймфунт-сила футфунт-сила дюйм Преобразованная величина ньютон-метрньютон-сантиметрньютон-миллиметркилоньютон-метрдина-метрдина-сантиметрдина-миллиметркилограмм-сила-метркилограмм-сила-сантиметркилограмм-сила-миллиметрграмм-сила-метрграмм-сила-сантиметрграмм-сила-миллиметрунция-сила-футунция-сила-дюймфунт-сила футфунт-сила дюйм TCTermsВопросы и ответы — профессиональные переводчики помогут перевести сложные термины В этом историческом двигателе используется маховик Общие сведения Использование момента силы в быту и технике Велосипедные педали Гаечный ключ Маховик Качели и рычаги Рычаги первого рода Рычаги второго рода Рычаги третьего рода Пример Общие сведенияКода на тело действует сила в определенном направлении — тело поворачивается. Момент силы имеет наибольшую величину, если сила, действующая на тело, перпендикулярна отрезку, соединяющему точку вращения и точку приложения силы. Давайте посмотрим на эту взаимосвязь на иллюстрации. Здесь силы F2, F3 и F5 перпендикулярны отрезку между осью вращения, обозначенной голубым цветом в центре штурвала, и точкой приложения силы. Создаваемый ими момент силы — максимален. С другой стороны, силы F1 и F4 приложены под углом, отличным от 90°, и создаваемый ими момент силы не максимален. То есть, момент силы этих двух сил отличается от момента силы других трех сил, хотя величина всех сил на рисунке — одинакова. Чтобы повернуть тело под воздействием силы с заданными условиями, необходимо создать момент силы. Так как эта величина зависит и от расстояния, и от силы, то для получения заданного момента можно изменять либо силу, либо расстояние от точки приложения до точки вращения. Люди используют эту зависимость испокон веков. Использование момента силы в быту и техникеОбычно легче увеличить расстояние между телом и точкой приложения силы, чем саму силу. Ведущие колеса помогают велосипедисту поддерживать оптимальную скорость вращения педалей, и используют момент вращения для преодоления местности с разным рельефом, от ровного до холмистого Велосипедные педалиМомент силы используется также в педалях велосипедов. Чем дальше ступня от центра велосипедного колеса, тем меньше нужно силы, чтобы повернуть это колесо с помощью педали. Длина наших ног ограничивает максимальную длину педалей — если сделать педали длиннее, чем делают их сейчас на современных велосипедах, то крутить их будет неудобно. Гаечный ключГайку намного легче открутить гаечным ключом, чем голыми руками Гаечные ключи используют момент силы, чтобы уменьшить силу, необходимую для затягивания или откручивания гайки или болта. Гаечный ключ сделан так, чтобы его удобно было держать, но в то же время его длинная ручка увеличивает силу, к нему приложенную, чтобы затянуть или открутить болт или гайку. Иногда достаточно маленького ключа с короткой ручкой, но в некоторых случаях нужна ручка длиннее, например, если мы пытаемся открутить заржавевшую гайку. Реверсивный ключ похож по методу работы на обычные гаечные ключи — он, как и гаечный ключ, позволяет увеличить момент силы Удобство гаечного ключа в том, что когда он подобран по размеру к гайке, сила нужна только для того, чтобы повернуть ключ, но не для того, чтобы удерживать его на гайке. Плоскогубцы, наоборот, нужно удерживать вокруг гайки, чтобы они не сорвались, и на это тратится дополнительная сила. Именно поэтому во многих случаях гаечный ключ более экономичен с точки зрения затраченной энергии. С другой стороны, в некоторых случаях плоскогубцы удобнее — например их можно использовать под углом в труднодоступных местах, в то время как гаечный ключ часто работает только в одной плоскости с гайкой. Если откручивать гайку под наклоном, то момент силы уменьшится, но это лучше, чем совсем не иметь возможности ее отвернуть. Аналогично работают и инструменты, предназначенные для отвинчивания крышек с законсервированных банок. Обычно это резиновый жгут, прикрепленный к ручке так, что жгут образует петлю, диаметр которой регулируется. Сама петля закрепляется на крышке и не влияет на момент силы, а вот ручка как раз помогает создать нужный момент. Чем она больше, тем больше момент силы. Благодаря ему, банку открыть намного легче, чем руками, с использованием полотенца или материала с высоким коэффициентом трения. Этот маховик, находящийся внутри двигателя, накапливает энергию, которую двигатель вырабатывает неравномерно, бросками. По мере необходимости маховик выделяет эту энергию более равномерно МаховикВ этом историческом двигателе используется маховик Хороший пример устройства, которое использует момент силы — маховик. Момент силы приводит его в движение, а также помогает ускорить маховик и, благодаря этому движению, получить энергию. Маховик накапливает и хранит ее для дальнейшего использования. Маховик используется для хранения энергии В некоторых случаях нужен обратный эффект, то есть необходимо кратковременно подать большое количество энергии, обычно больше, чем источник энергии может выработать в течение заданного промежутка времени. В такой ситуации маховик на протяжении некоторого времени накапливает энергию, поступающую небольшими порциями, чтобы потом отдать нужное количество. Качели и рычагиСила, с которой два ребенка надавливают на качели-балансир, когда сидят по обе стороны от центра, двигает эти качели вверх и вниз. То есть, при этом происходит частичное вращение качелей вокруг своей оси. Рычаги действуют аналогично: момент силы в них используется для того, чтобы уменьшить силу, нужную для совершения определенной работы. Обычно рычаг — это продолговатый предмет, например ручка или планка, которая вращается вокруг точки, называемой центром вращения или точкой опоры. К другой точке рычага прикладывают силу, которая, благодаря длине рычага, увеличивается или уменьшается в зависимости от конструкции рычага и его назначения. Рычаги делят на три рода, в зависимости от того, где точка опоры, как приложена сила, которая их поворачивает, и где приложена сила сопротивления. Обычно их называют рычагами первого, второго, и третьего рода. Иногда не совсем понятно, при чем тут сила сопротивления, но она действительно есть. Она противодействует силе, которая направлена на то, чтобы повернуть рычаг. Когда приложенная сила больше силы сопротивления, рычаг поворачивается. Мы, а также другие животные, используем эти принципы в организме, и части нашего тела становятся рычагами, как показано на примерах ниже. Точка опоры рычагов первого рода находится в середине рычага. На иллюстрации она обозначена буквой F. Сила сопротивления, R, действует на один конец рычага, в то время как сила, действующая на рычаг, E, приложена к противоположному концу рычага. Примеры рычагов первого рода — это ножницы, весы, лом, и голова человека и животных. Рычаг первого рода похож по конструкции на детские качели-балансир, описанные выше. Рычаги первого родаРавноплечие весы с чашками — пример рычагов первого рода. Ножницы — тоже, только они состоят из двух рычагов, соединенных между собой. С их помощью намного легче, чем ножом, аккуратно разрезать некоторые материалы, например бумагу или ткань. Чем длиннее ручки, тем более толстые и твердые материалы можно разрезать. С другой стороны, чем дальше поместить от оси вращения материал, который нужно разрезать, тем труднее это сделать. Весы с двумя чашками — пример рычага первого рода Ножницы-болторезы предназначены для резки толстой проволоки и болтов, с использованием силы мышц, поэтому у них длинные ручки, чтобы увеличить момент силы Чем толще материал, который нужно разрезать, тем больший момент силы необходим для этого, и тем длиннее должны быть ручки ножниц и прочнее материал, из которых они сделаны. Лом-монтировку или лом-гвоздодер, называемый также «фомкой» тоже можно считать рычагом первого рода, хотя иногда, в зависимости от использования, он может быть и рычагом второго или третьего рода. Пример рычага первого рода в организме людей и некоторых животных — голова. Она находится в равновесии на шее. Шея — центр вращения, сила мышц прилагается с одной стороны головы, сила сопротивления — с другой. Когда приложенная сила достаточно велика, голова наклоняется в сторону направления этой силы. Точка опоры рычагов второго рода находится на одном конце рычага, а сила прикладывается к другому концу. Сила сопротивления возникает между силой, действующей на рычаг, и осью вращения. Рычаги второго родаПримеры рычагов второго рода — челюсти людей и животных, и клювы птиц. Являются ими и щипцы для орехов, а также декоративные щелкунчики. Клешни этого краба — рычаги второго рода. Они нужны крабам для того, чтобы обороняться от других крабов. У некоторых видов крабов клешни также привлекают самок во время брачного периода. Чеснокодавилка — еще один пример рычагов второго ряда. По устройству она похожа на щипцы для орехов. Ее часто используют в быту, хотя некоторые повара предпочитают мелко резать чеснок, и считают, что чеснокодавилка портит вкус чеснока. Другие, наоборот, пользуются только чеснокодавилкой, так как вкус чеснока при ее использовании усиливается. Ступня людей и некоторых животных — тоже рычаг второго типа. Точка опоры в этом случае в районе пальцев, мышцы ноги прикладывают силу около пятки, а сила сопротивления — это наш вес. Этот «рычаг» позволяет нам держать равновесие, а также подниматься и опускаться на пальцах. Другие примеры рычагов второго класса — тачки, тормоза в автомобиле и двери. Если толкнуть дверь рядом с осью вращения, то она вряд ли откроется, но если толкать как можно дальше от этой оси, то даже тяжелая дверь легко поддается. Именно поэтому ручки делают со стороны, противоположной расположению петель. Чтобы даже тяжелую дверь было легко открывать, ее можно сделать шире. Открывалки для бутылок — тоже рычаги второго класса, особенно те, что не прикреплены к стене, как в некоторых барах и ресторанах. В некоторых перочинных ножах имеются маленькие открывалки; также популярны брелки-открывалки. Если под рукой нет открывалки, то иногда получается использовать подручные материалы, например нож или вилку. Сами открывалки можно в некоторых случаях использовать, чтобы поддеть закрученную крышку на банке — если сделать это удачно, то банка легче откроется. Иногда открывалки используют как рычаги первого класса. В этом случае открывалку закрепляют на крышке иначе и давят на нее снизу, а не сверху, как с рычагами второго рода. Примеры рычагов третьего ранга Рычаги третьего родаЕсли поднимать рукой тяжелые предметы, сгибая локоть, то рука становится рычагом третьего рода. Во время бега и ходьбы, ноги тоже становятся рычагами. Точка опоры рычага в этом случае — в локтях и коленях. Если «продлить» руку инструментом, например бейсбольной битой или теннисной ракеткой, то опять получится рычаг третьего рода. Другие примеры рычагов третьего рода — молоток, и аналогичные инструменты, такие как лопаты, грабли, веники, и мухобойки. Некоторые инструменты состоят сразу из двух рычагов, действующих по направлению друг к другу. Так устроены, например, пинцет, степлер и щипцы. ПримерТеперь давайте рассмотрим пример. Представим, что обычный человек среднего телосложения может поднять камень весом в 20 кг. Конечно, это будет нелегко, и придется сильно напрячь мышцы, но поднять такой камень вполне возможно. С другой стороны, маленький ребенок такой камень поднять не в состоянии. Если же дать ребенку достаточно длинный и прочный лом и научить его, как им пользоваться, то он справится с этой задачей, так как сила, нужная для того, чтобы поднять камень, намного уменьшится. Литература Автор статьи: Kateryna Yuri Вас могут заинтересовать и другие конвертеры из группы «Механика»:Плоский угол Конвертер угловой скорости и частоты вращения Конвертер ускорения Конвертер углового ускорения Конвертер площади Конвертер плотности Конвертер энергии и работы Конвертер силы Конвертер длины и расстояния Конвертер массы Конвертер момента инерции Конвертер момента силы Конвертер мощности Конвертер давления, механического напряжения, модуля Юнга Конвертер удельного объема Конвертер объема и единиц измерения в кулинарных рецептах Конвертер мер объема сыпучих продуктов и продуктов питания Конвертер линейной скорости Компактный калькулятор Полный калькулятор Определения единиц Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. |
ВРАЩАЮЩИЙ МОМЕНТ — это что такое ВРАЩАЮЩИЙ МОМЕНТ
Значение слова «ВРАЩАЮЩИЙ МОМЕНТ» найдено в 32 источниках
найдено в «Большой Советской энциклопедии»
мера внешнего воздействия, изменяющего угловую скорость вращающегося тела. В. м. равен алгебраической сумме моментов всех действующих на вращающееся тело сил относительно оси вращения (см. Момент силы, Вращательное движение). В. м. связан с угловым ускорением тела ε равенством Мвр = Iε, где I — Момент инерции тела относительно оси вращения.
найдено в «Большой советской энциклопедии»
ВРАЩАЮЩИЙ МОМЕНТ, мера внеш. воздействия, изменяющего угловую скорость вращающегося тела. В. м. равен алгебраич. сумме моментов всех действующих на вращающееся тело сил относительно оси вращения (см.

найдено в «Физической энциклопедии»
мера внеш. воздействия, изменяющего угл. скорость вращающегося тела. В. м. равен алгебр. сумме моментов всех действующих на вращающееся тело сил относительно оси вращения (см. МОМЕНТ СИЛЫ, ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ). В. м. связан с угл. ускорением тела e равенством: Mвp=Ie, где I — момент инерции тела относительно оси вращения.
Физический энциклопедический словарь. — М.: Советская энциклопедия.Главный редактор А. М. Прохоров.1983.
найдено в «Научно-техническом энциклопедическом словаре»
ВРАЩАЮЩИЙ МОМЕНТ, вращающее действие силы. Так, турбина при повороте генератора создает вращающий момент по оси вращения. Мощность ротационного двигателя, к примеру, ЧЕТЫРЕХТАКТНОГО ДВИГАТЕЛЯ или электрического мотора, определяется вращающим моментом, который он способен создавать. Единица измерения — нм (ньютон на метр).
найдено в «Естествознании. Энциклопедическом словаре»
мера внеш. воздействия, изменяющего угловую скорость вращающегося тела. В. м. Мвр равен сумме моментов всех действующих на тело сил относительно оси вращения и связан с угловым ускорением тела Е равенством Мвр = IE, где I — момент инерции тела относительно оси вращения.
В. м. Мвр равен сумме моментов всех действующих на тело сил относительно оси вращения и связан с угловым ускорением тела Е равенством Мвр = IE, где I — момент инерции тела относительно оси вращения.
найдено в «Современном энциклопедическом словаре»
ВРАЩАЮЩИЙ МОМЕНТ, мера внешнего воздействия, изменяющего угловую скорость вращающегося тела. Вращающий момент Мвр равен сумме моментов всех действующих на тело сил относительно оси вращения и связан с угловым ускорением тела ? равенством Мвр = I?, где I — момент инерции тела относительно оси вращения.
найдено в «Большом Энциклопедическом словаре»
ВРАЩАЮЩИЙ момент — мера внешнего воздействия, изменяющего угловую скорость вращающегося тела. Вращающий момент Мвр равен сумме моментов всех действующих на тело сил относительно оси вращения и связан с угловым ускорением тела ? равенством Мвр = I?, где I — момент инерции тела относительно оси вращения.
найдено в «Энциклопедическом словаре естествознания»
ВРАЩАЮЩИЙ МОМЕНТ , мера внешнего воздействия, изменяющего угловую скорость вращающегося тела. Вращающий момент Мвр равен сумме моментов всех действующих на тело сил относительно оси вращения и связан с угловым ускорением тела ? равенством Мвр = I?, где I — момент инерции тела относительно оси вращения.
найдено в «Большом энциклопедическом словаре»
ВРАЩАЮЩИЙ МОМЕНТ, мера внешнего воздействия, изменяющего угловую скорость вращающегося тела. Вращающий момент Мвр равен сумме моментов всех действующих на тело сил относительно оси вращения и связан с угловым ускорением тела ? равенством Мвр = I?, где I — момент инерции тела относительно оси вращения.
найдено в «Большом энциклопедическом словаре»
— мера внешнего воздействия, изменяющего угловую скоростьвращающегося тела. Вращающий момент Мвр равен сумме моментов всехдействующих на тело сил относительно оси вращения и связан с угловымускорением тела ? равенством Мвр = I?, где I — момент инерции телаотносительно оси вращения.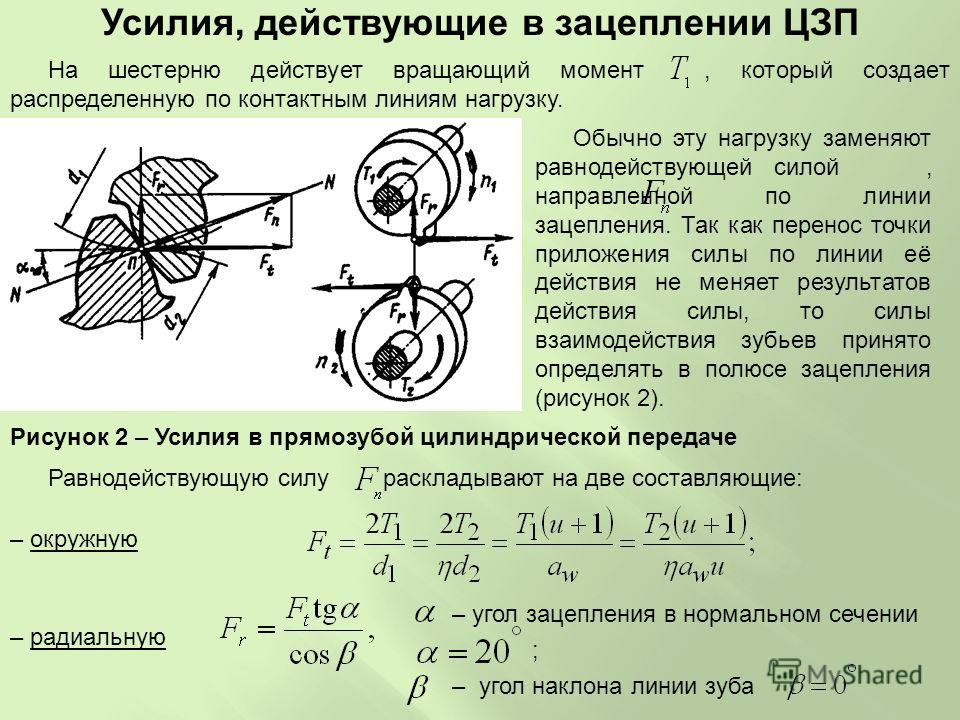
найдено в «Русско-английском словаре по физике»
torque moment, torsional moment, rotational moment, turning moment, torque, turning couple
АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
ABCDEFGHIJKLMNOPQRSTUVWXYZ
Крутящий момент — Энциклопедия Нового Света
Крутящий момент, приложенный с помощью регулируемого торцевого ключа вращательное движение. Эта сила определяется линейной силой, умноженной на радиус. Символ крутящего момента: τ , греческая буква тау . Понятие крутящего момента, также называемого моментом или парой, возникло в результате работы Архимеда над рычагами.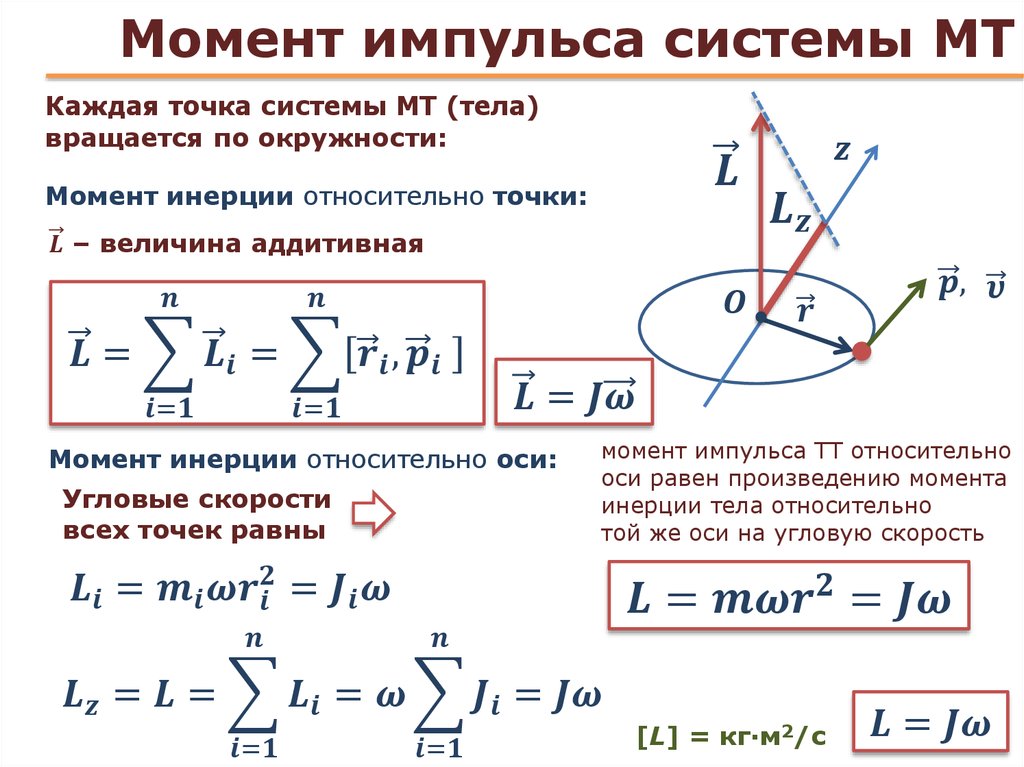 Вращательными аналогами силы, массы и ускорения являются крутящий момент, момент инерции и угловое ускорение соответственно.
Вращательными аналогами силы, массы и ускорения являются крутящий момент, момент инерции и угловое ускорение соответственно.
Содержимое
- 1 Пример
- 2 шт.
- 3 Особые случаи и другие факты
- 3.1 Формула плеча момента
- 3.2 Сила под углом
- 3.3 Статическое равновесие
- 3.4 Крутящий момент как функция времени
- 4 Крутящий момент машины
- 5 Связь между крутящим моментом, мощностью и энергией
- 5.1 Преобразование в другие единицы
- 5.2 Происхождение
- 6 См. также
- 7 Примечания
- 8 Каталожные номера
- 9 Внешние ссылки
- 10 кредитов
Связь между векторами силы, крутящего момента и количества движения во вращающейся системе
Пример
В случае рычага крутящий момент равен силе, приложенной к рычагу, умноженной на расстояние от точки опоры рычага. Например, сила в три ньютона, приложенная в двух метрах от точки опоры, создает такой же крутящий момент, как и сила в один ньютон, приложенная в шести метрах от точки опоры.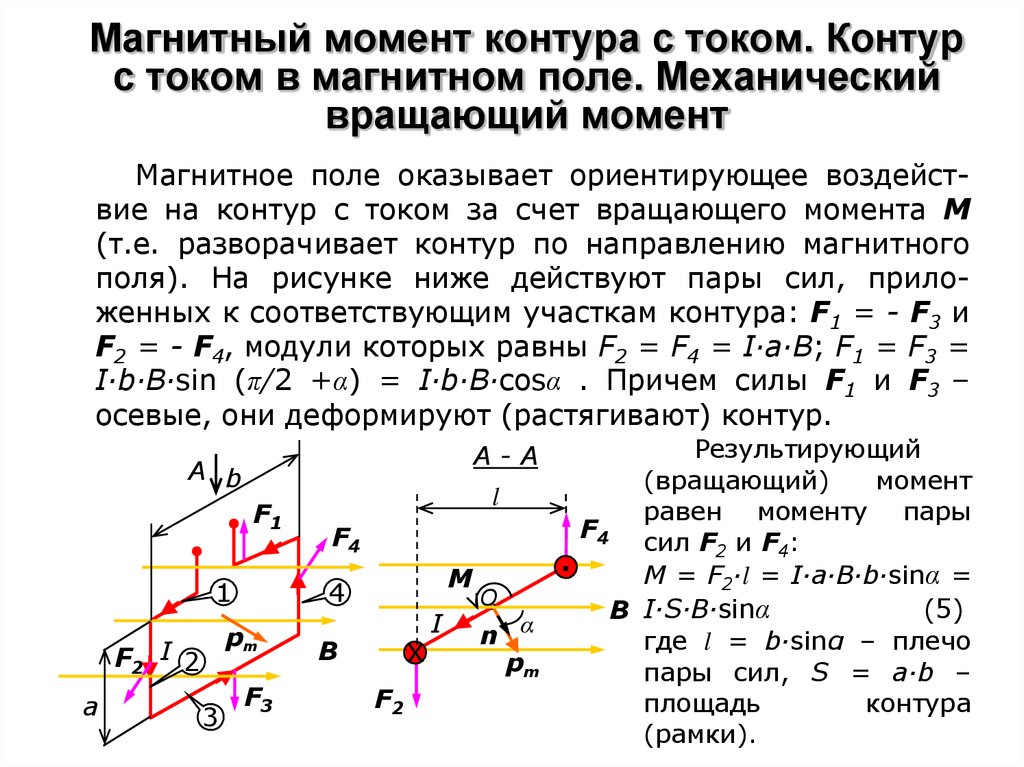 Это предполагает, что сила направлена под прямым углом к прямому рычагу.
Это предполагает, что сила направлена под прямым углом к прямому рычагу.
Направление крутящего момента можно определить с помощью правила правой руки: правой рукой согните пальцы в направлении вращения и вытяните большой палец так, чтобы он совпадал с осью вращения. Ваш большой палец указывает в направлении вектора крутящего момента. [1]
Математически крутящий момент на частице (имеющей положение r в некоторой системе отсчета) можно определить как векторное произведение:
- τ = r × F {\ displaystyle {\boldsymbol {\ tau}} = \ mathbf {r} \ times \ mathbf {F}}
где
- r вектор положения частицы
- F — сила, действующая на частицу,
или, в более общем смысле, крутящий момент можно определить как скорость изменения углового момента,
где
- L — вектор углового момента
- t обозначает время.

Как следствие любого из этих определений, крутящий момент представляет собой вектор, который указывает вдоль оси вращения, которое он стремится вызвать.
Единицы
Крутящий момент имеет размерность силы, умноженной на расстояние. Единицей СИ для крутящего момента является ньютон-метр (Н·м или Н·м). [2] В единицах измерения, принятых в Соединенных Штатах, он измеряется в фунтах-футах (lb-ft) (или фут-фунтах).
Хотя порядок «ньютонов» и «метров» математически взаимозаменяем, BIPM (Международное бюро мер и весов) указывает, что порядок должен быть N·m, а не m·N. [3]
Джоуль, который является единицей СИ для энергии или работы, также определяется как 1 Н·м, но эта единица не используется для крутящего момента. Поскольку энергию можно рассматривать как результат «расстояния между точками силы», энергия всегда является скаляром, тогда как крутящий момент представляет собой «поперечное расстояние силы», а значит, является (псевдо) векторной величиной.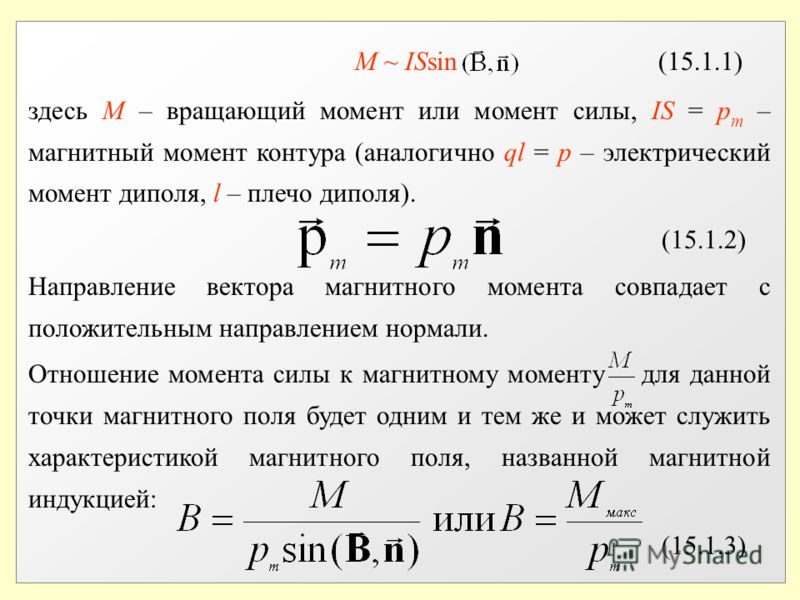 Конечно, размерная эквивалентность этих единиц не просто совпадение; крутящий момент в 1 Н·м, приложенный к полному обороту, потребует энергии ровно 2π джоулей. Математически,
Конечно, размерная эквивалентность этих единиц не просто совпадение; крутящий момент в 1 Н·м, приложенный к полному обороту, потребует энергии ровно 2π джоулей. Математически,
- E = τθ {\ displaystyle E = \ tau \ theta \}
, где
- E это энергия
- τ крутящий момент
- θ — угол перемещения в радианах.
Другие единицы крутящего момента, не входящие в систему СИ, включают «фунт-сила-фут», или «фут-фунт-сила», или «унция-сила-дюйм», или «метр-килограмм-сила».
Особые случаи и другие факты
Формула плеча момента
Диаграмма плеча момента
Очень полезный частный случай, часто приводимый в качестве определения крутящего момента в областях, отличных от физики, выглядит следующим образом:
- τ=(момент\плечо)×сила{\displaystyle {\boldsymbol {\tau}}=({\textrm{момент\плечо}})\times {\textrm{сила}}}
Конструкция «плеча момента» показано на рисунке ниже вместе с упомянутыми выше векторами r и F . Проблема с этим определением заключается в том, что оно дает не направление крутящего момента, а только его величину, и, следовательно, его трудно использовать в трехмерных случаях. Если сила перпендикулярна вектору смещения r плечо момента будет равно расстоянию до центра, а момент будет максимальным для данной силы. Уравнение для величины крутящего момента, возникающего от перпендикулярной силы:
Проблема с этим определением заключается в том, что оно дает не направление крутящего момента, а только его величину, и, следовательно, его трудно использовать в трехмерных случаях. Если сила перпендикулярна вектору смещения r плечо момента будет равно расстоянию до центра, а момент будет максимальным для данной силы. Уравнение для величины крутящего момента, возникающего от перпендикулярной силы:
- T = (расстояние \ до \ центра) × сила {\ displaystyle {\boldsymbol {T}} = ({\ textrm {расстояние \ до \ центра}}) \ times {\ textrm {force}}}
Например, если человек прикладывает усилие 10 Н к гаечному ключу длиной 0,5 м, крутящий момент составит 5 Н·м при условии, что человек тянет гаечный ключ, прилагая усилие перпендикулярно гаечному ключу.
Сила под углом
Если сила величины F находится под углом θ к плечу смещения длиной r (и в плоскости, перпендикулярной оси вращения), то из определения векторного произведения величина возникающего крутящего момента равна:
Статическое равновесие
Чтобы объект находился в статическом равновесии, необходима не только сумма сил равна нулю, но и сумма крутящих моментов (моментов) относительно любой точки.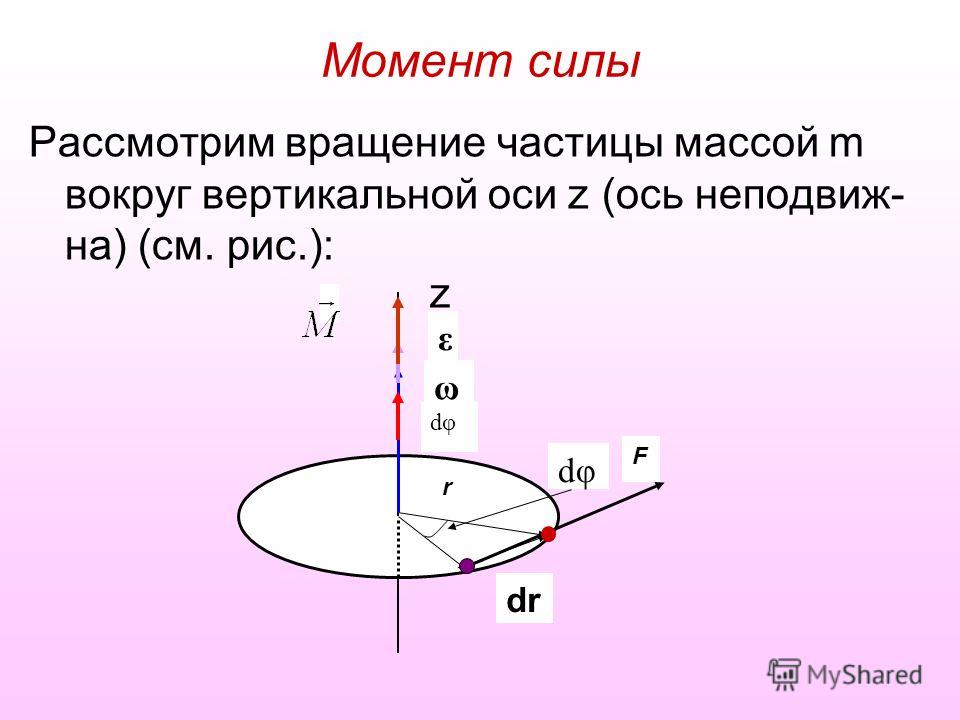 Для двухмерной ситуации с горизонтальными и вертикальными силами сумма требований к силам представляет собой два уравнения: Σ H = 0 и Σ V = 0, а для крутящего момента третье уравнение: Σ τ = 0. То есть для решения статически определимых задач равновесия в двух измерениях используем три уравнения.
Для двухмерной ситуации с горизонтальными и вертикальными силами сумма требований к силам представляет собой два уравнения: Σ H = 0 и Σ V = 0, а для крутящего момента третье уравнение: Σ τ = 0. То есть для решения статически определимых задач равновесия в двух измерениях используем три уравнения.
Крутящий момент как функция времени
Крутящий момент, вызванный двумя противодействующими силами F g и — F g , вызывает изменение углового момента L в направлении этого крутящего момента. Это приводит к прецессии верхней части.
Крутящий момент — это производная по времени от углового момента, так же как сила — это производная по времени от линейного количества движения: где
- L — угловой момент.
Угловой момент твердого тела можно записать через его момент инерции I {\ displaystyle {\boldsymbol {I}} \, \!} и его угловую скорость ω {\ displaystyle {\boldsymbol {\omega} }}:
- L = Iω {\ displaystyle \ mathbf {L} = I \, {\ boldsymbol {\ omega}} \, \!}
, поэтому, если !} постоянно,
- τ = Idωdt = Iα {\ displaystyle {\boldsymbol {\ tau}} = I {\ mathrm {d} {\boldsymbol {\omega}} \ over \ mathrm {d} t} = I {\boldsymbol { \alpha }}\,\!}
где α — угловое ускорение, величина, обычно измеряемая в радианах на секунду в квадрате.
Крутящий момент машины
Крутящий момент является частью базовой спецификации двигателя: выходная мощность двигателя выражается как его крутящий момент, умноженный на его скорость вращения. Двигатели внутреннего сгорания создают полезный крутящий момент только в ограниченном диапазоне скоростей вращения (обычно от 1000 до 6000 об / мин для небольшого автомобиля). Изменение выходного крутящего момента в этом диапазоне можно измерить с помощью динамометра и показать в виде кривой крутящего момента. Пик этой кривой крутящего момента обычно находится несколько ниже общего пика мощности. Пик крутящего момента не может по определению появляться при более высоких оборотах, чем пик мощности.
Понимание взаимосвязи между крутящим моментом, мощностью и частотой вращения двигателя имеет жизненно важное значение в автомобилестроении, поскольку оно связано с передачей мощности от двигателя через трансмиссию к колесам. Обычно мощность зависит от крутящего момента и частоты вращения двигателя.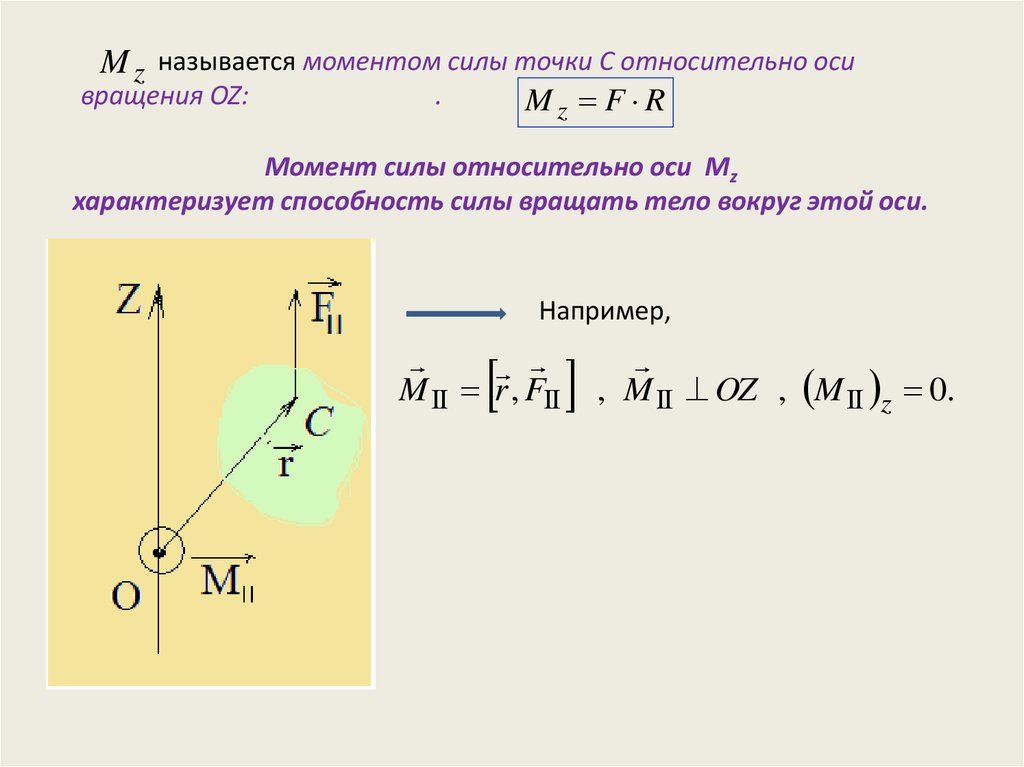 Зубчатая передача трансмиссии должна быть выбрана соответствующим образом, чтобы максимально использовать характеристики крутящего момента двигателя.
Зубчатая передача трансмиссии должна быть выбрана соответствующим образом, чтобы максимально использовать характеристики крутящего момента двигателя.
Паровые двигатели и электродвигатели, как правило, развивают максимальный крутящий момент вблизи нуля оборотов в минуту, при этом крутящий момент уменьшается по мере увеличения скорости вращения (из-за увеличения трения и других ограничений). Следовательно, эти типы двигателей обычно имеют совершенно другие типы трансмиссии, чем двигатели внутреннего сгорания.
Крутящий момент также является самым простым способом объяснить механическое преимущество почти каждой простой машины.
Соотношение между крутящим моментом, мощностью и энергией
Если сила действует на расстоянии, она совершает механическую работу. Точно так же, если крутящему моменту позволено действовать через расстояние вращения, он совершает работу. Мощность — это работа в единицу времени. Однако время и расстояние вращения связаны угловой скоростью, где каждый оборот приводит к тому, что длина окружности проходит под действием силы, создающей крутящий момент.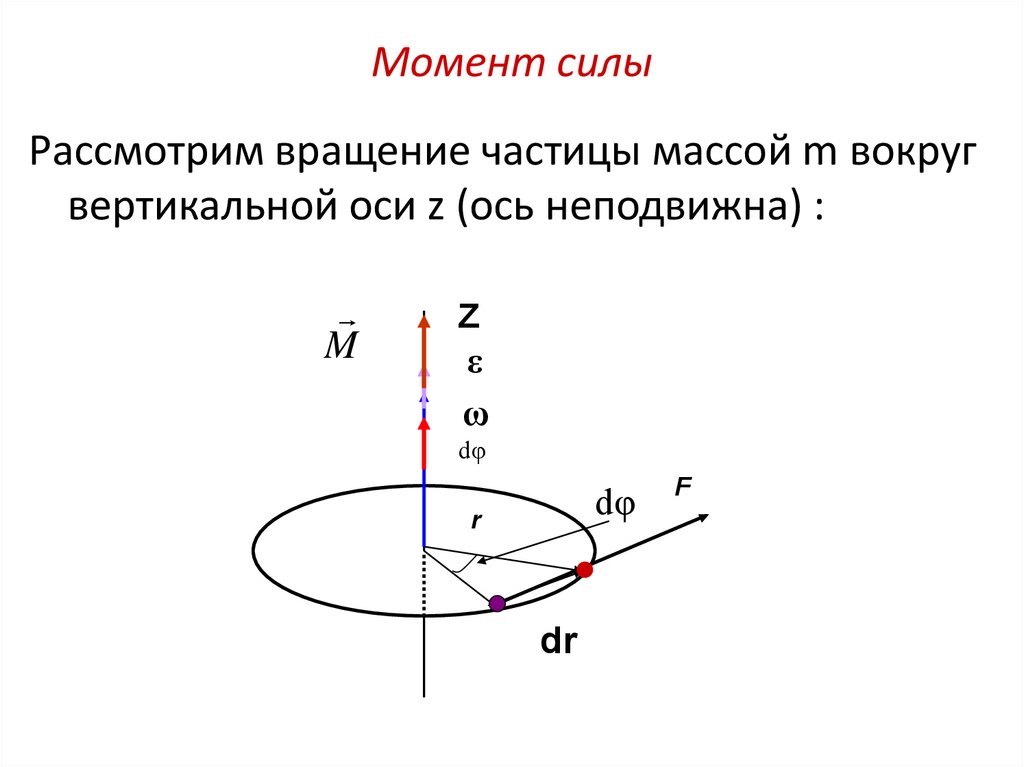 Это означает, что крутящий момент, вызывающий увеличение угловой скорости, совершает работу, и генерируемая мощность может быть рассчитана как:
Это означает, что крутящий момент, вызывающий увеличение угловой скорости, совершает работу, и генерируемая мощность может быть рассчитана как:
- Мощность = крутящий момент × угловая скорость {\ displaystyle {\ mbox {Мощность}} = {\ mbox {крутящий момент}} \ times {\ mbox {угловая скорость}} \,}
С правой стороны это является скалярным произведением двух векторов, дающим скаляр в левой части уравнения. Математически уравнение можно изменить, чтобы вычислить крутящий момент для заданной выходной мощности. Однако на практике нет прямого способа измерения мощности, тогда как крутящий момент и угловая скорость могут быть измерены напрямую.
На практике эту зависимость можно наблюдать на электростанциях, подключенных к крупной электрической сети. В такой схеме угловая скорость генератора определяется частотой сети, а выходная мощность установки определяется крутящим моментом, приложенным к оси вращения генератора.
Должны использоваться согласованные единицы измерения. Для метрических единиц СИ мощность — это ватты, крутящий момент — ньютон-метры, а угловая скорость — радианы в секунду (не об/мин и не обороты в секунду).
Для метрических единиц СИ мощность — это ватты, крутящий момент — ньютон-метры, а угловая скорость — радианы в секунду (не об/мин и не обороты в секунду).
Кроме того, единица измерения ньютон-метр эквивалентна джоулю, который является единицей энергии. Однако в случае крутящего момента единица присваивается вектору, тогда как для энергии она присваивается скаляру.
Преобразование в другие единицы
Для других единиц мощности, крутящего момента или угловой скорости в уравнение необходимо ввести коэффициент преобразования. Кроме того, если вместо угловой скорости (в радианах за время) используется скорость вращения (оборотов за время), необходимо добавить коэффициент преобразования 2π {\ displaystyle 2 \ pi}, поскольку существует 2π {\ displaystyle 2 \ pi} радиан. в революцию:
- Мощность = крутящий момент × 2π × скорость вращения {\ displaystyle {\ mbox {Power}} = {\ mbox {крутящий момент}} \ times 2 \ pi \ times {\ mbox {скорость вращения}} \,},
, где скорость вращения выражается в оборотах в единицу времени.
Полезная формула в единицах СИ:
- Мощность (кВт) = крутящий момент (Нм) × π × скорость вращения (об/мин) 30000 {\ displaystyle {\ mbox {Мощность (кВт)}} = {\ frac {{\ mbox {крутящий момент (Нм)}} \ times \pi \times {\mbox{скорость вращения (об/мин)}}}{30000}}}
Некоторые люди (например, американские автомобильные инженеры) используют лошадиные силы (британские механические единицы) для мощности, футо-фунты (lbf·ft) для крутящего момента и об/мин (оборотов в минуту) для угловой скорости. В результате формула меняется на:
- Мощность (л.с.) ≈ крутящий момент (фунт-сила-фут) × скорость вращения (об/мин) 5252 {\ displaystyle {\ mbox {Мощность (л. с.)}} \ приблизительно {\ frac {{\ mbox {крутящий момент (фунт-сила}} \ cdot {\mbox{ft}}}\times {\mbox{скорость вращения (об/мин)}}}{5252}}}
Этот коэффициент преобразования является приблизительным, поскольку в нем появляется трансцендентное число π; более точное значение — 5252,113 122 032 55.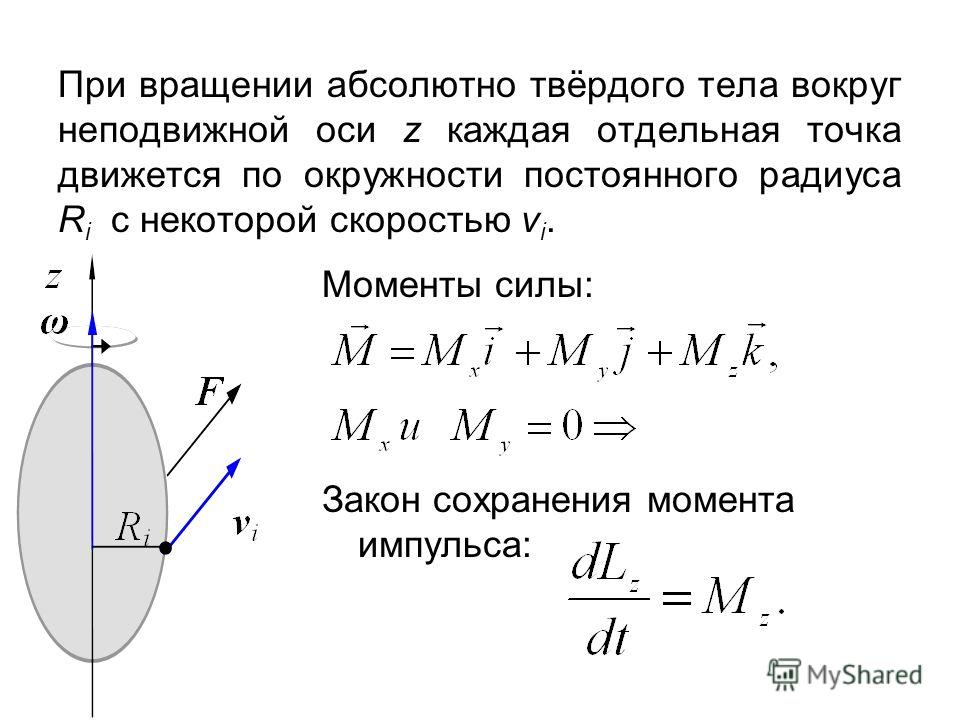 .. Оно, конечно, также меняется с определением лошадиных сил; например, используя метрическую мощность, она становится ~ 5180.
.. Оно, конечно, также меняется с определением лошадиных сил; например, используя метрическую мощность, она становится ~ 5180.
Использование других единиц (например, БТЕ/ч для мощности) потребует другого пользовательского коэффициента преобразования.
Вывод
Для вращающегося объекта линейное расстояние , проходимое по окружности в радианах вращения, является произведением радиуса на угловую скорость. То есть: линейная скорость = радиус x угловая скорость. По определению, линейное расстояние = линейная скорость х время = радиус х угловая скорость х время.
По определению крутящего момента: крутящий момент=сила x радиус. Мы можем изменить это, чтобы определить силу = крутящий момент / радиус. Эти два значения можно подставить в определение мощности:
- мощность = сила × линейное расстояние-время = (крутящий момент) × (r × угловая скорость × t) t = крутящий момент × угловая скорость {\ displaystyle {\ mbox {power}} = {\ frac {{\ mbox {force}} \times {\mbox{линейное расстояние}}}{\mbox{time}}}={\frac {\left({\frac {\mbox{крутящий момент}}{r}}\right)\times (r\times {\mbox{угловая скорость}}\times t}}{t}}={\mbox{крутящий момент}}\times {\mbox{угловая скорость}}}
Радиус r и время t выпали из уравнение.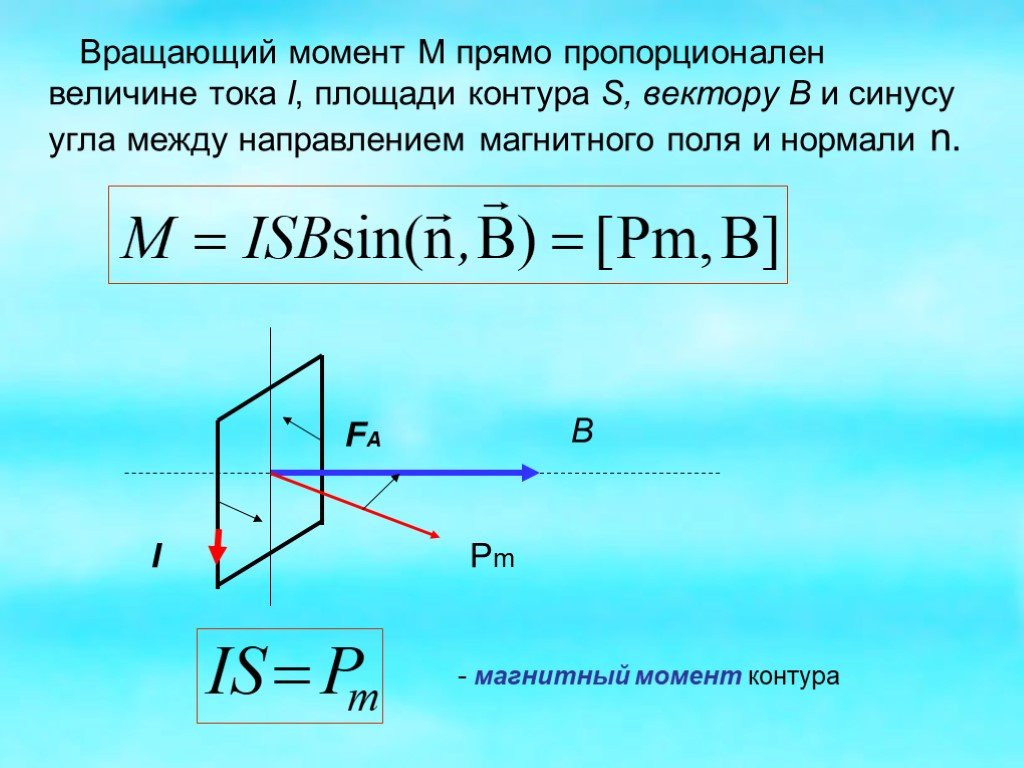 Однако угловая скорость должна быть в радианах из-за предполагаемой прямой зависимости между линейной скоростью и угловой скоростью в начале вывода. Если скорость вращения измеряется в оборотах в единицу времени, линейная скорость и расстояние увеличиваются пропорционально на 2π {\ displaystyle 2 \ pi} в приведенном выше выводе, чтобы получить:
Однако угловая скорость должна быть в радианах из-за предполагаемой прямой зависимости между линейной скоростью и угловой скоростью в начале вывода. Если скорость вращения измеряется в оборотах в единицу времени, линейная скорость и расстояние увеличиваются пропорционально на 2π {\ displaystyle 2 \ pi} в приведенном выше выводе, чтобы получить:
- мощность = крутящий момент × 2π × скорость вращения {\ displaystyle {\ mbox {мощность}} = {\ mbox {крутящий момент}} \ times 2 \ pi \ times {\ mbox {скорость вращения}} \,}
Если крутящий момент выражается в lbf·ft, а скорость вращения — в оборотах в минуту, приведенное выше уравнение дает мощность в ft·lbf/мин. Форма уравнения для лошадиных сил затем выводится путем применения коэффициента преобразования 33 000 фут·фунт-сила/мин на лошадиную силу:
- мощность = крутящий момент × 2π × скорость вращения⋅ft⋅lbfmin×лошадиная сила33000⋅ft⋅ lbfmin≈крутящий момент×RPM5252{\displaystyle {\mbox{power}}={\mbox{крутящий момент}}\times \ 2\pi \ \times {\mbox{скорость вращения}}\cdot {\frac {{\mbox{ft}}\cdot {\mbox{lbf}}}{\mbox{min}}}\times {\frac {\mbox{ лошадиных сил}} {33000 \ cdot {\ frac {{\ mbox {ft}} \ cdot {\ mbox {lbf}}}} {\ mbox {min}}}}} \ приблизительно {\ frac {{\ mbox {torque} }\times {\mbox{об/мин}}}{5252}}}
, потому что 5252,113 . .. = 33 0002 π {\ displaystyle 5252,113 … = {\ frac {33 000} {2 \ pi}} \,}.
.. = 33 0002 π {\ displaystyle 5252,113 … = {\ frac {33 000} {2 \ pi}} \,}.
См. также
- Угловой момент
- Механические работы
- Момент (физика)
- Статика
- Динамометрический ключ
- Torsion
Примечания
- ↑ Правило правой руки для Torque, HTTP-сервер Apache. Проверено 10 апреля 2008 г.
- ↑ Брошюра СИ Под ред. 8, раздел 5.1. Международное бюро мер и весов (2006 г.). Проверено 1 апреля 2007 г.
- ↑ Брошюра СИ Под ред. 8, раздел 2.2.2. Международное бюро мер и весов (2006 г.). Проверено 1 апреля 2007 г.
Ссылки
Ссылки ISBN поддерживают NWE за счет реферальных сборов
- Serway, Raymond A. и John W. Jewett. 2004. Физика для ученых и инженеров . 6-е изд. Брукс/Коул. ISBN 0534408427
- Типлер, Пол. 2004. Физика для ученых и инженеров: механика, колебания и волны, термодинамика . 5-е изд. WH Freeman.
 ISBN 0716708094.
ISBN 0716708094.
Внешние ссылки
Все ссылки получены 14 марта 2020 г.
- «Лошадиная сила и крутящий момент» — статья, показывающая, как мощность, крутящий момент и передача влияют на характеристики автомобиля.
- обсуждение крутящего момента и углового момента в онлайн-учебнике
- Интерактивное моделирование крутящего момента
Кредиты
Энциклопедия Нового Света Авторы и редакторы переписали и дополнили Википедия статья
в соответствии со стандартами New World Encyclopedia . Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с надлежащим указанием авторства. Упоминание должно осуществляться в соответствии с условиями этой лицензии, которая может ссылаться как на авторов New World Encyclopedia , так и на самоотверженных добровольных участников Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:
История более ранних вкладов википедистов доступна исследователям здесь:
- Крутящий момент история
История этой статьи с момента ее импорта в New World Encyclopedia :
- История «Torque»
Примечание. На использование отдельных изображений, лицензированных отдельно, могут распространяться некоторые ограничения.
В чем разница между моментом и крутящим моментом в приложениях линейного перемещения?
Даниэль Коллинз Оставить комментарий
В линейном движении мы часто имеем дело с приложениями, которые включают силы, приложенные на расстоянии от линейной направляющей, называемые консольными или моментными нагрузками. В этих случаях нас интересует допустимая нагрузка на направляющую или ее способность сопротивляться вращению. Но мы также имеем дело с компонентами, которые должен вращаться, когда сила приложена на расстоянии, например, вал шарико-винтовой передачи, передающий крутящий момент от двигателя для привода нагрузки.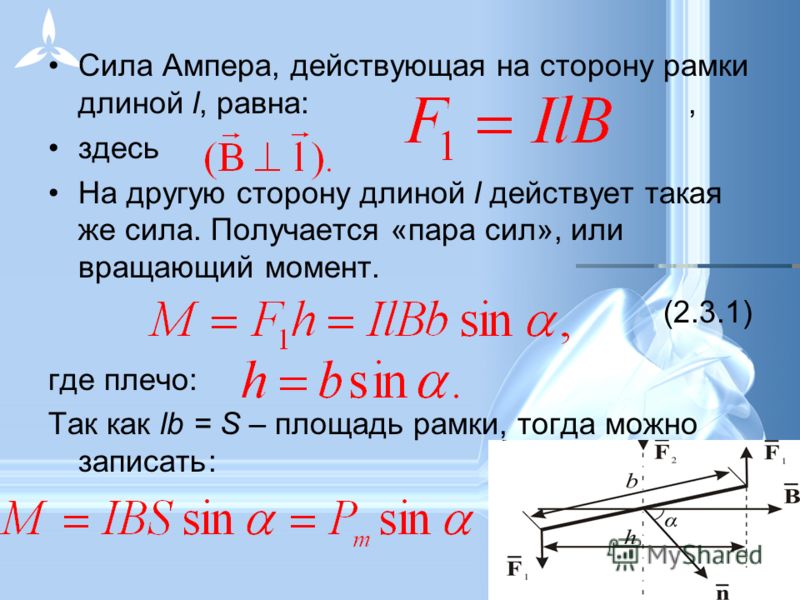 В этих случаях нас интересует количество крутящего момента, которое компонент может передать.
В этих случаях нас интересует количество крутящего момента, которое компонент может передать.
Момент на линейной направляющей и крутящий момент на валу вызываются силами, приложенными на расстоянии, и оба измеряются в ньютон-метрах (Нм) или фунт-футах (фунт-фут). Так в чем разница между моментом, приложенным к линейной направляющей, и моментом, приложенным к валу винта?
Основное различие между моментом и крутящим моментом можно найти, изучая реакцию объекта. Когда крутящий момент приложен к валу, вал вращается. Но когда к линейной направляющей приложена моментная нагрузка, направляющая остается неподвижной (если только момент не превышает номинальный допустимый момент направляющей, в этом случае направляющая может деформироваться или начать вращаться).
Крутящий момент производит вращение вокруг оси или точки вращения. Другими словами, крутящий момент вызывает изменение углового момента объекта, что приводит к вращению. С другой стороны, момент не вызывает изменения углового момента.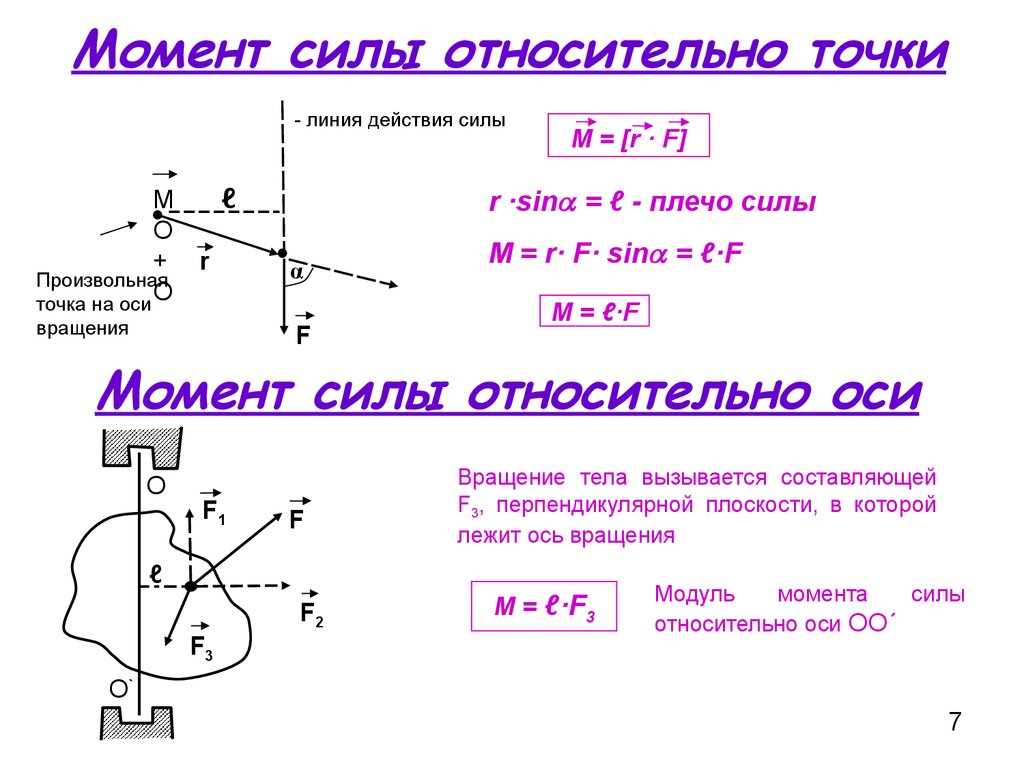 Тело, к которому приложен момент, остается неподвижным, а силы реакции, возникающие внутри объекта и его опорных элементов, препятствуют вращению объекта.
Тело, к которому приложен момент, остается неподвижным, а силы реакции, возникающие внутри объекта и его опорных элементов, препятствуют вращению объекта.
L = угловой импульс (KGM 2 /S)
I = Инерция (KGM 2 )
ω = Угловая Velocity (RAD /S)
ω = Angular Velocity (RAD /S)
ω = Angular Velocity (RAD /S)
ω = Angular (RAD /S)
ω = Angular (RAD /S)
ω = Angular. нагрузка, приложенная к консольной балке с опорой на конце, вызовет силу реакции и изгибающий момент на балке, но не изменит ее угловой момент и, следовательно, не заставит балку вращаться.
Сила (F), приложенная к консольной балке, вызывает силу реакции (R) и момент (M), но не заставляет балку вращаться. Крутящий момент иногда называют моментом силы, потому что так же, как приложенная сила заставляет объект двигаться линейно, приложенный крутящий момент заставляет объект вращаться вокруг оси или точки поворота.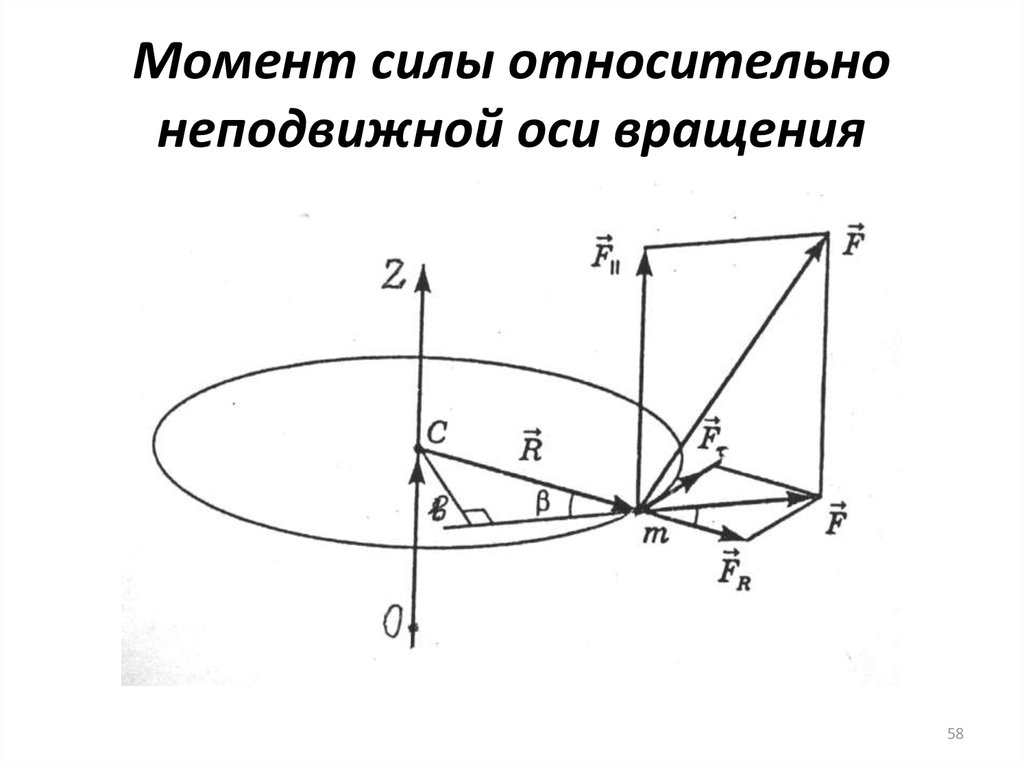



 Это стремление силы поворачивать тело описывается физической величиной — вращающим моментом или моментом силы. Сама сила, которая вызывает поворот или кручение, а также расстояние между точкой ее приложения и точкой вращения тела влияют на момент силы. В данном случае сила — векторная величина, поэтому важно также и направление силы, то есть угол между направлением силы и отрезком, соединяющим точку приложения силы и центр вращения тела. Если этот угол прямой, то есть сила приложена перпендикулярно отрезку, то момент силы — максимальный. По мере того, как сила становится параллельной отрезку, момент силы уменьшается. То есть, чем ближе угол к 0° или 180°, тем слабее момент силы, пока он не становится равным нулю, когда направление силы параллельно отрезку. Удобно представить момент силы, как комбинацию расстояния, на которое удалена сила от точки вращения, и силы, которая необходима, чтобы заставить тело вращаться с определенной интенсивностью.
Это стремление силы поворачивать тело описывается физической величиной — вращающим моментом или моментом силы. Сама сила, которая вызывает поворот или кручение, а также расстояние между точкой ее приложения и точкой вращения тела влияют на момент силы. В данном случае сила — векторная величина, поэтому важно также и направление силы, то есть угол между направлением силы и отрезком, соединяющим точку приложения силы и центр вращения тела. Если этот угол прямой, то есть сила приложена перпендикулярно отрезку, то момент силы — максимальный. По мере того, как сила становится параллельной отрезку, момент силы уменьшается. То есть, чем ближе угол к 0° или 180°, тем слабее момент силы, пока он не становится равным нулю, когда направление силы параллельно отрезку. Удобно представить момент силы, как комбинацию расстояния, на которое удалена сила от точки вращения, и силы, которая необходима, чтобы заставить тело вращаться с определенной интенсивностью. На рисунке силы F2, F3, и F5 создают наибольший момент силы.
На рисунке силы F2, F3, и F5 создают наибольший момент силы.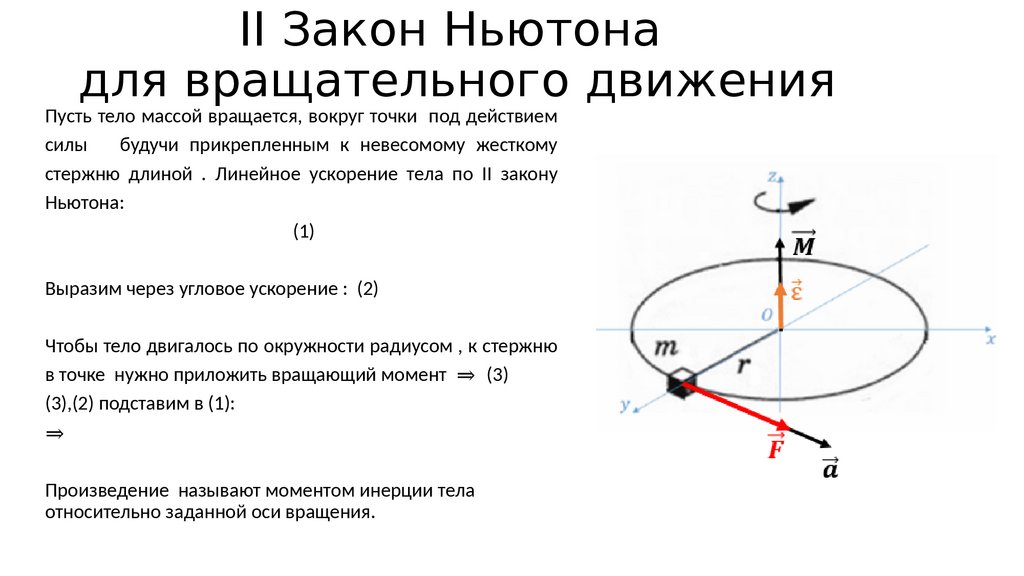 Поэтому чаще всего, когда силы человека или животного недостаточно для того или иного задания, которое включает вращение, используют рычаги и другие устройства, чтобы увеличить расстояние между силой и осью вращения, и тем самым увеличить момент силы. Например, чтобы повернуть мельницу или колесо, на которое наматывают цепь, чтобы поднять тяжелый мост, люди или животные вращают устройства с длинными ручками или рычагами. Длинные рычаги и ручки позволяют увеличить приложенное усилие. Это увеличение пропорционально расстоянию между осью вращения тела и точкой приложения силы.
Поэтому чаще всего, когда силы человека или животного недостаточно для того или иного задания, которое включает вращение, используют рычаги и другие устройства, чтобы увеличить расстояние между силой и осью вращения, и тем самым увеличить момент силы. Например, чтобы повернуть мельницу или колесо, на которое наматывают цепь, чтобы поднять тяжелый мост, люди или животные вращают устройства с длинными ручками или рычагами. Длинные рычаги и ручки позволяют увеличить приложенное усилие. Это увеличение пропорционально расстоянию между осью вращения тела и точкой приложения силы. Несмотря на эти ограничения, педали сильно облегчают передвижение на велосипеде. Конструкция велосипедных педалей настолько удобна, что некоторые люди, особенно в развивающихся странах, где не всегда есть доступ к новейшей технике, используют велосипедные педали в конструкции других устройств, где нужно ножное или ручное управление. Иногда такие педали устанавливают на инвалидные коляски, чтобы облегчить ручное кручение колес. В этом случае можно немного удлинить педали, чтобы увеличить момент силы, хотя это может несколько затруднить управление коляской.
Несмотря на эти ограничения, педали сильно облегчают передвижение на велосипеде. Конструкция велосипедных педалей настолько удобна, что некоторые люди, особенно в развивающихся странах, где не всегда есть доступ к новейшей технике, используют велосипедные педали в конструкции других устройств, где нужно ножное или ручное управление. Иногда такие педали устанавливают на инвалидные коляски, чтобы облегчить ручное кручение колес. В этом случае можно немного удлинить педали, чтобы увеличить момент силы, хотя это может несколько затруднить управление коляской. Если под рукой не оказалось гаечного ключа, можно использовать плоскогубцы. Их длинные ручки создают достаточно высокий момент силы, хотя иногда они сжимают гайку или винт недостаточно сильно, и могут их повредить.
Если под рукой не оказалось гаечного ключа, можно использовать плоскогубцы. Их длинные ручки создают достаточно высокий момент силы, хотя иногда они сжимают гайку или винт недостаточно сильно, и могут их повредить.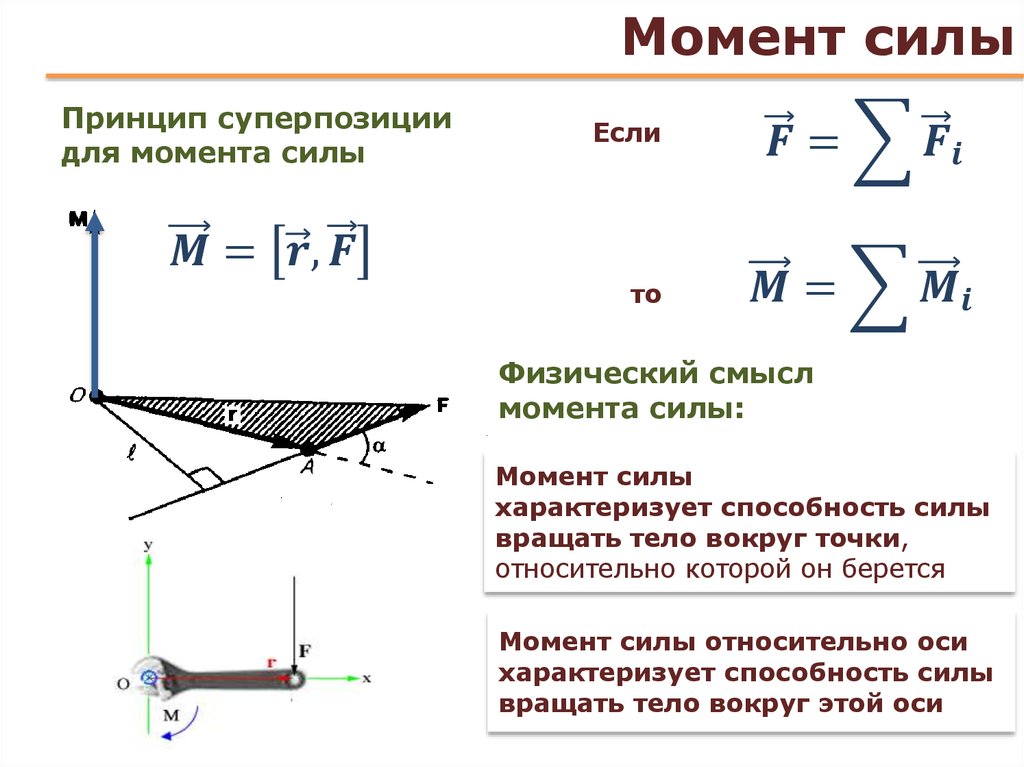
 Если эта энергия нужна для других целей, то момент силы, наоборот, замедляет скорость маховика, и вырабатывается энергия, которую потом используют по назначению. Маховики используют в случае, если источник энергии работает в прерывистом режиме, а энергия нужна постоянно. Именно так используют маховики в двигателях автомобилей, где энергия выделяется «вспышками», при сгорании топлива.
Если эта энергия нужна для других целей, то момент силы, наоборот, замедляет скорость маховика, и вырабатывается энергия, которую потом используют по назначению. Маховики используют в случае, если источник энергии работает в прерывистом режиме, а энергия нужна постоянно. Именно так используют маховики в двигателях автомобилей, где энергия выделяется «вспышками», при сгорании топлива.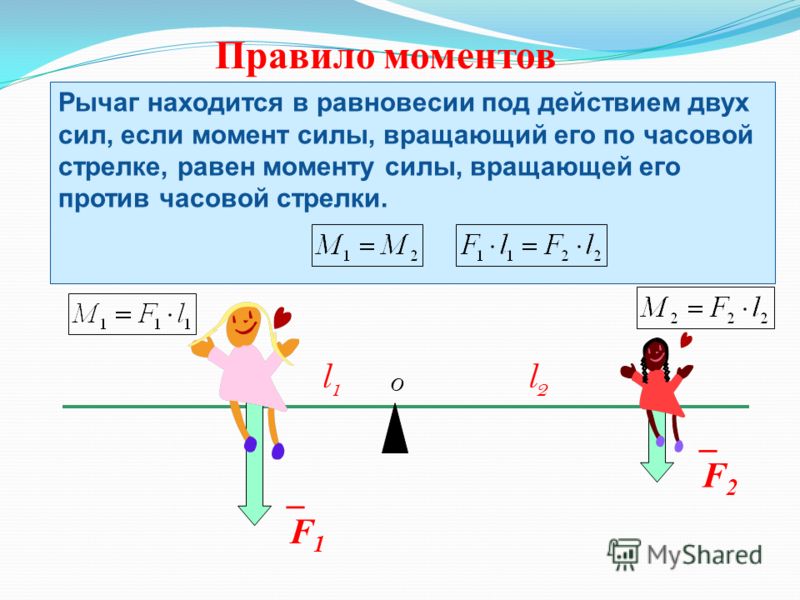 Если вес обоих детей приблизительно одинаков, то они легко могут качаться на таких качелях. Детям разного веса намного труднее — более тяжелый ребенок тянет качели со своей стороны вниз, а более легкому ребенку не хватает веса, чтобы опустить качели в свою сторону. Это происходит потому, что вес тяжелого ребенка производит больший момент силы. Чтобы решить эту проблему, большому ребенку нужно пересесть ближе к центру настолько, насколько его вес превышает вес второго ребенка. Например, если большой ребенок в три раза тяжелее, то пересесть ему нужно в три раза ближе, и тогда качели придут в равновесие.
Если вес обоих детей приблизительно одинаков, то они легко могут качаться на таких качелях. Детям разного веса намного труднее — более тяжелый ребенок тянет качели со своей стороны вниз, а более легкому ребенку не хватает веса, чтобы опустить качели в свою сторону. Это происходит потому, что вес тяжелого ребенка производит больший момент силы. Чтобы решить эту проблему, большому ребенку нужно пересесть ближе к центру настолько, насколько его вес превышает вес второго ребенка. Например, если большой ребенок в три раза тяжелее, то пересесть ему нужно в три раза ближе, и тогда качели придут в равновесие.
 точка опоры в них посередине, сила приложена на одном конце, а сопротивление возникает на другом конце. Ось вращения в рычаге второго рода находится с одного края рычага, и рядом с ним возникает сопротивление. Сила прилагается к такому рычагу на другом конце. Рычаг третьего рода устроен похоже, но ближе к центру вращения, находящемуся у конца рычага, не сопротивление, а сила, прикладываемая к рычагу. Сопротивление возникает на другом конце рычага.
точка опоры в них посередине, сила приложена на одном конце, а сопротивление возникает на другом конце. Ось вращения в рычаге второго рода находится с одного края рычага, и рядом с ним возникает сопротивление. Сила прилагается к такому рычагу на другом конце. Рычаг третьего рода устроен похоже, но ближе к центру вращения, находящемуся у конца рычага, не сопротивление, а сила, прикладываемая к рычагу. Сопротивление возникает на другом конце рычага.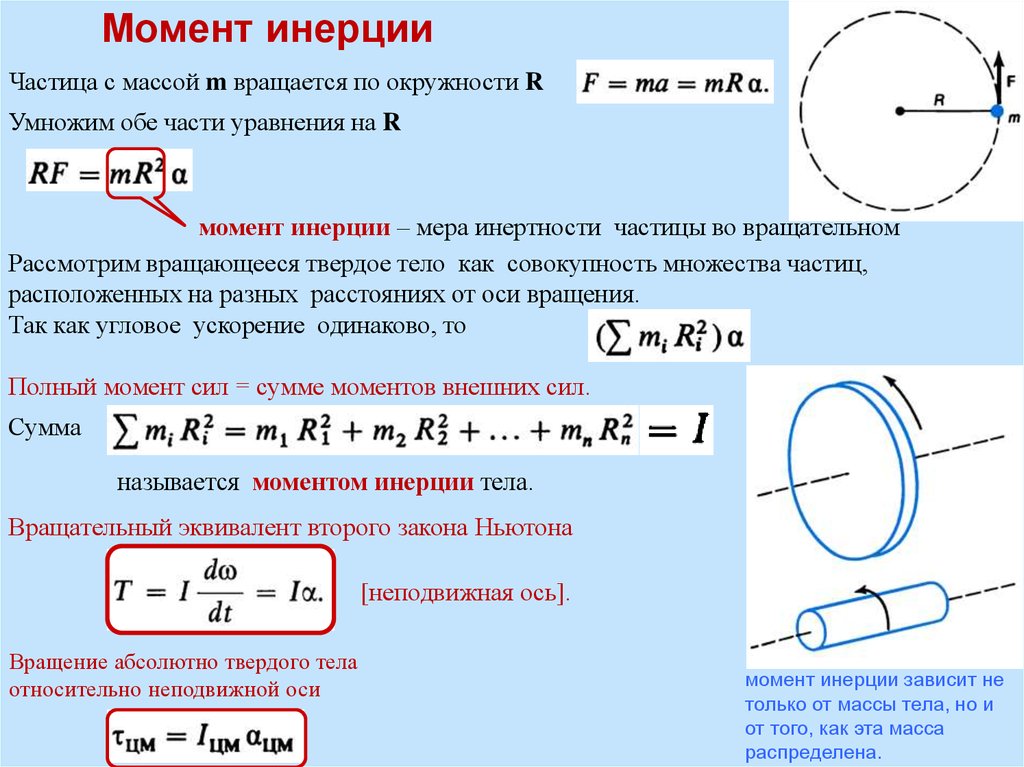 В некоторых случаях к ножницам добавляют пружину, которая делает их более удобными в использовании. Так, например, устроен садовый секатор. Кроме этого у специализированных ножниц бывают и другие особенности. В медицине используют ножницы с закругленными, тупыми и острыми концами, в зависимости от их назначения. В отличие от скальпеля, ими удобнее работать и у них механическое преимущество над скальпелем, хотя скальпель тоже широко используется, так как в некоторых случаях он удобнее ножниц. Медицинские ножницы, предназначенные для использования врачами скорой помощи, закруглены на конце, чтобы можно было разрезать ими одежду, не повредив кожи. Некоторые медицинские ножницы — очень маленькие. Например, офтальмологические хирургические ножницы могут быть всего 6 сантиметров длиной, с лезвием до 2 сантиметров, и даже короче.
В некоторых случаях к ножницам добавляют пружину, которая делает их более удобными в использовании. Так, например, устроен садовый секатор. Кроме этого у специализированных ножниц бывают и другие особенности. В медицине используют ножницы с закругленными, тупыми и острыми концами, в зависимости от их назначения. В отличие от скальпеля, ими удобнее работать и у них механическое преимущество над скальпелем, хотя скальпель тоже широко используется, так как в некоторых случаях он удобнее ножниц. Медицинские ножницы, предназначенные для использования врачами скорой помощи, закруглены на конце, чтобы можно было разрезать ими одежду, не повредив кожи. Некоторые медицинские ножницы — очень маленькие. Например, офтальмологические хирургические ножницы могут быть всего 6 сантиметров длиной, с лезвием до 2 сантиметров, и даже короче. Чаще всего его используют, чтобы вынуть забитые гвозди, или разобщить два предмета, соединенных клеем, гвоздями, скрепками, и аналогичными способами. Лом получил дурную репутацию, как инструмент воров, взломщиков, и других преступников, хотя на самом деле преступники используют любые подручные материалы и инструменты, лишь бы они помогли добиться конечного результата.
Чаще всего его используют, чтобы вынуть забитые гвозди, или разобщить два предмета, соединенных клеем, гвоздями, скрепками, и аналогичными способами. Лом получил дурную репутацию, как инструмент воров, взломщиков, и других преступников, хотя на самом деле преступники используют любые подручные материалы и инструменты, лишь бы они помогли добиться конечного результата.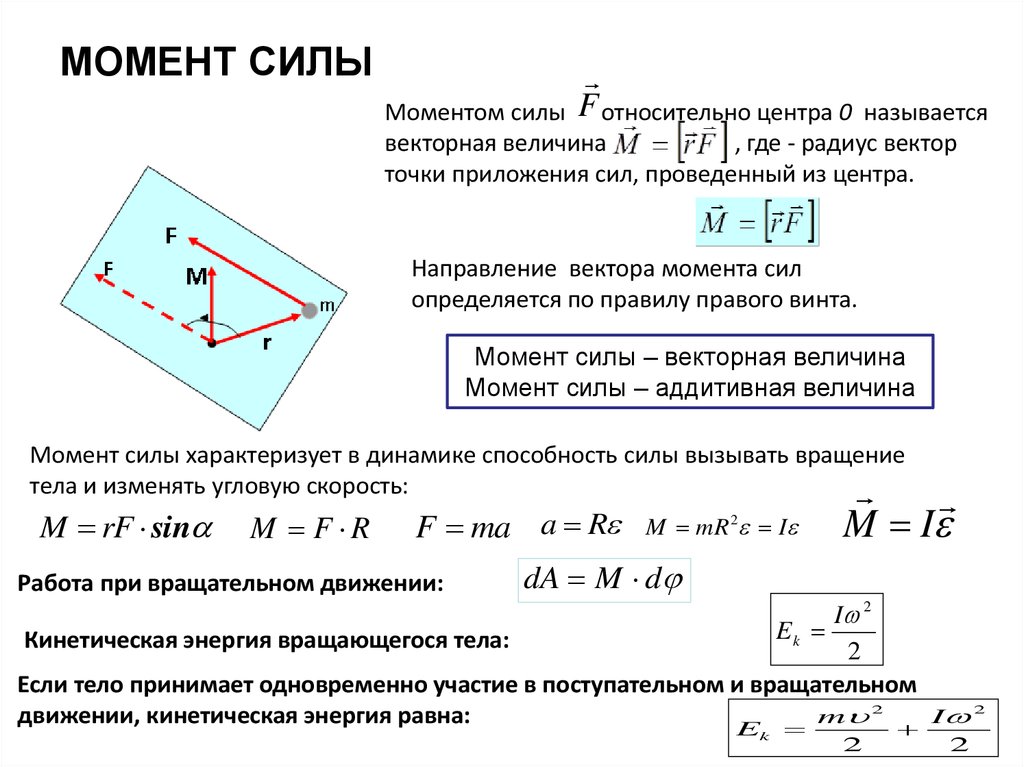 Щипцы чаще всего делают из металла, хотя иногда встречаются изделия и из других материалов, например из дерева. Щелкунчики — стилизованные щипцы, сделанные из дерева, и украшенные наподобие кукол. Раньше их использовали по прямому назначению, но сейчас это по большей части украшения. Чаще всего их делают в форме солдат, королей, и других фигурок. В США и Канаде такие фигурки часто используют как новогодние украшения. Считается, что щелкунчиков начали делать в лесистых районах Германии. Их там делают на продажу как сувениры и до сих пор. Сейчас для расщепления орехов чаще всего используют обычные щипцы, а не щелкунчиков. Такие щипцы похожи на щипцы для расщепления клешней крабов и омаров. Кстати, сами крабовые и омаровые клешни — тоже рычаги второго ряда, и работают по тому же принципу, что и щипцы для орехов.
Щипцы чаще всего делают из металла, хотя иногда встречаются изделия и из других материалов, например из дерева. Щелкунчики — стилизованные щипцы, сделанные из дерева, и украшенные наподобие кукол. Раньше их использовали по прямому назначению, но сейчас это по большей части украшения. Чаще всего их делают в форме солдат, королей, и других фигурок. В США и Канаде такие фигурки часто используют как новогодние украшения. Считается, что щелкунчиков начали делать в лесистых районах Германии. Их там делают на продажу как сувениры и до сих пор. Сейчас для расщепления орехов чаще всего используют обычные щипцы, а не щелкунчиков. Такие щипцы похожи на щипцы для расщепления клешней крабов и омаров. Кстати, сами крабовые и омаровые клешни — тоже рычаги второго ряда, и работают по тому же принципу, что и щипцы для орехов.

 Чтобы заставить этот рычаг двигаться, силу прикладывают возле центра вращения. При этом сопротивление образуется на другом конце. В случае с ракеткой и битой, сопротивление — в месте, где они соприкасаются с мячом. Удочка — тоже рычаг третьего рода, и сила прикладывается к ней в районе запястья.
Чтобы заставить этот рычаг двигаться, силу прикладывают возле центра вращения. При этом сопротивление образуется на другом конце. В случае с ракеткой и битой, сопротивление — в месте, где они соприкасаются с мячом. Удочка — тоже рычаг третьего рода, и сила прикладывается к ней в районе запястья. Архимед говорил, что он может сдвинуть Землю, если встанет достаточно далеко от нее, и возьмет длинный рычаг. Это утверждение основано на таком же принципе. После того, как мы поднимем наш 20-ти-киллограммовый камень с помощью лома — рычага первого рода — мы можем погрузить его на тачку — рычаг второго рода — и отвезти, куда необходимо, поднимая за ручки руками — рычагами третьего рода.
Архимед говорил, что он может сдвинуть Землю, если встанет достаточно далеко от нее, и возьмет длинный рычаг. Это утверждение основано на таком же принципе. После того, как мы поднимем наш 20-ти-киллограммовый камень с помощью лома — рычага первого рода — мы можем погрузить его на тачку — рычаг второго рода — и отвезти, куда необходимо, поднимая за ручки руками — рычагами третьего рода. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
 », то есть «…умножить на десять в степени…». Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах.
», то есть «…умножить на десять в степени…». Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах. com на YouTube
com на YouTube
 ISBN 0716708094.
ISBN 0716708094.