Ошибка

• Автомобиль — модели, марки
• Устройство автомобиля
• Ремонт и обслуживание
• Тюнинг

• Аксессуары и оборудование
• Компоненты
• Безопасность
• Физика процесса

• Новичкам в помощь
• Приглашение
• Официоз (компании)
• Пригородные маршруты

• Персоны
• Наши люди
• ТЮВ
• Эмблемы

•  
• А
• Б
• В
• Г
• Д
• Е
• Ё
• Ж
• З
• И
• Й
• К
• Л
• М
• Н
• О
• П
• Р
• С
• Т
• У
• Ф
• Х
• Ц
• Ч
• Ш
• Щ
• Ъ
• Ы
• Ь
• Э
• Ю
• Я

Навигация

• Заглавная страница
• Сообщество
• Текущие события
• Свежие правки
• Случайная статья
• Справка

Личные инструменты

• Представиться системе

Инструменты

• Спецстраницы

Пространства имён

• Служебная страница

Просмотры

Перейти к: навигация, поиск

Запрашиваемое название страницы неправильно, пусто, либо неправильно указано межъязыковое или интервики название. Возможно, в названии используются недопустимые символы.

Возврат к странице Заглавная страница.

Если Вы обнаружили ошибку или хотите дополнить статью, выделите ту часть текста статьи, которая нуждается в редакции, и нажмите Ctrl+Enter. Далее следуйте простой инструкции.

формула, направление, единицы измерения и физический смыл

От Masterweb

31.01.2019 15:00

При изучении динамики в физике большое внимание уделяют рассмотрению законов Ньютона применительно к прямолинейному перемещению тел. Тем не менее вращательное движения также играет важную роль в технике и природе. В данной статье ответим на вопрос, связанный с динамикой вращательного движения, разберемся, что такое момент сил.

О какой величине пойдет речь?

Начнем статью с определения, что такое момент силы. Под ним понимают физическую величину, которая получается, если умножить радиус-вектор на вектор силы. В данном случае речь идет о векторном умножении. Математически момент M¯ записывается так:

M¯ = [r¯*F¯].

Поясним значение каждого множителя в правой части равенства. Радиус-вектор r¯ — это вектор, который направлен от оси вращения к точке приложения внешней силы F¯. Последняя, собственно, действуя на систему, имеющую ось вращения, заставляет ее совершать вращательные движения.

В соответствии с определением векторного произведения, абсолютное значение момента силы может быть вычислено по такой формуле:

M = r*F*sin(φ).

Здесь φ — это угол между векторами r¯ и F¯. Если рассмотреть с точки зрения геометрии эту ситуацию, то можно записать формулу выше в виде:

M = d*F*, где d = r*sin(φ).

Величина d называется плечом момента или плечом силы. Она равна дистанции между осью вращения и вектором силы F¯. От значения плеча зависит возможность силы создать вращательный момент.

Направление величины M¯

Разобравшись, что такое момент силы в физике, необходимо пояснить, куда он направлен.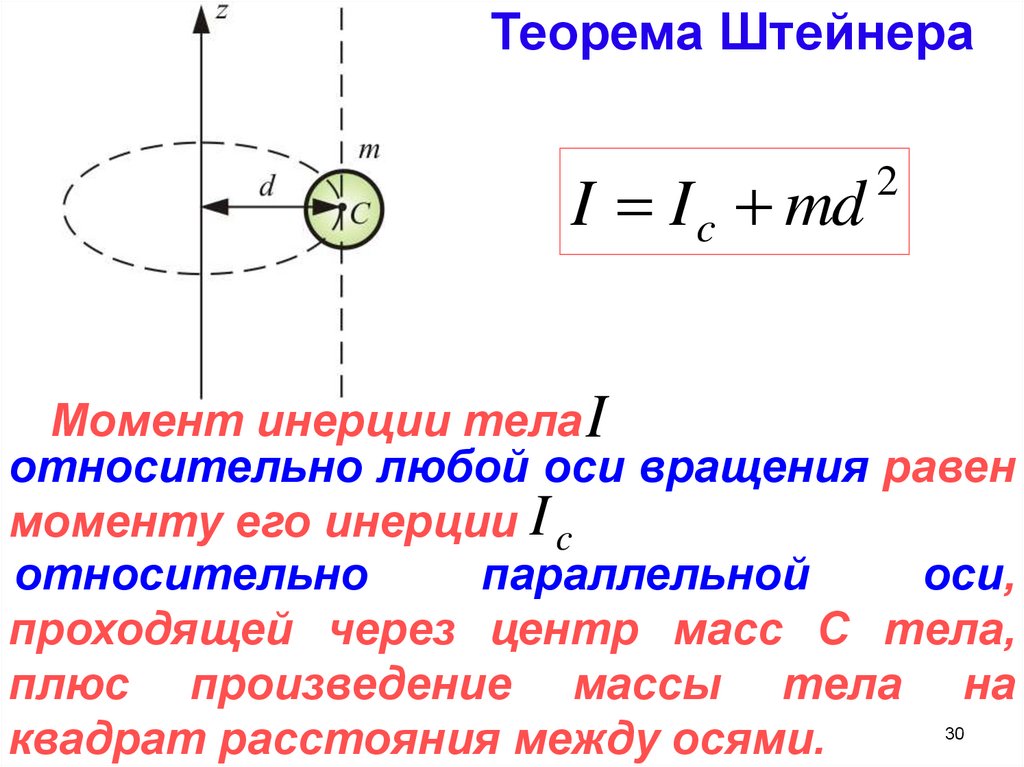 Как известно, результатом векторного произведения является направленный отрезок, перпендикулярный плоскости, в которой лежат исходные вектора. Например, если речь идет о горизонтальном вращающемся диске на вертикальной оси, то M¯ будет направлен вдоль этой оси. Вверх или вниз — это уже зависит от направления действующей силы. Определить это можно по правилу правой руки: направляя четыре пальца правой руки по ходу вектора r¯ к вектору F¯, оттопыренный большой палец покажет, куда действует момент силы.

Существует еще один способ определения направления величины M¯. Для этого следует представить, что если смотреть с конца вектора M¯ на приложенную силу, то система должна поворачиваться против часовой стрелки. Если же она поворачивается по часовой стрелки, значит, момент направлен в противоположную сторону.

Во время решения задач полагают, что если сила создает вращение против часовой стрелки, то такой момент считается положительным, и наоборот.

Единицы измерения

Раскрывая вопрос о том, что такое момент силы, следует несколько слов сказать о его единицах измерения.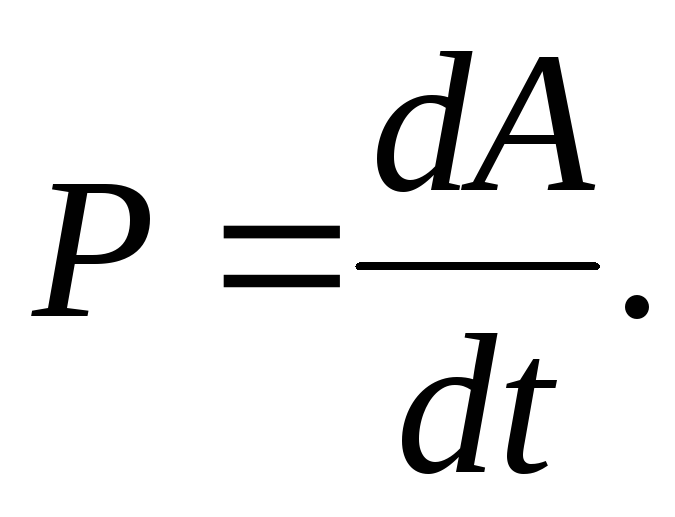 Если исходить из формулы, то можно сказать, что рассматриваемая величина измеряется в ньютонах на метр и записывается сокращенно Н*м. Однако, это единица измерения совпадает с работой в физике, которая выражается в джоулях (Дж). Для описания момента сил используют именно Н*м, поскольку джоуль по своему смыслу является энергетической величиной, а не силовой характеристикой.

Если момент силы, действуя на систему, приводит к ее повороту на некоторый угол θ, то произведение этого угла в радианах на M в Н*м даст величину работы в джоулях.

Физический смысл

Выше мы дали математическое определение, что такое момент силы, но практически ничего не сказали о том, какой смысл он несет. Изучаемая величина определяет возможность совершения поворота в системе. Чтобы понять лучше, о какой возможности идет речь, рассмотрим следующий пример: известно, что дверь все открывают за ручку. Сделать это может даже ребенок, поскольку плечо силы d велико, а значит, большим будет и создаваемый крутящий момент. Предлагается читателю попытаться открыть дверь, надавливая на нее близко от петель. В этом случае выполнить задачу гораздо труднее, поскольку для создания того же крутящего момента, необходимо приложить большую силу, компенсирующую маленькое плечо.

Другими примерами момента силы в действии является использование гаечных ключей или удержание человеком веса на вытянутой или на прижатой к телу руке.

калькулятор крутящего момента

, созданный Bogna Szyk

, рассмотрено Стивеном Вудлингом

Последнее обновление: 20 июня 2022 г.

Соглашение:
• Уравнение крутящего момента
• Как вычислять крутящий момент
• FAQ

Это крутой момент. найти крутящий момент, возникающий при вращении тела. Что именно представляет собой этот крутящий момент? Представьте себе объект, который может вращаться вокруг некоторой точки, называемой точкой вращения. Если приложить силу на некотором расстоянии от точки опоры, то хоть сила и будет действовать по прямой линии, объект начнет вращаться. Продолжайте читать, если вы хотите узнать, как рассчитать крутящий момент, и получить подробное объяснение формулы крутящего момента.

Уравнение крутящего момента

Крутящий момент (склонность объекта к вращению) зависит от трех разных факторов:

τ = rFsin(θ)

где:

• r расстояние между плечом рычага точка поворота и точка приложения силы;
• F — сила, действующая на объект;
• θ — угол между вектором силы и плечом рычага. Обычно он равен 90°; и
• τ — крутящий момент. Единицами крутящего момента являются ньютон-метры (обозначение: Н·м).

Представьте, что вы пытаетесь открыть дверь. Точка поворота — это просто место, где расположены петли. Чем ближе вы к петлям, тем большее усилие вы должны приложить. Однако, если вы используете ручку, плечо рычага увеличится, и дверь откроется с меньшим усилием.

Не путайте это понятие с центробежной силой — центробежная сила направлена ​​к точке поворота, параллельно плечу рычага. Такая сила не вызывает крутящего момента (это можно проверить, подставив угол 0° в формулу крутящего момента).

Как рассчитать крутящий момент

1. Начните с определения силы, действующей на объект. Предположим, что F = 120 N .
2. Выберите длину плеча рычага. В нашем примере r = 0,5 м .
3. Выберите угол между вектором силы и плечом рычага. Если он не равен 90° по умолчанию, откройте расширенный режим калькулятора, чтобы изменить его. Предположим, что θ = 90° . Используйте расширенный режим для изменения значения θ.
4. Введите эти значения в наш калькулятор крутящего момента. В нем используется уравнение крутящего момента: τ = rFsin(θ) = 0,5 * 120 * sin(90°) = 60 Н·м .
5. Калькулятор крутящего момента также может работать в обратном направлении, определяя силу или плечо рычага, если задан крутящий момент.

Если вы хотите узнать больше о концепции силы и втором законе Ньютона, попробуйте калькулятор ускорения.

Часто задаваемые вопросы

Как рассчитать крутящий момент?

Для расчета крутящего момента следуйте приведенным инструкциям:

1. Узнать величину приложенной силы, F .

2. Измерьте расстояние , r , между точкой вращения и точкой приложения силы.

3. Определите угол θ между направлением приложенной силы и вектором между точкой приложения силы и точкой поворота.

4. Умножение r на F и sin θ и вы получите крутящий момент.

Что такое единица крутящего момента в системе СИ?

Единицей крутящего момента в системе СИ является ньютон-метр или Н⋅м . Чтобы выразить крутящий момент в имперских единицах , мы используем фунт-сила-фут или lbf·ft .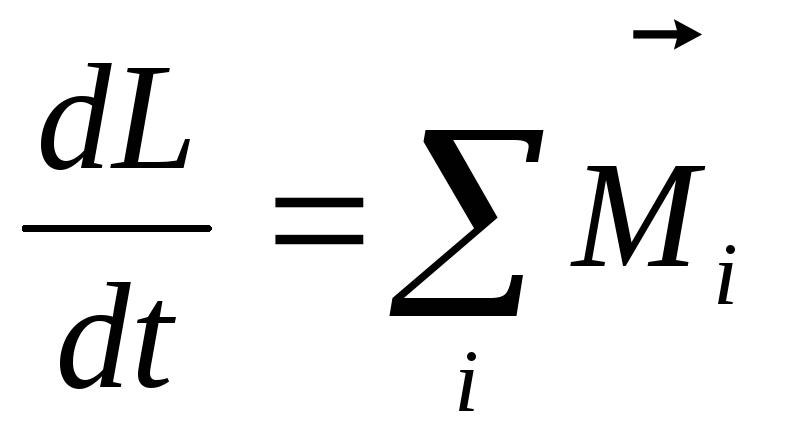

Какова формула измерения крутящего момента?

Величина крутящего момента равна произведению величины силы на плечо рычага. Формула измерения силы — [M¹L¹T⁻²], а для плеча рычага — [L]. Следовательно, 9Размерная формула 0085 для крутящего момента равна [M¹L²T⁻²] .

Как преобразовать крутящий момент в lbf·ft из Н⋅м?

Как мы знаем, 1 фунт-сила (фунт-сила) = 4,448 ньютона (Н) и 1 фут (фут) = 0,3048 метра (м). Следовательно, To преобразует крутящий момент из Н⋅м в фунт-сила-фут, разделив на 1,355818 или умножив на 0,737562.

Bogna Szyk

τ = rFsin(θ)

Расстояние (r)

Сила (F)

Крутящий момент (τ)

92002 Калькуляторы периодического и вращательного движения0003

Угловое ускорениеУгловое смещениеУгловая частота… Еще 17

10.7: Крутящий момент — Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

• Идентификатор страницы

  4032

• ОпенСтакс
• ОпенСтакс

Цели обучения

• Описать, как величина крутящего момента зависит от величины плеча рычага и угла, который вектор силы образует с плечом рычага
• Определите знак (положительный или отрицательный) крутящего момента с помощью правила правой руки
• Рассчитайте отдельные крутящие моменты относительно общей оси и просуммируйте их, чтобы найти чистый крутящий момент

Важной величиной для описания динамики вращающегося твердого тела является крутящий момент.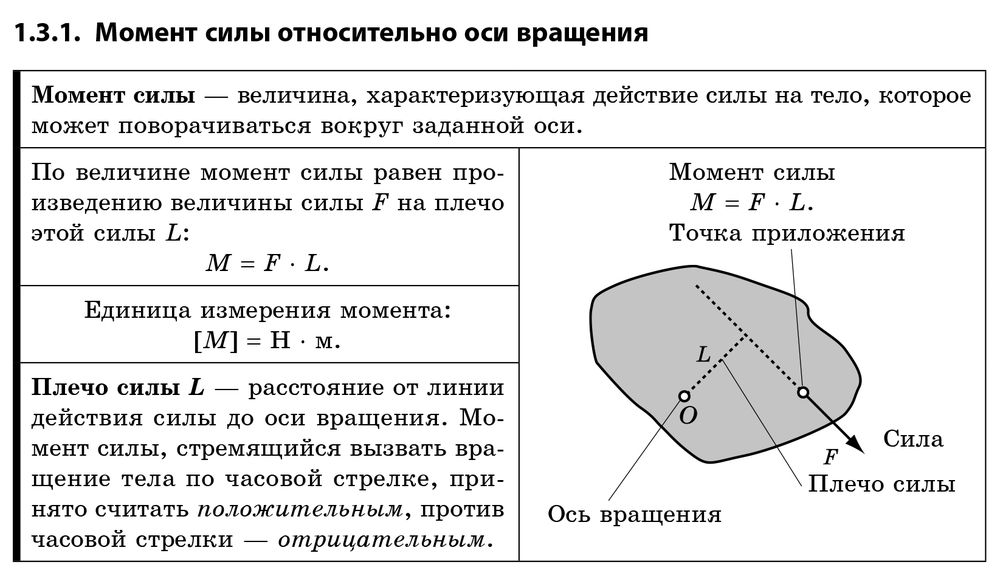 Мы видим применение крутящего момента во многих отношениях в нашем мире. У всех нас есть интуитивное представление о крутящем моменте, например, когда мы используем большой гаечный ключ, чтобы открутить упрямый болт. Крутящий момент действует невидимым образом, например, когда мы нажимаем на педаль акселератора в автомобиле, заставляя двигатель передавать дополнительный крутящий момент на трансмиссию. Или каждый раз, когда мы перемещаем свое тело из положения стоя, мы прикладываем крутящий момент к нашим конечностям. В этом разделе мы определяем крутящий момент и аргументируем уравнение для расчета крутящего момента для твердого тела с вращением с фиксированной осью.

Определение крутящего момента

До сих пор мы определили множество переменных, которые являются вращательными эквивалентами своих поступательных аналогов. Рассмотрим, каким должен быть аналог силы. Поскольку силы изменяют поступательное движение объектов, вращательный аналог должен быть связан с изменением вращательного движения объекта вокруг оси.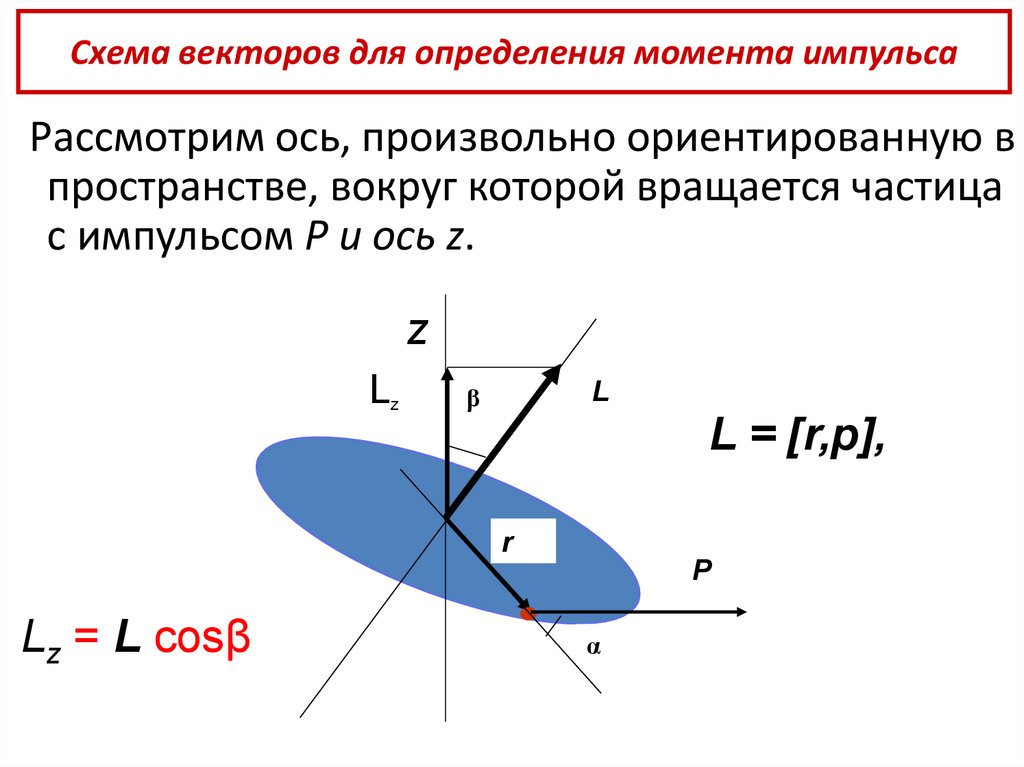 Мы называем этот вращательный аналог крутящим моментом .

В повседневной жизни мы постоянно вращаем объекты вокруг оси, поэтому интуитивно мы уже многое знаем о крутящем моменте. Рассмотрим, например, как мы поворачиваем дверь, чтобы открыть ее. Во-первых, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям; более эффективно повернуть дверь, если мы нажмем далеко от петель. Во-вторых, мы знаем, что толкать надо перпендикулярно плоскости двери; если мы нажмем параллельно плоскости двери, мы не сможем ее повернуть. В-третьих, чем больше сила, тем эффективнее она открывает дверь; чем сильнее вы нажимаете, тем быстрее открывается дверь. Первый пункт подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; второй подразумевает, что эффективность зависит от угла приложения силы; третий подразумевает, что величина силы также должна быть частью уравнения. Обратите внимание, что при вращении в плоскости крутящий момент имеет два возможных направления. Крутящий момент либо по часовой стрелке, либо против часовой стрелки относительно выбранной точки поворота. На рисунке \(\PageIndex{1}\) показано вращение против часовой стрелки.

Рисунок \(\PageIndex{1}\): Крутящий момент — это эффективность силы при повороте или скручивании, показанная здесь для вращения двери на петлях (если смотреть сверху). Крутящий момент имеет как величину, так и направление. (a) Крутящий момент против часовой стрелки создается силой \(\vec{F}\), действующей на расстоянии r от шарниров (точки поворота). (b) Меньший крутящий момент против часовой стрелки создается, когда меньшая сила \(\vec{F}′\) действует на том же расстоянии r от шарниров. (c) Та же сила, что и в (a), создает меньший крутящий момент против часовой стрелки, когда она приложена на меньшем расстоянии от шарниров. (d) Меньший крутящий момент против часовой стрелки создается силой той же величины, что и (а), действующей на том же расстоянии, что и (а), но под углом \(\theta\), который меньше 90°.

Теперь рассмотрим, как определить крутящие моменты в общем трехмерном случае.

Крутящий момент

Когда сила \(\vec{F}\) приложена к точке P, положение которой равно \(\vec{r}\) относительно точки O (рисунок \(\PageIndex{2}\)) , крутящий момент \(\vec{\tau}\) вокруг O равен

\[\vec{\tau} = \vec{r} \times \vec{F} \ldotp \label{10.22}\]

Рисунок \(\PageIndex{2}\): направление определяется по правилу правой руки.

Из определения векторного произведения крутящий момент \(\vec{\tau}\) перпендикулярен плоскости, содержащей \(\vec{r}\) и \(\vec{F}\), и имеет величина

\[|\vec{\tau}| = |\vec{r} \times \vec{F}| = rF \sin \theta,\]

, где \(\theta\) — угол между векторами \(\vec{r}\) и \(\vec{F}\). Единицей крутящего момента в СИ является ньютон, умноженный на метр, обычно записывается как Н • м. Величина r _\(\perp\) = rsin \(\theta\) представляет собой перпендикулярное расстояние от O до линии, определяемой вектором \(\vec{F}\), и называется рычаг . Обратите внимание, что чем больше плечо рычага, тем больше величина крутящего момента. В терминах плеча рычага величина крутящего момента составляет

\[|\vec{\tau}| = r_{\perp} F \ldotp \label{10.23}\]

Перекрестное произведение \(\vec{r} \times \vec{F}\) также сообщает нам знак крутящего момента. На рисунке \(\PageIndex{2}\) векторное произведение \(\vec{r} \times \vec{F}\) расположено вдоль положительной оси z, что по соглашению представляет собой положительный крутящий момент. Если \(\vec{r} \times \vec{F}\) вдоль отрицательной оси z, это создает отрицательный крутящий момент.

Если мы рассмотрим диск, который может свободно вращаться вокруг оси, проходящей через центр, как показано на рисунке \(\PageIndex{3}\), мы увидим, как угол между радиусом \(\vec{r}\ ), а сила \(\vec{F}\) влияет на величину крутящего момента. Если угол равен нулю, крутящий момент равен нулю; если угол равен 90°, крутящий момент максимальный. Крутящий момент на рисунке \(\PageIndex{3}\) положительный, потому что направление крутящего момента по правилу правой руки выходит за пределы страницы вдоль положительной оси z.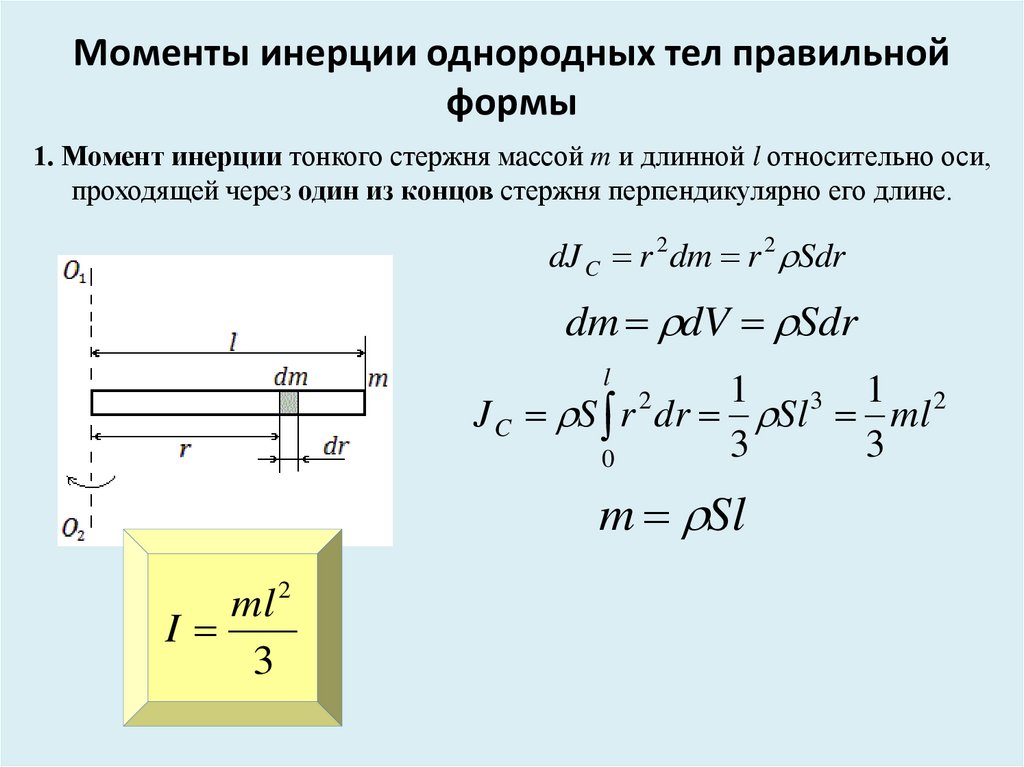 Диск вращается против часовой стрелки за счет крутящего момента в том же направлении, что и положительное угловое ускорение.

Рисунок \(\PageIndex{3}\): Диск может свободно вращаться вокруг своей оси, проходящей через центр. Величина крутящего момента на диске равна rFsin \(\theta\). Когда \(\theta\) = 0°, крутящий момент равен нулю и диск не вращается. Когда \(\theta\) = 90°, крутящий момент максимален и диск вращается с максимальным угловым ускорением.

Любое количество крутящих моментов может быть рассчитано относительно данной оси. Отдельные крутящие моменты складываются, чтобы создать чистый крутящий момент вокруг оси. Когда соответствующий знак (положительный или отрицательный) присваивается величинам отдельных крутящих моментов относительно заданной оси, чистый крутящий момент вокруг оси представляет собой сумму отдельных крутящих моментов:

\[\vec{\tau}_{net} = \sum_{i} |\vec{\tau}_{i}| \ldotp \label{10.24}\]

Расчет чистого крутящего момента для твердых тел на неподвижной оси

В следующих примерах мы вычисляем крутящий момент как абстрактно, так и применительно к твердому телу. Сначала мы вводим стратегию решения проблем.

Стратегия решения проблем: определение чистого крутящего момента

1. Выберите систему координат с точкой вращения или осью вращения в качестве начала выбранной системы координат.
2. Определите угол между плечом рычага \(\vec{r}\) и вектором силы.
3. Возьмите векторное произведение \(\vec{r}\) и \(\vec{F}\), чтобы определить, является ли крутящий момент положительным или отрицательным относительно точки вращения или оси.
4. Оценить величину крутящего момента с помощью r _\(\perp\) F.
5. Присвойте величине соответствующий знак, положительный или отрицательный.
6. Суммируйте крутящие моменты, чтобы найти чистый крутящий момент.

Пример 10.14: Расчет крутящего момента

Четыре силы показаны на рисунке \(\PageIndex{4}\) в определенных местах и ​​ориентациях по отношению к данной системе координат xy. Найдите крутящий момент, вызванный каждой силой относительно начала координат, а затем используйте полученные результаты, чтобы найти чистый крутящий момент вокруг начала координат.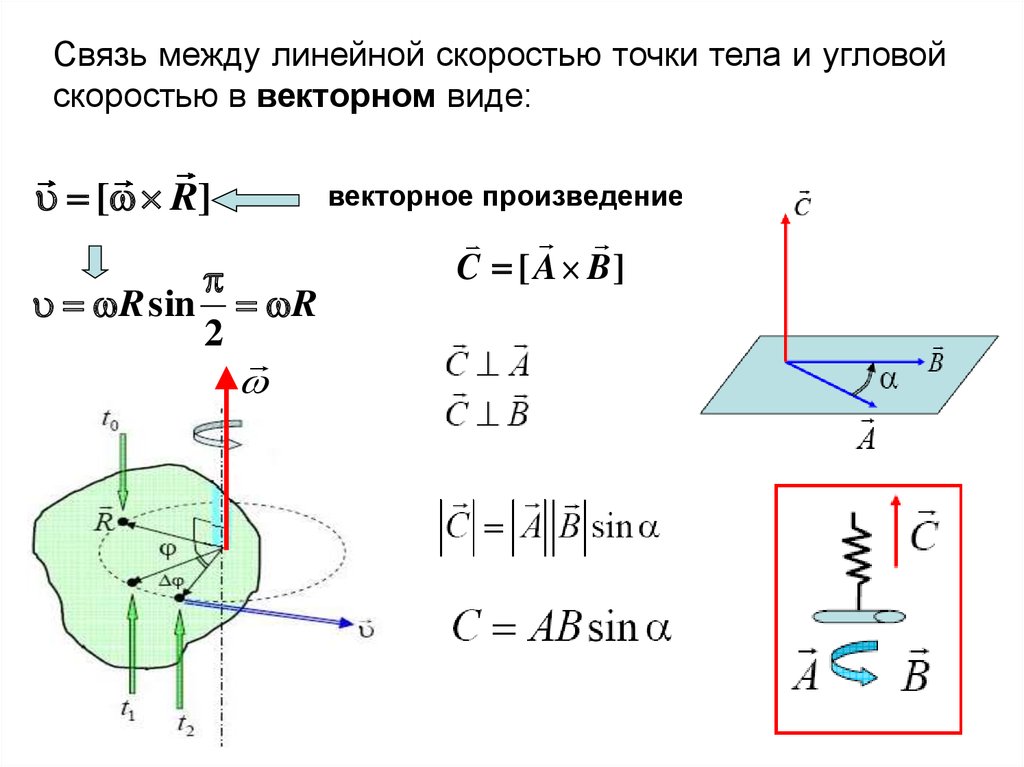

Рисунок \(\PageIndex{4}\): Четыре силы, создающие крутящие моменты.

Стратегия

Эта задача требует расчета крутящего момента. Все известные величины — силы с направлениями и плечами рычага — приведены на рисунке. Цель состоит в том, чтобы найти каждый отдельный крутящий момент и чистый крутящий момент путем суммирования отдельных крутящих моментов. Будьте осторожны, чтобы присвоить правильный знак каждому крутящему моменту, используя векторное произведение \(\vec{r}\) и вектора силы \(\vec{F}\).

Решение

Использование |\(\vec{\tau}\)| = r _\(\perp\) F = rFsin \(\theta\) для нахождения величины и \(\vec{r} = \vec{r} \times \vec{F}\) для определения знака крутящего момента.

Крутящий момент от силы 40 Н в первом квадранте определяется формулой (4)(40)sin 90° = 160 Н • м.

Перекрестное произведение \(\vec{r}\) и \(\vec{F}\) вне страницы, положительное.

Крутящий момент от силы 20 Н в третьем квадранте определяется выражением −(3)(20)sin 90° = − 60 Н • м.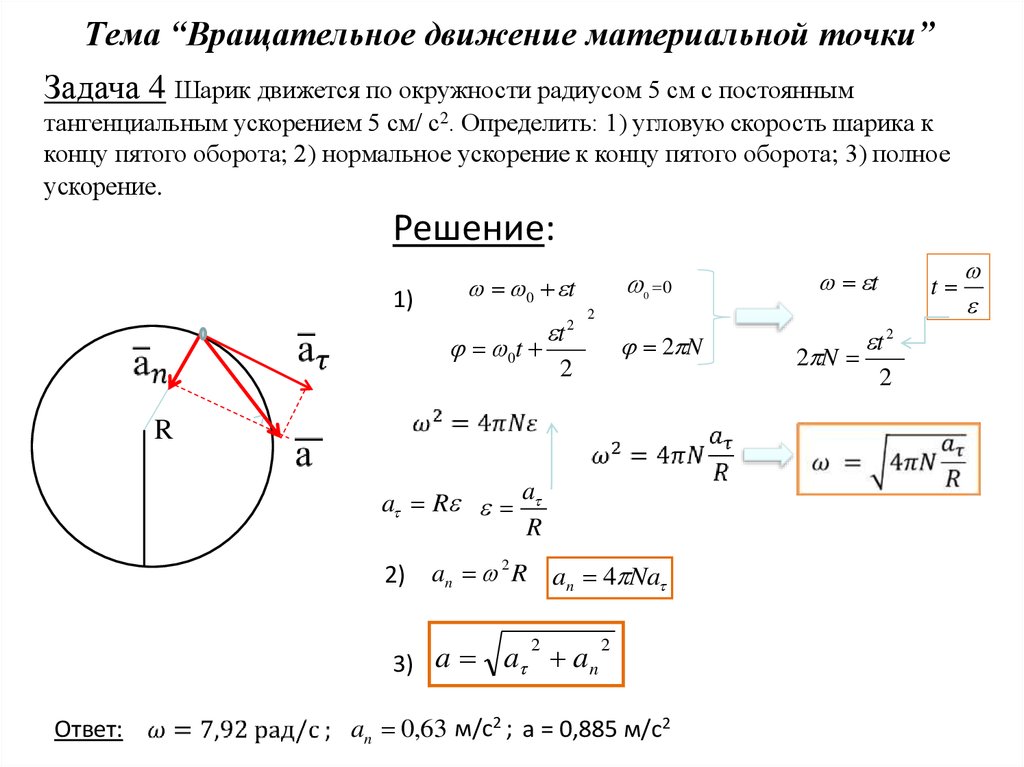

Перекрестное произведение \(\vec{r}\) и \(\vec{F}\) находится на странице, поэтому оно отрицательно.

Крутящий момент от силы 30 Н в третьем квадранте определяется выражением (5)(30)sin 53° = 120 Н • м.

Перекрестное произведение \(\vec{r}\) и \(\vec{F}\) вне страницы, положительное.

Крутящий момент от силы 20 Н во втором квадранте определяется выражением (1)(20)sin 30° = 10 Н • м.

Перекрестное произведение \(\vec{r}\) и \(\vec{F}\) находится за пределами страницы.

Таким образом, чистый крутящий момент равен \(\tau_{net} = \sum_{i} |\tau_{i}|\) = 160 − 60 + 120 + 10 = 230 Н • м.

Значение

Обратите внимание, что каждая сила, действующая против часовой стрелки, имеет положительный крутящий момент, тогда как каждая сила, действующая по часовой стрелке, имеет отрицательный крутящий момент. Крутящий момент больше, когда расстояние, сила или перпендикулярные компоненты больше.

Пример 10.15: Расчет крутящего момента на твердом теле

На рисунке \(\PageIndex{5}\) показано несколько сил, действующих в разных местах и ​​под разными углами на маховике. Имеем \(|\vec{F}_{1}|\) = 20 Н, \(|\vec{F}_{2}|\) = 30 Н, \(|\vec{F}_{ 3}|\) = 30 Н, r = 0,5 м. Найдите чистый крутящий момент на маховике относительно оси, проходящей через центр.

Рисунок \(\PageIndex{5}\): Три силы, действующие на маховик.

Стратегия

Мы рассчитываем каждый крутящий момент отдельно, используя векторное произведение, и определяем знак крутящего момента. Затем мы суммируем крутящие моменты, чтобы найти чистый крутящий момент. Решение Начнем с \(\vec{F}_{1}\). Если мы посмотрим на рисунок \(\PageIndex{5}\), то увидим, что \(\vec{F}_{1}\) составляет угол 90° + 60° с радиус-вектором \(\vec{r }\). Взяв векторное произведение, мы видим, что оно находится вне страницы и, следовательно, является положительным. Мы также видим это из расчета его величины: 9{о} = (-0,5\; m)(30\; N) = -15,0\; Н\; \cdotp m \ldotp\]

Когда мы оцениваем крутящий момент из-за \(\vec{F}_{3}\), мы видим, что угол, который он образует с \(\vec{r}\), равен нулю, поэтому \(\vec{r} \times \vec{F}_{3}\) = 0. Следовательно, \(\vec{F}_{3}\) не создает крутящего момента на маховике.

Оцениваем сумму моментов:

\[\tau_{net} = \sum_{i} |\tau_{i}| = 5 — 15 = -10\; Н\; \cdotp m \ldotp\]

Значение

Ось вращения находится в центре масс маховика. Поскольку маховик находится на неподвижной оси, он не может свободно перемещаться. Если бы он находился на поверхности без трения и не был зафиксирован на месте, \(\vec{F}_{3}\) вызвал бы перемещение маховика, а также \(\vec{F}_{1}\). Его движение было бы комбинацией поступательного движения и вращения.

Упражнение 10.6

Большое океанское судно садится на мель у береговой линии, как и Costa Concordia , и лежит под углом, как показано ниже. Спасательные бригады должны приложить крутящий момент, чтобы выровнять судно, чтобы поднять его на воду для транспортировки. Чтобы выровнять судно, необходимо приложить силу 5,0 x 10

5 Н, действующую в точке А. Каков крутящий момент в точке контакта корабля с землей (рис.