Краткий курс высшей математики
Краткий курс высшей математики
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. МЕТОД КООРДИНАТ. ПОНЯТИЕ ФУНКЦИИ § 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. КООРДИНАТЫ ТОЧКИ НА ПРЯМОЙ 2. Геометрическое изображение действительных чисел. Координаты точки на прямой 3. Абсолютная величина действительного числа  Расстояние между двумя точками на прямой§ 2. КООРДИНАТЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ 2. Расстояние между двумя точками на плоскости 3. Деление отрезка в данном отношении 4. Координаты точки в пространстве 5. Расстояние между двумя точками в пространстве § 3. УГОЛ МЕЖДУ ДВУМЯ ОСЯМИ. ПОЛЯРНЫЕ КООРДИНАТЫ 2. Полярные координаты 3. Зависимость между декартовыми и полярными координатами § 4. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ 2. Понятие функции 3. График функции 4. Способы задания функций 5. Основные элементарные функции и их графики 6. Сложные функции. Элементарные функции 7. Целые и дробно-рациональные функции 8. Функции четные и нечетные. Периодические функции 2. Нахождение уравнения линии по ее геометрическим свойствам § 6 ПРЕОБРАЗОВАНИЕ КООРДИНАТ 2. Поворот осей координат ГЛАВА II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ § 1. ПРЯМАЯ 2. Уравнение прямой с угловым коэффициентом 3. Уравнение прямой, параллельной оси ординат 4.  Общее уравнение прямой и его частные случаи5. Точка пересечения прямых. Построение прямой по ее уравнению 6. Вычисление угла между двумя прямыми. Условия параллельности и перпендикулярности двух прямых 7. Уравнение прямой, проходящей через данную точку в заданном направлении 9. Уравнение прямой, проходящей через две данные точки 10. Расстояние от точки до прямой § 2. КРИВЫЕ ВТОРОГО ПОРЯДКА 2. Окружность 3. Эллипс 4. Гипербола 5. Парабола 6. Окружность, эллипс, гипербола и парабола как конические сечения 7. Упрощение уравнения кривой второго порядка. График квадратного трехчлена 8. Уравнение равносторонней гиперболы, асимптоты которой приняты за оси координат 9. График дробно-линейной функции 10. Преобразование уравнения кривой второго порядка, не содержащего члена с произведением координат ГЛАВА III. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЫ § 1. ЭЛЕМЕНТЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ 2. Определитель третьего порядка  Понятие об определителях высших порядков§ 2. СИСТЕМЫ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ 2. Однородная система двух уравнений первой степени с тремя неизвестными 3. Система трех уравнений первой степени с тремя неизвестными 4. Однородная система трех уравнений первой степени с тремя неизвестными § 3. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ 2. Линейные операции над векторами 4. Проекция вектора на ось и составляются вектора по оси 5. Разложение вектора на составляющие по осям координат 6. Направляющие косинусы вектора 7. Условие коллинеарности двух векторов 8. Скалярное произведение 10. Косинус угла между двумя векторами 11. Векторное произведение 12. Выражение векторного произведения через проекции перемножаемых векторов 13. Смешанное произведение трех векторов 14. Геометрический смысл смешанного произведения 15. Условие компланарности трех векторов § 4. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ 2.  Равенство матриц. Действия над матрицами3. Обратная матрица 4. Матричная запись и матричное решение системы уравнений первой степени § 5. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ 2. Преобразование координат 3. Приведение квадратичной формы к каноническому виду ГЛАВА IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ § 1. ПЛОСКОСТЬ 2. Нормальный вектор плоскости. Уравнение плоскости, проходящей через данную точку 3. Общее уравнение плоскости и его частные случаи 4. Построение плоскости по ее уравнению 5. Угол между плоскостями. Условия параллельности и перпендикулярности двух плоскостей 6. Точка пересечения трех плоскостей § 2. ПРЯМАЯ В ПРОСТРАНСТВЕ 2. Общие уравнения прямой 3. Векторное уравнение прямой. Параметрические уравнения прямой 4. Канонические уравнения прямой 5. Уравнения прямой, проходящей через две точки 6. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых  Прямая и плоскость в пространстве2. Точка пересечения прямой с плоскостью 3. Расстояние от точки до плоскости 4. Пучок плоскостей § 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА 2. Цилиндрические поверхности 3. Конические поверхности 4. Поверхность вращения 6. Гиперболоиды 7. Параболоиды ГЛАВА V. ТЕОРИЯ ПРЕДЕЛОВ § 1. ПРЕДЕЛ ФУНКЦИИ 2. Предел функции при х -> -оо 3. Предел функции при х->х0 4. Бесконечно малые функции. Ограниченные функции 5. Бесконечно большие функции и их связь с бесконечно малыми функциями 7. Предел функции при x -> 0 8. Последовательность. Число e 9. Натуральные логарифмы 10. Сравнение бесконечно малых функций § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ 2. Операции над непрерывными функциями. Непрерывность элементарных функций 3. Свойства функций, непрерывных на сегменте 4. Понятие об обратной функции 5. Обратные тригонометрические функции 6. Показательная и логарифмическая функции 7.  Понятие о гиперболических функцияхГЛАВА VI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ 1. Приращение аргумента и приращение функции 3. Задачи, приводящие к понятию производной 4. Определение производной и ее механический смысл 5. Дифференцируемость функции 6. Геометрический смысл производной 7. Производные некоторых основных элементарных функций 8. Основные правила дифференцирования 9. Производная обратной функции 10. Производные обратных тригонометрических функций 11. Производная сложной функции § 12. Производные гиперболических функций 13. Производная степенной функции с любым показателем 14. Сводная таблица формул дифференцирования 15. Неявные функции и их дифференцирование 17. Графическое дифференцирование § 2. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ 1. Нахождение производных высших порядков 2.  Механический смысл второй производной§ 3. ДИФФЕРЕНЦИАЛ ФУНКЦИИ 2. Производная как отношение дифференциалов 3. Дифференциал суммы, произведения и частного функций 4. Дифференциал сложной функции. Инвариантность формы дифференциала 5. Применение дифференциала к приближенным вычислениям 6. Дифференциалы высших порядков § 4. ФУНКЦИИ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ, И ИХ ДИФФЕРЕНЦИРОВАНИЕ 2. Дифференцирование функций, заданных параметрически 2. Векторная функция скалярного аргумента и ее производная 3. Уравнения касательной прямой и нормальной плоскости к пространственной кривой 4. Механический смысл первой и второй производных векторной функции скалярного аргумента § 6. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ 2. Теорема Ролля 3. Теорема Лагранжа 4. Правило Лопиталя § 7. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ 2. Максимум и минимум функции 3. Достаточный признак существования экстремума, основанный на знаке второй производной 4.  5. Применение теории максимума и минимума к решению задач 6. Выпуклость и вогнутость графика функции. Точки перегиба 7. Асимптоты графика функции 8. Общая схема исследования функции и построение ее графика § 8. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ 2. Уточнение найденных значений корней методом хорд и касательных § 9. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА ГЛАВА VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА 2. Геометрический смысл неопределенного интеграла 3. Таблица основных интегралов 4. Основные свойства неопределенного интеграла § 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ 3. Интегрирование по частям § 3. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ 2. Рациональные дроби. Выделение правильной рациональной дроби 3. Интегрирование простейших рациональных дробей 4. Разложение правильной рациональной дроби на простейшие дроби 5.  Метод неопределенных коэффициентов6. Интегрирование рациональных дробей § 4. Интегрирование тригонометрических функций 2. Рациональные функции двух переменных 3. Интегралы вида § 5. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ 2. Интеграл вида 3. Интегралы видов 4. Интегралы вида § 6. ОБЩИЕ ЗАМЕЧАНИЯ О МЕТОДАХ ИНТЕГРИРОВАНИЯ. ИНТЕГРАЛЫ, НЕ БЕРУЩИЕСЯ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ 2. Понятие об интегралах, не берущихся в элементарных функциях ГЛАВА VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. ЗАДАЧИ, ПРИВОДЯЩИЕ К ОПРЕДЕЛЕННОМУ ИНТЕГРАЛУ 2. Задача о работе переменной силы § 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 2. Свойства определенного интеграла 3. Производная интеграла по переменной верхней границе 4. Формула Ньютона—Лейбница 5. Замена переменной в определенном интеграле 6. Интегрирование по частям в определенном интеграле § 3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 2. Вычисление площади в полярных координатах 3.  Вычисление объема тела по известным поперечным сечениям4. Объем тела вращения 5. Длина дуги кривой 6. Дифференциал дуги 7. Площадь поверхности вращения 8. Общие замечания о решении задач методом интегральных сумм § 4. КРИВИЗНА ПЛОСКОЙ КРИВОЙ 2. Вычисление кривизны 3. Радиус кривизны. Круг кривизны. Центр кривизны 4. Эволюта и эвольвента § 5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 2. Интегралы от разрывных функций 3. Признаки сходимости несобственных интегралов § 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 2. Метод трапеций 3. Метод параболических трапеций (метод Симпсона) ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2. График функции двух переменных 3. Функции трех и большего числа переменных § 2. Предел функции нескольких переменных. Непрерывность функции. Точки разрыва 2. Непрерывность функции нескольких переменных 3. Понятие области 4.  Точки разрыва5. Свойства функций, непрерывных в ограниченной замкнутой области § 3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ 2. Геометрический смысл частных производных функции двух переменных 3. Частные производные высших порядков § 4. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2. Полный дифференциал функции 3. Приложение полного дифференциала к приближенным вычислениям § 5. Дифференцирование сложных и неявных функций 2. Инвариантность формы полного дифференциала 3. Дифференцирование неявных функций § 6. СКАЛЯРНОЕ ПОЛЕ 2. Производная по направлению 3. Градиент 4. Касательная плоскость а нормаль к поверхности 5. Геометрический смысл полного дифференциала функции двух переменных § 7. ЭКСТРЕМУМ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ 2. Наибольшее и наименьшее значения функции двух переменных ГЛАВА X. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ § 1. ДВОЙНОЙ ИНТЕГРАЛ 2. Двойной интеграл. Теорема существования 3. Свойства двойного интеграла 4.  Вычисление двойного интеграла в декартовых координатах5. Вычисление двойного интеграла в полярных координатах 6. Приложения двойного интеграла § 2. ТРОЙНОЙ ИНТЕГРАЛ 2. Тройной интеграл и его свойства 3. Вычисление тройного интеграла в декартовых координатах 4. Вычисление тройного интеграла в цилиндрических координатах 5. Приложения тройного интеграла § 3. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ 2. Задача о работе. Криволинейный интеграл 3. Вычисление криволинейного интеграла 4. Формула Остроградского — Грина 5. Независимость криволинейного интеграла от пути интегрирования 6. Отыскание первообразной по полному дифференциалу 7. Криволинейный интеграл по длине дуги ГЛАВА XI. РЯДЫ § 1. ЧИСЛОВЫЕ РЯДЫ 2. Геометрическая прогрессия 3. Простейшие свойства числовых рядов 4. Необходимый признак сходимости ряда 5. Достаточные признаки сходимости знакоположительных рядов 6. Знакопеременные ряды 7. Остаток ряда и его оценка § 2.  ФУНКЦИОНАЛЬНЫЕ РЯДЫ2. Правильно сходящиеся функциональные ряды и их свойства § 3. СТЕПЕННЫЕ РЯДЫ 2. Свойства степенных рядов 3. Ряды по степеням разности х-а 4. Разложение функций в степенные ряды. Ряд Тейлора 5. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена § 4. ПРИЛОЖЕНИЕ РЯДОВ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ 2. Приближенное вычисление интегралов § 5. ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ. СТЕПЕННЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ 2. Числовые ряды с комплексными членами 3. Степенные ряды в комплексной области § 6. РЯДЫ ФУРЬЕ 2. Ряд Фурье 3. Сходимость ряда Фурье 4. Ряды Фурье для четных и нечетных функций 5. Разложение в ряд Фурье функций с периодом 2l ГЛАВА XII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 2. Дифференциальные уравнения первого порядка 3. Уравнения с разделяющимися переменными 4. Однородные уравнения 5. Линейные уравнения 6. Уравнение в полных дифференциалах 7.  Особые решения8. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 2. Простейшие уравнения второго порядка, допускающие понижение порядка 3. Понятие о дифференциальных уравнениях высших порядков § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 2. Линейные однородные дифференциальные уравнения второго порядка 3. Линейные неоднородные дифференциальные уравнения второго порядка 4. Метод вариации произвольных постоянных § 4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 2. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами 3. Приложение линейных дифференциальных уравнений второго порядка к изучению механических и электрических колебаний § 5. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ 2. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами § 6.  ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ РЯДОВ§ 7. ПОНЯТИЕ О СИСТЕМАХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 2. Системы линейных дифференциальных уравнений с постоянными коэффициентами ПРИЛОЖЕНИЕ 1. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА ПРИЛОЖЕНИЕ 2. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ |
Массив Numpy
Содержание страницы
- 1 Списки и массивы
- 2 Скалярное произведение, часть 1. Цикл for, метод косинусов, функция dot
- 3 Скалярное произведение, часть 2. Сравнение скорости работы
Здравствуйте и вновь добро пожаловать на занятия по теме «Инструментарий Numpy на языке Python».
В этой статье мы сравним списки и массивы, и разберем скалярное произведение.
Первое,что приходит в голову, – а какой смысл использовать массив Numpy? Разве он не похож в точности на список? Давайтезапустим Ipython и выполним несколько примеров.
ИмпортируемNumpy и создадим список, а затем – такой же массив:
import numpy as np
L = [1,2,3]
A = np.
array([1,2,3])
Обаони дают одно и тоже – объект с тремя элементами 1, 2 и 3. Часто встречающаязадача – пройтись по списку. Так и сделаем:
for ein L:
print e
Всёработает. Теперь то же самое, но с массивом:
for e in A:
print e
Тожеработает нормально. Итак, работают они одинаково, так что остаётся вопрос, вчём смысл?
Допустим,нам нужно что-то добавить в наш список. В случае обычного списка используетсякоманда append:
L.append(4)
ТеперьL содержит ещё и элемент 4. Но что будет, сделать тоже самое с массивом?
A.append(4)
Оказывается,нет метода append для массива Numpy.
Ноесть ещё один способ добавить элемент в список – объединить два списка. Сначалапопробуем со списком:
L = L + [5]
ТеперьL содержит и 5. Теперь попробуем это же с Numpy. Попробуем добавить 4 и 5, поскольку в массиве ещёнет четвёрки:
A = A + [4,5]
Иэто не работает. Похоже, что мы вообще не можем ничего добавить к массиву Numpy.
Вероятно, в этот момент вы решили, что Numpy – дрянь, ведь он не может даже того, что можетсписок. Но давайте попробуем кое-что ещё. Давайте попробуем сложение векторов.Чтобы было совсем просто, просто добавим вектор к самому себе. В случаем спискаPython мы знаем, что использование знака «плюс» простодаёт нам новый список с объединением всех элементов. Но нам нужно не это. Намнужно складывать каждый элемент по отдельности.
Итак,создадим пустой список и пройдёмся по каждому элементу eсписка L, добавляя e к e:
L2 = []
for e in L:
L2.append(e+ e)
Витоге L2 будет равно L+ L. А как это сделать в Numpy?Попробуем
A + A
Ив результате получаем именно то, что нужно. Итак, урок первый: знак «плюс» вслучае списка приводит к добавлению, а знак «плюс» в массиве Numpy даёт векторное сложение. Если бы у нас быламатрица, которая представляет собой двухмерный массив, то у нас получилось бысложение матриц. Обобщая понятие, можно сказать, что происходит поэлементноесложение.
Какойещё есть способ удвоения вектора без сложения его с самим собой? Ну, его можнопросто умножить на 2, то есть скалярную величину умножить на вектор. Сначалапопробуем с массивом Numpy.
2*A
Чтодаёт нам ожидаемое. Теперь попробуем список.
2*L
Интересно:содержимое списка было просто повторено два раза. Но то обстоятельство, чтополучился другой результат, не значит, что это бесполезная операция. Вдействительности я довольно часто пользуюсь умножением числа на список. Если женужно умножить на число каждый элемент списка, придётся использовать цикл for, как мы сделали в случае L+ L.
Вкачестве последнего упражнения попробуем сделать поэлементное возведение вквадрат каждой величины вектора. Сначала попробуем со списком, хотя мыдогадываемся, что, вероятно, получим некорректный результат.
L**2
Неработает. Мы не можем список возвести в степень. Вернее, можем, но придётсяиспользовать цикл for:
L2 = []
for e in L:
L2.append(e*e)
ТеперьL2 содержит ожидаемые элементы.
Попробуем теперь Numpy:
A**2
Каки ожидалось, всё работает, но куда проще.
Поповоду Numpy нужно помнить, что большинство функций работаютпоэлементно, как мы убедились в случае возведения во вторую степень. А как насчётизвлечения квадратного корня?
np.sqrt(A)
Врезультате извлекается квадратный корень из каждого элемента вектора. Какнасчёт логарифма?
np.log(A)
Берётсялогарифм каждого элемента. А что с экспонентой?
np.exp(A)
Получимпоэлементное экспонирование.
Длявсех этих действий в случае списка приходится использовать цикл for и производить операцию по отдельности над каждымэлементом.
Подведём итог. На этой лекции мы узнали, что если нужно представить вектор, то массив Numpy несколько более удобен, поскольку при действиях с ним мы получаем ожидаемый результат, когда применяем операции вроде сложения, умножения и возведения в квадрат. Списки тоже неплохи – во многих случаях на самом деле нам нужен именно список, а не массив Numpy.
Обычно список можно рассматривать как массив, но массив Numpy можно рассматривать как вектор – математический объект. Для выполнения операций над списками приходится использовать цикл for, а как вы увидите позже, цикл for в Python очень медлителен, так что следует всячески его избегать при выполнении математических операций.
Скалярное произведение, часть 1. Цикл for, метод косинусов, функция dot
Здесь мы обсудим скалярное произведение – вид умножения, который можно применить по отношению к векторам. Напомню, что есть два эквивалентных определения скалярного произведения. Первое – это сумма поэлементных произведений двух векторов. Если использовать d в качестве индекса каждого компонента, то получится
Обратитевнимание, что запись aTb подразумевает, что по умолчанию векторысчитаются векторами-столбцами. Следовательно, результат будет иметь размерность1×1 – то есть это скалярная величина.
Второеопределение – это модуль a, умноженный на модуль b и умноженный на косинус угла между a и b:
Обратитевнимание, что запись aTb подразумевает, что по умолчанию векторысчитаются векторами-столбцами.
Следовательно, результат будет иметь размерность1×1 – то есть это скалярная величина.
Второеопределение – это модуль a, умноженный на модуль b и умноженный на косинус угла между a и b:
Второйспособ не очень удобен, если только мы не знаем величин, указанных в правойчасти равенства. На самом деле обычно, скомбинировав эти два определения,находят собственно угол:
Этовведение в лекцию очень удачно позволит нам изучить больше возможностей Numpy. Сделаем это прямо в коде.
Начнёмс двух векторов:
a = np.array([1,2])
b = np.array([2,1])
Предположим,мы используем прямое определение скалярного произведения. Нужно одновременнопройтись по обоим массивами, перемножить соответствующие элементы и прибавитьрезультат к окончательной сумме. Для начала так и сделаем.
dot = 0
for e,f inzip(a,b)
dot += e*f
Ответ4, что и ожидалось. Но над массивами Numpy можнопроизвести ещё одну интересную операцию – перемножение двух массивов.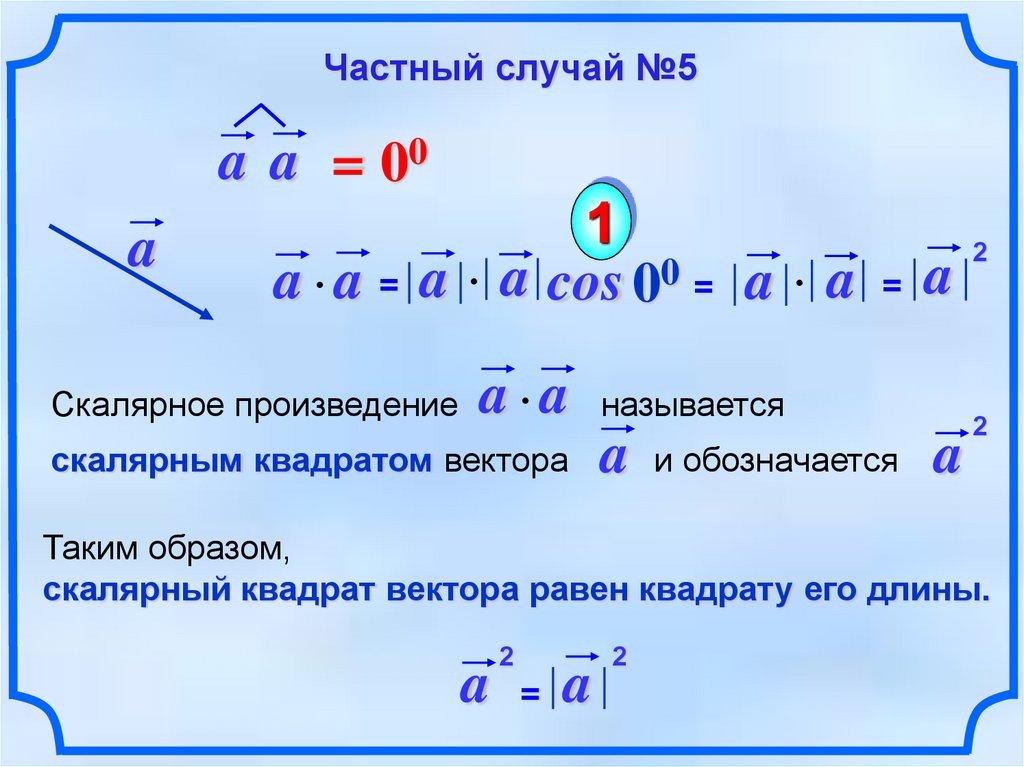
Ранее мывидели только умножение вектора на скалярную величину. Попробуем умножить a и bи посмотрим, что получится
a*b
Мывидим, что это, как и следовало ожидать, дало нам поэлементное умножение двухмассивов. Это также означает, что нельзя выполнить такую операцию над двумямассивами, имеющими разные длины. Сейчас же нам нужно лишь просуммировать всеэлементы. К счастью, Numpy имеет функцию sum, позволяющую это сделать:
np.sum(a*b)
Этодаёт нам ожидаемый результат. Интересно, что функция sumявляется методом экземпляра самого массива Numpy,так что в качестве альтернативы можно использовать команду
(a*b).sum()
Этодаёт нам тот же результат.
Наконец,в то время как оба эти способа дают правильный ответ, есть и ещё более удобныйспособ вычисления скалярного произведения с помощью функции dot:
np.dot(a, b)
Иэто вновь-таки даёт нам ожидаемый результат. Как и функция sum, функция dot также являетсяметодом экземпляра массива Numpy, так что мыможем вызвать её для самого объекта:
a.
dot(b)
Иполучаем всё тот же ответ. Это также эквивалентно команде
a.dot(b)
Теперьвоспользуемся альтернативным определением скалярного произведения, чтобывычислить угол между a и b. Для этого надовыяснить, как рассчитать длину вектора. Мы можем это сделать, пользуясь лишьимеющимися данными – длина равна квадратному корню, извлечённому из суммыквадратов каждого элемента. Так, например, для a имеем:
amag = np.sqrt( (a*a).sum() )
Каки ожидалось, длина вектора а равна2,236. На самом деле в Numpy для этогоимеется специальная функция, поскольку это достаточно распространённаяоперация. Функция является частью модуля linalgбиблиотеки Numpy, в состав которого входят также множество другихраспространённых функций линейной алгебры. Попробуем ещё раз с помощью linalg:
amag = np.linalg.norm(a)
Иполучаем тот же ответ. Итак, теперь мы готовы вычислить угол:
cosangle = a.dot(b) / (np.linalg.norm(a) *np.linalg.norm(b) )
Итак,косинус угла равен 0,8.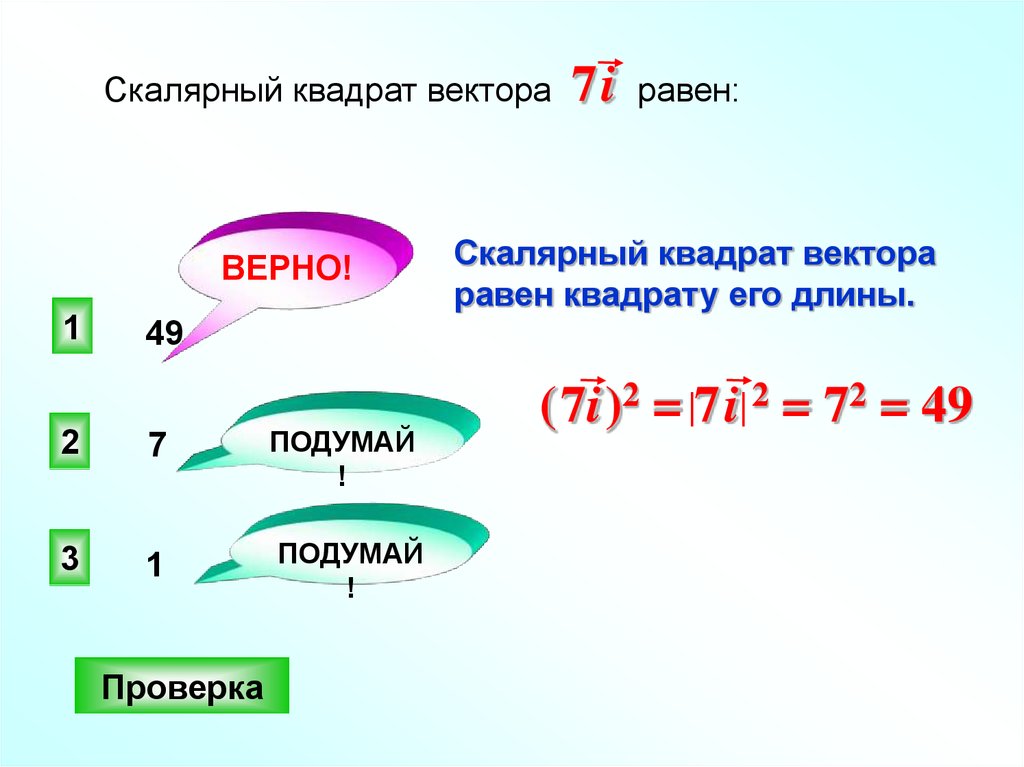
А сам угол равен
angle = np.arccos(cosangle)
Итак, угол равен 0,643 – по умолчанию, ответ даётся в радианах.
Скалярное произведение, часть 2. Сравнение скорости работы
Теперь нам нужно сравнить два способа вычисления скалярного произведения и посмотрим, сколько времени займёт их выполнение.
В первом случае используется цикл for с умножением каждого из соответствующих элементов одной размерности за раз и накапливанием результата. Во втором же будет использоваться функция dot библиотеки Numpy. В конце мы поделим время, потраченное в первом случае, на время, потраченное во втором. Это примерно покажет, во сколько раз способ с Numpy работает быстрее.
Итак, запустим файл. Он называется dot_for.py.
Запустимещё раз, чтобы убедиться, что это не случайность.
Итак,при первом запуске способ с Numpy оказался в 37раз быстрее, при втором – в 25 раз быстрее, при третьем – в приблизительно 33раза быстрее.
Результат всегда будет где-то в этом диапазоне. Как видите,функция dot библиотеки Numpyработает на несколько порядков быстрее, чем цикл for.Отсюда урок: не пользуйтесь циклом for, если этогоможно избежать.
Этовведение в лекцию очень удачно позволит нам изучить больше возможностей Numpy. Сделаем это прямо в коде.
Предположим,мы используем прямое определение скалярного произведения. Нужно одновременнопройтись по обоим массивами, перемножить соответствующие элементы и прибавитьрезультат к окончательной сумме. Для начала так и сделаем.
Ответ4, что и ожидалось. Но над массивами Numpy можнопроизвести ещё одну интересную операцию – перемножение двух массивов. Ранее мывидели только умножение вектора на скалярную величину. Попробуем умножить a и bи посмотрим, что получится
Мывидим, что это, как и следовало ожидать, дало нам поэлементное умножение двухмассивов. Это также означает, что нельзя выполнить такую операцию над двумямассивами, имеющими разные длины. Сейчас же нам нужно лишь просуммировать всеэлементы.
К счастью, Numpy имеет функцию sum, позволяющую это сделать:
Этодаёт нам ожидаемый результат. Интересно, что функция sumявляется методом экземпляра самого массива Numpy,так что в качестве альтернативы можно использовать команду
Наконец,в то время как оба эти способа дают правильный ответ, есть и ещё более удобныйспособ вычисления скалярного произведения с помощью функции dot:
Иэто вновь-таки даёт нам ожидаемый результат. Как и функция sum, функция dot также являетсяметодом экземпляра массива Numpy, так что мыможем вызвать её для самого объекта:
Теперьвоспользуемся альтернативным определением скалярного произведения, чтобывычислить угол между a и b. Для этого надовыяснить, как рассчитать длину вектора. Мы можем это сделать, пользуясь лишьимеющимися данными – длина равна квадратному корню, извлечённому из суммыквадратов каждого элемента. Так, например, для a имеем:
Каки ожидалось, длина вектора а равна2,236. На самом деле в Numpy для этогоимеется специальная функция, поскольку это достаточно распространённаяоперация.
Функция является частью модуля linalgбиблиотеки Numpy, в состав которого входят также множество другихраспространённых функций линейной алгебры. Попробуем ещё раз с помощью linalg:
Теперь нам нужно сравнить два способа вычисления скалярного произведения и посмотрим, сколько времени займёт их выполнение.
В первом случае используется цикл for с умножением каждого из соответствующих элементов одной размерности за раз и накапливанием результата. Во втором же будет использоваться функция dot библиотеки Numpy. В конце мы поделим время, потраченное в первом случае, на время, потраченное во втором. Это примерно покажет, во сколько раз способ с Numpy работает быстрее.
Итак,при первом запуске способ с Numpy оказался в 37раз быстрее, при втором – в 25 раз быстрее, при третьем – в приблизительно 33раза быстрее. Результат всегда будет где-то в этом диапазоне. Как видите,функция dot библиотеки Numpyработает на несколько порядков быстрее, чем цикл for.
Отсюда урок: не пользуйтесь циклом for, если этогоможно избежать.
Возведение вектора в квадрат? — Математический стек Exchange
спросил
Изменено 6 лет, 7 месяцев назад
Просмотрено 98 тысяч раз
$\begingroup$
Итак, это базовый. И должно быть довольно быстро. Допустим, у меня есть вектор $\vec{r}$: 92$, когда понятно, что ты не имеешь в виду $$ {\ bf r} {\ bf r} = \ sum_ {i, j} r_i r_j {\ bf e} _i {\ bf e} _j $$ что равно вполне допустимой величине [1].
Что касается ${\bf r} = {\bf x} + {\bf y} + {\bf z}$,
$$
\begin{выравнивание}
{\bf r} \cdot {\bf r} &=& {\bf x} \cdot {\bf x} + {\bf x} \cdot {\bf y} + {\bf x} \cdot {\ bf z} + {\bf y} \cdot {\bf x} + {\bf y} \cdot {\bf y} + {\bf y} \cdot {\bf z} + {\bf z} \cdot {\bf x} + {\bf z} \cdot {\bf y} + {\bf z} \cdot {\bf z} \\
&=& {\bf x} \cdot {\bf x} + {\bf y} \cdot {\bf y} + {\bf z} \cdot {\bf z} + 2\left( {\bf x } \cdot {\bf y} + {\bf x} \cdot {\bf z} + {\bf y} \cdot {\bf z}\right)
\end{эквнаррай}
$$
равно ${\bf x} \cdot {\bf x} + {\bf y} \cdot {\bf y} + {\bf z} \cdot {\bf z}$ для всех $\bf x$, $ \bf y$, $\bf z$ тогда и только тогда, когда ${\bf x} \cdot {\bf y} + {\bf x} \cdot {\bf z} + {\bf y} \cdot {\bf z} = 0$ — особый случай, когда ${\bf x} \cdot {\bf y} = {\bf x} \cdot {\bf z} = {\bf y} \cdot {\bf z} = 0$.
2 + 2 \left((\vec{x} \cdot\vec{z}) +(\vec{y}\cdot\vec{z}) + (\vec{x} \cdot\vec{y}) \ справа)$$ 92$$
$\endgroup$
$\begingroup$
Существует два основных способа умножения вектора, скалярного произведения, как показано в ссылке Скалярное произведение, которое дает скаляр, независимо от того, умножаете ли вы A.B или возводите его в квадрат, A.A.
Или у вас может быть перекрестное произведение, то есть A X B, которое дает вам другой вектор, перпендикулярный обоим перекрестным произведениям.
Причина, по которой существуют два разных способа умножения векторов, заключается в том, что они имеют дело с различными физическими ситуациями, поэтому скалярное произведение может использоваться для работы, которая является скалярной, F.D, а векторное произведение используется для крутящего момента, скажем, или углового скорости, которые являются векторами.
$\endgroup$
4
алгебр Клиффорда — Возведение вектора в квадрат; почему бы не использовать геометрическое произведение с самим собой вместо скалярного произведения с самим собой?
Задать вопрос
спросил
Изменено 2 года, 4 месяца назад 92 := \mathbf{A}\cdot \mathbf{A} $$
Однако при таком определении $\sqrt{\mathbf{A}\cdot \mathbf{A}} = A \neq \mathbf{A}$.
