Тест по информатике на тему «Системы счисления» (8 класс)

8 класс. Системы счисления.

Тест

1. В какой системе счисления представлена информация, хранящаяся в компьютере?

а) троичной; б) двоичной; в) десятичной; г) двенадцатеричной.

2. Преимущество двоичной системы счисления состоит в том, что

а) двоичный код позволяет экономить память компьютера;

б) электронные элементы с двумя состояниями наиболее просты в конструктивном исполнении;

в) электронные элементы с двумя состояниями потребляют меньше электроэнергии;

г) двоичный код не вызывает сбоя компьютера.

3. Восьмеричная система счисления отличается от шестнадцатеричной

а) количеством операций над числом в секунду;

б) глубиной вложенности операций;

в) количеством цифр, используемых для записи числа;

г) степенью компьютеризации.

4. Какое количество цифр используется в троичной системе счисления?

а) 3; б)11; в) 10;г) 2.

5. В шестнадцатеричной системе счисления символ F используется для обозначения

а) конца файла; б) числа 16;в) конца строки; г) числа 15.

6. Переведите из двоичной системы счисления в десятичную число 101010101.

а) 361; б) 564; в) 455; г) 341.

7. Переведите из десятичной системы счисления в двоичную число 216.

а) 11001100; б) 11011000; в) 11100000; г) 11001000.

8. Число 1116 в двоичной системе счисления равно

а) 1010101; б) 10011; в) 10001; г) 1000010.

9. Число ЕЕ16 в двоичной системе счисления равно

а) 110011; б) 11101110; в) 11110000; г) 10101010.

10. Число Е216 в десятичной системе счисления равно

а) 10000; б) 456; в) 226; г) 2310.

11. Число 3210 равно числу

а) 1000002; б) 358; в) 2116; г) 100002.

12. Сумма 1012 + 1002 + 1102, равна

а) 10112; б) 10012; в) 00012; г) 11112.

13. Выполните действие: 1111000012 + 1000112.

а) 10000001002; б) 10011001102; в) 10000111102; г) 10000011002.

14. Какое из равенств верно?

а) 510 = 000001112; б) 4710 = 1011112; в) 1310 = 000111112; г) 2 10 = 000010002.

15. Запись числа 100

а) отсутствует в двоичной системе счисления;

б) существует в двоичной, десятичной, восьмеричной и шестнадцатеричной системах счисления;

в) отсутствует в десятичной системе счисления;

г) отсутствует в восьмеричной системе счисления;

д) отсутствует в шестнадцатеричной системе счисления.

8 класс. Системы счисления.

Тест

1. В какой системе счисления представлена информация, хранящаяся в компьютере?

а) троичной; б) двоичной; в) десятичной; г) двенадцатеричной.

2. Преимущество двоичной системы счисления состоит в том, что

а) двоичный код позволяет экономить память компьютера;

б) электронные элементы с двумя состояниями наиболее просты в конструктивном исполнении;

в) электронные элементы с двумя состояниями потребляют меньше электроэнергии;

г) двоичный код не вызывает сбоя компьютера.

3. Восьмеричная система счисления отличается от шестнадцатеричной

а) количеством операций над числом в секунду;

б) глубиной вложенности операций;

в) количеством цифр, используемых для записи числа;

г) степенью компьютеризации.

4. Какое количество цифр используется в троичной системе счисления?

а) 3; б)11; в) 10;г) 2.

5. В шестнадцатеричной системе счисления символ F используется для обозначения

а) конца файла; б) числа 16;в) конца строки; г) числа 15.

6. Переведите из двоичной системы счисления в десятичную число 101010101.

а) 361; б) 564; в) 455; г) 341.

7. Переведите из десятичной системы счисления в двоичную число 216.

а) 11001100; б) 11011000; в) 11100000; г) 11001000.

8. Число 1116 в двоичной системе счисления равно

а) 1010101; б) 10011; в) 10001; г) 1000010.

9. Число ЕЕ16 в двоичной системе счисления равно

а) 110011; б) 11101110; в) 11110000; г) 10101010.

10. Число Е216 в десятичной системе счисления равно

а) 10000; б) 456; в) 226; г) 2310.

11. Число 3210 равно числу

а) 1000002; б) 358; в) 2116; г) 100002.

12. Сумма 1012 + 1002 + 1102, равна

а) 10112; б) 10012; в) 00012; г) 11112.

13. Выполните действие: 1111000012 + 1000112.

а) 10000001002; б) 10011001102; в) 10000111102; г) 10000011002.

14. Какое из равенств верно?

а) 510 = 000001112; б) 4710 = 1011112; в) 1310 = 000111112; г) 2 10 = 000010002.

15. Запись числа 100

а) отсутствует в двоичной системе счисления;

б) существует в двоичной, десятичной, восьмеричной и шестнадцатеричной системах счисления;

в) отсутствует в десятичной системе счисления;

г) отсутствует в восьмеричной системе счисления;

д) отсутствует в шестнадцатеричной системе счисления.

Ответы:

1 – б

2 – б

3 – в

4 – а

5 – г

6 – г

7 – б

8 – в

9 – б

10 – в

11 – а

12 – г

13 – а

14 – б

15 – б

Восьмеричная система счисления отличается от шестнадцатеричной

Двоичная система счисления

Для представления чисел в микропроцессоре используется двоичная система счисления .
При этом любой цифровой сигнал может иметь два устойчивых состояния: «высокий уровень» и «низкий уровень». В двоичной системе счисления для изображения любого числа используются две цифры, соответственно: 0 и 1. Произвольное число x=a_na_n-1..a₁a_{,a-1a-2…a-m} запишется в двоичной системе счисления как

где a_i — двоичные цифры (0 или 1).

Восьмеричная система счисления

В восьмеричной системе счисления базисными цифрами являются цифры от 0 до 7. 8 единиц младшего разряда объединяются в единицу старшего.

Шестнадцатеричная система счисления

В шестнадцатеричной системе счисления базисными цифрами являются цифры от 0 до 15 включительно. Для обозначения базисных цифр больше 9 одним символом кроме арабских цифр 0…9 в шестнадцатеричной системе счисления используются буквы латинского алфавита:

Например, число 175₁₀ в шестнадцатеричной системе счисления запишется как AF₁₆. Действительно,

10·16 1 +15·16 0 =160+15=175

В таблице представлены числа от 0 до 16 в десятичной, двоичной, восьмеричной и шестнадцатеричной системах счисления.

Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F
16	10000	20	10

Двоично-восьмеричные и двоично-шестнадцатеричные преобразования

Двоичная система счисления удобна для выполнения арифметических действий аппаратными средствами микропроцессора, но неудобна для восприятия человеком, поскольку требует большого количества разрядов. Поэтому в вычислительной технике помимо двоичной системы счисления широкое применение нашли восьмеричная и шестнадцатеричная системы счисления для более компактного представления чисел.

Три разряда восьмеричной системы счисления реализуют все возможные комбинации восьмеричных цифр в двоичной системе счисления: от 0 (000) до 7(111). Чтобы преобразовать двоичное число в восьмеричное, нужно объединить двоичные цифры в группы по 3 разряда (триады) в две стороны, начиная от разделителя целой и дробной части. При необходимости слева от исходного числа нужно добавить незначащие нули. Если число содержит дробную часть, то справа от него тоже можно добавить незначащие нули до заполнения всех триад. Затем каждая триада заменяется восьмеричной цифрой.

Пример: Преобразовать число 1101110,01₂ в восьмеричную систему счисления.

Объединяем двоичные цифры в триады справа налево. Получаем

Чтобы перевести число из восьмеричной системы в двоичную, нужно каждую восьмеричную цифру записать ее двоичным кодом:

Четыре разряда шестнадцатеричной системы счисления реализуют все возможные комбинации шестнадцатеричных цифр в двоичной системе счисления: от 0 (0000) до F(1111). Чтобы преобразовать двоичное число в шестнадцатеричное, нужно объединить двоичные цифры в группы по 4 разряда (тетрады) в две стороны, начиная от разделителя целой и дробной части. При необходимости слева от исходного числа нужно добавить незначащие нули. Если число содержит дробную часть, то справа от нее тоже нужно добавить незначащие нули до заполнения всех тетрад. Затем каждая тетрада заменяется шестнадцатеричной цифрой.

Пример: Преобразовать число 1101110,11₂ в шестнадцатеричную систему счисления.

Объединяем двоичные цифры в тетрады справа налево. Получаем

Чтобы перевести число из шестнадцатеричной системы в двоичную, нужно каждую шестнадцатеричную цифру записать ее двоичным кодом:

Такие системы счисления относятся к двоично-кодированным системам, когда основание системы счисления представляют целые степени двойки: 2 3 — для восьмеричной и 2 4 — для шестнадцатеричной систем счисления. Изображения целых чисел в восьмеричной и шестнадцатеричной системах счисления вместе с их двоичным и десятичными эквивалентами представлены в табл. 2.4 и 2.6

Большим достоинством восьмеричной и шестнадцатеричной систем счисления является:

-возможность более ком­пактно представить запись двоичного числа. Запись од­ного и того же двоичного числа в восьмеричной в 3 раза, а в шестнадцатерич­ной системе в 4 раза короче двоичной;

-сравнительно просто осуществляется преобразование чисел из двоичной в восьмеричную и шестнадцатеричную системы и наоборот.

Действительно, так как для восьмеричного числа каж­дый разряд представляется группой из трех двоичных разрядов (триад), а для шестнадцатеричного — группой из четырех двоич­ных разрядов (тетрад), то для такого преобразования достаточно объединить двоичные цифры в группы по 3 и 4 бита соответственно, продвигаясь от разделительной запятой вправо и влево. При этом в случае необходимости добавляют нули в начале и в конце числа и каждую такую группу — триаду или тетраду — заменяют экви­валентной восьмеричной или шестнадцатеричной цифрой.

Указанные достоинства восьмеричных и шестнадцатеричных систем счисления определили использование их при составлении программ для более короткой и удобной записи двоичных чисел, команд и специальных двоичных слов, с которыми оперирует ЭВМ. Особенно оказалось удобным использование шестнадцатеричной системы, когда разрядность чисел и команд выбрана кратной бай­ту, при этом каждый двоичный код байта запишется в виде 2-раз­рядного шестнадцатеричного числа.

Использование шестнадцатеричной системы счисления в ЭВМ общего назначения, как будет видно из дальнейшего изложения, позволяет расширить допустимый диапазон представления норма­лизованных чисел.

Шестнадцатеричная система счисления.

Наиболее удобной и короткой по записи является шестнадцатеричной СС. Данная СС имеет набор цифр <0, 1, 2, 3,. . ., 9, А, В, С, D, Е, F>, т.е основание системы р = 16. Для изображения чисел в шестнадцатеричной СС требуются 16 цифр. Для обозначения первых десяти цифр используются цифры десятичной СС, а для изображения шести ос­тальных — шесть заглавных (прописных) букв латинского алфавита А, В, С, D, Е, F, хотя можно было бы использовать любые другие шесть знаков.

По формуле (2.2) шестнадцатеричное число можно представить так:

А 16 = an 16 n + an-1 16 n-1 + an-2 16 n-2 + … + a1 16 1 + a 16 0 + a-1 16 -1 + a-2 16 -2 + … + a-m 16 -m

Не нашли то, что искали? Воспользуйтесь поиском:

Идёт приём заявок

Подать заявку

Для учеников 1-11 классов и дошкольников

8 класс. Системы счисления.

1. В какой системе счисления представлена информация, хранящаяся в компьютере?

а) троичной; б) двоичной; в) десятичной; г) двенадцатеричной.

2 . Преимущество двоичной системы счисления состоит в том, что

а) двоичный код позволяет экономить память компьютера;

б) электронные элементы с двумя состояниями наиболее просты в конструктивном исполнении;

в) электронные элементы с двумя состояниями потребляют меньше электроэнергии;

г) двоичный код не вызывает сбоя компьютера.

3. Восьмеричная система счисления отличается от шестнадцатеричной

а) количеством операций над числом в секунду;

б) глубиной вложенности операций;

в) количеством цифр, используемых для записи числа;

г) степенью компьютеризации.

4. Какое количество цифр используется в троичной системе счисления?

а) 3; б)11; в) 10;г) 2.

5. В шестнадцатеричной системе счисления символ F используется для обозначения

а) конца файла; б) числа 16;в) конца строки; г) числа 15.

6. Переведите из двоичной системы счисления в десятичную число 101010101.

а) 361; б) 564; в) 455; г) 341.

7. Переведите из десятичной системы счисления в двоичную число 216.

а) 11001100; б) 11011000; в) 11100000; г) 11001000.

8. Число 1116 в двоичной системе счисления равно

а) 1010101; б) 10011; в) 10001; г) 1000010.

9. Число ЕЕ16 в двоичной системе счисления равно

а) 110011; б) 11101110; в) 11110000; г) 10101010.

10. Число Е216 в десятичной системе счисления равно

а) 10000; б) 456; в) 226; г) 2310.

11. Число 3210 равно числу

а) 1000002; б) 358; в) 2116; г) 100002.

12. Сумма 1012 + 1002 + 1102, равна

а) 10112; б) 10012; в) 00012; г) 11112.

13. Выполните действие: 1111000012 + 1000112.

а) 10000001002; б) 10011001102; в) 10000111102; г) 10000011002.

14. Какое из равенств верно?

а) 510 = 000001112; б) 4710 = 1011112; в) 1310 = 000111112; г) 2 10 = 000010002.

15. Запись числа 100

а) отсутствует в двоичной системе счисления;

б) существует в двоичной, десятичной, восьмеричной и шестнадцатеричной системах счисления;

в) отсутствует в десятичной системе счисления;

г) отсутствует в восьмеричной системе счисления;

д) отсутствует в шестнадцатеричной системе счисления.

8 класс. Системы счисления.

1. В какой системе счисления представлена информация, хранящаяся в компьютере?

а) троичной; б) двоичной; в) десятичной; г) двенадцатеричной.

2 . Преимущество двоичной системы счисления состоит в том, что

а) двоичный код позволяет экономить память компьютера;

б) электронные элементы с двумя состояниями наиболее просты в конструктивном исполнении;

в) электронные элементы с двумя состояниями потребляют меньше электроэнергии;

г) двоичный код не вызывает сбоя компьютера.

3. Восьмеричная система счисления отличается от шестнадцатеричной

а) количеством операций над числом в секунду;

б) глубиной вложенности операций;

в) количеством цифр, используемых для записи числа;

г) степенью компьютеризации.

4. Какое количество цифр используется в троичной системе счисления?

а) 3; б)11; в) 10;г) 2.

5. В шестнадцатеричной системе счисления символ F используется для обозначения

а) конца файла; б) числа 16;в) конца строки; г) числа 15.

6. Переведите из двоичной системы счисления в десятичную число 101010101.

а) 361; б) 564; в) 455; г) 341.

7. Переведите из десятичной системы счисления в двоичную число 216.

а) 11001100; б) 11011000; в) 11100000; г) 11001000.

8. Число 1116 в двоичной системе счисления равно

а) 1010101; б) 10011; в) 10001; г) 1000010.

9. Число ЕЕ16 в двоичной системе счисления равно

а) 110011; б) 11101110; в) 11110000; г) 10101010.

10. Число Е216 в десятичной системе счисления равно

а) 10000; б) 456; в) 226; г) 2310.

11. Число 3210 равно числу

а) 1000002; б) 358; в) 2116; г) 100002.

12. Сумма 1012 + 1002 + 1102, равна

а) 10112; б) 10012; в) 00012; г) 11112.

13. Выполните действие: 1111000012 + 1000112.

а) 10000001002; б) 10011001102; в) 10000111102; г) 10000011002.

14. Какое из равенств верно?

а) 510 = 000001112; б) 4710 = 1011112; в) 1310 = 000111112; г) 2 10 = 000010002.

15. Запись числа 100

а) отсутствует в двоичной системе счисления;

б) существует в двоичной, десятичной, восьмеричной и шестнадцатеричной системах счисления;

в) отсутствует в десятичной системе счисления;

г) отсутствует в восьмеричной системе счисления;

д) отсутствует в шестнадцатеричной системе счисления.

• Гончаровская Светлана АнатольевнаНаписать 4424 10.12.2015

Номер материала: ДВ-247864

Не нашли то что искали?

Вам будут интересны эти курсы:

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

3.6. Восьмеричная и шестнадцатеричная системы счисления

При наладке аппаратных средств и написании новых программ (особенно на языках низкого уровня типа ассемблера) часто возникает необходимость посмотреть содержимое той или иной ячейки памяти машины. Но там все заполнено длинными последовательностями нулей и единиц, очень неудобных для восприятия. Кроме того, естественные восможности человеческого мышления не позволяют быстро и точно оценить величину числа, представленного, например, комбинацией из 16 нулей и единиц. Для облегчения восприятия двоичного числа решили разбить его на группы разрядов, например по три и четыре разряда. Разбив таким образом число можно закодировать каждую группу разрядов отдельно, сократив при этом количество символов необходимых для записи числа. Последовательность из 3-х бит имеет 8 комбинаций, а из 4-х – 16 комбинаций. Для кодирования трех битов (триад) используются цифры от 0 до 7, а для кодирования четырех битов (тетрад) – цифры от 0 до 9 и буквы A, B, C, D, E, F (таблица 3.4). Полученные системы, имеющие в основании 8 и 16, назвали соответственно восьмиричной и шестнадцатиричной.

Таблица 3.4.

Восьмиричная система счисления		Шестнадцатиричная система счисления
Цифра	Триада	Цифра	Тетрада
0	000	0	0000
1	001	1	0001
2	010	2	0010
3	011	3	0011
4	100	4	0100
5	101	5	0101
6	110	6	0110
7	111	7	0111
		8	1000
		9	1001
		A	1010
		B	1011
		C	1100
		D	1101
		E	1110
		F	1111

Для перевода восьмиричного или шестнадцатиричного числа в двоичную форму достаточно заменить каждую цифру этого числа соответствующим трехзначным двоичным числом или четырехзначным двоичным числом (таблица 3.4). При этом отбрасываются ненужные нули в старших и младших (для дробной части) разрядах.

Пример. Перевести .

.

Пример. Перевести .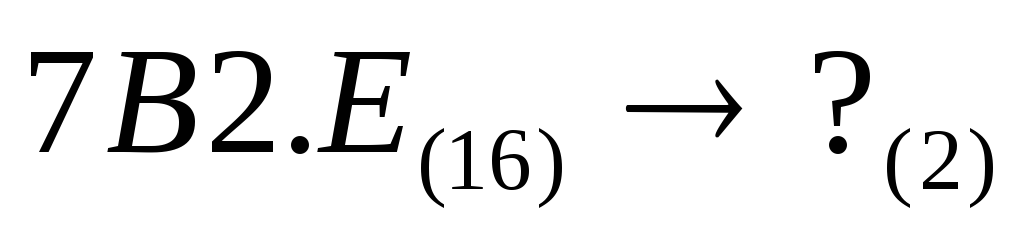

.

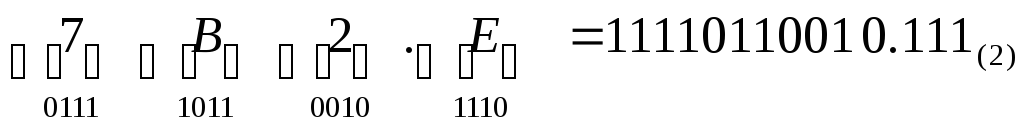Для перехода от двоичной к восмиричной (шестнадцатиричной) системе поступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмиричной (шестнадцатиричной) цифрой.

Пример. Перевести .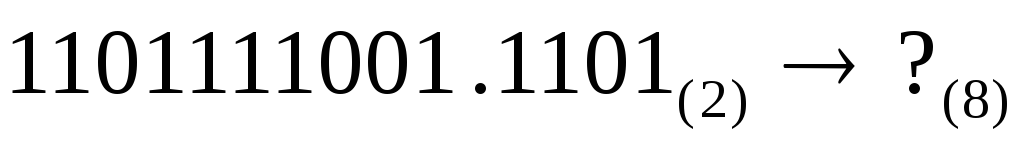

.

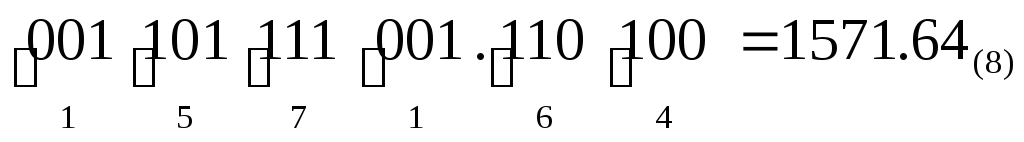Пример. Перевести .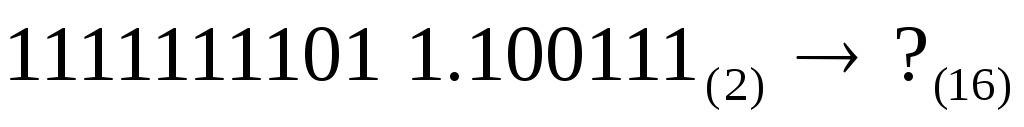

.

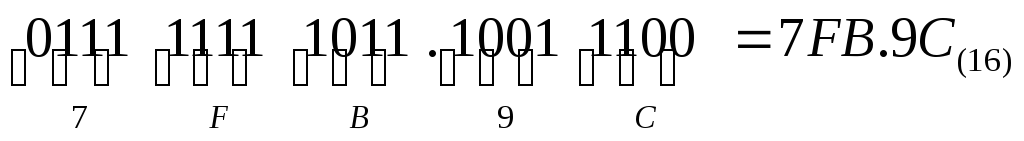Перевод из восьмиричной системы в шестнадцатиричную и обратно осуществляется через двоичную систему при помощи триад и тетрад.

Пример. Перевести .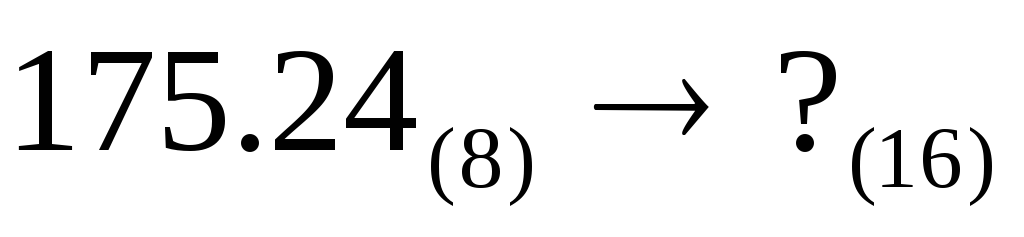

.

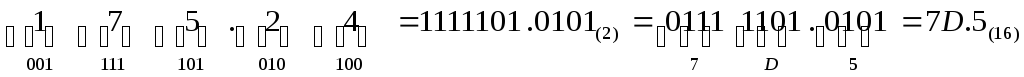3.7. Перевод чисел из системы с основанием p в систему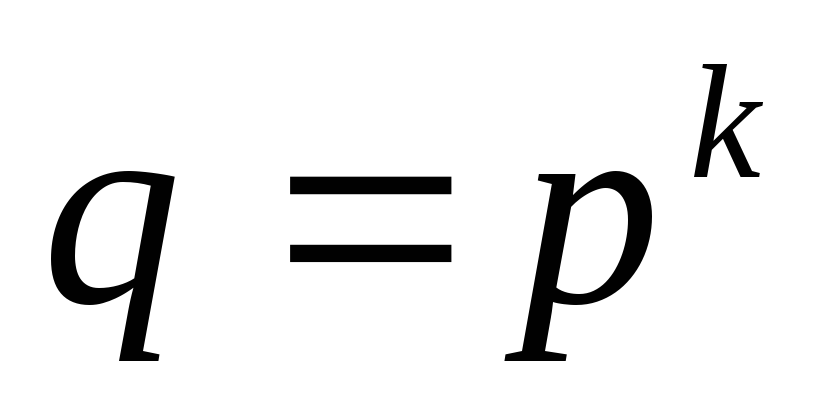

Рассмотренный выше метод взаимного перевода чисел между двоичной и восьмиричной (шестнадцатиричной) системами счисления заслуживает более детального рассмотрения. Обозначим основание двоичной системы через p. Тогда основание восьмиричной системы , а для шестнадцатиричной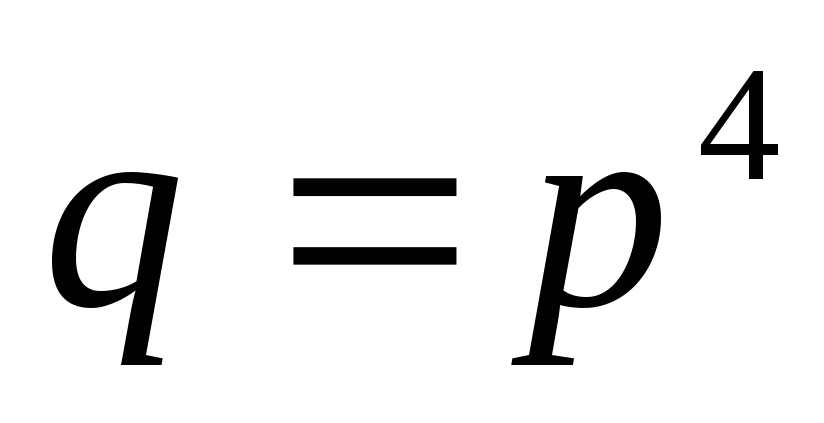. Именно поэтому перевод чисел между двоичной и восьмиричной (шестнадцатиричной) системами осуществляется простой группировкой цифр. При этом показатель степени определяет по сколько цифр системы с меньшим основанием необходимо группировать, чтобы получить одну цифру системы с большим основанием. Аналогичный метод справедлив для любыхp и q, связанных соотношением .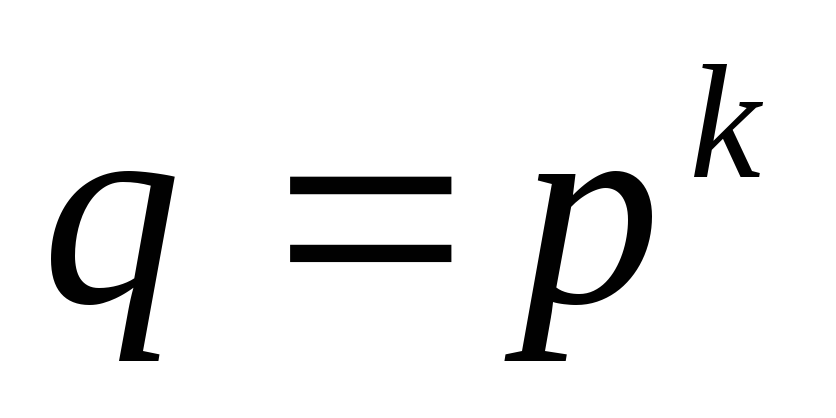

Пример. Перевести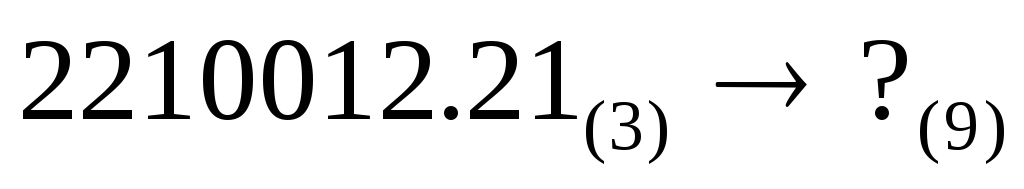

Здесь p= 3, q= 9, k= 2. Составляем таблицу соответствия между системой с основанием 3 и системой с основанием 9.

Девятиричная система	Троичная система
0	00
1	01
2	02
3	10
4	11
5	12
6	20
7	21
8	22

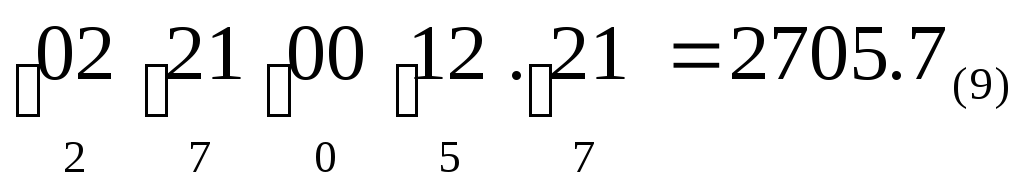
3.8. Перевод чисел из системы основанием p в систему q (общий случай)

Предположим, что мы выполняем преобразование из системы с основанием p в систему с основанием q, когда p и q произвольные целые положительные числа. В основе большинства методов лежат операции умножения и деления, которые выполняются по одной из следующих схем (преобразование целых чисел).

Метод 1. Деление на q, при помощи арифметических действий над величинами с позиционным представлением по основанию p. Выше он рассматривался (метод деления для перевода чисел из десятичного представления в недесятичное) для частного случая когда p= 10, а q произвольно.

Метод 2. Умножение на p, при помощи арифметики основания q. Выше он рассматривался (метод перевода чисел из недесятичного представления в десятичное) для частного случая когда p произвольно, а q= 10.

Заметим, что на практике достаточно сложно выполнять арифметические действия над числами, записанными в системе счисления с произвольным основанием. Поэтому преобразование из системы с основанием p в систему с основанием q, когда p и q произвольные целые положительные числа, выполняется с использованием промежуточной системы счисления, выбираемой по соображениям удобства (десятичной, если вычисления производятся вручную и двоичной, если на компьютере).

Двоичная, восьмеричная и шестнадцатеричная системы счисления

Замечание 1

Данные системы счисления относятся к позиционным.

Двоичная система счисления

Эта система счисления свое название получила в результате того, что содержит в своем основании всего две цифры – $0$ и $1$. Таким образом, число $2$ и его степени $2, 4, 8$ и т.д. играют особую роль. Самая правая цифра числа показывает число единиц, следующая – число двоек, следующая — число четверок и т.д.

В двоичной системе счисления для формирования числа используются всего две цифры: $0$ и $1$. Пределом разряда является $1$, и как только при счете разряд достигает своего максимального значения, он обнуляется, а при этом образуется новый разряд. Ниже в таблице приведены соответствия двоичных и десятичных чисел.

Рисунок 1.

Замечание 2

Используя двоичную систему счисления, можно закодировать любое натуральное число, представляя его как последовательность нулей и единиц. В двоичном виде можно представить не только числа, но и любую другую информацию: тексты, изображения, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что оно легко реализуется технически.

Именно на принципе двоичного кодирования работает вся вычислительная техника: $1$ означает, что электрический сигнал прошел, а $0$ – сигнал отсутствует. Наглядно это можно рассмотреть на примере перфокарт, которые использовались в вычислительных машинах первых поколений. Как уже упоминалось выше: в перфокартах пробивались отверстия в соответствующих рядах и столбцах цифр, таким образом, кодировались и сохранялись программы, поскольку жестких дисков, и тем более оптических, в те времена не было. Затем программы считывались при помощи электрического сигнала, который, если проходил в отверстие, значит, это был код $1$ и, наоборот, если не проходил сигнал – это был код $0$. Аналогичным способом в настоящее время записываются оптические диски при помощи лазерного луча, прожигающего невидимые микроотверстия на поверхности специальных дисков. Принцип считывания закодированной информации с диска аналогичен предыдущему.

Из всего вышесказанного можно сделать вывод, что компьютер «понимает» всего два числа: $0$ и $1$. И именно один двоичный разряд и является минимальной единицей измерения памяти компьютера, которая называется «бит», т.е. бит – это ячейка памяти компьютера, в которую можно записать $1$ или $0$.

Другой единицей измерения информации является байт.

Байт – это восемь подряд расположенных битов. Общее количество комбинаций двоичных значений в байте равно $28 = 256$.

$1 \ байт = 8 \ битам$; $1 \ Кб = 210 \ байта = 1024 \ байта$; $1 \ Мб = 210 \ Кбайт = 1024 \ Кбайта$; $1 \ Гб = 210 \ байта = 1024 \ килобайта$; $1 \ Тб = 210 \ гигабайта = 1024 \ гигабайта$.

Замечание 3

Достоинства двоичной системы счисления заключаются в ее простоте, благодаря которой она широко используется в технике. Устройства, работающие в двух состояниях (включено, выключено), наиболее помехоустойчивы, и, как следствие, более надежны.

Восьмеричная система счисления

В основе данной системы счисления находятся $8$ цифр: от $0$ до $7$. Цифра $1$, указанная в самом младшем разряде, означает, как и в десятичном числе просто $1$. Та же цифра $1$ в следующем разряде означает $8$, в следующем $64$ и т.д. Число $100$ (восьмеричное) – это число $64$ (десятичное). Чтобы перевести в двоичную систему, например, число $611$ (восьмеричное), необходимо каждую цифру числа заменить эквивалентной тройкой двоичных чисел. Для перевода многозначного двоичного числа в восьмеричную систему счисления необходимо разбить его на тройки по правую сторону и по левую и заменить каждую тройку соответствующей восьмеричной цифрой.

В таблице приведены соответствия чисел в восьмеричной и десятичной системах.

Рисунок 2.

В технике данная система находит широкое применение, так с помощью нее можно компактно записывать двоичные числа.

Шестнадцатеричная система счисления

Запись числа в восьмеричной системе счисления достаточно компактная, но еще компактнее она выглядит в шестнадцатеричной системе. В основу данной системы входят цифры от $0$ до $9$ и первые буквы латинского алфавита: $A$, $B$, $C$, $D$, $E$, $F$.

Цифра $1$, записанная в самом младшем разряде, означает просо единицу. Цифра $1$ в следующем разряде – $16$ (десятичное число), в следующем – $256$ и т.д. Цифра, обозначенная латинской буквой $F$, расположенная в самом младшем разряде означает $15$ ( десятичное число).

В таблице приведены соответствия чисел в шестнадцатеричной и десятичной системах.

Рисунок 3.

Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является $8$-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы $IBM/360$, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с $8$-битными символами, как, например, $PDP-11$ или $БЭСМ-6$) использовали восьмеричную систему.

Системы счисления: двоичная, восьмеричная, десятичная, шестнадцатеричная

«Системы счисления: двоичная, восьмеричная, десятичная, шестнадцатеричная».

Автор: Гребенников Александр Николаевич
Должность: учитель информатики

Учебное заведение: ГБОУ школа – интернат № 67
Населённый пункт: Пушкинский район Санкт–Петербурга
Наименование материала: статья
Тема: «Системы счисления: двоичная, восьмеричная, десятичная, шестнадцатеричная».

Системы счисления: двоичная, восьмеричная, десятичная, шестнадцатеричная.

Система счисления – это способ записи чисел. Обычно, числа записываются с помощью специальных знаков – цифр (хотя и не всегда). Если вы никогда не изучали данный вопрос, то, по крайней мере, вам должны быть известны две системы счисления – это арабская и римская. Следует отметить, важную роль нуля. «Открытие» этой цифры в истории человечества сыграло большую роль в формировании позиционных систем счисления.

Каждая позиционная система использует определенный алфавит цифр и основание. В позиционных системах счисления основание системы равно количеству цифр (знаков в ее алфавите) и определяет, во сколько раз различаются значения цифр соседних разрядов числа.

В первой используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 (10 цифр) — это позиционная система счисления. А во второй – I, V, X, L, C, D, M (1, 5, 10, 50, 100, 500, 1000) — это непозиционная система счисления.

В позиционных системах счисления количество, обозначаемое цифрой в числе, зависит от ее позиции, а в непозиционных – нет.

Например:

11 – здесь первая единица обозначает 10, а вторая – 1.
I I – здесь обе единицы обозначают единицу.

Основание системы счисления – это количество знаков, которое используется для записи цифр.

Разряд — это позиция цифры в числе. Разрядность числа — количество цифр, из которых состоит число (например, 362 — трехразрядное число, 1001101 — восьмиразрядное число). Разряды нумеруются справа на лево (например, в числе 793 семёрка занимает первый разряд, а тройка — третий).

Итак, в позиционной системе счисления числа записываются таким образом, что каждый следующий (движение справа на лево) разряд больше другого на степень основания системы счисления.

456, 567, 678 – здесь цифра 6 в первом случае обозначает 6, во втором – 60, а в третьем – 600.

XXV, XVI, XII – здесь, где бы ни стояла цифра X, она везде обозначает десять единиц. Другими словами, величина, обозначаемая знаком X, не зависит от его позиции.

В мире наиболее распространены позиционные системы счисления. Помимо знакомой всем с детства десятичной (где используется 10 цифр от 0 до 9), в технике широкое распространение нашли такие системы счисление как двоичная (используются цифры 0 и 1), восьмеричная (используются 8 цифр от 0 до 7), шестнадцатеричная (используются 16 цифр 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F).

Сложение, умножение и другие математические операции в позиционных системах счисления выполнить легче, чем в непозиционных, т.к. математические операции осуществляются по несложным алгоритмам (например, умножение в столбик, сравнение двух чисел). 

Одно и тоже число (значение) можно представить в различных системах счисления. Представление числа при этом различно, а значение остается неизменным.

Двоичная система счисления.

Почему двоичная система счисления так распространена?

Двоичной системой счисления люди начали пользоваться очень давно. Древние племена Австралии и островов Полинезии использовали эту систему в быту. Так, полинезийцы передавали необходимую  информацию, выполняя два вида ударов по барабану: звонкий и глухой. Это было примитивное представление двоичной системы счисления.

Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания. Поэтому для кодирования информации в компьютере вместо привычной десятичной системы счисления используется двоичная система счисления.

В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)

Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.

В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни. 

Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.

Для обозначения системы счисления, в которой представляется число, используют нижний индекс, указывающий основание системы. Например, 11011 ₂   —  число в двоичной системе счисления.

Цифры в двоичном числе являются коэффициентами его представления в виде суммы степеней с основанием ₂, например:

2 1 0

101 ₂ =1⋅2 ² +0⋅2 ¹ +1⋅2 ⁰ .

 В десятичной системе счисления это число будет выглядеть так:

2 1 0 

110 ₂ =4+0+1=5 .

 Для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на 2  до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример:

Переведём десятичное число 15 в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так:

 

-14

7

2

1

-6

3

2

1

-2

1

1

 

Получили 15 ₁₀ =1111 ₂.

Попробуем считать в двоичной системе:
 0 – это ноль
 1 – это один (и это предел разряда)
 10 – это два
 11 – это три (и это снова предел)
 100 – это четыре
 101 – пять
 110 – шесть
 111 – семь и т.д.
Перевод чисел из двоичной системы счисления в десятичную.

Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные. 

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:

1567 = 1000 + 500 + 60 + 7

Можно пойти еще дальше и разложить так:

3 2 1 0

1567 ₁₀= 1 * 10³ + 5 * 10² + 6 * 10¹ + 7 * 10⁰

Посмотрите на эту запись внимательно. Здесь цифры 1, 5, 6 и 7 — это набор цифр из которых состоит число 1567. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.

Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:

6 5 4 3 2 1 0

1000101₂ = 1*2⁶ + 0*2⁵ + 0*2⁴ + 0*2³ + 1*2² + 0*2¹ + 1*2⁰

Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:

1*2⁶ + 0*2⁵ + 0*2⁴ + 0*2³ + 1*2² + 0*2¹ + 1*2⁰ = 64 + 0 + 0 + 0 + 4 + 0 + 1 = 69₁₀

Т.е. число 10001001 по основанию 2 равно числу 69 по основанию 10. Записать это можно так:

1000101₂ = 69₁₀

Восьмеричная система счисления

Итак, современное «железо понимает» лишь двоичную систему счисления. Однако человеку трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводит числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко. В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко.

В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствуют набор из трех цифр в двоичной системе счисления:

000 – 0
001 – 1
 010 – 2
 011 – 3
 100 – 4
 101 – 5
 110 – 6
 111 – 7

Для преобразования двоичного числа в восьмеричное достаточно разбить его на тройки (триады) и заменить их соответствующими им цифрами из восьмеричной системы счисления. Разбивать на тройки нужно начинать с конца, а недостающие цифры в начале заменить нулями. Например:

2²2¹2⁰

4 2 1 4 2 1 4 2 1 4 2 1 (Складываем цифры над единицами)

1110101₂ = 1 011 101 = 001 110 101 = 1 6 5 = 165₈

Т.е число 1011101 в двоичной системе счисления равно числу 165 в восьмеричной системе счисления. Или 1110101₂ = 165₈.

Обратный перевод. Допустим, требуется перевести число 103₈ (не заблуждайтесь! 100 в восьмеричной системе – это не 103 в десятичной) в двоичную систему счисления.

2²2¹2⁰

4 2 1 4 2 1  4 2 1 4 2 1 (1=421, 0=421, 3=42+1 зелёные – 0, красные – 1)

103₈ = 1 0 3 = 001 000 011 = 001000011 = 1000011₂ 

Перевод восьмеричного числа в десятичное можно осуществить по уже знакомой схеме:

2 1 0

672₈ = 6 * 8² + 7 * 8¹ + 2 * 8⁰ = 6 * 64 + 56 + 2 = 384 + 56 + 2 = 442₁₀
2 1 0

100₈ = 1 * 8² + 0 * 8¹ + 0 * 8⁰ = 64₁₀

Шестнадцатеричная система счисления

Шестнадцатеричная система счисления, так же как и восьмеричная, широко используется в компьютерной науке из-за легкости перевода в нее двоичных чисел. При шестнадцатеричной записи числа получаются более компактными.

В шестнадцатеричной системе счисления используются цифры от 0 до 9 и шесть первых латинских букв – A (10), B (11), C (12), D (13), E (14), F (15). 

При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда (тетрады), начиная с конца. В случае, если количество разрядов не делится нацело, то первая четверка дописывается нулями впереди. Каждой четверке соответствует цифра шестнадцатеричной системе счисления:

Например:

2³2²2¹2⁰

8 4 2 1 8 4 2 1 8 4 2 1 8 4 2 1 (Складываем цифры над единицами)

 _11011010101 = 0110 1101 0101 = 6 13 5 = 6D5

Если потребуется, то число 6D5 можно перевести в десятичную систему счисления следующим образом (D следует заменить на соответствующее данному символу число в десятичной системе счисления – это 13):

2 1 0

6D5₁₆ = 6 * 16² + 13 * 16¹ + 5 * 16⁰ = 6 * 256 + 208 + 5 = 1749₁₀

Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи — это FF.

1 0

FF₁₆ = 15 * 16¹ + 15 * 16⁰ = 240 + 15 = 255 

255 – это максимальное значение одного байта, равного 8 битам: 1111 1111 = FF. Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов. Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние

Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?

Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.

Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.

Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 – соответственно, третья и четвертая степени числа 2).

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

Например:

Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответ-ствующей восьмеричной (шестнадцатеричной) цифрой.

Например,

Как перевести целое число из десятичной системы в любую другую позиционную систему счисления?

При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q–1. Число в системе с основанием q записывается как последо-вательность остатков от деления, записанных в обратном порядке, начиная с последнего.

Пример: Перевести число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Ответ: 75₁₀ = 1 001 011₂ = 113₈ = 4B₁₆.

Как пеpевести пpавильную десятичную дpобь в любую другую позиционную систему счисления?

Пpи переводе правильной десятичной дpоби в систему счисления с основанием q необходимо сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть пpоизведения. Число в новой системе счисления записывается как последовательность полученных целых частей пpоизведения.

Умножение пpоизводится до тех поp, пока дpобная часть пpоизведения не станет pавной нулю. Это значит, что сделан точный пеpевод. В пpотивном случае пеpевод осуществляется до заданной точности. Достаточно того количества цифp в pезультате, котоpое поместится в ячейку.

Пример: Перевести число 0,35 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Ответ: 0,35₁₀ = 0,01011₂ = 0,263₈ = 0,59₁₆ .

Как пеpевести число из двоичной (восьмеpичной, шестнадцатеpичной) системы в десятичную?

При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления.

Примеpы:

4.9. Сводная таблица переводов целых чисел из одной системы счисления в другую

Рассмотрим только те системы счисления, которые применяются в компьютерах — десятичную, двоичную, восьмеричную и шестнадцатеричную.

Для определенности возьмем произвольное десятичное число, например 46, и для него выполним все возможные последовательные переводы из одной системы счисления в другую.

Порядок переводов определим в соответствии с рисунком:

На этом рисунке использованы следующие обозначения:

· в кружках записаны основания систем счисления;

· стрелки указывают направление перевода;

· номер рядом со стрелкой означает порядковый номер соответствующего примера в сводной таблице 4.1.

Например: означает перевод из двоичной системы в шестнадцатеричную, имеющий в таблице порядковый номер 6.

Сводная таблица переводов целых чисел

Таблица 4.1.

Как производятся арифметические операции в позиционных системах счисления?

Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.

Сложение

Таблицы сложения легко составить, используя Правило Счета.

Сложение в двоичной системе

Сложение в восьмеричной системе

Сложение в шестнадцатиричной системе

 

При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.

Пример 1. Сложим числа 15 и 6 в различных системах счисления.

 

 

Шестнадцатеричная: F16+616

Ответ: 15+6 = 2110 = 101012 = 258 = 1516. Проверка. Преобразуем полученные суммы к десятичному виду: 101012 = 24 + 22 + 20 = 16+4+1=21, 258 = 2*81 + 5*80 = 16 + 5 = 21, 1516 = 1*161 + 5*160 = 16+5 = 21.

Пример 2. Сложим числа 15, 7 и 3.

Шестнадцатеричная: F16+716+316

Ответ: 5+7+3 = 2510 = 110012 = 318 = 1916. Проверка: 110012 = 24 + 23 + 20 = 16+8+1=25, 318 = 3*81 + 1*80 = 24 + 1 = 25, 1916 = 1*161 + 9*160 = 16+9 = 25.

Пример 3. Сложим числа 141,5 и 59,75.

Ответ: 141,5 + 59,75 = 201,25₁₀ = 11001001,01₂ = 311,2₈ = C9,4₁₆

Проверка. Преобразуем полученные суммы к десятичному виду:
11001001,01₂ = 2⁷ + 2⁶ + 2³ + 2⁰ + 2^-2 = 201,25
311,2₈ = 3*8² + 1•8¹ + 1*8⁰ + 2*8^-1 = 201,25
C9,4₁₆ = 12*16¹ + 9*16⁰ + 4*16^-1 = 201,25

Вычитание

Пример 4. Вычтем единицу из чисел 10₂, 10₈ и 10₁₆

Пример 5. Вычтем единицу из чисел 100₂, 100₈ и 100₁₆.

Пример 6. Вычтем число 59,75 из числа 201,25.

Ответ: 201,25₁₀ – 59,75₁₀ = 141,5₁₀ = 10001101,1₂ = 215,4₈ = 8D,8₁₆.

Проверка. Преобразуем полученные разности к десятичному виду:
10001101,1₂ = 2⁷ + 2³ + 2² + 2⁰ + 2^–1 = 141,5;
215,4₈ = 2*8² + 1*8¹ + 5*8⁰ + 4*8^–1 = 141,5;
8D,8₁₆ = 8*16¹ + D*16⁰ + 8*16^–1 = 141,5.

Умножение

Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.

Умножение в двоичной системе

Умножение в восьмеричной системе

Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям.

Пример 7. Перемножим числа 5 и 6.

Ответ: 5*6 = 30₁₀ = 11110₂ = 36₈.

Проверка. Преобразуем полученные произведения к десятичному виду:
11110₂ = 2⁴ + 2³ + 2² + 2¹ = 30;
36₈ = 3•8¹ + 6•8⁰ = 30.

Пример 8. Перемножим числа 115 и 51.

Ответ: 115*51 = 5865₁₀ = 1011011101001₂ = 13351₈.

Проверка. Преобразуем полученные произведения к десятичному виду:
1011011101001₂ = 2¹² + 2¹⁰ + 2⁹ + 2⁷ + 2⁶ + 2⁵ + 2³ + 2⁰ = 5865;
13351₈ = 1*8⁴ + 3*8³ + 3*8² + 5*8¹ + 1*8⁰ = 5865.

Деление

Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.

Пример 9. Разделим число 30 на число 6.

 

Ответ: 30 : 6 = 5₁₀ = 101₂ = 5₈.

Пример 10. Разделим число 5865 на число 115.

Восьмеричная: 13351₈ :163₈

Ответ: 5865 : 115 = 51₁₀ = 110011₂ = 63₈.

Проверка. Преобразуем полученные частные к десятичному виду:
110011₂ = 2⁵ + 2⁴ + 2¹ + 2⁰ = 51; 63₈ = 6*8¹ + 3*8⁰ = 51.

Пример 11. Разделим число 35 на число 14.

Восьмеричная: 43₈ : 16₈

Ответ: 35 : 14 = 2,5₁₀ = 10,1₂ = 2,4₈.

Проверка. Преобразуем полученные частные к десятичному виду:
10,1₂ = 2¹ + 2 ^-1 = 2,5;
2,4₈ = 2*8⁰ + 4*8^-1 = 2,5.

Тестовые задания на тему Системы счисления

Тест «Системы счисления»

1. Системой счисления называют:

а) алфавит; б) способ представления чисел; в) способ представления чисел и соответствующие ему правила действия над числами; г) набор чисел в определенной последовательности;

1. Системы счисления делятся на:

а) четные и нечетные; б) позиционные и непозиционные; в) троичные, семеричные, десятичные; г) двоичные, восьмеричные, шестнадцатеричные;

1. В восьмеричной системе счисления присутствуют символы:

а) 0, 1, 2, 3, 4, 5, 6, 7, 8; б) 0, 1, 2, 3, 4, 5, 6, 7; в) 1, 2, 3, 4, 5, 6, 7, 8; г) 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F

1. В шестнадцатеричной системе счисления присутствуют символы:

а) 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16; б) 0, 1, 2, 3, 4, 5, 6, 7; в) 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F; г) 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, А, В, С, D, E, F;

1. В двоичной системе счисления присутствуют символы:

а) 1, 2; б) 0, 1; в) а, в; в) все перечисленные

1. Числу 10010₂ соответствует число … в десятичной системе счисления:

а) 18; б) 17; в) 100; г) 36;

1. Числу 126₈ соответствует число … в десятичной системе счисления:

а) 15; б) 86; в) 688; г) 200;

1. Числу 243₁₀ соответствует число … в восьмеричной системе счисления:

а) 179; б) 342; в) 100110; г) 363;

1. Числу 823₁₀ соответствует число … в шестнадцатеричной системе счисления:

а) 10011; б) 337; в) АВ; г) 12С;

1. Римская система относится к:

а) непозиционной системе; б) позиционной системе; в) другой вариант;

1. Десятичная система относится к:

а) непозиционной системе; б) позиционной системе; в) другой вариант;

1. Числу МСХХIII соответствует десятичное число:

а) 34; б) 1117; в) 1123; г) 73;

1. Числу 1968 соответствует римское:

а) нет правильного ответа; б) MDCCCCLXIIIV; в) MMLXVIII; г) МСМLXVIII;

1. Числу CXIX соответствует десятичное число:

а) 119; б) 129; в) 69; г) 59;

1. Жители Древнего Египта использовали при счете:

а) позиционную систему счисления; б) непозиционную систему счисления;

1. Единичная система счисления относится к:

а) позиционной системе счисления; б) непозиционной системе счисления;

1. Самая древняя система записи чисел:

а) древнеегипетская; б) римская; в) единичная; г) десятичная;

1. ЭВМ выполняет арифметические расчеты в системе счисления:

а) десятичной; б) двоичной; в) единичной; г) шестнадцатеричной;

19. Самая древняя система счисления –

а) двоичная; б) римская; в) древнеегипетская; г) единичная;

20. В исчислении времени, в чередовании месяцев года сохранились остатки СС:

а) десятичной; б) двенадцатеричной; в) двоичной; г) восьмеричной.

Ответы системы счисления

вопрос	Ответ
1	В
2	Б
3	Б
4	В
5	Б
6	А
7	Б
8	Г
9	Б
10	А
11	Б
12	В
13	Г
14	А
15	Б
16	Б
17	В
18	Б
19	Г
20	Б