Восьмеричная и шестнадцатеричные системы счисления. Компьютерные системы счисления. Правило перевода целых десятичных чисел

Похожие презентации:

Пиксельная картинка

Информационная безопасность. Методы защиты информации

Электронная цифровая подпись (ЭЦП)

Этапы доказательной медицины в работе с Pico. Первый этап

История развития компьютерной техники

От печатной книги до интернет-книги

Краткая инструкция по CIS – 10 шагов

Информационные технологии в медицине

Информационные войны

Моя будущая профессия. Программист

Восьмеричная и
шестнадцатеричные системы
счисления. Компьютерные системы
счисления.
Правило перевода целых
десятичных чисел в систему
счисления с основанием q.
Цели урока:
образовательные – выяснить, почему именно двоичная
система счисления используется в компьютере, показать
связь между двоичной, восьмеричной и
шестнадцатеричной системами счисления;
сформировать знания и умения перевода небольших
десятичных и двоичных чисел в восьмеричную и

шестнадцатеричную системы счисления.
развивающие – умение анализировать любую
позиционную систему счисления как знаковую систему;
воспитательные – понимание роли фундаментальных
знаний как основы современных информационных
технологий.
Задачи:
1) рассмотрение восьмеричной системы счисления как
знаковой системы;
2) рассмотрение правила перевода целых десятичных
чисел в восьмеричную систему счисления
3) рассмотрение шестнадцатеричной системы
счисления как знаковой системы;
4) рассмотрение правила перевода целых десятичных
чисел в шестнадцатеричную систему счисления;
5) рассмотрение правила перевода двоичных чисел в
шестнадцатеричную и восьмеричную системы

счисления;
6) характеристика двоичной, восьмеричной и
шестнадцатеричной систем счисления с точки зрения их
использования в компьютерной технике.
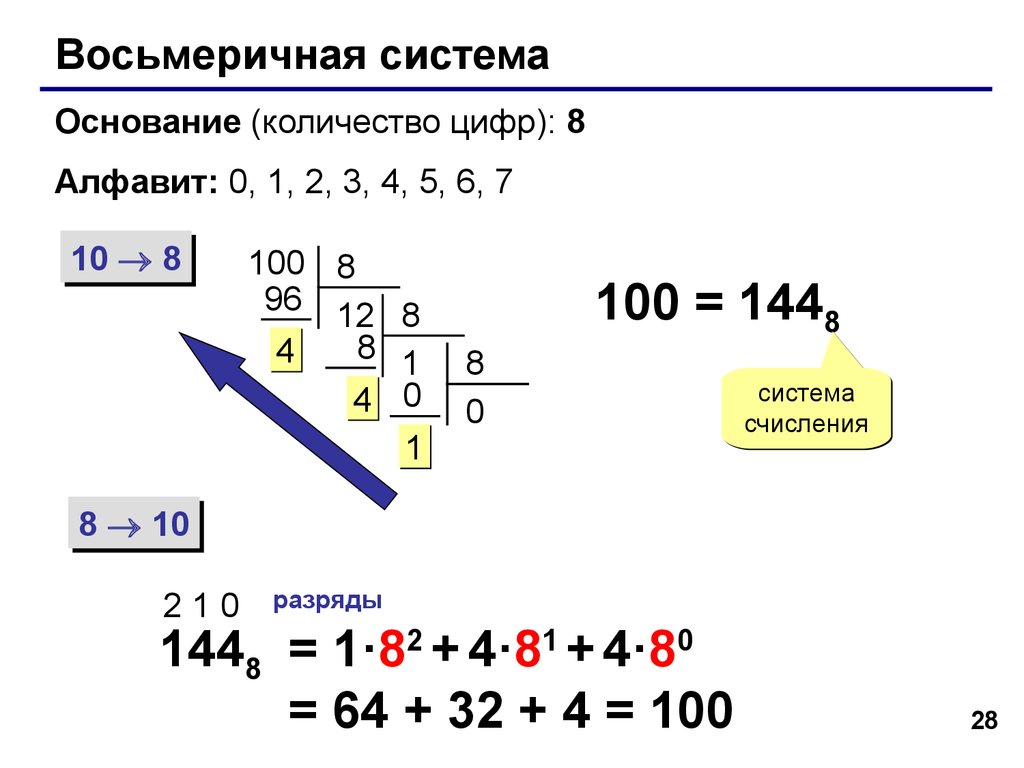
Восьмеричная система
счисления
Восьмеричной системой счисления называется
позиционная система счисления с основанием 8.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.
an–1an–2…a1a0 = an–1 8n–1+an–2 8n–2+…+a0 80
Пример: 10638 =1 83 +0 82+6 81+3 80=56310.
Для перевода целого восьмеричного числа в десятичную
систему счисления следует перейти к его развёрнутой
записи и вычислить значение получившегося выражения.
Для перевода целого десятичного числа в восьмеричную
систему счисления следует последовательно выполнять
деление данного числа и получаемых целых частных на 8 до
тех пор, пока не получим частное, равное нулю.
Шестнадцатеричная
система счисления
Основание: q = 16.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
3АF16 =3 162+10 161+15 160 =768+160+15=94310.
Переведём десятичное число 154 в шестнадцатеричную
систему счисления:
154 16
-144
9
16
10
(А)
9
0
15410 = 9А16
Правило перевода целых десятичных чисел
в систему счисления с основанием q
1) последовательно выполнять деление данного числа и
получаемых целых частных на основание новой системы
счисления до тех пор, пока не получим частное, равное нулю;
2) полученные остатки, являющиеся цифрами числа в
новой системе счисления, привести в соответствие с
алфавитом новой системы счисления;
3) составить число в новой системе счисления, записывая
его, начиная с последнего полученного остатка.
Цифровые весы
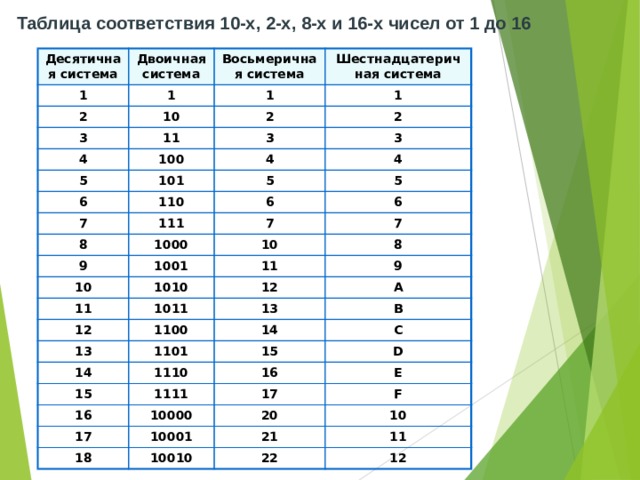
Таблица соответствия 10-х, 2-х, 8-х и 16-х чисел от 1 до 16
Десятичная
система
Двоичная
система
Восьмеричная
система
Шестнадцатеричная
система
1
1
1
1
2
10
2
2
3
11
3
3
4
100
4
4
5
101
5
5
6
110
6
6
7
111
7
7
8
1000
10
8
9
1001
11
9
10
1010
12
A
11
1011
13
B
12
1100
14
C
13
1101
15
D
14
1110
16
E
15
1111
17
F
16
10000
20
10
17
10001
21
11
18
10010
22
12
Двоичная арифметика
Арифметика двоичной системы счисления основывается
на использовании следующих таблиц сложения и
умножения:
+
0
1
0
1
0
0
1
0
0
0
1
1
10
1
0
1
«Компьютерные» системы счисления
Двоичная система используется в компьютерной технике,
так как:
двоичные числа представляются в компьютере с
помощью простых технических элементов с двумя
устойчивыми состояниями;
представление информации посредством только двух
состояний надёжно и помехоустойчиво;
двоичная арифметика наиболее проста;
существует математический аппарат, обеспечивающий
логические преобразования двоичных данных.
Двоичный код удобен для компьютера.
Человеку неудобно пользоваться длинными и
однородными
кодами.
Специалисты

заменяют
двоичные коды на величины в восьмеричной или
шестнадцатеричной системах счисления.

English     Русский Правила

4.4. Почему люди пользуются десятичной системой, а компьютеры — двоичной? 4.5. Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?

Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.

А компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:

•  
  • для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т. п.), а не, например, с десятью, — как в десятичной;
  • представление информации посредством только двух состояний надежно и помехоустойчиво;
  • возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
  • двоичная арифметика намного проще десятичной.

Недостаток двоичной системы — быстрый рост числа разрядов

, необходимых для записи чисел.4.5. Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?
Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.

Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.

Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно

в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, третья и четвертая степени числа 2).

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

Например:

Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответ-ствующей восьмеричной (шестнадцатеричной) цифрой.

Например,

Краткая информация о восьмеричной и шестнадцатеричной системах счисления

Компьютеры созданы человеком, но они работают на языке чисел. Когда мы набираем на компьютере букву, цифру или специальный символ, операционная система преобразует ввод в числа. Это связано с тем, что компьютер может понимать только позиционную систему счисления, в которой есть некоторые символы, называемые цифрами. Символы, используемые в системе счисления, отображают различные значения.

Величина каждой цифры в числе определяется с помощью цифры, места цифры в числе и основания системы счисления. Существует несколько типов систем счисления, таких как десятичная система счисления, двоичная система счисления и т. д. 

В этой статье мы обсудим восьмеричную и шестнадцатеричную системы счисления. Сначала мы поговорим о том, что такое восьмеричная система счисления и ее представление. Затем мы перейдем к обсуждению шестнадцатеричной системы счисления и ее представления.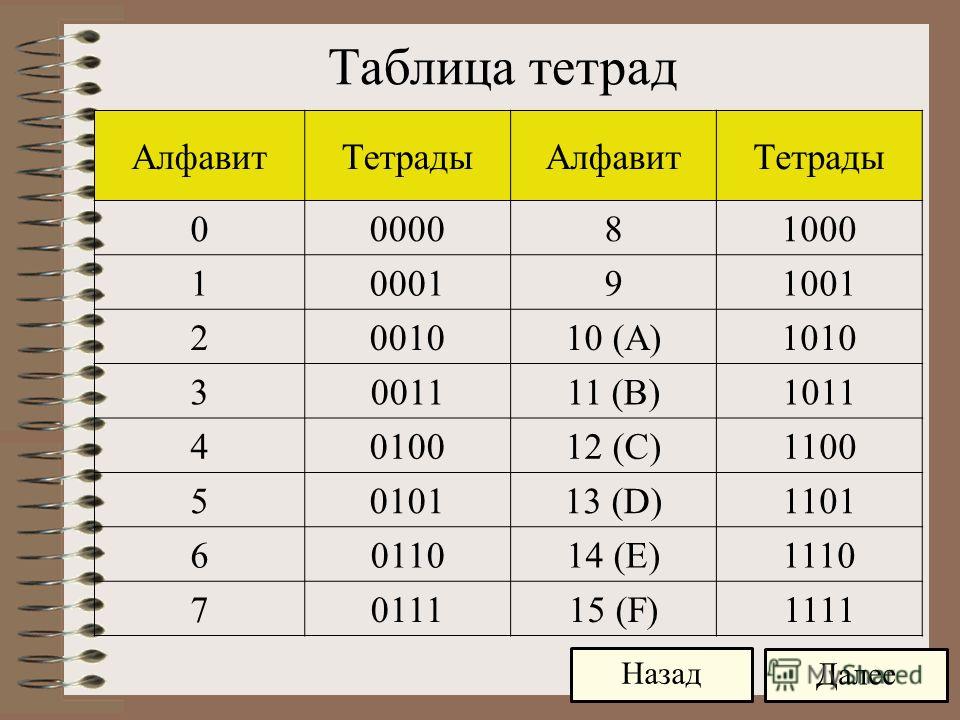

Восьмеричная система счисления

Восьмеричная система счисления, также известная как октальная, представляет собой систему счисления с основанием 8. В системе используются цифры от 0 до 7. Поэтому, если мы пишем восьмеричное число 10, оно изображает 8, а если мы записываем восьмеричное число 100, оно представляет 64. Когда мы изучаем десятичную систему счисления, каждый разряд представляется в степени 10. Но когда мы внедряем восьмеричную систему счисления, каждый разряд равен степени числа 8. 9.0003

Преобразование восьмеричных чисел очень просто. Для преобразования восьмеричного числа все, что нам нужно сделать, это сгруппировать двоичные цифры в группу из трех. Примером восьмеричной системы счисления является представление десятичного числа 74. Десятичное представление числа 74 – 1001010. В этой системе перед двоичной цифрой 1 можно поставить два нуля, и теперь мы преобразуем 74 в восьмеричное. Восьмеричное число равно 112.

Основная характеристика восьмеричной системы счисления состоит в том, что она имеет 8 различных счетных цифр от 0 до 7. В первые дни вычислений восьмеричные числа и восьмеричная система счисления считали входы и выходы. Восьмеричное число было введено для удобного преобразования больших двоичных чисел. Однако восьмеричная система счисления постепенно вымирает из-за более популярной шестнадцатеричной системы счисления.

Представление восьмеричного числа

Система не использует числа или алфавиты выше 8. Кроме того, преобразование восьмеричных чисел в двоичные числа аналогично шестнадцатеричным числам. Восьмеричные числа представляются следующим образом.

0003

Decimal number	3-bit binary number	Octal number
0	000	0
1	001	1
2	010	2
3	011	3
4	100	9000 4	100	9000 4	100	9000 4
5	101	5
6	110	6
7	111	7
8	001 000	10 (1+0)
	0019		9001 0019		0019
	0003	11 (1+1)

При написании 10 или 20 не путайтесь, потому что число 10 и число 20 представляют собой использование (1+0) и (2+0) в восьмеричная система счисления. Восьмеричное число равно 8octal. Значение восьмеричной системы счисления варьируется от 0 до 7.

Шестнадцатеричная система счисления

Шестнадцатеричная система счисления — это система счисления, в которой базовое значение равно 16. Это означает, что в шестнадцатеричной системе используется 16 символов. Шестнадцатеричные символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9., A, B, C, D, E и F. Алфавиты, используемые в шестнадцатеричной системе, представляют собой однобитовое представление десятичных чисел 10, 11, 12, 13, 14 и 15. Шестнадцатеричная система требует 4 бита для изобразить любую цифру. Поскольку существует так много систем счисления, шестнадцатеричная система счисления обычно обозначается буквой h.

В шестнадцатеричной системе счисления каждая цифра имеет вес, эквивалентный степени 16. Таким образом, в шестнадцатеричной системе счисления каждая цифра в 16 раз ценнее предыдущей. Числовое значение каждой цифры в шестнадцатеричной последовательности получается путем умножения числа в степени 16, которая зависит от положения числа, и последующего прибавления числа к сумме.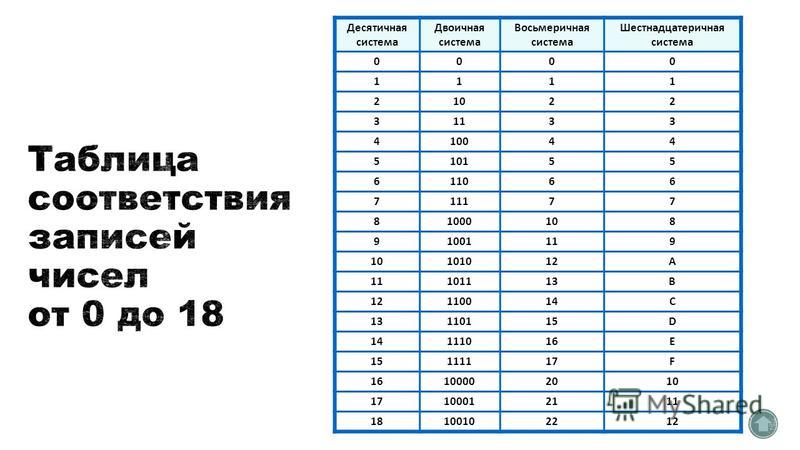

Разработчики программного обеспечения широко используют шестнадцатеричную систему счисления, потому что она удобно представляет значения в двоичном коде.

Представление шестнадцатеричных чисел

Из приведенного выше определения ясно, что шестнадцатеричная система счисления представляет собой набор из 4 битов. Каждый набор битов в шестнадцатеричных числах равен 0 и 15. Шестнадцатеричные числа широко используются в современных компьютерах и цифровых системах, поскольку их удобно интерпретировать.

Представление шестнадцатеричных чисел следующее:

Hex	0	1	2	3	4	5	6	7	8
	00003 9003 0033	0001	0010	0011	0100	0101	0110	0111	1000

HEX		10 = A	11 = B	10 = A	0003	12 = C	13 = D	14 = E	15 = F
Binary	1001	1010	1011	1100	1101	1110	1111

В основном.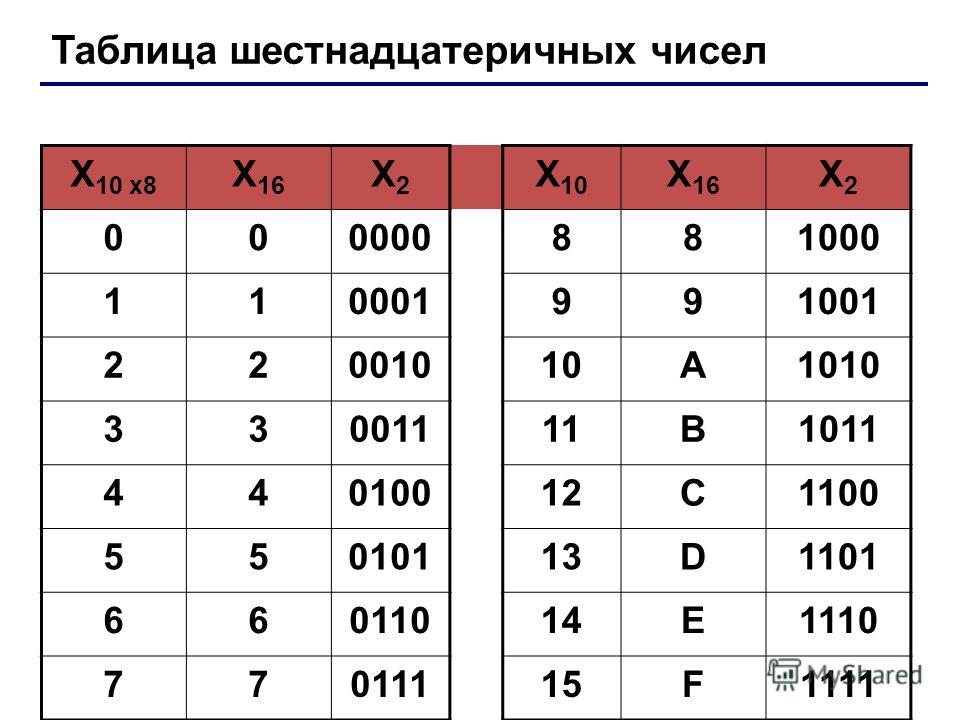 Используя эту систему счисления, мы можем легко объединить двоичные цифры в группу из 4 и записать их в шестнадцатеричном формате.

Заключение

Изучение различных систем счисления, таких как десятичная система счисления, шестнадцатеричная

система счисления и восьмеричная система счисления, необходимо для понимания работы компьютеров и других электронных устройств. В этой статье мы узнали о восьмеричной системе счисления, шестнадцатеричной системе счисления и различных способах их представления.

Прочитав эту статью, вы узнаете следующее:

• Разница между десятичной, шестнадцатеричной и восьмеричной системами в том, что основание в каждой системе разное

• Шестнадцатеричная система имеет основание 16, восьмеричная система имеет основание 8 и десятичная система имеет основание 10 цифры соединены вместе

Системы счисления (двоичная, восьмеричная, десятичная, шестнадцатеричная)

Прежде чем мы сможем объяснить некоторые конкретные системы счисления, нам нужно знать, что такое система счисления. Проще говоря, система счисления — это способ представления чисел.

Мы можем классифицировать системы счисления по типу записи в зависимости от того, используют ли они позиционную запись (также известную как запись разрядного значения), а также проводить дальнейшую категоризацию по основанию или основанию.

1. Непозиционная система счисления

Чтобы объяснить непозиционную систему счисления, в качестве примера возьмем римские цифры. В таблице ниже вы можете найти десятичные значения основных символов в римской системе счисления.

Вы можете спросить, есть ли какой-то шаблон для формирования всех остальных символов? Ответ положительный.

• Когда символ с меньшим значением помещается после символа, имеющего равное или большее значение, значения складываются. Примеры приведены в таблице ниже.

• Когда символ с меньшим значением помещается перед символом с большим значением, меньшее значение вычитается из большего. Примеры приведены в таблице ниже.

 

2. Позиционная система счисления

Позиционная система счисления позволяет расширить исходный набор символов, чтобы их можно было использовать для представления любого произвольно большого (или малого) значения. Число может быть представлено по-разному в разных системах.
Например, два числа $(2A)_{16}$ и $(52)_{8}$ относятся к одному и тому же количеству, $(42)_{10}$.

Система счисления, которую мы используем каждый день, называется десятичной системой счисления или системой счисления с основанием десять. Как видно из названия системы счисления, основание определяет всю систему.

Десятичная система счисления имеет основание 10, потому что мы работаем с 10 цифрами (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), и любое другое большее число может быть составлено из этих 10 цифр. Другими словами, мы используем тот же набор символов, но присваиваем символу другое значение в зависимости от его положения в числе.

Положение символа по отношению к другим символам в номере позволяет отдельному символу представлять большее (или меньшее) значение. Это также означает, что каждая цифра умножается на соответствующую степень числа 10 в зависимости от ее положения в числе. 9{0} $

$= 3 \cdot 100+4 \cdot 10+2 \cdot 1$ ​​

$=300 + 40 + 2$

В этом уроке мы не будем подробно объяснять десятичную систему, так как она много уроков на странице, посвященной этому.

Помимо десятичной системы счисления существует множество других систем счисления. Мы упомянем только три из них, поскольку они являются наиболее часто используемыми системами счисления после десятичной. Это: двоичная система счисления, восьмеричная система счисления и шестнадцатеричная система счисления. Мы дадим краткое объяснение каждому из них и научимся преобразовывать числа из одной системы в другую.

 

2.1. Двоичная система счисления

Двоичная система счисления содержит две уникальные цифры (0 и 1). Таким образом, эта система является системой счисления с основанием 2. Относительные величины символов равны 0 < 1. Символы в этой системе часто называют двоичными цифрами или просто битами. Двоичная система счисления является позиционной системой счисления. Позже мы увидим, что, например, $1010_{2}\neq 1100_{2}$.

 

2.2. Восьмеричная система счисления

Восьмеричная система счисления содержит 8 уникальных цифр (0, 1, 2, 3, 4, 5, 6, 7). Таким образом, эта система является системой счисления с основанием 8. Относительные величины символов равны 0 < 1 < 2 < 3 < 4 < 5 < 6 < 7. Восьмеричная система счисления — еще один пример позиционной системы счисления.

 

2.3. Шестнадцатеричная система счисления

Шестнадцатеричная система счисления содержит 16 уникальных цифр. Поскольку в десятичной системе всего 10 арабских цифр, нам нужно использовать другие символы для представления оставшихся 6 цифр. Мы используем алфавитные
символов от A до F, чтобы расширить систему до 16 цифр. 16 цифр в шестнадцатеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F. Относительные величины символов равны
0 < 1 < 2 < 3 < 4 < 5 < 6 < 7 < 8 < 9< A < B < C < D < E < F.
Шестнадцатеричная система счисления также является позиционной системой счисления.

3. Преобразование основания

Каждая позиция цифры в числе с основанием b представляет собой степень $b$. Таким образом, когда мы записываем число с основанием b, каждая цифра с основанием b умножается на соответствующую степень $b$ в зависимости от позиции в числе.

 

3.1. Преобразование в десятичное число

Преобразование числа из любой системы счисления в десятичное число довольно просто. Мы знаем, что значение каждой цифры в числе основано на значении отдельной цифры и позиции цифры. Мы узнали это, изучая десятичные числа. Используя это правило, мы можем преобразовать число из любой системы счисления в десятичное число. 9{-2}=3\cdot 8+4\cdot 1+1\cdot \displaystyle{\frac{1}{8}}+5\cdot \displaystyle{\frac{1}{64}}=28,203125$

 

3.

2. Преобразование десятичного числа в любое другое основание

Мы можем преобразовать десятичное число в любое другое основание, используя всего несколько простых шагов:

1. Разделите десятичное число, которое нужно преобразовать, на значение нового основания.
2. Запишите остаток в сторону
3. Разделите частное предыдущего деления на новое основание.
4. Запишите остаток в сторону
5. Повторяйте шаги 3 и 4, пока частное не станет равным нулю на шаге 3.

Требуемое число состоит из остатков, записанных снизу вверх и слева направо.

Пример 2. Преобразование 25 в двоичное число.

Следуя правилу преобразования десятичных чисел в любую другую систему счисления, необходимое число равно $11001_{2}$.

Пример 3. Преобразование 2489 в шестнадцатеричное число.

Помните, что эквивалентом числа 11 в шестнадцатеричной системе счисления является буква B.

Следуя правилу преобразования десятичных чисел в любую другую систему счисления, необходимое число равно $9B9_{16}$.

 

3.3. Эквивалентность между различными системами счисления

4. Сокращения для переключения между основанием 2 и основанием 8 и между основанием 2 и основанием 16

Мы узнали, что можем преобразовать число из любого основания в число с любым основанием с помощью сначала преобразовать его в десятичное. Например, если мы хотим преобразовать число с основанием 3 в число с основанием 7, первым шагом будет преобразование числа с основанием 3 в десятичное, а затем преобразование этого десятичного числа в число с основанием 7.

Мы можем использовать ту же процедуру для преобразования двоичного числа в восьмеричное или шестнадцатеричное число, но есть несколько полезных сокращений, которые упростят этот процесс. Рассмотрим следующий пример:

Пример 4. Преобразование $100100010101111_{2}$ в шестнадцатеричное число.

Чтобы преобразовать двоичное число в шестнадцатеричное, мы могли бы просто разбить двоичное число на группы из 4 цифр (начиная справа и добавив ведущие нули, если цифры заканчиваются), а затем интерпретировать эти группы из 4 цифр как шестнадцатеричные значения. перечислены в таблице выше. При этом имеем:

$ 1001000101011111111_ {2} = 0100 1000 1010 1111 $

$ 0100 = 4 $, $ 1000 = 8 $, 1010 $. к этому, чтобы преобразовать двоичное число в восьмеричное число, мы могли бы просто разбить двоичное число на группы из 3 цифр, а остальная часть процедуры такая же, как преобразование двоичного числа в шестнадцатеричное число. Преобразуем то же двоичное число в восьмеричное:

$100100010101111_{2}=100 100 010 101 111$

$100=4$

$010=2$

$101=5$

$111=7$

$100100010101111_{2}=44257_{8}$

Обратный процесс еще проще. Предположим, мы хотим преобразовать $FC7_{16}$ в двоичную форму. Из таблицы мы можем прочитать двоичные значения для каждой цифры шестнадцатеричного числа:

$F_{16} = 1111_{2}$ $C_{16} = 1100_{2}$ $7_{16} = 0111_{2} $

$FC7_{16}=111111000111_{2}$

Процесс преобразования восьмеричного числа в двоичную форму точно такой же.