Как измерить внутреннее сопротивление аккумулятора?

Главная » Интересные статьи

На чтение 2 мин Просмотров 37

Данное сопротивление обозначается на схемах буквой «R». В данной статье мы разберемся как его измерить в аккумуляторах и расскажем на что оно влияет.

Чтобы определить внутреннее сопротивление аккумулятора достаточно взять простую лампочку от автомобильной фары. Главное, чтобы она была не светодиодной. Галогеновая вполне подойдет.

Известно, что лампочка на 60 ват съедает ток в 5 ампер. Когда ток 100 ампер на внутреннем «R» не должно расходоваться больше 1 V. Применяем эти значения к току в 5 А и получаем что потеря не должна составлять 0,05 в. Это можно оформить так (1В * 5А / 100А).

Сопротивление внутри аккумулятора не должно быть более 0. 05В / 5А = 0.01 Ома.

Подсоедините параллельно АКБ мультиметр в режиме измерения напряжения и лампочку. Посмотрите какое напряжение будет. Выключите осветительный прибор. Теперь посмотрите каким стало напряжение. Если оно без этой нагрузки увеличилось на 0,2 V (Re = 0.04 Ома), то это означает что АКБ уже не годен. Ну а если на 0,02 то его внутреннее сопротивление будет Re = 0.04 Ома и это говорит о том что он вполне себе работоспособен.

Со 100 ампер будет теряться 0,02 вольта умноженное на 100 ампер и деленное га 5 ампер. В результате этих вычислений получится 0,4 вольта.

Более подробно читайте по этой ссылке: http://photo-ek.ru/workshop/internal-resistance.html

 

Batareykaa.ru

window.yaContextCb.push(()=>{ Ya.Context.AdvManager.render({ renderTo: ‘yandex_rtb_R-A-277958-196’, blockId: ‘R-A-277958-196’ })})»+»ipt>»; cachedBlocksArray[80628] = «window.yaContextCb.push(()=>{ Ya.Context.AdvManager.render({ renderTo: ‘yandex_rtb_R-A-277958-191’, blockId: ‘R-A-277958-191’ })})»+»ipt>»; cachedBlocksArray[80625] = «window.

yaContextCb.push(()=>{ Ya.Context.AdvManager.render({ renderTo: ‘yandex_rtb_R-A-277958-69’, blockId: ‘R-A-277958-69’ })})»+»ipt>»; cachedBlocksArray[80615] = «window.yaContextCb.push(()=>{ Ya.Context.AdvManager.render({ renderTo: ‘yandex_rtb_R-A-277958-48’, blockId: ‘R-A-277958-48’ })})»+»ipt>»; cachedBlocksArray[80614] = «window.yaContextCb.push(()=>{ Ya.Context.AdvManager.render({ renderTo: ‘yandex_rtb_R-A-277958-44’, blockId: ‘R-A-277958-44’ })})»+»ipt>»; cachedBlocksArray[80613] = «window.yaContextCb.push(()=>{ Ya.Context.AdvManager.render({ renderTo: ‘yandex_rtb_R-A-277958-40’, blockId: ‘R-A-277958-40’ })})»+»ipt>»; cachedBlocksArray[80612] = «window.yaContextCb.push(()=>{ Ya.Context.AdvManager.render({ renderTo: ‘yandex_rtb_R-A-277958-36’, blockId: ‘R-A-277958-36’ })})»+»ipt>»; cachedBlocksArray[80611] = «window.yaContextCb.push(()=>{ Ya.Context.AdvManager.render({ renderTo: ‘yandex_rtb_R-A-277958-35’, blockId: ‘R-A-277958-35’ })})»+»ipt>»; cachedBlocksArray[80610] = «window. yaContextCb.push(()=>{ Ya.Context.AdvManager.render({ renderTo: ‘yandex_rtb_R-A-277958-30’, blockId: ‘R-A-277958-30’ })})»+»ipt>»; cachedBlocksArray[284597] = «window.yaContextCb.push(()=>{ Ya.Context.AdvManager.render({ renderTo: ‘yandex_rtb_R-A-277959-6’, blockId: ‘R-A-277959-6’ })})»+»ipt>»;

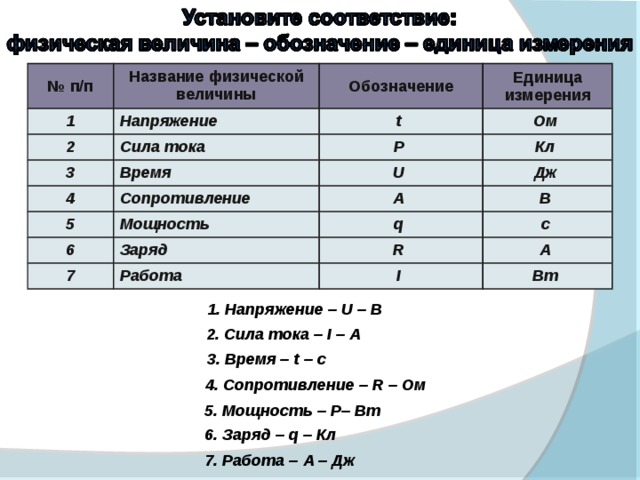
5Формула индуктивного сопротивления:

1 Реальные и идеальные источники эл. энергии. Схемы замещения. Любой источник электрической энергии преобразует другие виды энергии (механическую, световую, химическую и др.) в электрическую. Ток в источнике электрической энергии направлен 

от отрицательного вывода к положительному за счет сторонних сил, обусловленных видом энергии, которую источник преобразует в электрическую. Реальный источник электрической энергии при анализе электрических цепей можно представить либо в виде источника напряжения, либо в виде источника тока. Ниже это показано на примере обыкновенной батарейки.

Рис. 14. Представление реального источника электрической энергии либо в виде источника напряжения, либо в виде источника тока

Способы представления реального источника электрической энергии отличаются друг от друга схемами замещения (расчетными схемами). На рис. 15 реальный источник представлен (замещен) схемой источника напряжения, а на рис. 16 реальный источник представлен (замещен) схемой источника тока.

	Рис. 15. Схема замещения реального источника  напряжения		Рис. 16. Схема замещения реального источника  тока

Как видно из схем на рис. 15 и 16, каждая из схем имеет идеальный источник (напряжения или тока) и собственное внутреннее сопротивление r_ВН. Если внутреннее сопротивление источника напряжения равно нулю (r_ВН=0), то получается идеальный источник напряжения (источник ЭДС). Если внутреннее сопротивление источника тока бесконечно велико (r_ВН=), то получается идеальный источник тока

 (источник задающего тока). Схемы идеальных источника напряжения и идеального источника тока показаны на рис. 17 и 18. Отметим особо, что обозначать идеальный источник тока будем буквой J.

 

 

Рис. 17. Схема замещения идеального источника  напряжения (источника ЭДС)

Рис. 18. Схема замещения идеального источника  тока

2. Цепи переменного тока. Однофазный переменный ток. Основные хар-ки, частоты фазы, начальная фаза. ПЕРЕМЕННЫЙ ОДНОФАЗНЫЙ ТОК. Ток, изменяющийся во времени по значению и направлению, называется переменным. В практике применяют периодически

из

меняющийся по синусоидальному закону переменный ток (рис. 1).Синусоидальные величины характеризуются следующими основными параметрами: периодом, частотой, амплитудой, начальной фазой или сдвигом фаз.

Рис. 1   График синусоидальной величины

Период (T) — время (с), в течение которого переменная величина совершает полное колебание. Частота — число периодов в секунду. Единица измерения частоты — Герц (сокращенно Гц), 1 Гц равен одному колебанию в секунду. Период и частота связаны зависимостью T = 1 / f. Изменяясь с течением времени, синусоидальная величина (напряжение, ток, ЭДС) принимает различные значения. Значение величины в данный момент времени называют мгновенным.

Амплитуда — наибольшее значение синусоидальной величины. Амплитуды тока, напряжения и ЭДС обозначают прописными буквами с индексом: I_m, U_m, E_m, а их мгновенные значения — строчными буквами i, u, e. Мгновенное значение синусоидальной величины, например тока, определяют по формуле i = I_msin(ωt + ψ), где ωt + ψ — фаза-угол, определяющий значение синусоидальной величины в данный момент времени; ψ — начальная фаза, т. е. угол, определяющий значение величины в начальный момент времени. Синусоидальные величины, имеющие одинаковую частоту, но разные начальные фазы, называются сдвинутыми по фазе.

3 На рис. 2 приведены графики синусоидальных величин (тока, напряжения), сдвинутых по фазе. Когда же начальные фазы двух величин равны ψ_i = ψ_u, то разница ψ_i − ψ_u = 0 и, значит, сдвига фаз нет φ = 0 (рис. 3). Эффективность механического и теплового действия переменного тока оценивается действующим его значением. Действующее значение переменного тока равно такому значению постоянного тока, который за время, равное одному периоду переменного тока, выделит в том же сопротивлении такое же количество тепла, что и переменный ток. Действующее значение обозначают прописными буквами без индекса: I, U, E. Рис. 2   Графики синусоидальных тока и напряжения, сдвинутых по фазе. Рис. 3   Графики синусоидальных тока и напряжения, совпадающих по фазе

Для синусоидальных величин действующие и амплитудные значения связаны соотношениями:

I=I_M/√2;   U=U_M/√2;   E=E_M√2.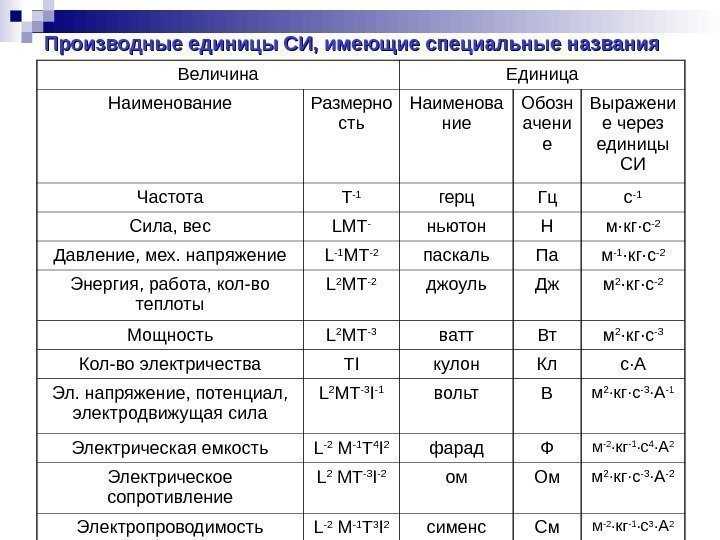 Действующие значения тока и напряжения измеряют амперметрами и вольтметрами переменного тока, а среднее значение мощности — ваттметрами.

4.Действующим (эффективным) значением силы переменного тока называют величину постоянного тока, действие которого произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток за время одного периода. В современной литературе чаще используется математическое определение этой величины — среднеквадратичное значение силы переменного тока. Иначе говоря, действующее значение тока можно определить по формуле:

.

Для гармонических колебаний тока

 

где L — индуктивность.

Формула емкостного сопротивления:

где С — емкость.

Предлагаем рассмотреть цепь переменного тока, в которую включено одно активное сопротивление, и нарисовать ее в тетрадях. После проверки рисунка рассказываю, что в электрической цепи (рис. 1, а) под действием переменного напряжения протекает переменный ток, изменение которого зависит от изменения напряжения. Если напряжение увеличивается, ток в цепи возрастает, а при напряжении, равном нулю, ток в цепи отсутствует. Изменение направления его также будет совпадать с изменением направления напряжения

(рис. 1, в).

Рис 1. Цепь переменного тока с активным сопротивлением: а – схема; б – векторная диаграмма; в – волновая диаграмма

Графически изображаю на доске синусоиды тока и напряжения, которые совпадают по фазе, объясняя, что хотя по синусоиде можно определить период и частоту колебаний, а также максимальное и действующее значения, тем не менее построить синусоиду довольно сложно. Более простым способом изображения величин тока и напряжения является векторный. Для этого вектора напряжения (в масштабе) следует отложить вправо из произвольно выбранной точки. Вектор тока преподаватель предлагает учащимся отложить самостоятельно, напомнив, что напряжение и ток совпадают по фазе. После построения векторной диаграммы (рис. 1, б) следует показать, что угол между векторами напряжения и тока равен нулю, т. е. ? = 0. Сила тока в такой цепи будет определяться по закону Ома: Вопрос 2. Цепь переменного тока с индуктивным сопротивлением Рассмотрим электрическую цепь переменного тока (рис. 2, а), в которую включено индуктивное сопротивление. Таким сопротивлением является катушка с небольшим количеством витков провода большого сечения, в которой активное сопротивление принято считать равным 0.

Рис. 2. Цепь переменного тока с индуктивным сопротивлением

Вокруг витков катушки при прохождении тока и будет создаваться переменное магнитное поле, индуктирующее в витках эдс самоиндукции. Согласно правилу Ленца, эде индукции всегда противодействует причине, вызывающей ее. А так как эде самоиндукции вызвана изменениями пе-ременного тока, то она и препятствует его прохождению. Сопротивление, вызываемое эде самоиндукции, называется индуктивным и обозначается буквой x_L. Индуктивное со-противление катушки зависит от скорости изменения то-ка в катушке и ее индуктивности L: где Х_L– индуктивное сопротивление, Ом; – угловая частота переменного тока, рад/с; L–индуктивность ка-тушки, Г.

Угловая частота == ,

следовательно, .

Емкостное сопротивление в цепи переменного тока. Перед началом объяснения следует напомнить, что имеется ряд случаев, когда в электрических цепях, кроме активного и индуктивного сопротивлений, имеется и емкостное сопротивление. Прибор, предназначенный для накопления электрических зарядов, называется конденсатором. Простейший конденсатор – это два проводка, разделенных слоем изоляции. Поэтому многожильные провода, кабели, обмотки электродвигателей и т. д. имеют емкостное сопротивление. Объяснение сопровождается показом конденсатора различных типов и емкостных сопротивлений с подключением их в электрическую цепь. Предлагаю рассмотреть случай, когда в электрической цепи преобладает одно емкостное сопротивление, а активным и индуктивным можно пренебречь из-за их малых значений (рис. 6, а). Если конденсатор включить в цепь постоянного тока, то ток по цепи проходить не будет, так как между пластинами конденсатора находится диэлектрик. Если же емкостное сопротивление подключить к цепи переменного тока, то по цепи будет проходить ток /, вызванный перезарядкой конденсатора. Перезарядка происходит потому, что переменное напряжение меняет свое направление, и, следовательно, если мы подключим амперметр в эту цепь, то он будет показывать ток зарядки и разрядки конденсатора. Через конденсатор ток и в этом случае не проходит. Сила тока, проходящего в цепи с емкостным сопротивлением, зависит от емкостного сопротивления конденсатора Хс и определяется по закону Ома 

где U – напряжение источника эдс, В; Хс – емкостное сопротивление, Ом; / – сила тока, А.

Рис. 3. Цепь переменного тока с емкостным сопротивлением

Емкостное сопротивление в свою очередь определяется по формуле 

где С – емкостное сопротивление конденсатора, Ф. Предлагаю учащимся построить векторную диаграмму тока и напряжения в цепи с емкостным сопротивлением. Напоминаю, что при изучении процессов в электрической цепи с емкостным сопротивлением было установлено, что ток опережает напряжение на угол ф = 90°. Этот сдвиг фаз тока и напряжения следует показать на волновой диаграмме. Графически изображаю на доске синусоиду напряжения (рис. 3, б) и дает задание учащимся самостоятельно нанести на чертеж синусоиду тока, опережающую напряжение на угол 90°

Вопрос Видео: Определение внутреннего сопротивления батареи

Стенограмма видео

Батарея с электродвижущей силой 4,50 В подключена к цепи с сопротивлением 2,75 Ом. Сила тока в цепи 1,36 ампера. Чему равно внутреннее сопротивление батареи? Дайте ответ с точностью до двух знаков после запятой.

Поскольку этот вопрос касается схемы, давайте начнем с рисования схемы. Нам говорят, что в схеме задействована батарея. Итак, мы можем начать с символа цепи для батареи. Затем нам говорят, что эта батарея подключена к цепи с сопротивлением 2,75 Ом. На самом деле нам не сказали ни о каком из компонентов этой схемы. Однако, поскольку мы знаем сопротивление всей цепи, мы можем просто рассматривать остальную часть схемы, как если бы это был один резистор 2,75 Ом. Вопрос также говорит нам о том, что сила тока в цепи составляет 1,36 ампера. Таким образом, мы можем обозначить этот ток на нашей принципиальной схеме, отметив, что, поскольку цепь представляет собой единую петлю, ток будет одинаковым в каждой точке цепи.

Мы также можем отметить, что мы нарисовали наши стрелки, указывающие в направлении обычного тока, который течет от положительной клеммы батареи к отрицательной клемме. Это направление противоположно направлению потока электронов. Хотя направление, в котором, как мы говорим, движется течение, на самом деле не меняет того, как мы решаем этот вопрос. Последняя часть информации, которую нам дают в этом вопросе, заключается в том, что электродвижущая сила батареи составляет 4,50 вольта. В этот момент может возникнуть соблазн пометить нашу батарею этой разностью потенциалов. Однако важно помнить, что электродвижущая сила батареи — это не то же самое, что ее разность потенциалов, когда она находится в цепи. Поэтому мы пока не будем маркировать нашу батарею.

Вопрос заключается в том, чтобы рассчитать внутреннее сопротивление батареи. Для этого нам нужно тщательно подумать о том, как работают батареи. Мы можем вспомнить, что роль батареи заключается в обеспечении разности потенциалов в цепи. И эта разность потенциалов создает ток в цепи. В этом смысле батарея очень похожа на ячейку, которая имеет очень похожий символ цепи. Однако между этими двумя компонентами есть некоторые важные различия.

Ячейка, или идеальная ячейка, — это своего рода теоретический компонент, который мы обычно используем в принципиальных схемах. Идеальная ячейка обеспечивает разность потенциалов в цепи. И что особенно важно, мы относимся к нему так, как будто оно не имеет никакого сопротивления. Важно отметить, что, хотя идеальные ячейки очень часто встречаются на принципиальных схемах, в реальной жизни их не существует. Вот где на помощь приходят батареи. Батарея — это настоящее устройство, и она преобразует химическую энергию в электрическую, чтобы фактически выполнять роль ячейки в реальной цепи. Таким образом, батарея обеспечивает разность потенциалов. Но, в отличие от идеальной клетки, она имеет некоторое электрическое сопротивление. И мы называем это его внутренним сопротивлением.

Итак, поскольку батарея в основном такая же, как идеальная ячейка, но с сопротивлением, мы можем фактически рассматривать батарею, как если бы это была идеальная ячейка, подключенная к постоянному резистору. В частности, сопротивление этого резистора будет равно внутреннему сопротивлению батареи, которое мы обычно обозначаем строчной буквой 𝑟. А разность потенциалов этой ячейки была бы равна электродвижущей силе батареи, обозначаемой греческой буквой 𝜀. И нам сказали, что в этом случае электродвижущая сила батареи составляет 4,50 вольта. Поскольку батарея в нашем вопросе эквивалентна этой комбинации элемента и резистора, мы можем заменить эти компоненты на нашу принципиальную схему.

Итак, мы показали, что описание схемы в вопросе эквивалентно этой принципиальной схеме. Что нам нужно выяснить, так это сопротивление резистора, который мы нарисовали здесь, который представляет собой внутреннее сопротивление батареи. Мы можем сделать это, используя закон Ома, который выражается уравнением 𝑉 равно 𝐼𝑅. Это говорит нам о том, что разность потенциалов на компоненте 𝑉 равна току в этом компоненте 𝐼, умноженному на сопротивление этого компонента 𝑅. Мы можем применить закон Ома к любому резистору или группе резисторов в цепи.

Есть по крайней мере несколько способов решить эту проблему. Но что мы собираемся сделать, так это применить закон Ома к обоим резисторам в цепи одновременно. В этом случае закон Ома говорит нам, что разность потенциалов на обоих резисторах равна току через оба резистора, умноженному на сопротивление обоих резисторов. Таким образом, в этом конкретном случае разность потенциалов, с которой мы имеем дело, на самом деле является электродвижущей силой 𝜀 батареи, поскольку она обеспечивает разность потенциалов на обоих резисторах на нашей принципиальной схеме. Ток одинаков во всех точках цепи, поэтому мы можем просто назвать это 𝐼. А сопротивление 𝑅, с которым мы имеем дело, — это комбинированное сопротивление цепи и внутреннее сопротивление батареи. Мы можем назвать это полное сопротивление 𝑅 tot.

Можно вспомнить, что при последовательном соединении нескольких резисторов общее сопротивление 𝑅tot равно сумме индивидуальных сопротивлений всех последовательно соединенных резисторов. Таким образом, для трех или более резисторов общее уравнение, которое мы используем для расчета общего сопротивления последовательных резисторов, выглядит следующим образом. Но в этом случае, поскольку у нас есть только два последовательно соединенных резистора, мы можем немного упростить уравнение. В этом случае два сопротивления, которые мы суммируем, — это внутреннее сопротивление элемента, обозначенное строчной буквой 𝑟, и сопротивление остальной части цепи, которое, как нам сказали, составляет 2,75 Ом. А пока давайте назовем эту столицу сопротивления 𝑅. Это означает, что общее сопротивление обоих резисторов в нашей схеме равно прописной 𝑅 плюс строчная 𝑟.

Мы можем подставить это в нашу формулировку закона Ома, чтобы получить 𝜀 равно 𝐼 умноженной на заглавную 𝑅 плюс строчную 𝑟. Таким образом, используя закон Ома и правило для последовательных резисторов, мы получили уравнение, содержащее все известные в задаче величины, а именно электродвижущую силу, ток в цепи и сопротивление остальной части цепи. и неизвестная величина, которую мы ищем, которая является внутренним сопротивлением батареи. Все, что нам нужно сделать, это изменить это уравнение так, чтобы строчная буква 𝑟 была предметом, а затем подставить известные значения.

Первым шагом в преобразовании этого уравнения является деление обеих частей уравнения на 𝐼. И делая это, мы можем видеть, что множитель 𝐼 в числителе и знаменателе в правой части уравновешивается, в результате чего 𝜀 над 𝐼 равно заглавной 𝑅 плюс строчной 𝑟. На этом этапе мы можем избавиться от круглых скобок, а затем вычесть заглавную 𝑅 из обеих частей уравнения, чтобы получить 𝜀 сверх 𝐼 минус заглавная 𝑅 равно строчной 𝑟. Наконец, мы просто поменяем местами левую и правую части уравнения. Все, что осталось сделать сейчас, это подставить значения 𝜀, 𝐼 и заглавной 𝑅. Таким образом, значение 𝜀, то есть электродвижущая сила батареи, составляет 4,50 вольта. А значение 𝐼, то есть ток в цепи, составляет 1,36 ампер. Затем нам нужно вычесть заглавную 𝑅, это сопротивление остальной части цепи, которое составляет 2,75 Ом.

На этом этапе мы можем отметить, что, поскольку все величины используют единицы СИ, нам не нужно выполнять какие-либо преобразования единиц измерения. Поскольку этот расчет покажет нам сопротивление, оно будет указано в омах. Оценив сначала эту дробь, 4,50 вольта, разделенные на 1,36 ампера, дают нам 3,309, а затем еще несколько знаков после запятой, и эта величина измеряется в омах. Затем вычитание из этого значения 2,75 Ом дает нам результат 0,559 и так далее Ом. Единственное, что осталось сделать сейчас, это округлить это значение до двух знаков после запятой, как указано в вопросе, что даст нам окончательный ответ для внутреннего сопротивления батареи 0,56 Ом.

Если аккумулятор с электродвижущей силой 4,50 вольта подключить к цепи с сопротивлением 2,75 Ом и сила тока в цепи 1,36 ампер, то мы знаем, что внутреннее сопротивление аккумулятора должно быть 0,56 Ом.

[Заметки для класса физики] о формуле внутреннего сопротивления Pdf для экзамена 2023

Соотношение между внутренним сопротивлением, обозначенным r, и ЭДС, обозначенной e ячейки, определяется следующим образом:

e = I (r + R)

Где мы можем заметить, что термин, обозначенный буквой e = ЭДС, известная как электродвижущая сила Вольт, записывается как: I = ток, который обозначается буквой A буква R = сопротивление нагрузки, а буква r обозначает Внутреннее сопротивление ячейки измеряется в омах.

Преобразовав приведенное выше уравнение, мы получим следующее:

То есть e = IR + Ir или, e = V + Ir

Формула внутреннего сопротивления

В приведенном выше уравнении мы можем сказать, что буква  V равна клемма разности потенциалов на ячейке, когда ток, обозначенный буквой I, протекает через цепь.

Мы можем отметить: ЭДС, обозначенная буквой e ячейки, всегда больше, чем разность потенциалов, обычно на конце ячейки.

Пример: 1 — это разность потенциалов на ячейке, когда через цепь не протекает ток, равный 3 В. Когда протекает ток I = 0,37, т. е. ампер, эта разность потенциалов на клеммах падает до 2,8. вольт. Определить внутреннее сопротивление, обозначенное буквой r ячейки?

Решение:

То есть e = V + Ir

Или мы видим e – V = Ir

Или это (e – V)/I = r

Следовательно, мы видим, что r = (3,0 – 2,8)/0,37 = 0,54 Ом .

Теперь, благодаря внутреннему сопротивлению ячейки, электроны, движущиеся через ячейку, превращают часть электрической энергии в тепловую. Следовательно, мы видим, что разность потенциалов доступна для остальной части цепи, то есть:

То есть V = E, что означает ЭДС ячейки – Ir, то есть p.d. через внутренний резистор

Электродвижущая сила, которая обозначается буквой e или э.д.с. это энергия, которая обычно обеспечивается элементом или батареей на кулон проходящего через них заряда. Таким образом, мы можем сказать, что оно измеряется в вольтах, то есть в В. Говорят, что оно равно разности потенциалов на клеммах ячейки, когда ток не течет.

ε=E/Q

• Можно сказать, что e = электродвижущая сила в вольтах, В

• И тогда E = энергия в джоулях, Дж

• Тогда буква Q = заряд в кулонах, Кл

Батареи и элементы имеют внутреннее сопротивление, обозначаемое буквой r, которое измеряется в омах, обозначаемых буквой W. Когда поток электричества течет по цепи, внутреннее сопротивление самой ячейки сопротивляется потоку тока и настолько тепловое, что называется теплом, то есть энергия тратится впустую в самой клетке.

ε=I(R+r)

• Буква e = электродвижущая сила в вольтах, В

• Буква I = ток в амперах, А

• Буква R = сопротивление нагрузки в цепи в Ом, Вт

• Буква r = Внутреннее сопротивление элемента в Ом, Вт

Здесь преобразование приведенного выше уравнения:

ε=IR+Ir

и затем к следующему: разность потенциалов, которая обычно измеряется в вольтах, то есть в вольтах. Это разность потенциалов, которая, как говорят, возникает на клеммах ячейки, когда в цепи протекает ток, то есть она всегда меньше, чем ЭДС. клетки.

Мы можем сказать Например:

1. Мы можем сказать, что p.d. То есть на клеммах ячейки 3,0 вольта, когда она не подключена к цепи и ток не течет. Здесь, когда говорят, что ячейка подключена к цепи и через клемму p.d. течет ток 0,37 А. Это обычно падает до 2,8 В. Мы можем сказать, что такое внутреннее сопротивление ячейки?

Граф терминала, который имеет п.д. против тока

Таким образом, мы можем сказать, что если мы построим график разности потенциалов на клеммах, обозначенной буквой V, в зависимости от тока в цепи, обозначенного буквой I, мы получим прямую линию с отрицательным градиентом.

Здесь можно сказать, что они вообще перестраивают Э.Д.С. уравнение, приведенное выше, чтобы соответствовать общему выражению для прямой линии, то есть мы можем сказать y = mx +c.

Мы можем отметить, что это из красных прямоугольников, что выше:

• Отрезок, который, как говорят, находится на оси у, равен Э.Д.С. Это ячейка

• Градиент графика равен -r, где r — внутреннее сопротивление ячейки.

Можно сказать, что сайт Physics net Search.

Формула внутреннего сопротивления клетки

Электродвижущая сила, называемая ЭДС, незнакома большинству учащихся. Эти вещи тесно связаны с более привычной концепцией напряжения. Понимание разницы между ними и того, что обычно означает ЭДС, дает нам инструменты, необходимые для решения многих задач в физике, а также в электронике. Также будет введено понятие внутреннего сопротивления батареи. Здесь снова мы можем сказать, что ЭДС говорит о напряжении батареи без учета внутреннего сопротивления, уменьшающего значение. Говорят, что в этой теме объясняется формула ЭДС с примерами. Итак, снова мы можем видеть, что давайте учиться этому.

Уже сказано, что электродвижущая сила определяется как разность потенциалов на клеммах батареи, то есть мы можем сказать, когда через нее не протекает ток. Говорят, что это не похоже на это, поскольку это имело бы значение, но мы можем сказать, что каждая батарея имеет внутреннее сопротивление. Можно сказать, что оно похоже на обычное сопротивление, уменьшающее ток в цепи, но существует внутри самой батареи.

Через ячейку, которая называется внутренним сопротивлением, не протекает ток, который ничего не изменит, потому что нет тока, который мог бы его замедлить.

Определение внутреннего сопротивления

Формула внутреннего сопротивления — это математическое уравнение, которое можно использовать для расчета сопротивления движущегося объекта. Внутреннее сопротивление вызвано потерей тепла, трением и другими процессами, которые замедляют или останавливают движение. Формула внутреннего сопротивления часто используется в инженерных приложениях при проектировании двигателей и силовых агрегатов для легковых или грузовых автомобилей, но ее также можно применять во многих других ситуациях. В этой статье я объясню, что означает формула внутреннего сопротивления, как она рассчитывается, и приведу примеры с решениями, чтобы вы поняли, как работает внутреннее сопротивление!

Внутреннее сопротивление важно изучать следующими способами:

1. Для повышения эффективности электродвигателя или любого другого электрического устройства
   важно понимать, какое внутреннее сопротивление имеет это устройство и как его можно уменьшить.

2. Внутреннее сопротивление применяется при изучении внутреннего сопротивления батарей. Внутреннее сопротивление является важным понятием в электротехнике, и его можно применять ко многим типам проектов или экспериментов, связанных с электричеством.

3. Внутреннее сопротивление

   также имеет жизненно важное значение при проектировании двигателей легковых автомобилей, грузовиков или других крупных транспортных средств. Внутреннее сопротивление может применяться в двигателях внутреннего сгорания (ДВС) для повышения производительности и топливной экономичности двигателя.

Вот несколько важных советов по изучению внутреннего сопротивления:

1. Изучите основы. Формула внутреннего сопротивления — это концепция, которую можно применять ко многим типам двигателей и электрических устройств. Для начала следует понять формулы внутреннего сопротивления в их простейшей форме, прежде чем пробовать более сложные приложения. Формула внутреннего сопротивления показывает взаимосвязь между напряжением, током, потребляемой мощностью и внутренним сопротивлением: Внутреннее сопротивление = напряжение – ток

2. Практика внутреннего сопротивления. Формулу внутреннего сопротивления можно применять ко многим различным типам проектов и экспериментов, но формулы внутреннего сопротивления следует сначала практиковать на более простых задачах, прежде чем переходить к более сложным. Практикуйте формулы внутреннего сопротивления, используя их в простых цепях или используя батареи, для которых вы знаете внутреннее сопротивление! Это поможет формуле внутреннего сопротивления стать второй натурой, когда вам понадобится использовать ее позже в дороге.

3. Поймите, где применять Формулу внутреннего сопротивления можно применять разными способами, но важно понимать, где и как следует применять внутреннее сопротивление. Внутреннее сопротивление чаще всего используется в электродвигателях или электрических устройствах, но его также можно применять при изучении внутреннего сопротивления аккумуляторов.