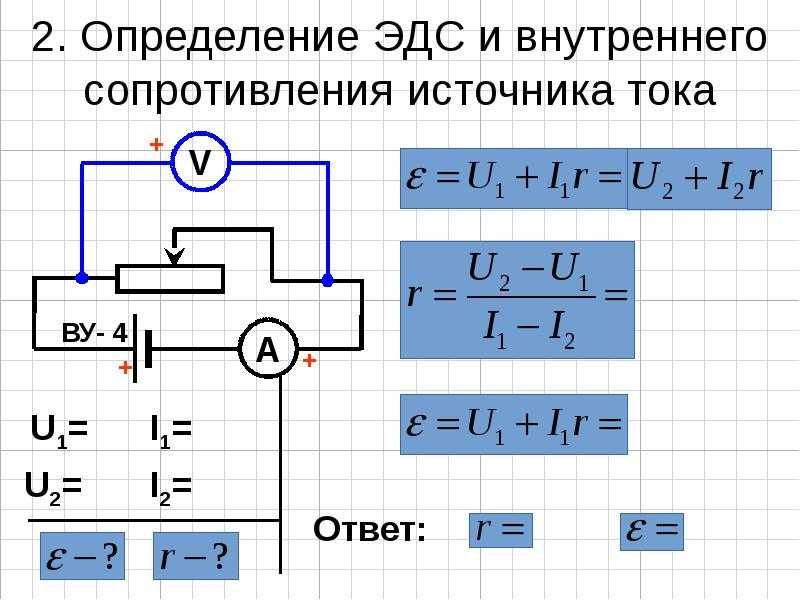
Внутреннее сопротивление химических источников тока и его измерение
Внутреннее сопротивление химических источников тока (ХИТ) — параметр, на который
многие пользователи не обращают внимания. Однако его величина существенно влияет
на работоспособность устройств с автономным питанием.
Многие радиостанции получали питание
от батарей, состоящих из никель-кадмиевых аккумуляторов емкостью 700 мА.ч (ти-
поразмер АА).
При замене деградировавшей батареи пользователь часто выбирает современные никель-металлгидридные аккумуляторы того же типоразмера, емкость которых достигает 2000–2200 мА·ч. Однако может оказаться, что продолжительность работы новых
батарей (особенно при низкой температуре) значительно меньше ожидаемой. И объясняется это более
высоким внутренним сопротивлением новых аккумуляторов, из-за чего при большом энергопотреблении в режиме передачи радиостанция отключается, хотя ее емкость еще не исчерпана.
Напряжение химического источника тока при разряде может быть записано в виде уравнения
U = НРЦ – IR = НРЦ – I (RΩ + Rпол),
где I — разрядный ток, R — полное сопротивление
ХИТ, RΩ — чисто омическое сопротивление, определяемое сопротивлением токоподводящих деталей
электродов, их активных масс и сопротивлением электролита, Rпол — поляризационное сопротивление,
отражающее скорость электрохимических реакций.
Сопротивление Rпол представляется сложной эквивалентной схемой, содержащей емкость двойного
электрического тока, активное сопротивление переноса заряда и RС-цепочки, отражающие диффузионное сопротивление, адсорбционные процессы
и другие особенности электрохимического процесса. Оно зависит от тока разряда.
Для оценки сопротивления ХИТ может использоваться регистрация его отклика на подачу импульса
постоянного тока и на воздействие переменного тока в некотором диапазоне частот.
В первом случае при анализе отклика ХИТ на импульс постоянного тока можно оценить составляющие его полного сопротивления: на RΩ происходит
мгновенное изменение напряжение, Rпол обеспечивает экспоненциальное изменение напряжения ХИТ
до его нового стационарного состояния. Аппаратура для таких измерений достаточно проста, проблема состоит только в способе и скорости регистрации
отклика, а также в задании продолжительности периода регистрации.
Регистрация отклика на переменный синусоидальный сигнал дает более детальное представление о поляризационном сопротивлении и позволяет оценить
 Отклик обычно представляется в виде годографа импеданса (на плоскости в координатах действительной и реактивной составляющих полного комплексного сопротивления).
Отклик обычно представляется в виде годографа импеданса (на плоскости в координатах действительной и реактивной составляющих полного комплексного сопротивления).Измерения производятся при последовательном
тестировании на разных частотах из диапазона от десятков килогерц до сотых долей герца. Тестовый сигнал должен быть очень малым, что приводит к очень
сложной аппаратурной реализации метода и делает
его исключительно лабораторным.
Оценка внутреннего сопротивления ХИТ
как одной из его электрических
характеристик
В настоящее время характеристика внутреннего
параметра и необходимо понять, можно ли сравнивать характеристики сопротивления аналогичной
продукции отечественных и зарубежных производителей.
Величина импеданса ХИТ, которая дается в каталогах зарубежных производителей, оценивается при измерениях на переменном токе частотой 1000 ±100 Гц
(в течение 1–5 с).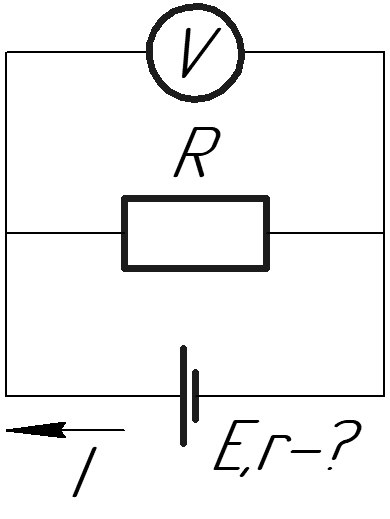
R1000 Гц = U—/I—;,
где I~и U~ — переменный ток и напряжение с откли-
ком на него источника тока. Переменный ток выбирается так, чтобы пиковое значение напряжения
не превышало 20 мВ. Для широкого спектра
источников тока величина R1000 Гц соответствует их омическому сопротивлению RΩ.
В России характеристика внутреннего сопротивления ХИТ обычно измеряется при подаче импульса постоянного тока. Оценивается величина сопротивления
R= (U1–U2)/(I2–I1) (1)
где U1 и U2 — напряжение, которое регистрируется после пропускания тока I
Таблица
При такой методике измеренная величина
включает кроме RΩ еще и поляризационное
сопротивление. Она заметно больше величины R1000 Гц. А так как стационарное состояние
Она заметно больше величины R1000 Гц. А так как стационарное состояние
источника тока к моменту Τ
2 может и не до-
стигаться, эта величина не всегда характеризует и полное сопротивление источника тока.
Использование параметра
внутреннего сопротивления
при отработке технологии
изготовления источников тока
и диагностике их состояния
Измерения внутреннего сопротивления ХИТ
могут быть использованы разработчиками при
случае наиболее полезной является информация о сопротивлении RΩ, так как она дает возможность лучше выявить все зависимости
между конструктивными и технологическими
параметрами и конечными характеристиками
изделия. Такая информация помогает быстрее
выбрать лучший сепарационный материал, определить допуски при дозировке электролита,
оценить плотность сборки.
Для диагностики технического состояния
ХИТ (степени разряженности, степени деградации, состояния после длительного хранения) в зависимости от природы источников
тока разных электрохимических систем полезной может быть информация и об омическом сопротивлении, и о поляризационном.
У герметичных источников тока с водным
электролитом (щелочных и свинцово-кислотных) осушение сепаратора в результате разбухания электродов и некоторых потерь воды,
изменение плотности сборки электродов и деформация аккумуляторов в результате повышенного давления приводят к увеличению
омического сопротивления. У литиевых источников тока этот эффект выражен меньше, а изменение поверхностной анодной пленки сказывается на поляризационном сопротивлении.
К сожалению, изменения параметров внутреннего сопротивления ХИТ в литературе обычно описывают только качественно.
возможной лишь при накоплении данных относительно конкретных источников тока [1],
так как:
- разброс RΩ свежеизготовленных ХИТ конкретного типа может быть соизмерим с изменением RΩ этого источника тока в процессе разряда; это в наибольшей степени касается отечественных аккумуляторов;
- разброс внутреннего сопротивления аккумуляторов ведущих зарубежных компаний, таких как SAFT, SANYO, PANASONIC, обычно не превышает 20%;
- изменения RΩ при изменении степени разряженности зависят от типа источника тока и его емкости;
- изменения RΩ при изменении степени разряженности и степени деградации различны у разных производителей;
- диагностика литиевых источников тока по их внутреннему сопротивлению затруднена из-за быстрой пассивации анода, а разброс сопротивления пассивной пленки значительно увеличивается со временем хранения.

Возможности диагностирования состояния
литий-ионных аккумуляторов изучены плохо, но известно, что их омическое сопротивление в процессе разряда увеличивается мало,
Из сказанного следует, что определение состояния источника тока с неизвестной предысторией эксплуатации весьма проблематично.
Однако при периодическом измерении RΩ
ХИТ в процессе эксплуатации (при одинаковой высокой степени заряженности и температуре) можно прогнозировать его работоспособность. Обычно источники тока считаются работоспособными до тех пор, пока их
фактическая разрядная емкость Сраз не станет
менее 60–50% от номинальной емкости (Сн).
Зависимость Сраз и омического сопротивления в пределах этого периода эксплуатации
уравнением
Сраз RΩ = const
Поэтому, измерив омическое сопротивление
RΩ используемого источника тока в начале эксплуатации, при периодических последующих
его измерениях можно с достаточной точностью предсказывать реальную емкость ХИТ.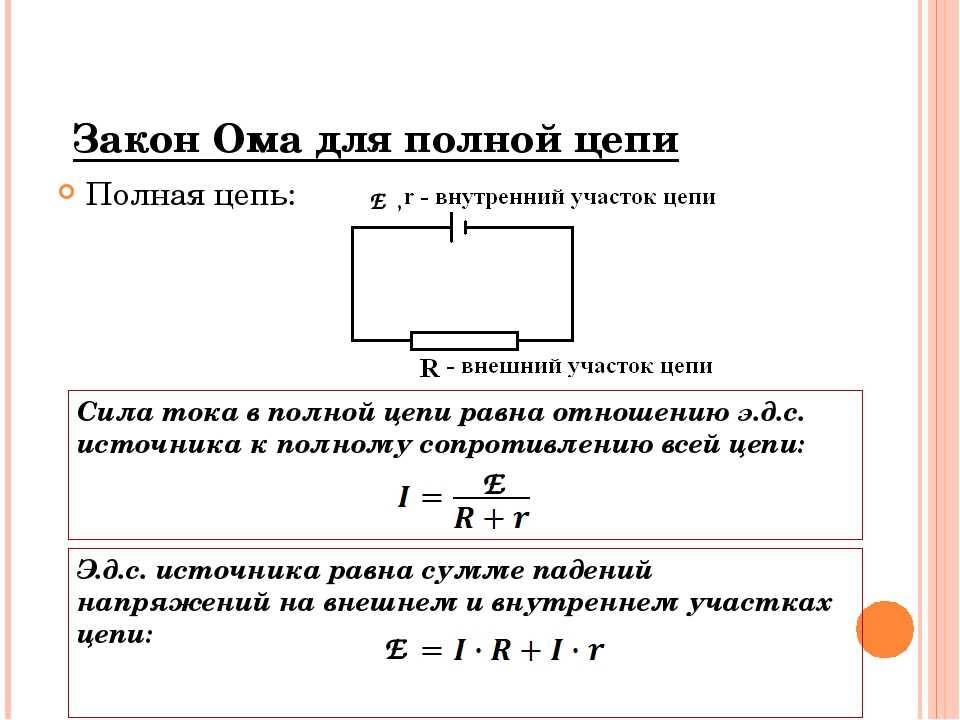
И эта процедура занимает всего несколько секунд. Измерения сопротивления возможны
и на работающих в буферном режиме батареях.
Выявление момента ускорения деградации
источников тока позволяет своевременно принять меры по восстановлению их работоспособности или замене.
По скорости изменения сопротивления в течение срока службы можно судить и о правильности условий эксплуатации.
Сравнение величин RΩ аккумуляторов в составе батареи можно использовать для быстрого выявления «слабых». Деформация аккумуляторов или высыхание сепаратора приводит
к значительному увеличению сопротивления
относительно среднего его значения для всех
аккумуляторов батареи.
Аппаратура для измерений внутреннего сопротивления источников тока
В России до настоящего времени стандартизованной аппаратуры для измерений внутреннего сопротивления ХИТ на постоянном
токе нет. А аппаратура для импедансных исследований очень дорога и используется только в исследовательских центрах.
Измерения сопротивления источников тока, которые реализованы в зарубежной диагностической аппаратуре для ХИТ небольшой
емкости, привязаны к методике измерений
на постоянном токе, но обычно не к стандарту, и потому разрешают вопрос только сравнительных испытаний однотипных источников тока.
В настоящее время, когда стала обязательной оценка характеристики внутреннего сопротивления выпускаемых источников тока,
и вопросы диагностирования технического состояния массовой продукции требуют решения, необходима аппаратура, достаточно простая и универсальная, доступная как компаниям, производящим источники тока, так
и сервисным службам.
В ООО «Мегарон» разработан тестер-анализатор внутреннего сопротивления химических источников тока, который осуществляет измерения сопротивления как постоянному току, так и переменному частотой 1 кГц.
Технические характеристики:
Внешний вид тестера показан на рисунке.
Рисунок. Тестер для измерения внутреннего сопротивления источников тока
Временная диаграмма соответствует ГОСТу
на щелочные аккумуляторы.
Омическое сопротивление, а также импеданс на частоте 1000 Гц измеряются в гальваностатическом режиме при токе разряда I1 в течение первых десяти секунд. За это время производится несколько измерений с усреднением результатов. Полное сопротивление вычисля-
ется в соответствии с формулой (1). Поляризационное сопротивление вычисляется как
разница полного и омического сопротивлений.
Тестер обеспечивает точные измерения омического сопротивления и сопротивления на частоте 1000Гц, а полное и поляризационное сопротивления вычисляются при токах меньше
регламентированных, однако и эти параметры
могут использоваться для сравнительных оценок однотипных источников тока.
Результаты измерений (НРЦ, величины
омического сопротивления, поляризационного и полного, импеданса при 1000 Гц) считываются поочередно с 4-разрядного дисплея.
Разработан измеритель позволяющий работать автономно и совместно с компьютером.
При подключении к компьютеру имеются
дополнительные возможности:
- Автоматическая регистрация и сохранение параметров ХИТ.

- Ведение базы обслуживавшихся ХИТ
- Отбраковка ХИТ. Параметры по которым ведется отбраковка и их величины могут задаваться во всем рабочем диапазоне.
- При подключении внешнего зарядно-разрядного устройства снятие зависимостей измеряемых параметров от степени заряженности ХИТ.
Разрабатывается модификация тестера для
измерения сопротивления герметизированных свинцово-кислотных батарей, которая дает возможность также и измерения тока короткого замыкания.
Разрабатываются модификации тестера:
- с подключением к компьютеру через СОМ- порт для мониторинга всех параметров сопротивления в процессе заряда-разряда;
- Пригодные для измерения сопротивления герметизированных свинцово-кислотных батарей, которые дают возможность также и измерения тока короткого замыкания.
Расширение диапазона обследуемых в соответствии со стандартом МЭК источников
тока возможно при создании универсального
стационарного прибора, где тестовый ток для
измерений внутреннего сопротивления на постоянном токе будет задаваться вшироком диапазоне, а временная его диаграмма будет соответствовать стандарту на любые источники
тока. Изготовление такого прибора планируется в самое ближайшее время.
Изготовление такого прибора планируется в самое ближайшее время.
Авторы выражают благодарность А. А. Тагановой за помощь в подготовке материала.
Литература
- Таганова А. А., Бубнов Ю. И., Орлов
Б. Герметичные химические источники тока: элементы и аккумуляторы, оборудование для испытаний и эксплуатации. СПб:Химиздат. 2005. - Таганова А. А., Пак И. А. Герметичные химические источники тока для портативной аппаратуры: Справочник. СПб: Химиздат. 2003.
- Таганова А. А., Бубнов Ю. И. Герметичные химические источники тока: элементы и аккумуляторы, способы и устройства заряда. СПб: Химиздат. 2002.
Как найти внутреннее сопротивление формула. Как рассчитать внутреннее сопротивление источника питания
Закон Ома для полной цепи, определение которого касается значения электрического тока в реальных цепях, находится в зависимости от источника тока и от сопротивления нагрузки. Этот закон носит и другое название — закон Ома для замкнутых цепей.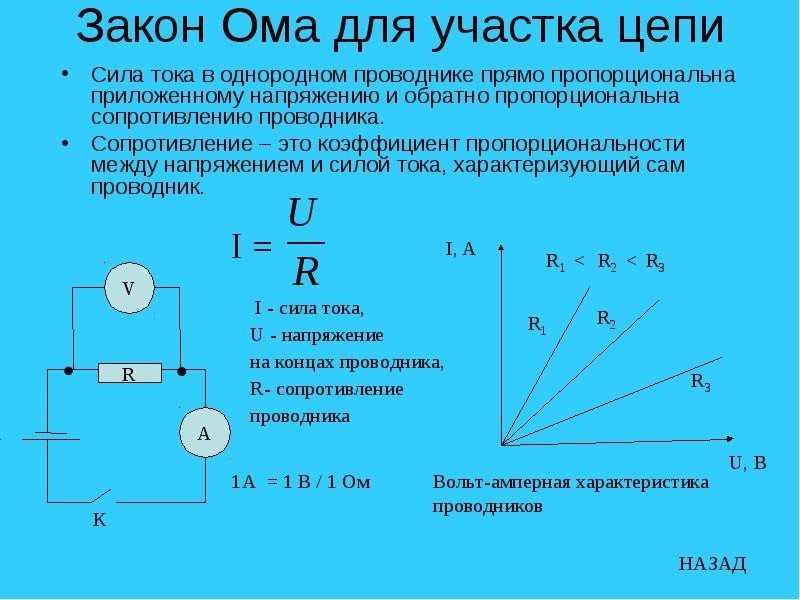 Принцип действия данного закона заключается в следующем.
Принцип действия данного закона заключается в следующем.
В качестве самого простого примера, электрическая лампа, являющаяся потребителем электрического тока, совместно с источником тока есть не что иное, как замкнутая . Данная электрическая цепь наглядно показана на рисунке.
Электроток, проходя через лампочку, также проходит и через сам источник тока. Таким образом, во время прохождения по цепи, ток испытает сопротивление не только проводника, но и сопротивление, непосредственно, самого источника тока. В источнике сопротивление создается электролитом, находящимся между пластинами и пограничными слоями пластин и электролита. Отсюда следует, что в замкнутой цепи, ее общее сопротивление будет состоять из суммы сопротивлений лампочки и источника тока.
Внешнее и внутреннее сопротивление
Сопротивление нагрузки, в данном случае лампочки, соединенной с источником тока, носит название внешнего сопротивления. Непосредственное сопротивление источника тока называется внутренним сопротивлением. Для более наглядного изображения процесса, все значения необходимо условно обозначить. I — , R — внешнее сопротивление, r — внутреннее сопротивление. Когда по электрической цепи протекает ток, то для того, чтобы поддерживать его, между концами внешней цепи должна присутствовать разность потенциалов, которая имеет значение IхR. Однако, протекание тока наблюдается и во внутренней цепи. Значит, для того, чтобы поддержать электроток во внутренней цепи, также необходима разность потенциалов на концах сопротивления r. Значение этой разности потенциалов равно Iхr.
Для более наглядного изображения процесса, все значения необходимо условно обозначить. I — , R — внешнее сопротивление, r — внутреннее сопротивление. Когда по электрической цепи протекает ток, то для того, чтобы поддерживать его, между концами внешней цепи должна присутствовать разность потенциалов, которая имеет значение IхR. Однако, протекание тока наблюдается и во внутренней цепи. Значит, для того, чтобы поддержать электроток во внутренней цепи, также необходима разность потенциалов на концах сопротивления r. Значение этой разности потенциалов равно Iхr.
Электродвижущая сила аккумулятора
Аккумулятор должен иметь следующее значение электродвижущей силы, способной поддерживать необходимый ток в цепи: Е=IхR+Iхr
. Из формулы видно, что электродвижущая сила аккумулятора составляет сумму внешнего и внутреннего . Значение тока нужно вынести за скобки: Е=I(r+R)
. Иначе можно представить: I=Е/(r+R)
. Двумя последними формулами выражается закон Ома для полной цепи, определение которого звучит следующим образом: в замкнутой цепи сила тока прямо пропорциональна электродвижущей силе и обратно пропорциональна сумме сопротивлений этой цепи.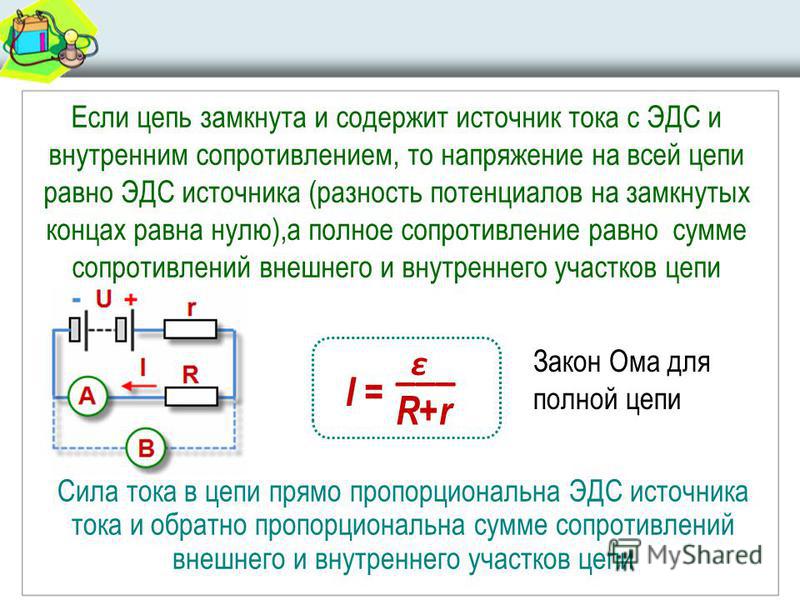
Двухполюсник и его эквивалентная схема
Вну́треннее сопротивле́ние двухполюсника — импеданс в эквивалентной схеме двухполюсника, состоящей из последовательно включенных генератора напряжения и импеданса (см. рисунок). Понятие применяется в теории цепей при замене реального источника идеальными элементами, то есть при переходе к эквивалентной схеме.
Введение
Рассмотрим пример. В легковом автомобиле запитаем бортовую сеть не от штатного свинцово-кислотного аккумулятора напряжением 12 вольт и ёмкостью 55 А·ч, а от последовательно соединённых восьми батареек (например, типоразмера АА, ёмкостью около 1 А·ч). Попробуем завести двигатель. Опыт показывает, что при питании от батареек вал стартера не повернётся ни на градус. Более того, не сработает даже втягивающее реле.
Интуитивно понятно, что батарейка «недостаточно мощная» для подобного применения, однако рассмотрение её заявленных электрических характеристик — напряжения и заряда (ёмкости) — не даёт количественного описания данного явления.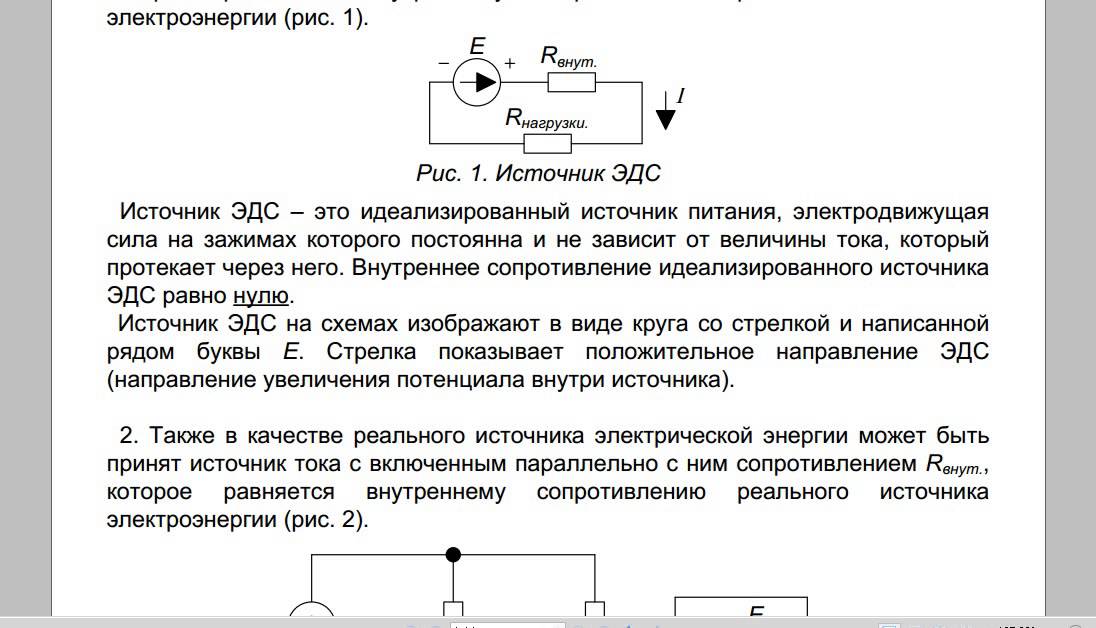 Напряжение в обоих случаях одинаково:
Напряжение в обоих случаях одинаково:
Аккумулятор: 12 вольт
Гальванические элементы: 8·1,5 вольт = 12 вольт
Ёмкости также вполне достаточно: одного ампер·часа в батарейке должно хватить, чтобы вращать стартер в течение 14 секунд (при токе 250 ампер).
Казалось бы, в соответствии с законом Ома ток в одинаковой нагрузке при электрически одинаковых источниках также должен быть одинаковым. Однако в действительности это не совсем так. Источники вели бы себя одинаково, если бы были идеальными генераторами напряжения. Для описания степени отличия реальных источников от идеальных генераторов и применяется понятие внутреннее сопротивление.
Сопротивление и внутреннее сопротивление
Основной характеристикой двухполюсника является его сопротивление (или импеданс). Однако характеризовать двухполюсник одним только сопротивлением не всегда возможно. Дело в том, что термин сопротивление примени́м только для чисто пассивных элементов, то есть не содержащих в себе источников энергии. Если двухполюсник содержит источник энергии, то понятие «сопротивление» к нему просто не применимо, поскольку закон Ома в формулировке U=Ir не выполняется.
Если двухполюсник содержит источник энергии, то понятие «сопротивление» к нему просто не применимо, поскольку закон Ома в формулировке U=Ir не выполняется.
Таким образом, для двухполюсников, содержащих источники (то есть генераторы напряжения и генераторы тока) необходимо говорить именно о внутреннем сопротивлении (или импедансе). Если же двухполюсник не содержит источников, то «внутреннее сопротивление» для такого двухполюсника означает то же самое, что и просто «сопротивление».
Родственные термины
Если в какой-либо системе можно выделить вход и/или выход, то часто употребляются следующие термины:
Входное сопротивление — внутреннее сопротивление двухполюсника, которым является вход системы.
Выходное сопротивление — внутреннее сопротивление двухполюсника, которым является выход системы.
Физические принципы
Несмотря на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (причем активное сопротивление, то есть резистор в нем присутствует обязательно), внутреннее сопротивление не сосредоточено в каком-либо одном элементе. Двухполюсник лишь внешне ведет себя так, словно в нем имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности внутреннее сопротивление является внешним проявлением совокупности физических эффектов:
Двухполюсник лишь внешне ведет себя так, словно в нем имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности внутреннее сопротивление является внешним проявлением совокупности физических эффектов:
Если в двухполюснике имеется только источник энергии без какой-либо электрической схемы (например, гальванический элемент), то внутреннее сопротивление чисто активное, оно обусловлено физическими эффектами, которые не позволяют мощности, отдаваемой этим источником в нагрузку, превысить определенный предел. Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в химическом источнике мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.
В случае двухполюсника, содержащего внутри электрическую схему, внутреннее сопротивление «рассредоточено» в элементах схемы (в дополнение к перечисленным выше механизмам в источнике).
Отсюда также следуют некоторые особенности внутреннего сопротивления:
Внутреннее сопротивление невозможно убрать из двухполюсника
Внутреннее сопротивление не является стабильной величиной: оно может изменяться при изменении каких-либо внешних условий.
Влияние внутреннего сопротивления на свойства двухполюсника
Эффект внутреннего сопротивления является неотъемлемым свойством любого двухполюсника. Основной результат наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.
Если к источнику с ЭДС генератора напряжения E и активным внутренним сопротивлением r подключена нагрузка с сопротивлением R, то ток, напряжение и мощность в нагрузке выражаются следующим образом.
Расчёт
Понятие расчёт применимо к схеме (но не к реальному устройству). Расчёт приведён для случая чисто активного внутреннего сопротивления (отличия реактивного сопротивления будут рассмотрены далее).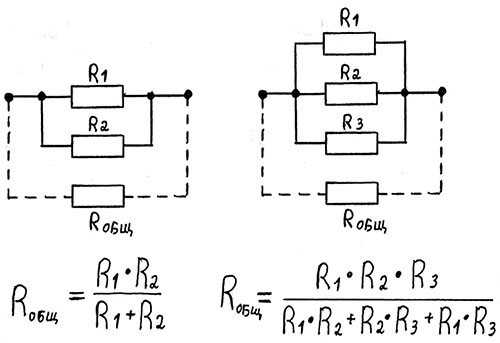
Пусть, имеется двухполюсник, который может быть описан приведенной выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:
ЭДС генератора напряжения U
Внутреннее сопротивление r
В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов Uout = φ2 − φ1) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:
где Uout1 — выходное напряжение при токе I1, Uout2 — выходное напряжение при токе I2. Решая систему уравнений, находим искомые неизвестные:
Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система (1) записывается следующим образом:
где Uoc — выходное напряжение в режиме холостого хода (англ. open circuit), то есть при нулевом токе нагрузки; Isc — ток нагрузки в режиме короткого замыкания (англ. short circuit), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:
short circuit), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:
Измерение
Понятие измерение применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение, которое принципиально не отличается от расчета — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощенной формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.
Часто применяется следующий простой способ измерения, не требующий вычислений:
Измеряется напряжение холостого хода
В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нем составило половину от напряжения холостого хода.
После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.
Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.
Реактивное внутреннее сопротивление
Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности, то расчет реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды, то есть расчет производится методом комплексных амплитуд.
Измерение реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией, а не скалярным значением:
Можно искать различные параметры комплексного значения: модуль, аргумент, только вещественную или мнимую часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.
Соответственно, методика измерений будет зависеть от того, что хотим получить.
Необходимость введения термина можно проиллюстрировать следующим примером. Сравним два химических источника постоянного тока с одинаковым напряжением:
- Автомобильный свинцово-кислотный аккумулятор напряжением 12 вольт и ёмкостью 55 А·ч
- Восемь батареек типоразмера АА, соединенных последовательно. Суммарное напряжение такой батареи также 12 вольт, ёмкость значительно меньше — примерно 1 А·ч
Несмотря на одинаковое напряжение, эти источники значительно отличаются при работе на одинаковую нагрузку. Так, автомобильный аккумулятор способен отдать в нагрузку большой ток (от аккумулятора заводится двигатель автомобиля, при этом стартер потребляет ток 250 ампер), а от цепочки батареек стартер вообще не вращается. Относительно небольшая емкость батареек не является причиной: одного ампер-часа в батарейках хватило бы для того, чтобы вращать стартер в течение 14 секунд (при токе 250 ампер).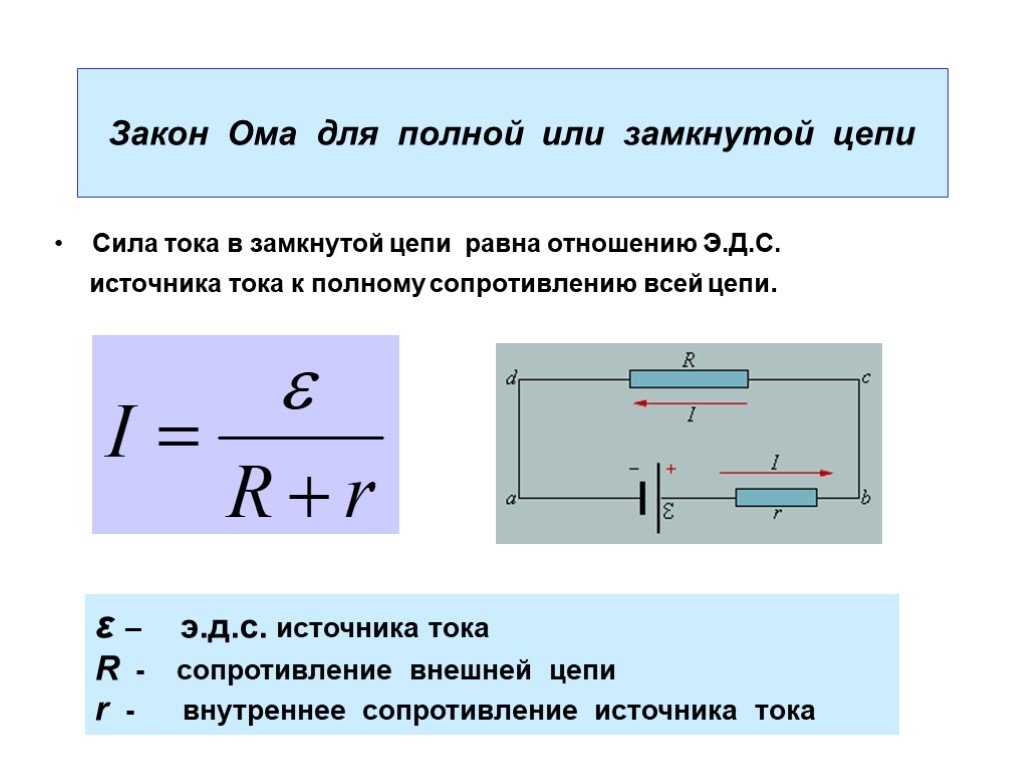
Таким образом, для двухполюсников, содержащих источники (то есть генераторы напряжения и генераторы тока) необходимо говорить именно о внутреннем сопротивлении (или импедансе). Если же двухполюсник не содержит источников, то «внутреннее сопротивление» для такого двухполюсника означает то же самое, что и просто «сопротивление».
Родственные термины
Если в какой-либо системе можно выделить вход и/или выход, то часто употребляются следующие термины:
Физические принципы
Несмотря на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (причём активное сопротивление , то есть резистор в нём присутствует обязательно), внутреннее сопротивление не сосредоточено в каком-либо одном элементе. Двухполюсник лишь внешне ведёт себя так, словно в нём имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности внутреннее сопротивление является внешним проявлением совокупности физических эффектов:
- Если в двухполюснике имеется только источник энергии без какой-либо электрической схемы (например, гальванический элемент), то внутреннее сопротивление практически чисто активное (если только речь не идет об очень высоких частотах), оно обусловлено физическими эффектами, которые не позволяют мощности , отдаваемой этим источником в нагрузку, превысить определённый предел.
 Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.
Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д. - В случае двухполюсника, содержащего внутри электрическую схему , внутреннее сопротивление «рассредоточено» в элементах схемы (в дополнение к перечисленным выше механизмам в источнике).
Отсюда также следуют некоторые особенности внутреннего сопротивления:
Влияние внутреннего сопротивления на свойства двухполюсника
Эффект внутреннего сопротивления является неотъемлемым свойством любого активного двухполюсника. Основной результат наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.
Пусть, имеется двухполюсник, который может быть описан приведённой выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:
- ЭДС генератора напряжения U
- Внутреннее сопротивление r
В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов U out = φ 2 − φ 1 ) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:
| (Напряжения) |
где U out1 I 1 , U out2 — выходное напряжение при токе I 2 . Решая систему уравнений, находим искомые неизвестные:
Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система () записывается следующим образом:
где U oc — выходное напряжение в режиме холостого хода (англ. open circuit ), то есть при нулевом токе нагрузки; I sc — ток нагрузки в режиме короткого замыкания (англ. short circuit ), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:
open circuit ), то есть при нулевом токе нагрузки; I sc — ток нагрузки в режиме короткого замыкания (англ. short circuit ), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:
| (ВнутрСопр) |
Измерение
Понятие измерение применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение , которое принципиально не отличается от расчёта — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощённой формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.
Иногда применяется следующий простой способ измерения, не требующий вычислений:
- Измеряется напряжение холостого хода
- В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нём составило половину от напряжения холостого хода.

После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.
Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.
Реактивное внутреннее сопротивление
Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности , то расчет реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды , то есть расчет производится методом комплексных амплитуд .
Измерение реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией , а не скалярным значением:
- Можно искать различные параметры комплексного значения: модуль , аргумент , только вещественную или мнимую часть, а также комплексное число полностью.
 Соответственно, методика измерений будет зависеть от того, что хотим получить.
Соответственно, методика измерений будет зависеть от того, что хотим получить. - Любой из перечисленных параметров зависит от частоты. Теоретически, чтобы получить путем измерения полную информацию о реактивном внутреннем сопротивлении, необходимо снять зависимость от частоты, то есть провести измерения на всех частотах, которые может генерировать источник данного двухполюсника.
Применение
В большинстве случаев следует говорить не о применении внутреннего сопротивления, а об учете его негативного влияния, поскольку внутреннее сопротивление является скорее негативным эффектом. Тем не менее, в некоторых системах наличие внутреннего сопротивления с номинальным значением является просто необходимым.
Упрощение эквивалентных схем
Представление двухполюсника как совокупность генератора напряжения и внутреннего сопротивления является наиболее простой и часто используемой эквивалентной схемой двухполюсника.
Согласование источника и нагрузки
Согласование источника и нагрузки — это выбор соотношения сопротивления нагрузки и внутреннего сопротивления источника с целью достижения заданных свойств полученной системы (как правило, стараются достичь максимального значения какого-либо параметра для данного источника).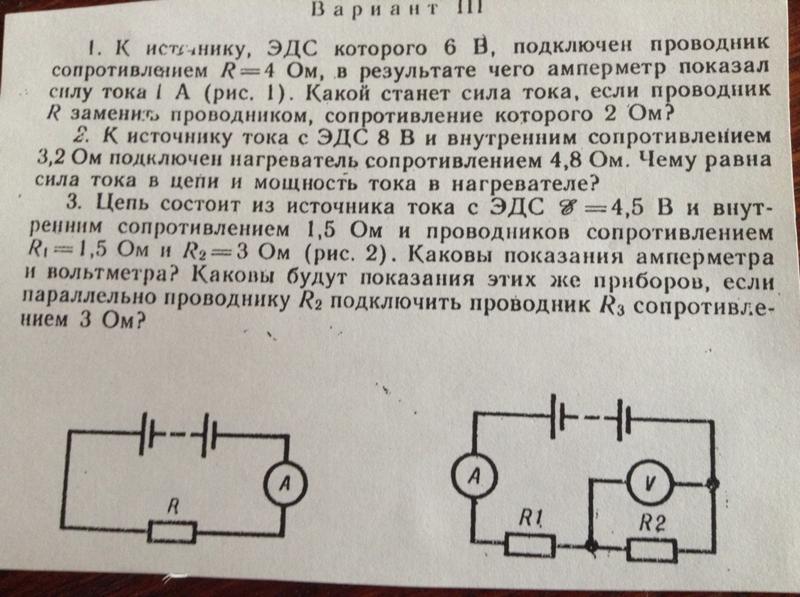 Наиболее часто используются следующие типы согласования:
Наиболее часто используются следующие типы согласования:
Согласование по току и мощности следует использовать с осторожностью, так как есть опасность перегрузить источник.
Понижение высоких напряжений
Иногда к источнику искусственно добавляют большое сопротивление (оно добавляется к внутреннему сопротивлению источника) для того, чтобы значительно понизить получаемое от него напряжение. Однако добавление резистора в качестве дополнительного сопротивления (так называемый гасящий резистор) ведёт к бесполезному выделению мощности на нём. Чтобы не расходовать энергию впустую, в системах переменного тока используют реактивные гасящие импедансы, чаще всего конденсаторы . Таким образом строятся конденсаторные блоки питания. Аналогично, при помощи ёмкостного отвода от высоковольтной ЛЭП можно получить небольшие напряжения для питания каких-либо автономных устройств.
Минимизация шума
При усилении слабых сигналов часто возникает задача минимизации шума, вносимого усилителем в сигнал. Для этого используются специальные малошумящие усилители , однако они спроектированы таким образом, что наименьший коэффициент шума достигается лишь в определенном диапазоне выходного сопротивления источника сигнала. Например, малошумящий усилитель обеспечивает минимальный шум только в диапазоне выходных сопротивлений источника от 1 кОм до 10 кОм; если источник сигнала обладает меньшим выходным сопротивлением (например, микрофон с выходным сопротивлением 30 Ом), то следует применить между источником и усилителем повышающий трансформатор , который повысит выходное сопротивление (а также напряжение сигнала) до необходимого значения.
Для этого используются специальные малошумящие усилители , однако они спроектированы таким образом, что наименьший коэффициент шума достигается лишь в определенном диапазоне выходного сопротивления источника сигнала. Например, малошумящий усилитель обеспечивает минимальный шум только в диапазоне выходных сопротивлений источника от 1 кОм до 10 кОм; если источник сигнала обладает меньшим выходным сопротивлением (например, микрофон с выходным сопротивлением 30 Ом), то следует применить между источником и усилителем повышающий трансформатор , который повысит выходное сопротивление (а также напряжение сигнала) до необходимого значения.
Ограничения
Понятие внутреннего сопротивления вводится через эквивалентную схему, поэтому имеют силу те же ограничения , что и для применимости эквивалентных схем.
Примеры
Значения внутреннего сопротивления относительны: то, что считается малым, например, для гальванического элемента, является очень большим для мощного аккумулятора. Ниже приведены примеры двухполюсников и значения их внутреннего сопротивления r . Тривиальные случаи двухполюсников без источников оговорены особо.
Ниже приведены примеры двухполюсников и значения их внутреннего сопротивления r . Тривиальные случаи двухполюсников без источников оговорены особо.
Малое внутреннее сопротивление
Большое внутреннее сопротивление
Отрицательное внутреннее сопротивление
Существуют двухполюсники, внутреннее сопротивление которых имеет отрицательное значение. В обычном активном сопротивлении происходит диссипация энергии, в реактивном сопротивлении энергия запасается, а затем выделяется обратно в источник. Особенность отрицательного сопротивления в том, что оно само является источником энергии. Поэтому отрицательное сопротивление в чистом виде не встречается, оно может быть только имитировано электронной схемой, которая обязательно содержит источник энергии. Отрицательное внутреннее сопротивление может быть получено в схемах путём использования:
- элементов с отрицательным дифференциальным сопротивлением , например, туннельных диодов
Системы с отрицательным сопротивлением потенциально неустойчивы и поэтому могут быть использованы для построения автогенераторов .
См. также
Ссылки
Литература
- Зернов Н. В., Карпов В.Г. Теория радиотехнических цепей. — М. — Л.: Энергия, 1965. — 892 с.
- Джонс М. Х. Электроника — практический курс. — М.: Техносфера, 2006. — 512 с. ISBN 5-94836-086-5
Примечания
Wikimedia Foundation . 2010 .
- Политехнический терминологический толковый словарь
ЭДС и напряжение. Внутреннее сопротивление источников питания.
Ликбез так ликбез!
Закон Ома. Вот я о чем.
О законе Ома мы уже говорили. Поговорим еще раз — с несколько иной стороны. Не вдаваясь в физические подробности и выражаясь простым кошачьим языком, закон Ома гласит: чем больше э.д.с. (электродвижущая сила), тем больше ток, чем больше сопротивление, тем меньше ток.
Переведя сие заклинание на язык сухих формул получаем:
I=E/R
где:I — сила тока,E — Э.Д.С. — электродвижущая силаR — сопротивление
Ток измеряется в амперах, э. д.с. — в вольтах, а сопротивление носит гордое имя товарища Ома.Э.д.с. — это есть характеристика идеального генератора, внутренне сопротивление которого принято считать бесконечно малым. В реальной жизни такое бывает редко, поэтому в силу вступает закон Ома для последовательной цепи (более знакомый нам):
д.с. — в вольтах, а сопротивление носит гордое имя товарища Ома.Э.д.с. — это есть характеристика идеального генератора, внутренне сопротивление которого принято считать бесконечно малым. В реальной жизни такое бывает редко, поэтому в силу вступает закон Ома для последовательной цепи (более знакомый нам):
I=U/R
где:U — напряжение источника непосредственно на его клеммах.
Рассмотрим простой пример.
Представим себе обычную батарейку в виде источника э.д.с. и включенного последовательно с ним некоего резистора, который будет олицетворять собой внутреннее сопротивление батарейки. Подключим параллельно батарейке вольтметр. Его входное сопротивление значительно больше внутреннего сопротивления батарейки, но не бесконечно большое — то есть, через него потечет ток. Величина напряжения, которую покажет вольтметр будет меньше величины э.д.с. как раз на величину падения напряжения на внутреннем воображаемом резисторе при данном токе.Но, тем не менее именно эта величина и принимается за напряжение батарейки.
Формула конечного напряжения при этом будет иметь следующий вид:
U(бат)=E-U(внутр)
Так как со временем у всех элементов питания внутреннее сопротивление увеличивается, то и падение напряжения на внутреннем сопротивлении тоже увеличивается. При этом напряжение на клеммах батарейки уменьшается. Мяу!
Разобрались!
Что же происходит, если вместо вольтметра к батарейке подключить амперметр? Так как собственное сопротивление амперметра стремится к нулю, мы фактически будем измерять ток, протекающий через внутреннее сопротивление батарейки. Так как внутренне сопротивление источника очень небольшое, измеренный при этом ток может достигать н ескольких ампер.
Однако следует заметить, что внутреннее сопротивление источника является таким же элементом цепи, как и все остальные. Поэтому при увеличении тока нагрузки падение напряжения на внутреннем сопротивлении также увеличится, что приводит к уменьшению напряжения на нагрузке. Или как мы, радиокоты, любим выражаться — к просадке напруги.
Чтобы изменение нагрузки как можно меньше влияло на выходное напряжение источника его внутреннее сопротивление стараются свести к минимуму.
Можно так подобрать элементы последовательной цепи, чтобы на каком-нибудь из них получить напряжение, уменьшенное, по сравнению с исходным, во сколько угодно раз.
На концах проводника, а значит, и тока необходимо наличие сторонних сил неэлектрической природы, с помощью которых происходит разделение электрических зарядов .
Сторонними силами называются любые силы, действующие на электрически заряженные частицы в цепи, за исключением электростатических (т. е. кулоновских).
Сторонние силы приводят в движение заряженные частицы внут-ри всех источников тока: в генераторах, на электростанциях, в гальванических элементах, аккумуляторах и т. д.
При замыкании цепи создается электрическое поле во всех про-водниках цепи. Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил (электроны движут-ся от положительно заряженного электрода к отрицательному), а во всей остальной цепи их приводит а движение электрическое поле (см. рис. выше).
рис. выше).
В источниках тока в процессе работы по разделению заряженных частиц происходит превращение разных видов энергии в электричес-кую. По типу преобразованной энергии различают следующие виды электродвижущей силы:
— электростатическая — в электрофорной машине, в которой происходит превращение механической энергии при трении в электрическую;
— термоэлектрическая — в термоэлементе — внутренняя энергия нагретого спая двух проволок, изготовленных из разных металлов, превращается в электрическую;
— фотоэлектрическая — в фотоэлементе. Здесь происходит превращение энергии света в элек-трическую: при освещении некоторых веществ, например, селена, оксида меди (I) , кремния наблюдается потеря отрицательного электрического заряда;
— химическая — в гальванических элементах, аккумуляторах и др. источниках, в которых происходит превращение химической энергии в электрическую.
Электродвижущая сила (ЭДС) — характеристика источников тока. Понятие ЭДС было введено Г. Омом в 1827 г. для цепей постоянного тока. В 1857 г. Кирхгофф определил ЭДС как работу сторонних сил при переносе единичного электрического заряда вдоль замкнутого контура:
Понятие ЭДС было введено Г. Омом в 1827 г. для цепей постоянного тока. В 1857 г. Кирхгофф определил ЭДС как работу сторонних сил при переносе единичного электрического заряда вдоль замкнутого контура:
ɛ = A ст /q ,
где ɛ — ЭДС источника тока, А ст — работа сторонних сил , q — количество перемещенного заряда.
Электродвижущую силу выражают в вольтах.
Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил (работа по перемещению единичного заряда) не во всем контуре, а только на данном участке.
Внутреннее сопротивление источника тока.
Пусть имеется простая замкнутая цепь, состоящая из источника тока (например, гальванического элемента, аккумулятора или генератора) и резистора с сопротивлением R . Ток в замкну-той цепи не прерывается нигде, следовательно, oн существует и внутри источника тока. Любой источник представляет собой некоторое сопротивление дли тока. Оно называется внутренним сопротивлением источника тока и обозначается буквой r .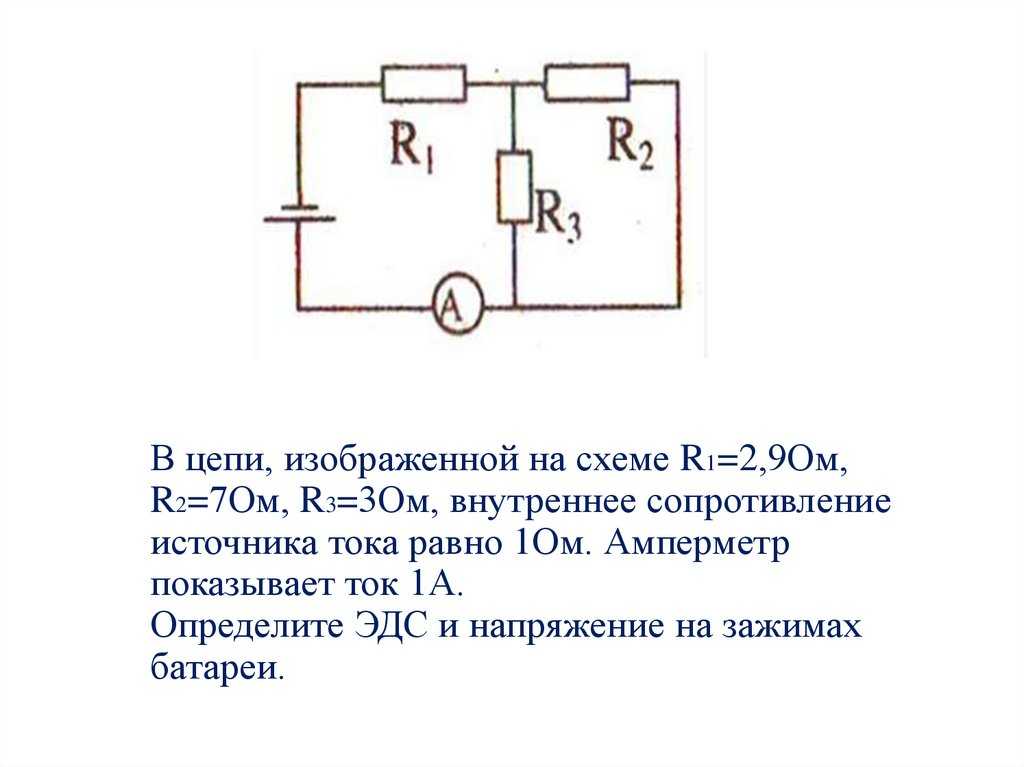
В генераторе r — это сопротивление обмотки, в гальваническом элементе — сопротивление раствора электролита и электродов.
Таким образом, источник тока характеризуется величинами ЭДС и внутреннего сопротивлении, которые определяют его качество. Например, электростатические машины имеют очень большую ЭДС (до десятков тысяч вольт), но при этом их внутреннее сопротивление огромно (до со-тни Мом). Поэтому они непригодны для получения сильных токов. У гальванических элементов ЭДС всего лишь приблизительно 1 В, но зато и внутреннее сопротивление мало (приблизительно 1 Ом и меньше). Это позволяет с их помощью получать токи, измеряемые амперами.
Внутреннее сопротивление источника постоянного тока формула
P.S. общее сопротивление можно находить и через использование закона Ома, который гласит, что сопротивление равно напряжение деленное на силу тока. Следовательно, берем мультиметр, измеряем ток и напряжение в том месте цепи, где хотим узнать сопротивление. Воспользовавшись формулой Ома находим (определяем) электрическое сопротивление нужного участка цепи. Напомню, что при использовании закона ома нужно применять основные единицы измерения — ток в амперах, напряжение в вольтах, а сопротивление в омах.
Напомню, что при использовании закона ома нужно применять основные единицы измерения — ток в амперах, напряжение в вольтах, а сопротивление в омах.
Его можно находить двумя путями: рассчитать или измерить. Первым путём идут при работе с электрическими схемами, второй – выбирают, занимаясь с реальными устройствами.
Простой расчёт производится с использованием формулы Закона Ома для участка полной цепи:
Комплекс измерений этого параметра у настоящего устройства не подразумевает непосредственных замеров. Тестируются напряжения на нагрузочном сопротивлении в двух режимах тока: холостом и КЗ.
Так как не любой источник может выдержать даже кратковременный режим замыкания, берётся метод измерения без вычислений.
В схему включается внешнее сопротивление нагрузки в виде подстроечного резистора Rн. Выставляется такое значение, при котором падение напряжения на резисторе равнялось бы 1/2 U холостого хода. Тогда измеренное омметром Rн будет соответствовать внутреннему сопротивлению источника.
Эксплуатация батарей приводит к их разрядке. Восстановление аккумуляторов, зарядка малогабаритных элементов осуществляется при помощи тока, значение силы которого не превышает одной десятой емкости источника.
Кроме гальванических и электролитических двухполюсников, существуют источники питания, схемы которых включают в себя реактивные элементы. При определении их внутреннего сопротивления используют метод комплексных амплитуд. Он подразумевает использовать при расчётах комплексные сопротивления элементов, включённых в схему. Величины токов и напряжений заменяются значениями их комплексных амплитуд. Сам алгоритм вычисления такой же, как при расчёте активного сопротивления.
Процесс измерений r-реактивного немного отличается от измерения активной составляющей сопротивления. Методы зависят от того, какие параметры этой комплексной функции нужно узнать: отдельные составляющие или комплексное число.
На эти параметры влияет частота, поэтому, чтобы при тестировании добиться информации о внутреннем реактивном значении r, нужно убрать частотную зависимость. Это достигается комплексом замеров на всём диапазоне частот, генерируемых таким двухполюсником.
Это достигается комплексом замеров на всём диапазоне частот, генерируемых таким двухполюсником.
В принципе, любая из возможных окислительно-восстановительных реакций может быть использована в батареях. Но веществ, способных работать в ценных технически элементах, не так уж и много. Более того, многие реакции требуют затрат дорогостоящих веществ.
Современные аккумуляторные батареи имеют более простое строение. Два электрода, помещенные в один электролит, заполняют сосуд — корпус батареи. Такие конструктивные особенности упрощают строение и удешевляют аккумуляторы.
Сопротивление тока не позволяет всем ионам одновременно оказаться на электродах, поэтому элемент работает достаточно долго. Химические реакции образования ионов рано или поздно прекращаются, элемент разряжается.
Источника тока имеет большое значение.
Большое внутреннее сопротивление
Пьезоэлектрические датчики, конденсаторные микрофоны и другие источники импульсов обладают повышенным внутренним импедансом. Чтобы эффективно использовать такие устройства, нужно правильно согласовать схему считывания сигнала. При неудачном согласовании неизбежны потери.
Чтобы эффективно использовать такие устройства, нужно правильно согласовать схему считывания сигнала. При неудачном согласовании неизбежны потери.
Важно! Удачное согласование по напряжению получается при использовании для снятия сигнала устройства, с большим входным сопротивлением, чем у источника сигнала. В случае высокоомного источника для считывания сигнала применяется буферный усилитель.
ИНФОФИЗ — мой мир.
Весь мир в твоих руках — все будет так, как ты захочешь
Весь мир в твоих руках — все будет так, как ты захочешь
- Главная
- Мир физики Физика в формулах
- Теоретические сведения
- Физический юмор
- Физика вокруг нас
- Физика студентам Для рефератов
- Экзамены
- Лекции по физике
- Естествознание
- Солнечная система
- Физика и психология
- World Wide Web
- Мои лекции
«Инфофиз» — это сайт для тех, кто учится сам и учит других
Ведь «обучать — значит вдвойне учиться» (Ж. Жубер)
Жубер)
Раздел «Архитектура ЭВМ и ВС»
Материал для изучения по дисциплине «Архитектура ЭВМ и вычислительные сети»
Раздел «Программное обеспечение компьютерных сетей»
Материал для изучения дисциплины «Программное обеспечение компьютерных сетей»
Раздел «Информатика»
Материалы для изучения дисциплины «Информатика»
Раздел «Физика»
Физика — одна из самых удивительных наук!
Надеюсь, данный раздел поможет Вам эффективно и интересно изучать физику.
Учите физику!
- Физика школьникам
- Физика студентам
- Астрономия
- Информатика
- ПОКС
- Арх ЭВМ и ВС
- Методические материалы
- Медиа-файлы
- Тестирование
Как сказал.
Если вы студент, значит перед вами стоит тысяча возможностей. Найдите в себе силы, чтобы использовать хотя бы одну из них.
Вопросы к экзамену
Для всех групп технического профиля
Законы и формулы
- Механика Кинематика
- Динамика
- Законы сохранения
- Статика, гидростатика и гидродинамика
Влияние внутреннего сопротивления на свойства двухполюсника
Чем оно выше, тем меньшую мощность выдаёт источник при подключении нагрузки.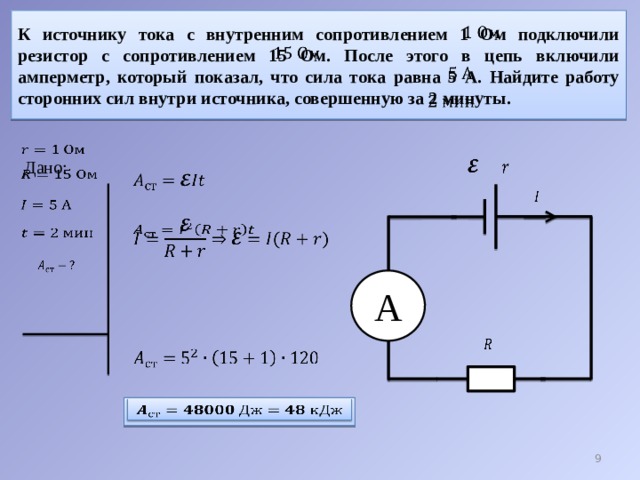 Определить мощность в нагрузке можно по формуле:
Определить мощность в нагрузке можно по формуле:
где:
- E – напряжение ЭДС;
- R – сопротивление нагрузки;
- r – активное внутреннее сопротивление двухполюсника.
Формула применима к двухполюсникам, не отдающим энергию.
К сведению. Когда величина внутреннего сопротивления двухполюсника приближается по своему значению к сопротивлению нагрузки, передача мощности достигает максимума.
Лаб. 4
= E/I — R; R = 4; 4.3/0.65 — 4 = 6.62 — 4 = 2.62 Ом.
| № опыта | Измерено | Вычислено | |
| E, В | I, А | r, Ом | |
| 1 | 4,3 | 0,65 | |
| 2 | 4,3 | 0,65 | |
| 3 | 4,3 | 0,65 | |
| 4 | 4,3 | 0,65 | |
| 5 | 4,3 | 0,65 | |
| Среднее | 4,3 | 0,65 | 2,62 |
- ΔE = ΔиE + ΔоE; ΔE = 0.
 15 В + 0,18 В = 0,26 В;
15 В + 0,18 В = 0,26 В; - ΔI = ΔиI + ΔоI; ΔI = 0.05 А + 0,025 А = 0,075 А.
Er = 0.25/4.3 + 0.075/0.65 + 0.1/4 = 0.06 + 0.12 + 0.025 = 0.21 В.
Δr = 0.21 В · 2,62 Ом = 0,55 Ом.
1. Почему вольтметр включают в цепь параллельно потребителю? Что произойдет, если вольтметр включить в цепь последовательно?
Вольтметр включают параллельно участку цепи, на котором измеряют напряжение. Напряжение на измеренном участке и напряжение на вольтметре будет одним и тем же, т.к. вольтметр и напряжение на вольтметре подключены к общим точкам.
Т.к. вольтметр обладает большим сопротивлением, то при его последовательном подключении к электрической цепи увеличится внешнее сопротивление цепи, а, значит, сила тока в цепи значительно уменьшится.
2. Почему сопротивление амперметра должно быть значительно меньше сопротивления цепи, в которой измеряют ток? Что произойдет, если амперметр включить параллельно потребителю?
Поскольку включение амперметра в электрическую цепь не должно изменять силу тока в ней, то сопротивление амперметра должно быть как можно меньше.
Сопротивление амперметра гораздо меньше сопротивления потребителя, поэтому при таком неправильном подключении почти весь ток пойдёт через амперметр. В итоге «зашкалит» и может перегореть, если вовремя не отключить. Такое включение амперметра недопустимо.
3. Почему показания вольтметра при разомкнутом и замкнутом ключе различаются?
Потому что у источника питания появляется нагрузка в виде резистора. Вольтметр, подключённый к полюсам источника питания ЭДС источника ε. При подключении нагрузки (резистора) напряжение на источнике будет падать, т.к. источник не идеальный.
4. Как можно повысить точность измерения ЭДС источника тока?
Самый простой способ — взять вольтметр с меньшей приборной погрешностью, т.е. более высокого класса точности.
Также повысить точность можно путём совершенствования методики измерения и обработки результатов, таким образом можно уменьшить систематические погрешности.
5. При каком значении КПД будет получена максимальная полезная мощность от данного источника тока? Каким должно быть при этом сопротивление внешней цепи по отношению ко внутреннему сопротивлению источника тока?
Коэффициент полезного действия источника тока определяется как отношение полезной мощности к полной, и зависит от сопротивления нагрузки и внутреннего сопротивления источника тока. Можно доказать, что КПД оказывается равным 50%.
Можно доказать, что КПД оказывается равным 50%.
Источник
Разрядная емкость источника
Величина, зависящая от силы тока разряда, называется разрядной ёмкостью источника. Это электрический заряд, который отдаёт источник в процессе эксплуатации в зависимости от тока нагрузки. Эту величину можно считать постоянной условно. Так, стартерный аккумулятор, имеющий разрядную ёмкость С = 55 А*ч, при токе разряда 5,5 А проработает 10 часов. При запусках холодного или имеющего неисправность автомобиля аккумулятор можно разрядить за несколько минут.
Для того чтобы найти остаточную разрядную ёмкость, производят циклы «заряд – разряд». Они выполняются при помощи нагрузочных сопротивлений. Разряд на нагрузочное сопротивление производят до минимально допустимых значений плотности электролита. При этом замеряется время работы под нагрузкой. Это актуально при сезонном обслуживании аккумуляторов для выявления процессов саморазряда.
Внутреннее сопротивление источников тока – важная величина.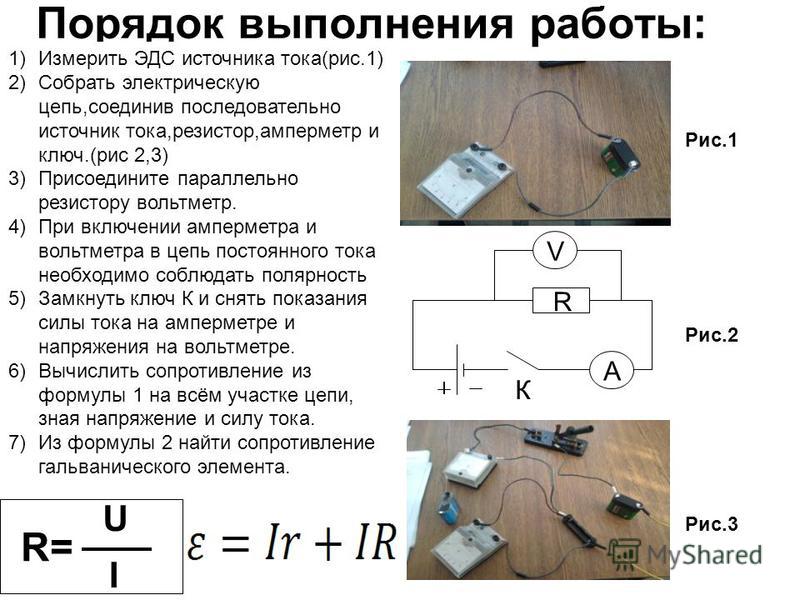 Методы, применяемые для её снижения, являются прямыми путями увеличения отдаваемой мощности источника, значит, повышения производительности двухполюсников. Правильное измерение и вычисление импеданса эквивалентных схем позволяют приблизить двухполюсник к идеальному источнику.
Методы, применяемые для её снижения, являются прямыми путями увеличения отдаваемой мощности источника, значит, повышения производительности двухполюсников. Правильное измерение и вычисление импеданса эквивалентных схем позволяют приблизить двухполюсник к идеальному источнику.
Медно-цинковый элемент
Принцип действия гальванических элементов интересно рассмотреть на примере медно-цинкового гальванического элемента, действие которого идет в счет энергии цинка и сульфата меди. В этом источнике пластина из меди помещена в раствор сульфата меди, а цинковый электрод погружен в раствор сульфата цинка. Растворы разделены пористой прокладкой во избежание смешивания, но обязательно соприкасаются.
Если цепь замкнута, поверхностный слой цинка окисляется. В процессе взаимодействия с жидкостью атомы цинка, превратившись в ионы, появляются в растворе. На электроде высвобождаются электроны, которые могут принимать участие в образовании тока.
Попадая на медный электрод, электроны принимают участие в восстановительной реакции.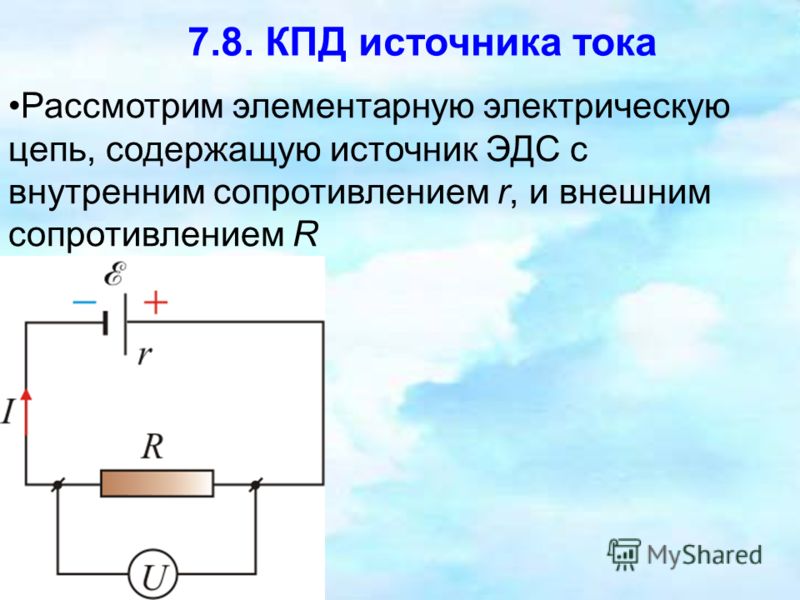 Из раствора на поверхностный слой поступают ионы меди, в процессе восстановления они превращаются в атомы меди, осаждаясь на медной пластине.
Из раствора на поверхностный слой поступают ионы меди, в процессе восстановления они превращаются в атомы меди, осаждаясь на медной пластине.
Суммируем происходящее: процесс работы гальванического элемента сопровождается переходом электронов восстановителя к окислителю по внешней части цепи. Реакции идут на обоих электродах. Внутри источника протекает ионный ток.
Видео
Величина, характеризующая количество энергетических потерь, возникающих при протекании тока через его источник, определяется как внутреннее сопротивление источника тока. Как и обычное сопротивление, имеет единицу измерения, равную 1 Ом. Ток, двигаясь через источник, теряет часть своей энергии, которая переходит в тепло, точно так же, как на любом нагрузочном сопротивлении. Это значит, что величина напряжения на выводах источника зависит от величины тока, а не от ЭДС.
Если рассмотреть замкнутую электрическую цепь, в которую включён источник тока (батарейка, аккумулятор или генератор), и нагрузку R, то ток течёт и внутри источника.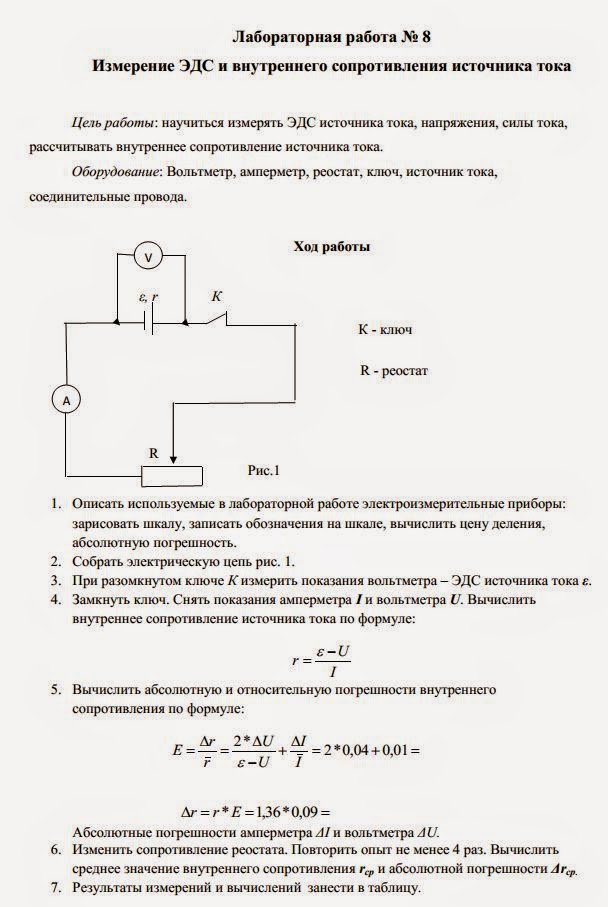 Внутреннее сопротивление источника, обозначаемое буквой r, ему препятствует.
Внутреннее сопротивление источника, обозначаемое буквой r, ему препятствует.
У генератора r – это внутреннее сопротивление обмоток статора, у аккумулятора – сопротивление электролита.
Обработка и анализ результатов проверки аккумуляторов
К одному UPS подключены две аккумуляторные батареи, состоящие из одинаковых
герметичных свинцовых кислотных аккумуляторов. Не известно, введены ли они в эксплуатацию одновременно и из одной ли партии эти аккумуляторы. Поэтому примем предложенное автором запроса разбиение аккумуляторов на две батареи и будем анализировать их по-отдельности.
Поместим все полученные данные в электронную таблицу и проведем несложный статистический анализ.
Минимальное и максимальное напряжение на аккумуляторе
| Батарея | 1 | 2 |
| Umin, В | 11,19 | 13,38 |
| Umax, В | 13,6 | 13,59 |
Сразу бросается в глаза большой разброс минимальных напряжений.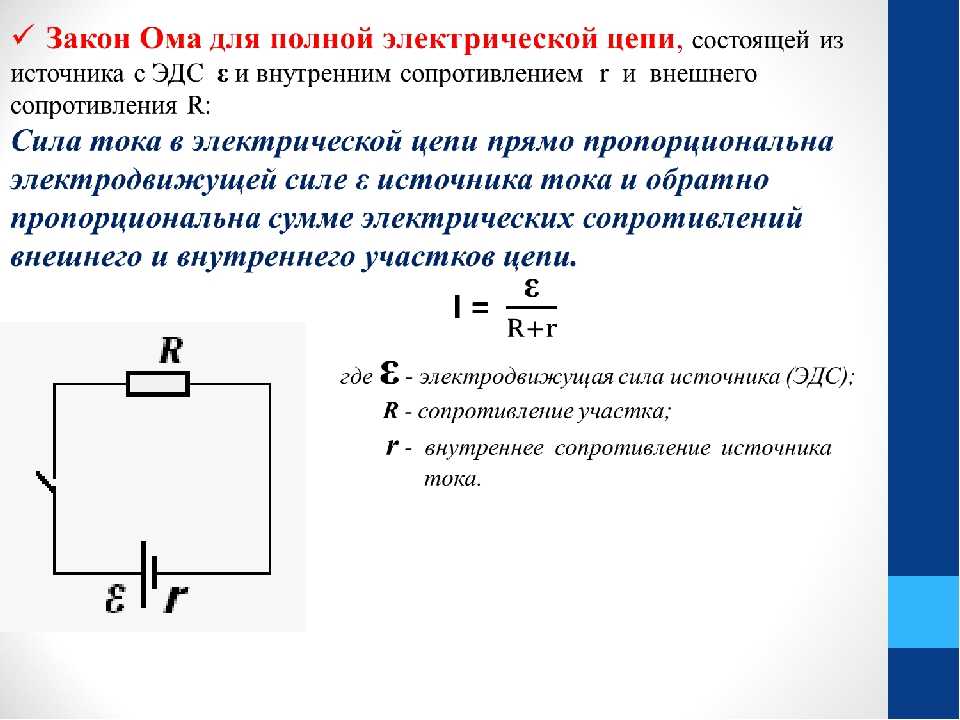 Смотрим на исходные данные и видим, что у одного из аккумуляторов батареи 1 напряжение понижено примерно на 2.2 В, по сравнению с другими аккумуляторами. Из-за пониженного напряжения, Кулон не смог оценить емкость этого аккумулятора. Напряжение на аккумуляторе 1-5 понижено примерно на величину напряжения одного элемента. Можно предположить, что в имеется короткое замыкание одного из элементов — этот аккумулятор следует заменить немедленно.
Смотрим на исходные данные и видим, что у одного из аккумуляторов батареи 1 напряжение понижено примерно на 2.2 В, по сравнению с другими аккумуляторами. Из-за пониженного напряжения, Кулон не смог оценить емкость этого аккумулятора. Напряжение на аккумуляторе 1-5 понижено примерно на величину напряжения одного элемента. Можно предположить, что в имеется короткое замыкание одного из элементов — этот аккумулятор следует заменить немедленно.
Среднее и медианное значение напряжения на аккумуляторе
| Батарея | 1 | 2 |
| Uсред, В | 13,42 | 13,52 |
| Uмедиан, В | 13,53 | 13,53 |
У нас есть большой выброс (аккумулятор 1-5), который сильно смещает величину среднего напряжения. Обычно для данных с выбросами правильнее использовать медиану, а не среднее. Для расчета отклонений напряжения, так сделаем и мы — примем за напряжение группы медианное значение напряжения.
Отклонения напряжения (аккумулятор 1-5 отброшен)
| Батарея | 1 | 2 |
Станд. откл. U (без выброса), В откл. U (без выброса), В | 0,04 | 0,04 |
| Относит. ст. Откл. | 0,32% | 0,31% |
Разбросы напряжения на аккумуляторах небольшие, это характерно для аккумуляторов из одной партии, до окончания ресурса которых еще остается некоторое время (старение аккумуляторов еще не вступило в финальную стадию). О наиболее интересующей нас величине — емкости аккумуляторов, напряжение или разброс напряжений не говорит ничего.
Минимальная и максимальная емкость аккумуляторов, среднее и медианное значение емкости.
| Батарея | 1 | 2 |
| Еmin, А*час | 32 | 32 |
| Emax, А*час | 39,2 | 39,4 |
| Eсред, А*час | 36,28 | 37,08 |
| Емедиан, А*час | 37,6 | 38 |
Максимальная и минимальная емкости аккумуляторов заметно различаются, поэтому отклонения мы будем мы рассчитывать относительно медианного значения.
Отклонения емкости аккумуляторов.

| Батарея | 1 | 2 |
| Станд.откл. Е (без 1-5), А*час | 2,64 | 1,93 |
| Относит. ст. Откл. | 7,03% | 5,07% |
| Макс.отклонение Е, А*час | 5,6 | 6 |
| Относит.макс.отклон.Е | 14,9% | 15,8% |
Стандартное отклонение емкости аккумуляторов 5-7% — это неплохо. Но максимальные отклонения емкости — великоваты для 10-летних аккумуляторов, простоявших в буфере всего 2 года. Похоже, что эти аккумуляторные батареи испытали на себе какое-то вредное воздействие (неправильные режимы зарядки или, скорее всего, повышенную температуру). Но сейчас, по утверждениям автора запроса, с температурой и режимами все нормально.
Сами по себе 15% отклонения емкости от медианы не являются причиной выводить аккумуляторы из эксплуатации. Поэтому можно считать состояние аккумуляторных батарей 1 и 2 (за исключением аккумулятора 1-5) удовлетворительным.
Измерение сопротивления петли фаза-нуль
Петля «фаза – нуль» – это электрическая цепь переменного тока, которая может возникнуть в результате короткого замыкания между проводами: «фаза» и «ноль» или «фаза» и «фаза». Разрушение изоляции, механические повреждения или случайное соединение оголённых участков кабеля между собой могут стать этому причиной. В установках с глухо заземлённой нейтралью нулевой проводник физически связан с нейтралью трансформатора, она подключена к контуру заземления. При замыкании на корпус или соединении фаз между собой образуется цепь (петля).
Разрушение изоляции, механические повреждения или случайное соединение оголённых участков кабеля между собой могут стать этому причиной. В установках с глухо заземлённой нейтралью нулевой проводник физически связан с нейтралью трансформатора, она подключена к контуру заземления. При замыкании на корпус или соединении фаз между собой образуется цепь (петля).
Главная задача проводимых измерений – узнавать, каким будет величина тока через петлю при КЗ. Это обязательно для расчёта и подбора защитного оборудования. Хорошим результатом будет маленькое сопротивление петли, тогда ток Iк.з. будет наибольшим. От его величины зависит, как быстро сработает защитный автоматический выключатель.
Чем меньше времени будет затрачено на отключение повреждённой или закороченной цепи, тем больше шансов предотвратить пожар от возгорания кабельной сети. При попадании человека под удар электрического тока в результате прикосновения или короткого замыкания автоматическое снятие напряжения спасёт ему жизнь.
На предприятиях ежегодно проводится комплекс измерений защитного заземления и сопротивления петли фаза – ноль. При неудовлетворительных результатах проводится ряд мероприятий:
- заменяются участки провода, не отвечающие требованиям по диаметру сечения;
- перекручиваются болтовые соединения с обязательной установкой врезных шайб;
- вскрываются контуры защитных заземлений и осматриваются на предмет целостности сварных соединений и состояния элементов заземления;
- при необходимости в контур защитного заземления добавляются дополнительные элементы;
- исключается последовательное подключение корпусов устройств к общей шине заземления.
После выполнения комплекса мероприятий измерения проводятся повторно.
Первые попытки
Первые попытки «накопить электричество» для дальнейшего его исследования и использования были предприняты в Голландии. Немец Эвальд Юрген фон Клейст и голландец Питер ван Мушенбрук, проводившие свои исследования в городке Лейден, создали первый в мире конденсатор, названный позже «лейденской банкой».
Накопление электрического заряда уже проходило под действием механического трения. Использовать разряд через проводник можно было в течение некоторого, достаточно короткого, промежутка времени.
Победа человеческого разума над такой эфемерной субстанцией, как электричество, оказалась революционной.
К сожалению, разряд (электрический ток, создаваемый конденсатором) длился настолько коротко, что создать постоянный ток не мог. Кроме того, напряжение, даваемое конденсатором, постепенно понижается, что не оставляет возможности получать длительный ток.
Нужно было искать иной способ.
Реактивное внутреннее сопротивление
Кроме гальванических и электролитических двухполюсников, существуют источники питания, схемы которых включают в себя реактивные элементы. При определении их внутреннего сопротивления используют метод комплексных амплитуд. Он подразумевает использовать при расчётах комплексные сопротивления элементов, включённых в схему. Величины токов и напряжений заменяются значениями их комплексных амплитуд. Сам алгоритм вычисления такой же, как при расчёте активного сопротивления.
Сам алгоритм вычисления такой же, как при расчёте активного сопротивления.
Процесс измерений r-реактивного немного отличается от измерения активной составляющей сопротивления. Методы зависят от того, какие параметры этой комплексной функции нужно узнать: отдельные составляющие или комплексное число.
На эти параметры влияет частота, поэтому, чтобы при тестировании добиться информации о внутреннем реактивном значении r, нужно убрать частотную зависимость. Это достигается комплексом замеров на всём диапазоне частот, генерируемых таким двухполюсником.
Закон Ома в комплексной форме
Чтобы провести анализ электрических цепей синусоидального тока, комфортнее использовать закон Ома в комплексной форме. Для лучшего понимания введем основное понятие, фигурирующее в данной интерпретации закона: синусоидальный ток – это линейные цепи с установившимся режимом работы, после того, как переходные процессы в них завершены, уровень напряжения резко уменьшается на конкретной дистанции, токи в ветвях и ЭДС источников являются синусоидальными функциями времени. В противном случае, когда данные параметры не соблюдаются, закон не может быть применим. Чем отличается эта форма от обычной? Ответ прост: токи, сопротивление и ЭДС фиксируются как комплексные числа. Это обусловлено тем, что существуют как активные так и реактивные значения напряжений, токов и сопротивлений, а в результате этого требуется внесение определенных коррективов.
В противном случае, когда данные параметры не соблюдаются, закон не может быть применим. Чем отличается эта форма от обычной? Ответ прост: токи, сопротивление и ЭДС фиксируются как комплексные числа. Это обусловлено тем, что существуют как активные так и реактивные значения напряжений, токов и сопротивлений, а в результате этого требуется внесение определенных коррективов.
Вместо активного сопротивления используется полное, то есть комплексное сопротивление цепи Z. Падение напряжения, ток и ЭДС тоже превращаются в комплексные величины. При реальных расчетах лучше и удобнее применять действующие значения. Итак, закон в комплексной форме выглядит так:
i = U/Z, i = UY
В данной формуле Z – комплексное сопротивление, Y – комплексная проводимость.
Чтобы выявить эти величины, выведены формулы. Пропустим шаги их создания и приведем готовые формулы:
Z = ze = z cosф + jz sinф = r + jx
Y = 1/ ze = ye = y cos ф — jy sin ф = g + jb
Большое внутреннее сопротивление
Пьезоэлектрические датчики, конденсаторные микрофоны и другие источники импульсов обладают повышенным внутренним импедансом. Чтобы эффективно использовать такие устройства, нужно правильно согласовать схему считывания сигнала. При неудачном согласовании неизбежны потери.
Чтобы эффективно использовать такие устройства, нужно правильно согласовать схему считывания сигнала. При неудачном согласовании неизбежны потери.
Важно! Удачное согласование по напряжению получается при использовании для снятия сигнала устройства, с большим входным сопротивлением, чем у источника сигнала. В случае высокоомного источника для считывания сигнала применяется буферный усилитель.
Двухполюсник и его эквивалентная схема
Двухполюсник представляет собой электрическую цепь, содержащую две точки присоединения к другим цепям. Бывает два вида электрических цепей:
- цепи, содержащие источник тока или напряжения;
- двухполюсники, не являющиеся источниками.
Первые характеризуются электрическими параметрами: силой тока, напряжением и импедансом. Для расчёта параметров таких двухполюсников предварительно производят замену реальных элементов цепи на идеальные элементы. Комбинация, которая получается в результате подобной замены, называется эквивалентной схемой.
Внимание! При работе со сложными электрическими схемами с учётом того, что устройство работает на одной частоте, допустимо преобразовывать последовательные и параллельные ветви до получения простой схемы, доступной для расчёта параметров.
Второй вид двухполюсников можно охарактеризовать только величиной внутреннего сопротивления.
Как написать жалобу
Заявление пишется в свободной форме, лучше делать его в печатном виде, чтобы избежать вопросов о неразборчивости почерка. Собрать подписи всех неравнодушных, если это коллективная жалоба, и отнести в управляющую организацию либо выслать заказным письмом почтой. Заказное письмо оформляется для того, чтобы быть уверенным, что адресат получил заявление. Квитанция почты потом может пригодиться при обращении в прокуратуру или в суд.
В заявлении должны быть указаны:
- Наименование организации.
- ФИО руководителя организации, куда направляется жалоба.
- ФИО заявителя и контактные данные – адрес и телефон.

- Подробное изложение проблемы.
- Подписи и дата написания.
В готовом виде заявление на низкое напряжение в сети может выглядеть так: образец.
Если жалоба пишется в электронном виде на сайте управляющей компании, достаточно заполнить все предложенные поля.
Влияние внутреннего сопротивления на свойства двухполюсника
Чем оно выше, тем меньшую мощность выдаёт источник при подключении нагрузки. Определить мощность в нагрузке можно по формуле:
где:
- E – напряжение ЭДС;
- R – сопротивление нагрузки;
- r – активное внутреннее сопротивление двухполюсника.
Формула применима к двухполюсникам, не отдающим энергию.
К сведению. Когда величина внутреннего сопротивления двухполюсника приближается по своему значению к сопротивлению нагрузки, передача мощности достигает максимума.
Вывод
Внутреннее сопротивление бывает не только у различных химических источников напряжения.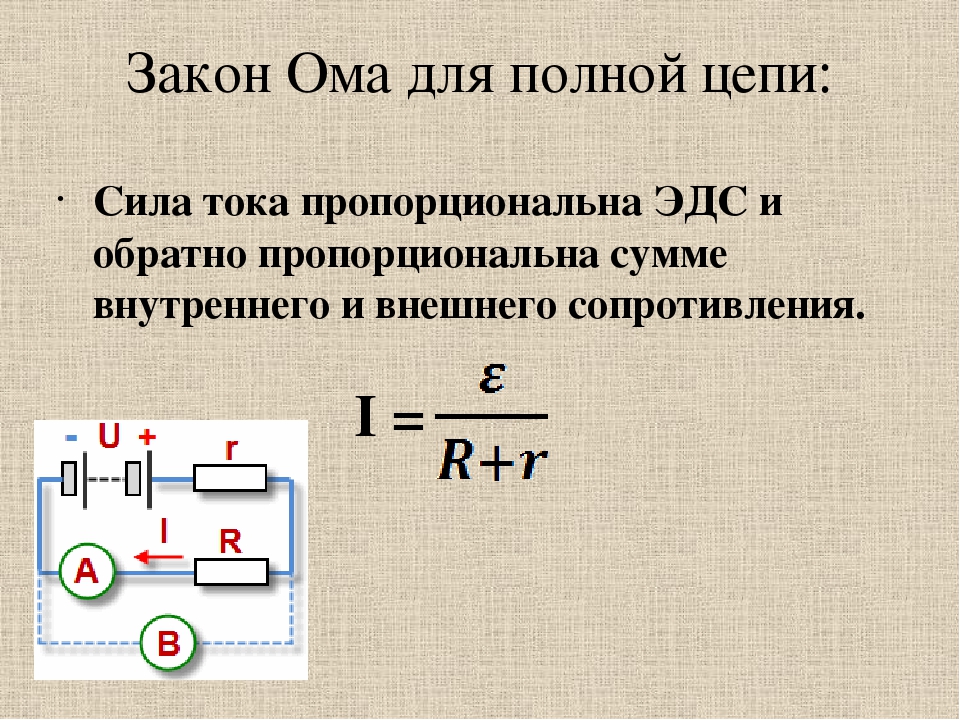 Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.
Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.
Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник электрической энергии.
Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.
Источник
Разрядная емкость источника
Величина, зависящая от силы тока разряда, называется разрядной ёмкостью источника. Это электрический заряд, который отдаёт источник в процессе эксплуатации в зависимости от тока нагрузки. Эту величину можно считать постоянной условно. Так, стартерный аккумулятор, имеющий разрядную ёмкость С = 55 А*ч, при токе разряда 5,5 А проработает 10 часов. При запусках холодного или имеющего неисправность автомобиля аккумулятор можно разрядить за несколько минут.
Это электрический заряд, который отдаёт источник в процессе эксплуатации в зависимости от тока нагрузки. Эту величину можно считать постоянной условно. Так, стартерный аккумулятор, имеющий разрядную ёмкость С = 55 А*ч, при токе разряда 5,5 А проработает 10 часов. При запусках холодного или имеющего неисправность автомобиля аккумулятор можно разрядить за несколько минут.
Для того чтобы найти остаточную разрядную ёмкость, производят циклы «заряд – разряд». Они выполняются при помощи нагрузочных сопротивлений. Разряд на нагрузочное сопротивление производят до минимально допустимых значений плотности электролита. При этом замеряется время работы под нагрузкой. Это актуально при сезонном обслуживании аккумуляторов для выявления процессов саморазряда.
Внутреннее сопротивление источников тока – важная величина. Методы, применяемые для её снижения, являются прямыми путями увеличения отдаваемой мощности источника, значит, повышения производительности двухполюсников. Правильное измерение и вычисление импеданса эквивалентных схем позволяют приблизить двухполюсник к идеальному источнику.
Какая организация отвечает за напряжение в сети
При обнаружении в многоквартирном доме проблем в сети, не связанными с проводкой в определенной квартире, следует вопрос решать всем домом совместно с соседями. Обращаться следует в управляющую организацию, проще говоря туда, куда производится оплата за электроэнергию.
Первым делом необходимо написать письмо-претензию, при этом будет лучше, если оно будет подписано подавляющим большинством жильцов дома. Обязательно следует получить входящий номер регистрации, а копию письма оставить себе с отметкой регистратора.
По закону срок рассмотрения такого письма составляет 30 суток, по истечении которых организация обязана предоставить какой-либо ответ или уведомить о продлении срока рассмотрения.
Если ответа нет, тогда следует направить письмо в прокуратуру с описанием проблемы и указанием, что ответ от управляющей стороны не получен, желательно с приложением копии, на которой будет проставлен регистрационный номер письма в управляющую компанию.
В зависимости от решения вопроса прокуратурой или параллельно с отправленным письмом можно оформить запросы в Роспотребнадзор и администрацию населенного пункта. Общественная палата тоже может оказать определенное воздействие. Запрос в Энергонадзор поможет прояснить ситуацию, на каком этапе проседает электричество.
Последней инстанцией в этом вопросе будет суд, для которого необходимо будет собрать дополнительно документы.
Если бытовая техника при скачке напряжения вышла из строя, тогда следует:
- Уведомить поставщика электроэнергии о произошедшем для фиксации факта и составлении акта.
- Получить в сервисном центре документ, в котором указана причина выхода из строя техники.
- Подать поставщику претензию с требованием возмещения нанесенного ущерба.
- В случае отказа нужно обратиться в суд.
внутреннее сопротивление источников напряжения
Когда используется источник постоянного тока, такой как генератор, аккумулятор, вы изначально предполагаете, что он обеспечит желаемое напряжение для
любую резистивную нагрузку независимо от того, какую нагрузку вы можете применить. К сожалению,
Это не всегда так. Например, если мы применим резистор 1 кОм
к лабораторному источнику постоянного тока довольно легко установить напряжение на
резистор на 20 В. Однако, если мы удалим резистор 1 кОм и
замените его на резистор 100 Ом и не трогайте элементы управления на источнике питания
вообще, мы можем обнаружить, что напряжение упало до 19.14 В. Изменение
нагрузку на резистор 68 Ом, и напряжение на клеммах падает до 18,72 В.
Мы обнаруживаем, что приложенная нагрузка влияет на напряжение на клеммах источника питания.
К сожалению,
Это не всегда так. Например, если мы применим резистор 1 кОм
к лабораторному источнику постоянного тока довольно легко установить напряжение на
резистор на 20 В. Однако, если мы удалим резистор 1 кОм и
замените его на резистор 100 Ом и не трогайте элементы управления на источнике питания
вообще, мы можем обнаружить, что напряжение упало до 19.14 В. Изменение
нагрузку на резистор 68 Ом, и напряжение на клеммах падает до 18,72 В.
Мы обнаруживаем, что приложенная нагрузка влияет на напряжение на клеммах источника питания.
Этот пример показывает, что сеть всегда должна быть подключена к источнику питания до уровня устанавливается напряжение питания.
Причина, по которой напряжение на клеммах падает при изменении нагрузки (ток спрос) это
Каждый практический (реальный) источник питания имеет внутреннее сопротивление, включенное последовательно с идеализированным источником напряжения.
Уровень сопротивления зависит от типа питания,
но он всегда присутствует. Каждый год выходят новые поставки, которые меньше
чувствителен к приложенной нагрузке, но даже в этом случае некоторая чувствительность все же остается.
Каждый год выходят новые поставки, которые меньше
чувствителен к приложенной нагрузке, но даже в этом случае некоторая чувствительность все же остается.
Из-за внутреннего сопротивления источника питания идеальный внутренний источник питания должен быть установлен на некоторое значение выше фиксированного значения. Внутреннее сопротивление улавливает дополнительное значение приложенного напряжения. Поясним идею внутреннего сопротивления и идеального значения напряжения на следующем примере.
(a) Идеальный источник напряжения
(b) Батарея с внутренним сопротивлением
Рис.№1: Идеальные и практичные источники напряжения.
Ток в цепи определяется с учетом идеального напряжения на рис. № 1 (а). просто глядя на нагрузку и используя закон Ома; то есть,
$ I_L = {20 В \ более 1000 Ом} = 20 мА $, что является относительно низким током.
Но практически не существует идеального источника напряжения, опять же, каждый источник напряжения имеет некоторое внутреннее сопротивление, как показано на рис.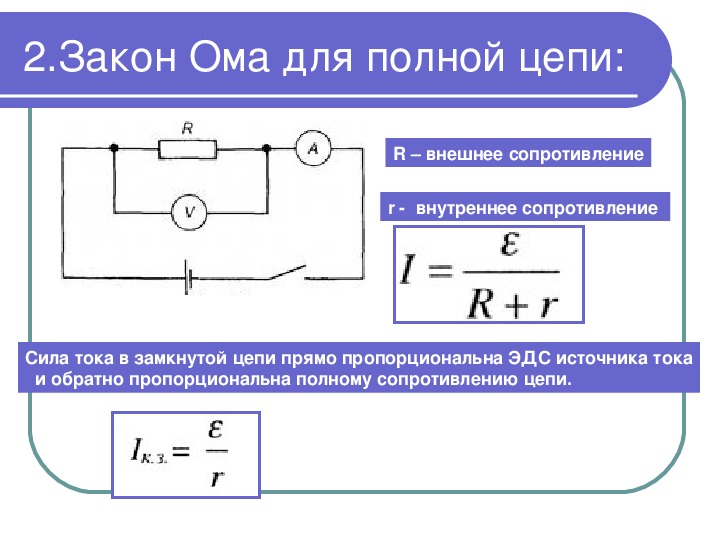 № 1 (б). Внутреннее сопротивление батареи на рисунке принято равным 5 Ом. Чтобы рассчитать протекание тока в цепи, теперь мы должны посчитать значение внутреннего сопротивления, а также определить влияние внутреннего сопротивления источника напряжения в цепи.
$$ I_L = {20В\свыше 1000Ом+5Ом} =190,9 мА$$
Падение напряжения на сопротивлении нагрузки может быть равно $V_L = 1000 Ом \× 19,9 мА = 19,9 В$, что показывает, что внутреннее сопротивление источника напряжения влияет на падение напряжения нагрузки до некоторого значения, зависящего от сопротивления нагрузки. Увеличение значения сопротивления нагрузки имеет смысл игнорировать внутреннее сопротивление и полагаться только на сопротивление нагрузки. Но уменьшение сопротивления нагрузки окажет значительное влияние на последовательный ток в цепи, что повлияет на напряжение на клеммах нагрузки.
№ 1 (б). Внутреннее сопротивление батареи на рисунке принято равным 5 Ом. Чтобы рассчитать протекание тока в цепи, теперь мы должны посчитать значение внутреннего сопротивления, а также определить влияние внутреннего сопротивления источника напряжения в цепи.
$$ I_L = {20В\свыше 1000Ом+5Ом} =190,9 мА$$
Падение напряжения на сопротивлении нагрузки может быть равно $V_L = 1000 Ом \× 19,9 мА = 19,9 В$, что показывает, что внутреннее сопротивление источника напряжения влияет на падение напряжения нагрузки до некоторого значения, зависящего от сопротивления нагрузки. Увеличение значения сопротивления нагрузки имеет смысл игнорировать внутреннее сопротивление и полагаться только на сопротивление нагрузки. Но уменьшение сопротивления нагрузки окажет значительное влияние на последовательный ток в цепи, что повлияет на напряжение на клеммах нагрузки.
Чтобы преодолеть этот эффект, к источнику напряжения добавляется дополнительное значение источника напряжения. Следовательно, эффект внутреннего сопротивления компенсируется за счет этого дополнительного значения напряжения, добавленного к напряжению источника.
Например, в приведенном выше примере, если напряжение источника составляет 20,1 В, и закон Ома снова применяется таким же образом. Напряжение на клеммах сопротивления нагрузки теперь будет равно 20 вольтам, что является требуемым напряжением на сопротивлении нагрузки.
$$ I_L = {20,1 В \ более 1005 Ом} = 20 мА$$
$$ V_L = 20 мА \× 1000 Ом = 20 В$$
Следовательно, эффект внутреннего сопротивления компенсируется за счет этого дополнительного значения напряжения, добавленного к напряжению источника.
Например, в приведенном выше примере, если напряжение источника составляет 20,1 В, и закон Ома снова применяется таким же образом. Напряжение на клеммах сопротивления нагрузки теперь будет равно 20 вольтам, что является требуемым напряжением на сопротивлении нагрузки.
$$ I_L = {20,1 В \ более 1005 Ом} = 20 мА$$
$$ V_L = 20 мА \× 1000 Ом = 20 В$$
Что такое условия без нагрузки и полной нагрузки
Без нагрузки (NL) — это состояние выходных клемм источника питания, которые не подключены к какой-либо нагрузке, ток будет 0А из-за отсутствия полной цепи показано на рис.№3(а). Выходное напряжение будет внутренним идеальным уровнем питания.
Условия полной нагрузки (FL) определяются максимальным током, который источник питания может непрерывно подавать в подключенную к нему цепь, показанную на рис. № 3 (b).
(a)
(b)
Рис. №3: Условия без нагрузки и полной нагрузки
№3: Условия без нагрузки и полной нагрузки
Как найти внутреннее сопротивление источника напряжения?
Внутреннее сопротивление можно определить путем испытаний в условиях холостого хода и полной нагрузки. В условиях холостого хода питание на выходных клеммах дает полное напряжение питания с нулевым током из-за разомкнутой цепи, показанной на рис. № 2 (а). Когда мы замыкаем цепь с некоторым сопротивлением выходной нагрузки, уровень тока увеличивается, а напряжение на выходных клеммах падает аналогичным образом. График показан на рис. № 2 (b), где по оси x показан ток, а по оси y — напряжение на выходных клеммах источника питания.
(a)
(b)
Рис. № 2: График зависимости VL от IL для подачи.
Наклон линии определяется внутренним сопротивлением источника питания. То есть, (1)
что для графика на рис. № 2 (б) дает
$$ \begin{array} {rcl}R_{int} &=& {\Delta V_L \over \Delta I_L}\\
& = &{20,1 В — 18,2 В \более 275,2 мА — 0 А}\\
&=&6 Ом \end{массив}$$ Для поставок любого рода сюжетом особое значение имеет выход
напряжение по отношению к току, потребляемому от источника питания. Обратите внимание, что максимальное значение достигается в условиях холостого хода (NL). Условия полной нагрузки (FL) определяются максимальным током, который источник питания может обеспечить.
непрерывная основа.
Обратите внимание, что максимальное значение достигается в условиях холостого хода (NL). Условия полной нагрузки (FL) определяются максимальным током, который источник питания может обеспечить.
непрерывная основа.
Реальный аналог: глава 2 — справочник Digilent
В главе 1 мы представили законы Кирхгофа (которые регулируют взаимодействие между элементами цепи) и закон Ома (который регулирует отношения напряжения и тока для резисторов). Эти аналитические инструменты дают нам возможность анализировать любую схему, содержащую только резисторы и идеальные источники питания. Однако в главе 1 мы также видели, что анализ схемы, основанный исключительно на грубом применении этих инструментов, может быстро усложниться — мы, по сути, должны использовать в качестве неизвестных разность напряжений на все резисторы и токи через все резисторы . Обычно это приводит к большому количеству неизвестных и, соответственно, большому количеству уравнений, которые необходимо написать и решить для анализа любой схемы, кроме самой простой.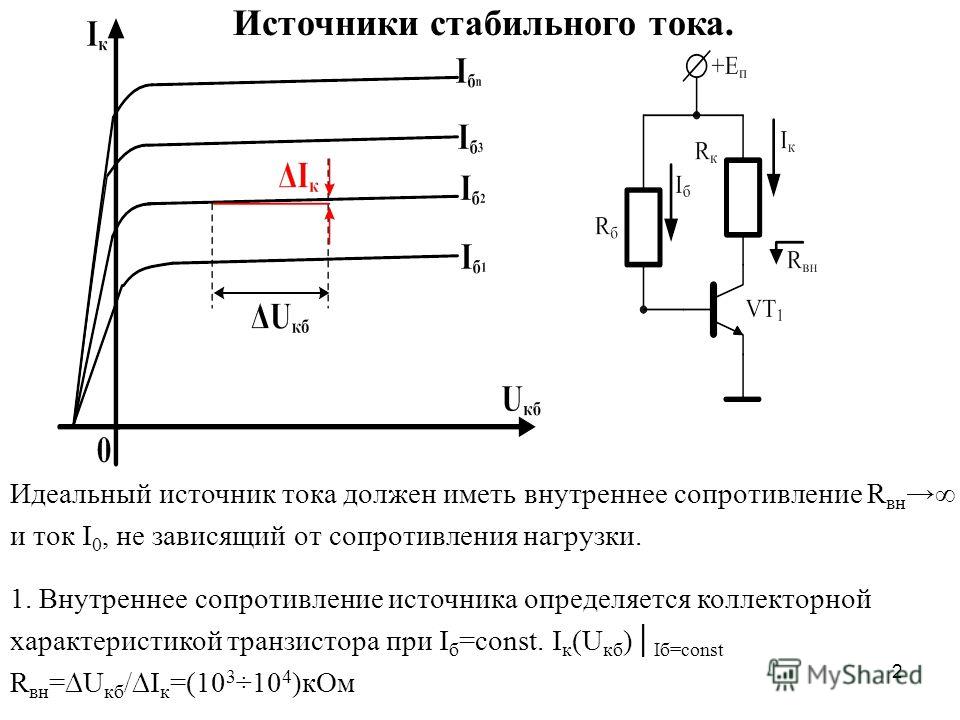
В следующих нескольких главах мы по-прежнему будем применять законы Кирхгофа и закон Ома при анализе цепей, но сосредоточимся на повышении эффективности нашего анализа. Как правило, это повышение эффективности достигается за счет уменьшения количества неизвестных в схеме, что уменьшает количество уравнений, которые необходимо написать для описания работы схемы.
В этой главе мы представляем методы анализа, основанные на сокращении схемы . Сокращение цепи состоит из объединения сопротивлений в цепи с меньшим количеством резисторов, которые (в некотором смысле) эквивалентны исходной резистивной сети. Уменьшение количества резисторов, конечно, уменьшает количество неизвестных в цепи.
Мы начнем обсуждение методов сокращения цепей с представления двух конкретных, но очень полезных концепций: Series 9.0072 и параллельные резисторы . Эти концепции приведут нас к формулам напряжения и делителя тока . Затем мы рассматриваем сокращение более общих схем, что обычно соответствует идентификации нескольких наборов последовательных и параллельных сопротивлений в сложной резистивной сети. Затем эта глава завершается двумя важными примерами применения методов уменьшения схемы: анализ неидеальных источников питания и неидеальное измерение 9устройства 0072; без понимания этих устройств невозможно построить практические схемы или понять
последствия измерения напряжения или тока.
Затем эта глава завершается двумя важными примерами применения методов уменьшения схемы: анализ неидеальных источников питания и неидеальное измерение 9устройства 0072; без понимания этих устройств невозможно построить практические схемы или понять
последствия измерения напряжения или тока.
После завершения этой главы вы должны уметь:
Определять последовательные и параллельные комбинации элементов схемы
Определение эквивалентного сопротивления комбинаций последовательных резисторов
Определение эквивалентного сопротивления параллельных комбинаций резисторов
Соотношение делителя напряжения и тока из памяти
Определение эквивалентного сопротивления электрических цепей, состоящих из последовательных и параллельных комбинаций резисторов
Схема эквивалентных схем для неидеальных измерителей напряжения и тока
Анализ цепей, содержащих неидеальные источники напряжения или тока
Определение влияния неидеальных счетчиков на измеряемый параметр
2.
 1 Элементы последовательной цепи и разделение напряжения
1 Элементы последовательной цепи и разделение напряженияСуществует ряд распространенных комбинаций элементов схемы, которые довольно легко анализировать. Эти «особые случаи» заслуживают внимания, поскольку многие сложные схемы содержат эти комбинации схем в качестве подсхем. Распознавание этих подсхем и их соответствующий анализ могут значительно упростить анализ схемы.
В этой главе особое внимание уделяется двум важным комбинациям элементов схемы: элементам, включенным последовательно, и элементам, включенным параллельно. Также обсуждается использование этих комбинаций элементов схемы для уменьшения сложности анализа схемы.
Соединения серииГоворят, что элементы цепи соединены в ряды и , если все элементы имеют одинаковый ток. Пример двух последовательно соединенных элементов схемы показан на рис. 2.1. Применяя KCL в узле a и принимая токи из узла за положительные, мы видим, что:
$$-i_1+i_2=0$$
или же
$$i_1=i_2 \qquad (уравнение 2. 1)$$
1)$$
Уравнение (2.1) является прямым следствием того, что (единственный) узел а на рис. 2.1 соединяет между собой только два элемента — к этому узлу не подключены другие элементы, через которые можно отвести ток. Это наблюдение настолько очевидно (во многих случаях 1) ), что уравнение (2.1) обычно записывается путем проверки для последовательных элементов, таких как те, что показаны на рис. 2.1 без явного написания KCL.
При последовательном соединении резисторов возможно упрощение схемы. Рассмотрим резистивную цепь, показанную на рис. 2.2 (а). Так как резисторы включены последовательно, они оба пропускают один и тот же ток. Закон Ома дает:
\начать{выравнивать*} v_1 = R_1i\ v_2=R_2i \\ (Уравнение 2.2) \конец{выравнивание*}
Применение KVL вокруг цикла:
$$ -v+v_1+v_2=0 \Rightarrow v=v_1+v_2 \qquad (уравнение 2.3)$$
Подстановка уравнений (2.2) в уравнение (2.3) и решение текущих i приводит к:
$$ i = \frac{v}{R_1+R_2} \qquad (уравнение 2. 4) $$
4) $$
Теперь рассмотрим схему на рис. 2.2(b). Применение закона Ома к этой цепи и решение для тока i дает:
$$ i = \frac{v}{R_{eq}} \qquad (уравнение 2.5) $$
Сравнивая уравнение (2.4) с уравнением (2.5), видим, что схемы рис. 2.2(а) и 2.2(б) неразличимы, если мы выберем:
$$R_{eq}=R_1+R_2 \qquad (уравнение 2.6)$$
Рисунки 2.2(a) и 2.2(b) называются эквивалентными схемами , если эквивалентное сопротивление на рис. 2.2(b) выбрано, как показано в уравнении (2.6). R экв уравнения (2.6) называется эквивалентным сопротивлением последовательного соединения резисторов R 1 и R 2 .
Этот результат можно обобщить на последовательную комбинацию сопротивлений N следующим образом:
Последовательную комбинацию резисторов N R 1 , R 2 , …, R N можно заменить одним эквивалентным сопротивлением $R_{eq}=R_1+R_2+ \cdots + R_N$. Эквивалентная схема может быть проанализирована для определения тока через последовательную комбинацию резисторов.
Эквивалентная схема может быть проанализирована для определения тока через последовательную комбинацию резисторов.
Раздел напряжения
Объединение уравнений (2.2) с уравнением (2.4) приводит к следующим выражениям для V i и v 2 :
$$v_1= \frac{R_1}{R_1+R_2}v \qquad (уравнение 2.7)$$
$$v_2= \frac{R_2}{R_1+R_2}v \qquad (уравнение 2.8)$$
Эти результаты обычно называют отношениями делителя напряжения , потому что они показывают, что общее падение напряжения на последовательной комбинации резисторов делится между отдельными резисторами в комбинации. Отношение падения напряжения каждого отдельного резистора к общему падению напряжения такое же, как отношение отдельного сопротивления к общему сопротивлению.
Приведенные выше результаты можно обобщить для последовательной комбинации сопротивления N следующим образом:
Падение напряжения на любом резисторе в последовательной комбинации N сопротивлений пропорционально общему падению напряжения на комбинации резисторов.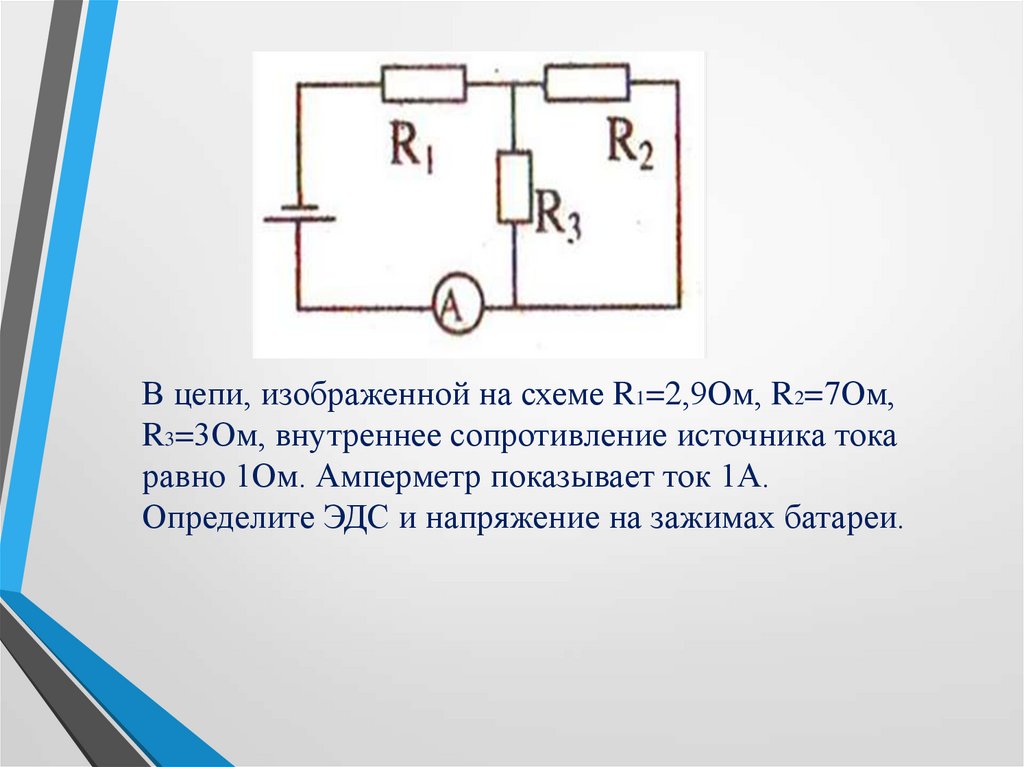 Константа пропорциональности такая же, как отношение значения отдельного резистора к общему сопротивлению последовательной комбинации. Например, падение напряжения на сопротивлении k th в последовательном соединении резисторов определяется выражением:
Константа пропорциональности такая же, как отношение значения отдельного резистора к общему сопротивлению последовательной комбинации. Например, падение напряжения на сопротивлении k th в последовательном соединении резисторов определяется выражением:
$$ v_k=\frac{R_k}{R_1+R_2+ \cdots +R_N}v \qquad (уравнение 2.9)$$
Пример 2.1
Для приведенной ниже схемы определите напряжение на резисторе 5 Ом, v , ток, подаваемый источником, i , и мощность, подаваемую источником.
Напряжение на резисторе 5 Ом можно определить из отношения делителя напряжения:
$$ v = [\frac{5Ω}{5Ω + 15Ω + 10Ω}] \cdot 15V= \frac{5}{30} \cdot 15V = 2,5V $$
Ток, подаваемый источником, можно определить, разделив общее напряжение на эквивалентное сопротивление:
$$i= \frac{15V}{R_{eq}}= \frac{15V}{5Ω+15Ω+10Ω}= \frac{15V}{30Ω}=0,5A$$
Мощность, отдаваемая источником, является произведением напряжения источника и тока источника:
$$P=iv=(0,5 А)(15 В)=7,5 Вт$$
Мы можем перепроверить соответствие между напряжением и и током и с помощью закона Ома. Применение закона Ома к резистору 5 Ом с током 0,5 А дает $v=(5 Ом)(0,5 А)=2,5 В$, что согласуется с результатом, полученным с использованием соотношения делителя напряжения.
Применение закона Ома к резистору 5 Ом с током 0,5 А дает $v=(5 Ом)(0,5 А)=2,5 В$, что согласуется с результатом, полученным с использованием соотношения делителя напряжения.
Резюме раздела
Если только два элемента соединяются в одном узле, эти два элемента относятся к серии . Однако более общее определение состоит в том, что все последовательно соединенные элементы цепи имеют один и тот же ток — это определение позволяет нам определять последовательные комбинации, содержащие более двух элементов. Идентификация последовательных элементов цепи позволяет упростить наш анализ, так как происходит сокращение числа неизвестных: для всех последовательных элементов имеется только один неизвестный ток.
Последовательная комбинация резисторов при желании может быть заменена одним эквивалентным сопротивлением . Эквивалентное сопротивление — это просто сумма отдельных сопротивлений в последовательной комбинации. Таким образом, последовательное сочетание N резисторов $R_1,R_2, \cdots, R_N$ можно заменить одним эквивалентным сопротивлением $R_{eq}=R_1+R_2+\cdots + R_N$.

Если общая разность напряжений на наборе последовательностей известна, разность напряжений на любом отдельном резисторе может быть определена по принципу деление напряжения . Термин деление напряжения происходит от того факта, что падение напряжения на последовательной комбинации резисторов делится между отдельными резисторами. Соотношение между разностью напряжений на конкретном резисторе и общей разностью напряжений такое же, как отношение между сопротивлением этого резистора и общим сопротивлением комбинации. Если v k это напряжение на к ом резисторе, а R ТОТ — общее сопротивление последовательной комбинации, математическая формулировка этой концепции:
$$ \frac{v_k}{v_{TOT}} = \frac{R_k}{R_{TOT}} $$
Упражнения
1. Определить напряжение В 1 в приведенной ниже схеме.
2.2 Элементы параллельной цепи и разделение тока
Говорят, что элементы схемы соединены параллельно , если все элементы имеют одну и ту же пару узлов. Пример двух элементов схемы, соединенных параллельно, показан на рис. 2.3. Применение КВЛ вокруг контура рис. 2.3 приводит к:
Пример двух элементов схемы, соединенных параллельно, показан на рис. 2.3. Применение КВЛ вокруг контура рис. 2.3 приводит к:
$$ v_1=v_2 \qquad (уравнение 2.10)$$
Этот результат настолько распространен, что уравнение (2.10) обычно записывается путем проверки параллельных элементов, таких как показанные на рис. 2.3 без явного написания KVL.
Мы можем упростить схемы, состоящие из параллельно соединенных резисторов. Рассмотрим резистивную цепь, показанную на рис. 2.4 (а). Резисторы соединены параллельно, поэтому оба резистора имеют разность напряжений В·9.0072 . Закон Ома, примененный к каждому резистору, приводит к:
$$ i_1= \frac{v}{R_1} \\ i_2= \frac{v}{R_2} \\ \qquad (уравнение 2.11) $$
Применение KCL в узле a:
$$i=i_1 + i_2 \qquad (уравнение 2.12)$$
Подставляя уравнения (2.11) в уравнение (2.12):
$$ i = \left[ \frac{1}{R_1} + \frac{1}{R_2} \right] v \qquad (уравнение 2.13)$$
или же
$$v= \frac{1}{\frac{1}{R_1}+\frac{1}{R_2}}\cdot i \qquad (уравнение 2. 14)$$
14)$$
Если мы установим $ R_{eq} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2}}$, мы можем изобразить рис. 2.4(b) как эквивалентный рис. 2.4(б).
Мы можем обобщить этот результат для параллельных сопротивлений N :
Параллельную комбинацию резисторов N $R_1, R_2, \cdots, R_N$ можно заменить одним эквивалентным сопротивлением:
$$ R_{eq} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2}+ \cdots \frac{1}{R_N}} \qquad (уравнение 2.15)$ $
Для частного случая двух параллельных сопротивлений, $R_1$ и $R_2$, эквивалентное сопротивление обычно записывается как:
$$R_{eq}= \frac{R_1R_2}{R_1+R_2} \qquad (уравнение 2.16)$$
Этот альтернативный способ расчета $R_{eq}$ можно также использовать для расчета $R_{eq}$ для большего количества параллельных резисторов, поскольку любое количество резисторов можно комбинировать по два одновременно.
Текущий отдел
Подстановка уравнения (2.14) в уравнения (2.11) приводит к:
$$i_1 = \frac{1}{R_1}\cdot \frac{i}{ \frac{1}{R_1} + \frac{1}{R_2}} \qquad (уравнение 2.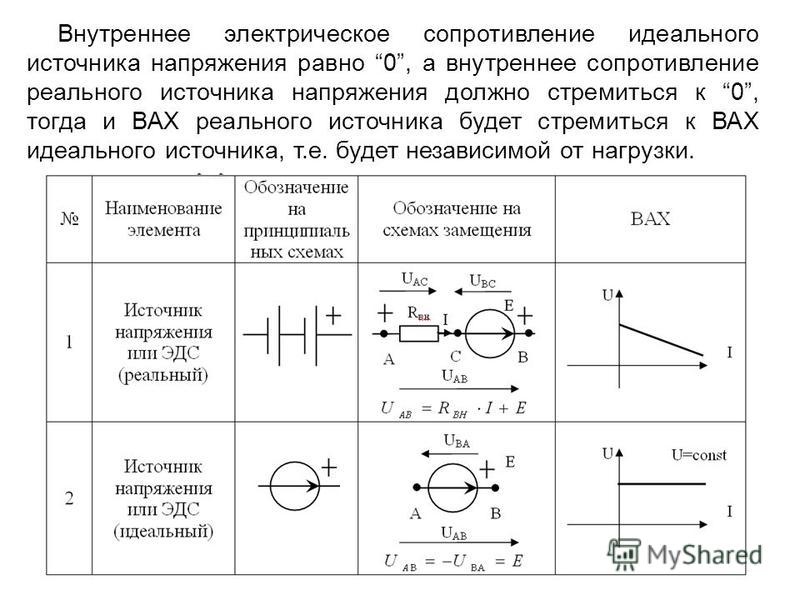 17)$$
17)$$
Упрощение:
$$i_1=\frac{R_2}{R_1+R_2} \qquad (уравнение 2.18)$$
Аналогично для текущего $i_2$:
$$i_2 = \frac{R_1}{R_1+R_2} \qquad (уравнение 2.19)$$
Уравнения (2.18) и (2.19) представляют собой отношения делителя тока для двух параллельных сопротивлений, называемые так потому, что ток в комбинации параллельных сопротивлений делится между двумя резисторами. Отношение тока одного резистора к общему току такое же, как отношение другие сопротивления к общему сопротивлению.
Приведенные выше результаты можно обобщить для последовательной комбинации сопротивлений N . По закону Ома $v = R_{eq} i$. Подставив наш предыдущий результат для эквивалентного сопротивления для параллельной комбинации резисторов N , мы получим:
$$v= \frac{1}{\frac{1}{R_1}+\frac{1}{R_2} + \cdots \frac{1}{R_N}} \cdot i \qquad (уравнение 2.20)$ $
Поскольку разность напряжений на всех резисторах одинакова, ток через k -й резистор составляет по закону Ома:
$$i_k=\frac{v}{R_k} \qquad (уравнение 2. 21)$$
21)$$
Где $R_k$ — сопротивление резистора k th . Объединение уравнений (2.20) и (2.21) дает:
$$i_k= \frac{\frac{1}{R_k}}{\frac{1}{R_1}+\frac{1}{R_2}+ \cdots \frac{1}{R_N}} \cdot i \ qquad (уравнение 2.22)$$
Часто удобнее представить обобщенный результат уравнения (2.20) в терминах проводимости отдельных резисторов. Напомним, что проводимость обратно пропорциональна сопротивлению, $G=\frac{1}{R}$. Таким образом, уравнение (2.22) можно переформулировать следующим образом:
Ток через любой резистор в параллельной комбинации сопротивлений N пропорционален общему току в комбинации резисторов. Константа пропорциональности равна отношению проводимости отдельного резистора к общей проводимости параллельной комбинации. Например, ток через сопротивление кОм при параллельном соединении резисторов определяется по формуле:
$$i_k=\frac{G_k}{G_1+G_2+ \cdots + G_N}i \qquad (уравнение 2.23)$$
Где i — это общий ток через параллельную комбинацию резисторов.
И последнее замечание об обозначениях: две параллельные полосы обычно используются в качестве сокращенного обозначения, чтобы указать, что два элемента схемы параллельны. Например, запись $R_1 \parallel R_2$ означает, что резисторы $R_1$ и $R_2$ включены параллельно. Обозначение $R_1 \parallel R_2$ часто используется как сокращенное обозначение эквивалентного сопротивления комбинации параллельных сопротивлений вместо уравнения (2.16).
Результаты двойной проверки для параллельных сопротивлений:
Эквивалентное сопротивление для параллельной комбинации резисторов N всегда будет меньше наименьшего сопротивления в комбинации. На самом деле эквивалентное сопротивление всегда будет подчиняться следующим неравенствам:
$$\frac{R_{min}}{N} \leq R_{eq} \leq R_{min}$$
Где $R_{min}$ — наименьшее значение сопротивления в параллельной комбинации.
При параллельной комбинации сопротивлений резистор с наименьшим сопротивлением будет иметь наибольший ток , а резистор с наибольшим сопротивлением будет иметь наименьший ток .

Резюме раздела
Если несколько элементов соединяют одни и те же два узла, два элемента параллельны . Однако более общее определение состоит в том, что все элементы схемы, соединенные параллельно, имеют одинаковую разность напряжений. Как и в случае с последовательными элементами цепи, идентификация параллельных элементов цепи позволяет нам упростить наш анализ, поскольку количество неизвестных сокращается: существует только одна неизвестная разность напряжений для всех параллельных элементов.
Параллельная комбинация резисторов может быть заменена одним эквивалентным сопротивлением , если это необходимо. Проводимость параллельной комбинации — это просто сумма индивидуальных проводимостей параллельных резисторов. Следовательно, параллельную комбинацию N резисторов $R_1$, $R_2$, $\cdots$, $R_N$ можно заменить одним эквивалентным сопротивлением:
$$R_{eq} = \frac{1}{\frac{1}{R_1}+\frac{1}{R_2}+\cdots\frac{1}{R_N}}$$
Если известен общий ток через набор параллельно включенных резисторов, то ток через любой отдельный резистор можно определить с помощью концепции деления тока .
 Термин «деление тока» происходит от того факта, что ток через параллельную комбинацию резисторов делится между отдельными резисторами. Соотношение между током через конкретный резистор и полным током такое же, как отношение между проводимостью этого резистора и общей проводимостью комбинации. Если $i_k$ — напряжение на k -й резистор , $i_{TOT}$ — общий ток через параллельную комбинацию, $G_k$ — проводимость резистора k -й , а $G_{TOT}$ — общая проводимость параллельной комбинации, математическая формулировка этой концепции:
Термин «деление тока» происходит от того факта, что ток через параллельную комбинацию резисторов делится между отдельными резисторами. Соотношение между током через конкретный резистор и полным током такое же, как отношение между проводимостью этого резистора и общей проводимостью комбинации. Если $i_k$ — напряжение на k -й резистор , $i_{TOT}$ — общий ток через параллельную комбинацию, $G_k$ — проводимость резистора k -й , а $G_{TOT}$ — общая проводимость параллельной комбинации, математическая формулировка этой концепции:
$$\frac{v_k}{i_{TOT}}=\frac{G_k}{G_{TOT}}$$
Упражнения
1. Определите значение I в схеме ниже.
2. Определить значение R в схеме ниже, что дает I=2 мА.
2.3 Сокращение и анализ схемы
Предыдущие результаты дают нам возможность потенциально упростить анализ некоторых схем. Это упрощение получается, если мы можем использовать методы уменьшения схемы для преобразования сложной схемы в более простую, но эквивалентную схему, которую мы можем использовать для выполнения необходимого анализа. Сокращение цепи не всегда возможно, но когда оно применимо, оно может значительно упростить анализ цепи.
Сокращение цепи не всегда возможно, но когда оно применимо, оно может значительно упростить анализ цепи.
Сокращение схемы основано на идентификации параллельных и последовательных комбинаций элементов схемы. Параллельные и последовательные элементы затем объединяются в эквивалентные элементы, и анализируется полученная в результате схема уменьшенного размера . Принципы сокращения схемы проиллюстрированы ниже на ряде примеров.
Пример 2.2
Определите эквивалентное сопротивление на клеммах резистивной сети, показанной ниже.
Последовательность выполняемых операций показана ниже. Сопротивления 6 Ом и 3 Ом соединяются параллельно, чтобы получить эквивалентное сопротивление 2 Ом. Это сопротивление 2 Ом и оставшееся сопротивление 6 Ом включены последовательно, они объединяются в эквивалентное сопротивление 8 Ом. Наконец, этот резистор 8 Ом и резистор 24 Ом соединяются параллельно, чтобы получить эквивалентное сопротивление 6 Ом. Таким образом, эквивалентное сопротивление всей сети составляет 6 Ом.
Таким образом, эквивалентное сопротивление всей сети составляет 6 Ом.
Пример 2.3
В приведенной ниже схеме определите мощность, отдаваемую источником.
Чтобы определить подачу мощности, нам нужно определить общий ток, подаваемый источником на остальную часть цепи. Мы можем легко определить ток, если преобразуем сеть резисторов в одно эквивалентное сопротивление. Набор шагов для этого описан ниже.
Шаг 1: Резисторы на четыре и два Ома, выделенные на рисунке слева внизу синим цветом, соединены последовательно. Последовательные сопротивления добавляются напрямую, поэтому их можно заменить одним резистором на шесть Ом, как показано на рисунке справа ниже.
Шаг 2: Резистор с тремя омами и два резистора по 6 Ом теперь соединены параллельно, как показано на рисунке слева ниже. Эти сопротивления можно объединить в один эквивалентный резистор $R_{eq}=\frac{1}{\frac{1}{3}+\frac{1}{6}+\frac{1}{6}}= 1,5\Омега$. Получившаяся эквивалентная схема показана справа внизу.
Ток от источника теперь можно легко определить по рисунку справа вверху. Падение напряжения на резисторе 1,5 Ом составляет 6 В, поэтому закон Ома дает $i=\frac{6V}{1,5\Omega}=4A$. Таким образом, мощность, отдаваемая источником, составляет $P=(4A)(6V)=24W$. Так как знак тока по отношению к току равен , а не согласуется с соглашением о пассивном знаке, мощность генерируется источником.
Пример 2.4
Для схемы, показанной ниже, определите напряжение $v_s$ на источнике 2А.
Два резистора 1 Ом и два резистора 2 Ом включены последовательно друг с другом, как показано на рисунке слева ниже. Их можно комбинировать, просто добавляя последовательные сопротивления, что приводит к эквивалентной схеме, показанной справа ниже.
Три оставшихся резистора подключены параллельно (все они имеют одни и те же узлы), поэтому их можно комбинировать с помощью соотношения $R_{eq}=\frac{1}{\frac{1}{2}+\frac{1} {4}+\frac{1}{4}}=1\Omega$. Учтите, что не обязательно сочетать все три одновременно, тот же результат получается при последовательных комбинациях двух сопротивлений. Например, два резистора по 4 Ом можно объединить с помощью уравнения (2.16), чтобы получить: $R_{eq1}=\frac{4 \cdot 4}{4+4}=2\Omega$. Общее эквивалентное сопротивление может быть определено параллельной комбинацией $R_{eq1}$ и резистора 2 Ом: $R_{eq}=\frac{2 \cdot 2}{2+2}=1 \Omega$.
Учтите, что не обязательно сочетать все три одновременно, тот же результат получается при последовательных комбинациях двух сопротивлений. Например, два резистора по 4 Ом можно объединить с помощью уравнения (2.16), чтобы получить: $R_{eq1}=\frac{4 \cdot 4}{4+4}=2\Omega$. Общее эквивалентное сопротивление может быть определено параллельной комбинацией $R_{eq1}$ и резистора 2 Ом: $R_{eq}=\frac{2 \cdot 2}{2+2}=1 \Omega$.
Напряжение на источнике теперь можно определить по закону Ома: $v_s=(1\Omega)(2A)=2V$. Предполагаемая полярность источника напряжения правильная.
Пример 2.5: Мост Уитстона
Схема моста Уитстона показана ниже. Мост обычно представлен так, как показано на рисунке слева; обычно мы будем использовать эквивалентную схему, показанную справа. Мост Уитстона обычно используется для преобразования изменения сопротивления в изменение напряжения. На схему подается постоянное напряжение питания $V_s$. Все резисторы в цепи имеют номинальное сопротивление R; переменный резистор имеет отклонение $\Delta R$ от этого номинала. Выходное напряжение $v_{ab}$ показывает изменение $\Delta R$ на переменном резисторе. Переменный резистор в сети часто является преобразователем, сопротивление которого изменяется в зависимости от какой-либо внешней переменной, такой как температура.
Выходное напряжение $v_{ab}$ показывает изменение $\Delta R$ на переменном резисторе. Переменный резистор в сети часто является преобразователем, сопротивление которого изменяется в зависимости от какой-либо внешней переменной, такой как температура.
По делению напряжения напряжения $v_b$ и $v_a$ (относительно земли) равны:
$$v_b=\frac{(R+\Delta R)}{2R+\Delta R}V_s$$
а также
$$v_a=Ri_2=\frac{V_s \cdot R}{2R}=\frac{V_s}{2}$$
Тогда напряжение $v_{ab}$ равно:
$$v_{ab}=v_a-v_b= \left( \frac{1}{2} — \frac{R+ \Delta R}{2R + \Delta R} \right) V_s = \left( \frac{( 2R+ \Delta R) — 2(R+ \Delta R)}{2(2R+ \Delta R)} \right) V_s = — \frac{\Delta R}{2(2R+ \Delta R)} \cdot V_s $$
Для случая, когда $\Delta R << 2R$, это упрощается до:
$$v_{ab} \приблизительно — \frac{V_s}{4R}\Delta R$$
А выходное напряжение пропорционально изменению сопротивления переменного резистора.
Практическое применение:
Ряд распространенных датчиков приводит к изменению сопротивления в результате некоторого внешнего воздействия. Термисторы изменяют сопротивление в результате изменения температуры; тензорезисторы сопротивление изменению в результате деформации, как правило, из-за приложения нагрузки к части, к которой приклеен тензорезистор; 9Фоторезисторы 0071 или фоторезисторы изменяют сопротивление в результате изменения интенсивности света. Мосты Уитстона обычно используются в сочетании с этими типами датчиков.
Термисторы изменяют сопротивление в результате изменения температуры; тензорезисторы сопротивление изменению в результате деформации, как правило, из-за приложения нагрузки к части, к которой приклеен тензорезистор; 9Фоторезисторы 0071 или фоторезисторы изменяют сопротивление в результате изменения интенсивности света. Мосты Уитстона обычно используются в сочетании с этими типами датчиков.
Резюме раздела
В цепи, которая содержит очевидные последовательные и/или параллельные комбинации резисторов, анализ может быть упрощен путем объединения этих сопротивлений в эквивалентные сопротивления. Уменьшение общего количества сопротивлений уменьшает количество неизвестных в цепи с соответствующим уменьшением количества определяющих уравнений. Уменьшение количества уравнений и неизвестных обычно упрощает анализ схемы.
Не все схемы можно сокращать.
Упражнения
Для показанной цепи определите:
$R_{eq}$ (эквивалентное сопротивление, видимое источником)
Токи $I_1$ и $I_2$
2.
 4 Неидеальные блоки питания
4 Неидеальные блоки питанияВ разделе 1.2 мы обсуждали идеальные источники питания. В этом разделе идеальный источник напряжения был охарактеризован как обеспечивающий заданное напряжение независимо от текущих требований к устройству . Аналогично, идеальный источник тока был определен как обеспечивающий заданное напряжение независимо от разности потенциалов на источнике . Эти модели нереалистичны — поскольку идеальный источник напряжения может обеспечивать бесконечный ток при ненулевой разности напряжений, а идеальный источник тока может обеспечивать бесконечную разность напряжений при ненулевой токе, любое устройство способно обеспечивать бесконечную мощность. Во многих случаях идеальные модели источников напряжения и тока будут адекватными, но в тех случаях, когда нам нужно более точно воспроизвести работу реальных источников питания, нам потребуется модифицировать наши модели этих устройств.
В этом разделе мы представляем простые модели источников напряжения и тока, которые включают более реалистичные предположения относительно поведения этих устройств.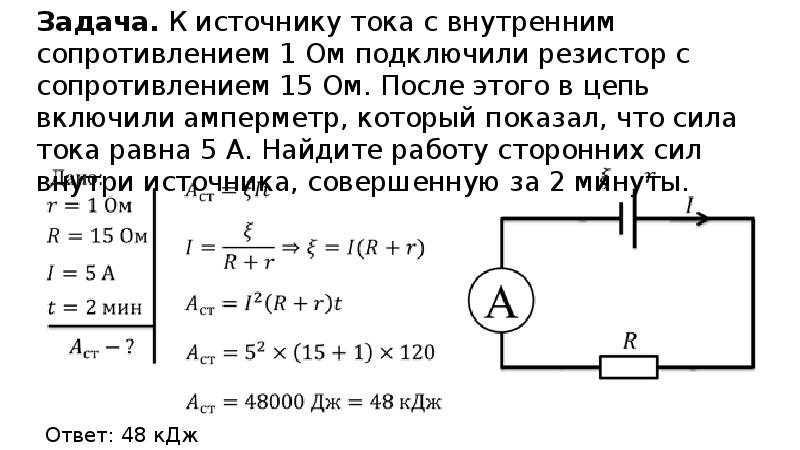
Неидеальные источники напряжения
Идеальный источник напряжения был определен в разделе 1.2 как обеспечивающий заданное напряжение, независимо от тока, протекающего через устройство. Например, батарея perfect 12 В будет обеспечивать 12 В на своих клеммах, независимо от нагрузки, подключенной к клеммам. Однако настоящая батарея на 12 В обеспечивает 12 В на своих клеммах только тогда, когда ее клеммы разомкнуты. Поскольку мы потребляем ток от клемм, батарея будет давать менее 12 В — напряжение будет уменьшаться по мере того, как от батареи потребляется все больше и больше тока. Таким образом, реальная батарея имеет внутреннее падение напряжения, которое увеличивается с увеличением тока.
Мы смоделируем реальный или практический источник напряжения как последовательное соединение идеального источника напряжения и внутреннего сопротивления . Эта модель схематически изображена на рис. 2.5, в котором неидеальный источник напряжения содержит идеальный источник напряжения, обеспечивающий напряжение $V_s$ и внутреннее сопротивление $R_s$. Неидеальный источник напряжения обеспечивает напряжение V и ток i , где:
Неидеальный источник напряжения обеспечивает напряжение V и ток i , где:
$$V=V_s-i \cdot R_s \qquad (уравнение 2.24)$$
Уравнение (2.24) показывает, что напряжение, создаваемое нашей неидеальной моделью источника напряжения, уменьшается по мере увеличения тока, выходящего из источника напряжения, что согласуется с ожиданиями.
Пример 2.6
Рассмотрим случай, когда мы подключаем резистивную нагрузку к неидеальному источнику напряжения. На рисунке ниже представлена схема всей системы; $R_L$ — сопротивление нагрузки, $V_L$ — напряжение, подаваемое на нагрузку, а $i_L$ — ток, подаваемый на нагрузку.
В приведенном выше случае ток, подаваемый на нагрузку, равен $i=\frac{V_s}{R_s+R_L}$, а напряжение нагрузки равно $V_L=V_s \frac{R_L}{R_s+R_L}$. Таким образом, если сопротивление нагрузки бесконечно (нагрузка представляет собой разомкнутую цепь), $V_L=V_S$, но источник питания не подает ток и, следовательно, не подает питание на нагрузку.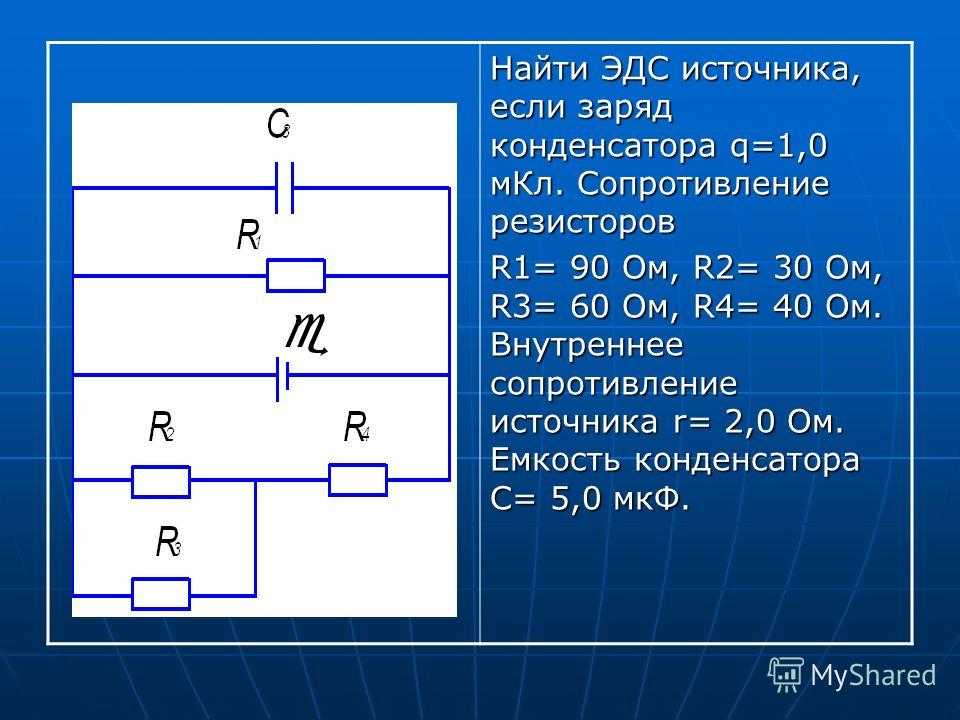 Если сопротивление нагрузки равно нулю (нагрузка короткое замыкание), $V_L=0$ и источник питания подает ток $i_L=\frac{V_s}{R_s}$ в нагрузку; однако мощность, подаваемая на нагрузку, по-прежнему равна нулю.
Если сопротивление нагрузки равно нулю (нагрузка короткое замыкание), $V_L=0$ и источник питания подает ток $i_L=\frac{V_s}{R_s}$ в нагрузку; однако мощность, подаваемая на нагрузку, по-прежнему равна нулю.
Пример 2.7: Зарядка аккумулятора
У нас есть «мертвый» автомобильный аккумулятор, который обеспечивает только 4 В на своих клеммах. Мы хотим зарядить батарею, используя запасную батарею, которая обеспечивает 12 В на своих клеммах. Для этого мы соединяем две батареи, как показано ниже:
Если мы попытаемся проанализировать эту схему, применяя КВЛ вокруг петли, мы получим 12В=4В. Это явно неверно, и мы не можем продолжать наш анализ — наша модель не соответствует действительности!
Для решения этого вопроса включим внутреннее сопротивление аккумуляторов. Предполагая, что внутреннее сопротивление каждой батареи равно 3 Ом, мы получаем следующую модель системы:
Применение КВЛ вокруг контура и использование закона Ома для записи напряжений на внутренних сопротивлениях батареи через ток между батареями приводит к:
$$-12В+(3\Омега)я+(3\Омега)я+4В=0$$
Что можно решить для текущего i для получения:
$$i= \frac{12V-4V}{6\Omega}=1,33A$$
Обратите внимание, что по мере увеличения напряжения «разряженной» батареи в процессе зарядки ток, подаваемый на «разряженную» батарею, уменьшается.
Неидеальные источники тока
Идеальный источник тока был определен в разделе 1.2 как обеспечивающий определенный ток, независимо от разницы напряжений на устройстве. Эта модель страдает тем же основным недостатком, что и наша модель идеального источника напряжения — модель может обеспечивать бесконечную мощность, что несовместимо с возможностями реального источника тока.
Мы будем использовать схему, схематически показанную на рис. 2.6, для моделирования неидеального источника тока. Неидеальная модель состоит из идеального источника тока $i_s$, подключенного параллельно внутреннему сопротивлению $R_s$. Источник выдает напряжение В и ток i . Выходной ток определяется как:
$$i=i_S-\frac{V}{R_S} (уравнение 2.25)$$
Уравнение (2.25) показывает, что ток, подаваемый источником, уменьшается по мере увеличения подаваемого напряжения.
Пример 2.8
Рассмотрим случай, когда мы подключаем резистивную нагрузку к неидеальному источнику тока.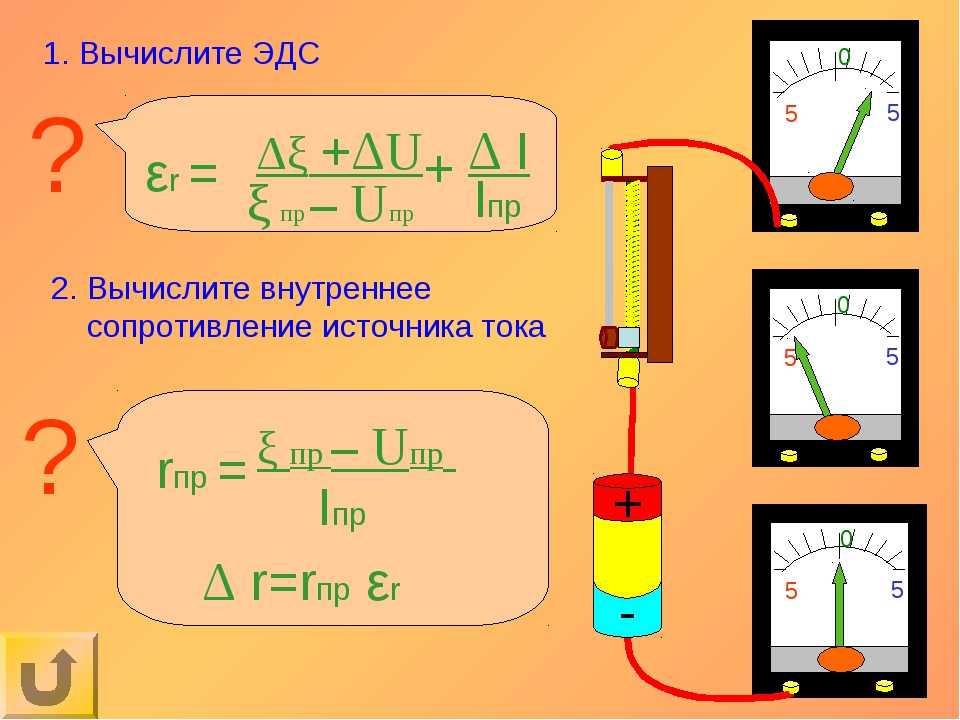 На рисунке ниже представлена схема всей системы; $R_L$ — сопротивление нагрузки, $V_L$ — напряжение, подаваемое на нагрузку, а $i_L$ — ток, подаваемый на нагрузку.
На рисунке ниже представлена схема всей системы; $R_L$ — сопротивление нагрузки, $V_L$ — напряжение, подаваемое на нагрузку, а $i_L$ — ток, подаваемый на нагрузку.
В приведенном выше случае ток, подаваемый на нагрузку, может быть определен из соотношения делителя тока как $i_l=i_s \cdot \frac{R_s}{R_s+R_L}$, а напряжение на нагрузке по закону Ома равно $V_L= i_L R_L = i_s \frac{R_S R_L}{R_s + R_L}$. Если сопротивление нагрузки равно нулю (нагрузка имеет короткое замыкание), $i_L=i_s$, но источник питания не подает напряжение и, следовательно, не подает питание на нагрузку. В случае бесконечного сопротивления нагрузки (нагрузка разомкнута) $i_L = 0$. В этом случае мы можем пренебречь $R_s$ в знаменателе уравнения напряжения нагрузки, чтобы получить $V_L \приблизительно i_s \frac{R_S R_L}{R_L}$, так что $V_L \приблизительно i_s R_S$. Однако, поскольку ток равен нулю, мощность, подаваемая на нагрузку, по-прежнему равна нулю.
9{2} \frac{R_S R_L}{R_s + R_L} \cdot \frac{R_s}{R_s+R_L}$. График зависимости мощности, подаваемой на нагрузку, от сопротивления нагрузки показан ниже; логарифмическая шкала используется на горизонтальной оси, чтобы сделать график более читаемым. Как и ожидалось, мощность равна нулю для высоких и низких сопротивлений нагрузки. Пик кривой возникает, когда сопротивление нагрузки равно сопротивлению источника, $R_L=R_s$.
График зависимости мощности, подаваемой на нагрузку, от сопротивления нагрузки показан ниже; логарифмическая шкала используется на горизонтальной оси, чтобы сделать график более читаемым. Как и ожидалось, мощность равна нулю для высоких и низких сопротивлений нагрузки. Пик кривой возникает, когда сопротивление нагрузки равно сопротивлению источника, $R_L=R_s$.
Резюме раздела
Во многих случаях блоки питания можно смоделировать как идеальные блоки питания, как показано в разделе 1.2. Однако в некоторых случаях представление источника питания как идеального приводит к недопустимым ошибкам. Например, идеальные блоки питания могут выдавать бесконечную мощность, что явно нереально.
В этом разделе мы представляем простую модель неидеального источника питания.
Наш неидеальный источник напряжения состоит из идеального источника напряжения, соединенного последовательно с внутренним сопротивлением источника питания.

Наш неидеальный источник тока состоит из идеального источника тока, подключенного параллельно с внутренним сопротивлением источника питания.
Формулы делителя напряжения и тока позволяют нам легко определить влияние внутренних сопротивлений неидеальных источников питания. Наш анализ показывает, что неидеальными эффектами можно пренебречь, пока сопротивление нагрузки велико по сравнению с внутренним сопротивлением источника питания.
Упражнения
1. Источник напряжения с внутренним сопротивлением 2 Ом, как показано ниже, используется для подачи питания на резистор 3 Ом. Какое напряжение вы бы измерили на резисторе 3 Ом?
2. Источник напряжения из упражнения 1 выше используется для подачи питания на резистор 2 кОм. Какое напряжение вы бы измерили на резисторе 2 кОм?
2.5 Практические измерения напряжения и тока
Процесс измерения физического параметра почти всегда меняет измеряемый параметр. Этот эффект и нежелателен, и, вообще говоря, неизбежен. Одной из целей любого измерения является воздействие на измеряемый параметр как можно меньше .
Этот эффект и нежелателен, и, вообще говоря, неизбежен. Одной из целей любого измерения является воздействие на измеряемый параметр как можно меньше .
Вышеприведенное утверждение справедливо для измерений напряжения и тока. Идеальный вольтметр , подключенный параллельно к некоторому элементу цепи, будет измерять напряжение на элементе, не влияя на ток, протекающий через элемент. К сожалению, любой реальный или практический вольтметр потребляет некоторый ток из цепи, к которой он подключен; этот эффект нагрузки изменит условия работы схемы, вызывая некоторую разницу между измеренным напряжением и соответствующим напряжением без вольтметра, присутствующего в цепи. Точно так же идеальный амперметр, включенный последовательно с каким-либо элементом цепи, будет измерять ток, не влияя на напряжение в цепи. Практический амперметр, как и практический вольтметр, вводит эффекты нагрузки, которые изменяют работу цепи, в которой производится измерение.
В этом разделе мы познакомим вас с некоторыми эффектами измерения напряжения и тока практическими измерителями.
Модели вольтметра и амперметра
Мы будем моделировать как вольтметры, так и амперметры как имеющие некоторое внутреннее сопротивление и способ отображения измеренной разности напряжений или тока. На рис. 2.7 показаны схематические изображения вольтметров и амперметров.
Амперметр на рис. 2.7(а) имеет внутреннее сопротивление $R_M$; ток через амперметр равен $i_A$, а разность напряжений на амперметре равна $V_M$. Разность напряжений амперметра должна быть как можно меньше, поэтому амперметр должен иметь чрезвычайно малое внутреннее сопротивление.
Вольтметр на рис. 2.7(b) также представлен имеющим внутреннее сопротивление $R_M$; ток через счетчик равен $i_v$, а разность напряжений на счетчике равна $V_v$. Ток через вольтметр должен быть как можно меньше — вольтметр должен иметь чрезвычайно высокое внутреннее сопротивление.
Эффекты ненулевых напряжений амперметра и ненулевых токов вольтметра более подробно рассматриваются в следующих подразделах.
Измерение напряжения
Рассмотрим схему, показанную на рис. 2.8(а). Источник тока $i_s$ подает ток на элемент схемы с сопротивлением R. Мы хотим измерить падение напряжения V на элементе схемы. Мы делаем это, присоединяя вольтметр к элементу цепи, как показано на рис. 2.8 (b).
На рис. 2.8(b) сопротивление вольтметра параллельно элементу цепи, напряжение на котором мы хотим измерить, и комбинация элемента цепи и вольтметра становится делителем тока. Тогда ток через резистор R будет равен:
$$i=i_s \frac{R_M}{R+R_M} \qquad (уравнение 2.26)$$
Тогда напряжение на резисторе R по закону Ома равно:
$$V=i_s \frac{R \cdot R_M}{R+R_M} \qquad (уравнение 2.27)$$
Если $R_M >>R$, это выражение упрощается до:
$$V \приблизительно i_s \frac{R \cdot R_M}{R_M} = R \cdot i_s \qquad (уравнение 2.28)$$
И в измерение вносится незначительная погрешность — измеряемое напряжение примерно равно напряжению без вольтметра. Если же сопротивление вольтметра сравнимо с сопротивлением R, то упрощение уравнения (2. 28) нецелесообразно и наличие вольтметра вносит существенные изменения в систему.
28) нецелесообразно и наличие вольтметра вносит существенные изменения в систему.
Измерение тока
Рассмотрим схему, показанную на рис. 2.9(а). Источник напряжения $V_s$ подает питание на элемент цепи с сопротивлением R. Мы хотим измерить ток $i$ через элемент цепи. Мы делаем это, присоединяя амперметр последовательно к элементу цепи, как показано на рис. 2.9 (б).
На рис. 2.9(b) последовательная комбинация сопротивления амперметра и элемента цепи, ток которого мы хотим измерить, создает делитель напряжения. КВЛ по одноцепной петле обеспечивает:
$$V_s=i(R_M+R) (уравнение 2.29)$$
Решение для текущих результатов в:
$$i= \frac{V_s}{R_M+R} (уравнение 2.30)$$
Если $R_M << R$, это упрощается до:
$$i \ приблизительно \frac{V_s}{R} (уравнение 2.31)$$
И измеренный ток является хорошим приближением к току в цепи рис. 2.9 (а). Однако, если сопротивление амперметра не мало по сравнению с сопротивлением R, аппроксимация уравнения (2. 31) не подходит, и измеренный ток больше не отражает работу цепи без амперметра.
31) не подходит, и измеренный ток больше не отражает работу цепи без амперметра.
Осторожно
Неправильное подключение амперметров или вольтметров может привести к повреждению счетчика. Например, рассмотрим подключение амперметра параллельно с относительно большим сопротивлением, как показано ниже.
В этой конфигурации ток амперметра $i_M= \frac{V_S}{R_M}$. Поскольку сопротивление амперметра обычно очень мало, это может привести к тому, что на амперметр будут подаваться большие токи. Это, в свою очередь, может привести к тому, что на амперметр будет подаваться чрезмерная мощность, что приведет к повреждению устройства.
Амперметры обычно предназначены для подключения в серии к элементу (элементам) цепи, ток которых измеряется. Вольтметры обычно предназначены для подключения в параллельно с элементом (элементами) цепи, напряжение которых измеряется. Альтернативные соединения могут привести к повреждению счетчика.
Резюме раздела
Измерение напряжения и/или тока в цепи всегда приводит к некоторому влиянию на поведение цепи, т. е. наше измерение всегда будет изменять измеряемый параметр. Одна из целей при измерении напряжения или тока состоит в том, чтобы гарантировать, что эффект измерения будет незначительным.
В этом разделе мы представляем простые модели вольтметров и амперметров (устройства измерения напряжения и тока соответственно).
Наш неидеальный вольтметр состоит из идеального вольтметра (имеющего бесконечное сопротивление и, таким образом, не потребляющего ток из цепи) параллельно с сопротивлением, которое является внутренним для вольтметра. Эта модель воспроизводит конечный ток, который обязательно снимается с цепи реальным вольтметром.
Наш неидеальный амперметр состоит из идеального амперметра (имеющего нулевое сопротивление и, таким образом, не вызывающего падения напряжения в цепи) последовательно соединенного с внутренним сопротивлением амперметра.
 Это сопротивление позволяет нам смоделировать конечное падение напряжения, которое вводится в цепь при измерении реального тока.
Это сопротивление позволяет нам смоделировать конечное падение напряжения, которое вводится в цепь при измерении реального тока.
Формулы делителя напряжения и тока позволяют нам легко определить влияние внутренних сопротивлений измерителей напряжения и тока. Наш анализ показывает, что неидеальными эффектами можно пренебречь, если:
Сопротивление вольтметра велико по сравнению с сопротивлением, на котором производится измерение напряжения.
Сопротивление амперметра мало по сравнению с общим сопротивлением цепи.
Упражнения
Вольтметр с внутренним сопротивлением 10 МОм используется для измерения напряжения $v_{ab}$ в цепи ниже. Какое измеренное напряжение? Какое измерение напряжения вы ожидаете от идеального вольтметра?
Назад к главе 1 Перейти к главе 3
1) Если есть сомнения в последовательном соединении элементов, используйте KCL! Предполагая, что элементы находятся в ряду, который не находится в ряду, может иметь катастрофические последствия.
Различия в источниках напряжения и тока • Инженерные каракули
Перейти к содержимомуПредыдущий Следующий
Различия источников напряжения и токаИсточники напряжения и источники тока являются источниками энергии. Оба имеют положительную/отрицательную клемму, напряжение питания и ток , выходящий из них обоих. Но в чем разница?
По своей природе мы больше знакомы с источниками напряжения. Пример: аккумуляторов . Есть разные типы, подумайте о Батарея 9В . Это означает, что он обеспечивает 9 вольт! Но вот в чем хитрость. 9 вольт НЕ всегда 9 вольт. Это когда у нас есть разомкнутая цепь, да, но как только вы добавляете нагрузку, это совсем другая история.
Кратко:
- Источник напряжения
- поддерживает постоянное напряжение независимо от нагрузки
- Внутреннее сопротивление << нагрузки для стабильного напряжения
- Источник тока
- поддерживает постоянный ток независимо от нагрузки
- Внутреннее сопротивление >> нагрузка для стабильного тока
По существу, сопротивление нагрузки определяет точность источника. Источник напряжения будет пытаться поддерживать постоянное напряжение, но изменять ток, тогда как источник тока будет обеспечивать постоянный ток, но будет изменять напряжение, которое он может обеспечить.
Источник напряжения будет пытаться поддерживать постоянное напряжение, но изменять ток, тогда как источник тока будет обеспечивать постоянный ток, но будет изменять напряжение, которое он может обеспечить.
Итак, что часто сбивает с толку: они оба делают одно и то же: подают напряжение и ток, но
- источник напряжения хорошо обеспечивает постоянное напряжение
- источник тока обеспечивает постоянный ток
Символы
Источник напряжения
- Хороший (стабильный) источник напряжения независимо от нагрузки
- Ток меняется
- Внутреннее сопротивление r равно последовательно с ЭДС E
- Если схема ниже представляет собой аккумулятор, A и B являются клеммами аккумулятора
- r внутри аккумулятора
- Если подключена нагрузка, в цепи будет течь ток.

- Из закона Ома V=IR или I=V/R видно, что ток обратно пропорционален сопротивлению: чем меньше RLoad, тем больше ток .
- Нагрузка не получит все напряжение, которое может обеспечить E . Почему? Из-за падения напряжения на внутреннем сопротивлении. Нагрузка будет получать напряжение только на AB :
- Закон Ома также применяется к внутреннему сопротивлению Ом. Итак, чем больше ток, тем больше падение напряжения на r. Следовательно, Vab будет меньше. Это не то, чего мы хотим.
- Хотим большую нагрузку по сравнению с r !
На изображении выше вы можете увидеть общее представление источника напряжения. График справа показывает, что если мы увеличим ток, напряжение AB упадет. Мы можем предотвратить это, выбрав r << Rload
- Ниже приведен расчет, математически показывающий, почему мы должны выбирать нагрузку с гораздо большим сопротивлением, чем внутреннее сопротивление источника.

- В идеале Vab равно ЭДС. Но добиться этого мы не можем из-за падения напряжения на r . Единственный способ добиться этого — иметь высокое значение Rнагрузка , поэтому (Vab/Rнагрузка)*r будет очень маленьким. Таким образом, мы вычитаем небольшое число из E , так что Vab почти равно E .
Источник тока
- Хороший (стабильный) источник тока независимо от нагрузка
- Изменение напряжения
- Идеальный источник тока I — это параллельно с внутренним сопротивлением r .
Поскольку r и Rload подключены параллельно, ток будет разделяться между этими двумя ветвями.
- Я = И1+И2
- где I2 течет в ответвлении Rload
В идеале мы хотим, чтобы I1 был очень маленьким, чтобы большая часть тока текла к нагрузке
- Итак, мы хотим I = I2 , но никогда не сможем этого добиться из-за r .

- Итак, мы хотим I = I2 , но никогда не сможем этого добиться из-за r .


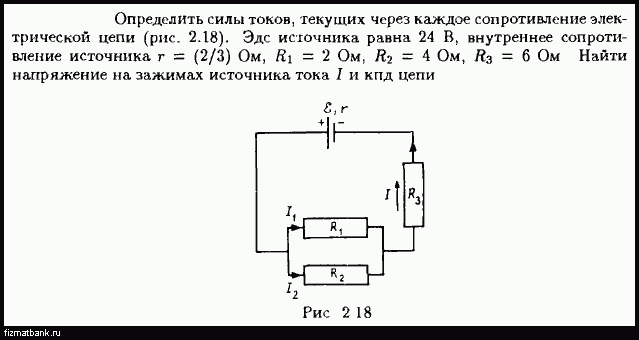
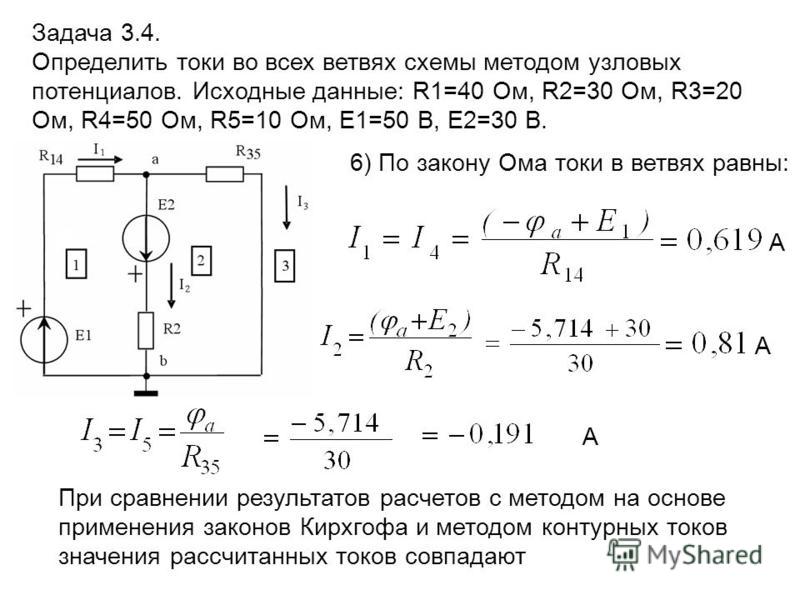
 Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.
Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.
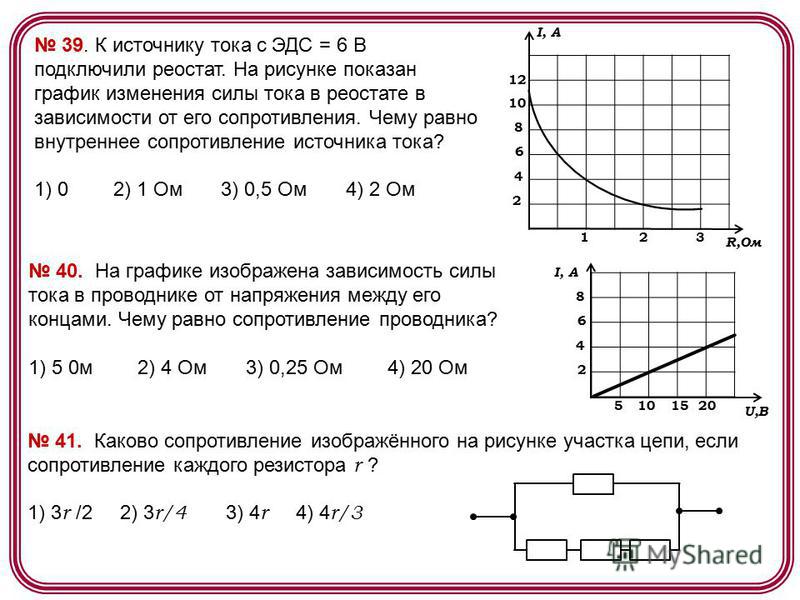 Соответственно, методика измерений будет зависеть от того, что хотим получить.
Соответственно, методика измерений будет зависеть от того, что хотим получить.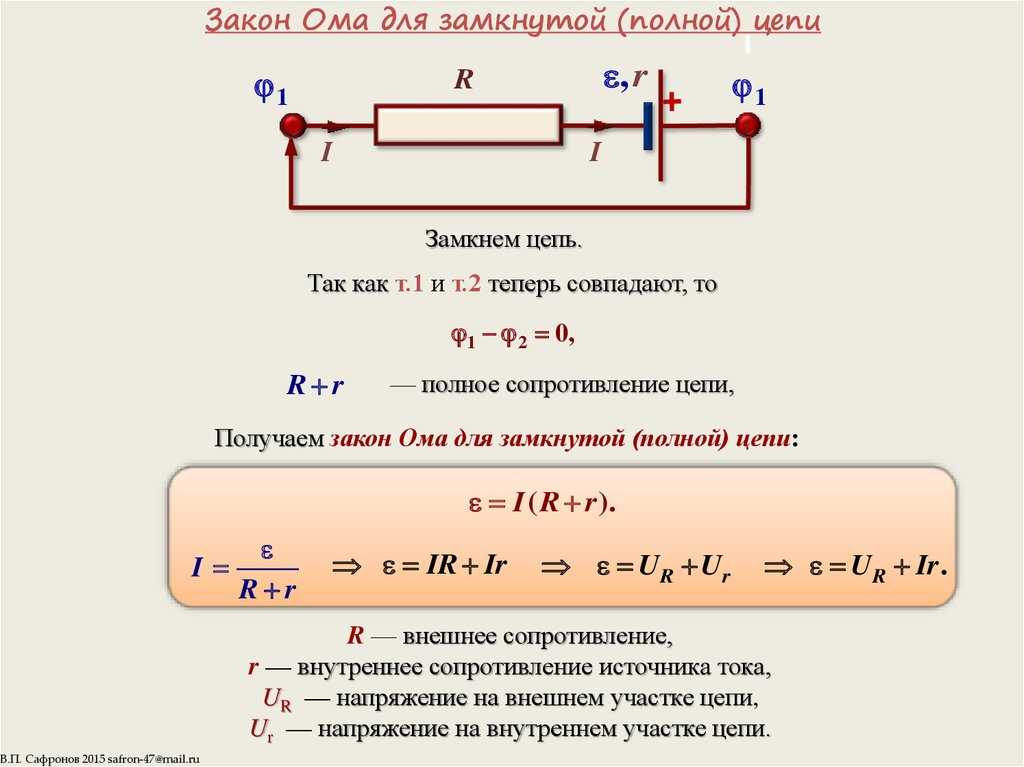 15 В + 0,18 В = 0,26 В;
15 В + 0,18 В = 0,26 В;


 Термин «деление тока» происходит от того факта, что ток через параллельную комбинацию резисторов делится между отдельными резисторами. Соотношение между током через конкретный резистор и полным током такое же, как отношение между проводимостью этого резистора и общей проводимостью комбинации. Если $i_k$ — напряжение на k -й резистор , $i_{TOT}$ — общий ток через параллельную комбинацию, $G_k$ — проводимость резистора k -й , а $G_{TOT}$ — общая проводимость параллельной комбинации, математическая формулировка этой концепции:
Термин «деление тока» происходит от того факта, что ток через параллельную комбинацию резисторов делится между отдельными резисторами. Соотношение между током через конкретный резистор и полным током такое же, как отношение между проводимостью этого резистора и общей проводимостью комбинации. Если $i_k$ — напряжение на k -й резистор , $i_{TOT}$ — общий ток через параллельную комбинацию, $G_k$ — проводимость резистора k -й , а $G_{TOT}$ — общая проводимость параллельной комбинации, математическая формулировка этой концепции:
 Это сопротивление позволяет нам смоделировать конечное падение напряжения, которое вводится в цепь при измерении реального тока.
Это сопротивление позволяет нам смоделировать конечное падение напряжения, которое вводится в цепь при измерении реального тока.