Внешнее магнитное поле — Справочник химика 21

    По отношению к внешнему магнитному полю различают диамагнитные и парамагнитные веш,ества. Диамагнитные вещества оказывают прохождению магнитных силовых линий большее сопротивление, чем вакуум, и поэтому внешнее магнитное поле их выталкивает. Парамагнитные вещества, напротив, проводят магнитные силовые линии лучше, чем вакуум, и поэтому магнитное поле втягивает такие вещества. [c.155]

    По характеру взаимодействия с внешним магнитным полем различают парамагнитные и диамагнитные вещества. Парамагнитные вещества втягиваются в магнитное поле, а диамагнитные — слабо выталкиваются из него. [c.204]

    Для атомов и молекул со спином /г во внешнем магнитном поле возникает не два, а 25 + 1 уровней, отличающихся значением спинового магнитного числа, и соответственно в спектре ЭПР не одна, а несколько близлежащих полос — так называемая тонкая структура спектра ЭПР, связанная с мультиплетностью уровня. Если к тому же ядерный спин отличен от нуля, то у ядра существует собственное магнитное поле, в котором каждая линия тонкой структуры спектра ЭПР расщепляется на 2У + 1 компонент (сверхтонкая структура спектра). 

[c.148]

    Парамагнитные частицы в постоянном внешнем магнитном поле [c.229]

    Здесь 0B.V — угол между направлением внешнего магнитного поля Во и направлением нормали к границе раздела N S — параметр остаточной анизотропии [c.235]

    Для ядра с / = 1 квадрупольный спектр с двумя линиями может возникнуть в случае г / О, как отмечалось выше (рис. 14.6,Б), или для ядер с л = О, находящихся в двух неэквивалентных центрах решетки. Исследование спектра образца, находящегося во внешнем магнитном поле, позволяет различить эти два варианта. В первом случае (г / 0) снова должны наблюдаться две линии, но с энергиями, отличающимися от тех, что наблюдались в отсутствие поля во втором случае каждый двукратно вырожденный уровень должен расщепляться, приводя к спектру с четырьмя линиями. 

[c.269]

    Если в атоме или молекуле момент импульса L = О и спин 5=0, частица не обладает собственным магнитным моментом (диамагнетик). Во внешнем магнитном поле в такой частице наводится индуцированный магнитный момент 1,м(инд). пропорциональный напряженности поля Н [c.42]

    С. Феррожидкости. Феррожидкости [40[ весьма перспективны для использования в качестве высокоэффективных теплоносителей. Специфическая температурная зависимость намагниченности благоприятствует хорошему их перемешиванию даже в отсутствие сил тяжести, поскольку на неодинаково нагретые объемы жидкости со стороны внешнего магнитного поля действуют различные силы. За счет неоднородных магнитных полей удается частично или полностью компенсировать силу тяжести в земных условиях, искусственно создавая в неизотермической среде ту или иную степень невесомости. 

[c.187]

    Величина вектора намагниченности, очевидно, аналогична вектору поляризации. Наличие вектора намагниченности означает, что элементарный объем горной среды, попадая во внешнее магнитное поле, создает свое собственное магнитное иоле. В первом приближении наблюдается прямо пропорциональная зависимость между векторами намагниченности и суммой напряженностей внешнего п собственного магнитных полей   [c.140]

    Экспериментально установлено, что снижение температуры горных пород во внешнем магнитном поле сопровождается появлением собственной остаточной намагниченности. В связи с этим основным источником высокой собственной намагниченности изверженных пород, видимо, являлись процессы их остывания во внешнем магнитном поле Земли. [c.142]

    Поведение парамагнитной частицы с невырожденными орбитальными уровнями во внешнем магнитном поле показывает, что благодаря спин-орбитальной связи внешнее поле индуцирует слабое орбитальное движение. Это приводит к отклонению значения -фактора от чисто спинового значения и появлению пространственной анизотропии -фактора. 

[c.226]

    Различие в ориентации электронных облаков относительно друг друга позволяет объяснить спектры атомов в магнитном поле. В спектрах атомов, помещенных во внешнее магнитное поле, происходит расщепление линий — возникновение новых близлежащих линий, поскольку в магнитном поле энергия электронов изменяется. Энергетические изменения при действии магнитного поля можно объяснить ра зличием в характере расположения электронных облаков относительно друг друга (рис. 7), а следовательно, и различными дозволенными углами поворота каждого из них в магнитном поле. 

[c.18]

   &en

Влияние — внешнее магнитное поле

Влияние — внешнее магнитное поле

Cтраница 1

Влияние внешнего магнитного поля на элементарные токи в веществе состоит в том, что изменяется ориентация осей вращения частиц так, что их магнитные моменты оказываются направленными в одну сторону. Интенсивность и характер намагничивания у различных веществ в одинаковом внешнем магнитном поле значительно отличаются. С этой точки зрения различают диамагнитные, парамагнитные и ферромагнитные вещества.  [1]

Влияние внешнего магнитного поля заметно лишь в преобразователях из специальных материалов ( см. гл.  [2]

Влияние внешнего магнитного поля на показания такого прибора незначительно, так как собственное магнитное поле в зазоре достаточно сильное.  [4]

Влияние внешнего магнитного поля также отражается на показании электроизмерительных приборов, особенно электромагнитной и электродинамической систем. Внешние магнитные поля изменяют собственное магнитное поле измерительного устройства, чем и вносят дополнительную погрешность. Для уменьшения влияния внешнего магнитного поля применяют железные экраны. В щитовых приборах с железным кожухом последний, хотя и в небольшой степени, служит магнитным экраном.  [5]

Влияние внешнего магнитного поля на туннельный ток может быть существенно усилено, если использовать интерференцию волн де Бройля куперовских пар в сверхпроводящем кольце, содержащем два последовательных симметрично расположенных туннельных контакта.  [6]

Под влиянием внешнего магнитного поля изменяется ориентация магнитных моментов части доменов, причем магнитные моменты всех электронов в пределах каждого домена остаются синпа-раллельными. С усилением намагничивающего поля магнитные моменты все большего числа доменов поворачиваются параллельно направлению внешнего поля, пока не наступит насыщение.  [7]

Под влиянием внешнего магнитного поля в ферромагнетиках происходит поворот вдоль поля магнитных моментов не отдельных атомов или молекул, как в парамагнетиках ( 111.6.4.3), а целых областей самопроизвольной намагниченности — доменов. Поворот вдоль поля векторов Ргад происходит прежде всего в тех доменах, у которых направление Ротд наиболее близко к направлению вектора индукции В0 внешнего поля.  [8]

Под влиянием внешнего магнитного поля в ферромагнетиках происходит поворот вдоль поля магнитных моментов не отдельных атомов или молекул, как в парамагнетиках ( 111.6.4.3), а целых областей самопроизвольной намагниченности — доменов. Поворот вдоль поля векторов Ртд происходит прежде всего в тех доменах, у которых направление Ртд наиболее близко к направлению вектора индукции В0 внешнего поля. При увеличении внешнего поля размеры доменов, намагниченных вдоль внешнего поля, растут за счет уменьшения размеров доменов с другими ориентациями векторов Ртд. При достаточно сильном внешнем магнитном поле все ферромагнитное тело оказывается намагниченным.  [9]

Под влиянием внешнего магнитного поля в системе электронов индуцируются токи, которые в свою очередь генерируют магнитное поле.  [10]

Для учета влияния внешнего магнитного поля используется численное решение уравнения движения электрона на отрезке методом Рунге-Кутта. Алгоритм построения траектории электрона состоит из двух этапов. На первом этапе решается уравнение движения электрона на отрезке траектории, на втором — рассматривается укрупненное столкновение электрона, причем, входными параметрами ( координаты, импульс) для него служат конечные параметры электрона на первом этапе. Величина шага траектории не должна превышать максимальной, определяемой из теории многократного рассеяния и в то же время ограничена точностью алгоритма Рунге Кутта интегрирования уравнения движения электрона.  [11]

Для исключения влияния внешнего магнитного поля на показания прибора обычно производят два измерения одного и того же значения: первый раз при произвольном положении прибора, а второй после поворота его на 180 вокруг вертикальной оси. Среднее из результатов отсчетов этих двух измерений будет свободно от влияния магнитного поля.  [12]

Диамагнетизм обусловлен влиянием внешнего магнитного поля на орбитальное движение электронов. Каждый электрон можно рассматривать как заряд, двигающийся по круговой орбите. Компонент внешнего поля в плоскости этой орбиты не влияет на этот заряд. Однако перпендикулярный компонент индуцирует дополнительное движение электрона с дополнительным магнитным моментом. По закону Ленца этот дополнительный момент всегда направлен точно против приложенного поля; более того, он строго пропорционален полю. Следовательно, диамагнитная восприимчивость отрицательна и не зависит ни от Я, ни от температуры.  [13]

Изменение показаний от влияния внешнего магнитного поля напряженностью 5 э не превышает 2 5 % от верхнего предела измерения.  [15]

Страницы:      1    2    3    4

Магнитное поле в веществе. Часть 1

Всем доброго времени суток. В прошлой статье я рассказывал о основной характеристике магнитного поля – магнитной индукции, однако приведённые расчётные формулы соответствуют магнитному полю в вакууме. Что в практической деятельности встречается довольно редко. Когда проводники с током находятся в какой–либо среде, даже в воздухе, магнитное поле, которое они создают, претерпевает некоторые, а иногда и существенные изменения. Какие изменения происходят с магнитным полем, и от чего это зависит, я расскажу в данной статье.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Как связана индукция и напряженность магнитного поля?

Магнетиком называется вещество, которое под действием магнитного поля способно намагничиваться (или как говорят физики приобретать магнитный момент). Магнетиками являются практически все вещества. Намагничивание веществ объясняется тем, что в веществах присутствуют свои собственные микроскопические магнитные поля, которые создаются вращением электронов по своим орбитам. Когда внешнее магнитное поле отсутствует, то микроскопические поля расположены произвольным образом, а под воздействием внешнего магнитного поля соответствующим образом ориентируются.

Для характеристики намагничивания различных веществ используют так называемый вектор намагничивания J.

Таким образом, под действием внешнего магнитного поля с магнитной индукцией В₀, магнетик намагничивается и создает свое магнитное поле с магнитной индукцией В’. В итоге общая индукция В будет состоять из двух слагаемых

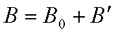
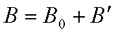
Тут возникает проблема вычисления магнитной индукции намагниченного вещества В’, для решения которой необходимо считать электронные микротоки всего вещества, что практически нереально.

Альтернативой данного решения есть ввод вспомогательных параметров, а именно напряженность магнитного поля Н и магнитная восприимчивость χ. Напряженность связывает магнитную индукцию В и намагничивание вещества J следующим выражением

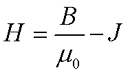
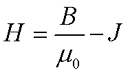
где В – магнитная индукция,

μ₀ – магнитная постоянная, μ₀ = 4π*10^-7 Гн/м.

В то же время вектор намагничивания J связан с напряженность магнитного поля В параметром, характеризующим магнитные свойства вещества и называемым магнитной восприимчивостью χ

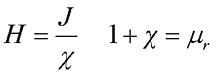
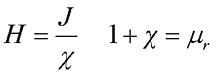
где J – вектор намагничивания вещества,

μ_r – относительная магнитная проницаемость вещества.

Однако наиболее часто для характеристики магнитных свойств веществ используют относительную магнитную проницаемость μ_r.

Таким образом, связь между напряженностью и магнитной индукцией будет иметь следующий вид

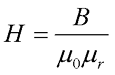
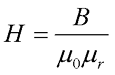
где μ₀ – магнитная постоянная, μ₀ = 4π*10^-7 Гн/м,

μ_r – относительная магнитная проницаемость вещества.

Так как намагничивание вакуума равна нулю (J = 0), то напряженность магнитного поля в вакууме будет равна

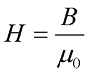
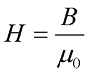
Отсюда можно вывести выражения напряженности для магнитного поля, создаваемого прямым проводом с током:

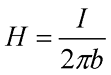
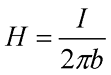
где I – ток протекающий по проводнику,

b – расстояние от центра провода до точки, в которой считается напряженность магнитного поля.

Как видно из данного выражения единицей измерения напряженности является ампер на метр (А/м) или эрстед (Э)

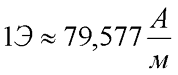
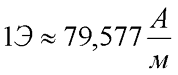
Таким образом, магнитная индукция В и напряженность Н являются основными характеристиками магнитного поля, а магнитная проницаемость μ_r – магнитной характеристикой вещества.

Намагничивание ферромагнетиков

В зависимости от магнитных свойств, то есть способности намагничиваться под действием внешнего магнитного поля, все вещества делятся на несколько классов. Которые характеризуются разной величиной относительной магнитной проницаемости μ_r и магнитной восприимчивости χ. Большинство веществ являются диамагнетиками (χ = -10^-8 … -10^-7 и μ_r < 1) и парамагнетиками (χ = 10^-7 … 10^-6 и   μ_r > 1), несколько реже встречаются ферромагнетики (χ = 10³ … 10⁵ и   μ_r >> 1). Кроме данных классов магнетиков существует ещё несколько классов магнетиков: антиферромагнетики, ферримагнетики и другие, однако их свойства проявляются только при определённых условиях.

Особый интерес в радиоэлектронике ферромагнитные вещества. Основным отличием данного класса веществ является нелинейная зависимость намагничивания, в отличие от пара- и диамагнетиков, имеющих линейную зависимость намагничивания J от напряженности Н магнитного поля.

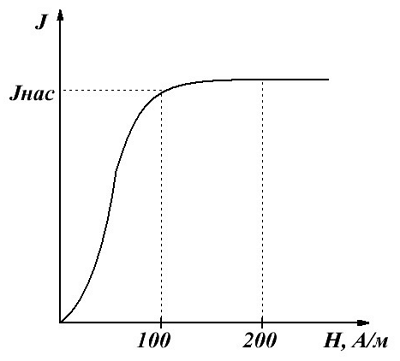
Зависимость намагничивания J ферромагнетика от напряженности Н магнитного поля.

На данном графике показана основная кривая намагничивания ферромагнетика. Изначально намагниченность  J, в отсутствие магнитного поля (Н = 0), равна нулю. По мере возрастания напряженности намагничивание ферромагнетика проходит довольно интенсивно, вследствие того что его магнитная восприимчивость и проницаемость очень велика. Однако по достижении напряженности магнитного поля порядка H ≈ 100 А/м увеличение намагниченности прекращается, так как достигается точка насыщения J_НАС. Данное явление называется магнитным насыщением. В данном режиме магнитная проницаемость ферромагнетиков сильно падает и при дальнейшем увеличении напряженности магнитного поля стремится к единице.

Гистерезис ферромагнетиков

Еще одной особенностью ферромагнетиков является наличие петли гистерезиса, которая является основополагающим свойством ферромагнетиков.

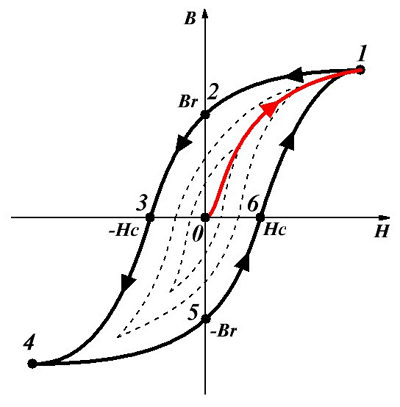
Петля гистерезиса ферромагнетика.

Для понимания процесса намагничивания ферромагнетика изобразим зависимость индукции В от напряженности Н магнитного поля, где красным цветом выделим основную кривую намагничивания. Данная зависимость довольно неопределенна, так как зависит от предыдущего намагничивания ферромагнетика.

Возьмём образец ферромагнитного вещества, которое не подвергалось намагничиванию (точка 0) и поместим его в магнитное поле, напряженность Н которого начнем увеличивать, то есть зависимость будет соответствовать кривой 0 – 1, пока не будет достигнуто магнитное насыщение (точка 1). Дальнейшее увеличение напряженности не имеет смысла, потому как намагниченность J практически не увеличивается, а магнитная индукция увеличивается пропорционально напряженности Н. Если же начинать уменьшать напряженность, то зависимость В(Н) будет соответствовать кривой 1 – 2 – 3, при этом когда напряженность магнитного поля упадёт до нуля (точка 2), то магнитная индукция не упадёт до нуля, а будет равна некоторому значению B_r, которое называется остаточной индукцией, а намагничивание будет иметь значение J_r, называемое остаточным намагничиванием.

Для того чтобы снять остаточное намагничивание и уменьшить остаточную индукцию B_r до нуля, необходимо создать магнитное поле, противоположное полю, вызвавшему намагничивание, причем напряженность размагничивающего поля должна составлять Н_с, называемая коэрцитивной силой. При дальнейшем росте напряженности магнитного поля, которое противоположно первоначальному полю, происходит насыщение ферромагнетика (точка 4).

Таким образом, при действии на ферромагнетик переменного магнитного поля зависимость индукции от напряженности будет соответствовать кривой 1 – 2 – 3 – 4 – 5 – 6 – 1, которая называется петлёй гистерезиса. Таких петель для ферромагнетика может быть множество (пунктирные кривые), называемые частными циклами. Однако, если при максимальных значениях напряженности магнитного поля происходит насыщение, то получается максимальная петля гистерезиса (сплошная кривая).

Так как магнитная проницаемость μ_r ферромагнетиков имеет довольно сложную зависимость от напряженности магнитного поля, поэтому нормируются два параметра магнитной проницаемости:

μ_н – начальная магнитная проницаемость соответствует напряженности Н = 0;

μ_max – максимальная магнитная проницаемость достигается в магнитном поле при приближении магнитного насыщения.

Таким образом, у ферромагнетиков величины B_r, Н_с и μ_н (μ_max) являются основными характеристиками, влияющими на выбор вещества в конкретном случае.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Эффект Мейснера — Википедия

Материал из Википедии — свободной энциклопедии

Схема Эффекта Мейснера. Показаны линии магнитного поля и их вытеснение из сверхпроводника, находящегося ниже своей критической температуры

Эффект Мейснера, эффект Мейсснера (от нем. Meißner) — полное вытеснение магнитного поля из объёма проводника при его переходе в сверхпроводящее состояние. Впервые явление наблюдалось в 1933 году немецкими физиками В. Мейснером и Р. Оксенфельдом.

При охлаждении сверхпроводника, находящегося во внешнем постоянном магнитном поле, в момент перехода в сверхпроводящее состояние магнитное поле полностью вытесняется из его объёма. Этим сверхпроводник отличается от идеального проводника, у которого при падении сопротивления до нуля индукция магнитного поля в объёме должна сохраняться без изменения.

Отсутствие магнитного поля в объёме проводника позволяет заключить из общих законов магнитного поля, что в нём существует только поверхностный ток. Он физически реален и поэтому занимает некоторый тонкий слой вблизи поверхности. Магнитное поле тока уничтожает внутри сверхпроводника внешнее магнитное поле. В этом отношении сверхпроводник ведёт себя формально как идеальный диамагнетик. Однако он не является диамагнетиком, так как внутри него намагниченность равна нулю.

Эффект Мейснера не может быть объяснён только бесконечной проводимостью. Впервые его природу объяснили братья Фриц и Хайнц Лондоны^[en] c помощью уравнения Лондонов. Они показали, что в сверхпроводнике поле проникает на фиксированную глубину от поверхности — лондоновскую глубину проникновения магнитного поля λ{\displaystyle \lambda }. Для металлов λ∼10−2{\displaystyle \lambda \sim 10^{-2}} мкм.

Чистые вещества, у которых наблюдается явление сверхпроводимости, немногочисленны. Чаще сверхпроводимость бывает у сплавов. У чистых веществ имеет место полный эффект Мейснера, а у сплавов не происходит полного выталкивания магнитного поля из объёма (частичный эффект Мейснера). Вещества, проявляющие полный эффект Мейснера, называются сверхпроводниками первого рода, а частичный — сверхпроводниками второго рода. Однако стоит отметить, что в низких магнитных полях полным эффектом Мейснера обладают все типы сверхпроводников.

У сверхпроводников второго рода в объёме имеются круговые токи, создающие магнитное поле, которое, однако, заполняет не весь объём, а распределено в нём в виде отдельных нитей вихрей Абрикосова. Что же касается сопротивления, оно равно нулю, как и в сверхпроводниках первого рода, хотя движение вихрей под действием текущего тока создаёт эффективное сопротивление в виде диссипативных потерь на передвижение магнитного потока внутри сверхпроводника, чего избегают вводом в структуру сверхпроводника дефектов — центров пиннинга, за которые вихри «цепляются».

«Гроб Магомета» — опыт, демонстрирующий эффект Мейснера в сверхпроводниках^[1].

Происхождение названия[править | править код]

По преданию, гроб с телом пророка Магомета висел в пространстве без всякой поддержки, поэтому этот эксперимент называют «Гроб Магомета».

Постановка опыта[править | править код]

Сверхпроводимость существует только при низких температурах (в ВТСП-керамиках — при температурах ниже 150 К), поэтому предварительно вещество охлаждают, например, при помощи жидкого азота. Далее магнит кладут на поверхность плоского сверхпроводника. Даже в полях, магнитная индукция которых составляет 0,001 Тл, заметно смещение магнита вверх на расстояние порядка сантиметра. При увеличении поля вплоть до критического магнит поднимается всё выше.

Объяснение[править | править код]

Одним из свойств сверхпроводников является выталкивание магнитного поля из области сверхпроводящей фазы. Отталкиваясь от неподвижного сверхпроводника, магнит «всплывает» сам и продолжает «парить» до тех пор, пока внешние условия не выведут сверхпроводник из сверхпроводящей фазы. В результате этого эффекта магнит, приближающийся к сверхпроводнику, «видит» магнит одинаковой полярности и точно такого же размера, — что и вызывает левитацию.

Магнитное поле Википедия

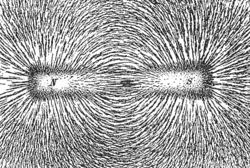
Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения^[1]; магнитная составляющая электромагнитного поля^[2].

Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, что обычно проявляется в существенно меньшей степени) (постоянные магниты).

Кроме этого, оно возникает в результате изменения во времени электрического поля.

Основной силовой характеристикой магнитного поля является вектор магнитной индукции B{\displaystyle \mathbf {B} } (вектор индукции магнитного поля)^[3]. С математической точки зрения B=B(x,y,z){\displaystyle \mathbf {B} =\mathbf {B} (x,y,z)} — векторное поле, определяющее и конкретизирующее физическое понятие магнитного поля.

Ещё одной фундаментальной характеристикой магнитного поля (альтернативной магнитной индукции и тесно с ней взаимосвязанной, практически равной ей по физическому значению) является векторный потенциал.

Нередко в литературе в качестве основной характеристики магнитного поля в вакууме (то есть в отсутствие магнитной среды) выбирают не вектор магнитной индукции B,{\displaystyle \mathbf {B} ,} а вектор напряжённости магнитного поля

Магнетосопротивление — Википедия

Магнитосопротивление (магниторезистивный эффект) — изменение электрического сопротивления материала в магнитном поле. Впервые эффект был обнаружен в 1856 Уильямом Томсоном. В общем случае можно говорить о любом изменении тока через образец при том же приложенном напряжении и изменении магнитного поля. Все вещества в той или иной мере обладают магнетосопротивлением. Для сверхпроводников, способных без сопротивления проводить электрический ток, существует критическое магнитное поле, которое разрушает этот эффект и вещество переходит в нормальное состояние, в котором наблюдается сопротивление. В нормальных металлах эффект магнитосопротивления выражен слабее. В полупроводниках относительное изменение сопротивления может быть в 100—10 000 раз больше, чем в металлах.

Магнитосопротивление вещества зависит и от ориентации образца относительно магнитного поля. Это связано с тем, что магнитное поле не изменяет проекцию скорости частиц на направление магнитного поля, но благодаря силе Лоренца закручивает траектории в плоскости, перпендикулярной магнитному полю. Это объясняет, почему поперечное поле действует сильнее продольного. Здесь^[где?] речь пойдёт в основном о поперечном магнитосопротивлении двумерных систем, когда магнитное поле ориентировано перпендикулярно к плоскости движения частиц.

На основе магниторезистивного эффекта создают датчики магнитного поля.

Качественно понять это явление можно, если рассмотреть траектории положительно заряженных частиц (например, дырок) в магнитном поле. Пусть через образец проходит ток j{\displaystyle j} вдоль оси X. Частицы обладают тепловой скоростью или, если дырочный газ вырожден, то средняя скорость частиц равна фермиевской скорости (скорости частиц на уровне Ферми), которые должны быть много больше скорости их направленного движения (дрейфа). Без магнитного поля носители заряда движутся прямолинейно между двумя столкновениями.

Во внешнем магнитном поле B{\displaystyle B} (перпендикулярном току) траектория будет представлять собой в неограниченном образце участок циклоиды длиной l{\displaystyle l} (длина свободного пробега), и за время свободного пробега (время между двумя столкновениями) вдоль поля E{\displaystyle E} частица пройдет путь меньший, чем l{\displaystyle l}, а именно

lx≈lcos⁡ϕ≈l(1−μ2B22).(1.1){\displaystyle l_{x}\approx l\cos \phi \approx l(1-{\frac {\mu ^{2}B^{2}}{2}}).\qquad (1.1)}

Поскольку за время свободного пробега τ{\displaystyle \tau } частица проходит меньший путь вдоль поля E{\displaystyle E}, то это равносильно уменьшению дрейфовой скорости, или подвижности, а тем самым и проводимости дырочного газа, то есть сопротивление должно возрастать. Разницу между сопротивлением при конечном магнитном поле и сопротивлением в отсутствие магнитного поля принято называть магнетосопротивлением.

Также удобно рассматривать не изменение полного сопротивления, а локальную характеристику проводника — удельное сопротивление в магнитном поле ρ(B) и без магнитного поля ρ(0). При учете статистического разброса времен (и длин) свободного пробега, получим

Δρ(B)=ρ(B)−ρ(0)=ρ(0)μ2B2,(1.2){\displaystyle \Delta \rho (B)=\rho (B)-\rho (0)=\rho (0)\mu ^{2}B^{2},\qquad (1.2)}

где μ{\displaystyle \mu } — подвижность заряженных частиц, а магнитное поле предполагается малым: μB≪1{\displaystyle \mu B\ll 1}. Это приводит к положительному магнетосопротивлению. В трёхмерных ограниченных образцах на боковых гранях возникает разность потенциалов благодаря эффекту Холла, в результате чего носители заряда движутся прямолинейно, поэтому магнетосопротивление с этой точки зрения должно отсутствовать. На самом деле оно имеет место и в этом случае, поскольку холлово поле компенсирует действие магнитного поля лишь в среднем, как если бы все носители заряда двигались с одной и той же (дрейфовой) скоростью. Однако скорости электронов могут быть различны, поэтому на частицы, движущиеся со скоростями, большими средней скорости, магнитное поле действует сильнее, чем холлово. Наоборот, более медленные частицы отклоняются под действием превалирующего холлова поля. В результате разброса частиц по скоростям уменьшается вклад в проводимость быстрых и медленных носителей заряда, что приводит к увеличению сопротивления, но в значительно меньшей степени, чем в неограниченном образце^[1].

Вывод[править | править код]

В модели Друде уравнение для дрейфовой скорости vd{\displaystyle v_{d}} частицы (для простоты рассмотрим дырку) в электрическом E→{\displaystyle {\vec {E}}} и магнитных полях B→{\displaystyle {\vec {B}}} имеет вид:

mv→dτ=e(E→+[v→d×B→]),(2.1){\displaystyle {\frac {m{\vec {v}}_{d}}{\tau }}=e\left({\vec {E}}+[{\vec {v}}_{d}\times {\vec {B}}]\right),\qquad (2.1)}

где m — эффективная масса дырки, e — элементарный заряд, τ — время релаксации по импульсам (время между столкновениями, когда происходит существенное изменение импульса). Решение этого уравнения можно искать в виде суммы трёх векторов, которые определяют базис трёхмерного пространства.

v→d=a1E→+a2B→+a3[E→×B→].(2.2){\displaystyle {\vec {v}}_{d}=a_{1}{\vec {E}}+a_{2}{\vec {B}}+a_{3}[{\vec {E}}\times {\vec {B}}].\qquad (2.2)}

Здесь ai{\displaystyle a_{i}} — искомые коэффициенты. Если подставить это выражение в исходное (2.1) получим

a1E→+a2B→+a3[E→×B→]=eτm(E→+[(a1E→+a2B→+a3[E→×B→])×B→]).(2.3){\displaystyle a_{1}{\vec {E}}+a_{2}{\vec {B}}+a_{3}[{\vec {E}}\times {\vec {B}}]={\frac {e\tau }{m}}\left({\vec {E}}+\left[\left(a_{1}{\vec {E}}+a_{2}{\vec {B}}+a_{3}[{\vec {E}}\times {\vec {B}}]\right)\times {\vec {B}}\right]\right).\qquad (2.3)}

Используя формулу двойного векторного произведения

[E→×B→]×B→=−[B→×[E→×B→]]=−E→B2+B→(B→⋅E→),(2.4){\displaystyle [{\vec {E}}\times {\vec {B}}]\times {\vec {B}}=-[{\vec {B}}\times [{\vec {E}}\times {\vec {B}}]]=-{\vec {E}}B^{2}+{\vec {B}}({\vec {B}}\cdot {\vec {E}}),\qquad (2.4)}

приведём выражение (2.3) к следующему виду:

(a1−μ+a3μB2)E→+(a2−a3μ(B→⋅E→))B→+(a3−μa1)[E→×B→]=0,(2.5){\displaystyle (a_{1}-\mu +a_{3}\mu B^{2}){\vec {E}}+(a_{2}-a_{3}\mu ({\vec {B}}\cdot {\vec {E}})){\vec {B}}+(a_{3}-\mu a_{1})[{\vec {E}}\times {\vec {B}}]=0,\qquad (2.5)}

собрав коэффициенты при базисных векторах. Приравняв коэффициенты при базисных векторах нулю найдём значения

a1=μ1+(μB)2,(2.6){\displaystyle a_{1}={\frac {\mu }{1+(\mu B)^{2}}},\qquad (2.6)}

a2=μ3(B→⋅E→)1+(μB)2,(2.7){\displaystyle a_{2}={\frac {\mu ^{3}({\vec {B}}\cdot {\vec {E}})}{1+(\mu B)^{2}}},\qquad (2.7)}

a3=μ21+(μB)2.(2.8){\displaystyle a_{3}={\frac {\mu ^{2}}{1+(\mu B)^{2}}}.\qquad (2.8)}

Ток и дрейфовая скорость связана соотношением

ȷ→=nev→d.(2.9){\displaystyle {\vec {\jmath }}=ne{\vec {v}}_{d}.\qquad (2.9)}

где n — концентрация электронов участвующих в проводимости. Выразим проводимость через подвижность μ=eτm{\displaystyle \mu ={\frac {e\tau }{m}}}

σ0=neμ.(2.10){\displaystyle \sigma _{0}=ne\mu .\qquad (2.10)}

Теперь, зная дрейфовую скорость, запишем общее выражение для плотности тока^[2]

ȷ→=σ01+(μB)2E→+σ0(μB→⋅E→)1+(μB)2μB→+σ01+(μB)2[E→×μB→].(2.11){\displaystyle {\vec {\jmath }}={\frac {\sigma _{0}}{1+(\mu B)^{2}}}{\vec {E}}+{\frac {\sigma _{0}(\mu {\vec {B}}\cdot {\vec {E}})}{1+(\mu B)^{2}}}\mu {\vec {B}}+{\frac {\sigma _{0}}{1+(\mu B)^{2}}}[{\vec {E}}\times \mu {\vec {B}}].\qquad (2.11)}

В ограниченном образце с двумерным электронным газом в поперечном магнитном поле холловское поле компенсирует действие магнитного поля, когда выполняются следующие условия:

• Двумерный электронный газ вырожден, то есть температура достаточно низка по сравнению с энергией Ферми и нет энергетического разброса носителей, то есть они обладают одинаковой фермиевской скоростью.
• Существует только один тип носителей, поскольку холловское поле не может скомпенсировать дрейф носителей с разными подвижностями или зарядом. Система также должна быть однородна по распределению концентрации носителей, поскольку разная концентрация соответствует различным энергиям и скоростям частиц.
• Поле не может быть квантующим, то есть когда наблюдается эффект Шубникова — де Гааза.
• Эффект магнетосопротивления оказывается чувствительным к форме образца. Длина образца прямоугольной формы должна быть много больше его ширины, поскольку вблизи токовых контактов наблюдается искажение линий токов. Соответственно все измерения должны производиться в четырёхконтактной схеме при постоянном токе.
• Ещё одно ограничение существует на размер образца. Он должен быть макроскопическим. Транспорт в нём должен быть диффузионным и длина фазовой когерентности (длина сбоя фазы) должна быть много меньше размера образца.

Собственно говоря, выполнение этих условий является необходимым условием отсутствия положительного магнетосопротивления. Но существуют эффекты как классические, так и квантовые (слабая локализация) и многочастичные (электрон-электронные взаимодействия в Ферми жидкости), которые могут приводить к магнетосопротивлению в двумерной системе.

Неограниченный образец можно моделировать в виде диска (диск Корбино). Так как ток имеет радиальный характер, то отклонение носителей заряда под действием магнитного поля происходит в перпендикулярном к радиусу направлении, поэтому не происходит разделения и накопления зарядов, и холлово поле не возникает. В геометрии диска Корбино эффект магнетосопротивления максимален.

Если магнитное поле направлено вдоль тока j, то в этом случае изменения сопротивления не должно было бы быть. Однако в ряде веществ магнетосопротивление наблюдается, что объясняется сложной формой поверхности Ферми .

Тензор проводимости[править | править код]

Выражение (2.11) существенно упрощается, если рассматривать двумерный дырочный газ (в плоскости XY) помещённый в поперечное магнитное поле. То есть магнитное поле направлено по оси Z

B→=(0,0,Bz)(3.1){\displaystyle {\vec {B}}=(0,0,B_{z})\qquad (3.1)}

и магнитное поле и электрическое ортогональны между собой

(B→⋅E→)=0.(3.2){\displaystyle ({\vec {B}}\cdot {\vec {E}})=0.\qquad (3.2)}

Тогда выражение (2.11) записанное в матричной форме примет вид

(jxjy)=σ(ExEy)=σ01+(μBz)2(1μBz−μBz1)(ExEy),(3.3){\displaystyle \left({\begin{array}{c}j_{x}\\j_{y}\\\end{array}}\right)=\sigma \left({\begin{array}{c}E_{x}\\E_{y}\\\end{array}}\right)={\frac {\sigma _{0}}{1+(\mu B_{z})^{2}}}\left({\begin{array}{cc}1&\mu B_{z}\\-\mu B_{z}&1\\\end{array}}\right)\left({\begin{array}{c}E_{x}\\E_{y}\\\end{array}}\right),\qquad (3.3)}

где тензор σ называют тензором проводимости двумерного дырочного газа в магнитном поле.

Если рассмотреть достаточно длинный образец прямоугольной формы, такой, что линии тока вдали от контактов параллельны боковым сторонам образца, то в этой системе отсутствует ток j_y. Можно записать связь между компонентами электрического поля (E_y называют холловским полем)

Ey=μBzEx,(3.4){\displaystyle E_{y}=\mu B_{z}E_{x},\qquad (3.4)}

которая приводит к выражению для тока j_x

jx=σ0Ex,(3.5){\displaystyle j_{x}=\sigma _{0}E_{x},\qquad (3.5)}

не зависящему от магнитного поля, то есть к отсутствию магнетосопротивления.^[2]

Обратная матрица к матрице проводимости называется тензором сопротивлений

ρ=σ−1,(3.4){\displaystyle \rho =\sigma ^{-1},\qquad (3.4)}

и в общем случае для обращения нужно использовать формулы

ρxx=σxxσxx2+σxy2,(3.5){\displaystyle \rho _{xx}={\frac {\sigma _{xx}}{\sigma _{xx}^{2}+\sigma _{xy}^{2}}},\qquad (3.5)}

ρxy=−σxyσxx2+σxy2,(3.6){\displaystyle \rho _{xy}=-{\frac {\sigma _{xy}}{\sigma _{xx}^{2}+\sigma _{xy}^{2}}},\qquad (3.6)}

где вместо компонент тензора проводимости следует использовать компоненты в уравнении (3.3) или в явном виде

ρ=1σ0(1−μBzμBz1).(3.7){\displaystyle \rho ={\frac {1}{\sigma _{0}}}\left({\begin{array}{cc}1&-\mu B_{z}\\\mu B_{z}&1\\\end{array}}\right).\qquad (3.7)}

Для двумерного электронного газа используются формулы (3.3), где изменён знак на противоположный перед подвижностью в тензоре проводимости (или просто транспонированная матрица проводимости).

Геометрическое магнетосопротивление[править | править код]

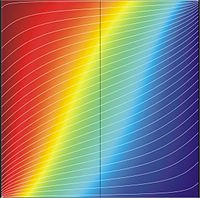Рис. 1. Распределение потенциала (красный цвет соответствует максимуму, а синий — минимуму) в однородном квадратном образце с двумерным дырочным газом в поперечном магнитном поле (μB=1). Белыми линиями показаны искривлённые в магнитном поле линии тока. Рис. 2. Распределение потенциала в однородном прямоугольном образце с двумерным дырочным газом в поперечном магнитном поле (μB=1). Белыми линиями показаны линии тока, которые в середине образца практически параллельны боковым сторонам (сравните с Рис. 1.).

Если рассмотреть прямоугольный образец (длиной L и шириной d) с двумерным электронным газом (магнитное поле направлено перпендикулярно плоскости образца), то в образце наблюдается магнитосопротивление связанное с перераспределением токов в магнитном поле^[3]:

R(B)−R(0)R(0)=g(Ld)(μBz)2,(4.1){\displaystyle {\frac {R(B)-R(0)}{R(0)}}=g\left({\frac {L}{d}}\right)(\mu B_{z})^{2},\qquad (4.1)}

где

g(Ld)=16π31L/d∑k=0∞th(π2Ld(2k+1))(2k+1)3.(4.2){\displaystyle g\left({\frac {L}{d}}\right)={\frac {16}{\pi ^{3}}}{\frac {1}{L/d}}\sum _{k=0}^{\infty }{\frac {\mathrm {th} \left({\frac {\pi }{2}}{\frac {L}{d}}(2k+1)\right)}{(2k+1)^{3}}}.\qquad (4.2)}

Классификацию магнетосопротивлений производят по знаку изменения сопротивления образца в магнитном поле и по различиям в причинах, обуславливающих спин-зависимое рассеяние носителей тока.

Отрицательное магнетосопротивление[править | править код]

Среди эффектов, которые приводят к магнетосопротивлению можно выделить слабую локализацию, как наиболее известный эффект приводящий к отрицательному магнетосопротивлению, то есть наблюдается увеличение проводимости при приложении магнитного поля. Это одноэлектронный квантовый интерференционный эффект, приводящий к дополнительному рассеянию носителей, что уменьшает проводимость.

Анизотропное магнетосопротивление[править | править код]

Особенностью ферромагнитных материалов является зависимость их электрического сопротивления от угла между направлением движения носителей тока и направлением намагниченности в образце вследствие спин-орбитального взаимодействия^[4]. Эффект является довольно слабым (изменение сопротивления не превышает нескольких процентов), но тем не менее это позволяло использовать его в датчиках магнитного поля до открытия эффекта гигантского магнитного сопротивления^[5].

Гигантское магнетосопротивление[править | править код]

Было экспериментально открыто двумя научными группами под руководством Альбера Фера и Петера Грюнберга независимо друг от друга в 1988 году. За открытие эффекта гигантского магнетосопротивления Феру и Грюнбергу была присуждена Нобелевская премия по физике за 2007 год^[6].

Эффект проявляется в многослойных структурах (сверхрешетках), состоящих из чередующихся ферромагнитных и немагнитных слоев. Подбором толщины немагнитного слоя можно достичь того, что основным состоянием будет антипараллельная направленность намагниченности в соседних магнитных слоях (антиферромагнитная структура). Приложением внешнего магнитного поля можно ориентировать намагниченность параллельно во всех слоях. В этом случае часть электронов будет проходить сквозь структуру рассеиваясь очень слабо^[7][8].

Колоссальное магнетосопротивление[править | править код]

Под эффектом колоссального магнетосопротивления понимают сильную зависимость электрического сопротивления некоторых манганитах со структурой перовскита. В отличие от эффекта гигантского магнетосопротивления, здесь не требуется многослойных структур^[9].

Туннельное магнетосопротивление[править | править код]

Туннельное магнитное сопротивление так же, как и гигантское, наблюдается в многослойных структурах ферромагнитных материалов, где в качестве прослойки между ними используется диэлектрик, через который происходит туннелирование электронов при прохождении электрического тока через образец. Эффект был открыт Мишелем Жюльером в 1975 году, однако в то время не привлек к себе внимания, так как проявлялся лишь при гелиевых температурах^[10]. В настоящее время, после открытия высокотемпературных материалов, позволяющих его наблюдать, датчики на его основе заменили приборы, использующие гигантское магнетосопротивление.

1. ↑ Kireev, P. S. (англ.)русск.. Semiconductor physics, 2nd ed (неопр.). — Moscow: Mir Publishers, 1978. — С. 696.
2. ↑ ^{1 2} Askerov, B. M. (англ.)русск.. Electron Transport Phenomena in Semiconductors, 5-е изд (англ.). — Singapore: World Scientific, 1994. — P. 416.
3. ↑ Vorob’ev V. N. and Sokolov Yu. F. «Determination of the mobility in small sample of gallium arsenide from magnetoresistive effects» Sov. Phys. Semiconductors 5, 616 (1971).
4. ↑ Hari Singh Nalwa. Handbook of thin film materials: Nanomaterials and magnetic thin films. — Academic Press, 2002. — Vol. 5. — P. 514. — 633 p. — ISBN 9780125129084.
5. ↑ Claude Chappert, Albert Fert and Frédéric Nguyen Van Dau. The emergence of spin electronics in data storage (англ.) // Nature Materials : journal. — 2007. — Vol. 6. — P. 813—823. — DOI:10.1038/nmat2024.
6. ↑ The Nobel Prize in Physics 2007 (англ.). The Official Web Site of the Nobel Prize. Дата обращения 27 февраля 2011. Архивировано 10 августа 2011 года.
7. ↑ .
8. ↑ С.А. Никитин. МАГНИТНЫЕ СТРУКТУРЫ В КРИСТАЛЛИЧЕСКИХ И АМОРФНЫХ ВЕЩЕСТВАХ (неопр.). Соросовский образовательный журнал. Русский переплет (1996).
9. ↑ Colossal Magnetoresistance, Charge Ordering and Related Properties of Manganese Oxides / Ed. by C. N. R. Rao and B. Raveau. — World Scientfic Publishing Co., 1998. — P. 1—2. — 356 p. — ISBN 978-981-02-3276-4.
10. ↑ M. Jullière. Tunneling between ferromagnetic films (англ.) // Phys. Lett. (англ.)русск. : journal. — 1975. — Vol. 54A. — P. 225—226. sciencedirect Архивная копия от 8 июля 2009 на Wayback Machine