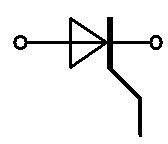
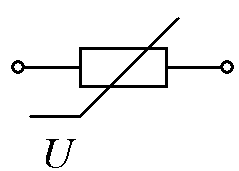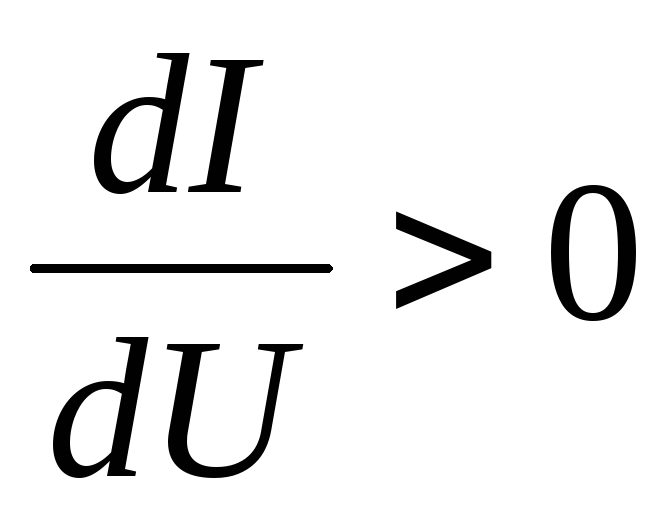2.1. Классификация нелинейных элементов

Свойства нелинейных двухполюсников обычно описывают их статическими характеристиками. Общепринятой характеристикой нелинейного резистивного двухполюсника является его вольт-амперная характеристика (ВАХ).

Статическая ВАХ – это зависимость тока, протекающего через нелинейный резистивный элемент, от приложенного к нему напряжения в установившемся режиме (или наоборот – зависимость падения напряжения на элементе от протекающего через него тока).

Статическая ВАХ определяет свойства элемента при переменном напряжении (токе) низкой частоты, значение которой не превышает предельно допустимого значения.

В зависимости от числа внешних выводов различают нелинейные двухполюсные элементы (резисторы с нелинейным сопротивлением, электровакуумные и полупроводниковые диоды) и

нелинейные многополюсные элементы (транзисторы и тиристоры различных типов, электровакуумные триоды и пентоды).

ВАХ нелинейного двухполюсного элемента может быть симметричной (рис.15.2,а) или несимметричной (рис.15.2,б,в) относительно начала координат.

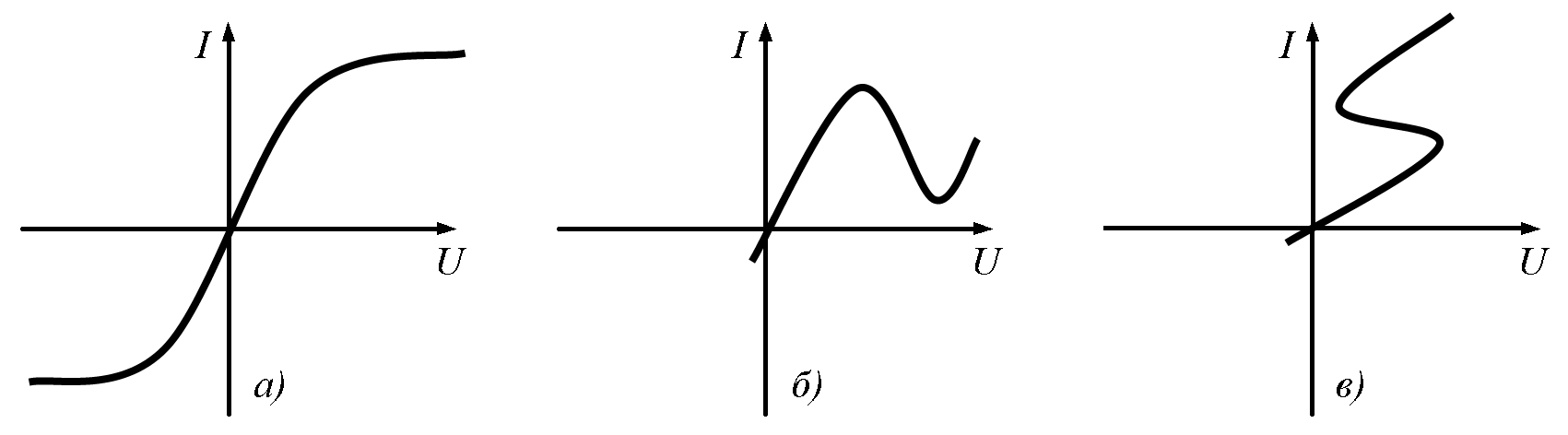
Рис.15.2 – Статические вольт-амперные характеристики различных

резистивных элеметов

Для симметричной ВАХ справедливо условие I(U) = —I(-U), а для несимметричной

I(U)  —I(-U).

Очевидно, что режим работы нелинейной цепи не изменится, если выводы нелинейного резистивного элемента с симметричной характеристикой поменять местами.

Различают нелинейные резистивные элементы с монотонной (рис.15.2,а) и немонотонной (рис.15.2,б,в) ВАХ.

У элементов с монотонной ВАХ увеличение приложенного к элементу напряжения приводит к росту (или хотя бы не уменьшению) тока и, наоборот, увеличение тока приводит к возрастанию напряжения на элементе.

Напряжение и ток на зажимах такого элемента связаны между собой однозначной зависимостью

, причем производные ВАХ во всех ее токах принимают только неотрицательные значения, т.е.

,.

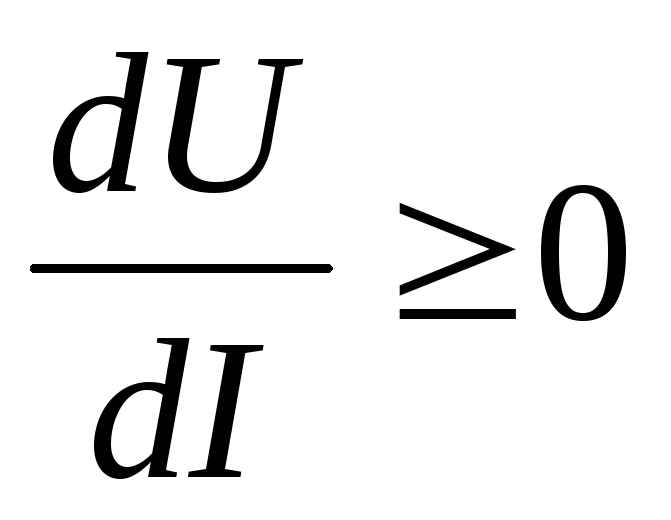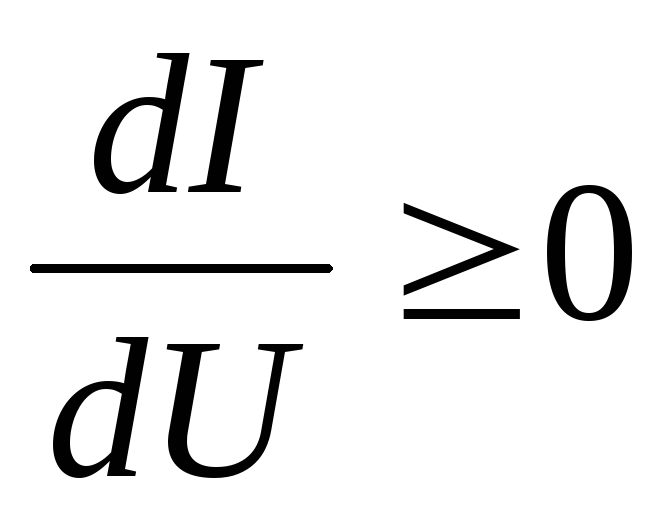ВАХ нелинейного элемента является немонотонной, если хотя бы в ограниченном диапазоне изменения токов и напряжений рост напряжения на зажимах элемента приводит к уменьшению тока или, наоборот, увеличение тока приводит к снижению напряжения.

Ток и напряжение нелинейного резистивного элемента с немонотонной ВАХ не связаны между собой взаимно однозначной зависимостью (рис.15.2,б,в).

Многообразие всех ВАХ нелинейных двухполюсников можно свести к шести основным типам (рис.15.3,а-е).

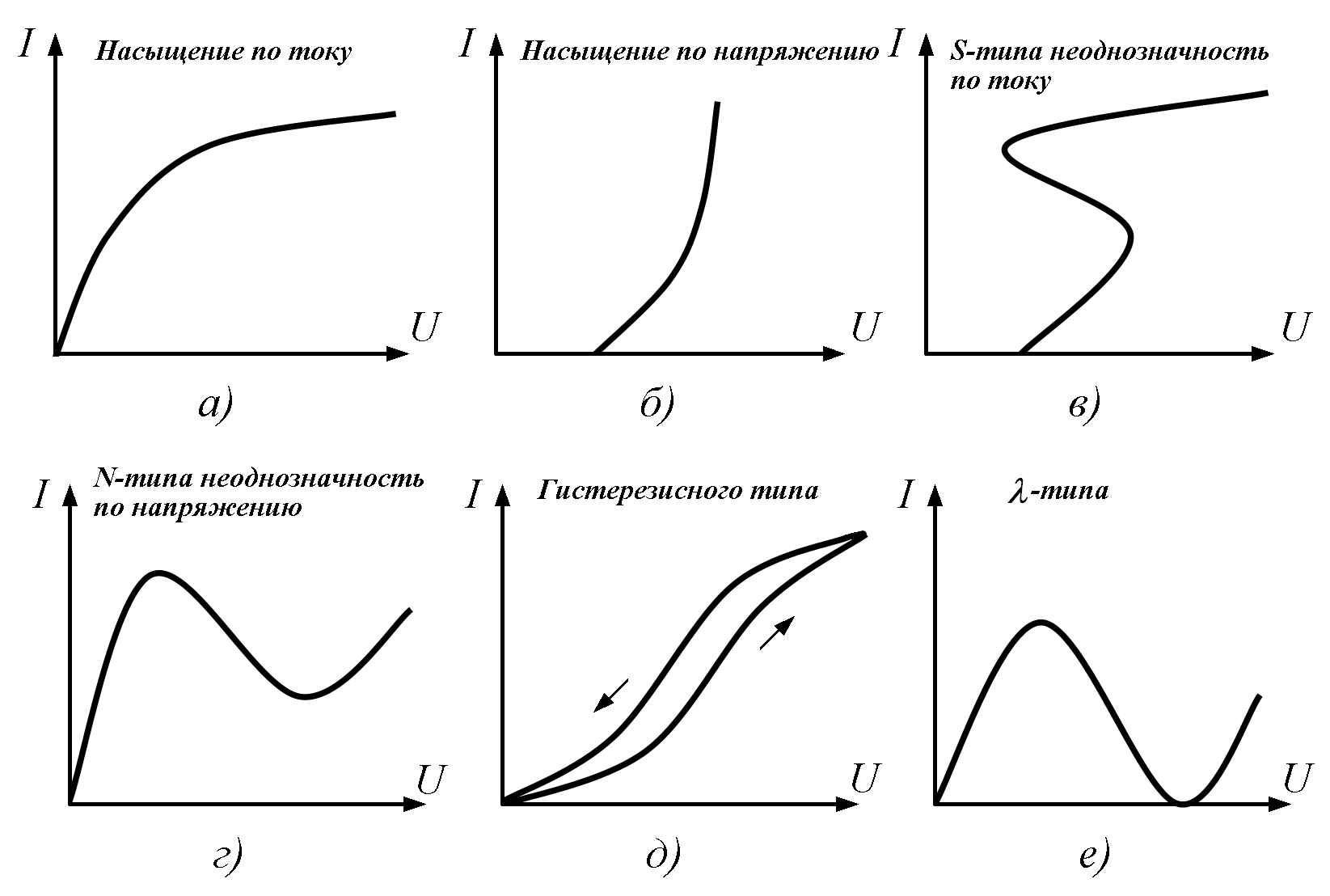
Рис.15.3

ВАХ могут иметь зон нечувствительности, т.е. «ступеньку» по напряжению или по току (рис.15.4,а,б)

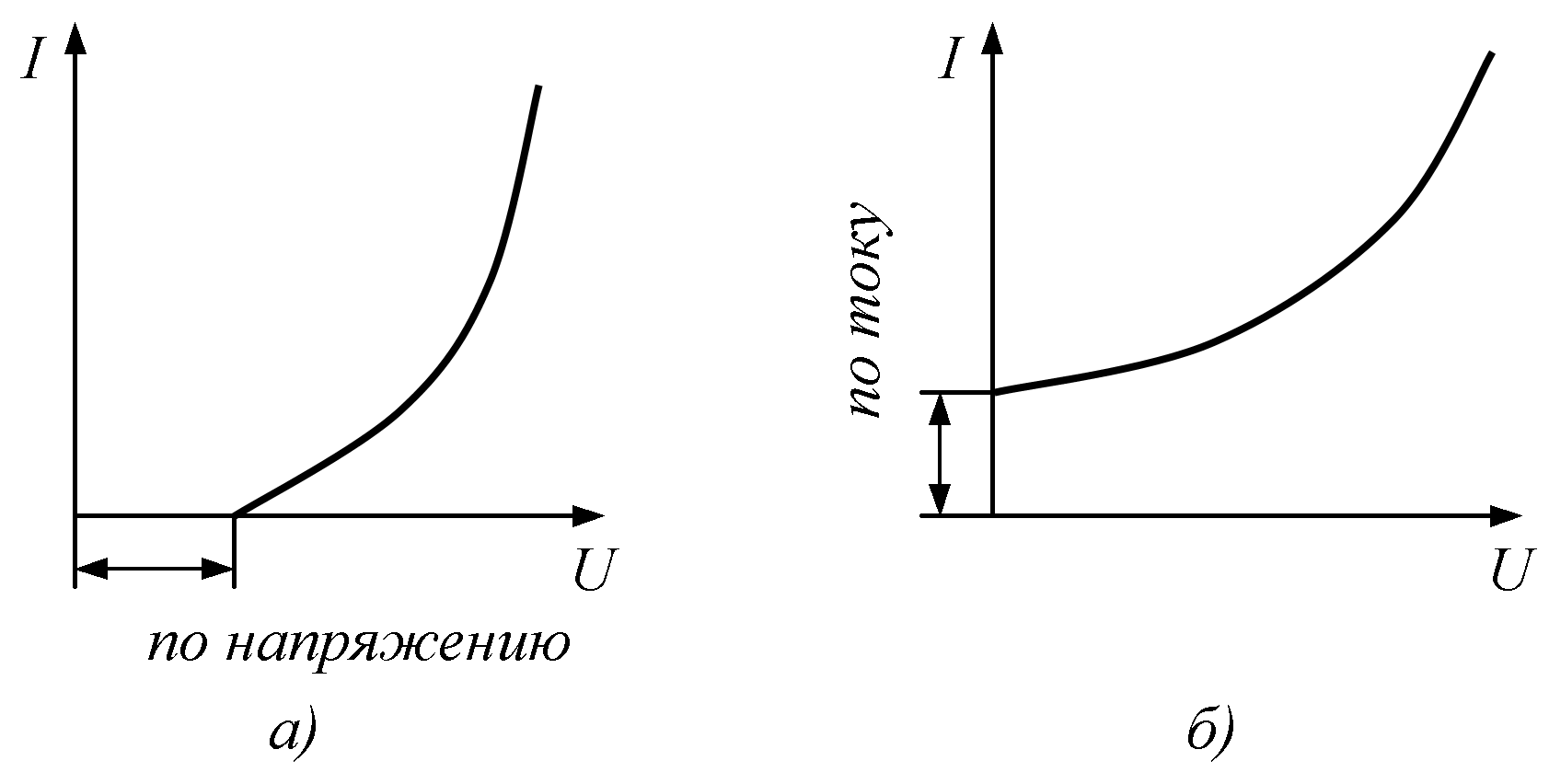
Рис.15.4

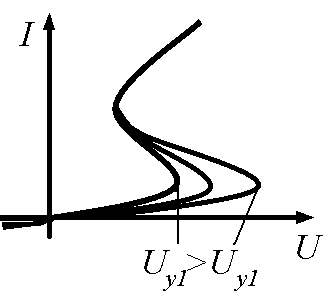
Вид ВАХ нелинейного резистивного двухполюсника может зависеть от некоторой величины, не связанной непосредственно с токами или напряжениями цепи, в которую включен данный элемент, в частности от температуры, освещенности, давления и др. Такие элементы относятся к

неэлектрически управляемым двухполюсникам.

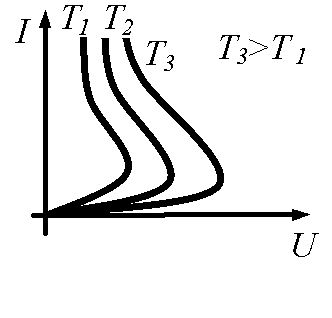
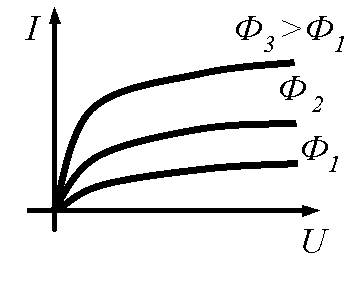
Так как каждому значению управляющей величины соответствует своя кривая, характеризующая зависимость между током и напряжением на зажимах неэлектрически управляемого резистивного двухполюсника, также двухполюсники характеризуются не одной ВАХ, а семейством ВАХ (рис.15.5).

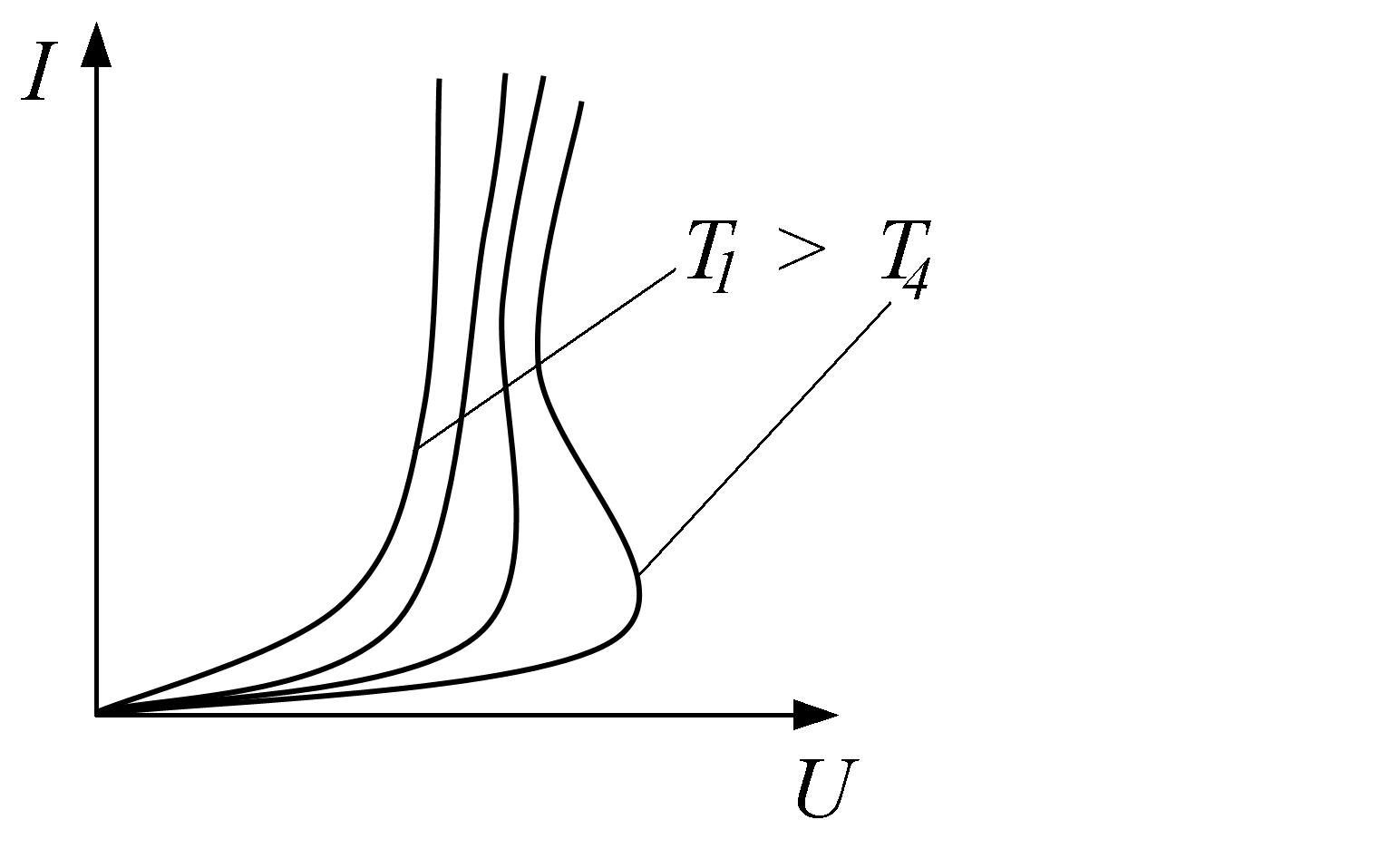
Рис.15.5 – Семейство ВАХ термистора.

Важнейший класс нелинейных резистивных элементов составляют

электрически управлямые элементы (транзисторы различных типов, вакуумные и газоразрядные трехэлектродные и многоэлектродные приборы. Элементы этого типа содержат два основных электрода:

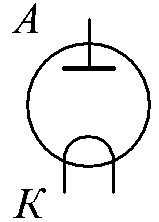
— катод и анод у электронных ламп;

— эмиттер и коллектор у биполярных транзисторов;

— сток и исток у полевых транзисторов.

Сопротивление между основными электродами изменяется под действием тока или напряжения одного или нескольких управляющих электродов:

— сетки у электронных ламп;

— базы у биполярных транзисторов;

— затвора или подложки у полевых транзисторов.

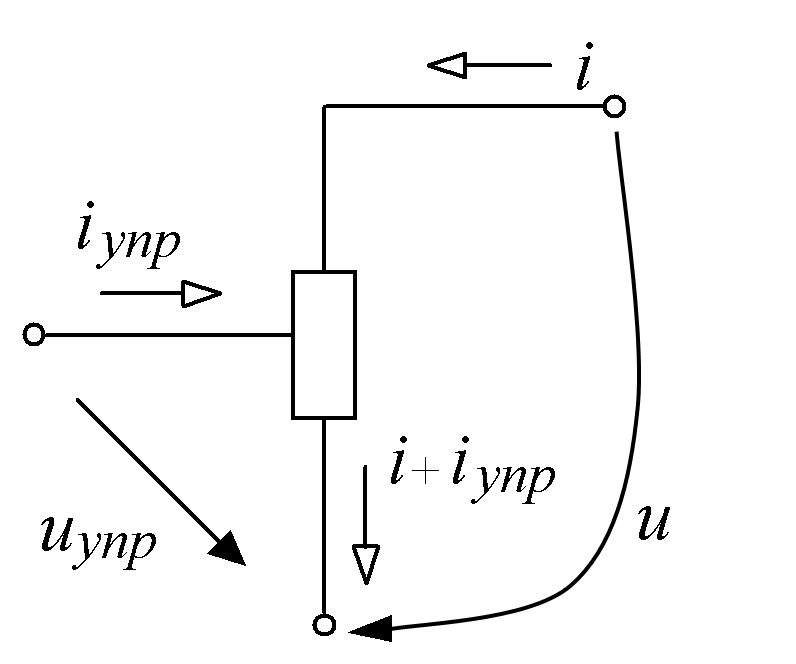
В частности, ток i нелинейного резистивного трехполюсника (рис.15.6), имеющего два основных и один управляющий электрод, является функцией напряжения между основными электродами u и тока управления i_упр или напряжения u_упр управляющего электрода:

i = i(u, iупр) или i = i (u, uупр).

Рис.15.5 – Электрически управляемый нелинейный трехполюсник

Как видно из рис.15.5, электрически управляемый нелинейный резистивный трехполюсник имеет две стороны: входную (управляющую) и выходную (управляемую), причем один из выводов трехполюсника является общим для обеих сторон.

Электрически управляемые нелинейные резистивные элементы могут быть охарактеризованы различными семействами ВАХ.

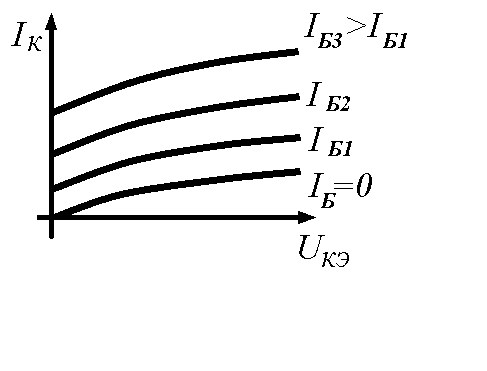
Выходные ВАХ отображают зависимость между выходным током i и выходным напряжением u при различных значениях входного тока

i_упр или напряжения u_упр.

Типовые выходные ВАХЪ биполярного транзистора в схеме с общим эмиттером (рис.15.6,а) представлены на рис.15.6,б.

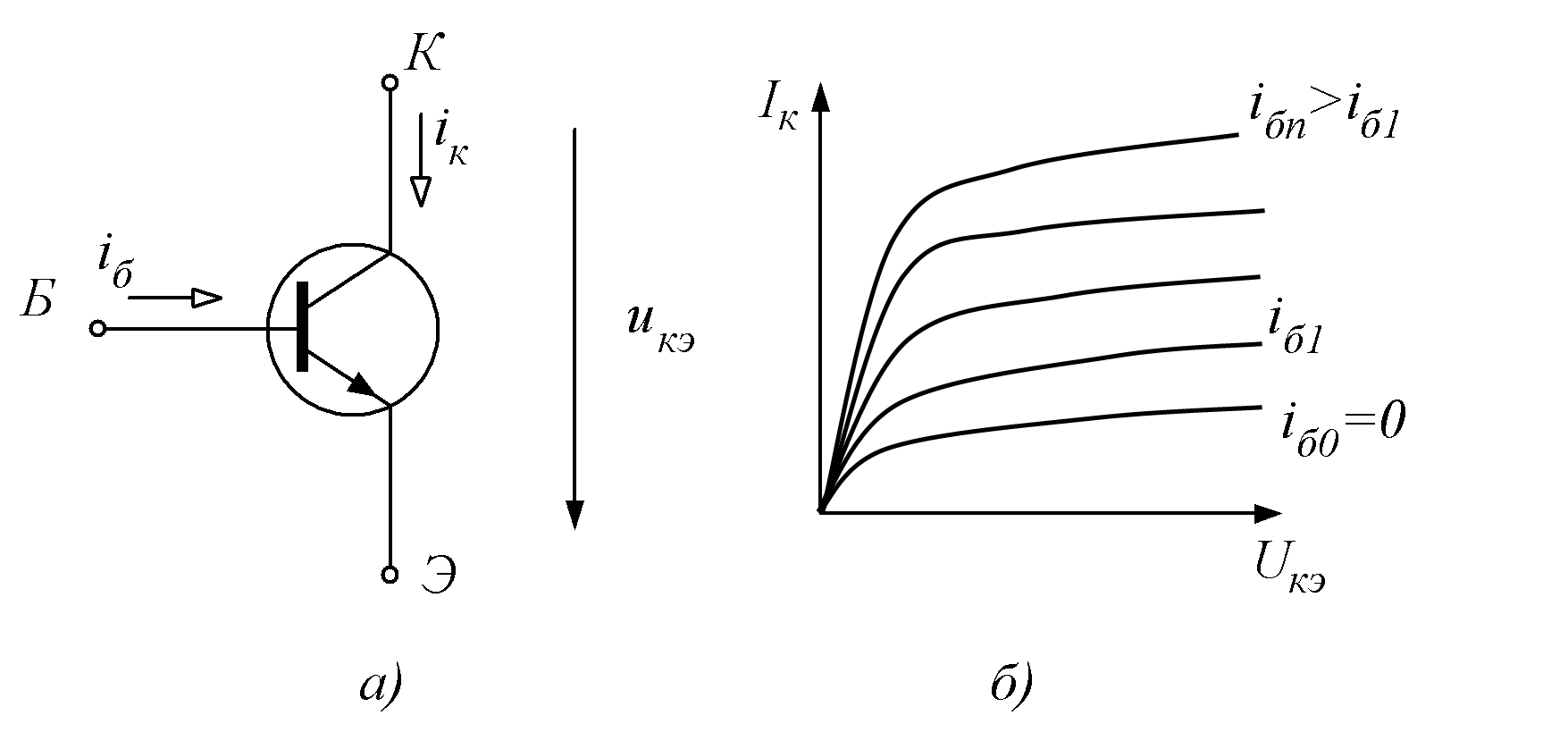
Рис.15.6

Полная классификация нелинейных элементов представлена в таблице 15.1, а примеры нелинейных резистивных элементов с их условными графическими обозначениями и вольт-амперными характеристиками приведены в таблице 15.2.

Резистивные	1. По виду параметра	Признаки классификации	Табл.29.1 – Классификация нелинейных элементов
Индуктивные
Емкостные
Двухполюсные	2. По количес-тву внешних выводов
Многополюсные
Симметричные	3. По наличию симмет-рии ВАХ
Несимметричные
Монотонные	4. По наличию монотон-ности ВАХ
Немонотонные
С насыщением по току	5. По типу ВАХ
С насыщением по напряжению
S-типа (неоднозначность по току)
N-типа (неоднозначность по напряжению)
-типа
С зоной нечувствительности по току	6. По наличию зоны нечувствитель-ности
С зоной нечувствительности по напряжению
Без зоны нечувствительности
Неэлектрически управляемые	7. По способу управления
Электрически управляемые

Таблица 15.1 – Резистивные НЭ

Элемент, графическое обозначение	Вид ВАХ	Характеристика ВАХ
1	2	3
Двухполюсные резистивные элементы
Варистор		Симметричная I(U) = —I(-U), монотонная
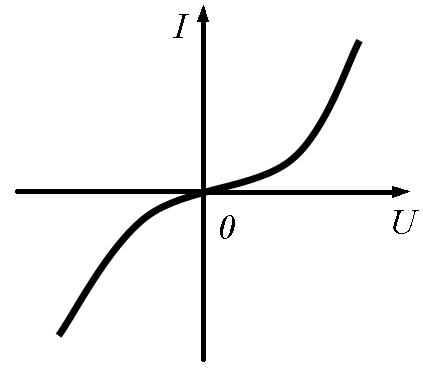
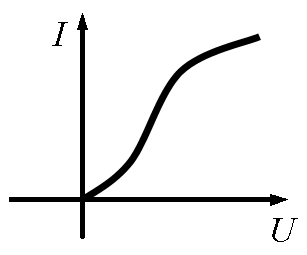
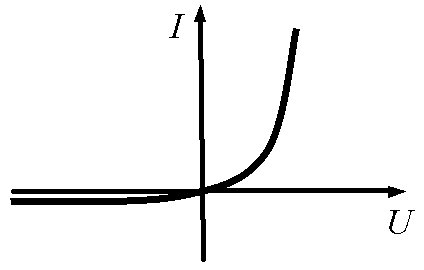
Электровакуумный диод		Несимметричная, монотонная ВАХ (dI/dU) > 0
1	2	3
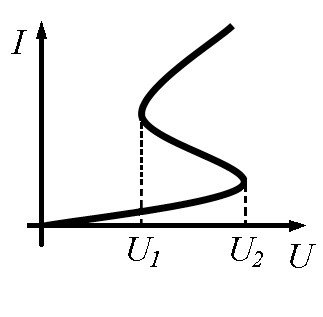
Неоновая лампа		ВАХ с падающим участком (dI/dU) < 0, несимметричная, немонотонная, S-типа
Полупровод-никовый диод		ВАХ несимметричная, монотонная
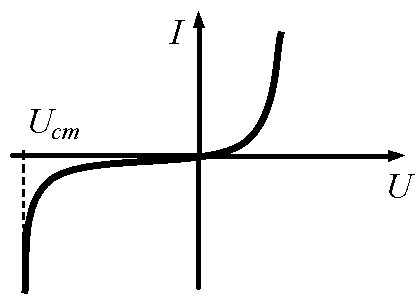
Стабилитрон		ВАХ несимметричная, монотонная
Тоннельный диод		ВАХ с падающим участком, несимметричная, немонотонная, N-типа
1	2	3
Неэлектрически управляемые двухполюсные резистивные элементы
Терморезистор		ВАХ с падающим участком, сопротивление зависит от температуры
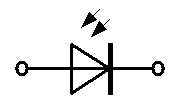
Фотодиод		ВАХ несимметрична, монотонна, с насыщением по току. Сопротивление зависит от светового потока
Электрически управляемые трехполюсные резистивные элементы
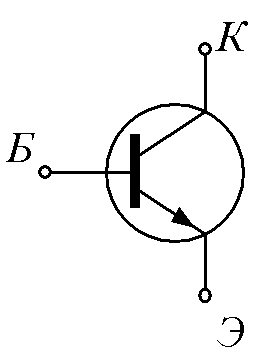
Биполярный транзистор типа n—p—n	Выходные ВАХ	ВАХ несимметрична, монотонна, с насыщением по току. Выходной ток зависит от напряжения и от входного тока: Iк = I(IБ, Uкэ)
Тиристор		ВАХ несимметрична, немонотонна, S-типа, зависит от напряжения на управляющем электроде

2.2. СТАТИЧЕСКИЕ И ДИФФЕРЕНЦИАЛЬНЫЕ ПАРАМЕТРЫ

Для резистивных нелинейных элементов важным параметром является их сопротивление, которое в отличие от линейных резисторов не является постоянным, а зависит от того, в какой точке ВАХ оно определяется. Различают два вида сопротивлений: статическое и дифференциальное (динамическое).

Статическое сопротивление характеризует рабочую точку нелинейного элемента по постоянному току, а дифференциальное – работу нелинейного элемента в окрестности этой рабочей точки.

Пусть резистивный нелинейный элемент имеет вольт-амперную характеристику, указанную на рисунке 15.8.

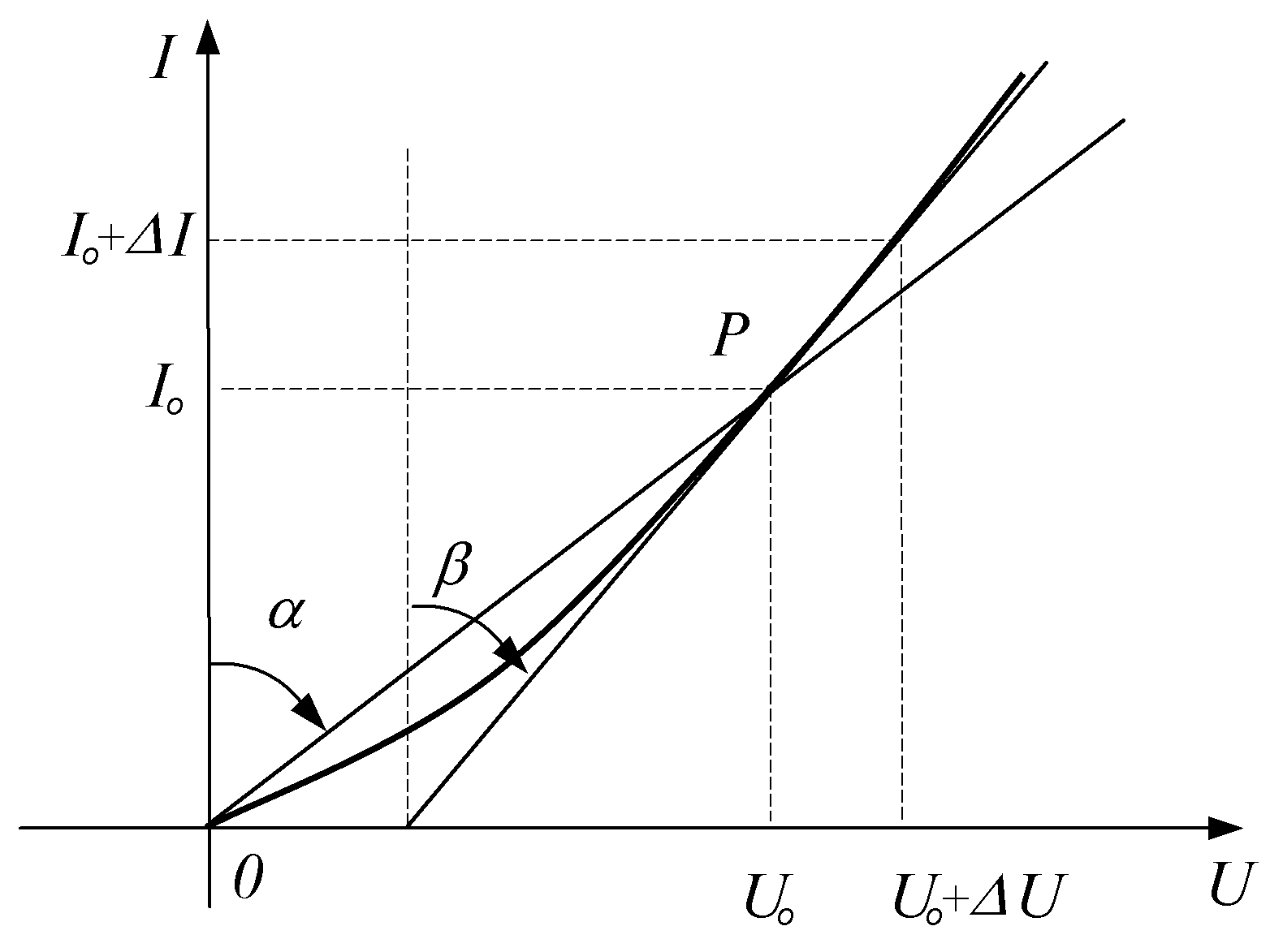
Рис.15.8

Статическое сопротивление – это соотношение напряжения к току в данной точке ВАХ.

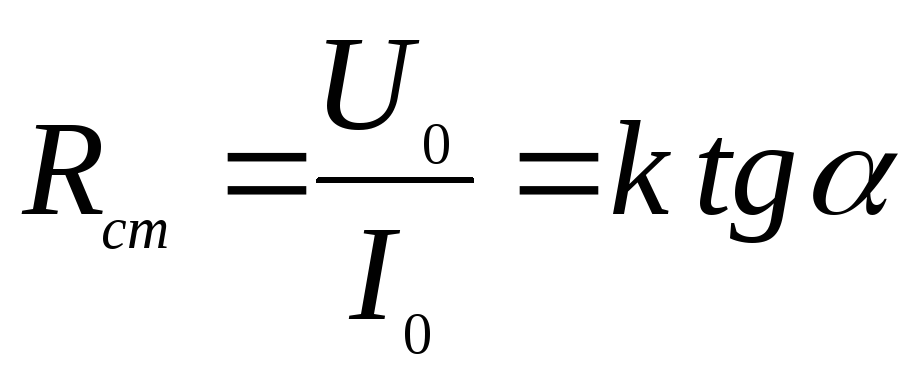(15.1)

где 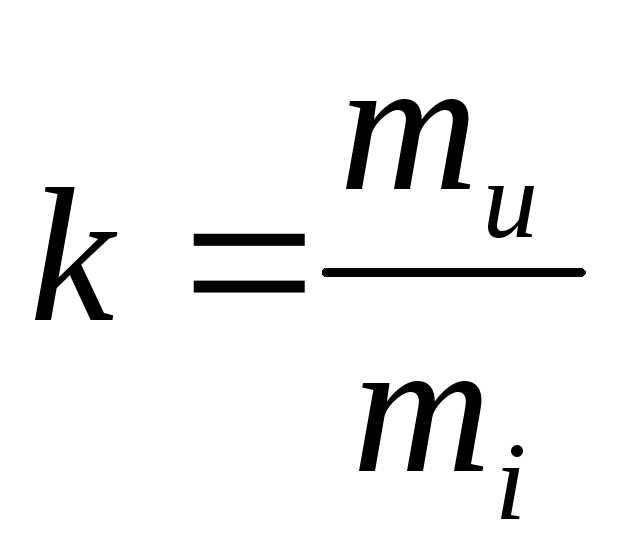— масштабный коэффициент;

m_u, m_i – масштабы по напряжению и току;

 — угол наклона секущей, проведенной через начало координат и рабочую точку, к оси токов.

Статическое сопротивление – это сопротивление нелинейного элемента постоянному току.

Очевидно статическая проводимость есть величина, обратная статическому сопротивлению

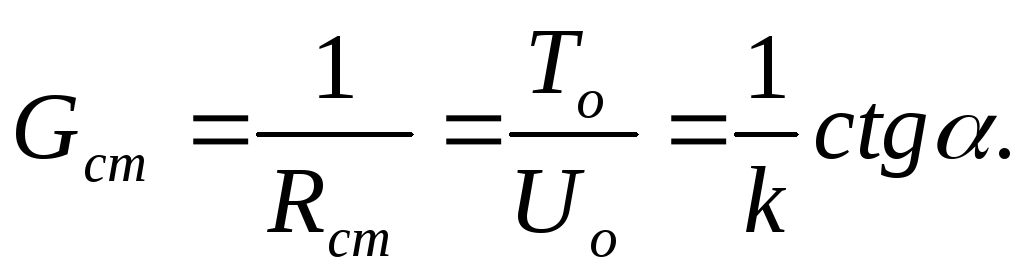(15.2)

Дифференциальное сопротивление – это предел отношения приращения напряжения к соответствующему приращению тока при небольшом смещении рабочей точки на ВАХ под воздействием переменного напряжения малой амплитуды:

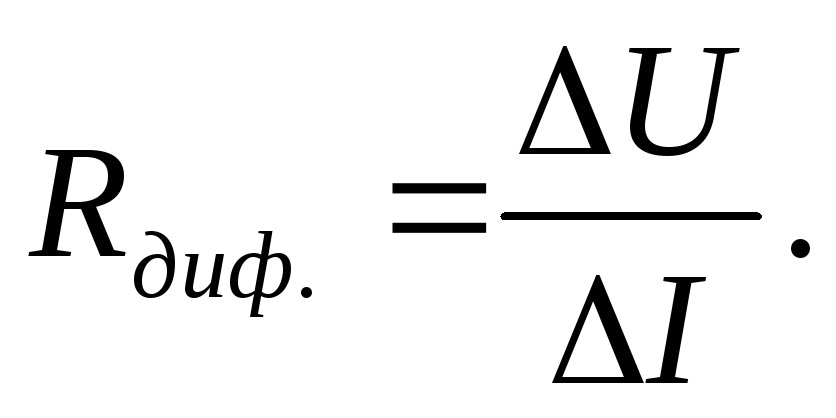
Дифференциальное сопротивление – это сопротивление нелинейного элемента переменному току малой амплитуды.

Вольт-амперная характеристика — Википедия

Материал из Википедии — свободной энциклопедии

Пример ВАХ для полупроводникового диода c p-n переходом. Зелёная область — прямая ветвь ВАХ (слева — участок обратного напряжения, справа — участок прямого тока), голубая область — область допустимых напряжений на обратной ветви ВАХ, розовая область — обратный лавинный пробой p-n перехода. Масштабы по оси тока для прямого и обратного тока разные.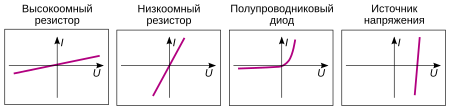 Пример 4 различных ВАХ Пример сток-затворной ВАХ (слева) и семейство стоковых ВАХ (справа) полевого транзистора с затвором в виде p-n перехода и каналом n-типа

Вольт-ампе́рная характери́стика (ВАХ) — зависимость тока, протекающего через двухполюсник, от напряжения на этом двухполюснике. Описывает поведение двухполюсника на постоянном токе. Также ВАХ называют функцию, выражающую (описывающую) эту зависимость и график этой функции.

Обычно рассматривают ВАХ нелинейных элементов (степень нелинейности определяется коэффициентом нелинейности β=UI⋅dIdU{\displaystyle \beta ={\frac {U}{I}}\cdot {\frac {dI}{dU}}}), поскольку для линейных элементов ВАХ представляет собой прямую линию (описывающуюся законом Ома) и потому тривиальна.

Примеры элементов, обладающих существенно нелинейной ВАХ: диод, тиристор, стабилитрон.

Для трёхполюсных элементов с управляющим электродом (таких, как транзистор, тиристор или электровакуумный триод) часто строят семейства кривых, являющимися ВАХ для двухполюсника при заданном токе или напряжении на третьем управляющем электроде элемента.

Необходимо отметить, что в реальной схеме, особенно работающей с относительно высокими частотами (близкими к границам рабочего частотного диапазона) для данного устройства рабочая точка на ВАХ может пробегать по траекториям, отклоняющимся от ВАХ, измеренной на постоянном токе или низких частотах. Обычно такое отклонение связано с присущими инерционными свойствами прибора или ёмкостью и индуктивностью присоединённой к прибору цепи или паразитными ёмкостью и индуктивностью.

Форма ВАХ полупроводниковых приборов зависит от температуры его полупроводниковой структуры, например, от температуры p-n перехода. Для полупроводниковых диодов с p-n переходом при увеличении температуры угол наклона прямой и обратной ветвей ВАХ увеличивается.

При последовательном или параллельном включении двух или нескольких двухполюсников вид ВАХ результирующего двухполюсника изменяется.

При параллельном соединении двух двухполюсников, напряжения на обоих приборах равны и при этом общий ток равен сумме токов, при последовательном — токи через каждый прибор равны, а общее напряжение на такой цепи равно сумме напряжений на элементах.

Классификация нелинейных элементов — Студопедия.Нет

Нелинейные элементы могут быть классифицированы по разным признакам. Если нелинейность вольт-амперной характеристики (ВАХ) обусловлена тепловыми процессами, то такие элементы называют инерционными (лампы накаливания, бареттеры, газоразрядные приборы и др.).

Если же нелинейность ВАХ обусловлена не тепловыми, а иными процессами, то такие элементы называют безынерционными (полупроводниковые и электронные приборы). Однако полупроводниковые приборы при импульсном или высокочастотном воздействии переключаются с задержкой из-за наличия нелинейной емкости p-n перехода, то есть приборы становятся инерционными.

Различают управляемые и неуправляемые НЭ. Неуправляемыми, как правило, бывают двухполюсные НЭ. Характеристика неуправляемого НЭ изображается одной кривой. Управляемыми являются многополюсные НЭ: транзисторы, тиристоры, электронные лампы, операционные усилители и т.д., которые кроме основной цепи имеют хотя бы еще одну управляющую цепь, ток или напряжение которой влияют на ВАХ основной цепи. Поэтому управляемый НЭ характеризуется семейством нелинейных характеристик, параметром которых является управляющий фактор.

В зависимости от вида ВАХ различают НЭ с симметричной и несимметричной характеристикой.

На рис. 11.1, а показана симметричная характеристика лампы накаливания с металлической нитью. Загиб кривой I(U) объясняется тем, что по мере увеличения тока нить нагревается сильнее и ее сопротивление возрастает.

Рис. 11.1

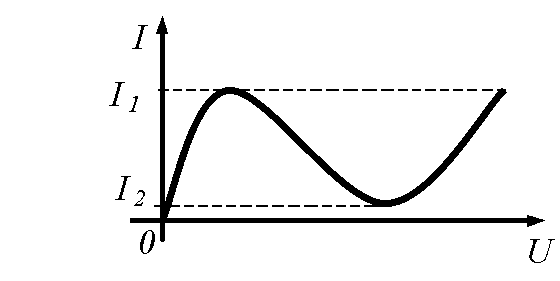
Характеристику, представленную на рис. 11.1, б, имеет бареттер, с помощью которого поддерживается неизменный ток при колебаниях напряжения на его зажимах в определенных пределах от U₁ до U₂.

На рис. 11.2 показаны несимметричные характеристики. Вольт-амперную характеристику, изображенную на рис. 11.2, а, имеет выпрямительный диод. Для удобства изображения характеристики прямой и обратный токи, а также прямое и обратное напряжение даны на одном рисунке в разных масштабах.

На рис. 11.2, б показана вольт-амперная характеристика полупроводникового стабилитрона – прибора, напряжение на котором в некотором диапазоне изменения тока остается практически неизменным.

При постоянном токе не имеет принципиального значения, является ли характеристика НЭ симметричной или несимметричной. В цепях переменного тока зависимость ВАХ от полярности приложенного напряжения или направления тока очень существенна. Приборы с несимметричной характеристикой используются для преобразования переменного тока в постоянный, для выделения четных гармоник тока при синусоидальном напряжении источника и для других целей.

Экспериментальное получение ВАХ

Вольтамперные характеристики НЭ могут быть получены экспериментально. Для этого собирают электрическую цепь по одной из двух схем, показанных на рис. 11.3, а, б.

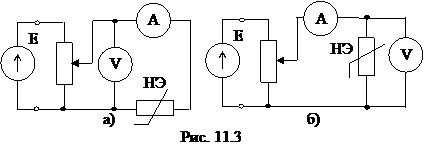
При этом следует иметь в виду, что измерительные приборы обладают сопротивлениями, указанными на их лицевой стороне. Сопротивления амперметра R_A и вольтметра R_V могут быть соизмеримы с сопротивлениями НЭ, поэтому при снятии ВАХ следует производить перерасчет данных для построения характеристик.

Так, при снятии ВАХ по схеме рис. 11.3, а следует учесть, что вольтметр покажет суммарное напряжение амперметра и нелинейного элемента

     .

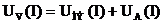Поэтому при заданных значениях тока напряжение на НЭ определяют по формуле

    

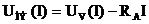
 и только после этого строят вольтамперную характеристику.

В случае, если сопротивление нелинейного элемента намного больше сопротивления амперметра, то напряжением амперметра можно пренебречь и считать, что

     .

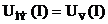При снятии ВАХ по схеме рис. 11.3, б получают погрешность вследствие того, что амперметр измеряет суммарный ток            .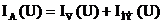

Поэтому при заданных значениях напряжения определяют ток НЭ по формуле

     ,

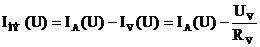после чего строят зависимость I_НЭ(U).

В случае, если сопротивление нелинейного элемента намного меньше сопротивления вольтметра, то током вольтметра можно пренебречь и считать, что

     .

Полученные экспериментальным способом вольт-амперные характеристики НЭ используют далее для описания свойств НЭ и для расчета электрической цепи, содержащей нелинейные элементы.

1. Нелинейные радиотехнические цепи. Радиотехнические цепи и сигналы. Учебное пособие

1.1. Нелинейные элементы и их характеристики. Способы аппроксимации характеристик нелинейных элементов

1.2. Анализ преобразования гармонического сигнала НЭ при степенной аппроксимации ВАХ

1.3. Анализ преобразования гармонического сигнала НЭ при кусочно-линейной аппроксимации ВАХ

1.1. Нелинейные элементы и их характеристики. Способы аппроксимации характеристик нелинейных элементов

В общем случае нелинейная цепь описывается оператором преобразования W_нц:

u_вых(t) = W_нц[U_вх(t),t], (1.1)

для которого свойство линейности не выполняется. В состав такой цепи входят один или несколько нелинейных элементов (НЭ). Различают резистивные и реактивные НЭ. В качестве резистивных НЭ выступают транзисторы, полупроводниковые диоды, электронные лампы. Примером реактивного НЭ является варикап.

При анализе НЭ предполагается, что переходные процессы в НЭ заканчиваются практически с окончанием изменения входного сигнала, т.е. НЭ является безынерционным.

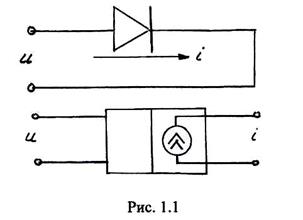В подавляющем большинстве задач радиотехники рассматриваются резистивные безынерционные НЭ. В таких элементах в качестве входного сигнала выступает напряжение, а в качестве выходного – ток, протекающий по элементу. На Рис.1.1 показаны: нелинейный двухполюсник – полупроводниковый диод и четырехполюсник, которым может быть представлен транзистор. Основной характеристикой НЭ является его вольт-амперная характеристика (ВАХ), т.е. зависимость тока, протекающего через НЭ, от приложенного к нему напряжения:

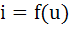
Другими характеристиками НЭ являются (Рис 1.2):

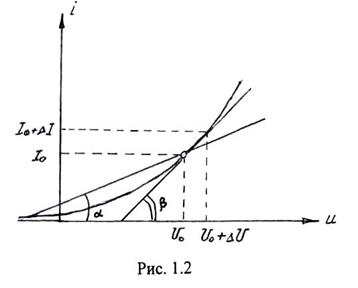– статическое сопротивление или сопротивление НЭ по постоянному току:

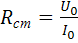, (1.2)

– статическая крутизна:

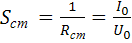, (1.3)

– дифференциальное сопротивление:

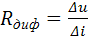, (1.4)

– дифференциальная крутизна:

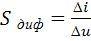. (1.5)

Статическая крутизна пропорциональна тангенсу угла α, а динамическая тангенсу угла β – угла наклона касательной ВАХ в рабочей точке.

Замена истинной (реальной) ВАХ приближенно представляющей функцией называется аппроксимацией характеристики.

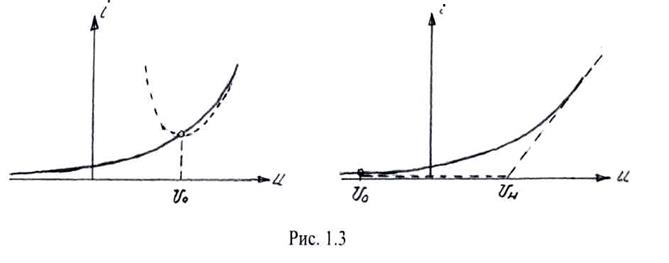
Степенная аппроксимация – представление ВАХ в виде ряда Тейлора в окрестности рабочей точки (I₀, U₀):

i=f(u)=a₀+a₁(u-U₀)+a₂(u-U₀)²+… (1.6)

Кусочно-линейная аппроксимация – представление ВАХ отрезками прямых с различными наклонами. На практике ограничиваются двумя отрезками:

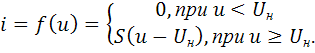(1.7)

Здесь 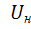– напряжение начала характеристики;

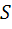– крутизна наклона характеристики;

Аппроксимации (1.6) и (1.7) показаны на Рис. 1.3.

1.2. Анализ преобразования гармонического сигнала НЭ при степенной аппроксимации ВАХ

На Рис. 1.4 изображены ВАХ нелинейного элемента, график входного сигнала:

u(t)=U₀+U_mcosω₀t, (1.8)

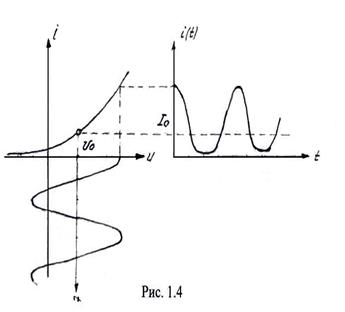и график выходного сигнала (тока, протекающего через НЭ). Форма тока существенно отличается от формы напряжения приложенного к нему. Воспользуемся степенной аппроксимацией ВАХ, ограничившись слагаемым третьей степени. Подставляя (1.8) в (1.6) и используя тригонометрические соотншения:

,

.

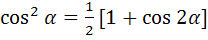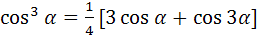получим выражение для тока, протекающего через нелинейный элемент:

i(t)=I₀+I₁cosω₀t+I₂cos2ω₀t+ I₃cos3ω₀t+…, (1.9)

где 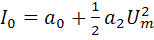; ; 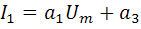; 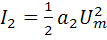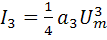(1.10)

Ток, протекающий через НЭ, содержит постоянную составляющую 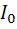и совокупность гармоник, количество которых определяется наибольшей степенью аппроксимирующего полинома. При этом амплитуды четных гармоник определяются четными коэффициентами аппроксимирующего полинома, а нечетных гармоник – нечетными коэффициентами.

Анализ преобразования суммы двух гармонических сигналов при степенной аппроксимации ВАХ полиномом второй степени:

i=a₀+a₁(u—U₀)+a₂(u—U₀)². (1.11)

Входным сигналом в этом случае является колебание:

u(t)=U₀+U_m1cosω₁t+U_m2cosω₂t. (1.12)

Подстановка (1.12) в (1.11) и использование ранее приведенных тригонометрических соотношений и соотношения:

,

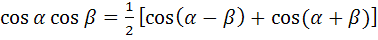дает выражение для тока, протекающего через НЭ:

i(t)=I₀+I₁₁cosω₁t+I₁₂cosω₂t+I₂₁cos2ω₁t+I₂₂cos2ω₂t+

I_pcos(ω₁ – ω₂)t+ I_ccos(ω₁ + ω₂)t, (1.13)

где: ]; ; ; ; ; ;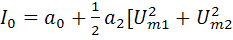

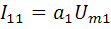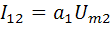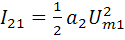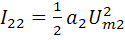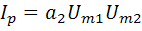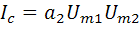. (1.14)

В этом случае ток, протекающий через НЭ содержит постоянную составляющую 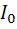, гармоники кратных частот ω₁ , ω₂ , 2ω_{1 ,} 2ω₂ с амплитудами соответственно 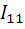, , 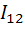, 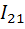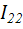и гармоники комбинационных частот: разностной частоты ω_p= ω₁ – ω₂ с амплитудой 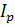и суммарной частоты ω_с= ω₁ + ω₂ с амплитудой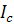

1.3. Анализ преобразования гармонического сигнала НЭ при кусочно-линейной аппроксимации ВАХ

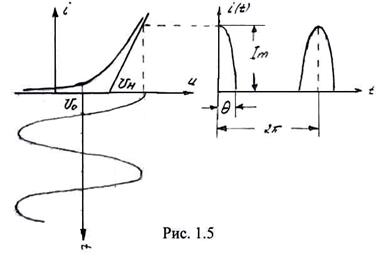При кусочно-линейной аппроксимации вольт-амперная характеристика описывается выражением (1.7). Так же, как и в предыдущем случае, входной сигнал представляет собой сумму напряжения смещения U₀ и гармонического сигнала (выражение 1.8).

На Рис. 1.5 изображена вольт-амперная характеристика, а также графики входного сигнала и тока, протекающего через нелинейный элемент.

Ток, протекающий через НЭ имеет вид периодической последовательности импульсов косинусоидальной формы, ограниченных по амплитуде.

Подстановка (1.8) в (1.7) дает следующее выражение для тока:

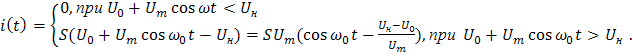(1.15)

Вводится специальный параметр – угол отсечки θ, определяемый из соотношения:

.

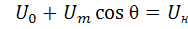Откуда:

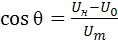. (1.16)

В соответствии с этим величина 2θ равна длительности одного импульса, выраженного в угловой мере, т.е. ωτ_и = 2θ.

Для определения спектрального состава тока необходимо провести разложение периодической последовательности косинусоидальных импульсов в ряд Фурье, которое приводит к следующему результату:

i(t)=I₀+I₁cosω₀t+ I₂cos2ω₀t+…+ I_kcoskω₀t ,

где I₀=SU_mγ₀(θ), I₁=SU_mγ₁(θ), I₂=SU_mγ₂(θ) , … , I_k=SU_mγ_k(θ), — амплитуды соответствующих гармоник,

γ₀(θ), γ₁(θ), γ₂(θ), … , γ_k(θ), – функции Берга.

Значения функций Берга рассчитаны для различный значений K и Θ и сведены в таблицу (табулированы).

Зависимости γ_k(θ) показывают, как изменяется амплитуда к-той гармоники тока, если амплитуда входного сигнала постоянна, а угол отсечки изменяется за счет изменения напряжения смещения .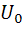

Для получения наибольшей амплитуды желаемой гармоники тока необходимо обеспечить оптимальный угол отсечки. Так, например для второй гармоники при 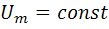, оптимальный угол отсечки Θ=90⁰.

3.1.     Нелинейный элемент и воздействие на него единичного сигнала

Нелинейный элемент

Нелинейным элементом  называют элемент, параметры которого зависят от протекающего через него тока или от приложенного к нему напряжения. Типичными нелинейными элементами являются диод и транзистор. Их параметры существенно изменяются при воздействии рабочих токов и напряжений.

Ранее рассматривались линейные элементы, параметры которых не зависят от протекающего тока и приложенного напряжения. Например, в рабочем диапазоне напряжений и токов такие радиоэлементы, как резисторы и конденсаторы, считаются линейными элементами. На рис. 3.1 приведены вольт-амперные характеристики (ВАХ) нелинейного (1) и линейного (2) резисторов. Только при воздействии малых напряжений нелинейные элементы можно приб­лиженно заменять линейными элементами. Например, характеристики  диодов  и  транзисторов  линеаризуются,  если  воздействует напряжение DU < 0,1 В.

Отметим, что кроме линейных и нелинейных элементов использу­ются параметрические элементы, параметры которых зависят от вре­мени. Некоторые свойства параметрических элементов близки к свой­ствам нелинейных элементов, так как на практике изменений параметров добиваются подачей дополнительных сигналов на пара­метрический элемент, и параметры параметрических элементов в ито­ге оказываются зависимыми от напряжений или токов в цепи.

Если в цепи, кроме линейных элементов, содержатся нелинейные резисторы и (или) нелинейные конденсаторы и (или) нелинейные катушки, то такая цепь называется нелинейной. Процессы в такой цепи в общем случае описываются нелинейным дифференциальным урав­нением. Общих аналитических методов решения этих уравнений не существует. Как правило, эти уравнения решают на ЭВМ с помощью численных методов. Например, с помощью численных методов анали­зируются нелинейные цепи в программах схемотехнического модели­рования.

Основные явления, свойственные любой нелинейной цепи, не обя­зательно изучать, составляя и решая сложные нелинейные дифферен­циальные уравнения. Общие свойства нелинейной цепи будут прояв­ляться в простых цепях, содержащих один нелинейный резистор. Кстати, простые нелинейные цепи наиболее часто используются в ра­диоэлектронике. Для их анализа используют один из аналити­ческих методов – метод тригонометрических формул.

В соответствии с методом тригонометрических формул вольт-амперную характеристику нелинейного резистора аппроксимируем полиномом:

,                                            (3.1)

где коэффициенты а_i (i = 0, 1, 2, …, n) зависят от вида ВАХ.

Пусть к нелинейному элементу приложено гармоническое напря­жение  Для простоты начальная фаза этого напря­жения выбрана равной нулю. Подставляя это напряжение в формулу (3.1), получим ток, протекающий через нелинейный элемент:

Используя известные тригонометрические формулы:

перепишем выражение для тока в виде суммы постоянной состав­ляющей и гармоник тока с кратными частотами (в виде ряда Фурье):

(3.2)

где

Из анализа выражения (3.2) следует общее свойство нелинейных це­пей – порождать в спектре выходного сигнала новые частоты, кото­рых не было в спектре входного сигнала. Номер наивысшей гармони­ки в спектре выходного сигнала соответствует степени аппроксимирующего полинома.

Как известно, сумма гармоник различных, но кратных частот об­разует периодический сигнал, форма которого отличается от формы гармонического колебания. Следовательно, в нелинейных цепях в об­щем случае искажается форма сигнала. Гармонический сигнал при этом становится негармоническим, треугольный сигнал может стать трапецеидальным и т.п.

На рис. 3.2 показаны спектры входного (рис. 3.2, а) и выходного (рис. 3.2, б) сигналов нелинейной цепи, описываемой полиномом треть­ей степени. Как видим, в выходном сигнале появилась по
стоянная со­ставляющая, а также вторая и третья гармоники. Отметим, что воз­никновение новых гармоник, которых не было во входном сигнале, не нарушает законов причинности и сохранения энергии.

Новые частоты, постоянную составляющую и вторую гармонику, можно получить с помощью параметрического элемента – аналогового перемножителя, подавая на него управляющий гармонический сигнал с частотой, точно равной частоте приложенного к элементу входного напряжения.

Свойство нелинейных цепей порождать новые гармоники и иска­жать форму сигнала широко используется в радиоэлектронике при создании разнообразных устройств. Рассмотрим некоторые из этих устройств, наиболее часто встречающиеся на практике.

Нелинейный усилитель

Нелинейный усилитель – это усилитель на работающем в нели­нейном режиме транзисторе, имеющий увеличенный коэффициент полезного действия (рис. 3.3).

Отличительной особенностью схемы является отсутствие по­стоянного напряжения смещения на базе транзистора. Поэтому тран­зистор при отсутствии входного сигнала будет закрыт, и его постоянные токи базы, коллектора и эмиттера будут практически рав­ны нулю. Транзистор будет открываться только при подаче положи­тельной полуволны большого по амплитуде входного напряжения (амплитуда должна быть много больше 0,1 В). Отметим, что в некото­рых нелинейных усилителях может использоваться источник напря­жения смещения. В этом случае напряжение выбирается или запи­рающим, или небольшим открывающим.

Работа нелинейного усилителя описывается с помощью диаграм­мы токов и напряжений (рис. 3.4). На рис. 3.4, а приведена передаточная ВАХ транзистора. Зависимость от времени напряжения на базе транзистора приведена на рис. 3.4, в. Это гармоническое напря­жение поступило через разделительный конденсатор с входных зажи­мов каскада. Как видим, только положительные полуволны вход­ного напряжения открывают транзистор.

Зависимость возникающего тока коллектора от времени (рис. 3.4, б) получена на основе кривых рис. 3.4, а и 3.4, в. Последовательность построения пока­зана стрелками. Ток коллектора, протекая по резистору R_Н (см. рис. 3.3), создает на коллекторе транзистора переменное напряжение (рис. 3.4, г). Отме­тим, что при увеличении тока коллектора напряжение на коллекторе уменьшается, так как увеличивается падение напряжения на резисторе R_Н. Этим объясняется эффект инвертирования фазы сигнала, возни­кающий в каскадах ОЭ.

Форма напряжения на коллекторе транзистора существенно отли­чается от формы гармонического входного сигнала. В этих искажени­ях формы сигнала проявляется свойство нелинейных цепей, обуслов­ленное возникновением в токе транзистора дополнительных гармоник. Для уменьшения искажений используют двухтактную схе­му. В схеме используются два транзистора разных типов, ра­ботающие на общую нагрузку. Причем если транзистор типа п-р-п от­крывается при подаче положительной полуволны напряжения, то другой, р-п-р-транзистор, открывается при подаче отрицательной по­луволны входного напряжения.

Основное преимущество нелинейного усилителя – увеличенный коэффициент полезного действия (КПД). Увеличение КПД объясняется тем, что существенную часть времени транзистор в работающем нелинейном усилителе закрыт и не потребляет энергии от источника питания.

Нелинейные усилители используются в автогенераторах (напри­мер, в импульсных источниках питания ЭВМ), в усилителях мощности (например, в мощных усилителях звуковой частоты), в качестве усилителей-ограничителей, в передатчиках и т.д.

Умножитель частоты

Умножитель частоты – это нелинейное устройство, частота на выходе которого в несколько раз больше частоты входного сигнала. В умножителе частоты используется свойство нелинейных элементов – порождать гармоники с частотами, кратными частоте входного сигна­ла.

Простейшая схема умножителя частоты строится на основе схемы резонансного усилителя (рис. 3.5). При подаче на вход каскада гармо­нического сигнала с большой амплитудой в составе тока коллектора транзистора возникают гармоники с частотами, в целое число раз превышающими частоту входного сигнала. Резонансный контур (нагрузку каскада) настраивают на частоту одной из в
ысших гармоник. На этой частоте в контуре возникает резонанс, а на колебательном контуре и на выходе каскада появляется гармоническое напряжение, частота которого в целое число раз больше частоты входного сигнала. Отметим, что полоса пропускания контура должна быть достаточно малой, чтобы выделялась только одна высшая гармоника.

Расчет выходного напряжения умножителя частоты проводится по формуле:

,

где  – комплексное сопротивление параллельного колебательного контура,  – амплитуда n-й гармоники тока коллектора транзистора. При точной настройке параллельного контура на частоту выделяемой гармоники получим:  так как реактивное сопротивление катушки индуктивности компенсируется реактивным сопротивлением конденсатора контура.

Умножение частоты в два раза можно получить, используя параметрическую цепь (аналоговый перемножитель) и подавая гармонический сигнал одновременно на оба входа перемножителя. Умножители частоты широко используются в компьютерах для получения увеличенных тактовых частот при использовании относительно низкочастотного задающего кварцевого генератора.

Лекция №31

6

ЛЕКЦИЯ №31

4. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

4.1. Общая характеристика нелинейных цепей

Электрические цепи, параметры которых зависят от тока или напряжения, называются нелинейными. Процессы в таких цепях описываются нелинейными дифференциальными уравнениями, к которым неприменим принцип наложения. Общих методов решения нелинейных уравнений не существует. Лишь для небольшого числа частных случаев могут быть найдены точные решения.

Нелинейности могут быть как полезными, так и вредными. В области передачи и преобразования энергии примерами отрицательных нелинейных эффектов могут служить: насыщение магнитопроводов электрических машин и связанные с этим искажения формы кривых тока и напряжения, увеличение тока холостого хода и потерь в стали. Положительная роль нелинейностей проявляется в таких важнейших электротехнических устройствах, как стабилизаторы, преобразователи частоты, выпрямители, статические генераторы и др.

Физические процессы, определяющие характеристики нелинейных элементов, часто настолько сложны, что не удается установить аналитическое выражение этих характеристик и получить уравнения, описывающие цепь. В этом случае, чаще всего на основе экспериментальных данных, приходится прибегать к приближенному аналитическому или графическому выражению нелинейных зависимостей. При этом важным моментом является рациональное упрощение или идеализация.

4.2. Примеры нелинейных элементов и их вольтамперных характеристик

Зарисуем некоторые типы наиболее часто встречающихся вольтамперных характеристик неуправляемых нелинейных элементов (рис. 4.1).

Вольтамперные характеристики типа показанных на рис. 4.1а имеют, например, лампы накаливания с металлической нитью. Чем больше протекающий через них ток, тем сильнее нагревается нить и тем больше становится ее сопротивление.

Вольтамперные характеристики типа показанных на рис. 4.1б имеют тиритовые и вилитовые сопротивления, некоторые типы терморезисторов и лампы накаливания с угольной нитью. Сопротивление таких элементов с ростом тока уменьшается.

Вольт-амперной характеристикой типа, изображенной рис. 4.1в, обладает бареттер, который используется в цепях стабилизации тока накала электронных ламп.

Для этих характеристик справедливо условие: f(I) = – f(–I). Такие нелинейные элементы называются элементами с симметричной вольт-амперной характеристикой.

Вольтамперная характеристика, представленная на рис. 4.1г несимметрична. Ею обладают полупроводниковые диоды. На рис. 4.1д изображена вольтамперная характеристика туннельного диода, на рис. 4.1е – вольтамперная характеристика динистора (неуправляемого тиристора).

4.3. Основные явления в нелинейных цепях и их особенности

В нелинейных цепях могут быть получены явления принципиально недостижимые в линейных цепях. Более того, на нелинейности цепи основывается принцип действия устройства.

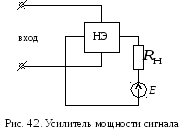
С помощью нелинейного элемента возможно усиление мощности сигнала (рис. 4.2).

Нелинейный элемент включен в цепь нагрузки R_н и источника ЭДС E достаточно большой мощности. В зависимости от сопротивления нелинейного элемента в сопротивлении R_н будет меняться ток и, соответственно, выделяемая мощность. Сопротивлением нелинейного элемента управляет входной сигнал, обычно имеющий много меньшую мощность.

При определенном соотношении параметров нелинейной цепи могут возникнуть самовозбуждающиеся колебания (автоколебания). Выходное напряжение или ток при этом будут иметь заданную форму. Следовательно, можно генерировать сигналы.

Напряжение на некоторых нелинейных элементах слабо зависит от величины протекающего тока, или наоборот ток практически не зависит от приложенного напряжения. На таких элементах можно получить стабилизацию напряжения или тока.

С помощью нелинейных элементов можно получать функциональные преобразования, т.е. получать определенную зависимость между входной и выходной величинами, например, U₁ = k lg U₂. Так характеристика полупроводникового диода в прямом направлении выражается зависимостью U_д = a lg I_д.

При плавном изменении входной величины может происходить скачкообразное изменение выходной величины. Возникает так называемый релейный эффект. Примером могут служить триггеры.

Гистерезисные явления в нелинейных элементах дают возможность запоминать сигнал. В качестве примера можно привести запоминающие устройства на основе явления остаточного магнетизма, триггеры Шмидта.

При питании нелинейного элемента от источника синусоидальной ЭДС возникают токи различных частот, которые можно выделить и использовать в качестве вторичных источников других частот, т.е. производить спектральное изменение входного сигнала.

4.4. Статические, дифференциальные,

динамические и эквивалентные параметры нелинейных элементов

У нелинейных элементов нет прямой пропорциональности между током и напряжением, поэтому нельзя пользоваться известными понятиями сопротивления, индуктивности и емкости. Нелинейные элементы нельзя охарактеризовать одним параметром.

Если рассматривать безынерционный нелинейный элемент, то его статическая вольтамперная характеристика, снятая при постоянном токе и напряжении, совпадает с динамической характеристикой, отображающей связь между мгновенными значениями тока и напряжения. В этом случае нелинейный элемент характеризуется двумя параметрами: статическим сопротивлением

R_ст = u/I (4.1)

и дифференциальным сопротивлением

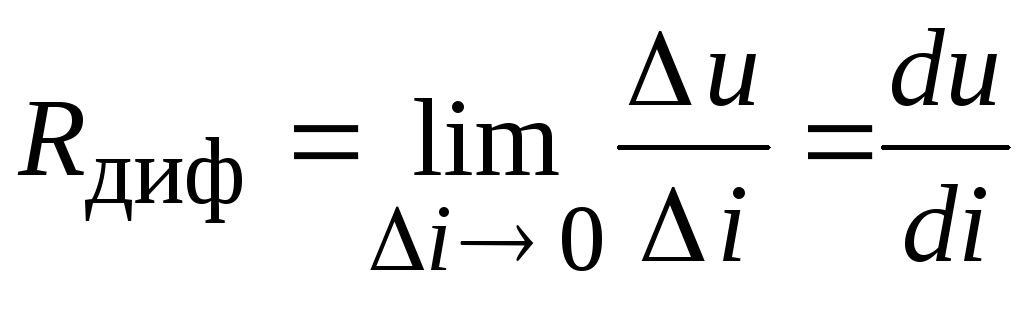. (4.2)

На рис. 4.3 показано, как по статической ВАХ определяются параметры нелинейного элемента.

Графически R_ст определяется тангенсом угла , а R_диф – тангенсом угла . На графике:

А – рабочая точка;

прямая К – касательная к вольт-амперной характеристике в точке А;

прямая С – секущая, проходящая через начало координат и точку А.

Рис. 4.3. Характеристика для определения параметров

нелинейного элемента

Статическое и дифференциальное сопротивления не равны друг другу и зависят от положения рабочей точки на вольт-амперной характеристике. статическое сопротивление у неуправляемого элемента всегда конечно и положительно. Дифференциальное сопротивление может равняться нулю (точка В), бесконечности и даже становиться отрицательной (на падающем участке BC).

В случае инерционного нелинейного элемента соотношение между током и напряжением в общем виде зависит не только от соотношения их величин, но и от их производных и интегралов по времени. Поэтому вводят понятие о динамическом сопротивлении, которое является сопротивлением для переменной составляющей тока. Если период переменного тока очень мал по сравнению с постоянной времени изменения величины нелинейного элемента, то динамическое сопротивление будет равно статическому (R_дин = R_ст). А если период велик – то дифференциальному (R_дин = R_диф).

В общем случае форма кривой напряжения нелинейного элемента отличается от формы кривой тока, что сильно усложняет анализ и расчет цепей с нелинейными элементами. Иногда целесообразно ради упрощения полагать токи и напряжения синусоидальными. Это позволяет применить для анализа и расчета мощные линейные методы, например, комплексный. При этом реальные несинусоидальные токи и напряжения заменяют эквивалентными синусоидальными. Вводят понятие об эквивалентных сопротивлениях R_э, X_Lэ, X_Cэ и эквивалентных (динамических) параметрах R_э, L_э, C_э. Эквивалентные параметры – это тем или иным способом усредненные динамические параметры. Часто пользуются эквивалентными величинами, определяемыми по действующим значениям тока и напряжения:

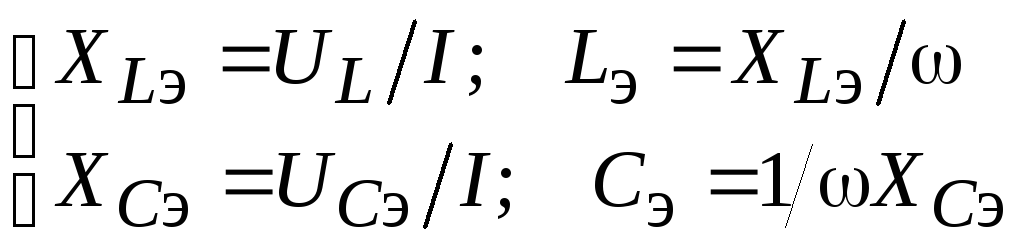. (4.3)

39.Классификация нелинейных элементов

Нелинейным элементом электрической цепи считается элемент, значения параметров которого зависят от значения тока данного элемента или напряжения на его выводах.

К нелинейным элементам электрических целей относятся разнообразные электронные, полупроводниковые и ионные приборы, устройства, содержащие намагничивающие обмотки с ферромагнитными магнитопроводами (при переменном токе), лампы накаливания, электрическая дуга и др.

Нелинейные элементы можно разделить: Нелинейные элементы можно разделить на двух – и многополюсные, можно разделить на инерционные и безынерционные. Инерционными называются элементы, характеристики которых зависят от скорости изменения переменных. Для таких элементов статические характеристики, определяющие зависимость между действующими значениями переменных, отличаются от динамических характеристик, устанавливающих взаимосвязь между мгновенными значениями переменных. Безынерционными называются элементы, характеристики которых не зависят от скорости изменения переменных. Для таких элементов статические и динамические характеристики совпадают. В зависимости от вида характеристик различают нелинейные элементы с симметричными и  несимметричными характеристиками. Наконец, все нелинейные элементы можно разделить на управляемые и неуправляемые. В отличие от неуправляемых управляемые нелинейные элементы (обычно трех- и многополюсники) содержат управляющие каналы, изменяя напряжение, ток, световой поток и др. в которых, изменяют их основные характеристики: вольт-амперную, вебер-амперную или кулон-вольтную.

40.Характеристики нелинейных элементов, статистические и дифференциальные параметры.

Типичными динамическими нелинейными элементами электрической цепи являются катушки с сердечниками из ферромагнитных материалов. Их нелинейность обусловлена характеристикой намагничивания материала сердечника В(Н). Вольтамперные характеристики нелинейных резисторов обычно монотонны, и с ростом приложенного напряжения ток резистора увеличивается. Однако существуют элементы с немонотонными на отдельных участках характеристиками, у которых с ростом напряжения ток уменьшается. К ним относится, например, туннельный диод, имеющий N-образную характеристику (рис. 27.2, а), а также динистор или неоновая лампа с S-образной характеристикой (рис. 27.2, б). Такая особенность характеристики проводит к тому, что у элементов первого типа в некотором интервале одному и тому же току отвечают три различных значения напряжения, т. е. зависимость и(i) не однозначна. Их зависимость i(u) однозначна, и такие элементы и характеристики (см. рис. 27.2, а) называются управляемыми напряжением. Элементы с S-образной характеристикой, наоборот, называются управляемыми током — они имеют однозначную зависимость и(i), а обратная функция i(и) неоднозначна.

Рис. 27.2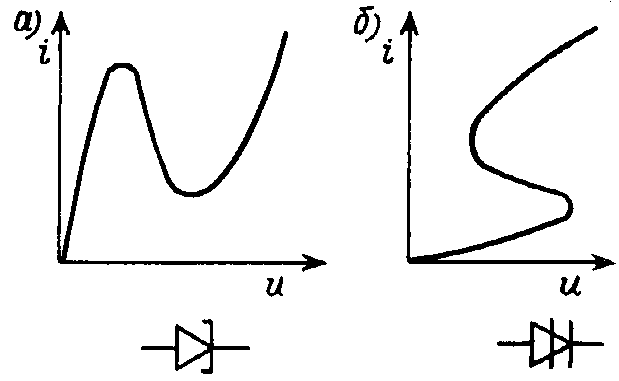

Различают статические и дифференциальные параметры нелинейных элементов. Статическое сопротивление R_ст = u/i, дифференциальное сопротивление R_д = du/di и проводимости G_ст = i/u и G_д = di/du нелинейных элементов являются функциями тока в элементе. Падающему участку немонотонных характеристик (см. рис. 27.2) отвечают отрицательные значения дифференциальных параметров (R_д < 0, G_д < 0). Статические сопротивления и проводимости нелинейных элементов в общем случае не равны соответствующим дифференциальным параметрам. У линейного элемента оба параметра совпадают.