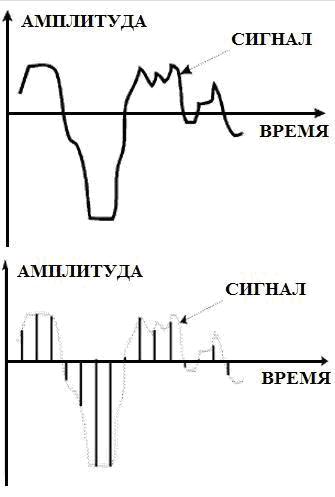
Урок 8.1 — Аналоговые и цифровые сигналы

8. Основы цифровой схемотехники

Цифровая схемотехника – важнейшая дисциплина, которую изучают во всех высших и средних учебных заведениях, готовящих специалистов в электронике. Настоящий радиолюбитель тоже должен хорошо разбираться в этом вопросе. Но большинство книг и учебных пособий написаны очень сложным для понимания языком, и начинающему электронщику (возможно, школьнику) будет тяжело освоить новую информацию. Цикл новых обучающих материалов от Мастер Кит призван восполнить этот пробел: в наших статьях о сложных понятиях рассказывается самыми простыми словами.

8.1. Аналоговые и цифровые сигналы

Сначала надо разобраться, чем вообще аналоговая схемотехника отличается от цифровой. И главное отличие – в сигналах, с которыми работают эти схемы.
Все сигналы можно разделить на два основных вида: аналоговые и цифровые.

Аналоговые сигналы

Аналоговые сигналы наиболее привычны для нас. Можно сказать, что весь окружающий природный мир вокруг нас – аналоговый. Наши зрение и слух, а также все остальные органы чувств воспринимают поступающую информацию в аналоговой форме, то есть непрерывно во времени. Передача звуковой информации – речь человека, звуки музыкальных инструментов, рёв животных, звуки природы и т.п. – также осуществляется в аналоговом виде.
Чтобы ещё лучше понять этот вопрос, нарисуем аналоговый сигнал (рис.1.):

 

 

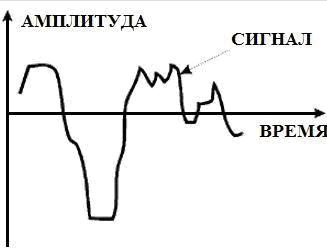
Рис.1. Аналоговый сигнал

Мы видим, что аналоговый сигнал непрерывен во времени и по амплитуде. Для любого момента времени можно определить точное значение амплитуды аналогового сигнала.

 

Цифровые сигналы

Давайте будет анализировать амплитуду сигнала не постоянно, а дискретно, через фиксированные промежутки времени. Например, раз в секунду, или чаще: десять раз в секунду. То, как часто мы будем это делать, называется частотой дискретизации: один раз в секунду – 1 Гц, тысячу раз в секунду – 1000 Гц или 1 кГц.

Для наглядности нарисуем графики аналогового (вверху) и цифрового (внизу) сигналов (рис.2.):

 

Рис.2. Аналоговый сигнал (вверху) и его цифровая копия (внизу)

Мы видим, что в каждый мгновенный промежуток времени можно узнать мгновенное цифровое значение амплитуды сигнала. Что происходит с сигналом (по какому закону он меняется, какова его амплитуда) между интервалами «проверки», мы не знаем, эта информация потеряна для нас. Чем реже мы проверяем уровень сигнала (чем ниже частота дискретизации), тем меньше имеем информации о сигнале. Разумеется, справедливо и обратное: чем выше частота дискретизации, тем лучше качество представления сигнала. В пределе, увеличивая частоту дискретизации до бесконечности, мы получаем практически тот же аналоговый сигнал.
Значит ли это, что аналоговый сигнал в любом случае качественнее цифрового? В теории, пожалуй, да. Но на практике современные аналого-цифровые преобразователи (АЦП) работают с такой высокой частотой дискретизации (до нескольких миллионов выборок в секунду), так качественно описывают аналоговый сигнал в цифровой форме, что органы чувств человека (глаза, уши) уже не могут почувствовать разницу между оригинальным сигналом и его цифровой моделью. Цифровой сигнал обладает очень существенным достоинством: его легче передавать по проводам или радиоволне, помехи не оказывают на такой сигнал существенного влияния. Поэтому вся современная мобильная связь, теле- и радиовещание — цифровая.

Нижний график на рис. 2 легко представить и в другом виде – как длинную последовательность пары цифр: время/амплитуда. А цифры – это как раз то, что нужно цифровым схемам. Правда, цифровые схемы предпочитают работать с цифрами в особом представлении, но об этом мы поговорим в следующем уроке.

Сейчас мы можем сделать важные выводы:

— цифровой сигнал дискретен, его можно определить только для отдельных моментов времени;
— чем выше частота дискретизации – тем лучше точность представления цифрового сигнала.

Виды сигналов — Студопедия

Назначение радиоэлектронных устройств, как известно, — получение, преобразование, передача и хранение информации, представленной в форме электрических сигналов. Сигналы, действующие в электронных устройствах, и соответственно сами устройства делят на две большие группы: аналоговые и цифровые.

Аналоговый сигнал — сигнал, непрерывный по уровню и во времени, т. е. такой сигнал существует в любой момент времени и может принимать любой уровень из заданного диапазона.

Квантованный сигнал — сигнал, который может принимать только определенные квантованные значения, соответствующие уровням квантования. Расстояние между двумя соседними уровнями — шаг квантования.

Дискретизированный сигнал — сигнал, значения которого заданы только в моменты времени, называемые моментами дискретизации. Расстояние между соседними моментами дискретизации — шаг дискретизации

. При постоянном применима теорема Котельникова: , где — верхняя граничная частота спектра сигнала.

Цифровой сигнал — сигнал, квантованный по уровню и дискретизированный во времени. Квантованные значения цифрового сигнала обычно кодируются некоторым кодом, при этом каждый выделенный в процессе дискретизации отсчет заменяется соответствующим кодовым словом, символы которого имеют два значения — 0 и 1 (рис. 2.1).

Типичными представителями устройств аналоговой электроники являются устройства связи, радиовещания, телевидения. Общие требования, предъявляемые к аналоговым устройствам, — минимальные искажения. Стремление выполнить эти требования приводит к усложнению электрических схем и конструкции устройств. Другая проблема аналоговой электроники — достижение необходимой помехоустойчивости, ибо в аналоговом канале связи шумы принципиально неустранимы.

Цифровые сигналы формируются электронными схемами, транзисторы в которых либо закрыты (ток близок к нулю), либо полностью открыты (напряжение близко к нулю), поэтому на них рассеивается незначительная мощность и надежность цифровых устройств получается более высокой, чем аналоговых.

Цифровые устройства более помехоустойчивы, чем аналоговые, так как небольшие посторонние возмущения не вызывают ошибочного срабатывания устройств. Ошибки появляются только при таких возмущениях, при которых низкий уровень сигнала воспринимается как высокий, или наоборот. В цифровых устройствах можно также применить специальные коды, позволяющие исправить ошибки. В аналоговых устройствах такой возможности нет.

Цифровые устройства нечувствительны к разбросу (в допустимых пределах) параметров и характеристик транзисторов и других элементов схем. Безошибочно изготовленные цифровые устройства не нужно настраивать, а их характеристики полностью повторяемы. Все это очень важно при массовом изготовлении устройств по интегральной технологии. Экономичность производства и эксплуатации цифровых интегральных микросхем привела к тому, что в современных радиоэлектронных устройствах цифровой обработке подвергаются не только цифровые, но и аналоговые сигналы. Распространены цифровые фильтры, регуляторы, перемножители и др. Перед цифровой обработкой аналоговые сигналы преобразуются в цифровые с помощью аналого-цифровых преобразователей (АЦП). Обратное преобразование — восстановление аналоговых сигналов по цифровым — выполняется с помощью цифроаналоговых преобразователей (ЦАП).

При всем многообразии задач, решаемых устройствами цифровой электроники, их функционирование происходит в системах счисления, оперирующих всего двумя цифрами: нуль (0) и единица (1).

Работа цифровых устройств обычно тактируется достаточно высокочастотным генератором тактовых импульсов. В течение одного такта реализуется простейшая микрооперация — чтение, сдвиг, логическая команда и т. п. Информация представляется в виде цифрового слова. Для передачи слов используются два способа — параллельный и последовательный. Последовательное кодирование применяется при обмене информацией между цифровыми устройствами (например, в компьютерных сетях, модемной связи). Обработка информации в цифровых устройствах реализуется при использовании параллельного кодирования информации, обеспечивающего максимальное быстродействие.

Элементную базу для построения цифровых устройств составляют интегральные микросхемы (ИМС), каждая из которых реализуется с использованием определенного числа логических элементов — простейших цифровых устройств, выполняющих элементарные логические операции.

Курс лекций «Основы цифровой обработки сигналов» / Хабр

Всем привет!

Часто ко мне обращаются люди с вопросами по задачам из области цифровой обработки сигналов (ЦОС). Я подробно рассказываю нюансы, подсказываю нужные источники информации. Но всем слушателям, как показало время, не хватает практических задач и примеров в процессе познания этой области. В связи с этим я решил написать краткий интерактивный курс по цифровой обработке сигналов и выложить его в открытый доступ.

Большая часть обучающего материала для наглядного и интерактивного представления реализована с использованием Jupyter Notebook. Предполагается, что читатель имеет базовые знания из области высшей математики, а также немного владеет языком программирования Python.

Список лекций

Этот курс содержит материалы в виде законченных лекций по разным тематикам из области цифровой обработки сигналов. Материалы представлены с использованием библиотек на языке Python (пакеты numpy, scipy, matplotlib, и т.д.). Основная информация для этого курса взята из моих лекций, которые я, будучи аспирантом, читал студентам Московского Энергетического Института (НИУ МЭИ). Частично информация из этих лекций была использована на обучающих семинарах в Центре Современной Электроники, где я выступал в качестве лектора. Кроме того, в этот материал входит перевод различных научных статей, компиляция информации из достоверных источников и литературы по тематике цифровой обработки сигналов, а также официальная документация по прикладным пакетам и встроенным функциям библиотек scipy и numpy языка Python.

Для пользователей MATLAB (GNU Octave) освоение материала с точки зрения программного кода не составит труда, поскольку основные функции и их атрибуты во многом идентичны и схожи с методами из Python-библиотек.

Все материалы сгруппированы по основным тематикам цифровой обработки сигналов:

1. Сигналы: аналоговые, дискретные, цифровые. Z-преобразование,
2. Преобразование Фурье: амплитудный и фазовый сигнала, ДПФ и БПФ,
3. Свертка и корреляция. Линейная и циклическая свертка. Быстрая свёртка,
4. Случайные процессы. Белый шум. Функция плотности вероятностей,
5. Детерминированные сигналы. Модуляция: АМ, ЧМ, ФМ, ЛЧМ. Манипуляция,
6. Фильтрация сигналов: БИХ, КИХ фильтры,
7. Оконные функции в задачах фильтрации. Детектирование слабых сигналов,
8. Ресемплинг: децимация и интерполяция. CIC-фильтры, фильтры скользящего среднего,
9. Непараметрические методы спектрального анализа,
10. Усреднение по частоте и по времени. Полифазный БПФ.

Список лекций — достаточный но, разумеется, неполный для вводного знакомства с областью ЦОС. При наличии свободного времени я планирую поддерживать и развивать этот проект.

Где найти?

Все материалы — абсолютно бесплатны и доступны в виде открытого репозитория на моем гитхабе как opensource проект. Материалы представлены в двух форматах — в виде тетрадок Jupyter Notebook для интерактивной работы, изучения и редактирования, и в виде скомпилированных из этих тетрадок HTML-файлов (после скачивания с гитхаба имеют вполне пригодный формат для чтения и для печати).

Ниже приводится очень краткое описание разделов курса с небольшими пояснениями, терминами и определениями. Основная информация доступна в исходных лекциях, здесь представлен лишь краткий обзор!

Сигналы. Z-преобразование

Вводный раздел, в котором содержится основная информация по типам сигналов. Вводится понятие дискретной последовательности, дельта-функции и функции Хевисайда (единичный скачок).

Все сигналы по способу представления на множестве можно разделить на четыре группы:

• аналоговые — описываются непрерывными во времени функциями,
• дискретные — прерываются во времени с шагом заданным дискретизации,
• квантованные — имеют набор конечных уровней (как правило, по амплитуде),
• цифровые — комбинация свойств дискретных и квантованных сигналов.

Для правильного восстановления аналогового сигнала из цифрового без искажений и потерь используется теорема отсчетов, известная как Теорема Котельникова (Найквиста-Шеннона).

Любой непрерывный сигнал с ограниченным спектром может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой строго больше удвоенной верхней частоты спектра непрерывного сигнала.

Такая трактовка справедлива при условии, что непрерывная функция времени занимает полосу частот от 0 до значения верхней частоты. Если шаг квантования и дискретизации выбраны неправильно, преобразование сигнала из аналоговой формы в дискретную будет происходить с искажениями.

Также в этом разделе описывается Z-преобразование и его свойства, показывается представление дискретных последовательностей в Z-форме.

Пример конечной дискретной последовательности:

x(nT) = {2, 1, -2, 0, 2, 3, 1, 0}

.
Пример этой же последовательности в Z-форме:

X(z) = 2 + z^-1 — 2z^-2 + 2z^-4 + 3z^-5 + 1z^-6

Преобразование Фурье. Свойства. ДПФ и БПФ

В этом разделе описывается понятие временной и частотной области сигнала. Вводится определение дискретного преобразования Фурье (ДПФ). Рассмотрены прямое и обратное ДПФ, их основные свойства. Показан переход от ДПФ к алгоритму быстрого преобразования Фурье (БПФ) по основанию 2 (алгоритмы децимации по частоте и по времени). Отражена эффективность БПФ в сравнении с ДПФ.

В частности, в этом разделе описывается Python пакет scipy.ffpack для вычисления различных преобразований Фурье (синусное, косинусное, прямое, обратное, многомерное, вещественное).

Преобразование Фурье позволяет представить любую функцию в виде набора гармонических сигналов! Преобразование Фурье лежит в основе методов свертки и проектировании цифровых корреляторов, активно применяется при спектральном анализе, используется при работе с длинными числами.

Особенности спектров дискретных сигналов:
1. Спектральная плотность дискретного сигнала – периодическая функция с периодом, равным частоте дискретизации.
2. Если дискретная последовательность вещественная, то модуль спектральной плотности такой последовательности есть четная функция, а аргумент – нечетная функция частоты.

Спектр гармонического сигнала:

Сравнение эффективности ДПФ и БПФ

Эффективность алгоритма БПФ и количество выполняемых операций линейно зависит от длины последовательности N:
Как видно, чем больше длина преобразования, тем больше экономия вычислительных ресурсов (по скорости обработки или количеству аппаратных блоков)!

Любой сигнал произвольной формы можно представить в виде набора гармонических сигналов разных частот. Иными словами, сигнал сложной формы во временной области имеет набор комплексных отсчетов в частотной области, которые называются *гармоники*. Эти отсчеты выражают амплитуду и фазу гармонического воздействия на определенной частоте. Чем больше набор гармоник в частотной области, тем точнее представляется сигнал сложной формы.

Свертка и корреляция

В этом разделе вводится понятие корреляции и свертки для дискретных случайных и детерминированных последовательностей. Показана связь автокорреляционной и взаимнокорреляционной функций со сверткой. Описываются свойства свертки, в частности, рассмотрены методы линейной и циклической свертки дискретного сигнала с подробным разбором на примере дискретной последовательности. Кроме того, показан метод вычисления «быстрой» свертки с помощью алгоритмов БПФ.

В реальных задачах часто ставится вопрос о степени похожести одного процесса на другой или же о независимости одного процесса от другого. Иными словами, требуется определить взаимосвязь между сигналами, то есть найти корреляцию. Методы корреляции используются в широком диапазоне задач: поиск сигналов, компьютерное зрение и обработка изображений, в задачах радиолокации для определения характеристик целей и определения расстояния до объекта. Кроме того, с помощью корреляции производится поиск слабых сигналов в шумах.

Свертка описывает взаимодействие сигналов между собой. Если один из сигналов — импульсная характеристика фильтра, то свертка входной последовательности с импульсной характеристикой есть ни что иное, как реакция цепи на входное воздействие. Иными словами, результирующий сигнал отражает прохождение сигнала через фильтр.

Автокорреляционная функция (АКФ) находит применение в кодировании информации. Выбор кодирующей последовательности по параметрам длины, частоты и формы во многом обусловлен корреляционными свойствами этой последовательности. Наилучшая кодовая последовательность обладает наименьшим значением вероятности ложного обнаружения или срабатывания (для детектирования сигналов, для пороговых устройств) или ложной синхронизации (для передачи и приема кодовых последовательностей).

В этом разделе представлена таблица сравнения эффективности быстрой свертки и свертки, вычисляемой по прямой формуле (по числу вещественных умножений).

Как видно, для длин БПФ до 64, быстрая свёртка проигрывает у прямого метода. Однако, при увеличении длины БПФ результаты меняются в обратную сторону — быстрая свертка начинает выигрывать у прямого метода. Очевидно, чем больше длина БПФ, тем лучше выигрыш частотного метода.

Случайные сигналы и шум

В этом разделе вводится понятие случайных сигналов, плотности распределения вероятностей, закона распределения случайной величины. Рассматриваются математические моменты — среднее (математическое ожидание) и дисперсия (или корень этой величины — среднеквадратическое отклонение). Также в этом разделе рассматривается нормальное распределение и связанное с ним понятие белого шума, как основного источника шумов (помех) при обработке сигналов.

Случайным сигналом называют функцию времени, значения которой заранее неизвестны и могут быть предсказаны лишь с некоторой вероятностью. К основным характеристикам случайных сигналов относятся:

• закон распределения (относительное время пребывания значения сигнала в определенном интервале),
• спектральное распределение мощности сигнала.

В задачах ЦОС случайные сигналы делятся на два класса:

• шумы — беспорядочные колебания, состоящие из набора разных частот и амплитуд,
• сигналы, несущие информацию, для обработки которых требуется прибегать к вероятностным методам.

С помощью случайных величин можно моделировать воздействие реальной среды на прохождение сигнала от источника к приёмнику данных. При прохождении сигнала через какое-то шумящее звено, к сигналу добавляется так называемый белый шум. Как правило, спектральная плотность такого шума равномерно (одинаково) распределена на всех частотах, а значения шума во временной области распределены нормально (Гауссовский закон распределения). Поскольку белый шум физически добавляется к амплитудам сигнала в выбранные отсчеты времени, он называется аддитивный белый гауссовский шум (AWGN — Additive white Gaussian noise).

Сигналы, модуляция и манипуляция

В этом разделе показаны основные способы изменения одного или нескольких параметров гармонического сигнала. Вводятся понятия амплитудной, частотной и фазовой модуляции. В частности, выделяется линейная частотная модуляция, применяемая в задачах радиолокации. Показаны основные характеристики сигналов, спектры модулированных сигналов в зависимости от параметров модуляции.

Для удобства на языке Python создан набор функций, осуществляющих перечисленные виды модуляции. Пример реализации ЛЧМ-сигнала:

def signal_chirp(amp=1.0, freq=0.0, beta=0.25, period=100, **kwargs):
    """
    Create Chirp signal

    Parameters
    ----------
    amp : float
        Signal magnitude
    beta : float
        Modulation bandwidth: beta < N for complex, beta < 0.5N for real
    freq : float or int
        Linear frequency of signal
    period : integer
        Number of points for signal (same as period)
    kwargs : bool
        Complex signal if is_complex = True
        Modulated by half-sine wave if is_modsine = True
    """
    is_complex = kwargs.get('is_complex', False)
    is_modsine = kwargs.get('is_modsine', False)

    t = np.linspace(0, 1, period)
    tt = np.pi * (freq * t + beta * t ** 2)
    
    if is_complex is True:
        res = amp * (np.cos(tt) + 1j * np.sin(tt))
    else:
        res = amp * np.cos(tt)

    if is_modsine is True:
        return res * np.sin(np.pi * t)
    return res

Также в этом разделе из теории передачи дискретных сообщений описаны виды цифровой модуляции — манипуляции. Как и в случае с аналоговыми сигналами, цифровые гармонические последовательности могут быть манипулированы по амплитуде, фазе и частоте (либо по нескольким параметрам сразу).

Цифровые фильтры — БИХ и КИХ

Достаточно большой раздел, посвященный вопросам цифровой фильтрации дискретных последовательностей. В задачах цифровой обработки сигналов данные проходят через цепи, которые называются фильтрами. Цифровые фильтры, как и аналоговые, обладают различными характеристиками — частотные: АЧХ, ФЧХ, временная: импульсная характеристика, а также передаточная характеристика фильтра. Цифровые фильтры используются в основном для улучшения качества сигнала — для выделения сигнала из последовательности данных, либо для ухудшения нежелательных сигналов — для подавления определенных сигналов в приходящих последовательностях отсчетов.

В разделе перечислены основные преимущества и недостатки цифровых фильтров (в сравнении с аналоговыми). Вводится понятие импульсной и передаточной характеристик фильтра. Рассматривается два класса фильтров — с бесконечной импульсной характеристикой (БИХ) и конечной импульсной характеристикой (КИХ). Показан способ проектирования фильтров по канонической и прямой форме. Для КИХ фильтров рассматривается вопрос о способе перехода к рекурсивной форме.

Для КИХ фильтров показан процесс проектирования фильтра от стадии разработки технического задания (с указанием основных параметров), до программной и аппаратной реализации — поиска коэффициентов фильтра (с учетом формы представления числа, разрядности данных и т.д.). Вводятся определения симметричных КИХ фильтров, линейной ФЧХ и её связи с понятием групповой задержки.

Оконные функции в задачах фильтрации

В задачах цифровой обработки сигналов используются оконные функции различной формы, которые при наложении на сигнал во временной области, позволяют качественно улучшить его спектральные характеристики. Большое количество всевозможных окон обусловлено в первую очередь одной из главных особенностей любого оконного наложения. Эта особенность выражается во взаимосвязи уровня боковых лепестков и ширины центрального лепестка. Правило:

Чем сильнее подавление боковых лепестков спектра, тем шире главный лепесток спектра и наоборот.

Одно из применений оконных функций: обнаружение слабых сигналов на фоне более сильных путём подавления уровня боковых лепестков. Основные оконные функции в задачах ЦОС — **треугольное, синусоидальное, окно Ланцоша, Ханна, Хэмминга, Блэкмана, Харриса, Блэкмана-Харриса, окно с плоской вершиной, окно Наталла, Гаусса, Кайзера** и множество других. Большая часть из них выражена через конечный ряд путём суммирования гармонических сигналов с определенными весовыми коэффициентами. Такие сигналы отлично реализуются на практике на любых аппаратных устройствах (программируемые логические схемы или сигнальные процессоры).

Ресемплинг. Децимация и интерполяция

В этом разделе рассматриваются вопросы многоскоростной обработки сигналов — изменения частоты дискретизации. Многоскоростная обработка сигналов (multirate processing) предполагает, что в процессе линейного преобразования цифровых сигналов возможно изменение частоты дискретизации в сторону уменьшения или увеличения, либо в дробное число раз. Это приводит к более эффективной обработке сигналов, так как открывается возможность использования минимально допустимых частот дискретизации и, как следствие, значительного уменьшения требуемой вычислительной производительности проектируемой цифровой системы.

Децимация (прореживание) – понижение частоты дискретизации. Интерполяция – повышение частоты дискретизации.

Также в разделе рассматривается класс однородных КИХ фильтров, которые называются интегрально-гребенчатыми фильтрами (CIC, Cascaded integrator–comb). Показана реализация, основные свойства и особенности CIC фильтров. В силу линейности математических операций, происходящих в CIC фильтре возможно каскадное соединение нескольких фильтров подряд, что дает пропорциональное уменьшение уровня боковых лепестков, но также увеличивает «завал» главного лепестка амплитудно-частотной характеристики.

График АЧХ фильтра в зависимости от коэффициента децимации:

Также в этом разделе обсуждается вопрос увеличения разрядности данных на выходе CIC фильтра в зависимости от его параметров. Это особенно важно в задачах программной реализации, в частности на ПЛИС.

Для практической реализации CIC фильтров на Python разработан отдельный класс CicFilter, реализующий методы децимации и интерполяции. Также показаны примеры изменения частоты дискретизации с помощью встроенных методов из scipy пакета Python.

Python CicFilter Class for Digital Signal Processing

class CicFilter:
    """
    Cascaded Integrator-Comb (CIC) filter is an optimized class of
    finite impulse response (FIR) filter.
    CIC filter combines an interpolator or decimator, so it has some
    parameters:

    R - decimation or interpolation ratio,
    N - number of stages in filter (or filter order)
    M - number of samples per stage (1 or 2)*

    * for this realisation of CIC filter just leave M = 1.

    CIC filter is used in multi-rate processing. In hardware
    applications CIC filter doesn't need multipliers, just only
    adders / subtractors and delay lines.

    Equation for 1st order CIC filter:
    y[n] = x[n] - x[n-RM] + y[n-1].


    Parameters
    ----------
    x : np.array
        input signal
    """

    def __init__(self, x):
        self.x = x

    def decimator(self, r, n):
        """
        CIC decimator: Integrator + Decimator + Comb

        Parameters
        ----------
        r : int
            decimation rate
        n : int
            filter order
        """

        # integrator
        y = self.x[:]
        for i in range(n):
            y = np.cumsum(y)

        # decimator

        y = y[::r]
        # comb stage
        return np.diff(y, n=n, prepend=np.zeros(n))

    def interpolator(self, r, n, mode=False):
        """
        CIC inteprolator: Comb + Decimator + Integrator

        Parameters
        ----------
        r : int
            interpolation rate
        n : int
            filter order
        mode : bool
            False - zero padding, True - value padding.
        """

        # comb stage
        y = np.diff(self.x, n=n,
                    prepend=np.zeros(n), append=np.zeros(n))

        # interpolation
        if mode:
            y = np.repeat(y, r)
        else:
            y = np.array([i if j == 0 else 0 for i in y for j in range(r)])

        # integrator
        for i in range(n):
            y = np.cumsum(y)

        if mode:
            return y[1:1 - n * r]
        else:
            return y[r - 1:-n * r + r - 1]

Наконец, в этом разделе приведен особый класс фильтров — скользящего среднего. Показано три способа реализации: через свертку сигналов, с помощью КИХ-фильтра и БИХ-фильтра.

Заключение

Надеюсь, этот курс лекций в совокупности с моими предыдущими статьями по цифровой обработке сигналов на ПЛИС принесет практическую пользу и поможет читателю лучше понять основы цифровой обработки сигналов. Этот проект будет улучшаться и дополняться новым полезным и не менее интересным материалом. Следите за развитием!

Дополнительно к этому материалу я поддерживаю и развиваю свой проект по основным модулям ЦОС (на языке Python). Он содержит пакет генерации различных сигналов, класс CIC фильтров для задач децимации и интерполяции, алгоритм расчета коэффициентов корректирующего КИХ-фильтра, фильтр скользящего среднего, алгоритм вычисления сверх-длинного БПФ через методы двумерного преобразования (последнее очень пригодилось в работе при аппаратной реализации на ПЛИС).

UPD: 20.04.2020

В курс добавлено две лекции:

1. Непараметрические методы спектрального анализа (Владимир Фадеев)
2. Усреднение по частоте и по времени. Полифазный БПФ.

TODO:

1. Вейвлет анализ
2. STFT, мел-спектрограммы, преобразование Гриффина-Лима

Спасибо за внимание!

Отличия аналогового звука от цифрового / Блог компании Soundpal / Хабр

Очень часто мы слышим такие определения, как «цифровой» или «дискретный» сигнал, в чем его отличие от «аналогового»?

Суть различия в том, что аналоговый сигнал непрерывный во времени (голубая линия), в то время как цифровой сигнал состоит из ограниченного набора координат (красные точки). Если все сводить к координатам, то любой отрезок аналогового сигнала состоит из бесконечного количества координат.

У цифрового сигнала координаты по горизонтальной оси расположены через равные промежутки времени, в соответствии с частотой дискретизации. В распространенном формате Audio-CD это 44100 точек в секунду. По вертикали точность высоты координаты соответствует разрядности цифрового сигнала, для 8 бит это 256 уровней, для 16 бит = 65536 и для 24 бит = 16777216 уровней. Чем выше разрядность (количество уровней), тем ближе координаты по вертикали к исходной волне.

Аналоговыми источниками являются: винил и аудиокассеты. Цифровыми источниками являются: CD-Audio, DVD-Audio, SA-CD (DSD) и файлы в WAVE и DSD форматах (включая производные APE, Flac, Mp3, Ogg и т.п.).

Преимущества и недостатки аналогового сигнала

Преимуществом аналогового сигнала является то, что именно в аналоговом виде мы воспринимаем звук своими ушами. И хотя наша слуховая система переводит воспринимаемый звуковой поток в цифровой вид и передает в таком виде в мозг, наука и техника пока не дошла до возможности именно в таком виде подключать плееры и другие источники звука напрямик. Подобные исследования сейчас активно ведутся для людей с ограниченными возможностями, а мы наслаждаемся исключительно аналоговым звуком.

Недостатком аналогового сигнала являются возможности по хранению, передаче и тиражированию сигнала. При записи на магнитную ленту или винил, качество сигнала будет зависеть от свойств ленты или винила. Со временем лента размагничивается и качество записанного сигнала ухудшается. Каждое считывание постепенно разрушает носитель, а перезапись вносит дополнительные искажения, где дополнительные отклонения добавляет следующий носитель (лента или винил), устройства считывания, записи и передачи сигнала.

Делать копию аналогового сигнала, это все равно, что для копирования фотографии ее еще раз сфотографировать.

Преимущества и недостатки цифрового сигнала

К преимуществам цифрового сигнала относится точность при копировании и передачи звукового потока, где оригинал ничем не отличается от копии.

Основным недостатком можно считать то, что сигнал в цифровом виде является промежуточной стадией и точность конечного аналогового сигнала будет зависеть от того, насколько подробно и точно будет описана координатами звуковая волна. Вполне логично, что чем больше будет точек и чем точнее будут координаты, тем более точной будет волна. Но до сих пор нет единого мнения, какое количество координат и точность данных является достаточным для того, что бы сказать, что цифровое представление сигнала достаточно для точного восстановления аналогового сигнала, неотличимого от оригинала нашими ушами.

Если оперировать объемами данных, то вместимость обычной аналоговой аудиокассеты составляет всего около 700-1,1 Мб, в то время как обычный компакт диск вмещает 700 Мб. Это дает представление о необходимости носителей большой емкости. И это рождает отдельную войну компромиссов с разными требованиями по количеству описывающих точек и по точности координат.

На сегодняшний день считается вполне достаточным представление звуковой волны с частотой дискретизации 44,1 кГц и разрядности 16 бит. При частоте дискретизации 44,1 кГц можно восстановить сигнал с частотой до 22 кГц. Как показывают психоакустические исследования, дальнейшее повышение частоты дискретизации мало заметно, а вот повышение разрядности дает субъективное улучшение.

Как ЦАП строят волну

ЦАП – это цифро-аналоговый преобразователь, элемент, переводящий цифровой звук в аналоговый. Мы рассмотрим поверхностно основные принципы. Если по комментариям будет виден интерес более подробно рассмотреть ряд моментов, то будет выпущен отдельный материал.

Мультибитные ЦАП

Очень часто волну представляют в виде ступенек, что обусловлено архитектурой первого поколения мультибитных ЦАП R-2R, работающих аналогично переключателю из реле.

На вход ЦАП поступает значение очередной координаты по вертикали и в каждый свой такт он переключает уровень тока (напряжения) на соответствующий уровень до следующего изменения.

Хотя считается, что ухо человека слышит не выше 20 кГц, и по теории Найквиста можно восстановить сигнал до 22 кГц, остается вопрос качества этого сигнала после восстановления. В области высоких частот форма полученной «ступенчатой» волны обычно далека от оригинальной. Самый простой выход из ситуации – это увеличивать частоту дискретизации при записи, но это приводит к существенному и нежелательному росту объема файла.

Альтернативный вариант – искусственно увеличить частоту дискретизации при воспроизведении в ЦАП, добавляя промежуточные значения. Т.е. мы представляем путь непрерывной волны (серая пунктирная линия), плавно соединяющий исходные координаты (красные точки) и добавляем промежуточные точки на этой линии (темно фиолетовые).

При увеличении частоты дискретизации обычно необходимо повышать и разрядность, чтобы координаты были ближе к аппроксимированной волне.

Благодаря промежуточным координатам удается уменьшить «ступеньки» и построить волну ближе к оригиналу.

Когда вы видите функцию повышения частоты с 44.1 до 192 кГц в плеере или внешнем ЦАП, то это функция добавления промежуточных координат, а не восстановления или создание звука в области выше 20 кГц.

Изначально это были отдельные SRC микросхемы до ЦАП, которые потом перекочевали непосредственно в сами микросхемы ЦАП. Сегодня можно встретить решения, где к современным ЦАП добавляется такая микросхема, это сделано для того, чтобы обеспечить альтернативу встроенным алгоритмам в ЦАП и порой получить еще более лучший звук (как например это сделано в Hidizs AP100).

Основной отказ в индустрии от мультибитных ЦАП произошел из-за невозможности дальнейшего технологического развития качественных показателей при текущих технологиях производства и более высокой стоимости против «импульсных» ЦАП-ов с сопоставимыми характеристиками. Тем не менее, в Hi-End продуктах предпочтение отдают зачастую старым мультибитным ЦАП-ам, нежели новым решениям с технически более хорошими характеристиками.

Импульсные ЦАП

В конце 70-тых широкое распространение получил альтернативный вариант ЦАП-ов, основанный на «импульсной» архитектуре – «дельта-сигма». Технология импульсных ЦАП-ов стала возможной появлению сверх-быстрых ключей и позволила использовать высокую несущую частоту.

Амплитуда сигнала является средним значением амплитуд импульсов (зеленым показаны импульсы равной амплитуды, а белым итоговая звуковая волна).

Например последовательность в восемь тактов пяти импульсов даст усредненную амплитуду (1+1+1+0+0+1+1+0)/8=0,625. Чем выше несущая частота, тем больше импульсов попадает под сглаживание и получается более точное значение амплитуды. Это позволило представить звуковой поток в однобитном виде с широким динамическим диапазоном.

Усреднение возможно делать обычным аналоговым фильтром и если такой набор импульсов подать напрямую на динамик, то на выходе мы получим звук, а ультра высокие частоты не будут воспроизведены из-за большой инертности излучателя. По этому принципу работают ШИМ усилители в классе D, где плотность энергии импульсов создается не их количеством, а длительностью каждого импульса (что проще в реализации, но невозможно описать простым двоичным кодом).

Мультибитный ЦАП можно представить как принтер, способный наносить цвет пантоновыми красками. Дельта-Сигма – это струйный принтер с ограниченным набором цветов, но благодаря возможности нанесению очень мелких точек (в сравнении с пантовым принтером), за счет разной плотности точек на единицу поверхности дает больше оттенков.

На изображении мы обычно не видим отдельных точек из-за низкой разрешающей способности глаза, а только средний тон. Аналогично и ухо не слышит импульсов по отдельности.

В конечном итоге при текущих технологиях в импульсных ЦАП можно получить волну, близкую к той, что теоретически должна получится при аппроксимации промежуточных координат.

Надо отметить, что после появления дельта-сигма ЦАП исчезла актуальность рисовать «цифровую волну» ступеньками, т.к. так ступеньками волну современные ЦАП не строят. Правильно дискретный сигнал строить точками соединенной плавной линией.

Являются ли идеальными импульсные ЦАП?

Но на практике не все безоблачно, и существует ряд проблем и ограничений.

Т.к. подавляющее количество записей сохранено в многоразрядном сигнале, то перевод в импульсный сигнал по принципу «бит в бит» требует излишне высокую несущую частоту, которую современные ЦАП не поддерживают.

Основной функцией современных импульсных ЦАП является перевод многоразрядного сигнала в однобитный с относительно невысокой несущей частотой с прореживанием данных. В основном именно эти алгоритмы и определяют конечное качество звучания импульсных ЦАП-ов.

Чтобы уменьшить проблему высокой несущей частоты, звуковой поток разбивается на несколько однобитных потоков, где каждый поток отвечает за свою группу разряда, что эквивалентно кратному увеличению несущей частоты от числа потоков. Такие ЦАП называются мультибитными дельта-сигма.

Сегодня импульсные ЦАП-ы получили второе дыхание в быстродействующих микросхемах общего назначения в продуктах компаний NAD и Chord за счет возможности гибко программировать алгоритмы преобразования.

Формат DSD

После широкого распространения дельта-сигма ЦАП-ов вполне логичным было и появления формата записи двоичного кода напрямую дельта-сигма кодировке. Этот формат получил название DSD (Direct Stream Digital).

Широкого распространения формат не получил по нескольким причинам. Редактирование файлов в этом формате оказалось излишне ограниченным: нельзя микшировать потоки, регулировать громкость и применять эквализацию. А это значит, что без потери качества можно лишь архивировать аналоговые записи и производить двухмикрофонную запись живых выступлений без последующей обработки. Одним словом – денег толком не заработать.

В борьбе с пиратством диски формата SA-CD не поддерживались (и не поддерживаются до сих пор) компьютерами, что не позволяет делать их копии. Нет копий – нет широкой аудитории. Воспроизвести DSD аудиоконтент можно было только с отдельного SA-CD проигрывателя с фирменного диска. Если для PCM формата есть стандарт SPDIF для цифровой передачи данных от источника к отдельному ЦАП, то для DSD формата стандарта нет и первые пиратские копии SA-CD дисков были оцифровками с аналоговых выходов SA-CD проигрывателей (хоть ситуация и кажется глупой, но на деле некоторые записи выходили только на SA-CD, либо та же запись на Audio-CD специально была сделана некачественно для продвижения SA-CD).

Переломный момент произошел с выходом игровых приставок SONY, где SA-CD диск до воспроизведения автоматически копировался на жесткий диск приставки. Этим воспользовались поклонники формата DSD. Появление пиратских записей простимулировало рынок на выпуск отдельных ЦАП для воспроизведения DSD потока. Большинство внешних ЦАП с поддержкой DSD на сегодняшний день поддерживает передачу данных по USB используя формат DoP в виде отдельного кодирования цифрового сигнала через SPDIF.

Несущие частоты для DSD сравнительно небольшие, 2.8 и 5.6 МГц, но этот звуковой поток не требует никаких преобразований с прореживанием данных и вполне конкурентно-способен с форматами высокого разрешения, такими как DVD-Audio.

На вопрос что лучше, DSP или PCM однозначного ответа нет. Все упирается в качество реализации конкретного ЦАП и таланта звукорежиссера при записи конечного файла.

Общий вывод

Аналоговый звук – это то, что мы слышим и воспринимаем, как окружающий мир глазами. Цифровой звук, это набор координат, описывающих звуковую волну, и который мы напрямую услышать не можем без преобразования в аналоговый сигнал.

Аналоговый сигнал, записанный напрямую на аудиокассету или винил нельзя без потери качества перезаписать, в то время как волну в цифровом представлении можно копировать бит в бит.

Цифровые форматы записи являются постоянным компромиссом между количеством точностью координат против объема файла и любой цифровой сигнал является лишь приближением к исходному аналоговому сигналу. Однако при этом разный уровень технологий записи и воспроизведения цифрового сигнала и хранения на носителях для аналогового сигнала дают больше преимуществ цифровому представлению сигнала, аналогично цифровой фотокамере против пленочного фотоаппарата.

Автор Кузнецов Роман romanrex

Ликбез №5. Модуляция и передача цифровых сигналов по каналам связи (Часть 1).

Лет 15 тому назад один из бывших сотрудников ведущего европейского поставщика оборудования связи (Ericsson) рассказывал мне, как они поставляли систему радиодоступа DECT в одну из российских «электросвязей». Когда шведы приехали подписывать контракт, то главный инженер российского оператора во время церемонии подписания вдруг произнёс: «Что-то мне кажется, вы нас обманываете – как это можно голос в цифре передавать, да ещё по воздуху?». Немая сцена…

Вот и попробуем разобраться, как «голос преобразуется в цифру».

Методы модуляции аналоговых сигналов

Любой аналоговый сигнал, например, электрический ток из микрофона, при передаче по цифровым каналам связи нужно, как говорят, «оцифровать». То есть, выполнить цифровую модуляцию. Можно, конечно, и в аналоговом виде сигнал передавать, но с середины прошлого века так уже никто не делает – это чревато высокими затратами и очень низким качеством связи.

Для оцифровки аналоговый сигнал А (рис. 1) нужно подвергнуть модуляции. Например, существует Импульсно-Амплитудная Модуляция (ИАМ), по-английски PAM (Pulse Amplitude Modulation), что показано на графике В. По сути, это просто выборка (дискретизация) значений амплитуды сигнала через равные промежутки времени. В результате сигнал все равно остаётся аналоговым, только представленным в виде «столбиков», высота которых представляет собой амплитуду сигнала в момент выборки.

Теперь по одному проводу можно передавать несколько сигналов, если в промежутке между двумя выборками сигнала А передавать выборки от других сигналов.

Другой вид модуляции – широтно-импульсная модуляция (ШИМ), или PWM – Pulse Width Modulation, что мы видим на графике С. Здесь амплитуда А сигнала в каждый момент выборки представлена длительностью («шириной») импульсов, амплитуда которых всегда постоянная.

На графике D показана фазовая модуляция, или PPM – Pulse Position Modulation. Дословно сиё переводится как «модуляция по положению импульса». Фактически, амплитуда сигнала А здесь представлена фазой (сдвигом) импульсов равной амплитуды относительно момента дискретизации исходного сигнала А.

Ну и наконец, есть ещё импульсно-кодовая модуляция (ИКМ), которая показана на графике Е. По-английски она называется PСM (Pulse Сode Modulation).

Вот эта модуляция нас и будет больше всего интересовать, поскольку она и есть цифровая!

Рис. 1. Виды модуляции аналогового сигнала.

Заметим, что и цифровой сигнал тоже можно различным образом модулировать.

 

Преобразование аналогового сигнала в цифровой

Чтобы преобразовать аналоговой сигнала в цифровую форму, нужно его, во-первых, сделать выборку его величины (амплитуды) через равные промежутки времени. Это процесс называется «семплированием» (от слова sample – «образец») и показан на рис. 2.

Рис. 2. Преобразование аналогового сигнала в цифровой

Во-вторых, нужно сделать квантование, т.е. измерение величины амплитуды сигнала в моменты выборки и округление результата измерения до ближайшего значения ступени квантования.

И в-третьих, полученные кванты нужно представить в цифровой форме, т.е. закодировать тем или иным способом. На рисунке 2 показано кодирование в виде трёхразрядного (трёхбитового) двоичного числа.  Вообще, этого очень мало, на практике обычно применяют 8-битное кодирование. Поэтому, как видим, полученный результат довольно сильно отличается от формы исходного сигнала.

Что нужно, чтобы повысить точность, т.е. соответствие полученных значений исходному сигналу? Очевидно, нужно увеличить частоту семплирования. То есть, чаще производить выборку. Здесь можно воспользоваться теоремой, у которой аж целых три автора: два зарубежных, Найквист и Шэннон, и наш, российский Котельников. Поэтому в России эту теорему называют теоремой Котельникова, а за рубежом – Найквиста-Шэннона. И гласит эта теорема следующее: «сигнал, спектр которого ограничен частотой среза (f_ср), может быть восстановлен без потерь, если частота дискретизации составляет не менее fд = 2f_ср». То есть, берём самую высокую гармонику сигнала (как известно, сигнал любой практически формы можно разложить на сумму синусоидальных гармоник с различными амплитудами), и умножаем её на два. После этого, можем считать, что мы адекватно преобразовали аналоговый сигнал в цифровую форму. Ну, если не считать т.н. «шумов квантования», о которых речь немного позже.

Например, если частотный диапазон телефонного сигнала ограничен частотой 3400 Гц (а он именно такой частотой и ограничен, на входе ставят частотный фильтр), то частота выборки (семплирования) должна быть не менее 6800 Гц. На практике обычно делают семплирование с частотой 8000 Гц.

И ещё, как уже отмечалось, нужно повысить разрядность кодирования, то есть кодировать выборки не трёхразрядным двоичным числом, а восьмиразрядным (байтом).

Восстановление формы исходного аналогового сигнала на приёмном конце линии связи

Затем, полученный цифровой сигнал передают тем или иным способом по линии связи. Как это делается, нас пока не интересует. Однако, на приёмном конце линии связи форму сигнала нужно восстановить. Вот что при этом получается (рис. 3).

Рис. 3. Восстановление исходной аналогового формы сигнала.

Как видим, при трёхразрядном кодировании (семь уровней квантования) исходную форму сигнала удаётся восстановить лишь приблизительно. На рис. 3. даже на глаз видны существенные различия полученного сигнала от исходного, хотя общая форма сигнала похожа. Например, если исходный аналоговый сигнал представляет речь, то собеседник на приёмном конце при этом сможет понять, о чем его визави говорит, но тембр голоса может сильно измениться, и возможно, некоторые слова придётся повторять.

Шумы квантования

При квантовании аналогового сигнала, как показано на рис.1, реальное значение сигнала заменяется ближайшим ему уровней квантования. При этом, реальная волнообразная форма аналогового сигнала заменяется «лесенкой», ступени которой соответствуют уровням квантования.

Рис. 4. Аппроксимация аналогового сигнала уровнями квантования.  

Ясно, что такая «пилообразная» кривая отличается от исходной формы аналогового сигнала. Различие (ошибка) между аналоговым сигналом и его ступенчатой аппроксимацией и есть шумы квантования.

Чем больше уровней квантования, тем точнее аппроксимация аналогового сигнала при квантовании, что видно на рис. 5.

Рис. 5. Точность аппроксимации повышается с увеличением числа уровней квантования.  

 

Импульсно-кодовая модуляция ИКМ (PCM, Pulse Code Modulation)

Импульсно-кодовая модуляция – и есть цифровизация аналогового сигнала, то есть, представление аналогового сигнала, вернее его квантованных значений, в цифровой форме. По линии связи при этом передаётся последовательность нолей и единиц (битов), которая представляет собой двоичное число, равное значению уровня квантования в момент квантования.

Рис. 6. Принцип импульсно-кодовой модуляции ИКМ (источник: Н.Н. Слепов. Современные технологии цифровых оптоволоконных сетей связи, 2000 г.).

Квантование, в соответствии с теоремой Котельникова (или Шеннона-Найквиста), производится с частотой 8000 Гц, то есть период квантования составляет 125 мкс. Длительность передачи 8-битового кода выборки квантования составляет 3,91 мкс.

Почему именно 8000 Гц? Потому, что частота среза в телефонном канале составляет 3400 Гц. С «запасом прочности» величина частота среза выбрана равной 4000 Гц, поэтому частота дискретизации выбрана 8000 Гц.

 

Методы двоичного кодирования.

Двоичное кодирование сигнала для передачи его по каналам связи производится различными методами.

Рис. 7. Методы двоичного кодирования.

• Самый простой метод кодирования – униполярный код NRZ (Non-Return to Zero), «без возврата к нулю». Единица представлена высоким уровнем сигнала, тока или напряжения, ноль – нет тока, либо напряжения. Впрочем, может быть и наоборот, это непринципиально.
• Биполярный код NRZ (Non-Return to Zero), «без возврата к нулю». Единица представлена положительным значением тока в цепи, ноль – отрицательным.
• Униполярный код RZ (Return to Zero) «с возвратом к нулю». После обозначения единицы, сигнал в течение периода такта возвращается к нулевому значению сигнала (не ноля, как числа, а лишь величины модулирующего сигнала).
• Биполярный код RZ (Return to Zero) «с возвратом к нулю». То же самое, только две идущие подряд единицы обозначаются разнополярными импульсами с чередованием. Ноль обозначается отсутствием тока или напряжения.
• И наконец, самый экстравагантный код – «Манчестерский» (Manchester Code). Читателю предлагается самому разобраться в методе кодирования по рисунку.

 

Дилемма между сильным и слабым сигналом

Метод ИКМ не лишен недостатков. Кроме шумов квантования, есть ещё и проблема возрастания ошибок квантования, если сигнал имеет низкую амплитуду. В случае телефонного разговора, это будет означать, что если собеседник будет говорить негромко, то его речь может стать совсем неразборчивой.

Рис. 8. Линейное и нелинейное кодирование.

Это может произойти при линейном кодировании, когда все уровни квантования имеют одинаковый шаг по амплитуде сигнала. На рис. 8 видно, что при линейном квантовании слабый сигнал сильно искажается.

Поэтому применяется нелинейное кодирование (компандирование) сигнала.

 

Компандирование: А-закон и μ-закон

Существует два метода компандирования: А-закон (используется в Европе и России) и μ-закон (используется в Северной Америке и Японии).

А-закон командирования выглядит, как показано на рис. 9, и выражается следующей математической формулой:

Рис. 9. А-закон компандирования 

В правой части рис. 9 показана кривая А-закона только для положительных значений входного сигнала. Такая же кривая имеется для отрицательных значений, которая будет «смотреть» вниз.

По вертикальной оси отложено 128 ступеней квантования. Если учесть нижнюю часть кривой, ступеней будет 256. В двоичной форме число 256 можно представить байтом из 8 разрядов. Принцип кодирования показан в таблице в левой части рисунка 9.

При 256 ступенях квантования можно обеспечить довольно хорошее соответствие квантованных значений сигнала его исходной кривой.

Компандирование сигнала и формула μ-закона показано на рисунке 10. Принципиальных отличий от А-закона здесь нет.

Рис. 10. Компандирование по μ-закону.

При восстановлении аналогового сигнала из цифровой формы на стороне приёма выполняется обратное компандирование, таким образом, удаётся получить довольно хорошее соответствие полученного сигнала исходному за счёт двух факторов:

• Достаточного количества уровней квантования – 256 (2⁸)
• Применения компандирования, которое обеспечивает достаточно хорошее качество передачи сигналов малой амплитуды.

В следующей статье Ликбеза рассмотрим методы формирования цифровых трактов.

— Ты прошёл через мой беспроводной цифровой поток и промодулировался!

Like this:

Like Loading…

Related

Объясните простыми словами, что такое аналоговый сигнал и чем он отличается от цифрового?

Применительно к звуку и видео это можно объяснить так. В аналоговом звуковом тракте сигнал от источника передаётся по тракту как непрерывная последовательность изменения тока, напряжения, напряженности магнитного поля (при записи на ленту), радиосигнала, по сути описывающего зависимость частоты и громкости сигнала от времени. Сигнал может подвергаться изменению только фильтрами (ограничивается или изменяется полоса сигнала), усилителями, и иными аналоговыми преобразователями, но формально сама последовательность сохраняется. Если кто не видел сигнал на экране осциллографа, то свою кардиограмму — наверняка. Для видеосигнала это выглядит немного сложнее, так как изображение сканируется по строкам, а между ними вводятся специальные сигналы — синхроимпульсы, чтобы на приёме телевизор мог разобраться какую строку где показывать. Там есть ещё спецсигналы для цветности и некоторые другие, но в строке сигнал — это тоже непрерывная последовательность сигнала, в данном случае описывающего яркость изображения. На аналоговый сигнал прямо воздействуют шум в канале передаче и различные помехи: всё это «собирается» по всему тракту и вместе с музыкой и видео доставляется получателю; также искажают сигнал «неточности» тракта передачи — это, к примеру, неравномерность характеристики в зависимости от частоты сигнала (АЧХ), нелинейности модуляторов-демодуляторов и др. Поэтому качество аппаратуры на стадии первичного источника должно быть сильно выше, чем качество аппаратуры получателя.
 При цифровой передаче после источника  происходит перевод сигнала в цифровой вид — оцифровка. Далее сигнал проходит через любой тракт передачи и на приёме у получателя (абонента) переводится в аналоговый вид: в звук в колонках и видеокартинку на экране. При этом к тракту передачи требования по шуму, искажениям АЧХ и др. очень сильно снижаются, искажения перестают накапливаться по всему тракту,  но появляются некоторые другие, которые влияют на цифровой сигнал (джиттер, фазовый шум, к примеру) — эти искажения влияют на точность восстановления исходного сигнала у получателя. Главные  преимущества цифровых сигналов в том, что они экономят ресурсы: меньше ширина каналов связи или, по-другому, по тому же каналу связи можно передавать больше информации, можно почти бесконечное количество раз перезаписывать,  хранить на различных носителях, передача цифровых сигналов через Интернет может происходить с гарантированной доставкой (протокол TCP). Недостатки: неизбежное невосстановимое внесение искажений в сигнал при оцифровке, необходимость обработки сигналов по всему тракту хранения-передачи, сложные методы кодирования и восстановления исходного сигнала при передаче через некоторые среды передачи, дополнительные требования к некоторым абонентским устройствам (спутниковые конверторы), нетерпимость к некоторым нарушениям согласования в трактах передачи и т.д., но главный недостаток для пользователя — резкое падение качества при сильных искажениях в каналах связи. Объясню проще: аналоговый звук и видео можно продолжать слушать и смотреть даже в шуме, то есть информация до вас доходит, а цифровой вы видите и слышите отлично, даже когда аналоговый уже в шуме, но потом резко раз, и всё пропало — информация теряется. Шум на картинке и на звуке воспринимается людьми более приемлемо, чем расквадрачивание картинки, или, что даже ещё хуже, щелкание и пропадание звука.
 Надо заметить, что, строго говоря, никаких цифр нигде не хранится и не передаётся. В памяти чисто цифровых устройств хранятся состояния: есть заряд — нет заряда, и это и есть условные 1 и 0. При аналоговой записи существует много уровней той же намагниченности, а при цифровой — только 2 крайних состояния. А вот в каналах связи «цифровой код» передаётся не состояния

Основные принципы цифровой беспроводной связи. Ликбез / Хабр

Всем привет. В этой статье я хотел бы рассказать немного об основных приемах и идеях современной цифровой беспроводной связи — на примере стандарта IEEE 802.11. В наше время очень часто люди живут на довольно высоких уровнях абстракции, плохо представляя как именно работают окружающие нас вещи. Ну что ж — попытаюсь принести в массы свет просвещения. В статье будут использоваться вещи и терминология, объясненные в этой статье. Так что людям, далеким от радиотехники рекомендуется сначала прочитать её.
DANGER: в статье присутствует матан — особо впечатлительным не нажимать на эту кнопку:

Цифровые сигналы и спектры

Аналоговые сигналы

До развития компьютеров — посредством радиоволн передавались обычно аналоговые сигналы — то есть сигналы, множество значений которых непрерывно.

Например — звук — зависимость давления от времени. Полученный с приемника сигнал (напряжение) поступает на усилитель звуковой частоты и заставляет колебаться динамик.

Или видеосигнал для кинескопа. Уровень сигнала определяет значение мощности, бегающего по экрану лучика, который в нужные моменты времени засвечивает люминофор, формируя изображение на экране

Основной минус такого способа передачи информации — низкая помехоустойчивость — передающая среда всегда вносит в наш сигнал какую то случайную составляющую — изменение формы видеосигнала меняет цвета отдельных пикселей(все мы помним шумы радиоприемника и рябь на экране телевизора).

Цифровые сигналы

Цифровые сигналы — то есть сигналы, имеющие дискретное множество значений — по этому параметру значительно лучше аналоговых, так как нас интересует не непосредственно значение сигнала, а диапазон в котором находится это значение и помеха нам не страшна(например в диапазоне напряжений 0В — 1.6В мы считаем, что это лог 0, а в диапазоне 3.3В — 5В лог 1). Расплата за это — увеличение требуемой скорости передачи и обработки информации.

Первое, что люди научились делать — естественно передавать такие сигналы по проводам, просто переключая состояние линии данных и синхронизации из единицы в ноль.
На этом небольшой ликбез закончен — далее речь пойдет о том — а как же передается цифровой сигнал при помощи радиоволн. Как работает WiFi.

Спектр единичного импульса

В радиосвязи нас часто интересует спектр сигнала — цифровой сигнал — последовательность прямоугольных импульсов — для начала рассмотрим спектр одного прямоугольного импульса.
Вспомним — что такое спектр(коэффициент перед интегралом опущен):

Спектр прямоугольного импульса длительностью T и амплитудой A:

Таак — а как же быть с отрицательной амплитудой? Вспомним что в действительных числах спектр раскладывается на сумму синусов и косинусов с нулевыми фазами —

в такой форме на самом деле удобней представлять в компьютере, но для анализа такая форма совершенно неудобна — при изменениях сигнала во временнОй области — спектры будут меняться совершенно непонятным для человека образом, поэтому два спектра синусных компонент и косинусных компонент преобразуют в полярные координаты, сворачивая пары синусов и косинусов с нулевой фазой в синус с ненулевой фазой, получая амплитудный спектр и фазовый, а теперь вспомним, что домножение сигнала на -1 — эквивалентно скачку фазы на 180 градусов, поэтому отрицательная часть отразится относительно горизонтальной оси, а в точках перегиба — фаза будет испытывать скачок на 180 градусов.

Также видим, что спектр одиночного импульса представляет собой sinc функцию, довольно часто встречающуюся в цифровой обработке сигналов и радиотехнике.

Почти вся энергия импульса содержится в центральном пике спектра — его ширина обратно пропорциональна длительности импульса. А высота — прямо пропорциональна — то есть — чем длиннее импульс — тем уже и выше его спектр, а чем короче — тем ниже и шире.
Спектр последовательности импульсов с хорошей степенью точности можно считать совокупностью гармоник в спектральной полосе, ширина которой обратно пропорциональна длительности импульса T.

Итак — вывод — уменьшая длину импульсов нашего цифрового сигнала мы можем размазывать сигнал по широкой полосе спектра — при этом пропорционально уменьшается его высота — при увеличении полосы в N раз — во столько же уменьшится высота спектра вплоть до уровня шумов. Широкополосная передача имеет довольно много плюсов — один из них — устойчивость к узкополосным помехам — так как информация размазана по спектру — узкополосная помеха портит только малую часть этой информации.

Если тупо уменьшить длину импульсов нашего информационного сигнала — спектр, конечно, уширится, но ведь приемник не знает какую информацию мы ему передаем и не сможет выделить её из шумов. Поэтому необходим способ — преобразовать узкополосный сигнал в широкополосный шумоподобный — для передачи по радиоканалу, а после приема преобразовать обратно в узкополосный — нужно добавлять в сигнал избыточную информацию, то есть информацию, известную и приемнику и передатчику, при помощи которой приемник может отличить сигнал от шумов. Закодируем каждый бит информации известной и приемнику и передатчику последовательностью.

Автокорреляционная функция. Коды Баркера

Наша задача — найти в длинной последовательности входных данных заранее известную короткую последовательность.
Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом.
Особое значение данный параметр имеет в локации — вот сгенерировали мы какой то сигнал и засекли время — скорость распространения сигнала нам известна, значит зная время, которое потребовалось сигналу, чтобы сбегать до препятствия и обратно — мы можем вычислить расстояние для препятствия. Но вот незадача — идеальных условий в жизни не бывает — как правило вокруг очень много шумов и вместе с отраженным сигналом на вход приемника поступает всякий мусор. А мы во-первых не должны спутать наш сигнал ни с чем другим, во вторых — достаточно точно определить момент времени, когда он вернулся назад.

Математически — автокорреляция определяется так:

То есть мы накладываем функцию на саму себя, но со сдвигом — перемножаем и вычисляем интеграл, отмечаем точку, затем опять сдвигаем, опять вычисляем интеграл и так для всех возможных сдвигов. Если мы прикладываем функцию не к самой себе, а к какой то другой, то это называется просто корреляция.
На приведенной ниже картинке демонстрируются операции свертки, корреляции и автокорреляции.
Отличие свертки и корреляции — в направлении — свертка функций f(x) и g(x) — это та же корреляция, только функций f(x) и g(-x), автокорреляция — корреляция функции с самой собой

То есть в момент времени, когда входной сигнал наиболее похож на нужную нам функцию — корреляционная функция будет иметь пик. Ширина этого пика, если не брать во внимание шум — будет равна удвоенной длине зондирующего импульса и будет симметричной относительно центрального пика — даже если исследуемый сигнал не является симметричным. К слову — пиков может быть несколько — центральный пик и так называемые боковые лепестки — зависит от функции. Корреляционный метод является самым оптимальным методом определения сигнала известной формы на фоне белого шума — другими словами метод имеет наилучшее отношение сигнал/шум. Зондирующий импульс должен удовлетворять следующим требованиям — иметь как можно более узкий центральный пик и при этом иметь минимальный уровень боковых лепестков, то есть функция похожа сама на себя только в очень коротком интервале времени — чуть сдвинуть и она становится совершенно непохожа. В локации этим требованиям удовлетворяет ЛЧМ сигнал.
Имеющий минимальный уровень боковых лепестков, автокорреляционная функция ЛЧМ сигнала имеет следующий вид:

Аналогом ЛЧМ сигнала в дискретных системах является последовательность Баркера
Например — известная последовательность длинной 11 бит: 11100010010.
Найдем автокорреляционную функцию этой последовательности, циклически сдвигая её и считая сумму попарных произведений, при этом заменив 0 на -1
11100010010
11100010010
11
11100010010
01110001001
-1
11100010010
10111000100
-1
11100010010
01011100010
-1
11100010010
00101110001
-1
11100010010
10010111000
-1
…
И так далее — в общем автокорреляционная функция имеет значение 11 только при полном совпадении, во всех остальных случаях — -1.
То же самое справедливо и для инверсии последовательности, то есть для 00011101101. Плюс ко всему — прямая и инверсная последовательности слабо коррелируют между собой — мы их не спутаем.
Получается, что мы можем каждый бит информации кодировать 11 битами последовательности Баркера — прямой для единиц и инверсной для нулей. Элементы последовательности Баркера называют чипами.На практике кодирование происходит примерно так:

Приемник просто может считать корреляцию последовательностей Баркера(прямой и инверсной) и входного сигнала и по пикам корреляционной функции определять — где во входном сигнале закодированы нули, а где — единицы

Модуляция

В общем — как сделать из узкополосного информационного сигнала — широкополосный шумоподобный, а потом его восстановить — разобрались. Теперь поговорим немного о способах передачи данных через среду — средой может быть вакуум, воздух, оптоволокно, провод и т.д. Для того чтобы передавать сигнал при помощи радиоволн нам нужна несущая частота, промодулировав её — мы насаживаем нашу информацию на несущую. Есть 3 основных типа модуляции — амплитудная, частотная и фазовая.
Можно наш готовый к передаче сигнал направить на переключатель и просто включать-выключать передачу несущей — тем самым промодулировав амплитуду

Достоинства и недостатки амплитудной модуляции рассматривались в этой статье, так что подробно здесь останавливаться на ней не будем — в настоящее время амплитудная модуляция почти не применяется.

Следующий тип модуляции — частотная, когда сигнал данных управляет частотой несущей — либо напрямую (ГУН), либо переключаясь между двумя разными генераторами(при этом происходит скачок фазы)

Тут тоже есть что сказать, но как нибудь в другой раз — иначе статья получится слишком уж большой.

Фазовая модуляция

Несложно догадаться — что тут мы кодируем информацию в фазе сигнала — например нуль соответствует нулевому сдвигу по фазе, а единица — сдвигу на 180 градусов — такой способ кодировки легко реализовать технически — например умножая сигнал на 1 — имеем нулевой фазовый сдвиг, а умножая на -1 — сдвиг на 180 градусов. Такая модуляция называется Binary Phase Shift Key или BPSK

А что если мы хотим иметь больше фазовых сдвигов? Для начала объясню логику инженеров, которые придумали следующие танцы с бубном — у вас всего 2 управляющих сигнала — 1 и -1 и при помощи них нужно наиболее простым способом закодировать произвольное число фазовых сдвигов — можно конечно поставить какой нибудь супер ЦАП и управлять генерируемой частотой напрямую, но математика предлагает нам кое что получше. А именно вот эту формулу:

К слову — на ее основе мы произвели переход от спектров синусоид и косинусоид с нулевыми фазами к спектру синусоид с ненулевыми фазами и фазовому спектру — теперь мы просто делаем обратное преобразование.

На этом основана Квадратурная Модуляция

— вместе с несущей мы генерируем еще один сигнал, который сдвинут относительно несущей на 90 градусов, то есть находится с ней в квадратуре. Теперь — управляя амплитудой каждого сигнала(In phase и Quadrature) — умножая на 1 или -1, а затем суммируя — мы можем получить уже 4 возможных фазовых сдвига.

Теперь за раз мы можем кодировать 2 бита. То есть скорость передачи возрастает вдвое. Но и вероятность ошибки при тоже неизбежно возрастет.

Аналогичным образом можно получить большее число фазовых сдвигов. Возможные состояния сигнала обычно показывают на векторной диаграмме или на плоскости сигнального созвездия

Обратите внимание, что последовательность бинарных слов на диаграмме представляет собой Код Грея, что минимизирует вероятность ошибки. Кроме того — есть дополнительный сдвиг на 45 градусов — это делается для того, чтобы уменьшить паразитную амплитудную модуляцию при скачках фазы на 180 градусов

На практике синхронный способ передачи не используется — потому что есть привязка к какой то начальной фазе, а со временем набегает ошибка и фаза уплывает, нужно постоянно переустанавливать начальную фазу — синхронизировать приемник и передатчик. Поэтому носителем информации в реальных системах является не фаза, а изменение фазы — дифференциальный способ передачи сигнала позволяет избавиться от синхронизации. Например при каждом появлении нуля — фаза делает скачок на 180 градусов (BPSK).

Далее уже можно начать говорить о тонкостях реализации — как всегда — на практике все оказывается сложнее, чем в теории, данная статья — скорее небольшой ликбез для расширения кругозора.

Сигналы в электронике — Аналоговые и цифровые типы сигналов

Электрические сигналы (в электронике) — различные напряжения и токи в электрической сети, называемые электрическими «цепями» или «устройствами», которые в дальнейшем можно описать как процесс изменений определенное физическое количество или состояние физического объекта в течение определенного периода времени. Используются с целью визуализации, регистрации и передачи сообщений (информации). Сигнал может быть носителем различной информации e.грамм. электрические, магнитные и акустические сигналы и содержит информационный параметр, например амплитуда, частота или ширина импульса. В электронике наиболее важными сигналами являются изменения электрического заряда, тока, напряжения и электромагнитного поля. Они используются для анализа поведения электронных схем или для измерения изменяющихся электрических значений.

Периодический сигнал

Периодический сигнал — это сигнал, который может повторяться в одних и тех же неизменных временных интервалах. Эти интервалы называются периодами сигнала и обозначаются символом «Т».

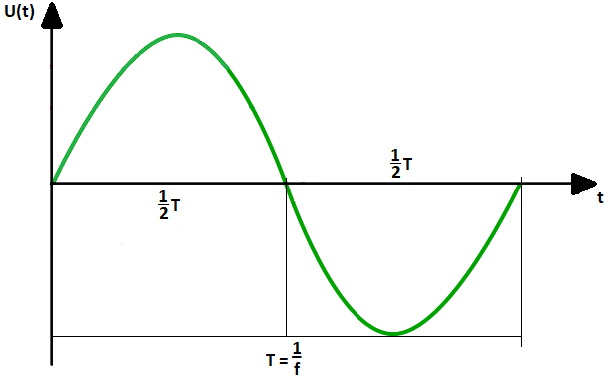
Рис. 1. Пример формы периодического сигнала

Сигналы в электронике — раздел

Самым основным делением электрических сигналов является разделение на аналоговые и цифровые сигналы. В электронике мы различаем несколько типов сигналов, которые включают:

• Аналоговые сигналы — непрерывные по значениям и времени,
• Цифровые сигналы — дискретные по значениям и времени,
• Дискретные сигналы — непрерывные по времени. дискретные по времени значения
• Квантованные сигналы — дискретные по значениям, непрерывные во времени.

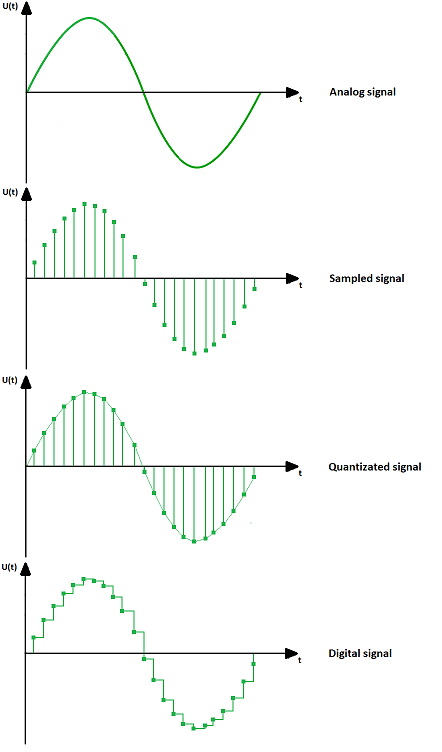
Рис. 2. Пример преобразования сигнала из аналоговой формы в цифровую. Так работает аналого-цифровой преобразователь (АЦП).

Сигналы в электронике — Основные параметры

Наиболее важные параметры электронных сигналов следующие:

• Среднее значение сигнала ,
• Среднее значение сигнала в определенном диапазоне ,
• Энергия сигнал ,
• Мощность сигнала ,
• Средняя мощность сигнала в определенном диапазоне .

Сигналы в электронике — Аналоговые сигналы

Синусоидальный сигнал — Описание

Синусоидальный сигнал (волна) — это непрерывная периодическая волна, описываемая двумя параметрами: амплитудой и частотой. Следующее уравнение описывает синусоидальный сигнал:

Если предположить, что ω = 2πf , то синусоидальный сигнал может быть описан следующей формулой:

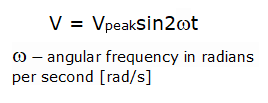
Иногда вместо амплитуды корень -Используется среднеквадратичное значение напряжения В RMS или размах напряжения В pp .Среднеквадратичное значение равно пиковому напряжению, умноженному на √2:

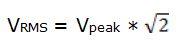
Пиковое значение равно удвоенному значению амплитуды В пик (пиковое напряжение):

среднеквадратичных значений используются при расчете энергии или мощности. Во время измерения электрического напряжения и тока мультиметры обычно показывают среднеквадратичные значения.

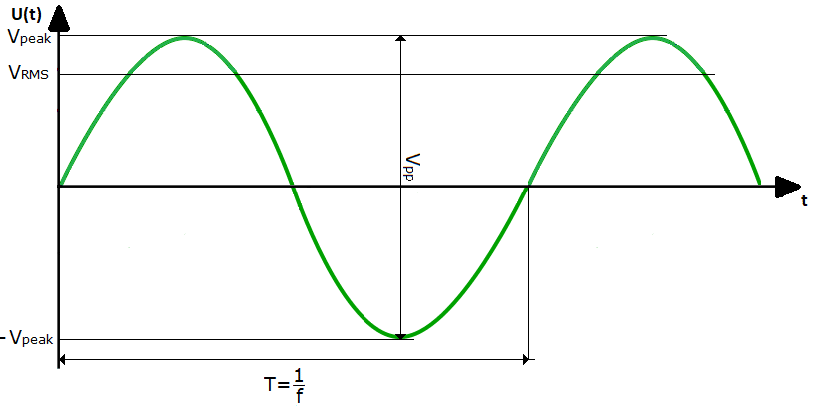
Рис. 3. Пример синусоиды

Квадратный сигнал — Описание

Квадратный сигнал (волна) — аналогично синусоиде, описывается двумя параметрами: амплитудой и частотой, с той разницей, что среднеквадратичное значение напряжения прямоугольной волны равно ее амплитуде.Частота «f» часто заменяется периодом «T», который равен:

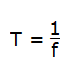
Квадратный сигнал состоит из нарастающего фронта, высокого уровня, спадающего фронта и низкого уровня. Квадратные сигналы «обычно видны» только с положительными половинами, что означает, что низкий уровень сигнала близок к 0В.

Квадратные сигналы используются как в цифровой электронике, так и на границе с системами аналоговой электроники, такими как компараторы, преобразователи АЦП (аналого-цифровой преобразователь) или ЦАП (цифро-аналоговый преобразователь).

На самом деле форма волны отличается от идеальной формы склона, так как на самом деле невозможно быть полностью перпендикулярным, но она близка к.

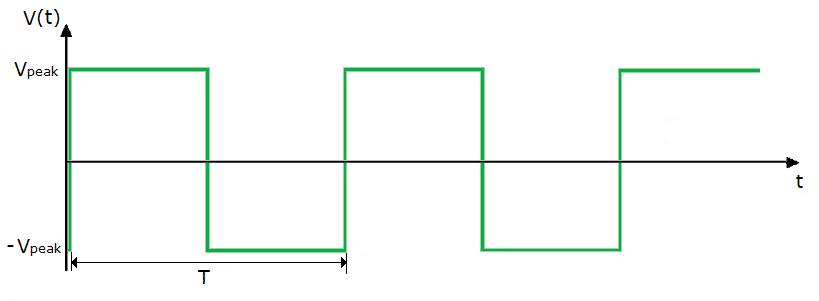
Рис. 4. Пример идеальной прямоугольной волны

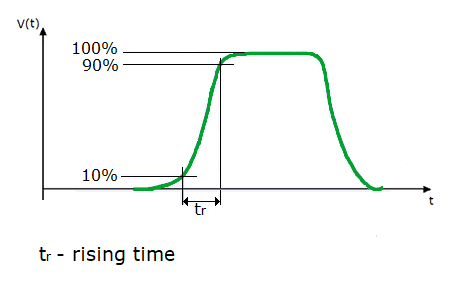
Рис. 5. Пример реального прямоугольного сигнала

Треугольный сигнал — Описание

Треугольный сигнал — треугольная волна, восходящая и падающая. линейно с определенной скоростью. Его можно получить (очень упрощенно) путем интегрирования прямоугольной формы волны.

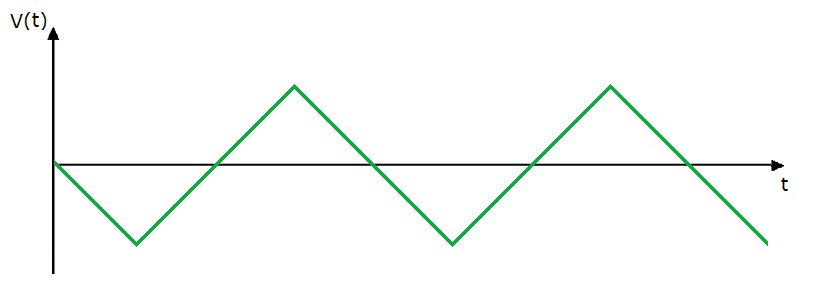
Рис. 6. Пример треугольной волны

Пилообразный сигнал — Описание

Пилообразный сигнал (волна) — как следует из названия, по форме напоминает зуб пилы. Этот сигнал имеет линейную форму волны — напряжение изменяется с фиксированной скоростью до определенного значения и периодически повторяется.

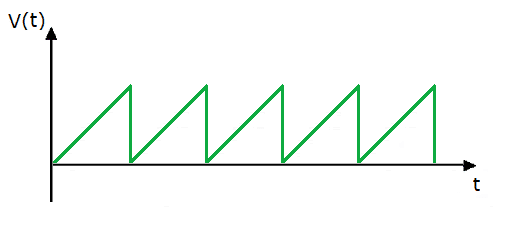
Рис. 7. Пример пилообразного сигнала

Шумовой сигнал — Описание

Шум — является неотъемлемой частью каждого сигнала и обычно нежелателен в электронных схемах.

Рис. 8. Пример шумового сигнала

Импульсный сигнал — Описание

Импульсные сигналы — большинство из них не являются периодическими сигналами. Они описываются двумя параметрами: амплитудой и шириной этих импульсов. Импульсные сигналы делятся на положительные и отрицательные. В случае цифровой электроники нам также потребуется анализировать периодические импульсы, которые в дальнейшем описываются частотой и коэффициентом заполнения.

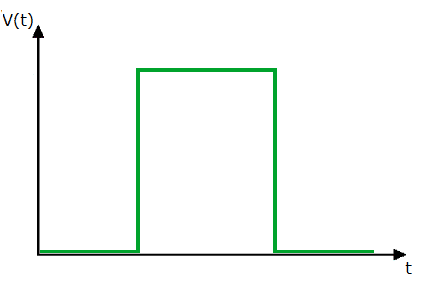
Рис. 9. Пример прямоугольного импульса

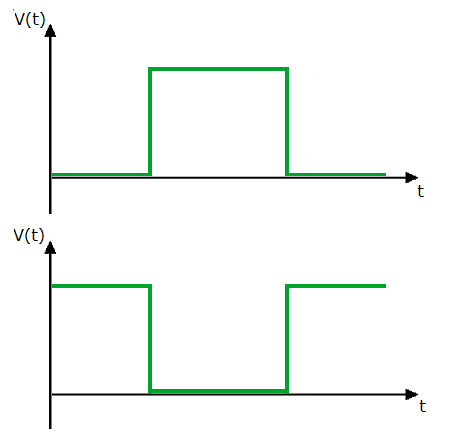
Рис.10. Примеры положительных импульсов

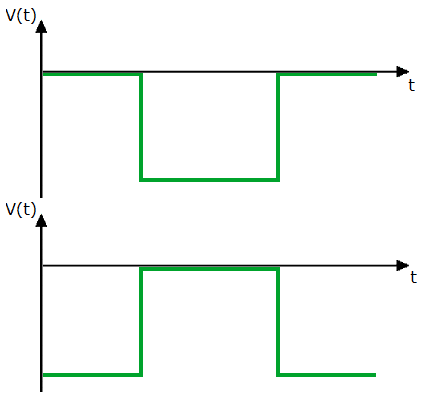
Рис. 11. Примеры отрицательных импульсов

Модульные шаги и пиковые сигналы — Описание

Модульные шаги и пиковые сигналы — можно сказать, что эти сигналы практически не используются в электронные системы, но используются для их описания и анализа.

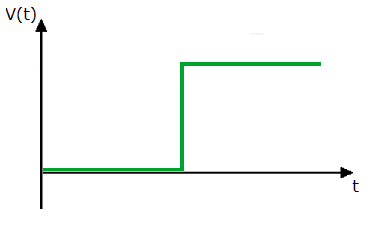
Рис. 12. Пример единичного шага — часть квадратного сигнала

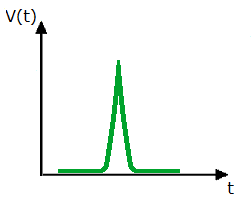
Рис. 13. Пример пикового сигнала — очень узкий импульс

Сигналы в электронике — цифровые сигналы

На следующем рисунке показано цифровой сигнал, состоящий из четырех 3-битных слов в двоичном коде.

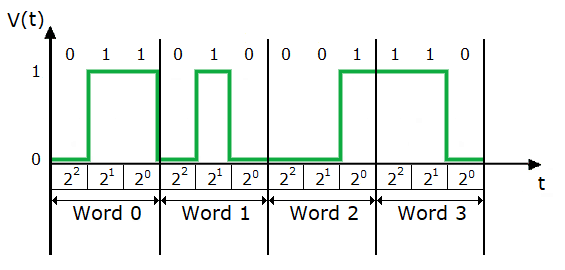
Рис. 14. Пример цифрового сигнала — двоичный код

.

Знакомство с сигналами

Введение в сигналы

• Определение сигналов
  • Типы сигналов
  • Свойства сигнала
• Пример сигналов
  • Различные сигналы
  • Свойство периодичности
  • Разница между системами CT и DT
• Дельта функция

Свойства и типы сигналов

Управление сигналами

• разворот времени
• сдвиг во времени
• замедление / сокращение времени
  • Разница между CT и DT

Составные сигналы

Почему цифровая обработка сигналов?

Если вы работаете на компьютере или используете компьютер для манипулирования данными, вы почти наверняка работаете с цифровыми сигналами.Все манипуляции с данными являются примерами цифровой обработки сигналов (для нашей цели обработка сигналов с дискретным временем как экземпляры цифровой обработки сигналов). Примеры использования DSP:

• Фильтрация: устранение шума из сигналов, таких как речевые сигналы и другие аудиоданные, астрономические данные, сейсмические данные, изображения.
• Синтез и манипуляции: например, синтез речи, синтез музыки, графика.
• Анализ: сейсмические данные, атмосферные данные, анализ фондового рынка.
• Голосовая связь: обработка, кодирование и декодирование для хранения и пересылки.
• Кодирование голоса, звука и изображений для сжатия.
• Активное шумоподавление: наушники, глушители в автомобилях
• Обработка изображений, компьютерное зрение
• Компьютерная графика
• Промышленное применение: анализ вибрации, химический анализ
• Biomed: МРТ, сканирование кошек, визуализация, анализы, ЭКГ, ЭМГ и т. Д.
• Радар, сонар
• Сейсмология.

Определение сигналов

Что такое сигнал?

Сигнал — это способ передачи информации. Жесты, семафоры, изображения, звук — все может быть сигналами.

Технически — функция времени, пространства или другой переменной наблюдения, которая передает информацию

Распишем 3 форм сигналов:

• Непрерывный / аналоговый сигнал
• Дискретно-временной сигнал
• Цифровой сигнал

Непрерывный (CT) / аналоговый сигнал

конечный , действительный , гладкий функция $ s (t) $ переменной t , которая обычно представляет время.И s , и t в $ s (t) $ являются непрерывными

Почему на самом деле ?

Обычно явления реального мира имеют реальную ценность.

Почему конечный ?

Реальные сигналы обычно имеют ограниченную энергию просто потому, что для нас нет бесконечного источника энергии.
В качестве альтернативы, особенно когда они характеризуют долговременные явления (например, солнечное излучение), они будут ограничены по мощности.
Реальные сигналы также будут ограничены по амплитуде — их значения никогда не будут бесконечными.

Чтобы утверждать, что сигнал «конечен», нам нужна некоторая характеристика его «размера». Утверждать, что сигнал конечен, значит утверждать, что размер сигнала ограничен — он никогда не уходит в бесконечность.2 (\ тау), д \ тау. $

Амплитуда = $ max | s (t) | $

Почему гладкий ?

Реальные сигналы никогда не изменяются внезапно / мгновенно. Чтобы быть более техническим, у них есть конечная пропускная способность .

Обратите внимание, что, хотя мы сделали предположения о сигналах (конечность, реальные, гладкие), при реальном анализе и разработке методов обработки сигналов эти соображения обычно игнорируются.

Дискретный сигнал (DT)

Сигнал с дискретным временем — это ограниченная последовательность с непрерывными значениями $ s [n] $. С другой стороны, его можно рассматривать как непрерывную функцию от дискретного индекса $ n $. Мы часто ссылаемся на индекс $ n $ как на , время , так как сигналы с дискретным временем часто получаются путем создания снимков сигнала с непрерывным временем, как показано ниже.Однако более правильно, $ n $ — это просто индекс, который представляет последовательность чисел в $ s [n] $.

Если они DT-сигналы являются снимками реальных сигналов, применяются , реальность и конечность , .

Ниже приведены несколько характеристик размера сигнала DT.

1. Энергия

$ E = \ sum_n s ^ 2 [n] $

2. Мощность

$ P = \ lim_ {N \ to \ infty} \ frac {1} {2N + 1} \ sum_ {n = -N} ^ {N} s ^ 2 [n].$

3. Амплитуда = $ max | s [n] | $

Гладкость неприменима.

Цифровой сигнал

Мы будем работать с с цифровыми сигналами, но будем развивать теорию в основном вокруг сигналов с дискретным временем .

Цифровые компьютеры работают с цифровыми сигналами , а не с сигналами дискретного времени.Цифровой сигнал представляет собой последовательность $ s [n] $, где index значения $ s [n] $ не только конечны, но могут принимать только конечный набор значений. Например, в цифровом сигнале, где отдельные числа $ s [n] $ хранятся с использованием 16-битных целых чисел, $ s [n] $ может принимать одно из 2 ¹⁶ значений.

В числовом ряду $ s [n] $ значения s могут принимать только фиксированный набор значений.

Цифровые сигналы — это сигналы с дискретным временем, полученные после «оцифровки». Цифровые сигналы также обычно получают путем измерения от явления реального мира. Однако, в отличие от принятой нормы для аналоговых сигналов, цифровые сигналы могут принимать комплексные значения.

Выше представлены некоторые критерии для реальных сигналов. Теоретические сигналы не ограничены

реальный — это часто нарушается; работаем с комплексными числами

конечное / ограниченное

энергия — ВСЕГДА нарушается

. Сигналы, которые имеют бесконечную временную протяженность, , то есть , которые простираются от $ — \ infty $ до $ \ infty $, могут иметь бесконечную энергию.

мощность — почти никогда: почти все сигналы, с которыми мы столкнемся, имеют ограниченную мощность

плавность — это часто нарушается многими из рассматриваемых нами сигналов непрерывного времени.

Примеры «стандартных» сигналов

Мы перечисляем некоторые основные типы сигналов, которые часто встречаются в DSP. Мы перечисляем их версии для непрерывного и дискретного времени. Обратите внимание, что аналоговые версии с непрерывным временем некоторых из этих сигналов являются искусственными конструкциями — они нарушают некоторые из условий, которые мы указано выше для сигналов реального мира и фактически не может быть реализовано.

Типы сигналов

Мы можем классифицировать сигналы по их свойствам, которые позже повлияют на наш анализ этих сигналов.

Периодические сигналы

Сигнал является периодическим, если он повторяется ровно через некоторый промежуток времени. Однако значение периодичности различается для сигналов с непрерывным и дискретным временем.Мы рассмотрим каждый из них по очереди.

Сигналы непрерывного времени Таким образом, в непрерывном времени сигнал, если он называется периодическим, если существует какое-либо значение $ T $ такое, что \ [ s (t) = s (t + MT), ~~~~~ — \ infty \ leq M \ leq \ infty, ~~ \ text {integer} ~ M \] Наименьшее значение $ T $, для которого указанное выше соотношение удерживает период сигнала.

Дискретные временные сигналы

Определение периодичности для сигналов с дискретным временем аналогично определению периодичности для сигналов с непрерывным временем с одним ключевым отличием: период должен быть целым числом.Как мы увидим, это приводит к некоторым неинтуитивным выводам.

Дискретный сигнал времени $ x [n] $ называется периодическим, если существует положительное целое значение $ N $ такое, что \ [ x [n] = x [n + MN] \] для всех целых $ M $. Наименьшее значение $ N $, для которого справедливо указанное выше, является периодом сигнала.

Четные и нечетные сигналы

Симметический сигнал или — это сигнал, который зеркально отражается в момент времени $ t = 0 $.Сигнал считается, даже если он имеет следующее свойство: \ [ \ text {Непрерывное время:} ~ s (t) = s (-t) \\ \ text {Дискретное время:} ~ s [n] = s [-n] \]

Сигнал является нечетным симметическим сигналом, если он имеет следующее свойство: \ [ \ text {Непрерывное время:} ~ s (t) = -s (-t) \\ \ text {Дискретное время:} ~ s [n] = -s [-n] \]

На рисунке ниже показаны примеры четных и нечетных симметричных сигналов.Например, косинус даже симметричен, поскольку $ \ cos (\ theta) = \ cos (- \ theta) $, что приводит к $ \ cos (\ omega t) = \ cos (\ omega (-t)) $ , С другой стороны, синус нечетно симметричен, поскольку $ \ sin (\ theta) = — \ sin (- \ theta) $, что приводит к $ \ sin (\ omega t) = — \ sin (\ omega (-t) ) $.

Разложение сигнала на четные и нечетные составляющие Любой сигнал $ x [n] $ может быть выражен как сумма четного и нечетного сигналов следующим образом. \ [ x [n] = x_ {четное} [n] + x_ {нечетное} [n] \] где \ [ x_ {даже} [n] = 0.5 (х [п] + х [-n]) \\ x_ {odd} [n] = 0,5 (x [n] — x [-n]) \]

Управляющие сигналы

Сигналы можно составлять путем манипулирования и комбинирования других сигналов. Кратко рассмотрим эти манипуляции.

Масштабирование

Простое масштабирование сигнала вверх или вниз по коэффициенту усиления.

Непрерывное время: $ y (t) = a x (t) $

Дискретное время: $ y [n] = a x [n] $

$ a $ может быть реальным / мнимым, положительным / отрицательным. Когда $ a отрицательно, сигнал переворачивается по оси y.

Разворот времени

Переворот сигнала слева направо.

Непрерывное время: $ y (t) = x (-t) $

Дискретное время: $ y [n] = x [-n] $

Сдвиг во времени

Сигнал смещен вдоль оси индента на $ \ tau $ (или N для дискретного времени). Если $ \ tau $ положительно, сигнал задерживается, а если $ \ tau $ — отрицательный сигнал продвигается.

Непрерывное время: $ y (t) = x (t- \ tau) $

Дискретное время: $ y [n] = x [n — N] $

Расширение

Саму временную ось можно масштабировать на $ \ alpha $.

Непрерывное время: $ y (t) = x (\ alpha t) $

Дискретное время: $ y [n] = x [/ alpha n] $

Расширение DT отличается от расширения CT, потому что $ x [n] $ определяется ТОЛЬКО в целом числе n, поэтому для существования $ y [n] = x [\ alpha n] $ «an» должно быть целым числом.

Однако $ x [\ alpha n] $ при $ a \ neq 1 $ проигрывает некоторым семплам. Вы никогда не сможете полностью восстановить x [n] из него. Этот процесс часто называют дециминкацией .

Для сигналов DT $ y [n] = x [\ alpha n] $ для $ \ alpha интерполировать нули для неопределенных значений, если $ an $ не является целым числом.

Составные сигналы

Сигналы могут быть составлены путем манипулирования и комбинирования других сигналов. Есть несколько способов комбинирования сигналов, и мы рассматриваем следующие два:

ДОПОЛНЕНИЕ

Непрерывное время: $ y (t) = x_1 (t) + x_2 (t) $ Дискретное время: $ y [n] = x_1 [n] + x_2 [n] $

УМНОЖЕНИЕ

Непрерывное время: $ y (t) = x_1 (t) x_2 (t) $ Дискретное время: $ y [n] = y_1 [n] y_2 [n] $

$ x_1 [n] $ и $ x_2 [n] $ сами могут быть получены путем манипулирования другими сигналами.{\ alpha t} u (t) $ для $ \ alpha

На самом деле односторонние сигналы могут быть получены умножением на u [n] (или сдвинутые / обращенные во времени версии u [n] или u (t)).

Получение основных сигналов друг от друга

Можно получить один сигнал из другого просто с помощью математических манипуляций.{\ infty} u [k] \ delta [n-k] $

На этом завершается введение в сигналы. В обзоре мы обсудили важность DSP, типы сигналов и их свойства, манипуляции с сигналами, и состав сигнала. Далее мы обсудим системы.

,

Digital Signals — Signal Identification Wiki

Щелкните имя сигнала, чтобы просмотреть более подробную информацию, возможное декодирование и дополнительные образцы звука и водопада

Цветовая легенда

Неактивно (больше не используется)

Активно (В настоящее время активно используется)

Статус Неизвестно или периодически

Имя сигнала	Описание	Частота	Режим	Модуляция	Пропускная способность	Расположение	Пример аудио	Изображение водопада
CDMA 2 Гбит / с (IS-95)	CDMAOne, также известная как IS-95, была первой в истории сотовой стандартной технологией, основанной на множественном доступе с кодовым разделением CDMAC.6 Гц	по всему миру

.

Руководство для начинающих по цифровой обработке сигналов (DSP) | Дизайн-центр

Что такое DSP?

Цифровые сигнальные процессоры (DSP)

принимают реальные сигналы, такие как голос, аудио, видео, температура, давление или положение, которые были оцифрованы, а затем математически обрабатывают их. DSP разработан для очень быстрого выполнения математических функций, таких как «сложение», «вычитание», «умножение» и «деление».

Сигналы необходимо обрабатывать, чтобы информацию, которую они содержат, можно было отображать, анализировать или преобразовывать в другой тип сигнала, который может оказаться полезным. В реальном мире аналоговые устройства обнаруживают такие сигналы, как звук, свет, температура или давление, и управляют ими. Преобразователи, такие как аналого-цифровой преобразователь, затем принимают реальный сигнал и преобразуют его в цифровой формат единиц и нулей. Отсюда DSP захватывает оцифрованную информацию и обрабатывает ее.Затем он возвращает оцифрованную информацию для использования в реальном мире. Это делается одним из двух способов: в цифровом или аналоговом формате с помощью цифро-аналогового преобразователя. Все это происходит на очень высоких скоростях.

Для иллюстрации этой концепции на схеме ниже показано, как DSP используется в аудиоплеере MP3. Во время фазы записи аналоговый звук вводится через ресивер или другой источник. Этот аналоговый сигнал затем преобразуется в цифровой сигнал аналого-цифровым преобразователем и передается на DSP.DSP выполняет кодирование MP3 и сохраняет файл в памяти. Во время фазы воспроизведения файл берется из памяти, декодируется DSP, а затем преобразуется обратно в аналоговый сигнал через цифро-аналоговый преобразователь, чтобы его можно было выводить через акустическую систему. В более сложном примере DSP будет выполнять другие функции, такие как регулировка громкости, эквализация и пользовательский интерфейс.

Информация DSP может использоваться компьютером для управления такими вещами, как безопасность, телефон, системы домашнего кинотеатра и сжатие видео.Сигналы могут быть сжаты, чтобы их можно было быстро и более эффективно передавать из одного места в другое (например, телеконференции могут передавать речь и видео по телефонным линиям). Сигналы также могут быть усилены или обработаны для повышения их качества или предоставления информации, не воспринимаемой людьми (например, эхоподавление для сотовых телефонов или компьютерные медицинские изображения). Хотя реальные сигналы можно обрабатывать в их аналоговой форме, цифровая обработка сигналов обеспечивает такие преимущества, как высокая скорость и точность.

Благодаря тому, что ЦСП является программируемым, он может использоваться в самых разных приложениях. Вы можете создать собственное программное обеспечение или использовать программное обеспечение, предоставленное ADI и ее третьими сторонами, для разработки решения DSP для приложения. Для получения более подробной информации о преимуществах использования DSP для обработки реальных сигналов, пожалуйста, прочтите часть 1 статьи из Analog Dialogue под названием: Зачем использовать DSP? Цифровая обработка сигналов 101 — Вводный курс по проектированию систем DSP.

,