3. Виды информации и сигналов

Информация может быть двух видов: дискретная (импульсная и цифровая) и не­прерывная (аналоговая). Дискретная информация характеризуется по­следовательными точными значениями некоторой величины, а непре­рывная — непрерывным процессом изменения некоторой величины. Не­прерывную информацию может, например, выдавать датчик атмосфер­ного давления или датчик скорости автомашины. Дискретную инфор­мацию можно получить от любого цифрового индикатора: электронных часов, счетчика магнитофона и т. п.

Сигнал всегда является функцией времени. В зависимости от того, какие значения могут принимать аргумент (время t) и уровни сигналов их делят на 4 типа.

1) Непрерывный или аналоговый сигнал (случайный сигнал этого типа называется непрерывным случайным процессом). Эти сигналы определены для всех моментов времени и могут принимать все значения из заданного диапазона.

Чаще всего физические процессы, порождающие сигналы являются непрерывными. Этим и объясняется второе название сигналов данного типа аналоговый т.е. аналогичные порождающим процессам.

2) Дискретизированный или дискретно непрерывные сигналы (случайные сигналы этого типа называют процессами с дискретным временем или непрерывными случайными последовательностями). Они определены лишь в отдельные моменты времени и могут принимать любые значения уровня.

3) Дискретные по уровню или квантованные сигналы (случайные сигналы этого типа называют дискретными случайными процессами). Они определены для всех моментов времени и принимают лишь разрешенные значения уровней отделенные от друг друга на величину шага квантования.

4) Дискретные по уровню и по времени сигналы (случайные сигналы этого типа называют дискретными случайными последовательностями). Они определены лишь в отдельные разрешенные моменты времени и могут принимать лишь разрешенные значения уровней.

Совокупность технических средств используемых для передачи сообщений от источника к потребителю информации называется системой связи. Общая схема системы связи состоит из 5 частей.

1) Источник сообщений

создающий сообщения или последовательность сообщений, которые должны быть переданы. Сообщения могут быть разных типов: последовательность букв или цифр как в системах телеграфа и передачи данных. Одна или более функций времени как в системах передачи звука в моно и стерео звучаниях и т.д.

2) Передатчик, который перерабатывает некоторым образом сообщения в сигналы соответственного типа определенного характеристиками используемого канала.

3) Канал связи — это комплекс технических средств, обеспечивающий передачу сигналов от передатчика к приемнику. В состав канала входит каналообразующая аппаратура, осуществляющая сопряжение выходного и входного сигналов соответственно передатчика и приемника с линией связи, и самой линии связи.

Линией связи (ЛС) называется среда, используемая для передачи сигнала от передатчика к приемнику. Это может быть, например: пара поводов, коаксиальный кабель, область распространения радиоволн, световод и т.д. Обычно входными и выходными сигналами линии связи является сигналы типа один, т.е. непрерывный. Вместе с тем на входе и выходе канала могут присутствовать сигналы и других типов. Канал называется дискретным, если на его входе и выходе присутствуют сигналы дискретные по уровню. Если сигналы на входе и выходе канала непрерывны по времени, то он называется непрерывным. В общем случае в процессе передачи в канале сигнал искажается шумом, что соответствует наличию источника шума.

4) Приемник обычно выполняет операцию обратную по отношению к операции, производимой передатчиком, т.е. восстанавливается сообщение по сигналам. Сложность построения приемника обусловлена изменением формы принимаемых сигналов, что связано с наличием шума.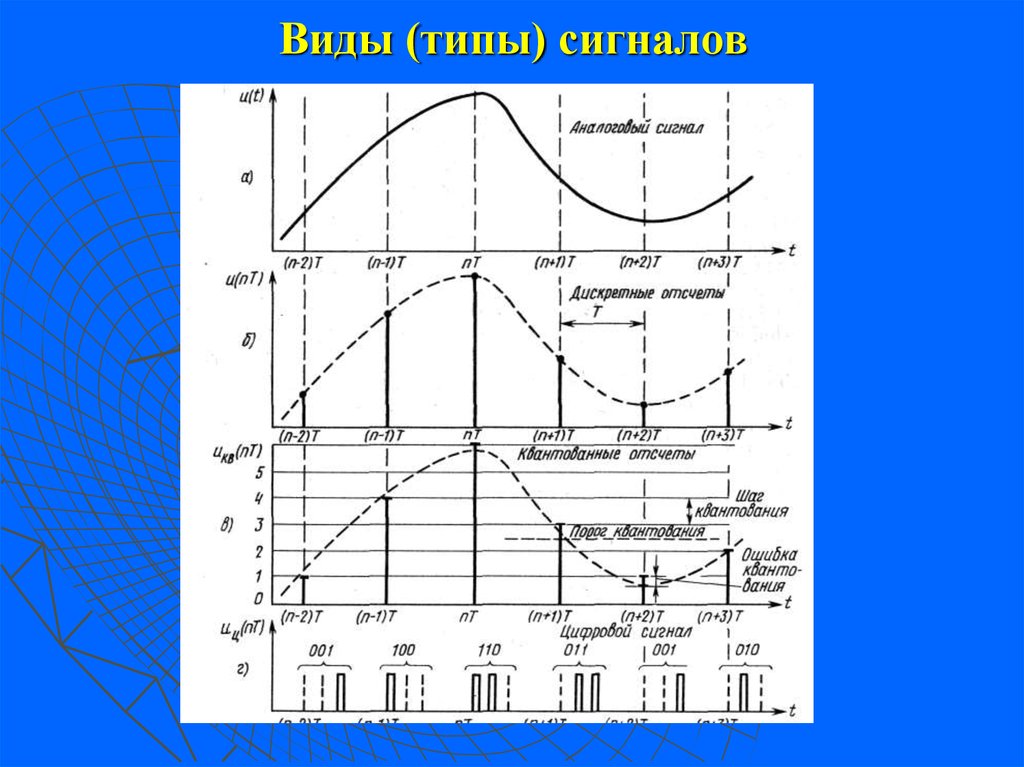

5) Получатель это лицо или аппарат, для которого предназначено сообщение. Процесс преобразования сообщения в сигнал, осуществляющий в передатчике и обратный ему процесс, реализующий в приемнике назовем соответственно кодированием и декодированием.

Виды сигналов. Назначение радиоэлектронных устройств

Похожие презентации:

3D печать и 3D принтер

Видеокарта. Виды видеокарт

Анализ компании Apple

Трансформаторы тока и напряжения

Транзисторы

Устройство стиральной машины LG. Электрика

Конструкции распределительных устройств. (Лекция 15)

Электробезопасность. Правила технической эксплуатации электроустановок

Магнитные пускатели и контакторы

Работа на радиостанциях КВ и УКВ диапазонов. Антенны военных радиостанций. (Тема 5.1)

1. Виды сигналов

• Назначение радиоэлектронных
устройств — получение,
преобразование, передача и хранение
информации, представленной в форме
электрических сигналов.
• Сигналы, действующие в электронных
устройствах, и соответственно сами
устройства делят на две большие
группы: аналоговые и цифровые.

3. Аналоговый сигнал

— сигнал, непрерывный по уровню и во
времени, т. е. такой сигнал существует в
любой момент времени и может принимать
любой уровень из заданного диапазона.

4. Квантованный сигнал

— сигнал, который может принимать только
определенные квантованные значения,
соответствующие уровням квантования. Расстояние
между двумя соседними уровнями — шаг
квантования.

5. Дискретизированный сигнал

— сигнал, значения которого заданы только в
моменты времени, называемые моментами
дискретизации. Расстояние между соседними
моментами дискретизации — шаг
дискретизации Td .

6. Цифровой сигнал

— сигнал, квантованный по уровню и
дискретизированный во времени.
Квантованные значения цифрового сигнала обычно
кодируются некоторым кодом, при этом каждый
выделенный в процессе дискретизации отсчет заменяется
соответствующим кодовым словом, символы которого
имеют два значения — 0 и 1.
Последовательность
таких кодовых слов и
будет являться
цифровым сигналом.

7. Аналоговые устройства

• Типичными представителями устройств аналоговой
электроники являются устройства связи,
радиовещания, телевидения. Общие требования,
предъявляемые к аналоговым устройствам, —
минимальные искажения. Стремление выполнить эти
требования приводит к усложнению электрических
схем и конструкции устройств. Другая проблема
аналоговой электроники — достижение необходимой
помехоустойчивости, ибо в аналоговом канале связи
шумы принципиально неустранимы.

8. Цифровые устройства

• Цифровые сигналы формируются электронными схемами,
транзисторы в которых либо закрыты (ток близок к нулю),
либо полностью открыты (напряжение близко к нулю),
поэтому на них рассеивается незначительная мощность и
надежность цифровых устройств получается более
высокой, чем аналоговых.
• Цифровые устройства более помехоустойчивы, чем
аналоговые, так как небольшие посторонние возмущения
не вызывают ошибочного срабатывания устройств.
• Безошибочно изготовленные цифровые устройства не
нужно настраивать, а их характеристики полностью
повторяемы.

9. Цифровые устройства

• Работа цифровых устройств обычно тактируется достаточно
высокочастотным генератором тактовых импульсов. В течение
одного такта реализуется простейшая микрооперация — чтение,
сдвиг, логическая команда и т. п. Информация представляется в
виде цифрового слова. Для передачи слов используются два
способа — параллельный и последовательный.
• Последовательное кодирование применяется при обмене
информацией между цифровыми устройствами (например, в
компьютерных сетях, модемной связи). Обработка информации в
цифровых устройствах реализуется при использовании
параллельного кодирования информации, обеспечивающего
максимальное быстродействие.

English     Русский Правила

Какие бывают типы сигналов?

Непрерывные и дискретные сигналы

Если значение сигнала определено для каждого момента времени в рассматриваемом интервале, каким бы малым он ни был, такой сигнал называется «непрерывным сигналом». Сигнал с дискретным временем выводится из сигнала с непрерывным временем с помощью процесса, называемого равномерной выборкой, поэтому он определяется для дискретных значений времени.

Для модуля сигнала с дискретным временем f(n) аргумент ‘n’ должен быть целым числом, в отличие от аргумента ‘t’ сигнала с непрерывным временем может быть любым действительным значением.

Если временной сигнал непрерывного времени f(t) равномерно дискретизируется для формирования дискретного сигнала времени f(nT _s ), так что t=nT _s

f(nT _s ) = f (t), n = 0, ±1, ±2, ±3,….

, где T _с  — период выборки (сек/выборка).

Если T _с = 1 с/отсчет, то f(nT _с )=f(n)

На приведенном ниже рисунке показан сигнал с непрерывным временем f(t)=sin t и его версия с дискретным временем. f(nT _с )

Непрерывный сигнал f(t) может быть определен либо в виде математического уравнения, либо в графической форме. С другой стороны, наряду с математической формой и графическим представлением сигнал дискретного времени f(n) может быть представлен в наборе значений, как показано ниже.

Здесь стрелка указывает амплитуду выборки в начале координат, а значения справа от стрелки представляют амплитуду выборки для положительных значений ‘n’, а значения слева от нее будут амплитудами выборки для отрицательных значений. значения «n».

Четные и нечетные сигналы

Четный сигнал

Если f(t) является непрерывным во времени сигналом, который симметричен относительно вертикальной оси, так что он визуально идентичен своей версии с обращением во времени, такой сигнал называется четным сигналом.

F (−T) = F (T)

для сигнала дискретного времени

F (−n) = F (n)

Пример:

ODD Сигнал

Если f(t) является сигналом с непрерывным временем, он будет называться нечетным сигналом, если он антисимметричен относительно своей вертикальной оси, так что

f(−t)=−f(t)

Для того, чтобы дискретный сигнал был нечетным сигналом

f(−n)=−f(n)

Пример:

Но на практике большинство сигналов не являются ни четными, ни нечетными , для таких сигналов мы можем найти четные и нечетные части таких сигналов, чтобы использовать симметрию при анализе сигналов и систем. Если

f(t) — любой непрерывный сигнал, который не является ни четным, ни нечетным сигналом, тогда

• Четная часть сигнала равна
• Нечетная часть сигнала равна

Тогда f(t) можно представить в виде суммы его четной составляющей (f _e (t)) и нечетной составляющей (f _o (t)).

f(t) = (f _e (t))+(f _o (t))

Периодические и апериодические сигналы

интервал, такой сигнал известен как периодический сигнал. Если он не имеет такой картины, то он известен как апериодический сигнал. Если f(t) — непрерывный периодический сигнал, то

f(t)= f(t±kT)

Где «T» — основной период времени сигнала f(t), а «k» — целое число.

T=1/частота(f)=2π/ω

Где ω — угловая частота, ω=2πf, и не путать с сигналом f(t) и частотой «f».

Если f(n) — сигнал дискретного времени,

f(n) = F(n+N)

Где «n» — целое число, а «N» — основной период времени. Здесь N — количество отсчетов, принимаемых сигналом для повторения одного и того же шаблона, это целое число, в отличие от «T» может быть любым реальным значением для сигнала с непрерывным временем.

Рассмотрим следующий пример для лучшего понимания.

>

Сигналы энергии и сигналы мощности

Если полная энергия сигнала конечна, то такие сигналы называются энергетическими сигналами, мощность таких сигналов равна нулю. Сигналы, имеющие бесконечную энергию и конечную мощность, известны как сигналы мощности. Чтобы иметь точную ясность в этом, мы должны знать, как рассчитать мощность и энергию сигнала, для этого понимания рассмотрим электрическую цепь, имеющую сопротивление сопротивления (R), приложенное напряжение v(t) и ток, протекающий через резистор i(t). Мгновенная мощность равна

Для расчета нормированной мощности предположим, что сопротивление R=1

Путем накопления мгновенной мощности в интервале [уравнение] до [уравнение] мы можем получить энергию, рассеиваемую в этом интервале, E(t).

Следовательно, используя этот пример, мы можем обобщить энергию любого непрерывного сигнала f(t)

Полная нормализованная энергия
Затем мы вычислим мощность

Следовательно, мы должны сначала вычислить энергию, если энергия сигнал конечен, то это энергетический сигнал, мощность энергетического сигнала почти незначительна, поэтому мы можем считать его равным нулю.

Если энергия сигнала бесконечна, то мы не можем вычислить мощность такого сигнала напрямую, так как

Для таких сигналов мы должны вычислить мощность косвенно, как показано ниже

Если сигнал имеет бесконечную энергию и конечной мощности такой сигнал можно назвать сигналом мощности. Если сигнал имеет бесконечную энергию и бесконечную мощность, такие сигналы не являются ни энергетическими, ни энергетическими сигналами.

• Как правило, сигналы мощности имеют бесконечную продолжительность, а их значение стремится к ненулевому постоянному значению по мере того, как время стремится к бесконечности. Следовательно, периодические сигналы в целом являются сигналами мощности.
• Сигналы, имеющие бесконечную длительность со своими значениями, также стремятся к бесконечности, такие сигналы не называются ни энергетическими, ни силовыми.

Если f(n) является сигналом с дискретным временем, то энергия и мощность сигнала определяются выражением

Детерминированные и случайные сигналы

называется детерминированным сигналом.

Пример: f(t) = 3t + 6

При t=0; f(t) = 3(0) + 6 = 6 (текущая стоимость)

При t=10; f(t) = 3(10) + 6 = 36 (будущее значение)

Если будущее значение сигнала не может быть определено в настоящее время, такие сигналы называются случайными сигналами, такие сигналы можно только ожидать или оценивать.

Причинные и непричинные сигналы

Если f(t) является сигналом таким, что

f(t)= 0; t<0

Тогда f(t) называется причинным сигналом.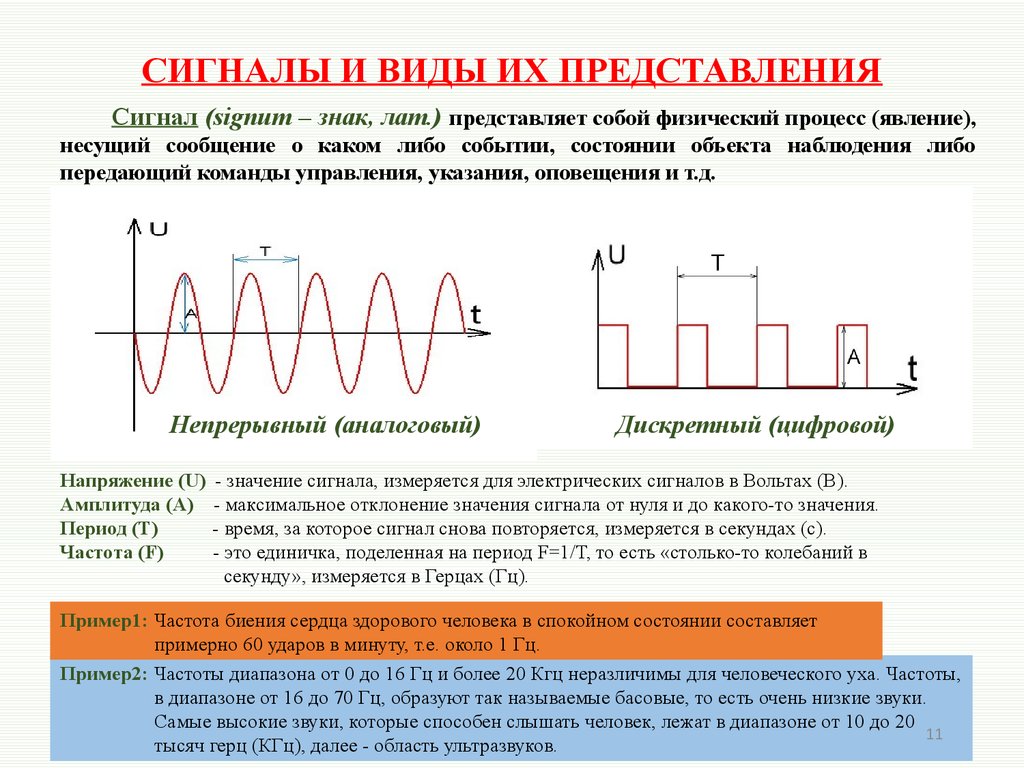

Пример:

Если f(t) является сигналом, который имеет определенное значение в интервале t<0; такие сигналы известны как некаузальные сигналы.

f(t) ≠ 0; t < 0

Пример:

Аналоговые и цифровые сигналы

По времени сигналы подразделяются на сигналы с непрерывным временем и сигналы с дискретным временем. Аналогично по значению сигналы классифицируются на аналоговые и цифровые. Если значение сигнала может быть любым действительным значением в его динамическом диапазоне, такие сигналы известны как аналоговые сигналы. В то время как, если сигналу разрешено учитывать определенные значения в его динамическом диапазоне, такие сигналы называются цифровыми сигналами.

Что такое сигнал? Типы сигналов, их свойства, действие и применение

Что такое сигнал?

Сигнал определяется как любая физическая или виртуальная величина , которая изменяется в зависимости от времени или пространства или любой другой независимой переменной или переменных.

Графически независимая переменная представлена ​​ горизонтальной осью или осью x. И зависимая переменная

представлена ​​ вертикальной осью или осью Y.

Математически сигнал является функцией одной или нескольких независимых переменных.

Содержание

Сигнал с одной переменной

Зависит от одной независимой переменной. Он либо изменяется линейно, либо нелинейно в зависимости от выражения сигнала. Примеры сигнала с одной переменной:

S(x) = x+5

S (x) = x ² +5 , где x является переменной

s (t) = cos (wt +θ) , где t является переменным

.

Сигнал с двумя переменными изменяется при изменении двух независимых переменных. Пример сигнала с двумя переменными:

S(x,y) = 2x+ 5y

• По теме: Что такое квантизация и выборка? Типы и законы сжатия

Характеристики сигнала

Сигнал определяется его характеристиками.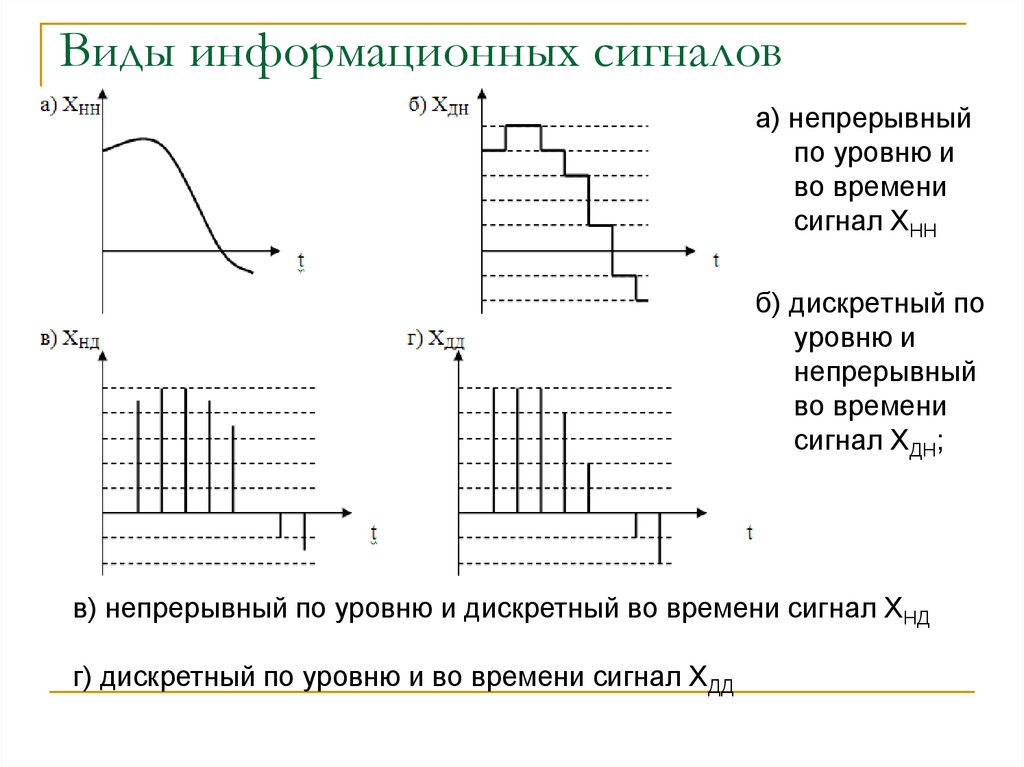 Он показывает характер сигнала. Эти характеристики приведены ниже:

Амплитуда

Амплитуда – это сила или высота формы волны сигнала. Визуально это высота сигнала от его центральной линии или оси x. Ось Y формы волны сигнала показывает амплитуду сигнала. Амплитуда сигнала меняется со временем.

Например, амплитуда синусоиды — это максимальная высота формы волны по оси Y.

Сила сигнала обычно измеряется в децибелах дБ .

Частота

Частота — это частота повторений сигнала в секунду.

Периодические сигналы повторяют свой цикл через некоторое время. Число циклов в секунду известно как Частота . Единицей частоты является герц (Гц) и один герц равен одному циклу в секунду. Он измеряется по оси x формы волны.

Например, синусоида 5 герц завершит свои 5 циклов за одну секунду .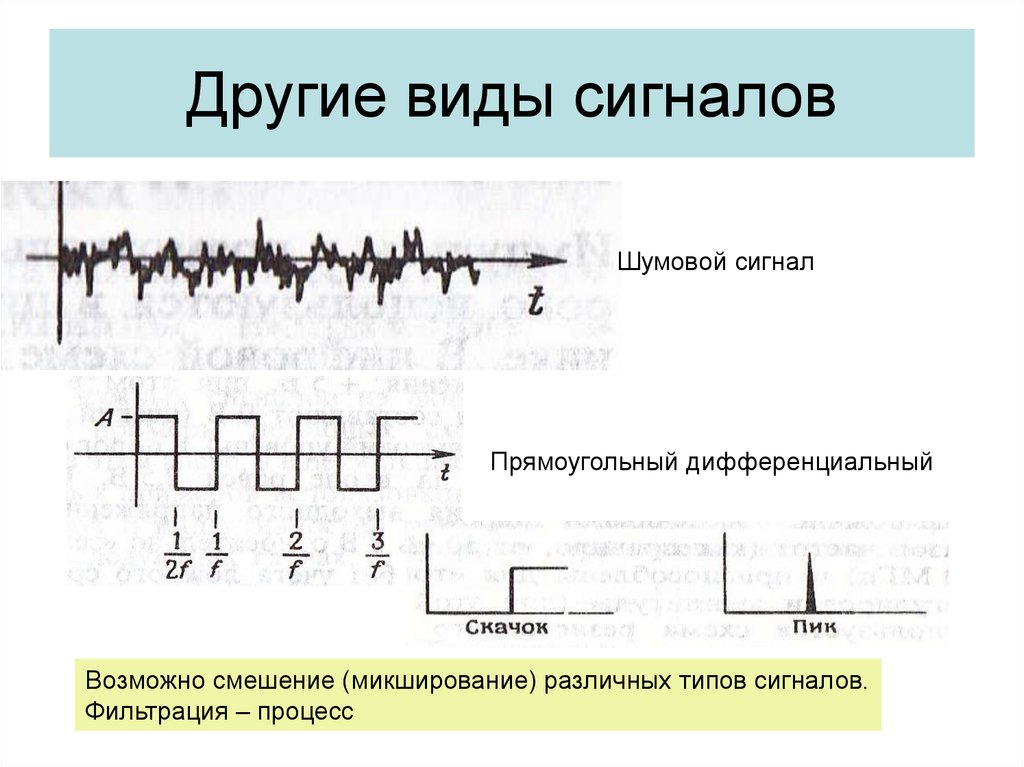

Время Период

Период времени сигнала – это время, за которое он совершает один полный цикл. Единицей периода времени является секунды . Период времени обозначается цифрой 9.0003 ‘T’ и это инверсия частоты . т.е.

T=1/F

Например, синусоида с периодом времени 10 секунд завершит свой один полный цикл за 10 секунд .

Фаза

Фаза синусоидального сигнала представляет собой сдвиг или смещение в исходной или начальной точке. Фазовый сдвиг может быть с отставанием или с опережением . Обычно исходные синусоидальные сигналы имеют фазу 0° градусов и начинаются с амплитуды 0, но смещение по фазе сдвинет его начальную амплитуду не на 0.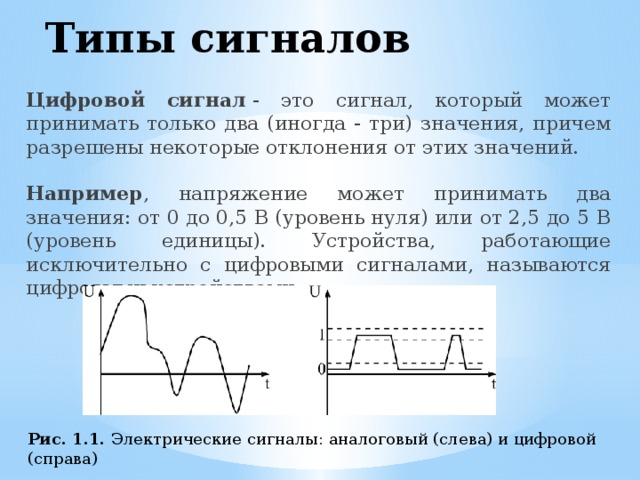

Пример фазового сдвига 45° приведен ниже. Сигнал остается прежним, но его источник смещается на 45° .

Фазовый сдвиг может быть от 0° до 360° градусов или 0 до 2π радиан . 360° градусов или 2π радиан — это один полный период.

Запись по теме: Что такое GSM и как он работает?

Размер сигнала

Размер сигнала — это число, которое показывает силу или размер этого сигнала. Как известно, амплитуда сигнала меняется со временем. Из-за этого изменения мы не можем сказать, что его амплитуда может быть его размером. Чтобы измерить размер сигнала, мы должны принять во внимание площадь , покрытую амплитудой сигнала в течение времени.

В зависимости от размера сигнала есть два параметра.

Энергия сигнала

Энергия сигнала представляет собой площадь сигнала под его кривой.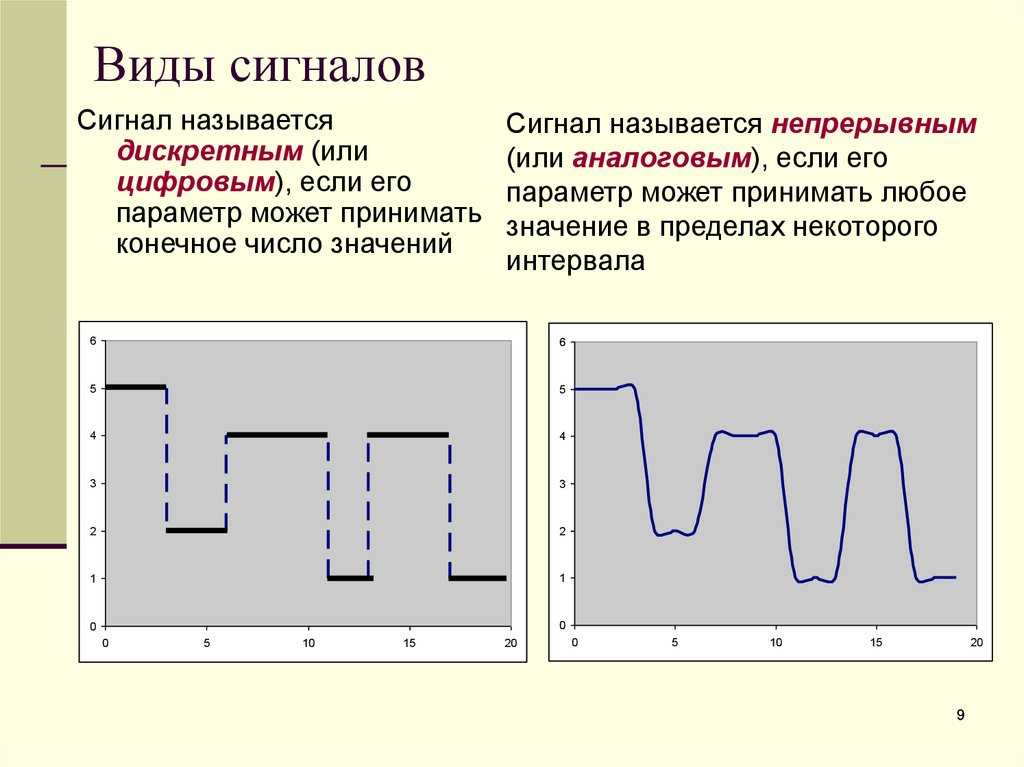 Но сигнал может быть как в положительной, так и в отрицательной области. Из-за чего они будут компенсировать эффект друг друга, что приведет к меньшему сигналу. Чтобы устранить эту проблему, мы возьмем квадрат амплитуды сигнала , которая всегда положительна.

Для сигнала g(t) площадь под г ² (t) известен как Энергия сигнала .

Единица Энергии Сигнала

Эта энергия не берется в обычном смысле, но она показывает величину сигнала. Следовательно, его единицей измерения не является джоуль. Единица энергии зависит от сигнала . Если это сигнал напряжения , то его единицей измерения будет вольт ² /секунда .

Ограничение

Энергия сигнала может быть измерена, только если сигнал является конечным.   бесконечный сигнал будет иметь бесконечную энергию

, что абсурдно. Амплитуда конечного сигнала достигает 0 по мере того, как время (t) приближается к бесконечности (∞).

Итак, необходимо , чтобы сигнал был конечным   сигналом , если вы хотите измерить его энергию.

• Запись по теме: Что такое WiMAX? Разница между широкополосным WiMax и WiFi

Мощность сигнала

Если сигнал является бесконечным сигналом , то есть его амплитуда не достигает 0 по мере того, как время t приближается к ∞ , мы не можем измерить его энергию. В таком случае мы берем среднее время ( Период времени ) энергии сигнала как мощность сигнала.

Единица мощности

Подобно энергии сигнала, эта мощность также не принимается в общепринятом смысле. также будет зависят от измеряемого сигнала . Если сигнал сигнал напряжения , то мощность будет в вольт ² .

Ограничение

Точно так же, как и энергия сигнала, измерение мощности сигнала также имеет некоторые ограничения, заключающиеся в том, что сигнал должен быть периодической природы . бесконечный и непериодический сигнал не имеют ни энергии, ни мощности .

Классификация сигналов

Сигналы классифицируются по различным категориям в зависимости от их характеристик. Некоторые из этих категорий приведены ниже.

Аналог. Цифровой сигнал

Сигнал можно разделить на аналоговый или цифровой на основании его амплитуды . Эта классификация основана только на вертикальной оси (амплитуда) сигнала. И это не имеет никакого отношения к горизонтальной оси (оси времени).

Амплитуда аналогового сигнала может иметь любое значение (включая дроби) в любой момент времени. Это означает, что аналоговый сигнал имеет бесконечных значения .

Однако амплитуда цифрового сигнала может иметь только конечных и дискретных значений.

Особый случай Цифрового сигнала, имеющего два дискретных значения, известен как Двоичный сигнал

. Однако количество значений амплитуды в цифровом сигнале равно 9.0003 не ограничено до только два .

Аналоговый сигнал преобразуется в цифровой с помощью аналого-цифрового преобразователя (АЦП) .

• Запись по теме: Что такое промышленные коммуникационные сети? Обзор

Сигнал непрерывного и дискретного времени

Эта классификация основана на горизонтальной оси (оси времени) сигнала.

Непрерывные и дискретные сигналы времени не следует путать с аналоговыми и цифровыми сигналами соответственно.

Сигнал непрерывного времени — это сигнал, значение (амплитуда) которого существует в течение каждой доли от времени t.

Сигнал дискретного времени существует только для дискретного значения из времени t .

Помните , нет ограничений на амплитуду сигнала. Вот почему его не следует путать с аналоговым или цифровым сигналом.

Энергия против. Сигнал мощности

Сигнал равен Сигнал энергии , если его амплитуда достигает 0 , когда время приближается к ∞ . Энергетические сигналы имеют конечную энергию.

Точно так же сигнал с конечной мощностью называется сигналом мощности.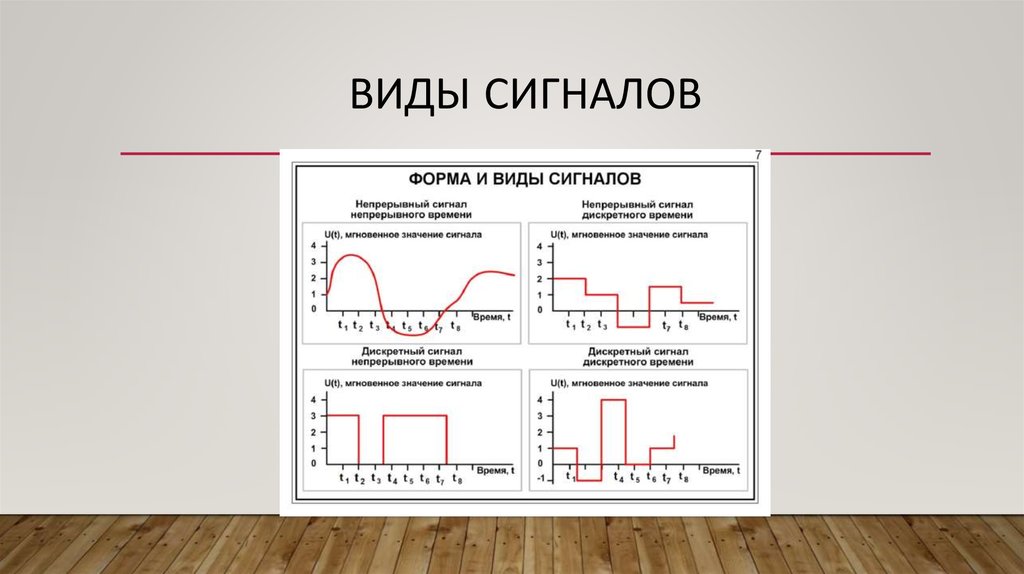

Сигнал мощности является периодическим сигналом , то есть он имеет период времени.

Сигнал Energy имеет конечную энергию , но нулевую мощность . А сигнал мощности имеет конечную мощность , но бесконечную энергию . Таким образом, сигнал может быть либо сигналом энергии , либо сигналом мощности , но не может быть одновременно . .

• Запись по теме: Интернет вещей (IOT) и его приложения в электроэнергетике

Периодический против. Апериодический сигнал

Периодический сигнал — это сигнал, который поддерживает повторение своего шаблона после минимального фиксированного времени . Это время известно как период времени «T»  для этого сигнала.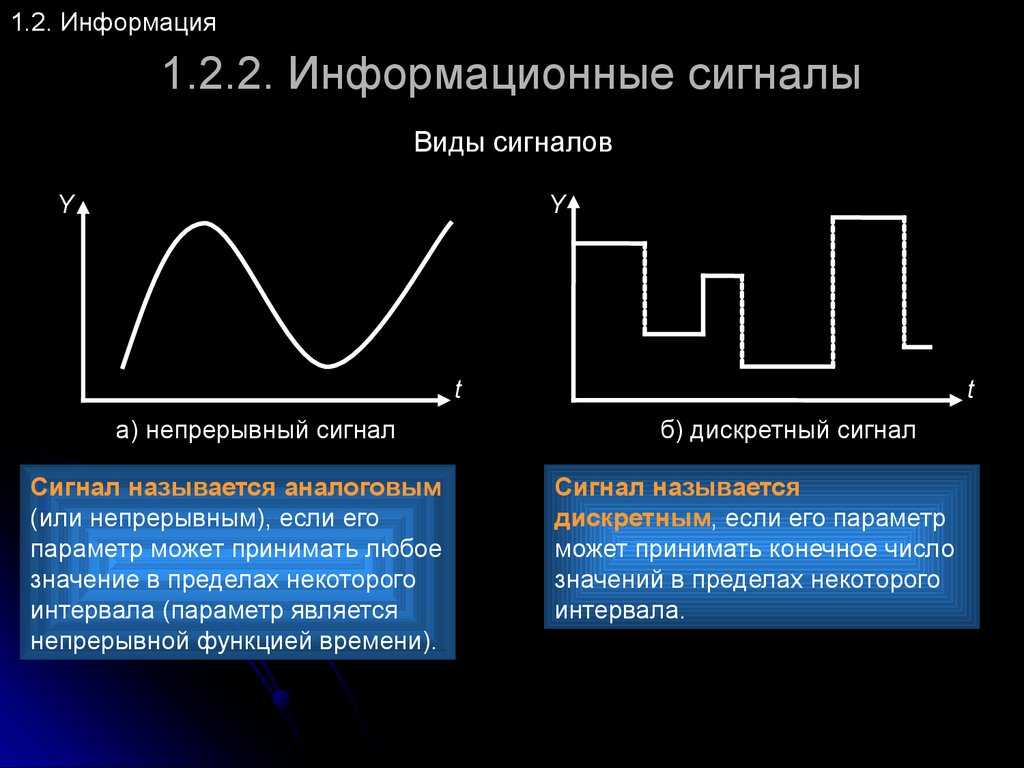 Периодический сигнал не изменяется, если он сдвинут во времени на любое число, кратное периоду времени «T».

Математическое выражение для периодического сигнала g(t) :

T ₀ — период времени сигнала g(t) .

Периодический сигнал начинается с t=-∞ и продолжается до t=+∞ . Сигнал, который начинается с t=0 , не будет тем же самым сигналом, если он сдвинут во времени на +T, потому что он не существовал для отрицательных t.

Апериодический или непериодический сигнал — это сигнал, который не повторяет через определенное время. Эти сигналы имеют без повторений любой шаблон.

Детерминированный и случайный сигнал

Сигнал, который может быть представлен в математической или графической форме , называется детерминированным сигналом .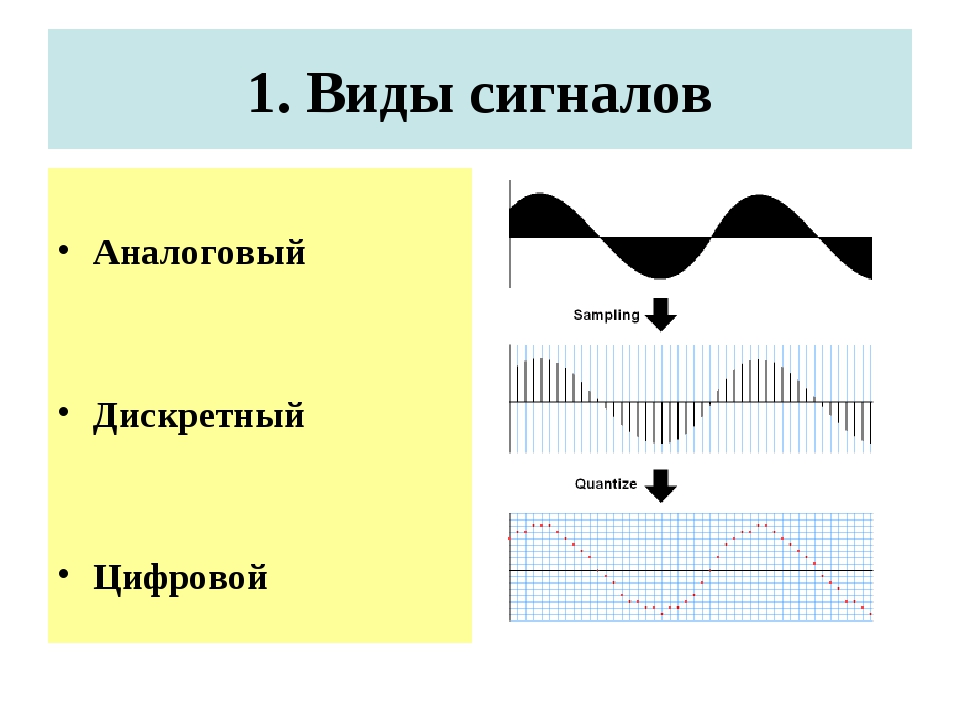 Детерминированные сигналы имеют заданную амплитуду , частоту и т. д. Их легко обрабатывать, поскольку они определяются в течение длительного периода времени, и мы можем Оценить его результат , если они применяются к конкретной системе на основе ее выражения.

Случайный или недетерминированный сигнал — это сигнал, который может быть представлен только вероятностным выражением , а не его полным математическим выражением. Каждый сигнал, который имеет какую-то неопределенность , является случайным сигналом . Шумовой сигнал — лучший пример случайного сигнала.

Как правило, каждый сигнал сообщения является случайным сигналом, потому что мы не уверены в информации, которая должна быть передана другой стороне.

• Связанная запись: Что такое нечеткая логическая система — работа, примеры, преимущества и приложения

Работа сигнала

Некоторые базовые операции сигналов приведены ниже

Время смены

Сдвиг времени означает Движение сигнала через Time Axis ( Horizontal Axis ). Сдвиг сигнала во времени не изменяет сам сигнал, а только сдвигает источник сигнала из исходной точки по оси времени.

По сути, сложение во времени — это сдвиг во времени. Для сдвига во времени сигнал g(t) , t следует заменить на (t-T) , где T — секунды сдвига во времени . Следовательно, g(t-T) — это сигнал, сдвинутый во времени на T секунд.

Временной сдвиг может быть сдвиг вправо (задержка) или сдвиг влево (ускорение).

Если временной сдвиг T равен положительному , то сигнал сдвинется на справа (задержка). Например, сигнал g(t-4) является сдвинутой версией g(t) с задержкой 4 секунд .

Если временной сдвиг T равен отрицательному , то сигнал сдвинется на влево (вперед). Сигнал g(t+4) является сдвинутой версией g(t) с 4 секунды до слева .

Масштабирование времени

Временное масштабирование сигнала означает сжатие или расширение сигнала. Это достигается умножением временной переменной сигнала на коэффициент . Сигнал расширяется или сжимается в зависимости от фактора.

Предположим, что сигнал g(t) , тогда его масштабированная версия равна g(at) .

Если коэффициент a>1 , то сигнал будет сжиматься . А операция называется сжатие сигнала . Сжатие сигнала сделает сигнал быстрым , так как он станет меньше, а его продолжительность станет меньше.

Если a<1 , то сигнал будет расширяться .