Входное сопротивление
У любого электрического устройства, для работы которого требуется сигнал, имеется входное сопротивление. Точно так же, как и любое другое сопротивление, входное сопротивление устройства есть мера тока, текущего по входной цепи, когда ко входу приложено определенное напряжение.
Например, входное сопротивление 12-вольтовой осветительной лампы, потребляющей 0,5 А, равно 12/0,5 = 24 Ом. На первый взгляд, наличие в схеме конденсаторов, резисторов и полупроводниковых p-n переходов делает определение входного сопротивления трудным. Однако любую входную цепь, какой бы сложной она ни была, можно представить в виде простого импеданса (рис9.5).
Рис. 9.5. Схема с парой входных клемм, иллюстрирующая понятие входного импеданса Zin.
Если Vin — напряжение переменного входного сигнала, а Iin — переменный ток, текущий по входной цепи, то входной импеданс равен
Zin = Vin/Iin
У
большинства схем входной импеданс имеет
резистивный (омический) характер в
широком диапазоне частот, в пределах
которого сдвиг по фазе между входным
напряжением и входным током пренебрежимо
мал.
В этом случае справедлив закон
Ома и нет необходимости в алгебре
комплексных чисел и в векторных
диаграммах, применяемых к цепям с
реактивными элементами. Важно отметить,
однако, что из омического характера
входного импеданса не обязательно
следует возможность его измерения на
постоянном токе; на пути входного сигнала
могут находиться реактивные компоненты
(например, разделительный конденсатор),
которые несущественны в отношении
переменного сигнала на средних
частотах, но не позволяют проводить
измерения во входной цепи на постоянном
токе.
Измерение входного сопротивления
Cпособ измерения входного сопротивления показан на рис. 9.6.
Рис. 9.6. Измерение входного сопротивления
Резистор
с известным сопротивлением R
Ом включают между генератором и входом
схемы. Затем с помощью осциллографа
или вольтметра переменного напряжения
с высокоомным входом измеряются
напряжения V1,
и V2 по обе стороны резистора R.
Если Iin — переменный входной ток (в амперах), то, согласно закону Ома, на резисторе R падает напряжение, равное
V1 – V2 = RIin вольт.
Поэтому
Iin = (V1 – V2)/R ампер.
Входное сопротивление
Zin = V2/Iin,
следовательно,
Zin = V2R/(V1 – V2) = R/(V1/V2 – 1) Ом.
Если
схема является усилителем, то V1,
и V2,
удобнее измерять на выходе усилителя:
V
V1/V2 = Vвых1/Vвых2 .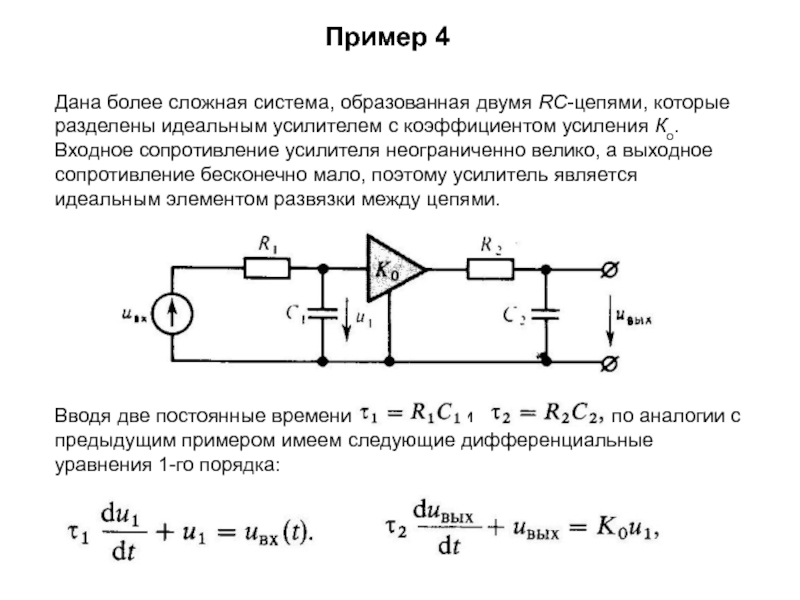
Пример: если включение последовательно со входом резистора с сопротивлением 10 кОм вызывает уменьшение напряжения на выходе усилителя наполовину, то V1
Выходное сопротивление
Пример, дающий представление о выходном сопротивлении: свет фар автомобиля тускнеет при работе стартера. Большой ток, потребляемый стартером, вызывает падение напряжения внутри аккумулятора, в результате чего напряжение на его клеммах уменьшается и свет фар становится менее ярким. Это падение напряжения происходит на выходном сопротивлении аккумулятора, возможно, более известном как внутреннее сопротивление или сопротивление источника. Этот пример можно распространить на все выходные цепи, включая цепи постоянного и переменного тока, у которых всегда имеется определенное выходное сопротивление, соединенное с источником напряжения.
9.7), где Zout —
выходной импеданс, а V- выходное напряжение
холостого хода, то есть напряжение на
выходе разомкнутой цепи.Рис. 9.7. Эквивалентная схема, применимая к любой паре выходных клемм в соответствии с теоремой Тевенина
Из
рис. 9.7, видно, что, когда к выходным
клеммам подключается резистор или
входные клеммы другого устройства,
часть напряжения источника V падает на
внутреннем импедансе Z
13.5. Входное сопротивление линии. 13. Цепи с распределенными параметрами. Теория электрических цепей. Курс лекций
- Главная
- Теория электрических цепей
- 13. Цепи с распределенными параметрами
- Категория: 13. Цепи с распределенными параметрами
Входное сопротивление линии определяется отношением напряжения и тока в начале линии. Найдем выражение для Zвх, используя уравнения передачи линии в форме (13.9 в):
Рассмотрим некоторые частные режимы работы линии.
При согласованном включении линии (Zн = Zв) из (13.16) получим, что Zвх = Zв как и было установлено ранее.
Если выходные зажимы линии замкнуты накоротко (Zн = 0), формула (13.
16) упрощается и принимает вид
В случае разомкнутых выходных зажимов (Zн = бесконечность)
Когда линия нагружена на произвольное сопротивление, не равное волновому (Zн <> Zв), можно пользоваться для расчетов общей формулой (13.16). Однако иногда удобно выразить Zвх через параметры XX и КЗ. Для этого разделим числитель и знаменатель (13.16) на
Данная формула позволяет по измеренным значениям сопротивлений XX и КЗ рассчитать входное сопротивление линии.
Существует еще одна форма представления входного сопротивления. Для получения ее перепишем выражение (13.16) после деления на
в другом виде:
Обозначим
.
Тогда
Эта формула дает возможность по заданным параметрам Zв и Zн определить
и затем найти входное сопротивление линии.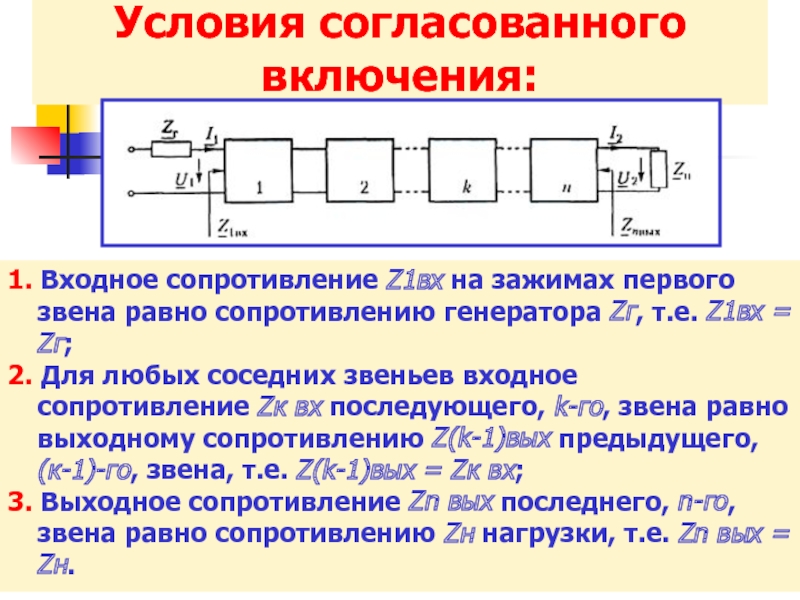
Во всех случаях, когда нагрузка на конце линии не равна ее волновому сопротивлению, входное сопротивление определяется гиперболическим тангенсом комплексного аргумента. Чтобы дать представление о характере изменения входного сопротивления линии, на рис. 13.7, а показаны зависимости модулей сопротивлений XX и КЗ от длины линии, построенные в соответствии с формулами (13.17), а на рис. 13.7, б изображена зависимость модуля Zвх от частоты из (13.18) при несогласованной нагрузке линии.
- Главная
- Радиотехника и Электроника
- 13. Цепи с распределенными параметрами
org/ListItem»>
Теория электрических цепейВходное сопротивление | bartleby
Что такое входной импеданс?РасчетВходной импеданс усилителяВходной и выходной импедансВажность импедансовВходной импеданс линии передачи и операционного усилителяКонтекст и применениеПрактические задачиСвязанные понятия
Что такое входной импеданс?
Это сопротивление, оказываемое потоку тока как статическим, так и динамическим сопротивлением в сеть, которая является внешней по отношению к источнику. Свойства источника для нагрузки были бы такими же, если бы сеть на стороне нагрузки была заменена устройством, у которого выходное сопротивление равно входному сопротивлению эквивалентной схемы. Следовательно, напряжение и ток через входные клеммы будут такими же, как и в выбранной эквивалентной сети нагрузки.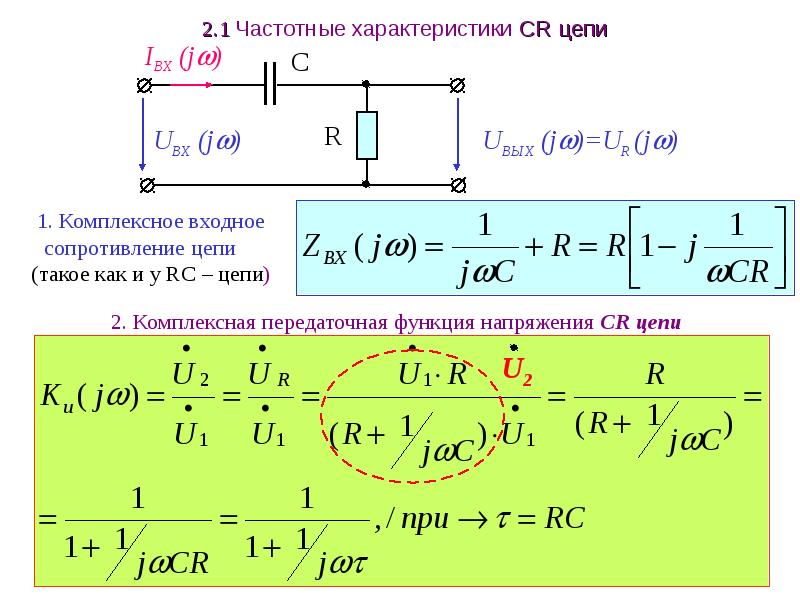
Входное сопротивление и выходное сопротивление определяют, как изменяются ток и напряжение в цепи.
CC BY-SA 4.0 | Изображение предоставлено: https://en.m.wikipedia.org/wiki/Input_impedance | Cjp24Расчет
Закон Ома можно использовать для расчета передаточной функции, если мы собираемся создать с одинаковыми характеристиками на стороне входа, поместив входное сопротивление на стороне нагрузки сети, а выходное сопротивление последовательно с источником.
Электрическая эффективность
Значения Zin и Zout часто используются для определения эффективности электрических сетей, и каждый этап оценивается независимо путем разбиения нескольких этапов. Электрические потери сведены к минимуму, когда Zout незначителен по сравнению с Zin. В этом случае Zin>>Zout, которое представляет собой входное сопротивление, намного больше, чем выходное сопротивление.
Коэффициент мощности
В цепях переменного тока потери, вызванные реактивными компонентами, могут быть незначительными.
Это называется дисбалансом фаз, когда ток не совпадает по фазе с потенциалом. Поэтому по этой причине произведение тока и потенциала меньше исходного значения, если бы ток и потенциал находились в фазе друг с другом. В случае источника постоянного тока коррекция коэффициента мощности не требуется, так как нет влияния реактивных цепей.
Передача мощности
Когда сопротивление источника равно сопротивлению нагрузки, говорят, что мощность передается в максимальном количестве. Коэффициент мощности корректируется путем компенсации реактивного сопротивления цепи. Схема называется комплексно-сопряженной, когда это происходит. Это не максимизирует эффективность схемы, а максимизирует только передачу мощности. Схема работает с половинной эффективностью, когда передача мощности оптимизирована.
Входное сопротивление усилителя
Входное сопротивление — это входная характеристика усилителя относительно напряжения от источника питания и тока от источника тока на входных клеммах усилителя.
Входное сопротивление является одним из важных параметров при разработке усилителей. Он характеризует усилитель в соответствии с эффективным выходным и входным сопротивлениями, включая их мощность и номинальные токи. Входное сопротивление обозначается как Zin, а выходное сопротивление обозначается как Zout.
Чтобы свести к минимуму искажения сигнала, значение импеданса усилителя очень важно для анализа каскадных каскадов усилителя вместе друг за другом. Зин — это сопротивление, которое видит источник. Если значение слишком низкое, это может иметь неблагоприятный эффект нагрузки, и это может повлиять на предыдущий каскад, возможно, повлиять на уровень выходного сигнала и частотно-зависимую характеристику каскада. Усилители с общим эмиттером и общим коллектором обычно имеют высокое значение Zin, любое произвольное синфазное усиление и низкий выходной импеданс, но если Zin ниже желаемого значения, выходное сопротивление предыдущего каскада можно отрегулировать, чтобы нейтрализовать его или каскады можно использовать буферный усилитель.
Схема усилителя должна иметь усиление тока наряду с усилением напряжения. Схема также может иметь усиление мощности. Идеальный усилитель должен иметь бесконечный Zin и нулевой выходной импеданс, то есть каждый усилитель должен иметь эти три параметра: высокий входной импеданс, низкий выходной импеданс и полосу пропускания.
Входной и выходной импеданс
Схема усилителя может рассматриваться или представляться как черный ящик с двумя входными и двумя выходными клеммами. Здесь резистор ZS – это выходной резистор, а резистор ZL – входной резистор на первом рисунке.
Если мы посмотрим на эти клеммы схемы, то увидим, что входное и выходное сопротивление представляют собой отношение напряжения к току, протекающему через эти клеммы. Zin зависит от источника, но выходное сопротивление зависит от сопротивления нагрузки. Усиленные входные сигналы представляют собой переменные токи с эквивалентной схемой усилителя, представляющей собой нагрузку. Входное сопротивление может быть от омов (Ом) до килоомов (кОм) для биполярных транзисторов и мегаомов (МОм) для транзисторов на основе полевых транзисторов.
Зин котируется на указанной частоте сигнала. Zin — это отношение входного синусоидального напряжения слабого сигнала к току, протекающему через входные клеммы в заданном диапазоне частотной характеристики. Импеданс выхода также указан для указанной частоты сигнала. Кроме того, если в цепи присутствуют емкость и индуктивность, то на них влияет частота, поэтому Zin также изменяется.
Важность импедансов
Концепция сопротивления входа и выхода очень важна для согласования импедансов. Согласование импеданса — это концепция, согласно которой передача мощности максимальна, когда мощность передается от сопротивления внутреннего источника к сопротивлению нагрузки, то есть когда ZS = ZL.
Входное сопротивление линии передачи и операционного усилителя
Входное сопротивление линии передачи — это сопротивление, воспринимаемое любым входящим в нее сигналом. Затухания нет, если линия идеально подходит для передачи амплитуд сигнала. Когда линия имеет бесконечную длину, входное сопротивление равно волновому сопротивлению.
Характеристическое сопротивление определяется как отношение напряжения к току бегущей волны, входящей в линию. Это важный параметр при проектировании этих линий.
Импеданс источника, видимый управляющим устройством операционного усилителя, — это Zin, который должен обеспечиваться источником сигнала. Для неинвертирующего режима входное сопротивление представляет собой сопротивление входной клеммы, измененное эффектами обратной связи, тогда как для инвертирующего режима может быть сложно достичь высокого сопротивления из-за токов утечки в проводке или печатных платах.
Контекст и приложения
Эта тема имеет важное значение на профессиональных экзаменах для бакалавриата, магистратуры и аспирантуры.
- Бакалавр электротехники
- Магистр электротехники
Практические задачи
1. Каково значение входного сопротивления согласованной линии?
- Сопротивление нагрузки
- Характеристическое сопротивление
- Выходное сопротивление
- Сопротивление усилителя напряжения
Ответ: Вариант b
Объяснение: Значение входного импеданса для согласованной линии будет равно характеристическому сопротивлению, поскольку согласованная линия относится к той же характеристике и входному сопротивлению.
2. Какое сопротивление видит источник?
- Вход
- Выход
- Оба
- Нет
Ответ: Вариант a
Объяснение: сопротивление, видимое источником, является импедансом входной клеммы.
3. Что важно для минимизации искажений?
- Значение импеданса усилителя
- Резонанс цепи
- Значение напряжения питания
- Значение реактивного сопротивления цепи
Ответ: Вариант а
Пояснение: Для минимизации искажения сигнала значение импеданса усилителя очень важно для анализа последовательно соединенных каскадов усилителя
4. От чего зависит входное сопротивление?
- Источник
- Вход напряжения Thevenin
- Оба
- Нет
Ответ: Вариант a
Объяснение: 90 076 Входное сопротивление зависит от источника, поскольку источник подключен только к входным клеммам.
5. Когда передача мощности максимальна?
- RL>RS
- RL=RS
- RL
- Нет
Ответ: Вариант b
Объяснение ation: Максимальная передача мощности при RL=RS
- Выходное сопротивление
- Транзисторы
- Делитель напряжения
Мы обеспечим вас пошаговыми решениями миллионов задач из учебников, 24 часа в сутки, 7 дней в неделю, когда вы в тупике, и многое другое.
Ознакомьтесь с примером решения вопросов и ответов по электротехнике здесь!*Время ответа зависит от темы и сложности вопроса. Среднее время отклика составляет 34 минуты для платных подписчиков и может быть больше для рекламных предложений.
Изучайте умный доступ к миллионам пошаговых учебников, нашей библиотеке вопросов и ответов и математическому решателю на основе искусственного интеллекта. Кроме того, вы ежемесячно получаете 30 вопросов, которые нужно задать эксперту.
МашиностроениеЭлектротехника
Микроволновая техника
Линия передачи
Входное сопротивление
Входное и выходное сопротивление — Вики курса
Материал из Вики курса
Перейти к: навигация, поиск
Что происходит, когда мы соединяем один компонент схемы с другим? Иногда компонент схемы ведет себя по-разному, когда он сам по себе, и когда он подключен к другому компоненту. Чтобы понять, как будет вести себя схема, мы должны рассмотреть входное и выходное сопротивление различных частей. выходной импеданс относится к импедансу или противодействию протеканию тока компонента, который часто имеет электрический источник для «управления» компонентом нагрузки. Между тем, входное сопротивление относится к сопротивлению компонента нагрузки току, протекающему от источника электричества. Во многих случаях вы захотите иметь высокое входное сопротивление по сравнению с выходным сопротивлением, и в следующих разделах вы поймете, почему.
Давайте рассмотрим пример подключения батареи к резистору. Когда мы видим батарею на 9 В, мы часто думаем, что она должна выдавать 9 В на своих клеммах. Это действительно так, но только тогда, когда он не получает никакого тока. Оказывается, внутри батареи есть некоторый внутренний импеданс, который не позволяет выходному напряжению оставаться на уровне 9 В, когда начинает течь ток. Таким образом, мы можем смоделировать батарею как источник чистого напряжения, соединенный последовательно с резистором, где значение сопротивления $ R_{out} $ равно выходному сопротивлению батареи. Вот пример 9ВАХ батареи V (соотношение ток-напряжение).
Модель батареи 9 В, показывающая внутреннее сопротивление в виде резистора со значением $ R_{out} $. $ I_{SC} $ относится к току короткого замыкания (если провод был помещен между выходными клеммами), а $ V_{OC} $ относится к напряжению холостого хода (напряжение, измеренное между выходными клеммами при отсутствии тока).
течет)Теперь подключим к этому источнику нагрузку. Для простоты подключим резистор сопротивлением $R_{in}$. Следовательно, входное сопротивление этой нагрузки равно $R_{in}$. Когда мы строим ВАХ нагрузки с источником, пересечение двух линий является рабочей точкой.
Выходное сопротивление нагрузки равно $ R_{out} $. Когда нагрузка подключена к источнику, рабочая точка определяется пересечением двух линий на графике ВАХ. Рабочая точка дает напряжение, приложенное к нагрузке, а также количество тока, протекающего через нее. Здесь мы видим, что после подключения нагрузки к источнику выходное напряжение больше не равно 9 В; скорее это задается рабочей точкой. В приведенном выше примере показана батарея 9 В, имеющая выходное сопротивление 1,5 Ом, и нагрузка, имеющая входное сопротивление 3 Ом. Если вы используете соотношения делителя напряжения для расчета напряжения, приложенного к нагрузке, и тока, протекающего через нее, вы обнаружите, что оно составляет 6 В и 2 Ом соответственно, как указано в рабочей точке графически.
Это показывает нам, что хотя 9Батарея V выдает 9 В, когда ток отсутствует, как только мы применяем нагрузку, выходное напряжение падает до 6 В, чтобы учесть увеличенный ток.
Что произошло бы, если бы сопротивление нагрузки было очень высоким? Подумайте, как изменение наклона ВАХ для нагрузки повлияет на рабочую точку.
Изучив предыдущий пример, вы можете увидеть, что нагрузка на источник, входной импеданс которого по величине аналогичен выходному импедансу источника, приводит к падению выходного напряжения. Как можно нагрузить источник таким образом, чтобы поддерживать выходное напряжение?
Если $ Z_{in} >> Z_{out} $ (входной импеданс нагрузки >> выходной импеданс источника), , то выходное напряжение источника может быть достаточно близко к его напряжению холостого хода, что мы можем игнорировать изменения, вызванные Загрузка. Один из способов думать об этом состоит в том, что если входное сопротивление нагрузки очень велико по сравнению с выходным сопротивлением источника, то он не будет потреблять большой ток от источника, и напряжение в точке подключения будет поддерживаться.
Это хороший принцип, которому следует следовать при соединении различных компонентов вместе.
1. Каково выходное сопротивление $ Z_{out} $ следующей цепи? Мы хотим подключить еще один контур к синим узлам.
Решение: При нахождении выходного импеданса мы «заглядываем» в синие выходные узлы схемы. Помните из показанной ранее кривой ВАХ, что $ Z_{out} = {V_{oc} \over I_{sc}} $, где $ V_{oc} $ — напряжение холостого хода (когда синие узлы остаются открытыми). , $V_{oc}=V_{in}{Z_2 \over Z_1 + Z_2}$) и $I_{sc}$ — ток короткого замыкания (при замыкании синих узлов $I_{sc}={V_ {in}\over Z_1}$). Другими словами, выходное сопротивление аналогично эквивалентному сопротивлению Thevenin. Кратчайший способ найти $Z_{out}$ — заменить источник напряжения проводом и найти эквивалентное сопротивление или импеданс. Здесь, если мы заменим источник напряжения проводом, схема будет выглядеть как параллельные резистор и конденсатор, где $ Z_{out} = {Z_1 Z_2 \над Z_1 + Z_2} $ .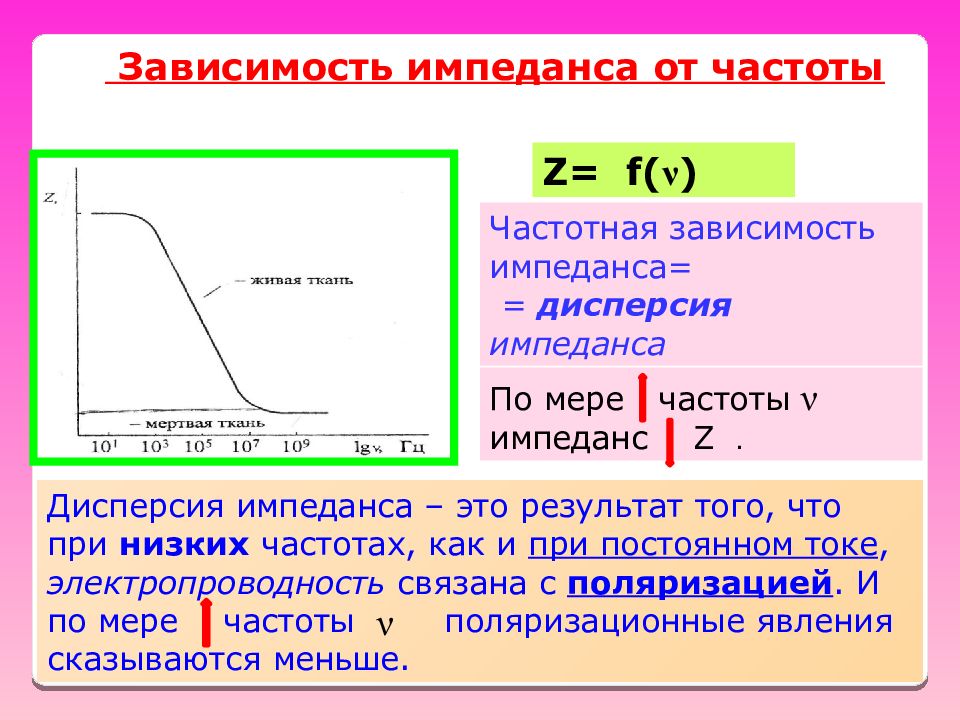
2. Если мы хотим подключить еще один фильтр нижних частот (контур 2) последовательно со схемой из вопроса 1 (контур 1), какой критерий должен соблюдаться, чтобы мы могли игнорировать влияние нагрузки второго контура? Запишите ответ в виде $Z_1, Z_2, Z_3, Z_4$.
Решение: Мы знаем, что для игнорирования нагрузки нам нужно $ Z_{out} << Z_{in} $. Поскольку мы уже нашли $ Z_{out} $ в вопросе 1, теперь нам нужно найти $ Z_{in} $. Глядя на узлы схемы 2, она выглядит как последовательно соединенные резистор и конденсатор. Здесь нет источников напряжения, которые можно заменить проводами, у нас есть просто разомкнутая цепь с резистором, подключенным к конденсатору. Таким образом, $ Z_{in} = Z_3 + Z_4 $. Заменяя $ Z_{out} $ и $ Z_{in} $, критерием для нас, чтобы игнорировать эффекты загрузки схемы 2, является, если: $ {Z_1 Z_2 \over Z_1 + Z_2} << Z_3 + Z_4 $ .
3. Если мы обнаружим, что критерий из вопроса 2 не соответствует действительности, и контур 2 загружает контур 1, что мы можем поместить между двумя контурами, чтобы изолировать их эффекты?
Решение: Буфер, состоящий из операционного усилителя.
