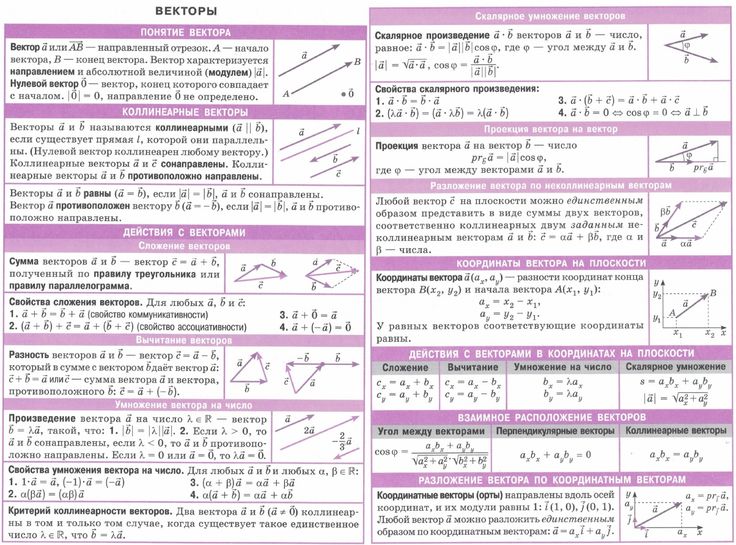
Векторы для чайников. Часть 1. Сложение, разность, умножение на число. — Блог
Векторы для чайников. Часть 1. Сложение, разность, умножение на число.
18 июня 2021 0 Marina Pashnina
Есть на баше одна уже старая шутка про черного кота, которая звучит как-то так:
— Если чёрный кот перешел дорогу туда и обратно, это значит, что он удвоил наказание или отменил своё решение?
— Кот скалярный или векторный? Если скалярный — то удвоил, если векторный — то отменил.
В общем, с этой ноты и начинается статья про то, что было бы, если бы уже знакомый нам кот по имени Котаненс был векторным или скалярным, или статья о векторах.
Вектор — это направленный отрезок и главное, что нужно знать о векторе — у него есть величина и направление. Тут пока все сходится с котом, переходящим дорогу: кот идет в определенном направлении и проходит при этом определенное расстояние.
В школьном курсе геометрии рассматриваются некоторые действия над векторами: сложение векторов, умножение вектора на число, разность векторов. В основном, эти действия интуитивно понятные, достаточно только представить или нарисовать вектор или пару векторов. Давайте коротко рассмотрим эти действия.
Отдельно оговорюсь о существовании нулевых векторов — таких векторов, у которых начало и конец находятся в одной точке. Для упрощения материала этот нулевой вектор будет местами игнорироваться ввиду малой практической значимости.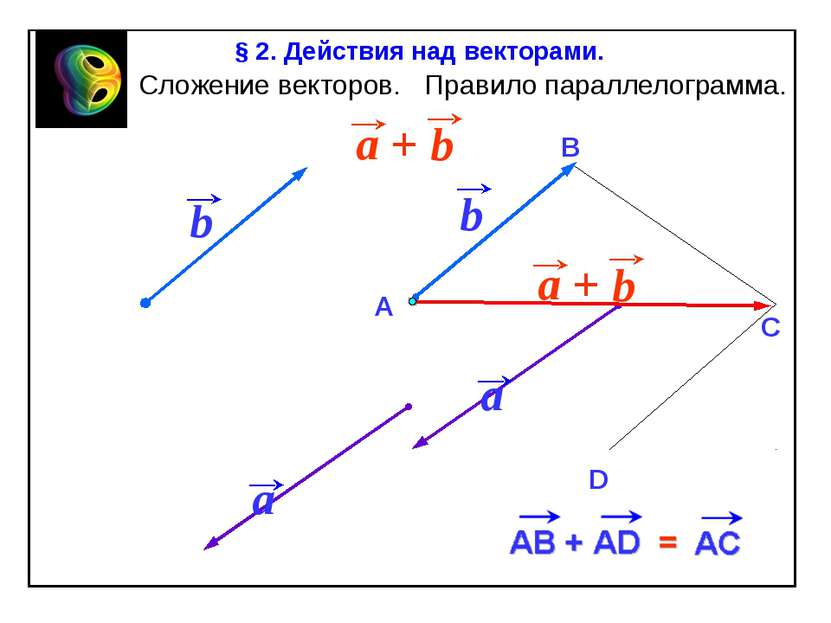
Что ж, начнем.
Сложение векторов
Есть несколько методов сложения векторов, которые руководствуются похожими принципами.
Для сложения двух векторов нам понадобятся вектора ā и b̅ (кто бы мог подумать?) .
Отложим вектор b̅ от вектора ā и проведем от конца вектора ā до начала вектора b̅ результирующий вектор. Этот прием называется правило треугольника.
Результатом сложения будет вектор ā + b̅. Всё также, как с котом: сначала кот прошел по вектору ā (определенное расстояние в определенном направлении), затем по вектору b̅. То, что он прошел в итоге — это и есть результирующий вектор ā + b̅.
Это же работает и для сложения нескольких векторов: кот может пробежать по зиг-загу, или же статно пройти по результирующему вектору.
Если же вектор b̅ отложить не от конца, а от начала вектора ā, то получится правило параллелограмма.
Тут можно вспомнить векторного кота из шутки — если векторный кот пройдет туда-обратно, результирующий вектор, по которому он пройдет — будет равняться 0, а значит — кот отменит свое проклятье.
Скалярный же кот при проходе туда-обратно сложит длины векторов и получит число в 2 раза больше изначального, а значит и проклятье удвоится.
Разность векторов
Разность векторов ā и b̅ также можно рассчитать несколькими способами.
ā — b̅, как частный случай сложения — это сложение вектора ā с вектором, обратному b̅, т.е. ā + (-b̅).
Вектор -b̅, обратный к вектору b̅ сделать просто: кот просто должен пойти в обратную сторону.
А дальше просто складываем этот вектор с вектором ā.
Второй способ получить разность векторов чуть сложнее для осознания: разностью векторов ā и b̅ называется такой вектор, сумма которого с вектором b̅ дает вектор ā. Для понимания достаточно просто нарисовать на листочке и все станет ясно.
Умножение вектора на число
Умножение вектора a на число n создает такой вектор, длина которого равна |ā| * | n |, где |ā| — это длина вектора a, а направление сохраняется при n >= 0 и меняется при n < 0.
Эта статья оказалась достаточно объемной, поэтому я рещила разделить ее на 2 части: во второй части статьи будет рассказано про векторное и скалярное произведение векторов и об этом можно почитать в статье «Векторы для чайников. Часть 2.».
Краткое введение в тензоры / Хабр
В заметке Магия тензорной алгебры было дано очень неплохое введение в математику тензоров. Но, как мне кажется, этот текст все-равно несколько сложен для понимания. В нем не до конца понятно, что же это такое тензор и зачем он вообще нужен.
Сейчас я попытаюсь дать совсем простое введение в тензоры. Я не претендую на математическую строгость, поэтому некоторые термины могут употребляться не совсем корректно.
Откуда появился термин тензор
Насколько я помню, термин тензор происходит от латинского tensus или английского слова tension — напряжение.
Термин возник в процессе осмысления следующей задачи. Пусть нам дано некоторое твердое тело произвольной формы в трехмерном пространстве. К разным концам тела приложены некоторые силы. Как описать возникающие напряжения в некотором сечении этого тела? Ответ на эту задачу — напряжения описываются тензорным полем. Но для понимания этого ответа давайте рассмотрим более простые задачи.
Тензор нулевого ранга
Пусть нам дан в трехмерном пространстве однородный кубик. Давайте его начнем нагревать с какой-либо стороны. Теперь зафиксируем какой-либо момент времени и попробуем описать значения температуры в каждой точке кубика.
Температура — это скаляр, нам нужно только одно число. Введем произвольную систему координат. В рамках этой системы координат температура будет описываться как скалярная функция от
А давайте теперь возьмем другую систему координат. Что изменится? А ничего! Температура в каждой точке пространства осталась таким же скаляром и при смене системы координат не поменялась.
Вот уже интересно! Мы получили некоторый математический объект, скаляр, который не изменяется при смене системы координат. Назовем его тензором нулевого ранга. Идем дальше.
(Уточнение из комментариев: координаты точек изменятся, но температура в этих точках от поворота системы координат не изменится. Именно температура и есть тензор ранга (0,0))
Тензор первого ранга
Итак, мы нагрели наш однородный кубик. Под действием температуры молекулы какого-либо вещества в нем начали как-то двигаться. Опять зафиксируем какой-либо момент времени и попробуем описать значения скоростей молекул в каждой точке кубика.
Скорость — это вектор. Введем произвольную систему координат. В рамках этой системы скорости в каждой точке пространства будут описываться как векторные функции от (x, y, z). А давайте теперь возьмем другую систему координат? Что изменится? Давайте рассуждать.
Векторное поле скоростей в кубике не изменилось, оно осталось таким же, мы просто взяли другую линейку (другую систему координат) для измерения скоростей.
Таким образом, мы получили математический объект, вектор, который опять же не изменяется при смене системы координат, но изменяются его компоненты, причем по заранее определенному закону. Это тензор первого ранга. Теперь начинается самое интересное.
Тензор второго ранга
Мы нагрели наш кубик, молекулы начали двигаться. Но представим теперь, что наш кубик перестал быть однородным. Он теперь пористый, внутри состоит из разных каналов с разной ориентацией. Скорость движения молекулы вдоль канала гораздо больше, чем скорость движения поперек канала. Как нам описать такую неоднородную среду?
Зафиксируем какой-либо момент времени, возьмем одну молекулу со своим вектором скорости. Вопрос, как этот вектор скорости изменится в следующий момент времени? Если молекула попала в канал и вектор ее скорости направлен вдоль канала, то скорость не изменится, если вектор направлен поперек канала, то уменьшится в несколько раз, а если под углом, то вектор скорости вообще изменит свое направление.
Это очень похоже на то, что в каждой точке кубика задано нечто, что умеет поворачивать и масштабировать вектора. Да, да, это матрица! Но не произвольная, а специальная, которая не уничтожает вектора, а преобразовывает.
Хорошо, а что будет с нашей матрицей, если мы возьмем другую систему координат, что изменится? Конфигурация каналов в кубике осталась такой же, и эта матрица должна поворачивать вектора скоростей точно таким же образом. Да, компоненты этой матрицы изменятся, но само ее действие на вектора останется таким же.
Таким образом, мы опять же имеем математический объект, матрицу специального вида, действие которой на вектор не зависит от смены системы координат, а ее компоненты пересчитываются по определенному закону. Назовем его тензором второго ранга.
Так что же такое тензор?
Итак, тензор это математический объект, который как объект не зависит от смены системы координат, но его компоненты при смене системы координат преобразуются по определенному математическому закону.
В трехмерном пространстве тензор второго ранга проще всего представить как матрицу, заданную в каждой точке пространства, которая описывает неоднородность этого пространства и действует на входящий вектор, изменяя его направление и масштаб.
Free Higher Mathematics — весь курс
Добро пожаловать на highmathematics.co.uk
Бесплатные веб-сайты по математике любезно предоставлены Inigo Media, SQA и всеми авторами, которые любезно предоставили свои ресурсы в свободный доступ.
Прохождение ускоренного курса высшей математики значительно расширит ваши карьерные возможности, помогая вам поступить в колледж/университет, пройти стажировку или даже устроиться на работу. «Хороший» результат по высшей математике поможет вам хорошо подготовиться к курсу AH Maths в следующем году, если вы заинтересованы. Пожалуйста, сделайте все возможное, чтобы продолжать учебу.
Для студентов, которым нужна дополнительная помощь по курсу высшей математики, вы можете рассмотреть возможность подписки на фантастические дополнительные ресурсы, ориентированные на экзамен, доступные в онлайн-пакете для изучения высшей математики.
Чтобы получить доступ к множеству дополнительных бесплатных ресурсов по теме , воспользуйтесь расположенной выше панелью поиска или нажмите ЗДЕСЬ, выбрав тему, которую хотите изучить.
Мы надеемся, что вы найдете этот веб-сайт полезным, и желаем вам всего наилучшего в изучении курса высшей математики в 2023 году. Ниже вы найдете:
1. Онлайн-учебный пакет, посвященный экзамену по высшей математике
2. Изменения даты курса и экзамена в 2023 г. — новые
3. Полезные ссылки по высшей математике
4. Буклет для подготовки к курсу высшей математики — рекомендуется
Экзамен по высшей математике по темам – Экзамен 2022 года включен!
6. Heinemann Higher Text Book Solutions — обновленные решения
7. Higher Math Essential Skills
8. Практика экзамена Higher Math Essential Skills — New
9. Leckie & Leckie Higher Math Book Solutions — New
10. Higher Maths SQA Past & Practice Papers
11.
12. Higher Math Practice Papers A to H & Prelim Special
13. Higher Maths Дополнительные практические работы от A до M
14. 40 вопросов по высшей математике без калькулятора
15. 200 экзаменационных вопросов по высшей математике
16. 178 повторных вопросов по высшей математике без ответов – новые
17. 264 экзаменационных вопроса с несколькими вариантами ответов
18. Прошлые и практические документы по высшей математике по темам
19. Видео по высшей математике, руководства по теории, интеллект-карты и рабочие листы
20. Старые рабочие листы для экзаменов по высшей математике по темам
21. Контрольные списки экзаменов по высшей математике – новые 9005
22. Руководства по теории высшей математики
23. Интеллект-карты высшей математики
24. Оценки практических занятий по высшей математике – решения включены
25. Высшая математика.0005
27. Учебный пакет, ориентированный на экзамен – Студенты, которым нужен «хороший» пропуск
.
.
1. Онлайн-учебный пакет, посвященный экзамену по высшей математике
Пожалуйста, предоставьте себе все возможности для успешной сдачи высшей математики в 2023 году, поговорите со своими родителями и рассмотрите возможность подписки на отличный онлайн-учебный пакет, посвященный экзамену по высшей математике, уже сегодня.
Всего за 20 фунтов стерлингов у вас будет мгновенный неограниченный доступ к онлайн-учебному пакету по высшей математике с настоящего момента и до окончания экзамена в мае 2023 года. Нажмите ЗДЕСЬ , чтобы узнать, что входит в онлайн-учебный пакет.
Пожалуйста, подпишитесь ниже:
Вам не нужна учетная запись PayPal,
просто используйте свою дебетовую или кредитную карту.
Мы обещаем никому не передавать вашу информацию.
Ваш очень ценный вклад реинвестируется в расходы на разработку веб-сайта, плату за хостинг, дальнейшее обогащение и гарантированное продолжение этого фантастического ресурса.
Онлайн-учебный пакет, посвященный экзамену по высшей математике . Здесь вы найдете четкие, простые в использовании, пошаговые решения для всех экзаменационных/практических работ CfE по высшей математике (бумага 2022 г. включена!), экзаменационных вопросов по высшей математике. разбито на темы, 14 заданий для повышения квалификации, 8 заданий по высшей математике от A до H, специальный предварительный экзамен 2021 г. (54 страницы), все 33 рабочих листа по основным навыкам, 13 Экзамен Таблицы основных навыков, 40 вопросов экзамена по высшей математике без калькулятора, 200 вопросов экзамена по высшей математике с калькулятором, руководства по теории, интеллект-карты по темам и многое другое! Нажмите ЗДЕСЬ, чтобы получить дополнительную информацию, в том числе снимок экрана учебного пакета и несколько примеров.
.
2. Изменения даты экзамена и курса в 2023 году — новые
В соответствии с расписанием SQA экзамен по высшей математике будет проходить в , четверг, 4 мая 2023 года: Документ 1 (09:00–10:15) и Документ 2 (10:45 – 12:15).
SQA заявило: Мы не будем оценивать следующее содержание в контрольных листах:
- Векторы
- Рекуррентные соотношения
.
3. Полезные ссылки по высшей математике
Студенты и преподаватели — Нажмите на любую из зеленых ссылок ниже или воспользуйтесь строкой поиска вверху этой страницы, где вы найдете множество бесплатных ресурсов по темам. . Ресурсы включают теоретические руководства, видеоролики, презентации в формате PowerPoint, интеллект-карты и рабочие листы по темам.
Высшая домашняя страница
Бесплатные руководства по теории HSN
Бесплатные высшие математики по теме
БЕСПЛАТНЫЕ математические математики прошлые документы
Бесплатные математические навыки Essential Essential Skill Видео и рабочие листы по высшей математике
Бесплатный учебник Heinemann с рабочими решениями
Бесплатный учебник Leckie & Leckie с рабочими решениями
Нажмите ЗДЕСЬ, чтобы просмотреть все доступные бесплатные онлайн-курсы по математике
.
4. Буклет для подготовки к курсу высшей математики – Рекомендуется
Если вы не уверены в какой-либо из тем N5 по математике в брошюре «Подготовка к высшей математике» ниже, пожалуйста, используйте всю возможную помощь, чтобы обеспечить успех высшей математики, и подпишитесь к онлайн-учебному пакету, посвященному экзамену по высшей математике, сегодня.
| Подготовительный буклет по высшей математике _________________________________ | Ответы ___________ | Любезность ________________________ |
| Буклет — Вопросы и ответы | Ответы | Буклет предоставлен ЗИПТ |
.
5. Рабочие листы экзамена по высшей математике по темам – Экзамен 2022 года включен!
Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Рабочие листы по темам являются фантастическим учебным ресурсом, поскольку они являются реальными вопросами прошлых бумажных экзаменов.
Четкие, простые в использовании, пошаговые решения для всех новых вопросов CfE по высшей математике, приведенных ниже, доступны в онлайн-пакете для изучения.
.
6. Решения Heinemann Higher Text Book Solutions – Обновленные решения
Приведенные ниже высококачественные обновленные рабочие решения окажутся чрезвычайно полезными для улучшения ваших знаний по высшей математике. Решения, а также отличные ресурсы, ориентированные на экзамены, также доступны в пакете для онлайн-обучения.
.
7. Высшие математические навыки
Спасибо г-ну Г. Ренни за то, что он предоставил в свободный доступ приведенные ниже отличные ресурсы. Рабочие листы основных навыков можно использовать для подготовки к оценкам, тестам и экзаменам. Четкие, простые в использовании, пошаговые решения для всех 33 рабочих листов основных навыков, приведенных ниже, доступны в онлайн-пакете для изучения.
.
8.
Практика сдачи экзамена по высшей математике по основным навыкам – Новый
Спасибо г-ну Г. Ренни за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Вопросы демонстрируют контексты, которые вы, скорее всего, встретите на экзаменах SQA. Четкие, простые в использовании, пошаговые решения для всех 13 практических рабочих листов для экзамена по основным навыкам, приведенные ниже, доступны в онлайн-учебном пакете.
.
9. Leckie & Leckie Higher Text Book Solutions – Новый
Спасибо Madras College за предоставленные решения для учебника Leckie & Leckie Higher Maths, указанные ниже. Они окажутся чрезвычайно полезными для улучшения ваших знаний по высшей математике. Обратите внимание, что некоторые упражнения могут быть неполными и может быть случайная ошибка.
.
10. Higher Maths SQA Past & Practice Papers
Спасибо SQA за то, что они предоставили в свободном доступе превосходные ресурсы, указанные ниже.
Четкие, простые в использовании, пошаговые решения для всех представленных ниже документов CfE Higher Papers доступны в пакете онлайн-обучения.
.
11. Учебные пособия по высшей математике – новые
Благодарим Madras College за предоставление бесплатного доступа к превосходным ресурсам, приведенным ниже. Пожалуйста, используйте для повторения перед оценками, тестами и выпускным экзаменом. Четкие, простые в использовании, пошаговые решения для всех 14 приведенных ниже заданий для повышения оценок доступны в пакете онлайн-обучения.
.
12. Практические экзаменационные работы по высшей математике от A до H и специальный предварительный экзамен
Спасибо SQA и Larkhall Academy за предоставление в свободном доступе превосходных ресурсов, указанных ниже. Пожалуйста, регулярно используйте для повторения перед оценками, тестами и выпускным экзаменом. Четкие, простые в использовании, пошаговые решения для практических работ от A до E и специального предварительного задания (54 страницы) доступны в пакете онлайн-обучения.
.
13. Дополнительные практические документы по высшей математике от A до M
Благодарим SQA, SPTA и авторов за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Эти работы основаны на старом стиле высшего экзамена и обеспечат отличную подготовку к выпускным экзаменам в 2021 году.
.
14. 40 вопросов по высшей математике без калькулятора
Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Четкие, простые для понимания, пошаговые решения всех 40 приведенных ниже вопросов доступны в пакете онлайн-обучения.
.
15. 200 вопросов по высшей математике
Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Четкие, простые в использовании, пошаговые решения всех 200 приведенных ниже вопросов доступны в пакете онлайн-обучения.
.
16. 178 Высшая математика. Повторные вопросы без ответов – New
Спасибо автору за предоставление бесплатного доступа к приведенному ниже превосходному ресурсу. Этот ресурс не имеет ответов и идеально подходит для учителей, желающих задавать вопросы для домашнего задания или повторения, чтобы у учащихся не возникало соблазна проверить отработанные решения.
178 Контрольные вопросы по высшей математике
.
17. Экзамен 264 SQA Вопросы и ответы с несколькими вариантами ответов
Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Множественный выбор — это, прежде всего, вопросы уровня C, и это отличное место для начала проверки. Если вы застряли, всегда обращайтесь к учителю за помощью как можно скорее.
18. Higher Maths SQA Past & Practice Papers by Topic
Спасибо SQA за то, что они предоставили в свободный доступ превосходные ресурсы, указанные ниже.
Вопросы и ответы разделены по темам для удобства поиска. Четкие, простые в использовании, пошаговые решения всех приведенных ниже вопросов доступны в пакете онлайн-обучения.
| . Бумага _____________ | . Маркировка __________ | . Круги ______ | Дифференциация и оптимизация ____________ | Exp’s & Logs ________ | . Интегрирование _________ | Многочлены и квадратичные уравнения ____________ 9. Векторы ________ | Волна Функция _________ | ||||||
| 2019 P1 | Marking P1 | Q3,16 | Q1 | Q14 | Q10,12 | Q6,11,17b | Q8 | Q2 | Q4 | Q5,7 | Q13,15,17a | Q9 | |
| 2019 P2 | Marking P2 | Q15 | Q7b,11 | Q9,12 | Q5,8 | Q2,13 | Q7,10 | Q4 | Q1 | Q6b | Q3 ,14 | Q6a | |
| 2018 P1 | Marking P1 | Q4 | Q6,11 | Q2,11,15 | Q3,14 | Q10 | Q7 | Q1,8 | Q13 | Q5,9,12 | |||
| 2018 P2 | Marking P2 | Q5c,12 | Q3,9 | Q11 | Q6 | Q1 | Q4,7a,10 | 7b,c | Q5a,b | Q2 | Q8 | ||
| 2017 P1 | Marking P1 | Q2 | Q8,15c | Q12 | Q1,6,15a | Q3,13 | Q10,15b | Q4 | Q9 | Q7,11 | Q5 | Q14 | |
| 2017 P2 | Marking P2 | Q3,10 | Q4,7 | Q9 | Q2 | Q8 | Q1 | Q6,11 | Q5 | ||||
| 2016 P1 | Marking P1 | Q4,8 | Q2,9 | Q14 | Q6,10,12 | Q5 | Q15 | Q3 | Q1 | Q13 | Q7,11 | ||
| 2016 P2 | Marking P2 | Q4 | Q7 | Q6 | Q10,11b | 3b,9 | Q2,3a | Q1 | Q8b,11a | Q5 | Q8a | ||
| 2015 P1 | Marking P1 | Q11,14 | Q2,7 | Q6 | Q4,5,13 | Q12,15 | Q3,8 | Q9 | Q10 | Q1 | |||
| 2015 P2 | Marking P2 | Q5 | Q8 | Q2 | Q7a | Q4 | Q3 | Q1 | Q7b | Q6 | Q9 | ||
| Specimen P1 | Marking P1 | Q11 | Q8 | Q10 | Q1 | Q4,7 | Q2,5,9 | Q6,12 | Q3 | ||||
| Specimen P2 | Marking P2 | Q5 | Q3b,8 | Q4,7 | Q9 | Q3a | Q2 | Q1,6 | Q10 | ||||
| Exemplar P1 | Marking P1 | Q1 | Q8,11 | Q10 | Q3 | Q2,5 | Q6 | Q4,7 | Q9 | ||||
| Образец P2 | Маркировка P2 | Q2 | Q9,10 | Q7 | Q8 | Q4 | Q3 | Q1 | Q5,6 | Q5,6 |
.
19. Видео по высшей математике, руководства по теории, интеллект-карты и рабочие листы
Десятки видео по высшей математике содержат качественные уроки по темам. Также включены отличные руководства по теории, интеллект-карты и рабочие листы с актуальными экзаменационными вопросами по высшей математике. Пожалуйста, нажмите на нашу новую страницу с видео и рабочими таблицами по высшей математике по темам.
.
20. Старые экзаменационные листы по высшей математике по темам
Спасибо SQA за то, что они предоставили в свободный доступ превосходные ресурсы, указанные ниже. Рабочие листы по темам являются фантастическим дополнительным учебным ресурсом.
| Тема ________ | Название темы ___________________________ | Ссылка ________ | Примечания ___________________ |
| Тема 1 | Круги | ЗДЕСЬ | Ответы включены |
| Тема 2 | Дифференциация | ЗДЕСЬ | Ответы включены |
| Тема 3 | Экспоненты и логарифмы | ЗДЕСЬ | Ответы включены |
| Тема 4 | Функции | ЗДЕСЬ | Ответы включены |
| Тема 5 | Дальнейшее исчисление | ЗДЕСЬ | Ответы включены |
| Тема 6 | Графики функций | ЗДЕСЬ | Ответы включены |
| Тема 7 | Интеграция | ЗДЕСЬ | Ответы включены |
| Тема 8 | Полиномы | ЗДЕСЬ | Ответы включены |
| Тема 9 | Квадратика | ЗДЕСЬ | Ответы включены |
| Тема 10 | Рекуррентные соотношения | ЗДЕСЬ | Ответы включены |
| Тема 11 | Прямая линия | ЗДЕСЬ | Ответы включены |
| Тема 12 | Триггерные формулы сложения | ЗДЕСЬ | Ответы включены |
| Тема 13 | Триггерные графики и уравнения | ЗДЕСЬ | Ответы включены |
| Тема 14 | Векторы | ЗДЕСЬ | Ответы включены |
| Тема 15 | Волновая функция | ЗДЕСЬ | Ответы включены |
.
21. Контрольные списки экзамена по высшей математике
Спасибо SQA и авторам за то, что они предоставили в свободный доступ приведенные ниже отличные ресурсы. Это фантастические контрольные списки для оценки ваших знаний по высшей математике. Пожалуйста, старайтесь регулярно использовать их для повторения перед тестами, предварительными экзаменами и выпускным экзаменом.
.
22. Справочники по высшей математике
Спасибо HSN за то, что они сделали превосходные руководства по высшей математике бесплатными для всех. Они окажутся фантастическим ресурсом, который поможет вам закрепить ваше понимание высшей математики.
| Теоретические руководства _________________ | Тема ____________________________________________ | Ссылка _______ |
| Руководство по теории 1 | Все темы Раздел 1 Теория (HSN) | ЗДЕСЬ |
| Теоретическое руководство 2 | Все темы, раздел 1 — Краткое руководство на одной странице (HSN) | ЗДЕСЬ |
| Руководство по теории 3 | Все темы Раздел 2 Теория (HSN) | ЗДЕСЬ |
| Теоретическое руководство 4 | Все темы, раздел 2 — краткое руководство на одной странице (HSN) | ЗДЕСЬ |
| Руководство по теории 5 | Все темы Раздел 3 Теория (HSN) | ЗДЕСЬ |
| Теоретическое руководство 6 | Все темы, раздел 3 — краткое руководство на одной странице (HSN) | ЗДЕСЬ |
| Руководство по теории 7 | Все темы Разделы 1, 2 и 3 Теория (HSN) | ЗДЕСЬ |
| Руководство по теории 8 | Теория кругов (HSN) | ЗДЕСЬ |
| Руководство по теории 9 | Теория дифференцировки (HSN) | ЗДЕСЬ |
| Руководство по теории 10 | Теория экспонент и логарифмов (HSN) | ЗДЕСЬ |
| Руководство по теории 11 | Теория функций и графиков (HSN) | ЗДЕСЬ |
| Руководство по теории 12 | Дальнейшая теория исчисления (HSN) | ЗДЕСЬ |
| Руководство по теории 13 | Теория трансформации графиков (движение и отражение) | ЗДЕСЬ |
| Теоретическое руководство 14 | Сводная таблица преобразований графиков | ЗДЕСЬ |
| Теоретическое руководство 15 | Теория интеграции (HSN) | ЗДЕСЬ |
| Руководство по теории 16 | Теория многочленов и квадратичных уравнений (HSN) | ЗДЕСЬ |
| Руководство по теории 17 | Теория последовательностей (HSN) | ЗДЕСЬ |
| Руководство по теории 18 | Теория прямых линий (HSN) | ЗДЕСЬ |
| Руководство по теории 19 | Теория тригонометрии (HSN) | ЗДЕСЬ |
| Теоретическое руководство 19 | Теория векторов (HSN) | ЗДЕСЬ |
| Руководство по теории 20 | Теория волновых функций (HSN) | ЗДЕСЬ |
.
23. Интеллект-карты высшей математики
Спасибо авторам за предоставленные ниже отличные ресурсы. Интеллект-карты — отличный способ систематизировать ключевые идеи или понятия из уроков/учебников в виде диаграмм.
.
24. Оценки по высшей математике – решения включены
Спасибо авторам за то, что они сделали приведенные ниже отличные ресурсы бесплатными для всех. Пожалуйста, регулярно используйте для повторения перед оценками, тестами и выпускным экзаменом.
.
25. Higher Maths Past Paper Video Solutions
Щелкните DLB Maths, чтобы просмотреть видеорешения Higher Maths Past Paper. Это отличный ресурс, который поможет вам подготовиться к оцениванию, тестам и выпускному экзамену.
.
26. Рекомендуемый учебник по высшей математике
Ниже вы найдете рекомендуемый учебник, который можно заказать, нажав на книгу/ссылку.
.
.
27. Учебный онлайн-пакет по высшей математике
Благодаря пошаговым решениям экзаменационных вопросов, доступным в онлайн-учебном пакете, мы охватим все, что вам нужно знать о высшей математике, чтобы сдать выпускной экзамен.
Для студентов, которые ищут «хороший» проход по высшей математике, вы можете рассмотреть возможность подписки на фантастические дополнительные ресурсы, ориентированные на экзамены, доступные в Online Study Pack. Подписка может стать одной из ваших лучших инвестиций.
Пожалуйста, предоставьте себе все возможности для достижения успеха, поговорите со своими родителями и подпишитесь на ориентированный на экзамен Online Study Pack сегодня.
Мы надеемся, что ресурсы на этом веб-сайте окажутся полезными, и желаем вам всего наилучшего в изучении курса высшей математики в 2023 году.
Документация Godot обновляется, чтобы отразить последние изменения в версии 4,0 .
Некоторые страницы документации могут
до сих пор указывают устаревшую информацию. Этот баннер сообщит вам, читаете ли вы одну из таких страниц.
Содержание этой страницы до даты . Если вы все еще можете найти устаревшую информацию, пожалуйста, открыть вопрос.
Самолеты
У скалярного произведения есть еще одно интересное свойство единичных векторов. Представьте, что перпендикулярно этому вектору (и через начало координат) проходит самолет. Плоскости делят все пространство на положительные (над плоскостью) и отрицательное (под плоскостью), и (вопреки распространенное мнение) вы также можете использовать их математику в 2D:
Единичные векторы, перпендикулярные поверхности (таким образом, они описывают
ориентация поверхности) называются единичными векторами нормалей . Хотя,
обычно они просто обозначаются как normals . Нормали появляются в
плоскости, трехмерная геометрия (чтобы определить, где каждая грань или вершина имеет боковую сторону),
и т.
д. нормальный — это единичный вектор , но он называется нормальный из-за его использования. (Точно так же, как мы называем (0,0) Происхождением!).
Самолет проходит через начало координат и его поверхность перпендикулярна единичному вектору (или обычный ). сторона, обращенная к вектору, указывает на положительное полупространство, а другая сторона — отрицательное полупространство. В 3D это точно так же, за исключением того, что плоскость представляет собой бесконечную поверхность (представьте себе бесконечную плоскую лист бумаги, который можно сориентировать и который закреплен в исходной точке) вместо линии.
Расстояние до плоскости
Теперь, когда стало понятно, что такое плоскость, вернемся к скалярному произведению. Скалярное произведение между единичным вектором и любыми точка в пространстве (да, на этот раз мы делаем скалярное произведение между вектором и позицией), возвращает расстояние от точки до плоскости :
var Distance = normal.dot(точка)
dot(точка)
Но не только абсолютное расстояние, если точка находится в отрицательной половине space расстояние тоже будет отрицательным:
Это позволяет нам определить, с какой стороны плоскости находится точка.
Вдали от источника
Я знаю, о чем ты думаешь! Пока это хорошо, но настоящие самолёты везде в пространстве, не только проходя через начало координат. Вы хотите настоящего самолет действие и вы хотите теперь .
Помните, что самолеты не только делят пространство надвое, но и имеют полярность . Это означает, что можно иметь полностью перекрывающиеся плоскости, но их отрицательное и положительное полупространства меняются местами.
Имея это в виду, давайте опишем полную плоскость как нормальный N и расстояние от начала координат скаляр D . Таким образом, наша плоскость представлена по N и D. Например:
Для трехмерной математики Годо предоставляет плоскость
встроенный тип, который обрабатывает это.
По сути, N и D могут представлять любую плоскость в пространстве, будь то 2D или 3D. (в зависимости от количества измерений N) и математика такая же для обоих. То же, что и раньше, но D — это расстояние от начала координат. к самолету, летящему в направлении N. Например, представьте, что вы хотите чтобы добраться до точки на плоскости, вы просто сделаете:
переменная точка_в_плоскости = N*D
Это растянет (изменит размер) вектор нормали и заставит его касаться самолет. Эта математика может показаться запутанной, но на самом деле все намного проще. чем кажется. Если мы хотим сказать, опять же, расстояние от точки до самолет, делаем то же самое, но с поправкой на расстояние:
переменная дистанция = N.dot(точка) - D
То же самое, но встроенной функцией:
var Distance = plane.distance_to(точка)
Это снова вернет либо положительное, либо отрицательное расстояние.
Изменение полярности плоскости может быть выполнено отрицанием обоих
N и D.
Это приведет к тому, что плоскость окажется в том же положении, но с
перевернутые отрицательные и положительные полупространства:
Н = -Н Д = -Д
Godot также реализует этот оператор в Plane. Таким образом, использование следующего формата будет работать как положено:
.вар инвертированная_плоскость = -плоскость
Итак, помните, главное практическое применение самолета в том, что мы можем рассчитать расстояние до него. Итак, когда полезно рассчитывать расстояние от точки до плоскости? Давайте посмотрим на некоторые примеры.
Построение плоскости в 2D
Самолеты явно не берутся из ниоткуда, поэтому их надо строить. Построить их в 2D легко, это можно сделать либо из обычного (единичный вектор) и точка, или из двух точек в пространстве.
В случае нормали и точки большая часть работы выполнена, так как нормаль уже вычислена, поэтому вычислите D из скалярного произведения норма и точка.
вар N = нормальный var D = normal.
dot(точка)
Для двух точек в пространстве на самом деле есть две плоскости, которые проходят через их, разделяя одно и то же пространство, но с нормальным указанием на противоположное направления. Чтобы вычислить нормаль из двух точек, направление вектор нужно сначала получить, а потом его нужно повернуть 90° градусов в обе стороны:
# Вычислить вектор от `a` до `b`. var dvec = (point_b - point_a).normalized() # Повернуть на 90 градусов. var normal = Vector2(dvec.y, -dvec.x) # Альтернативно (в зависимости от желаемой стороны нормали): # var normal = Vector2(-dvec.y, dvec.x)
Остальное аналогично предыдущему примеру. Либо point_a, либо point_b будет работать, так как они находятся в одной плоскости:
вар N = нормальный var D = normal.dot(point_a) # это работает так же # var D = normal.dot(point_b)
То же самое в 3D немного сложнее и объясняется дальше.
Некоторые образцы самолетов
Вот пример того, чем могут быть полезны самолеты.
Представьте, что у вас есть
выпуклый
полигон. Например, прямоугольник, трапеция, треугольник или просто любой
многоугольник, в котором ни одна грань не загибается внутрь.
Для каждого сегмента многоугольника мы вычисляем плоскость, которая проходит мимо тот сегмент. Когда у нас есть список самолетов, мы можем делать аккуратные вещи, например, проверка того, находится ли точка внутри многоугольника.
Проходим все плоскости, если найдем плоскость, где расстояние до точка положительна, то точка находится вне многоугольника. Если мы не может, то дело внутри.
Код должен быть примерно таким:
переменная внутри = истина
для p в плоскостях:
# проверяем, положительно ли расстояние до плоскости
если (p.distance_to(точка) > 0):
внутри = ложь
break # с тем, который не работает, этого достаточно
Довольно круто, да? Но это становится намного лучше! Приложив немного больше усилий,
аналогичная логика даст нам знать, когда два выпуклых многоугольника перекрываются
слишком.
Это называется теоремой о разделяющей оси (или SAT).
физические движки используют это для обнаружения столкновений.
С точкой, просто проверяя, есть ли самолет возвращает положительное расстояние, которого достаточно, чтобы определить, находится ли точка снаружи. С другим многоугольником мы должны найти плоскость, где все другие полигон точки возвращают к нему положительное расстояние. Этот чек выполняются плоскостями А против точек В, а затем с плоскости B относительно точек A:
Код должен быть примерно таким:
var перекрытие = правда
для p в planes_of_A:
переменная all_out = истина
для v в точках_из_В:
если (p.distance_to(v) < 0):
все_выход = ложь
перерыв
если (все_из):
# найдена разделяющая плоскость
# не продолжать тестирование
перекрытие = ложь
перерыв
если (перекрываются):
# делаем эту проверку, только если нет разделяющей плоскости
# был найден в самолетах A
для p в planes_of_B:
переменная all_out = истина
для v в точках_из_А:
если (p. distance_to(v) < 0):
все_выход = ложь
перерыв
если (все_из):
перекрытие = ложь
перерыв
если (перекрываются):
print("Многоугольники столкнулись!")
distance_to(v) < 0):
все_выход = ложь
перерыв
если (все_из):
перекрытие = ложь
перерыв
если (перекрываются):
print("Многоугольники столкнулись!")
Как видите, самолеты весьма полезны, и это вершина айсберг. Вам может быть интересно, что происходит с невыпуклыми многоугольниками. Обычно это просто обрабатывается путем разбиения вогнутого многоугольника на меньшие выпуклые многоугольники или с использованием такой техники, как BSP (которая не широко используется в настоящее время).
Обнаружение столкновений в 3D
Это еще один бонусный бит, награда за терпение и не отставание. с этим длинным учебником. Вот еще одна мудрость. Это может не быть чем-то с прямым вариантом использования (Годо уже делает коллизию обнаружение довольно хорошо), но он используется почти всеми физическими движками и коллизионными библиотеки обнаружения 🙂
Помните, что преобразование выпуклой формы в 2D в массив 2D-плоскостей
был полезен для обнаружения столкновений? Вы можете определить, была ли точка
внутри любой выпуклой формы или если две двумерные выпуклые формы перекрываются.
Ну, это работает и в 3D, если сталкиваются две 3D многогранные фигуры, вы не сможете найти разделяющую плоскость. Если разделяющая плоскость найдено, то фигуры определенно не сталкиваются.
Немного обновить разделяющую плоскость означает, что все вершины многоугольника A лежат по одну сторону от плоскости, а все вершины многоугольника B лежат в Другая сторона. Эта плоскость всегда является одной из лицевых плоскостей любой многоугольник A или многоугольник B.
Однако в 3D у этого подхода есть проблема, потому что он возможно, что в некоторых случаях разделяющая плоскость не может быть найдена. Это пример такой ситуации:
Чтобы этого избежать, некоторые дополнительные плоскости необходимо испытать в качестве разделителей, эти плоскости являются векторным произведением между ребрами многоугольника A и ребра многоугольника B
Таким образом, окончательный алгоритм выглядит примерно так:
var перекрытие = правда для p в planes_of_A: переменная all_out = истина для v в точках_из_В: если (p.
distance_to(v) < 0):
все_выход = ложь
перерыв
если (все_из):
# найдена разделяющая плоскость
# не продолжать тестирование
перекрытие = ложь
перерыв
если (перекрываются):
# делаем эту проверку, только если нет разделяющей плоскости
# был найден в самолетах A
для p в planes_of_B:
переменная all_out = истина
для v в точках_из_А:
если (p.distance_to(v) < 0):
все_выход = ложь
перерыв
если (все_из):
перекрытие = ложь
перерыв
если (перекрываются):
для советника в edge_of_A:
для eb в edge_of_B:
var n = ea.cross(eb)
если (n.length() == 0):
продолжать
var max_A = -1e20 # маленькое число
var min_A = 1e20 # огромное число
# мы используем скалярный продукт напрямую
# чтобы мы могли отобразить максимальный и минимальный диапазон
# для каждого полигона, затем проверяем,
# перекрывать.
