Векторы вокруг нас | Образовательная социальная сеть
НАЦИОНАЛЬНАЯ ОБРАЗОВАТЕЛЬНАЯ ПРОГРАММА
«ИНТЕЛЛЕКТУАЛЬНО-ТВОРЧЕСКИЙ ПОТЕНЦИАЛ РОССИИ»
Конкурс исследовательских работ «ЮНОСТЬ, НАУКА, КУЛЬТУРА-СЕВЕР»
Секция: математика
Векторы вокруг нас
Неклюдова Юлия
СОШ №8, 11 класс, г. Елизово, Камчатский край
Научный руководитель:
Голованева Любовь Викторовна
учитель математики, высшая квалификационная категория,
почётный работник общего образования РФ,
победитель конкурса лучших учителей РФ
г. Санкт-Петербург
2008-2009 учебный год
Содержание:
- Введение 3
- Векторы в предметах естественнонаучного цикла 5
- Векторы вокруг нас 8
- Векторы в знаках дорожного движения 9
- Заключение 10
- Список литературы 11
- Приложение 12
Введение
ХХI ВЕК – век новых технологий и я, уже нынешняя одиннадцатиклассница, продолжаю усердно «грызть» гранит науки.
С темой «Вектор» я познакомилась на уроке математики в 8-ом классе. Особого интереса она у меня не вызвала, но без неё я не могла изучать раздел физики «Механика» в 9-ом классе. После предпрофиля в 9-ом классе я решила продолжить обучение в 10-ом классе естественнонаучного профиля, где встретилась с векторами не только на физике уже в теме «Электричество», но и на химии, биологии и опять на математике, но уже в пространстве. Тогда я решила посмотреть, в каких ещё областях знаний можно встретить это понятие и насколько оно актуально в жизни.
Проект назвала «Векторы вокруг нас». Я работала по следующим направлениям:
- «Векторы в предметах естественнонаучного цикла»
- «Векторы вокруг нас»
- «Векторы в знаках дорожного движения».
Я поставила перед собой цели:
- Проследить важность понятия «Вектор» в предметах естественно-научного цикла
- Рассмотреть при получении, каких специальностей будет происходить развитие понятия «вектор» в высшей школе.
- Обратить внимание одноклассников и окружающих на векторы вокруг нас.
Внимательно изучив различные материалы из книг, поработав в Интернете, я узнала, что понятие «Вектор» — относительно новое математическое понятие и его изучает раздел математики «Векторное исчисление».
Векторное исчисление, математическая дисциплина, в которой изучают свойства операций над векторами евклидова пространства. При этом понятие вектора представляет собой математическую абстракцию величин, характеризующихся не только численным значением, но и направленностью (например, сила, ускорение, скорость).
Я проделала эксперименты по химии, посетила строящийся мост через реку Авача, прошла с фотоаппаратом по магазинам и улицам г. Елизова, проехала по дорогам Елизовского района и, используя собственные наблюдения, я пришла к выводу, что понятия вектора очень распространены, и мы буквально сталкиваемся с ними на каждом шагу. Кроме того, мне предстоит продолжить их изучение в высших учебных заведениях (например, в векторной алгебре).
В жизни векторы помогают найти нужный объект, сэкономить время, они даже выполняют предписывающую функцию (в знаках дорожного движения), тем самым, предотвращая аварии на дорогах и сохраняя жизни участников движения.
Меня заинтересовала книга «Правила дорожного движения», а если конкретно, то:
- дорожные знаки и их значение;
- пешеходные переходы и места остановок маршрутных транспортных средств;
- обязанности пешеходов;
- обязанности пассажиров;
- дополнительные требования к движению велосипедистов, мопедов;
- таблица штрафов;
- оформление квитанции оплаты штрафов ГИБДД.
Векторы в предметах естественнонаучного цикла.
Возникновение векторного исчисления тесно связано с потребностями механики и физики. До XIX в. для задания векторов использовался лишь координатный способ, и операции над векторами сводились к операциям над их координатами. Лишь в середине XIX в. усилиями ряда учёных было создано векторное исчисление, в котором операции проводились непосредственно над векторами, без обращения к координатному способу задания.
Сам термин «вектор» впервые появился в 1845 году у английского математика и астронома Уильяма Гамильтона. Основы векторного исчисления были заложены исследованиями английского математика У. Гамильтона и немецкого математика Г. Грассмана. Их идеи были использованы английским физиком Дж. К. Максвеллом в его работах по электричеству и магнетизму. Современный вид векторам придал американский физик Дж. Гиббс (рис.1).
Я учусь в классе естественнонаучного профиля, а значит, буду связывать свои профессии с химией, физикой, биологией. Поэтому, мне предстоит изучать математику и в высших учебных заведениях. Я побеседовала с выпускниками 2003 г. нашей школы, которые учатся в КамГТУ и КамГУ на физико-математическом факультете и факультете «управление и информатика в технических системах». И выяснила, что одним из многих предметов будет «Векторная алгебра», элементы которой я уже изучила в школьном курсе математики и использую в физике в разделе «Механика», «Электричество», химии при составлении реакций, биологии и др.
Направленным отрезком или вектором называется отрезок, для которого указано какая из его граничных точек считается началом, а какая – концом. Направление вектора (от начала к концу) на рисунках отмечается стрелкой (рис.2). Длиной ненулевого вектора называется длина отрезка . В векторной алгебре важную роль играют линейные операции над векторами: операция сложения векторов и умножения вектора на действительное число. Суммой векторов и называют вектор, идущий из начала вектора в конец вектора при условии, что начало вектора приложено к концу вектора (рис. 2). Это правило используется нами при сложении сил в физике (векторных величин, рис.3).
Применение векторной алгебры тесно связано с различными типами векторных произведений: скалярного, векторного и смешанного. Понятие скалярного произведения векторов применяется, например, в физике, при рассмотрении работы силы F на заданном пути S: работа равна |F||S|cosj, где j — угол между векторами F и S. В механике, физике широко используются понятия векторного поля.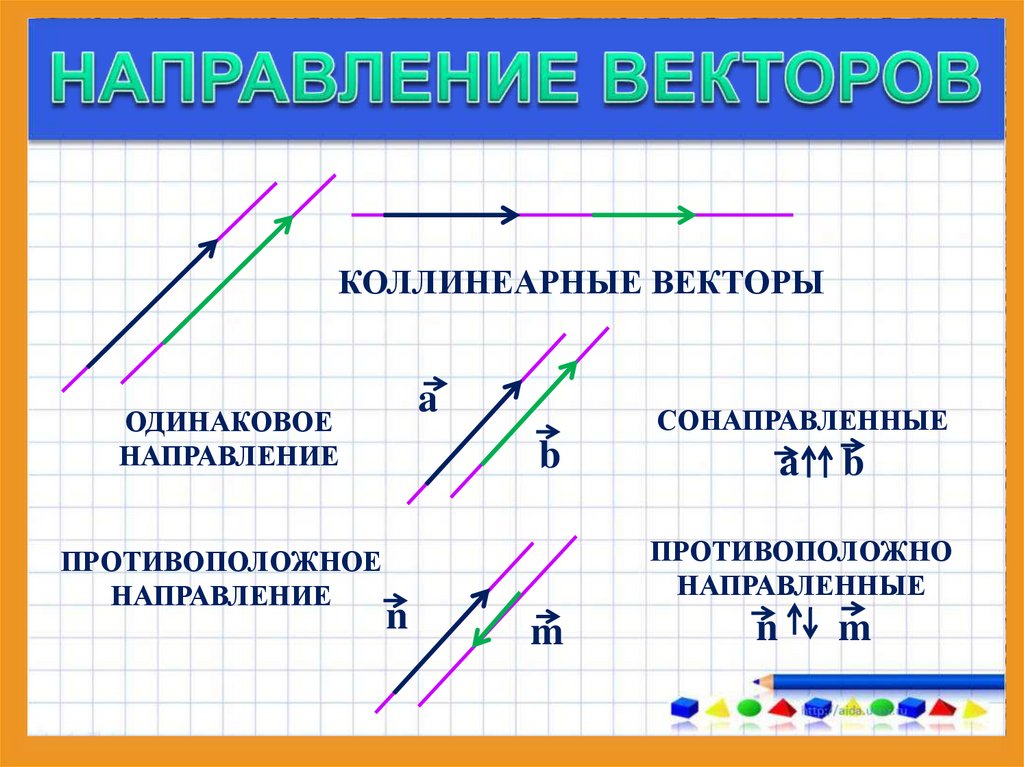
Примерами векторных полей могут служить также поле силы тяжести, магнитное и электрическое напряжение электромагнитного поля (рис.5).
Векторы, изучаемые в математике, помогают мне в физике. Физические формулы, законы, чаще всего изображаются математическими знаками, в частности векторами. Любая сила, например F тяжести, раскладывается по векторам. Это необходимо при расчётах в строительстве различных сооружений, например в построении моста, через реку Авача в г. Елизово (рис.4,6). Так неправильные расчёты могут привести к трагедиям и многочисленным жертвам (рис.7). Разложение векторов применяют при расчётах летательных аппаратов, например вектор скорости для круговых орбит (рис.8), в навигации морского и воздушного флота (рис.9). Планирую вместе с классом в этом учебном году совершить экскурсию в аэропорт в аэронавигационную службу и посмотреть практическое применение векторов при расчётах полётов истребительных самолётов.
Своё широкое применение векторы получили в химии.
Например, рассмотрим электронное строение атома азота (рис.10,11). Каждый электрон имеет свою собственную характеристику – спин. Спин – собственный момент импульса электрона, не связанный с движением в пространстве. Спины электронов складываются как вектора. Сумма спинов данного числа электронов на подуровне должна быть максимальной. Если в квантовой ячейке находятся два спаренных электрона, то их изображают противоположно направленными векторами.
Векторная модель атома. Модель основана на рассмотрении векторного сложения угловых моментов электронов в атоме. Силовой угловой момент имеет (2I+1) различных компонентов (рис.23).
Обратимость реакции. Обратимыми называются реакции, протекающие в двух взаимно противоположных направлениях. Такие реакции не доходят до конца и заканчиваются установлением химического равновесия, при котором скорости прямой и обратной реакций равны между собой.
Обратимые реакции не доходят до конца. Концентрации реагентов уменьшаются, что приводит к уменьшению скорости прямой реакции .
Скорость же обратной реакции постоянно возрастает, поскольку увеличиваются концентрации продуктов. Когда скорости прямой и обратной реакции станут одинаковыми ( ), наступает состояние химического равновесия. Человек научился направлять обратимые химические реакции в нужную для себя сторону, используя действие таких факторов, как температура, давление, концентрация.
Диссоциация. Диссоциация – распад молекул на ионы. Ассоциация – соединение ионов в молекулу.
HF H+ + F-
Уравнения химических реакций в органической химии. В органической химии уравнения химических реакций записывают, использую вектор между левой частью уравнения и правой. Объяснение этому факту состоит в том, что большинство химических реакций между органическими веществами имеют несколько направлений течения. Могут образовываться различные продукты реакции при взаимодействии одних и тех же веществ, только количественное соотношение продуктов реакций различно, поэтому записывают то уравнение химической реакции, в котором продуктами реакции являются вещества, выход которых больше.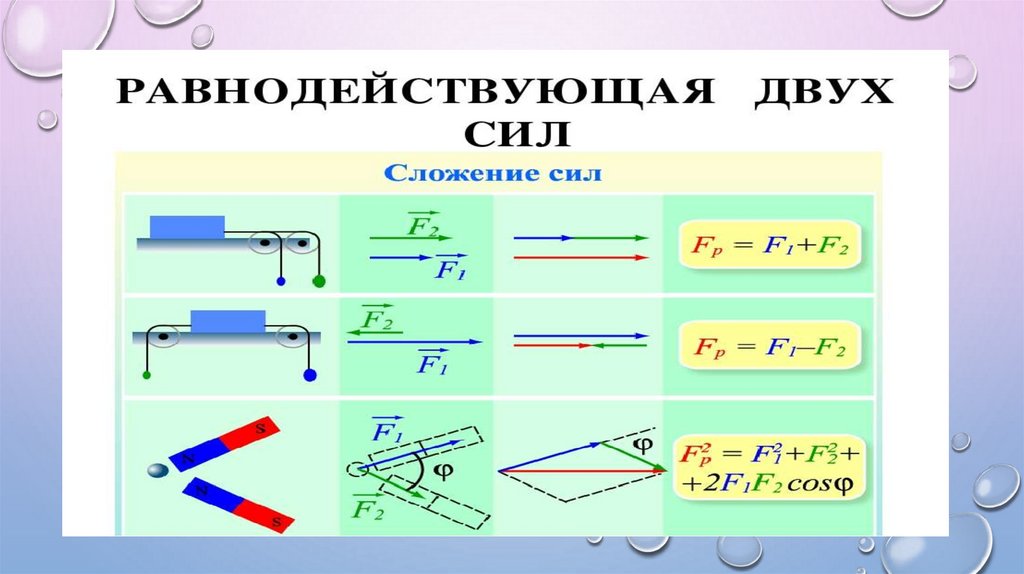
Это и будет являться основным уравнением. Чтобы указать на существование побочных процессов, используют знак вектора.
Ch4 Ch3 Ch3Cl
Ch4 CH Ch3 + HCl
Ch4 CHCl Ch4
Электролиз. Электролиз — это окислительно-восстановительный процесс, протекающий на электропроводах при прохождении электрического тока через расплав или раствор электролита.
NaCl
Катод Na+
Na+ + е = Na
Анод Cl-
2Cl— 2е = Cl2
Знаком вектора обозначается осадок, т.е. нерастворимое вещество, которое выпадает на дно сосуда, или газ, который уходит вверх, в атмосферный воздух (рис.12). Для проведения опыта я взяла мелко измельченный мрамор и прилила соляную кислоту, происходит бурная реакция c выделением углекислого газа, описываемая уравнением
CaCO3+2HCl=CaCl2+CO2 +h3O
Второй опыт я провела, используя раствор сульфата меди и гидроксида натрия, в котором наблюдала выпадение голубого осадка гидроксида меди:
CuSO4+2NaOH=Cu(OH)2 +Na2SO4 (рис.
13)
Интересно, но понятие «вектор» встречается даже в биологии. И вы будете ещё больше удивлены, когда узнаете, что эти векторы изображены на рисунках (рис.14). Это вошь, клещ, крыса…
Вектором (в биологии) называется организм, переносящий паразита от одного организма-хозяина к другому. Например, вши переносят возбудителей сыпного тифа, крысы – чумы, а клещи являются переносчиками вируса, вызывающего энцефалит. Так эти заболевания являются очень опасными для человека, поэтому необходимо досконально изучить механизм их передачи во избежание заражения. Существует ещё одно значение слова «вектор» в биологии. На этот раз немножко коснёмся генной инженерии.
Вектор – это автономная молекула ДНК, используемая в генной инженерии, для переноса генов от организма-донора в организм-реципиент, а также для клонирования нуклеиновых последовательностей (клонирующий вектор).
Вектором, например, является бактериальная плазмида. Плазмиды дают бактериям большие преимущества, например способность синтезировать вещества опасные для других бактерий – антибиотики, а так же быть устойчивыми к антибиотикам своих собратьев (рис.
15). Эти свойства научился использовать в своей деятельности человек, но они так же могут и вредить ей. Например, был получен антибиотик против бактерии, вызывающей туберкулёз, но эта бактерия эволюционировала и приобрела к нему невосприимчивость. Поэтому необходимо снова искать средство, что бы справиться с этой болезнью. Человек создаёт также искусственные векторы.
С помощью векторов синтезируются различные лекарства и антибиотики. Синтезируются ферменты или даже целые каскады ферментов, необходимые человеку (например, инсулин). В генной инженерии существует такое молодое развивающееся направление, как генотерапия, где векторы позволяют исправлять генетические дефекты. Эти молекулы ДНК (векторы) используются также при создании трансгенных растений и животных (например, генетически модифицированные овцы продуцируют человеческий ген альфа 1-антитрипсина в молоке). Люди, наследующие два нефункционирующих гена этого белка, страдают болезнью, называемой альфа 1-антитрипсиновой недостаточностью.
Она поражает легкие и иногда печень. Векторы применяются также при клонировании.
В обычном понимании клоном считается идентичная копия высшего организма. Молекулярные биологи, однако, клоном считают популяцию генетически идентичных организмов, клеток, вирусов или молекул ДНК. В генетической инженерии цель клонирования, как правило, — получение значительного количества копий специфического гена. Первый шаг на этом пути – создание библиотеки, для которого понадобятся векторы. Идеальный вектор для генетической инженерии должен иметь три характеристики:
- Хороший потенциал клонирования. То есть должен давать большое количество реплик в хозяйской клетке.
- Его геном должен иметь один сайт узнавания для каждого из многих ферментов рестрикции. Таким образом, чужой ген сможет встраиваться только в одну точку вектора.
- он должен иметь полезную информацию в клетке, например нести ген устойчивости к антибиотику, чтобы можно было легко отличить клетки, несущие вектор, и выделить встроенный в него ген.
Векторы вокруг нас.
С уверенностью можно сказать, что мало кто из людей задумывается о том, что векторы окружают нас повсюду и помогают нам в повседневной жизни. Я люблю свой город Елизово и часто гуляю по его улицам, хожу в магазины, посещаю театр, выставки, музеи и т. д. Я обратила внимание, что векторы, помимо точных наук, встречаются мне каждый день. Так, например, во время прогулки в парке, я заметила, что ель, оказывается, можно рассматривать как пример вектора в пространстве: нижняя её часть – начало вектора, а верхушка дерева является концом вектора (рис.16). А вывески с изображением вектора при посещении больших магазинов помогают нам быстро найти тот или иной отдел и сэкономить время. Но большинство векторов я встречаю на вывесках или баннерах на улицах. На баннере, например, можно увидеть преимущество того или иного банка (% кредита или накопительный) (рис.17). Вывески помогают мне найти местонахождение нужного магазина, службы или другого необходимого объекта (рис.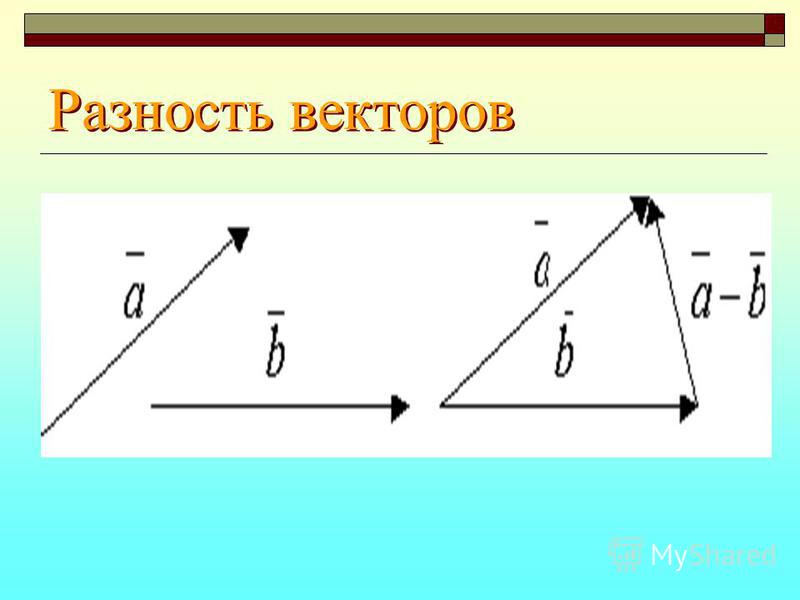
18).
Векторы в знаках дорожного движения.
Каждый день, выходя из дома, мы становимся участниками дорожного движения в роли пешехода либо в роли водителей (рис.19). В наше время практически каждая семья имеет машину, что, разумеется, не может не отразиться на безопасности всех участников дорожного движения. И, чтобы избежать казусов на дороге, стоит соблюдать все правила дорожного движения. Но не стоит забывать того, что в жизни всё взаимосвязано и, даже в простейших предписывающих знаках дорожного движения, мы видим указательные стрелки движения, в математике называемые – векторами. На примере знаков: 4.1.1 «Движение прямо», 4.1.2 «Движение направо», 4.1.3 «Движение налево», 4.1.4 «Движение прямо и налево» и другие (рис.20,21). Эти стрелки (векторы) указывают нам направления движения, стороны движения, стороны объезда, и ещё многое другое. Всю эту информацию можно прочитать на знаках дорожного движения на обочинах дорог. Не соблюдение этих правил и пренебрежение знаками приводит к необратимым последствиям (автокатастрофам), что, конечно же, не обходится без человеческих жертв, в том числе и детей (рис.
22).
Заключение.
Базовое понятие «вектор», рассмотренное на уроках математики, является основой для дальнейшего изучения в разделах общей химии, общей биологии, физики и других наук. Я наблюдаю необходимость векторов в жизни, которые помогают найти нужный объект, сэкономить время, они выполняют предписывающую функцию (в знаках дорожного движения), и избежать опасных ситуаций на дороге. Призываю всех, серьёзно отнестись к правилам дорожного движения, быть внимательными на дорогах, не проходить мимо детей, нарушающих их, и самим этого не делать.
Список литературы.
- Атанасян Л. С., В.Ф.Бутузов, С.Б.Кадомцев и др. Геометрия 7-9. Издательство «Просвещение», 2007г., 384с.
- Атанасян Л. С., В.Ф.Бутузов, С.Б.Кадомцев и др. Геометрия 10-11. Издательство «Просвещение», 2007г., 285с.
- Малугин В. А., Математика для экономистов: Линейная алгебра. Курс лекций. Глав 3. Векторная алгебра. Москва; Эксмо, 2006г., 224с.
- Беклемишев Д. В., Курс аналитической геометрии и линейной алгебры. Москва; Наука, 1988г.
- Перышкин А. В., Физика 9 класс: Учебник для общеобразовательных учреждений; М.: «Дрофа», 2004 г. – 256с.
- Мякишев Г. Я., Физика: учебник для 10 класса общеобразовательных учреждений; М.: «Просвещение», 2005г. – 366с.
- Мякишев Г. Я., Физика: учебник для 11 класса общеобразовательных учреждений; М.: «Просвещение», 2004г. – 382с.
- Габриелян О. С., Химия. 11 класс: учебник для общеобразовательных учреждений; М.: «Дрофа», 2005г. – 362[6]с.
- Лидин Р. А., Аликберова Л. Ю., Химия. Справочник для старшеклассников и поступающих в ВУЗы; М.: «АСТ-ПРЕСС ШКОЛА», 2006г. – 512 с.
- Кузьменко Н. Е., Ерёмин В. В., Попков В. А., Начала химии. Современный курс для поступающих в ВУЗы. Т.1; М.: «Экзамен», 2002г. – 384 с.
- Глинка Н. Л., Общая химия: Учебное пособие для вузов; М.: «Интеграл-Пресс», 2008 г. – 728 с.
- Уиллет Э., Генетика без тайн; М.: «Эксмо», 2008г. – 224с.
- Тейлор Д., Грин Н., Стаут У., Биология. Т.3; М.: «МИР», 2006г. – 451с.
- Правила дорожного движения Российской Федерации с иллюстрациями; М.; ООО «АТБЕРГ 98», 2007г.
В., Курс аналитической геометрии и линейной алгебры. Москва; Наука, 1988г.
Приложение
рис.1
рис.2
рис.4
рис.3
рис.6
рис.13
рис.11
рис.10
рис.8
рис.12
рис.14
рис.15
рис.18
рис.16
рис.20
рис.21
рис.19
Применение векторов в прикладных науках
Слайд 1
Описание слайда:
Применение векторов в прикладных науках Авторы: Аброськин Алексей Николаевич Рябуха Андрей Викторович
Слайд 2
Описание слайда:
План проекта:
1. Введение 2
2.
История возникновения понятия вектор. 3
3. Применение векторов в прикладн ых науках. 6
3.1 Векторы в математике 6
3.2.Вектор в географии 8
3.3.Векторы в физике 9
3.4.Векторы в навигации. 9
3.5.Векторы в экономике 11
3.6.Векторы в психологии 11
3.7. Векторы в проффесиях 11
4.Заключение 12
5. Литература:
Слайд 3
Описание слайда:
1. Введение
1. Введение
Данная работа посвящена рассмотрению векторного аппарата геометрии. С помощью векторов можно доказывать теоремы, решать геометрические, физические и другие задачи.
Слайд 4
Описание слайда:
Гипотеза Векторы находят широкое применение в геометрии и в прикладных науках.
Слайд 5
Описание слайда:
Задачи:
1. Провести исследования по данной теме.
2. Рассмотреть понятие «вектор» в предметах естественно-научного цикла.
3. Изучить осуществление моделирования с помощью векторов.
4. Показать применение векторов в прикладных науках.
Слайд 6
Описание слайда:
Описание слайда:
Слайд 8
Описание слайда:
История возникновения понятия вектор. Вектор – молодое математическое понятие. Этот термин впервые употребил ирландский математик Уильям Гамильтон в 1845 году в своих работах по построению числовых систем, обобщающих комплексные числа. Он же ввел термины «скаляр», «скалярное произведение», «векторное произведение».
Слайд 9
Описание слайда:
В 1587 г. был опубликован на голландском языке трактат фламандского ученого С. Стевина (1548-1620) «Начала статики». В нем автор, рассматривая сложение сил, приходит к выводу, что для нахождения результата сложения двух сил, действующих под углом 90, необходимо воспользоваться «параллелограммом сил», при этом для обозначения сил С.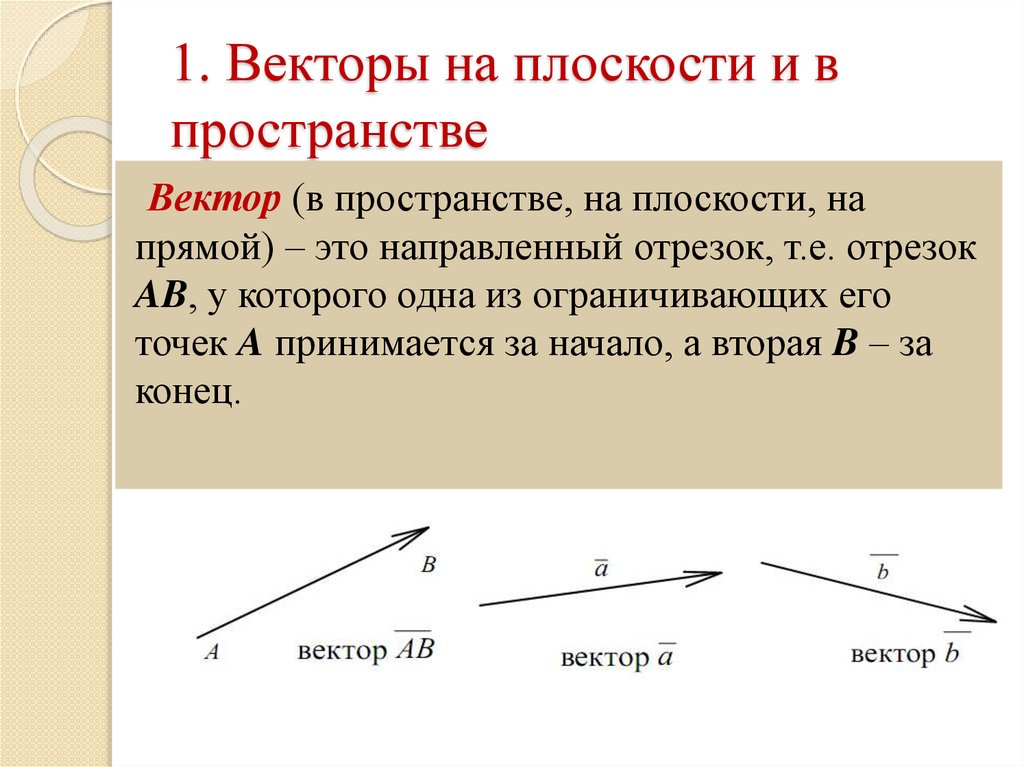
Слайд 10
Описание слайда:
Начала исчисления направленных отрезков были впервые изложены норвежцем Каспаром Весселем в мемуаре «Опыт об аналитическом представлении направления и его применениях, преимущественно к решению плоских и сферических многоугольников», опубликованном в «Трудах Датской Академии наук» в 1799 г.
Слайд 11
Система координат Р. Декарта основана на его концепции единой математики, объединяющей геометрию и алгебру. Развивая мысли Декарта о матемизации естествознания, Лейбниц писал: «Алгебра выражает величину необходим ещё иной, чисто геометрический анализ, непосредственно выражающий положение».
Система координат Р. Декарта основана на его концепции единой математики, объединяющей геометрию и алгебру.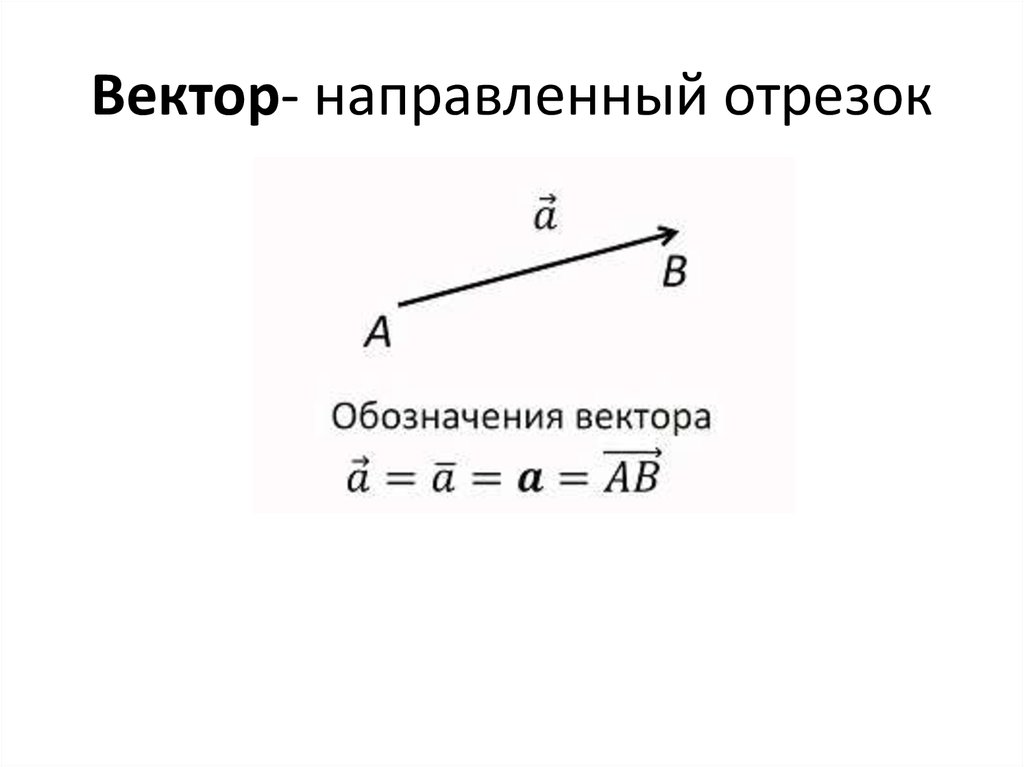
Развивая мысли Декарта о матемизации естествознания, Лейбниц писал: «Алгебра выражает величину необходим ещё иной, чисто геометрический анализ, непосредственно выражающий положение».
Слайд 12
Описание слайда:
Слайд 13
Описание слайда:
В конце 16- начале 17 в. многие ученые — физики, в том числе Леонардо да Винчи, и Галилео Галилей, пользовались направленными отрезками для наглядного представления сил. Формулируя свои законы движения планет, Кеплер по существу рассматривает направленный отрезок, началом которого является Солнце, а конец совпадает с движущейся точкой.
В конце 16- начале 17 в. многие ученые — физики, в том числе Леонардо да Винчи, и Галилео Галилей, пользовались направленными отрезками для наглядного представления сил. Формулируя свои законы движения планет, Кеплер по существу рассматривает направленный отрезок, началом которого является Солнце, а конец совпадает с движущейся точкой.
Слайд 14
Описание слайда:
Галиле́о Галиле́й— итальянский физик, механик, астроном, философ, математик, оказавший значительное влияние на науку своего времени. Он первым использовал телескоп для наблюдения небесных тел и сделал ряд выдающихся астрономических открытий. Галиле́о Галиле́й— итальянский физик, механик, астроном, философ, математик, оказавший значительное влияние на науку своего времени. Он первым использовал телескоп для наблюдения небесных тел и сделал ряд выдающихся астрономических открытий.
Слайд 15
Описание слайда:
Иога́нн Ке́плер— немецкий математик, астроном, механик, оптик, первооткрыватель законов движения планет Солнечной системы.(использовал векторное направление)
Иога́нн Ке́плер— немецкий математик, астроном, механик, оптик, первооткрыватель законов движения планет Солнечной системы.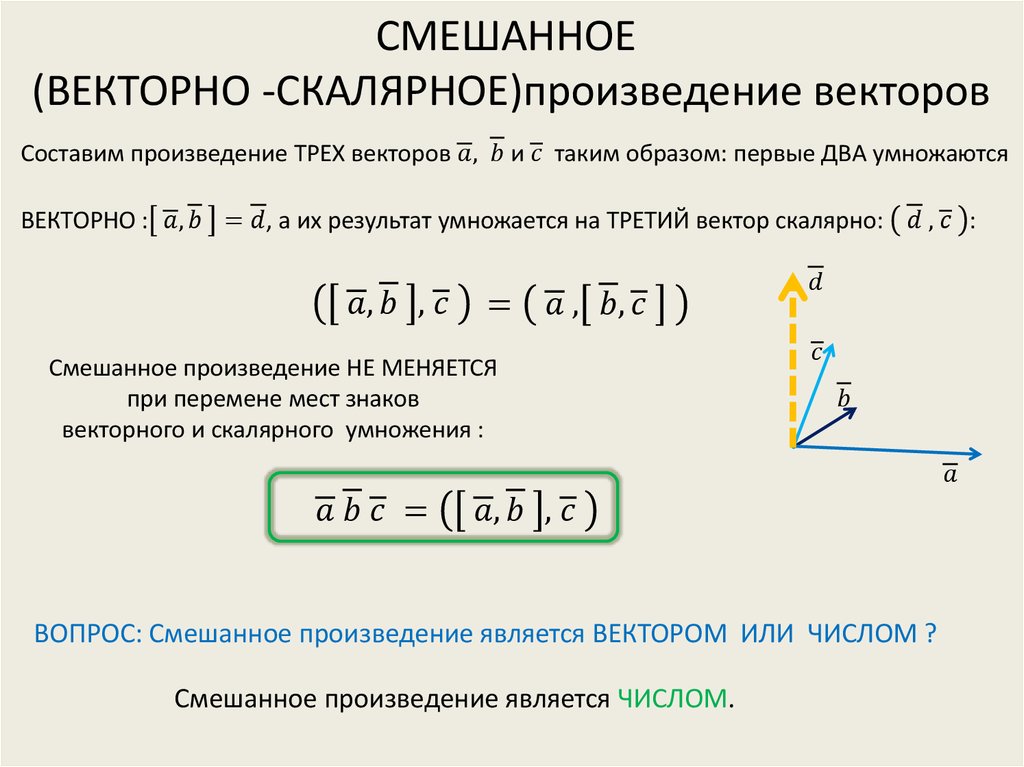
Слайд 16
Описание слайда:
В последней четверти 19 в. происходит слияние, синтез трех путей (геометрического, алгебраического и физического) исторического развития и трех источников формирования векторного исчисления. Векторное исчисление становится независимой ветвью математикиДжоза́йя Уи́ллард Гиббс — американский физик, физикохимик, математик и механик, один из создателей векторного анализа, статистической физики, математической теории термодинамики, что во многом предопределило развитие современных точных наук и естествознания в целом.
В последней четверти 19 в. происходит слияние, синтез трех путей (геометрического, алгебраического и физического) исторического развития и трех источников формирования векторного исчисления. Векторное исчисление становится независимой ветвью математикиДжоза́йя Уи́ллард Гиббс — американский физик, физикохимик, математик и механик, один из создателей векторного анализа, статистической физики, математической теории термодинамики, что во многом предопределило развитие современных точных наук и естествознания в целом.
Слайд 17
Описание слайда:
Применение векторов в прикладных науках.
Слайд 18
Описание слайда:
Векторы в географии
Оказывается, векторы, как отрезки, показывающие направление нашли своё отражение и в географии. Так, ветер – характеризуемый величиной и направлением, рассматривается как вектор. Распределение ветра исследуется в векторной форме. Таким образом, ветер (горизонтальное движение воздушных частиц относительно подстилающей поверхности) – векторная величина и описывается двумя параметрами – скоростью ( м/с) и направлением. Вектор – модель ветра. Аналогично, с помощью векторов показывают направление движения воздушных масс в циклонах и антициклонах.
С помощью векторов составляют карты миграции птиц и животных.
Используя действия над векторами можно рассчитать пролетные пути перелетных птиц.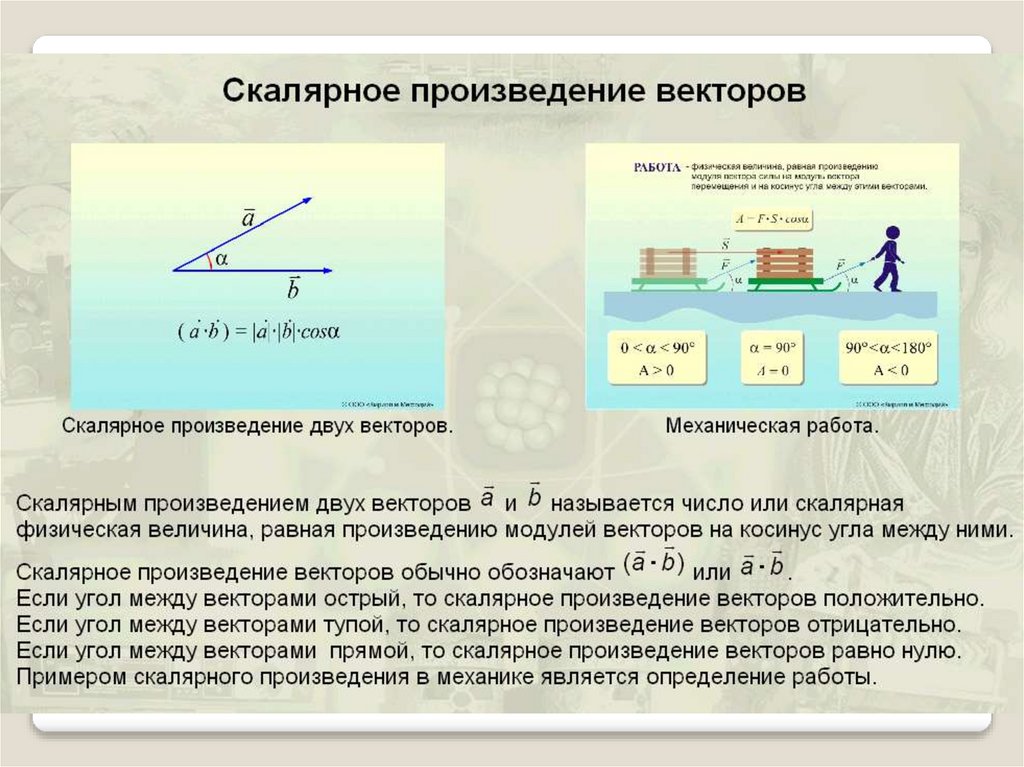
Слайд 19
Описание слайда:
Мы можем увидеть природное явление- молния, которая как-никак, вектор
Слайд 20
Описание слайда:
Векторы в физике Векторы — мощный инструмент не только математики, но и физики. Векторные величины в физике: скорость, перемещение, ускорение, сила, импульс, напряженность электрического поля, магнитная индукция, момент силы. Для этих величин важно «сколько» и «куда». Равномерным движением по окружности называется такое движение, при котором скорость не меняется по модулю, а меняется лишь её направление. При этом вектор ускорения перпендикулярен вектору скорости. Вектор скорости направлен по касательной к окружности.
Слайд 21
Описание слайда:
Электрический ток- также является вектором
Слайд 22
Описание слайда:
Векторы в навигации.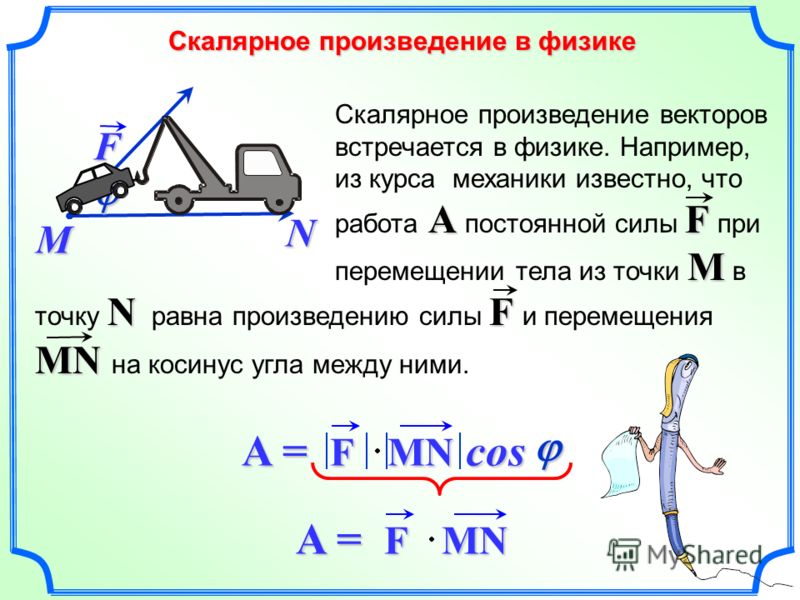
Часто для навигации в 3D программисты берут единичные вектора и, путём умножения их на матрицу вида камеры, получают вектора для навигации. Для навигации в трёхмерном пространстве, обычно так же необходимо иметь всего три вектора – один вбок (для стрейфа), один к камере либо от неё (что бы ходить вперёд/назад) и один вверх, либо вниз (для прыжков, например).
В практике судовождения довольно часто встречаются случаи, когда одновременно с учетом дрейфа судна от ветра приходится учитывать и снос течением.
Чтобы не ошибаться в последовательности действия при совместном учете течения и дрейфа, необходимо помнить, что в скоростном треугольнике одна из сторон всегда представляет собой вектор относительной скорости судна. В данном случае этот вектор направлен по линии пути при дрейфе.
Слайд 23
Описание слайда:
Векторы в экономике
Векторы можно рассматривать в качестве элементов любой природы, в том числе и экономической.
Предположим, что некоторая текстильная фабрика должна выпустить в одну смену 30 комплектов постельного белья, 150 полотенец, 100 домашних халатов, тогда производственную программу данной фабрики можно представить в виде вектора, где всё, что должна выпустить фабрика – это трехмерный вектор.
Слайд 24
Описание слайда:
Векторы в психологии Все больше обретает популярность такое необычное направление, как системно-векторная психология, в ней существует 8 вектор: -звуковой -зрительный -кожный и т.д. Все эти понятия характеризуют человека, его характер
Слайд 25
Описание слайда:
Мы встречаем векторы в знаках дорожного движения: Мы встречаем векторы в знаках дорожного движения:
Слайд 26
Описание слайда:
Векторы в профессиях
Векторы в профессиях
Мы выяснили, что векторы используются во многих науках для моделирования самых различных процессов и явлений.
Значит, это понятие потребуется во всех технических профессиях, профессиях, связанных с компьютерном деле, в медицине, химии и т.д. Векторы нужны для освоения профессии строителя и архитектора, так как особое место вектору отводится в сопромате, ведь нагрузка на разные элементы конструкций является разложением вектора по базису векторов силы тяжести и других приложенных к конструкции сил. В самолетостроении, судостроении, автомобилестроении при конструировании транспорта также применяются векторы и их свойства.
В науке судовождение используются векторы и их свойства для определения кажущегося ветра во время движения судна. В штилевую погоду на судне, имеющего ход, всегда ощущается встречный ветер, равный скорости судна. Он имеет название курсовой ветер и имеет направление, противоположное движению судна. Таким образом, на движущемся судне наблюдается кажущийся ветер, вектор которого равен геометрической сумме истинного и курсового ветров. Для определения направления ветра используется способ построения векторного треугольника.
Векторы понадобятся и портному для правильного составления выкроек одежды
Слайд 27
Описание слайда:
Заключение Каждый человек постоянно сталкивается с векторами в повседневной жизни. Векторы необходимы нам для изучения не только математики, но и других наук. Каждый должен знать, что такое вектор. Базовое понятие «вектор» является основой для изучения в разделах общей химии, общей биологии, физики и других наук. Мы наблюдаем необходимость векторов в жизни, которые помогают найти нужный объект, сэкономить время, они выполняют предписывающую функцию в знаках дорожного движения. С помощью векторов решаются многие математические и физические задачи. Встречается применение векторов к решению задач и на экзаменах ОГЭ и ЕГЭ,
Слайд 28
Описание слайда:
Литература:
1.
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.
2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
3. Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
4. Википедия
Как можно использовать векторы в повседневных жизненных ситуациях
Изучение математики необходимо для изучения физики. Основные понятия и принципы поддерживаются математическим фундаментом. По мере продвижения в изучении физики мы столкнемся с широким кругом понятий, основанных на математических принципах.
Слова могут использоваться для адекватного выражения движения объектов в некоторых ситуациях. Даже тот, кто никогда в жизни не посещал уроков физики, вероятно, имеет в своем лексиконе некоторые термины, которые они могут использовать для описания движущихся объектов.
Словарного запаса, включающего такие слова и фразы, как «двигаться быстро», «остановиться», «замедлить», «ускорить» и «повернуться», более чем достаточно, когда дело доходит до объяснения движения объектов. Это лишь некоторые из многих фраз, которые используются при изучении физики.
Вектор необходим для расчета любой векторной единицы. Например, масса шины движущегося автомобиля. Кроме того, она обладает начальной скоростью, конечной скоростью и ускорением, гравитационной реакцией, силами трения, а благодаря вращению обладает крутящим моментом. . Вектор необходим для того, чтобы мы могли получить результат.
Практическое применение вектора в повседневной жизни 1. ВОЕННОЕ ИСПОЛЬЗОВАНИЕ Любое артиллерийское орудие, стреляющее снарядами с использованием силы пушки или любого другого типа метательного заряда, обычно основанного на взрывчатых веществах, считается пушкой.
Калибр, дальность, подвижность, скорострельность и угол стрельбы орудий отличаются друг от друга. В зависимости от роли, которую каждый тип пушек должен играть на поле боя, разные типы пушек смешивают и уравновешивают эти характеристики в разной степени. Необходимо использовать этот вектор. Векторы определяют, куда направится снаряд и попадет в землю.
Вектор бейсбола автоматически используется игроками в таких видах спорта, как баскетбол и бейсбол. В конце концов, ученики либо стреляли в цель, либо бросали мяч в направлении под углом, и то, и другое выполнялось с использованием их понимания векторов. На самом деле, в таких играх, как «Метание копья», необходимо оценивать угол, который вектор снаряда образует с землей, чтобы копье могло лететь как можно дальше.
3. ВЕКТОР В ИГРАХ Векторы используются для хранения местоположений, направлений и скоростей в видеоиграх. Вектор положения говорит нам, как далеко находится объект, вектор скорости говорит нам, сколько времени это займет или какую силу нам нужно приложить, а вектор направления говорит нам, как мы должны приложить эту силу.
Большая часть движений, происходящих во время катания на американских горках, является реакцией на гравитационное притяжение земли. Когда поезд попадает в высшую точку, а затем едет вниз, он набирает достаточную скорость, чтобы на него повлияло гравитационное притяжение. С такой скоростью он достигнет вершины следующего холма. Этот процесс повторяется снова, пока вся энергия поезда не рассеется из-за трения. Однако поезд сможет продолжать движение до тех пор, пока на пути не будет точки, превышающей первоначальный пик. При построении системы безопасности важно учитывать векторы сил, ускорения и скорости. Это использует использование векторов при разработке аттракциона на американских горках.
5. ПРИ ИГРЕ В КРИКЕТ Если игрок с битой в крикете делает бросок с навеса, возможны три исхода: догнать, упасть раньше полевого игрока или максимальное количество очков. Когда игрок с битой бьет по мячу, угол, под которым он бьет, и скорость, с которой он бьет по мячу, являются важными факторами, определяющими, пересечет ли мяч границу.
Если оба этих фактора соответствуют требованиям максимальной силы, мяч переходит границу. Из-за шара все вращается вокруг вектора.
Когда лодка плывет по реке, скорость лодки и скорость реки влияют на общую скорость лодки. При изменении скорости течения реки меняется и курс, по которому идет лодка. Следовательно, лодочник должен определить угол переправы через реку, чтобы напрямую добраться до берега реки. Вектор играет здесь важную роль.
7. ПОПЕРЕЧНЫЙ ВЕТЕРПонятие бокового ветра нам знакомо. Ветер, который дует в направлении, перпендикулярном пути, по которому движется человек, называется боковым ветром. Когда самолет, наконец, приземлится, он иногда будет испытывать проблемы из-за бокового ветра. Используя вектор, пилот может определить результирующую скорость, а также направление.
Заключение Векторы используются в повседневной жизни для помощи в локализации людей, мест и вещей. Они также используются для описания вещей, которые действуют в ответ на приложенную к ним внешнюю силу. Величина, которая обладает как величиной, так и направлением, называется вектором. Первый, второй и третий законы Ньютона — это отношения между векторами, точно описывающие движение тел, когда на них действует внешняя сила. Законы Ньютона охватывают широкий спектр явлений и могут использоваться для описания чего угодно, от мяча в свободном падении до ракеты на пути к Луне.
Объяснение урока: Векторные приложения | Nagwa
В этом объяснителе мы узнаем, как использовать векторные операции для решения различных реальных задач.
В реальном мире некоторые величины являются скалярами, например масса,
длина или возраст, представленный одним числом, которое мы называем его величиной,
и другие, которые являются векторами, такими как перемещение, скорость или сила,
представлены как величиной, так и конкретным направлением. Используются векторы
широко в математике, технике, физике и вычислительной технике. Например,
в классической механике, если мы рассмотрим силы или импульс, действующие на
тела, мы должны принять во внимание как величину, так и направление, чтобы знать
куда тело будет двигаться в любой момент; если тело движется в свободном падении, то
учитывать не только направление силы тяжести, действующей на тело, но и
направление и величина других сил, таких как сопротивление воздуха или ветер.
Определение: Вектор
Вектор — это величина, которая имеет как величину, так и направление. Это может быть геометрически изображается в виде направленного отрезка, длина которого величина вектора и стрелка которого указывает его направление.
Это направление может быть указано с точки зрения севера, востока, запада и юга направления, или их комбинация, или, в более общем смысле, как угол или несущий. Например, объект может двигаться со скоростью 25 миль в час в восточное направление.
В качестве примера рассмотрим ситуацию, связанную со скоростью, и определим
величина и направление от данной информации.
Пример 1: Величина и направление скорости
Скорость — это векторная величина, которая объединяет скорость и направление. Например, скорость на участке реки Миссисипи около Нового Орлеана равна 3 мили в час восток.
- Какова величина этой скорости?
- Каково направление этой скорости?
Ответ
Часть 1
Давайте сначала определим величину скорости.
Величина скорости – это ее скорость, которая в данном случае для сечения реки Миссисипи недалеко от Нового Орлеана, 3 мили в час.
Часть 2
Как сказано в вопросе, скорость — это векторная величина, которая объединяет скорость и направление. Нам говорят, что скорость воды 3 мили в час в восточном направлении. Поэтому направление скорости на восток.
Другой способ представления вектора, вместо использования величины и направления,
имеет прямоугольную форму. В общем, векторы могут быть представлены в любом количестве
размеров, также известный как
степеней свободы, то есть количество
компоненты, необходимые для полного определения вектора. В этом объяснении мы будем
рассматривать векторы в одном и двух измерениях соответственно, но одинаковые
принципы справедливы для трех и более измерений.
В одном измерении векторы представлены одним числом 𝑣, которое может быть положительным или отрицательным в зависимости от направления вектора. В двух измерениях вектор ⃑𝑣 представлен двумя числами в прямоугольная форма. Прямоугольная форма вектора определяет положение как линейное расстояние от начала координат в двух или более взаимно перпендикулярных направления.
Стандартные единичные векторы в координатной плоскости ⃑𝑖=(1,0) и ⃑𝑗=(0,1) через два размеры, как показано на схемах.
Начало — это точка пересечения осей и векторов на координатной плоскости задаются линейной комбинацией единичные векторы с использованием обозначения ⃑𝑣=𝑥⃑𝑖+𝑦⃑𝑗=(𝑥,𝑦).
Направление закодировано в этой форме вектора: с запада на восток означает, что мы
двигаться в направлении ⃑𝑖, а с востока на запад означает, что мы
двигаться в направлении −⃑𝑖. Точно так же с юга на север
означает, что мы движемся в направлении ⃑𝑗 и с севера на юг
означает, что мы движемся в направлении −⃑𝑗. Двигаясь в любом другом направлении, скажем, на юго-восток,
будет сочетанием этих направлений.
Например, если мы хотим определить вектор смещения человека, который перемещается на 2 м на запад, а затем на 4 м на юг, мы можем сделать это с помощью эти взаимно перпендикулярные направления; 2 м к западу представляет собой смещение на −2⃑𝑖 и 4 м к югу представляет собой смещение −4⃑𝑗, так как берем север и восток направления как положительные. Собрав это вместе, вектор смещения будет быть ⃑𝑠=−2⃑𝑖−4⃑𝑗.
Добавление или вычитание векторов в одном измерении очень просто, так как мы просто добавляем или вычесть компоненты или числа, представленные каждым вектором. Напомним, что сложение или вычитание двух векторов, ⃑𝑢 и ⃑𝑣, в двух измерениях может быть представлен в векторная диаграмма выглядит следующим образом.
Сложение или вычитание двух векторов эквивалентно сложению или вычитанию их
составные части. Например, если
⃑𝑢=(𝑥,𝑦) и
⃑𝑣=(𝑥,𝑦), тогда
⃑𝑢+⃑𝑣=(𝑥,𝑦)+(𝑥,𝑦)=(𝑥+𝑥,𝑦+𝑦)=(𝑥+𝑥)⃑𝑖+(𝑦+𝑦)⃑𝑗,⃑𝑢-⃑𝑣=(𝑥),𝑦 (𝑥,𝑦)=(𝑥−𝑥,𝑦−𝑦)=(𝑥−𝑥)⃑𝑖+(𝑦−𝑦)⃑𝑗.
Мы также можем иметь вектор относительно другого, например, когда мы рассмотреть движение двух тел.
Определение: Вектор относительной скорости
Рассмотрим движение двух тел, тела 𝐴 и тела 𝐵.
Если эти тела движутся со скоростями ⃑𝑣 и ⃑𝑣 соответственно относительная скорость 𝐴 с по отношению к 𝐵, обозначаемому ⃑𝑣, есть разница между этими двумя скоростями: ⃑𝑣=⃑𝑣−⃑𝑣.
Аналогично, относительная скорость 𝐵 относительно 𝐴 может быть обозначается как ⃑𝑣 и определяется как ⃑𝑣=⃑𝑣−⃑𝑣.
Обратите внимание, что мы имеем ⃑𝑣=−⃑𝑣, что является интуитивным результатом, поскольку отрицание вектора представляет противоположное направление.
В простых ситуациях мы можем предположить, что разные тела
двигаться по прямой линии в двух направлениях, влево или вправо,
и что они движутся либо в одном направлении, либо в противоположных направлениях. Если они движутся в одном направлении,
скорости будут иметь один и тот же знак, а в противоположных направлениях
имеют разные знаки. Скорость — это просто величина скорости, т.
‖‖⃑𝑣‖‖.
Рассмотрим пример, где нам нужно определить относительные скорости двух мотоциклов, движущихся в одном направлении по прямой. скорости каждого мотоцикла, ⃑𝑣 и ⃑𝑣, будут даны как единичные число, представляющее вектор в одном измерении.
Пример 2. Определение относительной скорости двух тел, движущихся в одном направлении Направление
Два мотоцикла 𝐴 и 𝐵 движутся в одном направлении. Если скорость из 𝐴 это 30 км/ч и скорость 𝐵 равно 15 км/ч, найдите относительная скорость 𝐴 относительно 𝐵.
Ответ
В этом примере мы хотим найти относительную скорость мотоцикла 𝐴 в отношении мотоциклов 𝐵, которые движутся в то же направление.
Пусть скорость мотоцикла 𝐴 будет
⃑𝑣=30/км/ч
а скорость мотоцикла 𝐵 быть
⃑𝑣=15/км/ч,
так как мотоциклы движутся в одном направлении.
Относительная скорость мотоцикла 𝐴 относительно 𝐵 это ⃑𝑣=⃑𝑣−⃑𝑣=30−15=15.
Таким образом, относительная скорость равна 15 км/ч.
Теперь давайте рассмотрим пример, где нам нужно определить реальную скорость грузовик, учитывая информацию о скорости полицейской машины и относительной скорости.
Пример 3. Определение скорости движущегося тела по его относительной скорости
Полицейская машина двигалась по горизонтальному шоссе в точке 47 км/ч. Это использовали радар для измерения скорости грузовика, движущегося в том же направлении. Данный что показания на радаре были 50 км/ч, определить фактическая скорость грузовика.
Ответ
В этом примере мы хотим определить фактическую скорость грузовика с помощью информация о скорости полицейской машины и относительном скорость грузовика до полицейской машины, измеренная радаром.
Пусть ⃑𝑣=47/км/ч
быть скорость полицейской машины и
⃑𝑣=50/км/ч быть
скорость грузовика, измеренная радаром, то есть скорость
грузовика относительно скорости полицейской машины. Обе скорости имеют одинаковый знак
так как полицейская машина и грузовик движутся в одном направлении. Находим реальную скорость грузовика
путем перестановки
⃑𝑣=⃑𝑣−⃑𝑣 как
⃑𝑣=⃑𝑣+⃑𝑣=50+47=97.
Поскольку это положительное число, фактическая скорость грузовика равна 97 км/ч.
У нас также может быть вектор относительной скорости для прямоугольной формы в двух измерениях. Например, предположим два тела, 𝐴 и 𝐵, движутся со скоростями ⃑𝑣 и ⃑𝑣, соответственно, выраженные в прямоугольных форме или через два взаимно перпендикулярных единичных вектора. Это означает, что мы взять разницу каждого компонента в векторе ⃑𝑣 с соответствующим компонентом в вектор ⃑𝑣.
Нам не нужно записывать единичные векторы в терминах ⃑𝑖 и ⃑𝑗, которые являются стандартными единичными векторами. Мы могли бы также иметь их с точки зрения других векторов, скажем, ⃑𝑒 и ⃑𝑓, пока они перпендикулярны друг другу и имеют единичную длину.
Например, если тело 𝐴 движется со скоростью
⃑𝑣=𝑥⃑𝑒+𝑦⃑𝑓
а тело 𝐵 движется со скоростью
⃑𝑣=𝑥⃑𝑒+𝑦⃑𝑓,
скорость 𝐴 относительно 𝐵 можно обозначить
как ⃑𝑣 и определяется как
⃑𝑣 = ⃑𝑣 — ⃑𝑣 = 𝑥⃑𝑒+𝑦⃑𝑓 — 𝑥⃑𝑒+𝑦⃑𝑓 = (𝑥 — 𝑥) ⃑𝑒+(𝑦 — 𝑦) ⃑𝑓.
Теперь давайте посмотрим на примере, где мы должны определить относительную скорость в члены заданного единичного вектора двух автомобилей, движущихся в противоположных направлениях.
Пример 4. Определение относительной скорости двух тел, движущихся в противоположных направлениях в векторной форме
Две машины 𝐴 и 𝐵 движутся встречно направления по той же дороге в 62 км/ч и 31 км/ч соответственно. Учитывая, что ⃑𝑒 — единичный вектор в направлении движение автомобиля 𝐴, определить скорость автомобиля 𝐴 относительно автомобиля 𝐵.
Ответ
В этом примере мы хотим определить скорость автомобиля 𝐴 относительно автомобиля 𝐵 с точки зрения единичного вектора ⃑𝑒, направление движения автомобиля 𝐴, и машины движутся в противоположных направлениях.
Так как ⃑𝑒 задан единичный вектор в направлении
движения автомобиля 𝐴 и нам говорят, что этот автомобиль
движется со скоростью
62 км/ч,
вектор скорости автомобиля 𝐴 будет
⃑𝑣=62⃑𝑒.
Аналогично, поскольку автомобиль 𝐵 движется в противоположном направлении направление движения автомобиля 𝐴, со скоростью 31 км/ч, его вектор скорости будет отрицательным: ⃑𝑣=−31⃑𝑒.
Скорость автомобиля 𝐴 относительно автомобиля 𝐵 равна ⃑𝑣=⃑𝑣−⃑𝑣=62⃑𝑒−−31⃑𝑒=93⃑𝑒.
Таким образом, относительная скорость равна 93⃑𝑒/.км/ч
При рассмотрении двух или более сил, действующих на тело, результирующая сила, ⃑𝑅 — векторное сложение различных сил.
Определение: Результирующая сила
Если есть силы 𝑛, ⃑𝐹,⃑𝐹,…,⃑𝐹, действующий на одно тело, то равна равнодействующая сила ⃑𝑅 к ⃑𝑅=⃑𝐹+⃑𝐹+⋯+⃑𝐹.
Система с такими силами находится в равновесии, когда результирующая сила равна к нулевому вектору, ⃑𝑅=0.
Например, если есть две силы, ⃑𝐹 и ⃑𝐹, действующие на тело, то результирующая сила определяется выражением ⃑𝑅=⃑𝐹+⃑𝐹.
Теперь рассмотрим пример, где нам нужно определить неизвестные значения
входящие в векторы сил, заданные в условной единице
векторы ⃑𝑖 и
⃑𝑗, действующий на частицу, находящуюся в равновесии.
Пример 5: Нахождение неизвестных компонентов двух сил при заданном равновесии
Частица находится в равновесии под действием двух сил ⃑𝐹=3⃑𝑖+𝑥⃑𝑗N и ⃑𝐹=𝑦⃑𝑖+2⃑𝑗N. Найдите значения 𝑥 и 𝑦.
Ответ
В этом примере мы хотим определить значения 𝑥 и 𝑦 силы в направления ⃑𝑗 и ⃑𝑖 для ⃑𝐹 и ⃑𝐹 соответственно для частица, находящаяся в равновесии под действием двух сил.
Напомним, что результирующая сила, действующая на любое тело, есть сумма всех силы. Таким образом, равнодействующая двух сил, действующих на частица ⃑𝑅=⃑𝐹+⃑𝐹=3⃑𝑖+𝑥⃑𝑗+𝑦⃑𝑖+2⃑𝑗=(3+𝑦)⃑𝑖+(𝑥+2)⃑𝑗.
Силы находятся в равновесии, если результирующая сила, ⃑𝑅, равен нулевому вектору. Если вектор равный нулевому вектору, его отдельные компоненты должны быть равны нулю; следовательно, 3+𝑦=0𝑦=−3 и 𝑥+2=0𝑥=−2.
Таким образом, значения 𝑥=−2,𝑦=−3.
В следующем примере мы снова определим неизвестные значения, появляющиеся в
векторы сил, заданные в терминах стандартных единичных векторов
⃑𝑖 и
⃑𝑗, на этот раз с тремя силами, действующими на
частица с заданной равнодействующей силой.
Пример 6. Нахождение неизвестных компонентов трех сил по данным компонентам равнодействующей
Силы ⃑𝐹=−10⃑𝑖−7⃑𝑗, ⃑𝐹=𝑎⃑𝑖−⃑𝑗 и ⃑𝐹=5⃑𝑖+(𝑏−10)⃑𝑗 действуют на частицу, где ⃑𝑖 и ⃑𝑗 два перпендикулярных единичных вектора. Учитывая, что равнодействующая сил ⃑𝑅=−13⃑𝑖−3⃑𝑗, определить значения 𝑎 и 𝑏.
Ответ
В этом примере мы хотим определить неизвестные значения 𝑎 и 𝑏, встречающиеся в компонентах силы ⃑𝐹 и ⃑𝐹 соответственно, которые, вместе с ⃑𝐹 действуют на частицу с заданной равнодействующей силой.
Напомним, что результирующая сила, действующая на любое тело, есть сумма всех силы. Таким образом, равнодействующая трех сил, действующих на частица ⃑𝑅 = ⃑𝐹+⃑𝐹+⃑𝐹 = -10⃑𝑖 — 7⃑𝑗+𝑎⃑𝑖 — ⃑𝑗+5⃑𝑖+(𝑏 -10) ⃑𝑗 = (𝑎 -5) ⃑𝑖+(𝑏 -18) ⃑𝑗.
Так как нам сказали, что результирующий вектор силы равен ⃑𝑅=−13⃑𝑖−3⃑𝑗, мы приравниваем ⃑𝑖 и ⃑𝑗 компоненты отдельно для получения 𝑎−5=−13𝑎=−8 и 𝑏−18=−3𝑏=15.
Таким образом, значения
𝑎=−8, 𝑏=15.
Для вектора прямоугольной формы ⃑𝑣=𝑥⃑𝑖+𝑦⃑𝑗, величина ‖‖⃑𝑣‖‖=√𝑥+𝑦.
Это длина вектора или расстояние от начала координат, которое мы можем определить по теореме Пифагора о прямоугольном треугольнике со сторонами 𝑥 и 𝑦.
Величины единичных векторов равны ‖‖⃑𝑖‖‖=√1+0=1,‖‖⃑𝑗‖‖=√0+1=1, по этой причине их называют единичными векторами, поскольку они имеют единичную длину. Величина вектора смещения или скорости даст нам расстояние или скорость соответственно. Например, если вектор скорости объекта ⃑𝑣=3⃑𝑖+4⃑𝑗/, мс тогда скорость тела ‖‖⃑𝑣‖‖=√3+4=√25=5/.мс
Мы также можем указать направление в терминах угла против часовой стрелки от
положительное ⃑𝑖 направление. С помощью стандартных
тригонометрия, мы
загар𝜃=𝑦𝑥,
где 𝜃 известно как направление вектора. С использованием
величину и направление, мы можем перевести вектор, заданный в терминах единицы
векторов в прямоугольной форме к вектору, представленному его величиной и
направление. Фактически, это эквивалентно полярной форме вектора с
радиальная составляющая 𝑟≡‖‖⃑𝑣‖‖ и угловая составляющая
𝜃, где измеряется угол 𝜃
против часовой стрелки от положительной оси 𝑥.
Нам может понадобиться сначала нарисовать вектор, чтобы убедиться, что мы получаем правильный угол, так как взятия арктангенса может быть недостаточно. Диапазон для функция арктангенса равна −𝜋2,𝜋2 когда область определения касательной функции ограничена одним и тем же интервалом, называется основной ветвью.
Таким образом, пока 𝜃∈−𝜋2,𝜋2, мы можно взять арктангенс обеих частей уравнения, чтобы получить 𝜃=𝑦𝑥.tan
Угловые координаты 𝜃∈−𝜋2,𝜋2 соответствуют первому и четвертому квадранту или квадрантам, где 𝑥>0. Однако это уже не так, если вектор лежит в второй или третий квадрант. Для второго и третьего квадрантов значение 𝜋, в радианах или 180∘, дюйм градусов, необходимо прибавить к углу 𝜃, чтобы отрегулировать угол так, чтобы вектор лежал в правильном квадрант. Это не влияет на саму функцию тангенса, так как мы имеем личность тантан𝜃=(𝜃+180).∘
Например, рассмотрим вектор во втором квадранте.
Из эскиза видно, что
𝛼=−𝑦𝑥. tan
Сумма всех углов прямой составляет 180∘ и, следовательно, 𝛼+𝜃=180∘. Таким образом, для второго или третьего квадранта, где 𝑥0, угол будет 𝜃=−𝛼+180=𝑦𝑥+180.∘∘tan
Наконец, давайте рассмотрим пример, где мы определяем смещение, и следовательно, величина и направление конкретного тела из информации данный. Мы можем сделать это, сначала записав вектор смещения в терминах единичные векторы, а затем, используя теорему Пифагора и стандартный тригонометрия.
Пример 7. Решение текстовых задач путем сложения двух векторов в Форма
Величины и направления Тело продвинулось на 28 м строго на восток, а затем 14 м на север. Определять перемещение тела с указанием его направления до ближайшего минута.
Ответ
В этом примере мы хотим определить смещение и, следовательно, расстояние и направление тела, движущегося в определенных направлениях перпендикулярны друг другу.
Начнем с определения вектора смещения из информации
данный. Напомним, что мы можем представить вектор в прямоугольной форме через
два взаимно перпендикулярных направления,
⃑𝑖 и
⃑𝑗.
Мы принимаем направление с запада на восток (прямо на восток) как положительное в ⃑𝑖 направление и с юга на север (на север) как положительное в ⃑𝑗 направление.
Поскольку тело проходит 28 м, его смещение в этом направлении будет 28⃑𝑖 и тогда 14 м строго на север будет иметь водоизмещение 14⃑𝑗. Собрав это вместе, смещение вектор ⃑𝑠=28⃑𝑖+14⃑𝑗.
Расстояние — это величина вектора смещения, которую мы можем определить с помощью теоремы Пифагора как 𝑑=‖‖⃑𝑠‖‖=√28+14=14√5.
Направление задается как угол 𝜃, который может быть находится из стандартной прямоугольной тригонометрии как тантантан𝜃=1428𝜃=12𝜃=12=2634′.∘
Таким образом, водоизмещение равно 14√5 м, 2634′∘ к северу от востока.
Ключевые точки
- Векторы представлены величиной и направлением или в терминах
единичных векторов в координатной плоскости в двух взаимно перпендикулярных
направления. Стандартные единичные векторы для этих направлений:
⃑𝑖 и ⃑𝑗
а прямоугольную форму вектора можно записать как
⃑𝑣=𝑥⃑𝑖+𝑦⃑𝑗.
- Мы можем решать реальные проблемы, переводя информацию в векторы и применяя операции, в которых мы складываем или вычитаем разные векторы.
- Относительная скорость двух тел, 𝐴 и 𝐵, со скоростями ⃑𝑣 и ⃑𝑣, соответственно, обозначаются ⃑𝑣, это разница между двумя скорости: ⃑𝑣=⃑𝑣−⃑𝑣.
- Результирующая сила, действующая на частицу, ⃑𝑅, векторное сложение всех сил действует на частицу.
- Величина, ‖‖⃑𝑣‖‖, и
направление 𝜃 вектора в прямоугольной форме
можно найти по теореме Пифагора и стандартной тригонометрии как
‖‖⃑𝑣‖‖=√𝑥+𝑦
и
загар𝜃=𝑦𝑥.
Используя их, мы можем перевести вектор, заданный в терминах единичных векторов, в
прямоугольной формы к вектору, представленному его величиной и направлением. Угол 𝜃 будет зависеть от квадранта, в котором
вектор лежит, что может быть эффективно передано с помощью следующей диаграммы.
