Примеры решения задач с векторами
Примеры решения задач с векторами
Вектора применяются во многих науках, таких как: математика, физика, геометрия и многих других прикладных науках. На практике, они позволяют не делать лишних операций и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять теорию векторов и научиться решать задачи с ними.
Перед изучением примеров решения задач советуем изучить теоретический материал по векторам, прочитать все определения и свойства. Список тем находится в правом меню.
Координаты вектора
Теоретический материал по теме — координаты вектора.
Пример
Запись 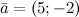 означает,
что вектор
означает,
что вектор 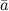
Пример
Задание. Заданы векторы 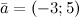 и
и 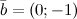 .
Найти координаты вектора
.
Найти координаты вектора 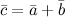
Решение. 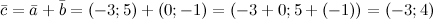
Пример
Задание. Вектор 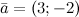
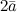
Решение. 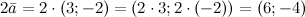
Пример
Задание. Найти координаты вектора  ,
если
,
если 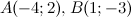
Решение. 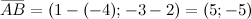
Длина (модуль) вектора
Теоретический материал по теме — длина вектора.
Пример
Задание. Найти длину вектора 
Решение. Используя формулу, получаем:

Пример
Задание. Найти длину вектора 
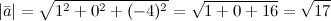
Угол между векторами
Теоретический материал по теме — угол между векторами.
Пример
Задание. Известно, что скалярное произведение
двух векторов 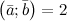 ,
а их длины
,
а их длины  .
Найти угол между векторами
.
Найти угол между векторами 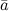
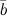 .
.Решение. Косинус искомого угла:

Пример
Задание. Найти угол между векторами  и
и 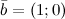
Решение. Косинус искомого угла

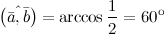
Пример
Задание. Найти угол между векторами 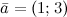 и
и 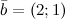
Решение. Косинус искомого угла:
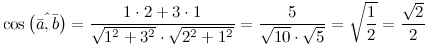
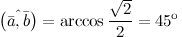
Разложение вектора по ортам координатных осей
Теоретический материал по теме — разложение вектора по ортам.
Пример
Задание. Зная разложения вектора 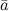 по
базисной системе векторов:
по
базисной системе векторов: 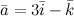 ,
записать координаты этого вектора в
пространстве.
,
записать координаты этого вектора в
пространстве.
Решение. Коэффициенты при ортах и есть координатами
вектора, поэтому из того, что 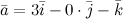 ,
получаем, что
,
получаем, что 
Пример
Задание. Вектор  задан
своими координатами:
задан
своими координатами:  .
Записать разложение данного вектора
по ортам осей координат.
.
Записать разложение данного вектора
по ортам осей координат.
Решение. Координаты вектора — это коэффициенты при ортах координатных осей в разложении вектора по базисной системе векторов, поэтому искомое разложение:

Теоретический материал по теме — скалярное произведение векторов.
Пример
Задание. Вычислить скалярное произведение
векторов  и
и  ,
если их длины соответственно равны 2 и
3, а угол между ними 60°.
,
если их длины соответственно равны 2 и
3, а угол между ними 60°.
Решение. Так как из условия 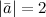 ,
, 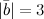
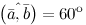 ,
то
,
то 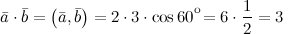
Пример
Задание. Найти скалярное произведение векторов 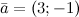 и
и 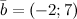
Решение. Скалярное произведение
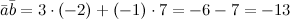
Векторное произведение векторов
Теоретический материал по теме — векторное произведение векторов.
Пример
Задание. Найти векторное произведение векторов  и
и 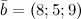
Решение. Составляем определитель и вычисляем его:
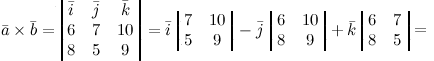
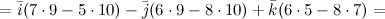
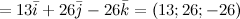
Смешанное произведение векторов
Теоретический материал по теме — смешанное произведение векторов.
Пример
Задание. Вычислить объем пирамиды, построенной
на векторах 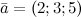 ,
,  ,
, 
Решение. Найдем смешанное произведение заданных
векторов, для это составим определитель,
по строкам которого запишем координаты
векторов 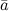
 и
и 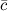 :
: 
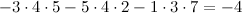
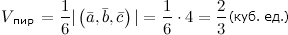
Примеры решения задач с векторами — онлайн справочник для студентов
Векторы используются во многих науках, таких как: математика, физика, геометрия и многие другие прикладные науки. На практике они позволяют не выполнять ненужных операций и сокращают время на выполнение задач. Поэтому для будущих специалистов очень важно понять теорию векторов и научиться решать с ними проблемы.
Прежде чем изучать примеры решения проблем, советуем вам изучить теоретический материал по векторам, прочитать все определения и свойства. Список тем находится в правом меню.
Векторные координаты
пример
Запись \(\ \overline{a}=(5 ;-2) \) означает, что вектор \(\ \overline{a} \) имеет следующие координаты: абсцисса равна 5, ордината равна -2.
пример
Векторы и дан \(\ \overline{a}=(-3 ; 5) \) и \(\ \overline{b}=(0 ;-1) \) . Найти векторные координаты \(\ \overline{c}=\overline{a}+\overline{b} \)
\(\ \overline{c}=\overline{a}+\overline{b}=(-3 ; 5)+(0 ;-1)=(-3+0 ; 5+(-1))=(-3 ; 4) \)
Пример
Вектор \(\ \overline{a}=(3 ;-2) \) Найти векторные координаты \(\ 2 \overline{a} \)
\(\ 2 \overline{a}=2 \cdot(3 ;-2)=(2 \cdot 3 ; 2 \cdot(-2))=(6 ;-4) \)
Пример
Найти координаты вектора \(\ \overline{A B} \), если \(\ A(-4 ; 2), B(1 ;-3) \)
\(\ \overline{A B}=(1-(-4) ;-3-2)=(5 ;-5) \)
Длина (модуль) вектора
пример
Найти длину вектора \(\ \overline{a}=(-4 ; 3) \)
Используя формулу, получаем:
\(\ |\overline{a}|=\sqrt{(-4)^{2}+3^{2}}=\sqrt{16+9}=\sqrt{25}=5 \)
Пример
Найти длину вектора\(\ \overline{a}=(1 ; 0 ;-4) \)
Используя формулу, получаем:
\(\ |\overline{a}|=\sqrt{1^{2}+0^{2}+(-4)^{2}}=\sqrt{1+0+16}=\sqrt{17} \)
Угол между векторами
пример
Известно, что скалярное произведение двух векторов \(\ (\overline{a} ; \overline{b})=2 \) и их длины \(\ |\overline{a}|=2,|\overline{b}|=2 \). Найти угол между векторами \(\ \overline{a} \) и \(\ \overline{b} \).
Косинус необходимого угла:
\(\ \cos (\overline{a}, \overline{b})=\frac{(\overline{a} ; \overline{b})}{|\overline{a}| \cdot|\overline{b}|}=\frac{2}{2 \cdot 2}=\frac{1}{2} \Rightarrow(\overline{a}, \overline{b})=60^{\circ} \)
Пример
Найти угол между векторами \(\ \overline{a}=(1 ; \sqrt{3}) \) и \(\ \overline{b}=(1 ; 0) \)
Косинус желаемого угла
\(\ \cos (\overline{a}, \tilde{b})=\frac{1 \cdot 1+\sqrt{3} \cdot 0}{\sqrt{1^{2}+(\sqrt{3})^{2}} \cdot \sqrt{1^{2}+0^{2}}}=\frac{1}{2} \)
\(\ (\overline{a}, \overline{b})=\arccos \frac{1}{2}=60^{\circ} \)
Разложение вектора по ортам координатных осей
пример
Зная разложение вектора \(\ \overline{a} \) на базисной системе векторов: \(\ \overline{a}=3 \overline{i}-\overline{k} \)запишите координаты этого вектора в пространстве.
Коэффициенты ортов являются координатами вектора, поэтому из того, что \(\ \overline{a}=3 \overline{i}-0 \cdot \overline{j}-\overline{k} \) мы получаем \(\ \overline{a}=(3 ; 0 ;-1) \)
Пример
Вектор \(\ \overline{a} \) определяется его координатами: \(\ \overline{a}=(2 ;-1 ; 5) \) запишите разложение этого вектора по осям осей.
Координаты вектора представляют собой коэффициенты по осям координатных осей при разложении вектора в основную систему векторов, поэтому требуется разложение:
\(\ \overline{a}=2 \overline{i}-\overline{j}+5 \overline{k} \)
Скалярное произведение векторов
Пример
Рассчитайте скалярное произведение векторов \(\ \overline{a} \) и \(\ \overline{b} \) , если их длины равны 2 и 3 соответственно, а угол между ними равен 60 °.
С условием \(\ |\overline{a}|=2,|\overline{b}|=3 \), а \(\ (\widehat{a}, \overline{b})=60^{\circ} \) затем \(\ \overline{a} \cdot \overline{b}=(\overline{a}, \overline{b})=2 \cdot 3 \cdot \cos 60^{\circ}=6 \cdot \frac{1}{2}=3 \)
Пример
Найти скалярное произведение векторов \(\ \overline{a}=(3 ;-1) \) и \(\ \overline{b}=(-2 ; 7) \)
Скалярное произведение
\(\ \overline{a} \overline{b}=3 \cdot(-2)+(-1) \cdot 7=-6-7=-13 \) Векторное произведение векторов пример
Найти векторное произведение векторов \(\ \overline{a}=(6 ; 7 ; 10) \) и \(\ \overline{b}=(8 ; 5 ; 9) \)
Составляем определитель и вычисляем его:
\(\ \overline{a} \times \overline{b}=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {6} & {7} & {10} \\ {8} & {5} & {9}\end{array}\right|=\overline{i} \left| \begin{array}{cc}{7} & {10} \\ {5} & {9}\end{array}\right|-\overline{j} \left| \begin{array}{cc}{6} & {10} \\ {8} & {9}\end{array}\right|+\overline{k} \left| \begin{array}{cc}{6} & {7} \\ {8} & {5}\end{array}\right|= \)
\(\ =\overline{i}(7 \cdot 9-5 \cdot 10)-\overline{j}(6 \cdot 9-8 \cdot 10)+\overline{k}(6 \cdot 5-8 \cdot 7)= \)
\(\ =13 \overline{i}+26 \overline{j}-26 \overline{k}=(13 ; 26 ;-26) \)
Смешанное произведение векторов
Пример
Рассчитать объем пирамиды, построенной на векторах \(\ \overline{a}=(2 ; 3 ; 5), \overline{b}=(1 ; 4 ; 4), c=(3 ; 5 ; 7) \)
Мы находим смешанное произведение указанных векторов, для этого составляем определитель, в строки которого записываем координаты векторов \(\ \overline{a}, \overline{b} \) и \(\ \overline{c} \):
\(\ (\overline{a}, \overline{b}, \overline{c})=\left| \begin{array}{ccc}{2} & {3} & {5} \\ {1} & {4} & {4} \\ {3} & {5} & {7}\end{array}\right|=2 \cdot 4 \cdot 7+1 \cdot 5 \cdot 5+3 \cdot 4 \cdot 3- \)
\(\ -3 \cdot 4 \cdot 5-5 \cdot 4 \cdot 2-1 \cdot 3 \cdot 7=-4 \)
\(\ V_{\mathrm{пир}}=\frac{1}{6}|(\overline{a}, \overline{b}, \overline{c})|=\frac{1}{6} \cdot 4=\frac{2}{3}(\mathrm{куб} . \mathrm{ед.}) \)
1. Основные понятия векторной алгебры; примеры решения задач.
Основные понятия включают в себя: понятие вектора, разложение вектора по другим векторам, модуль вектора, скалярное произведение, векторное произведение и смешанное произведение, а также их приложения для решения задач.
Пример 1. Задание.
Разложить вектор  по векторам
по векторам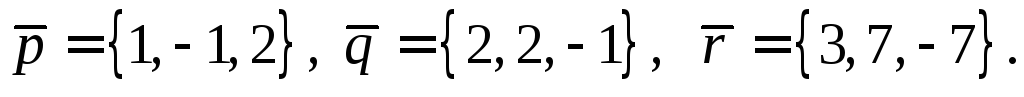
Прежде чем привести решение задачи напомним понятие линейной зависимости системы векторов.
Рассмотрим систему
векторов 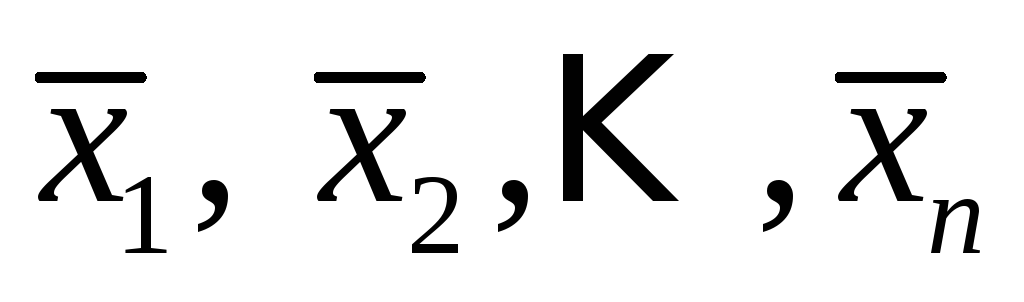 и составим равенство вида:
и составим равенство вида:
 –постоянные величины.
Если это равенство выполняется только
при одновременном равенстве нулю всех
–постоянные величины.
Если это равенство выполняется только
при одновременном равенстве нулю всех 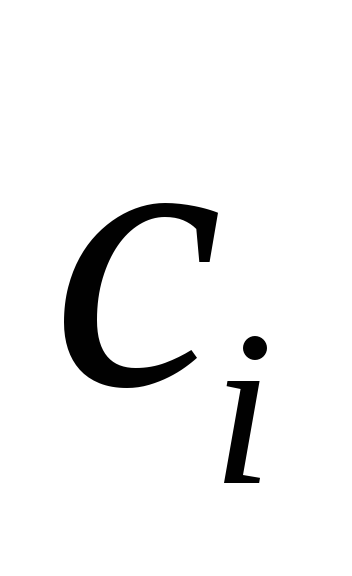 ,
,
 ,
тогда система векторов называется
линейно независимой , в противном случае
– система векторов линейно зависима,
то есть один вектор можно представить
в виде линейной комбинации других
векторов.
,
тогда система векторов называется
линейно независимой , в противном случае
– система векторов линейно зависима,
то есть один вектор можно представить
в виде линейной комбинации других
векторов.
 .
Разделим левую и правую части равенства
на
.
Разделим левую и правую части равенства
на  ,
получим:
,
получим:

то есть вектор 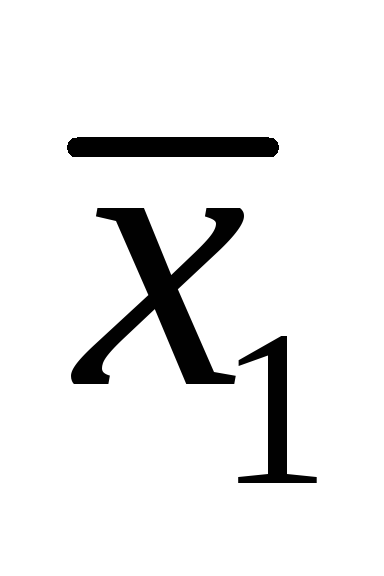 представлен в виде линейной комбинации
представлен в виде линейной комбинации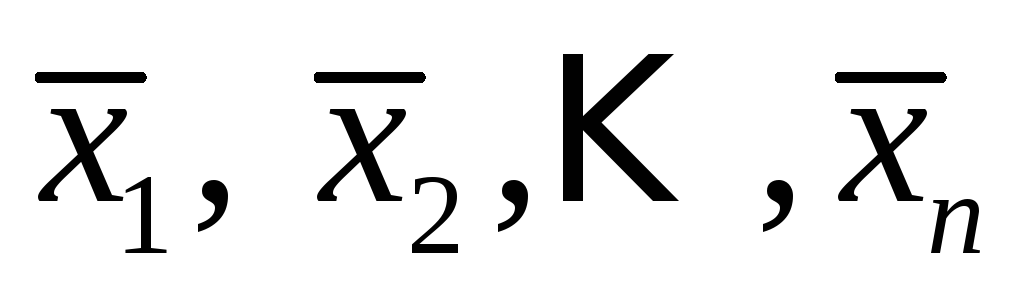 .
.
Решение.
Разложить вектор  по векторам
по векторам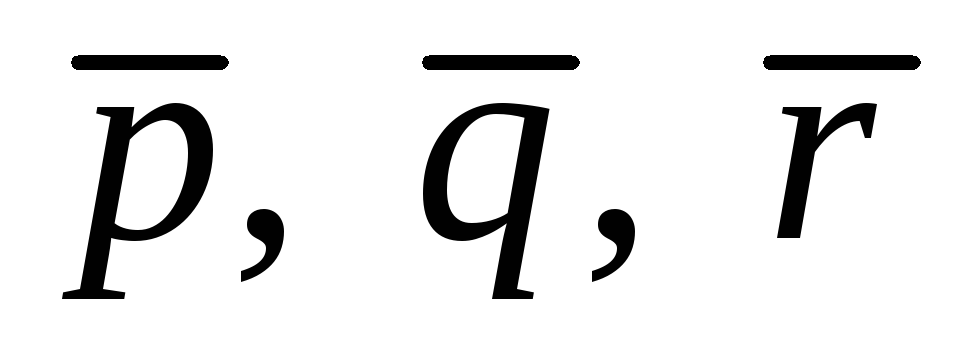 это значит представить его в виде
линейной комбинации
это значит представить его в виде
линейной комбинации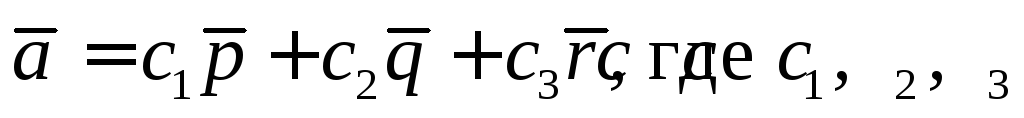 – искомые числа.
– искомые числа.
Представим линейную комбинацию в координатной форме
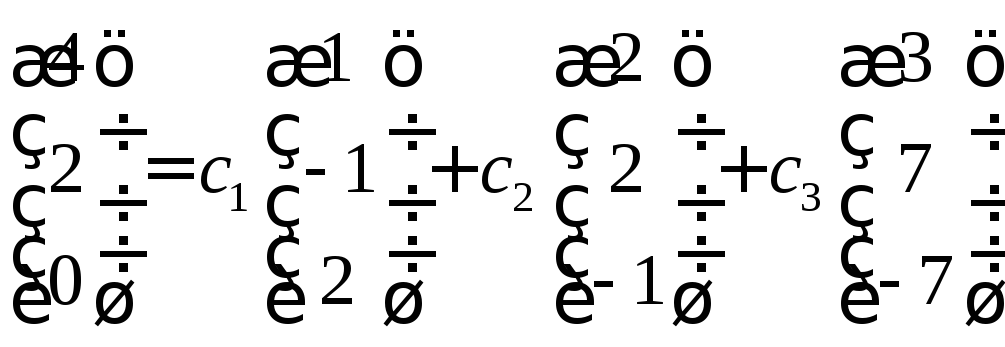
И получим систему линейных уравнений
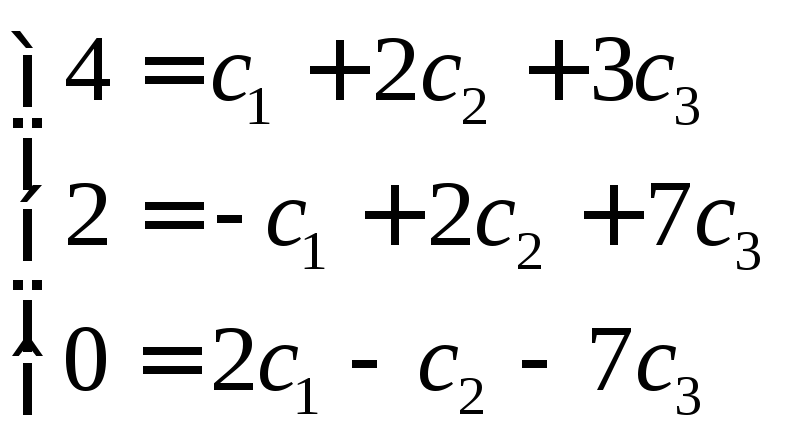
Решение системы
имеет вид: 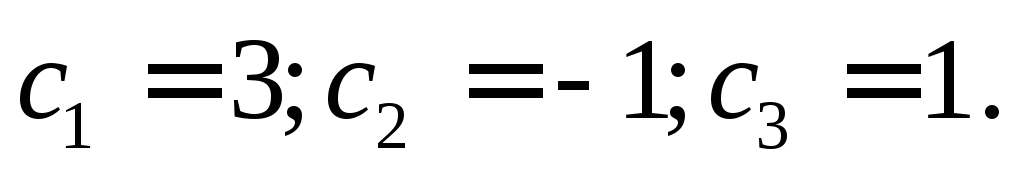
Следовательно: 
Пример 2.
Напомним понятие длины вектора (модуля вектора)
Если  ,
то
,
то
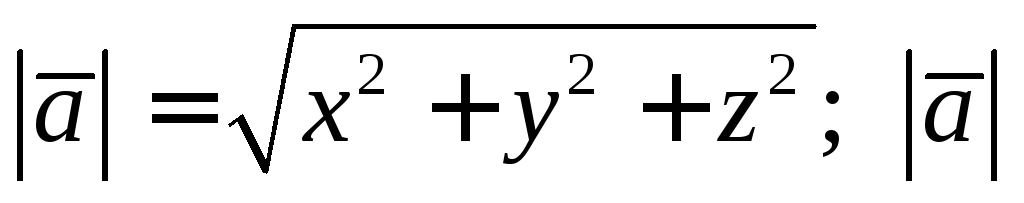 –называется
длиной вектора.
–называется
длиной вектора.
Рассмотрим свойство
скалярного произведения: 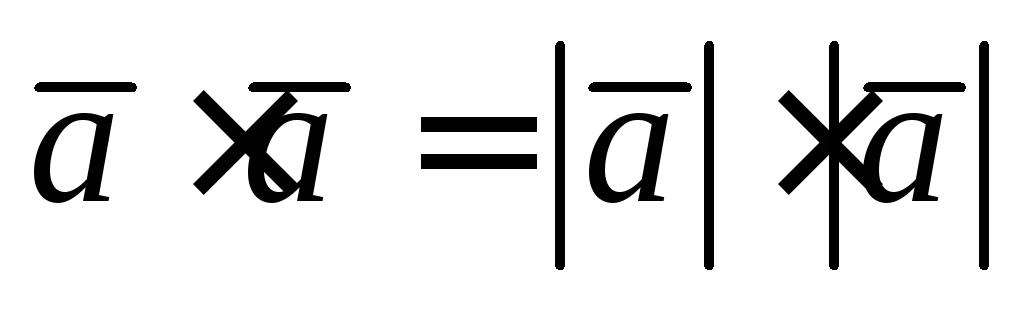 ,
то есть
,
то есть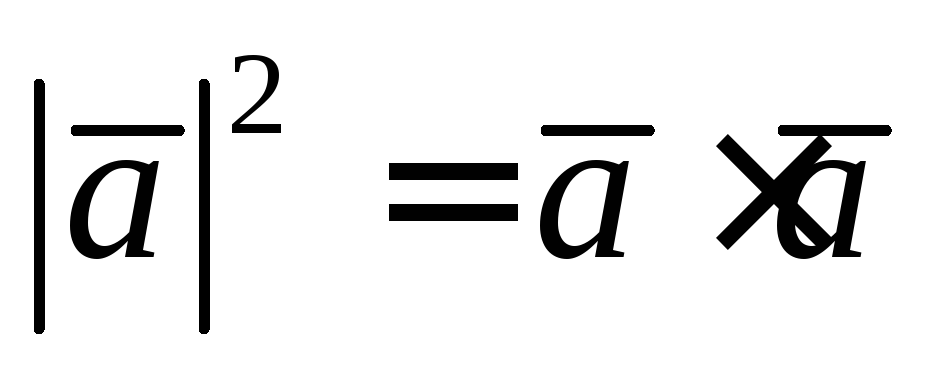 .
.
Задание.
Найти длину вектора 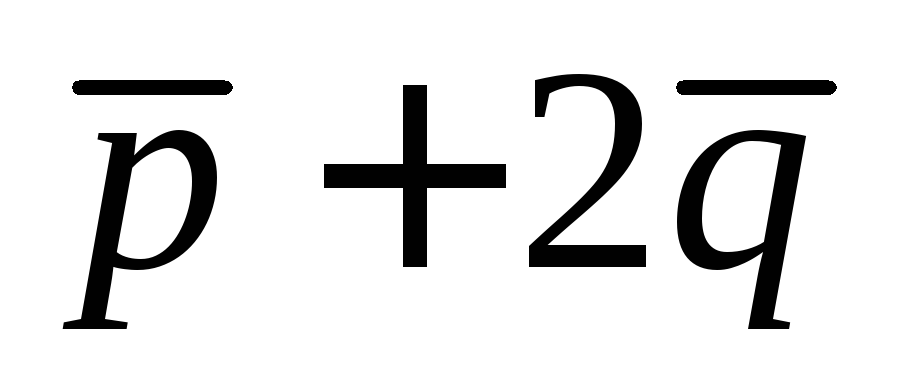 ,
если
,
если
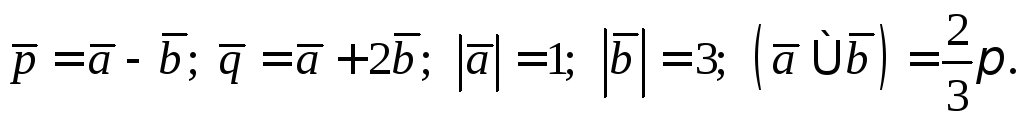
Решение. Имеем
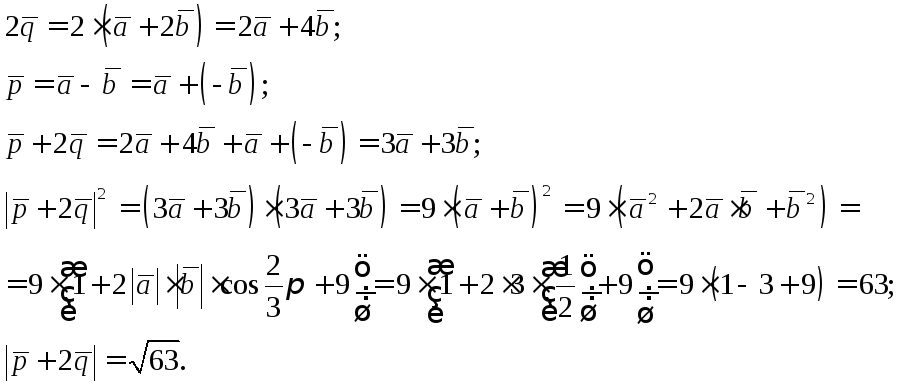
Пример 3.
Напомним определение
коллинеарности двух векторов 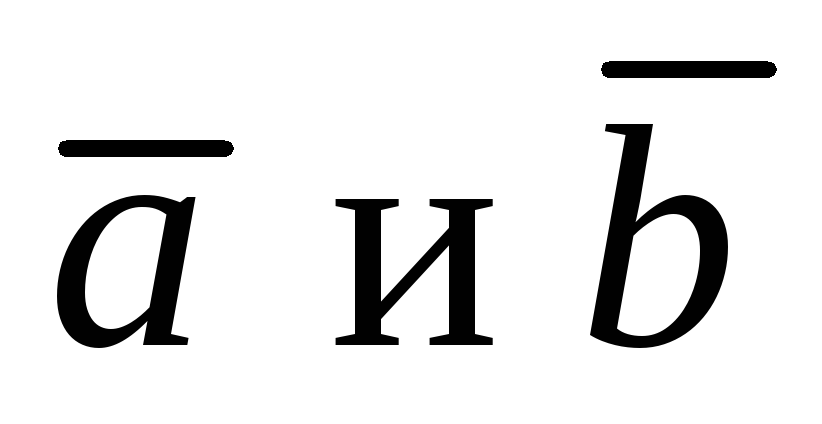 отличных от нуля: два вектора
отличных от нуля: два вектора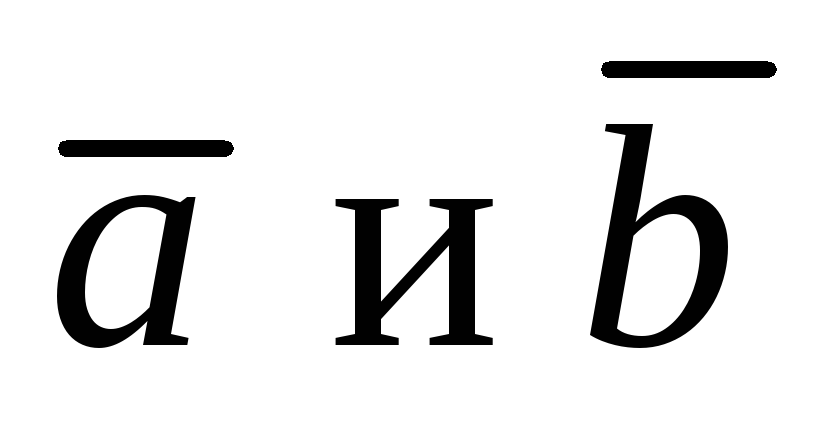 называются коллинеарными, если
называются коллинеарными, если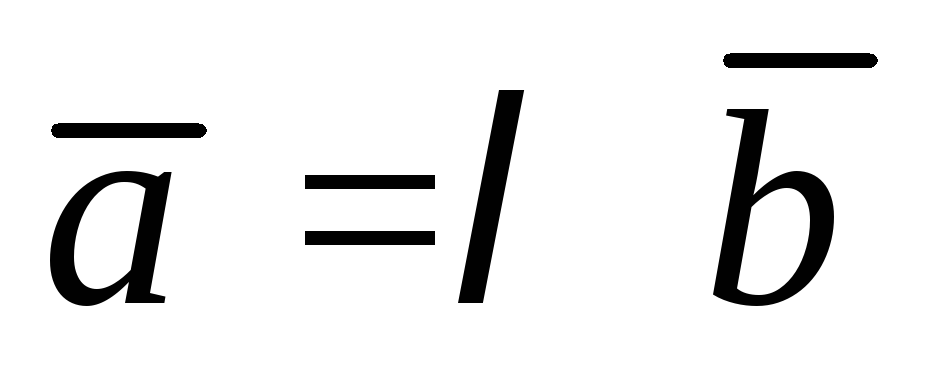 ,
где
,
где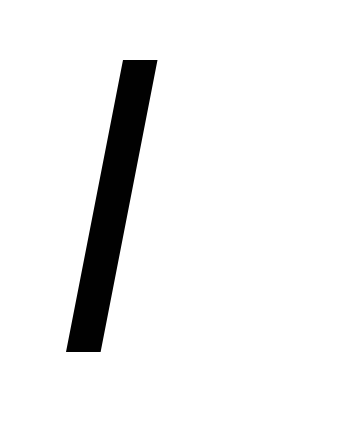 – некоторый постоянный множитель.
– некоторый постоянный множитель.
Задание.
Найти вектор  ,
коллинеарный вектору
,
коллинеарный вектору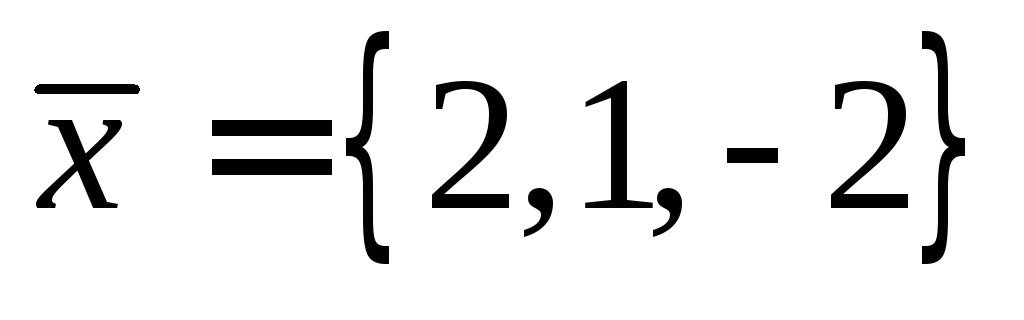 и
удовлетворяющий условию: скалярное
произведение векторов
и
удовлетворяющий условию: скалярное
произведение векторов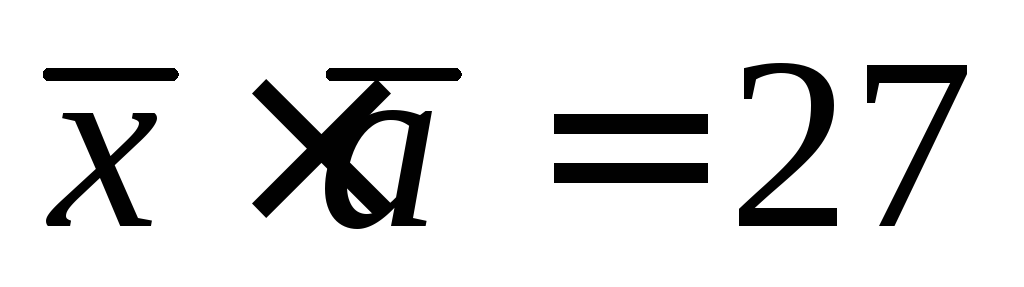 .
.
Решение.
Запишем условие
коллинеарности двух векторов 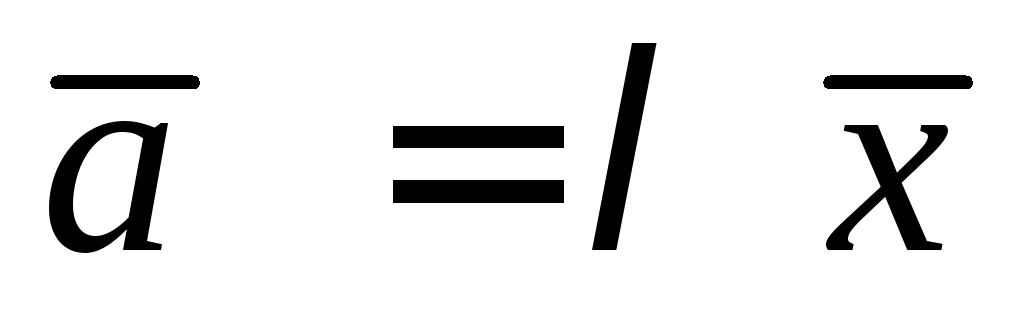 и полученный вектор
и полученный вектор подставим в условие
подставим в условие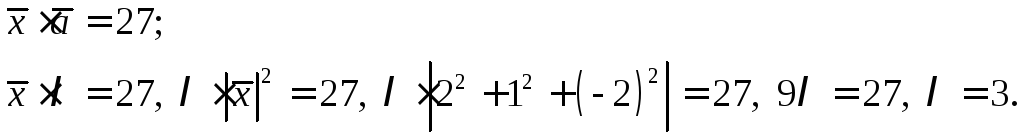
Следовательно 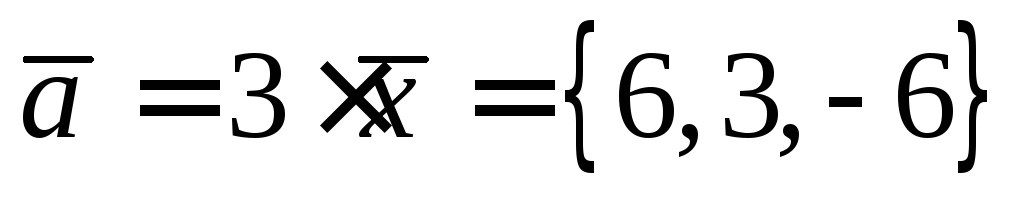 .
.
Пример 4.
Напомним определение скалярного произведения векторов:
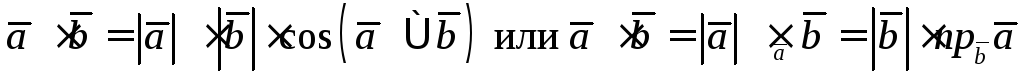 .
.
Задание.
Вычислить проекцию
вектора  на направление вектора
на направление вектора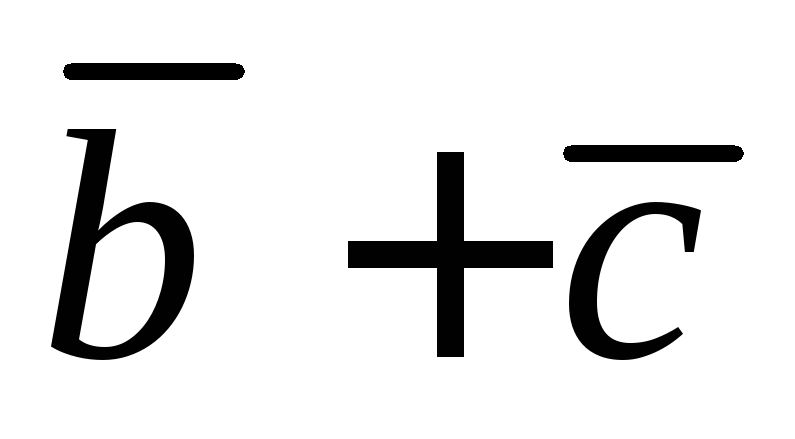 ,
если
,
если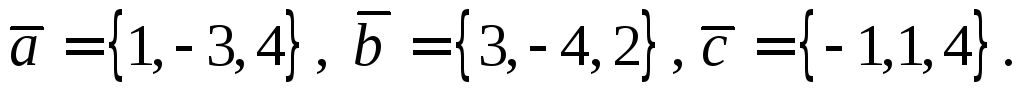
Решение.
Обозначим 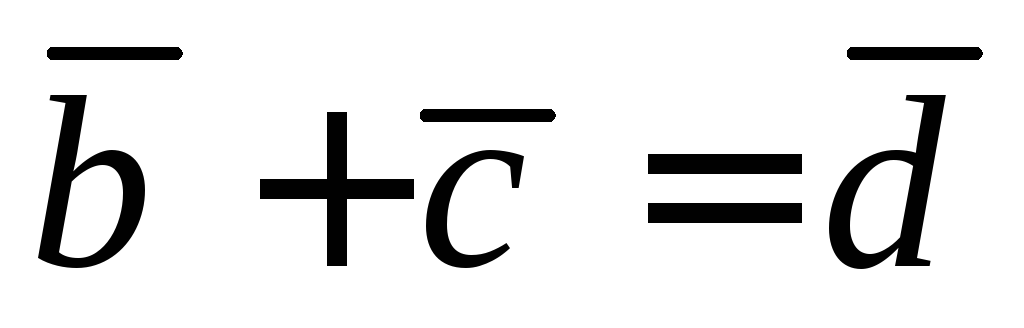 ,
тогда
,
тогда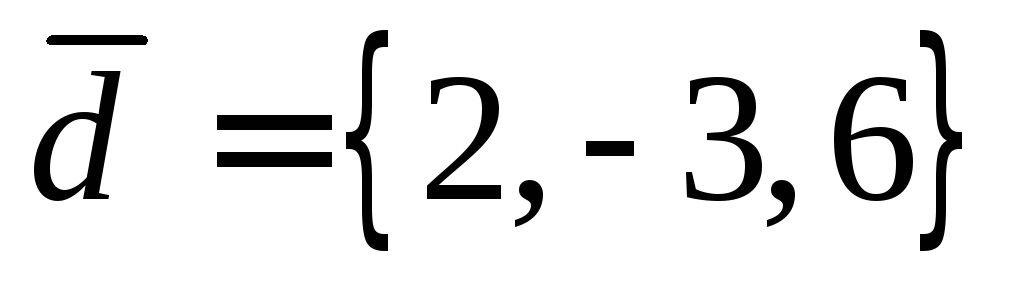
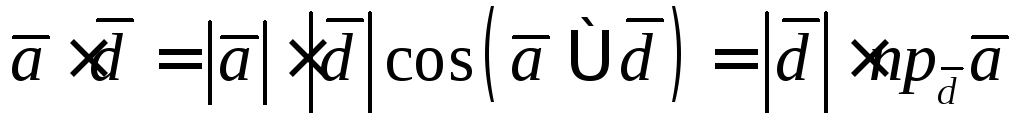 ,
отсюда
,
отсюда
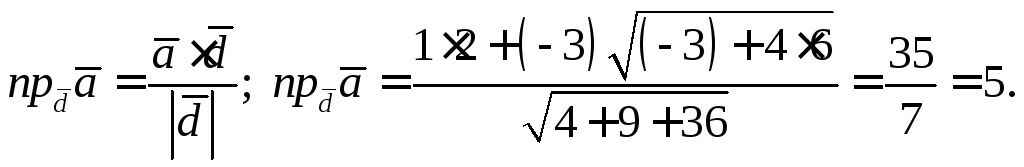
Ответ: 
Пример 5.
Пусть 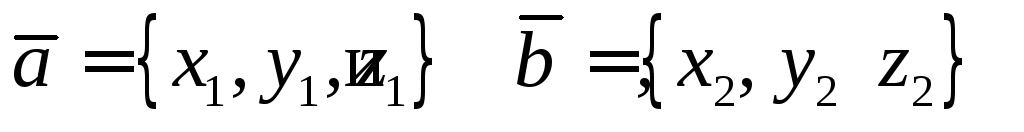 .
Напомним, что векторное произведение
двух векторов
.
Напомним, что векторное произведение
двух векторов и
и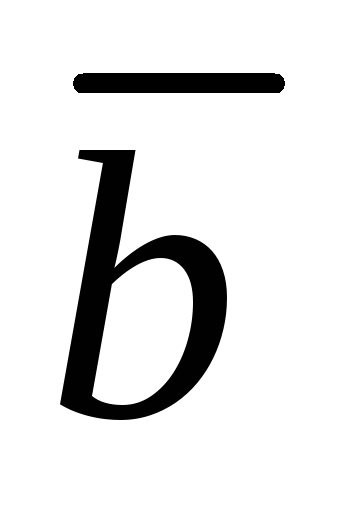 равно:
равно: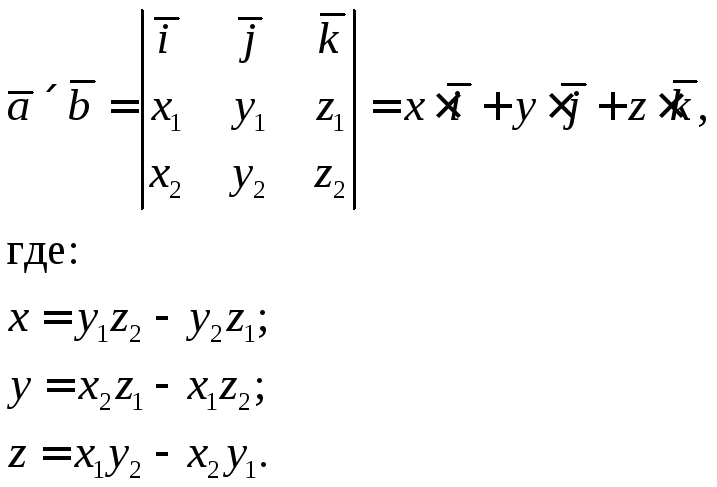
Модуль векторного произведения равен площади параллелограмма, построенного на этих векторах.
Задание.
Найти площадь
треугольника 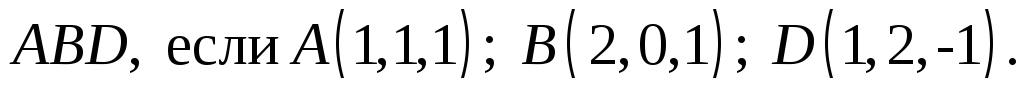
Решение.
Построим
параллелограмм  на векторах
на векторах (рис. 1):
(рис. 1):

рис. 1 

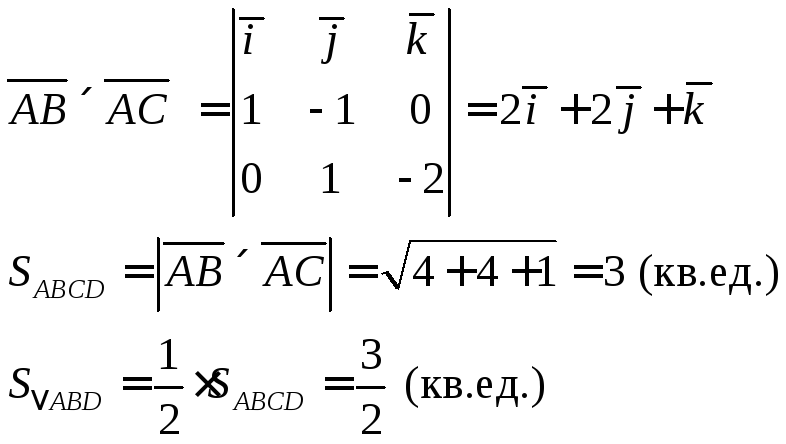
Пример 6.
Задание.
Найти вектор 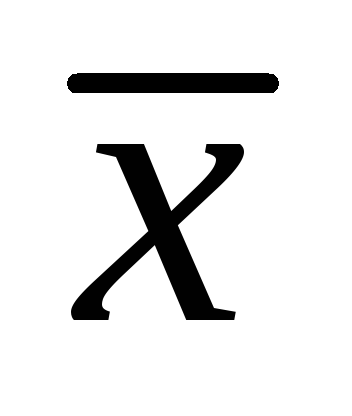 ,
перпендикулярный векторам
,
перпендикулярный векторам и образующий с осью
и образующий с осью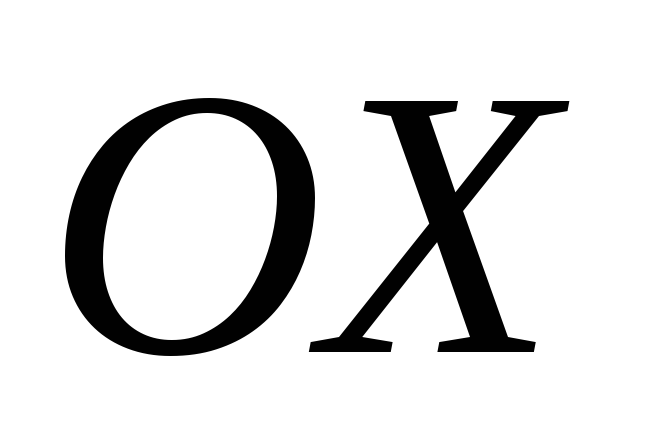 тупой угол, если
тупой угол, если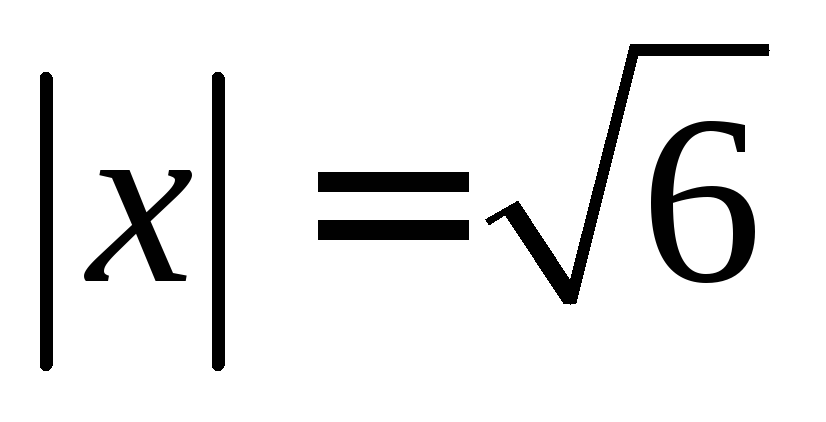 .
.
Решение.
Если 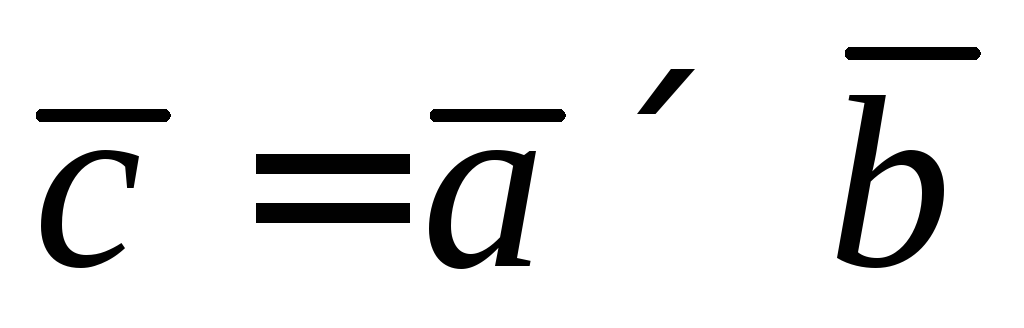 ,
тогда вектор
,
тогда вектор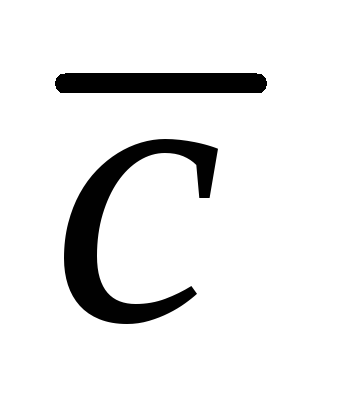 перпендикулярен векторам
перпендикулярен векторам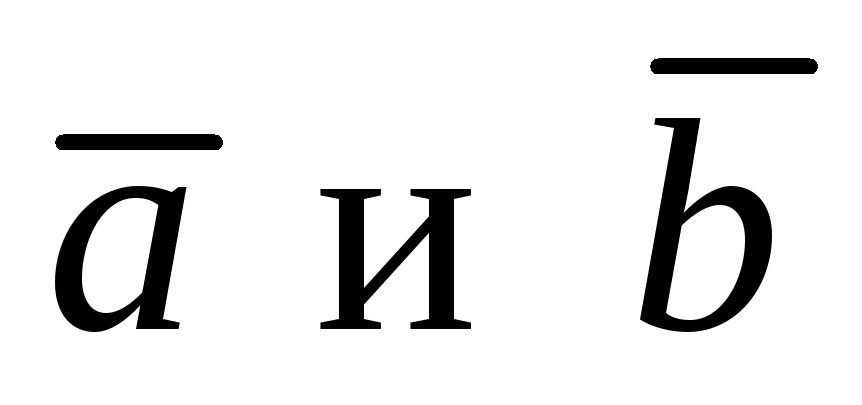 .
.
Найдем вектор 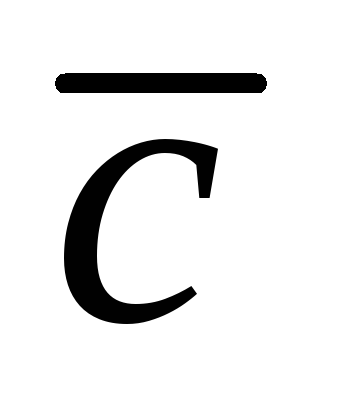 :
: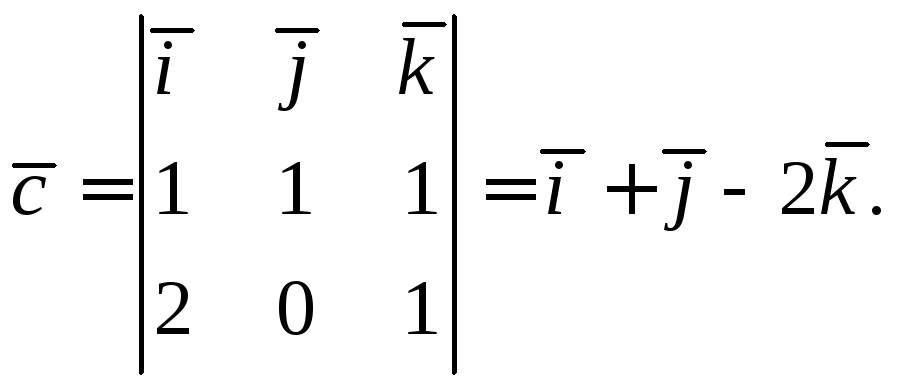
Так как  тоже перпендикулярен
тоже перпендикулярен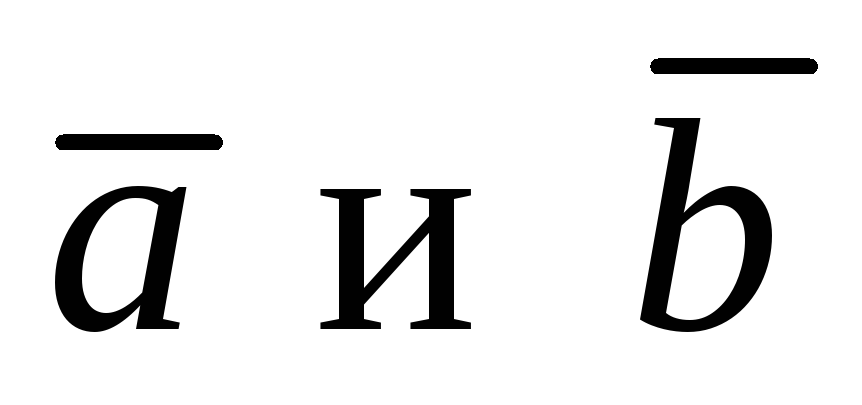 ,
следовательно вектора
,
следовательно вектора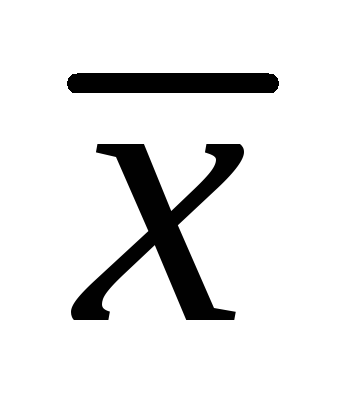 и
и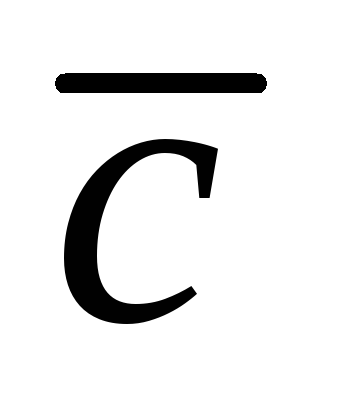 — коллинеарны. Запишем условие
коллинеарности векторов:
— коллинеарны. Запишем условие
коллинеарности векторов: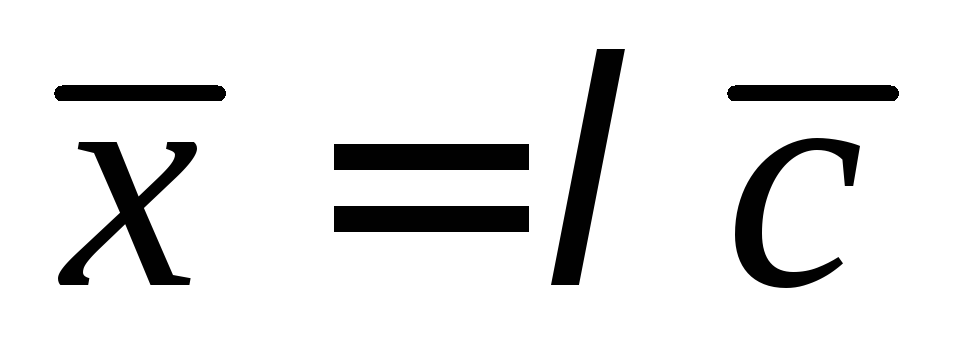 ,
,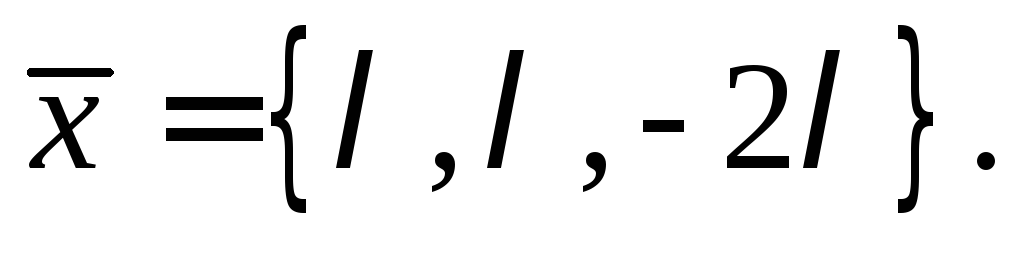
По условию 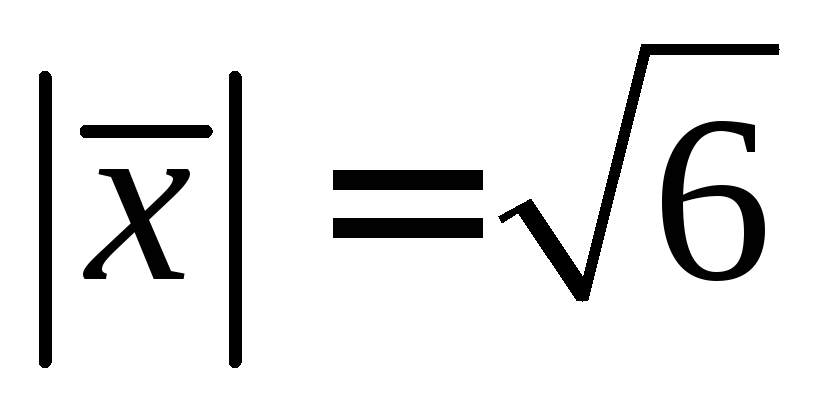 ,
то есть
,
то есть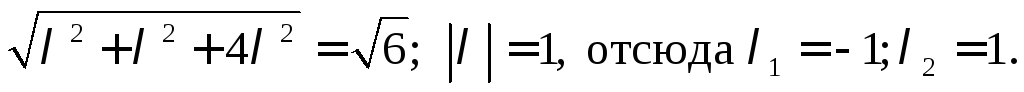
Так как вектор 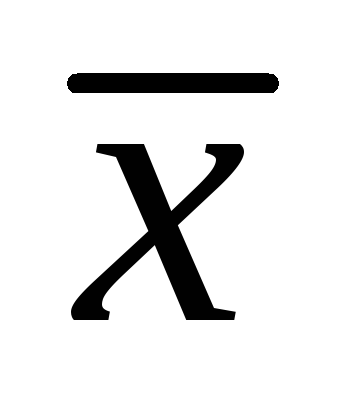 образует с осью
образует с осью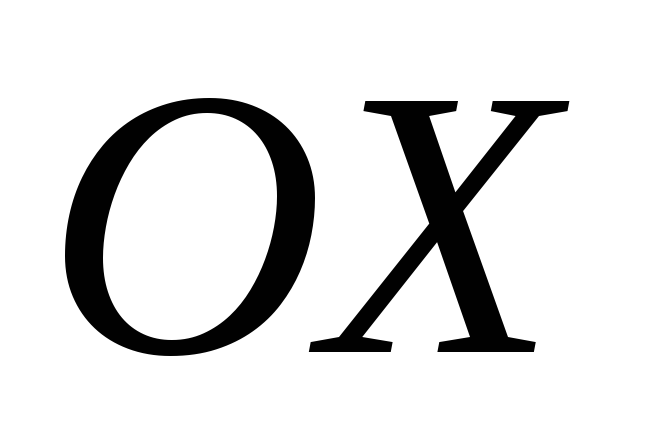 тупой угол, то его проекция на ось
тупой угол, то его проекция на ось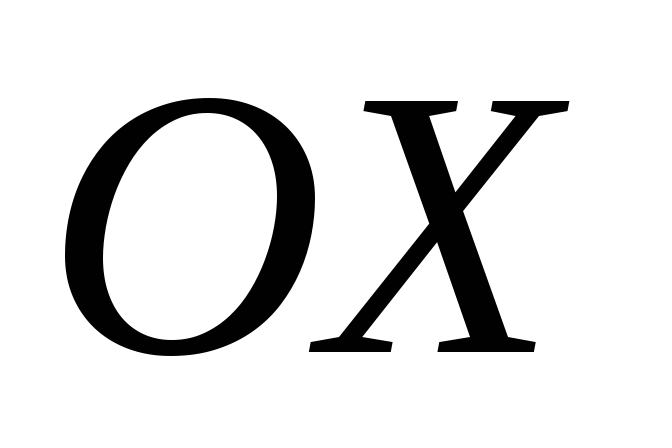 должна быть отрицательной.
должна быть отрицательной.
Отсюда 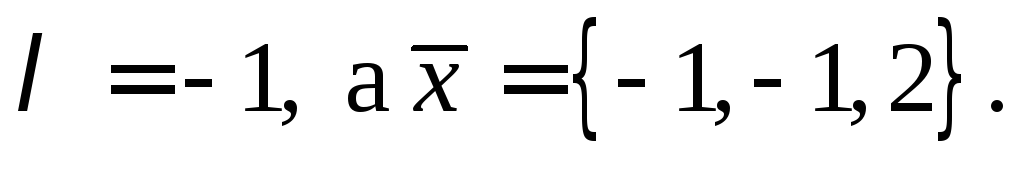
Пример 7.
Рассмотрим вектор 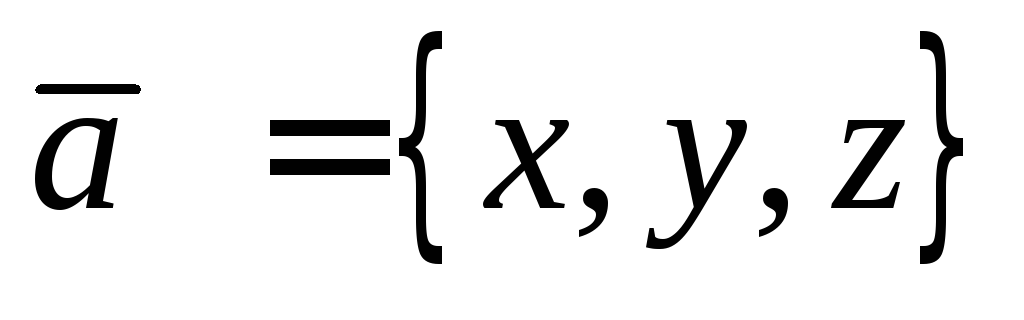 .
Вектор
.
Вектор образует с осями координат углы
образует с осями координат углы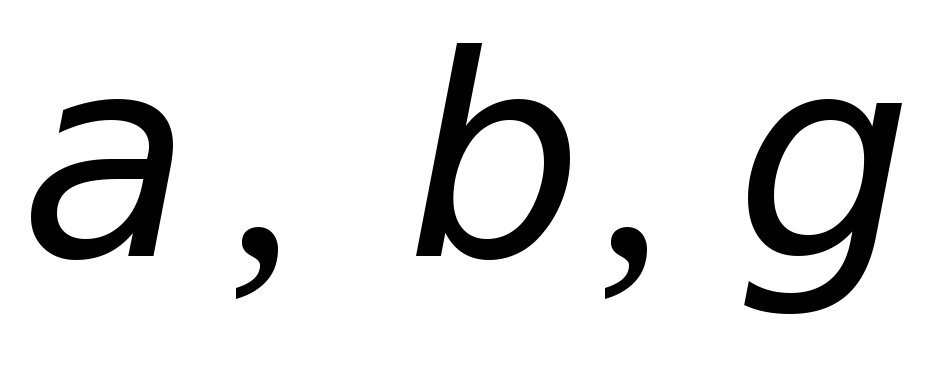 ,
а
,
а называются направляющими косинусами,
при этом
называются направляющими косинусами,
при этом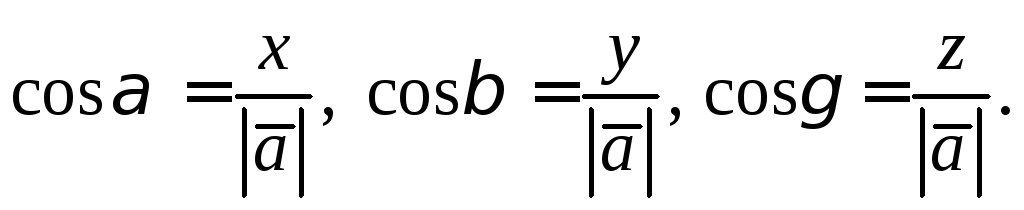
Задание.
Найти направляющие
косинусы вектора силы 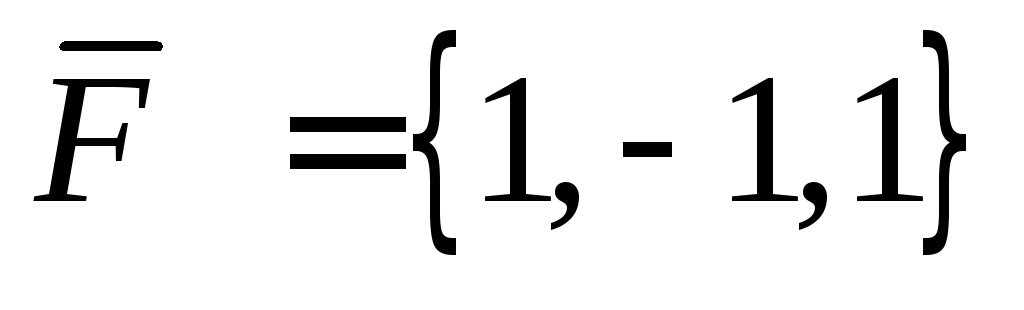 ,
приложенной в точке
,
приложенной в точке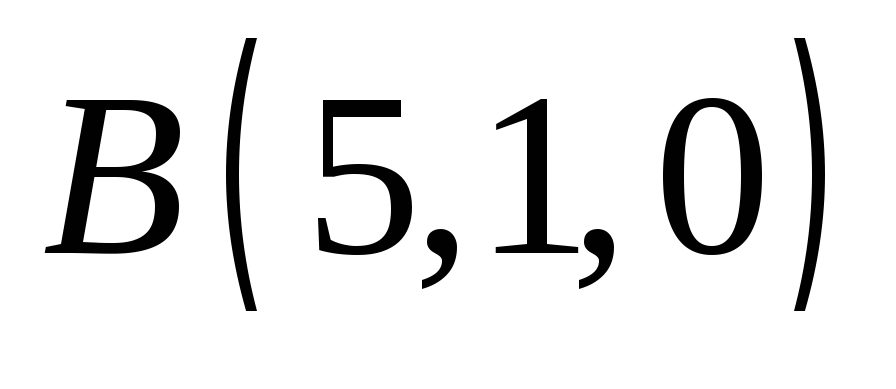 ,
и момент этой силы относительно точки
,
и момент этой силы относительно точки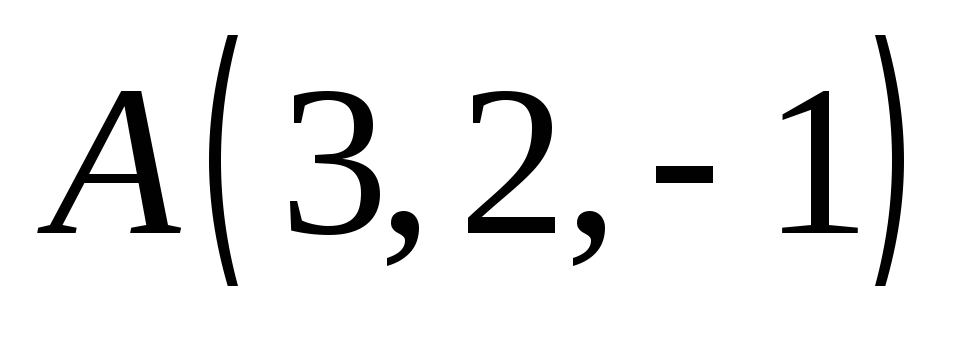 .
.
Решение.
Найдем направляющие косинусы вектора силы:
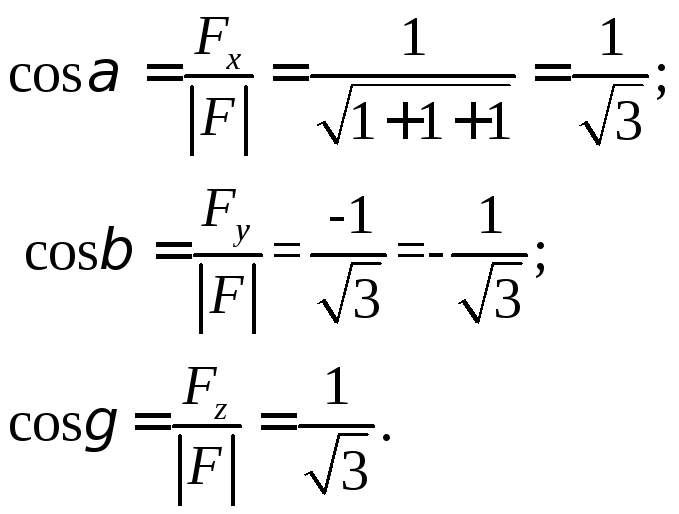
Момент силы
определим как векторное произведение
вектора 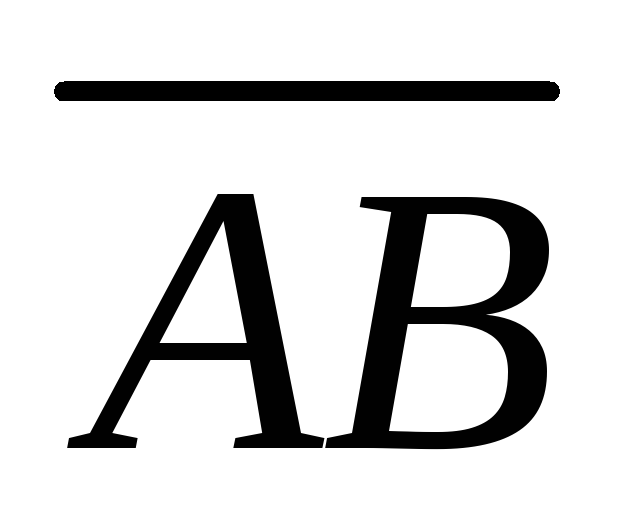 на вектор
на вектор .
Имеем
.
Имеем
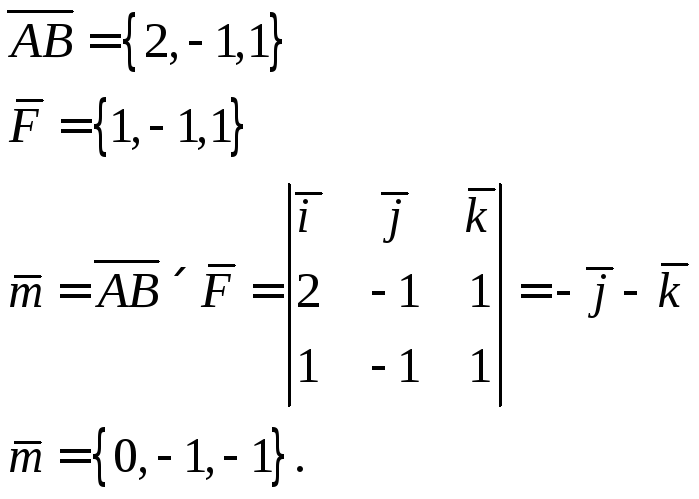
Пример 8.
Напомним формулу
смешанного произведения трех векторов 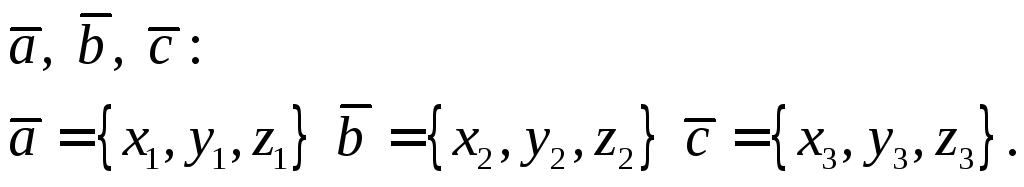
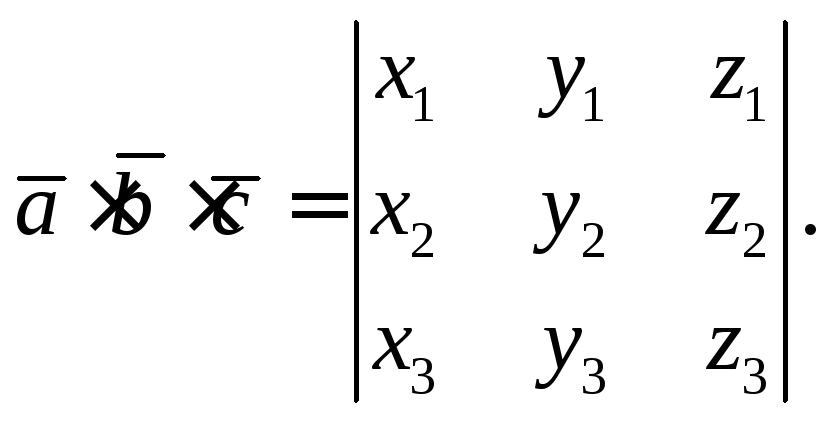
Известно, что
модуль смешанного произведения  равен объему параллелепипеда, построенного
на этих векторах.
равен объему параллелепипеда, построенного
на этих векторах.
Задача.
Найти длину высоты
пирамиды, опущенной из вершины 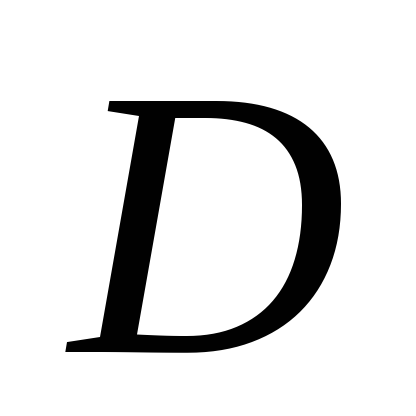 (рис. 2), если ее вершины
(рис. 2), если ее вершины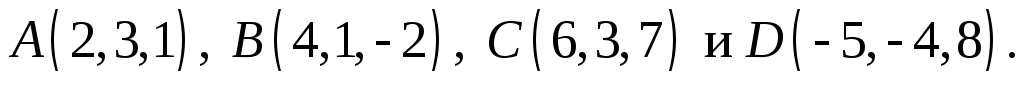
Решение.
рис. 2
Найдем векторы:

Объем пирамиды,
построенной на векторах 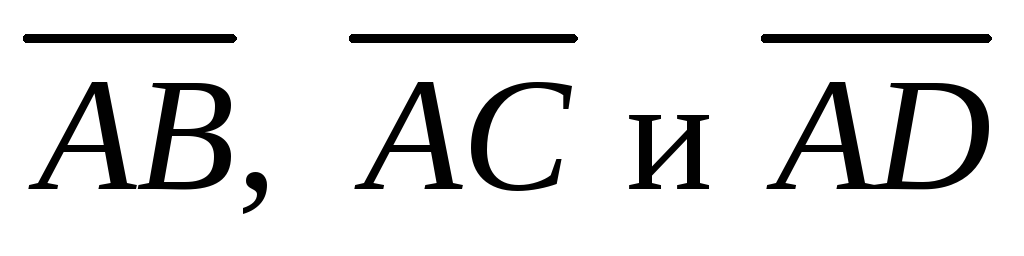 ,
равен одной шестой модуля смешанного
произведения этих векторов.
,
равен одной шестой модуля смешанного
произведения этих векторов.
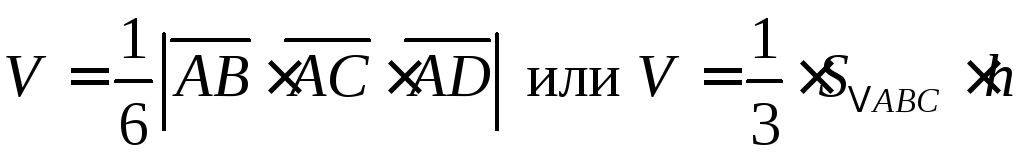 , где
, где  – высота пирамиды, а площадь прямоугольника,
построенного на векторах
– высота пирамиды, а площадь прямоугольника,
построенного на векторах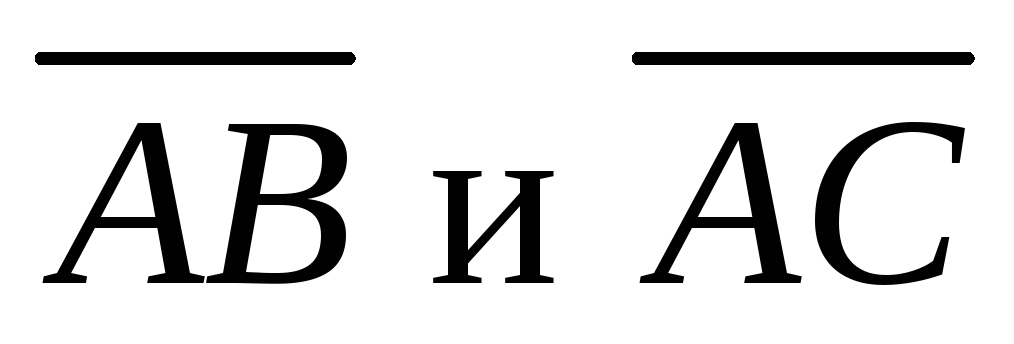 равна одной второй векторного произведения
равна одной второй векторного произведения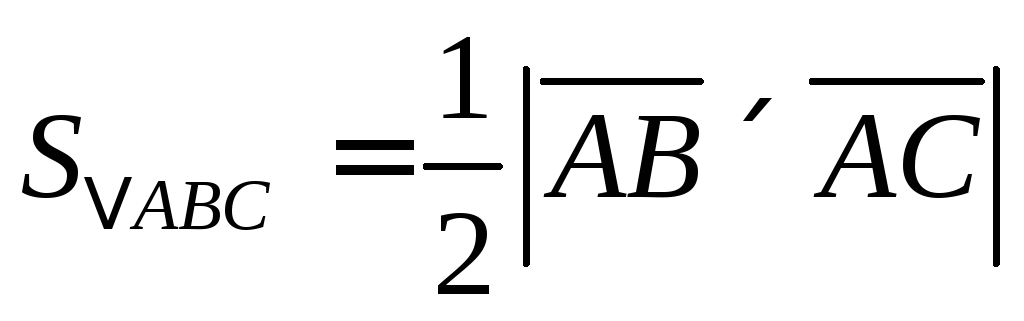 .
.
Вычислим смешанное произведение векторов
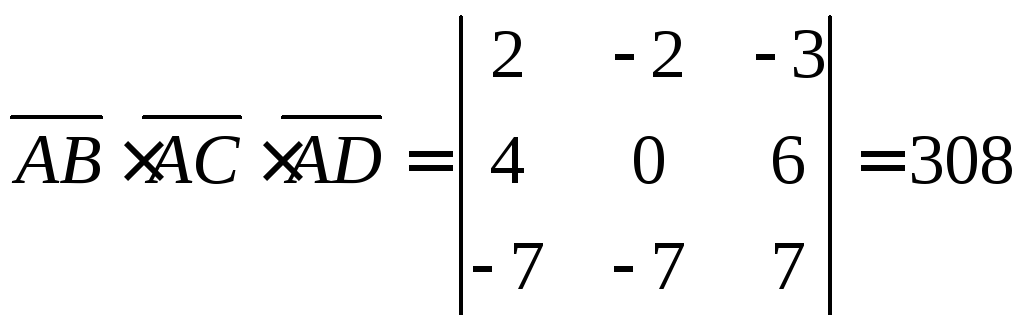
Отсюда  пирамиды
пирамиды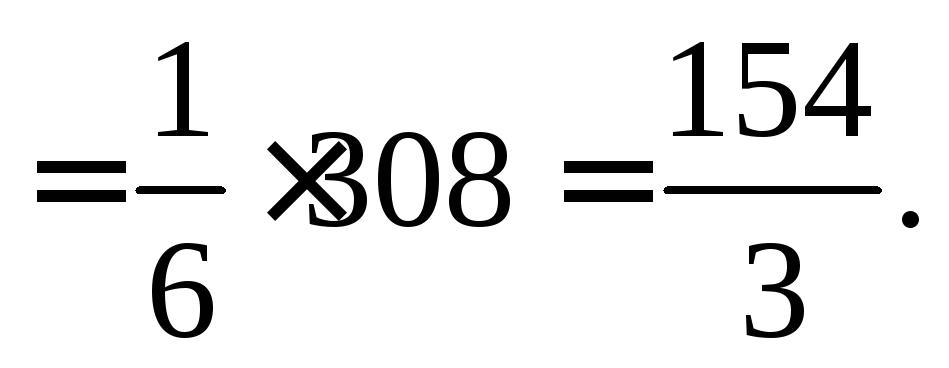
Вычислим векторное произведение векторов:
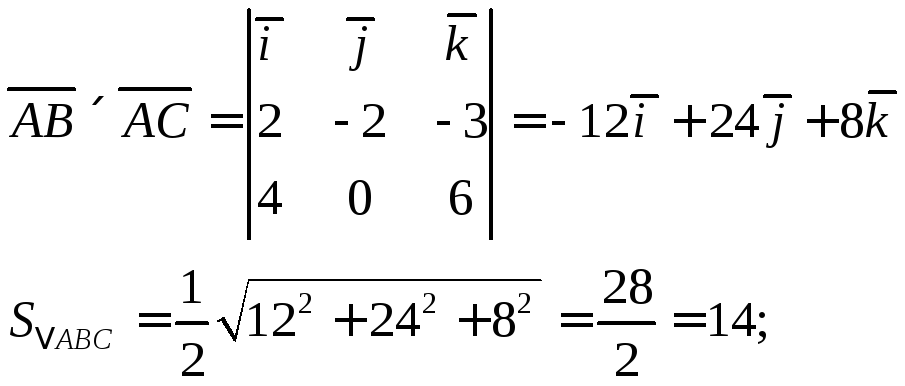
Найдем высоту пирамиды:
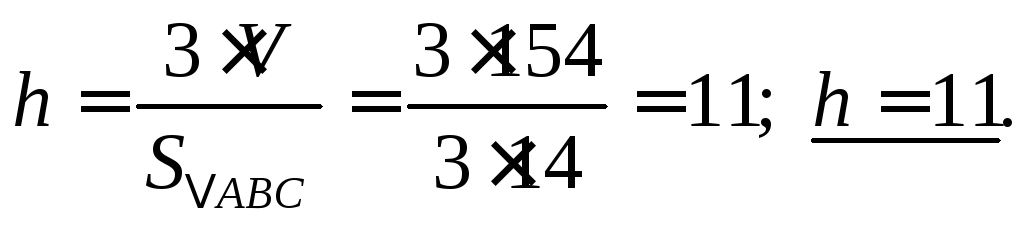
Лекция 3 Векторы. Вопросы:
Элементы векторной алгебры.
1. Векторы. Основные понятия. 2. Линейные операции над векторами. 3. Проекция вектора на ось. 4. Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы. 5. Действие над векторами, заданными проекциями. 6. Скалярное произведение векторов и его свойства. Определение скалярного произведения. Свойства скалярного произведения. Выражение скалярного произведения через координаты. Некоторые приложения скалярного произведения. 7. Векторное произведение векторов и его свойства. Определение векторного произведения. Некоторые приложения векторного произведения. 8. Смешанное произведение векторов. Определение смешанного произведения, его геометрический смысл. Свойства смешанного произведения. Выражение смешанного произведения через координаты. Некоторые приложения смешанного произведения.
Обычно в естественных науках рассматривают величины двух видов:
скалярные, они определены числовым значением — площадь, объем, температура, масса, и векторные, которые определяются не только численным значением, но и направлением — это сила, скорость, ускорение и другие.
Определение. Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают.
Определение. Длиной (модулем) вектора называется расстояние между началом и концом вектора.
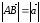
Определение. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.

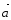


Определение. Векторы называются компланарными, если существует плоскость, которой они параллельны




.
Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
Определение. Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.
Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему.
Определение. Линейными операциями над векторами называется сложение и умножение на число.
Суммой
векторов является вектор — 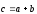
Суммой векторов 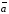 ,
,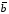 ,…
,
,…
,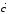 называют вектор
называют вектор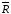 ,
замыкающий ломаную линию, построенную
из данных векторов так, что начало
каждого последующего вектора совпадает
с концом предыдущего.
,
замыкающий ломаную линию, построенную
из данных векторов так, что начало
каждого последующего вектора совпадает
с концом предыдущего.

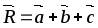
В
частности, суммой двух векторов  и
и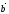 ,
имеющих общее начало, является диагональ
параллелограмма, построенного на этих векторах, начало
которой совпадает с началом векторов
ā
и
,
имеющих общее начало, является диагональ
параллелограмма, построенного на этих векторах, начало
которой совпадает с началом векторов
ā
и  .
.
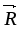 =
=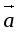 +
+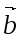

Произведение
— 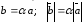 ,
при этом
,
при этом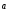 коллинеарен
коллинеарен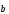 .
.
Вектор
сонаправлен с вектором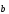 (
(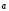
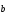 ),
если
> 0.
),
если
> 0.
Вектор 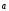 противоположно направлен с вектором
противоположно направлен с вектором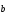 (
(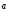
 ),
если
< 0.
),
если
< 0.
Свойства.
1) 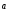 +
+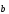 =
=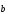 +
+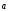 — коммутативность.
— коммутативность.
2) 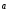 + (
+ ( +
+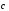 )
= (
)
= (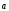 +
+ )+
)+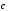
3) 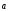 +
+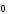 =
=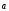
4) 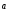 +(-1)
+(-1)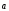 =
=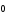
5)
() =(
=( )
– ассоциативность
)
– ассоциативность
6)
(+)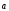 =
=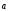 +
+ 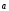 — дистрибутивность
— дистрибутивность
7)
(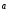 +
+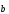 )
=
)
= +
+ 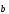
8)
1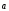 =
= 
Определение.
1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.
2) Базисом на плоскости называются любые 2 неколлинеарные вектора, взятые в определенном порядке.
3)Базисом на прямой называется любой ненулевой вектор.
Определение. Если 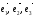 — базис в пространстве и
— базис в пространстве и , то числа,
и
— называются компонентами
или координатами вектора
, то числа,
и
— называются компонентами
или координатами вектора 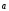 в этом базисе.
в этом базисе.
В связи с этим можно записать следующие свойства:
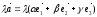 =
=  .
.
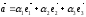 ;
; 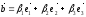 ;
;
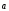 +
+ 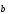 =
= .
.
Линейная зависимость векторов.
Определение. Векторы 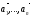 называютсялинейно
зависимыми,
если существует такая линейная комбинация
называютсялинейно
зависимыми,
если существует такая линейная комбинация 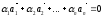 ,
при не равных нулю одновременноi , т.е.
,
при не равных нулю одновременноi , т.е.  .
.
Если
же только при i = 0 выполняется 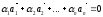 ,
то векторы называются линейно
независимыми.
,
то векторы называются линейно
независимыми.
Свойство
1. Если среди векторов 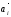 есть нулевой вектор, то эти векторы
линейно зависимы.
есть нулевой вектор, то эти векторы
линейно зависимы.
Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.
Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.
Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.
Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.
Свойство 6. Любые 4 вектора линейно зависимы.
Система координат.
Для определения положения произвольной точки могут использоваться различные системы координат. Положение произвольной точки в какой- либо системе координат должно однозначно определяться. Понятие системы координат представляет собой совокупность точки начала отсчета (начала координат) и некоторого базиса. Как на плоскости, так и в пространстве возможно задание самых разнообразных систем координат. Выбор системы координат зависит от характера поставленной геометрической, физической или технической задачи. Рассмотрим некоторые наиболее часто применяемые на практике системы координат.
Декартова система координат.
Зафиксируем в пространстве точку О и рассмотрим произвольную точку М.
Вектор 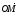 назовем радиус- вектором точки М. Если
в пространстве задать некоторый базис,
то точке М можно сопоставить некоторую
тройку чисел – компоненты ее радиус-
вектора.
назовем радиус- вектором точки М. Если
в пространстве задать некоторый базис,
то точке М можно сопоставить некоторую
тройку чисел – компоненты ее радиус-
вектора.
Определение. Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка называется началом координат. Прямые, проходящие через начало координат называются осями координат.
1-я ось – ось абсцисс
2-я ось – ось ординат
3-я ось – ось апликат
Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала.
Если
заданы точки А(x1,
y1,
z1),
B(x2,
y2,
z2),
то 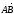 =
(x2 –
x1,
y2 – y1,
z2 – z1).
=
(x2 –
x1,
y2 – y1,
z2 – z1).
Определение. Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.
Определение. Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат.
Пример.
Даны векторы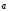 (1;
2; 3),(-1;
0; 3),
(1;
2; 3),(-1;
0; 3),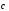 (2;
1; -1) и
(2;
1; -1) и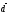 (3;
2; 2) в некотором базисе. Показать, что
векторы
(3;
2; 2) в некотором базисе. Показать, что
векторы ,
,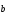 и
и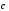 образуют
базис и найти координаты вектора
образуют
базис и найти координаты вектора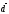 в этом базисе.
в этом базисе.
Векторы образуют базис, если они линейно независимы, другими словами, если уравнения, входящие в систему:
 линейно
независимы.
линейно
независимы.
Тогда 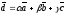 .
.
Это условие выполняется, если определитель матрицы системы отличен от нуля.
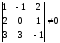


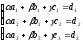 Для
решения этой системы воспользуемся
методом Крамера.
Для
решения этой системы воспользуемся
методом Крамера.
1 = 
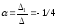 ;
;
2 = 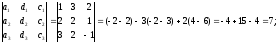
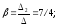
3 = 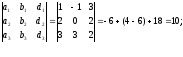
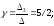
Итого,
координаты вектора 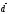 в
базисе
в
базисе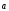 ,
,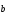 ,
,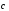 :
: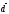 { -1/4, 7/4, 5/2}.
{ -1/4, 7/4, 5/2}.
Длина
вектора в координатах определяется как расстояние между
точками начала и конца вектора. Если
заданы две точки в пространстве А(х1,
y1,
z1),
B(x2,
y2,
z2),
то 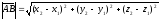 .
.
Если точка М(х, у, z) делит отрезок АВ в соотношении /, то координаты этой точки определяются как:
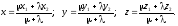
В частном случае координаты середины отрезка находятся как:
x = (x1+ x2)/2; y = (y1 + y2)/2; z = (z1 + z2)/2.
Линейные операции над векторами в координатах.
2.1. Понятие вектора и линейные операции над векторами.
1. Понятие вектора. При изучении различных разделов физики, механики и технических наук встречаются величины, которые полностью определяются заданием их числовых значений. Такие величины называютсяскалярнымиили, короче,скалярами . Скалярными величинами, например, являются длина, площадь, объем, масса, температура тела и др. Помимо скалярных величин, в различных задачах встречаются величины, для определения которых, кроме числового значения, необходимо знать также их направление. Такие величины называютсявекторными. Физическими примерами векторных величин могут служить смещение материальной точки, двигающейся в пространстве, скорость и ускорение этой точки, а также действующая на нее сила. Векторные величины используются, например, и в климатологии. Рассмотрим простой пример из климатологии. Если мы скажем, что ветер дует со скоростью 10 м/с, то тем самым введем скалярную величину скорости ветра, но если мы скажем, что дует северный ветер со скоростью 10 м/с, то в этом случае скорость ветра будет уже векторной величиной.
Векторные величины изображаются с помощью векторов.
Векторомназывается направленный отрезок, имеющий
определенную длину, т.е. отрезок
определенной длины, у которого одна из
ограничивающих его точек принимается
за начало, а вторая — за конец. ЕслиА
— начало вектора иВ — его конец,
то вектор обозначается символом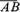 . Вектор можно обозначать и одной малой
латинской буквой с чертой над ней
(например,
. Вектор можно обозначать и одной малой
латинской буквой с чертой над ней
(например, ).
Изображается вектор отрезком со стрелкой
на конце (рис. 24). Начало вектора называютточкой его приложения. Если точкаА является началом вектора
).
Изображается вектор отрезком со стрелкой
на конце (рис. 24). Начало вектора называютточкой его приложения. Если точкаА является началом вектора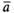 , то мы будем говорить, что вектор
приложен в точкеА.
, то мы будем говорить, что вектор
приложен в точкеА.
Длина
вектора  называется
егомодулем и обозначается символом
называется
егомодулем и обозначается символом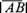 .Модуль вектора
.Модуль вектора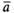 обозначается
обозначается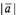 . Вектор
. Вектор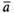 , для которого
, для которого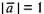 ,
называетсяединичным
,
называетсяединичным
Вектор
называется нулевым(обозначается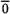 ),
если начало и конец его совпадают.
Нулевой вектор не имеет определенного
направления и имеет длину, равную нулю.
),
если начало и конец его совпадают.
Нулевой вектор не имеет определенного
направления и имеет длину, равную нулю.
Рис.24
Рис.25
Векторы 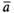 и
и ,
расположенные на одной прямой или на
параллельных прямых, называютсяколлинеарными.
,
расположенные на одной прямой или на
параллельных прямых, называютсяколлинеарными.
Два
вектора  и
и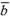 называютсяравными, если они коллинеарны, имеют
одинаковую длину и одинаковое направление.
называютсяравными, если они коллинеарны, имеют
одинаковую длину и одинаковое направление.
В
этом случае пишут: 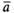 =
=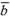 .
Все нулевые векторы считаются равными.
Из определения равенства векторов
следует, что вектор можно параллельно
переносить, помещая его начало в любую
точку пространства (в частности,
плоскости). Такой вектор называется
свободным.
.
Все нулевые векторы считаются равными.
Из определения равенства векторов
следует, что вектор можно параллельно
переносить, помещая его начало в любую
точку пространства (в частности,
плоскости). Такой вектор называется
свободным.
Пример.
Рассмотрим квадрат (рис. 25). На основании
определения равенства векторов можем
написать 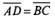 и
и ,
но
,
но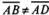 ,
,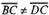 хотя
хотя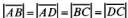 .
.
Два коллинеарных вектора (отличные от нулевых векторов), имеющие равные модули, но противоположно направленные, называются противоположными.
Вектор,
противоположный вектору  ,
обозначается
,
обозначается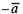 .
Для вектора
.
Для вектора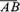 противоположным
будет вектор
противоположным
будет вектор .
.
2. Линейные операции над векторами.
Линейными операциями называются операции сложения и вычитания векторов и умножения вектора на число.
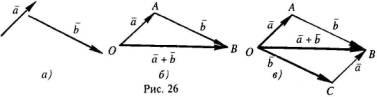
Определение.
Пусть 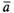 и
и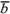 два
свободных вектора (рис. 26,а). Возьмем
произвольную точку О и построим вектор
два
свободных вектора (рис. 26,а). Возьмем
произвольную точку О и построим вектор 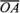 =
= ,затем от точки А отложим вектор
,затем от точки А отложим вектор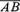 =
= 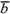 ,Вектор
,Вектор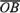 ,
соединяющий начало первого слагаемого
вектора с концом второго, называетсясуммойэтих векторов и обозначается
,
соединяющий начало первого слагаемого
вектора с концом второго, называетсясуммойэтих векторов и обозначается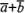 (рис.
26,б). Ту же самую сумму векторов
можно получить иным способом.
(рис.
26,б). Ту же самую сумму векторов
можно получить иным способом.
Отложим
от точки О векторы 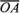 =
=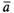 и
и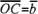 .
Построим на этих векторах как на сторонах
параллелограмм О ABC Вектор
.
Построим на этих векторах как на сторонах
параллелограмм О ABC Вектор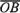 ,
служащий диагональю этого параллелограмма,
проведенной из вершиныО, является,
очевидно, суммой векторов
,
служащий диагональю этого параллелограмма,
проведенной из вершиныО, является,
очевидно, суммой векторов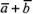 (рис.
26, в). Из рис. 26, в непосредственно следует,
что сумма двух векторов обладает
переместительным свойством:
(рис.
26, в). Из рис. 26, в непосредственно следует,
что сумма двух векторов обладает
переместительным свойством:
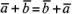 .
.
Действительно,
каждый из векторов  и
и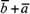 равен
одному и тому же вектору
равен
одному и тому же вектору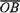 .
.
Понятие суммы векторов, введенное для двух слагаемых векторов, можно обобщить на случай любого конечного числа слагаемых векторов.
Пусть,
например, даны три вектора 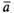 ,
, и
и (рис.
27,а). Построив сначала сумму векторов
(рис.
27,а). Построив сначала сумму векторов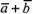 , а затем прибавив к этой сумме вектор
, а затем прибавив к этой сумме вектор получим
вектор
получим
вектор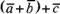 .
На рис. 27, б)
.
На рис. 27, б)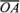 =
=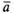 ,
,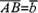 ,
,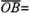
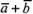 ,
,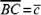 и
и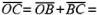
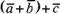 .
.
Из
рис. 27, б видно, что тот же вектор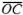 мы
получим, если к вектору
мы
получим, если к вектору =
=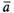 прибавим
вектор
прибавим
вектор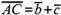 .
Таким образом,
.
Таким образом,
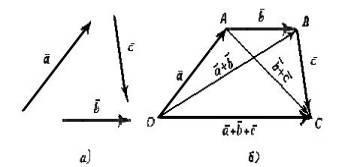
Рис.27
( 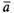 +
+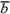 )
+
)
+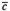 =
=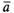 +
(
+
(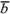 +
+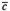 ),
),
т.е.
сумма векторов обладает сочетательнымсвойством. Поэтому сумму трех векторов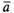 ,
, ,
,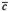 записывают
просто
записывают
просто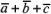 .
.
Итак, сумму трех векторов можно получить следующим образом. Из произвольной точки О откладывается вектор, равный первому слагаемому вектору. К концу первого вектора присоединяется начало второго; к концу второго — начало третьего. Вектор, соединяющий начало первого вектора с концом последнего, является суммой данных векторов. Подобным же образом строится сумма любого конечного числа векторов.
Если
при сложении нескольких векторов конец
последнего слагаемого вектора совпадает
с началом первого, то сумма векторов
равна нулевому вектору. Очевидно, что
для любого вектора имеет место равенство 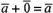 .
.
Определение. Разностью 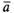 и
и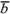 называется
третий вектор
называется
третий вектор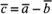 ,
сумма которого с вычитаемым вектором
,
сумма которого с вычитаемым вектором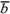 дает
вектор
дает
вектор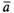 .
Таким образом, если,
.
Таким образом, если,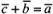 .
.
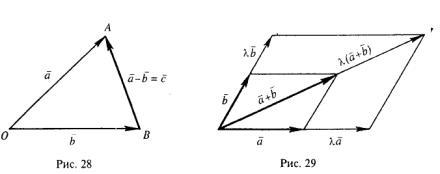
Из определения суммы двух векторов вытекает правило построения вектора-разности (рис. 28). Откладываем векторы
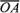 =
= 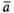 и
и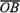 =
=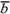 из
общей точкиО. Вектор
из
общей точкиО. Вектор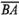 , соединяющий
, соединяющий
концы
уменьшаемого вектора 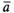 и
вычитаемого вектора
и
вычитаемого вектора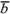 и
направленный от вычитаемого к уменьшаемому,
является разностью
и
направленный от вычитаемого к уменьшаемому,
является разностью .
Действительно, по правилу сложения
векторов
.
Действительно, по правилу сложения
векторов
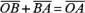 ,
или
,
или  .
.
Определение. Произведением 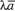 (
или
(
или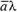 )
)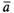 на
на ,
называется вектор
,
называется вектор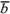 , коллинеарный вектору
, коллинеарный вектору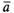 , имеющий длину, равную
, имеющий длину, равную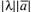 и
то же направление, что и вектор
и
то же направление, что и вектор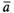 ,
если
,
если >
0, и направление, противоположное
направление
>
0, и направление, противоположное
направление <
0. Так, например, 2
<
0. Так, например, 2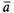 есть
вектор, имеющий то же направление, что
и вектор
есть
вектор, имеющий то же направление, что
и вектор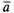 ,
а длину, вдвое большую, чем вектор
,
а длину, вдвое большую, чем вектор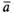 .
В случае, когда
.
В случае, когда =
0 или
=
0 или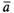 ,
произведение
,
произведение
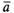 представляет
собой нулевой вектор. Противоположный
вектор
представляет
собой нулевой вектор. Противоположный
вектор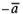 можно
рассматривать как результат умножения
вектора
можно
рассматривать как результат умножения
вектора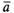 на
на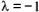
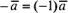
Так,
западный ветер можно представить как
отрицательный восточный ветер. Очевидно,
что 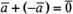 .
.
Пусть
дан вектор 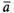 .
Рассмотрим единичный вектор
.
Рассмотрим единичный вектор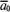 ,
коллинеарный вектору
,
коллинеарный вектору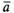 и
одинаково с ним направленный. Из
определения умножения вектора на число
следует, что
и
одинаково с ним направленный. Из
определения умножения вектора на число
следует, что
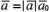 ,
,
т.е.
каждый вектор равен произведению его
модуля на единичный вектор того же
направления. Далее из того же определения
следует 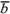 =
=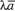 ,
где
,
где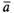 ненулевой
вектор, то векторы
ненулевой
вектор, то векторы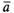 и
и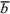 коллинеарны.
коллинеарны.
Очевидно,
что и, обратно, из коллинеарности векторов  и
и следует,
что
следует,
что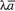 .
.
Таким
образом, два вектора 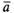 и
и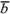 коллинеарны
тогда и только тогда, когда имеет место
равенство
коллинеарны
тогда и только тогда, когда имеет место
равенство
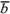 =
= 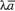 .
.
Легко убедиться, что умножение вектора на число обладает
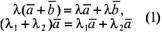 и
сочетательным свойством
и
сочетательным свойством
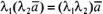 .
.
Справедливость,
например, равенства (1) при  следует
из того, что при изменении сторон
параллелограмма в
следует
из того, что при изменении сторон
параллелограмма в раз
в силу свойств подобия его диагональ
также изменяется в
раз
в силу свойств подобия его диагональ
также изменяется в
§8. Пространство геометрических векторов, как пример линейного пространства
1О. Направленные отрезки.
Рассмотрим в пространстве две точки АиВ. Они определяют отрезокАВ.
Определение 1. Отрезок АВназываетсянаправленным, если его концыАиВупорядочены; если при этом первой является точкаА, а второй – точкаВ, тоА– начало отрезка, аВ– его конец.
Направленный
отрезок обозначается AB (а также или
или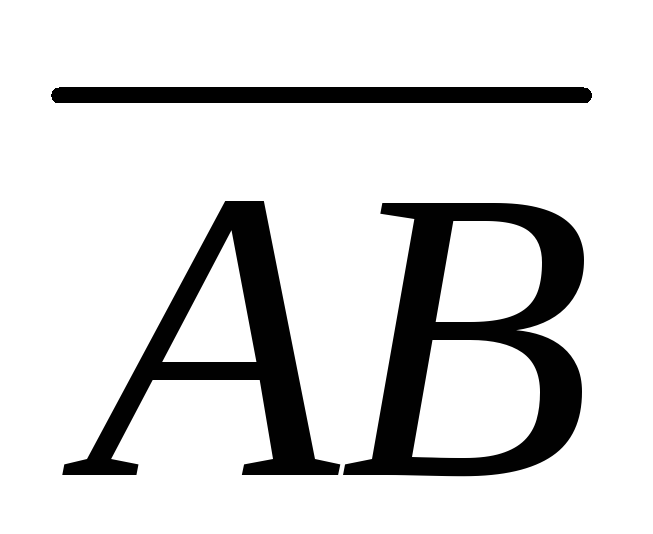 ).
На чертеже направленный отрезок снабжен
стрелкой на конце(см. рис.1)
).
На чертеже направленный отрезок снабжен
стрелкой на конце(см. рис.1)
Определение 2. Длиной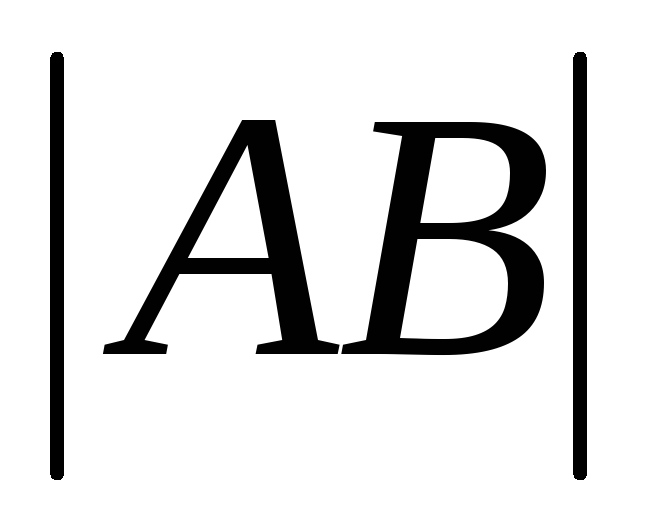 направленного отрезка
направленного отрезка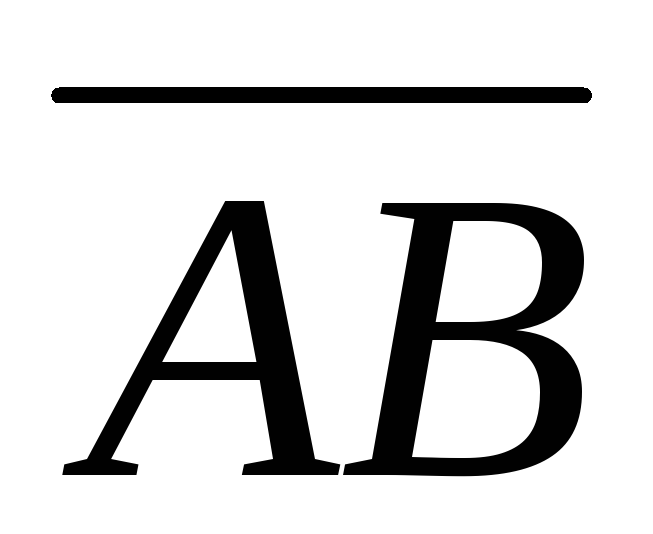 называетсядлина отрезка АВ.
называетсядлина отрезка АВ.
 Рис.1.
Направленный отрезокАВ.
Рис.1.
Направленный отрезокАВ.
Определение 3. Направленные отрезки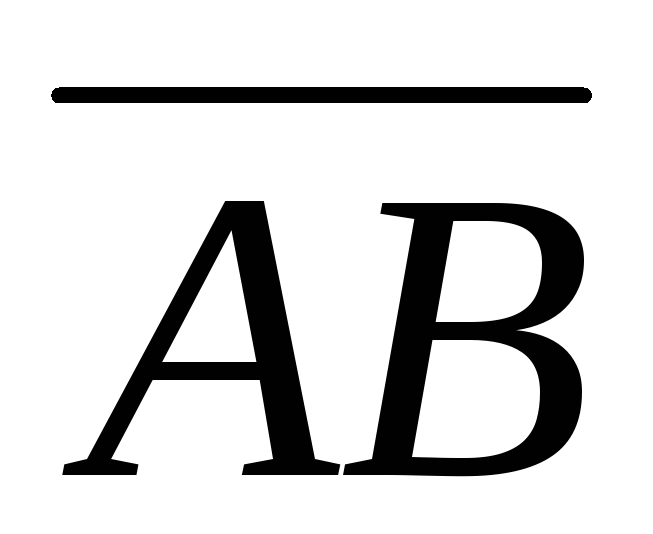 и
и называютсясонаправленными(обозначается
называютсясонаправленными(обозначается ),
если они лежат на параллельных прямых
и направлены в одну сторону.
),
если они лежат на параллельных прямых
и направлены в одну сторону.
Направленные
отрезки 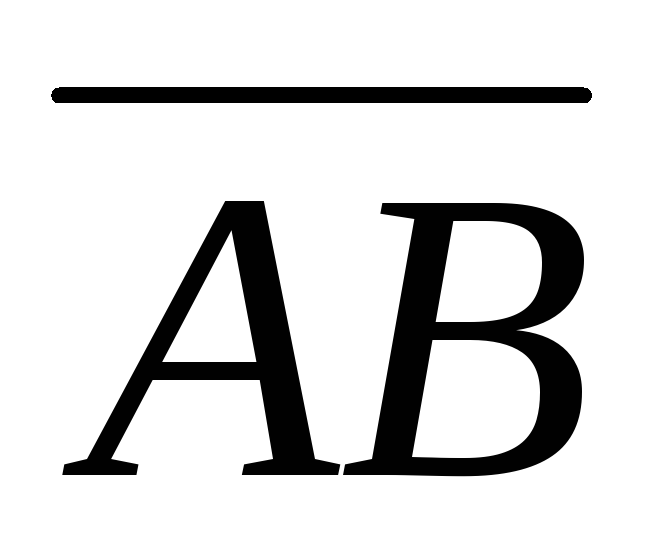 и
и называютпротивоположно направленными(пишут
называютпротивоположно направленными(пишут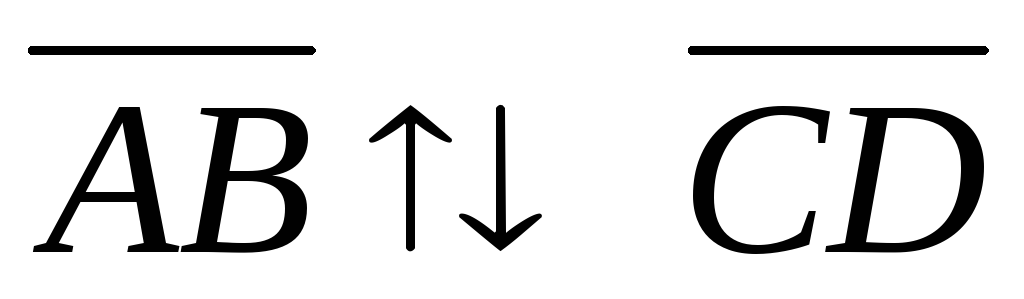 ),
если они лежат на параллельных прямых
и направлены в разные стороны.
),
если они лежат на параллельных прямых
и направлены в разные стороны.
Направленные
отрезки  и
и называютсяпротивоположными.
называютсяпротивоположными.
Каждую точку Апространства можно рассматривать как
направленный отрезок с совпадающим
началом и концом. Этот отрезок обозначается и называется нулевым направленным
отрезком. Его длина считается равной
нулю, а направление не определено.
и называется нулевым направленным
отрезком. Его длина считается равной
нулю, а направление не определено.
Определение 4. Два направленных отрезка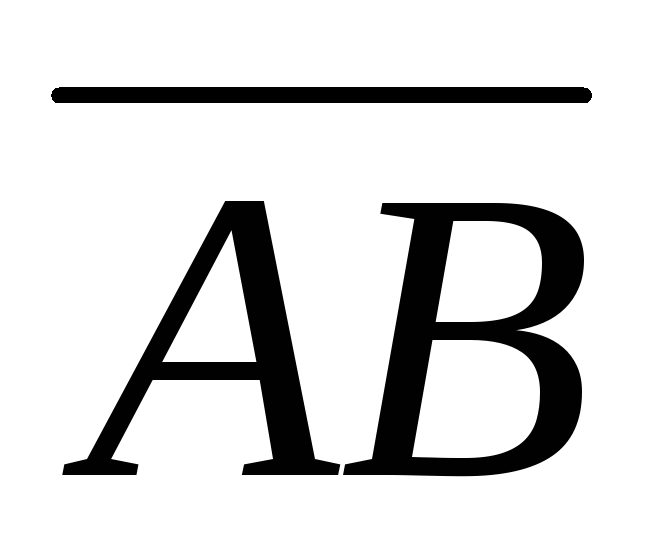 и
и считаютсяэквивалентными, если они
сонаправлены и имеют равные длины.
(Обозначают
считаютсяэквивалентными, если они
сонаправлены и имеют равные длины.
(Обозначают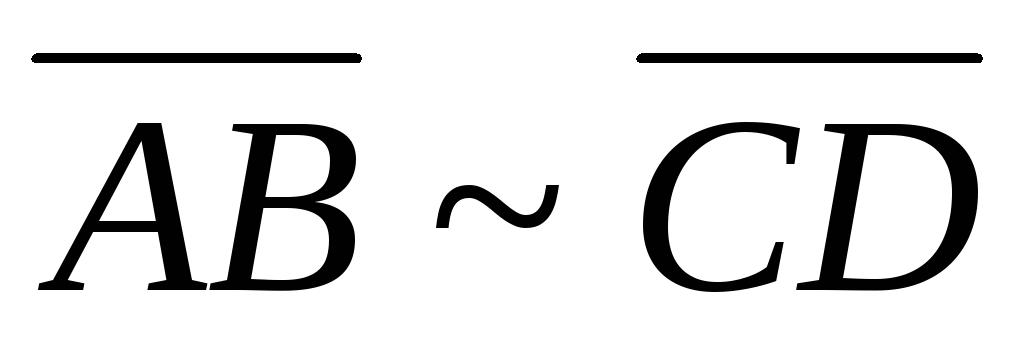 ).
).
Эквивалентностьявляется отношением эквивалентности в множестве всех направленных отрезков, т.к. из определения эквивалентности следует:
1) отрезок 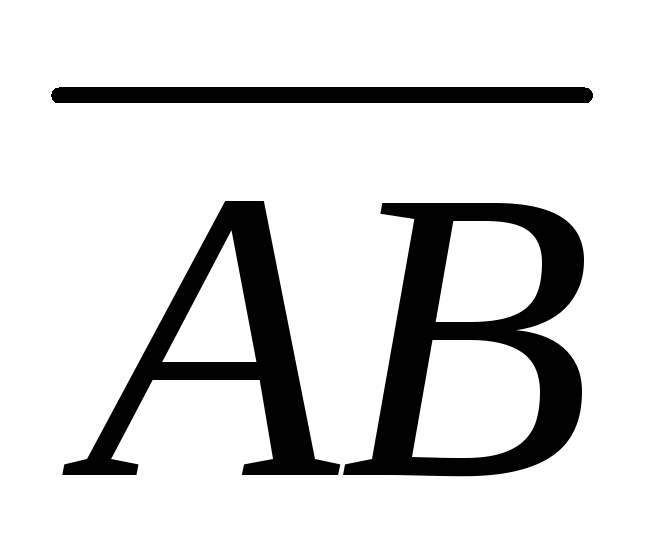 эквивалентен сам себе;
эквивалентен сам себе;
2) если
эквивалентен ,
то
,
то эквивалентен
эквивалентен ;
;
3) если  эквивалентен
эквивалентен и
и эквивалентен
эквивалентен ,
то
,
то эквивалентен
эквивалентен .
.
Так как эквивалентность направленных отрезков является отношением эквивалентности, то множество всех направленных отрезков пространства разбивается на непересекающиеся классы – классы эквивалентности. Классы эквивалентности образуют фактор-множество множества всех направленных отрезков пространства.
Определение 5. Множество всех эквивалентных направленных отрезков называетсявектором(или свободным вектором).
Замечание.Напомним, что в средней школе вектор характеризует параллельный перенос.
Направление эквивалентных направленных отрезков называется направлением вектора, а их длина –длиной вектора.
Таким образом, любой направленный отрезок однозначно определяет вектор, а вектор – это класс эквивалентных направленных отрезков.
Поэтому часто
пишут вектор 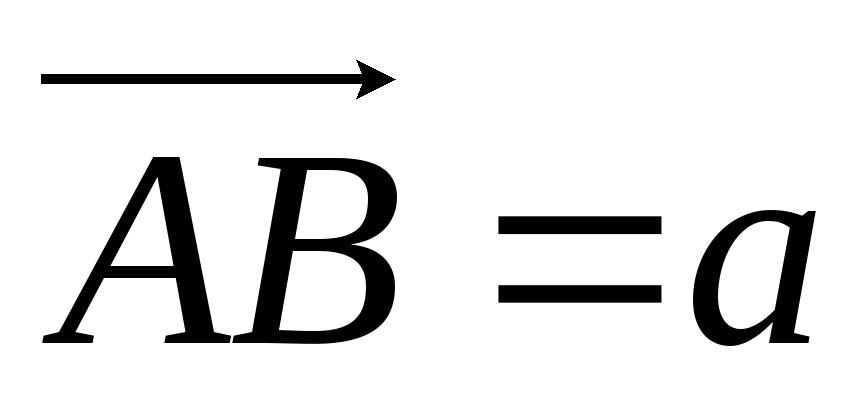 ,
,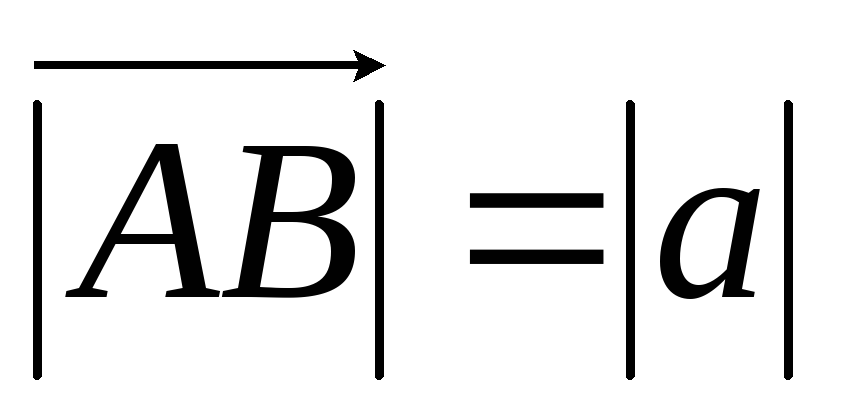 .
.
Определение 6. Векторaтакой, что называетсяединичным векторомилиортом. Множество нулевых отрезков
называетсянулевым вектором
называетсяединичным векторомилиортом. Множество нулевых отрезков
называетсянулевым вектором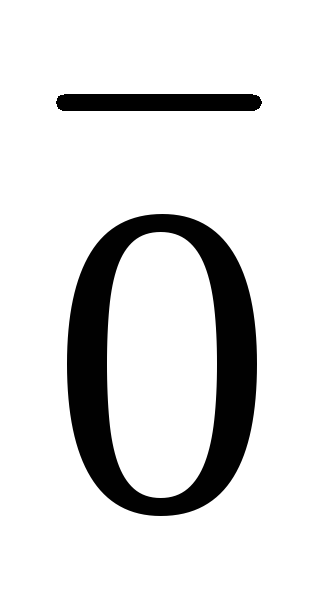 ;
Его длина равна нулю, а направление не
определено.
;
Его длина равна нулю, а направление не
определено.
Определение 7. Два ненулевых вектора, направления
которых совпадают или противоположны,
называютсяколлинеарными. Обозначают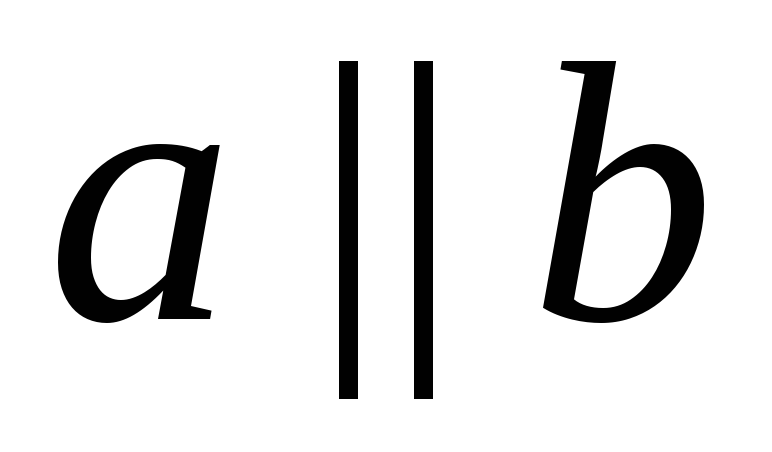 .
.
Нулевой вектор считается коллинеарным любому вектору.
Очевидно, что прямые, на которых лежат представители классов коллинеарных векторов, параллельны.
Определение 8. Три и более векторов называютсякомпланарными, если они параллельны некоторой плоскости.
Для определенности любую тройку векторов, содержащую нулевой вектор, считают компланарной.
Пусть даны два
вектора aиb.
Из произвольной точкиO пространства отложим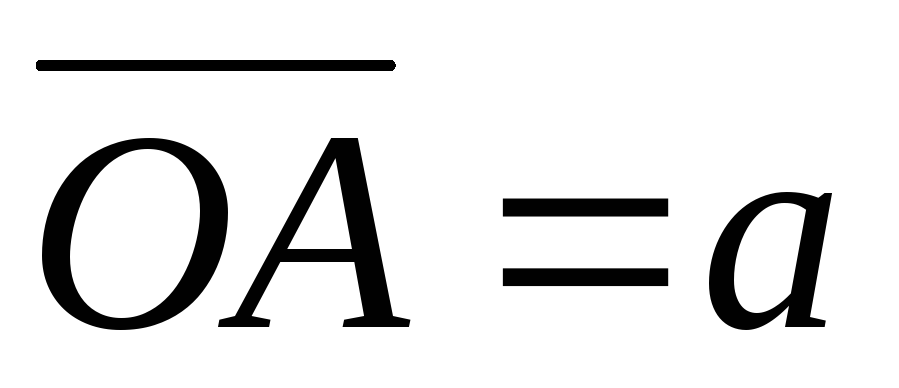 и
и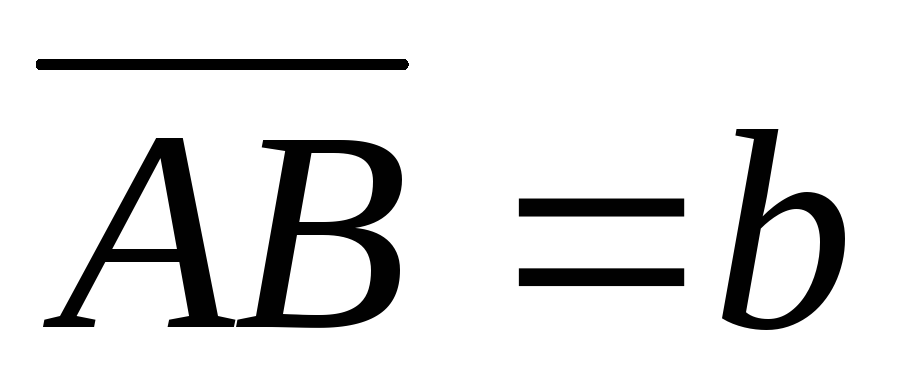 .
Тогда
.
Тогда есть направленный отрезок и значит,
определяет вектор.
есть направленный отрезок и значит,
определяет вектор.
Покажем, что
введенная операция сложения векторов
корректно определена, т.е. вектор  не зависит от выбора точкиO.
Для этого выберем другую точку
не зависит от выбора точкиO.
Для этого выберем другую точку  .
Пусть
.
Пусть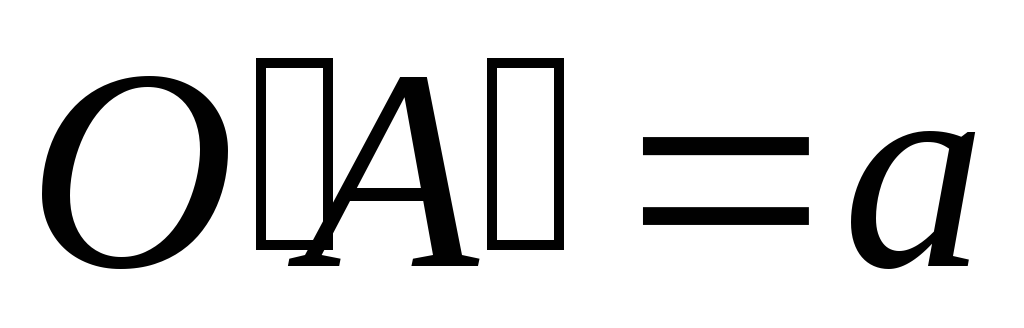 ,
, .
Тогда
.
Тогда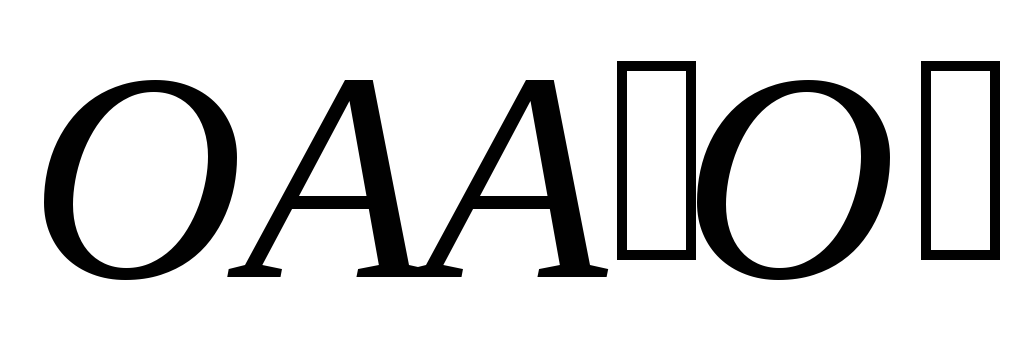 – параллелограмм; аналогично,
– параллелограмм; аналогично,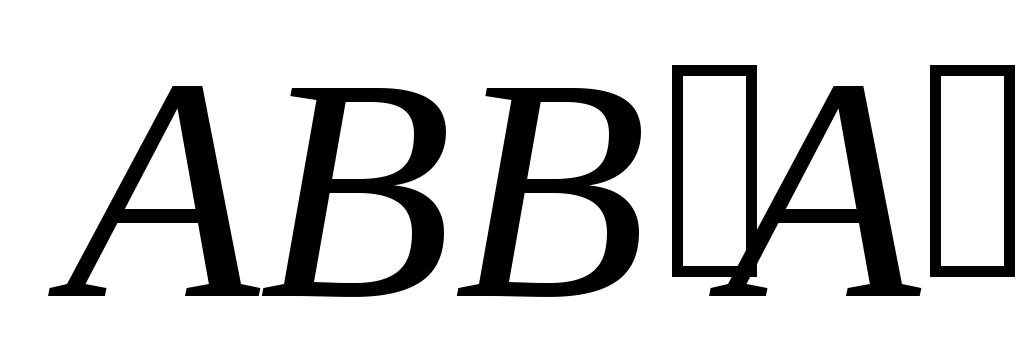 – параллелограмм
– параллелограмм
 – параллелограмм
– параллелограмм
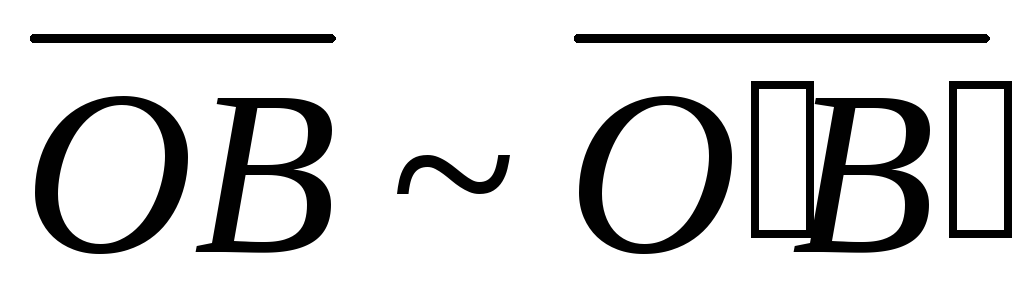 ,
то есть они определяют один и тот же
вектор.
,
то есть они определяют один и тот же
вектор.
Определение 9. Вектор называетсясуммойвекторов
называетсясуммойвекторов и
и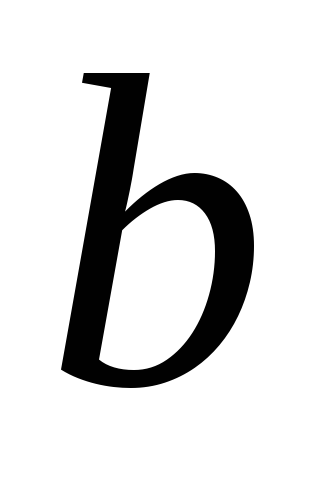 .
Пишут:
.
Пишут: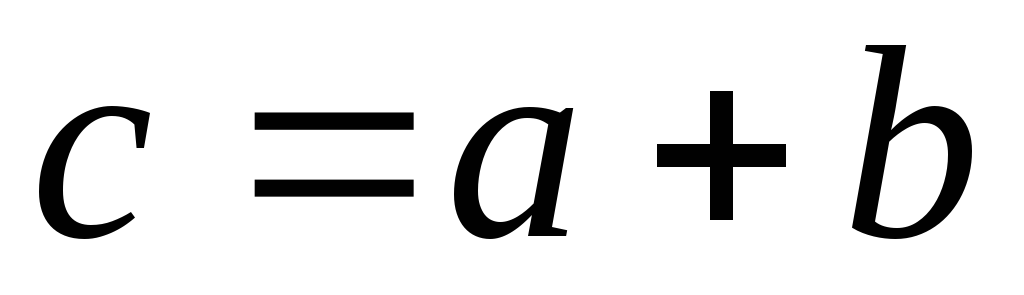 .
.
Способ сложения векторов, изложенный выше, называется правилом треугольника. Можно также использовать правило параллелограмма.
Свойства сложения векторов.
1. 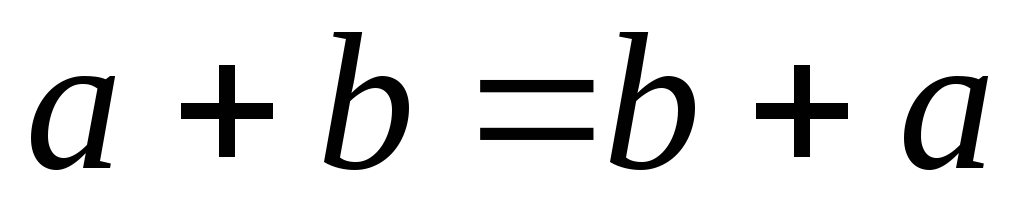 .
.
2. 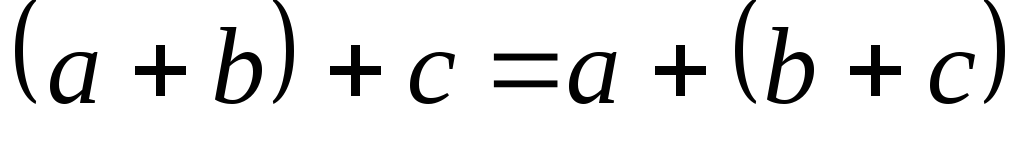 .
.
3. 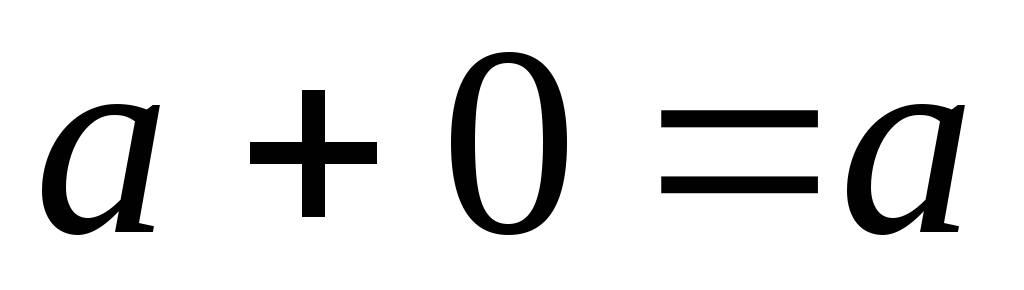 ,
так как
,
так как .
.
4. Для каждого
вектора 
 вектор, называемый вектором, противоположным
вектор, называемый вектором, противоположным ,
такой, что
,
такой, что 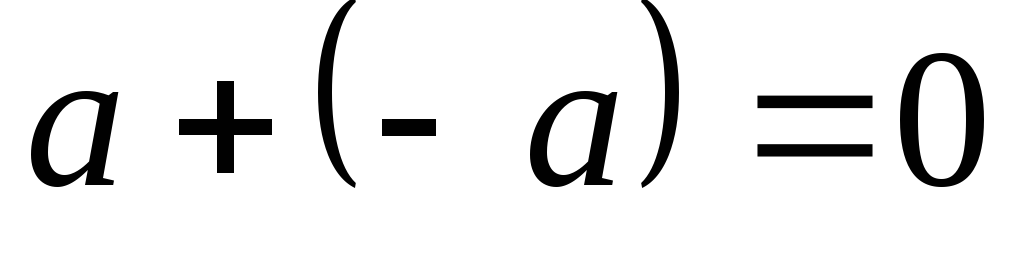 .
Доказательство свойств может быть
проиллюстрировано рис.2
.
Доказательство свойств может быть
проиллюстрировано рис.2
а
 )
б)
)
б)
Рис.2. Свойства сложения векторов: а) коммутативность, б) ассоциативность
Если 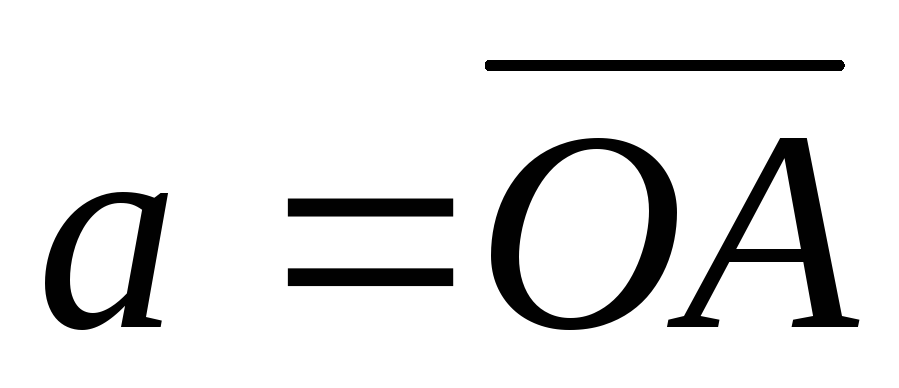 ,
то через
,
то через обозначим
обозначим .
Тогда
.
Тогда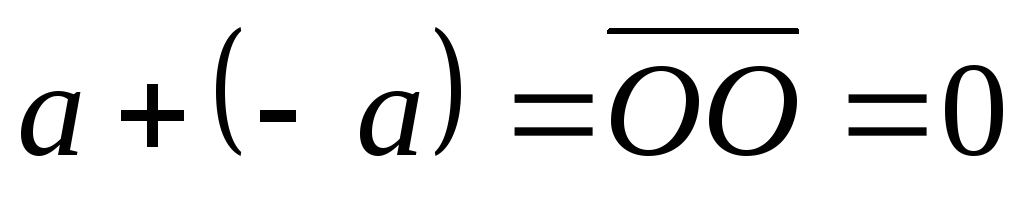 .
.
Определение 10. Произведениемвектора на число
на число
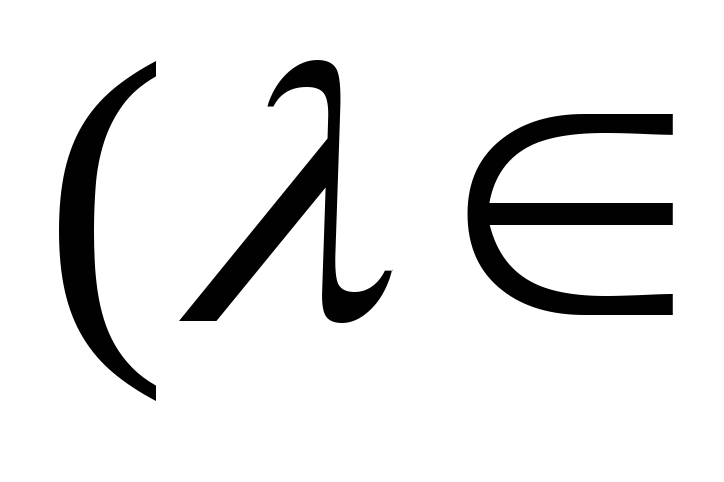 R,
R, 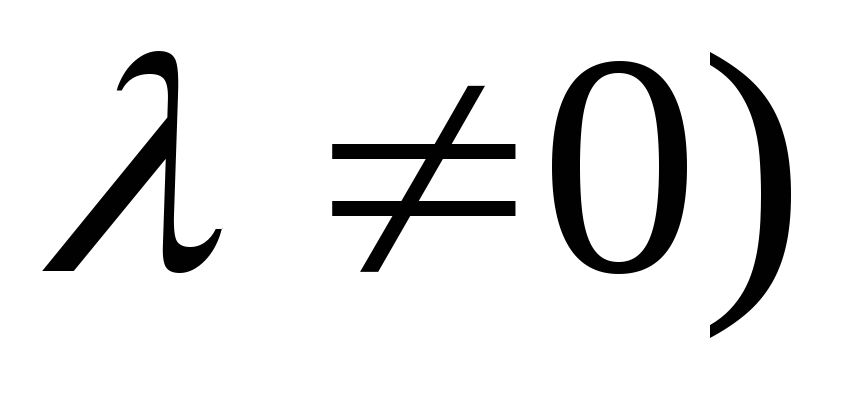 называется
вектор
называется
вектор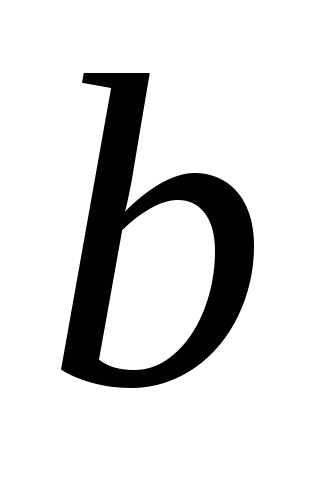 ,
удовлетворяющий следующим условиям:
,
удовлетворяющий следующим условиям:
векторы
 и
и сонаправлены, если
сонаправлены, если и противоположно направлены, если
и противоположно направлены, если ;
; .
.
Произведение
вектора на число 0 есть нулевой вектор.
Пишут 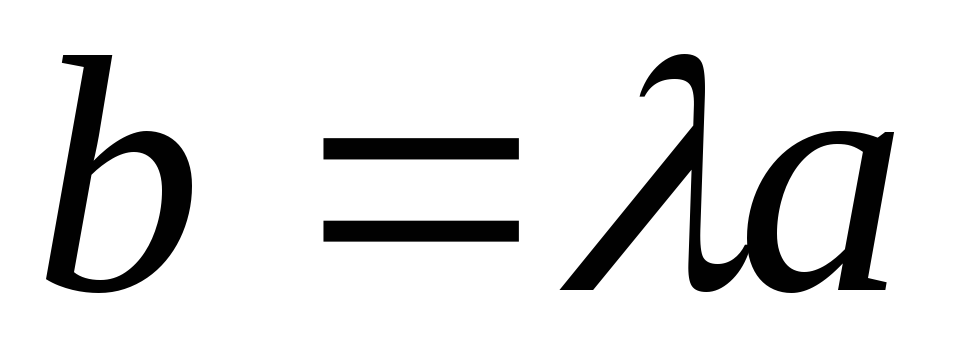 .
.
Свойства умножения вектора на число.
 и
и 

 .
. и
и  вектора
вектора

 .
. и
и  вектора
вектора

 .
. вектора
вектора 

 .
.
Доказательство
1). Пусть для простоты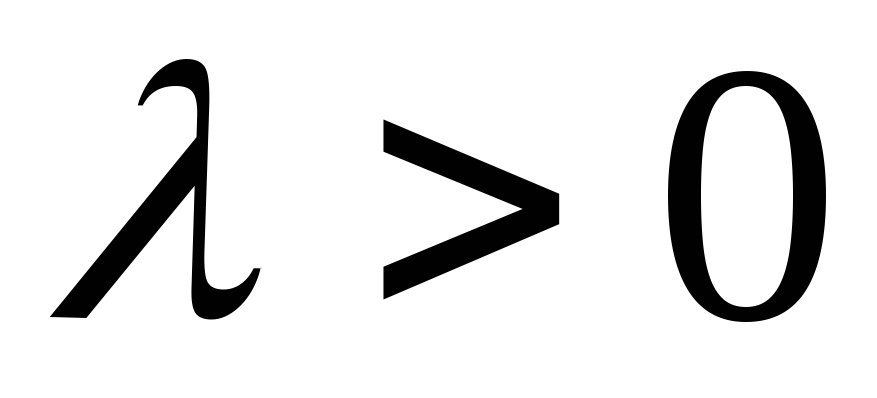 и будем использовать правило параллелограмма
для сложения векторов. Если вместо
и будем использовать правило параллелограмма
для сложения векторов. Если вместо и
и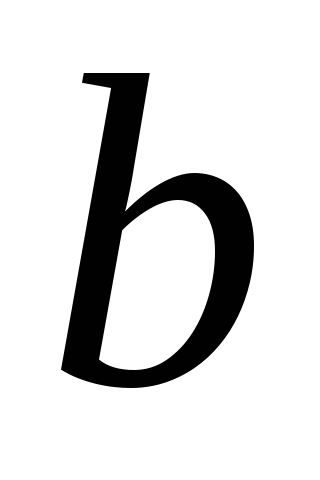 взять
взять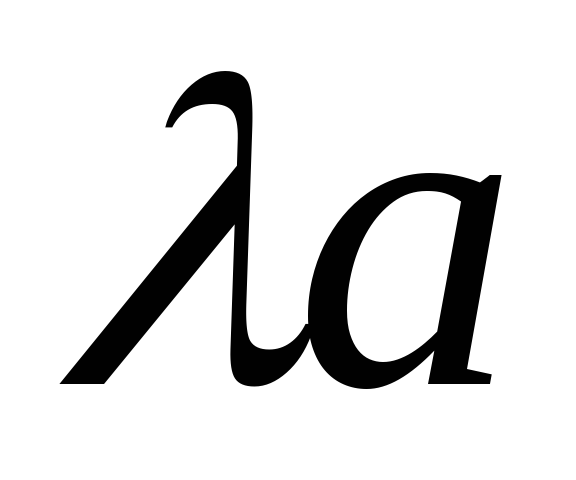 и
и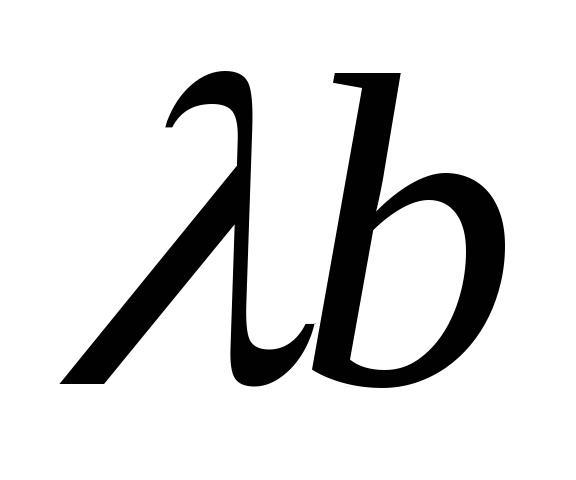 ,
то получим подобный параллелограмм и
его диагональ соответственно равна
,
то получим подобный параллелограмм и
его диагональ соответственно равна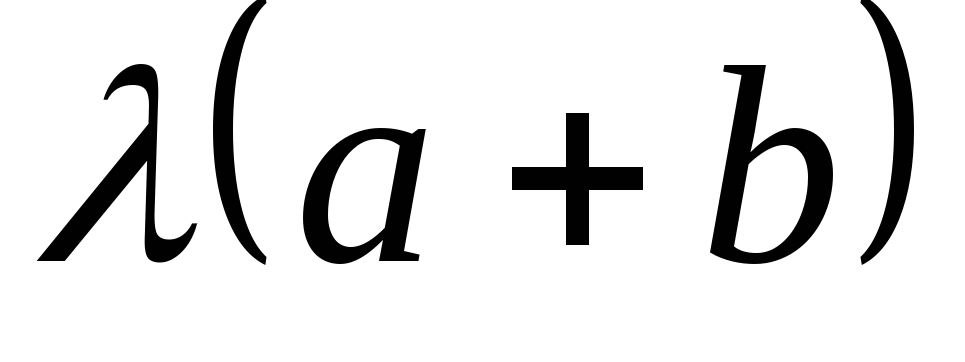 (см. рис.3).
(см. рис.3).

Рис.3.Иллюстрация
свойства сложения векторов 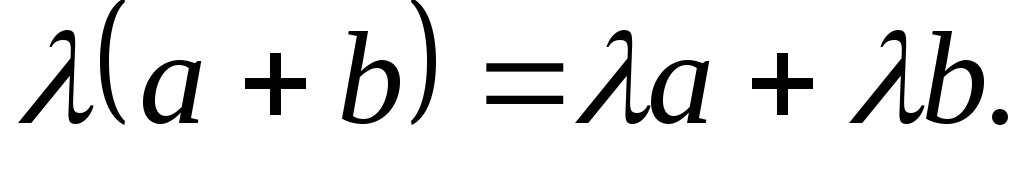
Доказательство 2)–4).Очевидно, и при этом получаются коллинеарные вектора.
Теорема 1.Множество векторов пространства образует линейное пространство.
Доказательство.Следует из свойств сложения векторов и умножения на число.∎
Замечание.Можно определить операцию вычитания
векторов по формуле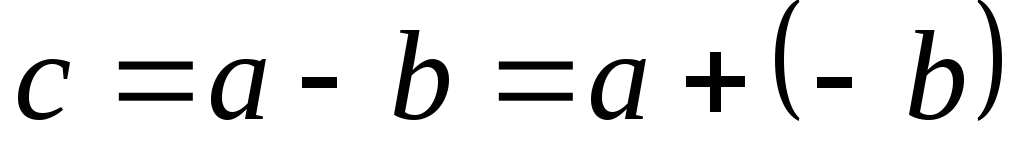 (см. рис.4)
(см. рис.4)
Р ис.
4. Вычитание векторов
ис.
4. Вычитание векторов
a) Множество коллинеарных векторов образует линейное пространство
б)Множество компланарных векторов образует линейное пространство.
Далее выясним размерности и базисы перечисленных пространств.


 и
и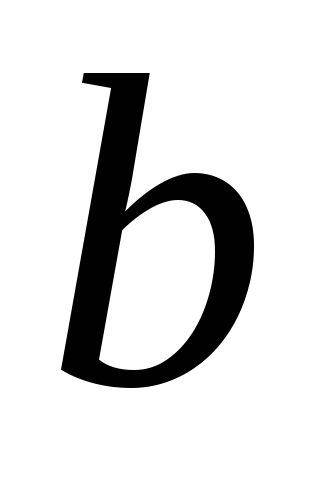 сонаправлены, если
сонаправлены, если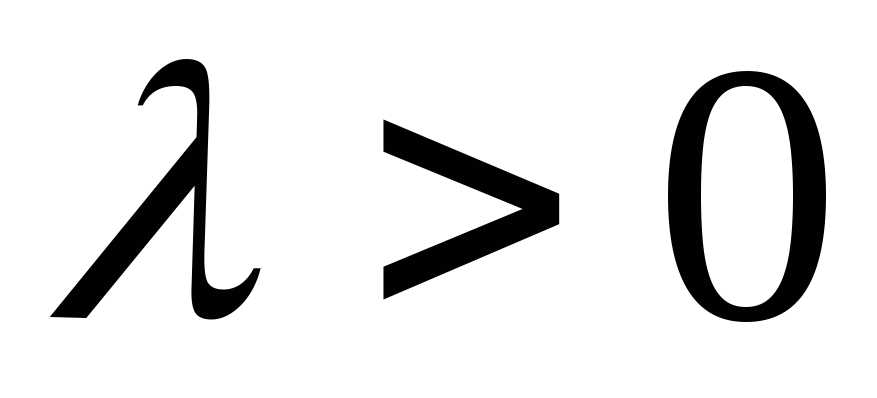 и противоположно направлены, если
и противоположно направлены, если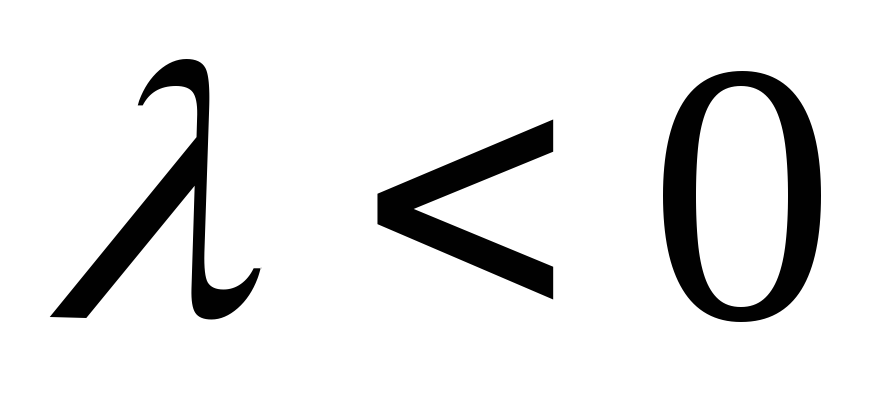 ;
;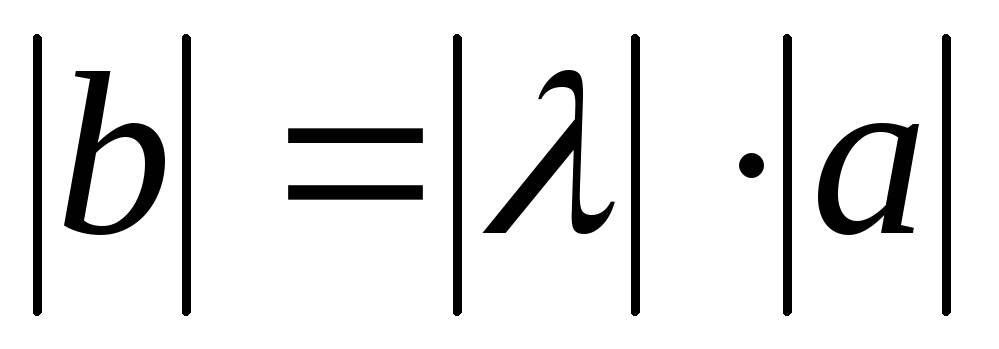 .
. и
и 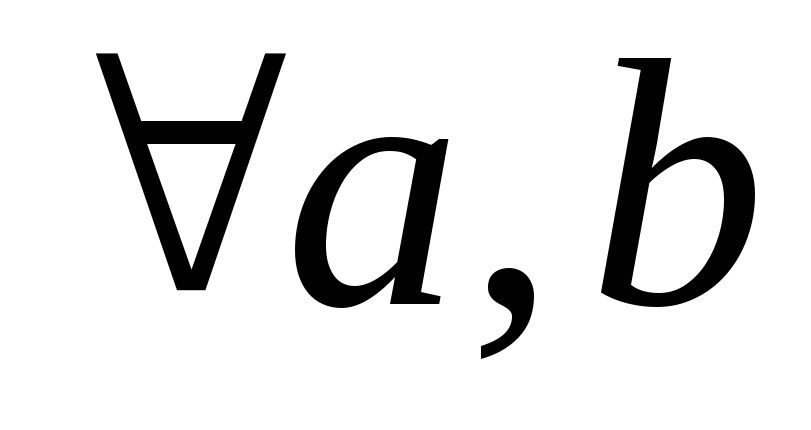

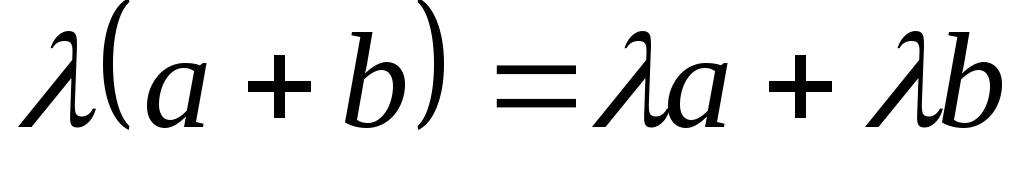 .
.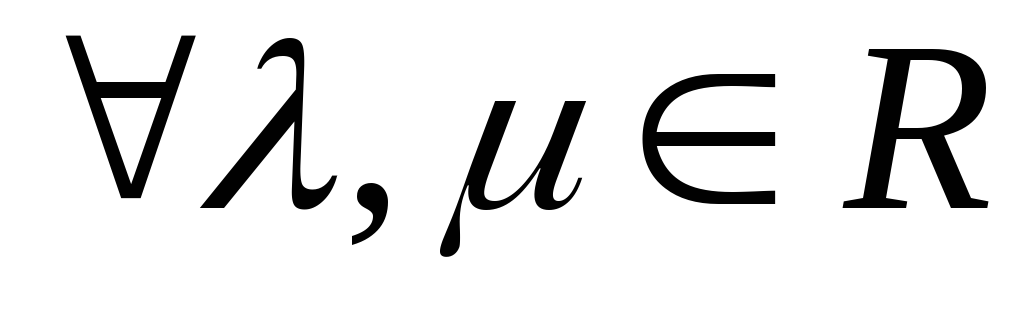 и
и  вектора
вектора

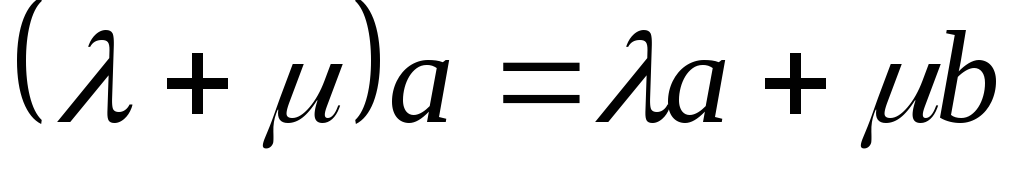 .
.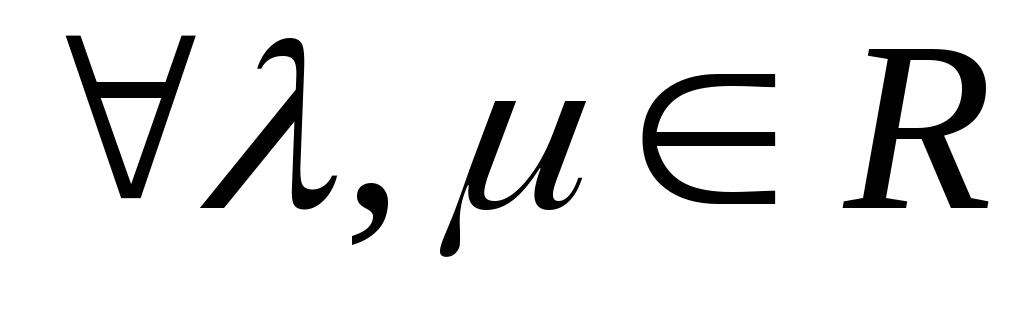 и
и  вектора
вектора

 .
. вектора
вектора 

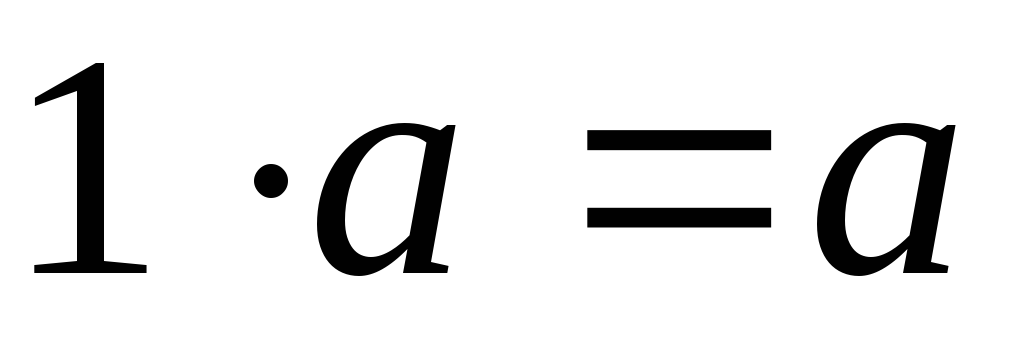 .
.