Ортогональные векторы и условие ортогональности: определение, примеры решения задач

В данной статье мы расскажем, что такое ортогональные векторы, какие существуют условия ортогональности, а также приведем подробные примеры для решения задач с ортогональными векторами.

Ортогональные векторы: определение и условие

Определение 1

Ортогональные векторы — это векторы a¯ и b¯, угол между которыми равен 900.

Примечание

Необходимое условие для ортогональности векторов — два вектора a¯ и b¯ являются ортогональными (перпендикулярными), если их скалярное произведение равно нулю.

a¯ × b¯=0

Примеры решения задач на ортогональность векторов

Плоские задачи на ортогональность векторов

Если дана плоская задача, то ортогональность для векторов a¯={ax×ay} и b¯={bx×by} записывают следующим образом:

a¯×b¯=ax×bx + ay×by=0

Пример 1

Задача 1.  Докажем, что векторы a¯={1;2} и b¯={2;-1} ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a¯×b¯=1×2+2×(-1)=2-2=0

Ответ: поскольку произведение равняется нулю, то векторы являются ортогональными.

Пример 2

Задача 2. Докажем, что векторы a¯={3;-1} и b¯={7;5} ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a¯×b¯=3×7+(-1)×5=21-5=16

Ответ: поскольку скалярное произведение не равняется нулю, то и векторы не являются ортогональными.

Пример 3

Задача 3. Найдем значение числа n, при котором векторы a¯={2;4} и b¯={n;1} будут ортогональными.

Как решить?

Найдем скалярное произведение данных векторов:

a¯×b¯=2×n+4×1=2n+42n+4=02n=-4n=-2

Ответ: векторы являются ортогональными при значении n=2.

Примеры пространственных задач на ортогональность векторов

При решении пространственной задачи на ортогональность векторов a¯={1;2;0} и b¯={2;-1;10} условие записывается следующим образом: a¯×b¯=ax×bx+ay×by+az×bz=0.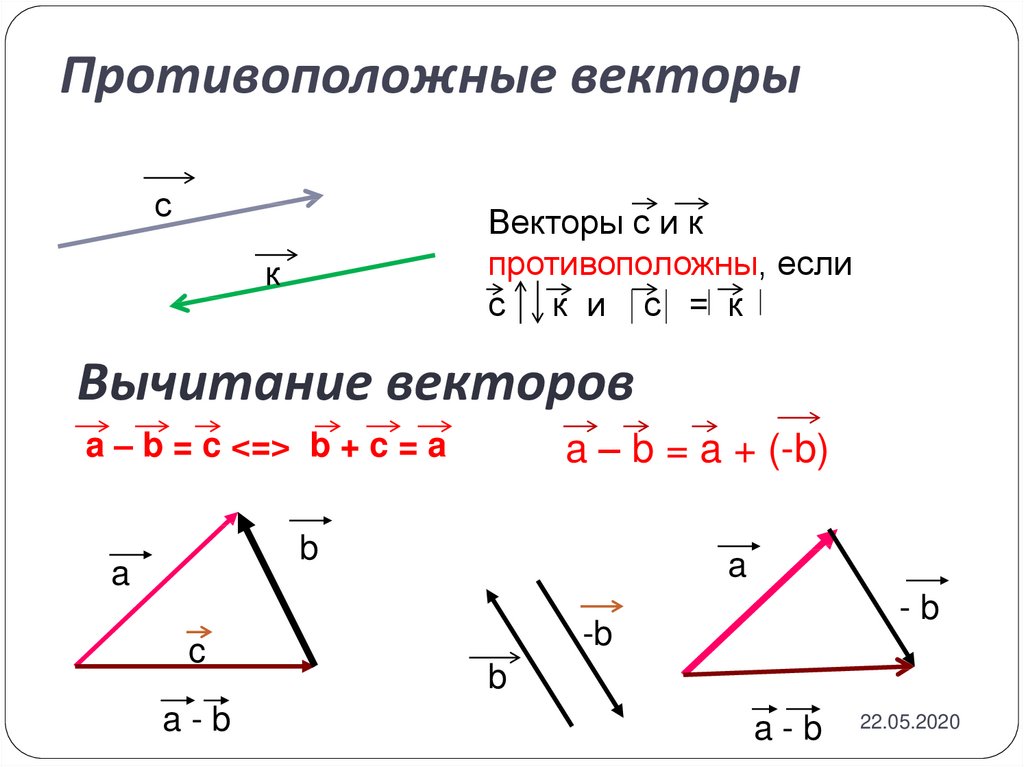

Пример 4

Задача 4. Докажем, что векторы a¯={1;2;0} и b¯={2;-1;10} являются ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a¯×b¯=1×2+2×(-1)+0×10=2-2=0

Ответ: поскольку произведение векторов  равняется нулю, то они являются ортогональными.

Пример 5

Задача 5. Найдем значение числа n, при котором векторы a¯={2;4;1} и b¯={n;1;-8} будут являться ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a¯×b¯=2×n+4×1+1×(-8)=2n+4-8=2n-42n-4=02n=4n=2

Ответ: векторы a¯ и b¯ будут ортогональными при значении n=2.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

какие двери открыл России визит Лаврова в Африку

На этой неделе министр иностранных дел России Сергей Лавров совершил турне в Африку. Он посетил ЮАР, Анголу, Эсватини и Эритрею. «Абзац» рассказывает, почему укрепление связей с африканскими странами важно для России.

Сегодня завершилось африканское турне главы МИД России Сергея Лаврова, в ходе которого он встретился с коллегами из ЮАР, Анголы, Эсватини и Эритреи. «Абзац» рассказывает, какие отношения сложились у Россией с каждой из стран.

У Эритреи с нашей страной была сложная история, учитывая, что Москва выступала в поддержку Эфиопии, а не Эритреи, когда та пыталась отделиться. Однако именно она стала единственной африканской страной, которая в марте 2022 года проголосовала против резолюции ООН, осуждающей начало спецоперации России на Украине.

Одним из главных аргументов в пользу сотрудничества с Эритреей является её выгодное стратегическое расположение. Страна занимает удобное для торговли и размещения баз положение на выходе из Красного моря в Индийский океан – у Баб-эль-Мандебского пролива.

По итогам визита Лавров сообщил, что Россия и Эритрея намерены изучить возможность использования логистического потенциала порта Массауа, а также транзита через аэропорт этого африканского города.

Фото: ТАСС / Илья Ермаков / Министр иностранных дел РФ Сергей Лавров (слева) во время прослушивания песни «Катюша» в исполнении учащихся школы при посольстве РФ в Анголе

Во время переговоров с ангольским коллегой Тете Антониу Лавров пообещал рассмотреть потенциал развития программы атомной энергетики в стране. Учитывая, что российская компания «Росатом» не присутствовала в Анголе до 2019 года, инициативу придётся разрабатывать практически с нуля.

«Договорились ускорить согласование целого ряда новых межправительственных соглашений, в том числе об открытии культурных центров, по атомной энергетике, гуманитарным операциям, торговому судоходству», – сказал глава российской дипломатии.

Партнёрские отношения с Анголой развивались ещё в СССР, Москва долгое время являлась крупнейшим поставщиком оружия в страну. Однако в последние годы США активно пытаются заменить Россию в этом качестве.

Ангола для Вашингтона – это новый и довольно крупный рынок вооружения. Многие эксперты предполагают, что глава российского МИД обсуждал с представителями страны тему о возобновлении крупных долгосрочных контрактов в сфере вооружения.

Почти каждая страна Африки имеет соглашение о безопасности с Москвой, многие направляют своих офицеров и специалистов для обучения в российские военные академии.

Даже у такой небольшой страны, как Королевство Эсватини, которое является одним из самых маленьких государств на африканском континенте, существуют тесные связи в оборонной сфере с Россией.

«На встрече с военным руководством мы договорились наращивать сотрудничество в сфере безопасности, у нас есть действующее межправительственное соглашение о военном сотрудничестве, о военно-техническом сотрудничестве, действуют рабочие группы по военно-техническому сотрудничеству», – сказал Лавров на брифинге по итогу визита.

О сотрудничестве России и ЮАР и о том, почему это очень беспокоит Соединённые Штаты, «Абзац» рассказывал ранее.

Фото: ТАСС / Пресс-служба МИД РФ

В ходе визита Лаврова стало понятно, что африканские страны принципиально иначе относятся к развитию сотрудничества с Россией. В Эритрее российского министра встретили национальными песнями и танцами у памятника Пушкину.

Руководитель экспертного совета Фонда стратегического развития Игорь Шатров в комментарии для «Абзаца» отметил, что коллективный Запад привык выстраивать с Африкой отношения по принципу принуждения и подчинения, а Россия выстраивает равноправные отношения.

«Россия в качестве правопреемницы Советского Союза имеет статус страны, которая поддерживала антиколониальное движение в Африке. СССР оказывал многим странам не только политическую поддержку, но и гуманитарную, а в некоторых случаях – даже военную. В советские годы об этом громко не говорилось, но уже сейчас ни для кого не является секретом, что многие освободительные движения в африканских странах проводились при поддержке СССР», – сказал эксперт.

После распада СССР, в 1990-е годы, Россия потерялась на международной арене, были прерваны тесные контакты со многими государствами. Однако даже сейчас отношение к русским в Африке отличается от отношения к другим представителям белой расы, потому что у нас нет колониального прошлого, отмечает Шатров.

«В течение последних пяти-десяти лет происходит резкое переориентирование многих франкоязычных африканских государств в сторону России. По такой сложившейся «традиции» Франция направляет во многие страны, являвшиеся раньше её колониями, свои контингенты, которые поддерживают правительства и якобы обеспечивают безопасность. Сейчас правительства этих стран начинают понимать, что такое влияние несёт только отрицательный эффект», – пояснил он.

Эксперт добавил, что ни для кого не секрет, что порядка десяти африканских стран поддерживают отношения с русскими военными советниками – там есть контингент того же самого ЧВК «Вагнер». Тем самым уважение к России возросло, а её статус в Африке стал ещё выше.

«У нас на глазах формируется многополярный мир, потому что африканские страны не поддерживают политику Запада в отношении России и активно идут на сотрудничество. На этом фоне особенно важен саммит Россия – Африка, который пройдёт этим летом в Санкт-Петербурге. Это ещё один способ укрепить наши связи», – сказал Шатров.

Он заключил, что Африке нужны инвестиции, её страны, так же как и Россия, богаты полезными ископаемыми. Однако их надо добывать и во многих случаях ещё и проводить геологоразведочные работы для их нахождения. В Африке очень хорошо развито сельское хозяйство, многие продукты могли бы импортировать и в Россию. У России и стран Африки действительно много векторов развития сотрудничества.

вектор по математике — определение, умножение и примеры (видео)

Написано

Малкольм МакКинси

12 января 2023

Проверка по фактам

Paul Mazzola

Определение вектора

A Vector . величина в математике, которая имеет величину  (расстояние, скорость или размер) и направление (как на стрелке компаса, например, запад, вверх, юго-восток, вниз или север через северо-запад).

Переплывая бухту на лодке, вы можете думать, что плывете прямо на юг со скоростью 3 узла, но если приливы отступают, вы можете двигаться со скоростью 5 узлов на юго-восток.

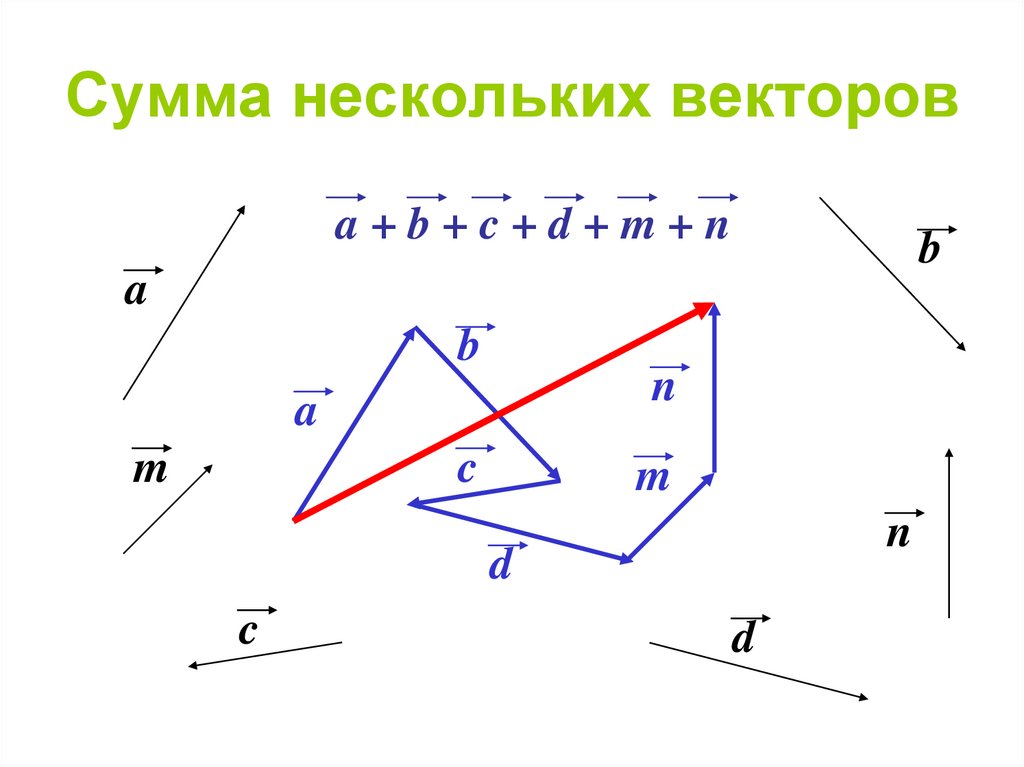
Вектор или несколько векторов, работающих вместе, будут учитывать расстояние, которое вы гребете, вашу скорость и фактическое направление.

Символ вектора

Для представления векторов математики, физики и инженеры используют лучи, обозначая их строчными или прописными буквами, например:

Символ вектора

Советы по маркировке векторов

• Все векторы называются от конца (начальной точки) до конца стрелки, поэтому у нас есть вектор AB , а не вектор BA .

• Если вы маркируете свои векторы, решение использовать прописные или строчные буквы остается за вами; если вам даны векторы, обратите внимание на направление вектора (посмотрите на стрелки).

• Векторы могут быть параллельны и указывать в одном или противоположном направлении (посмотрите на стрелки).

• Векторы одинаковой величины, но направленные в противоположные стороны, являются противоположными, поэтому вектор b можно также записать как -a , что отрицает величину a.

Репетиторы

Вектор единичной длины называется единичным вектором и обозначается так называемой шляпой: ˆ

Сложение и вычитание векторов

Простая векторная математика не слишком сложна.

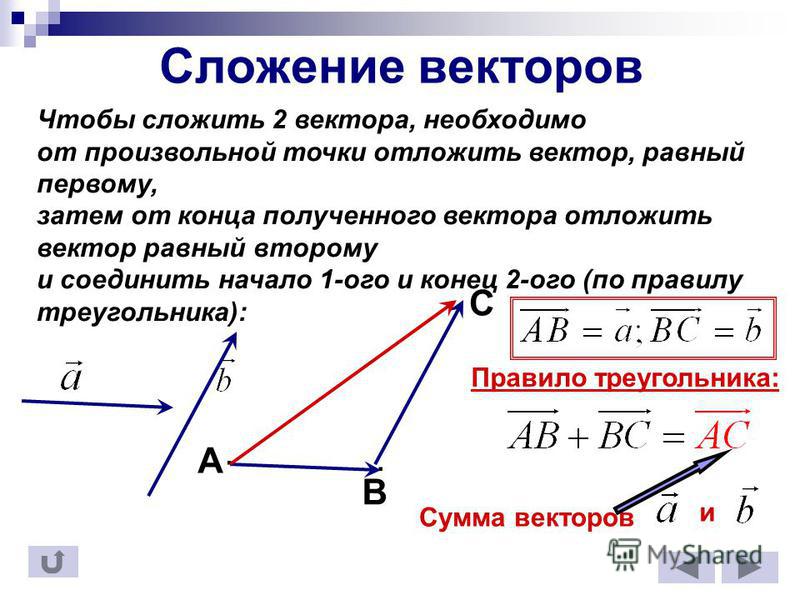
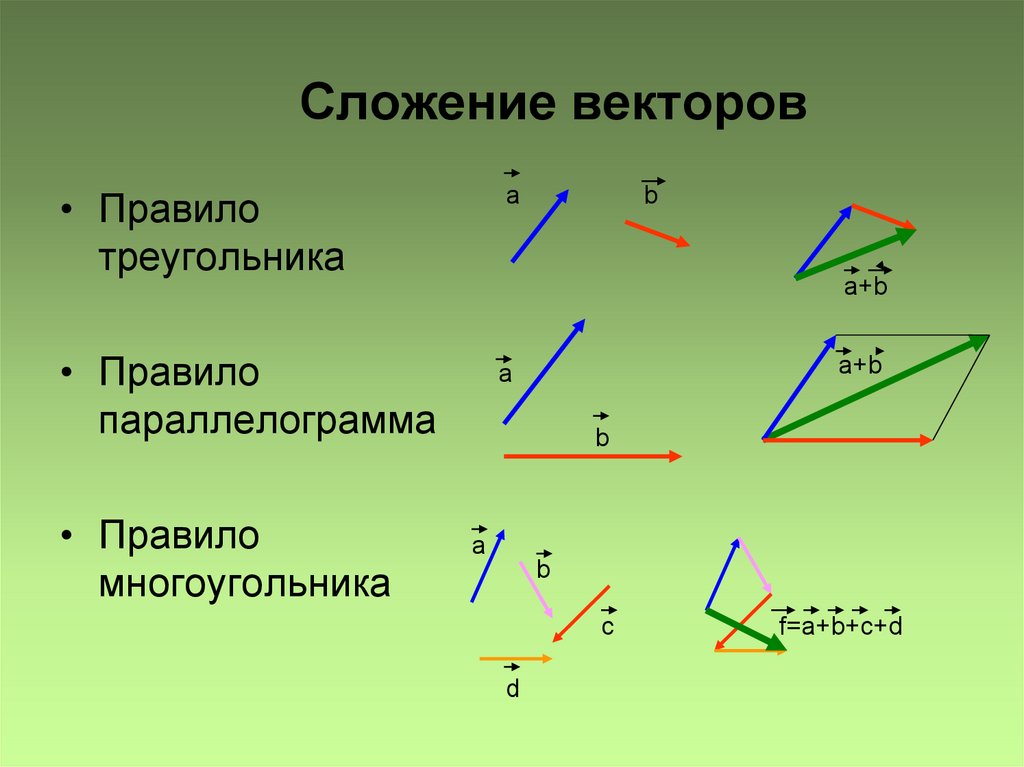
Чтобы добавить векторы, мы соединяем хвост одного вектора с головой другого, используя стрелку. Прямой луч, соединяющий два вектора, является равнодействующим, r , как на этом рисунке:

Пример сложения вектора

Добавляем вектор CD к вектору EF и получаем результат r .

Вот загадка: этот рисунок дает те же результаты, что и предыдущий?

Сложение вектора

Здесь мы добавляем вектор EF к вектору CD и еще получаем результирующее r . Векторы подчиняются тем же правилам арифметики, что и целые числа (в данном случае свойство коммутативности).

В реальном мире два путешествия вдоль векторов могут показать совершенно разные пейзажи. В математике, поскольку два вектора не изменили своего направления или величины, результаты идентичны: CD + EF = EF + CD = r .

Вычитание вектора состоит всего из двух шагов:

1. инвертируйте вектор, который вы хотите вычесть

2. затем сложите два вектора вместе

0017 IL , показывающий маршрут, по которому, как мы думали, мы плывем на парусной лодке:

Вычитание вектора

Мы не осознавали, что течение было сильным; мы заблудились в тумане; солнце ослепляло. По какой-то причине вместо того, чтобы следовать вектору IL , мы пошли в направлении , противоположном . Поэтому вместо добавления вектора IL нам нужно его вычесть. Мы делаем это, инвертируя вектор IL и добавляя его к вектору SA :

Умножая векторы на скаляр

Умножение вектора на скаляр (действительное число) называется скалярным умножением .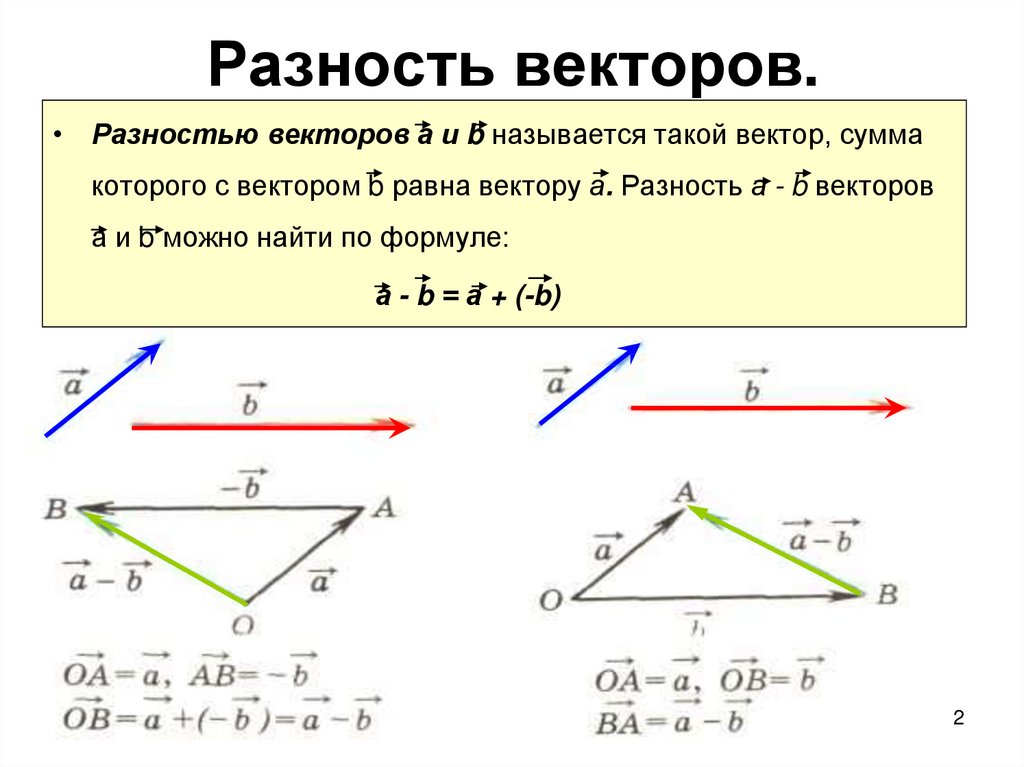

Векторы состоят из двух частей (величина и направление), но мы не можем умножить направление. Это не имеет смысла: два «юга» не обращены к югу больше, чем один «юг». Но мы можем умножить величину вектора:

• Умножение вектора на положительное целочисленное скалярное значение > 1 дает больший вектор.

• Умножение вектора на отрицательный целочисленный скаляр < −1 дает больший вектор в направлении , противоположном .

• Умножение векторов на 1 возвращает тот же вектор ( 0 смещение).

• Умножение вектора на положительный дробный скаляр < 1 дает меньший вектор.

• Умножение вектора на отрицательный дробный скаляр > −1 дает меньший вектор в направлении , противоположном .

Два вектора также можно умножить друг на друга с помощью векторного произведения или скалярного произведения.

Умножение двух векторов методом перекрестного произведения дает новый вектор, а скалярное произведение дает число, иногда называемое скалярным произведением.

Величина вектора

Величина вектора отображается как абсолютное значение, |а| или двумя строками, чтобы не спутать его с абсолютным значением, | |а|| .

Если вы знаете значения оси x и оси y вектора (как если бы он был на карте или в декартовой системе координат), вы можете легко вычислить его величину, применив теорему Пифагора к изменению положения от хвоста к наконечнику .0017 6  и изменение значения y на 4 , поэтому:

Величина вектора равна 7,2111 единиц .

Единица измерения определяется тем, что вы измеряете; дюймы, километры, мили в час (миль/ч) и т. д. Итак, если бы мы просто измерили расстояние в милях, то 7,2111 миль  было бы длиной вектора.

Скаляр против векторов

Чтобы было ясно, скалярные  величины — это только величины: масса, температура, скорость, объем, расстояние, энергия, работа и т. д. Думайте о них как о чистых числах.

Послушайте или прочитайте внимательно: Услышать или прочитать две величины, например скорость и  направление? Тогда вы имеете дело с вектором. Не читаешь и не слышишь две величины? Вероятно, вы имеете дело со скаляром.

Векторы смещения

Летающие супергерои редко выбирают кратчайший путь от Дэйли Бьюгл или Дэйли Плэнет до катастрофы того дня. Они налетают, петляют, прыгают и перекатываются, прежде чем, наконец, прибывают в самый последний момент.

Если бы мы использовали векторы для определения курса летающего супергероя, нам потребовалось бы пять или шесть векторов, чтобы учесть все эти обходные пути. А вектор смещения  от начала до конца пересекает прямую линию:

Определение вектора смещения и пример

Смещение в этом значении исходит из физики, означая изменение положения по сравнению с начальным положением.

Вы суете правую руку; вы убираете правую руку: нулевое смещение. Ты ча-ча три шага влево и два шага вправо: Вектор смещения на один шаг влево.

На этом рисунке мы видим, что вектор смещения также является результирующим.

Расчет смещения по-прежнему вектор n + вектор v = r , потому что векторы a и y отрицают друг друга!

Вы можете подумать, что мы потратили много усилий, чтобы преодолеть такое небольшое расстояние, но что, если бы мы находились на корабле ВМФ и должны были бы перемещаться вокруг пристани или охраняемого заповедника? Тогда мы можем увидеть, что это действительно был кратчайший путь

Примеры векторов

Все эти измерения являются примерами векторов, поскольку все они включают расстояние или размер силы и направление:

• Velocity

• Force

• Acceleration

• Momentum

• Displacement

Commercial airliners, fighter jets, boats, cars, bicyclists, runners, falling objects, rockets, hot air воздушные шары, бумажные самолетики и подводные лодки — все это примеры движущихся объектов, использующих векторы в повседневной жизни.

Пилоты и штурманы должны использовать векторы, чтобы добраться до места назначения. Ученые-ракетчики и аэрокосмические инженеры используют векторы для управления ракетами.

Существует одно исключение для векторов, имеющих длину и направление, и это нулевой вектор. Нулевой вектор не имеет длины, поэтому он не указывает ни в каком конкретном направлении. Это означает, что нулевой вектор имеет неопределенное направление.

Основные векторные задачи

1. Что произойдет, если мы умножим вектор на 4 ? Надеемся, вы сказали, что он будет указывать в том же направлении, но будет в четыре раза длиннее!

2. Является ли «25 узлов к югу на юго-запад» скаляром или вектором? Это вектор, поскольку он дает величину и направление.

3. Что произойдет с вектором, если мы умножим его на −12-\frac{1}{2}−21​? Мы надеемся, вы сказали, что он будет вдвое короче и пойдет в противоположном направлении!

4. Два вектора параллельны, но направлены в противоположные стороны. Один вектор z . Какой другой вектор? Мы надеемся, что вы помните об отрицании векторов, назвав его -z

Векторы и матрицы

Марко Табога, доктор философии

Эта лекция представляет собой неформальное введение в матрицы и векторы.

Table of contents

1. Matrix

2. Dimension of a matrix

3. Entries of a matrix

4. Vectors

5. Scalars

6. Equal matrices

7. Zero matrices

8. Square matrices

9. Diagonal and off-diagonal elements

10. Identity matrix

11. Transpose of a matrix

12. Symmetric matrices

13. Solved exercises

    1. Упражнение 1

    2. Упражнение 2

    3. Упражнение 3

Матрица

Матрица — это двумерный массив с фиксированным числом строк и столбцов и содержит число на пересечении каждой строки и столбца.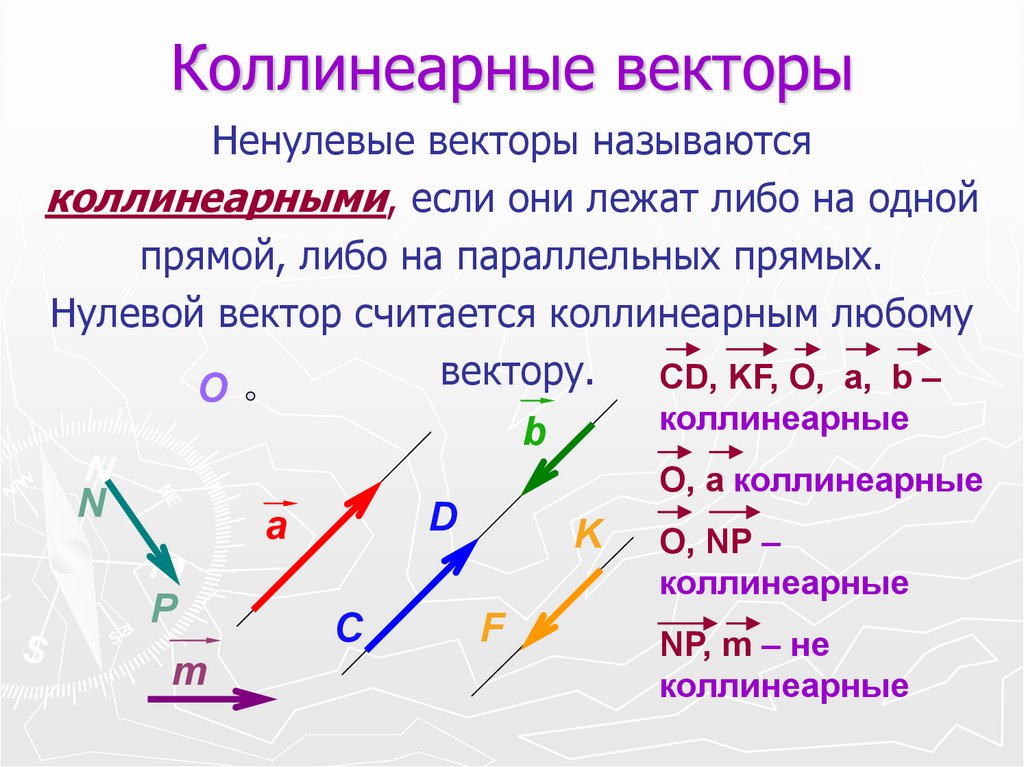

Матрица обычно ограничивается квадратными скобками.

Пример Вот пример матрицы с двумя строками и двумя столбцы:

Размерность матрицы

Если матрица имеет ряды и столбцы, мы говорим, что он имеет размерность , или что это матрица.

Пример матрица имеет ряды и столбцы. Итак, мы говорим, что это матрица.

Элементы матрицы

Числа, содержащиеся в матрице, называются элементами числа. матрица (или элементы, или компоненты).

Если является матрицей, запись на пересечении строки и колонка обычно обозначается (или ). Мы говорим, что это -й запись .

Пример Позволять быть матрица определяется как следует: элемент на пересечении третьей строки и первого столбца, т.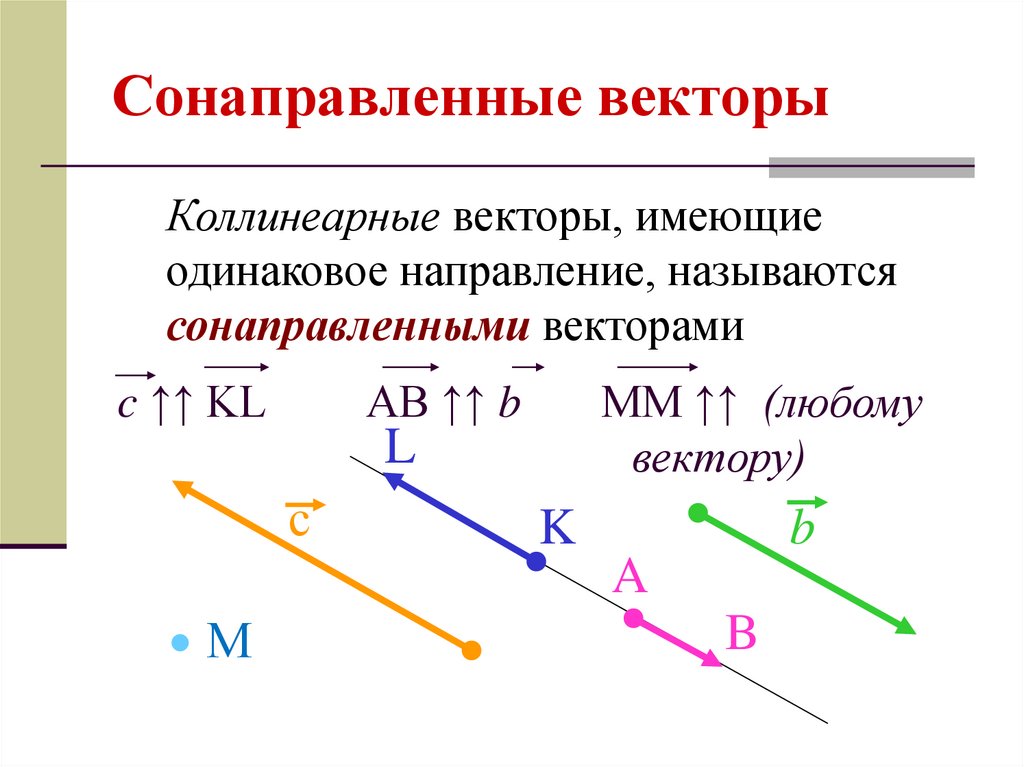 е. его -й вход

Векторы

Если матрица имеет только одну строку или только один столбец, она называется вектором.

Матрица, имеющая только одну строку, называется вектором-строкой .

Пример матрикс вектор-строку, потому что он имеет только одну строку.

Матрица, имеющая только один столбец, называется вектором-столбцом .

Пример матрикс вектор-столбец, потому что он имеет только один столбец.

Скаляры

Матрица, имеющая только одну строку и один столбец, называется скалярной.

Пример матрикс скаляр. Другими словами, скаляр — это одно число.

Равные матрицы

Равенство между матрицами определяется очевидным образом.

Два матрицы и имеют одинаковую размерность, называются равно тогда и только тогда, когда все их соответствующие элементы равны каждому другое:

Нулевые матрицы

Матрица является нулевой матрицей , если все ее элементы равны нулю, и мы пишем

Пример Если это матрица и , затем

Квадратные матрицы

А матрица называется квадратной матрицей , если количество его строк равно столько же, сколько и количество его столбцов, т.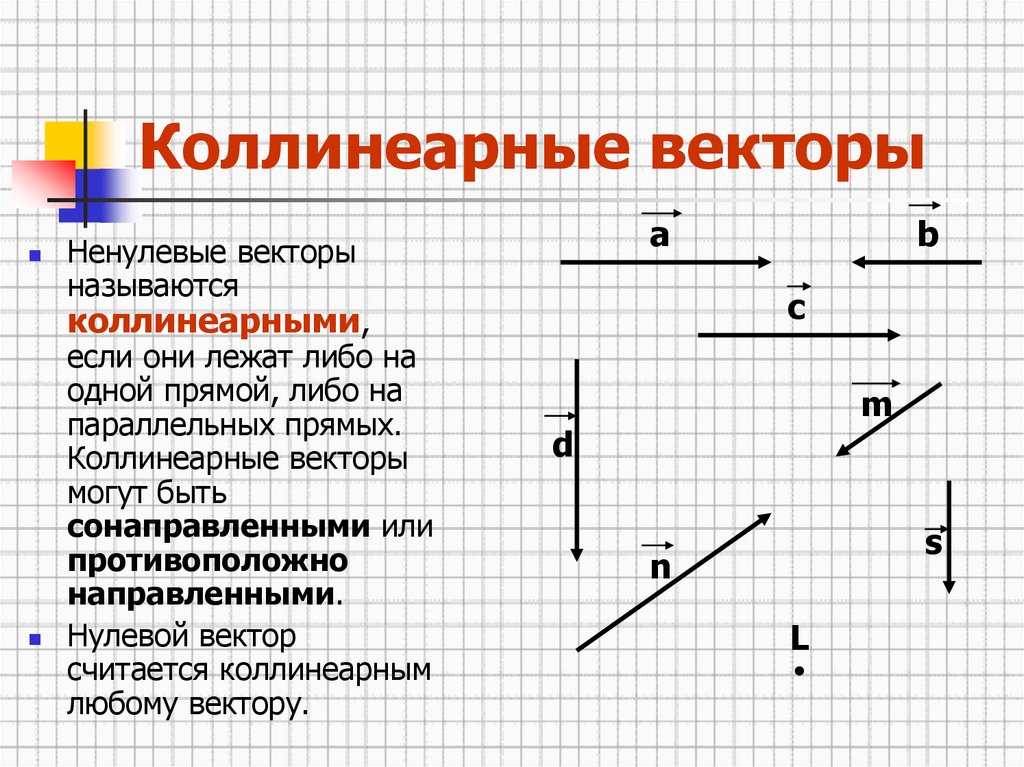

е. .

Пример матрикс квадратная матрица.

Пример матрикс квадратная матрица.

Диагональные и недиагональные элементы

Позволять быть квадратной матрицей.

Диагональ (или главная диагональ ) это набор всех записей такой, что .

Элементы, принадлежащие диагонали, называются диагональными элементами, и все остальные элементы называются недиагональными.

Пример Позволять быть матрица определена всем внедиагональные записи равны , а три диагональных элемента равны , , и , соответственно.

Идентификационная матрица

Квадратная матрица называется единичной матрицей , если все ее диагональные элементы равны и все его недиагональные элементы равны . Обычно обозначается буквой .

Пример матрикс в единичная матрица.

Транспонирование матрицы

Если это матрица, это транспонировать , обозначается , это матрица такая, что -й элемент равно -й элемент за Любые и удовлетворяющий и .

Другими словами, столбцы равны строкам (равнозначно ряды равны столбцам ).

Пример Позволять быть матрица определяется Его транспонировать следующее матрица:

Пример Позволять быть матрица определяется Его транспонировать следующее матрица:

Симметричные матрицы

Говорят, что квадратная матрица равна 9.0415 симметричный , если он равен его транспонировать.

Пример Позволять быть матрица определяется Его транспонировать следующее матрица: какая равно . Следовательно, симметричен.

Решенные упражнения

Ниже вы можете найти несколько упражнений с поясненными решениями.

Упражнение 1

Позволять быть матрица определена по

Найдите его транспонирование.

Решение

Транспонирование матрица такая, что ее столбцы равны строкам :

Упражнение 2

Позволять быть вектор-столбец определен по

Покажите, что его транспонирование является вектором-строкой.

Решение

Транспонирование матрица такая, что ее строки равны столбцам . Но имеет только один столбец, что означает, что имеет только одну строку. Следовательно, это ряд вектор:

Упражнение 3

Позволять быть матрица определена по

Является ли он симметричным?

Раствор

симметричен, если он равен своему транспонированному.