Решение задач по теме раздела. Продолжение 1 9 класс онлайн-подготовка на Ростелеком Лицей
Тема: Соотношения между сторонами и углами треугольника. Раздел 3. Скалярное произведение векторов
Урок: Решение задач по теме раздела. Продолжение 1
1. Тема урока, введение
Тема урока: «Решение задач по теме раздела. Продолжение 1». На этом уроке мы кратко повторим теорию и будем решать задачи с использованием метода координат.
2. Напоминание основных формул в координатной форме
Напомним, что вектор в координатной плоскости задается своими координатами. Координаты вектора – это коэффициенты разложения вектора по координатным векторам и .
Напомним основные формулы в координатной форме.
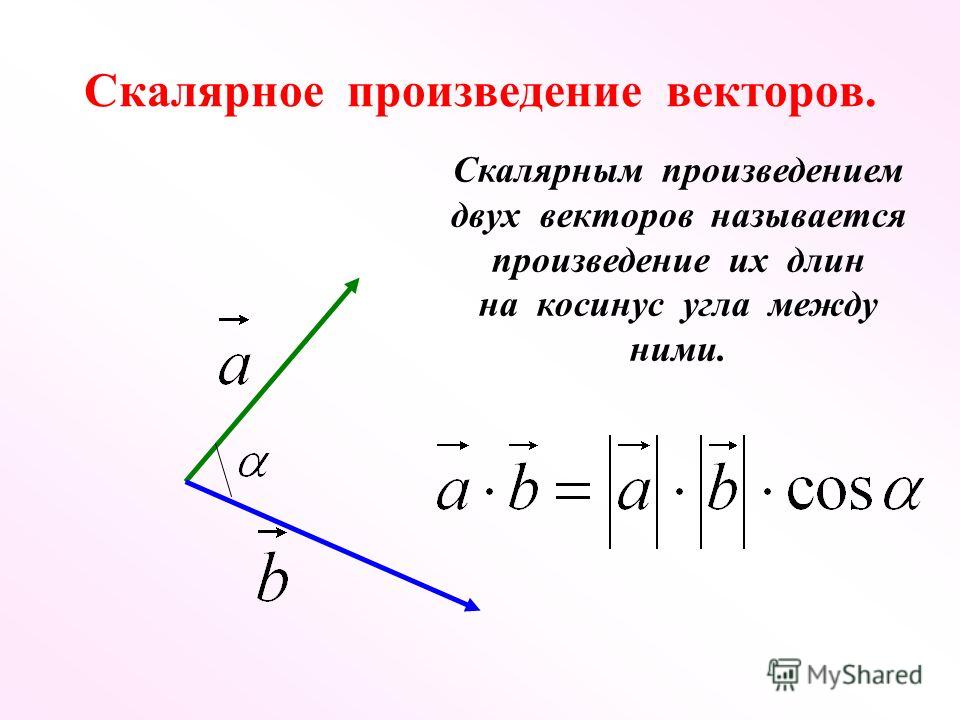
Скалярное произведение векторов:
;
Косинус угла между векторами:
Напомним, как найти координаты вектора через координаты его концов:
И напомним, что координаты середины отрезка определяются так:
Проекции вектора.
Проекция – это число, положительное или отрицательное в зависимости от знака .
3. Решение задач на скалярное произведение векторов методом координат
Рассмотрим решение задач координатным методом.
Задача. В треугольнике ABCAB=BC=AC=1, точки O, M, D – середины отрезков CB, CA, AO соответственно.
Найти:
1. длины отрезков BD и OM;
2.
3. проекцию вектора на вектор и проекцию вектора на вектор ;
4.
5. проекцию вектора на вектор и проекцию вектора на вектор .
Будем решать задачу методом координат.
1. Найти BD и OM.
Решение:
а) Для решения задачи координатным методом сначала на координатной плоскости требуется ввести систему координат.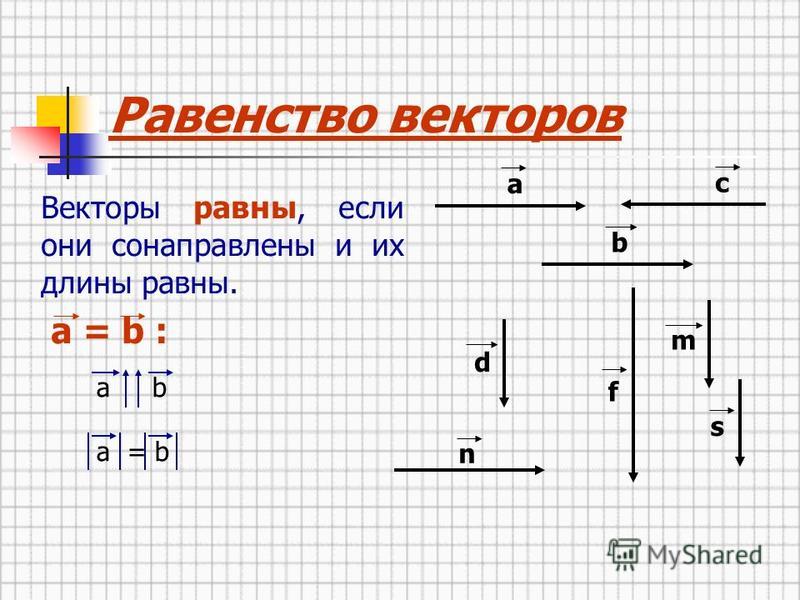 Введем систему координат, как показано на рисунке, тогда многие точки будут лежать на осях координат и, следовательно, иметь одну из координат, равную 0.
Введем систему координат, как показано на рисунке, тогда многие точки будут лежать на осях координат и, следовательно, иметь одну из координат, равную 0.
б) Найти координаты точек.
Найдем их из условия задачи с учетом выбранной системы координат.
в) Найти координаты векторов.
г) Найти длины векторов .
Ответ: Вернемся к длинам отрезков:
2. Дано:
Найти:
Решение:
Ответ:
3. Дано:
Найти:
а)
б)
Решение: Напомним, что
а)
б)
Ответ:
4. Дано:
Найти:
а)
б)
Решение:
а) ;
б)
Ответ:
а)
б)
5. Дано:
Найти:
а)
б)
Решение:
а)
б)
Ответ:
а)
б)
4.
 Заключение
Заключение
Итак, мы повторили теорию, напомнили основные формулы в координатах, решили ряд задач на скалярное произведение векторов с использованием метода координат. На следующем уроке мы продолжим решение задач по теме раздела.
Список литературы
- Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
- Фарков А. В. Тесты по геометрии: 9 класс. К учебнику Л. С. Атанасяна и др. – М.: Экзамен, 2010.
- Погорелов А. В. Геометрия. Уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- E-science.ru (Источник).
- Mathematics.ru (Источник).
Домашнее задание
- Атанасян Л. С. и др. Геометрия 7–9 классы. №№1050, 1051.
✅ Векторы
На данной онлайн странице электронного справочника по математике для школьников представлены следующие готовые домашние задания, решения тестовых заданий по геометрии 9 класса:
- – представлены определения вектора, скалярных и векторных величин;
- – в примерах с номерами 9 — 12 рассматривается, как решать геометрию по теме «Коллинеарные векторы»;
- – решения векторов представлены в теме «Разложение вектора по двум неколлинеарным векторам».
 Контрольные работы 13 — 15;
Контрольные работы 13 — 15; - – тема «Координаты вектора» объясняется в работах 16 — 22 учебника. В данной рабочей тетради показываются ответы к вопросам, как решать задачи, если требуется найти координаты суммы, разности векторов и произведения вектора на число;
- – задачи 1 — 8 показывают примеры решений и ответы по математике, изученных на материале курса геометрии 8 класса. Здесь рассматриваются тесты и задания по таким разделам, как средняя линия треугольника, параллелограмм, площадь треугольника, равнобедренная трапеция, вписанные и описанные окружности.
Понятие вектора
Автобус едет из города Анск в город Бинск. На карте город Анск обозначим латинской буквой A, город Бинск – буквой B латинского алфавита.
Соединив точки A и B, получаем отрезок AB. При этом точка A – начало отрезка или пункт отправления автобуса, т.е. откуда едет автобус, точка B – конец отрезка или пункт назначения автобуса, куда движется автобус.
При этом точка A – начало отрезка или пункт отправления автобуса, т.е. откуда едет автобус, точка B – конец отрезка или пункт назначения автобуса, куда движется автобус.
Отрезок AB изображает схему маршрута автобуса.
Направление движения автобуса, или направление маршрута, или направление отрезка AB обозначим стрелкой –>.
Выражение «A –> B» обозначает схематичное движение автобуса из пункта A в пункт B.
Отрезок со стрелкой – направленный отрезок.
Определение:
Вектор – направленный отрезок.
В математике принято обозначать вектор как , две латинские буквы со одной стрелкой сверху (произносится: вектор а-б.).
указывает на направление движения: A – начальная точка отрезка, B – конечная точка отрезка.
Часто вектор могут обозначать маленькой буквой (произносится: вектор а).
Когда A – начальная точка отрезка и B – конечная точка отрезка совпадают, то есть когда отрезок отсутствует, тогда вектор считается нулевым и обозначается как
, ноль со одной стрелкой сверху. Любая точка на карте, в тетради, на плоскости чертежной доски – нулевой вектор.
Любая точка на карте, в тетради, на плоскости чертежной доски – нулевой вектор.
Длина отрезка AB, расстояние между городом Анск и Бинск, – абсолютная величина вектора , или модуль вектора
, или длина вектора .
Модуль вектора обозначается как .
Например, дано = 1,7 км,
= 6 км. В этом случае говорят, что длина вектора а равна 1,7 км (одна целая семь десятых километра), длина вектора AB равна шести километрам.
Длина нулевого вектора обозначается как
и равна нулю:
= 0.
Скалярные и векторные величины
Величина может быть скалярной или векторной.
Величина является скалярной, если содержит численное значение, но не указывает на направление. Например, 5 книг, 10 метров ткани, где цифры «5», «10» – скалярные величины.
Векторная величина или вектор – величина, которая содержит количественное значение и указывает на направление.
Например, автобус едет или совершает перемещение из пункт A в пункт B со скоростью 30 км/ч.
Цифра «30» – скорость автобуса в км/ч – пример векторной величины, так как дано численное значение и указывается направление движения.
Перемещение точки, которая движется в данный момент времени, – вектор с начальной точкой в точке старта движения и с конечной точкой в точке, где данная точка находится в это время.
Например, AB = 5 км, BC = 5 км, CD = 3 км, DE = 2 км, AE = 4 км.
Длина маршрута движения автобуса из пункта A в пункт E составляет
L = AB + BC + CD + DE = 15 км.
Длина маршрута – скалярная величина, так как дано только количество километров – «15» без указания на направление движения.
Перемещение – вектор
, который соединяет A – точку начала движения автобуса, E – точку остановки движения.
AE = 4 км. Перемещение – векторная величина, где число «4» – количество километров, АЕ – указывает на направление движения, из пункта Анск в пункт Eнск.
Допустим, автобус проехал 30 км: в одну сторону, из Анска в Енск – 15 км, а также обратно, из Енска в Анск – 15 км. В этом примере перемещение равно 0 км и является нулевым вектором.
В этом примере перемещение равно 0 км и является нулевым вектором.
Коллинеарные векторы
Лемма – теорема, вспомогательная для доказательства следующей теоремы.
Лемма о коллинеарных векторах:
Если векторы и коллинеарны (где ), то можно найти такое число k, что верно равенство (вектор равен произведению числа k на вектор )
Дано: вектор a, вектор b
Векторы и – коллинеарные, т.е. вектор b коллинеарен вектору a
Доказать: есть такое число k, что верно равенство
Доказательство:
1 случай.Пусть векторы a и b — сонаправленные векторы, т.е.
.
, где k>0,т.к. . Тогда и сонаправленные векторы.
Значит,
***
2 случай.
Пусть a, b — противоположные векторы, т.е.
Возьмем , где k<0
Следовательно,
***
Задача 9.
Дано:
вектор m, вектор n
1) – противоположно направленные векторы ,
= 0,5 см, = 2 см
2) – сонаправленные векторы ,
= 12 см, = 240 см
Найти: k – ?
Решение: 1) Т.к. , то k<0. Тогда
= – = – 4
Ответ: k = – 4.
Решение: 2) Т.к. , то k>0. Тогда = = 20.
Ответ: k = 20.
***
Задача 10.
Дано:
ABCD – параллелограмм
BD AC = O
M – середина отрезка AO
1)
2)
Найти: k – ?
Решение:
1) Т.к. , то k>0.
По свойству параллелограмма
, тогда
Ответ: k=
2) Т.к. , то k<0. , – коллинеарные, т.к. лежат на одной прямой. Найдем середину OC и обозначим ее точкой N.
Тогда AM=MO=ON=NC
Т.к. k<0, то
Ответ: k=
***
Задача 11.
Дано:
1) – противоположно направленные векторы,
= 400 мм, = 4дм = 400мм
2) – сонаправленные векторы , = , =
Найти: k – ?
Решение: 1) Т. к. , то k<0. Тогда
к. , то k<0. Тогда
= – = –1
Ответ: k = –1.
Решение: 2) Т.к. , то k>0. Тогда = = =5.
Ответ: k = 5.
***
Задача 12.
Решить уравнение: найти значения x, y.
Решение: 1)
y=3
Ответ: x=0, y=3
***
Решить уравнение: найти значения x, y.
Решение: 2)
–3y = –1 , x= –1
y =
Ответ: x= – 1, y=
***
Разложение вектора по двум неколлинеарным векторам
Определение: Если , где и – данные векторы, x и y – некоторые числа, то говорят, что вектор разложен на векторы и , причем x и y – коэффициенты разложения
Выразить вектор:
через векторы и
через и
через и
через и
Решение:
а) По правилу параллелограмма (x= 1, y= 1)
б) , (x=y= 2)
в) = + , = 2 – (x= 2, y = –1)
г) Т. к. = 2 – = 2 +
к. = 2 – = 2 +
= – 2(x= 1, y = –2)
***
Задача 13.
Дано: ABCD – параллелограмм
;
M; AM : MC = 4 : 1
Найти:
Решение:
По правилу параллелограмма
или
Но , тогда
Ответ:
***
Задача 14.
Дано: векторы и – неколлинеарные
а)
б)
Найти: коэффициенты разложения x, y – ?
Решение:
а)
3 – y = 0, x+1=0 y= 3, x= – 1
б)
4 – x = 0, 5+y=0 x = 4, y= –5
Ответ: a) x= –1, y= 3 б) x = 4, y= –5
***
Задача 15.
Дано: ABCD – трапеция
EF – средняя линия трапеции
Доказать: EFAD — т.е. средняя линия трапеции параллельна её основанию,
— т.е. длина средней линии трапеции равна полусумме основанию трапеции.
Доказательство:
По правилу многоугольника
+
Сложив оба выражения, получаем
Т. к. E и F – середины сторон AB и CD, тогда
к. E и F – середины сторон AB и CD, тогда
Т.к. , то , а
Поэтому EF || AD и
***
Теорема: Любой вектор можно разложить по двум неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.
Дано:
вектор a, вектор b
и – неколлинеарные векторы
Доказать:
Доказательство:
Через точку А и точку В проведем прямые, параллельные прямым, содержащих векторы и . Найдем точку С.
Тогда по правилу треугольника
Заметим, что векторы и – коллинеарные, также векторы и – коллинеарные
По лемме о коллинеарных векторах
,
Тогда
Единственность разложения
Доказательство:
Знаем, что (1)
Пусть есть (2)
В результате разности выражений (1) и (2) получаем
Это равенство возможно
;
Т.е ;
***
Координаты вектора
Определение: Единичным вектором называется вектор, длина которого равна единице.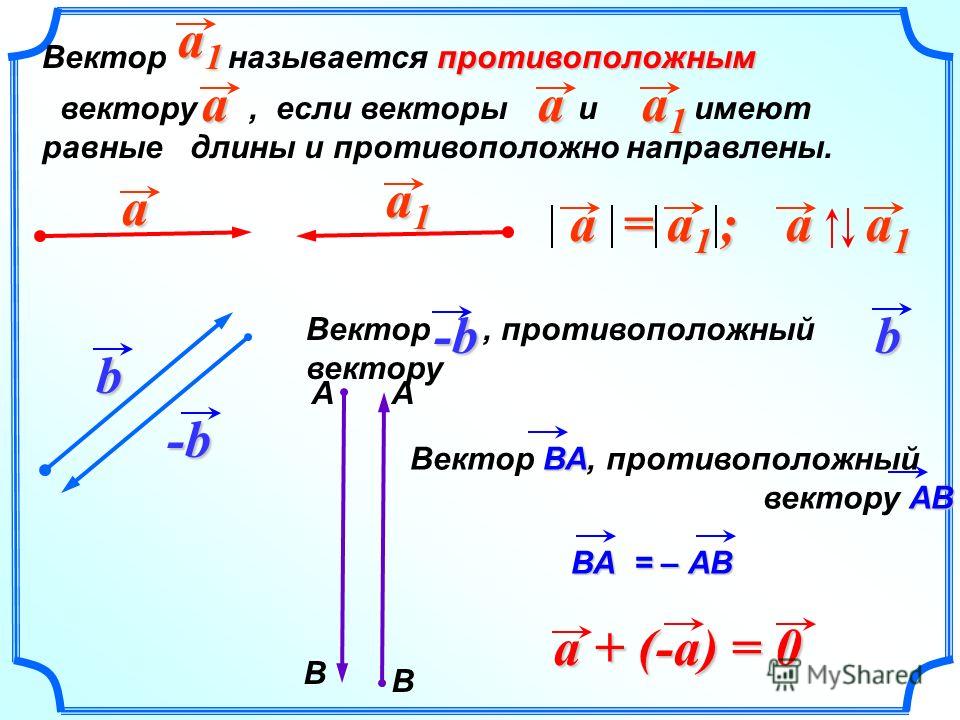
i и j – координатные векторы
Т.к. и – неколлинеарные векторы, то любой вектор можно разложить через векторы и .
Т.е. , где x и y – координаты вектора.
{1:2}
{2:–3}
{0;0}
Если и ,
то , если и
***
Задача 16.
Найти координаты векторов.
Решение:
{2;3}
{–2;3}
{2;0}
{–3;–4}
{2;–2}
{–4;–5}
***
Задача 17.
Найти координаты векторов.
Решение:
{2;3}
{–;–2}
{8;0}
{1;–1}
{0;–2}
{–1;0}
***
Задача 18.
Найти сумму вектора по его координатам.
Решение:
{–3;}
{–2;–3}
{–1;0}
{0;3}
{0;1}
***
Правила, позволяющие по координатам векторов находить координаты суммы, разности векторов и произведения вектора на число.
1. Суммой векторов и с координатами (a1;a2) и (b1;b2) называется вектор с координатами (a1+ b1;a2 +b2).
Дано:
{a1;a2}; {b1;b2};
Доказать: { a1+ b1;a2 +b2}
— сумма координат вектора, т.е. формула, как найти координаты вектора через сложение
Доказательство:
{ a1+ b1;a2 +b2}
***
Пример 1 — сложение векторов, как найти координаты векторов:
Если даны координаты векторов {3;2}; {2;5}, то
2. Разностью векторов и с координатами {a1; a2} и {b1; b2} называется вектор с координатами {a1 – b1; a2 – b2}.
3. Произведением вектора с координатами {a1; a2} на произвольное число k называется вектор с координатами {ka1; ka2}.
Дано:
{a1;a2}
k – произвольное число
Доказать: {ka1; ka2}
— умножение вектора на число
Доказательство:
Значит, вектор {ka1; ka2}
Пример 2 — как находить координаты вектора:
Найти координаты вектора , если
{1;2}; {0;3}; {–2;3}
Решение:
{0;6}
{0;6}
Ответ: {0;6}
***
Задача 19.
Найти координаты вектора , если даны векторы
{–7;–1}; {–1;7}; {4;–6}
Решение:
= {–21;–14}
Ответ: {–21;–14}
***
Задача 20.
Дано:
1)
2)
Найти: коэффициенты разложения x, y – ?
Решение:
1)
По теореме о разложении вектора по двум неколлинеарным векторам:
x=–3, y=7
2)
По теореме о разложении вектора по двум неколлинеарным векторам:
x= –4, y=0
***
Задача 21.
Дано: координаты векторов
1) {3;6}; {4;–3}
2) {–5;–6}; {2;–4}
Найти: разность векторов –
Решение:
1) –= = {–1;9}
–{–1;9}
2) –= ={–7;–2}
–{–7;–2}
***
Задача 22.
Дано: координаты векторов
{–2;–3}; {2;–3}; {0;5}
Найти: координаты векторов, противоположных данным.
Решение:
{–2;–3}{2;3}
{2;–3}{–2;3}
{0;5}{0;–5}
***
Задача 1.
Дано:
Четырехугольник ABCD
M, N, K, E – середины сторон AB, BC, DC, AD
Доказать:
Четырехугольник MNKE – параллелограмм
Доказательство:
Соединим точку А и точку С.
Получим треугольник Δ ABC, где MN – средняя линия треугольника Δ ABC и треугольник Δ ADC, где EK – средняя линия треугольника Δ ADC.
По свойству средней линии треугольника Δ следует, что
MN || AC – параллельны и MN= AC,
EK || AC – параллельны и EK= AC.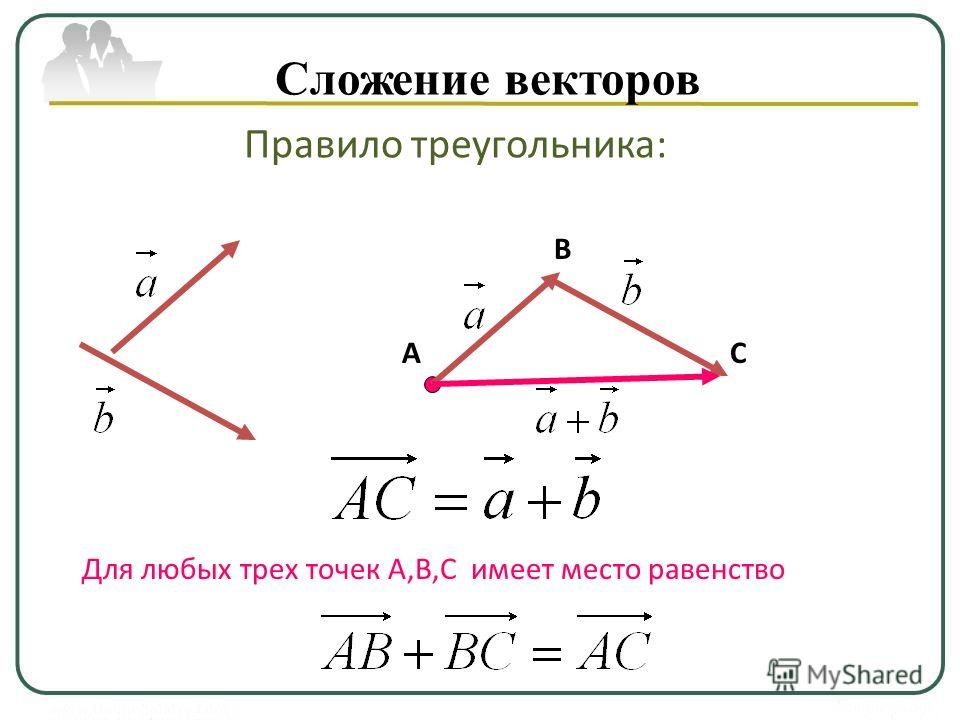
Тогда MN || EK – параллельны и MN=EK, поэтому
MNKE – параллелограмм (по первому признаку параллелограмма).
***
Задача 2.
Дано:
Треугольник Δ ABC
Сторона треугольника AB = 8,5 см
Сторона треугольника AC = 5 см
Высота AH = 4 см, т.е отрезок AH перпендикулярен стороне BC
HBC, т.е. точка H лежит на стороне BC
Найти:
Площадь треугольника S ΔABC – ?
Решение:
S ΔABC = BC • AH
По теореме Пифагора
BH = = = = 7,5 см
По теореме Пифагора
CH = = = 3 см
BC = BH + CH = 3 +7,5 = 10,5 см
S ΔABC = • 10,5 • 4 = 21
Ответ: S ΔABC = 21
***
Задача 3.
Доказать, что отрезки, соединяющие середины противоположных сторон равнобедренной трапеции, взаимно перпендикулярны.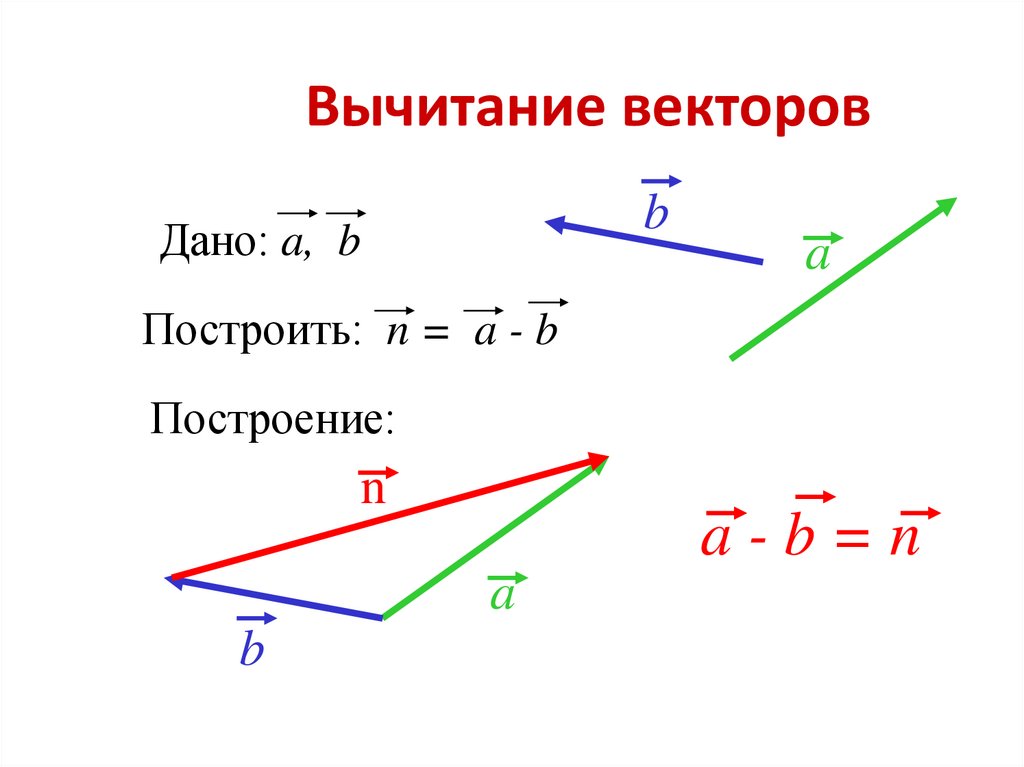
Дано:
ABCD – равнобедренная трапеция
Доказать: NE KM =
Доказательство:
Проведем перпендикуляры BH и CH1, то есть BHAD перпендикулярны; также CH1AD перпендикулярны.
Но BH и CH1 проходят через NE тогда перпендикулярны BRNE и CR1NE.
Стороны BH = CH1 равны параллельны BH || CH1
Поэтому BH = KM = CH1 равны параллельны BH KM CH1 как отрезок, заключенный между параллельными прямыми.
Следовательно углы равны KON = NR1C = 90° как соответственные.
ТогдаKON = EOM = 90°, как вертикальные.
***
Задача 4.
Дано:
AB – отрезок
AC = CB
O – произвольная точка
Доказать:
Вектор OC равен половине суммы двух других векторов OA и OB, исходящих из одной и той же точки O
Доказательство: По правилу треугольника
(1)
+
(2)
Сложив выражения (1) и (2), получаем
***
Задача 5.
Дано:
векторы a, b, c
Три вектора и – неколлинеарные векторы.
Построить:
Суммы и разности векторов.
Построение:
По правилу многоугольника
a)
б)
=
***
Задача 6.
Доказать, что отрезки, соединяющие середины противоположных сторон равнобедренной трапеции, взаимно перпендикулярны.
Дано:
четырехугольник ABCD – равнобедренная трапеция
Доказать: EF NM = , т.е. угол пересечения двух отрезков в равнобедренной трапеции равен 90°.
Доказательство:
Проведем параллельные прямые
MK || AB
MR || CD
Получим равнобедренный треугольник ΔMKR
AB=MK, так как трапеция равнобедренная,
CD=MR, т.к. трапеция равнобедренная.
Следовательно, EF – средняя линия треугольника ΔMKR, поэтому
MH=HR и OK=MO.
BM=MC=AK=RD, т.к. ABMK и MCDR – параллелограммы.
Поэтому HR=KO.
Тогда MN – медиана, биссектриса и высота равнобедренного треугольника ΔMKR.
Т.к. MN – высота, то отрезки MNAD – перпендикулярны.
По свойству средней линии треугольника Δ следует, что
EF || KR.
Тогда EF NM =
***
Задача 7.
Доказать, что центр окружности, вписанной в равнобедренный треугольник, лежит на медиане, проведенной к основанию.
Дано:
вписанная окружность в равнобедренном треугольнике
ΔABC – равнобедренный треугольник
BH2 – медиана
Доказать: O BH2, т.е. центр вписанной окружности лежит на медиане равнобедренного треугольника
Доказательство:
Проведем перпендикуляры OH1 ; OH2 ; OH3 к сторонам BC, AC, AB.
Здесь из двух точек проведен один и тот же перпендикуляр к стороне AC, но в треугольнике можно провести только один перпендикуляр к стороне и только из одной точки.
Следовательно, что O BH2
***
Задача 8.
Доказать, что центр окружности, описанной около равнобедренного треугольника, лежит на медиане, проведенной к основанию или на ее продолжение.
Дано:
Описанная окружность около равнобедренного треугольника
Δ ABC – вписанный равнобедренный треугольник
BH3 – медиана
Доказать: O BH3
Доказательство:
Проведем из центра окружности перпендикуляры
OH1 ; OH2 ; OH3 к сторонам BC, AC, AB.
Здесь проведен из двух точек перпендикуляр к стороне AC, но в треугольнике можно провести только один перпендикуляр к стороне и только из одной точки.
Следовательно, что O BH3
***
Векторные уравнения – Объяснение и примеры
В векторной геометрии одной из самых важных концепций при решении реальных задач является использование векторных уравнений. Векторное уравнение определяется как:
Векторное уравнение определяется как:
«Векторное уравнение — это уравнение векторов, решение которого дает результат в виде вектора».
В этом разделе мы кратко обсудим следующие упомянутые понятия:
- Что такое векторное уравнение?
- Как решить векторное уравнение?
- Что такое векторное уравнение прямой?
- Что такое векторное уравнение окружности?
- Примеры
- Задачи
Что такое векторное уравнение?
Векторное уравнение — это уравнение, содержащее n векторов. Более формально его можно определить как уравнение, включающее линейную комбинацию векторов с возможными неизвестными коэффициентами, и при решении оно возвращает вектор.
Обычно векторное уравнение определяется как «любая функция, которая принимает одну или несколько переменных и взамен дает вектор».
Любое векторное уравнение, включающее векторы с n числом координат, похоже на систему линейных уравнений с n числом координат, включающую числа. Например,
Например,
Рассмотрим векторное уравнение:
r <4,5,6> + t<3,4,1> = <8,5,9>
Его также можно записать как
<4r,5r,6r> + <3t,4t,1t> =<8,5,9>
Или
<4r+3t, 5r+4t, 6r+1t> = <8,5,9 >
Чтобы два вектора были равны, все координаты должны быть равны, поэтому его также можно записать в виде системы линейных уравнений. Такое представление имеет следующий вид:
4r+3t = 8
5r+4t = 5
6r+1t = 9
Итак, векторное уравнение можно решить, преобразовав его в систему линейных уравнений. Следовательно, это упрощается и становится легче решать.
В нашей повседневной жизни переносчики играют жизненно важную роль. Большинство используемых физических величин являются векторными величинами. Векторы имеют много реальных применений, включая ситуации, обозначенные силой и скоростью. Например, если автомобиль движется по дороге, на него будут действовать различные силы. Некоторые силы действуют в прямом направлении, а некоторые в обратном направлении, чтобы уравновесить систему. Итак, все эти силы являются векторными величинами. Мы используем векторные уравнения для нахождения различных физических величин в 2D или 3D, таких как скорость, ускорение, импульс и т. д.
Итак, все эти силы являются векторными величинами. Мы используем векторные уравнения для нахождения различных физических величин в 2D или 3D, таких как скорость, ускорение, импульс и т. д.
Векторные уравнения дают нам разнообразный и более геометрический способ рассмотрения и решения линейной системы уравнений.
В целом, мы можем заключить, что векторное уравнение имеет вид:
x1.t1+x2.t2+···+xk.tk = b
x 1,x 2,…,xk — неизвестные скаляры, имеет то же множество решений, что и линейная система с расширенной матрицей данного уравнения.
Таким образом, векторное уравнение записывается как
r = r 0 +k v
Давайте разберемся с этой концепцией на примерах.
Пример 1
Автомобиль движется с постоянной скоростью по прямой дороге. Первоначально в момент времени t=2 вектор положения автомобиля равен (1,3,5), затем через некоторое время в момент времени t=4 вектор положения описывается как (5,6,8). Запишите векторное уравнение положения объекта. Кроме того, выразить его в виде параметрических уравнений.
Запишите векторное уравнение положения объекта. Кроме того, выразить его в виде параметрических уравнений.
Решение
С момента уравнения вектора прямой линии дано
R = R 0 +T V
С
R 0 = <1,3,5. >
r = <5,6,8>
<5,6,8> = <1,3,5> + 4 v
<5,6,8> – <1,3 ,5> = 4 v
<4,3,3> = 4 v
v = <1,3/4,3/4>
Теперь, нахождение векторного уравнения положения объекта 4>
где вектор r равен
Выражение в форма параметрического уравнения:
Поскольку два вектора эквивалентны, только если их координаты равны. Итак, из-за равенства мы можем написать как,
x = 1+t
y = 3+3/4t
z = 5+3/4t
Векторное уравнение линий определяет вектор положения линии относительно вектора начала координат и направления, и мы можем найти из размеров векторов, соответствующих любой длине. Это работает для прямых линий и кривых.
Это работает для прямых линий и кривых.
Примечание: Вектор положения используется для описания положения вектора. Это прямая линия, один конец которой зафиксирован, а другой прикреплен к движущемуся вектору, чтобы указать его положение.
Давайте разберемся с этой концепцией на примерах.
Пример 2
Запишите следующие уравнения как векторные уравнения сначала рассмотрим уравнение 1:
x = -2y+7
Поскольку приведенное выше уравнение является уравнением прямой:
y = mx+c
Сначала выберем две точки на заданной линия.
Упростим уравнение,
x = -2y+7
пусть y = 0
x = 7
Итак, первая точка s (7,0) или OS (7,0)
Теперь найдем вторую точку, которая находится на полпути через первую точку, тогда
Пусть x = 14
14 = -2y + 7
-2y = 7
y = -3,5
Итак, вторая точка Т (14, -3,5) или ОТ (14, -3,5)
Затем,
ОС – ОТ = (7,0) – (14, -3,5)
OS – OT = (-7, 3,5)
Итак, форма векторного уравнения приведенного выше уравнения:
R = <7,0> + k<-7,3,5>
R = <7-7k, 3. 5k>
5k>
Теперь решим уравнение 2:
3x = -8y+6
приведенное выше уравнение является уравнением прямой
y = mx+c
Сначала выберем две точки на данной прямой. 9Упростим уравнение
Теперь давайте найдем вторую точку, которая находится на полпути через первую точку, тогда
Пусть x = 4
12 = -2y+7
-2y = 12-7
y = -5/2
Итак , вторая точка Т (4, -5/2) или ОТ (4, -5/2)
Затем,
ОС – ОТ = (2,0) – (4, -5/2)
OS – OT = (-2, 5/2)
Итак, форма векторного уравнения приведенного выше уравнения:
R = <2,0> + k<-2,5/2>
R = <2-2k, 5/2k>
Теперь составим уравнение 3:
x = -3 /5-8
Поскольку приведенное выше уравнение является уравнением прямой
y = mx+c
Сначала выберем две точки на данной прямой.
Упростим уравнение,
x = -3/5y+8
пусть y = 0
x = 8
Итак, первая точка равна s (8,0) или OS (8,0 )
Теперь найдем вторую точку, которая находится на полпути через первую точку, тогда
Пусть x=16
16 = -3/5y+8
-3/5y = 16-8
y = — 13. 33
33
Итак, вторая точка Т (16, -13,33) или ОТ (16, -13,33)
Затем,
ОС – OT = (8,0) – (16, -13,33)
OS – OT = (-8, 13,33)
Итак, форма векторного уравнения приведенного выше уравнения:
R = <8,0> + k<-8,13,33>
R = <8-8k, 13,33k>
Векторное уравнение прямой линииВсе мы знакомы с уравнением линия, имеющая y=mx+c, обычно называемая формой пересечения наклона, где m — наклон линии, а x и y — координаты точки или точки пересечения, определенные на осях x и y. Однако этой формы уравнения недостаточно, чтобы полностью объяснить геометрические особенности линии. Вот почему мы используем векторное уравнение, чтобы полностью описать положение и направление линии.
Для нахождения точек на прямой воспользуемся методом сложения векторов. Нам нужно найти вектор положения и вектор направления. Для вектора положения мы добавим вектор положения известной точки на прямой к вектору v , лежащему на прямой, как показано на рисунке ниже.
Итак, вектор положения r для любой точки задается как r = op + v
Тогда векторное уравнение задается как
R = op + k v
Где k — скалярная величина, принадлежащая RN, op — вектор положения относительно начала координат O, а v — вектор направления. По сути, k говорит вам, сколько раз вы пройдете расстояние от p до q в указанном направлении. Может быть и ½, если будет пройдена половина дистанции и так далее.
Если известны две точки на прямой, мы можем найти векторное уравнение прямой. Точно так же, если мы знаем векторы положения двух точек op и oq на линии, мы также можем определить векторное уравнение линии, используя метод векторного вычитания.
Где,
V = OP — OQ
Следовательно, уравнение вектора приведено,
R = OP +K V
LETSO SOLVE некоторые примеры на некоторые примеры к некоторым примерам на некоторые примеры на некоторые примеры к некоторым примерам на некоторые примеры к некоторым примерам на некоторые примеры к некоторым примерам. понять это понятие.
понять это понятие.
Пример 3
Запишите векторное уравнение прямой через точки P (2,4,3) и Q (5, -2,6).
Решение
Пусть вектор положения заданных точек P и Q относительно начала координат задан как OP и OQ, соответственно.
ОП = (2,4,3) – (0,0,0)
ОП = (2,4,3)
ОК = (5, -2,6) – ( 0,0,0)
OQ = (5, -2 ,6)
Поскольку мы знаем, что векторное уравнение прямой определяется как
R = OP + k v
Где v = OQ – OP
v = (5, -2,6) – (2,4,3)
= 3 (3, ) )
Итак, векторное уравнение прямой имеет вид уравнение прямой, где k=0,75. Если точки, указанные на линии, определены как A (1,7) и B (8,6).
Решение:
k — это шкала, которая может варьироваться от -∞ до +∞. В этом случае k принимается равным 0,75, что представляет собой расстояние, пройденное на AB в заданном направлении.
Пусть вектор положения заданных точек A и B относительно начала координат равен OA и OB, соответственно.
ОА = (1,7) – (0,0)
ОА = (1,7)
ОВ = (8,6) – (0,0)
4 0 9 ОБ = (8,6)
Поскольку мы знаем, что векторное уравнение линии определяется как
R = OA +K V
, где V = OB — OA
V = (8,6) — (1,7)
V = (8,6) — (1,7)
V = (7, -1)
Таким образом, векторное уравнение прямой имеет вид Пример 5
Запишите векторное уравнение прямой через точки P (-8,5) и Q (9,3).
Решение
Пусть вектор положения данных точек P и Q относительно начала координат задан как OP и OQ, соответственно.
ОП = (-8,5) – (0,0)
ОП = (-8,5)
ОК = (9,3) – (0,0)
3 OQ
= (9,3)Поскольку мы знаем, что векторное уравнение прямой определяется как
R = OP + k v
Где v = OQ – OP
v = (9,3) – (-8,5)
v = (17, -2)
5 Итак, уравнение
R = <-8,5> + k<17, -2>
Векторное уравнение окружности Ранее мы обсуждали векторное уравнение прямая линия. 2 = 25 92 = 25
2 = 25 92 = 25
Пример 6
Определите, лежит ли точка (2,5) на окружности с векторным уравнением окружности, заданным как | р —<-6,2>| = 3.
Решение
Нужно выяснить, лежит ли заданная точка внутри окружности или нет при заданном векторном уравнении окружности.
С подстановкой значения точки в заданное векторное уравнение
= |<2,5>—<-6,2>|
= |<2+6,5-2>|
= |<8,3>| 92)
= √ (64+9)
= √ (73) ≠ 3
Следовательно, точка не лежит внутри круга.
Практические задачи- Запишите следующие уравнения в виде векторных уравнений: x=3y+5 x=-9/5y+3 x+9y=4 (3,4,5) и Б (8,6,7). Найдите вектор положения точки, находящейся посередине между двумя точками.
- Напишите векторное уравнение прямой, параллельной вектору Q и прохождение через точку o с заданным вектором положения P . Запишите векторное уравнение прямой через точки P(-8/3,5) и Q(5,10).

- Автомобиль движется с постоянной скоростью по прямой дороге. Первоначально в момент времени t=2 вектор положения автомобиля равен (1/2,8), затем через некоторое время в момент t=4 вектор положения автомобиля описывается как ( 5,10). Запишите векторное уравнение положения объекта. Кроме того, выразить его в виде параметрических уравнений.
- Запишите векторное уравнение и декартово уравнение окружности с центром c в точке (8,0) и радиусом 7м.
- Определите, лежит ли точка (3,-5) на окружности с векторным уравнением окружности, заданным как | р —<-3,4>| = 4.
- (i) . r = <5 – 5k , (-5/3)k (ii) . r = <3 – 3k, (15/9)k > (iii) . r = <4 – 4k, (4/9)k >
- r = <11/2 , 5, 6 >
- (i) . r = <3, -1> + t<-2, 6> (ii) . r = <9, -3> + t<1, 8>
- R = <-8/3, 5> + k<23/3, 5>
- r = <5, 10 > +t <-9/8, -1/2> и x = 5 – (9/8)t , y = 10 – (1/2)t
- |r – <8, 0>| = 7 и (x – 8)2 + y2 =49
- НЕТ.

Все векторные диаграммы построены с использованием GeoGebra.
Предыдущий урок | Главная страница | Следующий урокКак найти величину и направление вектора
: Стивен Холцнер и
Обновлен: 10-29-2021
Из книги: .
Рабочая тетрадь по физике I для чайников с онлайн-практикой
Например, взгляните на вектор на изображении.
Предположим, вам известны координаты конца вектора и вы хотите найти его величину v и угол тета. Благодаря вашим познаниям в тригонометрии вы знаете
Где тангенс тета — тангенс угла. Это означает, что
Это означает, что
тета = тангенс –1 ( y / x )Предположим, что координаты вектора равны (3, 4). Вы можете найти угол тета как загар
Вы можете использовать теорему Пифагора, чтобы найти гипотенузу — величину, v — треугольника, образованного x, y, и v:
Подставьте числа для этого примера, чтобы получить
Итак, если у вас есть вектор, заданный координатами (3, 4), его величина равна 5, а его угол равен 53 градусам.
Пример вопроса
Преобразование вектора, заданного координатами (1.0, 5.0), в формат величина/угол.
Правильный ответ: звездная величина 5,1, угол 79 градусов.
Примените теорему Пифагора, чтобы найти величину. Подставьте числа, чтобы получить 5.1.
Примените уравнение theta= tan –1 ( y / x ), чтобы найти угол.
 Подставьте числа, чтобы получить тангенс –1 (5,0/1,0) = 79 градусов.
Подставьте числа, чтобы получить тангенс –1 (5,0/1,0) = 79 градусов.
Практические вопросы
Преобразование вектора (5.0, 7.0) в форму величины/угла.
Преобразование вектора (13.0, 13.0) в форму величины/угла.
Преобразование вектора (–1,0, 1,0) в форму величины/угла.
Преобразование вектора (–5,0, –7,0) в форму величины/угла.
Величина 8,6, угол 54 градуса
Применить уравнение
, чтобы найти звездную величину, которая равна 8,6.
Примените уравнение theta = tan –1 ( y / x ), чтобы найти угол: tan –1 (7,0/5,0) = 54 градуса.
Магнитуда 18,4, угол 45 градусов
Применить уравнение
, чтобы найти звездную величину, которая равна 18,4.

Примените уравнение theta = tan
Величина 1,4, угол 135 градусов
Применить уравнение
, чтобы найти звездную величину, которая равна 1,4.
Примените уравнение theta = tan –1 ( y / x ), чтобы найти угол: tan –1 (1,0/–1,0) = –45 градусов.
Однако обратите внимание, что угол действительно должен быть между 90 и 180 градусами, потому что первая составляющая вектора отрицательна, а вторая положительна. Это означает, что вы должны добавить 180 градусов к –45 градусам, что даст вам 135 градусов (тангенс 135 градусов также равен 1,0/–1,0 = –1,0).
Величина 8,6, угол 234 градуса
Применить уравнение
, чтобы найти звездную величину, которая равна 8,6.
Примените уравнение theta = tan–1(y/x), чтобы найти угол: tan–1(–7,0/–5,0) = 54 градуса.



 Контрольные работы 13 — 15;
Контрольные работы 13 — 15;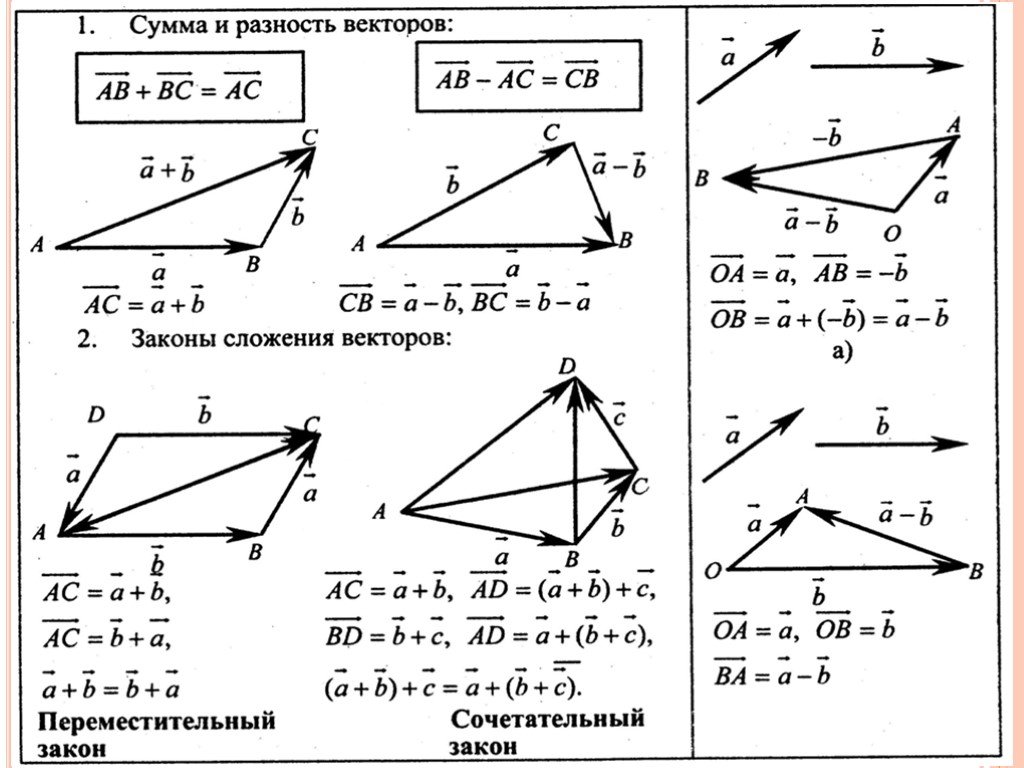

 Подставьте числа, чтобы получить тангенс –1 (5,0/1,0) = 79 градусов.
Подставьте числа, чтобы получить тангенс –1 (5,0/1,0) = 79 градусов.
