Векторы: третий уровень сложности
Для большинства людей искусственный интеллект — это нечто сложное и таинственное. А для математиков это синоним фразы «перемножение матриц». С точки зрения человека, который владеет линейной алгеброй, в искусственном интеллекте нет ничего загадочного.
Мы хотим, чтобы вы тоже смогли понять искусственный интеллект на уровне математики. Для этого у нас идёт цикл статей про линейную алгебру:
Сама тема несложная, но конкретно этот шаг вам ничего не даст в практическом смысле. Но если вам хватит терпения, на базе этих знаний мы уже перейдём к матрицам.
Что за коллинеарность
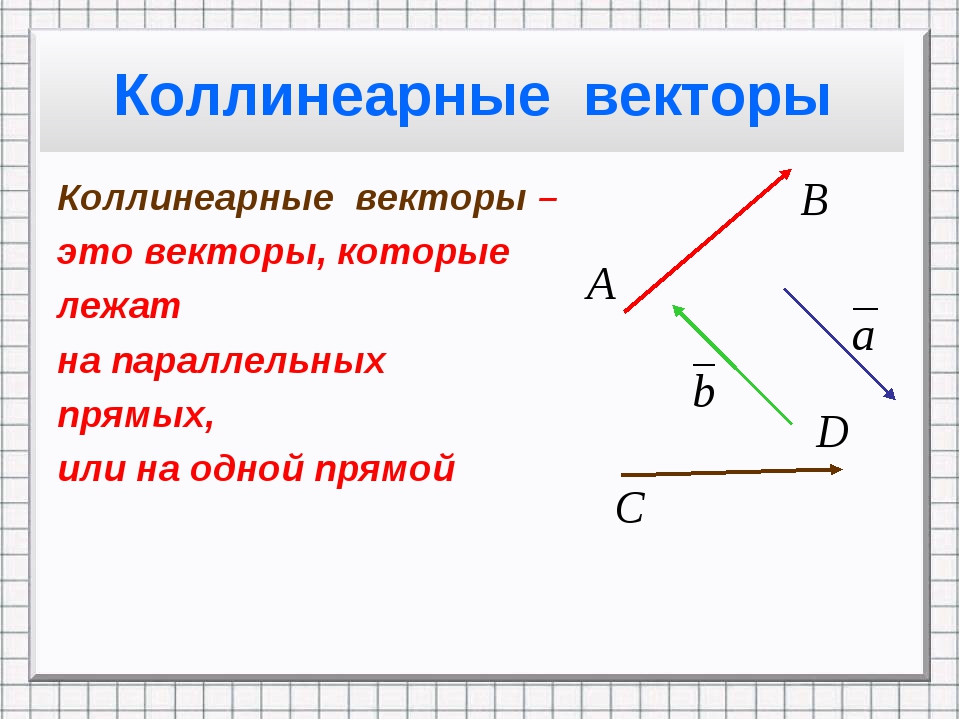
Представьте два вектора, которые находятся в одной плоскости и располагаются параллельно друг другу. При этом у них может быть разная длина. Такое расположение делает связку векторов коллинеарными, или, по-простому, линейно зависимыми.
И наоборот: если вектора находятся в одной плоскости и располагаются не параллельно друг относительно друга, то их считают линейно независимыми — неколлинеарными. Пока что ничего сложного.
Пока что ничего сложного.
Сложение коллинеарных и неколлинеарных векторов
Очевидно, что сложить два коллинеарных вектора очень легко: откладываем второй вектор от начала первого, получится новый вектор. Он будет коллинеарным своим слагаемым, они все будут лежать, грубо говоря, на одной линии.
Можно представить, что вы идёте прямо: каждый ваш шаг — это вектор. Каждый новый шаг — новый вектор. Но если все их сложить, получится один большой прямой вектор длиной как все ваши шаги.
Теперь попробуем сложить пару неколлинеарных векторов. Это как если бы мы сначала сделали шаг немного правее, а потом сделали бы шаг влево. Шага два, но если соединить начало и конец пути, он не будет совпадать с траекториями наших шагов. Появится какой-то новый вектор, с новым направлением, и он будет неколлинеарным по отношению к своим слагаемым.
Также пару неколлинеарных векторов из одной плоскости можно растянуть и развернуть в пространстве. Если их сложить, также появится новый вектор.
У математиков такой вектор называют базисом. Когда базис находится на плоскости или в пространстве, то он может единственным образом превращаться обратно в пару неколлинеарных векторов, которые его сформировали.
Правило работает, когда мы масштабируем и меняем расположение векторов в пространстве. Если мы изменим направление исходных векторов, то получим новый базис.
Базис — понятие из высшей математики, поэтому, если сейчас сложно, не отчаивайтесь. Студенты-математики когда-то тоже отчаивались.
Мы изменили пару неколлинеарных векторов и сформировали из них базис — получили новый фиолетовый вектор с собственной системой координат Теперь мы изменили исходные неколлинеарные векторы и получили новый базис — это оранжевый векторКак определять неколлинеарность
Когда мы работаем с короткими векторами, всё очевидно: нарисовали систему координат, отложили на ней векторы, они либо совпали, либо не совпали. Если совпали — коллинеарные, если нет — неколлинеарные.
Если совпали — коллинеарные, если нет — неколлинеарные.
А теперь представьте, что вектора настолько огромные, что мы физически не можем их нарисовать и сопоставить. Например,
Как такое нарисовать? Как проверить коллинеарность? Вот тут начинается магия алгебры.
Есть три способа проверки линейной зависимости векторов. Для простоты вычислений проверим эти три способа на вот этих всё ещё простых векторах:
По этим координатам ответим на два вопроса: являются ли предложенные вектора линейно зависимыми (то есть коллинеарными) и можно ли их раскладывать по базису.
Первый способ. Запишем простую систему уравнений: возьмём первую координату каждого вектора и приравняем её ко второй координате каждого вектора, умноженной на неизвестное число λ. Вычислим λ и сравним результаты.
👉 Знак λ здесь по традиции и для удобства. На самом деле это просто некое неизвестное число. Вместо этой буквы могли быть X, Y, Z или N, но так как у нас вектора уже называются X и Y, а N в математике используется для других целей, возьмём λ — это греческая буква «лямбда», давний предок нашей русской буквы «Л».
На самом деле это просто некое неизвестное число. Вместо этой буквы могли быть X, Y, Z или N, но так как у нас вектора уже называются X и Y, а N в математике используется для других целей, возьмём λ — это греческая буква «лямбда», давний предок нашей русской буквы «Л».
Составляем систему уравнений:
Вычисляем значение λ:
Сравниваем результат и делаем вывод:
Мы получили разное значение для неизвестного числа λ и поэтому наши векторы будут считаться линейно независимыми. Из них можно получить базис.
Если бы значение λ совпало, то мы бы имели дело с линейно зависимыми векторами.
Второй способ. Проверяем координаты векторов на пропорциональность: берём первую координату первого вектора, делим её на первую координату второго вектора. Повторяем это же действие со вторыми координатами: берём вторую координату первого вектора и делим её на вторую координату второго вектора.
Получаем такую пропорцию:
Считаем значение и сравниваем результат:
Равенство не выполняется, и поэтому между векторами нет зависимости.
Третий способ. Используем четыре элемента наших координат для поиска определителя — скалярной величины, с которой мы подробно познакомимся в следующих статьях во время решения матричных уравнений. Сейчас нам не нужны подробности, и для проверки линейной зависимости достаточно формулы.
Записываем в две строки координаты наших векторов:
Переводим координаты векторов в определитель — добавляем с двух сторон вертикальную черту и получаем простую квадратную матрицу размером 2 на 2:
В полученной матрице две диагонали. Числа −6 и −1 образуют главную диагональ; числа −4 и 5 — вторую диагональ. Чтобы найти определитель, нам нужно умножить числа главной и второй диагонали, а затем вычесть их разницу.
Если из координат вектора мы получили определитель и он не равен нулю, то векторы считаются линейно независимыми и подходят для разложения по базису.
И наоборот: нулевой определитель указывает на линейную зависимость векторов.
Что из этого нужно запомнить
- С точки зрения векторов важно, они сонаправленные или нет. По-другому — они коллинеарны или нет.
- Коллинеарность влияет на то, что можно делать с этими векторами. Например, неколлинеарные векторы можно разложить по базису.
- Базис — это вектор, который можно разложить на те самые неколлинеарные векторы.
- Коллинеарность легко проверяется через уравнения. Строить векторы на координатной плоскости необязательно.
Что дальше
Следующий шаг — матрицы. Это те самые, которые лежат в основе всех нейронок и искусственного интеллекта. Матрица — это таблица чисел, с которыми можно проводить различные вычисления.
Текст:
Александр Бабаскин
Редактура:
Максим Ильяхов
Художник:
Даня Берковский
Корректор:
Ирина Михеева
Вёрстка:
Мария Дронова
Соцсети:
Олег Вешкурцев
Векторы. Что такое вектор и как его обазначают
1. ВЕКТОРЫ
2. 1.1Какова разница между векторными и скалярными величинами? Скалярные величины определяются заданием своих численных величин, а
1.1КАКОВА РАЗНИЦА МЕЖДУ ВЕКТОРНЫМИ И СКАЛЯРНЫМИВЕЛИЧИНАМИ?
СКАЛЯРНЫЕ ВЕЛИЧИНЫ ОПРЕДЕЛЯЮТСЯ ЗАДАНИЕМ СВОИХ ЧИСЛЕННЫХ ВЕЛИЧИН, А
ХАРАКТЕРИЗУЮТСЯ НЕ ТОЛЬКО СВОИМ ЧИСЛОВЫМ ЗНАЧЕНИЕМ, НО И НАПРАВЛЕНИЕМ В
ПРОСТРАНСТВЕ.
1.2. ЧТО ТАКОЕ ВЕКТОР И КАК ЕГО ОБАЗНАЧАЮТ?
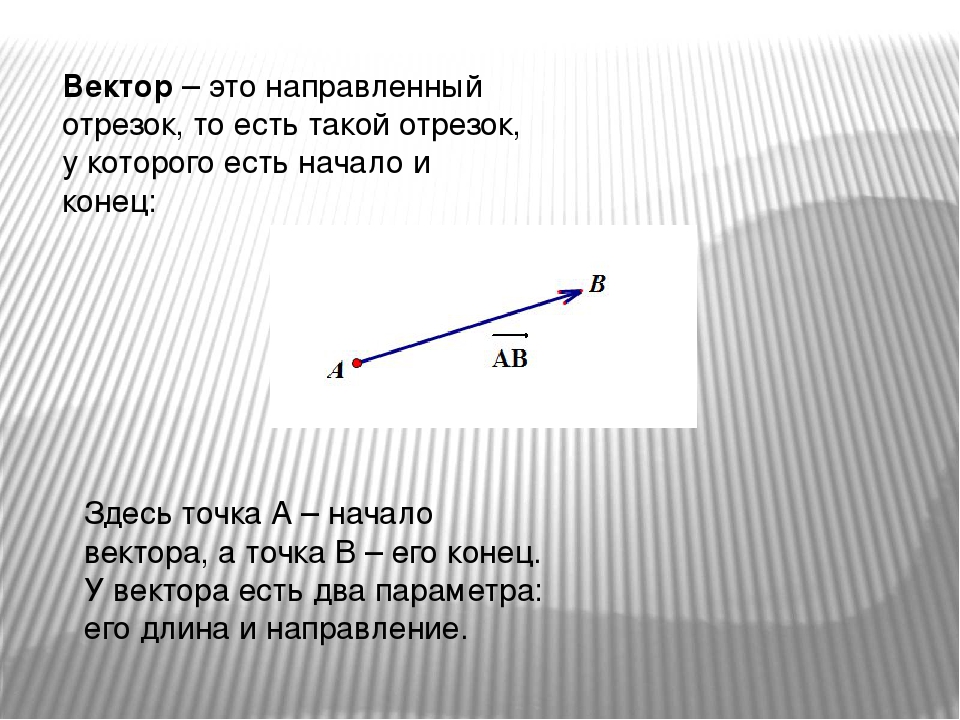
ВЕКТОР-ЛЮБОЙ НАПРАВЛЕННЫЙ ОТРЕЗОК. ОБОЗНАЧАЮТ АВ ИЛИ a.
1.3.КАКИЕ ВЕКТОРЫ НАЗЫВАЮТСЯ КОЛЛИНЕАРНЫМИ? ПРИВЕДИТЕ ПРИМЕР СОНАПРАВЛЕННЫХ
И ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫХ.
ЕСЛИ 2 ВЕКТОРЫ ЛЕЖАТ НА ОДНОЙ ПРЯМОЙ ИЛИ НА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ , ТО ТАКИЕ
ВЕКТОРЫ НАЗЫВАЮТЯ КОЛЛИНЕАРНЫМИ(рис 1 )
СОНАПРАВЛЕННЫЕ ВЕКТОРЫ (рис2)
ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫЕ (рис3)
1.
 4. КАКИЕ ВЕКТОРЫ НАЗЫВАЮТСЯ РАВНЫМИ?
4. КАКИЕ ВЕКТОРЫ НАЗЫВАЮТСЯ РАВНЫМИ?ВЕКТОРЫ НАЗЫВАЮТСЯ РАВНЫМИ, ЕСЛИ ОНИ СОНАПРАВЛЕННЫЕ И ИХ МОДУЛИ РАВНЫ. (рис4)
1.5. КАКАЯ СВЯЗЬ МЕЖДУ РАВЕНСТВОМ ВЕКТОРОВ И ПАРАЛЛЕЛЬНЫМ ПЕРЕНОСОМ?
РАВНЫЕ ВЕКТОРЫ МОЖНО СОВМЕСТИТЬ ПАРАЛЛЕЛЬНЫМ ПЕРЕНОСОМ,И, ОБРАТНО, ЕСЛИ
1.6. ЧТО ТАКОЕ МОДУЛЬ ВЕКТОРА?
ДЛИНА ОТРЕЗКА АВ НАЗЫВАЕТСЯ МОДУЛЕМ ВЕКТОРА АВ И ОБОЗНАЧАЕТСЯ /AB/.
1.7. ЧТО ВЫ ЗНАЕТЕ О НУЛЕВОМ ВЕКТОРЕ?
НУЛЕВОЙ ВЕКТОР – КОНЕЦ И НАЧАЛО КОТОРОГО СОВПАДАЮТ. ОБАЗНАЧАЕТСЯ 0.
2.1 СФОРМУЛИРУЙТЕ ПРАВИЛО ТРЕУГОЛЬНИКА И ПАРАЛЛЕЛОГРАММА СЛОЖЕНИЯ
ВЕКТОРОВ.
ПРАВИЛО ТРЕУГОЛЬНИКА
Для того чтобы сложить два вектора a⃗ и b нужно переместить вектор b⃗
параллельно самому себе так, чтобы его начало совпадало с концом вектора
a⃗.Тогда их суммой будет вектор c⃗ , начало которого совпадает с началом
вектора a⃗ , а конец — с концом вектора b⃗ (рис1)
Для того чтобы сложить два вектора a⃗ и b⃗ нужно переместить их параллельно самим
себе так, чтобы начала векторов a⃗ и b⃗ находились в одной точке.
 Затем построить
Затем построитьпараллелограмм, сторонами которого будут эти вектора. Тогда суммой a⃗ +b⃗ будет
вектор c⃗ , начало которого совпадает с общим началом векторов, а конец — с
противоположной вершиной параллелограмма. (рис2)
2.2 КАКИМИ СВОЙСТВАМИ ОБЛАДАЕТ СУММА ВЕКТОРОВ.
Для любых векторов а , b и с верно:
1.а + b=b + а
2.(а+b)+c=а+(b+c)
2.3. КАК ОПРЕДЕЛЯЕТСЯ РАЗНОСТЬ ВЕКТОРОВ?
Разностью a – b векторов a и b называется такой вектор c, что c + b = a. Если
треугольника» (рис1)
2.4. 2 ВЕКТОРА ,ИМЕЮЩИЕ РАВНЫЕ МОДУЛИ И ПРОТИВОПОЛОЖНО
НАПРАВЛЕННЫЕ , НАЗЫВАЮТСЯ ПРОТИВОПОЛОЖНЫМИ. (рис2)
2.5. КАК МОЖНО РАЗЛОЖИТЬ ВЕКТОР НА СУММУ СОСТАВЛЯЮЩИХ ПО ДВУМ
ПЕРЕСЕКАЮЩИМСЯ ПРЯМЫМ?
ПУСТЬ ДАНЫ ДВЕ ПЕРЕСЕКАЮЩИЕСЯ ПРЯМЫЕ. ТОГДА ЛЮБОЙ ВЕКТОР МОЖНО
РАЗЛОЖИТЬ НА СУММУ СОСТАВЛЯЮЩИХ , РАСПОЛОЖЕННЫХ НА ДАННЫХ
ПРЯМЫХ.
3.1 КАКИМ МОЖЕТ БЫТЬ ПРОИЗВЕДЕНИЕ K*A, ЕСЛИ: 1) a=0; 2) K=0?
Произведением вектора а≠0 на число к называется вектор , модуль которого равен
числу /к/*/а/ и сонаправлен с вектором а при к>0 , противоположно направлен с
3.
 2 КАК УМНОЖИТЬ НЕНУЛЕВОЕ ЧИСЛО НА НЕНУЛЕВОЙ ВЕКТОР?
2 КАК УМНОЖИТЬ НЕНУЛЕВОЕ ЧИСЛО НА НЕНУЛЕВОЙ ВЕКТОР?ПРОИЗВЕДЕНИЕ НЕНУЛЕВОГО ВЕКТОРА НА ЧИСЛО- ЭТО ВЕКТОР, КОЛЛИНЕАРНЫЙ
ДАННОМУ , А МОДУЛЬ РАВЕН МОДУЛЮ ДАННОГО ВЕКТОРА , УМНОЖЕННОМУ НА
МОДУЛЬ ЧИСЛА.
3.3 КАКИМИ СВОЙСТВАМИ ОБЛАДАЕТ УМНОЖЕНИЕ ЧИСЛА НА ВЕКТОР?
Свойства умножения вектора на число:
Если вектор b равен произведению ненулевого числа k и ненулевого вектора a, то
есть b = k · a, тогда:
b || a — вектора b и a параллельны
a↑↑b, если k > 0 — вектора b и a сонаправленные, если число k > 0
a↑↓b, если k
числа k.
3.4 ДОКАЖИТЕ ПРИЗНАКИ КОЛЛИНЕАРНОСТИ ВЕКТОРОВ.
Два вектора будут коллинеарны при выполнении любого из этих условий:
1. Два вектора a и b коллинеарны, если существует число n такое, что a = n · b
2. Два вектора коллинеарны, если отношения их координат равны.
ПРИЗНАК неприменимо, если один из компонентов вектора равен нулю.

Условия коллинеарности векторов 3. Два вектора коллинеарны, если их векторное произведение
равно нулевому вектору.
3.5. КАКОЕ УСЛОВИЕ ЯВЛЯЕТСЯ НЕОБХОДИМЫМ И ДОСТАТОЧНЫМ ДЛЯ ТОГО , ЧТОБЫ ТОЧКИ A,
Для того чтобы точка С лежала на прямой АВ , необходимо и достаточно , чтобы существовала
число а такое, что АС=АВ
4.1 КАКОЙ УГОЛ НАЗЫВАЕТСЯ УГОЛ МЕЖДУ ВЕКТОРАМИ AB И AC ?
УГЛОМ МЕЖДУ ВКТОРАМИ AB И AC НАЗЫВАЕТСЯ УГОЛ BAC. УГЛОМ МЕЖДУ НЕНУЛЕВЫМИ
ВЕКТОРАМИ a И b НАЗЫВАЕТСЯ УГОЛ ,ОБРАЗОВАННЫЙ ПРИОТКЛАДЫВАНИИ ЭТИХ ВЕКТОРОВ
ОТ ОДНОЙ ТОЧКИ. ОБОЗНАЧАЕТСЯ (a,b)
4.2. КАК ОПРЕДЕЛЯЕТСЯ УГОЛ МЕЖДУ ВЕКТОРАМИ a И b В ОБЩЕМ СЛУЧАЕ?
Углом между двумя ненулевыми векторами называется величина заданного ими угла , когда они
отложены от одной точки.
4.3 ЧТО НАЗЫВАЕТСЯ СКАЛЯРНЫМ ПРОИЗВЕДЕНИЕМ ДВУХ ВЕКТОРОВ ?
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ ЯВЛЯЕТСЯ ЧИСЛОМ ИЛИ ВЕКТОРОМ?
ПРОИЗВЕДЕНИЮ МОДУЛЕЙ ЭТИХ ВЕКТОРОВ НА КОСИНУС УГЛА МЕЖДУ НИМИ ЭТО
ЧИСЛО.

4.4 СФОРМУЛИРУЙТЕ СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЕ.
1.Скалярное произведение вектора самого на себя равно нулю тогда и
только тогда, когда вектор равен нулевому вектору:
a · a = 0 a = 0
Операция скалярного умножения коммуникативна:
a·b=b·a
Если скалярное произведение двух не нулевых векторов равно нулю, то эти
вектора ортогональны:
a ≠ 0, b ≠ 0, a · b = 0 a ┴ b
(a + b) · c = a · c + b · c
4.5. КАКОЕ УСЛОВИЕ ЯВЛЯЕТСЯ НЕОБХОДИМЫМ И ДОСТАТОЧНЫМ ДЛЯ ПЕРПЕНДИКУЛЯРНОСТИ
ДВУХ ВЕКТОРОВ?
ДЛЯ ПЕРПЕНДИКУЛЯРНОСТИ ДВУХ ВЕКТОРОВ НЕОБХОДИМО И ДОСТАТОНО, ЧТОБЫ ИХ
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ РАВНЯЛОСЬ НУЛЮ.
4.6. УКАЖИТЕ ПРИНЦИПЫ ПРИМЕНЕНИЯ ЭЛЕМЕНТОВ ВЕКТОРНОЙ АЛГЕБРЫ.
1. ВВОДЯ ВЕКТОРЫ В УДОБНОЙ ДЛЯ НАС ФОРМЕ , НУЖНО ПЕРЕПИСАТЬ УСЛОВИЕ ЗАДАЧИ С
ПОМОЩЬЮ ВЕКТОРОВ.
2. ПРЕОБРАЗОВЫВАЯ ЗАДАЧУ , ЗАПИСАННУЮ В ВЕКТОРОЙ ФОРМЕ ,ПОЛУЧАЕМ ЕЕ РЕШИЕМ В
ВЕКТОРНОЙ ФОРМЕ.
3. РЕШЕНИЕ ЗАДАЧИ, ПОЛУЧЕННОЕ В ВЕКТОРНЫХ СООТНОШЕНИЯХ , НУЖНО ПЕРЕВЕСТИ НА
ИСХОДНЫЙ «ЯЗЫК» ЗАДАЧИИ ЗАПИСАТЬ ОТВЕТ.

5.1 СФОРМУЛИРУЙТЕ И ДОКАЖИТЕ ТЕОРЕМУ О РАЗЛОЖЕНИИ ВЕКТОРА ПО ДВУМ
НЕКОЛЛИНЕАРНЫМ ВЕКТОРАМ.
ЕСЛИ НЕНУЛЕВЫЕ ВЕКТОРЫ a И b, ТО ДЛЯ ЛЮБОГО ВЕКТОРA c НАЙДУТСЯ ЧИСЛА x И y ТАКИЕ,
ЧТО ВЫПОЛНЯЕТСЯ РАВЕНСТВО c=xa+yb; ПРИЧЕМ КОЭФФИЦЕНТ РАЗЛОЖЕНИЯ x и y,
ОПРЕДЕЛЯЮТСЯ ЕДИНСТВЕННЫМ ОБРАЗОМ.
5.2 КАКИЕ ВЕКТОРЫНАЗЫВАЮТСЯ БАЗИСНЫМИ ВЕКТОРАМИ НА ПЛОСКОСТИ?
ИЗ ЭТОЙ ТЕОРЕМЫ ВЫТЕКАЕТ, ЧТО ЛЮБОЙ ВЕКТОР МОЖНО РАЗЛОЖИТЬ ПО ДВУМ
ПРОИЗВОЛЬНЫМНЕКОЛЛИНЕАРНЫМ ВЕКТОРАМ. ЕСЛИ НА ПЛОСКОСТИ ВЫБРАНЫ ТАКИЕ ЖЕ
ДВА НЕКОЛЛИНЕАРНЫХ ВЕКТОРОВ, ТО ОНИ НАЗЫВАЮТСЯ БАЗИСНЫМИ ВЕКТОРАМИ
5.3 ЧТО ТАКОЕ КООРДИНАТЫ ВЕКТОРА И КАК ИХ ОБОЗНАЧАЮТ?
КООРДИНАТАМИ ВЕКТОРА НАЗЫВАЮТСЯ КОЭФФИЦЕНТЫ ЕГО РАЗЛОЖЕНИЯ ПО БАЗИСНЫМ
ВЕКТОРАМ.ОБОЗНАЧЕНИЕ: а=(х;у)
5.4. НАПИШИТЕ КООРДИНАТЫ КООРДИНАТНЫХ ВЕКТОРОВ.
Координаты нулевого вектора равны нулю.
Координаты равных векторов соответственно равны.
Координаты вектора суммы двух векторов равны сумме соответствующих координат этих
векторов.

Координаты вектора разности двух векторов равны разностям соответствующих координат этих
векторов.
Координаты вектора произведения данного вектора на число равны произведениям
соответствующих координат этого вектора на данное число.
1.У РАВНЫХ ВЕКТОРОВ СООТВЕТСТВУЮЩИЕ КООРДИНАТЫ РАВНЫ.
2.ПРИ СЛОЖЕНИИ ВЕКТОРОВ СКЛАДЫВАЮТСЯ ИХ СОТВЕТСТВУЮЩИЕ КООРДИНАТЫ.
3.ПРИ УМНОЖЕНИИ ВЕКТОРА НА ЧИСЛО ЕГО КООРДИНАТЫ УМНОЖАЮТСЯ НА ЭТО ЖЕ ЧИСЛО.
5.6. КАКОЙ ВЕКТОР НАЗЫВАЕТСЯ РАДИУС-ВЕКТОРОМ ТОЧКИ А?
ЕСЛИ НА ПЛОСКОСТИ Оху ЗАДАНА ТОЧКА А(х;у) , ТО ВЕКТОР ОА НАЗЫВАЕТСЯ РАДИУСВЕКТОРОМ ТОЧКИ А.
5.7. КАК ОПРЕДЕЛЯЮТСЯ КООРДИНАТЫ ВЕКТОРА ,ЕСЛИ ЗАДАНЫ КООРДИНАТЫ ЕГО КОНЦОВ ?
КООРДИНАТЫ ВЕКТОРА ОПРЕДЕЛЯЮТСЯ КАК РАЗНОСТИ СООТВЕТСТВУЮЩИХ КООРДИНАТ
КОНЦА И НАЧАЛА ВЕКТОРА.
5.8. ПО КАКОЙ ФОРМУЛЕ ОПРЕДЕЛЯЕТСЯ МОДУЛЬ ВЕКТОРА?
6.1. КАК МОЖНО ОПРЕДЕЛИТЬ СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ ПО ИХ КООРДИНАТАМ?
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ a=(x1;y1), и b(x2;y2) ОТЛОЖИТЬ ОТ НАЧАЛА
КООРДИНАТ, ТО ОНИ ОПРЕДЕЛЯЮТСЯ ПО ФОРМУЛЕ: a*b=x1*x2+y1*y2
6.2 НАПИШИТЕ УСЛОВИЯ ПЕРПЕНДИКУЛЯРНОСТИ ВЕКТОРОВ.
ВЕКТОРЫ ЯВЛЯЮТСЯ ПЕРПЕНДИКУЛЯРНЫМИ ТОГДА И ТОЛЬКО, КОГДА ИХ СКАЛЯРНОЕ
ПРОИЗВЕДЕНИЕ РАВНО НУЛЮ. ДАНЫ 2 ВЕКТОРА a(xa;ya) и b(xb;yb). ЭТИ ВЕКТОРЫ БУДУТ
ПЕРПЕНДИКУЛЯРНЫ , ЕСЛИ ВЫРАЖЕНИЕ xa xb + ya yb =0
6.3. НАПИШИТЕ УСЛОВИЯ КОЛЛИНЕАРНОСТИ ВЕКТОРОВ.
1. ДВА ВЕКТОРА a И B КОЛЛИНЕАРНЫ, ЕСЛИ СУЩЕСТВУЕТ ЧИСЛО n ТАКОЕ, ЧТО a = n · b.
3. ДВА ВЕКТОРА КОЛЛИНЕАРНЫ, ЕСЛИ ИХ ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ РАВНО НУЛЕВОМУ
ВЕКТОРУ. (рис1)
6.4. ПО КАКОЙ ФОРМУЛЕ ОПРЕДЕЛЯЮТСЯ УГОЛ МЕЖДУ ВЕКТОРАМИ?
РИС1
7.1. КАКОЙ ВЕКТОР НАЗЫВАЕТСЯ НАПРАВЛЯЮЩИМ ВЕКТОРОМ ПРЯМОЙ?
НАПРАВЛЯЮЩИЙ ВЕТОР ПРЯМОЙ- ЭТО ЛЮБОЙ НЕНУЛЕВОЙ ВЕКТОР, ЛЕЖАЩИЙ НА ДАННОЙ
ПРЯМОЙ ИЛИ ПАРАЛЛЕЛЬНОЙ ЕЙ ПРЯМОЙ.(рис1)
7.2. КАКАЯ ТОЧКА НАЗЫВАЕТСЯ НАЧАЛЬНОЙ ТОЧКОЙ ПРЯМОЙ?
ТОЧКА М0 НАЗЫВАЕТСЯ НАЧАЛЬНОЙ ТОЧКОЙ ПРЯМОЙ l.

7.3. НАПИШИТЕ УРАВНЕНИЕ ПРЯМОЙ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ДВЕ ЗАДАННЫЕ ТОЧКИ?
УРАВНЕНИК ПРЯМОЙ,ПРОХОДЯЩИЙ ЧЕРЕЗ ДВЕ ЗАДАННЫЕ ТОЧКИ (x1,y1) и (x2,y2),
ЗАПИСЫВАЕТСЯ ТАК:
7.4. ЧТО ТАКОЕ ВЕКТОР НОРМАЛИ ПРЯМОЙ? НАПИШИТЕ УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И
ВЕКТОРУ НОРМАЛИ.
ВЕКТОР НОРМАЛИ- ЭТО ВЕКТОР, КОТОРЫЙ ПЕРПЕНДИКУЛЯРЕН ДАННОЙ ПЛОСКОСТИ .
УРАВНЕНИЕ ПРЯМОЙ ПО ВЕКТОРУ НОРМАЛИ: а(Х-Х0)+в(У-У0)=0
7.5. ПО КАКОЙ ФОРМУЛЕ ОПРЕДЕЛЯЕТСЯ УГОЛ МЕЖДУ ПРЯМЫМИ?
Рис 2
7.6. КАК ОПРЕДЕЛЯЕТСЯ РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ?
РАССТОЯНИЕ ОТ Т. ДО ПРЯМОЙ –РАВНО ДЛИНЕ ПЕРПЕНДИКУЛЯРА ОПУЩЕННОГО ИЗ Т. НА
ПРЯМУЮ.
d = |A·Mx + B·My + C|
√A2 + B2
СПАСИБО ЗА ВНИМАНИЕ!
Понятие вектора. Равенство векторов. Откладывание вектора от данной точки 9 класс онлайн-подготовка на Ростелеком Лицей
Тема 23.
Понятие вектора. Равенство векторов. Откладывание вектора от данной точки.
Сегодня мы вспомним что такое вектор, дадим определение равным векторам.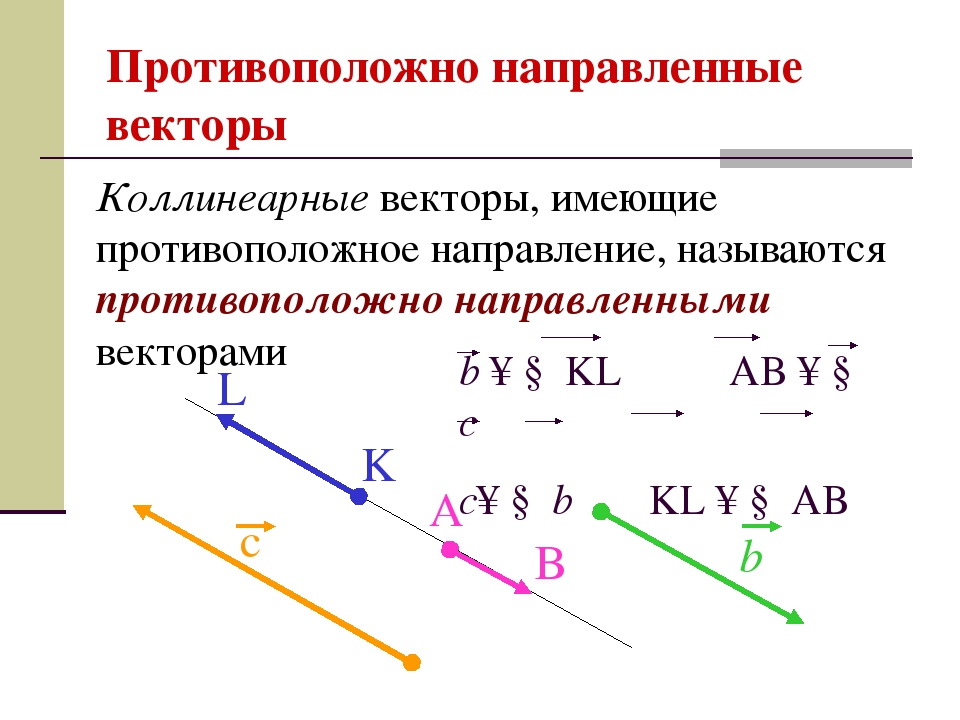
Многие физические величины, скорость, характеризуется не только своим числовым значением, но и направлением в пространстве. Такие физические величины называются векторными величинами или векторами.
Рассмотрим произвольный отрезок. Его концы называются так же граничными точками отрезка.
На отрезке можно указать два направления: от одной граничной точки до другой и наоборот.
Чтобы выбрать одно из направлений, одну граничную точку назовем началом отрезка, а другую – концом и будем считать, что отрезок направлен от начала к концу.
Определение:
Отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом, называется направленным отрезком или вектором.
Вектор изображается отрезком со стрелкой, показывающей направление вектора. Векторы обозначают двумя заглавными латинскими буквами со стрелками над ними, например, АВ⃗. Первая буква обозначает начало вектора, вторая – конец. Векторы часто обозначают и одной строчной латинской буквой со стрелкой над ней: a,⃗b⃗,c⃗.
Первая буква обозначает начало вектора, вторая – конец. Векторы часто обозначают и одной строчной латинской буквой со стрелкой над ней: a,⃗b⃗,c⃗.
Любая точка плоскости также является вектором. В этом случае вектор называется нулевым. Начало нулевого вектора совпадает с его концом, на рисунке такой вектор изображается одной точкой. Если, например, точка, изображающая нулевой вектор, обозначена буквой М, то данный нулевой вектор можно обозначить так: ММ⃗. Нулевой вектор обозначается так же символом 0⃗.
Длиной или модулем ненулевого вектора АВ⃗ называется длина отрезка АВ. Обозначается так: АВ⃗. Длина нулевого вектора ММ⃗=0.
Рассмотрим движение тела, при котором все его точки движутся с одной и той же скоростью и в одном и том же направлении.
Скорость каждой точки М тела является векторной величиной, поэтому ее можно изобразить направленным отрезком, начало которого совпадает с точкой М. Так как все точки тела движутся с одной и той же скоростью, то все направленные отрезки, изображающие скорости этих точек, имеют одно и то же направление и длины их равны.
Введем понятие коллинеарных векторов.
Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых; нулевой вектор считается коллинеарным любому вектору.
Если два ненулевых вектора коллинеарны, то они могут быть направлены либо одинаково, либо противоположно. В первом случае векторы называются сонаправленными, а во втором – противоположно направленными. Сонаправленность векторов a⃗ и b⃗ обозначается следующим образом: a⃗↑↑b⃗. Если же векторы a⃗ и b⃗ противоположно направлены, то обозначают так: a⃗↑↓b⃗.
Дадим теперь определение равных векторов.
Определение: Векторы называются равными, если они сонаправлены и их длины равны.
Таким образом векторы a⃗ и b⃗ равны, если a⃗↑↑b⃗ и a⃗=b⃗. Равенство векторов обозначается так: a⃗=b⃗.
Если точка А – начало вектора a⃗, то говорят, что вектор a⃗ отложен от точки А.
Итак, от любой точки М можно отложить вектор, равный данному вектору a⃗ и притом только один.
Замечание:
Равные векторы, отложенные от разных точек, часто обозначают одной и той же буквой. Иногда про такие векторы говорят, что это один и тот же вектор, но отложенный от разных точек.
Вектор, действия с векторами, сложение и вычитание
Тестирование онлайн
Проекция вектора
Сложение и вычитание векторов
Вектор
Вектор — это отрезок, который имеет направление. Конец вектора совпадает со стрелкой, начало — точка. Модуль вектора (абсолютная величина) — длина этого направленного отрезка.
Если начало вектора совпадает с его концом, получим нулевой вектор.
Два вектора являются равными, если их длина одинаковая и они имеют одинаковое направление. Они совмещаются при переносе.
На рисунке только вектор a равен вектору b. Вектор c им не равен, так как направлен в противоположную сторону
Вектор c им не равен, так как направлен в противоположную сторону
Вектор -c — это вектор c, но противоположного направления. Тогда
Проекция вектора
Проекция вектора на ось имеет положительное значение в том случае, когда направление вектора совпадает с направлением оси. Отрицательное значение — в противоположном случае.
Спроецируем вектор перемещения на ось Ox и на ось Oy. Для того, чтобы получить проекцию необходимо из координаты конца вектора отнять координату начала. На ось ОХ: sx=x-x0, на ось ОУ: sy=y-y0.
Рассмотрим примеры
Частные случаи, когда проекция на ось Ox или Oy нулевая.
Сумма составляющих вектора по осям равна данному вектору, т.е.
Сложение векторов
Правило параллелограмма: диагональ параллелограмма — сумма двух векторов с общим началом.
Правило треугольника: от конца первого вектора отложить второй вектор, тогда их суммой будет вектор, начало которого совпадает с началом первого вектора, а конец с концом второго вектора.
Рассмотрим правила на примерах.
Вычитание векторов
Вычитание векторов — это сумма положительного и отрицательного вектора.
Упражнения
Может ли при сложении двух векторов по правилу параллелограмма равнодействующая быть численно равной одному из составляющих векторов?
Может ли при сложении двух векторов по правилу параллелограмма равнодействующая быть меньше меньшего из составляющих векторов?
Вектор: определение и основные понятия.
Определение вектора
Определение. Вектор — это направленный отрезок, то есть отрезок, имеющий длину и определенное направление. Графически вектора изображаются в виде направленных отрезков прямой определенной длины. (рис.1)
| рис. 1 |
Обозначение вектора
Вектор началом которого есть точка А, а концом — точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a.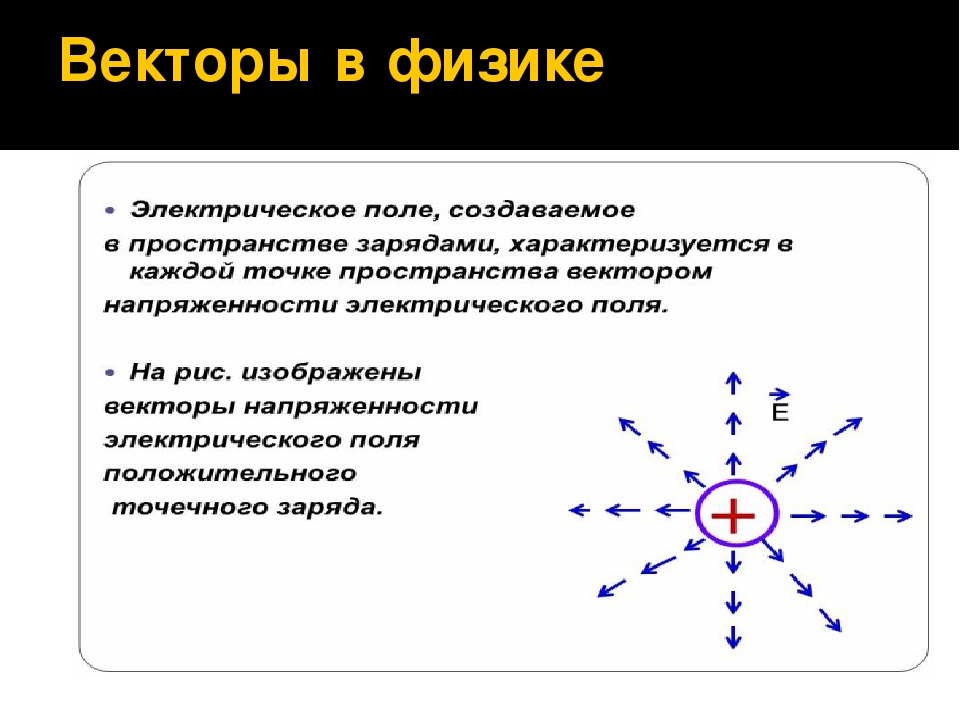
Длина вектора
Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.
Нулевой вектор
Определение. Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.
Нулевой вектор обычно обозначается как 0.
Длина нулевого вектора равна нулю.
Коллинеарные вектора
| рис. 2 |
Сонаправленные вектора
Определение. Два коллинеарных вектора a и b называются сонаправленными векторами, если их направления совпадают: a↑↑b (рис. 3).
| рис. 3 |
Противоположно направленные вектора
Определение. Два коллинеарных вектора a и b называются противоположно направленными векторами, если их направления противоположны: a↑↓b (рис. 4).
| рис. 4 |
Компланарные вектора
Определение.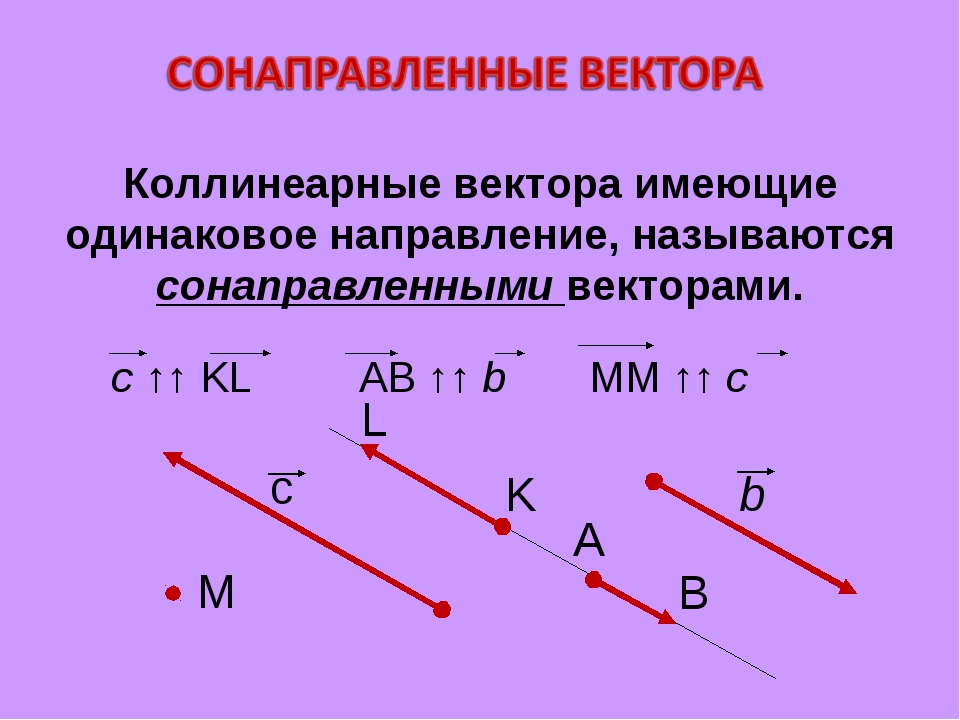 Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 5).
Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 5).| рис. 5 |
Всегда возможно найти плоскости параллельную двум произвольным векторам, по-этому любые два вектора всегда компланарные.
Равные вектора
Определение. Вектора a и b называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны (рис. 6).
| рис. 6 |
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b, если a↑↑b и |a| = |b|.
Единичный вектор
Определение. Единичным вектором или ортом — называется вектор, длина которого равна единице.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Что такое векторы и как они используются в программировании?
Я знаком с математической / физической концепцией вектора как величины и направления, но я также постоянно сталкиваюсь со ссылками на векторы в контексте программирования (например, C++, кажется, имеет библиотеку stl::vector, которая довольно часто появляется на SO).
Моя интуиция из контекста заключалась в том, что они представляют собой довольно примитивную конструкцию, чаще всего используемую для представления чего-то вроде массива переменной длины (я предполагаю, что его размер хранится как величина), но было бы очень полезно, если бы кто-то мог дать мне более полное объяснение, предпочтительно включая то, как и почему они используются на практике.
computer-science vectorПоделиться Источник Lawrence Johnston 03 февраля 2009 в 18:44
11 ответов
47
Из http:/ / www.cplusplus.com / ссылка / stl / вектор/
Векторные контейнеры реализуются как динамические массивы; как и обычные массивы, векторные контейнеры имеют свои элементы, хранящиеся в непрерывном хранилище местоположения, что означает, что их элементы могут быть доступны не только с помощью итераторов, но и с помощью смещений на обычных указателях на элементы.
Но в отличие от обычных массивов, хранение в векторах обрабатывается автоматически, что позволяет расширять и сжимать его по мере необходимости.
Кроме того, векторы обычно могут содержать любой объект — поэтому вы можете создать класс для хранения информации о транспортных средствах, а затем сохранить парк в векторе.
Хорошие вещи о векторах, помимо изменения размера, заключаются в том, что они все еще позволяют получить доступ в постоянное время к отдельным элементам через индекс, точно так же, как массив.
Компромисс для изменения размера заключается в том, что когда вы достигаете текущей емкости, она должна перераспределять, а иногда и копировать в большую память. Однако большинство алгоритмов увеличения емкости удваивают емкость каждый раз, когда вы попадаете в барьер, поэтому вы никогда не попадаете в него больше log2(доступная куча), что в худшем случае оказывается примерно в дюжину раз на протяжении всей работы программы.
-Adam
Поделиться Adam Davis 03 февраля 2009 в 18:47
24
В математике вектор можно рассматривать как комбинацию направления и величины. Однако его также можно рассматривать как координату. Например, вектор с величиной 5 и углом около 37 градусов от горизонтали представляет собой точку на плоскости 2D. Эта точка также может быть представлена декартовой парой координат (3, 4). Эта пара (3, 4) также является математическим вектором.
В программировании это имя «vector» первоначально использовалось для описания любой последовательности чисел scalar фиксированной длины. Вектор длины 2 представляет точку в плоскости 2D, вектор длины 3 представляет точку в пространстве 3D и так далее. Вектор длиной 100 представляет собой точку в 100-мерном пространстве (математикам нетрудно думать о таких вещах).
В современных библиотеках программирования это имя «vector» обычно означает последовательность значений переменного размера (не обязательно чисел). Изменение размера (длины или размерности) математического вектора-это не то, что вы обычно делаете, если только вы не выполняете какую-то проекционную операцию. Но изменение длины вектора программирования, содержащего последовательность строк, может быть обычной операцией.
Изменение размера (длины или размерности) математического вектора-это не то, что вы обычно делаете, если только вы не выполняете какую-то проекционную операцию. Но изменение длины вектора программирования, содержащего последовательность строк, может быть обычной операцией.
Поделиться Greg Hewgill 03 февраля 2009 в 18:59
7
Математические векторы, к которым вы привыкли, являются тензорами первого ранга ; структуры данных в информатике не обязательно подчиняются правилам тензорного преобразования. Это просто массивы, которые могут расширяться и сжиматься, как отмечалось ранее.
Поделиться duffymo 03 февраля 2009 в 18:51
- Что такое псевдоклассы и для чего они используются?
Я здесь совсем недавно. Я видел много вопросов и ответов на них. Но у меня есть вопрос, так как я открыл сайт блога.
 Мой вопрос заключается в том, что такое псевдоклассы и для чего они используются?
Мой вопрос заключается в том, что такое псевдоклассы и для чего они используются? - Что такое векторы в программировании (LibGDX)?
Я довольно часто видел векторы в свое время, изучая LibGDX и кодирование в целом. Но я никогда не мог понять, что это такое. Я знаю: В других языках программирования они являются (амортизированным) способом работы со списками массивов. В физике они представляют собой величину и направление. В…
4
Векторные контейнеры реализуются как динамические массивы; как и обычные массивы, векторные контейнеры имеют свои элементы, хранящиеся в смежных местах хранения, что означает, что их элементы могут быть доступны не только с помощью итераторов, но и с помощью смещений регулярных указателей на элементы.
Но в отличие от обычных массивов, хранение в векторах обрабатывается автоматически, что позволяет расширять и сжимать его по мере необходимости.
Векторы хороши в:
- Доступ к отдельным элементам по их индексу положения (постоянное время).
- Повторение элементов в любом порядке (линейное время).
- Добавление и удаление элементов с его конца (постоянное амортизируемое время).
REF
Поделиться cgreeno 03 февраля 2009 в 18:47
3
Я могу понять вашу путаницу по именам (меня это тоже смущало). Этому не помогает идея вектора в графическом программировании 3D, которая ближе к математическому определению. В математике вектор можно представить как 1-мерную матрицу произвольной длины (длина-это число измерений вашей системы координат). В большинстве языков OO векторы по существу являются 1-мерными матрицами (массивами), отсюда и название. Они не имеют ничего общего с координатами, если только программист не решит использовать их для этой задачи (что бывает редко — я никогда этого не видел). Они также обычно не имеют никаких математических операторов для выполнения матричного умножения или любых подобных операций. Таким образом, 1-мерная природа их примерно там, где сходство заканчивается. Я оставлю это другим ответам, чтобы объяснить особенности и использование контейнера OO, с которым у них уже есть ручка.
Они также обычно не имеют никаких математических операторов для выполнения матричного умножения или любых подобных операций. Таким образом, 1-мерная природа их примерно там, где сходство заканчивается. Я оставлю это другим ответам, чтобы объяснить особенности и использование контейнера OO, с которым у них уже есть ручка.
Поделиться rmeador 03 февраля 2009 в 18:52
2
Поскольку по крайней мере два других ответа вставлены с этого сайта , вы также можете прочитать rest описания там… 🙂
Поделиться Adrian Grigore 03 февраля 2009 в 18:49
2
Из книги SICP :
Для моделирования компьютерной памяти мы используем новый тип структуры данных, называемый вектором. Абстрактно, вектор-это сложный объект данных, отдельные элементы которого могут быть доступны с помощью целочисленного индекса за время, не зависящее от индекса.
Поделиться Nemanja Trifunovic 03 февраля 2009 в 19:04
1
Чтобы помочь вам запомнить CS значение слова “vector”, может быть полезно обратиться к латинскому корню vehere, что означает передавать или переносить. Таким образом, вектор несет или содержит вещи, вообще говоря.
Поделиться Ezra Justin Lee 20 октября 2017 в 05:31
0
https://isocpp.org/wiki/faq/containers содержит много информации, необходимой для понимания того, что окружает этот вопрос. Он будет противопоставлять векторы связанным спискам, массивам и т. д.
Кроме того, из тура Страуструпа (http: / / www.stroustrup.com / Tour. html ), Глава 9:
Большинство вычислений включает в себя создание коллекций значений.
… Класс с основной целью хранения объектов … называется контейнером . … Самый полезный контейнер
stl-этоvector. Astl::vector-это последовательность элементов данного типа. Элементы хранятся последовательно в памяти.
Таким образом, вектор STL — это набор значений одного и того же типа —таким образом, это похоже на математическое значение vector/module—but .
Поделиться isomorphismes 31 августа 2015 в 21:23
0
Помимо структуры данных в C++, вектор также является термином для указателя на код. F.e. вектор прерывания указывает на код прерывания, который будет вызван.
Поделиться Azure 20 июля 2017 в 23:41
0
Векторы в программировании-это в основном динамические массивы, в которых хранение обрабатывается автоматически, позволяя ему расширяться и сжиматься по мере необходимости. Лучше всего то, что они также позволяют получить доступ в постоянное время к отдельным элементам через индекс, как и обычный массив.
Лучше всего то, что они также позволяют получить доступ в постоянное время к отдельным элементам через индекс, как и обычный массив.
Поделиться Budhathoki Bijaya 20 марта 2016 в 17:52
Похожие вопросы:
Что такое модули слияния и как они используются?
Что такое модули слияния и как они используются? Я слышал, что это файлы .msm, но я никогда не видел этого раньше (я видел только файл .msi). Используются ли они при создании msi-файлов?…
Что такое веб-сервисы и как они используются?
Я пытаюсь понять Что такое веб-сервис Как они используются Все, что я знаю, это то, что они закодированы в SOAP/XML и не зависят от языка, то есть я мог бы написать программу в Java и создать…
Что такое матрицы совместного возникновения и как они используются в NLP?
В документах pypi для загрузчика google ngram говорится, что иногда вам нужны агрегированные данные по набору данных. Например, чтобы построить матрицу совпадений. Википедия для матрицы cooccurance…
Например, чтобы построить матрицу совпадений. Википедия для матрицы cooccurance…
Что такое функции ‘abstract’ в PHP и когда они используются?
Я знаю, что абстрактные классы предназначены только для использования родительскими классами и не могут иметь своих собственных экземпляров, но что такое абстрактные functions/methods?, каково их…
Что такое MultiPartEntity и данные формы? Как они используются для загрузки изображений в android?
Я искал в интернете, но смог найти только код, связанный с данными составных форм, а не объяснение того, что это такое и как они используются?
Что такое псевдоклассы и для чего они используются?
Я здесь совсем недавно. Я видел много вопросов и ответов на них. Но у меня есть вопрос, так как я открыл сайт блога. Мой вопрос заключается в том, что такое псевдоклассы и для чего они используются?
Что такое векторы в программировании (LibGDX)?
Я довольно часто видел векторы в свое время, изучая LibGDX и кодирование в целом. Но я никогда не мог понять, что это такое. Я знаю: В других языках программирования они являются (амортизированным)…
Но я никогда не мог понять, что это такое. Я знаю: В других языках программирования они являются (амортизированным)…
Что такое Systick во встраиваемых системах и для чего они используются?
Я изучаю курс по встроенным системам и перебираю прерывания. Я сталкивался с временами Systick и цикла. Что это такое, когда и почему они используются?
Что такое OpenSSL BIOs? Как они работают? Как BIOs используется в OpenSSL?
Мне нужна общая информация о OpenSSL био. Какое-то введение в нее. Что такое OpenSSL BIO? Какова его общая идея? Я знаю, что это какой-то API для input/output., но чем он отличается от stdio или…
Что такое векторы и < > в C?
Я смотрел на исходный код для gcc (из любопытства) и заметил структуру данных, которую никогда раньше не видел в C. В строках 80 и 129 (и во многих других местах) синтаксического анализатора они,…
Векторы и операции над векторами
Будут и задачи для самостоятельного решения, к которым можно
посмотреть ответы.
Прежде чем Вы узнаете всё о векторах и операциях над ними, настройтесь на решение несложной задачи. Есть вектор Вашей предприимчивости и вектор Ваших инновационных способностей. Вектор предприимчивости ведёт Вас к Цели 1, а вектор инновационных способностей — к Цели 2. Правила игры таковы, что Вы не можете двигаться сразу по направлениям двух этих векторов и достигнуть сразу двух целей. Векторы взаимодействуют, или, если говорить математическим языком, над векторами производится некоторая операция. Результатом этой операции становится вектор «Результат», который приводит Вас к Цели 3.
А теперь скажите: результатом какой операции над векторами «Предприимчивость» и «Инновационные способности» является вектор «Результат»? Если не можете сказать сразу, не унывайте. По мере изучения этого урока Вы сможете ответить на этот вопрос.
Как мы уже увидели выше, вектор обязательно идёт от некоторой точки A по прямой к некоторой точке
B. Следовательно, каждый вектор имеет не только числовое значение — длину, но также физическое и
геометрическое — направленность. Из этого выводится первое, самое простое определение вектора. Итак, вектор —
это направленный отрезок, идущий от точки A к точке B. Обозначается он так:
.
Следовательно, каждый вектор имеет не только числовое значение — длину, но также физическое и
геометрическое — направленность. Из этого выводится первое, самое простое определение вектора. Итак, вектор —
это направленный отрезок, идущий от точки A к точке B. Обозначается он так:
.
А чтобы приступить к различным операциям с векторами, нам нужно познакомиться с ещё одним определением вектора.
Вектор — это вид представления точки, до которой требуется добраться из некоторой начальной точки. Например, трёхмерный вектор, как правило, записывается в виде (х, y, z). Говоря совсем просто, эти числа означают, как далеко требуется пройти в трёх различных направлениях, чтобы добраться до точки.
Пусть дан вектор. При этом x = 3 (правая рука указывает направо), y = 1 (левая рука указывает
вперёд), z = 5 (под точкой стоит лестница, ведущая вверх). По этим данным вы найдёте точку,
проходя 3 метра в направлении, указываемом правой рукой, затем 1 метр в направлении,
указываемом левой рукой, а далее Вас ждёт лестница и, поднимаясь на 5 метров, Вы, наконец,
окажетесь в конечной точке.
По этим данным вы найдёте точку,
проходя 3 метра в направлении, указываемом правой рукой, затем 1 метр в направлении,
указываемом левой рукой, а далее Вас ждёт лестница и, поднимаясь на 5 метров, Вы, наконец,
окажетесь в конечной точке.
Все остальные термины — это уточнения представленного выше объяснения, необходимые для различных операций над векторами, то есть, решения практических задач. Пройдёмся по этим более строгим определениям, останавливаясь на типичных задачах на векторы.
Физическими примерами векторных величин могут служить смещение материальной точки, двигающейся в пространстве, скорость и ускорение этой точки, а также действующая на неё сила.
Геометрический вектор представлен в двумерном и трёхмерном пространстве в виде направленного отрезка. Это отрезок, у которого различают начало и конец.
Если A — начало вектора, а B — его конец, то вектор обозначается
символом или одной строчной буквой . На рисунке
конец вектора указывается стрелкой (рис. 1)
На рисунке
конец вектора указывается стрелкой (рис. 1)
Длиной (или модулем) геометрического вектора называется длина порождающего его отрезка
Два вектора называются равными, если они могут быть совмещены (при совпадении направлений) путём параллельного переноса, т.е. если они параллельны, направлены в одну и ту же сторону и имеют равные длины.
В физике часто рассматриваются закреплённые векторы, заданные точкой приложения, длиной и направлением. Если точка приложения вектора не имеет значения, то его можно переносить, сохраняя длину и направление в любую точку пространства. В этом случае вектор называется свободным. Мы договоримся рассматривать только свободные векторы.
Умножение вектора на число
Сложение и вычитание векторов
Слагаемые называются составляющими вектора , а
сформулированное правило — правилом многоугольника. Этот многоугольник может и не быть плоским.
Этот многоугольник может и не быть плоским.
Пример 1. Упростить выражение:
.
Решение:
,
то есть, векторы можно складывать и умножать на числа так же, как и многочлены (в частности, также задачи на упрощение выражений). Обычно необходимость упрощать линейно подобные выражения с векторами возникает перед вычислением произведений векторов.
Пример 2. Векторы и служат диагоналями параллелограмма ABCD (рис. 4а). Выразить через и векторы , , и , являющиеся сторонами этого параллелограмма.
Решение. Точка пересечения диагоналей параллелограмма делит каждую диагональ пополам.
Длины требуемых в условии задачи векторов находим либо как половины сумм векторов, образующих с искомыми треугольник, либо как половины разностей (в зависимости
от направления вектора, служащего диагональю), либо, как в последнем случае, половины суммы, взятой со знаком минус.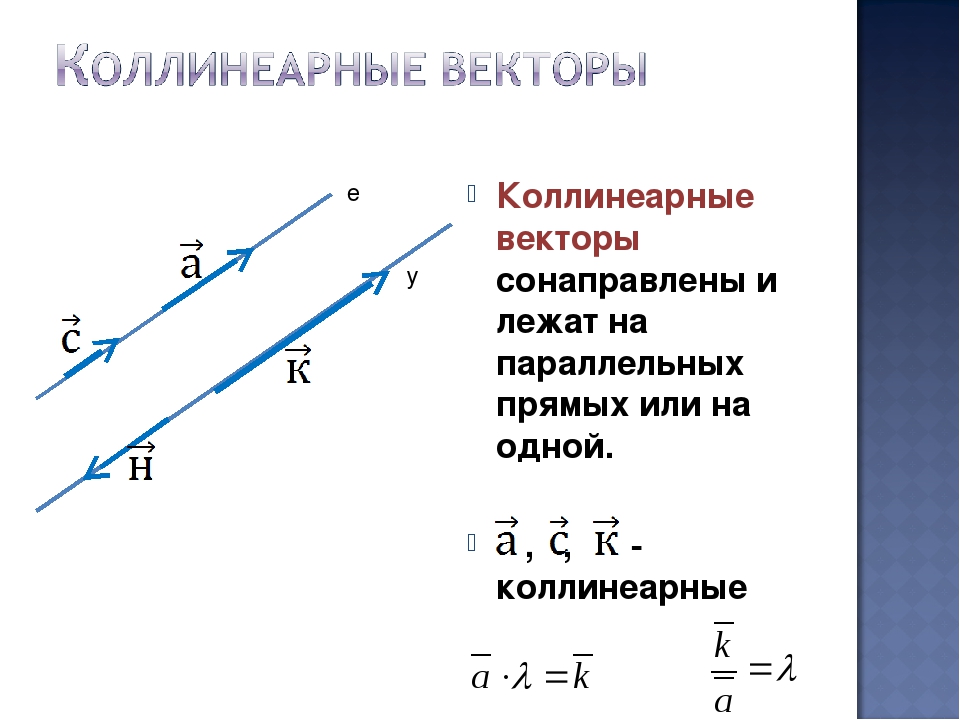 Результат —
требуемые в условии задачи векторы:
Результат —
требуемые в условии задачи векторы:
Есть все основания полагать, что теперь Вы правильно ответили на вопрос о векторах «Предприимчивость» и «Инновационные способности» в начале этого урока. Правильный ответ: над этими векторами производится операция сложения.
Решить задачи на векторы самостоятельно, а затем посмотреть решения
Как найти длину суммы векторов?
Эта задача занимает особое место в операциях с векторами, так как предполагает использование тригонометрических свойств. Допустим, Вам попалась задача вроде следующей:
Даны длины векторов и длина суммы этих векторов . Найти длину разности этих векторов .
Решения этой и других подобных задач и объяснения, как их решать — в
уроке «Сложение векторов: длина суммы векторов и теорема косинусов«.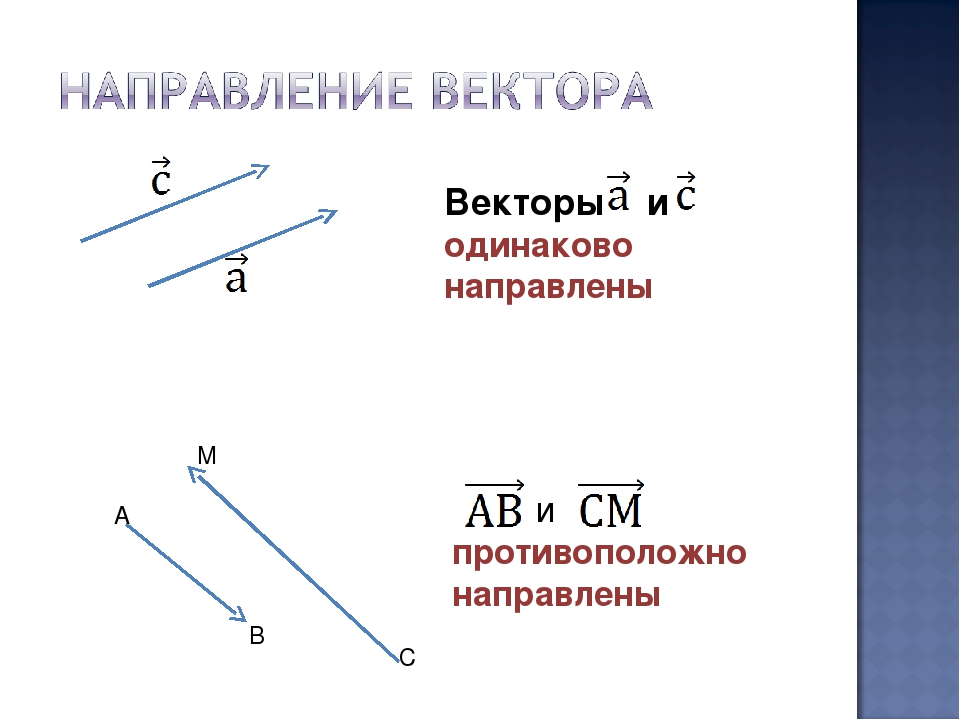
А проверить решение таких задач можно на Калькуляторе онлайн «Неизвестная сторона треугольника (сложение векторов и теорема косинусов)».
А где произведения векторов?
Произведения вектора на вектор не являются линейными операциями и рассматриваются отдельно. И у нас есть уроки «Скалярное произведение векторов» и «Векторное и смешанное произведения векторов».
Проекция вектора на ось равна произведению длины проектируемого вектора на косинус угла между вектором и осью:
Как известно, проекцией точки A на прямую (плоскость) служит основание перпендикуляра , опущенного из этой точки на прямую (плоскость).
Пусть —
произвольный вектор (Рис. 5), а и —
проекции его начала (точки A) и конца (точки B) на ось l. (Для построения проекции точки A) на прямую проводим
через точку A плоскость, перпендикулярную прямой. Пересечение прямой и плоскости определит требуемую проекцию.
Пересечение прямой и плоскости определит требуемую проекцию.
Составляющей вектора на оси l называется такой вектор , лежащий на этой оси, начало которого совпадает с проекцией начала, а конец — с проекцией конца вектора .
Проекцией вектора на ось l называется число
,
равное длине составляющего вектора на этой оси, взятое со знаком плюс, если направление составляюшей совпадает с направлением оси l, и со знаком минус, если эти направления противоположны.
Основные свойства проекций вектора на ось:
1. Проекции равных векторов на одну и ту же ось равны между собой.
2. При умножении вектора на число его проекция умножается на это же число.
3. Проекция суммы векторов на какую-либо ось равна сумме проекций на эту же ось слагаемых векторов.
4.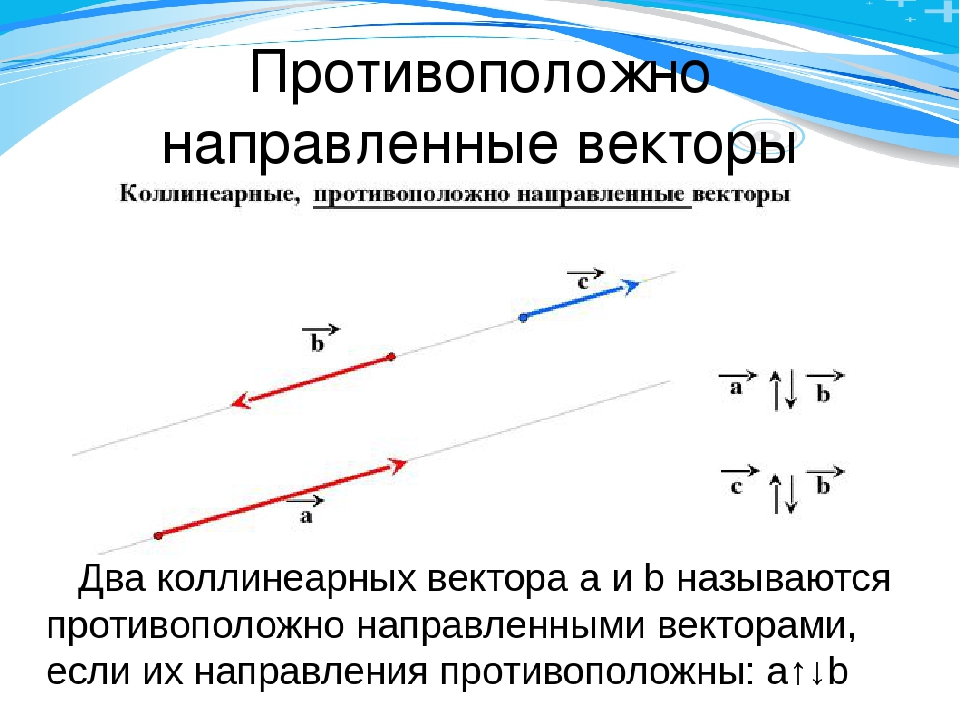 Проекция вектора на ось равна произведению длины проектируемого вектора на косинус
угла между вектором и осью:
Проекция вектора на ось равна произведению длины проектируемого вектора на косинус
угла между вектором и осью:
Пример 5. Рассчитать проекцию суммы векторов на ось l, если , а углы —
.
Решение. Спроектируем векторы на ось l как определено в теоретической справке выше. Из рис.5а очевидно, что проекция суммы векторов равна сумме проекций векторов. Вычисляем эти проекции:
Находим окончательную проекцию суммы векторов:
.
Знакомство с прямоугольной декартовой системой координат в пространстве состоялось в соответствующем уроке, желательно открыть его в новом окне.
В упорядоченной системе координатных осей 0xyz ось Ox называется осью абсцисс, ось 0y – осью ординат, и ось 0z – осью аппликат.
С произвольной точкой М пространства свяжем вектор
,
называемый радиус-вектором точки М и спроецируем его на каждую из координатных осей. Обозначим величины соответствующих проекций:
Числа x, y, z называются координатами точки М , соответственно абсциссой, ординатой и аппликатой, и записываются в виде упорядоченной точки чисел: M (x; y; z) (рис.6).
Вектор единичной длины, направление которого совпадает с направлением оси, называют единичным вектором(или ортом) оси. Обозначим через
Соответственно орты координатных осей Ox, Oy, Oz
Теорема. Всякий вектор может быть разложен по ортам координатных осей:
(2)
Равенство (2) называется разложением вектора по координатным осям.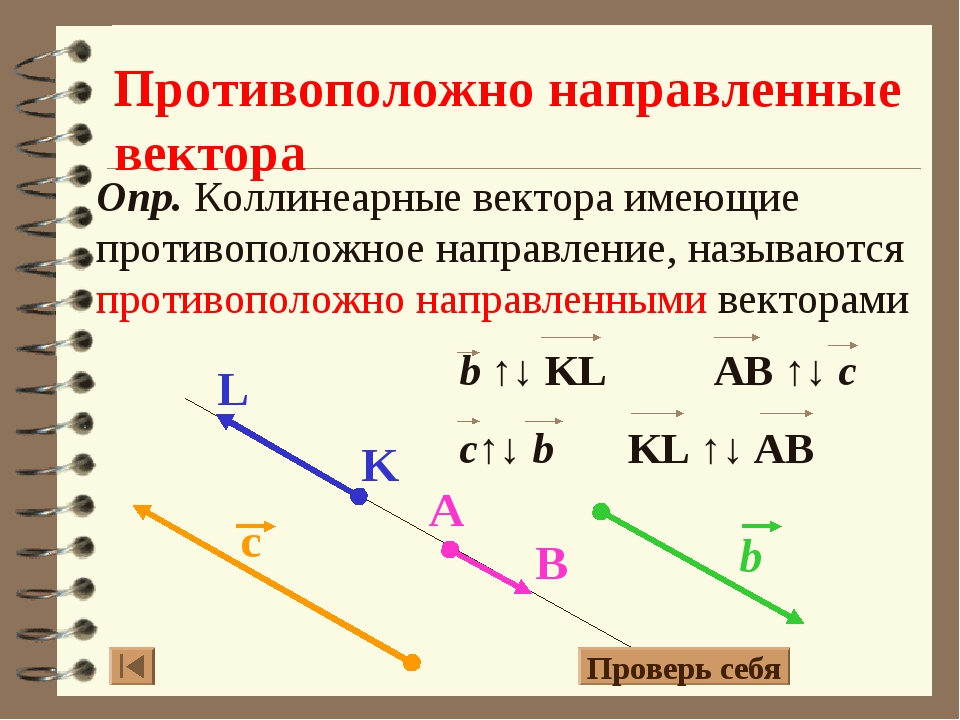 Коэффициентами этого разложения являются проекции вектора на координатные оси. Таким образом, коэффициентами разложения (2) вектора по координатным осям являются координаты вектора.
Коэффициентами этого разложения являются проекции вектора на координатные оси. Таким образом, коэффициентами разложения (2) вектора по координатным осям являются координаты вектора.
После выбора в пространстве определённой системы координат вектор и тройка его координат однозначно определяют друг друга, поэтому вектор может быть записан в форме
(3)
Представления вектора в виде (2) и (3) тождественны.
Как мы уже отмечали, векторы называются коллинеарными, если они связаны отношением
.
Пусть даны векторы . Эти векторы коллинеарны, если координаты векторов связаны отношением
,
то есть, координаты векторов пропорциональны.
Пример 6. Даны векторы . Коллинеарны ли эти векторы?
Решение. Выясним соотношение координат данных векторов:
.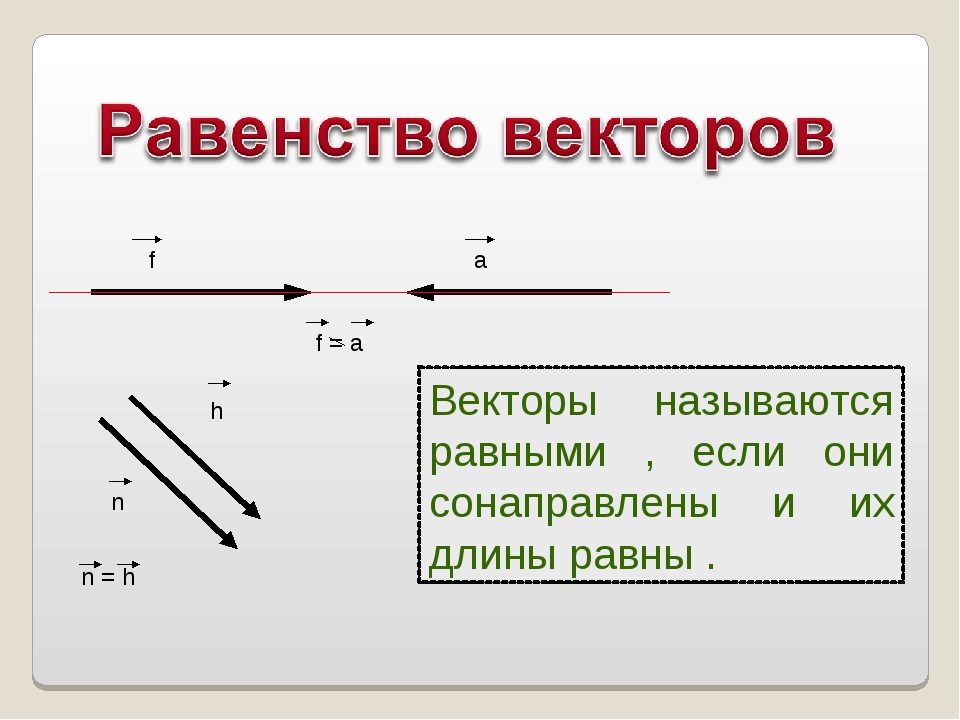
Координаты векторов пропорциональны, следовательно, векторы коллинеарны, или, что то же самое, параллельны.
Вследствие взаимной перпендикулярности координатных осей длина вектора
равна длине диагонали прямоугольного параллелепипеда, построенного на векторах
и выражается равенством
(4)
Вектор полностью определяется заданием двух точек (начала и конца), поэтому координаты вектора можно выразить через координаты этих точек.
Пусть в заданной системе координат начало вектора находится в точке
а конец – в точке
(рис.8).
Тогда
Из равенства
следует, что
Отсюда
или в координатной форме
(5)
Следовательно, координаты вектора равны разностям одноимённых координат конца и начала вектора. Формула (4) в этом случае примет вид
Формула (4) в этом случае примет вид
(6)
Направление вектора определяют направляющие косинусы. Это косинусы углов, которые вектор образует с осями Ox, Oy и Oz. Обозначим эти углы соответственно α, β и γ. Тогда косинусы этих углов можно найти по формулам
,
,
.
Направляющие косинусы вектора являются также координатами орта этого вектора и, таким образом, орт вектора
или
.
Учитывая, что длина орта вектора равна одной единице, то есть
,
получаем следующее равенство для направляющих косинусов:
.
Пример 7. Найти длину вектора x = (3; 0; 4).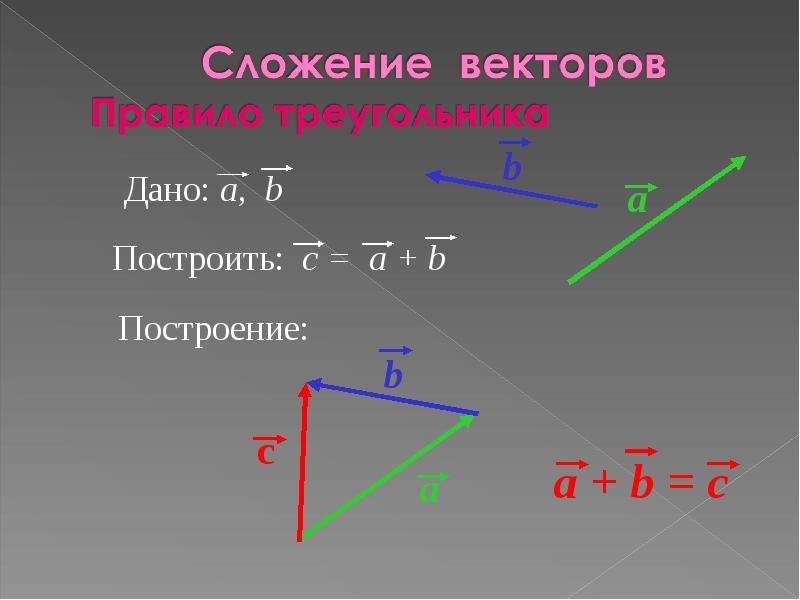
Решение. Длина вектора равна
Пример 8. Даны точки:
Выяснить, равнобедренный ли треугольник, построенный на этих точках.
Решение. По формуле длины вектора (6) найдём длины сторон и установим, есть ли среди них две равные:
Две равные стороны нашлись, следовательно необходимость искать длину третьей стороны отпадает, а заданный треугольник является равнобедренным.
Пример 9. Найти длину вектора и его направляющие косинусы, если .
Решение. Координаты вектора даны:
.
Длина вектора равна квадратному корню из суммы квадратов координат вектора:
.
Находим направляющие косинусы:
Решить задачу на векторы самостоятельно, а затем посмотреть решение
Пусть даны два вектора и , заданные своими проекциями:
или
или
Укажем действия над этими векторами.
1.Сложение:
или, что то же
(при сложении двух векторов одноимённые координаты складываются).
2.Вычитание:
или, что то же
,
(при вычитании двух векторов одноимённые координаты вычитаются).
3.Умножение вектора на число:
или, что то же
,
(при умножении вектора на число все координаты умножаются на это число).
Пример 11. Даны два вектора, заданные координатами:
.
Найти заданный координатами вектор, являющийся суммой этих векторов: .
Решение:
.
Решить задачи на координаты векторов самостоятельно, а затем посмотреть решение
При изучении многих вопросов, в частности, экономических, оказалось удобным
обобщить рассмотренные приёмы установления соответствия между числами и точками двумерного и трёхмерного пространства
и рассматривать последовательности n действительных чисел как «точки» некоторого абстрактного
«n-мерного пространства», а сами числа — как «координаты» этих точек. За составляющие n-мерного вектора можно принимать такие данные, как урожайность различных культур, объёмы продаж товаров, технические коэффициенты, номенклатура товаров на складах и т.д.
За составляющие n-мерного вектора можно принимать такие данные, как урожайность различных культур, объёмы продаж товаров, технические коэффициенты, номенклатура товаров на складах и т.д.
n-мерным вектором называется упорядоченный набор из n действительных чисел, записываемых в виде
,
где - i – й элемент (или i – я координата) вектора x.
Возможна и другая запись вектора – в виде столбца координат:
Размерность вектора определяется числом его координат и является его отличительной характеристикой. Например, (2; 5) – двухмерный вектор, (2; -3; 0) – трёхмерный, (1; 3; -2; -4; 7) – пятимерный,
—
n – мерный вектор.
Нулевым вектором называется вектор, все координаты которого равны нулю:
0 = (0; 0; …; 0).
Введём операции над n-мерными векторами.
Произведением вектора
на действительное число называется вектор
(при умножении вектора на число каждая его координата умножается на это число).
Зная вектор
можно получить противоположный вектор
Суммой векторов
и
называется вектор
,
(при сложении векторов одной и той же размерности их соответствующие координаты почленно складываются).
Если в плане продаж сети торговых предприятий продажи товаров определить как положительные уровни товаров, а затраты на продажи – как отрицательные, то получим вектор затрат-продаж
,
где
—
продажи (затраты) k – м предприятием товара i, а k = 1, 2, 3,…, m .
Суммарный вектор затрат-продаж y определяется суммированием векторов затрат-продаж всех m предприятий сети:
Сумма противоположных векторов даёт нулевой вектор:
При вычитании двух векторов одной и той же размерности их соответствующие координаты почленно вычитаются:
Операции над n-мерными векторами удовлетворяют следующим свойствам.
Свойство 1.
Свойство 2.
Свойство 3.
Свойство 4.
Свойство 5.
Свойство 6.
Поделиться с друзьями
Весь блок «Аналитическая геометрия»
- Векторы
- Плоскость
- Прямая на плоскости
Векторов
Это вектор:
Вектор имеет величину , (размер) и направление :
Длина линии показывает ее величину, а стрелка указывает направление.
Мы можем сложить два вектора, соединив их голова к хвосту:
И неважно, в каком порядке мы их добавляем, результат будет тот же:
Пример: самолет летит на север, но ветер дует с северо-запада.
Два вектора (скорость, создаваемая воздушным винтом, и скорость ветра) приводят к немного более низкой путевой скорости при движении немного к востоку от севера.
Если бы вы смотрели на самолет с земли, казалось бы, он немного скользит в сторону.
Вы когда-нибудь видели это? Возможно, вы видели птиц, борющихся с сильным ветром, которые, кажется, летят боком. Векторы помогают это объяснить.
Скорость, ускорение, сила и многое другое — векторы.
Вычитание
Мы также можем вычесть один вектор из другого:
- сначала мы меняем направление вектора, который мы хотим вычесть,
- , затем добавьте их как обычно:
а — б
Обозначение
Вектор часто пишется жирным шрифтом , например a или b .
| Вектор также может быть записан как буквы в его голове и хвосте со стрелкой над ним, например: |
Расчеты
Сейчас… как мы делаем расчеты?
Самый распространенный способ — сначала разбить векторы на части x и y, например:
Вектор a разбит на
, два вектора a x и a y
(Позже мы увидим, как это сделать.)
Добавление векторов
Затем мы можем сложить векторы на , добавив части x и , добавив части y :
Вектор (8, 13) и вектор (26, 7) складываются в вектор (34, 20)
Пример: складываем векторы
a = (8, 13) и b = (26, 7)c = a + b
c = (8, 13) + (26, 7) = (8 + 26, 13 + 7) = (34, 20)
Когда мы разбиваем такой вектор, каждая часть называется компонентом :
Вычитание векторов
Для вычитания сначала переверните вектор, который мы хотим вычесть, а затем сложите.
Пример: вычесть
k = (4, 5) из v = (12, 2)a = v + — k
a = (12, 2) + — (4, 5) = (12, 2) + (−4, −5) = (12−4, 2−5) = (8, −3)
Величина вектора
Величина вектора показана двумя вертикальными полосами по обе стороны от вектора:
| a |
ИЛИ можно написать с двойной вертикальной чертой (чтобы не путать с абсолютным значением):
|| a ||
Для его вычисления мы используем теорему Пифагора:
| a | = √ (х 2 + у 2 )
Пример: какова величина вектора
b = (6, 8)?| b | = √ (6 2 + 8 2 ) = √ (36 + 64) = √100 = 10
Вектор с величиной 1 называется единичным вектором.
Вектор против скалярного
Скаляр имеет величину (размер) только .
Скаляр: просто число (например, 7 или -0,32) … определенно не вектор.
Вектор имеет величину и направление и часто выделяется полужирным шрифтом , поэтому мы знаем, что это не скаляр:
- , поэтому c — вектор, он имеет величину и направление
- , но c — это просто значение, например 3 или 12.4
Пример: k
b на самом деле является скаляром k, умноженным на вектор b .Умножение вектора на скаляр
Когда мы умножаем вектор на скаляр, это называется «масштабированием» вектора, потому что мы меняем размер вектора.
Пример: умножить вектор
m = (7, 3) на скаляр 3| a = 3 м = (3 × 7, 3 × 3) = (21, 9) |
Он все еще указывает в том же направлении, но в 3 раза длиннее
(И теперь вы знаете, почему числа называются «скалярами», потому что они «масштабируют» вектор вверх или вниз.)
Умножение вектора на вектор (скалярное произведение и перекрестное произведение)
Как умножить два вектора вместе? Есть несколько способов! (Подробности см. |
Более двух размеров
Векторы также отлично работают в трех и более измерениях:
Вектор (1, 4, 5)
Пример: складываем векторы
a = (3, 7, 4) и b = (2, 9, 11)c = a + b
c = (3, 7, 4) + (2, 9, 11) = (3 + 2, 7 + 9, 4 + 11) = (5, 16, 15)
Пример: какова величина вектора
w = (1, −2, 3)?| w | = √ (1 2 + (−2) 2 + 3 2 ) = √ (1 + 4 + 9) = √14
Вот пример с 4-мя измерениями (но его сложно нарисовать!):
Пример: вычесть (1, 2, 3, 4) из (3, 3, 3, 3)
(3, 3, 3, 3) + — (1, 2, 3, 4)
= (3, 3, 3, 3) + (−1, −2, −3, −4)
= (3 −1, 3−2, 3−3, 3−4)
= (2, 1, 0, −1)
Звездная величина и направление
Мы можем знать величину и направление вектора, но нам нужны его длины по осям x и y (или наоборот):
| <=> | ||
| Вектор a в полярных координатах Координаты | Вектор a в декартовых координатах |
Вы можете прочитать, как преобразовать их в полярные и декартовы координаты, но вот краткое описание:
| От полярных координат (r, θ ) до декартовых координат (x, y) | От декартовых координат (x, y) до полярных координат (r, θ) | |
|---|---|---|
|
|
Пример
Сэм и Алекс тянут ящик.
- Сэм тянет с силой 200 Ньютонов при 60 °
- Алекс тянет с силой 120 Ньютонов под углом 45 °, как показано на рисунке
Что такое объединенная сила и ее направление?
Давайте сложим два вектора голова к хвосту:
Первое преобразование из полярной системы в декартовую (до 2 десятичных знаков):
Вектор Сэма:
- x = r × cos ( θ ) = 200 × cos (60 °) = 200 × 0,5 = 100
- y = r × sin ( θ ) = 200 × sin (60 °) = 200 × 0.8660 = 173,21
Вектор Алекса:
- x = r × cos ( θ ) = 120 × cos (-45 °) = 120 × 0,7071 = 84,85
- y = r × sin ( θ ) = 120 × sin (-45 °) = 120 × -0,7071 = -84,85
Теперь у нас:
Добавьте их:
(100, 173,21) + (84,85, -84,85) = (184,85, 88,36)
Этот ответ действителен, но давайте вернемся к полярному, поскольку вопрос был в полярном:
- r = √ (x 2 + y 2 ) = √ (184.
 85 2 + 88,36 2 ) = 204,88
85 2 + 88,36 2 ) = 204,88 - θ = tan -1 (y / x) = tan -1 (88,36 / 184,85) = 25,5 °
И у нас есть результат (округленный):
А для Сэма и Алекса это выглядит так:
Они могли бы получить лучший результат, если бы стояли плечом к плечу!
вектор | Определение, физика и факты
Вектор , в физике величина, имеющая как величину, так и направление.Обычно он представлен стрелкой, направление которой совпадает с направлением количества, а длина пропорциональна величине величины. Хотя вектор имеет величину и направление, у него нет позиции. То есть, пока его длина не изменяется, вектор не изменяется, если он смещается параллельно самому себе.
В отличие от векторов, обычные величины, которые имеют величину, но не направление, называются скалярами. Например, смещение, скорость и ускорение — векторные величины, а скорость (величина скорости), время и масса — скаляры.
Чтобы считаться вектором, величина, имеющая величину и направление, также должна подчиняться определенным правилам комбинирования. Одним из них является сложение векторов, символически записываемое как A + B = C (векторы обычно обозначаются жирным шрифтом). С геометрической точки зрения векторную сумму можно визуализировать, поместив хвост вектора B в начало вектора A и нарисовав вектор C, начиная с хвоста A и заканчивая в голове B, так, чтобы он завершал треугольник. Если A, B и C — векторы, должна быть возможность выполнить ту же операцию и получить тот же результат (C) в обратном порядке, B + A = C.Величины, такие как смещение и скорость, обладают этим свойством (законом коммутативности), но есть величины (например, конечные вращения в пространстве), которые не являются векторами и, следовательно, не являются векторами.
Векторный параллелограмм для сложения и вычитания Один из методов сложения и вычитания векторов состоит в том, чтобы соединить их хвосты вместе, а затем подвести еще две стороны, чтобы сформировать параллелограмм.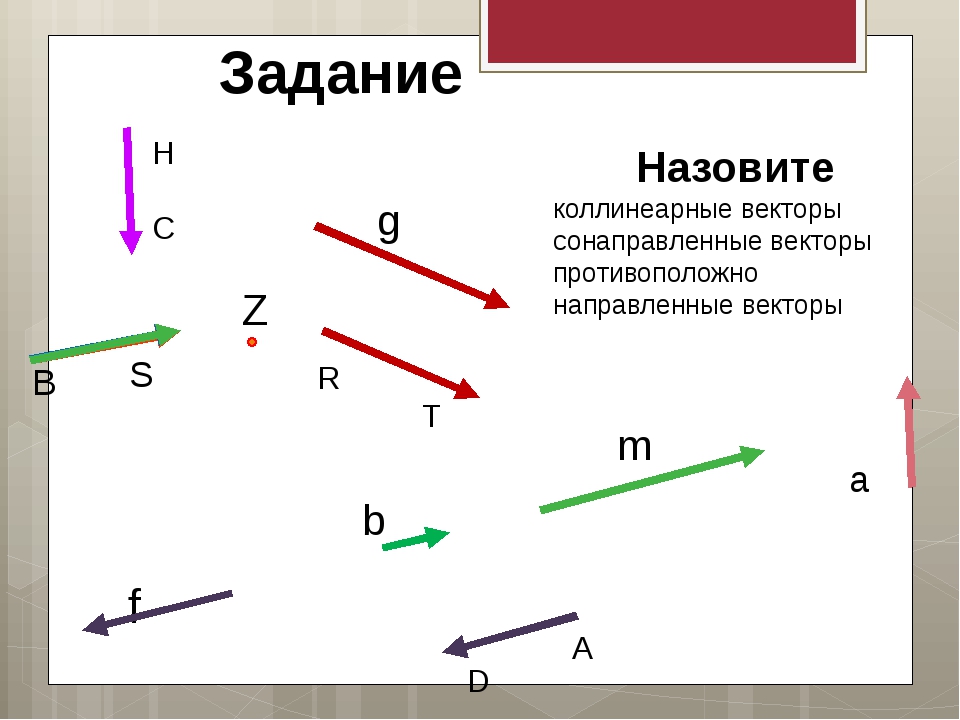 Вектор от их хвостов к противоположному углу параллелограмма равен сумме исходных векторов.Вектор между их головами (начиная с вычитаемого вектора) равен их разности.
Вектор от их хвостов к противоположному углу параллелограмма равен сумме исходных векторов.Вектор между их головами (начиная с вычитаемого вектора) равен их разности.
Другими правилами обработки векторов являются вычитание, умножение на скаляр, скалярное умножение (также известное как скалярное произведение или внутреннее произведение), векторное умножение (также известное как перекрестное произведение) и дифференцирование. . Нет операции, соответствующей делению на вектор. См. Векторный анализ для описания всех этих правил.
Правило правой руки для векторного векторного произведения Обычное, или точечное, произведение двух векторов — это просто одномерное число или скаляр. Напротив, перекрестное произведение двух векторов приводит к другому вектору, направление которого ортогонально обоим исходным векторам, как показано правилом правой руки. Величина или длина вектора векторного произведения равна v w sin θ , где θ — это угол между исходными векторами v и w .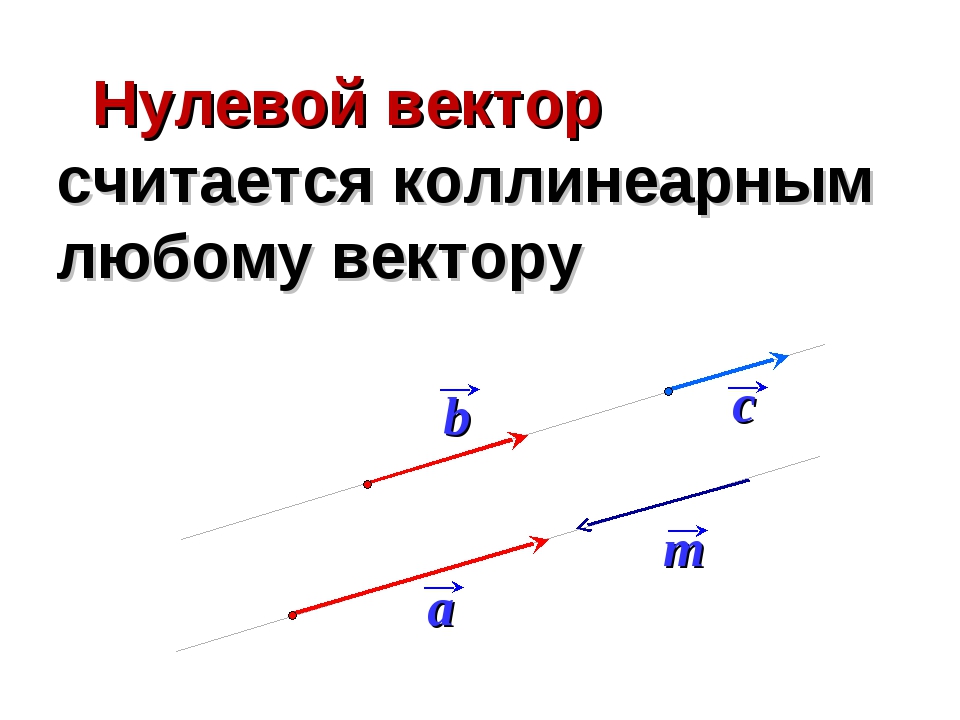
Хотя векторы математически просты и чрезвычайно полезны при обсуждении физики, они не были разработаны в их современной форме до конца XIX века, когда Джозайя Уиллард Гиббс и Оливер Хевисайд (из США и Англии соответственно) применили векторный анализ в чтобы помочь выразить новые законы электромагнетизма, предложенные Джеймсом Клерком Максвеллом.
Что такое векторы и как они используются?
В эпизоде Vectors телеканала NBC Learn «Наука о футболе НФЛ» вы видите, что квотербэки должны учитывать свое собственное движение при выполнении передачи, и что движение игрока и траектория мяча могут быть представлены стрелками, известными как векторы.
nbcunifiles.com/icue/files/ari/NBC_Learn/NBC_Learn_Video_Widget.swf?VIDEO_ID=1248081″/>
Векторы используются в науке для описания всего, что имеет как направление, так и величину. Обычно они изображаются в виде заостренных стрелок, длина которых представляет величину вектора.Передача квотербека — хороший пример, потому что у него есть направление (обычно где-то в поле) и величина (насколько сильно брошен мяч).
Вне поля векторы могут использоваться для представления любого количества физических объектов или явлений. Например, ветер является векторной величиной, потому что в любом данном месте он имеет направление (например, северо-восток) и величину (скажем, 45 километров в час). Затем вы можете составить карту воздушного потока в любой момент времени, нарисовав векторы ветра для ряда различных географических мест.
Многие свойства движущихся объектов также являются векторами. Возьмем, к примеру, бильярдный шар, катящийся по столу. Вектор скорости мяча описывает его движение — направление векторной стрелки указывает направление движения мяча, а длина вектора представляет скорость мяча.
Импульс бильярдного шара также является векторной величиной, потому что импульс равен массе, умноженной на скорость. Следовательно, вектор импульса мяча указывает в том же направлении, что и вектор его скорости, а величина или длина вектора импульса является произведением скорости мяча и его массы.
Векторы импульса полезны, когда вы хотите предсказать, что произойдет, когда два объекта соприкоснутся. Вспомните из видео, что векторы можно сложить вместе, соединив их в форму, называемую параллелограммом, и найдя диагональ этого параллелограмма. Диагональ — это сумма двух векторов, образующих стороны параллелограмма.
Допустим, катящийся бильярдный шар движется навстречу скользящему столкновению с неподвижным бильярдным шаром. При ударе движущийся шар передает часть своего импульса неподвижному шару, и оба откатываются от столкновения в разных направлениях.После удара оба шара имеют скорость и, следовательно, импульс. Фактически, сумма векторов импульса двух шаров после столкновения равна вектору импульса первого шара до столкновения, без учета небольших потерь из-за трения, а также звуковой и тепловой энергии, возникающей во время удара.
Итак, с пониманием векторов, игроки в бильярд могут предсказать, куда пойдут оба шара после столкновения, что позволит им утопить больше целевых шаров, сохраняя при этом биток на столе.
Что такое вектор? — Объяснение и примеры
Векторы эффективно передают информацию о математическом или физическом элементе. В частности:
Векторы — это математические величины, используемые для представления объектов, имеющих как величину, так и направление.
Вы когда-нибудь задумывались, что отличает скорость от скорости или массу от веса? Подсказка: ответ связан с векторами! Мы рассмотрим эти и другие вопросы, когда будем обсуждать следующие векторные темы в этой статье:
- Векторное определение
- Введение в векторы
Векторное определение
В физике и математике вектор определяется как:
«Объект или физическая величина, которые могут быть представлены как величиной, так и направлением. ”
”
Используя приведенное выше определение, мы видим, что представление векторов требует наличия двух компонентов, а именно:
- Величина (или размер)
- Направление
Введение в векторы
Исторически векторы использовались в геометрии, физике и механике. Однако со временем векторы стали широко использоваться во многих областях, включая линейную алгебру, инженерию, информатику, структурный анализ и навигацию.
Поскольку векторы выражают два понятия, а именно величину и направление, они могут создавать широкий спектр математических моделей для различных проблем и сценариев.
В этом разделе мы узнаем о следующих важных векторных концепциях:
- Геометрические и математические представления векторов
- Скаляры против векторов
- Различные типы векторов
Геометрическое и математическое представление векторов
Векторы могут быть геометрически представлены прямыми стрелками определенной длины, указывающими в определенном направлении с определенными начальной и конечной точками. Длина вектора представляет его величину, тогда как направление указывает его направление относительно набора координат. На изображении ниже показан пример геометрического представления вектора.
Длина вектора представляет его величину, тогда как направление указывает его направление относительно набора координат. На изображении ниже показан пример геометрического представления вектора.
Рассмотрим следующий рисунок, где A — вектор. | A | представляет его длину (или величину), а стрелка, указывающая от точки a к точке b, представляет его направление. Точка a называется начальной или начальной точкой, а точка b называется конечной или конечной точкой вектора A .Хотя этот пример показывает вектор в двух измерениях, он также может иметь трех-, четырех- или более высокие измерения.
Величина вектора в основном такая же, как длина отрезка ab. Направление вектора в основном такое же, как направление стрелки.
Алгебраически вектор может быть выражен как упорядоченная пара. Это представление называется вектором-столбцом. На изображении ниже вектор OA представлен как вектор-столбец.
OA = (2,3)
Это означает, что вектор смещен от начала координат на две точки по горизонтали (ось x) и четыре точки по вертикальной оси (ось y).
Векторы часто обозначаются полужирными буквами, например a или A. Если полужирный шрифт невозможен, например, при написании заметок от руки, вектор представлен буквой со стрелкой над ним.
Векторы против скаляров
Физические и математические величины классифицируются как векторы или скаляры.Хотя они связаны, векторы и скаляры используются в разных ситуациях.
Скалярная величина
Скалярная величина имеет величину, но не имеет направления.
Скаляры представлены простыми буквами, такими как a или A, и обычно состоят из действительных чисел. Некоторые общие примеры скаляров: время, скорость, энергия, масса, объем, площадь и высота.
Число векторов
Векторная величина имеет как величину, так и направление.
В отличие от скалярных величин, которые имеют только одну составляющую, векторные величины состоят из двух составляющих. Некоторые общие примеры векторов включают скорость, смещение и ускорение.
Некоторые общие примеры векторов включают скорость, смещение и ускорение.
Чтобы лучше понять разницу между скалярными и векторными величинами, рассмотрим несколько примеров:
Определите, является ли данная величина вектором или скаляром.
V = 10 м, восток
Чтобы классифицировать это количество, нам нужно рассмотреть определения векторов и скаляров и выяснить, сколько в нем компонентов. Сначала разложим данное количество на части.Данная величина имеет составляющую величины | V | = 10м. Он также указывает на восток. Таким образом, можно сделать вывод, что данная величина является вектором, поскольку она имеет две составные части.
A = 5 см
В этом примере присутствует только составляющая величины. Поскольку направление не упоминается, эта величина является скаляром.
Величина скаляра A равна 5 см.
Различные типы векторов
В математике используются различные типы векторов:
- Нулевой вектор
- Единичные векторы
- Равные векторы
- Векторы смещения
- Негатив вектора
- Векторы положения
- Совместные инициалы векторов
- Коллинеарные векторы
- Копланарные векторы
Каждый из этих типов векторов очень важен и имеет различные приложения. Их описание можно найти ниже.
Их описание можно найти ниже.
Нулевой вектор
Вектор называется нулевым вектором, если его величина равна нулю. Нулевой вектор начинается и заканчивается в одной и той же точке, что означает, что он имеет координаты (0,0). У него также нет определенного направления. Например: A = (0,0) и A = 0 — разные способы записи нулевых векторов.
Единичный вектор
Единичный вектор — это вектор, длина или величина которого равна 1. Нахождение единичного вектора с тем же направлением, что и другой вектор, может быть полезным инструментом, и мы называем его нормализованным вектором.Такой вектор находится путем деления данного вектора на его величину:
Y шляпа = Y / | Y |
Примечание: помните, что единичные векторы равны друг другу, только если они указывают в одном направлении.
Равный вектор
Два или более вектора считаются равными, если они имеют одинаковую величину и указывают в одном направлении. Два вектора, A и B, на изображении, показанном ниже, равны, поскольку их величина и направление одинаковы.
Два вектора, A и B, на изображении, показанном ниже, равны, поскольку их величина и направление одинаковы.
Вектор смещения
Если точка X перемещается (перемещается) из одной позиции в другую позицию Y, то смещение между двумя точками может быть представлено в виде вектора смещения.В этом случае вектор смещения будет записан как XY.
Отрицательный вектор
Два вектора одинаковой величины, но в противоположных направлениях называются отрицаниями друг друга. Пусть a и b — два вектора с одинаковой величиной. Если направление b противоположно направлению a, , тогда a и b являются противоположностями друг друга. Связь между этими двумя векторами:
a = -b
Вектор положения
Вектор положения используется для указания положения объекта в трехмерных декартовых координатах относительно указанной опорной точки.
Совместные инициалы Векторов
Два или более вектора, имеющих одинаковую начальную или начальную точку, называются ко-начальными векторами. На изображении, приведенном ниже, векторы AC и AB являются векторами со-начальными.
Коллинеарные векторы
Векторы, которые параллельны друг другу или лежат на одной прямой, называются коллинеарными векторами.
Копланарные векторы
Два или более трехмерных вектора, лежащих в одной плоскости, называются компланарными векторами.
Примеры
В этом разделе мы обсудим некоторые векторные примеры задач и их пошаговые решения.
Пример 1
Выразите данный вектор AD , как показано на изображении ниже, как вектор-столбец.
Решение
По определению вектор-столбец выражается как упорядоченная пара. Из рисунка видно, что AD начинается в точке A и заканчивается в точке D. Он смещен на 3 единицы вправо по оси x и на 4 единицы вверх по оси y.
Он смещен на 3 единицы вправо по оси x и на 4 единицы вверх по оси y.
Таким образом, данный вектор AD , записанный как вектор-столбец:
н.э. = (3,4)
Пример 2
Выразите данный вектор UV , как показано на изображении ниже, как вектор-столбец.
Решение
По определению вектор-столбец выражается как упорядоченная пара.Из рисунка видно, что UV начинается в точке U и заканчивается в точке V. Он смещен на 3 единицы вправо по оси x и на 2 единицы вниз по оси y.
Таким образом, данный вектор UV , записанный как вектор-столбец:
УФ = (5, -2)
Обратите внимание, что отрицательный знак указывает на то, что вектор движется вниз по оси y.
Пример 3
Определяет данную величину как скаляр или вектор.
S = 40 минут
Решение
Данная величина является скаляром, потому что она имеет только величину и не имеет направления. Его величина | S | = 40,
Пример 4
Определяет данную величину как скаляр или вектор.
OW = (2, -3)
Решение
Данная величина является векторной. Он выражается как вектор-столбец, OW, , где O — начальная точка, а W — конечная точка.Это показывает, что перевод от O к W составляет 2 точки вправо по горизонтальной оси и 3 точки вниз по оси y.
Пример 5
Определяет данную величину как скаляр или вектор.
В = 0
Решение
Данная величина является векторной. Величина вектора V задается как | V | = 0, так что это фактически нулевой вектор. Следовательно, направление этого вектора не определено, поскольку нулевой вектор не имеет направления.
Пример 6
Определяет данную величину как скаляр или вектор.
F = 20N, вниз
Решение
Данная величина является векторной. Величина вектора F, равна | F | = 20, а направление указано вниз.
Практические вопросыОпределите следующие величины как векторы или скаляры и определите их величины и направления.2, вертикально вверх.
Ответы
- Вектор: Величина | X | = 2 м, а направление указано как север.2)
- Вектор: величина | V | = 20 миль в час, направление — северо-восток.
- Вектор PQ можно представить в виде упорядоченной пары:
PQ = (5,5).
Это означает, что вектор PQ начинается в точке P и заканчивается в точке Q. Он перемещается на 5 точек вправо по горизонтальной оси и на 5 точек вверх.
- Вектор MN может быть выражен в виде упорядоченной пары:
MN = (-2, -4).
Это означает, что вектор MN начинается в точке M и заканчивается в точке N.Он перемещается на 2 точки влево по горизонтальной оси и на 4 точки вниз по оси Y.
Предыдущий урок | Главная страница | Следующий урокВекторы
Нет, это не просто стрелы.
И нет, это не лучи.
Векторы — это математические элементы, используемые для представления объекта с указанием направления и величины.
Они нарисованы так, чтобы выглядеть как луч, поскольку векторы обычно представлены в виде отрезка линии с конечной точкой на одной стороне и стрелкой на другой.
Однако, в отличие от лучей, векторы имеют определенную длину, которая отражает их величину. Стрелка вместо того, чтобы символизировать бесконечное продолжение вектора, указывает направление вектора так, как это не может сделать обычный линейный сегмент.
Векторная математика использует некоторые концепции из таких тем, как геометрия и алгебра, для определения векторных пространств. Однако сама тема имеет множество приложений в физике.
Например, , скорость отличается от скорости, потому что у нее есть направление, обычно обозначаемое положительным или отрицательным знаком при представлении алгебраически.Математический подход к векторам часто включает координатную плоскость и геометрические концепции, но физика обычно отделяет концепцию от конкретных мест.
В этом справочнике векторы представлены с математической точки зрения . Он начинается с объяснения векторов в целом и того, как работают векторные операции. Первая тема также включает информацию о геометрических представлениях векторов. Вторая тема связывает векторы с параметрическими уравнениями, поскольку обе концепции могут использоваться для описания движения.
Он начинается с демонстрации различных стратегий для векторных операций. Затем объясняется, как векторы могут использоваться для представления сил. В разделе эта информация используется для определения взаимосвязи между параметрическими уравнениями и векторами.
Тема заканчивается обобщением векторов в двух измерениях на векторы в трех измерениях.
Введение в вектор
В геометрическом представлении длина вектора указывает его величину, а угол — его направление.Однако, в отличие от обычных геометрических элементов, операции могут выполняться с векторами почти так же, как они выполняются с обычными числами, функциями и даже матрицами. Например, можно складывать и вычитать векторы, а также умножать их на скаляр.
Изображение иллюстрирует интуитивно понятную концепцию сложения векторов, показывая сумму красного и синего вектора в виде фиолетового вектора. Хотя это может не совпадать с представлением многих людей о сумме, это имеет смысл в свете сил в физике.
В этом руководстве сначала объясняются векторы и значение вектора, имеющего величину. Затем объясняются векторные операции сложения, вычитания и скалярного умножения.
Тема заканчивается объяснением параллельных векторов, векторной геометрии и векторов положения.
Векторы и параметрические уравнения
Векторы обычно рисуются в виде стрелки, и это геометрическое представление более знакомо большинству людей. Однако их можно представить алгебраически, задав пару координат.
Обычно это делается, предполагая, что вектор имеет конечную точку в точке (0,0) на координатной плоскости, и используя метод, аналогичный поиску полярных координат, для определения направления и величины. Например, вектор, представленный координатами (3, 0), указывает прямо вправо и имеет величину 3.
В этом разделе также рассматривается, почему векторные операции работают и как их можно обобщить за пределами координатной плоскости, особенно в физических сценариях.
Параметрические уравнения, в которых переменная x зависит от третьей переменной, можно использовать для получения информации о векторах.Поскольку x зависит от третьей переменной, t, x записывается как функция от t. Следовательно, y считается функцией как x, так и t. Параметрические уравнения отлично подходят для описания движения, так как векторы отлично подходят для описания сил.
Наконец, большая часть обсуждения векторов в этом руководстве касается векторов в двух измерениях. Однако в приложениях трехмерные векторы довольно распространены.
Эти ресурсы по этой теме начинаются с объяснения различий между геометрическим и алгебраическим представлениями векторов и их отношения к векторным операциям.Затем он более подробно объясняет, как векторы используются для представления сил в физике. В следующей части рассматривается связь между параметрическими уравнениями и векторами.
Наконец, тема завершается объяснением трехмерных векторов.
векторов | Безграничная физика
Компоненты вектора
Векторы — это геометрические представления величины и направления, которые могут быть выражены в виде стрелок в двух или трех измерениях.
Цели обучения
Контрастность двумерных и трехмерных векторов
Основные выводы
Ключевые моменты
- Векторы можно разбить на две составляющие: величину и направление.
- Взяв вектор, который нужно проанализировать, как гипотенузу, можно найти горизонтальную и вертикальную составляющие, заполнив прямоугольный треугольник. Нижний край треугольника — это горизонтальная составляющая, а сторона, противоположная углу, — вертикальная составляющая.
- Угол, который вектор образует с горизонталью, можно использовать для вычисления длины двух компонентов.
Ключевые термины
- координаты : числа, указывающие положение относительно некоторой оси. Пример: [latex] \ text {x} [/ latex] и [latex] \ text {y} [/ latex] координаты указывают положение относительно [latex] \ text {x} [/ latex] и [latex] \ text {y} [/ latex] топоры.
- ось : воображаемая линия, вокруг которой объект вращается или симметрично расположен.
- величина : число, присвоенное вектору, указывающее его длину.
Обзор
Векторы — это геометрические представления величины и направления, которые часто представлены прямыми стрелками, начинающимися в одной точке на оси координат и заканчивающимися в другой точке. Все векторы имеют длину, называемую величиной, которая представляет некоторое интересное качество, так что вектор можно сравнивать с другим вектором. Векторы, будучи стрелками, тоже имеют направление.Это отличает их от скаляров, которые представляют собой простые числа без направления.
Вектор определяется его величиной и ориентацией относительно набора координат. При анализе векторов часто бывает полезно разбить их на составные части. Для двумерных векторов эти компоненты бывают горизонтальными и вертикальными. Для трехмерных векторов компонент величины такой же, но компонент направления выражается в терминах [латекс] \ text {x} [/ latex], [latex] \ text {y} [/ latex] и [latex] \ text {z} [/ латекс].
Разложение вектора
Чтобы визуализировать процесс разложения вектора на его компоненты, начните с рисования вектора из начала набора координат. Затем нарисуйте прямую линию от начала координат по оси x до тех пор, пока линия не сравняется с концом исходного вектора. Это горизонтальная составляющая вектора. Чтобы найти вертикальный компонент, нарисуйте линию прямо вверх от конца горизонтального вектора, пока не дойдете до конца исходного вектора. Вы должны обнаружить, что у вас есть прямоугольный треугольник, в котором исходный вектор является гипотенузой.
Разложение вектора на горизонтальные и вертикальные компоненты — очень полезный метод для понимания физических задач. Всякий раз, когда вы видите движение под углом, вы должны думать о нем как о движении одновременно по горизонтали и вертикали. Такое упрощение векторов может ускорить вычисления и помочь отслеживать движение объектов.
Скаляры и векторы : Г-н Андерсен объясняет различия между скалярными и векторными величинами.Он также использует демонстрацию, чтобы показать важность векторов и сложения векторов.
Компоненты вектора : исходный вектор, определенный относительно набора осей. Горизонтальный компонент простирается от начала вектора до его самой дальней координаты x. Вертикальный компонент простирается от оси x до самой вертикальной точки вектора. Вместе два компонента и вектор образуют прямоугольный треугольник.
Скаляры против векторов
Скаляры — это физические величины, представленные одним числом, а векторы представлены как числом, так и направлением.
Цели обучения
Определите разницу между скалярами величин и векторами, которые представляют
Основные выводы
Ключевые моменты
- Скаляры — это физические величины, представленные одним числом без направления.
- Векторы — это физические величины, требующие как величины, так и направления.
- Примеры скаляров: высота, масса, площадь и объем. Примеры векторов включают смещение, скорость и ускорение.
Ключевые термины
- Оси координат : набор перпендикулярных линий, определяющих координаты относительно начала координат. Пример: оси координат x и y определяют горизонтальное и вертикальное положение.
Физические величины обычно можно разделить на две категории: векторы и скаляры. Эти две категории типичны в зависимости от того, какая информация им требуется. Векторы требуют двух частей информации: величины и направления. Напротив, скаляры требуют только величины.Скаляры можно рассматривать как числа, тогда как векторы следует рассматривать как стрелки, указывающие в определенном направлении.
Вектор : пример вектора. Векторы обычно представлены стрелками, длина которых представляет величину, а их направление — направлением, указанным стрелкой.
Векторы требуют как величины, так и направления. Величина вектора — это число для сравнения одного вектора с другим. В геометрической интерпретации вектора вектор представлен стрелкой.Стрелка состоит из двух частей, определяющих ее. Две части — это его длина, которая представляет величину и направление относительно некоторого набора осей координат. Чем больше величина, тем длиннее стрелка. Физические понятия, такие как смещение, скорость и ускорение, являются примерами величин, которые могут быть представлены векторами. Каждая из этих величин имеет как величину (как далеко или как быстро), так и направление. Чтобы указать направление, должно быть что-то, относительно чего это направление.Обычно эта контрольная точка представляет собой набор осей координат, таких как плоскость x-y.
Скаляры отличаются от векторов тем, что у них нет направления. Скаляры используются в основном для представления физических величин, для которых направление не имеет смысла. Вот некоторые из них: масса, высота, длина, объем и площадь. Говорить о направлении этих величин не имеет смысла, и поэтому они не могут быть выражены в виде векторов.
Разница между векторами и скалярами, Введение и основы : В этом видео представлена разница между скалярами и векторами.Представлены идеи о величине и направлении, а также приведены примеры векторов и скаляров.
Сложение и вычитание векторов графически
Векторы могут быть добавлены или вычтены графически, положив их встык по набору осей.
Цели обучения
Смоделируйте графический метод сложения и вычитания векторов
Основные выводы
Ключевые моменты
- Чтобы добавить векторы, положите первую на наборе осей хвостом в начале координат.Поместите следующий вектор хвостом в голову предыдущего вектора. Когда векторов больше нет, проведите прямую линию от начала до конца последнего вектора. Эта линия представляет собой сумму векторов.
- Чтобы вычесть векторы, действуйте так, как если бы складывались два вектора, но переверните вектор, который нужно вычесть, по осям, а затем соедините его хвостом к голове, как будто складывая.
- Сложение или вычитание любого количества векторов дает результирующий вектор.
Ключевые термины
- начало координат : Центр координатной оси, определенный как координата 0 по всем осям.
- Оси координат : набор перпендикулярных линий, определяющих координаты относительно начала координат. Пример: оси координат x и y определяют горизонтальное и вертикальное положение.
Сложение и вычитание векторов
Одним из способов, которым представление физических величин в виде векторов упрощает анализ, является легкость, с которой векторы могут быть добавлены друг к другу. Поскольку векторы представляют собой графические визуализации, сложение и вычитание векторов можно выполнять графически.
Графический метод сложения векторов также известен как метод «голова к хвосту». Для начала нарисуйте набор осей координат. Затем нарисуйте первый вектор с его хвостом (основанием) в начале координат осей. Для сложения векторов не имеет значения, какой вектор вы рисуете первым, поскольку сложение коммутативно, но для вычитания убедитесь, что вектор, который вы рисуете первым, это тот, который вы вычитаете из . Следующий шаг — взять следующий вектор и нарисовать его так, чтобы его хвост начинался с головы предыдущего вектора (сторона стрелки).Продолжайте помещать каждый вектор в начало предыдущего, пока все векторы, которые вы хотите добавить, не будут объединены. Наконец, проведите прямую линию от начала координат до головы последнего вектора в цепочке. Эта новая линия является векторным результатом сложения этих векторов вместе.
Графическое сложение векторов : Метод сложения векторов «голова к хвосту» требует, чтобы вы расположили первый вектор вдоль набора осей координат. Затем поместите хвост следующего вектора на голову первого.Нарисуйте новый вектор от начала до конца последнего вектора. Этот новый вектор представляет собой сумму двух исходных.
Сложение векторов Урок 1 из 2: Метод сложения «голова к хвосту» : Это видео знакомит зрителей с добавлением и вычитанием векторов. В первом уроке показано графическое сложение, а во втором видео используется более математический подход и показано сложение векторов по компонентам.
Метод вычитания векторов аналогичен.Убедитесь, что первый вектор, который вы рисуете, — это тот, из которого нужно вычесть. Затем, чтобы вычесть вектор, действуйте так, как если бы добавляли напротив этого вектора. Другими словами, переверните вектор, который нужно вычесть, по осям, а затем соедините его хвостом к голове, как будто складывая. Чтобы перевернуть вектор, просто поместите его голову на место хвоста и хвост на место головы.
Сложение и вычитание векторов с использованием компонентов
Часто проще складывать или вычитать векторы, используя их компоненты.
Цели обучения
Продемонстрируйте, как складывать и вычитать векторы по компонентам
Основные выводы
Ключевые моменты
- Векторы можно разложить на горизонтальные и вертикальные компоненты.
- После того, как векторы разложены на компоненты, можно добавлять компоненты.
- Сложение соответствующих компонентов двух векторов дает вектор, который является суммой двух векторов.
Ключевые термины
- Компонент : часть вектора.Например, горизонтальная и вертикальная составляющие.
Использование компонентов для сложения и вычитания векторов
Другой способ добавления векторов — это добавление компонентов. Ранее мы видели, что векторы можно выразить через их горизонтальные и вертикальные компоненты. Чтобы добавить векторы, просто выразите их оба в терминах их горизонтальных и вертикальных компонентов, а затем сложите компоненты вместе.
Вектор с горизонтальными и вертикальными компонентами : Вектор на этом изображении имеет величину 10.3 единицы и направление на 29,1 градуса выше оси абсцисс. Его можно разделить на горизонтальную и вертикальную части, как показано на рисунке.
Например, вектор длиной 5 под углом 36,9 градуса к горизонтальной оси будет иметь горизонтальную составляющую 4 единицы и вертикальную составляющую 3 единицы. Если бы мы добавили это к другому вектору той же величины и направления, мы бы получили бы вектор вдвое большей длины под тем же углом. Это можно увидеть, сложив горизонтальные компоненты двух векторов ([latex] 4 + 4 [/ latex]) и двух вертикальных компонентов ([latex] 3 + 3 [/ latex]).Эти добавления дают новый вектор с горизонтальной составляющей 8 ([latex] 4 + 4 [/ latex]) и вертикальной составляющей 6 ([latex] 3 + 3 [/ latex]). Чтобы найти результирующий вектор, просто поместите хвост вертикального компонента в головку (сторона стрелки) горизонтального компонента, а затем проведите линию от начала до вершины вертикального компонента. Эта новая строка является результирующим вектором. Он должен быть вдвое длиннее оригинала, так как оба его компонента в два раза больше, чем были ранее.
Чтобы вычесть векторы по компонентам, просто вычтите два горизонтальных компонента друг из друга и сделайте то же самое для вертикальных компонентов. Затем нарисуйте получившийся вектор, как вы делали в предыдущей части.
Добавление векторов Урок 2 из 2: Как добавить векторы по компонентам : Это видео знакомит зрителей с добавлением векторов с использованием математического подхода и демонстрирует сложение векторов по компонентам.
Умножение векторов на скаляр
Умножение вектора на скаляр изменяет величину вектора, но не направление.
Цели обучения
Обобщить взаимодействие между векторами и скалярами
Основные выводы
Ключевые моменты
- Вектор — это величина, имеющая как величину, так и направление.
- Скаляр — это величина, имеющая только величину.
- Умножение вектора на скаляр эквивалентно умножению величины вектора на скаляр. Вектор удлиняется или сжимается, но не меняет направления.
Ключевые термины
- вектор : Направленная величина, имеющая как величину, так и направление; между двумя точками.
- величина : число, присвоенное вектору, указывающее его длину.
- скаляр : величина, имеющая величину, но не направление; сравнить вектор.
Обзор
Хотя векторы и скаляры представляют различные типы физических величин, иногда необходимо, чтобы они взаимодействовали. Хотя добавление скаляра к вектору невозможно из-за их различных пространственных размеров, вектор можно умножить на скаляр.Однако скаляр нельзя умножить на вектор.
Чтобы умножить вектор на скаляр, просто умножьте аналогичные компоненты, то есть величину вектора, на величину скаляра. Это приведет к новому вектору с тем же направлением, но произведению двух величин.
Пример
Например, если у вас есть вектор A с определенной величиной и направлением, умножение его на скаляр a с величиной 0,5 даст новый вектор с величиной, равной половине исходной.Точно так же, если вы возьмете число 3, которое является чистым скаляром без единиц измерения, и умножите его на вектор, вы получите версию исходного вектора, которая в 3 раза длиннее. В качестве более физического примера возьмем гравитационную силу, действующую на объект. Сила — это вектор, величина которого зависит от скаляра, известного как масса, и его направления вниз. Если масса объекта удваивается, сила тяжести также удваивается.
Умножение векторов на скаляры очень полезно в физике. Большинство единиц, используемых в векторных величинах, по своей сути являются скалярами, умноженными на вектор.Например, единица измерения скорости в метрах в секунду, которая является вектором, состоит из двух скаляров, которые являются величинами: скаляр длины в метрах и скаляр времени в секундах. Чтобы преобразовать величины в скорость, нужно умножить единичный вектор в определенном направлении на эти скаляры.
Скалярное умножение : (i) Умножение вектора [latex] \ text {A} [/ latex] на скаляр [latex] \ text {a} = 0,5 [/ latex] дает вектор [latex] \ text { B} [/ latex] который вдвое короче.(ii) Умножение вектора [латекс] \ text {A} [/ latex] на 3 увеличивает его длину в три раза. (iii) Удвоение массы (скаляр) удваивает силу (вектор) гравитации.
Единичные векторы и умножение на скаляр
Умножение вектора на скаляр — это то же самое, что умножение его величины на число.
Цели обучения
Предсказать влияние умножения вектора на скаляр
Основные выводы
Ключевые моменты
- Единичный вектор — это вектор величины (длины) 1.
- Скаляр — это физическая величина, которая может быть представлена одним числом. В отличие от векторов, скаляры не имеют направления.
- Умножение вектора на скаляр — это то же самое, что умножение величины вектора на число, представленное скаляром.
Ключевые термины
- скаляр : Величина, которая может быть описана одним числом, в отличие от вектора, который требует направления и числа.
- единичный вектор : вектор величины 1.
Помимо сложения векторов, векторы также можно умножать на константы, известные как скаляры. Скаляры отличаются от векторов тем, что они представлены величиной, но не направлением. Примеры скаляров включают массу, высоту или объем объекта.
Скалярное умножение : (i) Умножение вектора A на 0,5 уменьшает его длину вдвое. (ii) Умножение вектора A на 3 увеличивает его длину втрое. (iii) Увеличение массы (скаляр) увеличивает силу (вектор).
При умножении вектора на скаляр направление вектора не изменяется, а величина умножается на величину скаляра. Это приводит к тому, что новая векторная стрелка указывает в том же направлении, что и старая, но с большей или меньшей длиной. Вы также можете выполнить скалярное умножение с помощью компонентов вектора. Когда у вас есть компоненты вектора, умножьте каждый из компонентов на скаляр, чтобы получить новые компоненты и, следовательно, новый вектор.
Полезной концепцией при изучении векторов и геометрии является концепция единичного вектора. Единичный вектор — это вектор с длиной или величиной, равной единице. Единичные векторы различны для разных координат. В декартовых координатах направлениями являются x и y, обычно обозначаемые [latex] \ hat {\ text {x}} [/ latex] и [latex] \ hat {\ text {y}} [/ latex]. С треугольником над буквами называется «шляпа». Единичные векторы в декартовых координатах описывают круг, известный как «единичный круг» с радиусом один.Это можно увидеть, взяв все возможные векторы длины один под всеми возможными углами в этой системе координат и поместив их в координаты. Если бы вы провели линию, соединяющую все головы всех векторов вместе, вы бы получили круг радиуса один.
Положение, смещение, скорость и ускорение как векторы
Положение, смещение, скорость и ускорение могут быть показаны векторами, поскольку они определены в терминах величины и направления.
Цели обучения
Изучить применение векторов в анализе физических величин
Основные выводы
Ключевые моменты
- Векторы — это стрелки, состоящие из величины и направления. Они используются в физике для обозначения физических величин, которые также имеют как величину, так и направление.
- Смещение — это физический термин, означающий расстояние объекта от контрольной точки. Поскольку смещение содержит две части информации: расстояние от опорной точки и направление от точки, оно хорошо представлено вектором.
- Скорость определяется как скорость изменения смещения во времени. Чтобы узнать скорость объекта, нужно знать, как быстро изменяется смещение, и в каком направлении. Следовательно, он также хорошо представлен вектором.
- Ускорение, будучи скоростью изменения скорости, также требует как величины, так и направления относительно некоторых координат.
- При рисовании векторов часто не хватает места, чтобы нарисовать их в масштабе, который они представляют, поэтому важно где-нибудь указать, в каком масштабе они нарисованы.
Ключевые термины
- скорость : Скорость изменения смещения относительно изменения во времени.
- смещение : Длина и направление прямой линии между двумя объектами.
- ускорение : скорость, с которой скорость тела изменяется со временем
Использование векторов
Векторы могут использоваться для представления физических величин. Чаще всего в физике векторы используются для обозначения смещения, скорости и ускорения.Векторы представляют собой комбинацию величины и направления и отображаются в виде стрелок. Длина представляет собой величину, а направление этой величины — это направление, в котором указывает вектор. Поскольку векторы строятся таким образом, полезно анализировать физические величины (как с размером, так и с направлением) как векторами.
Приложения
В физике векторы полезны, потому что они могут визуально представлять положение, смещение, скорость и ускорение. При рисовании векторов часто не хватает места, чтобы нарисовать их в масштабе, который они представляют, поэтому важно где-то обозначить, в каком масштабе они нарисованы.Например, при рисовании вектора, представляющего величину 100, можно нарисовать линию длиной 5 единиц в масштабе [латекс] \ displaystyle \ frac {1} {20} [/ latex]. Когда величина, обратная шкале, умножается на нарисованную величину, она должна равняться действительной величине.
Положение и перемещение
Смещение определяется как расстояние объекта в любом направлении относительно положения другого объекта. Физики используют концепцию вектора положения как графический инструмент для визуализации смещений.Вектор положения выражает положение объекта от начала системы координат. Вектор положения также может использоваться для отображения положения объекта относительно опорной точки, вторичного объекта или исходного положения (при анализе того, насколько далеко объект переместился от своего исходного положения). Вектор положения — это прямая линия, проведенная от произвольной исходной точки к объекту. После рисования вектор имеет длину и направление относительно используемой системы координат.
Скорость
Скорость также определяется величиной и направлением.Чтобы сказать, что что-то набирает или теряет скорость, нужно также сказать, насколько и в каком направлении. Например, самолет, летящий в 200 [latex] \ frac {\ text {km}} {\ text {h}} [/ latex] на северо-восток, может быть представлен вектором, указывающим в северо-восточном направлении, с магнитудой 200 [латекс] \ frac {\ text {km}} {\ text {h}} [/ latex]. При рисовании вектора величина важна только как способ сравнения двух векторов одинаковых единиц. Итак, если бы другой самолет летел на 100 [latex] \ frac {\ text {km}} {\ text {h}} [/ latex] на юго-запад, векторная стрелка должна быть вдвое короче и указывать в направлении юго-запад.
Разгон
Ускорение, представляющее собой скорость изменения скорости во времени, складывается из величины и направления и строится по той же концепции, что и вектор скорости. Значение ускорения не помогло бы в физике, если бы величина и направление этого ускорения были неизвестны, поэтому эти векторы важны. На диаграмме свободного тела, например, падающего объекта, было бы полезно использовать вектор ускорения рядом с объектом, чтобы обозначить его ускорение по направлению к земле.2} [/ латекс] .
Векторная диаграмма : Мужчина поднимается на холм. Его направление движения определяется углом тета относительно вертикальной оси и длиной стрелки, идущей вверх по холму. Он также ускоряется вниз под действием силы тяжести.
Вектор по математике | Определение, умножение и примеры (видео)
Векторы в математике — это величины с двумя атрибутами: , величина и направление , . Здесь вы можете узнать о векторах, как складывать и вычитать векторы, как умножать векторы на скалярные величины и как векторы указывают путь в реальной жизни.
Содержание
- Векторное определение
- Векторный символ
- Сложение и вычитание векторов
- Векторы смещения
- Умножение векторов на скаляр
- Векторные примеры
Векторное определение
Вектор — величина в математике, которая имеет величину , (расстояние, скорость или размер) и направление (как на стрелке компаса, например, запад, вверх, юго-восток, вниз или север на северо-запад) .
Гребя на лодке через залив, вы можете подумать, что гребете строго на юг со скоростью 3 узла, но если приливы отступают, вы можете двигаться со скоростью 5 узлов на юго-восток.
Вектор или несколько векторов, работающих вместе, будут учитывать расстояние, на которое вы гребете, вашу скорость и ваше фактическое направление.
Векторный символ
Для представления векторов математики, физики и инженеры используют лучи, помечая их строчными или прописными буквами, например:
Советы по маркировке векторов:
- Все векторы называются хвостом (начальной точкой) до стрелки, поэтому у нас есть вектор AB, а не вектор BA
- Если вы маркируете свои векторы, решение использовать прописные или строчные буквы остается за вами; если вам заданы векторы, обратите внимание на направление вектора (посмотрите на стрелки)
- Векторы могут быть параллельны и указывать в одном или противоположных направлениях (посмотрите на стрелки)
- Векторы одинаковой величины, но направленные в противоположных направлениях, являются противоположными, поэтому вектор b также можно записать как -a , что отрицает величину a
Вектор единичной длины называется единичным вектором и обозначается так называемой шляпой: v ^
Сложение и вычитание векторов
Простая векторная математика не слишком сложна.
Чтобы сложить векторы, мы соединяем хвост одного вектора с головой другого, используя стрелку. Прямолинейный луч, соединяющий два вектора, является результирующим r, как на этом рисунке:
Добавляем вектор CD к вектору EF и получаем r.
Вот загвоздка: дает ли эта цифра те же результаты, что и предыдущая?
Здесь мы добавляем вектор EF к вектору CD, и по-прежнему получаем результирующий r. Векторы подчиняются тем же правилам арифметики, что и целые числа (здесь свойство коммутативности).
В реальном мире два путешествия по векторам могут показать вам совершенно разные пейзажи. В математике, поскольку два вектора не меняли своего направления или величины, результирующие идентичны: CD + EF = EF + CD = r.
Вычитание вектора занимает всего два шага:
- отрицать вектор, который вы хотите вычесть
- затем сложите два вектора вместе
Вот векторы SA и IL, показывающие маршрут, который, как мы думали, мы ехали на парусной лодке:
Мы не осознавали, что течение было сильным; мы заблудились в тумане; солнце слепило.По какой-то причине, вместо того, чтобы следовать вектору IL, мы пошли в направлении , противоположном направлению . Поэтому вместо того, чтобы добавлять вектор IL, нам нужно его вычесть. Мы делаем это, инвертируя вектор IL и добавляя его к вектору SA:
.SA + (-IL) = r
Умножение векторов на скаляр
Умножение вектора на скаляр (действительное число) называется скалярным умножением .
Векторы состоят из двух частей (величины и направления), но мы не можем, , умножить направление на .В этом нет смысла: два «юга» не более обращены на юг, чем один «юг». Но мы, , можем на умножить величину вектора:
- Умножение вектора на положительный целочисленный скаляр > 1 дает вектор большего размера
- Умножение вектора на отрицательный скаляр целого числа <-1 дает больший вектор в противоположном направлении
- Умножение вектора на 1 возвращает тот же вектор (смещение 0)
- Умножение вектора на положительный дробный скаляр <1 дает вектор меньшего размера
- Умножение вектора на отрицательный дробный скаляр > -1 дает меньший вектор в противоположном направлении
Два вектора также можно умножить друг на друга с помощью перекрестного произведения или скалярного произведения.
Перекрестное произведение двух векторов дает новый вектор, а скалярное произведение дает число, иногда известное как скалярное произведение.
Величина вектора
Величина вектора отображается как абсолютное значение: a, или двумя линиями, чтобы не путать его с абсолютным значением: ∥a∥.
Если вы знаете значения по оси x и оси y вектора (как если бы он был на карте или в декартовой системе координат), вы можете легко вычислить его величину, применив теорему Пифагора к изменению положения от хвоста к стрелке:
Итак, здесь, с хвостом в (1, 4) и стрелкой в (7, 8), у нас есть изменение значения x на 6 и изменение значения y на 4, поэтому:
∥u∥ = 62 + 42
∥u∥ = 36 + 16
∥u∥ = 52
∥u∥ = 7.2111 шт.
Величина вектора составляет 7,2111 единиц.
Единица измерения определяется тем, что вы измеряете; дюймы, километры, мили в час (миль / ч) и т. д. Итак, если бы мы просто измерили расстояние в милях, то длина вектора составила бы 7,2111 мили.
Скаляр против векторов
Для ясности, скалярные величины — это только величины: масса, температура, скорость, объем, расстояние, энергия, работа и так далее. Думайте о них как о чистых числах.
Слушайте или читайте внимательно : Слушайте или читайте две величины, например скорость и направление ? Тогда вы имеете дело с вектором.Не читаете и не слышите две величины? Вероятно, вы имеете дело со скаляром.
Векторы смещения
Летающие супергерои редко выбирают кратчайший путь от Daily Bugle или Daily Planet до бедствия того дня. Они прыгают, петляют, прыгают и перекатываются, прежде чем, наконец, прибывают в самый последний момент.
Если бы мы использовали векторы для построения курса летающего супергероя, нам могло бы потребоваться пять или шесть векторов, чтобы учесть все эти обходные пути. Вектор смещения разрезает от начала до конца по прямой линии:
Смещение в этом смысле исходит из физики, что означает изменение положения относительно исходного положения.
Вы вставляете правую руку; вы вытягиваете правую руку: нулевое смещение. Вы ча-ча три шага влево и два шага вправо: вектор смещения на один шаг влево.
На этом рисунке мы видим, что вектор смещения также является результирующим.
Расчет смещения по-прежнему осуществляется вектором n + вектором v = r, потому что векторы a и y отрицают друг друга!
Вы можете подумать, что мы потратили много усилий, чтобы переместиться на такое небольшое расстояние, но что, если бы мы были на корабле ВМФ и должны были обогнуть пристань или охраняемый заповедник? Тогда мы видим, что это действительно был кратчайший маршрут
.Примеры векторных изображений
Все эти измерения являются примерами векторов, потому что все они включают расстояние или величину силы и направление:
- Скорость
- Сила
- Разгон
- Импульс
- Рабочий объем
Коммерческие авиалайнеры, истребители, лодки, автомобили, велосипедисты, бегуны, падающие объекты, ракеты, воздушные шары, бумажные самолетики и подводные лодки — все это примеры движущихся объектов, которые используют векторы в повседневной жизни.
Пилоты и штурманы должны использовать векторы, чтобы добраться до места назначения. Ракетчики и аэрокосмические инженеры используют векторы для управления ракетами.
Есть одно исключение из векторов, имеющих длину и направление, и это нулевой вектор. У нулевого вектора нет длины, поэтому он не указывает в каком-либо конкретном направлении. Это означает, что нулевой вектор имеет неопределенное направление.
Основные векторные задачи
- Что будет, если мы умножим вектор на 4?
- «25 узлов к югу на юго-запад» — это скаляр или вектор?
- Что будет с вектором, если мы умножим его на -12?
- Два вектора параллельны, но указывают в противоположных направлениях.
Надеемся, вы сказали, что он будет указывать в том же направлении, но будет в четыре раза длиннее!
Это вектор, поскольку он дает величину и направление.
Надеемся, вы сказали, что он будет вдвое короче и пойдет в обратном направлении!



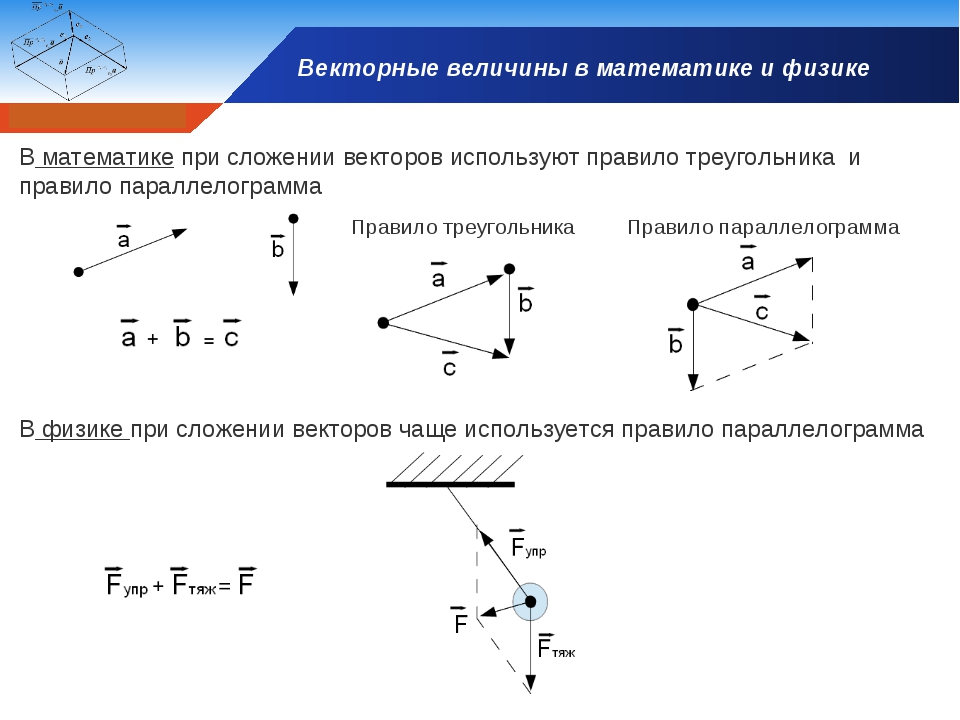 Мой вопрос заключается в том, что такое псевдоклассы и для чего они используются?
Мой вопрос заключается в том, что такое псевдоклассы и для чего они используются?
 … Класс с основной целью хранения объектов … называется контейнером . … Самый полезный контейнер
… Класс с основной целью хранения объектов … называется контейнером . … Самый полезный контейнер  На этих страницах.)
На этих страницах.) 85 2 + 88,36 2 ) = 204,88
85 2 + 88,36 2 ) = 204,88