2.2. Элементы векторной алгебры и аналитической геометрии в пространстве
Векторные величины (векторы) – это такие величины, которые характеризуются не только своими числовыми значениями, но и направлением.
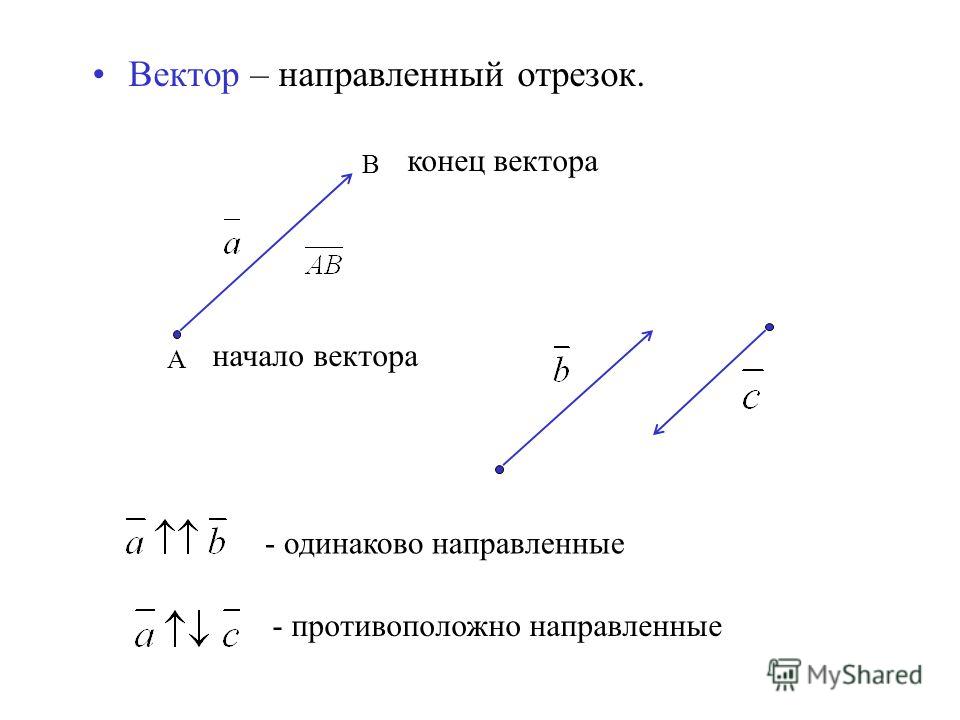
Для изображения векторных величин служат геометрические векторы. Геометрический вектор – это направленный отрезок.
Координатами вектора в прямоугольной системе координатназываются проекциивекторана оси координат. Записьозначает, что векторимеет координаты.
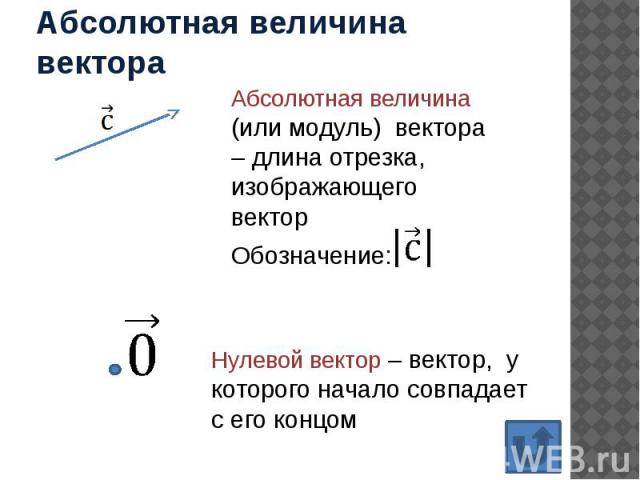
Модуль вектора (его длина) вычисляется по формуле
.
Чтобы найти координаты вектора, заданного координатами точек его начала и конца надо найти разности соответствующих координат его конца и начала, т.е. если задан вектор , где, то
.
Тогда модуль вектора находится по формуле
.
Скалярным
произведением двух векторов называется число, равное произведению
их модулей на косинус угла между ними.
Обозначают: () или. По определению
, где .
Пусть векторы заданы аналитически:
.
Выражение скалярного произведения через координаты перемноженных векторов:
.
Косинус угла между двумя векторами можно найти по формуле
.
Векторным произведением вектора на векторназывается вектор, обозначаемый символомили, определяемый условиями:
модуль этого вектора равен произведению модулей перемножаемых векторов на синус угла между ними, т.е.
;
этот вектор перпендикулярен каждому из перемножаемых векторов, т.е. плоскости, определяемой этими векторами;
направлен по перпендикуляру к этой плоскости так, что векторы исоставляют правую тройку (т.
е. если при
наблюдении с конца векторакратчайший поворот от векторак векторупроисходит против часовой стрелки.)
е. если при
наблюдении с конца векторакратчайший поворот от векторак векторупроисходит против часовой стрелки.)Модуль векторного произведения численно равен площади параллелограмма, построенного на векторах сомножителях – в этом состоит
.
Пусть даны два вектора и. Выражение векторного произведения через координаты перемножаемых векторов:
.
Смешанным произведением трех векторов называется число, равное скалярному произведению векторана вектор, т.е..
Если векторы заданы своими прямоугольными координатами, то их смешанное произведение вычисляется по формуле
.
Геометрический смысл смешанного произведения: объем параллелепипеда, построенного на 3-х некомпланарных векторах, равен абсолютной величине их смешанного произведения
.
Тогда объем треугольной пирамиды, построенной на этих же векторах, находится по формуле
.
Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Если ,три данные точки, не лежащие на одной прямой, апроизвольная точка плоскости, то уравнение плоскости, проходящей через три точки, имеет вид
.
Уравнение прямой, проходящей через две точки пространства имеет вид
.
Угол между прямой и плоскостью находится по формуле
,
где коэффициенты выбирают из канонических уравнений прямой
и общего уравнения плоскости
,
где — вектор нормали к плоскости.
Условие перпендикулярности прямой и плоскости:
.
Пример
Даны вершины треугольной пирамиды Найти:
1) угол между ребрами и;
2) площадь грани ;
3) объем пирамиды ;
5) угол между ребром и гранью;
6) уравнение высоты,
опущенной из вершины
на грань.
Решение
А4 А2 В А1А3 Рис. 2 | , найдем координаты векторов
тогда косинус угла между векторами . |
2) Площадь грани находим с помощью векторного произведения векторов. Найдем координаты вектора, тогда площадь треугольника находим по формуле
.
Найдем векторное произведение векторов
модуль векторного произведения равен
,
откуда находим площадь треугольника
3) Объем пирамиды находим с помощью смешанного произведения векторов по формуле
,
так как выше найдены координаты векторов
,
подставим координаты векторов в формулу, получим
.
4) Для нахождения длины высоты h, опущенной из вершины на граньприменим формулу
,
откуда находим
5) Общее уравнение плоскости :
,
нормальный вектор плоскости .
Уравнение высоты :.
Условие перпендикулярности прямой и плоскости: .
В нашем случае , тогда уравнение высоты имеет вид
Контрольная работа № 3. Предел и производная функции одной переменной
Вычислить предел
Вычислить предел .
Вычислить предел .
В точках идля функцииустановить непрерывность или определить характер точек разрыва.
Найти производную функции .
Найти производную функции
Найти производную функции , применяя метод логарифмического дифференцирования.
Найти производную функции, заданной неявно: .
Найти производную функции, заданной параметрически: .
С помощью методов дифференциального исчисления исследовать и построить график функции .
Стереометрия. Геометрия в пространстве
Стереометрия. Геометрия в пространстве
ОглавлениеПРЕДИСЛОВИЕ К ЧИТАТЕЛЮВВЕДЕНИЕ ГЛАВА 1. ПРЯМЫЕ И ПЛОСКОСТИ § 1. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ 1.2. Двугранный угол. Угол между плоскостями. 1.3. Плоскость и прямая в пространстве. 1.4. Аксиомы стереометрии. 1.5. Взаимное расположение двух прямых в пространстве. 1.6. Признаки скрещивающихся прямых. 1.7. Параллельные прямые. 1.8. Параллельное проектирование. § 2. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ 2.2. О значении перпендикуляра. 2.3. Теорема о трех перпендикулярах. 2.5. Построение плоскости, перпендикулярной данной прямой. 2.6. Связь между параллельностью прямых и перпендикулярностью прямой и плоскости.  2.7. Теорема о прямой, перпендикулярной плоскости. 2.8. Перпендикулярность плоскостей. 2.9. Ортогональное проектирование. § 3. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ 3.2. Параллельность и перпендикулярность. 3.3. Основная теорема о параллельных плоскостях. 3.4. Второй признак параллельности плоскостей. 3.5. Расстояние и параллельность. 3.6. Сонаправленность лучей и угол между прямыми. 3.7. Параллельность и углы. ЗАДАЧИ С РЕШЕНИЯМИ ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ГЛАВА 2. ВАЖНЕЙШИЕ ПРОСТРАНСТВЕННЫЕ ФИГУРЫ § 4. СФЕРА И ШАР 4.2. Взаимное положение шара и плоскости. 4.3. Сфера и многранники. 4.4. Вид и изображение шара и сферы. 4.5. Опорная плоскость. 4.6. Ограниченные фигуры. Диаметр фигуры. 4.7. Опорные плоскости в концах диаметра. 4.8. Сфера — фигура вращения. 4.9. Симметрия сферы и шара. 4.10. Сфера — центрально симметричная фигура. 4.11. Сфера — зеркально симметричная фигура. 4.12. Отражение в плоскости и отражение в зеркале.  § 5. ТРЕХГРАННЫЕ УГЛЫ И СФЕРИЧЕСКИЕ ТРЕУГОЛЬНИКИ 5.2. Тригонометрия трехгранного угла. 5.3. Равенство трехгранных углов. 5.4. Сферические треугольники. 5.5. “Неравенство треугольника” для трехгранных углов и сферических треугольников. § 6. ЦИЛИНДР 6.2. Другой подход к определению цилиндра. 6.3. Цилиндр вращения. 6.4. Эллипс как сечение цилиндра вращения. 6.5. Винтовые линии. 6.6. Цилиндры в практике. § 7. ПРИЗМА 7.2. Параллелепипед. 7.3. Прямоугольный параллелепипед. 7.4. Симметрия параллелепипеда. 7.5. Симметрия правильных призм. Поворот вокруг прямой. § 8. КОНУС 8.2. Сечение конуса плоскостью, параллельной плоскости основания. 8.3. Конус вращения. 8.4. Усеченный конус. § 9. ПИРАМИДА 9.2. Правильная пирамида. 9.3. Симметрия правильной пирамиды. 9.4. Конусы и пирамиды в практике. ЗАДАЧИ С РЕШЕНИЯМИ ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ГЛАВА 3. ТЕЛА, ПОВЕРХНОСТИ, МНОГОГРАННИКИ § 10.  ТЕЛА И ИХ ПОВЕРХНОСТИ10.2. Граница и внутренность. 10.3. Определение тела и замкнутой плоской области. 10.4. Выпуклые фигуры. 10.5. Выпуклые тела. § 11. МНОГОГРАННИКИ 11.2. Выпуклые многогранники. 11.3. Теорема Эйлера. 11.4. Выпуклые многогранники и выпуклые оболочки. 11.5. Многогранная поверхность и развертка. 11.6. Развертка выпуклого многогранника. § 12. ПРАВИЛЬНЫЕ И ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ 12.2. Классификация правильных многогранников. 12.3. Полуправильные многогранники. 12.4. Симметрия правильных многогранников. ЗАДАЧИ С РЕШЕНИЯМИ ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ГЛАВА 4. ОБЪЕМЫ ТЕЛ И ПЛОЩАДИ ИХ ПОВЕРХНОСТЕЙ § 13. ПОНЯТИЕ ОБЪЕМА 13.2. Определение объема. 13.3. Геометрические величины. § 14. ОБЪЕМ ПРЯМОГО ЦИЛИНДРА 14.2. Объем прямой призмы. § 15. ПРЕДСТАВЛЕНИЕ ОБЪЕМА ИНТЕГРАЛОМ 15.2. Выражение объема через площади сечений. § 16. ОБЪЕМ ЦИЛИНДРА, КОНУСА, ШАРА 16.2. Объем конуса 16.  3. Объем шара.16.4. Объем тел вращения. 16.5. Объем шарового сегмента и шарового сектора. § 17. ПЛОЩАДЬ ПОВЕРХНОСТИ 17.2. Площадь сферы. 17.3. Площадь сферических многоугольников. 17.4. Площадь сферического сегмента и сферического пояса. ЗАДАЧИ С РЕШЕНИЯМИ ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ГЛАВА 5. КООРДИНАТЫ И ВЕКТОРЫ § 18. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ 18.2. Другой способ нахождения координат точки. 18.3. Построение точки с данными координатами. 18.4. Выражение расстояния между точками. § 19. МЕТОД КООРДИНАТ 19.2. Уравнения без одной или двух координат. 19.3. Некоторые применения метода координат. § 20. РАЗЛИЧНЫЕ СИСТЕМЫ КООРДИНАТ 20.2. Полярные координаты. 20.3. Цилиндрические координаты. 20.4. Сферические координаты. 20.5. Координатная сеть. § 21. ПОНЯТИЕ ВЕКТОРА 21.2. Параллельность (коллинеарность) и перпендикулярность (ортогональность) векторов. 21.3. Сонаправленность и равенство векторов.  21.4. Признаки равенства векторов. 21.5. Радиус-вектор. § 22. ЛИНЕЙНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ 22.2. Разложение вектора на составляющие. 22.3. Умножение вектора на число. 22.4. Координаты вектора. 22.5. Равенство координат векторов и координат точек. 22.6. Разложение векторов по базису. 22.7. Ориентация базиса. § 23. СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ 23.2. Выражение скалярного произведения через координаты. 23.3. Свойства скалярного умножения. 23.4. Применения скалярного умножения. 23.5. Скалярное произведение и проекции. § 24. ВЕКТОРНЫЙ МЕТОД 24.2. Общее уравнение плоскости. 24.3. Векторное задание отрезка. 24.4. Некоторые теоремы о треугольниках и тетраэдрах. 24.5. Центр масс системы материальных точек. 24.6. Центры масс и выпуклые многогранники. ЗАДАЧИ С РЕШЕНИЯМИ ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ГЛАВА 6. ПРЕОБРАЗОВАНИЯ 25.1. Преобразования фигур. 25.2. Определения движения и равенства фигур.  25.3. Преобразования симметрии. 25.4. Параллельный перенос. 25.5. Поворот. § 26. СВОЙСТВА ДВИЖЕНИЙ 26.2. Общие свойства движений. 26.3. Теоремы о задании движений. 26.4. Неподвижные точки движений. 26.5. Два рода движений. 26.6. Теорема подвижности пространства. 26.7. Композиция отражений в плоскости. § 27. КЛАССИФИКАЦИЯ ДВИЖЕНИЙ ПРОСТРАНСТВА 27.2. Движения первого рода как винтовые движения. 27.3. Движение второго рода, имеющее неподвижную точку, как зеркальный поворот. 27.4. Движения второго рода, не имеющие неподвижных точек, как скользящие отражения. § 28. ПОДОБИЕ 28.2. Гомотетия. 28.3. Свойства подобия. 28.4. Группы преобразований. § 29. ИНВЕРСИЯ 29.2. Аналитическое задание инверсии. 29.3. Образы прямых и окружностей, плоскостей и сфер при инверсии. 29.4. Сохранение величин углов при инверсии. ЗАДАЧИ С РЕШЕНИЯМИ ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ОТВЕТЫ И УКАЗАНИЯ ОСНОВНЫЕ ТЕОРЕМЫ И ФОРМУЛЫ ПЛАНИМЕТРИИ |
В книге имеется около 100 задач с решениями и более 800 задач для самостоятельного решения. Приведены также задачи, которые использовались на вступительных экзаменах в различных вузах. Пособие рассчитано на учащихся школ, абитуриентов, преподавателей.
векторных величин | Решенные примеры | Геометрия
Предположим, что из своего начального положения X человек проходит расстояние 10 метров в северо-восточном направлении до своего конечного положения Y, как показано на рисунке ниже:
векторная величина , поскольку это величина, которая имеет как величину (10 метров), так и направление (северо-восток).
Без какой-либо части информации картина будет неполной. Например, если вам только говорят, что мужчина проходит 10 метров, не указывая направление этого движения, вы не сможете указать конечное положение человека.
Рассмотрим другой пример. Автомобиль проезжает 2 км на восток, затем 2 км на север, а затем 2 км на запад:
Чистое расстояние , пройденное автомобилем, равно 2 км + 2 км + 2 км = 6 км. Однако чистый водоизмещение автомобиля составляет 2 км севернее. Заметьте, что:
Другим примером векторной величины является скорость . Предположим, что автомобиль изначально находится в некоторой точке X и движется со скоростью 10 м/с. Можем ли мы указать положение автомобиля относительно X через, скажем, 3 секунды? Мы не можем, если не знаем направление, в котором движется машина. Если, например, нам говорят, что автомобиль движется в западном направлении, мы можем сказать, что через 3 секунды положение автомобиля будет в 30 метрах к западу от X.
Когда вы указываете скорость объекта, вы указываете его скорость, а также направление его движения (в этот момент). Обратите внимание, что скорость сама по себе является скалярной величиной. Скорость 9Направление 0007 и вместе становится скоростью — векторной величиной.
Рассмотрим еще один пример векторной величины. Вы уже читали о понятии силы и о том, что сила измеряется в ньютонах. Предположим, вам сказали, что к ящику приложена сила 10 Н. Это утверждение говорит нам только о величине силы, но не о ее направлении. Сила будет указана полностью только в том случае, если будет указано и ее направление. Например, сила 10 Н направлена вправо:
Мы видели три примера векторных величин, или величин, которые требуют полного указания как величины, так и направления:
смещение — векторная величина, позволяющая найти расположение конечной позиции относительно начальной позиции
скорость — векторная величина, которая сообщает нам (в любой момент) скорость объекта, а также направление его движения
сила — векторная величина, имеющая не только величину (измеряемую в ньютонах), но и направление приложения
Подводя итог:
Скалярные величины имеют только величины.
Например:на расстоянии 10 метров
скорость 10 метров в секунду
сила величиной 10 ньютонов
Векторные величины имеют как величину, так и направление. Например:
смещение 10 метров на северо-восток
скорость 10 метров в секунду на запад
сила 10 ньютонов вправо
Например:В этой главе мы узнаем, как математически обращаться с векторными величинами или векторами.
Вектор обычно обозначается буквой со стрелкой вверху: \(\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c \) и т. д. На рисунке ниже вектор \(\overrightarrow a \) представляет собой вектор величины 2 единицы, указывающий на север, а вектор \(\overrightarrow b \) имеет величину 3 единицы и указывает на юго-запад:
Величина вектора представляется путем заключения его в вертикальные полосы: \(\left| {\overrightarrow a} \right|,\,\left| {\overrightarrow b} \right|,\,\left| {\ overrightarrow c } \right|\) и т.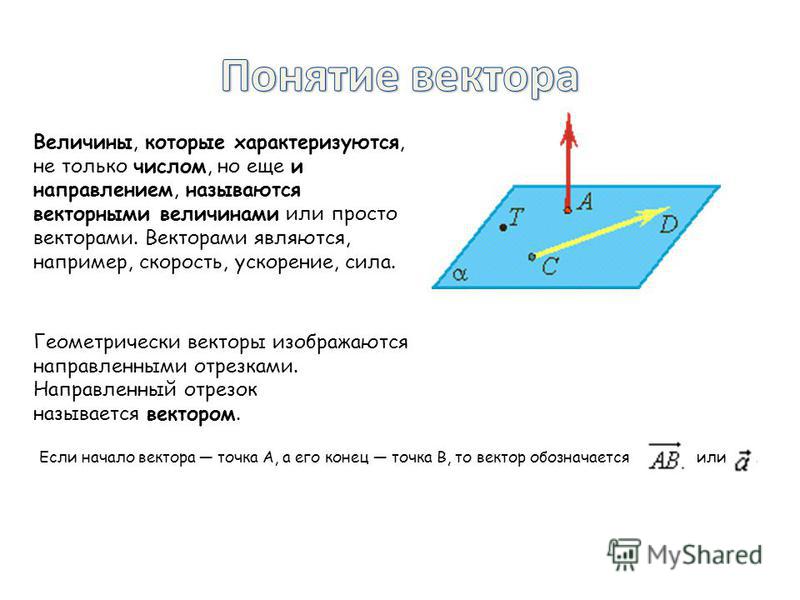
д. Для рисунка выше
\[\left| {\ overrightarrow а} \ справа | = 2 \, {\ rm {единицы,}} \ влево | {\ overrightarrow б } \ справа | = 3\, {\rm{единицы}}\]
Один из способов указать направление вектора — указать угол, который он образует с опорным направлением (скажем, x -ось в x — y системы координатных осей). Рассмотрим следующий рисунок, на котором показаны два вектора \(\overrightarrow p \) и \(\overrightarrow q \):
Обратите внимание, что \(\left| {\overrightarrow p } \right|\, = \,4 \) единиц и \(\left| {\overrightarrow q } \right|\, = \,3\) единиц. Кроме того, направление \(\overrightarrow p \) составляет 30° к горизонтали, а направление \(\overrightarrow q \) составляет 120° к горизонтали.
Позже мы увидим более лаконичные способы задания векторных величин.
Скаляры и векторы | Векторы и векторная геометрия
Все измеряемые физические величины можно разделить на три класса; скаляров , векторов и тензоров .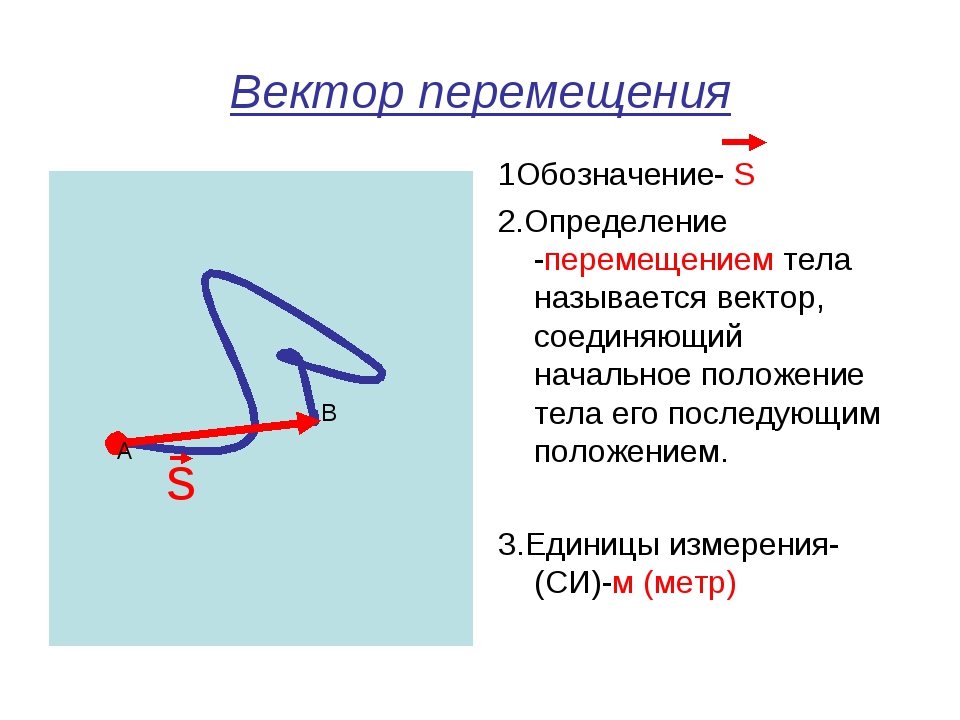
Скаляры
Те физические величины, которые имеют только величину, но не направление, называются скалярами . Масса, длина, время, плотность, скорость, работа и т. д. являются примерами скалярных величин.
Скаляр может быть полностью описан числовым значением, представляющим его величину. Оно может быть положительным или отрицательным. Их можно складывать, вычитать, умножать и делить по обычным правилам алгебры.
Векторы
Слово вектор происходит от латинского слова vehere , что означает «t или нести ». По мнению А.Н. Уайтхед, « Идея вектора, т. е. направленной величины, является корневой идеей физической науки. “
Векторы — это динамические понятия, которые обращаются непосредственно к нашей интуиции, а также дают нам яркие иллюстрации как физических, так и геометрических явлений.
Величины, которые имеют как величину, так и направление, а также могут подчиняться коммутативным законам сложения векторов, называются векторов .
Перемещение, скорость, ускорение [кинематика], импульс, сила, гравитационное поле, электрическое поле и т. д. являются примерами векторных величин.
Обозначения и представления
Как правило, векторы обозначаются полужирными буквами, известными как буквы Кларендона. Но поскольку жирный шрифт неудобен для письменного обозначения векторов, мы можем использовать следующие обозначения для представления вектора.
В математическом выражении векторная величина представлена буквой или комбинацией двух букв со стрелкой над ней. И скаляр представлен той же буквой или буквами без какой-либо стрелки над ней.
Геометрически вектор представлен отрезком направленной линии, т. е. отрезком линии со стрелкой на одном конце. Для этого нам потребуются две точки, скажем $O$ и $P$, такие, что модуль вектора равен длине отрезка $OP$, а его направление — от $O$ до $P$. Этот вектор представлен OP (буква Кларендона) или $\overrightarrow{OP}$. Если $\overrightarrow{OP}$ представляет собой вектор силы, то он также может быть представлен как F или $\overrightarrow{F}$.
